
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 23 February 2024
Sec. Medical Physics and Imaging
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1249393
 G. Franciosini1,2
G. Franciosini1,2 S. Muraro3
S. Muraro3 A. De Gregorio2,4
A. De Gregorio2,4 M. De Simoni2,5
M. De Simoni2,5 M. Di Francesco6
M. Di Francesco6 F. Di Martino7,8,9,10
F. Di Martino7,8,9,10 Y. Dong3
Y. Dong3 G. Felici6
G. Felici6 F. Galante6
F. Galante6 J. Harold Pensavalle6,8,9
J. Harold Pensavalle6,8,9 M. Marafini2,11
M. Marafini2,11 I. Mattei3
I. Mattei3 A. Muscato12
A. Muscato12 M. Pacitti6
M. Pacitti6 V. Patera1,2
V. Patera1,2 A. Sarti1,2
A. Sarti1,2 A. Schiavi1,2
A. Schiavi1,2 M. Toppi1,2
M. Toppi1,2 G. Traini2
G. Traini2 A. Trigilio1,13*
A. Trigilio1,13* G. Battistoni3
G. Battistoni3Purpose: Intraoperative electron radiotherapy (IOeRT) is considered the first clinical translation of FLASH with electrons. A crucial aspect is represented by the precise dose monitoring and measurement; to this aim, we propose a method fully based on Monte Carlo (MC) simulation that uses as input the beam current measurement and the beam optics simulation. To validate this approach, we chose the NOVAC11 (produced by Sordina IORT Technologies SpA) accelerator, which provides a well-studied model.
Methods: We used FLUKA and FRED MC software to simulate in detail the geometry of the NOVAC11 and the coupled applicator usually adopted in clinical practice to deliver the dose in the surgical bed. The simulation results of the longitudinal and off-axis profiles and dose per pulse obtained in a water phantom with different applicators are compared to the experimental data.
Results: A very good agreement not only for the relative dosimetry in both the longitudinal and off-axis profiles, with a gamma index pass rate of 100% with 3%/3 mm acceptance criteria, but also for the absolute dosimetry was obtained.
Conclusion: The results completely validate the MC description of the system and provide a reliable evaluation of the dose per pulse and output factor with an accuracy of the order of few % for different sets of applicator diameters and lengths.
Intraoperative electron radiotherapy (IOeRT), which plays a fundamental role in the treatment of prostate [1], breast [2], and rectal [3] cancer, is a technique that delivers a single high dose of ionizing radiation (10–25 Gy) directly to the surgical bed [4], after tumor removal. The objective of this therapy modality is to eradicate the microscopic residual tumor cells that surgery was not able to remove completely. IOeRT could be used alternatively in conjunction with other external beam radiotherapy (EBRT) techniques, to boost the efficacy of the treatment or to replace additional external radiotherapy cycles.
The dose is provided by an electron beam with uniform fluence produced by using dedicated linear accelerators (LINACs) with nominal energies between 4 and 12 MeV [5–7] covering tissue depths up to 5 cm.
In this procedure, a homogeneous dose is used to target the surgery bed and spare the surrounding healthy tissue. To achieve such radiation beam dose delivery, a polymethyl methacrylate (PMMA) cylindrical tube, called applicator, is used between the LINAC exit window and the patient surface.
The IOeRT treatment is performed directly in the surgery room in order to minimize the overall procedure duration. The development of specific portable accelerators allowed a significant improvement of this kind of treatments in terms of clinical logistics. Nevertheless, the IOeRT technique still has some limitations that make it difficult to fully exploit its potential.
In the current clinical practice, the main IOeRT issues are the unavailability of a treatment planning system (TPS) and the consequent absence of a dose planning optimized for the specific patient morphology. The difficulty in the development of an IOeRT TPS and the consequent technique limitations is mainly due to the time scarcity during the surgery (an order of 1–10 min [8]) to obtain both the image of the surgical field, needed to account for morphological changes due to the surgery itself, and the TPS computation.
As a consequence, during the standard IOeRT procedure, the patient is irradiated using a uniform electron beam, whose size and energy are evaluated according to the surgical bed dimension, and whenever possible, a metallic radioprotection disk, usually containing two layers of low and high atomic number (Z), respectively, is inserted under the target volume to preserve nearby critical organs [9]. The delivered dose (whose prescription is usually set to 90% isodose) is then evaluated according to measurements performed under reference conditions (i.e., in water target phantom). In this context, it is essential to perform the reference dosimetry measurements as accurately as possible.
A key issue for IOeRT accelerators is the electron beam dosimetry, which is quite different from that of the accelerators used in standard external beam radiotherapy. IOeRT has some specific characteristics that need to be taken into account such as the presence of the applicator and, hence, the lack of a “standard field size” used in EBRT dosimetry protocols and the high dose per pulse delivered. Monte Carlo (MC) simulations of the IOeRT accelerator head and electron beam are useful to improve the accuracy of knowledge of accelerator dosimetric characteristics.
Lately, a sudden interest arose around the IOeRT treatment in relationship with the new possibility of FLASH radiotherapy [10–16]. In this technique, the use of ultra-high-dose (
In this paper, we used the MC simulation to evaluate the radiation field produced by the NOVAC11 LINAC coupled with different applicators. This study provides the relative and absolute dosimetric characterization of the beam, i.e., percentage depth dose (PDD), off-axis profiles, dose per pulse (Dp), and output factor (OF) [17]. This paper also reports the validation of the MC simulation as a method to evaluate all the radiation field features.
The NOVAC11 LINAC [18], shown in Figure 1, provides an electron beam with four nominal energies: 4 MeV, 6 MeV, 8 MeV, and 10 MeV, allowing treating targets with a thickness of up to 2.6 cm within the 90% isodose or up to 3.0 cm within the 80% isodose.
The radiofrequency section of the accelerator provides a train of electron current pulses, each with approximately square shape in time and an approximate duration of 2.5 μs. The pulse repetition frequency has a range of 5–30 Hz.
This system does not use a scattering foil for beam broadening, but the electron beam crosses only the thin titanium window (60 μm thick) that seals the LINAC vacuum chamber and four steel plates (20 μm thick) which are the monitor ionization chamber electrodes. These elements also produce the beam scattering needed to spread the very narrow beam exiting from the RF section of the LINAC. At the same time, these materials modify the electron energy spectrum at the end of the accelerating structure and are the main source of emission of Bremsstrahlung photons.
The beam collimation system is purely passive and consists of a set of 5 mm-thick PMMA cylindrical applicators of different diameters ranging from 3 cm to 12 cm and of different lengths.
Each applicator consists of two parts: the upper part and the terminal section. The upper part, also called the applicator holder, is directly mounted to the radiant head, while the terminal part, also named the terminal applicator, is connected to the upper section via a ring nut. Both flat and beveled applicators are available, with possible inclination angles with respect to the surgical bed surface of 0°, 15°, 22.5°, 30°, and 45° offering both circular and elliptical fields. The source-to-surface distance (SSD) is 80 cm for the reference applicator (10 cm diameter) and 65 cm for the others.
Despite the relatively simple architecture of the cylindrical applicator, several collimation configurations (SSD, angle, etc.) can be obtained, with different outputs in terms of dose per pulse performance. It must be stressed that the dose per pulse outcome is a particularly relevant figure for an IOeRT system since it is directly proportional to the average dose rate DR delivered, as reported by Eq. 1:
where PRF is the pulse repetition frequency. Another important parameter of the system, the instantaneous dose rate (IDR), or dose rate within pulse, can be obtained by dividing the dose per pulse Dp by the pulse length (Δt). Taking into account that for the NOVAC11, the pulse length is about 2.5 μs, the IDR can be easily calculated as Eq. 2:
where the IDR is expressed in Gy/s when Dp is given in Gy. In the NOVAC11 system, despite a dose per pulse of up to 100 mGy, the average dose rate is quite limited, from 4 up to 30 Gy/min, due to the relatively low PRF (5 Hz in the clinical mode, up to 30 Hz in the service mode).
In this section, we describe the dosimetric characterization of the nominal 10 MeV electron beam of the NOVAC11 accelerator.
The beam current, pulse length, and delivered charge were measured by means of a Faraday cup, coupled with an oscilloscope and positioned after the titanium window. The Faraday cup employed for quantifying the NOVAC11 beam charge consists of a basic copper cup electrode linked to a Tektronix MDO4000C mixed domain oscilloscope [19]. Additionally, the Faraday cup features a suppressor plate set at a polarization of −80 V, serving to restrict the escape of induction electrons and maintain the integrity of charge collection. The utilization of the oscilloscope proves beneficial not only for charge measurement through waveform integration but also for assessing pulse length, thereby providing supplementary insights into the beam pulse characteristics.
The experimental setup for relative dosimetry, i.e., PDD and off-axis profiles, measurements consisted of a 3D motorized water phantom (MP3-XS, PTW, Freiburg, Germany [20]) equipped with an unshielded diode (Diode E, type 60017, PTW [21]) as the field detector and an ionization chamber (Semiflex Ionization Chamber, type 31010, PTW [22]) as the reference detector. The two detectors were connected to the dual-channel electrometer (UNIDOS E, PTW) [23].
The experimental measurements were performed using the reference applicator, which has a diameter of 10 cm, positioned to the water surface (no air gap) with a spatial resolution of 1.0 mm. The percentage depth dose was acquired along the beam axis perpendicular to the water phantom surface, while the transversal profiles were measured at the depths of maximum (R100), 80% (R80), and 50% (R50) of the PDD.
For absolute dosimetry measurements, the Advanced Markus ionization chamber (type 34045, PTW [24]) was used. This detector is a waterproof parallel plate chamber for the measurements of high-energy electron radiation. The small cylindrical sensitive volume of 0.02 cm3 with a diameter of 2.5 mm makes the chamber ideal for dose distribution measurements in a water phantom (the chamber has a protective acrylic cover of 0.87 mm for use in water), giving a good spatial resolution.
The absolute dose reference dosimetry was performed by positioning the ionization chamber at zmax, i.e., the depth of maximum dose value along the beam axes, according to the Italian National Health Institute [25].
In addition, to evaluate the output factor of the NOVAC11, the same absolute dosimetry measurements performed with the reference applicator were assessed for a smaller applicator with a diameter of 40 mm.
We evaluated the dosimetric quantities to be compared with experimental measurements by means of FLUKA [26, 27] Monte Carlo software (2020.0.10 version), which is widely used in medical applications and known to describe electromagnetic interactions with very high precision [28], and FRED, a GPU-accelerated MC-based dose engine [29–31].
As described in the previous section, the electron beam generated by the NOVAC11 with different nominal energies (4 MeV, 6 MeV, 8 MeV, and 10 MeV) is collimated on the surgical bed by a cylindrical applicator which can have different lengths and diameters.
In order to achieve the best possible agreement between the measurements and the simulation, we described the applicator geometry in great detail. In particular, the manufacturers provided all the information about the applicator structure and materials crossed by the beam.
For both MC simulations, the two applicators were modeled as a series of PMMA hollow cylinders of different dimensions and shapes centered on the beam axis (z-axis). The upper sections of the two applicators were both simulated as two sequential cylinders with diameters of 20 or 30 mm, a wall thickness of 5 mm, and lengths of 3.2 or 4.0 cm, respectively.
The terminal sections of the reference applicator were modeled using other three sequential cylinders with diameter equal to 27.5, 45, and 100 mm, wall thickness ranging from 5 to 15 mm, and lengths 2.2, 3.8, and 66.8 cm, respectively. The total applicator length, i.e., the SSD, was, thus, 80 cm. The terminal section of the 40 mm applicator was modeled as two PMMA cylinders with diameters of 30 and 40 mm with a wall thickness of 5–15 mm and a length of 3.6 and 54.2 cm, respectively. In this case, the SSD was equal to 65 cm.
In the upper section, the electron beam exits from the LINAC, passes through a 60 μm-thick titanium window that seals the LINAC vacuum chamber, and, after 16 mm, goes through four 20 μm-thick steel plates, which are the monitor ionization chamber electrodes. In the simulation, these elements were modeled as circular planes, inserted inside the applicator, with the same dimensions and material as those supplied by the manufacturer. In both simulations at the end of the applicator geometry, according to the setup used for the experimental data acquisition, a water phantom of 40 × 40 × 20 cm3 was placed. Figure 2 shows the FLUKA MC geometries for the 100 mm and 40 mm applicators in the plane containing the beam axis.
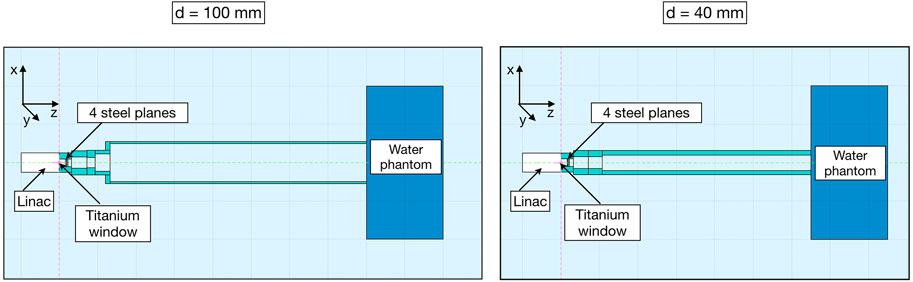
FIGURE 2. Cross-section of the 100 mm (left)- and 40 mm (right)-diameter applicators used in FLUKA simulation. The beam travels in the positive z-direction. The electron beam first crosses the LINAC titanium window and then the four steel plates of the monitor ionization chamber to propagate eventually through the air-filled PMMA applicator with 80 cm (left) or 65 cm (right) length.
For the input of the Monte Carlo calculation, a model of the electron beam impinging in the LINAC titanium window was provided by the manufacturer. The spatial beam profile was assumed to have Gaussian shape with an FWHM of 1.3 mm. The angular spread of the accelerated electrons was considered negligible. The 10 MeV electron energy spectrum used in the simulation is shown in Figure 3 and was obtained from the PARMELA code [32].
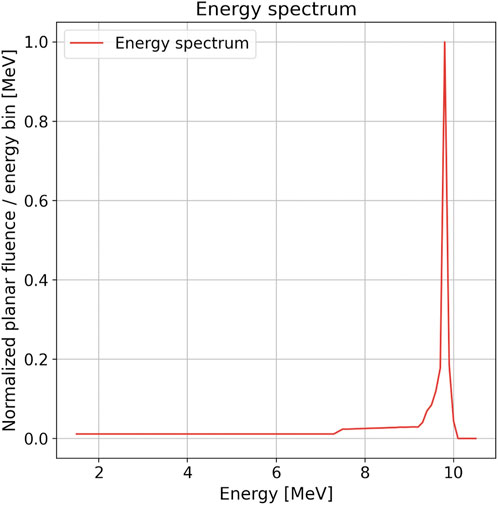
FIGURE 3. Distribution of planar fluence with respect to the energy of the electron beam impinging in the NOVAC11 LINAC titanium window for the 10 MeV modality. This distribution was obtained from PARMELA simulation [32]. In the graph, the distribution is plotted normalized to its maximum value with an energy bin of 50 keV.
The energy cutoffs for the transport and production of both electrons and photons were set to EMFCUT = 10 keV (kinetic energy). Particles with energy below this threshold are not transported anymore, and their energy is locally deposited.
We used the FLUKA MC simulation to investigate beam features such as the energy distribution inside the reference cylindrical applicators for both electrons and photons. Figure 4 shows the electron and photon distribution of fluence with respect to energy at the exit of the titanium window and at the surface of the water phantom, respectively, for the 10 MeV beam and the 100 mm-diameter applicator. The values of the total calculated electron fluence over the primary fluence are 1.03 and 0.32 at the exit of the titanium window and at the water phantom surface, respectively. As expected, the number of electrons decreases as the beam travels through the applicator due to absorption and scattering both on air and in the PMMA applicator walls. For the same reasons, the low-energy component of the beam also increases with respect to the initial one. For the photons, which are produced mainly from the interaction of the primary electrons with the titanium and steel plates, the integral value is 1.35 × 10−2 photon/primary and 3.24 × 10−2 photon/primary for the blue and red curve, respectively.
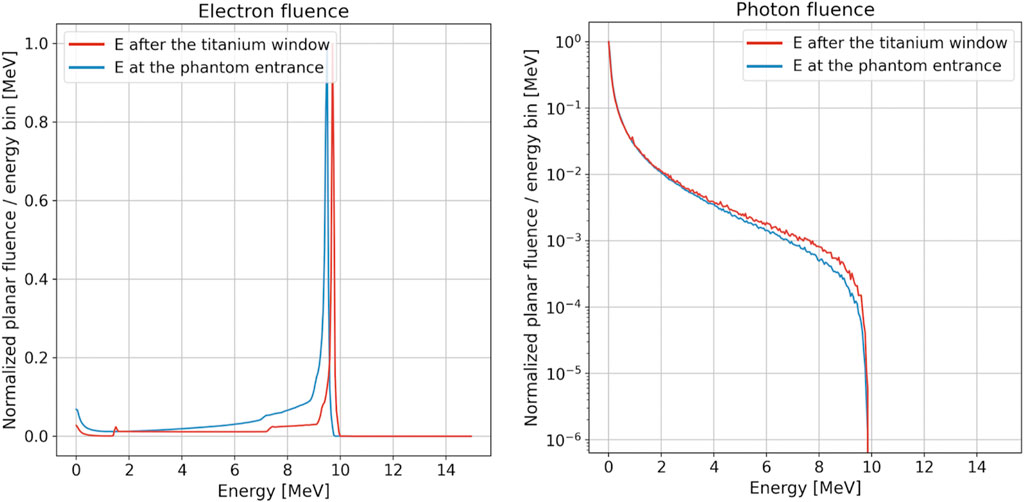
FIGURE 4. Electron (left) and photon (right) fluence as a function of energy at the exit of the titanium window (red line) and at the surface of the water phantom (blue line) for the 10 MeV modality and 100 mm-diameter applicator. For both plots, the energy bin is equal to 50 keV. Distributions were normalized to the peak value, and the photon plot is reported in the logarithmic scale.
Afterward, we studied the relative and absolute dosimetry comparing the FRED and FLUKA simulations with the experimental measurements.
The dose deposited in the water phantom at the applicator exit was calculated for each primary electron crossing the titanium window. In order to score the energy deposition, the phantom was divided into 201 × 201 × 200 voxels of size 2 × 2 × 1 mm3 in the x × y × z direction for both MC simulations. The FLUKA 2D dose distributions for the reference applicator are shown in Figure 5. To reduce the statistical MC fluctuation, the FRED and FLUKA simulations were performed using 109 histories (or primary electrons). The experimental measurements and simulated curves of the relative dosimetry, i.e., PDD along the beam axis and dose profiles at the depth of 15 ± 1 mm (R100), 28 ± 1 mm (R80), and 36 ± 1 mm (R50), are reported in Figures 6, 7 for the reference applicator.
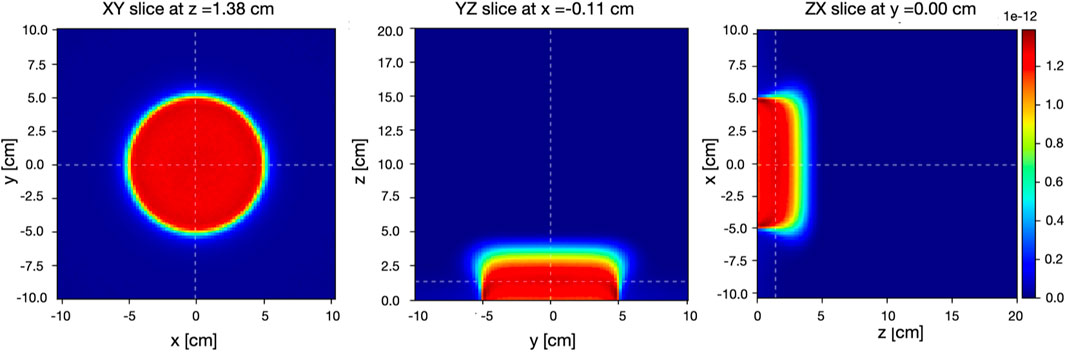
FIGURE 5. Two-dimensional FLUKA dose distributions on the XY slice at z = 1.35 cm (left), YZ slice at x = 0.00 cm (center), and ZX slice at y = 0.00 cm (right) per primary electron inside the water phantom for an electron beam having 10 MeV nominal energy collimated by the reference applicator. Origin of coordinates corresponds to the intersection of the water phantom surface and beam axis. The color linear scale represents the dose in Gy/primary units.
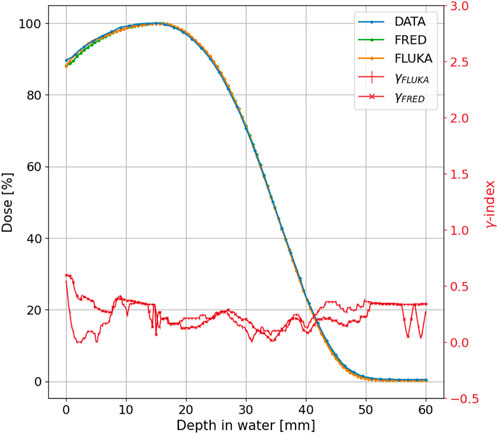
FIGURE 6. The measured (blue line), FRED (green line), and FLUKA (orange line) PDD distributions for the 10 MeV-nominal energy and 100 mm-diameter applicator of the NOVAC11. The γ index curve with 3 mm/3% criteria is also plotted in a red line with cross and horizontal line markers for FRED and FLUKA MC, respectively.
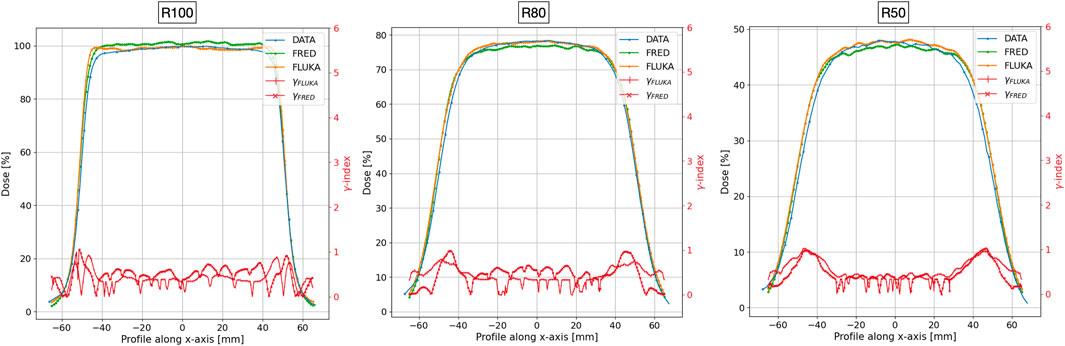
FIGURE 7. The measured (blue line), FRED (green line), and FLUKA (orange line) transverse profile at z = 15 mm (left), z = 28 mm (center), and z = 36 mm (right), corresponding to profiles at R100, R80, and R50, respectively. The red lines with cross and horizontal line markers for FRED and FLUKA MC, respectively, show the gamma index curve for acceptance criteria 3 mm/3%. The two simulations were performed using 109 primary electrons in order to reduce the impact of MC statistical fluctuations.
In the simulations, the dose in water was evaluated in volumes with a transverse area of 2 × 2 mm2, corresponding to the sensitive area of the diode used in the measurements.
To test the agreement between the simulated and measured distributions, we performed a gamma index [33] analysis comparing FRED and FLUKA with the experimental data separately. Such test is widely used in medical physics to assess the agreement between planned and measured dose distributions, by evaluating both spatial and dosimetric differences, comparing corresponding points in the two maps. The test was conducted employing distance-to-agreement (DTA) and dose difference acceptance criteria of 3 mm/3% (standard criteria) and 2 mm/2% (more stringent criteria). Figures 6, 7 display the gamma index curve for 3 mm/3%.
As observed in both MC simulations, the γ index curves for the PDD and the R100 and R80 transverse profiles show that the majority of points fall below 1. This indicates that for 100% or 99.45% of the points in the distribution, the difference between the measured and simulated curves is less than 3 mm/3% for FLUKA and slightly greater than 3 mm/3 for FRED. However, for the R50 transverse profile, only 98.8% for FLUKA and 98.30% for FRED of the points meet this criterion.
As can be observed for both MC simulations, the γ index curves for the PDD and the R100 and R80 transverse profiles show that the majority of points fall below 1. This indicates that for 100%, for FLUKA, and 99.45%, for FRED, of the points in the distribution, the difference between the measured and simulated curves is less than 3 mm/3% for FLUKA and slightly greater than 3 mm/3% for FRED. However, for the R50 transverse profile, only 98.8% for FLUKA and 98.30% for FRED of the points meet this criterion. Table 1 summarizes the results obtained from the gamma index analysis with 3%/3 mm and 2%/2 mm acceptance criteria for both MC simulations.
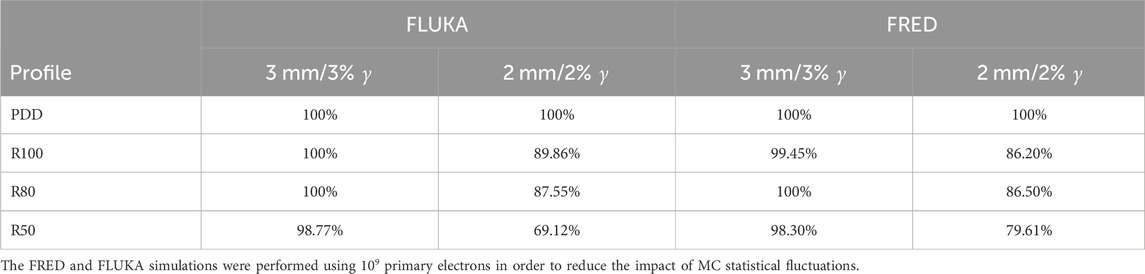
TABLE 1. Gamma index analysis with 3%/3 mm and 2%/2 mm acceptance criteria performed on the measured and simulated PDD and transverse profile curves.
For absolute dosimetry, the experimental measurements with the Advanced Markus at the peak values of the depth dose curves for both applicators were compared to the MC dose released in an ∼ 4.4 × 4.4 × 1 mm3 cubic voxel at the same position corresponding to the sensitive volume of the detector. From the two FLUKA simulations, we obtained a Dmax value equal to (1.285 ± 0.002) × 10–12 Gy/electron and (2.847 ± 0.004)× 10–12 Gy/electron for the applicator with 100 mm and 40 mm diameter, respectively. From the FRED one was instead obtained (1.269 ± 0.002) × 10–12 Gy/electron for the 100 mm applicator and (2.918 ± 0.004)× 10–12 Gy/electron for the 40 mm one. With these values, it is possible to compute the dose per pulse. To relate the dose in water to the current measurement at the NOVAC11 exit, the Dmax values per LINAC electron were rescaled in order to match the equivalent charge of Q = 3.88 ± 0.32 nC (corresponding to (2.422 ± 0.775) ⋅ 1010 electrons per pulse) as measured by the Faraday cup. Table 2 shows the estimated and measured dose per pulse values for the applicator with 100 and 40 mm diameter. It is worthwhile noticing that the uncertainty on the (MC/data) ratio is mainly due to the uncertainty of the charge measurement.
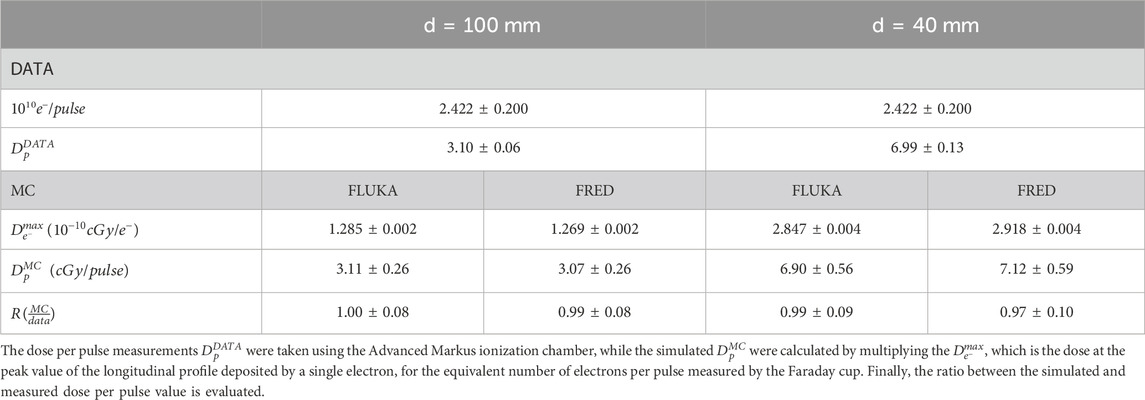
TABLE 2. The measured and simulated dose per pulse for the applicator with diameter equal to 100 and 40 mm.
To further test the agreement between the experimental data and the simulations, we compared the relative NOVAC11 output factor defined as
where D(d, zmax) is the absorbed dose at depth zmax in water for the beam collimated by an applicator with diameter d and D(dref, zmax) is the absorbed dose in water evaluated for the reference applicator at depth zmax [34]. In the present case, we considered the reference field as the 100 mm-diameter applicator and the field of interest as the 40 mm-diameter applicator. According to Eq. 3 and using the Dmax values reported in Table 2, the output factor evaluated from the simulation data is equal to 2.22 ± 0.01 and 2.22 ± 0.01 for FLUKA and FRED, respectively. This value was compared to the measured one, which is equal to 2.26 ± 0.06.
The goal of the present work goes significantly beyond the state of the art of the MC simulation for IOeRT LINACs. After the first pioneering works [34, 35], the work of Iaccarino et al. [36] established a benchmark leading to the development of dedicated software which has increased the safety and reduced the length of the commissioning process. Such approach, capable of determining the whole relative dosimetry (PDD, profiles, isodose curves, and output factors) of IOeRT LINACs by using a pre-validated MC library, has been widely adopted over the last years [37–39]. Nevertheless, in our best knowledge, there was no attempt to directly correlate the beam current with the dose in water. This possibility would be extremely relevant for the “FLASH” effect clinical application in IOeRT treatments as the ultra-high dose rates needed to trigger the effect are already available [40, 41]. A major challenge in that case is represented by the need of a reliable dose monitoring. Standard transmission ionization chambers are not adequate to monitor FLASH irradiations, as the detector response is heavily affected by saturation effects due to large recombination effects that have to be properly accounted for [42] and are, so far, resulting in substantial uncertainties [43]. Monitoring the total dose by means of a direct measurement of the beam current is being explored as a solution for this issue.
In this work, the verification of the reference and absolute dosimetry from the MC simulations was performed by comparing the obtained results directly with experimental measurements. The results show a successful agreement with both MC tools obtaining an ∼ 100% gamma index pass rate for the PDD, R100, and R80 profiles and ∼ 98% for the R50 one with 3 mm/3% acceptance criteria. The result obtained for profile R50 with both FLUKA and FRED, which is worse than that of the others, can be explained in the context of a limited accuracy in the positioning of the diode (±1 mm), at the required depth, along the beam axis that can easily account for the systematic shift observed in Figure 7.
Concerning absolute dosimetry, the comparison heavily depends on the uncertainties associated to the current and pulse length measurements. As shown in the previous section while the measured dose per pulse value
The agreement also between the measured and simulated output factor is excellent, confirming the accuracy of the FLUKA and FRED simulation in describing not only the relative but also the absolute dosimetry.
In this work, a dosimetric analysis of the NOVAC11 linear accelerator was performed by comparing a FLUKA and FRED MC simulation with the experimental measurements of the PDD and off-axis profiles for relative dosimetry and the dose per pulse and OF values for absolute dosimetry. The results of relative and absolute dosimetry reported here completely validate the FLUKA and FRED MC description of the system and provide a reliable evaluation of the dose per pulse and OF values for different sets of applicator diameters and lengths. In particular, we obtained a gamma index pass rate of ∼ 100% and ∼ 90% for the PDD and off-axis profiles using 3 mm/3% and 2 mm/2% acceptance criteria, respectively. The absolute dosimetry also validates the successful results achieved for the relative dosimetry: for both simulations (10 MeV electron beam collimated by the d = 100 and d = 40 mm diameter applicators), the ratio between the measured and simulated dose per pulse value is compatible with the one within the associated uncertainty.
These results should allow relying on FLUKA or FRED MC, or similar high-performance and accurate software, to characterize a new IORT accelerator and increase accuracy in dose reporting.
As the most promising beam-monitoring technique for electron FLASH LINACs is based on current transformers [43, 44] which provides a direct current measurement at the LINAC exit window, the possibility of relating such measurement to dose is particularly interesting and may even represent a solution to the actual difficulties in dose monitoring. The interested reader could find details about the current FLASH dosimetric challenges in [43, 45], together with some promising solutions: the FLASH diamond [46], FLASH ionization chambers [47–49], and using current technologies in the FLASH regimes [50, 51]. This work presents and validates the determination of the absorbed dose to water in any clinical configurations by means of a purely Monte Carlo simulation, once the beam optics geometry is known and the beam current at the exit window is available. The method was validated by using an IOeRT LINAC whose dose per pulse, even if greater than that of the conventional one, can still be safely measured with the standard technique. The next step will consist in adapting such approach to ultra-high-dose rate systems, such as electron FLASH [43, 44, 52].
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
GFr, AD, AT, Asa, VP, MP, FG, GFe, and GB wrote the main manuscript text. GFr, AM, MDS, MM, ASc, MT, and GT prepared the figures. GFe, FG, MP, JHP, MDF, and FD provided information about experimental data. SM, IM, GB, and YD provided information about the beam model to be used in the Monte Carlo simulations. GFr and AT implemented the simulation. All authors contributed to the article and approved the submitted version.
This work was partially funded by CSN5 of INFN in the context of the FRIDA project.
MDF, GFe, and JHP are employees of S.I.T.—Sordina IORT Technologies SpA. GFe is a shareholder of S.I.T.—Sordina IORT Technologies SpA. VP, ASc, and ASa received funds and royalties/patents from S.I.T.—Sordina IORT Technologies SpA. Authors FG and MP were employed by S.I.T.—Sordina IORT Technologies SpA.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Veronesi U, Orecchia R, Luini A, Galimberti V, Gatti G, Intra M, et al. Full-dose intraoperative radiotherapy with electrons during breast-conserving surgery: experience with 590 cases. Ann Surg (2005) 242(1):101–6. doi:10.1097/01.sla.0000167927.82353.bc
2. Saracino B, Gallucci M, De Carli P, Soriani A, Papalia R, Marzi S, et al. Phase I-ii study of intraoperative radiation therapy (IORT) after radical prostatectomy for prostate cancer. Int J Radiat Oncology*Biology*Physics (2008) 71:1049–56. doi:10.1016/j.ijrobp.2007.11.076
3. Roeder F, Treiber M, Oertel S, Dinkel J, Timke C, Funk A, et al. Patterns of failure and local control after intraoperative electron boost radiotherapy to the presacral space in combination with total mesorectal excision in patients with locally advanced rectal cancer. Int J Radiat Oncology*Biology*Physics (2007) 67:1381–8. doi:10.1016/j.ijrobp.2006.11.039
4. Calvo F, Gounderson L. Intraoperative irradiation. Techniques and results. 2nd ed. New York: Current Clinical Oncology (2011).
5. Ciocca M, Cantone M-C, Veronese I, Cattani F, Pedroli G, Molinelli S, et al. Application of failure mode and effects analysis to intraoperative radiation therapy using mobile electron linear accelerators. Int J Radiat Oncol Biol Phys (2012) 82:305–11. doi:10.1016/j.ijrobp.2011.05.010
6. Galimberti V, Ciocca M, Leonardi MC, Zanagnolo V, Paola B, Manuela S, et al. Is electron beam intraoperative radiotherapy (ELIOT) safe in pregnant women with early breast cancer? in vivo dosimetry to assess fetal dose. Ann Surg Oncol (2008) 16:100–5. doi:10.1245/s10434-008-0172-z
7. Beddar AS, Biggs PJ, Chang S, Ezzell GA, Faddegon BA, Hensley FW, et al. Intraoperative radiation therapy using mobile electron linear accelerators: report of AAPM Radiation Therapy Committee Task Group No. 72. Med Phys (2006) 33:1476–89. doi:10.1118/1.2194447
8. Baghani HR, Robatjazi M, Mahdavi SR, Nafissi N, Akbari ME. Breast intraoperative electron radiotherapy: image-based setup verification and in-vivo dosimetry. Physica Med (2019) 60:37–43. doi:10.1016/j.ejmp.2019.03.017
9. Robatjazi M, Baghani HR, Mahdavic SR, Felici G. Evaluation of dosimetric properties of shielding disk used in intraoperative electron radiotherapy: a Monte Carlo study. Appl Radiat Isot (2018) 139:107–13. doi:10.1016/j.apradiso.2018.04.037
10. Favaudon V, Caplier L, Monceau V, Pouzoulet F, Sayarath M, Fouillade C, et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci Translational Med (2014) 6:245ra93. doi:10.1126/scitranslmed.3008973
11. Montay-Gruel P, Acharya MM, Petersson K, Alikhani L, Yakkala C, Allen BD, et al. Long-term neurocognitive benefits of FLASH radiotherapy driven by reduced reactive oxygen species. Proc Natl Acad Sci (2019) 116:10943–51. doi:10.1073/pnas.1901777116
12. Vozenin M-C, Hendry J, Limoli C. Biological benefits of ultra-high dose rate FLASH radiotherapy: sleeping beauty awoken. Clin Oncol (2019) 31:407–15. doi:10.1016/j.clon.2019.04.001
13. Friedl AA, Prise KM, Butterworth KT, Montay-Gruel P, Favaudon V. Radiobiology of the FLASH effect. Med Phys (2022) 49:1993–2013. doi:10.1002/mp.15184
14. Schuler E, Acharya M, Montay-Gruel P, Loo BW, Vozenin M-C, Maxim PG. Ultra-high dose rate electron beams and the FLASH effect: from preclinical evidence to a new radiotherapy paradigm. Med Phys (2022) 49:2082–95. doi:10.1002/mp.15442
15. Esplen N, Mendonca MS, Bazalova-Carter M. Physics and biology of ultrahigh dose-rate (FLASH) radiotherapy: a topical review. Phys Med Biol (2020) 65:23TR03. doi:10.1088/1361-6560/abaa28
16. Bourhis J, Montay-Gruel P, Gonçalves Jorge P, Bailat C, Petit B, Ollivier J, et al. Clinical translation of FLASH radiotherapy: why and how? Radiother Oncol (2019) 139:11–7. FLASH radiotherapy International Workshop. doi:10.1016/j.radonc.2019.04.008
17. Björk P, Knöös T, Nilsson P. Measurements of output factors with different detector types and Monte Carlo calculations of stopping-power ratios for degraded electron beams. Phys Med Biol (2004) 49:4493–506. doi:10.1088/0031-9155/49/19/004
18. S.I.T. Sordina IORT Technologies SpA, Italy (2024). Available at: https://www.soiort.com (Accessed March 2, 2023). Sordina IORT technologies SpA, aprilia.
19. Tektronix. MDO4000C mixed Domain oscilloscope — Tektronix (2024). Available at: https://www.tek.com/en/datasheet/mixed-domain-oscilloscopes-0 (Accessed March 2, 2023).
20. Ptwdosimetry. MP3-XS water phantom system (2024). Available at: https://www.ptwdosimetry.com/products/mp3-xs-water-phantom-system/?L=0 (Accessed March 2, 2023).
21. Diode E. Biowel (2024). http://biowel.com/pdf/PTW/Field%20Detectors.pdf (Accessed March 2, 2023).
22. Semiflex Ionization Chamber. Semiflex ionization chamber 31010 (2024). https://www.ptwdosimetry.com/en/products/semiflex-ionization-chamber-31010/ (Accessed March 2, 2023).
23. UNIDOS E Universal Dosemeter. UNIDOS E universal dosemeter (2024). https://www.ptwdosimetry.com/en/products/unidos-e/ (Accessed March 2, 2023).
24. Advanced Markus Electron Chamber. Advanced Markus electron chamber (2024). https://www.ptwdosimetry.com/en/products/advanced-markus-electron-chamber/ (Accessed March 2, 2023).
25. Italin National Health Institute (2024). https://www.iss.it/rapporti-istisan (Accessed March 2, 2023).
26. Ferrari A, Sala PR, Fasso A, Ranft J. FLUKA: a multi-particle transport code (Program version 2005), CERN-2005-010, SLAC-R-773 (2005). INFN-TC-05-11 (2005).
27. Battistoni G, Bauer J, Boehlen TT, Cerutti F, Chin MPW, Dos Santos Augusto R, et al. The FLUKA code: an accurate simulation tool for particle therapy. Front Oncol (2016) 6:116. doi:10.3389/fonc.2016.00116
28. Rajabi R, Taherparvar P. Monte Carlo dosimetry for a new 32P brachytherapy source using FLUKA code. J Contemp Brachytherapy (2019) 11:76–90. doi:10.5114/jcb.2019.83002
29. Schiavi A, Senzacqua M, Pioli S, Mairani A, Magro G, Molinelli S, et al. Fred: a GPU-accelerated fast-Monte Carlo code for rapid treatment plan recalculation in ion beam therapy. Phys Med Biol (2017) 62:7482–504. doi:10.1088/1361-6560/aa8134
30. Simoni D, Battistoni G, De Gregorio A, De Maria P, Fischetti M, Franciosini G, et al. A data-driven fragmentation model for carbon therapy GPU-accelerated monte-carlo dose recalculation. Front Oncol (2022) 12:780784. doi:10.3389/fonc.2022.780784
31. Franciosini G, Battistoni G, Cerqua A, Gregorio AD, Maria PD, Simoni MD, et al. GPU-accelerated Monte Carlo simulation of electron and photon interactions for radiotherapy applications. Phys Med Biol (2023) 68:044001. doi:10.1088/1361-6560/aca1f2
32. Young LM, Billen JH. The particle tracking code Parmela. Proc 2003 Part Accelerator Conf (2003) 5:3521–3.
33. Low DA, Harms WB, Mutic S, Purdy JA. A technique for the quantitative evaluation of dose distributions. Med Phys (1998) 25:656–61. doi:10.1118/1.598248
34. Pimpinella M, Mihailescu D, Guerra A, Laitano R. Dosimetric characteristics of electron beams produced by a mobile accelerator for IORT. Phys Med Biol (2007) 52:6197–214. doi:10.1088/0031-9155/52/20/008
35. Righi S, Karaj E, Felici G, Di Martino F. Dosimetric characteristics of electron beams produced by two mobile accelerators, Novac7 and Liac, for intraoperative radiation therapy through Monte Carlo simulation. J Appl Clin Med Phys (2013) 14:6–18. doi:10.1120/jacmp.v14i1.3678
36. Iaccarino G, Strigari L, D’Andrea M, Bellesi L, Felici G, Ciccotelli A, et al. Monte Carlo simulation of electron beams generated by a 12 MeV dedicated mobile IORT accelerator. Phys Med Biol (2011) 56:4579–96. doi:10.1088/0031-9155/56/14/022
37. Baghani HR, Robatjazi M, Mahdavi SR, Hosseini Aghdam SR. Evaluating the performance characteristics of some ion chamber dosimeters in high dose per pulse intraoperative electron beam radiation therapy. Physica Med (2019) 58:81–9. doi:10.1016/j.ejmp.2019.01.019
38. Winkler P, Odreitz-Stark S, Haas E, Thalhammer M, Partl R. Commissioning, dosimetric characterization and machine performance assessment of the LIAC HWL mobile accelerator for Intraoperative Radiotherapy. Z f r Medizinische Physik (2020) 30:279–88. doi:10.1016/j.zemedi.2020.06.004
39. Mastella E, Szilagyi KE, De Guglielmo E, Fabbri S, Calderoni F, Stefanelli A, et al. Dosimetric characterization of a mobile accelerator dedicated for intraoperative radiation therapy: Monte Carlo simulations and experimental validation. Physica Med (2022) 104:167–73. doi:10.1016/j.ejmp.2022.11.006
40. Calvo FA, Serrano J, Cambeiro M, Aristu J, Asencio JM, Rubio I, et al. Intra-operative electron radiation therapy: an update of the evidence collected in 40 Years to search for models for electron-FLASH studies. Cancers (2022) 14:3693. doi:10.3390/cancers14153693
41. Calvo F, Ayestaran A, Serrano J, Cambeiro M, Palma J, Meirino R, et al. Practice-oriented solutions integrating intraoperative electron irradiation and personalized proton therapy for recurrent or unresectable cancers: proof of concept and potential for dual FLASH effect. Front Oncol (2022) 12:1037262. doi:10.3389/fonc.2022.1037262
42. Di Martino F, Giannelli M, Traino A, Lazzeri M. Ion recombination correction for very high dose-per-pulse high-energy electron beams: ksat evaluation for very high dose-per-pulse electron-beams. Med Phys (2005) 32:2204–10. doi:10.1118/1.1940167
43. Di Martino F, Barca P, Barone S, Bortoli E, Borgheresi R, De Stefano S, et al. FLASH radiotherapy with electrons: issues related to the production, monitoring, and dosimetric characterization of the beam. Front Phys (2020) 8. doi:10.3389/fphy.2020.570697
44. Faillace L, Barone S, Battistoni G, Di Francesco M, Felici G, Ficcadenti L, et al. Compact S-band linear accelerator system for ultrafast, ultrahigh dose-rate radiotherapy. Phys Rev Accel Beams (2021) 24:050102. doi:10.1103/physrevaccelbeams.24.050102
45. Schuller A, Heinrich S, Fouillade C, Subiel A, De Marzi L, Romano F, et al. The European Joint Research Project UHDpulse-Metrology for advanced radiotherapy using particle beams with ultra-high pulse dose rates. Physica Med (2020) 80:134–50. doi:10.1016/j.ejmp.2020.09.020
46. Marinelli M, Felici G, Galante F, Gasparini A, Giuliano L, Heinrich S, et al. Design, realization, and characterization of a novel diamond detector prototype for FLASH radiotherapy dosimetry. Med Phys (2022) 49:1902–10. doi:10.1002/mp.15473
47. Gómez F, Gonzalez-Castano D, Fernández N, Pardo-Montero J, Schüller A, Gasparini A, et al. Development of an ultra-thin parallel plate ionization chamber for dosimetry in FLASH radiotherapy. Med Phys (2022) 49:4705–14. doi:10.1002/mp.15668
48. Kranzer R, Schuller A, Gomez Rodriguez F, Weidner J, Paz-Martin J, Looe HK, et al. Charge collection efficiency, underlying recombination mechanisms, and the role of electrode distance of vented ionization chambers under ultra-high dose-per-pulse conditions. Physica Med (2022) 104:10–7. doi:10.1016/j.ejmp.2022.10.021
49. Di Martino F, Del Sarto D, Giuseppina Bisogni M, Capaccioli S, Galante F, Gasperini A, et al. A new solution for UHDP and UHDR (Flash) measurements: theory and conceptual design of ALLS chamber. Physica Med (2022) 102:9–18. doi:10.1016/j.ejmp.2022.08.010
50. Di Martino F, Del Sarto D, Barone S, Giuseppina Bisogni M, Capaccioli S, Galante F, et al. A new calculation method for the free electron fraction of an ionization chamber in the ultra-high-dose-per-pulse regimen. Physica Med (2022) 103:175–80. doi:10.1016/j.ejmp.2022.11.001
51. Cavallone M, Goncalves Jorge P, Moeckli A, Bailat C, Flacco A, Prezado Y, et al. Determination of the ion collection efficiency of the Razor Nano Chamber for ultra-high dose-rate electron beams. Med Phys (2022) 49:4731–42. doi:10.1002/mp.15675
Keywords: IORT, LINAC, dosimetry, Monte Carlo, FLASH
Citation: Franciosini G, Muraro S, De Gregorio A, De Simoni M, Di Francesco M, Di Martino F, Dong Y, Felici G, Galante F, Harold Pensavalle J, Marafini M, Mattei I, Muscato A, Pacitti M, Patera V, Sarti A, Schiavi A, Toppi M, Traini G, Trigilio A and Battistoni G (2024) Preliminary study on the correlation between accelerated current and dose in water for an electron-based LINAC. Front. Phys. 12:1249393. doi: 10.3389/fphy.2024.1249393
Received: 28 June 2023; Accepted: 29 January 2024;
Published: 23 February 2024.
Edited by:
Silvia Capuani, National Research Council (CNR), ItalyReviewed by:
Giovanni Romanelli, University of Rome Tor Vergata, ItalyCopyright © 2024 Franciosini, Muraro, De Gregorio, De Simoni, Di Francesco, Di Martino, Dong, Felici, Galante, Harold Pensavalle, Marafini, Mattei, Muscato, Pacitti, Patera, Sarti, Schiavi, Toppi, Traini, Trigilio and Battistoni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Trigilio, YW50b25pby50cmlnaWxpb0BsbmYuaW5mbi5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.