Hierarchical buckling of elastic fiber under transverse confinement

Hierarchical buckling is a novel phenomenon observed in elastic fibers subjected to transverse confinement; however, the deformation mechanisms and modal transitions of this unique phenomenon remain to be elucidated. This paper investigates the hierarchical buckling of elastic fibers with elliptical (circular) cross-sections under transverse confinement through analytical derivations and numerical simulations. Various magnitudes of hierarchical buckling of fibers are observed with the variation of the controlled elastic matrix stiffness. An analytical solution is first derived for the fiber’s buckling phenomenon, and the hierarchical buckling is accomplished through the superposition of buckling at various modes. The theoretical results are validated against the finite element simulations with good agreement. It is demonstrated from the parametric results that the hierarchical buckling phenomenon is primarily influenced by the stiffness of the external transverse confinement (matrix), which is defined as a dimensionless parameter. It is thus illustrated from the computational results that the buckling of elastic fibers within a solid or fluid matrix can be controlled and customized. The present work provides theoretical guidance for the application of elastic fibers in stretchable conductor fibers and flexible electronic devices.

1 Introduction

Elastic fibers lose stability under compression and undergo a buckling phenomenon to transition into a new minimum energy state. The buckling of fibers was previously considered as a form of failure, which was undesired due to the loss of the original configurations. However, this was later on demonstrated as a strategy to tailor the performance of soft and smart materials. Recently, shrinkage buckling has been employed in the preparation of conductors to improve tensile and ductile strengths [1–4]. Elastic fibers can be prepared to have various geometries, including U-shaped, spiral, and others [5–7], and to be extremely ductile. In recent work, it was observed that elastic fibers embedded in an external elastic matrix suffered from a wavy buckling configuration, resulting from shrinkage after the release of pre-stretch, as shown in Figure 1A. Through high-magnification SEM images, it can be observed that the elastic fiber is buckled into a wavy configuration superimposed with smaller waves, establishing a hierarchical buckling phenomenon [7], as illustrated in the conceptual diagram of Figure 1B. The hierarchy of buckling provides the option to customize the buckling phenomenon to achieve the functional requirements specific to certain scenarios. From a practical perspective, such buckling structures have been widely applied in electronic devices, including wearable electronics[8,9], flexible displays [10], energy devices, sensors [11], resonators, and electromagnetic wave absorbers [12–15]. By adopting a suitable buckling structure, the functionality of the devices can be further enhanced.

FIGURE 1

FIGURE 1. (A) SEM images of the fibers were prepared under 900% pre-stretching conditions. (Zhou et al. Copyright 2020); (B) Concept diagram of hierarchical buckling.

Until present, several analytical and numerical models have been developed to investigate the buckling and instability of fibrous materials. Dayan et al. [16] investigated the behavior of an elastic fiber constrained by flexible and rigid tubes under a compressive force through theoretical, numerical, and experimental methods. They emphasized the deviation in behavior between a compressed fiber constrained by a deformable tube and a fiber confined within a rigid cylinder. Su et al. [17] utilized the classical Euler beam theory to investigate the buckling problem of a slender elastic rod embedded in an elastic matrix. They determined the critical conditions for the transition of the rod from a planar wave to a non-planar coiled structure. Xiao et al. [18] categorized the buckling of an elastic rod under cylindrical transverse confinement into four specific deformation modes: initial two-dimensional (2D) shape, small three-dimensional (3D) shape, 3D helix shape and 3D alpha shape. They also investigated the critical axial displacement at the transitional point between those four deformation modes. Interestingly, a film [19,20] or ribbon [21–23] attached to an elastic substrate can also produce a buckling structure. The selection of substrates in these models is diverse, ranging from single-layered substrates and multilayered solid elastic substrates [20] to fluid substrates [23,24]. They exhibited similarities to the buckling of fibers under transverse confinement [6] and illustrated the varied structural responses among systems with different substrates. In addition, similar phenomena can be observed in studies with the same confinement conditions, such as cell microscopy [25,26], oil push rod [27] and plant root growth [28]. Most of the aforementioned studies focus on single-level buckling, with only a few analyzing hierarchical buckling. Based on this situation, in order to better explain the problem of hierarchical buckling of elastic fibers, the dimensionless theory is utilized in this paper for the analytical derivation. The dimensionless theory is a widely employed analytical method in the fields of mathematics and physics. It is utilized to enhance the comprehension and description of various problems. There has been considerable recent work on reducing the complexity of problems by removing the effects of scale in physical phenomena through the use of dimensionless theories, and this approach has yielded excellent results [29–35]. Therefore, we developed a dimensionless analytical solution to investigate the buckling hierarchy of elastic fibers with using elliptical cross-sections under transverse confinement, through the superposition of buckling of various buckling modes. For the establishment of a theoretical model, the fiber shape and elasticity are the critical parameters for the simulation of their counterparts. Moreover, in recent studies, the cross-section selection for the elastic fibers was basically the ideal circular or rectangular shape, which may affect the accuracy of the calculated results. Consequently, an irregular elliptical shape in this paper instead of the ideal circular shape to better reflect the actual situation.

In this paper, a theoretical model is established for the buckling phenomenon in sheath-core structural systems. The remainder of the paper is organized as follows: In Section 2, an analytical derivation of the hierarchical buckling phenomenon for elastic fibers with elliptical/circular cross-sections is conducted for the first time. The effect of the external solid/fluid substrates was investigated through their transformation to equivalent stiffness. A finite element (FE) model is established in Section 3 to verify the theoretical derivation. Finally, we present numerical examples to investigate several factors that may impact the hierarchical buckling effect observed in elastic fibers, and the mode transition law of buckling. We found that the morphology of buckling and its associated characteristic scales can be tailored by varying the geometric and material parameters of the system.

2 Theoretical framework

2.1 Model establishment

A 3D sheath-core theoretical model was established to analyze the aforementioned experimental buckling phenomenon, as shown in Figure 2A. Since the fibers were pre-stretched, dried, and then released, they experienced to axial compression. We adopted the Winkler foundation model to simulate the effect of the external confinement from either the elastic or fluid matrix [36–39]. The stiffness of the model is denoted as C that is acted only in the transverse direction. The external elastic matrix is shown in Figure 2B. For the sake of generality, fibers with elliptical cross sections were selected as the research of interests in the present work. The experimental phenomenon reveals that the buckling of the elastic fibers with elliptical cross-sections was different from the 3D buckling of fibers with circular cross-sections [17,18]. The elliptical fiber would buckle in the direction with the weaker moment of inertia (I_y > I_z), which is denoted as the y-direction in this particular situation. As shown in Figures 2C,D, I_y and I_z are the moments of inertia in two directions, respectively. It is equal to the average of the reconciliation between the main moment of inertia I_f = 2I_yI_z/(I_y + I_z). The fiber was simplified to a homogeneous fiber [40].

FIGURE 2

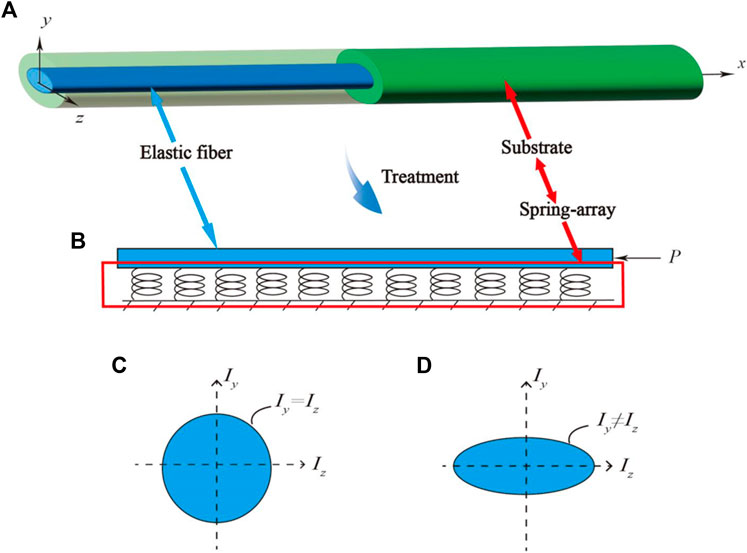
FIGURE 2. (A) Model of the sheath-core system; (B) simplified model of the sheath-core system with fibers (in blue) and the spring acting in the transverse direction attached to the fiber; (C, D) Moment of inertia of the y and z axes for different cross sections; (C) Round cross-section; (D) Elliptical cross-section.

2.2 Theoretical derivation

Here we start from the energy expression to analyze the critical buckling phenomenon of the elastic fibers with transverse confinement based on the theoretical model illustrated in Figure 2B. According to the principle of potential energy, it can be obtained:

$U_b+U_s-\Delta T=0(1)$

where U_b is the bending energy of the elastic fiber, U_s is the elastic energy of the matrix, ∆T is the external work done by the compression force. The bending energy U_b of the elastic fiber is expressed as:

$U_b=\frac{E_f{I}_f}{2}{\int }_0^L\left(\frac{d^{2}w}{{dx}^2}\right)dx(2)$

where E_f and I_f denote the Young’s modulus and moment of inertia of the fiber, respectively, w is the transverse deflection of the elastic fiber, and L is the length of the elastic fiber. In the meantime, the elastic energy of the matrix is expressed as:

$U_s=\frac{C}{2}{\int }_0^L{w}^{2}dx(3)$

where C is the stiffness of the spring, the magnitude of which represents the confinement of the matrix. Under a compression force P, ∆T can be expressed as:

$\Delta T=\frac{P}{2}{\int }_0^L{\left(\frac{dw}{dx}\right)}^{2}dx(4)$

Substituting Equations (2–4) into Eq. 1 yields the nonlinear equation for the deflection of the elastic fiber [41]:

$\frac{E_f{I}_f}{2}{\int }_0^L{\left(\frac{d^{2}w}{{dx}^2}\right)}^{2}dx+\frac{C}{2}{\int }_0^L{w}^{2}dx-\frac{P}{2}{\int }_0^L{\left(\frac{dw}{dx}\right)}^{2}dx=0(5)$

It was previously demonstrated in literature [41–46] that rod buckling could be solved by assuming trigonometric functions for the transverse deflection curve of a simply-supported fiber, which can thus be expressed in terms of a series expansion as [47]:

$w={\displaystyle \sum _{n=1}^{n=\infty }}{A}_n\mathit{sin}\frac{n\pi x}{L}(6)$

where A_n represents the amplitude of an elastic fiber buckling, and n is the modal number. By substituting Eq. 6 into Eq. 5, A_n is completely eliminated and the dimensionless critical buckling load of the fiber can be obtained as [48]:

$f_{cr}=n^2+\frac{c^2}{n^2{\pi }^4}(7)$

where f = PL²/π²E_fI_f and c = (CL⁴/E_fI_f)^1/2 are the dimensionless compression load and the dimensionless spring stiffness, respectively. It is thus demonstrated from Eq. 7 that the magnitudes of critical buckling loads at various modes are dependent on the dimensionless parameter c and modal number n. In the meantime, the hierarchical buckling phenomenon could be triggered through the superposition of buckling at two modal numbers.

Following the derivation in Eq. 7, we generated the dimensionless critical buckling load for each modal number utilizing the material properties of the polymer (poly (3,4-ethylenedioxythiophene)/polystyrene sulfonate (PEDOT/PSS)) [7]. We selected the elastic Young’s modulus and mean moment of inertia of the fiber as E_f = 59 GPa and I_f = 8.25 × 10⁻⁴ mm⁴, respectively. The length of the fiber was assumed as L = 100 mm. The dimensionless spring stiffness was assumed as c = 320.5. Figure 3 presents the dimensionless critical loads for various modal numbers, we discovered that the critical buckling load did not monotonically increased at increasing modal numbers. In this particular case, it could happen that buckling loads at two different modal numbers are coincident at the same value, leading to the existence of hierarchical buckling phenomenon.

FIGURE 3

FIGURE 3. Dimensionless critical buckling load f_cr for different values of modal number n.

To test this idea, we assumed two specific modes m and v (m≠v), the critical buckling load with the same magnitude was triggered, which indicates:

$m^{\mathit{2}}+\frac{c^2}{m^{\mathit{2}}{\pi }^{\mathit{4}}}=v^{\mathit{2}}+\frac{c^{\mathit{2}}}{v^{\mathit{2}}{\pi }^{\mathit{4}}}(8)$

more specifically, we have:

$c^2={\pi }^4{m}^2{v}^2(9)$

which is actually the condition that triggers the buckling of the same magnitude at two different modes. The superposition of the two buckling morphologies yields the hierarchical buckling configuration. Furthermore, it is obtained from Eq. 9 that the buckling phenomenon is also dependent on transverse confinement. Therefore, we analyzed the influence of the dimensionless spring stiffness c on the buckling phenomenon. Figure 4 illustrates the dimensionless critical buckling load f_cr as functions of dimensionless spring stiffness c. The critical buckling load at each mode was found to monotonically increase with the increase of dimensionless spring stiffness. In addition, the interjection of the curves indicates the triggering of two joint buckling phenomenon at different modes, which means the hierarchical buckling phenomenon appears at a given dimensionless spring stiffness c. Although the external elastic matrix was equated to a spring in this paper, there is still no explicit transformation relation between the stiffness and elastic matrix. For the purpose of establishing the FEA parameters for the spring in the subsequent section, we investigate this problem below.

FIGURE 4

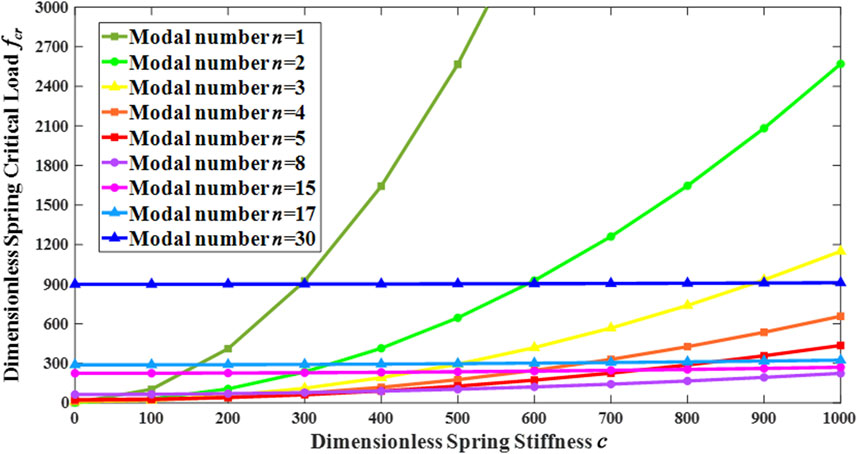
FIGURE 4. Dimensionless spring stiffness c versus dimensionless critical buckling load f_cr; The dimensionless critical buckling load was plotted for selected modes n = 1, 2, 3, 4, 5, 8,15, 17 and 30.

The effect of transverse confinement can be specialized as the elastic or fluid matrix. Therefore, it is important to characterize the effect of solid or fluid matrix on the buckling of fiber in a quantitative manner. For instance, in the case of a fluid substrate, [23,24]) was the first to realize that its weight could act as an effective stiffness, which indicates, for a fluid, we could assume the effective stiffness C = ρg, where ρ is the fluid density and g is the acceleration due to gravity. In the meantime, regarding the elastic matrix, the equivalent stiffness could be obtained in terms of the modulus of elastic matrix [49,50]:

$C=\frac{16\pi G_m\left(\mathit{1}-v_m\right)}{2\left(3-4v_m\right)K_0\left(l\right)+n\pi {rK}_1\left(n\pi r/l\right)/l}(10)$

where G_m = E_m/[2(1 + v_m)] and v_m are the shear modulus and Poisson’s ratio of the elastic matrix, K₀(*) and K₁(*) are modified Bessel functions of the second kind, r is the radius of the rod, and l is the length of the rod. For a slender elastic fiber (e.g., r/l ≈ 0) with an elliptical cross-section, Eq. 10 can be further optimized as:

$C=\frac{8\pi G_m\left(\mathit{1}-v_m\right)}{\mathit{ln}\left(2L/n\sqrt{a^2+b^2}\right)}(11)$

where a and b are the long and short semi-axes of the elliptical cross-section, respectively. In Figure 5, we plotted the dimensionless spring stiffness as a function of the dimensionless matrix stiffness e = E_mL⁴/E_fI_f and compared the simplified spring stiffness with the formula in literature. In Figure 5, it can be seen that the two curves provide almost identical predictions, proving that the optimization in Eq. 11 can also be employed in the calculation. FE simulations were subsequently conducted to validate the theoretical derivation.

FIGURE 5

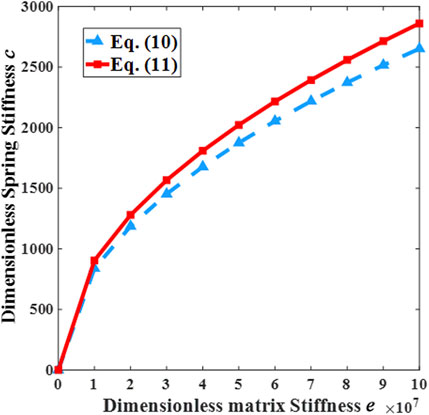
FIGURE 5. Comparison of spring estimation. The solid and dashed lines are the predictions applying Equation 10 and (11), respectively.

3 Numerical simulations

FE simulations were performed to validate the theoretical derivation through the commercial software package ABAQUS. In the simulations, small deformations were considered and the elastic fiber was modeled using element type C3D8R (an 8-node linear brick). Reduced integration and enhanced hourglass control are adopted to enable the elements to have an enhanced tolerance of distortion. The elastic Young’s modulus and Poisson’s ratio of the fiber were E_f = 59 GPa and v_m = 0.22 [5], respectively. The mean diameter and length of the fiber were R = 0.643 mm and L = 100 mm. Articulated boundary conditions were established at both ends of the elastic fibers (only the axial displacement being released) and a compressive tendency being imposed. To simulate the effect of transverse constraints on the elastic fibers, an array of springs was applied to the outside of the fibers using the elastic foundation module in the interaction. By utilizing the transformation relationship between the matrix stiffness and the spring stiffness discussed in the previous section, we were able to impose different spring stiffness values. To ensure accuracy and convergence reliability, we continuously debugged the number and size of cells. Ultimately, we used 22,000 meshes and 33,033 nodes with a mesh size of 0.1 mm. We checked the quality of the meshes using the mesh quality checking system in ABAQUS, which showed that the number of wrong and warning meshes was zero, indicating that our mesh setup was reasonable and correct. Finally, the buckling analysis was performed using a linear perturbation algorithm (via the BUCKLE module in ABAQUS).

Figure 6 illustrates the hierarchical buckling modes of the elastic fibers through the FEA results. In Figure 6, we show the buckling modes of elastic fibers with four representative configurations, which combinations of modal superpositions, say c² = 64π⁴, 5625π⁴, 4624π⁴ and 3600π⁴ (respectively, a, b, c, and d) in Figure 6. According to Eq. 9, it can be inferred that Figure 6 present joint buckling phenomenon by superposition of modes 1 and 8 (Figure 6A), modes 5 and 15 (Figure 6B), modes 4 and 17 (Figure 6C) as well as modes 2 and 30 (Figure 6D), respectively. It is observed that the hierarchical buckling phenomenon becomes more significant with the introduction of higher-order buckling modes. The FE simulations are employed to validate the present result by generating the dimensionless critical buckling loads as functions of dimensionless spring stiffness. Figure 7 compares the theoretical prediction and numerical ones, and it is found that the FE results do not closely fit with the theoretical calculations. We speculate that the reasons for the differences between the reduced model (Wrinkler foundation model) and the FE results is due to shear deformation in the matrix, which the Wrinkler model does not take into account. However, these simulation results are qualitatively consistent with the experimental results and supporting the theoretical analysis in Section 2.

FIGURE 6

FIGURE 6. FE simulation results: (A) c² = 64π⁴, (B) c² = 5625π⁴, (C) c² = 4624π⁴, (D) c² = 3600π⁴.

FIGURE 7

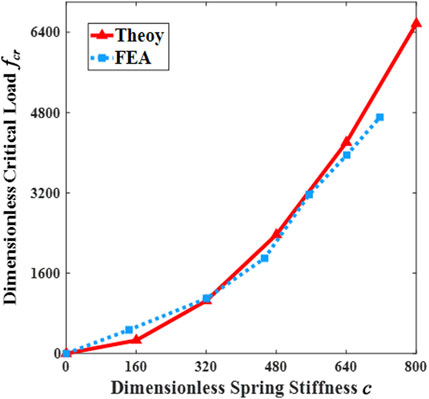
FIGURE 7. Comparison of theoretical and finite element results for the prediction of the dimensionless critical buckling load f_cr. The solid and dashed lines indicate theoretical results and FEA results for prediction, respectively.

4 Discussion and results

Based on the experimental observation, the hierarchical buckling of elastic fibers with elliptical and circular cross-sections, under transverse confinement, was investigated through analytical derivations. It was demonstrated that the elastic fibers’ hierarchical buckling phenomenon could be generated through triggering of superposition of buckling at two modes at the same time when the transverse confinement was satisfied c² = π⁴m²v². In addition, the hierarchical buckling phenomenon becomes more significant with the introduction of higher-order buckling modes. Moreover, hierarchical buckling can be effectively controlled by changing the Young’s modulus ratio (e = E_mL⁴/E_fI_f) between the matrix and the elastic fibers.

The analyses are in good qualitative agreement with the experimental results. However, a accurate quantitative comparison is challenging due to the important role played by imperfections and measurement uncertainties. We expect to take the following measures to improve the accuracy of the calculations in our subsequent work: Firstly, refining the computational grid to increase its density enables better capture of local details and structural deformations. Secondly, optimizing the accuracy of boundary conditions is crucial for precise calculation results. Additionally, selecting a more accurate material model that effectively describes the structural response during loading is essential. By combining these methods, the accuracy of the calculations can be significantly improved.

In addition, we have also found that the cross-sectional geometric characteristics of the fibers influence in the buckling configuration. In Figure 8, we plotted the relationship between dimensionless critical buckling loads for different b/a ratios, based on the theoretical results presented in this paper. For elliptical cross-sections elastic fibers, the ratio b/a of the short and long semi-axes of the elliptical cross-sections also affects the critical buckling load and buckling configuration of the elastic fiber. The critical buckling load increased as the cross-sections approached a circular shape. We speculate that when the fiber cross-sections are sufficiently close to a circular shape, the fibers undergo a transition from hierarchical buckling to 3D helical buckling [16,17]. However, the ratio of the short to the long axis of the elliptical cross-section mainly affects the buckling of the elastic fibers in the form of hierarchical buckling or 3D helical buckling. It is only a secondary factor affecting the modal superposition of the fibers. With the focus of this study being only the explanation of the hierarchical buckling phenomenon, the specific transition conditions were not thoroughly examined.

FIGURE 8

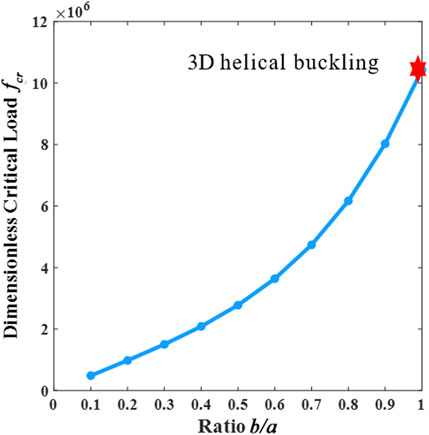
FIGURE 8. Relationship between the ratio of long and short axis b/a and dimensionless critical buckling load f_cr.

In summary, the analysis we proposed can be employed to predict the hierarchical buckling phenomenon observed in the experiment. The main reason in influencing the buckling phenomenon is the interaction of the matrix with the elastic fiber. By controlling the stiffness of the external matrix, the degree of hierarchical buckling of the elastic fibers could be tailored. It is shown that for a particular spring stiffness C, two different buckling modes can be simultaneously triggered at the onset of buckling, and the formation of hierarchical buckling is a result of the joint action of the two modes. This unique buckling phenomenon can motivate the development of new path for novel flexible electronic devices. Moreover, the present work provides theoretical guidance for the production, design and application of elastic/hyper-elastic fibers for the future use of buckling mechanisms to produce devices with controllable and sophisticated hierarchical structures.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

TZ: Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. JL: Conceptualization, Investigation, Supervision, Writing–review and editing. XW: Supervision, Writing–review and editing, Conceptualization, Funding acquisition, Methodology, Writing–original draft. PZ: Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China under Grant U1904175.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jiang H, Khang DY, Song J, Sun Y, Huang Y, Rogers JA. Finite deformation mechanics in buckled thin films on compliant supports. Proc Natl Acad Sci (2007) 104(40):15607–12. doi:10.1073/pnas.0702927104

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ko HC, Stoykovich MP, Song J, Malyarchuk V, Choi WM, Yu CJ, et al. A hemispherical electronic eye camera based on compressible silicon optoelectronics. Nature (2008) 454(7205):748–53. doi:10.1038/nature07113

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chen Y, Liu Y, Yan Y, Zhu Y, Chen X. Helical coil buckling mechanism for a stiff nanowire on an elastomeric substrate. J Mech Phys Sol (2016) 95:25–43. doi:10.1016/j.jmps.2016.05.020

CrossRef Full Text | Google Scholar

4. Chen Y, Zhu Y, Chen X, Liu Y. Mechanism of the transition from in-plane buckling to helical buckling for a stiff nanowire on an elastomeric substrate. J Appl Mech (2016) 83(4). doi:10.1115/1.4032573

CrossRef Full Text | Google Scholar

5. Miller JT, Su T, Pabon J, Wicks N, Bertoldi K, Reis PM. Buckling of a thin elastic rod inside a horizontal cylindrical constraint. Extreme Mech Lett (2015) 3:36–44. doi:10.1016/j.eml.2015.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Meng W, Nie M, Liu Z, Zhou J. Buckled fiber conductors with resistance stability under strain. Adv Fiber Mater (2021) 3(3):149–59. doi:10.1007/s42765-021-00067-x

CrossRef Full Text | Google Scholar

7. Zhou J, Tian G, Jin G, Xin Y, Tao R, Lubineau G. Buckled conductive polymer ribbons in elastomer channels as stretchable fiber conductor. Adv Funct Mater (2020) 30(5):1907316. doi:10.1002/adfm.201907316

CrossRef Full Text | Google Scholar

8. Ou M, Qiu W, Huang K, Feng H, Chu S. Ultrastretchable liquid metal electrical conductors built-in cloth fiber networks for wearable electronics. ACS Appl Mater Inter (2019) 12(6):7673–8. doi:10.1021/acsami.9b17634

CrossRef Full Text | Google Scholar

9. Chen G, Wang H, Guo R, Duan M, Zhang Y, Liu J. Superelastic EGaIn composite fibers sustaining 500% tensile strain with superior electrical conductivity for wearable electronics. ACS Appl Mater Inter (2020) 12(5):6112–8. doi:10.1021/acsami.9b23083

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kayser LV, Lipomi DJ. Stretchable conductive polymers and composites based on PEDOT and PEDOT: PSS. Adv Mater (2019) 31(10):1806133. doi:10.1002/adma.201806133

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang D, Hu N, Huang S, Nasab AM, Yang K, Abate MC, et al. Buckling and post-buckling of an elastic rod embedded in a bilayer matrix. Extreme Mech Lett (2018) 25:1–6. doi:10.1016/j.eml.2018.10.004

CrossRef Full Text | Google Scholar

12. Wang G, Wang W, Liu C, Chen W, Mei Y. Extended locally exact homogenization theory for effective coefficients and localized responses of piezoelectric composites. Adv Eng Mater (2022) 24(5):2101194. doi:10.1002/adem.202101194

CrossRef Full Text | Google Scholar

13. Chen Q, Chen W, Wang G. Fully-coupled electro-magneto-elastic behavior of unidirectional multiphased composites via finite-volume homogenization. Mech Mater (2021) 154:103553. doi:10.1016/j.mechmat.2020.103553

CrossRef Full Text | Google Scholar

14. Wang G, He Z, Chen Q. The surface effects on solid and hollow nanowires under diametral loading. Appl Math Model (2021) 96:697–718. doi:10.1016/j.apm.2021.03.039

CrossRef Full Text | Google Scholar

15. Chen W, Liu LX, Zhang HB, Yu ZZ. Kirigami-inspired highly stretchable, conductive, and hierarchical Ti₃C₂T_<i>x</i> MXene films for efficient electromagnetic interference shielding and pressure sensing. Acs Nano (2021) 15(4):7668–81. doi:10.1021/acsnano.1c01277

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Dayan Y, Durban D, Givli S. The postbuckling behavior of compressed elastica inside a flexible tube: experimental and numerical investigation. J Appl Mech (2022) 89(2). doi:10.1115/1.4052797

CrossRef Full Text | Google Scholar

17. Su T, Liu J, Terwagne D, Reis PM, Bertoldi K. Buckling of an elastic rod embedded on an elastomeric matrix: planar vs. non-planar configurations. Soft Matter (2014) 10(33):6294–302. doi:10.1039/c4sm00952e

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Xiao J, Chen Y, Lu X, Xu B, Chen X, Xu J. Three dimensional buckling beam under cylindrical constraint. Int J Mech Sci (2019) 150:348–55. doi:10.1016/j.ijmecsci.2018.10.041

CrossRef Full Text | Google Scholar

19. Song J. Mechanics of stretchable electronics. Curr Opin Solid State Mater Sci (2015) 19(3):160–70. doi:10.1016/j.cossms.2015.01.004

CrossRef Full Text | Google Scholar

20. Lin J, Liu X, Wang Y, Xu R, Wang G. Static and dynamic analysis of three-layered partial-interaction composite structures. Eng Structures (2022) 252:113581. doi:10.1016/j.engstruct.2021.113581

CrossRef Full Text | Google Scholar

21. Wang S, Song J, Kim DH, Huang Y, Rogers JA. Local versus global buckling of thin films on elastomeric substrates. Appl Phys Lett (2008) 93(2):023126. doi:10.1063/1.2956402

CrossRef Full Text | Google Scholar

22. Ma L, He L, Ni Y. Tunable hierarchical wrinkling: from models to applications. J Appl Phys (2020) 127(11):111101. doi:10.1063/1.5143651

CrossRef Full Text | Google Scholar

23. Pocivavsek L, Dellsy R, Kern A, Johnson S, Lin B, Lee KYC, et al. Stress and fold localization in thin elastic membranes. Science (2008) 320(5878):912–6. doi:10.1126/science.1154069

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Dillard DA, Mukherjee B, Karnal P, Batra RC, Frechette J. A review of Winkler's foundation and its profound influence on adhesion and soft matter applications. Soft matter (2018) 14(19):3669–83. doi:10.1039/c7sm02062g

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Brangwynne CP, MacKintosh FC, Kumar S, Geisse NA, Talbot J, Mahadevan L, et al. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J Cel Biol (2006) 173(5):733–41. doi:10.1083/jcb.200601060

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jiang H, Zhang J. Mechanics of microtubule buckling supported by cytoplasm. J Appl Mech (2008) 75(6). doi:10.1115/1.2966216

CrossRef Full Text | Google Scholar

27. Li SY, Chen JS. A twisted elastica constrained inside a tube. Eur J Mechanics-A/Solids (2014) 44:61–74. doi:10.1016/j.euromechsol.2013.10.006

CrossRef Full Text | Google Scholar

28. Zhang Y, Zhang S, Wang P. Growth induced buckling of morphoelastic rod in viscous medium. Chin Phys B (2020) 29(5):054501. doi:10.1088/1674-1056/ab7b4d

CrossRef Full Text | Google Scholar

29. Long X, Dong R, Su Y, Chang C. Critical review of nanoindentation-based numerical methods for evaluating elastoplastic material properties. Coatings (2023) 13(8):1334. doi:10.3390/coatings13081334

CrossRef Full Text | Google Scholar

30. Long X, Shen Z, Jia Q, Li J, Chen C, Liu Y, et al. Dimensionless analysis of the elastoplastic constitutive properties of single/multilayered films under nanoindentation. Scientia Sinica Physica, Mechanica & Astronomica (2023) 53(1):214606. doi:10.1360/sspma-2022-0203

CrossRef Full Text | Google Scholar

31. Long X, Shen Z, Jia Q, Li J, Dong R, Su Y, et al. Determine the unique constitutive properties of elastoplastic materials from their plastic zone evolution under nanoindentation. Mech Mater (2022) 175:104485. doi:10.1016/j.mechmat.2022.104485

CrossRef Full Text | Google Scholar

32. Long X, Li J, Shen Z, Su Y. Dimensionless analysis to determine elastoplastic properties of thin films by indentation. Coatings (2022) 12(11):1768. doi:10.3390/coatings12111768

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Long X, Jia Q, Shen Z, Liu M, Guan C. Strain rate shift for constitutive behaviour of sintered silver nanoparticles under nanoindentation. Mech Mater (2021) 158:103881. doi:10.1016/j.mechmat.2021.103881

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Long X, Shen Z, Lu C, Jia Q, Guan C, Chen C, et al. Reverse analysis of surface strain in elasto-plastic materials by nanoindentation. Int J Appl Mech (2021) 13(09):2150106. doi:10.1142/s1758825121501064

CrossRef Full Text | Google Scholar

35. Long X, Jia QP, Li Z, Wen SX. Reverse analysis of constitutive properties of sintered silver particles from nanoindentations. Int J Sol Structures (2020) 191:351–62. doi:10.1016/j.ijsolstr.2020.01.014

CrossRef Full Text | Google Scholar

36. Wang G, Zhang N, Huang G. Coupled effect of multi-factor on the vibration of submerged floating tunnel under impact load. Ocean Eng (2022) 262:112181. doi:10.1016/j.oceaneng.2022.112181

CrossRef Full Text | Google Scholar

37. Mojdehi AR, Tavakol B, Royston W, Dillard DA, Holmes DP. Buckling of elastic beams embedded in granular media. Extreme Mech Lett (2016) 9:237–44. doi:10.1016/j.eml.2016.03.022

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Wang Z, Gao W, Zhang Q, Zheng K, Xu J, Xu W, et al. 3D-printed graphene/polydimethylsiloxane composites for stretchable and strain-insensitive temperature sensors. ACS Appl Mater Inter (2018) 11(1):1344–52. doi:10.1021/acsami.8b16139

CrossRef Full Text | Google Scholar

39. Chen Y, Liao X, Liu Y, Chen X. Helical buckling of wires embedded in a soft matrix under axial compression. Extreme Mech Lett (2017) 17:71–6. doi:10.1016/j.eml.2017.09.010

CrossRef Full Text | Google Scholar

40. Wang Z, Wang W, Zhang Q. New effective bending rigidity and structural instability analysis of noncircular cross-section elastic rod model. Eur Phys J Spec Top (2022) 231(11):2325–34. doi:10.1140/epjs/s11734-021-00370-z

CrossRef Full Text | Google Scholar

41. Chai H. On the post-buckling behavior of bilaterally constrained plates. Int J Sol Structures (2002) 39(11):2911–26. doi:10.1016/s0020-7683(02)00253-6

CrossRef Full Text | Google Scholar

42. Xiao J, Chen X. Buckling morphology of an elastic beam between two parallel lateral constraints: implication for a snake crawling between walls. J R Soc Interf (2013) 10(85):20130399. doi:10.1098/rsif.2013.0399

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Pocheau A, Roman B. Uniqueness of solutions for constrained elastica. Physica D: Nonlinear Phenomena (2004) 192(3-4):161–86. doi:10.1016/j.physd.2003.12.013

CrossRef Full Text | Google Scholar

44. Chai H. The post-buckling response of a bi-laterally constrained column. J Mech Phys Sol (1998) 46(7):1155–81. doi:10.1016/s0022-5096(98)00004-0

CrossRef Full Text | Google Scholar

45. Chai H. On optimizing crash energy and load-bearing capacity in cellular structures. Int J Sol Structures (2008) 45(2):528–39. doi:10.1016/j.ijsolstr.2007.08.001

CrossRef Full Text | Google Scholar

46. Xiao J. The stability at the solid-solid and liquid-solid interfaces. New York, NY, USA: Columbia University (2016).

Google Scholar

47. Timoshenko S, Gere J. Theory of elasticty stability. Illinois, United States: Dover (1961).

Google Scholar

48. Tian L, Zhao H, Yuan M, Wang G, Zhang B, Chen J, et al. Global buckling and multiscale responses of fiber-reinforced composite cylindrical shells with trapezoidal corrugated cores. Compos Structures (2021) 260:113270. doi:10.1016/j.compstruct.2020.113270

CrossRef Full Text | Google Scholar

49. Herrmann LR, Mason WE, Chan STK. Response of reinforcing wires to compressive states of stress. J Compos Mater (1967) 1(3):212–26. doi:10.1177/002199836700100301

CrossRef Full Text | Google Scholar

50. Lanir Y, Fung YCB. Fiber composite columns under compression. J Compos Mater (1972) 6(3):387–401. doi:10.1177/002199837200600315

CrossRef Full Text | Google Scholar