FEM/Wideband FMBEM coupling based on subdivision isogeometry for structural-acoustic design sensitivity analysis

A computer simulation approach known as the isogeometric (IGA) method may directly use the surface information of geometric model. In 3D computer graphics, Loop subdivision surfaces are a common method for creating complicated shapes. In this study, we propose a coupling algorithm that utilizes Loop subdivision surfaces and a direct differentiation method for the computation of acoustic-fluid-structure interaction and the performance of structural-acoustic sensitivity analysis. This algorithm combines the finite element method (FEM) and wideband fast multipole boundary element method (FMBEM). Because of that the proposed method is of a great ability of integrating the numerical calculation and computer-aided modeling, the current technique can deliver results quickly and accurately. The numerical prediction of the effects of vibrating structures with arbitrary shape within sound field is made feasible by the FEM/Wideband FMBEM technique. Calculation examples are provided to show the applicability and effectiveness of the suggested method.

1 Introduction

The elastic structures in heavy fluid resulting in acoustic radiation or scattering is a common issue in underwater acoustics. It is possible to give the analytical solutions of the issues with acoustic fluid-structure interaction phenomenon while the structure is with simple boundary conditions and geometry [1,2]. However, as it comes for real-world issues which usually have complex geometries, providing an analytical solution becomes harder and even impossible, thus effective simulation techniques are needed.

FEM is extensively utilized to study the dynamic behavior of issues involving fluid-structure interactions, acoustics, and structures. The FEM has several drawbacks for modeling infinite domains, though. Because it offers good accuracy and simple mesh generation, BEM has been widely employed to calculate acoustic issues. The Sommerfeld radiation condition [3] is met, especially for external acoustic issues. The Galerkin technique has been frequently used in BEM implementation to solve the boundary integral problem numerically [4]. However, the collocation approach, has historically been popular in the engineering field. Hence, the coupled FEM/BEM technique [5,6] is suitable for studying fluid-structure interaction problems. However, the high computational expense remains a challenge when performing coupling analysis of underwater structural-acoustic problems using the FEM/Conventional BEM (CBEM) algorithm. This is primarily because CBEM generates a dense and non-symmetric coefficient matrix. Many techniques have been used to speed up the integral problem solution, including fast multipole method (FMM), the adaptive cross approximation methodology and fast direct solver. Martinsson and Rokhlin [7,8] introduced the fast direct solver, which works well for issues requiring moderately ill-conditioned matrices and immediately builds a compressed factorization of the matrix inverse. The adaptive cross approximation methodology [9], developed by Bebendorf and Rjasanow, has the capability to generate blockwise low-rank approximations from the BEM matrices. This methodology is particularly suitable for problems that require a large number of iterations. FMM [10–12] has been developed to reduce memory requirements while speeding up the solving of the CBEM system of equations. In reality, the Helmholtz equation has two versions of the Fast Multipole Method (FMM), namely, the original FMM and the diagonal form. However, it is well-known that both of these versions tend to fail outside of their optimal frequency ranges in some manner. On the other hand, the aforementioned issues can potentially be resolved by utilizing wideband FMM [13–18]. This advanced technique combines the original FMM with the diagonal form FMM, leading to more efficient solutions. Therefore, the challenges related to large-scale fluid-structure interaction problems can be effectively resolved through the utilization of the coupling approach based on FEM/fast multipole boundary element method (FEM/FMBEM) [19–23]. Furthermore, this study proposes the utilization of the FEM/Wideband FMBEM coupling method to tackle the intricate problems associated with fluid-structure interactions.

Through the use of appropriate software, FEM and BEM may be implemented—a process known as computer-aided engineering (CAE). Nowadays, industry 4.0 and digital twin technologies are being developed with the use of CAE simulation. The models created by CAD software must, however, be transformed into simulation-ready models as part of the preprocessing stage used by modern CAE. The CAE’s most time-consuming manual intervention phase, the geometric model data transfer stage produces geometry inaccuracies. The integration of geometric modeling and numerical simulation using isogeometric analysis [24–26] with boundary element method (IGABEM) [27,28] is suggested as a solution to this issue. By using IGABEM, geometric mistakes and time-consuming preprocessing steps may be avoided and numerical simulation can be carried out straight from the precise models. Since its inception, IGABEM has been used to address a variety of issues, including those related to elastic mechanics [27–30], potential issues [15], wave-resistance [31], fracture mechanics [32,33], electromagnetics [34–39], and structural optimization [40–46].

In addition to the benefits already discussed, IGABEM offers significant benefits for modelling acoustics issues. Numerous engineering fields have found extensive use for acoustics, including noise control, underwater navigation using sonar, ultrasound imaging for medical purposes, seismology, electroacoustic communications, etc. Numerous numerical simulation techniques have significant challenges when it comes to acoustics for that the sound wave may travel through semi-infinite domains. By shifting the acoustic field from a semi-infinite domain to the boundary of the domain, IGABEM can get around this problem. Simpson [16,47] applied IGABEM to acoustics. Acoustic optimization [37,48,49] with IGABEM was studied.

In the framework of the IGABEM, several sorts of geometric modeling approaches have been extensively researched. The ability to build multi-resolution geometries with complex forms and topologies makes the subdivision surface approach among them very promising [51–56]. There are two types of subdivision surfaces: Catmull-Clark and Loop method. Structure-acoustic interaction [1,57,58] and acoustic optimization [59–63] were both addressed using IGABEM based on Loop subdivision surfaces. The goal of the current effort is to merge Loop subdivision surfaces with IGABEM for sensitivity analysis. Additionally, we’ll speed up the solution process using wideband FMM.

Designers are increasingly considering passive noise management by altering the geometry of the construction. Particularly for thin shell structures, this structural-acoustic optimization has considerable promise for minimizing radiated noise [64]. Acoustic design sensitivity analysis is a crucial component in the process of acoustic design and optimization, as it allows for understanding the effect of geometry changes on the acoustic performance. In a comprehensive review by Marburg [65], advancements in structural-acoustic optimization for passive noise reduction were discussed. The global finite difference method (FDM) has been extensively employed for structural-acoustic optimization due to its ease of implementation [66–69]. However, this approach doesn’t work so well, particularly while considering several design elements simultaneously. To get over this issue, employ the adjoint variable approaches [70,71] or the direct differentiation method [72]. The sensitivity analysis for interaction issues is widely recognized as the most time-consuming step in gradient-based optimization. In our study, we aim to accelerate the calculation process by employing a direct differentiation approach for structural-acoustic sensitivity analysis in the FEM/Wideband FMBEM method.

In this study, we propose the incorporation of wideband FMBEM in the coupling of structural-acoustic sensitivity analysis and present the formulation for sensitivity analysis in the coupled FEM/BEM analysis. We advocate for the adoption of coupled FEM/Wideband FMBEM to address fluid-structure interaction problems and conduct structural-acoustic sensitivity analysis. To eliminate the geometry inaccurices, Loop subdivision scheme is applied to the sensitivity analysis of an underwater fluid-structure coupling problem. Through the computation of various numerical examples, we have demonstrated the accuracy and effectiveness of the proposed strategy.

2 Structural-acoustic coupling deduction

2.1 Subdivision scheme

In computer animation and graphics, it is of great advantages of using Subdivision surfaces [73,74] since their emergence in the 1970s. They may also be accessed in most industrial CAD solid modeling applications. Subdivision surfaces are frequently mentioned as a technique for continually fine-tuning and smoothing a control mesh so a smooth limit surface could be produced. They may also be regarded as the extension of splines to arbitrarily linked meshes for FEM and BEM.

A rough polygon mesh is transformed into a smooth surface using subdivision techniques. The creation of a smooth surface using subdivision method—which is usually classified as interpolating schemes—involves a constrained, repeating refinement process that starts with an initial control mesh. Due to the refinement characteristic inherited from splines, all control meshes generated during subdivision refinement accurately represent the same spline surface.

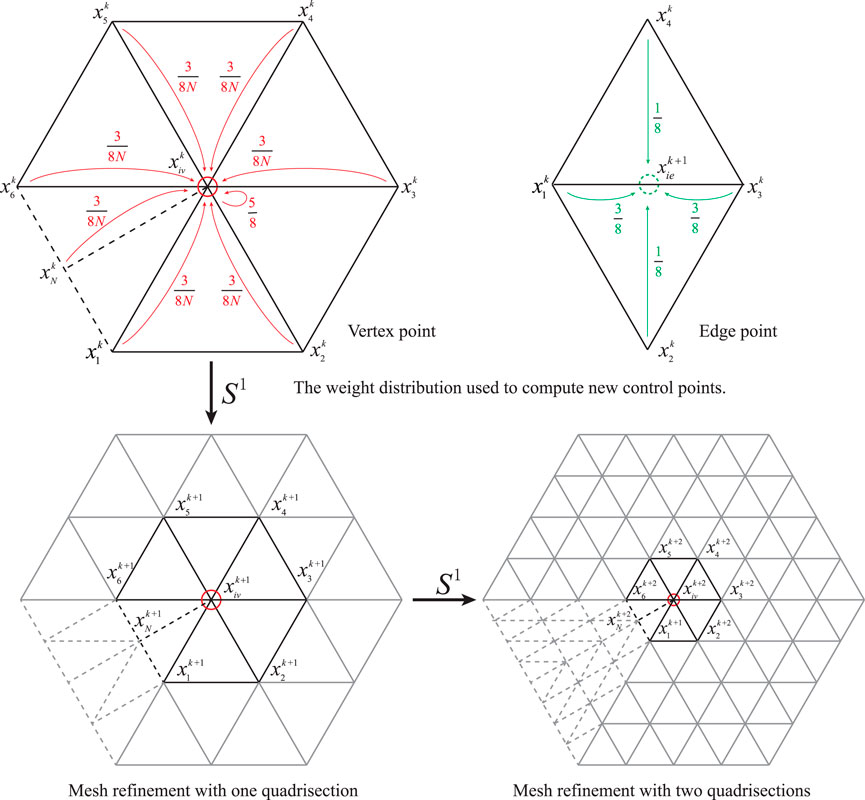
The structural-acoustic coupling analysis in this study is carried out utilizing the Loop subdivision scheme [59]. The quadrisection refinement of a triangular mesh in a construction of loop subdivision is shown in Figure 1. A vertex’s valence is the edges number that link it. When N = 6, a vertex is considered regular, and when N ≠ 6, it is considered irregular. Each triangle is split into four smaller triangles by adding a new vertex at the middle of each edge. As indicated in Eqs 1, 2, the positions of new vertices and edge points may be determined from the previous level.

$x_{iv}^{k+1}=\frac{5}{8}{x}_{iv}^k+\frac{3}{8N}{\displaystyle \sum _{i=1}^N}{x}_i^k,(1)$

$x_{ie}^{k+1}=\frac{3}{8}{x}_1^k+\frac{1}{8}{x}_2^k+\frac{3}{8}{x}_3^k+\frac{1}{8}{x}_4^k,(2)$

where

FIGURE 1

FIGURE 1. Templates for vertex and edge points with regular and irregular shapes.

In reality, there are too many nodes, making it impossible to achieve smooth surfaces with few subdivisions. Another method for creating limit surfaces for any degree of refinement is to create an elementwise map using linear combinations of Box-splines basis functions on triangular control meshes. For further details, please refer to Chen et al.[59].

2.2 BEM analysis

${\nabla }^{2}p\left(x\right)+k^{2}p\left(x\right)=0,(3)$

$\begin{array}{cc}\hfill p\left(x\right)& =\bar{p}\left(x\right)x\in {\mathrm{\Gamma }}_p,\hfill \\ \hfill q\left(x\right)& =\frac{\partial p\left(x\right)}{\partial n\left(x\right)}=\mathrm{i}\rho \omega \bar{v}\left(x\right)x\in {\mathrm{\Gamma }}_q,\hfill \\ \hfill p\left(x\right)& =zv\left(x\right)x\in {\mathrm{\Gamma }}_z,\hfill \end{array}(4)$

where

Equation 3 describes a acoustic wave which is time-harmonic in the Helmholtz equation, and Eq. 4 serves as an expression for the boundary conditions. A boundary integral equation (BIE) specified on the Γ can be created from Eqs 3–5.

$c\left(x\right)p\left(x\right)+{\int }_{\mathrm{\Gamma }}F\left(x,y\right)p\left(y\right)\mathrm{d}\mathrm{\Gamma }\left(y\right)={\int }_{\mathrm{\Gamma }}G\left(x,y\right)q\left(y\right)\mathrm{d}\mathrm{\Gamma }\left(y\right),(5)$

where

Equations 6, 7 gives the expression of Green’s function for acoustic problems in two and three dimensional problems, respectively.

$G\left(x,y\right)=\frac{i}{4}{H}_0^{\left(1\right)}\left(kr\right),(6)$

$G\left(x,y\right)=\frac{e^{ikr}}{4\pi r},(7)$

$r=\left|y-x\right|.$

When the boundary Γ is smooth around the source point x, the derivative of the integral representation in Eq. 5 with respect to the outer normal can be expressed as Eq. 8.

$\frac{1}{2}q\left(x\right)+{\int }_{\mathrm{\Gamma }}\frac{\partial F\left(x,y\right)}{\partial n\left(x\right)}p\left(y\right)\mathrm{d}\mathrm{\Gamma }\left(y\right)={\int }_{\mathrm{\Gamma }}\frac{\partial G\left(x,y\right)}{\partial n\left(x\right)}q\left(y\right)\mathrm{d}\mathrm{\Gamma }\left(y\right).(8)$

It is common knowledge that applying a single Helmholtz boundary integral equation to issues involving external boundary values may be challenging due to nonuniqueness. In order to effectively solve the nonuniqueness problem, the Burton-Miller approach [75]—which is a linear combination of Eqs 5, 8—is used in this study. The computation of the singular boundary integrals introduced by Eqs 5, 8 can also be performed directly and efficiently using the Cauchy principal value and the Hadamard finite part integral method [72].

If the boundary Γ is divided into elements, the system can be obtained [76] and can be expressed as Eq. 9 by assembling the equations for collocation points located in the center of each element.

$\mathbf{H}\mathbf{p}=\mathbf{G}\mathbf{q}+{\mathbf{p}}_{\mathbf{i}},(9)$

where

2.3 FEM analysis

The complete structural-acoustic simulation approach was described by Fritze et al. [6], and related expressions are supplied here. The structure response is determined by analyzing of frequency-response under the assumption that a harmonic load performs on the structure. Equation 10 derives the linear system of structural-acoustic equation.

$\left(\mathbf{K}+\mathrm{i}\omega \mathbf{C}-{\omega }^2\mathbf{M}\right)\mathbf{u}=\mathbf{f}(10)$

where

It is crucial to take into account that, because of damping, the steady-state response may have the same frequency as the applied load but a different phase angle. To handle non-harmonic imposed loads, the time-dependent forces can be examined in the frequency domain, enabling the use of Eq. 10. To address the effect of acoustic pressure on structural surfaces, a coupling matrix is introduced. This matrix facilitates the transfer of the structural nodal load from the fluid effect to the fluid nodal pressure. Then, Eq. 11 could be used to express the complete excitation, combining the acoustic load and the structural load.

$\begin{array}{ll}\hfill \mathbf{f}& ={\mathbf{C}}_{\mathbf{s}\mathbf{f}}\mathbf{p}+{\mathbf{f}}_{\mathbf{s}},\hfill \\ \hfill {\mathbf{C}}_{\mathbf{sf}}& ={\int }_{{\mathrm{\Gamma }}_{\mathit{int}}}{\mathbf{N}}_{\mathbf{s}}^{\mathbf{T}}\mathbf{n}{\mathbf{N}}_{\mathbf{f}}\mathrm{d}\mathrm{\Gamma },\hfill \end{array}(11)$

where

The structural nodal load from the fluid effect is directed to fluid nodal pressure via the coupling matrix C_sf. The nodal displacement could then be obtained from Eq. 10, as shown in Eq. 12.

$\mathbf{u}={\left(\mathbf{K}+\mathrm{i}\omega \mathbf{C}-{\omega }^2\mathbf{M}\right)}^{-1}\mathbf{f}.(12)$

2.4 FEM-BEM coupling analysis

The exact formulas of FEM/BEM modeling were published by Fritze et al. [6], and related expressions are supplied in this part. The continuity constraint over the interaction surface—as shown in Eq. 13—connects the governing equations as illustrated in the above section. Then, the normal velocity v may be written as a function with the displacement u, according to Eq. 14.

$\mathbf{q}=-\mathrm{i}\omega \rho \mathbf{v},(13)$

$\mathbf{v}=\mathrm{i}\omega {\mathbf{S}}^{-\mathbf{1}}{\mathbf{C}}_{\mathbf{fs}}\mathbf{u},(14)$

$\begin{array}{ll}\hfill \mathbf{S}& ={\int }_{{\mathrm{\Gamma }}_{\mathit{int}}}{\mathbf{N}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{N}}_{\mathbf{f}}\mathrm{d}\mathrm{\Gamma },\hfill \\ \hfill {\mathbf{C}}_{\mathbf{fs}}& ={\mathbf{C}}_{\mathbf{s}\mathbf{f}}^{\mathbf{T}}.\hfill \end{array}$

We can get Eq. 15 by inserting Eqs 13, 14 into Eq. 9.

$\mathbf{H}\mathbf{p}={\omega }^2\rho \mathbf{G}{\mathbf{S}}^{-\mathbf{1}}{\mathbf{C}}_{\mathbf{f}\mathbf{s}}\mathbf{u}+{\mathbf{p}}_{\mathbf{i}}.(15)$

Equations 10, 11, 15 can be connected to form a equation system, as shown in Eq. 16.

$\left[\begin{array}{cc}\hfill \mathbf{K}+\mathrm{i}\omega \mathbf{C}-{\omega }^2\mathbf{M}\hfill & \hfill -{\mathbf{C}}_{\mathbf{sf}}\hfill \\ \hfill -{\omega }^2\rho \mathbf{G}{\mathbf{S}}^{-\mathbf{1}}{\mathbf{C}}_{\mathbf{f}\mathbf{s}}\hfill & \hfill \mathbf{H}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \mathbf{u}\hfill \\ \hfill \mathbf{p}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\mathbf{f}}_{\mathbf{s}}\hfill \\ \hfill {\mathbf{p}}_{\mathbf{i}}\hfill \end{array}\right\}.(16)$

The direct iterations on Eq. 16 converge rather slowly, and directly solving the system equation would demand far more computational power and storage space. We present the following method as an alternative to utilizing an iterative solver to resolve the above non-symmetric linear equation. The coupled boundary element equation (6) shown in Eq. 17 may be obtained by putting Eq. 12 into Eq. 15.

$\begin{array}{ll}\hfill \mathbf{H}\mathbf{p}-\mathbf{G}\mathbf{W}{\mathbf{C}}_{\mathbf{s}\mathbf{f}}\mathbf{p}& ={\mathbf{G}\mathbf{W}\mathbf{f}}_{\mathbf{s}}+{\mathbf{p}}_{\mathbf{i}},\hfill \\ \hfill \mathbf{W}& ={\omega }^2\rho {\mathbf{S}}^{-\mathbf{1}}{\mathbf{C}}_{\mathbf{f}\mathbf{s}}{\mathbf{A}}^{-\mathbf{1}},\hfill \\ \hfill \mathbf{A}& =\mathbf{K}+\mathrm{i}\omega \mathbf{C}-{\omega }^2\mathbf{M}.\hfill \end{array}(17)$

By using a sparse direct solver, the equation linear system in Eq. 17 could be solved. To speed up the solution, FMM and the Generalized Minimum Residual (GMRES) iterative solver are used.

In this study, Loop subdivision is introduced in the model discretization in order to realize the FEM-BEM coupling and the ensuing sensitivity analysis.

3 Sensitivity analysis for shape design

Finding the optimum design parameters specifying the intended form of the given structure under specified restrictions is the aim of shape optimization. Calculating the gradients of stated cost functions is done using shape design sensitivity analysis. The direction in which to look for the best values of the design variables may then be decided using the acquired gradients. As a result, the first and most crucial phase in the design and optimization of acoustic shapes is often acoustic form sensitivity analysis [72,77]. The direct method utilizes the chain rule of differentiation to compute the sensitivity of the performance function. This process begins with determining the sensitivity of the variables before proceeding to compute the performance function sensitivity. Because it is so directly tied to the analytical process, this strategy is quite popular.

By differentiating Eqs 5, 8 with respect to any arbitrary design variable, assuming that the boundary Γ is smooth around the source point x, we can derive Eqs 18, 19.

$\begin{array}{ll}\hfill \frac{1}{2}\dot{p}\left(x\right)& ={\int }_{\mathrm{\Gamma }}\left[\dot{G}\left(x,y\right)q\left(y\right)-\dot{F}\left(x,y\right)p\left(y\right)\right]\mathrm{d}\mathrm{\Gamma }\left(y\right)\hfill \\ \hfill & +{\int }_{\mathrm{\Gamma }}\left[G\left(x,y\right)\dot{q}\left(y\right)-F\left(x,y\right)\dot{p}\left(y\right)\right]\mathrm{d}\mathrm{\Gamma }\left(y\right)\hfill \\ \hfill & +{\int }_{\mathrm{\Gamma }}\left[G\left(x,y\right)q\left(y\right)-F\left(x,y\right)p\left(y\right)\right]\mathrm{d}\dot{\mathrm{\Gamma }}\left(y\right).\hfill \end{array}(18)$

$\begin{array}{ll}\hfill \frac{1}{2}\dot{q}\left(x\right)& ={\int }_{\mathrm{\Gamma }}\left[\dot{\frac{\partial G\left(x,y\right)}{\partial n\left(x\right)}}q\left(y\right)-\dot{\frac{\partial F\left(x,y\right)}{\partial n\left(x\right)}}p\left(y\right)\right]\mathrm{d}\mathrm{\Gamma }\left(y\right)\hfill \\ \hfill & +{\int }_{\mathrm{\Gamma }}\left[\frac{\partial G\left(x,y\right)}{\partial n\left(x\right)}\dot{q}\left(y\right)-\frac{\partial F\left(x,y\right)}{\partial n\left(x\right)}\dot{p}\left(y\right)\right]\mathrm{d}\mathrm{\Gamma }\left(y\right)\hfill \\ \hfill & +{\int }_{\mathrm{\Gamma }}\left[\frac{\partial G\left(x,y\right)}{\partial n\left(x\right)}q\left(y\right)-\frac{\partial F\left(x,y\right)}{\partial n\left(x\right)}p\left(y\right)\right]\mathrm{d}\dot{\mathrm{\Gamma }}\left(y\right).\hfill \end{array}(19)$

For two dimensional problems, we have Eq. 20.

$\begin{array}{c}\dot{G}\left(x,y\right)=-\frac{ik}{4}{H}_1^{\left(1\right)}\left(kr\right)\dot{r},\hfill \\ \hfill \dot{F}\left(x,y\right)=-\frac{ik}{4}{H}_1^{\left(1\right)}\left(kr\right)\left[\frac{\left({\dot{y}}_j-{\dot{x}}_j\right)n_j\left(y\right)}{r}+r_{,j}{\dot{n}}_j\left(y\right)\right]\\ \hfill +\frac{i{k}^2}{4}{H}_2^{\left(1\right)}\left(kr\right)\dot{r}{r}_{,j}{n}_j\left(y\right),\hfill \\ \dot{r}=r_{,j}\left({\dot{y}}_j-{\dot{x}}_j\right).\hfill \end{array}(20)$

For three dimensional problems, we have Eq. 21.

$\begin{array}{c}\dot{G}\left(x,y\right)=-\frac{e^{ikr}}{4\pi r^2}\left(1-ikr\right)\frac{\partial r}{\partial y_i}\left({\dot{y}}_i-{\dot{x}}_i\right),\hfill \\ \hfill \dot{F}\left(x,y\right)=\frac{e^{ikr}}{4\pi r^3}\left[\left(3-3ikr-k^2{r}^2\right)\frac{\partial r}{\partial n\left(y\right)}\frac{\partial r}{\partial y_j}-\left(1-ikr\right)n_j\left(y\right)\right]\left({\dot{y}}_j-{\dot{x}}_j\right)\\ \hfill -\frac{e^{ikr}}{4\pi r^2}\left(1-ikr\right)\frac{\partial r}{\partial y_i}{\dot{n}}_i\left(y\right),\hfill \\ \dot{r}=r_{,j}\left({\dot{y}}_j-{\dot{x}}_j\right).\hfill \end{array}(21)$

The singular boundary integrals introduced by Eqs 18, 19 can be computed directly and efficiently using the Cauchy principal value and the Hadamard finite part integral method [72].

By differentiating Eq. 17 with respect to the design variable, the sensitivity analysis for shape design using the coupling FEM-BEM can yield Eq. 22.

$\begin{array}{ll}\hfill \mathbf{H}\dot{\mathbf{p}}-\mathbf{G}\mathbf{W}{\mathbf{C}}_{\mathbf{s}\mathbf{f}}\dot{\mathbf{p}}& =\dot{\mathbf{G}}\mathbf{X}+\mathbf{G}\mathbf{Y}-\dot{\mathbf{H}}\mathbf{p},\hfill \\ \hfill \mathbf{X}& =\mathbf{W}\left({\mathbf{C}}_{\mathbf{s}\mathbf{f}}\mathbf{p}+{\mathbf{f}}_{\mathbf{s}}\right),\hfill \\ \hfill \mathbf{Y}& =\dot{\mathbf{W}}\left({\mathbf{C}}_{\mathbf{s}\mathbf{f}}\mathbf{p}+{\mathbf{f}}_{\mathbf{s}}\right)+\mathbf{W}\left(\dot{{\mathbf{C}}_{\mathbf{sf}}}\mathbf{p}+\dot{{\mathbf{f}}_{\mathbf{s}}}\right),\hfill \\ \hfill \dot{\mathbf{W}}& ={\omega }^2\rho \left(\dot{{\mathbf{S}}^{-\mathbf{1}}}{\mathbf{C}}_{\mathbf{fs}}{\mathbf{A}}^{-\mathbf{1}}+{\mathbf{S}}^{-1}\dot{{\mathbf{C}}_{\mathbf{fs}}}{\mathbf{A}}^{-\mathbf{1}}+{\mathbf{S}}^{-1}{\mathbf{C}}_{\mathbf{fs}}\dot{{\mathbf{A}}^{-\mathbf{1}}}\right).\hfill \end{array}(22)$

Since the matrices are full and asymmetric, it takes a lot of computing time to directly solve Eq. 22 using conventional BEM. However, it is possible to speed up the computational process using FMM and GMRES. The matrix-vector products in Eqs 17, 22 are accelerated using wideband FMM, and the FEM-BEM coupling formula and the associated sensitivity equation are solved using the iterative solver GMRES.

4 Numerical examples

Several numerical tests are conducted to examine the validity and dependability of the established methodology in this section. In each case, the FEM uses shell elements whereas the discontinuous linear boundary elements are applied for acoustic analysis. All calculations are performed using a customized internal Fortran 95/2003 algorithm.

4.1 Sphere with an incoming sound wave

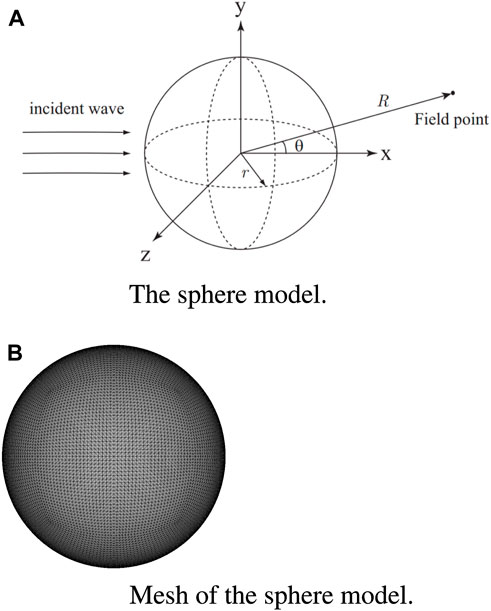
This section examines the sound field of an thin spherical shell that is centered at location (0, 0, 0), while accounting for an incoming sound wave with an amplitude of 1.0 in positive x direction, as shown in Figure 2. The following are the materials and geometrical elements used in this example.

FIGURE 2

FIGURE 2. The sphere model and its mesh plot. (A) The sphere model. (B) Mesh of the sphere model.

Figure 3 gives the results at position (10, 0, 0). Figure 3A displays the analytical and numerical solutions. The GMRES implementation with the wideband FMM technique is employed to accelerate the solution of linear systems without preconditioning. The discretized thin-shell model consists of 25,392 elements. The wideband FMM approach keeps the high accuracy of BEM, as the numerical and analytical answers present the good agreement which can seen in the figure.

FIGURE 3

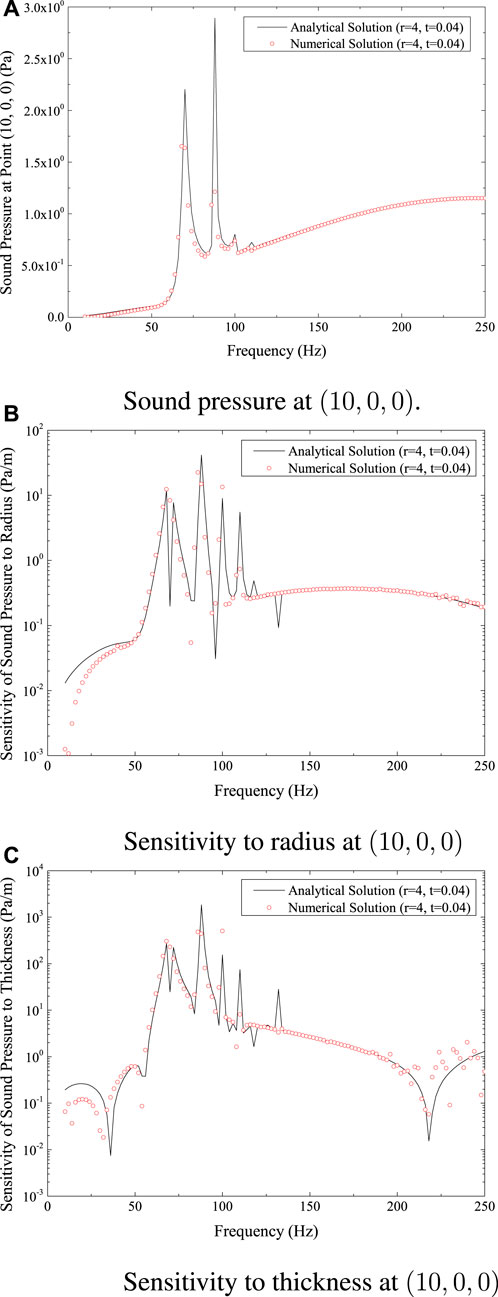
FIGURE 3. Sound pressure and sensitivity at (10,0,0) for spherical shell model. (A) Sound pressure at (10,0,0). (B) Sensitivity to radius at (10,0,0). (C) Sensitivity to thickness at (10,0,0).

Figures 3B, C shows, respectively, how sensitive the structure’s surface is to sound pressure in relation to the radius and thickness of the sphere. Basically, these graphs demonstrate a good agreement between the analytical and numerical results. Figure 3 shows that the sound pressure sensitivity grows significantly at resonance peaks, and the lower frequency range is crucial for this spherical shell model because the sound pressure there is substantially higher and more responsive to thickness and radius.

The results are shown in Figures 4, 5, respectively, for the positions (20, 0, 0) and (40, 0, 0). The curves for the same physical quantity at various locations, as shown in Figures 3, 4, 5—Figures 3A, 4A, 5A for sound pressure, Figures 3B, 4B, 5B for sensitivity to radius, and Figures 3C, 4C, 5C for sensitivity to thickness—all show a similar pattern of fluctuation.

FIGURE 4

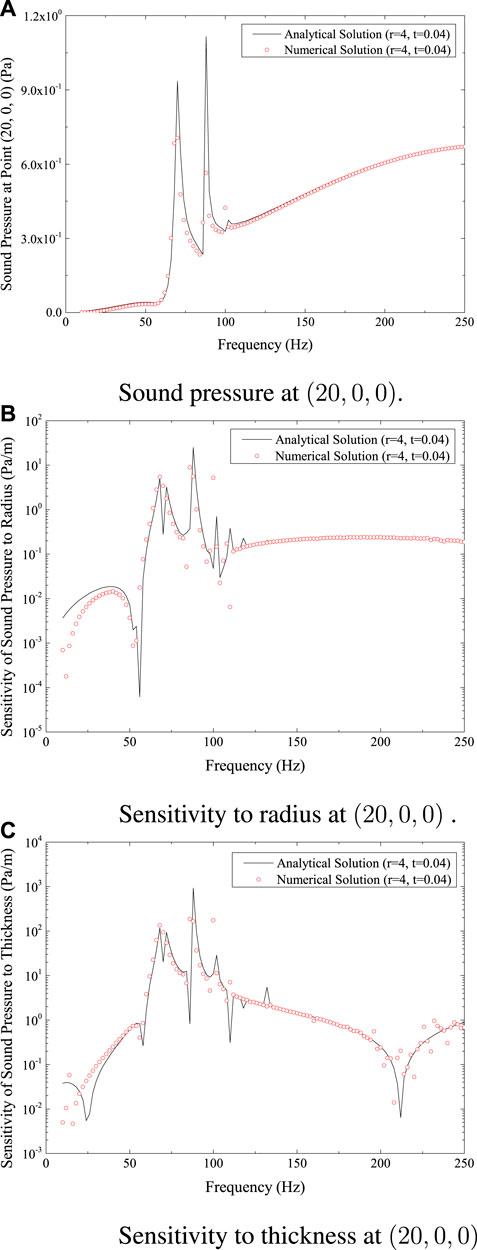
FIGURE 4. Sound pressure and sensitivity at (20,0,0) for spherical shell model. (A) Sound pressure at (20,0,0). (B) Sensitivity to radius at (20,0,0). (C) Sensitivity to thickness at (20,0,0).

FIGURE 5

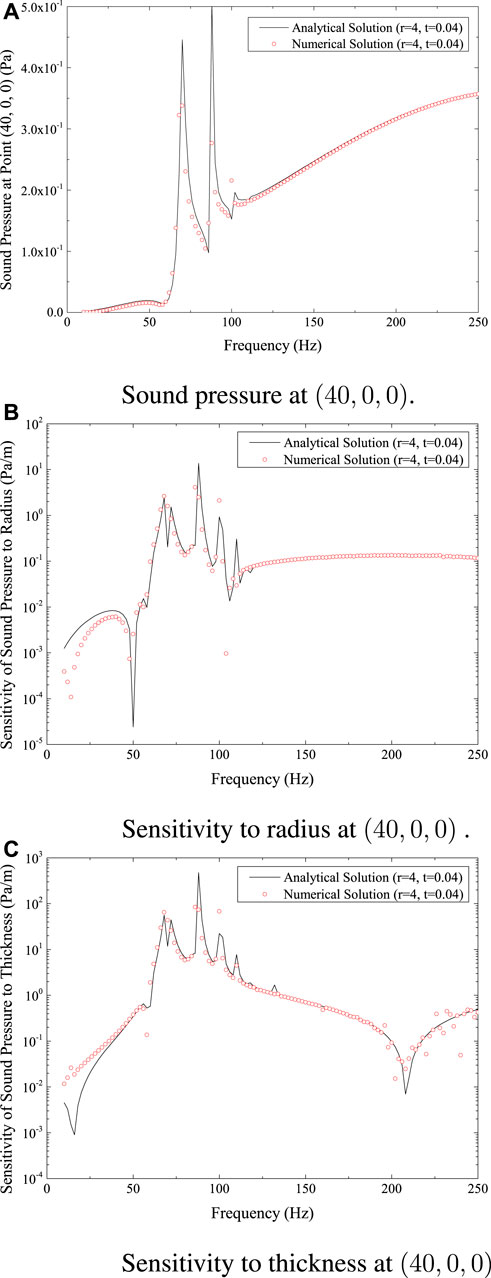
FIGURE 5. Sound pressure and sensitivity at (40,0,0) for spherical shell model. (A) Sound pressure at (40,0,0). (B) Sensitivity to radius at (40,0,0). (C) Sensitivity to thickness at (40,0,0).

4.2 Submarine model under an incoming sound wave

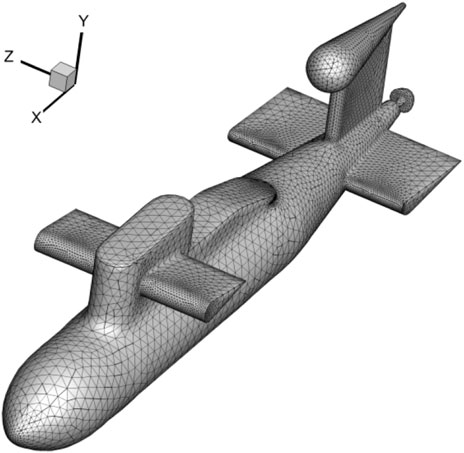
This section focuses on the underwater submarine model’s scattering sound field when influenced by an incoming plane wave [78]. The plane wave propagates predominantly along the x-axis and has an incidence wave amplitude of 1.0 Pa. The thickness of the submarine model is 0.01 m, and the sub has a length of 9.2 m. The origin of the coordinate is in the middle of the axial length of the submarine, and the x-axis is along the axial length of the submarine. The submarine model constructed using Loop subdivision scheme is shown in Figure 6, which has a total of 19,016 elements.

FIGURE 6

FIGURE 6. The submarine model.

Several calculation points are selected. Figure 7A gives the sound pressure changing with frequency at point (50, 0, 0) and Figure 7B illustrates the changing of its sensitivity to thickness. These two data demonstrate that the lower frequency range, given the existing material and geometrical parameters, is a vital region for this submarine model, as the sound pressure is noticeably greater and more sensitive to thickness there.

FIGURE 7

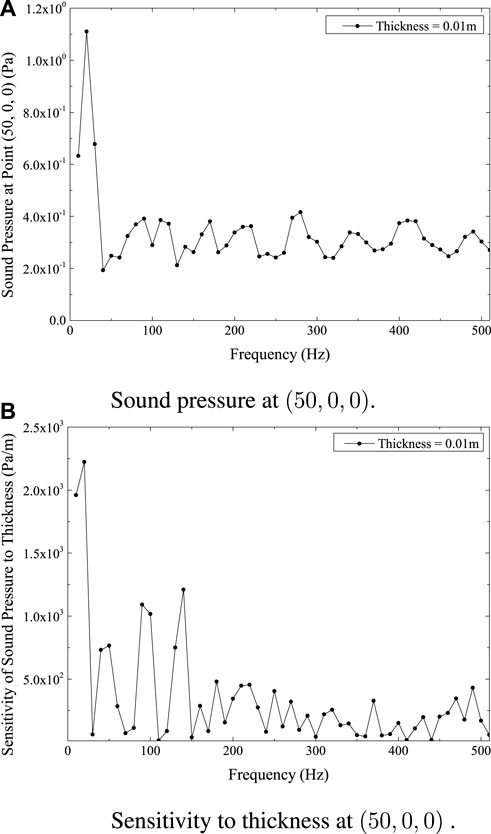
FIGURE 7. Sound pressure and sensitivity at point (50,0,0) for submarine model. (A) Sound pressure at (50,0,0). (B) Sensitivity to thickness at (50,0,0).

The computation of sound pressure at location (100, 0, 0) and (150, 0, 0) is shown in Figures 8A, 9A, respectively. Figures 8B, 9B depicts the sensitivity of sound pressure at point (100, 0, 0) and (150, 0, 0) to shell thickness, respectively. Figures 7A, 8A, 9A show comparable patterns in the sound pressure curves at the places (50, 0, 0), (100, 0, 0), and (150, 0, 0). As seen in Figures 7B, 8B, 9B, the sensitivity of sound pressure at (50, 0, 0), (100, 0, 0), and (150, 0, 0) also demonstrates a similar pattern. Additionally, and in line with predictions, the sound pressure and its sensitivity to thickness both decline with increasing distance from the structure.

FIGURE 8

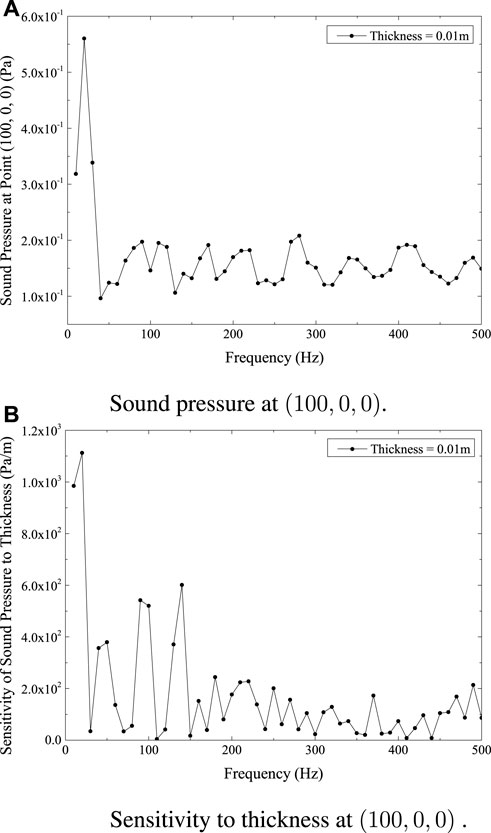
FIGURE 8. Sound pressure and sensitivity at point (100,0,0) for submarine model. (A) Sound pressure at (100,0,0). (B) Sensitivity to thickness at (100,0,0).

FIGURE 9

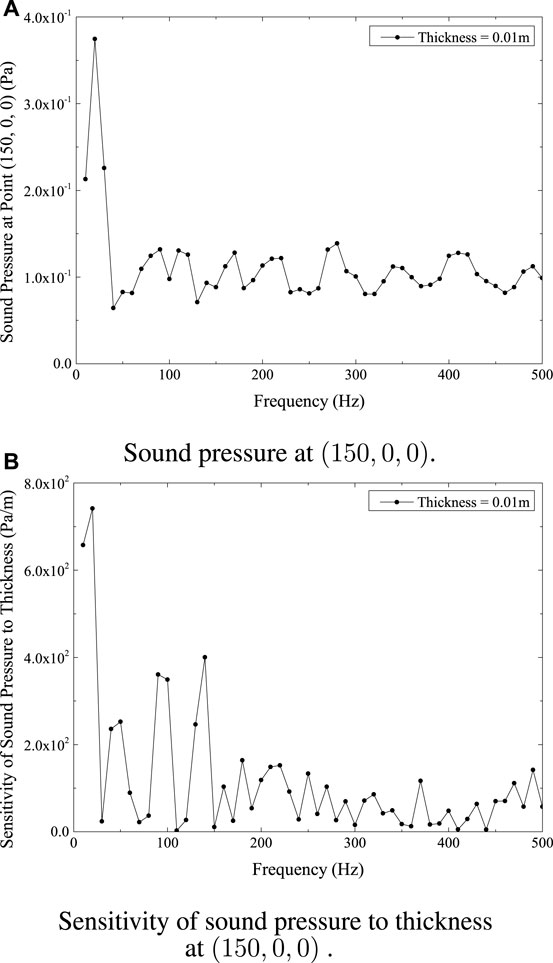
FIGURE 9. Sound pressure and sensitivity at point (150,0,0) for submarine model. (A) Sound pressure at (150,0,0). (B) Sensitivity of sound pressure to thickness at (150,0,0).

5 Conclusion

The simulation of acoustic-structure interaction and sensitivity analysis are conducted using a coupling approach that combines the Finite Element Method (FEM) and Boundary Element Method (BEM). FEM is applied to model structural elements of the issue. To eliminate the need for meshing the acoustic domain, the boundary of the structure being analyzed is discretized using the BEM. FMM is applied to expedite the matrix-vector output. IGABEM enables direct structural-acoustic interaction and sensitivity analysis from CAD models without the requirement for meshing, thereby eliminating any geometric errors. For coupled structural-acoustic systems, equations are derived for the sound pressure sensitivity. To prove the accuracy and practicality of the recommended strategy, calculation examples are given. The recommended method may be used to quantitatively predict how design parameters would affect the sound field in real-world scenarios.

Reduced order isogeometric boundary element methods for CAD-integrated shape optimization of electromagnetic scattering.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XC: Data curation, Formal Analysis, Writing–original draft. YH: Methodology, Resources, Software, Writing–original draft. ZZ: Investigation, Validation, Visualization, Writing–original draft. YX: Conceptualization, Project administration, Supervision, Writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors appreciate the financial support from Henan Provincial Key R&D and Promotion Project under Grant No. 232102220033.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chen L, Zheng C, Chen H, Marburg S. Structural-acoustic sensitivity analysis of radiated sound power using a finite element/discontinuous fast multipole boundary element scheme. Int J Numer Methods Fluids (2016) 82:858–78. doi:10.1002/fld.4244

CrossRef Full Text | Google Scholar

2. Junger MC, Feit D. Sound, structures, and their interaction, 225. Cambridge, MA: MIT press (1986).

Google Scholar

3. Sommerfeld A. Partial differential equations in Physics. Academic Press (1949). doi:10.1016/B978-0-12-654658-3.50003-3

CrossRef Full Text | Google Scholar

4. Engleder O, Steinbach S. Stabilized boundary element methods for exterior Helmholtz problems. Numerische Mathematik (2008) 110:145–60. doi:10.1007/s00211-008-0161-y

CrossRef Full Text | Google Scholar

5. Everstine GC, Henderson FM. Coupled finite element/boundary element approach for fluid-structure interaction. The J Acoust Soc America (1990) 87:1938–1947. doi:10.1121/1.399320

CrossRef Full Text | Google Scholar

6. Fritze D, Marburg S, Hardtke H-J (2005). FEM-BEM-coupling and structural-acoustic sensitivity analysis for shell geometries. Comput Structures 83, 143–54. doi:10.1016/j.compstruc.2004.05.019

CrossRef Full Text | Google Scholar

7. Martinsson P, Rokhlin V. A fast direct solver for boundary integral equations in two dimensions. J Comput Phys (2005) 205:1–23. doi:10.1016/j.jcp.2004.10.033

CrossRef Full Text | Google Scholar

8. Martinsson P, Rokhlin V. A fast direct solver for scattering problems involving elongated structures. J Comput Phys (2007) 221:288–302. doi:10.1016/j.jcp.2006.06.037

CrossRef Full Text | Google Scholar

9. Bebendorf S, Rjasanow M. Adaptive low-rank approximation of collocation matrices. Computing (2003) 70:1–24. doi:10.1007/s00607-002-1469-6

CrossRef Full Text | Google Scholar

10. Greengard L, Rokhlin V. A fast algorithm for particle simulations. J Comput Phys (1987) 73:325–48. doi:10.1016/0021-9991(87)90140-9

CrossRef Full Text | Google Scholar

11. Coifman R, Rokhlin V, Wandzura S. The fast multipole method for the wave equation: a pedestrian prescription. IEEE Antennas Propagation Mag (1993) 35:7–12. doi:10.1109/74.250128

CrossRef Full Text | Google Scholar

12. Rokhlin V. Diagonal forms of translation operators for the Helmholtz equation in three dimensions. Appl Comput Harmonic Anal (1993) 1:82–93. doi:10.1006/acha.1993.1006

CrossRef Full Text | Google Scholar

13. Cheng H, Crutchfield WY, Gimbutas Z, Greengard LF, Ethridge JF, Huang J, et al. A wideband fast multipole method for the Helmholtz equation in three dimensions. J Comput Phys (2006) 216:300–25. doi:10.1016/j.jcp.2005.12.001

CrossRef Full Text | Google Scholar

14. Gumerov NA, Duraiswami R. A broadband fast multipole accelerated boundary element method for the three dimensional Helmholtz equation. J Acoust Soc America (2009) 125:191–205. doi:10.1121/1.3021297

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Takahashi T, Matsumoto T. An application of fast multipole method to isogeometric boundary element method for Laplace equation in two dimensions. Eng Anal Boundary Elem (2012) 36:1766–75. doi:10.1016/j.enganabound.2012.06.004

CrossRef Full Text | Google Scholar

16. Simpson R, Liu Z. Acceleration of isogeometric boundary element analysis through a black-box fast multipole method. Eng Anal Boundary Elem (2016) 66:168–82. doi:10.1016/j.enganabound.2016.03.004

CrossRef Full Text | Google Scholar

17. Chen L, Lian H, Xu Y, Li S, Liu Z, Atroshchenko E, et al. Generalized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Appl Math Model (2023) 114:360–78. doi:10.1016/j.apm.2022.09.030

CrossRef Full Text | Google Scholar

18. Gao H, Chen L, Lian H, Zheng C, Xu H, Matsumoto T. Band structure analysis for 2d acoustic phononic structure using isogeometric boundary element method. Adv Eng Softw (2020) 149:102888. doi:10.1016/j.advengsoft.2020.102888

CrossRef Full Text | Google Scholar

19. Schneider S. FE/FMBE coupling to model fluid-structure interaction. Int J Numer Methods Eng (2008) 76:2137–56. doi:10.1002/nme.2399

CrossRef Full Text | Google Scholar

20. Liu C, Chen L, Zhao W, Chen H. Shape optimization of sound barrier using an isogeometric fast multipole boundary element method in two dimensions. Eng Anal Boundary Elem (2017) 85:142–57. doi:10.1016/j.enganabound.2017.09.009

CrossRef Full Text | Google Scholar

21. Chen L, Zhao J, Li H, Huang Y, Yuan X. A polynomial chaos expansion method for mechanical properties of flexoelectric materials based on the isogeometric finite element method. Sustainability (2023) 15:3417. doi:10.3390/su15043417

CrossRef Full Text | Google Scholar

22. Cao G, Yu B, Chen L, Yao W. Isogeometric dual reciprocity bem for solving non-fourier transient heat transfer problems in fgms with uncertainty analysis. Int J Heat Mass Transfer (2023) 203:123783. doi:10.1016/j.ijheatmasstransfer.2022.123783

CrossRef Full Text | Google Scholar

23. Chen L, Li H, Guo Y, Chen P, Atroshchenko E, Lian H. Uncertainty quantification of mechanical property of piezoelectric materials based on isogeometric stochastic fem with generalized n th-order perturbation. Eng Comput (2023) 1–21. doi:10.1007/s00366-023-01788-w

CrossRef Full Text | Google Scholar

24. Hughes T, Cottrell J, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng (2005) 194:4135–95. doi:10.1016/j.cma.2004.10.008

CrossRef Full Text | Google Scholar

25. Chen L, Lu C, Lian H, Liu Z, Zhao W, Li S, et al. Acoustic topology optimization of sound absorbing materials directly from subdivision surfaces with isogeometric boundary element methods. Comput Methods Appl Mech Eng (2020) 362:112806. doi:10.1016/j.cma.2019.112806

CrossRef Full Text | Google Scholar

26. Shen X, Du C, Jiang S, Sun L, Chen L. Enhancing deep neural networks for multivariate uncertainty analysis of cracked structures by pod-rbf. Theoretical and Applied Fracture Mechanics (2023).103925

CrossRef Full Text | Google Scholar

27. Simpson R, Bordas S, Trevelyan J, Rabczuk T. A two-dimensional isogeometric boundary element method for elastostatic analysis. Comput Methods Appl Mech Eng (2012) 209-212:87–100. doi:10.1016/j.cma.2011.08.008

CrossRef Full Text | Google Scholar

28. Simpson R, Bordas S, Lian H, Trevelyan J (2013). An isogeometric boundary element method for elastostatic analysis: 2D implementation aspects. Comput Structures 118, 2–12. doi:10.1016/j.compstruc.2012.12.021

CrossRef Full Text | Google Scholar

29. Scott M, Simpson R, Evans J, Lipton S, Bordas S, Hughes T, et al. Isogeometric boundary element analysis using unstructured T-splines. Comput Methods Appl Mech Eng (2013) 254:197–221. doi:10.1016/j.cma.2012.11.001

CrossRef Full Text | Google Scholar

30. Liu K, Meng L, Zhao A, Wang Z, Chen L, Li P. A hybrid direct fe2 method for modeling of multiscale materials and structures with strain localization. Comput Methods Appl Mech Eng (2023) 412:116080. doi:10.1016/j.cma.2023.116080

CrossRef Full Text | Google Scholar

31. Ginnis A, Kostas K, Politis C, Kaklis P, Belibassakis K, Gerostathis T, et al. Isogeometric boundary-element analysis for the wave-resistance problem using T-splines. Comput Methods Appl Mech Eng (2014) 279:425–39. doi:10.1016/j.cma.2014.07.001

CrossRef Full Text | Google Scholar

32. Peng X, Atroshchenko E, Kerfriden P, Bordas S. Linear elastic fracture simulation directly from CAD: 2D NURBS-based implementation and role of tip enrichment. Int J Fracture (2017) 204:55–78. doi:10.1007/s10704-016-0153-3

CrossRef Full Text | Google Scholar

33. Peng X, Atroshchenko E, Kerfriden P, Bordas S (2017). Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Comput Methods Appl Mech Eng 316, 151–85. doi:10.1016/j.cma.2016.05.038

CrossRef Full Text | Google Scholar

34. Simpson R, Liu Z, Vázquez R, Evans J. An isogeometric boundary element method for electromagnetic scattering with compatible B-spline discretizations. J Comput Phys (2018) 362:264–89. doi:10.1016/j.jcp.2018.01.025

CrossRef Full Text | Google Scholar

35. Qu Y, Pan E, Zhu F, Jin F, Roy A. Modeling thermoelectric effects in piezoelectric semiconductors: new fully coupled mechanisms for mechanically manipulated heat flux and refrigeration. Int J Eng Sci (2023) 182:103775. doi:10.1016/j.ijengsci.2022.103775

CrossRef Full Text | Google Scholar

36. Qu Y, Zhang G, Gao X, Jin F. A new model for thermally induced redistributions of free carriers in centrosymmetric flexoelectric semiconductor beams. Mech Mater (2022) 171:104328. doi:10.1016/j.mechmat.2022.104328

CrossRef Full Text | Google Scholar

37. Qu Y, Jin F, Yang J. Temperature effects on mobile charges in thermopiezoelectric semiconductor plates. Int J Appl Mech (2021) 13:2150037. doi:10.1142/s175882512150037x

CrossRef Full Text | Google Scholar

38. Xu Y, Li H, Chen L, Zhao J, Zhang X. Monte Carlo based isogeometric stochastic finite element method for uncertainty quantization in vibration analysis of piezoelectric materials. Mathematics (2022) 10:1840. doi:10.3390/math10111840

CrossRef Full Text | Google Scholar

39. Chen L, Wang Z, Ma Y, Lian H, Meng Z, Li P, et al. Reduced order isogeometric boundary element methods for CAD-integrated shape optimization in electromagnetic scattering. Comput Methods Appl Mech Eng (2023) 419:116654. doi:10.1016/j.cma.2023.116654

CrossRef Full Text | Google Scholar

40. Bandara K, Cirak F, Of G, Steinbach O, Zapletal J. Boundary element based multiresolution shape optimisation in electrostatics. J Comput Phys (2015) 297:584–98. doi:10.1016/j.jcp.2015.05.017

CrossRef Full Text | Google Scholar

41. Kostas K, Ginnis A, Politis C, Kaklis P (2015). Ship-hull shape optimization with a T-spline based BEM-isogeometric solver. Comput Methods Appl Mech Eng 284, 611–22. doi:10.1016/j.cma.2014.10.030

CrossRef Full Text | Google Scholar

42. Lian H, Kerfriden P, Bordas S. Shape optimization directly from CAD: an isogeometric boundary element approach using T-splines. Comput Methods Appl Mech Eng (2017) 317:1–41. doi:10.1016/j.cma.2016.11.012

CrossRef Full Text | Google Scholar

43. Xu G, Li M, Mourrain B, Rabczuk T, Xu J, Bordas SP. Constructing IGA-suitable planar parameterization from complex CAD boundary by domain partition and global/local optimization. Comput Methods Appl Mech Eng (2018) 328:175–200. doi:10.1016/j.cma.2017.08.052

CrossRef Full Text | Google Scholar

44. Li S, Trevelyan J, Zhang W, Wang D. Accelerating isogeometric boundary element analysis for 3-dimensional elastostatics problems through black-box fast multipole method with proper generalized decomposition. Int J Numer Methods Eng (2018) 114:975–98. doi:10.1002/nme.5773

CrossRef Full Text | Google Scholar

45. Li S, Trevelyan J, Wu Z, Lian H, Wang D, Zhang W. An adaptive SVD-Krylov reduced order model for surrogate based structural shape optimization through isogeometric boundary element method. Comput Methods Appl Mech Eng (2019) 349:312–38. doi:10.1016/j.cma.2019.02.023

CrossRef Full Text | Google Scholar

46. Lian H, Chen L, Lin X, Zhao W, Bordas SPA, Zhou M. Noise pollution reduction through a novel optimization procedure in passive control methods. Comput Model Eng Sci (2022) 131:1–18. doi:10.32604/cmes.2022.019705

CrossRef Full Text | Google Scholar

47. Simpson R, Scott M, Taus M, Thomas D, Lian H. Acoustic isogeometric boundary element analysis. Comput Methods Appl Mech Eng (2014) 269:265–90. doi:10.1016/j.cma.2013.10.026

CrossRef Full Text | Google Scholar

48. Chen L, Lian H, Liu Z, Chen H, Atroshchenko E, Bordas S. Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Comput Methods Appl Mech Eng (2019) 355:926–51. doi:10.1016/j.cma.2019.06.012

CrossRef Full Text | Google Scholar

49. Chen L, Lian H, Natarajan S, Zhao W, Chen X, Bordas S. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comput Methods Appl Mech Eng (2022) 395:114997. doi:10.1016/j.cma.2022.114997

CrossRef Full Text | Google Scholar

50. Chen L, Wang Z, Peng X, Yang J, Wu P, Lian H. Modeling pressurized fracture propagation with the isogeometric bem. Geomechanics Geophys Geo-Energy Geo-Resources (2021) 7:51. doi:10.1007/s40948-021-00248-3

CrossRef Full Text | Google Scholar

51. Burkhart D, Hamann B, Umlauf G. Iso-geometric finite element analysis based on catmull-clark: subdivision solids. Comput Graphics Forum (2010) 29:1575–84. doi:10.1111/j.1467-8659.2010.01766.x

CrossRef Full Text | Google Scholar

52. Wei X, Zhang Y, Hughes TJ, Scott MA. Truncated hierarchical Catmull-Clark subdivision with local refinement. Comput Methods Appl Mech Eng (2015) 291:1–20. doi:10.1016/j.cma.2015.03.019

CrossRef Full Text | Google Scholar

53. Wawrzinek A, Polthier K. Integration of generalized B-spline functions on Catmull-Clark surfaces at singularities. Computer-Aided Des (2016) 78:60–70. doi:10.1016/j.cad.2016.05.008

CrossRef Full Text | Google Scholar

54. Pan Q, Xu G, Xu G, Zhang Y. Isogeometric analysis based on extended Catmull-Clark subdivision. Comput Maths Appl (2016) 71:105–19. doi:10.1016/j.camwa.2015.11.012

CrossRef Full Text | Google Scholar

55. Bandara K, Rüberg T, Cirak F. Shape optimisation with multiresolution subdivision surfaces and immersed finite elements. Comput Methods Appl Mech Eng (2016) 300:510–39. doi:10.1016/j.cma.2015.11.015

CrossRef Full Text | Google Scholar

56. Bandara K, Cirak F. Isogeometric shape optimisation of shell structures using multiresolution subdivision surfaces. Computer-Aided Des (2018) 95:62–71. doi:10.1016/j.cad.2017.09.006

CrossRef Full Text | Google Scholar

57. Liu Z, Majeed M, Cirak F, Simpson NR. Isogeometric FEM-BEM coupled structural-acoustic analysis of shells using subdivision surfaces. Int J Numer Methods Eng (2018) 113:1507–30. doi:10.1002/nme.5708

CrossRef Full Text | Google Scholar

58. Chen L, Marburg S, Chen H, Zhang H, Gao H. An adjoint operator approach for sensitivity analysis of radiated sound power in fully coupled structural-acoustic systems. J Comput Acoust (2017) 25:1750003. doi:10.1142/s0218396x17500035

CrossRef Full Text | Google Scholar

59. Chen L, Cheng R, Li S, Lian H, Zheng C, Bordas S. A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic-vibration interaction problems. Comput Methods Appl Mech Eng (2022) 393:114784. doi:10.1016/j.cma.2022.114784

CrossRef Full Text | Google Scholar

60. Chen L, Liu C, Zhao W, Liu L. An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Comput Methods Appl Mech Eng (2018) 336:507–32. doi:10.1016/j.cma.2018.03.025

CrossRef Full Text | Google Scholar

61. Zhao W, Chen L, Chen H, Marburg S. An effective approach for topological design to the acoustic–structure interaction systems with infinite acoustic domain. Struct Multidisciplinary Optimization (2020) 62:1253–73. doi:10.1007/s00158-020-02550-2

CrossRef Full Text | Google Scholar

62. Chen L, Marburg S, Zhao W, Liu C, Chen H. Implementation of isogeometric fast multipole boundary element methods for 2d half-space acoustic scattering problems with absorbing boundary condition. J Theor Comput Acoust (2019) 27:1850024. doi:10.1142/s259172851850024x

CrossRef Full Text | Google Scholar

63. Chen L, Zhao J, Lian H, Yu B, Atroshchenko E, Li P. A bem broadband topology optimization strategy based on taylor expansion and soar method—application to 2d acoustic scattering problems. Int J Numer Methods Eng (2023) 124:5151–82. doi:10.1002/nme.7345

CrossRef Full Text | Google Scholar

64. Kim NH, Dong J. Shape sensitivity analysis of sequential structural-acoustic problems using FEM and BEM. J Sound Vibration (2006) 290:192–208. doi:10.1016/j.jsv.2005.03.013

CrossRef Full Text | Google Scholar

65. Marburg S. Developments in structural-acoustic optimization for passive noise control. Arch Comput Methods Eng (2002) 9:291–370. doi:10.1007/BF03041465

CrossRef Full Text | Google Scholar

66. Lamancusa J. Numerical optimization techniques for structural-acoustic design of rectangular panels. Comput Structures (1993) 48:661–75. doi:10.1016/0045-7949(93)90260-K

CrossRef Full Text | Google Scholar

67. Hambric SA. Sensitivity calculations for broad-band acoustic radiated noise design optimization problems. J Vibration Acoust (1996) 118:529–32. doi:10.1115/1.2888219

CrossRef Full Text | Google Scholar

68. Marburg S, Hardtke H-J. Shape optimization of a vehicle hat-shelf: improving acoustic properties for different load cases by maximizing first eigenfrequency. Comput Structures (2001) 79:1943–57. doi:10.1016/S0045-7949(01)00107-9

CrossRef Full Text | Google Scholar

69. Zhao W, Chen L, Chen H, Marburg S. Topology optimization of exterior acoustic-structure interaction systems using the coupled fem-bem method. Int J Numer Methods Eng (2019) 119:404–31. doi:10.1002/nme.6055

CrossRef Full Text | Google Scholar

70. Choi K, Shim I, Wang S. Design sensitivity analysis of structure-induced noise and vibration. J Vibration Acoust (1997) 119:173–9. doi:10.1115/1.2889699

CrossRef Full Text | Google Scholar

71. Wang S. Design sensitivity analysis of noise, vibration, and harshness of vehicle body structure. Mech Structures Machines (1999) 27:317–35. doi:10.1080/08905459908915701

CrossRef Full Text | Google Scholar

72. Zheng C, Matsumoto T, Takahashi T, Chen H. Explicit evaluation of hypersingular boundary integral equations for acoustic sensitivity analysis based on direct differentiation method. Eng Anal Boundary Elem (2011) 35:1225–35. doi:10.1016/j.enganabound.2011.05.004

CrossRef Full Text | Google Scholar

73. Schröder P. Subdivision for modeling and animation. In: Acm siggraph 1998 (1998).

Google Scholar

74. Cirak F, Ortiz M, Schröder P (2000). Subdivision surfaces: a new paradigm for thin-shell finite-element analysis. Int J Numer Methods Eng 47, 2039–72. doi:10.1002/(SICI)1097-0207(20000430)47:12¡2039::AID-NME872¿3.0.CO;2–1

CrossRef Full Text | Google Scholar

75. Burton AJ, Miller GF. The application of integral equation methods to the numerical solution of some exterior boundary-value problems. Proc R Soc Lond (1971) 323:201–10. doi:10.1098/rspa.1971.0097

CrossRef Full Text | Google Scholar

76. Ciskowski RD, Brebbia CA. Boundary element methods in acoustics. Springer (1991).

Google Scholar

77. Chen L, Lian H, Liu Z, Gong Y, Zheng C, Bordas S. Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric FEM-BEM. Eng Anal Boundary Elem (2022) 135:182–95. doi:10.1016/j.enganabound.2021.11.005

CrossRef Full Text | Google Scholar

78. Chen L, Lu C, Zhao W, Chen H, Zheng C. Subdivision surfaces - boundary element accelerated by fast multipole for the structural acoustic problem. J Theor Comput Acoust (2020) 28:2050011. doi:10.1142/S2591728520500115

CrossRef Full Text | Google Scholar