- 1Institute for Theoretical Physics, University of Göttingen, Göttingen, Germany
- 2Third Institute of Physics, University of Göttingen, Göttingen, Germany
We derive a bound for entropy production in terms of the mean of normalizable path-antisymmetric observables. The optimal observable for this bound is shown to be the signum of entropy production, which is often easier determined or estimated than entropy production itself. It can be preserved under coarse graining by the use of a simple path grouping algorithm. We demonstrate this relation and its properties using a driven network on a ring, for which the bound saturates for short times for any driving strength. This work can open a way to systematic coarse graining of entropy production.
1 Introduction
A common way of analyzing complex systems is observation of particle trajectories, e.g., via microscopy [1–3] in biological systems [4–8] or complex fluids [9, 10]. Detecting and quantifying the deviation from equilibrium, i.e., the violation of detailed balance, based on trajectories is, however, a challenging task, especially if relevant degrees of freedom are hidden, and non-equilibrium processes are random [11–17]. Several methods for such detection have been developed.
The fluctuation dissipation theorem (FDT) connects fluctuations and response functions [18], and it is violated out of equilibrium [19–21]. How far away from equilibrium a system is, e.g., has been quantified by using the so-called effective temperatures or effective energies [22–27].
Another way of detecting broken detailed balance is via entropy production, which has been found to obey a variety of theorems including the fluctuation theorems [28–31]. A number of important relations have been found that bound entropy production, such as the thermodynamic uncertainty relation (TUR) [32–38]. The TUR bounds mean and variance of currents by entropy production or vice versa. It has been extended and refined, including path antisymmetric observables (FTUR) or to more general path weights [39–42] and has been applied to experiments and numerical data [43–46]. Little is, however, known about how bounds behave under coarse graining.
In this paper, we derive an entropy bound in terms of the mean of path-antisymmetric observables, based on an integrated fluctuation theorem. In contrast to the TUR and FTUR, it does not involve the variance of the observable. We determine the optimal observable, i.e., the observable that maximizes the bound, to be the signum of entropy production so that a relation between entropy production and its sign appears. As this relation saturates for a binary process at short times, we argue that no better relation between entropy production and its sign can exist with the same range of validity. The sign of entropy production, and hence the bound for entropy production, can be preserved under coarse graining with a simple path grouping rule. We apply these results for a discrete network on a ring. For this network, the signum of entropy production is coarse-grained under preservation to the signum of the traveled distance, demonstrating how a bound for microscopic entropy production is obtained from a macroscopic observable. Under such coarse graining, entropy production can at most reduce to the original bound.
2 Setup and fluctuation theorem
A path observable
We introduced notation for path reversal, θω, including reversal of time and of kinematic reversal of momenta [49]. Validity of Eq. 1 requires the sum of paths to include θω for any included ω. Adding a zero yields
where the term
With detailed balance obeyed, i.e., p[ω] = p[θω], antisymmetric observables average to zero, and
Violations of Eq. 4, thus, indicate the breakage of detailed balance [50, 51]. Although the symmetric part O+ does not appear in the final result, Eq. 12 below, for the derivation, it is useful to start with O+ finite.
To quantify the path reversal properties of cases that break detailed balance, we introduce the stochastic change in entropy defined as the log ratio of path probabilities (kB = 1) [52–54].
For simplicity, we will, in the following, refer to s as the entropy production despite some caveats regarding this term1. The thermodynamic relevance of s is a topic of its own, which has been discussed in various works [52–54]. Substituting s into Eq. 2 yields
Reordering the terms yields a fluctuation theorem including O:
Equation 7 may be found equivalently from the so-called strong detailed fluctuation theorem [48] and has been stated in the similar form [50].
3 Entropy bound
Equation 7 can be used to find bounds for s, and we, therefore, restrict to positive observables, O[ω] ≥ 0. This allows Jensen’s inequality [55, 56] to be applied for the average
As expected from Jensen’s inequality, Eq. 8 saturates for small s, as seen by expanding it in this limit,
Taking the logarithm of Eq. 8 yields a lower bound for the correlation
Because the conjugate observable O*[ω] = O[θω] is non-negative if O is non-negative, Eq. 10 is also valid for O*. The bounds for
Notably, when adding Eq. 10 for
A direct way to extract a bound for
Equation 12 is a main result of this paper, a bound for entropy production
The condition of
Equation 12 can be read in the following two ways: (i) a given
The form of Eq. 12 is illustrated in Figure 1. For small
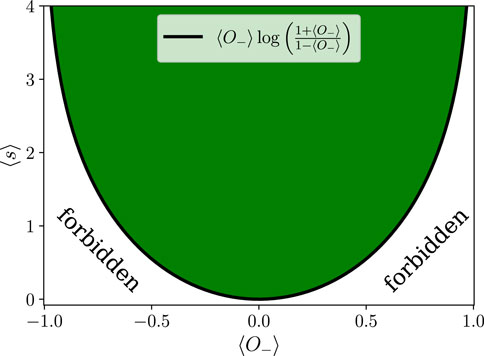
FIGURE 1. Illustration of Eq. 12 in terms of antisymmetric observable
4 Optimal observable: signum of entropy
Equation 12, as mentioned, is valid for any normalizable antisymmetric observable, and, naturally, the observable that maximizes the right hand side of it yields the best estimate for
In the second step, we used the anti-symmetry of O−. The inequality in the last step of Eq. 13 follows by noting that the sum is maximized if O−[ω] = 1 for p[ω] > p[θω] and O−[ω] = −1 for p[ω] < p[θω]. This is the definition of O− = sign(s)4.
As the right hand side of Eq. 12 is a monotonically growing function of
The first inequality of Eq. 14 bounds
5 Coarse graining
A bound of
Coarse graining, thus, leads, in general, to a decrease in
Under this “optimal” (index o) coarse graining, the bound provided by sign(s) is invariant so that the macroscopic
6 Example: network on a ring
To display this in an example, consider a network on a ring, where every state is connected to two neighbors (see inset sketch of Figure 2). In every discrete time step, a particle jumps to the left (right) with probability p (q). For q ≠ p, the system violates detailed balance and shows a directed flow. After N steps, the probability of finding a specific path with nL steps to the left is given by the binomial distribution
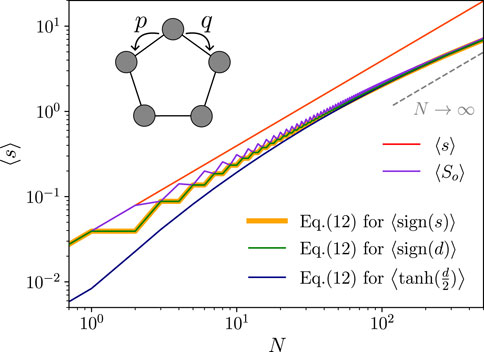
FIGURE 2. Network on a ring model: entropy production
Optimal coarse graining can be performed here in a straightforward manner: because s = d log(p/q), the sign of entropy production equals the sign of d = nL − nR (for p > q), with nR being the number of steps to the right, i.e., sign(d[ω]) = sign(s[ω]). This system, thus, allows coarse graining toward the measurement of the net displacement d, under preservation of the bound. We may expect that d is easier to measure than s.
Having established that Eq. 12 is maximal for O− = sign(d[ω]), we can test the quality of the estimate for
For N = 1, the bound of Eq. 12, thus, meets entropy production exactly, for any p and q, i.e., arbitrarily far from equilibrium. This is the abovementioned case of the binary process, where a particle either jumps right or left.
Figure 2 shows
i.e.,
Coarse graining groups paths according to their displacement, i.e., Ω for d > 0 and θΩ for d < 0. This way, the coarse-grained entropy
Notably, the bound shown in Eq. 12 is saturated with respect to So for odd N, as indicated. For N even, paths with zero entropy production exist, and the second equality shown in Eq. 21 is not valid, and Eq. 12 lies below
According to Eq. 13, any other normalizable antisymmetric observable should yield a lower bound, which we exemplify by using O− = tanh(d/2). Indeed, it lies lower but approaches the optimal bound for large N because then, a typical trajectory shows d ≫ 1 so that tanh(d/2) becomes equivalent to sign(d).
Although optimal coarse graining is possible in an exact manner in this model, we expect an approximate preservation of sign(s) to be possible in more complicated systems, which will be investigated in future works.
Can we compare to other relations such as TUR? The original TUR is not applicable to time-discrete dynamics, as used in this example. We, thus, compare to the so-called FTUR [40], as shown in Figure 3. Not knowing the optimal observable for FTUR, we use sign(s) and s, analytically computing the required variances for these two. Interestingly, for each of the three curves shown in the figure, there exists a regime of N, where it provides the highest estimate. It is also remarkable that FTUR used with sign(s) can provide a better estimate compared to using s. This shows the advantage of Eq. 17, for which the optimal observable is known, leading to the coarse-graining scheme. It also shows that the comparison between these relations is rich and non-trivial and needs to be studied in future works.
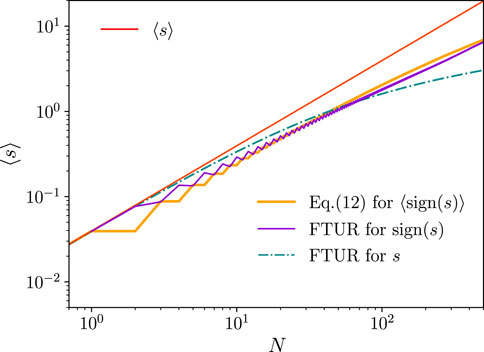
FIGURE 3. Network on a ring model, with identical parameters as shown in Figure 2, here focusing on the comparison to FTUR. FTUR is used with two different observables as indicated, sign(s) or s. For large N, Eq. 12 and FTUR for the sign(s) scale linearly in N, while FTUR for s scales with log(N).
7 Discussion
Entropy production is bound by the mean of normalizable antisymmetric observables. The optimal observable is identified to be the signum of entropy production so that we determine a bound between entropy production and its sign, sign(s). The latter may often be estimated from simple observables, like here, the displacement on a ring. The network example shows that measuring sign(s) (did the particle move left or right?) is expected to require a lower experimental resolution compared to measuring s (where did the particle move when?). One can also estimate ⟨sign(s)⟩ by the use of Eq. (13), i.e., by testing various observables O− and finding the maximum deviation from zero. For the investigated network,
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
GK: writing–original draft. TM: writing–review and editing. TB: writing–review and editing. MK: writing–original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors thank É. Fodor for a critical reading of the paper and Peter Sollich and Cai Dieball for insightful discussions. The authors acknowledge support by the Open Access Publication Funds of the Göttingen University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1The entropy defined in Eq. 5 corresponds to the total change in entropy in overdamped stationary systems. In underdamped or non-stationary systems, the boundary terms differ [54].
2A similar relation was derived in [57], however, with the left hand side always negative.
3Eq. 13 holds also for −O− and thus for
4The terms with p[ω] = p[θω] cancel in the sum in Eq. 13 due to O−[ω] = −O−[θω], and O−[ω] can be chosen arbitrarily in these cases.
References
1. Squires TM, Mason TG. Fluid mechanics of microrheology. Annu Rev Fluid Mech (2010) 42:413–38. doi:10.1146/annurev-fluid-121108-145608
2. Zia RN. Active and passive microrheology: theory and simulation. Annu Rev Fluid Mech (2018) 50:371–405. doi:10.1146/annurev-fluid-122316-044514
3. Bustamante CJ, Chemla YR, Liu S, Wang MD. Optical tweezers in single-molecule biophysics. Nat Rev Methods Primers (2021) 1:25. doi:10.1038/s43586-021-00021-6
4. Fang X, Wang J. Nonequilibrium thermodynamics in cell biology: extending equilibrium formalism to cover living systems. Annu Rev Biophys (2020) 49:227–46. doi:10.1146/annurev-biophys-121219-081656
5. Andrieux D, Gaspard P. Fluctuation theorems and the nonequilibrium thermodynamics of molecular motors. Phys Rev E (2006) 74:011906. doi:10.1103/PhysRevE.74.011906
6. Ahmed WW, Fodor É, Betz T. Active cell mechanics: measurement and theory. Biochim Biophys Acta (Bba) - Mol Cel Res (2015) 1853:3083–94. doi:10.1016/j.bbamcr.2015.05.022
7. Gladrow J, Broedersz CP, Schmidt CF. Nonequilibrium dynamics of probe filaments in actin-myosin networks. Phys Rev E (2017) 96:022408. doi:10.1103/PhysRevE.96.022408
8. Hurst S, Vos BE, Brandt M, Betz T. Intracellular softening and increased viscoelastic fluidity during division. Nat Phys (2021) 17:1270–6. doi:10.1038/s41567-021-01368-z
9. Mason TG, Weitz DA. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys Rev Lett (1995) 74:1250–3. doi:10.1103/PhysRevLett.74.1250
10. Ginot F, Caspers J, Krüger M, Bechinger C. Barrier crossing in a viscoelastic bath. Phys Rev Lett (2022) 128:028001. doi:10.1103/PhysRevLett.128.028001
11. Roldán É, Parrondo JMR. Estimating dissipation from single stationary trajectories. Phys Rev Lett (2010) 105:150607. doi:10.1103/PhysRevLett.105.150607
12. Mehl J, Lander B, Bechinger C, Blickle V, Seifert U. Role of hidden slow degrees of freedom in the fluctuation theorem. Phys Rev Lett (2012) 108:220601. doi:10.1103/PhysRevLett.108.220601
13. Basu U, Helden L, Krüger M. Extrapolation to nonequilibrium from coarse-grained response theory. Phys Rev Lett (2018) 120:180604. doi:10.1103/PhysRevLett.120.180604
14. Kahlen M, Ehrich J. Hidden slow degrees of freedom and fluctuation theorems: an analytically solvable model. J Stat Mech Theor Exp (2018) 2018:063204. doi:10.1088/1742-5468/aac2fd
15. Martínez IA, Bisker G, Horowitz JM, Parrondo JMR. Inferring broken detailed balance in the absence of observable currents. Nat Commun (2019) 10:3542. doi:10.1038/s41467-019-11051-w
16. Dieball C, Godec A. Coarse graining empirical densities and currents in continuous-space steady states. Phys Rev Res (2022) 4:033243. doi:10.1103/PhysRevResearch.4.033243
17. van der Meer J, Ertel B, Seifert U. Thermodynamic inference in partially accessible markov networks: a unifying perspective from transition-based waiting time distributions. Phys Rev X (2022) 12:031025. doi:10.1103/PhysRevX.12.031025
18. Kubo R. The fluctuation-dissipation theorem. Rep Prog Phys (1966) 29:255–84. doi:10.1088/0034-4885/29/1/306
19. Agarwal GS. Fluctuation-dissipation theorems for systems in non-thermal equilibrium and applications. Z für Physik A Hadrons nuclei (1972) 252:25–38. doi:10.1007/BF01391621
20. Speck T, Seifert U. Restoring a fluctuation-dissipation theorem in a nonequilibrium steady state. Europhysics Lett (Epl) (2006) 74:391–6. doi:10.1209/epl/i2005-10549-4
21. Baiesi M, Maes C, Wynants B. Fluctuations and response of nonequilibrium states. Phys Rev Lett (2009) 103:010602. doi:10.1103/PhysRevLett.103.010602
22. Martin P, Hudspeth AJ, Jülicher F. Comparison of a hair bundle’s spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process. Proc Natl Acad Sci (2001) 98:14380–5. doi:10.1073/pnas.251530598
23. Harada T, Si S. Equality connecting energy dissipation with a violation of the fluctuation-response relation. Phys Rev Lett (2005) 95:130602. doi:10.1103/PhysRevLett.95.130602
24. Toyabe S, Okamoto T, Watanabe-Nakayama T, Taketani H, Kudo S, Muneyuki E. Nonequilibrium energetics of a single F 1 -ATPase molecule. Phys Rev Lett (2010) 104:198103. doi:10.1103/PhysRevLett.104.198103
25. Krüger M, Fuchs M. Fluctuation dissipation relations in stationary states of interacting brownian particles under shear. Phys Rev Lett (2009) 102:135701. doi:10.1103/PhysRevLett.102.135701
26. Ahmed WW, Fodor É, Almonacid M, Bussonnier M, Verlhac MH, Gov N, et al. Active mechanics reveal molecular-scale force kinetics in living oocytes. Biophysical J (2018) 114:1667–79. doi:10.1016/j.bpj.2018.02.009
27. Muenker TM, Knotz G, Krüger M, Betz T. Onsager regression characterizes living systems in passive measurements (2022). bioRxiv. doi:10.1101/2022.05.15.491928
28. Jarzynski C. Nonequilibrium equality for free energy differences. Phys Rev Lett (1997) 78:2690–3. doi:10.1103/PhysRevLett.78.2690
29. Crooks GE. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys Rev E (1999) 60:2721–6. doi:10.1103/PhysRevE.60.2721
30. Speck T, Seifert U. The jarzynski relation, fluctuation theorems, and stochastic thermodynamics for non-markovian processes. J Stat Mech Theor Exp (2007) 2007:L09002. doi:10.1088/1742-5468/2007/09/L09002
31. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys (2012) 75:126001. doi:10.1088/0034-4885/75/12/126001
32. Barato AC, Seifert U. Thermodynamic uncertainty relation for biomolecular processes. Phys Rev Lett (2015) 114:158101. doi:10.1103/PhysRevLett.114.158101
33. Horowitz JM, Gingrich TR. Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nat Phys (2020) 16:15–20. doi:10.1038/s41567-019-0702-6
34. Van Vu T, Vo VT, Hasegawa Y. Entropy production estimation with optimal current. Phys Rev E (2020) 101:042138. doi:10.1103/PhysRevE.101.042138
35. Dechant A, Si S. Improving thermodynamic bounds using correlations. Phys Rev X (2021) 11:041061. doi:10.1103/PhysRevX.11.041061
36. Pietzonka P. Classical pendulum clocks break the thermodynamic uncertainty relation. Phys Rev Lett (2022) 128:130606. doi:10.1103/PhysRevLett.128.130606
37. Cao Z, Su J, Jiang H, Hou Z. Effective entropy production and thermodynamic uncertainty relation of active Brownian particles. Phys Fluids (2022) 34:053310. doi:10.1063/5.0094211
38. Koyuk T, Seifert U. Thermodynamic uncertainty relation in interacting many-body systems. Phys Rev Lett (2022) 129:210603. doi:10.1103/PhysRevLett.129.210603
39. Dechant A, Si S. Current fluctuations and transport efficiency for general Langevin systems. J Stat Mech Theor Exp (2018) 2018:063209. doi:10.1088/1742-5468/aac91a
40. Hasegawa Y, Van Vu T. Fluctuation theorem uncertainty relation. Phys Rev Lett (2019) 123:110602. doi:10.1103/PhysRevLett.123.110602
41. Dechant A, Si S. Fluctuation–response inequality out of equilibrium. Proc Natl Acad Sci (2020) 117:6430–6. doi:10.1073/pnas.1918386117
42. Ziyin L, Ueda M. Universal thermodynamic uncertainty relation in nonequilibrium dynamics. Phys Rev Res (2023) 5:013039. doi:10.1103/PhysRevResearch.5.013039
43. Li J, Horowitz JM, Gingrich TR, Fakhri N. Quantifying dissipation using fluctuating currents. Nat Commun (2019) 10:1666. doi:10.1038/s41467-019-09631-x
44. Manikandan SK, Ghosh S, Kundu A, Das B, Agrawal V, Mitra D, et al. Quantitative analysis of non-equilibrium systems from short-time experimental data. Commun Phys (2021) 4:258. doi:10.1038/s42005-021-00766-2
45. Otsubo S, Manikandan SK, Sagawa T, Krishnamurthy S. Estimating time-dependent entropy production from non-equilibrium trajectories. Commun Phys (2022) 5:11–0. doi:10.1038/s42005-021-00787-x
46. Roldán Barral J, Martin P, Parrondo JMR, Jülicher F, Jülicher F. Quantifying entropy production in active fluctuations of the hair-cell bundle from time irreversibility and uncertainty relations. New J Phys (2021) 23:083013. doi:10.1088/1367-2630/ac0f18
47. Altland A, Simons BD. Condensed matter field theory. 2 edn. Cambridge: Cambridge University Press (2010). doi:10.1017/CBO9780511789984
48. García-García R, Domínguez D, Lecomte V, Kolton AB. Unifying approach for fluctuation theorems from joint probability distributions. Phys Rev E (2010) 82:030104. doi:10.1103/PhysRevE.82.030104
49. Spinney RE, Ford IJ. Entropy production in full phase space for continuous stochastic dynamics. Phys Rev E (2012) 85:051113. doi:10.1103/PhysRevE.85.051113
50. Harris RJ, Schütz GM. Fluctuation theorems for stochastic dynamics. J Stat Mech Theor Exp (2007) 2007:P07020. doi:10.1088/1742-5468/2007/07/P07020
51. Zia RKP, Schmittmann B. Probability currents as principal characteristics in the statistical mechanics of non-equilibrium steady states. J Stat Mech Theor Exp (2007) 2007:P07012. doi:10.1088/1742-5468/2007/07/P07012
52. Maes C, Netočný K. Time-reversal and entropy. J Stat Phys (2003) 110:269–310. doi:10.1023/A:1021026930129
53. Seifert U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys Rev Lett (2005) 95:040602. doi:10.1103/PhysRevLett.95.040602
54. Fischer LP, Chun HM, Seifert U. Free diffusion bounds the precision of currents in underdamped dynamics. Phys Rev E (2020) 102:012120. doi:10.1103/PhysRevE.102.012120
55. Jensen JLWV. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Mathematica (1906) 30:175–93. doi:10.1007/BF02418571
56. Durrett R. Cambridge series in statistical and probabilistic mathematics. 5 edn. Cambridge, England: Cambridge University Press (2019).Probability:Theory and examples
57. Merhav N, Kafri Y. Statistical properties of entropy production derived from fluctuation theorems. J Stat Mech Theor Exp (2010) 2010:P12022. doi:10.1088/1742-5468/2010/12/P12022
58. Shiraishi N. Optimal thermodynamic uncertainty relation in markov jump processes. J Stat Phys (2021) 185:19. doi:10.1007/s10955-021-02829-8
59. Dieball C, Godec A. Direct route to thermodynamic uncertainty relations and their saturation. Phys Rev Lett (2023) 130:087101. doi:10.1103/PhysRevLett.130.087101
60. Seifert U. From stochastic thermodynamics to thermodynamic inference. Annu Rev Condensed Matter Phys (2019) 10:171–92. doi:10.1146/annurev-conmatphys-031218-013554
61. Arratia R, Gordon L. Tutorial on large deviations for the binomial distribution. Bull Math Biol (1989) 51:125–31. doi:10.1007/BF02458840
62. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active particles in complex and crowded environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/RevModPhys.88.045006
63. Esposito M, Harbola U, Mukamel S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev Mod Phys (2009) 81:1665–702. doi:10.1103/RevModPhys.81.1665
64. Landi GT, Paternostro M. Irreversible entropy production: from classical to quantum. Rev Mod Phys (2021) 93:035008. doi:10.1103/RevModPhys.93.035008
Keywords: entropy production, statistical physics, non-equilibrium, fluctuation theorems, coarse graining, detailed balance breakage
Citation: Knotz G, Muenker TM, Betz T and Krüger M (2024) Entropy bound for time reversal markers. Front. Phys. 11:1331835. doi: 10.3389/fphy.2023.1331835
Received: 01 November 2023; Accepted: 19 December 2023;
Published: 02 February 2024.
Edited by:
Juan Manuel López, Spanish National Research Council (CSIC), SpainReviewed by:
Ayan Banerjee, Indian Institute of Science Education and Research Kolkata, IndiaBiswajit Das, Indian Institute of Science Education and Research Kolkata, India, in collaboration with reviewer [AB]
Miguel Rubi, University of Barcelona, Spain
Copyright © 2024 Knotz, Muenker, Betz and Krüger. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gabriel Knotz, Zy5rbm90ekB0aGVvcmllLnBoeXNpay51bmktZ29ldHRpbmdlbi5kZQ==
 Gabriel Knotz
Gabriel Knotz Till Moritz Muenker2
Till Moritz Muenker2 Timo Betz
Timo Betz