Data-limited and imbalanced bladder wall segmentation with confidence map-guided residual networks via transfer learning

Purpose: To develop an algorithm using a residual base network guided by the confidence map and transfer learning for limited dataset size and imbalanced bladder wall segmentation.

Methods: The geometric transformation was made to the training data for data augmentation, and a pre-trained Resnet50 model on ImageNet was also adopted for transfer learning. Three loss functions were put into the pre-trained Resnet50 network, they are the cross-entropy loss function (CELF), the generalized Dice loss function (GDLF) and the Tversky loss function (TLF). Three models were obtained through training, and three corresponding confidence maps were output after entering a new image. By selecting the point with the maximum confidence values at the corresponding position, we merged the three images into one figure, performed threshold filtering to avoid external anomalies, and finally obtained the segmentation result.

Results: The average Jaccard similarity coefficient of model training based on the CELF, GDLF and TLF is 0.9173, 0.8355, 0.8757, respectively, and the average Jaccard similarity coefficient of our algorithm can be achieved at 0.9282. In contrast, the classical 2D U-Net algorithm can only achieve 0.518. We also qualitatively give the reasons for the improvement of model performance.

Conclusion: Our study demonstrates that a confidence map-assisted residual base network can accurately segment bladder walls on a limited-size data set. Compared with the segmentation results of each model alone, our method originally improves the accuracy of the segmentation results by combining confidence map guidance with threshold filtering.

Introduction

With the rapid development of computer and medical accelerator technology, radiotherapy plays a more and more important role in cancer treatment, including the pelvic cancers of cervical cancer, endometrial cancer, prostate cancer and rectal cancer. With the continuous increase of the dose and the growth of the patient’s survival time, the protection of the bladder, especially the bladder wall, has received more and more attention. So, it is necessary to outline the bladder wall in radiotherapy and reduce the accumulation of radiation dose in the bladder wall.

For example, prostate cancer is one of the most common cancers in male patients, and its 5-year survival rate has risen to more than 98% [1]. With prolonged survival, the quality of life after radiotherapy needs to be fully considered, so treatment-related toxicity has become a major concern for patients with high cancer survival rates. With the introduction of intensity-modulated radiotherapy, the genitourinary system toxicity has been significantly reduced compared with the past. However, according to several clinical trials, the 5-year toxicity rate greater than grade 2 is 12%–15%, and the common toxicity is dysuria, urinary retention, hematuria, and incontinence [2]. The main cause of toxicity is the high dose stacking in the bladder wall and urethra. According to relevant studies, the bladder is a hollow organ that stores urine, and the cumulative dose of the bladder wall can represent the truly involved dose [3]. In addition, the size, shape and position of the bladder will also be affected by factors such as patient positioning, bladder filling, and movement of surrounding organs during treatment. Therefore, it is of great clinical significance to study the spatial morphological changes of the bladder, especially the bladder wall during treatment, as well as superimposed dose analysis for the management of radiotherapy toxicity in the bladder. As an important part of bladder toxicity management, the accuracy of bladder wall segmentation directly affects the final spatial morphological changes and dose superposition analysis [4].

Conventional segmentation is time-consuming and labor-intensive, and the segmentation results are easily affected by the doctor’s temporal and spatial subjectivity. With the rapid development of artificial intelligence, especially the development of deep neural network algorithms, the automatic segmentation technology of medical images based on deep neural network algorithms has made great progress [5–8]. For segmentation studies of the bladder wall, there are mainly three types: model-based, data-driven, and methods that combine the two schemes. The typical scheme of the model-based methods has two branches, one is based on various prior models to adaptively extract the inner and outer boundaries of the bladder wall, and the other is mainly to train the classifier by selecting image low-order features, texture features, and wavelet features to reduce their features to the selection, thereby serving the bladder wall segmentation [9–11]. The advantage is that the relevant features are clearly defined, and easy to be used, and the disadvantage is that when the bladder wall and the surrounding background have similar grayscale and texture characteristics, the segmentation of the bladder wall often produces results with large errors. This data-driven approach is primarily based on the segmentation algorithm of U-Net and its modified deep neural networks, which can achieve a maximum similarity coefficient of 0.8 [12–14]. The advantage of this scheme is that deep neural networks can recognize multi-scale feature information, which is more conducive to segmentation, and the disadvantage is that it is limited by the training data, and the robustness and generalization performance needs to be improved. The combination of these two methods completes the segmentation task by organically combining the advantages of model-based and data-driven methods, avoiding their disadvantages, and achieving a maximum similarity coefficient of 0.9224 [15, 16]. Due to the smooth gradient of grayscale between adjacent areas, it is difficult to identify the weak boundary between the bladder wall and the surrounding soft tissues. In addition, complex backgrounds can easily affect the segmentation result. At the same time, the scarcity of medical data determines that it is difficult to have a large amount of medical data for segmentation training.

In addition, with the deepening of segmentation research based on deep neural networks, more and more networks have begun to be applied to clinical practice. However, the black box effect of the deep neural network algorithm limits its wide application in clinical practice [17, 18]. The ability to capture complex nonlinear relationships between input data and associated outputs often comes at the expense of the comprehensibility of the resulting model. Despite efforts to interpret relevant models in algorithmic interpretation and multi-scale analysis of segmentation results, deep neural network models notoriously evade direct human access.

There are many approaches to achieving explainability in deep learning models, but in this article, we will focus on two techniques that are relevant to our research: confidence maps and Grad-CAM. Confidence maps are a graphical representation of the model’s confidence or reliability. They help people better understand the model’s predictive ability and which data points or features have a significant impact on the model’s performance. In confidence maps, different colours or shades are used to represent different levels of confidence, making it easier for users to identify the model’s performance. In practical applications, confidence maps are often used in conjunction with other visualization techniques to help users better understand data features and model performance. In image segmentation tasks, confidence maps represent the probability distribution of each pixel belonging to a specific class. Typically, a neural network model generates confidence maps by classifying input images and outputting the probability values for each pixel belonging to each class. These probability values are then mapped to a grayscale image to obtain a confidence map. In a confidence map, areas with lighter colours represent uncertainty in the model’s classification of the pixel, while darker areas represent greater certainty in the model’s classification of the pixel. Post-processing methods such as threshold segmentation are often applied to confidence maps to obtain the final image segmentation result [19, 20].

Gradient-weighted Class Activation Mapping (Grad-CAM) is an explainable deep learning model technique used to determine which layers and positions are most critical for the model’s prediction of a particular class [21, 22]. This technique calculates the weights of each convolutional layer based on gradients and global average pooling and generates a heat map to visualize the regions that the model focuses on.

To address the limited data problem, we adopted geometric data augmentation and transfer learning techniques [23]. To solve the black box problem of deep learning models, we introduced confidence maps and Grad-CAM techniques. We also fused the strengths of three different loss functions based on confidence maps and ultimately developed our current solution.

We introduced the transfer learning algorithm to fine-tune the trained neural network model for bladder wall segmentation training with three loss functions: they are the cross-entropy loss function (CELF), the generalized Dice loss function (GDLF) and the Tversky loss function (TLF). Three models were obtained through training, and three corresponding confidence maps were output after entering a new image. By selecting the point with the maximum confidence values at the corresponding position, we merged the three images into one figure, performed threshold filtering to avoid external anomalies, and finally obtained the segmentation result. We also qualitatively gave the reasons for the improvement of model performance.

Material and methods

1088 T2 MRI images were used for model training. The data were divided into three parts: training data, validating data and testing data. 990 MRI images were used for training, 100 for validating and 88 used for model testing. To address the issue of insufficient data, we used data augmentation and transfer learning techniques. For data augmentation, we employed geometric augmentation techniques, including horizontal and vertical flipping, random rotation, and random horizontal and vertical shifting.

For transfer learning, a pre-trained Resnet50 model was utilized for deep neural network training. The pre-trained Resnet50 model is a three-channel, 50-layer deep model trained on the ImageNet database. The training period is 50 times, and 990 images are trained 49,500 times for a model in total. The learning rate is adaptive, and the final learning rate is 8.1e-6. Using NVIDIA 3070 graphics card, combined with 11th Gen Intel(R) Core (TM) i7-11800H @ 2.30 GHz processor, 32G RAM for training, a total of 265 min and 22 s were used for each model of the three.

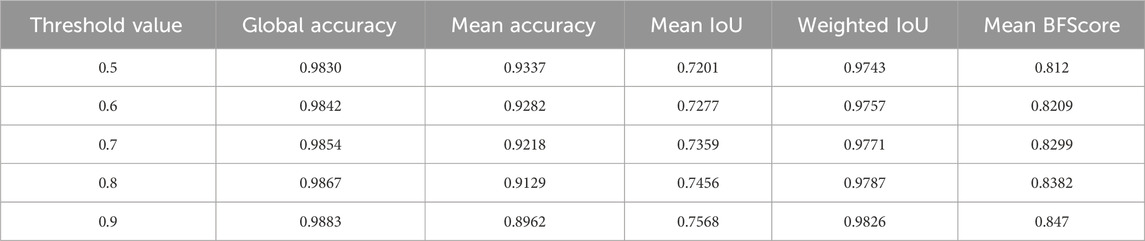
Figure 1 illustrates the workflow of our method, where 990 images were input into three pre-trained Resnet50 models with different loss functions (loss functions 1, 2, and 3 as shown in equations 2; (3); (4), respectively). Each model is a three-channel input architecture, so each image was duplicated as three identical images for training. 100 images were used for validation to prevent overfitting or excessive deviation, resulting in three models. 88 test images were pre-processed and sequentially input into the three trained models to obtain corresponding confidence distribution maps. For the three confidence distribution maps, we selected the points with the maximum confidence values at each corresponding position for integration to obtain a confidence distribution map. Considering the reliability of the confidence map, we needed to select a suitable threshold to perform image binarization on the confidence distribution map for image segmentation. We also provided a set of standards for selecting suitable thresholds. Figure 2 shows the size distribution of confidence maps between 0 and 1. By calculating the relevant indicators at the five thresholds of 0.9, 0.8, 0.7, 0.6, and 0.5, and considering that confidence values below 0.5 are not reliable, we compared and analyzed to find the optimal threshold of 0.6. The selection of 0.6 is more of a balance between segmentation accuracy and error. Threshold selection from 0.5 to 0.9 essentially resulted in a decrease in average segmentation accuracy, while other parameters showed some fluctuations, but the differences were not significant. Considering that confidence selection at 0.5 is not reliable enough, we chose 0.6 empirically as our segmentation threshold to balance segmentation accuracy and error. These relevant indicators include Global Accuracy, Mean Accuracy, Mean IoU, Weighted IoU, and Mean BFScore. Global Accuracy is the ratio of correctly classified pixels, regardless of class, to the total number of pixels. Intersection over union (IoU), also known as the Jaccard similarity coefficient, is the most commonly used metric. The IoU metric is a statistical accuracy measurement that penalizes false positives. For each class, IoU is the ratio of correctly classified pixels to the total number of ground truth and predicted pixels in that class. In other words,

$IoUscore=TP/\left(TP+FP+FN\right)(1)$

FIGURE 1

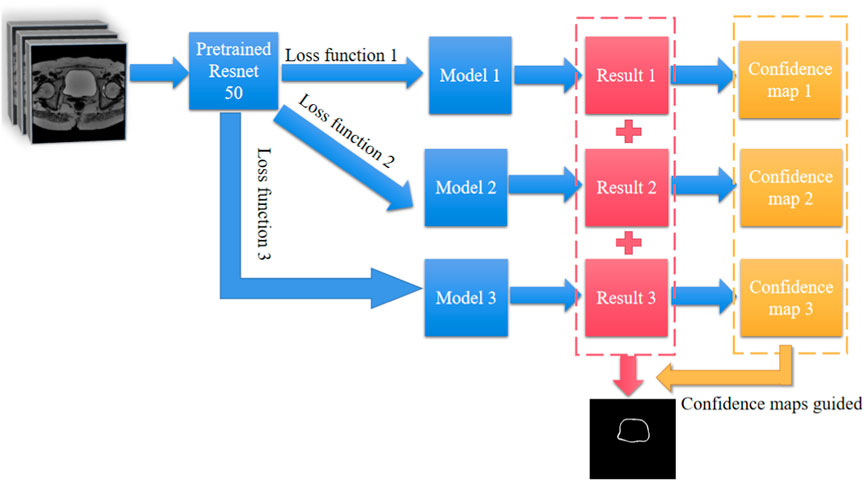
FIGURE 1. workflow of the confidence map-assisted residual base network for bladder wall segmentation.

FIGURE 2

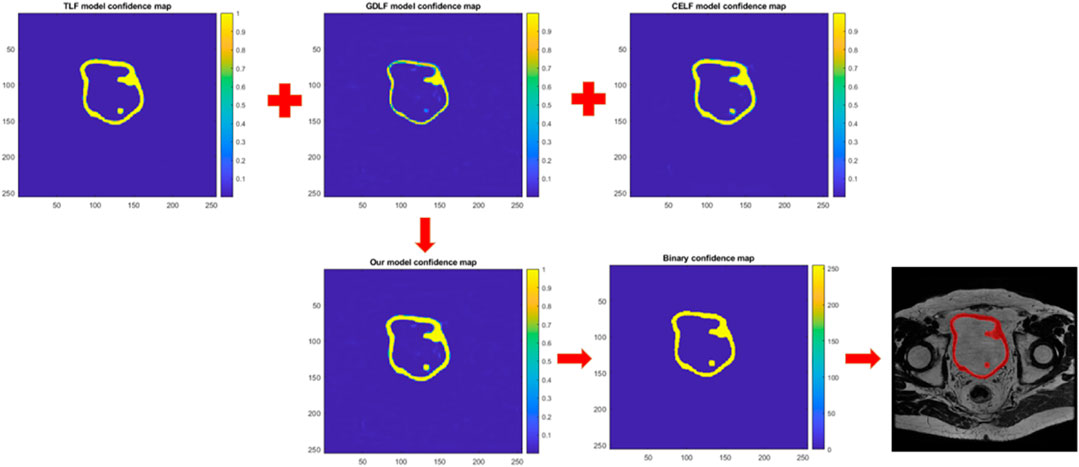
FIGURE 2. Shows a schematic diagram of how confidence maps guided image segmentation. The network generates the confidence map and represents the likelihood of each pixel belonging to a certain class. This map is then used to guide the segmentation process by assigning each pixel to the class with the highest confidence.

The image describes the true positives (TP), false positives (FP), and false negatives (FN). The average IoU of each class is weighted by the number of pixels in that class. This metric is used if images have disproportionally sized classes, to reduce the impact of errors in the small classes on the aggregate quality score. The boundary F1 (BF) contour matching score indicates how well the predicted boundary of each class aligns with the true boundary. The BF score is a metric that tends to correlate better with human qualitative assessment than the IoU metric. For each class, Mean BFScore is the average BF score of that class over all images.

To better understand the principle of image segmentation guided by confidence maps, we have depicted that in Figure 2. Figure 2 shows three confidence distribution maps were obtained by inputting a new test image into the three trained models. After selecting the maximum confidence values at the corresponding positions of the three confidence distribution maps, they were merged into a single confidence distribution map. Subsequently, the confidence distribution map was transformed into a binary image using a threshold of 0.6 as a standard to guide image segmentation.

The cross-entropy loss function described by Loss 1 is used to calculate the cross-entropy loss between the network-predicted values and the true values. The formula for calculating the cross-entropy loss function is:

$loss1=-\frac{1}{N}{\sum }_{n=1}^N{\sum }_{i=1}^K(T_{ni}\mathit{ln}\left(Y_{ni}\right)+\left(1-T_{ni}\right)\mathit{ln}\left(1-Y_{ni}\right)(2)$

Where N is the number of observations, K is the number of classes; T_ni is the true result, and Y_ni is the predicted result. The formula for calculating the generalized Dice similarity loss function described by Loss 2 is as follows:

$\mathit{\text{Loss}}2=1-\frac{2{\sum }_{k=1}^K{w}_k{\sum }_{m=1}^M{Y}_{\mathit{\text{km}}}{T}_{\mathit{\text{km}}}}{{\sum }_{k=1}^K{w}_k{\sum }_{m=1}^M{Y}_{\mathit{\text{km}}}^2+T_{\mathit{\text{km}}}^2}(3)$

Where K is the number of classes, M is the number of elements along the first two dimensions of the predicted result Y_km, W_k is a weight factor specific to each class that controls the contribution of each class to the result, and T_km is the true result. The generalized Dice similarity loss is based on the Sørensen-Dice similarity and is used to measure the overlap between two segmented images. The formula for calculating the Tversky loss function described by Loss 3 is as follows:

$Loss3=\frac{{\sum }_{m=1}^M{Y}_{cm}{T}_{cm}}{{\sum }_{m=1}^M{Y}_{cm}{T}_{cm}+\alpha {\sum }_{m=1}^M{Y}_{cm}{T}_{\stackrel{\_}{c}m}+\beta {\sum }_{m=1}^M{Y}_{\stackrel{\_}{c}m}{T}_{cm}}(4)$

Where c corresponds to the class, $\stackrel{\_}{c}$ corresponds to not being in class c; Y_cm is the predicted result, T_cm is the true result; M is the number of elements along the first two dimensions of the predicted result Y_cm; α is a weighted factor controlling the contribution of false positives for each class; β is a weighted factor controlling the contribution of false negatives for each class. The Tversky loss function described by Loss 3 is based on the Tversky index and is used to measure the overlap between two segmented images.

Table 1 displays the segmentation result metrics at different thresholds of 0.5, 0.6, 0.7, 0.8, and 0.9. The metrics include Global Accuracy, Mean Accuracy, Mean IoU, Weighted IoU, and Mean BFScore, which are commonly used to evaluate the accuracy of segmentation results. The table shows how the segmentation performance varies at different confidence thresholds, with lower thresholds generally resulting in better performance but potentially at the cost of reduced sensitivity. The metrics can be used to select an appropriate threshold for a specific application based on the desired trade-off between precision and recall.

TABLE 1

TABLE 1. The segmentation result metrics at different thresholds of 0.5, 0.6, 0.7, 0.8, and 0.9.

Results

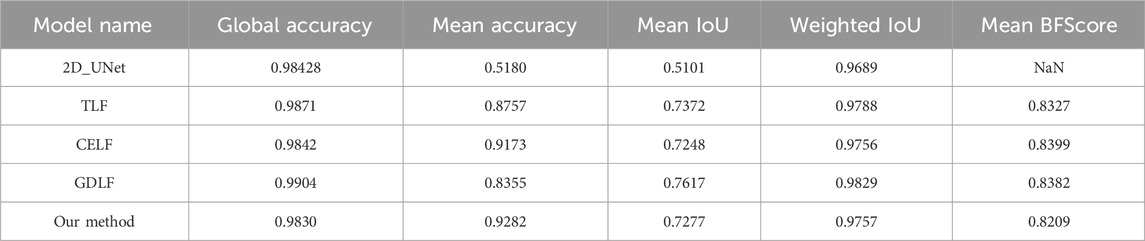
As shown in Figure 3, we selected one of the 88 images to display the results of our models and compared them with the results based on the 2D_UNet model. The quantitative analysis is shown in Table 2, which shows that our approach achieved the best performance.

FIGURE 3

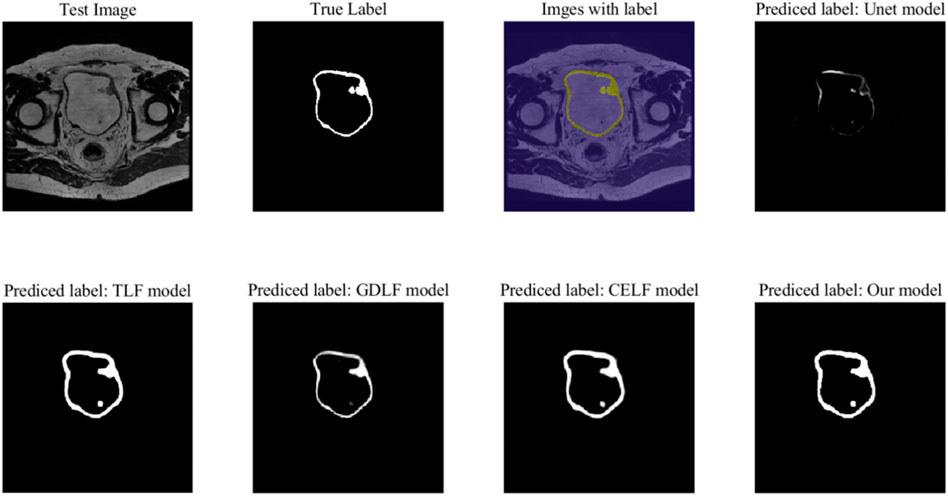
FIGURE 3. The segmentation performance on a test image. The Unet model is based on the training of the 2D_UNet neural network. The TLF model, GDLF model and CELF model are the corresponding models of Restnet50 with different loss functions: the Tversky loss function (TLF), the generalized Dice loss function (GDLF), and the cross-entropy loss function (CELF).

TABLE 2

TABLE 2. The segmentation result metrics for different models.

The Not a Number (NaN) problem with the Mean BFScore corresponding to 2D UNet is primarily due to the model segmenting fewer classified points. As shown in the prediction results of the UNet model in Figure 3, in some layers, the bladder wall cannot be properly segmented or visualized, resulting in the occurrence of NaN problems. This indicates that the classic 2D UNet neural network algorithm is unsuitable for bladder wall segmentation.

Table 2 displays the segmentation result metrics for different models. The metrics include Global Accuracy, Mean Accuracy, Mean IoU, Weighted IoU, and Mean BFScore, which are commonly used to evaluate the accuracy of segmentation results. The table shows how the segmentation performance varies in different models; our method has the highest mean accuracy at the cost of reduced sensitivity. Although our model did not achieve the best performance in terms of global accuracy, mean IOU, weighted IOU, and other parameters, the differences were not significant, and in some cases, even marginal. Furthermore, global accuracy represents the ratio of correctly classified pixels, regardless of class, to the total number of pixels. However, the increase in the proportion of background pixels does not significantly impact the accuracy of bladder wall segmentation, and similar trends were observed for other parameters. Therefore, we adopted mean accuracy as the primary evaluation metric, with other parameters serving as secondary evaluation metrics. Compared to the highest CELF model with a mean accuracy of 0.9173, our proposed algorithm achieved a mean accuracy of 0.9282. This 1% improvement in mean accuracy is based on the overall improvement of 88 test images, which demonstrates the effectiveness of our results.

Figure 4 shows the Grad-Cam maps analysis for four models. The heatmaps in the latter two columns are displayed on a Jet colour map scale, where blue represents low correlation, yellow represents medium correlation, and red represents high correlation. It has been shown that there is less red in the heatmap in small details and blurred border areas, indicating that the activation is weak there, and it also explains why the Resnet50 model still lacks accuracy in small detail segmentation, especially blurred borders. Through comparative analysis, it can be found that our proposed method does effectively integrate three models, but it may also amplify some minor errors, which will be analyzed in the limitation section.

FIGURE 4

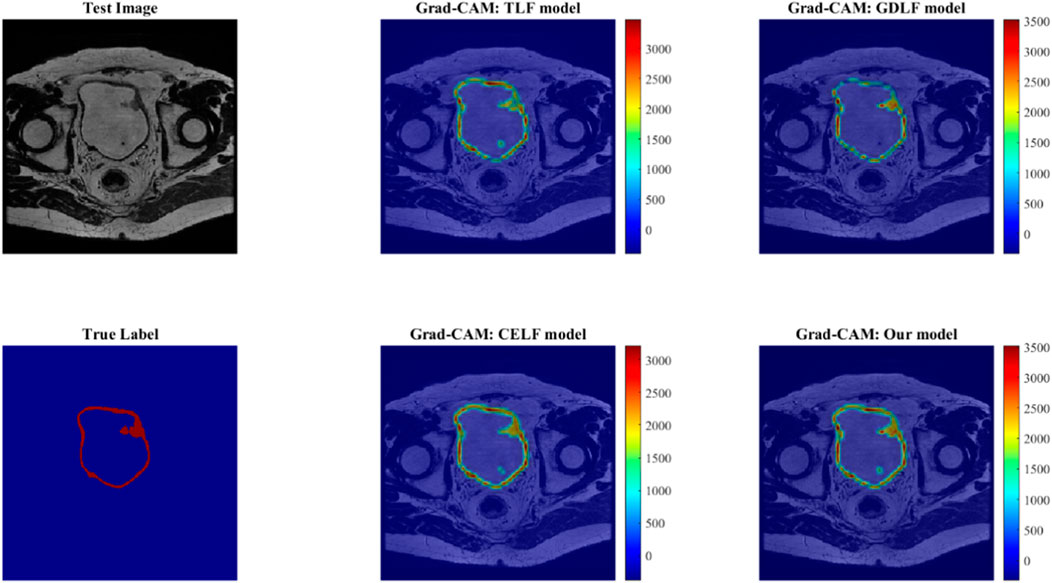
FIGURE 4. The Grad-Cam maps analysis for four models. The heatmaps in the latter two columns are displayed on a Jet colour map scale, where blue represents low correlation, yellow represents medium correlation, and red represents high correlation.

Table 2: The segmentation result metrics for different models. The metrics include Global Accuracy, Mean Accuracy, Mean IoU, Weighted IoU, and Mean BFScore, which are commonly used to evaluate the accuracy of segmentation results. The table shows how the segmentation performance varies in different models. Our method has the highest mean accuracy at the cost of reduced sensitivity.

Discussion

The proposed method in this paper aims to address the issue of bladder wall segmentation with limited data. Although geometric data augmentation and transfer learning are employed, along with confidence map-guided segmentation using three models based on different loss functions, there are still limitations. Firstly, it is inevitable that individual models have limitations, and their errors may be amplified when combined, resulting in a cascading effect. Although the three models are trained based on different loss functions and can extract different dimensions of information for image segmentation within a short training period, but how to further improve the utilization of the models and reduce the cascading effect of errors requires further research.

Due to limitations in the size of the datasets, our proposed solution is a two-dimensional approach, which has the following advantages compared to the currently popular 3D segmentation algorithms: 1. Fast computation: The 2D model only needs to process planar images, so the computation speed is usually relatively fast. 2. Simple algorithm: Since it only needs to process planar images, the algorithm is relatively simple, easy to implement, and debug. 3. More suitable for scenarios with limited data: When combined with transfer learning and data augmentation, it can achieve better results. However, it also has obvious disadvantages: 1. Information loss: Due to only processing planar images, some depth information may be lost, leading to less accurate segmentation results. 2. Not suitable for complex structures: The 2D model may not be able to accurately segment complex 3D structures. In summary, the 2D model is suitable for simple medical image segmentation, with fast computation speed and a simple algorithm, while the 3D model is suitable for complex medical image segmentation, providing more accurate segmentation results, but with higher computational complexity and difficulty in data acquisition. In practical applications, the appropriate model or a combination of 2D and 3D models can be selected based on the specific characteristics and requirements of the medical images.

Furthermore, for data augmentation and transfer learning, simple geometric data augmentation may not be sufficient. Other image augmentation techniques such as adversarial neural network techniques, style transfer, and stable diffusion should be considered to increase the richness of data augmentation. The selection and training of transfer learning models should also be reconsidered. In addition to the Resnet50 model, other pre-trained network models and models based on medical images that have already been trained should also be tried. Data augmentation and transfer learning should be organically combined rather than isolated techniques spliced together. The combination of these two techniques should be considered from the beginning, starting from the image training to obtain the pre-trained model, which may yield better results.

Finally, the introduction of confidence maps and Grad-CAM techniques is intended to better understand the internal operation mechanism of deep neural network models and provide a more hierarchical explanation of our new algorithm. However, existing explainable techniques lack a systematic explanation, only explaining or displaying the neural network model from a certain layer or result perspective. There is a lack of relevant explanatory theories for the overall understanding of model training. This requires us to develop relevant explanatory theories to reasonably control the model process at the training level. For example, how does the model change along with the decrease in loss function during model training? How to avoid suboptimal points reasonably during model training? How to prove that what we obtain is not a suboptimal model? Along with these issues, we also need to delve into the monitorability and explainability of the training process of deep learning models.

In addition to the calculation of cumulative bladder wall dose during patient radiotherapy and toxicity assessment, bladder wall segmentation has important applications in other medical scenarios, primarily in the following areas:

Bladder wall lesion diagnosis: Bladder wall segmentation can help doctors accurately analyze the condition of bladder wall lesions, such as tumors, ulcers, inflammation, etc. By segmenting the bladder wall, doctors can observe and analyze the morphological, size, and location characteristics of the lesion area in more detail. This allows for a comprehensive evaluation of the lesions, aiding in the diagnosis process. Moreover, it helps in determining the stage and severity of the lesions, providing valuable information for treatment planning.

Bladder wall disease treatment planning: In the treatment planning of bladder wall diseases, bladder wall segmentation plays a crucial role by providing important anatomical information to doctors. By segmenting the bladder wall, doctors can accurately determine the relationship between the lesion area and surrounding tissues. This information is essential in designing tailored treatment plans that ensure optimal outcomes. Furthermore, bladder wall segmentation helps in defining the extent of surgical procedures, minimizing the risk of complications and maximizing the effectiveness of the treatment.

Bladder wall surgical navigation: Accurate identification and segmentation of the bladder wall are vital in bladder wall surgery. By segmenting the bladder wall, doctors can provide precise information for surgical navigation and real-time positioning. This allows them to accurately locate the surgical resection area, ensuring the removal of all abnormal tissues while minimizing the damage to healthy bladder wall tissues. Ultimately, this improves the safety and accuracy of the surgery, leading to better patient outcomes.

Bladder wall lesion monitoring: Bladder wall segmentation aids doctors in monitoring bladder wall lesions regularly. By segmenting the bladder wall, doctors can accurately measure and compare the size, shape, and other key information of the lesion area. This enables them to monitor the progression of the lesions over time, evaluate the effectiveness of the ongoing treatment, and make necessary adjustments to subsequent treatment plans. This proactive approach ensures timely intervention and helps in optimizing patient care.

Overall, bladder wall segmentation serves as a versatile tool in various medical scenarios beyond calculating cumulative bladder wall dose during patient radiotherapy and toxicity assessment. It enables precise diagnosis, aids in treatment planning, enhances surgical navigation, and facilitates lesion monitoring, thereby promoting better patient care and outcomes.

Conclusion

Our study demonstrates that a confidence map-assisted residual base network can accurately segment bladder walls on a limited-size data set. Compared with the segmentation results of each model alone, our method originally improves the accuracy of the segmentation results by combining confidence map guidance with threshold filtering. Qualitative interpretability analysis also opens up the black box effect of neural network models and explains the reasons behind the improvement of the accuracy of our method.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/pea94/bladder-segmentation.

Author contributions

MW: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Writing–original draft. RY: Conceptualization, Formal Analysis, Funding acquisition, Project administration, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Our study demonstrates that a confidence map-assisted residual base network can accurately segment bladder walls on a limited-size data set. Compared with the segmentation results of each model alone, our method originally improves the accuracy of the segmentation results by combining confidence map guidance with threshold filtering. Qualitative interpretability analysis also opens up the black box effect of neural network models and explains the reasons behind the improvement of the accuracy of our method. This work was supported by the National Key Research and Development Program (No. 2021YFE0202500), Beijing Municipal Commission of Science and Technology Collaborative Innovation Project (Z221100003522028), the Non Profit Central Research Institute Fund of Chinese Academy of Medical Sciences (no. 2023-JKCS-10), and the Beijing Natural Science Foundation (no. Z230003).

Acknowledgments

We acknowledge the GitHub website for providing their platforms and contributors for uploading their meaningful datasets. The open dataset source: https://github.com/pea94/bladder-segmentation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lao Y, Cao M, Yang Y, Kishan AU, Yang W, Wang Y, et al. Bladder surface dose modeling in prostate cancer radiotherapy: an analysis of motion-induced variations and the cumulative dose across the treatment. Med Phys (2021) 48(12):8024–36. doi:10.1002/mp.15326

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yao HH-I, Hoe V, Shamout S, Sengupta S, O'Connell HE, Carlson KV, et al. Impact of radiotherapy for localized prostate cancer on bladder function as demonstrated on urodynamics study: a systematic review. Can Urol Assoc J (2021) 15(12):E664–E671. doi:10.5489/cuaj.7265

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chen H-H, Lin K-S, Lin P-T, Kuo L-T, Fang C-C, Chi C-C. Bladder volume reproducibility after water consumption in patients with prostate cancer undergoing radiotherapy: a systematic review and meta-analysis. Biomed J (2020) 44:S226–34. doi:10.1016/j.bj.2020.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Tamihardja J, Cirsi S, Kessler P, Razinskas G, Exner F, Richter A, et al. Cone beam CT-based dose accumulation and analysis of delivered dose to the dominant intraprostatic lesion in primary radiotherapy of prostate cancer. Radiat Oncol (2021) 16(1):205–9. doi:10.1186/s13014-021-01933-z

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Liu X, Li K-W, Yang R, Geng L-S. Review of deep learning based automatic segmentation for lung cancer radiotherapy. Front Oncol (2021) 11:717039. doi:10.3389/fonc.2021.717039

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Samarasinghe G, Jameson M, Vinod S, Field M, Dowling J, Sowmya A, et al. Deep learning for segmentation in radiation therapy planning: a review. J Med Imaging Radiat Oncol (2021) 65(5):578–95. doi:10.1111/1754-9485.13286

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Nikolov S, Blackwell S, Zverovitch A, Mendes R, Livne M, De Fauw J, et al. Clinically applicable segmentation of head and neck anatomy for radiotherapy: deep learning algorithm development and validation study. J Med Internet Res (2021) 23(7):e26151. doi:10.2196/26151

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Jin X, Thomas MA, Dise J, Kavanaugh J, Hilliard J, Zoberi I, et al. Robustness of deep learning segmentation of cardiac substructures in noncontrast computed tomography for breast cancer radiotherapy. Med Phys (2021) 48(11):7172–88. doi:10.1002/mp.15237

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Liu Y, Zheng H, Xu X, Zhang X, Du P, Liang J, et al. The invasion depth measurement of bladder cancer using T2-weighted magnetic resonance imaging. Biomed Eng Online (2020) 19(1):92–13. doi:10.1186/s12938-020-00834-8

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Qin X, Li X, Liu Y, Lu H, Yan P. Adaptive shape prior constrained level sets for bladder MR image segmentation. IEEE J Biomed Health Inform (2013) 18(5):1707–16. doi:10.1109/jbhi.2013.2288935

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Duan C, Liang Z, Bao S, Zhu H, Wang S, Zhang G, et al. A coupled level set framework for bladder wall segmentation with application to MR cystography. IEEE Trans Med Imaging (2010) 29(3):903–15. doi:10.1109/TMI.2009.2039756

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Dolz J, Xu X, Rony J, Yuan J, Liu Y, Granger E, et al. Multiregion segmentation of bladder cancer structures in MRI with progressive dilated convolutional networks. Med Phys (2018) 45(12):5482–93. doi:10.1002/mp.13240

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ma X, Hadjiiski LM, Wei J, Chan H, Cha KH, Cohan RH, et al. U-Net based deep learning bladder segmentation in CT urography. Med Phys (2019) 46(4):1752–65. doi:10.1002/mp.13438

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dong Q, Huang D, Xu X, Li Z, Liu Y, Lu H, et al. Content and shape attention network for bladder wall and cancer segmentation in MRIs. Comput Biol Med (2022) 148:105809. doi:10.1016/j.compbiomed.2022.105809

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Cha KH, Hadjiiski L, Samala RK, Chan H, Caoili EM, Cohan RH. Urinary bladder segmentation in CT urography using deep-learning convolutional neural network and level sets. Med Phys (2016) 43(4):1882–96. doi:10.1118/1.4944498

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xu X, Zhou F, Liu B. Automatic bladder segmentation from CT images using deep CNN and 3D fully connected CRF-RNN. Int J Comput Assist Radiol Surg (2018) 13(7):967–75. doi:10.1007/s11548-018-1733-7

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hayes TR, Henderson JM. Deep saliency models learn low-mid-and high-level features to predict scene attention. Sci Rep (2021) 11(1):18434. doi:10.1038/s41598-021-97879-z

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Liu G, Wang J. Dendrite net: a white-box module for classification, regression, and system identification. IEEE Trans Cybern (2021) 52:13774–87. doi:10.1109/TCYB.2021.3124328

CrossRef Full Text | Google Scholar

19. Jiang Y, Hauptmann AG. Salient object detection: a discriminative regional feature integration approach. IEEE Trans Pattern Anal Machine Intelligence (2017) 39(2):297–312. doi:10.1109/CVPR.2013.271

CrossRef Full Text | Google Scholar

20. Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; June 2015; Boston, MA, USA (2015). p. 3431–40.

CrossRef Full Text | Google Scholar

21. Jahmunah V, Ng EYK, Tan RS, Oh SL, Acharya UR. Explainable detection of myocardial infarction using deep learning models with Grad-CAM technique on ECG signals. Comput Biol Med (2022) 146:105550. doi:10.1016/j.compbiomed.2022.105550

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Jung W, Lee KE, Suh BJ, Seok H, Lee DW. Deep learning for osteoarthritis classification in temporomandibular joint. Oral Dis (2021) 29:1050–9. doi:10.1111/odi.14056

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tian S, Wang C, Zhang R, Dai Z, Jia L, Zhang W, et al. Transfer learning-based autosegmentation of primary tumor volumes of glioblastomas using preoperative MRI for radiotherapy treatment. Front Oncol (2022) 12:856346. doi:10.3389/fonc.2022.856346

PubMed Abstract | CrossRef Full Text | Google Scholar