Right partial rainbow refractometry for measuring droplet refractive index and size

Rainbow refractometry can be employed for measuring the parameters of droplets or sprays. Considering the diversity of different measurement environments and droplet components, there are instances in experiments where optics fail to record the complete rainbow signal. To enhance the experimental data utilization, this paper investigates rainbow refractometry using the incomplete rainbow signal on the right side, focusing on its feasibility and accuracy. The concept that defines the incompleteness of the right-sided rainbow signal is termed as the dimensionless right signal partial ratio (RSPR). The study conducts a comprehensive analysis of refractive index, droplet diameter, and size distributions retrieved from the partial rainbow signals simulated by the Lorenz-Mie theory with varying RSPR values. For both partial standard and global rainbows, the critical value of the retrieval error is found to be whether the primary peak of the rainbow is preserved or not, i.e., RSPR = 1. Laboratory experiments verify the feasibility and effectiveness of employing rainbow refractometry with right partial rainbow signals. The study addresses the challenge of incomplete recording of rainbow signals in experiments, and is expected to improve experimental efficiency and data utilization.

1 Introduction

Droplet measurement techniques are primarily categorized into traditional contact methods and non-contact methods, including acoustic, optical, and electromagnetic methods. Among these, optical measurement methods are preferred due to their high accuracy, non-destructiveness, and ability to provide in situ and on-line measurements. Noteworthy optical methods employed for droplet measurements encompass direct imaging [1, 2], shadowgraphy [3], laser interferometric particle imaging [4–6], phase doppler technique [7, 8], laser induced fluorescence [9–12], digital holography [13–16], Raman spectroscopy [17], and other light scattering techniques [18, 19]. Rainbow refractometry, a form of backscattered light interferometry, emerges as a pivotal optical technique. By analyzing the intensity distribution of backscattered signals in rainbow scattering region, this method enables the extraction of essential droplet parameters, including droplet size, droplet refractive index/temperature [20]. Some unique work has been done in measuring oblate droplets [21, 22], the refractive index (temperature) gradient within droplet [23], oscillating droplets [24] and colloidal droplets [25, 26].

The standard rainbow refractometry was initially introduced by Roth et al. in 1990 [27], focusing on the measurement of individual or monodisperse droplets. Subsequently, Van Beeck et al. [28] extended the technique’s capabilities by proposing global rainbow refractometry. This advancement involved extending the exposure time and enlarging the aperture size, thereby enabling the measurement of size distribution and mean refractive index/temperature for polydisperse droplets. To date, rainbow refractometry has further evolved to include one-dimensional [29] and planar [30] versions. Synthetic aperture rainbow refractometry [31] was developed for droplet measurement over wide working distances and large size ranges using dual-wavelength laser beams and color camera. Recent most advances have focused on the evaporation of nanofluid droplets [32] and multicomponent droplets [33–36] due to the availability of both time-resolved droplet size and temperature.

The scattering angle recording range of the measurement system is limited and decreases with increasing working distance. The rainbow signals of droplets with different temperature/composition (refractive index) actually exhibit distinct angular positions. Consequently, a measurement system with a fixed scattering angle recording range may not always capture the complete rainbow signal during experiments. These partial rainbow signals are usually discarded in the experimental data processing, leading to a deviation between the measured and actual values. Our prior work [37] introduced rainbow refractometry using left-sided incomplete rainbow signals, and extensively examined the errors in the inversion process with respect to refractive index, droplet size and size distribution using different inversion algorithms [38]. At the same time, the experiment also produces right-sided incomplete rainbow signals, which have not been thoroughly examined to date.

Therefore, this study aims to investigate the rainbow refractometry using the incomplete rainbow signal on the right side. Additionally, the findings highlighted that the accuracy of the inversion process significantly improves when employing signal fitting method as compared to methods solely relying on characteristic point estimation. To achieve better inversion accuracy and reduce unnecessary workload, this study directly adopts the signal fitting approach for signal retrieval.

Typical standard and global rainbow signals are simulated based on Lorenz-Mie scattering theory, and different inversion segments are intercepted by setting different RSPR. Section 2 briefly describes the principles of simulating and processing rainbow signals, and the definition of right-sided incomplete rainbow signal. Section 3 analyzes the results of processing the standard and global rainbow at different RSPR. Section 4 validates the conclusions in the simulation results through experiments. Finally, the laws and conclusions in this study are summarized in section 5.

2 Simulation and processing

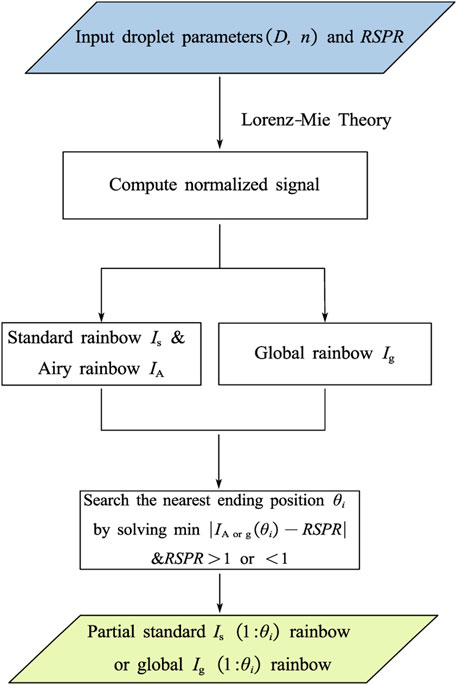
2.1 Simulation of partial rainbows

The standard and global rainbow signals of different preset refractive indices, droplet sizes and size distributions were simulated by the Lorenz-Mie scattering theory [39]. Notably, the global rainbow signal is synthesized through the numerical superposition of standard rainbows originating from individual droplet. The simulation was performed under the assumption of spherical droplets while ignoring multiple scattering and interference between droplets.

The level of right-sided incompleteness in the rainbow is determined by an introduced dimensionless variable, right signal partial ratio (RSPR), and is formulated as shown in Eq. 1

$RSPR=\left\{\begin{array}{l}R,0\le RSPR\le 1\\ 2.0-L,1\le RSPR<2\end{array}\right..(1)$

In this case, the range of RSPR is specified as 0 to 2. Figure 1 depicts the variation of normalized rainbow signal intensity with scattering angle. Here, L and R correspond to the normalized intensities of the left and right primary bows, respectively, serving as indicators of the partial degree of rainbow. An RSPR value of 0 indicates a complete primary bow. Specifically, the physical meaning of RSPR is the extent to which the primary bow is shifted within the receiving aperture such that the image on the detector no longer captures the entire primary bow. The simulation process of the partial standard rainbow and global rainbow signals is elucidated in Figure 2.

FIGURE 1

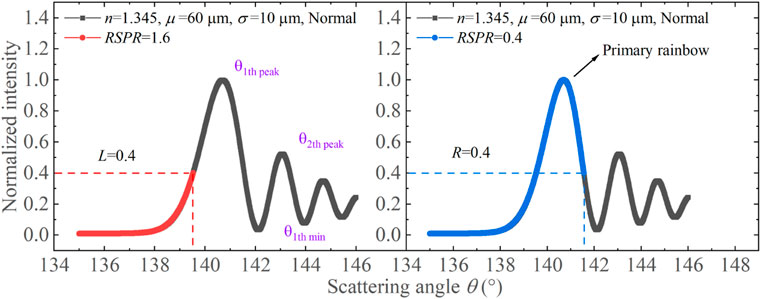
FIGURE 1. Right signal partial ratio is used to define and quantify the right-sided completeness of the rainbow signal.

FIGURE 2

FIGURE 2. The simulation flow for the partial standard and global rainbow signal.

Since the RSPR is defined independently of the ripple structure, the input chosen is the Airy rainbow I_A instead of the standard rainbow which contains high-frequency components. Notably, the global rainbow signal has no ripple structure and adheres to the defined criteria of RSPR. The minimization of $\left|I_{\mathrm{A}\text{or}\mathrm{g}}\left({\theta }_i\right)-RSPR\right|$ is determined through the preset RSPR values. Subsequently, the search is conducted to pinpoint the closest ending position θ_i of the inversion signal that aligns with the preset RSPR value. This process facilitates the creation of inversion segments from either the standard rainbow I_s(1:θ_i) or the global rainbow I_g(1:θ_i). When RSPR is less than 1, the position of θ_i is situated to the right of the primary bow. Conversely, the θ_i is to the left of the primary bow for RSPR exceeding 1. Note that the input signal is normalized by its maximum intensity.

2.2 Principle of signal fitting

Signal fitting was selected as the preferred method in the inversion of the rainbow signal in this study. This approach offers superior accuracy and precision in comparison to the conventional characteristic point estimation techniques [38, 40]. On the other hand, the characteristic points of incomplete signals such as primary peak and inflection points may not be available, making it difficult to study the effect of RSPR. By employing signal fitting, this study calculates the rainbow of a preset droplet diameter and refractive index through approximate or exact rainbow theory, using it to match the simulated or experimentally recorded input rainbow signal I to be processed. The described procedure is iterated over a prescribed range of droplet diameters D∈[D_min, D_max] and refractive indices n∈[n_min, n_max], with the aim of continuously refining the results. This iteration allows for a comprehensive exploration of potential parameter combinations to determine the optimal values of droplet diameter and refractive index to minimize the value of the objective function $\underset{n,N\left(D\right)}{\mathrm{argmin}}{‖\mathit{A}\cdot \mathit{N}-\mathit{I}‖}_2$. In this function, matrix A corresponds to the droplet diameter and refractive index related light intensity matrix, computed using the modified complex angular momentum theory; the N denotes a coefficient of the standard rainbow or an undetermined size distribution of the global rainbow. For a deeper understanding of the signal fitting algorithm, please refer to the literature [37].

This study complements previously published work [37], where they focused on the processing of incomplete rainbow signals on the right-sided and left-sided respectively. The formulas defining the degree of incompleteness and the simulation of partial signal interceptions are also different in the two papers. And obviously their conclusions in the following simulations and experiments will be somewhat different. This study is meaningful because the left and right sides of the primary bow have different physical implications. The left side of the primary bow covers more refractive index information of the droplets, while the right side contains subtle information such as droplet size distribution.

3 Simulation results and analysis

This section presents an in-depth analysis of the inversion results of the right-sided partial standard and global rainbows simulated and computed by above method. It investigates and compares the refractive indices, droplet sizes and size distributions obtained from the inversion of rainbow signals under different RSPR settings. Furthermore, it assesses the effect of fitting the inversed signals to the original ones during the inversion process. Additionally, this section conducts a comparison between the processing results of the right-sided partial rainbow signals and those of the left-sided partial rainbow signals.

3.1 Partial standard rainbow

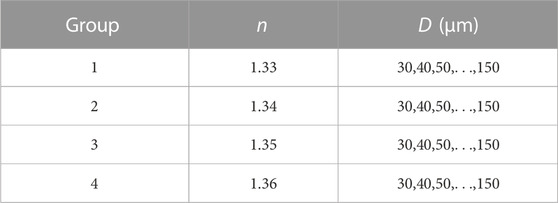
The standard rainbows of individual droplets under representative operational circumstances were simulated by Lorenz-Mie scattering theory. The simulations were carried out across a pre-defined range of refractive indices, spanning from 1.33 to 1.36, and droplet diameters ranging from 30 to 150 μm with 10 μm intervals. Table 1 details the simulations of the different scenarios and provides a comprehensive overview of the actual droplet parameters that may be encountered in the experiments. The droplet diameter range was chosen based on the measurable particle size range (20–200 μm) for which rainbow technique is suitable. The refractive indices of most frequently used water and ethanol are respectively about 1.33, 1.36 under the light illumination of 532 nm at temperature of 20°C. The range of refractive indices was thus chosen. The refractive index appears to have little effect on the inversion accuracy since it only translationally changes the scattering angle of the rainbow signal, whereas the droplet size changes the intensity and shape of the signal. And the selected parameters in the simulations will certainly cover the expected experimental conditions.

TABLE 1

TABLE 1. List of simulation parameters for standard rainbow.

Figure 3 illustrates the relative errors of diameter D and absolute errors of refractive index n processed from the right-sided partial standard rainbows at different RSPR. Evidently, both the absolute error of n and the relative error of D show an upward trend as RSPR value increases. The inversion accuracy of the right-sided incomplete standard rainbows is challenged in the range 1<RSPR ≤ 2. This is attributed to the absence of both the primary and secondary peaks within the Airy rainbow structure, coupled with the presence of the Ripple structure, collectively contributing to inaccuracies during signal inversion within this RSPR range. In Figure 4, the mean and maximum inversion errors are portrayed against the variation of pre-set droplet diameter and refractive index under different RSPR conditions. Notably, as the preset droplet diameter increases, there is an obvious downward trend in the mean and maximum values of relative error of D and absolute error of n. The inversion error for RSPR < 1 is analyzed in depth below. For a preset refractive index of n = 1.33, the absolute error of n remains below 8.38 × 10⁻⁴, with a relative error of D within 7.52%. Correspondingly, at a preset refractive index of n = 1.34, the two errors are both under 7.82 × 10⁻⁴ and 14.98%, respectively. While they are as high as 11.86 × 10⁻⁴ and 12.59% at n = 1.35, and 14.50 × 10⁻⁴ and 16.54% at n = 1.36. It is evident that the increase in error correlates with the increase in the preset refractive index.

FIGURE 3

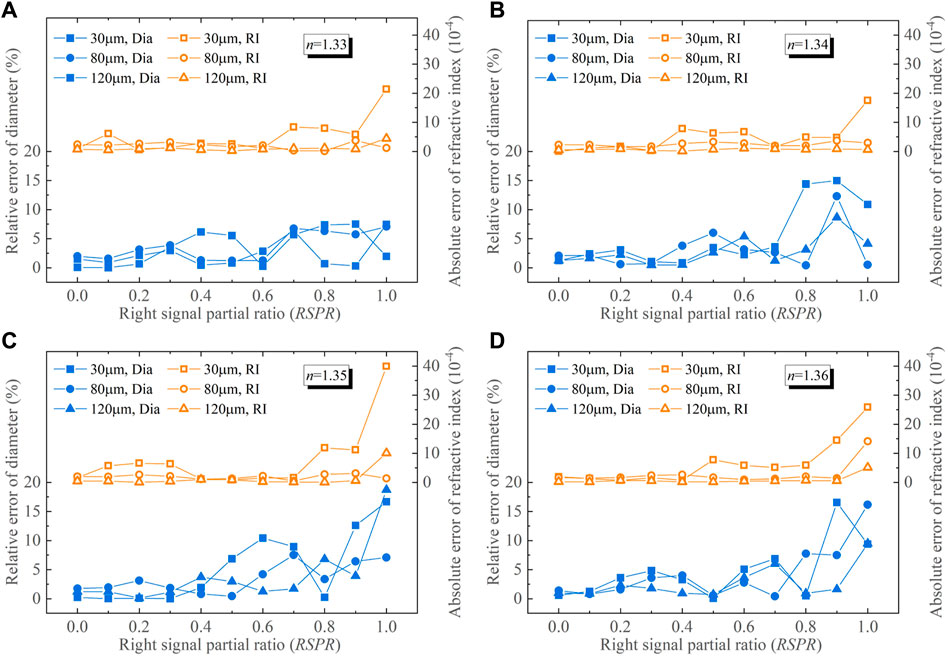
FIGURE 3. Relative errors of D and absolute errors of n for processing the right-sided partial standard rainbows. (A) n = 1.33, (B) n = 1.34, (C) n = 1.35, (D) n = 1.36.

FIGURE 4

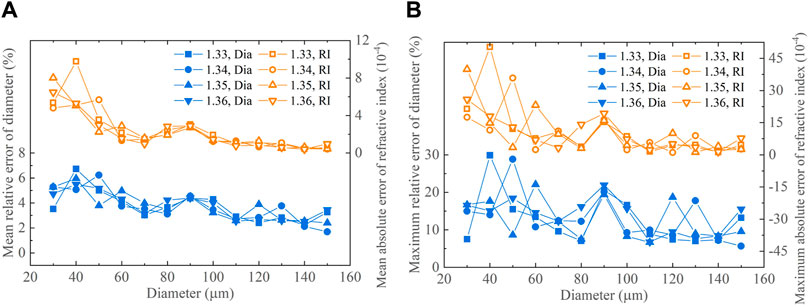
FIGURE 4. Mean (A) and maximum (B) errors of D and n retrieved from the right-sided partial standard rainbows.

For preset droplet diameters exceeding 60 μm, the mean relative error of D and the mean absolute error of n remain within the range of 4.96% and 3.04 × 10⁻⁴ under different RSPR values. Correspondingly, for preset droplet diameters greater than 100 μm, the maximum relative error of D and the maximum absolute error of n are predominantly below 13.23% and 5.71 × 10⁻⁴, respectively. The comprehensive analysis outlined above strongly indicates that using the right-sided incomplete standard rainbow signal allows successful retrieval of droplet parameters at RSPR values below 1. At 0≤RSPR ≤ 1, the absolute error of n and the relative error of D inversed from the left-sided incomplete standard rainbow are respectively within 6 × 10⁻⁴ and 3%, and most of them are less than 4 × 10⁻⁴ and 2%. It is concluded that the inversion error using the right-sided incomplete standard rainbow exceeds the inversion error using the left-sided incomplete standard rainbow. This difference in error could be attributed to the fact that the left-sided incomplete standard rainbow preserves the supernumerary peaks, while the right-sided incomplete standard rainbow experiences more pronounced signal loss.

3.2 Partial global rainbow

Global rainbows of spray droplets, characterized by three distinct size distributions (normal, lognormal, and bimodal normal distributions), were simulated using the Lorenz-Mie scattering theory. Each global rainbow is synthesized by numerically superimposing standard rainbows generated from 1000 droplets, regardless of the interference between droplet signals. The parameters for different size distributions are outlined in Table 2. For both normal and lognormal size distributions, the preset mean diameter μ assumes values of 60/100/140 μm, while the standard deviation σ takes on 10/15 μm and 0.2/0.3 μm respectively. The bimodal normal distribution is a composite of two normal distributions (μ₁ = 50 μm, σ₁ = 10 μm, μ₂ = 100 μm, σ₂ = 20 μm), with a number density ratio (Num₁: Num₂) of 60:100, 100:100, and 100:60. Notably, the refractive index and droplet size distribution are two independent parameters. Variations in the refractive index have a minimal impact on the size distribution retrieved from the simulated global rainbow. Therefore, in all cases, the refractive index was always set to 1.3450.

TABLE 2

TABLE 2. List of simulation parameters for global rainbow.

Figure 5 presents the scatter plots and error plots depicting the mean diameters μ and refractive indices n retrieved from the simulated global rainbows of droplets with normal size distributions at various RSPR values. As the RSPR increases, the data points in the graph become more scattered, accompanied by an increase in the µ and n errors. Notably, when RSPR ≤ 1 and σ = 10, the absolute errors of n and the relative errors of μ remain below 0.30 × 10⁻⁴ and 2.36%. Furthermore, as the preset μ increases, both the errors in μ and n exhibit a significant overall decrease. Under the conditions of RSPR ≤ 1 and σ = 15, errors in both n and μ are limited to less than 0.18 × 10⁻⁴ and 2.52%, respectively. A comprehensive evaluation of Figure 5 shows that the rainbow inversion exhibits relatively higher stability when σ = 5 than when σ = 10. The above error analysis shows the feasibility of using the signal fitting to retrieve the right-sided incomplete global rainbows of droplets with normal size distribution.

FIGURE 5

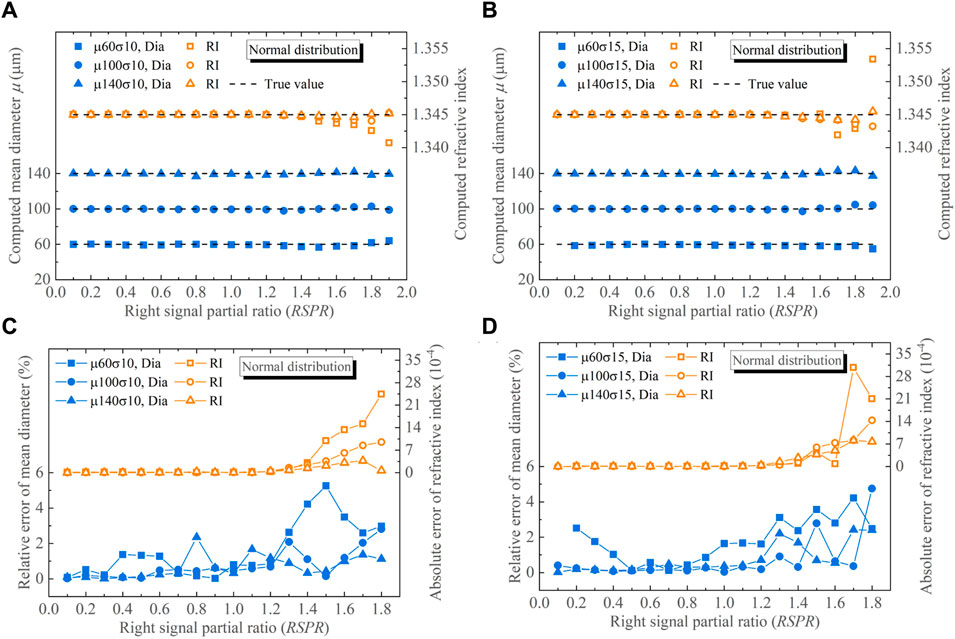
FIGURE 5. Processing results for global rainbows of droplets with normal size distributions. Retrieved mean diameters and refractive indices of (A) σ = 10 μm, (B) σ = 15 μm, and their errors of (C) σ = 10 μm, (D) σ = 15 μm.

The signal fitting and retrieved droplet size distributions at different RSPR are pictured as shown in Figure 6. The inverted signals are perfectly fitted to the simulated signals, and for RSPR ≤ 1, the retrieved size distributions agree well with the theoretical normal distributions. However, for RSPR > 1, the retrieved size distributions cannot be correctly identified as normal size distributions, which corresponds to an increase in their inversion errors. This emphasizes that the absence of the primary bow peak within the right-sided incomplete global rainbow can lead to an increased inversion error or even inversion failure.

FIGURE 6

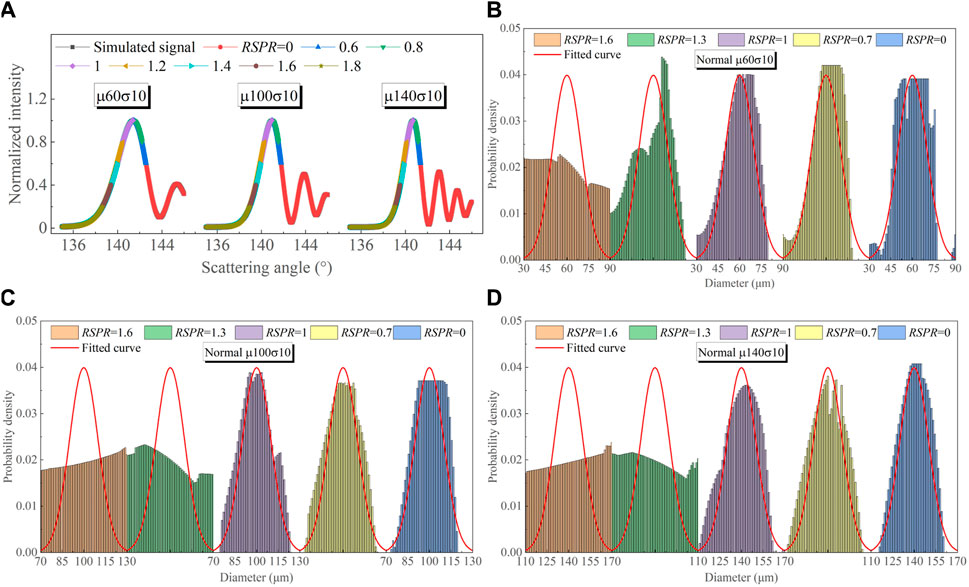
FIGURE 6. Signal fitting results for the simulated global rainbows of droplets with three different normal size distributions at different RSPR: fitted global rainbows for (A) μ = 60 μm, σ = 10 μm, μ = 100 μm, σ = 10 μm, μ = 140 μm, σ = 10 μm, and retrieved size distributions for (B) μ = 60 μm, σ = 10 μm, (C) μ = 100 μm, σ = 10 μm, (D) μ = 140 μm, σ = 10 μm.

Figure 7 illustrates scatter and error plots showing the mean diameters μ and refractive indices n retrieved from the simulated global rainbows of droplets with log-normal size distributions under different RSPR conditions. Similar to the case of droplets with normal size distributions, the errors of the retrieved μ and n ascend with increasing RSPR. For RSPR ≤ 1 and σ = 0.2, the absolute errors of n remain within 0.30 × 10⁻⁴, while the relative errors of μ are within 4.38%. Specifically, for μ = 60 μm, the errors in both n and μ are below 0.30 × 10⁻⁴ and 4.38%, while for μ = 100 μm, the errors remain within 0.26 × 10⁻⁴ and 3.01%. Remarkably, for μ = 140 μm, the errors are only 0.16 × 10⁻⁴ and 2.45%. The above analysis illustrates errors in retrieved μ and n experience a reduction when the preset mean diameter μ is increased. In the cases of RSPR ≤ 1 and σ = 0.3, the errors in n and μ are within 1.27 × 10⁻⁴ and 9.96%. Thus, it is obvious that the mean diameters and refractive indices of droplets obtained by signal fitting inversion at σ = 0.2 show higher stability and smaller errors compared to those at σ = 0.3 at different RSPR. Evidently, the errors in retrieved n and μ amplify as the preset droplet size standard deviation σ is increased.

FIGURE 7

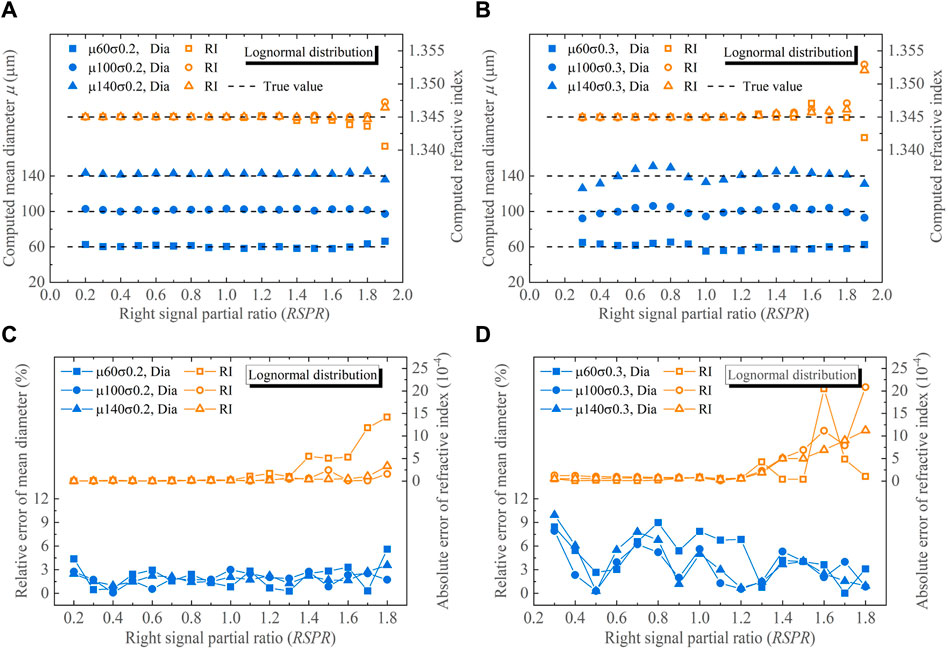
FIGURE 7. Processing results for the global rainbows of droplets with log-normal size distributions. Retrieved mean diameters and refractive indices of (A) σ = 0.2 μm, (B) σ = 0.3 μm, and their errors of (C) σ = 0.2 μm, (D) σ = 0.3 μm.

It is evident that the inverted rainbows fit remarkably well with the simulated global rainbows for different RSPR as shown in Figure 8, and the retrieved size distributions of droplets at RSPR ≤ 1 closely match the theoretical expectation of the log-normal distributions. It is worth noting that this consistency is not as precise as for droplets with normal size distributions. Importantly, with the increase in the preset mean diameter μ, the retrieved size distributions of droplets become more stable and more consistent with the theoretical log-normal size distributions. This observation also confirms the conclusion summarized earlier.

FIGURE 8

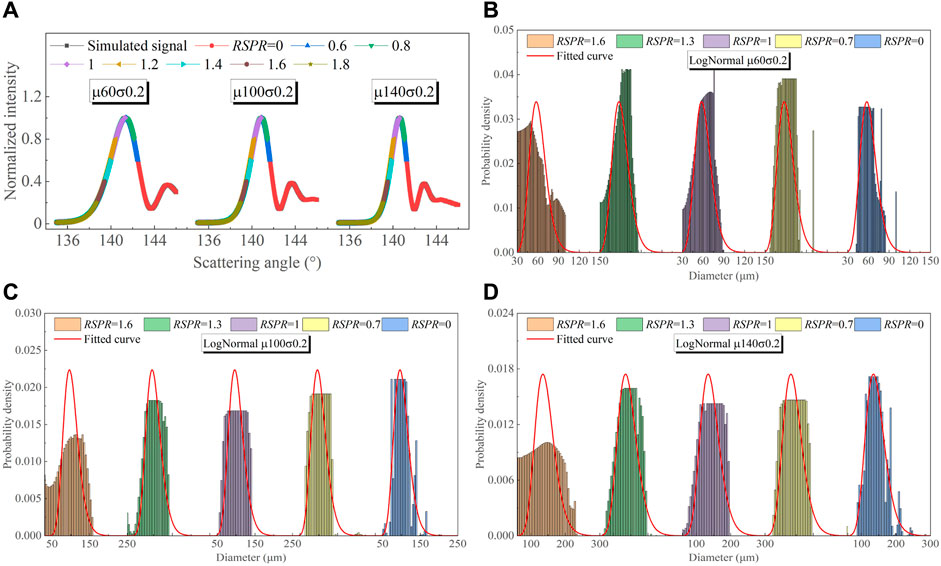
FIGURE 8. Signal fitting results of the simulated global rainbows of droplets with three different log-normal size distributions at different RSPR: fitted global rainbows for (A) μ = 60 μm, σ = 0.2 μm, μ = 100 μm, σ = 0.2 μm, μ = 140 μm, σ = 0.2 μm, and retrieved size distributions for (B) μ = 60 μm, σ = 0.2 μm, (C) μ = 100 μm, σ = 0.2 μm, (D) μ = 140 μm, σ = 0.2 μm.

Figure 9 presents scatter and error plots that depict the mean diameters μ and refractive indices n retrieved from the global rainbows of droplets characterized by bimodal normal size distributions at different RSPR. These bimodal normal distributions are composed of two independent normal distributions (μ₁ = 50 μm, σ₁ = 10 μm and μ₂ = 100 μm, σ₂ = 20 μm) with number density ratios of Num₁:Num₂ = 60:100, 100:100, and 100:60. Through simple mathematical calculations, their expected mean diameters are found to be 81.25 μm, 75 μm, and 68.75 μm. For RSPR ≤ 1 and Num₁:Num₂ = 60:100, the errors of the retrieved n and μ are both within 0.26 × 10⁻⁴ and 5.47%. For the cases of Num₁:Num₂ = 100:100, the errors in retrieved n and μ are notably smaller than 0.24 × 10⁻⁴ and 8.78%, respectively. Similarly, for Num₁:Num₂ = 100:60, the two errors are respectively less than 0.47 × 10⁻⁴ and 13.40%. Therefore, as the proportion of the normal distribution (μ₂ = 100 μm, σ₂ = 20 μm) decreases, the retrieved refractive index and mean diameter of the droplets tend to be more dispersed, accompanied by an increase in their errors.

FIGURE 9

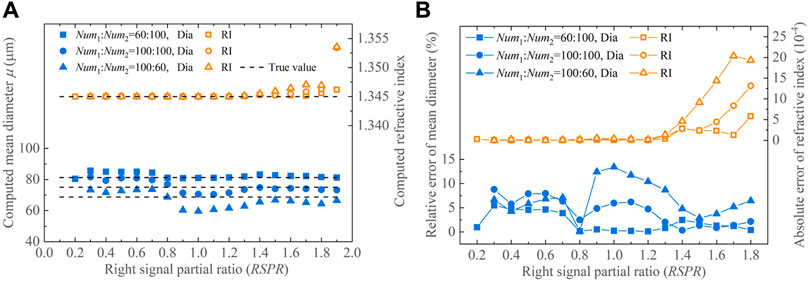
FIGURE 9. Processing results for the global rainbows of droplets with bimodal normal size distributions. (A) Retrieved mean diameters and refractive indices and (B) their errors.

Figure 10 shows the well signal fitting and size distribution of the inversion process at different RSPR. For the full rainbow, i.e., RSPR = 0, the retrieved bimodal normal size distribution fits well with the theoretical size distribution. However, when RSPR > 0, the retrieved size distribution is not satisfactory. This is due to the absence of the informative tail (the red part in Figure 10A) of the global rainbow signal of the bimodal normal distributed droplets. Meanwhile, the left incomplete rainbow signal preserves the information in the tail, and thus the retrieved bimodal distribution is normal. However, the parameter inversion errors shown in Figure 9 are reasonable, indicating that the mean diameter and refractive index obtained from the incomplete global rainbow of a bimodal normally distributed droplets are closely related to the primary bow peak, while the subsequent peaks are concerned with the droplet size distribution.

FIGURE 10

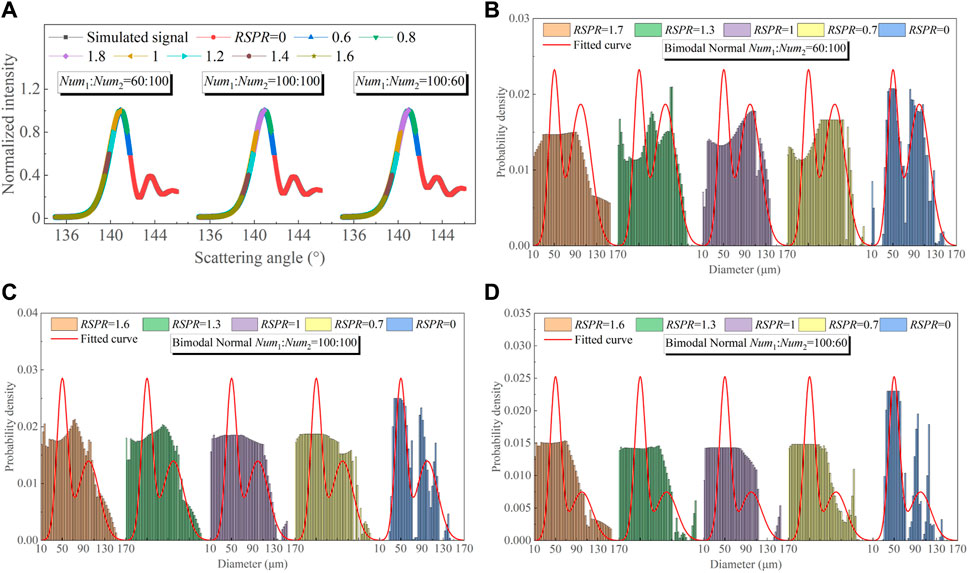
FIGURE 10. Signal fitting results of the simulated global rainbows of droplets with three different bimodal normal size distributions at different RSPR: fitted global rainbows when the number density ratios of the two distributions are (A) 60:100, 100:100, 100:60, and retrieved size distributions when the number density ratios of the two distributions are (B) 60:100, (C) 100:100, (D) 100:60.

By examining the simulated inversion results for the aforementioned three representative size distributions, it becomes evident that the errors in retrieving the mean diameter μ and refractive index n of the droplets with normal size distributions are relatively minimal compared to those with lognormal and bimodal normal distributions. Furthermore, it is worth noting that the normalized intensity value of the first trough in the global rainbow varies under different simulation conditions, and this difference imposes a limit on the setting range of the RSPR in different cases. In practical measurements, whether the incomplete signal is right-sided or left-sided depends on the actual situation, and what is needed is to determine whether the selected method is suitable for processing such signals. The inversions using the right-sided incomplete rainbow are generally less accurate than those using the left-sided incomplete rainbow because more information is preserved, especially in the cases of bimodal normal size distributions. But the processing result of the right-sided incomplete rainbows exhibits higher stability.

4 Experimental validation

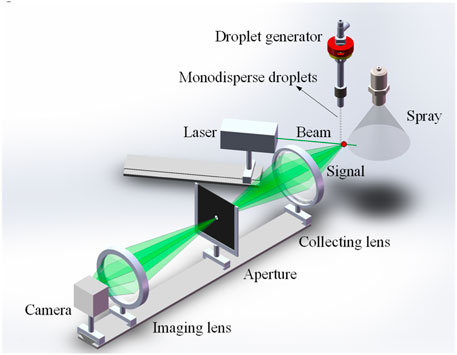
Experiments in laboratory have been conducted to further validate the conclusions drawn from the aforementioned simulation study. In Figure 11, a schematic of the experimental setup for the single-point rainbow measurement system is presented. The setup comprises a perpendicular polarized laser source (λ = 532 nm, maximum power = 200 mW, beam diameter = 2 mm, vertical polarization ratio>100:1), a collecting lens (plano-convex, D = 50 mm, f = 75 mm), an aperture, an imaging lens (plano-convex, D = 50 mm, f = 75 mm) and a recording CMOS camera (1392 × 1040, 6.45 μm/pixel, 15 fps). By illuminating droplets with the laser at a geometric rainbow angle of about 139°, the collecting lens captures the scattered rainbow signal, which is subsequently recorded on the camera via the imaging lens. The measurement volume is located 150 mm from the collecting lens, and the imaging lenses are 100 mm and 130 mm from the aperture and the camera, respectively. Placed at the conjugate position of the measurement point with respect to the collecting lens, the aperture effectively eliminates stray light from the surroundings and scattered light from droplets beyond the measurement point. This minimizes the influence of interfering light on the imaging signal camera through the imaging lens, achieving a spatial filtering effect.

FIGURE 11

FIGURE 11. Schematic of experimental setup.

Based on the measurement system described above, a monodisperse droplet stream and a hollow cone spray of deionized water are sequentially measured in ambient air at 10°C and 20°C, and the corresponding standard and global rainbows are recorded at camera exposure time of 0.2 ms and 100 ms, respectively.

4.1 Experimental partial standard rainbow

Figure 12A illustrates a pattern of typical standard rainbow captured during the experiment. It displays a low-frequency Airy structure with attached high-frequency Ripple structures. The input signal for the inversion analysis is averaged over 60 rows of pixels in the pattern, and appropriate signal inversion segments are intercepted according to the set RSPR. Figure 12B depicts the slightly noisy experimental standard rainbow signal after preprocessing, indicating that the experimentally measured droplets are highly spherical and monodisperse. Also shown is a good fit between the experimental standard rainbow signal and the calculated one at different RSPR. Subsequent analysis, as depicted in Figure 12C, D, reveals that in the range of RSPR = 0–1.0, the retrieved refractive indices are within 1.3354–1.3355, while the retrieved diameters range from 70 μm to 74 μm. These findings demonstrate the stability of the retrieved droplet parameters with only minor errors. However, when RSPR ≥ 1, the retrieved refractive indices and diameters exhibit significant fluctuations. As concluded in the previous simulation study, this phenomenon can be attributed to the absence of the primary bow peak in the standard rainbow signal, which leads to substantial inversion errors.

FIGURE 12

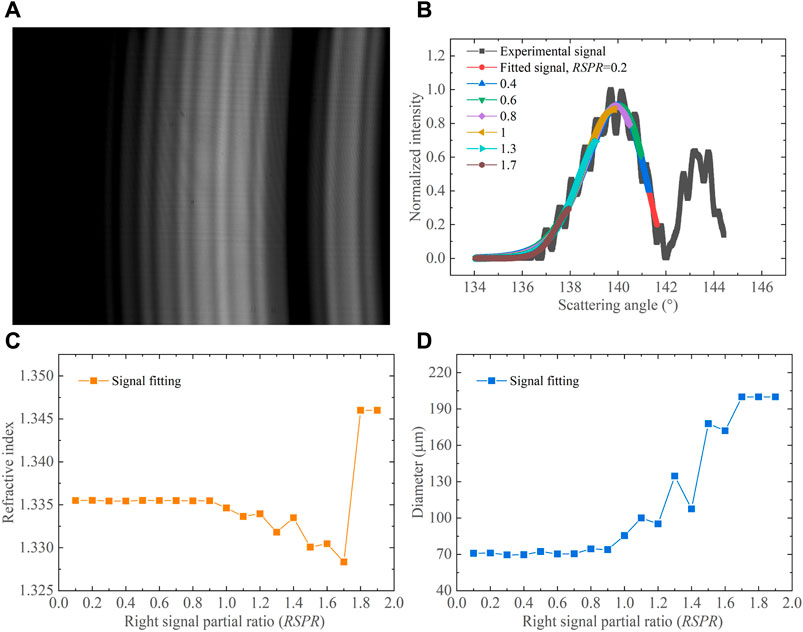
FIGURE 12. Experimental results of a typical standard rainbow of a monodisperse droplet stream: (A) experimental rainbow pattern, (B) fitted rainbows at different RSPR, (C) refractive indices, and (D) droplet diameters retrieved by signal fitting at different RSPR.

4.2 Experimental partial global rainbow

Figure 13A shows a typical experimental global rainbow pattern. It is recorded by extending the camera exposure time and enlarging the aperture size to synthetically capture numerous rainbow signals of droplets with a certain size distribution. Importantly, the global rainbow is smooth and does not contain the Ripple structure found in standard rainbow, indicating that the number of droplets is sufficient. The recorded original global rainbow signal in Figure 13B is faintly noisy, but the signals of the inversion process fit well at different RSPR. This favorable outcome is due to the ability of the signal fitting algorithm itself to eliminate weak noise when dealing with global rainbow signals [41]. Figure 13C shows the retrieved size distribution of the experimental global rainbow signal. The distribution is closer to the lognormal distribution. The right side of the experimental rainbow signal is incomplete and missing information from the right tail, which leads to an error in the retrieved size distribution. The retrieved size distributions remain stable until the RSPR = 1.5.

FIGURE 13

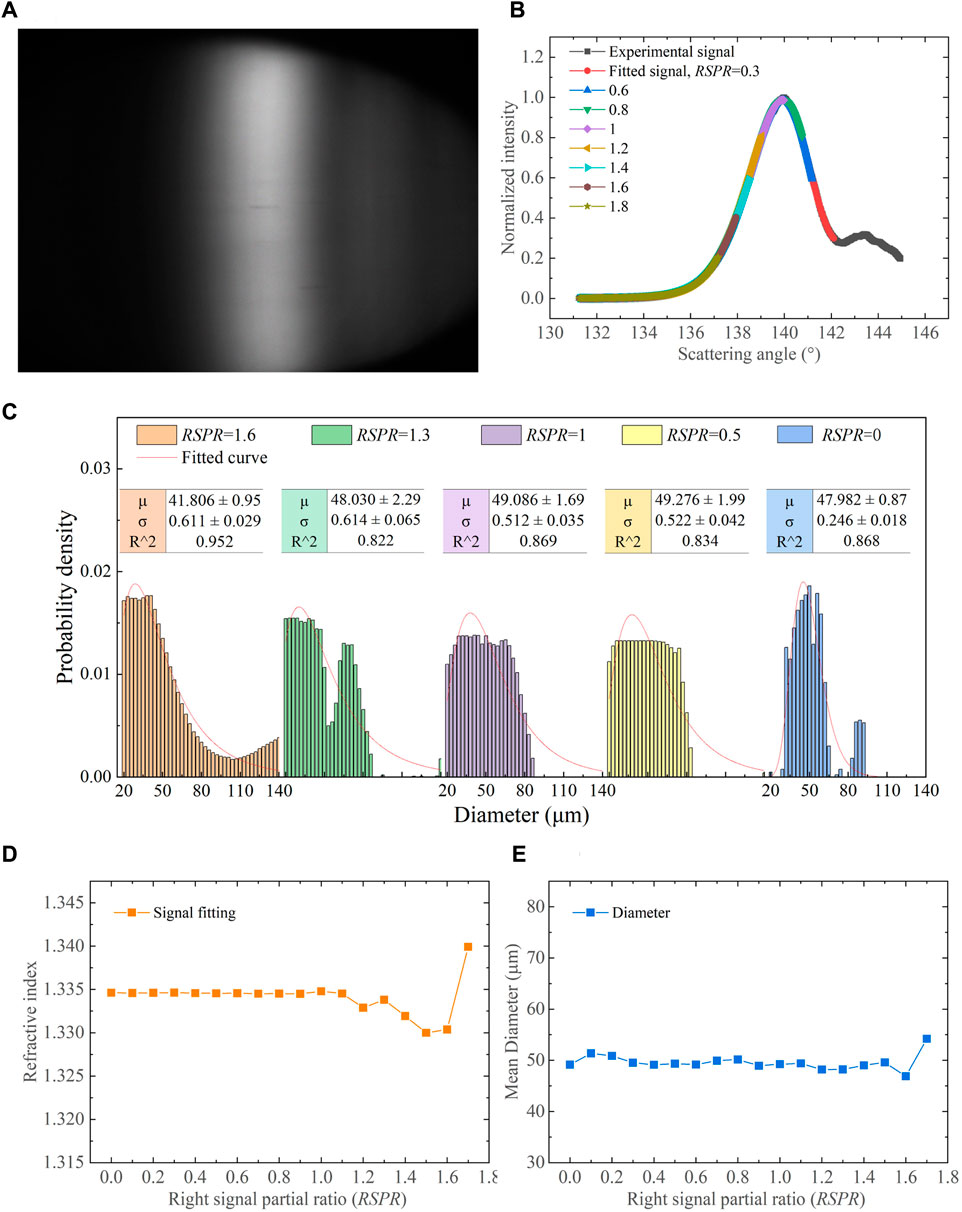
FIGURE 13. Experimental results of a typical global rainbow of spray droplets: (A) experimental rainbow pattern, (B) fitted rainbows at different RSPR, (C) size distributions, (D) refractive indices, and (E) mean diameters retrieved by signal fitting at different RSPR.

Figures 13D, E further display retrieved refractive indices n and the mean diameters μ for the right-sided incomplete global rainbow signal under different RSPR. At RSPR ≤ 1.1, the ranges of the n and μ are 1.3345–1.3348 and 48–51 μm, respectively, again demonstrating the satisfactory stability and accuracy. The retrieved refractive index fluctuates more as the RSPR increases. Whereas the retrieved mean diameters are more stable until the error reaches its maximum at RSPR of 1.5, indicating the mean diameter is more affected by the primary peak rather than the subsequent peaks. The aforementioned processed rainbow signals are laboratory ideal signals. The recorded rainbow signal from industrial spray would be noisier, partial, and maybe screened. And the detected droplets may have a refractive index gradient inside and be non-spherical. These effects should be considered.

Since this technique still depends on the assumption of spherical droplet, the upper limit of measurable droplet size is considered to be around 200 μm. Droplets larger than 200 μm have difficulty maintaining a spherical shape under their own surface tension. While the lower limit is 20 μm, because at this point the intensity of the primary rainbow is too weak to distinguish it from the ripple structures. With respect to the refractive index, it seems that the method is not limited by refractive index as long as the rainbow phenomenon exists.

5 Summary and concluding remarks

This study delves into the inversion process of the simulated and experimental right-sided incomplete standard and global rainbows, employing the signal fitting algorithm, with a focus on exploring its feasibility and accuracy. The incompleteness of the right-sided rainbow signal is characterized and defined by a dimensionless parameter, right signal partial ratio (RSPR). Typical standard and global rainbow signals, simulated by Lorenz-Mie theory, are divided into various inversion segments according to preset RSPR ranging from 0 to 2. The study analyzes in detail the retrieved refractive index, droplet size, size distribution and fitting process, and the simulation results are cross-validated by experiments, of which the main conclusions are as follows.

The errors of the droplet parameters (absolute error of the refractive index n and relative error of the droplet diameter D) retrieved from standard rainbows respectively show an increasing and decreasing trend with the preset n and D. When the preset D exceeds 60 μm and RSPR < 1, the average errors of D and n are within 4.96% and 3.04 × 10⁻⁴, respectively. In the RSPR range of 1-2, the inversion accuracy decreases significantly, resulting in large inversion errors.

In the range of 0<RSPR < 2, the errors in the refractive index n and average diameter μ of the right-sided partial incomplete global rainbow inversion increase with the RSPR. The retrieval errors for droplets with normal size distributions are smaller than that for droplets with lognormal distributions and bimodal normal distributions, with the values of respectively 0.30 × 10⁻⁴, 2.52% and 1.27 × 10⁻⁴, 9.96% and 0.47 × 10⁻⁴, 13.40% at RSPR ≤ 1. For 0<RSPR < 2, the overall trend of the errors in n and D decrease as the increased preset mean diameter μ, and the stability of the retrieved n and D decrease with the increased standard deviation σ of the size distribution.

A single-point rainbow measurement system is built to capture standard and global rainbows from monodisperse droplets and spray, respectively. In the RSPR range of 0–1.0, the refractive indices obtained from the inversion of a typical experimental standard rainbow remain stable around 1.3354–1.3355 and the diameters are between 70 and 74 μm. The refractive indices and mean diameters retrieved from an experimental global rainbow, also range from 1.3345–1.3348 and 48–51 μm, respectively. These experimental results further verify the above conclusions.

The investigation into the inversion using the right-sided incomplete rainbows presents a solution to address the challenge of incomplete recording of rainbow signals in experiments. This approach is expected to improve both experimental efficiency and utilization of experimental data. Scenarios such as different levels of noise effect, non-spherical droplets, droplets with gradient, insufficient number of recorded droplets should also be further considered when processing the partial rainbow signal.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

CL: Funding acquisition, Writing–original draft, Writing–review and editing. WP: Writing–original draft, Writing–review and editing. TL: Validation, Writing–review and editing. NL: Writing–review and editing, Resources.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (52206221); Natural Science Foundation of Jiangsu Province, China (BK20220952); Fundamental Research Funds for the Central Universities (30923011028, 2023203004); Shuangchuang Program of Jiangsu Province, China (JSSCBS20210207).

Acknowledgments

The authors would like to thank the editors and reviewers for their efforts in supporting the publication of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Cunningham MH, Frost DL. Fragmentation of a molten metal droplet in an ambient water flow. Front Phys (2023) 11:1171267. doi:10.3389/fphy.2023.1171267

CrossRef Full Text | Google Scholar

2. Itatani M, Nabika H. Self-propelled motion of an oil droplet containing a phospholipid and its stability in collectivity. Front Phys (2022) 10:849111. doi:10.3389/fphy.2022.849111

CrossRef Full Text | Google Scholar

3. Steinhausen C, Gerber V, Stierle R, Preusche A, Dreizler A, Gross J, et al. Characterisation of the transient mixing behaviour of evaporating near-critical droplets. Front Phys (2023) 11. doi:10.3389/fphy.2023.1192416

CrossRef Full Text | Google Scholar

4. Grandoni L, Méès L, Grosjean N, Leuzzi G, Monti P, Pelliccioni A, et al. Interferometric laser imaging for respiratory droplets sizing. Experiments in Fluids (2023) 64(4):80. doi:10.1007/s00348-023-03610-1

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Brunel M, Abad A, Delestre B, Frodello Q, Brunel R, Coëtmellec S, et al. Analysis and numerical correction of aberration in interferometric particle imaging. J Quantitative Spectrosc Radiative Transfer (2023) 302:108579. doi:10.1016/j.jqsrt.2023.108579

CrossRef Full Text | Google Scholar

6. Wu Y, Wen B, Zhuo Z, Wang X, Wu X. Accurate droplet depth displacement measurement with time-resolved astigmatic interferometric particle imaging. Opt Lett (2022) 47(13):3203–6. doi:10.1364/ol.461480

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sijs R, Kooij S, Holterman H, Van De Zande J, Bonn D. Drop size measurement techniques for sprays: comparison of image analysis, phase Doppler particle analysis, and laser diffraction. AIP Adv (2021) 11(1). doi:10.1063/5.0018667

CrossRef Full Text | Google Scholar

8. Mohammadi M, Nowak JL, Bertens G, Moláček J, Kumala W, Malinowski SP. Cloud microphysical measurements at a mountain observatory: comparison between shadowgraph imaging and phase Doppler interferometry. Atmos Meas Tech (2022) 15(4):965–85. doi:10.5194/amt-15-965-2022

CrossRef Full Text | Google Scholar

9. Prenting MM, Baik S-J, Dreier T, Endres T, Kempf A, Schulz C. Liquid-phase temperature in the spraysyn flame measured by two-color laser-induced fluorescence thermometry and simulated by les. Proc Combustion Inst (2023) 39(2):2621–30. doi:10.1016/j.proci.2022.07.131

CrossRef Full Text | Google Scholar

10. Guérin G, El Abed A. High throughput laser-induced fluorescence droplet micro-thermometry. Int J Heat Mass Transfer (2023) 212:124230. doi:10.1016/j.ijheatmasstransfer.2023.124230

CrossRef Full Text | Google Scholar

11. Parker HE, Sengupta S, Harish AV, Soares RR, Joensson HN, Margulis W, et al. A lab-in-a-fiber optofluidic device using droplet microfluidics and laser-induced fluorescence for virus detection. Scientific Rep (2022) 12(1):3539. doi:10.1038/s41598-022-07306-0

CrossRef Full Text | Google Scholar

12. Ulrich H, Sigl S, Möhnle M, Berrocal E, Zigan L. Droplet thermometry based on an optimized two dye two-color laser-induced fluorescence concept. Front Phys (2023) 11:11. doi:10.3389/fphy.2023.1235847

CrossRef Full Text | Google Scholar

13. Lin Z, Wu Y, Wu X, Jin J, Guan J. Holographic slurry droplet monitor: design and its application to 1000 Mw coal-fired power unit. Fuel (2022) 325:124813. doi:10.1016/j.fuel.2022.124813

CrossRef Full Text | Google Scholar

14. Asl MMZ, Dorao CA, Giacomello A, Fernandino M. Digital holographic microscopy for measurement of instantaneous contact angle of an evaporating droplet. Experiments in Fluids (2023) 64(9):152–11. doi:10.1007/s00348-023-03696-7

CrossRef Full Text | Google Scholar

15. Wang L, Li T, Zhao Y, Zhang H, Wu Y, Song G, et al. 65 khz picosecond digital off-Axis holographic imaging of 3d droplet trajectory in a kerosene swirl spray flame. Opt Lasers Eng (2023) 160:107236. doi:10.1016/j.optlaseng.2022.107236

CrossRef Full Text | Google Scholar

16. Pang Z, Zhang H, Wang Y, Zhang L, Wu Y, Wu X. Recognition of multiscale dense gel filament-droplet field in digital holography with Mo-U-net. Front Phys (2021) 9:742296. doi:10.3389/fphy.2021.742296

CrossRef Full Text | Google Scholar

17. Tong Y-K, Meng X, Zhou B, Sun R, Wu Z, Hu M, et al. Detecting the ph-dependent liquid-liquid phase separation of single levitated aerosol microdroplets via laser tweezers-Raman spectroscopy. Front Phys (2022) 10:969921. doi:10.3389/fphy.2022.969921

CrossRef Full Text | Google Scholar

18. Stiti M, Garcia S, Lempereur C, Doublet P, Kristensson E, Berrocal E. Droplet sizing in atomizing sprays using polarization ratio with structured laser illumination planar imaging. Opt Lett (2023) 48(15):4065–8. doi:10.1364/ol.495793

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Pan Y-L, Aptowicz K, Arnold J, Cheng S, Kalume A, Piedra P, et al. Review of elastic light scattering from single aerosol particles and application in bioaerosol detection. J Quantitative Spectrosc Radiative Transfer (2022) 279:108067. doi:10.1016/j.jqsrt.2022.108067

CrossRef Full Text | Google Scholar

20. Lv Q, Wu Y, Wu X. Surface temperature measurement of cooling and heating droplets by rainbow refractometry. Appl Opt (2022) 61(25):7455–62. doi:10.1364/ao.470123

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Onofri FR, Ren KF, Sentis M, Gaubert Q, Pelcé C. Experimental validation of the vectorial complex ray model on the inter-caustics scattering of oblate droplets. Opt Express (2015) 23(12):15768–73. doi:10.1364/oe.23.015768

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Duan Q, Onofri FR, Han X, Ren KF. Numerical implementation of three-dimensional vectorial complex ray model and application to rainbow scattering of spheroidal drops. Opt Express (2023) 31(21):34980–5002. doi:10.1364/oe.501640

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chiewudomrat S, Saengkaew S, Grehan G, Leveneur S, Estel L. Evaluation of refractive index gradients in droplets by rainbow technique: application to CO$$_2$$ capture by monoethanolamine aqueous spray. Experiments in Fluids (2022) 63(9):153. doi:10.1007/s00348-022-03495-6

CrossRef Full Text | Google Scholar

24. Lv Q, Wu Y, Li C, Wu X, Chen L, Cen K. Surface tension and viscosity measurement of oscillating droplet using rainbow refractometry. Opt Lett (2020) 45(24):6687–90. doi:10.1364/ol.412498

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Li C, Lv Q, Li N, Wu Y, Wu X, Weng C, et al. Dual-wavelength extinction rainbow refractometry for in-situ characterization of colloidal droplets. Powder Tech (2022) 399:117098. doi:10.1016/j.powtec.2021.117098

CrossRef Full Text | Google Scholar

26. Li C, Wu Y, Wu X, Tropea C. Simultaneous measurement of refractive index, diameter and colloid concentration of a droplet using rainbow refractometry. J Quantitative Spectrosc Radiative Transfer (2020) 245:106834. doi:10.1016/j.jqsrt.2020.106834

CrossRef Full Text | Google Scholar

27. Roth N, Anders K, Frohn A. Simultaneous measurement of temperature and size of droplets in the micrometer range. J Laser Appl (1990) 2(1):37–42. doi:10.2351/1.4745251

CrossRef Full Text | Google Scholar

28. Van Beeck J, Giannoulis D, Zimmer L, Riethmuller M. Global rainbow thermometry for droplet-temperature measurement. Opt Lett (1999) 24(23):1696–8. doi:10.1364/ol.24.001696

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wu X, Jiang H, Wu Y, Song J, Gréhan G, Saengkaew S, et al. One-dimensional rainbow thermometry system by using slit apertures. Opt Lett (2014) 39(3):638–41. doi:10.1364/ol.39.000638

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Li C, Lv Q, Li N, Wu Y, Wu X, Weng C, et al. Planar rainbow refractometry. Opt Lett (2021) 46(23):5898–901. doi:10.1364/ol.444013

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wang X, Wu Y, Xu D, Wen B, Lv Q, Wu X. Synthetic aperture rainbow refractometry. Opt Lett (2022) 47(20):5272–5. doi:10.1364/ol.471103

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Lv Q, Li C, Wu Y, Wang X, Wu X. Effect of aluminum nanoparticles addition on the evaporation of a monodisperse ethanol droplet stream. Int J Heat Mass Transfer (2022) 184:122275. doi:10.1016/j.ijheatmasstransfer.2021.122275

CrossRef Full Text | Google Scholar

33. Promvongsa J, Fungtammasan B, Gerard G, Saengkaew S, Vallikul P. A study on the evaporation of water–ethanol mixture using rainbow refractometry. J Energ Resour Tech (2017) 139(6):062002. doi:10.1115/1.4037157

CrossRef Full Text | Google Scholar

34. Lv Q, Wu Y, Wang X, Zeng L, Wu X. Measurement of interacting ethanol droplets evaporation at moderately elevated temperature and pressure using phase rainbow refractometry. Int J Heat Mass Transfer (2022) 196:123220. doi:10.1016/j.ijheatmasstransfer.2022.123220

CrossRef Full Text | Google Scholar

35. Ni Z, Hespel C, Han K, Foucher F. Evaluations of the preferential evaporation of binary droplet by rainbow technique and simulation. Exp Therm Fluid Sci (2022) 136:110649. doi:10.1016/j.expthermflusci.2022.110649

CrossRef Full Text | Google Scholar

36. Ni Z, Hespel C, Han K, Foucher F. Transient evaluations of the temperature and diameter of an evaporating droplet stream by using rainbow technique and simulation. Exp Therm Fluid Sci (2022) 131:110531. doi:10.1016/j.expthermflusci.2021.110531

CrossRef Full Text | Google Scholar

37. Li C, Peng W, Kang Y, Fan X, Huang X, Li N, et al. Rainbow refractometry using partial rainbow signals. Opt Laser Tech (2023) 158:108872. doi:10.1016/j.optlastec.2022.108872

CrossRef Full Text | Google Scholar

38. Wang W, Yu H, Shen J, Tropea C. Data inversion algorithms for droplet characterization based on simulated rainbows. J Quantitative Spectrosc Radiative Transfer (2022) 277:107986. doi:10.1016/j.jqsrt.2021.107986

CrossRef Full Text | Google Scholar

39. Laven P. Simulation of rainbows, coronas and glories using mie theory and the debye series. J Quantitative Spectrosc Radiative Transfer (2004) 89(1-4):257–69. doi:10.1016/j.jqsrt.2004.05.026

CrossRef Full Text | Google Scholar

40. Van Beeck J, Riethmuller M. Nonintrusive measurements of temperature and size of single falling raindrops. Appl Opt (1995) 34(10):1633–9. doi:10.1364/ao.34.001633

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Peng W, Li C, Li T, Huang L, Li N, Weng C. Anti-noise and denoising performance of global rainbow processing. J Quantitative Spectrosc Radiative Transfer (2023) 304:108619. doi:10.1016/j.jqsrt.2023.108619

CrossRef Full Text | Google Scholar