- 1Department of Chemical and Biological Engineering, University of Colorado Boulder, Boulder, CO, United States
- 2Biomedical Engineering Program, University of Colorado Boulder, Boulder, CO, United States
Swimming at the microscale typically involves two modes of motion: mechanical propulsion and propulsion due to field interactions. During mechanical propulsion, particles swim by reconfiguring their geometry. When propelled by field interactions, body forces such as phoretic interactions drive mobility. In this work, we employ slender-body theory to explore how a bent rod actuator propels due to a mechanical mode of swimming via hinge articulations and due to a chemical mode of swimming via diffusiophoretic interactions with a solute field. Although previous theoretical studies have examined mechanical and chemical modes of swimming in isolation, the simultaneous investigation of both modes has remained unexplored. For the mechanical mode of swimming, our calculations, both numerical and analytical, recover Purcell’s scallop theorem and show that the bent rod actuator experiences zero net displacement during reciprocal motion. Additionally, we calculate the trajectories traced by a bent rod actuator under a non-reciprocal hinge articulation, revealing that these trajectories are influenced by the amplitude of the hinge articulation, geometric asymmetry, and the angular velocity distribution between the two arms of the bent rod actuator. We provide intuitive explanations for these effects using free-body diagrams. Furthermore, we explore the motion induced by simultaneous hinge articulations and self-diffusiophoresis. We observe that hinge articulations can modify the effective phoretic forces and torques acting on the bent rod actuator, either supporting or impeding propulsion. Additionally, during self-diffusiophoretic propulsion, reciprocal hinge articulations no longer result in zero net displacement. In summary, our findings chart a new direction for designing micron-sized objects that harness both mechanical and chemical modes of propulsion synchronously, offering a mechanism to enact control over trajectories.
1 Introduction
Microscale entities orchestrate physical and biological phenomena. Bacteria play a key role in the spread of infection [1], macrophages have the capacity to affect tumor malignancy [2], T cells can infiltrate solid tumors and kill tumor cells [3], and subsurface microparticles influence contaminant transport in groundwater [4]. Inspired by these natural systems, efforts have been made to create artificial micron-sized objects endowed with programmable actions to influence phenomena at the microscale. Commonly called microrobots, these micron-sized objects are capable of treating diseases [5–9], acting as biological sensors [10, 11], and removing microplastics [12], among others. A key factor that influences the efficacy of microrobots is how capable they are at swimming in fluid environments. Due to the small length scales, viscous forces dominate over inertial forces, such that the Reynolds number (Re)
The two modes of swimming commonly used to impart motility at the microscale are, taxonomically, mechanical propulsion and propulsion due to field interactions. In the mechanical swimming mode, motility is induced by continuous geometric reconfiguration [16–20]. In field-driven propulsion, the geometry typically remains unchanged, but body forces due to interactions with a field induce motility [21–24]. In this paper, we explore how chemical fields leading to self-diffusiophoretic propulsion, i.e., a chemical mode of swimming, can be employed in concert with a mechanical mode of swimming to alter the motion of a bent rod actuator.
We first focus on the mechanical mode of swimming. In the seminal paper “Life at low Reynolds number,” Purcell outlined the scallop theorem and described the mechanical strategies that microscopic entities use to swim [15]. Purcell argued that any body with Re ≪ 1 experiences zero net displacement under reciprocal geometric reconfigurations, i.e., geometry changes that are identical when viewed forward or backward in time [15, 19]. Purcell illustrated this through the example of a microscopic scallop, whereupon opening and closing its shell, the scallop experienced zero net displacement [15]. More detailed mathematical works have confirmed the scallop theorem [25–27]. A consequence of the scallop theorem is that microscopic objects, both synthetic and biological, must use non-reciprocal swimming strokes to achieve non-zero net displacement. The simplest swimmer that Purcell described is a two-hinge swimmer that is able to achieve net displacement while still returning to the original configuration [15, 28]. In fact, microscopic biological organisms, such as Escherichia coli or spermatozoon, have developed strategies to swim by either rotating slender helical flagellar filaments or beating flexible flagella [29–33]. Advances in microfabrication and external field actuation techniques have enabled many of these biological swimming techniques to be replicated in synthetic systems [34–39].
In the field-driven mode of swimming, phoretic mechanisms, e.g., diffusiophoresis (the focus of this work) [40–52], thermophoresis [53–55], electrophoresis [56–64], and electrodiffusiophoresis [65, 66], are used to achieve directed motion at the microscale. Diffusiophoresis, the movement of particles in chemical gradients [67–80], has been a particularly rich area of research due to similarities with cell chemotaxis [81, 82]. Active diffusiophoretic particles use reactive patches on the particle surface, enabling the particle to generate local concentration gradients and achieve locomotion [40, 51, 83]. One key factor that influences self-diffusiophoretic particle motion is particle geometry [84–90]. Recently, Ganguly and Gupta have explored the effect of geometry on the diffusiophoretic motion of bent rod microparticles [42]. They found that bent rod particles with uniform or nonuniform surface activity, when constrained to move in two dimensions, have trajectories that are always circular, consistent with experimental reports [40, 55].
The aforementioned studies focus only on one mode of swimming. To the best of our knowledge, no study has explored low Re swimming due to a combination of a field-driven motion and mechanical reconfiguration. To this end, we extend the results from Ganguly and Gupta [42] by allowing the hinge connecting the self-propelling bent rod to articulate (Figure 1). We distinguish the articulating bent rod from the non-reconfigurable version by calling it a bent rod actuator. Here, hinge articulations facilitate the mechanical swimming mode, enabling the actuator to alter its geometry, whereas the surface reaction provides the field-driven mode via self-diffusiophoresis, herein called chemical swimming. The bent rod geometry is particularly useful because its configuration can be fully characterized by two dimensionless parameters, the length ratio of the two arms and the angle between the arms. In our framework, the mechanical mode is characterized by a normal surface velocity, whereas the chemical mode introduces a tangential surface velocity, see Figure 1, providing a convenient means to analyze the motion of the bent rod actuator.
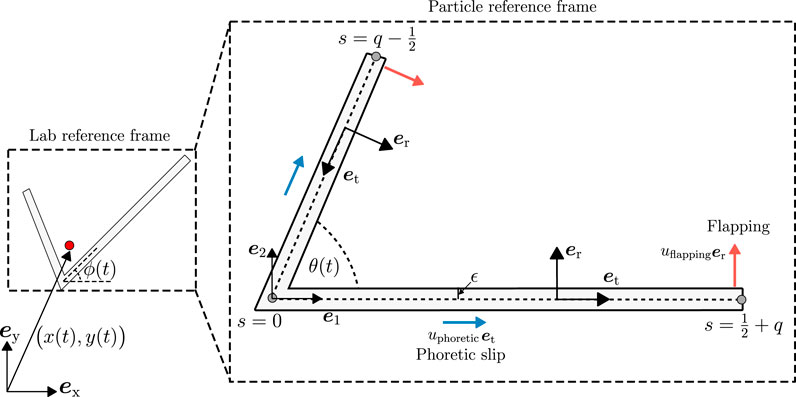
FIGURE 1. Non-dimensional geometry of a bent rod actuator. We consider the motion of a bent rod actuator with an angle θ(t) between the positive (s > 0) and negative (s < 0) arms. The angle θ(t) is allowed to vary in time via an articulating hinge at s = 0 that connects the positive and negative arms. Hinge articulations induce a normal velocity uflappinger on the surface of the actuator arms. We also consider the motion of the bent rod actuator due to a self-diffusiophoretic slip velocity uphoreticet in the direction tangential to the arms. The diffusiophoretic velocity is caused by a solute flux j(s) into the fluid surrounding the bent rod actuator imposing concentration gradients in the solution. We determine the velocity U and angular velocity Ω of the bent rod actuator in the particle frame of reference, as described with the e1 − e2 unit basis vectors. After calculating U and Ω, we integrate Eq. 14 to find the trajectory and orientation of the bent rod actuator in the laboratory frame of reference.
First, in Section 2, we expand the theoretical framework developed by Roggeveen and Stone [91] and Ganguly and Gupta [42] to compute the motion of the actuator due to both self-diffusiophoresis as well as hinge articulations. In Section 3.1 and Section 3.2, we calculate the trajectories of the actuator moving due to reciprocal hinge articulations (Figure 4) and non-reciprocal hinge articulations (Figure 5). We present an intuitive understanding of the trajectories by considering free-body diagrams (Figure 6). Lastly, we study the motion due to self-diffusiophoresis with hinge articulations to determine particle trajectories that combine mechanical and chemical modes of swimming (Section 3.3; Figures 7, 8).
2 Methods
2.1 Problem setup
We adapt the hydrodynamic calculations outlined by Roggeveen and Stone [91] and Ganguly and Gupta [42] to study the motion of a bent rod actuator, Figure 1. We employ the non-dimensional particle geometry as described by Ganguly and Gupta [42]. The bent rod actuator is composed of two arms connected with a hinge that articulates, allowing for the angle θ between the two arms to be varied in time. The two arms have a combined length ℓ, with each arm having a length of
The position along the center-line of the bent rod actuator is described by the non-dimensional arc-length s (scaled by ℓ), where
We extend the results of Ganguly and Gupta [42] to determine the dimensionless velocity U (scaled by
2.2 Slender-body theory
The velocity U and angular velocity Ω of the bent rod actuator, in the particle frame of reference, can be determined via the mobility relation,
where
The bent rod actuator can move with a velocity U1 in the e1 direction, U2 in the e2 direction, and angular velocity Ω3 about the e1 × e2 axis. The motion is caused by an effective force F1 in the e1 direction, F2 in the e2 direction, or an effective torque T3 about the e1 × e2 axis. The mobility coefficients
where xh(s) = set is the position of a point along the center-line of the bent rod and
Following similar treatments in the literature [42, 90, 94], we model the velocity induced by solute concentration gradients with
where Γ(s) is a lumped phoretic mobility parameter, cs(s) = c(s, ϵ), and
where
We note that all results shown are calculated with ϵ = 10–3. The framework is agnostic to the flux profile used; however, we use a uniform flux profile j(s) = 1 for simplicity. The concentration profile is derived for the case of small Péclet number, i.e.,
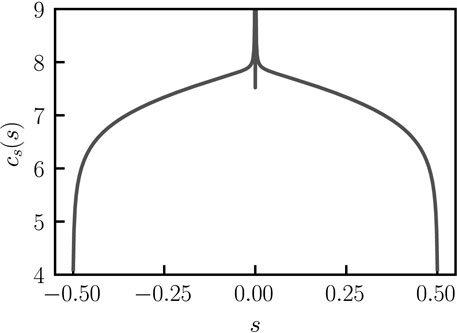
FIGURE 2. Concentration profile across the bent rod actuator. Concentration profile across the bent rod actuator for q = 0, θ = π/4, and j(s) = 1, as determined by solving Eq. 8 with Eq. 1 using the Scipy.integrate.quad function.
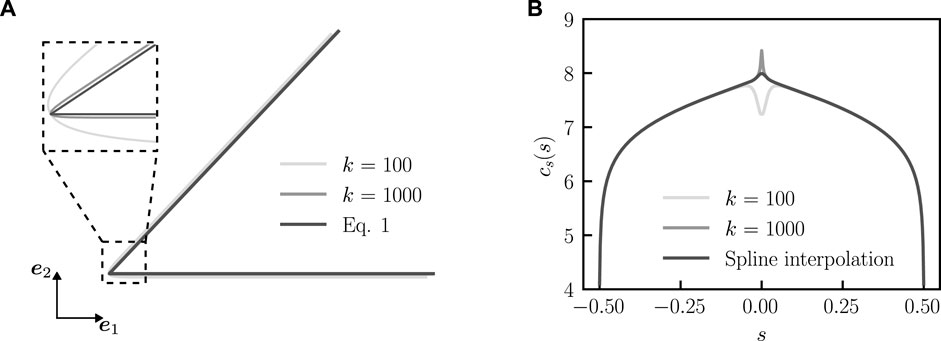
FIGURE 3. Determination of the concentration profile with approximated bent rod actuator geometry. (A) Comparison between bent rod actuator geometry, as approximated by Eq. 9 for k = 100 and k = 1,000 and Eq. 1. (B) Concentration profiles (q = 0, θ0 = π/4, and j(s) = 1) for the approximated bent rod actuator with k = 100 and k = 1,000 as well as the spline interpolated concentration profile near s = 0.
To achieve a numerical solution, we approximate the entire bent rod actuator center-line with the smooth continuous function
and k is a smoothness parameter that controls the curvature of the approximate bent rod actuator near s = 0. A larger k corresponds to a corner with higher curvature and a better approximated bent rod actuator, while a smaller k corresponds to a corner with lower curvature and a worse approximation of the bent rod actuator, see Figure 3A. To approximate the concentration profile near the hinge, we use Eq. 9 to calculate Eq. 8 with k = 100 and k = 1,000 (Figure 3B). We determine the values of s for s < 0 and s > 0, where the value of concentration profiles differs by 5% and fit the concentration profile for k = 1,000 with a fourth-order spline using the Scipy. interpolate.UnivariateSpline function (Figure 3B) between the two s values.
In addition to the phoretic contribution, we consider the motion of the bent rod actuator due to hinge articulations, θ → θ(t). The articulation of the hinge induces an angular velocity ωn for the negative arm and ωp for the positive arm. The angular velocity of each arm is related to the hinge articulation via
We write the flapping velocity as
Inserting Eq. 11 into Eq. 4 and integrating yields
The total velocity and angular velocity of the bent rod actuator is determined by a linear combination of Eqs. 7, 12:
We note that in order to use the combined phoretic and flapping contributions to the bent rod actuator motion, the Péclet number due to flapping must also be small. To justify, we briefly restore dimensions and note that
2.3 Numerical procedure
To calculate the bent rod actuator trajectory, we convert from the particle (e1 − e2) to the laboratory (ex − ey) frame of reference by employing the rotation matrix
where ϕ(t) is the angle between e1 and ex and t is the dimensionless timescale (scaled by
We apply the rotation matrix and translate the hinge and end points to determine the coordinates of the hinge and end points of the bent rod actuator in the laboratory frame of reference at each instant of time.
We then sequentially solve 14 and 16 to determine the trajectories of the bent rod actuator. Trajectories shown in Figure 4, Figure 5, Figure 6, and Figure 7 are ascertained from Eq. 16a, with the coordinates of the hinge and end points of the bent rod actuator drawn according to Eqs. 16b, 16c.
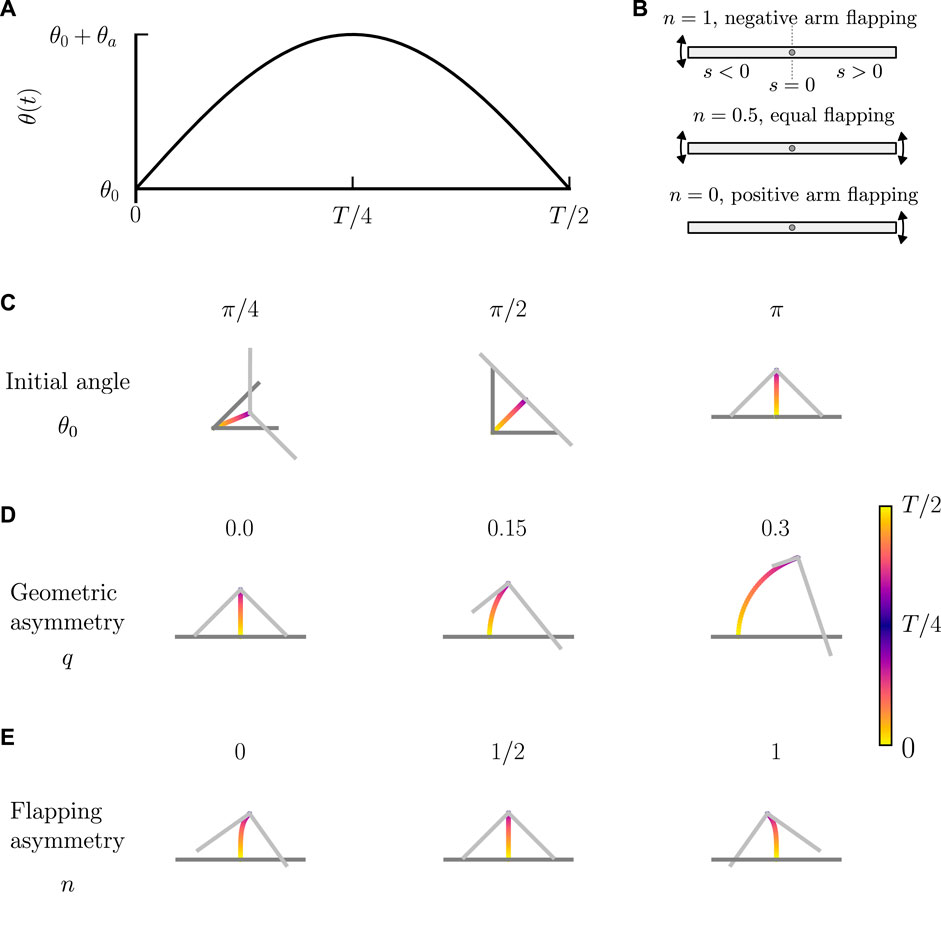
FIGURE 4. Motion of a bent rod actuator due to reciprocal hinge articulations. (A) θ(t) used for a bent rod actuator with reciprocal hinge articulations. θ(t) is characterized by an initial angle θ0, flapping amplitude θa, and period T. (B) Schematic illustration of flapping distribution between arms, as characterized by n. n = 1 describes a bent rod actuator where all changes in θ(t) are ascribed to the negative arm. n = 0.5 describes a bent rod actuator where the positive and negative arms are equally responsible for changes in θ(t). n = 0 describes a bent rod actuator where the positive arm is responsible for all changes in θ(t). Trajectory plots of rhinge over one half period for (C) θ0 ∈[π/4, π/2, π], θa = π/2, T = 1, q = 0, and n = 0.5. (D) θ0 = π, θa = π/2, T = 1, q ∈[0, 0.15, 0.3], and n = 0.5. (E) θ0 = π, θa = π/2, T = 1, q = 0, and n ∈[0, 1/2, 1].
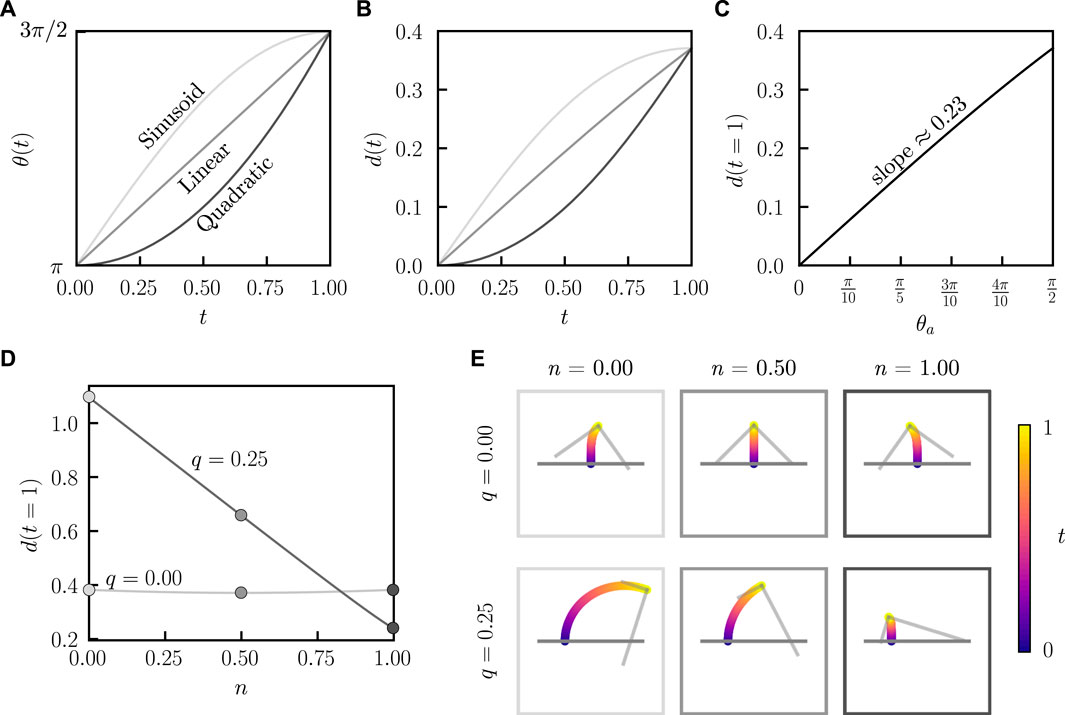
FIGURE 5. Distance traveled for a bent rod actuator with a single hinge articulation. (A) Variation of θ for a single hinge articulation from an initial angle π to a final angle 3π/2 under sinusoidal, linear, and quadratic temporal evolutions. (B) Distance traveled as a function of time for a bent rod actuator (q = 0, n = 0.5) undergoing a single hinge articulation from θ(t) = π to 3π/2 for sinusoidal, linear, and quadratic evolutions of θ(t). (C) Distance traveled at the end of a single articulation as a function of θa for linear hinge articulations (q = 0, n = 0.5, θ0 = π). (D) Distance traveled at the end of a single articulation for q = 0 and q = 0.25 as a function of n. (E) Bent rod actuator trajectories resulting from a single hinge articulation with an initial angle π and a final angle 3π/2 for q = 0, 0.25 and n = 0, 0.5, 1.
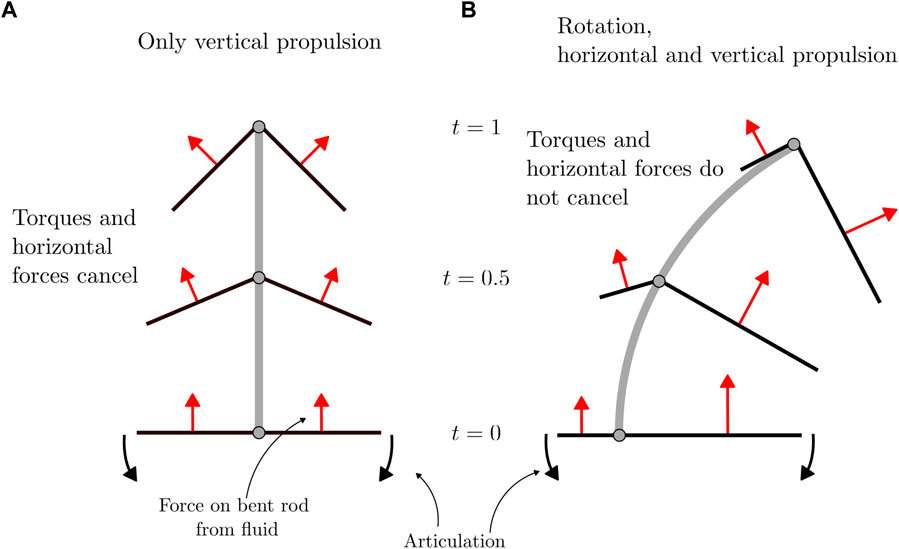
FIGURE 6. Free-body diagram of forces applied to a bent rod actuator due to hinge articulations. (A) Forces acting on a bent rod with geometric and flapping symmetry. (B) Forces acting on a bent rod with geometric asymmetry and flapping symmetry. The trajectories and bent rod are not to scale.
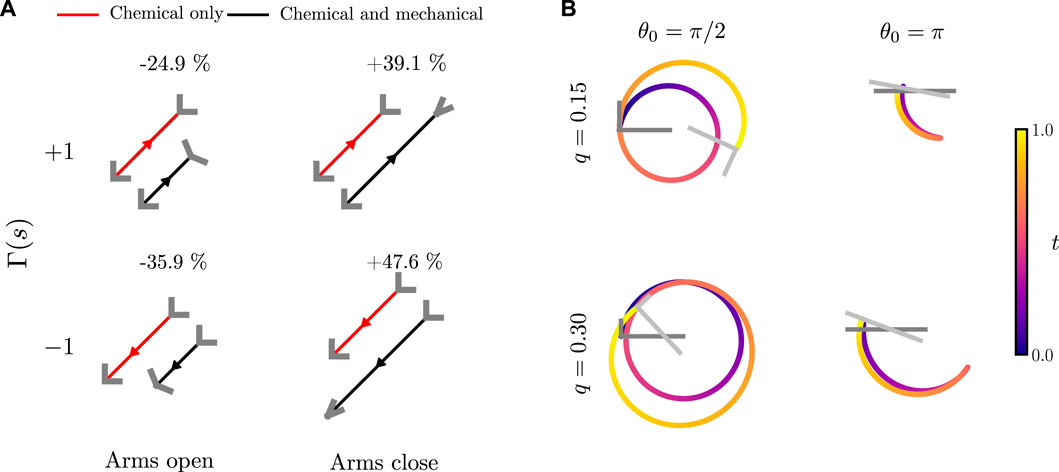
FIGURE 7. Trajectories of an active bent rod actuator undergoing hinge articulations. (A) Comparison between bent rod actuator motion due to a uniform surface activity (j(s) = 1) with a phoretic mobility Γ(s) = ±1, θ0 = π/2, q = 0, n = 0.5 and arms either opening or closing by θa = ±π/4 over t = 1 of linear temporal variation. (B) Trajectories for an active bent rod actuator undergoing sinusoidal hinge articulations, Γ(s) = 1, T = 1,
3 Results and discussion
3.1 Reciprocal motion
We first show that the bent rod actuator experiences zero net displacement while undergoing reciprocal hinge articulations without the contribution of diffusiophoresis (see Figure 4A). At t = 0, the hinge initiates articulation, changing θ(t) from an initial angle of θ0 to a final angle of θ0 + θa over a time
where
where n ∈ [0, 1] describes the distribution of angular velocities between the positive and negative arms, Figure 4B. When n = 1, only the articulation of the negative arm contributes to the changes in θ. When n = 0, only the positive arm articulates. When n = 0.5, both arms equally articulate. Thus, n = 0.5 distinguishes symmetric flapping, where both arms have the same angular velocity, and n ≠ 0.5 describes asymmetric flapping, where one arm has a larger angular velocity than the other. We solve Eq. 14, including no phoretic contributions, using Eq. 18. Figure 4C shows the trajectories of the hinge as well as the orientation of the bent rod actuator with an asymmetry parameter q = 0, flapping distribution n = 0.5, flapping amplitude
We also note that the bent rod actuator does return to its original position after undergoing a reciprocal hinge articulation. While known mathematically, to our knowledge, this is the first time where the trajectories of the bent rod actuator have been calculated numerically. It can be shown analytically via our framework that the bent rod actuator must return to its original location, as given in Eq. 14 and 12. We note that Eq. 12 can be expressed as
where
By integrating Eq. 20, we see that ϕ is a unique function of θ only (up to an arbitrary choice of ϕ(0), q, and n). Therefore, any trajectory characterized by a reciprocal choice of θ, i.e., θ(t = 0) = θ(tfinal), implies that
In summary, our framework using slender-body theory is able to recapitulate Purcell’s scallop theorem both numerically and analytically. In addition, we are able to numerically determine the trajectories taken by the bent rod actuator due to reciprocal hinge articulations. Either geometric or flapping asymmetry can be used to introduce rotation and motion along a curved trajectory.
3.2 Non-reciprocal articulation
To further understand the relationship between geometric and flapping asymmetry, we calculate the trajectories and cumulative distance traveled d(t) by a bent rod undergoing non-reciprocal hinge articulations, Figure 5A. In these simulations, the bent rod actuator starts with an initial angle of θ = π and the hinge articulates to a final angle of
An intuition for the motion of the bent rod actuator under non-reciprocal articulations can be understood by considering how forces are distributed across the bent rod arms as a function of geometric and flapping asymmetry, Figure 6. In the case of a bent rod actuator with both geometric (q = 0) as well as flapping (n = 0.5) symmetry, as the hinge articulates, the force applied to the bent rod actuator arms from the fluid is distributed across both arms, see Figure 6A. This leads to a net effective force in the ey direction. While the force does have a component in the ex direction, the contributions from the positive and negative arms cancel, leading to no net force in the ex direction. The same is true for the effective torque about the e1 × e2 axis applied to the center of mass of the bent rod actuator. As the arms are of the same length and flapping is symmetric, the torque produced by both arms is equal and opposite, leading to a net zero effective torque. When geometric (or similarly flapping) asymmetry is introduced (q > 0.5, Figure 6B), the effective force applied to the bent rod actuator due to hinge articulations is biased toward the longer arm. In this case, the effective force in the ey direction remains non-zero; however, the contributions to effective force in the ex direction as well as the effective torque about the e1 × e2 axis no longer cancels between the two arms.
In summary, an intuitive picture of bent rod actuator motion can be built by considering how forces acting on the bent rod from the fluid are distributed at each instant of time. In the case of flapping, this is done by considering normal force components distributed across the arms and decomposing the forces into their constitutive laboratory frame of reference components.
3.3 Phoretic motion with hinge articulations
To investigate interactions between the chemical mode of swimming from self-diffusiophoresis and the mechanical mode of swimming due to hinge articulations, we begin by comparing trajectories and the change in total distance traveled due to either a positive or negative Γ(s) when the arms open and close, Figure 7A. We notice that the bent rod actuator always moves further when closing its arms, independent of whether the phoretic mobility is positive or negative. This is due to two effects. First, as the angle between the arms decreases, the concentration difference between the hinge and end points increases [42]. As the effective phoretic forces, see Eq. 7, are proportional to the concentration differences, this leads to a larger effective force and, thus, a larger velocity. The inverse is true for the scenario when the arms are opening. As the arms open, the concentration difference between the hinge and end points decreases, leading to a smaller effective phoretic force and a shorter distance traveled. Second, as the arms close, the projected surface area along the direction of motion decreases, decreasing the drag and leading to a larger distance traveled over a given period of time.
While changes to phoretic motion are the primary reason for changes in the total distance traveled, a subtle effect involving the competition between mechanical and chemical swimming can also be noticed. When the arms open, the bent rod with a positive phoretic mobility experiences a smaller decrease in the total distance traveled when compared to the bent rod with a negative phoretic mobility. This is because the effective force acting on the bent rod actuator due to a positive phoretic mobility and the arms opening are in the same direction. Similarly, the bent rod actuator with a negative phoretic mobility and arms that close experiences a larger increase in the total distance traveled.
We also investigate how θ0 and q affect the motion of a self-diffusiophoretic bent rod actuator undergoing sinusoidal hinge articulations described by
We briefly discuss how the relative contributions of hinge articulations and diffusiophoresis impact the trajectory of the bent rod actuator. By increasing j(s), the contribution of diffusiophoresis relative to hinge articulations increases. Conversely, by increasing the articulation amplitude θa, the contribution of diffusiophoresis relative to hinge articulations decreases. Figure 8 shows the trajectories of a bent rod actuator moving due to both hinge articulations and diffusiophoresis, with j(s) increasing while keeping θa constant. As j(s) increases, the bent rod actuator traces a larger distance (though not necessarily displacement) during a given time period. This is attributed to the increase in the effective force and torque acting on the bent rod caused by the increasing j(s). Additionally, increasing j(s) causes the trajectories to become more circular and approach the trajectory of a self-diffusiophoretic bent rod without hinge articulations (refer to Supplementary Video S2) [42].
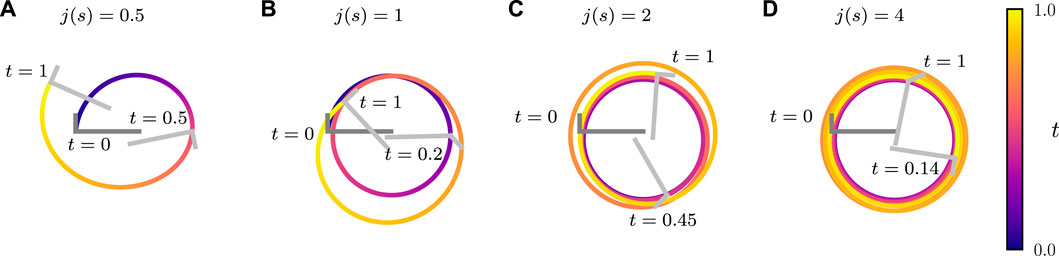
FIGURE 8. Trajectories of an active bent rod actuator undergoing sinusoidal hinge articulations with
4 Applications to biomedical microrobots
An improved understanding of the motion of a bent rod actuator with both mechanical and chemical swimming modes has direct applicability to the growing field of biomedical microrobots. Biomedical microrobots have found use in the delivery of small-molecule drugs, living cells, and contrast agents through complex biological media for precision medicine [8]. Primarily, the ability to enact real-time geometric changes and predict the resultant motion can have implications for the design of biomedical microrobots. First, real-time changes to microrobot geometry may allow the robot to switch between characteristic trajectories. In one sense, the ability to switch between straight-line trajectories and circular trajectories could enable enhanced motion through porous media [61]. In a similar manner, the direction of the microrobot for a given propulsion mechanism can be changed through flapping asymmetry and geometry alterations, for instance, by flapping a single arm to induce rotation that alters the direction of propulsion (Figure 5). This may be particularly useful for microrobots traversing through complex environments with multiple barriers, wherein real-time changes to trajectories may allow the swimmer to move around barriers and potentially escape confinement [96]. We note that the proposed hydrodynamic model of the bent rod actuator would need to be significantly modified to account for the presence of boundaries and is currently limited to two-dimensional motion. This warrants further studies that expand motion to three dimensions and include the effects of boundaries.
Experimental realizations of microrobots with similar geometries to the bent rod actuators exist [97–100]. These systems use polymeric cubes, typically fabricated at the micron scale with photolithography, coated with a ferromagnetic patch, that assemble into linear chains with hinges in a constant uniform magnetic field [97–99]. Systems could also be fabricated at the nanoscale using electron-beam lithography [101]. Upon turning the external magnetic field on and off, the assemblies open and close, allowing them to propel in non-Newtonian fluids, such as xanthan gum solutions for shear thinning fluids or fumed silica suspensions for shear thickening fluids, by using time asymmetric hinge articulations [97, 100]. Endowing such microrobots with a chemical mode of propulsion could be enabled by conjugating enzymes, such as urease, to the particles, allowing the microrobot to generate propulsion by converting urea, a chemical commonly found in the human body, to CO2 and NH3 [102]. In summary, our results will encourage scientists and engineers aiming to design microrobots with multiple swimming modalities for biomedical applications.
5 Conclusion
In this article, we have developed a mobility framework to calculate the trajectories taken by a bent rod actuator under chemical and mechanical modes of swimming. In the mechanical mode, where propulsion is induced by hinge articulations, we show numerically and analytically that Purcell’s Scallop theorem holds. To better understand the role of geometry on the bent rod actuator motion, we calculate the trajectories traced under non-reciprocal hinge articulations. Rotation and curved trajectories can be induced either through geometric or flapping asymmetry. This is explained through free-body diagrams that consider how forces are distributed across the bent rod actuator’s arms. To further explore the bent rod actuator’s motion, we also include self-diffusiophoresis to study the interplay between chemical and mechanical modes of swimming. We find that hinge articulations either aid or hinder self-diffusiophoretic motion. These effects are caused by changes to mobility, increasing or decreasing the effective phoretic force, and by the interference between the effective phoretic and flapping forces. Our work invites future studies to expand to swimmers with more than one hinge [28, 98, 99], to study swimmers in non-Newtonian fluids [48, 97, 103, 104], and to incorporate optimization schemes to control microrobot trajectories via hinge articulations. One intriguing direction is to extend the analysis to non-Newtonian fluids by scaling the applied forces in response to a viscosity that depends on the hinge articulation rate [100]. Another interesting possibility is to explore simultaneous mechanical reconfiguration with other methods of field-driven propulsion, such as electrochemical reactions [105], where the time dependence of the reactive flux [65, 66, 106] is known to impact the directed assembly of particles [107]. This may further influence the ability of swimmers to transport through confined porous media [108, 109], where it is known that both motion [110, 111] and the distribution of electrochemical species are altered [112, 113].
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
RR: writing–original draft and writing–review and editing. ArG: writing–review and editing. CB: writing–review and editing. CS: writing–review and editing. AnG: writing–original draft and writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. RR thanks the National Science Foundation (DGE—2040434) Graduate Research Fellowship for financial support. CB thanks the Discovery Learning Apprenticeship program for financial support. AG thanks the National Science Foundation (CBET—2238412) CAREER award for financial support. The authors acknowledge the donors of the American Chemical Society Petroleum Research Fund for partial support of this research. CS thanks the National Science Foundation (CBET—2143419) CAREER award for financial support. CS is a Pew Scholar in the Biomedical Sciences, supported by the Pew Charitable Trusts. He thanks the Packard Foundation for their support of this project.
Acknowledgments
The authors would like to acknowledge Filipe Henrique, Collin Kemper, and Gesse Roure for their insightful discussions leading to the completion of this work.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1307691/full#supplementary-material
References
1. Ribet D, Cossart P. How bacterial pathogens colonize their hosts and invade deeper tissues. Microbes Infect (2015) 17:173–83. doi:10.1016/j.micinf.2015.01.004
2. Williams CB, Yeh ES, Soloff AC. Tumor-associated macrophages: unwitting accomplices in breast cancer malignancy. NPJ Breast Cancer (2016) 2:15025. doi:10.1038/npjbcancer.2015.25
3. Lanitis E, Dangaj D, Irving M, Coukos G. Mechanisms regulating T-cell infiltration and activity in solid tumors. Ann Oncol (2017) 28:xii18–32. doi:10.1093/annonc/mdx238
4. Kanti Sen T, Khilar KC. Review on subsurface colloids and colloid-associated contaminant transport in saturated porous media. Adv Colloid Interf Sci (2006) 119:71–96. doi:10.1016/j.cis.2005.09.001
5. Cong Z, Tang S, Xie L, Yang M, Li Y, Lu D, et al. Magnetic-powered Janus cell robots loaded with oncolytic adenovirus for active and targeted virotherapy of bladder cancer. Adv Mater (2022) 34:2201042. doi:10.1002/adma.202201042
6. Gwisai T, Mirkhani N, Christiansen MG, Nguyen TT, Ling V, Schuerle S. Magnetic torque–driven living microrobots for increased tumor infiltration. Sci Robotics (2022) 7:eabo0665. doi:10.1126/scirobotics.abo0665
7. Lee JG, Raj RR, Thome CP, Day NB, Martinez P, Bottenus N, et al. Bubble-based microrobots with rapid circular motions for epithelial pinning and drug delivery. Small (2023) 19:2300409. doi:10.1002/smll.202300409
8. Lee JG, Raj RR, Day NB, Shields IVCW. Microrobots for biomedicine: unsolved challenges and opportunities for translation. ACS Nano (2023) 17:14196–204. doi:10.1021/acsnano.3c03723
9. De Ávila BEF, Angsantikul P, Li J, Angel Lopez-Ramirez M, Ramírez-Herrera DE, Thamphiwatana S, et al. Micromotor-enabled active drug delivery for in vivo treatment of stomach infection. Nat Commun (2017) 8:272. doi:10.1038/s41467-017-00309-w
10. Thome CP, Hoertdoerfer WS, Bendorf JR, Lee JG, Shields IVCW. Electrokinetic active particles for motion-based biomolecule detection. Nano Lett (2023) 23:2379–87. doi:10.1021/acs.nanolett.3c00319
11. Mohagheghian E, Luo J, Yavitt FM, Wei F, Bhala P, Amar K, et al. Quantifying stiffness and forces of tumor colonies and embryos using a magnetic microrobot. Sci Robotics (2023) 8:eadc9800. doi:10.1126/scirobotics.adc9800
12. Zhou H, Mayorga-Martinez CC, Pumera M. Microplastic removal and degradation by mussel-inspired adhesive magnetic/enzymatic microrobots. Small Methods (2021) 5:2100230. doi:10.1002/smtd.202100230
14. Abbott JJ, Peyer KE, Lagomarsino MC, Zhang L, Dong L, Kaliakatsos IK, et al. How should microrobots swim? Int J Robotics Res (2009) 28:1434–47. doi:10.1177/0278364909341658
16. Elfring GJ, Lauga E. Theory of locomotion through complex fluids. Complex Fluids Biol Syst Exp Theor Comput (2015) 283–317. doi:10.1007/978-1-4939-2065-5_8
17. Elfring GJ. A note on the reciprocal theorem for the swimming of simple bodies. Phys Fluids (2015) 27. doi:10.1063/1.4906993
18. Nasouri B, Khot A, Elfring GJ. Elastic two-sphere swimmer in Stokes flow. Phys Rev Fluids (2017) 2:043101. doi:10.1103/physrevfluids.2.043101
20. Lauga E, Powers TR. The hydrodynamics of swimming microorganisms. Rep Prog Phys (2009) 72:096601. doi:10.1088/0034-4885/72/9/096601
21. Moran JL, Posner JD. Phoretic self-propulsion. Annu Rev Fluid Mech (2017) 49:511–40. doi:10.1146/annurev-fluid-122414-034456
22. Michelin S, Lauga E. Phoretic self-propulsion at finite péclet numbers. J Fluid Mech (2014) 747:572–604. doi:10.1017/jfm.2014.158
23. Saha S, Yariv E. Phoretic self-propulsion of a slightly inhomogeneous disc. J Fluid Mech (2022) 940:A24. doi:10.1017/jfm.2022.237
24. Domínguez A, Popescu MN. A fresh view on phoresis and self-phoresis. Curr Opin Colloid Interf Sci (2022) 61:101610. doi:10.1016/j.cocis.2022.101610
25. Ishimoto K, Yamada M. A coordinate-based proof of the scallop theorem. SIAM J Appl Math (2012) 72:1686–94. doi:10.1137/110853297
26. Shapere A, Wilczek F. Geometry of self-propulsion at low Reynolds number. J Fluid Mech (1989) 198:557–85. doi:10.1017/S002211208900025X
27. Yariv E. Self-propulsion in a viscous fluid: arbitrary surface deformations. J Fluid Mech (2006) 550:139–48. doi:10.1017/S002211200500830X
28. Becker LE, Koehler SA, Stone HA. On self-propulsion of micro-machines at low Reynolds number: purcells three-link swimmer. J Fluid Mech (2003) 490:15–35. doi:10.1017/S0022112003005184
32. Lowe G, Meister M, Berg HC. Rapid rotation of flagellar bundles in swimming bacteria. Nature (1987) 325:637–40. doi:10.1038/325637a0
33. Ishijima S, Oshio S, Mohri H. Flagellar movement of human spermatozoa. Gamete Res (1986) 13:185–97. doi:10.1002/mrd.1120130302
34. Medina-Sánchez M, Schwarz L, Meyer AK, Hebenstreit F, Schmidt OG. Cellular cargo delivery: toward assisted fertilization by sperm-carrying micromotors. Nano Lett (2016) 16:555–61. doi:10.1021/acs.nanolett.5b04221
35. Gu H, Boehler Q, Cui H, Secchi E, Savorana G, De Marco C, et al. Magnetic cilia carpets with programmable metachronal waves. Nat Commun (2020) 11:2637. doi:10.1038/s41467-020-16458-4
36. Hou Y, Wang H, Zhong S, Qiu Y, Shi Q, Sun T, et al. Design and control of a surface-dimple-optimized helical microdrill for motions in high-viscosity fluids. IEEE/ASME Trans Mechatronics (2022) 28:429–39. doi:10.1109/TMECH.2022.3201012
37. Dillinger C, Nama N, Ahmed D. Ultrasound-activated ciliary bands for microrobotic systems inspired by starfish. Nat Commun (2021) 12:6455. doi:10.1038/s41467-021-26607-y
38. Orbay S, Ozcelik A, Bachman H, Huang TJ. Acoustic actuation of in situ fabricated artificial cilia. J Micromechanics Microengineering (2018) 28:025012. doi:10.1088/1361-6439/aaa0ae
39. Huang HW, Uslu FE, Katsamba P, Lauga E, Sakar MS, Nelson BJ. Adaptive locomotion of artificial microswimmers. Sci Adv (2019) 5:eaau1532. doi:10.1126/sciadv.aau1532
40. Venkateshwar Rao D, Reddy N, Fransaer J, Clasen C. Self-propulsion of bent bimetallic Janus rods. J Phys D: Appl Phys (2019) 52:014002. doi:10.1088/1361-6463/aae6f6
41. Zhou C, Zhang H, Tang J, Wang W. Photochemically powered AgCl Janus micromotors as a model system to understand ionic self-diffusiophoresis. Langmuir (2018) 34:3289–95. doi:10.1021/acs.langmuir.7b04301
42. Ganguly A, Gupta A. Going in circles: slender body analysis of a self-propelling bent rod. Phys Rev Fluids (2023) 8:014103. doi:10.1103/physrevfluids.8.014103
43. Golestanian R, Liverpool TB, Ajdari A. Propulsion of a molecular machine by asymmetric distribution of reaction products. Physcial Rev Lett (2005) 94:220801. doi:10.1103/PhysRevLett.94.220801
44. Howse JR, Jones RAL, Ryan AJ, Gough T, Vafabakhsh R, Golestanian R. Self-motile colloidal particles: from directed propulsion to random walk. Physcial Rev Lett (2007) 99:048102. doi:10.1103/PhysRevLett.99.048102
45. Rückner G, Kapral R. Chemically powered nanodimers. Physcial Rev Lett (2007) 98:150603. doi:10.1103/PhysRevLett.98.150603
46. Paxton WF, Kistler KC, Olmeda CC, Sen A, St Angelo SK, Cao Y, et al. Catalytic nanomotors: autonomous movement of striped nanorods. J Am Chem Soc (2004) 126:13424–31. doi:10.1021/ja047697z
47. Tătulea-Codrean M, Lauga E. Artificial chemotaxis of phoretic swimmers: instantaneous and long-time behaviour. J Fluid Mech (2018) 856:921–57. doi:10.1017/jfm.2018.718
48. Datt C, Natale G, Hatzikiriakos SG, Elfring GJ. An active particle in a complex fluid. J Fluid Mech (2017) 823:675–88. doi:10.1017/jfm.2017.353
49. Natale G, Datt C, Hatzikiriakos SG, Elfring GJ. Autophoretic locomotion in weakly viscoelastic fluids at finite péclet number. Phys Fluids (2017) 29. doi:10.1063/1.5002729
50. Uspal W, Popescu MN, Dietrich S, Tasinkevych M. Self-propulsion of a catalytically active particle near a planar wall: from reflection to sliding and hovering. Soft Matter (2015) 11:434–8. doi:10.1039/c4sm02317j
51. Popescu MN, Uspal WE, Bechinger C, Fischer P. Chemotaxis of active Janus nanoparticles. Nano Lett (2018) 18:5345–9. doi:10.1021/acs.nanolett.8b02572
52. Davis AM, Yariv E. Self-diffusiophoresis of Janus particles at large Damköhler numbers. J Eng Math (2022) 133:5. doi:10.1007/s10665-022-10213-y
53. Lin X, Si T, Wu Z, He Q. Self-thermophoretic motion of controlled assembled micro-/nanomotors. Phys Chem Chem Phys (2017) 19:23606–13. doi:10.1039/c7cp02561k
54. Jiang HR, Yoshinaga N, Sano M. Active motion of a Janus particle by self-thermophoresis in a defocused laser beam. Phys Rev Lett (2010) 105:268302. doi:10.1103/physrevlett.105.268302
55. Kümmel F, Ten Hagen B, Wittkowski R, Buttinoni I, Eichhorn R, Volpe G, et al. Circular motion of asymmetric self-propelling particles. Physcial Rev Lett (2013) 110:198302. doi:10.1103/physrevlett.110.198302
56. Shields IVCW, Han K, Ma F, Miloh T, Yossifon G, Velev OD. Supercolloidal spinners: complex active particles for electrically powered and switchable rotation. Adv Funct Mater (2018) 28:1803465. doi:10.1002/adfm.201803465
57. Gangwal S, Cayre OJ, Bazant MZ, Velev OD. Induced-charge electrophoresis of metallodielectric particles. Physcial Rev Lett (2008) 100:058302. doi:10.1103/physrevlett.100.058302
58. Squires TM, Bazant MZ. Breaking symmetries in induced-charge electro-osmosis and electrophoresis. J Fluid Mech (2006) 560:65–101. doi:10.1017/s0022112006000371
59. Bazant MZ, Squires TM. Induced-charge electrokinetic phenomena. Curr Opin Colloid Interf Sci (2010) 15:203–13. doi:10.1016/j.cocis.2010.01.003
60. Pascall AJ, Squires TM. Induced charge electro-osmosis over controllably contaminated electrodes. Physcial Rev Lett (2010) 104:088301. doi:10.1103/physrevlett.104.088301
61. Lee JG, Brooks AM, Shelton WA, Bishop KJ, Bharti B. Directed propulsion of spherical particles along three dimensional helical trajectories. Nat Commun (2019) 10:2575. doi:10.1038/s41467-019-10579-1
62. Lee JG, Al Harraq A, Bishop KJ, Bharti B. Fabrication and electric field-driven active propulsion of patchy microellipsoids. The J Phys Chem B (2021) 125:4232–40. doi:10.1021/acs.jpcb.1c01644
63. Brooks AM, Tasinkevych M, Sabrina S, Velegol D, Sen A, Bishop KJ. Shape-directed rotation of homogeneous micromotors via catalytic self-electrophoresis. Nat Commun (2019) 10:495. doi:10.1038/s41467-019-08423-7
64. Brooks AM, Sabrina S, Bishop KJ. Shape-directed dynamics of active colloids powered by induced-charge electrophoresis. Proc Natl Acad Sci (2018) 115:E1090–E1099. doi:10.1073/pnas.1711610115
65. Wang K, Leville S, Behdani B, Batista CAS. Long-range transport and directed assembly of charged colloids under aperiodic electrodiffusiophoresis. Soft Matter (2022) 18:5949–59. doi:10.1039/d2sm00631f
66. Jarvey N, Henrique F, Gupta A. Asymmetric rectified electric and concentration fields in multicomponent electrolytes with surface reactions. Soft Matter (2023) 19:6032–45. doi:10.1039/D3SM00823A
67. Velegol D, Garg A, Guha R, Kar A, Kumar M. Origins of concentration gradients for diffusiophoresis. Soft Matter (2016) 12:4686–703. doi:10.1039/C6SM00052E
68. Shim S. Diffusiophoresis, diffusioosmosis, and microfluidics: surface-flow-driven phenomena in the presence of flow. Chem Rev (2022) 122:6986–7009. doi:10.1021/acs.chemrev.1c00571
69. Shin S, Um E, Sabass B, Ault JT, Rahimi M, Warren PB, et al. Size-dependent control of colloid transport via solute gradients in dead-end channels. Proc Natl Acad Sci (2016) 113:257–61. doi:10.1073/pnas.1511484112
70. Shin S, Ault JT, Feng J, Warren PB, Stone HA. Low-cost zeta potentiometry using solute gradients. Adv Mater (2017) 29:1701516. doi:10.1002/adma.201701516
71. Gupta A, Rallabandi B, Stone HA. Diffusiophoretic and diffusioosmotic velocities for mixtures of valence-asymmetric electrolytes. Phys Rev Fluids (2019) 4:043702. doi:10.1103/physrevfluids.4.043702
72. Gupta A, Shim S, Stone HA. Diffusiophoresis: from dilute to concentrated electrolytes. Soft Matter (2020) 16:6975–84. doi:10.1039/d0sm00899k
73. Alessio BM, Shim S, Mintah E, Gupta A, Stone HA. Diffusiophoresis and diffusioosmosis in tandem: two-dimensional particle motion in the presence of multiple electrolytes. Phys Rev Fluids (2021) 6:054201. doi:10.1103/PhysRevFluids.6.054201
74. Alessio BM, Shim S, Gupta A, Stone HA. Diffusioosmosis-driven dispersion of colloids: a taylor dispersion analysis with experimental validation. J Fluid Mech (2022) 942:A23. doi:10.1017/jfm.2022.321
75. Raj RR, Shields IVCW, Gupta A. Two-dimensional diffusiophoretic colloidal banding: optimizing the spatial and temporal design of solute sinks and sources. Soft Matter (2023) 19:892–904. doi:10.1039/d2sm01549h
76. Banerjee A, Squires TM. Long-range, selective, on-demand suspension interactions: combining and triggering soluto-inertial beacons. Sci Adv (2019) 5:eaax1893. doi:10.1126/sciadv.aax1893
77. Banerjee A, Williams I, Azevedo RN, Helgeson ME, Squires TM. Soluto-inertial phenomena: designing long-range, long-lasting, surface-specific interactions in suspensions. Proc Natl Acad Sci (2016) 113:8612–7. doi:10.1073/pnas.1604743113
78. Banerjee A, Vogus DR, Squires TM. Design strategies for engineering soluto-inertial suspension interactions. Phys Rev E (2019) 100:052603. doi:10.1103/PhysRevE.100.052603
79. Alessio BM, Gupta A. Diffusiophoresis-enhanced turing patterns. Sci Adv (2023) 9:eadj2457. doi:10.1126/sciadv.adj2457
80. Ganguly A, Alessio BM, Gupta A. Diffusiophoresis: a novel transport mechanism - fundamentals, applications, and future opportunities. Front Sensors manuscript under final Rev Publ (2023). doi:10.3389/fsens.2023.1322906
81. Kalinin YV, Jiang L, Tu Y, Wu M. Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophysical J (2009) 96:2439–48. doi:10.1016/j.bpj.2008.10.027
82. Alessio BM, Gupta A. Diffusiophoresis-enhanced turing patterns (2023). arXiv preprint arXiv:2305.11372.
83. Sharifi-Mood N, Koplik J, Maldarelli C. Diffusiophoretic self-propulsion of colloids driven by a surface reaction: the sub-micron particle regime for exponential and van der Waals interactions. Phys Fluids (2013) 25:012001. doi:10.1063/1.4772978
84. Poehnl R, Popescu MN, Uspal WE. Axisymmetric spheroidal squirmers and self-diffusiophoretic particles. J Phys Condensed Matter (2020) 32:164001. doi:10.1088/1361-648x/ab5edd
85. Ebbens SJ, Howse JR. Direct observation of the direction of motion for spherical catalytic swimmers. Langmuir (2011) 27:12293–6. doi:10.1021/la2033127
86. Shemi O, Solomon MJ. Self-propulsion and active motion of Janus ellipsoids. J Phys Chem B (2018) 122:10247–55. doi:10.1021/acs.jpcb.8b08303
87. Hsu JP, Luu XC, Hsu WL. Diffusiophoresis of an ellipsoid along the axis of a cylindrical pore. J Phys Chem B (2010) 114:8043–55. doi:10.1021/jp1039157
88. Daddi-Moussa-Ider A, Nasouri B, Vilfan A, Golestanian R. Optimal swimmers can be pullers, pushers or neutral depending on the shape. J Fluid Mech (2021) 922:R5. doi:10.1017/jfm.2021.562
89. Shklyaev S, Brady JF, Córdova-Figueroa UM. Non-spherical osmotic motor: chemical sailing. J Fluid Mech (2014) 748:488–520. doi:10.1017/jfm.2014.177
90. Poehnl R, Uspal W. Phoretic self-propulsion of helical active particles. J Fluid Mech (2021) 927:A46. doi:10.1017/jfm.2021.801
91. Roggeveen JV, Stone HA. Motion of asymmetric bodies in two-dimensional shear flow. J Fluid Mech (2022) 939:A23. doi:10.1017/jfm.2022.203
92. Schnitzer O, Yariv E. Osmotic self-propulsion of slender particles. Phys Fluids (2015) 27. doi:10.1063/1.4914417
93. Yariv E. Self-diffusiophoresis of slender catalytic colloids. Langmuir (2019) 36:6903–15. doi:10.1021/acs.langmuir.9b02393
94. Katsamba P, Michelin S, Montenegro-Johnson TD. Slender phoretic theory of chemically active filaments. J Fluid Mech (2020) 898:A24. doi:10.1017/jfm.2020.410
95. Bender CM, Orszag SA. Advanced mathematical methods for scientists and engineers I: asymptotic methods and perturbation theory. Berlin, Germany: Springer Science and Business Media (1999).
96. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active particles in complex and crowded environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/RevModPhys.88.045006
97. Han K, Shields IVCW, Bharti B, Arratia PE, Velev OD. Active reversible swimming of magnetically assembled “microscallops” in non-Newtonian fluids. Langmuir (2020) 36:7148–54. PMID: 32011137. doi:10.1021/acs.langmuir.9b03698
98. Shields IVCW, Kim YK, Han K, Murphy AC, Scott AJ, Abbott NL, et al. Control of the folding dynamics of self-reconfiguring magnetic microbots using liquid crystallinity. Adv Intell Syst (2020) 2:1900114. doi:10.1002/aisy.201900114
99. Han K, IV CWS, Diwakar NM, Bharti B, López GP, Velev OD. Sequence-encoded colloidal origami and microbot assemblies from patchy magnetic cubes. Sci Adv (2017) 3:e1701108. doi:10.1126/sciadv.1701108
100. Qiu T, Lee TC, Mark AG, Morozov KI, Münster R, Mierka O, et al. Swimming by reciprocal motion at low Reynolds number. Nat Commun (2014) 5:5119. doi:10.1038/ncomms6119
101. Vieu C, Carcenac F, Pepin A, Chen Y, Mejias M, Lebib A, et al. Electron beam lithography: resolution limits and applications. Appl Surf Sci (2000) 164:111–7. doi:10.1016/s0169-4332(00)00352-4
102. Walker D, Käsdorf BT, Jeong HH, Lieleg O, Fischer P. Enzymatically active biomimetic micropropellers for the penetration of mucin gels. Sci Adv (2015) 1:e1500501. doi:10.1126/sciadv.1500501
103. Qin K, Pak OS. Purcell’s swimmer in a shear-thinning fluid. Phys Rev Fluids (2023) 8:033301. doi:10.1103/PhysRevFluids.8.033301
104. Shaik VA, Elfring GJ. Hydrodynamics of active particles in viscosity gradients. Phys Rev Fluids (2021) 6:103103. doi:10.1103/physrevfluids.6.103103
105. Jarvey N, Henrique F, Gupta A. Ion transport in an electrochemical cell: a theoretical framework to couple dynamics of double layers and redox reactions for multicomponent electrolyte solutions. J Electrochem Soc (2022) 169:093506. doi:10.1149/1945-7111/ac908e
106. Rath M, Weaver J, Wang M, Woehl T. pH-mediated aggregation-to-separation transition for colloids near electrodes in oscillatory electric fields. Langmuir (2021) 37:9346–55. doi:10.1021/acs.langmuir.1c00671
107. Wang K, Behdani B, Silvera Batista CA. Visualization of concentration gradients and colloidal dynamics under electrodiffusiophoresis. Langmuir (2022) 38:5663–73. doi:10.1021/acs.langmuir.2c00252
108. Alonso-Matilla R, Chakrabarti B, Saintillan D. Transport and dispersion of active particles in periodic porous media. Phys Rev Fluids (2019) 4:043101. doi:10.1103/physrevfluids.4.043101
109. Modica KJ, Xi Y, Takatori SC. Porous media microstructure determines the diffusion of active matter: experiments and simulations. Front Phys (2022) 10:232. doi:10.3389/fphy.2022.869175
110. Caprini L, Marconi UMB. Active particles under confinement and effective force generation among surfaces. Soft Matter (2018) 14:9044–54. doi:10.1039/c8sm01840e
111. Lee CF. Active particles under confinement: aggregation at the wall and gradient formation inside a channel. New J Phys (2013) 15:055007. doi:10.1088/1367-2630/15/5/055007
112. Henrique F, Zuk PJ, Gupta A. Kirchhoff’s laws for electric-double-layer charging in arbitrary porous networks (2023). arXiv preprint arXiv:2308.13100.
Keywords: microscale swimming, microrobots, self-diffusiophoresis, slender-body theory, Purcell’s scallop theorem
Citation: Raj RR, Ganguly A, Becker C, Shields CW IV and Gupta A (2023) Motion of an active bent rod with an articulating hinge: exploring mechanical and chemical modes of swimming. Front. Phys. 11:1307691. doi: 10.3389/fphy.2023.1307691
Received: 05 October 2023; Accepted: 13 November 2023;
Published: 18 December 2023.
Edited by:
Simon Rogers, University of Illinois at Urbana-Champaign, United StatesReviewed by:
Charles Reichhardt, Los Alamos National Laboratory (DOE), United StatesYongxiang Gao, Shenzhen University, China
Copyright © 2023 Raj, Ganguly, Becker, Shields and Gupta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ankur Gupta, QW5rdXIuR3VwdGFAY29sb3JhZG8uZWR1
 Ritu R. Raj
Ritu R. Raj Arkava Ganguly1
Arkava Ganguly1 C. Wyatt Shields IV
C. Wyatt Shields IV Ankur Gupta
Ankur Gupta