
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 01 November 2023
Sec. Complex Physical Systems
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1294451
Infectious diseases have constantly threatened human safety because the diffusion of the susceptible and infected may make more individuals infected and even die. In this paper, a modified SIR model with both external stimulus and diffusion is considered to illustrate the dynamical mechanism of the periodic outbreak and pattern formation. Firstly, we propose a modified SIR model based on the propagation behaviour of infectious diseases to show the effects of the different parameters and diffusion on the outbreak. The Hopf bifurcation and multiscale methods are performed to analyze the stability of this model, which explains the dynamical mechanism of the periodic outbreak. Then, the pattern formation and Turing instability are discussed through comparison principles to reveal the role of periodic disturbances and diffusion in selecting pattern formation. Also, we find rich patterns that may occur when the frequency modulation is close to the intrinsic frequency. Finally, our theoretical results are verified by numerical simulation.
Infectious diseases have always been a threat to human safety because the diffusion of the susceptible and the infected plays a vital role in spreading infectious diseases, which is hard to get a perfect solution. And mathematical models have long been proposed to show the evolution of infectious diseases [1–4]. The coronavirus outbreak has had an enormous impact on the global economy. There was a global economic downturn and mass unemployment. Many countries are already experiencing economic downturns due to the COVID-19 pandemic. Many scholars made use of the existing data to model and predict the development trend of the epidemic [5–7] and gave some suggestions on epidemic control from the perspective of mathematics. Xiao et al. analyzed the piecewise incidence rate in a SIR system to show the effect of threshold densities and control intensities on the outbreak of infectious disease [8]. The equilibrium states were investigated based on a Fourier analysis to show the dynamical mechanism of the seasonality of the disease in an SEIR model with delay [9]. But some challenges in understanding the spread of infectious diseases remain to be solved [10, 11]. An SIS model with delays is studied to show the effect of an awareness program on disease control through local stability, bifurcation analysis, and realistic simulations [12]. And the optimal control of a SIR model was proposed to study the existence, global stability, and backward bifurcation of the equilibrium [13], which is very important for the prevention of infectious diseases. Then an SVEIR was developed with the temporary immunity period to predict the dynamical behaviors and the evolution of the infectious diseases in the long run [14]. Zheng et al. constructed a network-organized SIR model to show the effects of the network structured entropy and diffusion on the bifurcation and Turing instability. They explained the dynamical mechanism of the periodic outbreak and endemic diseases through wavenumber [15], after that, the influences of directed network [16], driving factors [17] and time-delay network [18] on the pattern formation of epidemic model are given. Pattern formation provides new insight into the spread of infectious diseases, and relationships between pattern formation and the region of infectious diseases were introduced in the SIR reaction-diffusion model, which provided an optimal control method for the epidemic [19]. But some work on the SIR model with constant stimulation from other areas should be done further.
The study of system stability is a basic problem [20–22], and using pattern is an essential means to study stability. Patterns are a cluster phenomenon that could describe the distribution of the species, which had been used in biology, chemistry, population, etc. [23]. Turing first tried explaining the dynamical and biological mechanisms of pattern formation in the reaction-diffusion system [24]. Subsequently, much work about pattern and its dynamical behavior had been done [25–29]. It is found that the localized interactions (diffusion) could induce the spatial patterns in ecosystems through spatial self-organization, which is beneficial to explain the mechanism of regular pattern formation [30]. And a general delay was considered to show the stability of a reaction-diffusion population model through Hopf bifurcation [31]. Then studies showed that Turing instability was easier to occur in a stochastic activator-inhibitor system than the classic Turing system [32]. Turing instability generally occurs when the activator and inhibitor diffusion coefficients are sufficiently different, which is not physical in some systems. Haas and Goldstein found that Turing instability was more likely to happen and physical when the diffusing species increases [33]. Galbraith et al. showed that stochastic fluctuations could induce the switching between ordered and disordered patterns [34]. But how the external disturbance affects the pattern formation through the occurrence of Turing instability is still being explored.
The spread of infectious diseases is often disturbed by an external stimulus (diffusion, environmental factor, external input, vaccine, etc.), which may induce nonconstant parameters. The differences between external stimulus and prevention strategies could lead to the different distribution of infectious diseases in some areas. Meanwhile, the periodic behaviors and diffusion of the epidemic have always been an important feature of infectious diseases and are still in the research stage. To further study the effect of external stimulus and prevention strategies on the spread of the epidemic in different areas, we investigate the stability of a modified SIR model through multiscale methods and comparison principles. Firstly, a modified SIR model is proposed based on the actual situation, which could describe the periodic outbreak of infectious diseases through Hopf bifurcation. Then the form of bifurcation is analyzed and derived by multiscale methods to explain the function of parameters in the periodic behaviors. Also, the condition of Turing instability is given through comparison principles, which verifies the role of the disturbance parameters and diffusion coefficients in selecting pattern formation. Finally, numerical simulations are performed to prove our theoretical results.
Infectious diseases seriously threaten human health, which can’t even be eliminated. Therefore, we have to consider the individuals’ coexistence and the epidemic. Meanwhile, the importation of the infected will become the norm if the mortality stays lower. But the epidemic will still affect individuals’ everyday life. Therefore, we have to consider the effect of the imported on the SIR model based on the existing model [1–4],
where b1 is the birth of the susceptible, b2S represents the infected induced by the imported (or the natural source), b3SI2 is the infected influenced by the local cases, b4 is the recovery, θ is the natural mortality rate, b5 is the mortality rate caused by infectious diseases and associated sequelae. Also, bi ≥ 0 (i = 1, … , 5) and system (1) goes back to the most primitive version of SIR model [1–3] when b2 = 0 holds.
In general, the mortality of the susceptible θ is very low in comparison with the birth rate of the susceptible [35], which can be negligible compared to the overall population. Hence, we investigate the following system in this paper.
where the only equilibrium point is
For convenience, system (1) can be reducible to system (3) because
and the Jacobian matrix of system (3) at (S*, I*) is
where
and the characteristic equation is
where ν (ν is one of b1, b2, b3, b4 + b5) can be treated as the control parameter,
It is easy to know that α(νc) = 0 and β(νc) > 0 cause the occurrence of Hopf bifurcation [36]; Yang [37]. Meanwhile, the frequency value is
The critical value b21 of b2 is
The critical value b31, b32 of b3 is
The critical value of b4 + b5 meets
where Z = b4 + b5.
where
and
As an example, we take b2 (namely, ν = b2) as the control parameter to derive the normal form through the multiscale method, and assume
where
Substituting (5) into (4), we divide them by the series for ɛ, and obtain
where
The general solution of the series for ɛ can be read
where
The adjoint matrix of J (b21) is
Based on
where
Because (sin (nx), cos (nx)) is an orthogonal set, (u+, Nɛ2) = 0,
Substituting U1, U2 into O (ɛ2), we solve
and obtain
where
Substituting (7) and (9) into (8), and (u+, q3) = 0, we obtain
where
We can further rewrite it as
where
Assume C = ɛA,
Suppose C = reiϕ,
where Re (β1) > 0 means supercritical bifurcation occurs; Re (β1) < 0 means subcritical bifurcation occurs. Also, the above derivation process and conclusion apply to b1, b3, b4 + b5.
In this section, we consider the effect of the periodic perturbation and diffusion on pattern formation and Turing instability. The corresponding system is rewritten as
where γ is the perturbation amplitude, ϕ is the frequency modulation.
We perform a general perturbation [38, 39] of (11)
where 0 < ɛ ≪ 1,
where
Namely, the linearized dynamics of system (11) is
where
From (12), Dz1, z1 and Dz2, z2 can be represented as
We take the derivative of both sides of Eq. 12 when γ = 0, and obtain
Substituting (13) into (14), one has
According to the comparison principle [38, 39], Turing instability occurs when a T (k2) < 0 holds.
where the conditions of Turing instability in (16) bring into correspondence with the literatureOuyang [23].
The critical value is
where Turing instability may occur when
We take the derivative of both sides of Eq. 12 when γ ≠ 0, and obtain
where
Substituting (13) into (17) when J12J21 ≠ 0, one has
where
According to the comparison principle [38, 39], Turing instability may occur when T1 (k2) < 0 or T2 (k2) < 0 holds. And suppose
Based on theoretical results, we choose b1 = 1, b2 = 0.1, b3 = 1, b4 = 1, b5 = 0.1 as the default value in this paper. With the changing of parameters, the modified SIR model (1) presents the periodic behaviors, and the reaction-diffusion system (11) offers more complex patterns. In this section, we mainly show the effects of the parameters, diffusion coefficients, and periodic perturbation on stability and pattern formation. The initial conditions (S (0), I (0)) are the stochastic disturbance of the equilibrium point. The finite difference method is applied in our simulation.
where the amplitude is max{I(t)} − min{I(t)} and dt = 0.1 is time step.
Although infectious diseases are a severe threat to humans, we can’t eliminate them (SARS, Aids, etc.). The endemic or periodic outbreak usually happens unless everyone is immune to the virus (Variola virus). The presence of susceptible individuals is fundamental to the spread of infectious diseases and could make the infected continue to increase [Figure 1A]. Of course, endemic and periodic outbreaks can happen. When the susceptibility rate is relatively low, the endemic occurs [Figure 1B]. But the percentage of people infected would be inadequate, so the herd immunity strategy can be considered in this case. When the susceptibility rate becomes more prominent, the periodic outbreak of infectious diseases happens [Figure 1C], which may be like a seasonal cold. Also, the periodic outbreak can be treated as the recurrence of infectious diseases (like COVID-19), and some measures should be taken to contain the damage. After the occasional outbreak, there will be severe endemic diseases when the susceptibility becomes more and more [Figure 1D], which also means the early vaccination strategy is essential for prevention.
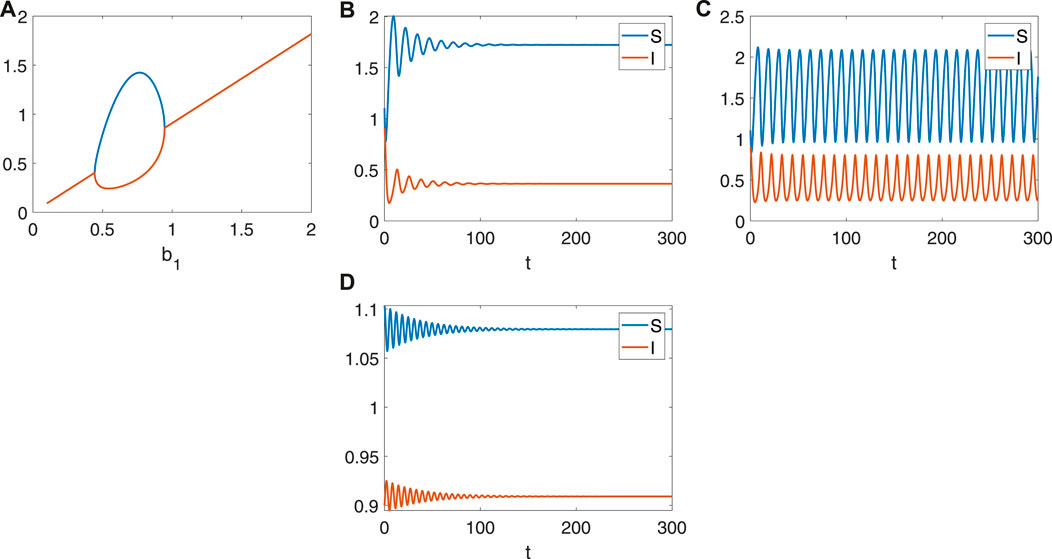
FIGURE 1. The stability and bifurcation diagram about b1 when b2= 0.1, b3=1, b4=1, b5=0.1. (A) The bifurcation diagram about b1 (b11=0.444 is the supercritical Hopf bifurcation point, b12=0.944 is the subcritical Hopf bifurcation point). (B) System (1) is stable when b1=0.4< b11. (C) System (1) is periodic when b11< b1=0.5< b12. (D) System (1) is stable when b1=0.4> b12.
The external environment (the imported, physical factor, human factor, viral properties, etc.) dramatically influences the transmission behavior of infectious diseases. Seasonal changes mainly affect the periodic behavior of influenza. When the external environment has little effect on the diffusion of infectious diseases, infectious diseases will vary with the external environment rather than cause a lot of severe consequences. When the external environment is dominant, the endemic occurs [Figure 2A], which is difficult to avoid. And the modified SIR model presents the periodic outbreak [Figure 2B] when b2 is relatively tiny.
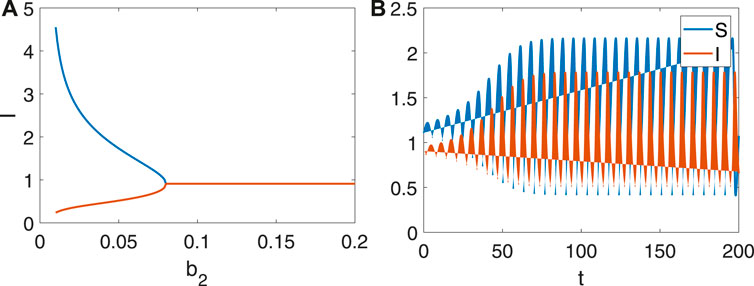
FIGURE 2. The stability and bifurcation diagram about b2 when b1=1, b3=1, b4=1, b5=0.1. (A) The bifurcation diagram about b2 (b21=0.08 is the subcritical Hopf bifurcation point). (B) System (1) is periodic when b2=0.05< b21.
Infectivity is an inherent characteristic of infectious diseases, and the transmission behavior is determined by external conditions (the susceptibility rate, the recovery rate, etc.). Although infectious diseases are highly contagious, they will rapidly disappear when the susceptibility rate is lower, and the recovery rate is higher. Therefore, the infectious rate does not affect the equilibrium point [Figure 3A], but the stability will vary with b3 [Figures 3B,C]. From Figure 3D, the endemic occurs when the amplitude tends to zero, and the periodic outbreak occurs when the amplitude is not zero. Also, the dynamic behaviors of infectious diseases are the results of multiple factors; maybe one or more factors determine the trend of infectious diseases [Figure 3D].
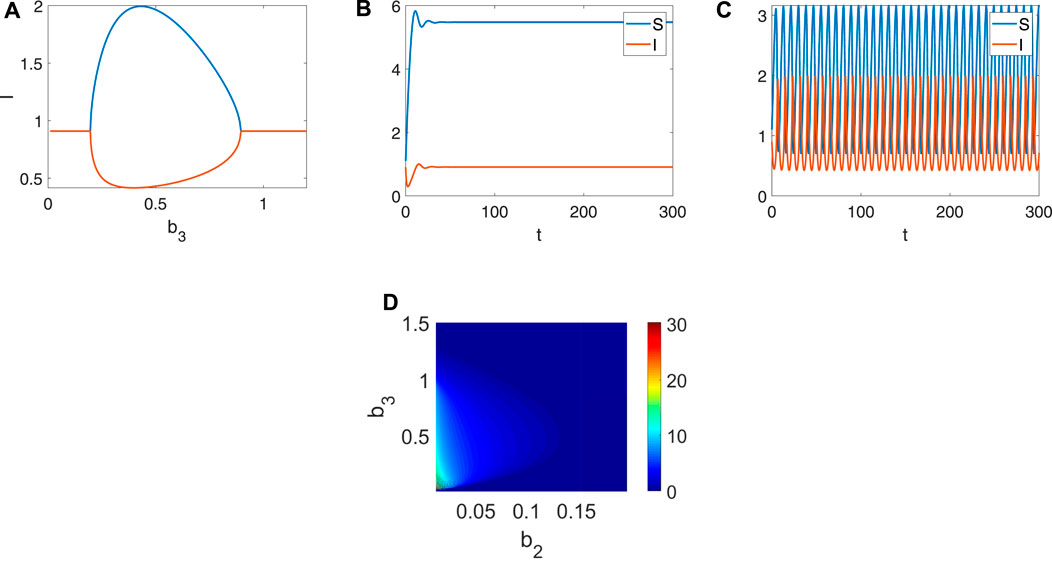
FIGURE 3. The stability and bifurcation diagram about b3 when b1=1, b2=0.1, b4=1, b5=0.1. (A) The bifurcation diagram about b3 (b31=0.197 is the supercritical Hopf bifurcation point, b32=0.892 is the subcritical Hopf bifurcation point). (B) System (1) is stable when b3=0.1< b31. (C) System (1) is periodic when b31< b3=0.5< b32. (D) The amplitude of the infected about b2, b3.
Finally, we consider the role of the recovery and death rates b4 + b5. From Figure 4, the effect of the recovery and death rates is the same. But the recovery rate increase is always treated as the ideal method to prevent the spreading of infectious diseases. A lot of infected individuals will exist when the recovery rate is lower and lead to endemic diseases [Figure 4A]. With the increase of the recovery rate, some of those infected will induce the periodic outbreak [Figure 4B]. Eventually, the impact of infectious diseases will be less and less [Figure 4C], even disappear. There’s no denying that the combination of b2, b5 expands the range of parameters for periodic behavior [Figure 4D]. If the model is given and the parameters bi, i = 1, 2, 3, 4, 5 are measured, the critical value of the bifurcation can be obtained. And then periodic outbreak phenomenon can be forecast through the bifurcation. Further, the purposeful human intervention can be done before the disease develops into periodic outbreaks in practice. Based on these numerical analyses, the external environment b2 plays a vital role in the generation of the periodic outbreak, which makes up for the shortcomings of the classical SIR model.
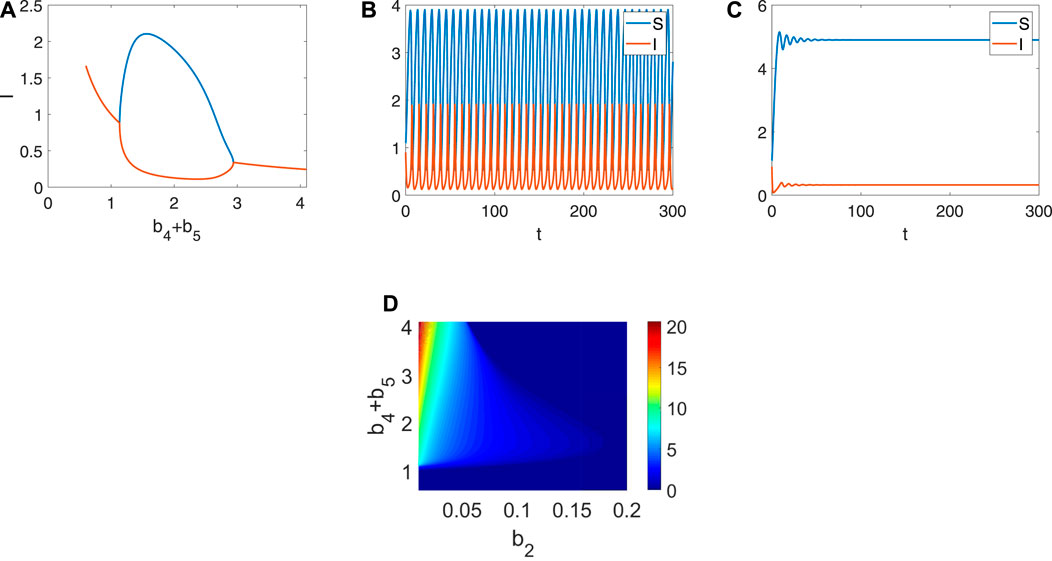
FIGURE 4. The stability and bifurcation diagram about b4+ b5 when b1=1, b2=0.1, b3=1. (A) The bifurcation diagram about b4+ b5 (1.135 is the supercritical Hopf bifurcation point, 2.938 is the subcritical Hopf bifurcation point). (B) System (1) is periodic when 1.135< b4+ b5=2<2.938. (C) System (1) is stable when b4+ b5=3<2.938. (D) The amplitude of the infected about b2, b4+ b5.
Diffusion is a common phenomenon in the spread of infectious diseases. Initially, the epidemic may occur in one city and further spread to other areas. This diffusion process plays an important role in the outbreak of infectious diseases. This section considers the effect of diffusion and periodic perturbation on pattern selection. It is well known that the necessary condition of Turing instability is T (k2) < 0. From Figure 5A, the minimum of T (k2) < 0 gets smaller and smaller as the diffusion parameter d1 increases. If T (k2) > 0 holds for every k, system (11) is stable [Figure 5B]. When a k could make T (k2) < 0, Turing instability occurs [Figures 5C,D]. Meanwhile, the diffusion may lead to a different pattern selection [Figures 5C,D], which is also consistent with the dynamic behavior of infectious diseases.
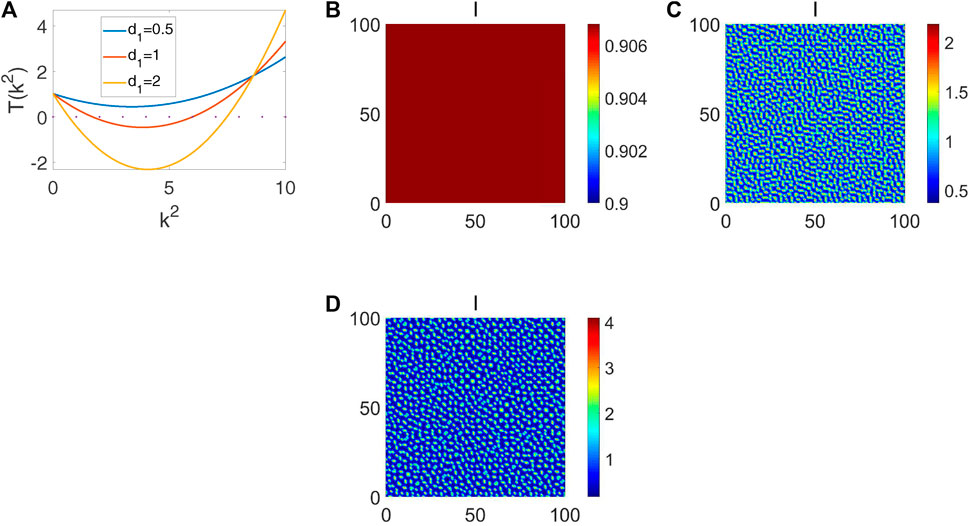
FIGURE 5. The stability and pattern formation when b1=1, b2=0.1, b3=1, b4=1, b5=0.1. (A) The dispersion equation T (k2) with k2. (B) The pattern formation when d1=0.5, d2=0.1. (C) The pattern formation when d1=1, d2=0.1. (D) The pattern formation when d1=2, d2=0.1.
Consider the pattern formation induced by the periodic perturbation and diffusion. Some parameters vary over time in a periodically perturbed system, which may lead to more complex dynamics through the sign of T (t, k2)[Figure 6, Figure 7, Figure 8]. If T (t, k2) > 0 always holds [Figure 6A], the corresponding pattern formation is uniform [Figure 6B]. If the disturbance amplitude makes a T (t, k2) < 0 hold [Figure 6C], Turing instability, stripe and spot pattern can occur [Figure 6D]. Especially γ = 2 [Figure 7A], the maze pattern occurs [Figure 7B]. Namely, the disturbance amplitude could make the distribution of infectious diseases reorganize, and the prevalence varies in different regions. If ϕ = 0.5 [Figure 7C], the corresponding pattern formation will become uniform again [Figure 7D], which means ϕ play a vital role in the pattern selection. Also, if we change μc from 0.1 to 0.4 [Figure 8A], the maze pattern occurs again [Figure 8B]. If we change ϕ from 0.5 to 0.45 [Figure 8C], the stripe and spot pattern coexist [Figure 8D]. From Figure 6 to Figure 8, we find that the pattern formation results from the combined interaction of ϕ, μc, and γ. So the periodic perturbation and diffusion could further explain why the distribution of infectious diseases varies in different regions. Meanwhile, under external factors, infectious diseases are more likely to break out periodically.
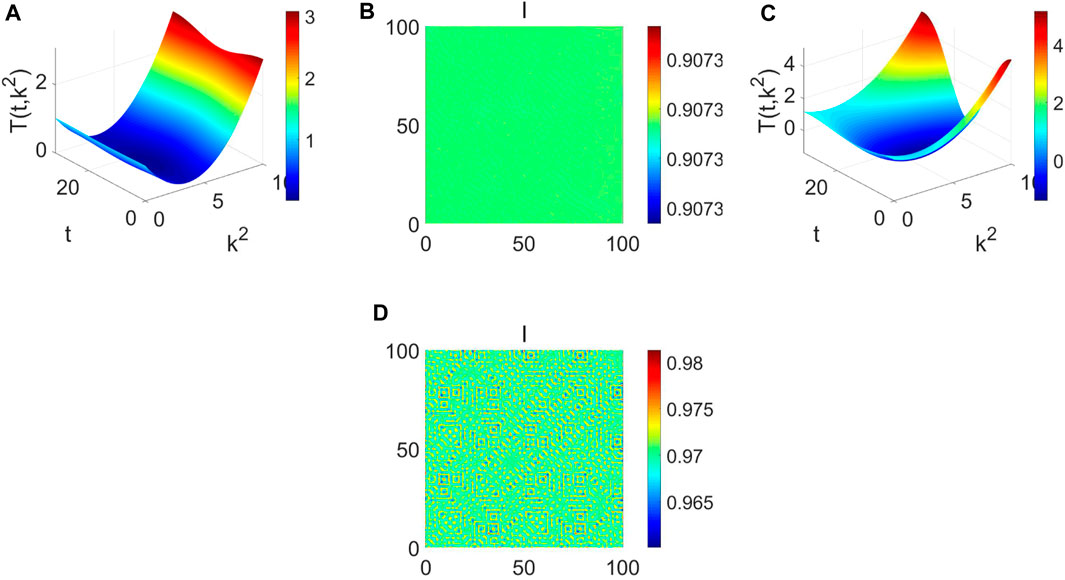
FIGURE 6. The dispersion equation and pattern formation when b1=1, b2=0.1, b3=1, b4=1, b5=0.1, d1=0.7, d2=0.1. (A) The dispersion equation Tk(t) about k2 and t (min (T (t, k2))=0.0151>0) when ϕ =1.1, μc =1, γ =0.1. (B) The pattern formation when ϕ =1.1, μc =1, γ =0.1. (C) The dispersion equation Tk(t) about k2 and t (min (Tk(t))=−1.3945<0) when ϕ =1.1, μc =1, γ =1.5. (D) The pattern formation when ϕ =1.1, μc =1, γ =1.5.
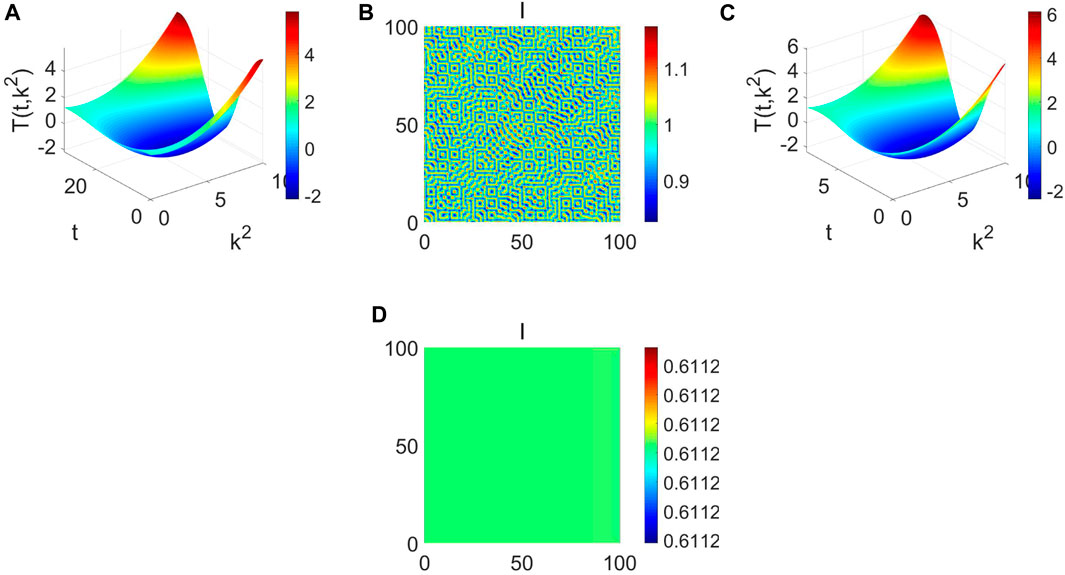
FIGURE 7. The dispersion equation and pattern formation when b1=1, b2=0.1, b3=1, b4=1, b5=0.1, d1=0.7, d2=0.1. (A) The dispersion equation Tk(t) about k2 and t (min (Tk(t))=−2.1698<0) when ϕ =1.1, μc =1, γ =2. (B) The pattern formation when ϕ =1.1, μc =1, γ =2. (C) The dispersion equation Tk(t) about k2 and t (min (Tk(t))=−2.3955<0) when ϕ =1.4, μc =1, γ =2. (D) The pattern formation when ϕ =1.4, μc =1, γ =2.
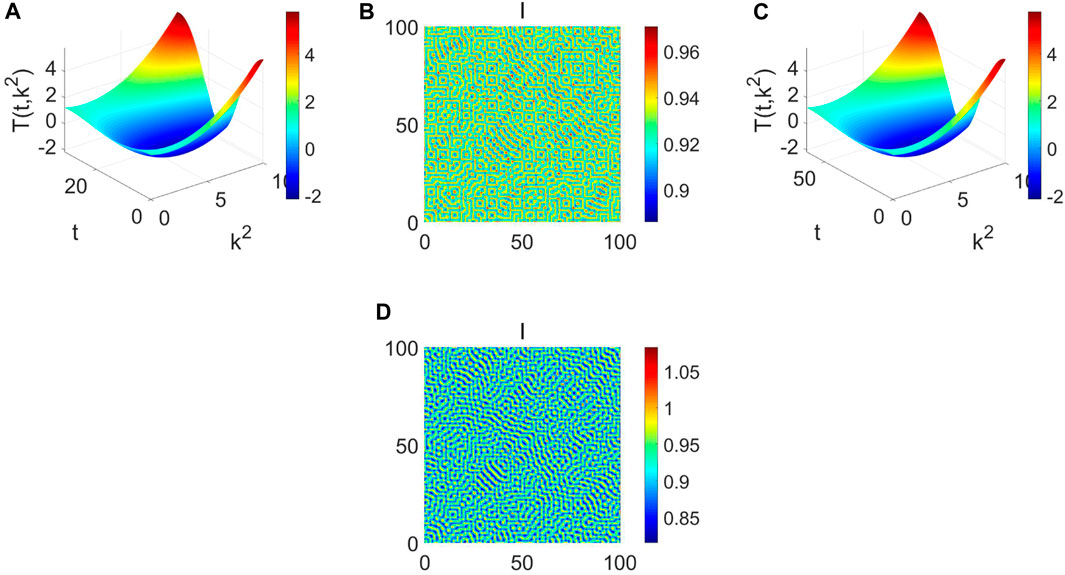
FIGURE 8. The dispersion equation and pattern formation when b1 = 1, b2 = 0.1, b3 = 1, b4 = 1, b5 = 0.1, d1 = 0.7, d2 = 0.1. (A) The dispersion equation Tk(t) about k2 and t (min(Tk(t)) = −2.1642 < 0<0) when min(Tk(t)) = −2.1642 < 0. (B) The pattern formation when ϕ = 1.08, μc = 1, γ = 2. (C) The dispersion equation Tk(t) about k2 and t (min(Tk(t)) = −2.1581 < 0) when ϕ = 1.05, μc = 1, γ = 2. (D) The pattern formation when ϕ = 1.05, μc = 1, γ = 2.
External stimulus and diffusion are vital in spreading infectious diseases, especially the periodic outbreak at the beginning. Still, the periodic behaviors can’t be described in the classical SIR model. To further study the effect of external stimulus and prevention strategies on the spread of the epidemic in different areas, we investigate the stability of a modified SIR model through multiscale methods and comparison principles. Firstly, a modified SIR model is proposed to describe the periodic outbreak of infectious diseases through Hopf bifurcation. The form of bifurcation is analyzed and derived by multiscale methods to explain the function of parameters in periodic behaviors. Then the condition of Turing instability is given through comparison principles, which verifies the role of the disturbance parameters and diffusion coefficients in selecting pattern formation. Also, we find rich patterns that may occur when the frequency modulation is close to the intrinsic frequency. The external environment plays a vital role in the generation of the periodic outbreak, which makes up for the shortcomings of the classical SIR model. The periodic perturbation and diffusion could further explain why the distribution of infectious diseases varies in different regions. Meanwhile, under external factors, infectious diseases are more likely to break out periodically. Our results provide a novel method to show the outbreak mechanism of infectious diseases.
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
WY: Writing–original draft, Writing–review and editing. QZ: Data curation, Writing–original draft. JS: Investigation, Writing–review and editing, Validation. LG: Writing–review and editing, Validation.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by National Natural Science Foundation of China (12002297, 12272135, 12202145), Basic research Project of Universities in Henan Province (21zx009), Program for Science and Technology Innovation Talents in Universities of Henan Province (22HASTIT018), Program for Innovative Research Team (in Science and Technology) in University of Henan Province (23IRTSTHN018), Outstanding Young Backbone Teacher of Xuchang University (2022), Innovative Training program for College students in Henan Province (S202210480058). Key scientific research projects of Henan Institutions of Higher learning in 2024 (24B110017), Wenjie Yang.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A (1927) 115:700–21. doi:10.1098/rspa.1927.0118
2. Hethcote HW. Qualitative analyses of communicable disease models. Math biosciences (1976) 28:335–56. doi:10.1016/0025-5564(76)90132-2
3. Liu W-m., Levin SA, Iwasa Y. Influence of nonlinear incidence rates upon the behavior of sirs epidemiological models. J Math Biol (1986) 23:187–204. doi:10.1007/bf00276956
4. Brauer F, Castillo-Chavez C, Feng Z, et al. Mathematical models in epidemiology. New York: Springer (2019).
5. Melek Manshouri N. Identifying covid-19 by using spectral analysis of cough recordings: a distinctive classification study. Cogn neurodynamics (2022) 16:239–53. doi:10.1007/s11571-021-09695-w
6. Pei L, Zhang M. Long-term predictions of current confirmed and dead cases of covid-19 in China by the non-autonomous delayed epidemic models. Cogn neurodynamics (2021) 16:229–38. doi:10.1007/s11571-021-09701-1
7. Zheng Q, Pandey V, Shen J, Xu Y, Guan L. Pattern dynamics in the epidemic model with diffusion network. Europhysics Lett (2022a) 137:42002. doi:10.1209/0295-5075/ac58bd
8. Xiao Y, Xu X, Tang S. Sliding mode control of outbreaks of emerging infectious diseases. Bull Math Biol (2012) 74:2403–22. doi:10.1007/s11538-012-9758-5
9. Nistal R, De la Sen M, Alonso-Quesada S, Ibeas A. Limit periodic solutions of a seir mathematical model for non-lethal infectious disease. Applled Math Sci (2013) 7:773–89. doi:10.12988/ams.2013.13070
10. Metcalf CJE, Andreasen V, Bjørnstad ON, Eames K, Edmunds WJ, Funk S, et al. Seven challenges in modeling vaccine preventable diseases. Epidemics (2015) 10:11–5. doi:10.1016/j.epidem.2014.08.004
11. Funk S, Bansal S, Bauch CT, Eames KT, Edmunds WJ, Galvani AP, et al. Nine challenges in incorporating the dynamics of behaviour in infectious diseases models. Epidemics (2015) 10:21–5. doi:10.1016/j.epidem.2014.09.005
12. Greenhalgh D, Rana S, Samanta S, Sardar T, Bhattacharya S, Chattopadhyay J. Awareness programs control infectious disease–multiple delay induced mathematical model. Appl Math Comput (2015) 251:539–63. doi:10.1016/j.amc.2014.11.091
13. Zhang Q, Tang B, Tang S. Vaccination threshold size and backward bifurcation of sir model with state-dependent pulse control. J Theor Biol (2018) 455:75–85. doi:10.1016/j.jtbi.2018.07.010
14. Zhang Z, Kundu S, Tripathi JP, Bugalia S. Stability and hopf bifurcation analysis of an sveir epidemic model with vaccination and multiple time delays. Chaos, Solitons & Fractals (2020) 131:109483. doi:10.1016/j.chaos.2019.109483
15. Zheng Q, Shen J, Xu Y, Pandey V, Guan L. Pattern mechanism in stochastic sir networks with er connectivity. Physica A: Stat Mech its Appl (2022c) 603:127765. doi:10.1016/j.physa.2022.127765
16. Zheng Q, Shen J, Xu Y, Pandey V, Guan L. Turing pattern induced by the directed ER network and delay. Math Biosciences Eng (2022b) 19:11854–67. doi:10.3934/mbe.2022553
17. Zheng Q, Shen J, Pandey V, Guan L, Guo Y. Turing instability in a network-organized epidemic model with delay. Chaos, Solitons & Fractals (2023a) 168:113205. doi:10.1016/j.chaos.2023.113205
18. Zheng Q, Shen J, Pandey V, Zhao Y, Guan L. Spatiotemporal dynamics of periodic waves in sir model with driving factors. New J Phys (2023b) 25:063028. doi:10.1088/1367-2630/acdb91
19. Chang L, Gao S, Wang Z. Optimal control of pattern formations for an sir reaction–diffusion epidemic model. J Theor Biol (2022) 536:111003. doi:10.1016/j.jtbi.2022.111003
20. Liebovitch LS, Peluso PR, Norman MD, Su J, Gottman JM. Mathematical model of the dynamics of psychotherapy. Cogn Neurodynamics (2011) 5:265–75. doi:10.1007/s11571-011-9157-x
21. Kumar RS, Sugumaran G, Raja R, Zhu Q, Raja UK. New stability criterion of neural networks with leakage delays and impulses: a piecewise delay method. Cogn Neurodynamics (2016) 10:85–98. doi:10.1007/s11571-015-9356-y
22. Song Z-G, Xu J. Stability switches and double hopf bifurcation in a two-neural network system with multiple delays. Cogn Neurodynamics (2013) 7:505–21. doi:10.1007/s11571-013-9254-0
23. Ouyang Q. Introduction to nonlinear science and pattern Dynamics. Beijing: Peking University Press (2010).
24. Turing AM. The chemical basis of morphogenesis. Bull Math Biol (1990) 52:153–97. doi:10.1007/bf02459572
25. Chen M, Wu R, Wang X. Non-constant steady states and hopf bifurcation of a species interaction model. Commun Nonlinear Sci Numer Simulation (2023) 116:106846. doi:10.1016/j.cnsns.2022.106846
26. Van Gorder RA. Pattern formation from spatially heterogeneous reaction–diffusion systems. Philosophical Trans R Soc A (2021a) 379:20210001. doi:10.1098/rsta.2021.0001
27. Zhang H-T, Wu Y-P, Sun G-Q, Liu C, Feng G-L. Bifurcation analysis of a spatial vegetation model. Appl Math Comput (2022) 434:127459. doi:10.1016/j.amc.2022.127459
28. Othmer HG, Scriven L. Instability and dynamic pattern in cellular networks. J Theor Biol (1971) 32:507–37. doi:10.1016/0022-5193(71)90154-8
29. Nakao H, Mikhailov AS. Turing patterns in network-organized activator–inhibitor systems. Nat Phys (2010) 6:544–50. doi:10.1038/nphys1651
30. Rietkerk M, Van de Koppel J. Regular pattern formation in real ecosystems. Trends Ecology Evolution (2008) 23:169–75. doi:10.1016/j.tree.2007.10.013
31. Su Y, Wei J, Shi J. Hopf bifurcations in a reaction–diffusion population model with delay effect. J Differential Equations (2009) 247:1156–84. doi:10.1016/j.jde.2009.04.017
32. Karig D, Martini KM, Lu T, DeLateur NA, Goldenfeld N, Weiss R. Stochastic turing patterns in a synthetic bacterial population. Proc Natl Acad Sci (2018) 115:6572–7. doi:10.1073/pnas.1720770115
33. Haas PA, Goldstein RE. Turing’s diffusive threshold in random reaction-diffusion systems. Phys Rev Lett (2021) 126:238101. doi:10.1103/physrevlett.126.238101
34. Galbraith M, Bocci F, Onuchic JN. Stochastic fluctuations promote ordered pattern formation of cells in the notch-delta signaling pathway. PLOS Comput Biol (2022) 18:e1010306. doi:10.1371/journal.pcbi.1010306
35. Song H, Jia Z, Jin Z, Liu S. Estimation of covid-19 outbreak size in harbin, China. Nonlinear Dyn (2021) 106:1229–37. doi:10.1007/s11071-021-06406-2
36. Kuznetsov YA, Kuznetsov IA, Kuznetsov Y. Elements of applied bifurcation theory. New York: Springer (1998).
37. Yang W. Bifurcation and dynamics in double-delayed chua circuits with periodic perturbation. Chin Phys B (2022) 31:020201. doi:10.1088/1674-1056/ac1e0b
38. Van Gorder RA. Turing and benjamin–feir instability mechanisms in non-autonomous systems. Proc R Soc A (2020) 476:20200003. doi:10.1098/rspa.2020.0003
Keywords: Turing instability, SIR model, Hopf bifurcation, multiscale methods, diffusion
Citation: Yang W, Zheng Q, Shen J and Guan L (2023) Hopf bifurcation and patterns in a modified SIR model. Front. Phys. 11:1294451. doi: 10.3389/fphy.2023.1294451
Received: 14 September 2023; Accepted: 20 October 2023;
Published: 01 November 2023.
Edited by:
Francisco Rodrigues, University of São Paulo, BrazilReviewed by:
Ranchao Wu, Anhui University, ChinaCopyright © 2023 Yang, Zheng, Shen and Guan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianwei Shen, eGNqd3NoZW5AZ21haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.