Competitive information propagation considering local-global prevalence on multi-layer interconnected networks

The popularity of online social networks (OSNs) promotes the co-propagation of multiple types of information. And there exist inevitably competitive interactions between these information, which will significantly affect the spreading trend of each information. Besides, the coupled topology of multi-layer interconnects exhibited in OSNs will also increase the research complexity of information propagation dynamics. To effectively address these challenges, we propose a novel competitive information propagation model on multi-layer interconnected networks, where the tendency of an individual to become a positive or negative spreader depends on the weighted consideration of local and global prevalence. Then the basic reproduction number is calculated via next-generation matrix method. And under the critical conditions of the basic reproduction number, the asymptotic stability of information-free and information-endemic equilibria is theoretically proven through Lyapunov stability theory. Besides, an optimal control problem involving two heterogeneous controls is formulated, aiming at achieving the best suppression performance of negative information with the minimum control cost. According to Cesari theorem and Pontryagin minimum principle, the existence and analytical formulation of optimal solutions are derived. Extensive numerical experiments are conducted to prove the correctness of our theoretical results, and evaluate the effectiveness of our proposed control strategies. This study can provide useful insights into the modeling and control of multiple information propagation considering multi-layer network topology and individual adaptive behavior.

1 Introduction

With the continuous development of modern technology, online social networks (OSNs) have gradually become essential mediums for people to exchange opinions, which contributes to large-scale information propagation in different forms including rumor, awareness, influence and so on. It is well-known that the ubiquitous information propagation will significantly affect human daily life in turn. In particular, the spread of positive influence involving a certain city will help it absorb more talents and accelerate its productivity [1–3]. The awareness propagation about COVID-19 protection may save many human lives and reduce unnecessary economic losses [4–7]. And the rumor spreading about side effects of vaccine therapy can decrease the vaccination rates and hinder the effectiveness of disease interventions [8–10]. Therefore, exploring the dynamical process of information propagation is of great practical significance and has attracted much attention from the academic community. A large number of related work has followed on the mathematical modeling of information propagation dynamics, employing classical SIS, SIR and other derivative models. For example, Yu et al. [11] established an ignorance-discussant-spreader-remover rumor spreading model, and analyzed the local asymptotic stability of four equilibria. Yin et al. [12] took into account the emotion categories and choices of user communities on OSNs, and constructed an emotion-based susceptible-forwarding-immune propagation dynamic model to investigate the evolution process of emotional information and guide public sentiment. Zhu et al. [13] proposed a novel susceptible-latent-breaking-recovered propagation model to explore the dynamic behavior of industrial viruses in the SCADA system.

However, a considerable amount of previous work assumes that only single information propagates on OSNs, which is far beyond the practical case. In view of the individuals’ differences including nationality, ethnicity, education and personality, their opinions towards a specific event is generally diverged into two opposite sides, which can be considered as positive information and negative information. Typically, different groups of people always have different evaluations on a city, where local residents tend to prefer good evaluations, while nonresidents may make bad evaluations due to their terrible experiences. Then good evaluations promote the spread of positive influences, and bad evaluations lead to the spread of negative influences [14–16]. The effectiveness of COVID-19 prevention measures, such as vaccination and physical distancing, also simultaneously spreads through the crowd in dual forms of rumor and truth [17–21]. In particular, the government will disclose the truth about the effectiveness of prevention measures, and the supporters may actively promote the spread of truth. However, some opponents inevitably worry about the side effects of prevention measures and spread rumors. More attention should be paid to the spreading process of competitive information, so that the interaction between multiple information can more truly reflect the complexity of information propagation on OSNs. On the other hand, OSNs also form a multi-layer structure due to the clustering nature of the population, and the coupling between any layers will significantly affect the dynamic trend and steady-state prevalence of information propagation compared to single-layer networks. Antonopoulos et al. [22] studied the opinion dynamics over multiplex networks with heterogeneous confidence thresholds and general initial opinion distributions. Through probability analysis, they derived the analytical expressions for the critical thresholds of confidence bound considering certain regularity conditions of the networks, which reveals the significant impacts of structural multiplexity and initial distribution on the critical thresholds. Furthermore, their numerical simulations also explored the consensus behavior of agents in diverse network topologies. Yin et al. [23] constructed an environment-based susceptible-forwarding-immune model of information propagation on multi-platform networks, which reflects the complexity of actual social network topologies and the interaction between various social platforms. They also parameterized the model using COVID-19 data, and conducted the parameter sensitivity analysis. Wang et al. [24] investigated the multi-lingual SIR dynamic process of rumor spreading, which regarded each language community as a layer, and establish the rumor cross-transmitted mechanism in different lingual environments. Both the basic reproduction number and the stability of the rumor-free/endemic equilibrium were systematically discussed. These studies reveal many new characteristics how multi-layer network topologies intervene information propagation trend. However, although lots of work has separately investigated the potential effects of multiple information coexistence and multi-layer network topology, the attempts to synthesize the two aspects may reveal more interesting conclusions, which have not been well explored. Therefore, in order to more comprehensively explore the information propagation dynamics on OSNs, an improved model taking both the multiple information interaction and multi-layer interconnected networks needs to be further developed and analyzed.

Actually, individuals in OSNs are not only the carriers of information propagation, but also take certain adaptive behaviors according to the information prevalence. The herd behavior that individuals tend to follow others when making decisions is one of the most common social behaviors, and has recently attracted substantial attention from the research community [25–28]. However, to the best of our knowledge, there is few work to introduce individual herd behavior into the multiple information propagation on multi-layer networks, where herd behavior may change the mechanism of state transition and thus determine the dominance relationship between multiple information. Under the framework of multiple information propagation, each individual may consider both the local situation of its neighbors and the global situation of all individuals before deciding which type of information to spread. This adaptive herd behavior will affect the coupling characteristics between multiple information, and interfere with the evolution trend and prevalence of various information. Therefore, the consideration of individual herd decision-making behavior will also improve our understanding of information propagation dynamics.

One of the primary purposes for modeling information propagation is to control the spreading processes of interest. There are two main streams of control strategies, namely, heuristic control and optimal control [29–33]. Heuristic control strategy employs the real-time information prevalence to construct adaptive control function, aiming to effectively suppress/promote the specific information spreading, while optimal control strategy constructs the adaptive control function to maximize/minimize a well-designed objective function. Lin et al. [34] established a novel SWIR model with uncertain mental state to describe the spreading process of fraudulent information, and further formulated an optimal problem of two synergistic control strategies to minimize the total cost constraint involving individual losses and control resource consumption. Li et al. [35] proposed a multifactor-based information model considering information content and node characteristics, and also constructed an efficient heuristic algorithm of seed nodes selection to solve the targeted influence maximization problem. Wang et al. [36] proposed a novel computational model to present the temporal dynamics of the positive and negative information spread, and devised a nonlinear feedback control mechanism to perform three synergetic intervention strategies with minimal system expenses. During multiple information propagation, our control strategies are aimed at promoting the diffusion of positive information and suppressing the outbreak of negative information. Due to the resource limitations in reality, decision-makers always attempt to achieve the most powerful suppress performance of negative information with the lowest control intensity, which forms a trade-off between control cost and propagation cost. This trade-off can be formulated as an optimization problem, and the corresponding optimal solutions need to be further discussed, which can provide theoretical guidance and reference significance for practical resource scheduling.

Motivated by the above analysis, we aim to develop a novel framework that can integrate competitive information propagation, multi-layer interconnected networks and individual adaptive behavior. Our main contributions are summarized as follows.

• We propose a novel competitive information propagation model on multi-layer interconnected networks. This model can not only efficiently describe the competing phenomenon of positive and negative information coexistence in the real world, but also analyze the correlation between information propagation and multi-layer topology in OSNs;

• We construct a novel compartmental model with individual herd behavior towards information propagation, where the individual’s inclination to be a positive or negative spreader depends on a weighted balance between global and local information prevalence. This consideration reflects the coupled characteristics of individual response and information propagation, that is, individuals generally take adaptive behavior towards the received information, and this behavior may further affect the trend of information propagation;

• We analytically deduce the basic reproduction number ${\mathcal{R}}_0$ of our proposed model, and respectively discuss the stability of information-free equilibrium and information-endemic equilibrium using Lyapunov theorem, that is, when ${\mathcal{R}}_0<1$, our dynamic system will converge to a stable information-free equilibrium; when ${\mathcal{R}}_0>1$, our dynamic system will also converge to a stable information-endemic equilibrium;

• We design two heterogeneous controls to suppress the prevalence of negative information. Considering the cost constraints in reality, we construct an optimization problem involving a trade-off between the negative propagation cost and the control cost. To solve the optimization problem, we further discuss the existence, the analytic formulation and the uniqueness of the optimal solution.

The rest of this paper is organized as follows. In Section 2, a competitive information propagation model is formulated within the framework of multi-layer interconnected network. Stability analysis of information-free and information-endemic equilibria is carried out in Section 3. The formulation of optimal control problem is conducted to discuss the existence, analytic formulation and uniqueness of the optimal solution in Section 4. Extensive numerical simulations are conducted to verify our presented theoretical results in Section 5. Some conclusions are drawn in Section 6.

2 Model formulation and Preliminaries

In this section, we formulate a spreading model SI^AI^BHR of competitive negative and positive information on multi-layer interconnected networks.

For simplicity, we here consider a two-layer interconnected network and denote them as layers 1 and 2 respectively, whose relevant conclusions can be easily generalized to the other cases of multi-layer networks with more layers. These two layers can be depicted as different countries, cities or communities in the real world. The individuals on two respective layers belong to different groups. Each individual has both the neighbors within the same layer and the acquaintances within other layer, which contributes to the intra-layer and inter-layer edges. Then denote the intra-layer average degree of the layer 1 and 2 as $⟨k_1⟩$ and $⟨k_2⟩$ respectively. And the inter-layer average degree from layer 1 to layer 2 is also denoted as $⟨k_{12}⟩$, and the similar definition holds for $⟨k_{21}⟩$. The diagram of multi-layer interconnected networks is shown in Figure 1A.

FIGURE 1

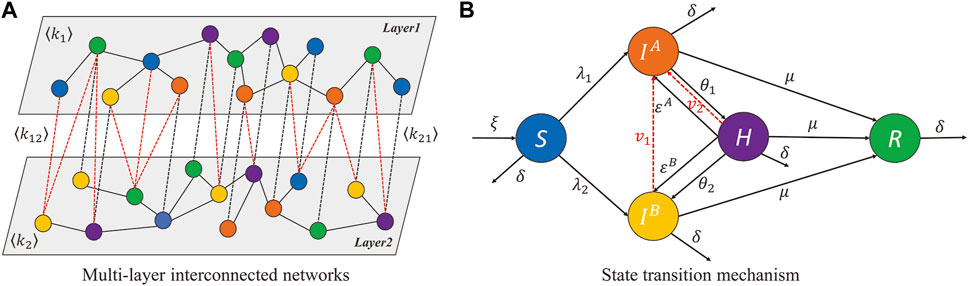
FIGURE 1. The schematic diagram of (A) multi-layer interconnected networks and (B) state transition mechanism.

During the spreading dynamics SI^AI^BHR, all individuals are divided into five status compartments: Susceptible (S), Infected by positive information (I^A), Infected by negative information (I^B), Hesitate (H) and Recovered (R). Specifically, S state represents an individual who is unknown to any type of information but potentially infected via its intra-layer or inter-layer edges; I^A state represents a spreader who is infected with positive information; I^B state represents a spreader who is infected with negative information; H state represents an individual who has received two types of information but is hesitant to become which one; R state represents an individual who has no interest in spreading either positive or negative information. We further define the state density of S, I^A, I^B, H, R in layer 1 and 2 at time t as S₁(t), S₂(t), $I_1^A(t)$, $I_2^A(t)$, $I_2^B(t)$, $I_2^B(t)$, H₁(t), H₂(t), R₁(t), R₂(t), respectively.

Considering that the dynamic process of information propagation has the same time scale as the evolution of involved population numbers, we introduce the birth and mortality rates of population dynamics. And the birth rate and mortality rate of our dynamics are presented as ξ and δ respectively. Denote $R_{+}^5$ the nonnegative cone and its lower dimensional face. Thus, we can study the SI^AI^BHR model in the following feasible region

$\mathrm{\Omega }=\left\{\left.\left(S_i\left(t\right),I_i^A\left(t\right),I_i^B\left(t\right),H_i\left(t\right),R_i\left(t\right)\right)\in R_{+}^5\right|S_i\left(t\right)+I_i^A\left(t\right)+I_i^B\left(t\right)+H_i\left(t\right)+R_i\left(t\right)\le \frac{\xi }{\delta }\right\}.(2.1)$

The birth rate will increase the quantitative basis of susceptible individuals, which can potentially raise the infection risk in the population and promote the information prevalence. And the opposite condition holds for the mortality rate. The relative size of birth and mortality rates determines the evolutionary trend of population numbers. In real life, both birth and mortality rates have two meanings: 1) For the birth rate, on the one hand, it refers to natural birth rate, which means that the initial population can give birth to newborns and these newborns can participate in the information propagation; on the other hand, it also refers to immigrated birth rate, which means that the external population may move to the regions where the initial population is located due to work, education and tourism. After their immigration, they can also participate in the information propagation. 2) For mortality rate, on the one hand, it refers to natural mortality rate, which means that some individuals in the initial population will die due to accidents and old age, and these deaths may be excluded for the information propagation; on the other hand, it also refers to emigration mortality rate, which means that some initial individuals may move to other regions for diverse reasons, and their emigration makes them no longer involved in the information propagation. Taking the propagation process in layer 1 as an example, the state transition mechanism of SI^AI^BHR model can be described as.

• Some newborn individuals will be filled into the network with birth rate ξ to participate in the information propagation process. Without loss of generality, these newborn individuals are assumed to be susceptible; Individuals in all five compartments are removed from the network with mortality rate δ;

• Individuals in S status may become infectious spreader of positive/negative information associating with their intra-layer infected neighbors in $I_1^A$ $(I_1^B)$ at infection rate λ₁ (λ₂). They can also be infected by their inter-layer acquaintances in $I_2^A$ $(I_2^B)$ at decay infection rate κλ₁ (κλ₂), κ < 1;

• Individuals in $I_1^A$ state may become hesitate ones after receiving the negative information from their neighbors (acquaintances) in $I_1^B$ $(I_2^B)$ state at transmission rate θ₁ (κθ₁); similarly, individuals in $I_1^B$ state also may become hesitate ones after receiving the positive information from their neighbors (acquaintances) in $I_1^A$ $(I_2^A)$ state at transmission rate θ₂ (κθ₂);

• Individuals in H status may tend to be the spreaders of positive (negative) information with transmission rate ${\epsilon }_1^A$ $({\epsilon }_1^B)$, which is driven by the weighted balance between the global and local prevalence scale of positive (negative) information;

• Individuals in $I_1^A$, $I_1^B$, H status may lose spreading interest at recovered rate μ, and be removed in the propagation processes of negative/positive information.

The similar state transition mechanism holds for layer 2. The state transition diagram of SI^AI^BHR model is shown in Figure 1B.

The dynamic evolution of information propagation for layers 1 and 2 can be derived as

$\left\{\begin{array}{c}\frac{d{S}_1\left(t\right)}{dt}=\xi -⟨k_1⟩{\lambda }_1{S}_1\left(t\right)I_1^A\left(t\right)-⟨k_1⟩{\lambda }_2{S}_1\left(t\right)I_1^B\left(t\right)-⟨k_{12}⟩\kappa {\lambda }_1{S}_1\left(t\right)I_2^A\left(t\right)-⟨k_{12}⟩\kappa {\lambda }_2{S}_1\left(t\right)I_2^B\left(t\right)-\delta S_1\left(t\right)\hfill \\ \frac{d{I}_1^A\left(t\right)}{dt}=⟨k_1⟩{\lambda }_1{S}_1\left(t\right)I_1^A\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_1{S}_1\left(t\right)I_2^A\left(t\right)+{\epsilon }_1^A\left(t\right)H_1\left(t\right)-⟨k_1⟩{\theta }_1{I}_1^A\left(t\right)I_1^B\left(t\right)-⟨k_{12}⟩\kappa {\theta }_1{I}_1^A\left(t\right)I_2^B\left(t\right)-\left(\delta +\mu \right)I_1^A\left(t\right)\hfill \\ \frac{d{I}_1^B\left(t\right)}{dt}=⟨k_1⟩{\lambda }_2{S}_1\left(t\right)I_1^B\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_2{S}_1\left(t\right)I_2^B\left(t\right)+{\epsilon }_1^B\left(t\right)H_1\left(t\right)-⟨k_1⟩{\theta }_2{I}_1^B\left(t\right)I_1^A\left(t\right)-⟨k_{12}⟩\kappa {\theta }_2{I}_1^B\left(t\right)I_2^A\left(t\right)-\left(\delta +\mu \right)I_1^B\left(t\right)\hfill \\ \frac{d{H}_1\left(t\right)}{dt}=⟨k_1⟩{\theta }_1{I}_1^A\left(t\right)I_1^B\left(t\right)+⟨k_{12}⟩\kappa {\theta }_1{I}_1^A\left(t\right)I_2^B\left(t\right)+⟨k_1⟩{\theta }_2{I}_1^B\left(t\right)I_1^A\left(t\right)+⟨k_{12}⟩\kappa {\theta }_2{I}_1^B\left(t\right)I_2^A\left(t\right)-\left({\epsilon }_1^A\left(t\right)+{\epsilon }_1^B\left(t\right)+\delta +\mu \right)H_1\left(t\right)\hfill \end{array}\right.(2.2)$

$\left\{\begin{array}{c}\frac{d{S}_2\left(t\right)}{dt}=\xi -⟨k_2⟩{\lambda }_1{S}_2\left(t\right)I_2^A\left(t\right)-⟨k_2⟩{\lambda }_2{S}_2\left(t\right)I_2^B\left(t\right)-⟨k_{21}⟩\kappa {\lambda }_1{S}_2\left(t\right)I_1^A\left(t\right)-⟨k_{21}⟩\kappa {\lambda }_2{S}_2\left(t\right)I_1^B\left(t\right)-\delta S_2\left(t\right)\hfill \\ \frac{d{I}_2^A\left(t\right)}{dt}=⟨k_2⟩{\lambda }_1{S}_2\left(t\right)I_2^A\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_1{S}_2\left(t\right)I_1^A\left(t\right)+{\epsilon }_2^A\left(t\right)H_2\left(t\right)-⟨k_2⟩{\theta }_1{I}_2^A\left(t\right)I_2^B\left(t\right)-⟨k_{21}⟩\kappa {\theta }_1{I}_2^A\left(t\right)I_1^B\left(t\right)-\left(\delta +\mu \right)I_2^A\left(t\right)\hfill \\ \frac{d{I}_2^B\left(t\right)}{dt}=⟨k_2⟩{\lambda }_2{S}_2\left(t\right)I_2^B\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_2{S}_2\left(t\right)I_1^B\left(t\right)+{\epsilon }_2^B\left(t\right)H_2\left(t\right)-⟨k_2⟩{\theta }_2{I}_2^B\left(t\right)I_2^A\left(t\right)-⟨k_{21}⟩\kappa {\theta }_2{I}_2^B\left(t\right)I_1^A\left(t\right)-\left(\delta +\mu \right)I_2^B\left(t\right)\hfill \\ \frac{d{H}_2\left(t\right)}{dt}=⟨k_2⟩{\theta }_1{I}_2^A\left(t\right)I_2^B\left(t\right)+⟨k_{21}⟩\kappa {\theta }_1{I}_2^A\left(t\right)I_1^B\left(t\right)+⟨k_2⟩{\theta }_2{I}_2^B\left(t\right)I_2^A\left(t\right)+⟨k_{21}⟩\kappa {\theta }_2{I}_2^B\left(t\right)I_1^A\left(t\right)-\left({\epsilon }_2^A\left(t\right)+{\epsilon }_2^B\left(t\right)+\delta +\mu \right)H_2\left(t\right)\hfill \end{array}\right.(2.3)$

where

${\epsilon }_1^A\left(t\right)={\beta }_1\left[{\omega }_1{I}_1^A\left(t\right)+\left(1-{\omega }_1\right)\frac{1}{2}\left(I_1^A\left(t\right)+I_2^A\left(t\right)\right)\right],{\epsilon }_1^B\left(t\right)={\beta }_1\left[{\omega }_1{I}_1^B\left(t\right)+\left(1-{\omega }_1\right)\frac{1}{2}\left(I_1^B\left(t\right)+I_2^B\left(t\right)\right)\right],(2.4)$

${\epsilon }_2^A\left(t\right)={\beta }_2\left[{\omega }_2{I}_2^A\left(t\right)+\left(1-{\omega }_2\right)\frac{1}{2}\left(I_1^A\left(t\right)+I_2^A\left(t\right)\right)\right],{\epsilon }_2^B\left(t\right)={\beta }_2\left[{\omega }_2{I}_2^B\left(t\right)+\left(1-{\omega }_2\right)\frac{1}{2}\left(I_1^B\left(t\right)+I_2^B\left(t\right)\right)\right].(2.5)$

For Eqs 2.4, 2.5, the local information prevalence is equivalent to the density of information spreaders in the layer where individuals reside, while the global information prevalence is defined as the average density of information spreaders in two layers. ω₁ and ω₂ are the weighted coefficients of local prevalence of negative/positive information in layer 1 and 2. β₁, β₂ are the scaling factors. Without loss of generality, we set β₁ = β₂ = 1 here.

3 Basic reproduction number and stability analysis

In this section, we firstly study the basic reproduction number of dynamical systems (2.2) and (2.3) through the next-generation matrix method [37]. Secondly, the existence and stability of information-free equilibrium and information-endemic equilibrium are discussed by means of analysis technique, Routh-Hurwitz judgment, Lyapunov method and LaSalle’s invariance principle.

In order to facilitate the calculation of the basic reproduction number, denote

$\mathcal{X}\left(t\right)={\left(I_1^A\left(t\right),I_2^A\left(t\right),I_1^B\left(t\right),I_2^B\left(t\right),H_1\left(t\right),H_2\left(t\right),S_1\left(t\right),S_2\left(t\right)\right)}^T.(3.1)$

Then we can rewrite the dynamical systems (2.2) and (2.3) as

$\frac{d\mathcal{X}\left(t\right)}{dt}=\mathcal{F}\left(\mathcal{X}\left(t\right)\right)-\mathcal{V}\left(\mathcal{X}\left(t\right)\right)(3.2)$

where

$\mathcal{F}=\left[\begin{array}{c}\hfill ⟨k_1⟩{\lambda }_1{S}_1\left(t\right)I_1^A\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_1{S}_1\left(t\right)I_2^A\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\lambda }_1{S}_2\left(t\right)I_2^A\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_1{S}_2\left(t\right)I_1^A\left(t\right)\hfill \\ \hfill ⟨k_1⟩{\lambda }_2{S}_1\left(t\right)I_1^B\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_2{S}_1\left(t\right)I_2^B\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\lambda }_2{S}_2\left(t\right)I_2^B\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_2{S}_2\left(t\right)I_1^B\left(t\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],(3.3)$

$\mathcal{V}=\left[\begin{array}{c}\hfill ⟨k_1⟩{\theta }_1{I}_1^A\left(t\right)I_1^B\left(t\right)+⟨k_{12}⟩\kappa {\theta }_1{I}_1^A\left(t\right)I_2^B\left(t\right)+\left(\delta +\mu \right)I_1^A\left(t\right)-{\epsilon }_1^A\left(t\right)H_1\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\theta }_1{I}_2^A\left(t\right)I_2^B\left(t\right)+⟨k_{21}⟩\kappa {\theta }_1{I}_2^A\left(t\right)I_1^B\left(t\right)+\left(\delta +\mu \right)I_2^A\left(t\right)-{\epsilon }_2^A\left(t\right)H_2\left(t\right)\hfill \\ \hfill ⟨k_1⟩{\theta }_2{I}_1^B\left(t\right)I_1^A\left(t\right)+⟨k_{12}⟩\kappa {\theta }_2{I}_1^B\left(t\right)I_2^A\left(t\right)+\left(\delta +\mu \right)I_1^B\left(t\right)-{\epsilon }_1^B\left(t\right)H_1\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\theta }_2{I}_2^B\left(t\right)I_2^A\left(t\right)+⟨k_{21}⟩\kappa {\theta }_2{I}_2^B\left(t\right)I_1^A\left(t\right)+\left(\delta +\mu \right)I_2^B\left(t\right)-{\epsilon }_2^B\left(t\right)H_2\left(t\right)\hfill \\ \hfill \left({\epsilon }_1^A\left(t\right)+{\epsilon }_1^B\left(t\right)+\delta +\mu \right)H_1\left(t\right)-\left({\theta }_1+{\theta }_2\right)⟨k_1⟩I_1^A\left(t\right)I_1^B\left(t\right)-\kappa ⟨k_{12}⟩\left({\theta }_1{I}_1^A\left(t\right)I_2^B\left(t\right)+{\theta }_2{I}_1^B\left(t\right)I_2^A\left(t\right)\right)\hfill \\ \hfill \left({\epsilon }_2^A\left(t\right)+{\epsilon }_2^B\left(t\right)+\delta +\mu \right)H_2\left(t\right)-\left({\theta }_1+{\theta }_2\right)⟨k_2⟩I_2^A\left(t\right)I_2^B\left(t\right)-\kappa ⟨k_{21}⟩\left({\theta }_1{I}_2^A\left(t\right)I_1^B\left(t\right)+{\theta }_2{I}_2^B\left(t\right)I_1^A\left(t\right)\right)\hfill \\ \hfill ⟨k_1⟩S_1\left(t\right)\left({\lambda }_1{I}_1^A\left(t\right)+{\lambda }_2{I}_1^B\left(t\right)\right)+\kappa ⟨k_{12}⟩S_1\left(t\right)\left({\lambda }_1{I}_2^A\left(t\right)+{\lambda }_2{I}_2^B\left(t\right)\right)+\delta S_1\left(t\right)-\xi \hfill \\ \hfill ⟨k_2⟩S_2\left(t\right)\left({\lambda }_1{I}_2^A\left(t\right)+{\lambda }_2{I}_2^B\left(t\right)\right)+\kappa ⟨k_{21}⟩S_2\left(t\right)\left({\lambda }_1{I}_1^A\left(t\right)+{\lambda }_2{I}_1^B\left(t\right)\right)+\delta S_2\left(t\right)-\xi \hfill \end{array}\right](3.4)$

Obviously, there exists an information-free equilibrium $E_0=\mathcal{X}(\infty )=\left(\mathrm{0,0,0,0,0,0},\frac{\xi }{\delta },\frac{\xi }{\delta }\right)$. Furthermore, the Jacobian matrices of $\mathcal{F}(\mathcal{X})$ and $\mathcal{V}(\mathcal{X})$ at E₀ are

$D\mathcal{F}\left(E_0\right)=\left[\begin{array}{cc}\hfill F\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],D\mathcal{V}\left(E_0\right)=\left[\begin{array}{cc}\hfill V\hfill & \hfill 0\hfill \\ \hfill J_1\hfill & \hfill J_2\hfill \end{array}\right],(3.5)$

where

$F=\left[\begin{array}{cccc}\hfill ⟨k_1⟩{\lambda }_1\frac{\xi }{\delta }\hfill & \hfill ⟨k_{12}⟩\kappa {\lambda }_1\frac{\xi }{\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⟨k_{21}⟩\kappa {\lambda }_1\frac{\xi }{\delta }\hfill & \hfill ⟨k_2⟩{\lambda }_1\frac{\xi }{\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill ⟨k_1⟩{\lambda }_2\frac{\xi }{\delta }\hfill & \hfill ⟨k_{12}⟩\kappa {\lambda }_2\frac{\xi }{\delta }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill ⟨k_{21}⟩\kappa {\lambda }_2\frac{\xi }{\delta }\hfill & \hfill ⟨k_2⟩{\lambda }_2\frac{\xi }{\delta }\hfill \end{array}\right],V=\left[\begin{array}{cccc}\hfill \delta +\mu \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \delta +\mu \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \delta +\mu \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \delta +\mu \hfill \end{array}\right].(3.6)$

Therefore, the next-generation matrix can be calculated as

$\mathrm{\Gamma }=F{V}^{-1}=\left[\begin{array}{cccc}\hfill \frac{⟨k_1⟩{\lambda }_1\frac{\xi }{\delta }}{\delta +\mu }\hfill & \hfill \frac{⟨k_{12}⟩\kappa {\lambda }_1\frac{\xi }{\delta }}{\delta +\mu }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{⟨k_{21}⟩\kappa {\lambda }_1\frac{\xi }{\delta }}{\delta +\mu }\hfill & \hfill \frac{⟨k_2⟩{\lambda }_1\frac{\xi }{\delta }}{\delta +\mu }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{⟨k_1⟩{\lambda }_2\frac{\xi }{\delta }}{\delta +\mu }\hfill & \hfill \frac{⟨k_{12}⟩\kappa {\lambda }_2\frac{\xi }{\delta }}{\delta +\mu }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{⟨k_{21}⟩\kappa {\lambda }_2\frac{\xi }{\delta }}{\delta +\mu }\hfill & \hfill \frac{⟨k_2⟩{\lambda }_2\frac{\xi }{\delta }}{\delta +\mu }.\hfill \end{array}\right](3.7)$

The basic reproduction number ${\mathcal{R}}_0$ is defined as the spectral radius of matrix Γ,namely,

${\mathcal{R}}_0=\rho \left(\mathrm{\Gamma }\right)=\rho \left(F{V}^{-1}\right)=\frac{\xi \max \left\{{\lambda }_1,{\lambda }_2\right\}}{2\delta \left(\delta +\mu \right)}\left(⟨k_1⟩+⟨k_2⟩+\sqrt{{\left(⟨k_1⟩-⟨k_2⟩\right)}^2+4{\kappa }^2⟨k_{12}⟩⟨k_{21}⟩}\right).(3.8)$

Combined the above analysis, the stability properties of the information-free equilibrium E₀ and information-endemic equilibrium E* are given in the following theorems.

3.1 Stability analysis of information-free equilibrium

With ${\mathcal{R}}_0<1$, our dynamical system will converge to the information-free equilibrium $E_0=\left(\mathrm{0,0,0,0,0,0},\frac{\xi }{\delta },\frac{\xi }{\delta }\right)$ when reaching a steady state. Next, we provide theorems 3.1 and 3.2 to prove its stability.

Theorem 3.1. For the dynamical systems (2.2) and (2.3), the information-free equilibrium E₀ is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

Proof: The local stability of the information-free equilibrium E₀ of the dynamical systems (2.2) and (2.3) is determined by the eigenvalues of the corresponding Jacobian matrix $J_{E_0}$. From the dynamic evolution of SI^AI^BHR, we can obtain

$J_{E_0=}\left[\begin{array}{cccccccc}\hfill ⟨k_1⟩{\lambda }_1\frac{\xi }{\delta }-\left(\delta +\mu \right)\hfill & \hfill ⟨k_{12}⟩\kappa {\lambda }_1\frac{\xi }{\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⟨k_{21}⟩\kappa {\lambda }_1\frac{\xi }{\delta }\hfill & \hfill ⟨k_2⟩{\lambda }_1\frac{\xi }{\delta }-\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill ⟨k_1⟩{\lambda }_2\frac{\xi }{\delta }-\left(\delta +\mu \right)\hfill & \hfill ⟨k_{12}⟩\kappa {\lambda }_2\frac{\xi }{\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill ⟨k_{21}⟩\kappa {\lambda }_2\frac{\xi }{\delta }\hfill & \hfill ⟨k_2⟩{\lambda }_2\frac{\xi }{\delta }-\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -⟨k_1⟩{\lambda }_1\frac{\xi }{\delta }\hfill & \hfill -⟨k_{12}⟩\kappa {\lambda }_1\frac{\xi }{\delta }\hfill & \hfill -⟨k_1⟩{\lambda }_2\frac{\xi }{\delta }\hfill & \hfill -⟨k_{12}⟩\kappa {\lambda }_2\frac{\xi }{\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\delta \hfill & \hfill 0\hfill \\ \hfill -⟨k_{21}⟩\kappa {\lambda }_1\frac{\xi }{\delta }\hfill & \hfill -⟨k_2⟩{\lambda }_1\frac{\xi }{\delta }\hfill & \hfill -⟨k_{21}⟩\kappa {\lambda }_2\frac{\xi }{\delta }\hfill & \hfill -⟨k_2⟩{\lambda }_2\frac{\xi }{\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\delta \hfill \end{array}\right].(3.9)$

Then the eigenvalues of $J_{E_0}$ can be provided as

$\begin{array}{c}{u}_{\mathrm{1,2}}=-\delta ,u_{\mathrm{3,4}}=\frac{1}{2\delta }\left[\left(⟨k_1⟩+⟨k_2⟩\pm \sqrt{{\left(⟨k_1⟩-⟨k_2⟩\right)}^2+4{\kappa }^2⟨k_{12}⟩⟨k_{12}⟩}\right)\xi {\lambda }_1-2\delta \left(\delta +\mu \right)\right],\hfill \\ u_{\mathrm{5,6}}=-\left(\delta +\mu \right),u_{\mathrm{7,8}}=\frac{1}{2\delta }\left[\left(⟨k_1⟩+⟨k_2⟩\pm \sqrt{{\left(⟨k_1⟩-⟨k_2⟩\right)}^2+4{\kappa }^2⟨k_{12}⟩⟨k_{12}⟩}\right)\xi {\lambda }_2-2\delta \left(\delta +\mu \right)\right].\hfill \end{array}$

Furthermore, we can derive the maximum eigenvalue

$u_{\max }=\frac{1}{2\delta }\left[\left(⟨k_1⟩+⟨k_2⟩+\sqrt{{\left(⟨k_1⟩-⟨k_2⟩\right)}^2+4{\kappa }^2⟨k_{12}⟩⟨k_{12}⟩}\right)\xi \max \left({\lambda }_1,{\lambda }_2\right)-2\delta \left(\delta +\mu \right)\right]=\left({\mathcal{R}}_0-1\right)\left(\delta +\mu \right)(3.10)$

Thus, it is obvious that as long as ${\mathcal{R}}_0<1$, all eigenvalues u₁, u₂, u₃, u₄, u₅, u₆, u₇, u₈ have negative real parts. Otherwise, at least one eigenvalue owns a positive real part. In conclusion, the information-free equilibrium E₀ is locally asymptotically stable for ${\mathcal{R}}_0<1$, and unstable for ${\mathcal{R}}_0>1$.

Next, we investigate the global stability of the information-free equilibrium E₀.

Theorem 3.2. The information-free equilibrium E₀ of the dynamical systems (2.2) and (2.3) is globally asymptotically stable if ${\mathcal{R}}_0<1$.

Proof: Construct the following Lyapunov function

$V\left(t\right)=\exp \left[\mathrm{\Xi }\left(t\right)-{\int }_0^t\left(\frac{2\xi \left(\delta +\mu \right)}{\delta }+\kappa \left(⟨k_{12}⟩+⟨k_{21}⟩\right)\right)dx\right]>0,(3.11)$

where $\mathrm{\Xi }(t)=\sum _{i=1}^2\left(I_i^A(t)+I_i^B(t)+H_i(t)\right)$, and $\frac{d\mathrm{\Xi }(t)}{dt}=\frac{d{I}_1^A(t)}{dt}+\frac{d{I}_1^B(t)}{dt}+\frac{d{I}_2^A(t)}{dt}+\frac{d{I}_2^B(t)}{dt}+\frac{d{H}_1(t)}{dt}+\frac{d{H}_2(t)}{dt}$.

The derivative of V(t) towards t can be calculated as

$\begin{array}{c}\begin{array}{cc}\hfill \frac{dV\left(t\right)}{dt}& =V\left(t\right)\left[\frac{d\mathrm{\Xi }\left(t\right)}{dt}-\frac{2\xi \left(\delta +\mu \right)}{\delta }-\kappa \left(⟨k_{12}⟩+⟨k_{21}⟩\right)\right]\hfill \\ \hfill & =V\left(t\right)S_1\left(t\right)\left[⟨k_1⟩\left({\lambda }_1{I}_1^A\left(t\right)+{\lambda }_2{I}_1^B\left(t\right)\right)+\kappa ⟨k_{12}⟩\left({\lambda }_1{I}_2^A\left(t\right)+{\lambda }_2{I}_2^B\left(t\right)\right)\right]\hfill \\ \hfill & +V\left(t\right)S_2\left(t\right)\left[⟨k_2⟩\left({\lambda }_1{I}_2^A\left(t\right)+{\lambda }_2{I}_2^B\left(t\right)\right)+\kappa ⟨k_{21}⟩\left({\lambda }_1{I}_1^A\left(t\right)+{\lambda }_2{I}_1^B\left(t\right)\right)\right]\hfill \\ \hfill & -V\left(t\right)\left[\left(\delta +\mu \right)\left(I_1^A\left(t\right)+I_1^B\left(t\right)+I_2^A\left(t\right)+I_2^B\left(t\right)+H_1\left(t\right)+H_2\left(t\right)\right)+\frac{2\xi \left(\delta +\mu \right)}{\delta }+\kappa \left(⟨k_{12}⟩+⟨k_{21}⟩\right)\right]\hfill \\ \hfill & \le V\left(t\right)\frac{\xi \max \left\{{\lambda }_1,{\lambda }_2\right\}}{\delta }\left[\left(⟨k_1⟩+\kappa ⟨k_{21}⟩\right)\left(I_1^A\left(t\right)+I_1^B\left(t\right)\right)+\left(⟨k_2⟩+\kappa ⟨k_{12}⟩\right)\left(I_2^A\left(t\right)+I_2^B\left(t\right)\right)\right]\hfill \\ \hfill & -V\left(t\right)\left[2\left(\delta +\mu \right)\mathrm{\Xi }\left(t\right)+\kappa \left(⟨k_{12}⟩+⟨k_{21}⟩\right)\right]\hfill \\ \hfill & \le V\left(t\right)\frac{\xi \max \left\{{\lambda }_1,{\lambda }_2\right\}}{\delta }\left[\left(⟨k_1⟩+⟨k_2⟩\right)\mathrm{\Xi }\left(t\right)+\kappa ⟨k_{21}⟩\left(I_1^A\left(t\right)+I_1^B\left(t\right)\right)+\kappa ⟨k_{12}⟩\left(I_2^A\left(t\right)+I_2^B\left(t\right)\right)\right]\hfill \\ \hfill & -V\left(t\right)\left[2\left(\delta +\mu \right)\mathrm{\Xi }\left(t\right)+\kappa \left(⟨k_{12}⟩+⟨k_{21}⟩\right)\right]\hfill \\ \hfill & \le V\left(t\right)\left\{\frac{\xi \max \left\{{\lambda }_1,{\lambda }_2\right\}}{\delta }\left(⟨k_1⟩+⟨k_2⟩+\sqrt{{\left(⟨k_1⟩-⟨k_2⟩\right)}^2+4{\kappa }^2⟨k_{12}⟩⟨k_{21}⟩}\right)-2\left(\delta +\mu \right)\mathrm{\Xi }\left(t\right)\right\}\hfill \\ \hfill & =V\left(t\right)\cdot 2\left(\delta +\mu \right)\left({\mathcal{R}}_0-1\right)\mathrm{\Xi }\left(t\right)\hfill \end{array}\hfill \end{array}$

Significantly, $\frac{dV(t)}{dt}\le 0$ if ${\mathcal{R}}_0<1$. Besides, $\frac{dV(t)}{dt}=0$ if and only if Ξ(t) = 0, namely, $I_i^A(t)=I_i^B(t)=H_i(t)=0$.Based on LaSalle’s invariance principle, it can be concluded that the information-free equilibrium E₀ is globally asymptotically stable if ${\mathcal{R}}_0<1$.

3.2 Stability analysis of information-endemic equilibrium

When ${\mathcal{R}}_0>1$, the system will deviate from the information-free equilibrium E₀, and point to an endemic equilibrium. We define information-endemic equilibrium $E^{*}=\left(I_1^{A*},I_2^{A*},I_1^{B*},I_2^{B*},H_1^{*},H_2^{*}\right)$, then dynamical system (2.2) satisfies the following conditions

$\begin{array}{c}\xi =⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}+⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}+⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}+⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}+\delta S_1^{*}\hfill \\ \left(\delta +\mu \right)I_1^{A*}=⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}+⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}+{\epsilon }_1^{A*}{H}_1^{*}-⟨k_1⟩{\theta }_1{I}_1^{A*}{I}_1^{B*}-⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}\hfill \\ \left(\delta +\mu \right)I_1^{B*}=⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}+⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}+{\epsilon }_1^{B*}{H}_1^{*}-⟨k_1⟩{\theta }_2{I}_1^{B*}{I}_1^{A*}-⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}\hfill \\ \left(\delta +\mu \right)H_1^{*}=⟨k_1⟩{\theta }_1{I}_1^{A*}{I}_1^{B*}+⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}+⟨k_1⟩{\theta }_2{I}_1^{B*}{I}_1^{A*}+⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}-\left({\epsilon }_1^{A*}+{\epsilon }_1^{B*}\right)H_1^{*}\hfill \end{array}(3.12)$

with the similar condition holding for system (2.3).

Theorem 3.3. The information-endemic equilibrium E* of the dynamical systems (2.2) and (2.3) is globally asymptotically stable if ${\mathcal{R}}_0>1$.

Proof: Construct the following Lyapunov function

$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),(3.13)$

for the dynamical system (2.2) in layer 1, we define

$V_1\left(t\right)=\exp \left[c_1{S}_1^{*}g\left(\frac{S_1\left(t\right)}{S_1^{*}}\right)+c_2{I}_1^{A*}g\left(\frac{I_1^A\left(t\right)}{I_1^{A*}}\right)+c_3{I}_1^{B*}g\left(\frac{I_1^B\left(t\right)}{I_1^{B*}}\right)+c_4{H}_1^{*}g\left(\frac{H_1\left(t\right)}{H_1^{*}}\right)-{\int }_0^t\mathrm{\Theta }\left(u\right)du\right]>0,(3.14)$

where g(x) = x − 1 − ln x ≥ g (1) = 0, and

$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{\Theta }\left(u\right)& =\left[\left(c_1-c_2\right)⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}+\left(c_2{\theta }_1+c_3{\theta }_2\right)⟨k_1⟩I_1^{A*}{I}_1^{B*}+c_2⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}\right]g\left(\frac{I_1^A\left(u\right)}{I_1^{A*}}\right)\hfill \\ \hfill & +\left[\left(c_1-c_3\right)⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}+\left(c_2{\theta }_1+c_3{\theta }_2\right)⟨k_1⟩I_1^{A*}{I}_1^{B*}+c_3⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}\right]g\left(\frac{I_1^B\left(u\right)}{I_1^{B*}}\right)\hfill \\ \hfill & +\left(c_4\frac{1-{\omega }_1}{2}\left(I_2^{A*}{H}_1^{*}+I_2^{B*}{H}_1^{*}\right)\right)g\left(\frac{H_1\left(u\right)}{H_1^{*}}\right)+\left(c_1⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}+c_4\frac{1-{\omega }_1}{2}{I}_2^{A*}{H}_1^{*}+c_3⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}\right)g\left(\frac{I_2^A\left(u\right)}{I_2^{A*}}\right)\hfill \\ \hfill & +\left(c_1⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}+c_4\frac{1-{\omega }_1}{2}{I}_2^{B*}{H}_1^{*}+c_2⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}\right)g\left(\frac{I_2^B\left(u\right)}{I_2^{B*}}\right).\hfill \end{array}\hfill \end{array}(3.15)$

Furthermore, we define

$q_1=\frac{S_1\left(t\right)}{S_1^{*}},x_1=\frac{I_1^A\left(t\right)}{I_1^{A*}},y_1=\frac{I_1^B\left(t\right)}{I_1^{B*}},z_1=\frac{H_1\left(t\right)}{H_1^{*}},(3.16)$

$V_1^S\left(t\right)=c_1{S}_1^{*}g\left(\frac{S_1\left(t\right)}{S_1^{*}}\right),V_1^A\left(t\right)=c_2{I}_1^{A*}g\left(\frac{I_1^A\left(t\right)}{I_1^{A*}}\right),V_1^B\left(t\right)=c_3{I}_1^{B*}g\left(\frac{I_1^B\left(t\right)}{I_1^{B*}}\right),V_1^H\left(t\right)=c_4{H}_1^{*}g\left(\frac{H_1\left(t\right)}{H_1^{*}}\right).(3.17)$

Then, we can obtain

$\begin{array}{c}\begin{array}{cc}\hfill V_1\left(t\right)& =\exp \left[V_1^S\left(t\right)+V_1^A\left(t\right)+V_1^B\left(t\right)+V_1^H\left(t\right)-{\int }_0^t\mathrm{\Theta }\left(u\right)du\right]\hfill \\ \hfill & =\exp \left[c_1{S}_1^{*}g\left(q_1\right)+c_2{I}_1^{A*}g\left(x_1\right)+c_3{I}_1^{B*}g\left(y_1\right)+c_4{H}_1^{*}g\left(z_1\right)-{\int }_0^t\mathrm{\Theta }\left(u\right)du\right].\hfill \end{array}\hfill \end{array}(3.18)$

The derivative of V₁(t) towards t can be calculated as

$\frac{d{V}_1\left(t\right)}{dt}=V_1\left(t\right)\left[\frac{d{V}_1^S\left(t\right)}{dt}+\frac{d{V}_1^A\left(t\right)}{dt}+\frac{d{V}_1^B\left(t\right)}{dt}+\frac{d{V}_1^H\left(t\right)}{dt}-\mathrm{\Theta }\left(t\right)\right],(3.19)$

where

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{V}_1^S\left(t\right)}{dt}& =c_1\left(1-\frac{1}{q_1}\right)\left[⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}\left(1-q_1{x}_1\right)+⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}\left(1-q_1{y}_1\right)\right.\hfill \\ \hfill & \left.+⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}\left(1-q_1{x}_2\right)+⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}\left(1-q_1{y}_2\right)+\delta S_1^{*}\left(1-q_1\right)\right],\hfill \end{array}\hfill \end{array}(3.20)$

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{V}_1^A\left(t\right)}{dt}& =c_2\left(1-\frac{1}{x_1}\right)\left[⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}\left(q_1{x}_1-x_1\right)+⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}\left(q_1{x}_2-x_1\right)+\frac{1+{\omega }_1}{2}{I}_1^{A*}{H}_1^{*}\left(x_1{z}_1-x_1\right)\right.\hfill \\ \hfill & \left.+\frac{1-{\omega }_1}{2}{I}_2^{A*}{H}_1^{*}\left(x_2{z}_1-x_1\right)-⟨k_1⟩{\theta }_1{I}_1^{A*}{I}_1^{B*}\left(x_1{y}_1-x_1\right)-⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}\left(x_1{y}_2-x_1\right)\right],\hfill \end{array}\hfill \end{array}(3.21)$

$\begin{array}{c}\begin{array}{c}\hfill \frac{d{V}_1^B\left(t\right)}{dt}=c_3\left(1-\frac{1}{y_1}\right)\left[⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}\left(q_1{y}_1-y_1\right)+⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}\left(q_1{y}_2-y_1\right)+\frac{1+{\omega }_1}{2}{I}_1^{B*}{H}_1^{*}\left(y_1{z}_1-y_1\right)\right.\\ \hfill \left.+\frac{1-{\omega }_1}{2}{I}_2^{B*}{H}_1^{*}\left(y_2{z}_1-y_1\right)-⟨k_1⟩{\theta }_2{I}_1^{B*}{I}_1^{A*}\left(y_1{x}_1-y_1\right)-⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}\left(y_1{x}_2-y_1\right)\right],\end{array}\hfill \end{array}(3.22)$

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{V}_1^H\left(t\right)}{dt}& =c_4\left(1-\frac{1}{z_1}\right)\left[⟨k_1⟩{\theta }_1{I}_1^{A*}{I}_1^{B*}\left(x_1{y}_1-z_1\right)+⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}\left(x_1{y}_2-z_1\right)-\frac{1+{\omega }_1}{2}{I}_1^{A*}{H}_1^{*}\left(x_1{z}_1-z_1\right)\right.\hfill \\ \hfill & -\frac{1-{\omega }_1}{2}{I}_2^{A*}{H}_1^{*}\left(x_2{z}_1-z_1\right)+⟨k_1⟩{\theta }_2{I}_1^{B*}{I}_1^{A*}\left(y_1{x}_1-z_1\right)+⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}\left(y_1{x}_2-z_1\right)\hfill \\ \hfill & \left.-\frac{1+{\omega }_1}{2}{I}_1^{B*}{H}_1^{*}\left(y_1{z}_1-z_1\right)-\frac{1-{\omega }_1}{2}{I}_2^{B*}{H}_1^{*}\left(y_2{z}_1-z_1\right)\right].\hfill \end{array}\hfill \end{array}(3.23)$

For convenience, we define

$\mathrm{\Lambda }\left(t\right)\triangleq \frac{d{V}_1^S\left(t\right)}{dt}+\frac{d{V}_1^A\left(t\right)}{dt}+\frac{d{V}_1^B\left(t\right)}{dt}+\frac{d{V}_1^H\left(t\right)}{dt}-\mathrm{\Theta }\left(t\right).(3.24)$

Therefore, combining Eq. 3.15 and Eqs 3.20—3.23, we can derive

$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{\Lambda }\left(t\right)& =-c_1\delta S_1^{*}\left(q_1-1\right)\left(1-\frac{1}{q_1}\right)-\left(c_1⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}+c_1⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}+c_1⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}+c_1⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}\right)g\left(\frac{1}{q_1}\right)\hfill \\ \hfill & -\left[c_2⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}+c_2\frac{1+{\omega }_1}{2}{I}_1^{A*}{H}_1^{*}\left(1-\frac{c_4}{c_2}\right)+c_2\frac{1-{\omega }_1}{2}{I}_2^{A*}{H}_1^{*}\right]g\left(x_1\right)-c_1⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}\left(1-\frac{c_2}{c_1}\right)g\left(q_1{x}_1\right)\hfill \\ \hfill & -\left(c_2⟨k_1⟩{\lambda }_1{S}_1^{*}{I}_1^{A*}+c_3⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}\right)g\left(q_1\right)-c_1⟨k_1⟩{\lambda }_2{S}_1^{*}{I}_1^{B*}\left(1-\frac{c_3}{c_1}\right)g\left(q_1{y}_1\right)\hfill \\ \hfill & -\left[c_3⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_1^{B*}+c_3\frac{1+{\omega }_1}{2}{I}_1^{B*}{H}_1^{*}\left(1-\frac{c_4}{c_3}\right)+c_3\frac{1-{\omega }_1}{2}{I}_2^{B*}{H}_1^{*}\right]g\left(y_1\right)-c_1⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}\left(1-\frac{c_2}{c_1}\right)g\left(q_1{x}_2\right)\hfill \\ \hfill & -c_2⟨k_{12}⟩\kappa {\lambda }_1{S}_1^{*}{I}_2^{A*}g\left(\frac{q_1{x}_2}{x_1}\right)-c_1⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}\left(1-\frac{c_3}{c_1}\right)g\left(q_1{y}_2\right)-c_3⟨k_{12}⟩\kappa {\lambda }_2{S}_1^{*}{I}_2^{B*}g\left(\frac{q_1{y}_2}{y_1}\right)\hfill \\ \hfill & +c_2\frac{1+{\omega }_1}{2}{I}_1^{A*}{H}_1^{*}\left(1-\frac{c_4}{c_2}\right)g\left(x_1{z}_1\right)+c_3\frac{1+{\omega }_1}{2}{I}_1^{B*}{H}_1^{*}\left(1-\frac{c_4}{c_3}\right)g\left(y_1{z}_1\right)+c_2\frac{1-{\omega }_1}{2}{I}_2^{A*}{H}_1^{*}\left(1-\frac{c_4}{c_2}\right)g\left(x_2{z}_1\right)\hfill \\ \hfill & -c_2\frac{1-{\omega }_1}{2}{I}_2^{A*}{H}_1^{*}g\left(\frac{x_2{z}_1}{x_1}\right)+c_3\frac{1-{\omega }_1}{2}{I}_2^{B*}{H}_1^{*}\left(1-\frac{c_4}{c_3}\right)g\left(y_2{z}_1\right)-c_3\frac{1-{\omega }_1}{2}{I}_2^{B*}{H}_1^{*}g\left(\frac{y_2{z}_1}{y_1}\right)\hfill \\ \hfill & -\left[\frac{1+{\omega }_1}{2}{H}_1^{*}\left(c_2{I}_1^{A*}\left(1-\frac{c_4}{c_2}\right)+c_3{I}_1^{B*}\left(1-\frac{c_4}{c_3}\right)\right)+c_4⟨k_1⟩\left({\theta }_1+{\theta }_2\right)I_1^{A*}{I}_1^{B*}+c_4⟨k_{12}⟩\kappa \left({\theta }_1{I}_1^{A*}{I}_2^{B*}+{\theta }_2{I}_1^{B*}{I}_2^{A*}\right)\right]g\left(z_1\right)\hfill \\ \hfill & -\left[c_2⟨k_1⟩{\theta }_1{I}_1^{A*}{I}_1^{B*}\left(1-\frac{c_4}{c_2}\right)+c_3⟨k_1⟩{\theta }_2{I}_1^{A*}{I}_1^{B*}\left(1-\frac{c_4}{c_3}\right)\right]g\left(x_1{y}_1\right)-c_4⟨k_1⟩\left({\theta }_1+{\theta }_2\right)I_1^{A*}{I}_1^{B*}g\left(\frac{x_1{y}_1}{z_1}\right)\hfill \\ \hfill & -⟨k_{12}⟩\kappa {\theta }_1{I}_1^{A*}{I}_2^{B*}\left[c_2\left(1-\frac{c_4}{c_2}\right)g\left(x_1{y}_2\right)+c_{4}g\left(\frac{x_1{y}_2}{z_1}\right)\right]-⟨k_{12}⟩\kappa {\theta }_2{I}_1^{B*}{I}_2^{A*}\left[c_3\left(1-\frac{c_4}{c_3}\right)g\left(y_1{x}_2\right)+c_{4}g\left(\frac{y_1{x}_2}{z_1}\right)\right].\hfill \end{array}\hfill \end{array}(3.25)$

Next, by taking c₁ ≥ c₂ = c₃ = c₄ > 0, we have

$\frac{d{V}_1\left(t\right)}{dt}=V_1\left(t\right)\mathrm{\Lambda }\left(t\right)\le 0.(3.26)$

Besides, $\frac{d{V}_1(t)}{dt}=0$ if and only if $S_1(t)=S_1^{*},I_1^A(t)=I_1^{A*},I_1^B(t)=I_1^{B*},H_1(t)=H_1^{*}$. And for the dynamical system (2.3) in layer 2, we can also construct the Lyapunov function V₂(t) which is similar to V₁(t), such that V₂(t) > 0 and $\frac{d{V}_2(t)}{dt}<0$. In other words, we achieve that V(t) = V₁(t) + V₂(t) > 0 and $\frac{dV(t)}{dt}=\frac{d{V}_1(t)}{dt}+\frac{d{V}_2(t)}{dt}<0$. Based on LaSalle’s invariance principle, it can be concluded that the information-endemic equilibrium E* is globally asymptotically stable if ${\mathcal{R}}_0>1$.

In conclusion, we have completed the proof of asymptotic stability for information-free and information-endemic equilibria. Note that the Lyapunov theory we employ is not the unique method to prove system stability. As an alternative, Shang [38] proposed a novel framework that can analytically obtain the explicit solutions of dynamical systems using Lie algebra methods. Once the explicit solutions can be available, an effort may be made to derive the limit values of these explicit solutions when t → ∞. And the convergence of the limit values can reflect the stability of dynamical systems.

4 Optimal control

In order to suppress the prevalence of negative information, we introduce two heterogeneous controls: one is direct control mode v₁(t), which persuades negative information spreaders to become positive information spreaders; the other is indirect control mode v₂(t), which guides hesitant individuals to become positive information spreaders. Define Q^C as the Lebesgue square integrable control set of all admissible values of v₁(t) and v₂(t) over time interval $\left[0,T\right]$, given as $Q^C=\left\{v_1(t),v_2(t)\in L^2\left[0,T\right]:0\le v_1(t),v_2(t)\le \mathrm{1,0}\le t\le T\right\}$. Based on the above considerations, we consider the optimization problems as follows:

$J={\int }_0^T\left\{d_1\left(I_1^B\left(t\right)+I_2^B\left(t\right)\right)+\frac{1}{2}{d}_2{v}_1^2\left(t\right)+\frac{1}{2}{d}_3{v}_2^2\left(t\right)\right\}dt.(4.1)$

where the first term corresponds to the infection cost of negative information propagation in the network, and the second and third terms are the costs brought by the implementation of controls. Our goal is to achieve the most powerful inhibition effect on negative information with the lowest control intensity, which forms a trade-off between the two kinds of costs. d₁, d₂ and d₃ are the weight factors of the three costs.

Correspondingly, the Lagrangian of our optimal problem can be formed as

$L=d_1\left(I_1^B\left(t\right)+I_2^B\left(t\right)\right)+\frac{1}{2}{d}_2{v}_1^2\left(t\right)+\frac{1}{2}{d}_3{v}_2^2\left(t\right),(4.2)$

then define adjoint functions $\phi (t)=\left({\phi }_1(t),{\phi }_2(t),{\phi }_3(t),{\phi }_4(t),{\phi }_5(t),{\phi }_6(t),{\phi }_7(t),{\phi }_8(t)\right)$, we can drive the Hamiltonian function as

$\begin{array}{c}\begin{array}{cc}\hfill H& =L+{\phi }_1\left(t\right)\frac{d{S}_1\left(t\right)}{dt}+{\phi }_2\left(t\right)\frac{d{I}_1^A\left(t\right)}{dt}+{\phi }_3\left(t\right)\frac{d{I}_1^B\left(t\right)}{dt}+{\phi }_4\left(t\right)\frac{d{H}_1\left(t\right)}{dt}\hfill \\ \hfill & +{\phi }_5\left(t\right)\frac{d{S}_2\left(t\right)}{dt}+{\phi }_6\left(t\right)\frac{d{I}_2^A\left(t\right)}{dt}+{\phi }_7\left(t\right)\frac{d{I}_2^B\left(t\right)}{dt}+{\phi }_8\left(t\right)\frac{d{H}_2\left(t\right)}{dt}.\hfill \end{array}\hfill \end{array}(4.3)$

4.1 The existence of optimal solution

Theorem 4.1. There exists a set of optimal controls $v^{*}(t)\in \left\{v_1^{*}(t),v_2^{*}(t)\right\}$ and corresponding solutions ${\bar{S}}_1(t)$, ${\bar{I}}_1^A(t)$, ${\bar{I}}_1^B(t)$, ${\bar{H}}_1(t)$, ${\bar{S}}_2(t)$, ${\bar{I}}_2^A(t)$, ${\bar{I}}_2^B(t),{\bar{H}}_2(t)$ such that $J(v^{*}(t))={\min }_{v(t)\in Q^C}J(v(t))$.

Proof: The existence of optimal control strategies can be proven by the Cesari theorem [39]. Cesari theorem indicates that if the optimization problem for our dynamical systems (2.2) and (2.3) satisfies the following five conditions, the optimal solutions of two controls v₁(t) and v₂(t) will exist.

(1) The control set and state variables are non-empty;

(2) The control set is closed and convex;

(3) The right-hand side of systems (2.2) and (2.3) is bounded above by a linear function with the state and control;

(4) The integrand in the objective function is convex with respect to the controls v₁(t), v₂(t);

(5) There exists a constant C₁ > 1 and positive number C₂ and C₃ such that

$L\ge C_2{\left({\left|v_1\left(t\right)\right|}^2+{\left|v_2\left(t\right)\right|}^2\right)}^{\frac{C_1}{2}}-C_3.$

Next, we will prove that the dynamical systems (2.2) and (2.3) satisfy the above five conditions. Obviously, if the system is uniformly Lipschitz continuous, the sets of Q^C and solutions to initial values are non-empty. Besides, state variables are non-empty such that condition (1) is satisfied. The characteristics of control space and objective function can be verified by definition, meeting conditions (2) and (4).

The systems (2.2) and (2.3) can be rewritten as

$D\left(\mathcal{X}\left(t\right)\right)=\frac{d\mathcal{X}\left(t\right)}{dt}=B\mathcal{X}\left(t\right)+G\left(\mathcal{X}\left(t\right)\right),(4.4)$

where

$B=\left[\begin{array}{cccccccc}\hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\left(\delta +\mu \right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\delta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\delta \hfill \end{array}\right],(4.5)$

$G\left(\mathcal{X}\right)=\left[\begin{array}{c}\hfill ⟨k_1⟩{\lambda }_1{S}_1\left(t\right)I_1^A\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_1{S}_1\left(t\right)I_2^A\left(t\right)+{\epsilon }_1^A\left(t\right)H_1\left(t\right)-⟨k_1⟩{\theta }_1{I}_1^A\left(t\right)I_1^B\left(t\right)-⟨k_{12}⟩\kappa {\theta }_1{I}_1^A\left(t\right)I_2^B\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\lambda }_1{S}_2\left(t\right)I_2^A\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_1{S}_2\left(t\right)I_1^A\left(t\right)+{\epsilon }_2^A\left(t\right)H_2\left(t\right)-⟨k_2⟩{\theta }_1{I}_2^A\left(t\right)I_2^B\left(t\right)-⟨k_{21}⟩\kappa {\theta }_1{I}_2^A\left(t\right)I_1^B\left(t\right)\hfill \\ \hfill ⟨k_1⟩{\lambda }_2{S}_1\left(t\right)I_1^B\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_2{S}_1\left(t\right)I_2^B\left(t\right)+{\epsilon }_1^B\left(t\right)H_1\left(t\right)-⟨k_1⟩{\theta }_2{I}_1^B\left(t\right)I_1^A\left(t\right)-⟨k_{12}⟩\kappa {\theta }_2{I}_1^B\left(t\right)I_2^A\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\lambda }_2{S}_2\left(t\right)I_2^B\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_2{S}_2\left(t\right)I_1^B\left(t\right)+{\epsilon }_2^B\left(t\right)H_2\left(t\right)-⟨k_2⟩{\theta }_2{I}_2^B\left(t\right)I_2^A\left(t\right)-⟨k_{21}⟩\kappa {\theta }_2{I}_2^B\left(t\right)I_1^A\left(t\right)\hfill \\ \hfill ⟨k_1⟩{\theta }_1{I}_1^A\left(t\right)I_1^B\left(t\right)+⟨k_{12}⟩\kappa {\theta }_1{I}_1^A\left(t\right)I_2^B\left(t\right)+⟨k_1⟩{\theta }_2{I}_1^B\left(t\right)I_1^A\left(t\right)+⟨k_{12}⟩\kappa {\theta }_2{I}_1^B\left(t\right)I_2^A\left(t\right)-\left({\epsilon }_1^A\left(t\right)+{\epsilon }_1^B\left(t\right)\right)H_1\left(t\right)\hfill \\ \hfill ⟨k_2⟩{\theta }_1{I}_2^A\left(t\right)I_2^B\left(t\right)+⟨k_{21}⟩\kappa {\theta }_1{I}_2^A\left(t\right)I_1^B\left(t\right)+⟨k_2⟩{\theta }_2{I}_2^B\left(t\right)I_2^A\left(t\right)+⟨k_{21}⟩\kappa {\theta }_2{I}_2^B\left(t\right)I_1^A\left(t\right)-\left({\epsilon }_2^A\left(t\right)+{\epsilon }_2^B\left(t\right)\right)H_2\left(t\right)\hfill \\ \hfill \xi -⟨k_1⟩{\lambda }_1{S}_1\left(t\right)I_1^A\left(t\right)-⟨k_1⟩{\lambda }_2{S}_1\left(t\right)I_1^B\left(t\right)-⟨k_{12}⟩\kappa {\lambda }_1{S}_1\left(t\right)I_2^A\left(t\right)-⟨k_{12}⟩\kappa {\lambda }_2{S}_1\left(t\right)I_2^B\left(t\right)\hfill \\ \hfill \xi -⟨k_2⟩{\lambda }_1{S}_2\left(t\right)I_2^A\left(t\right)-⟨k_2⟩{\lambda }_2{S}_2\left(t\right)I_2^B\left(t\right)-⟨k_{21}⟩\kappa {\lambda }_1{S}_2\left(t\right)I_1^A\left(t\right)-⟨k_{21}⟩\kappa {\lambda }_2{S}_2\left(t\right)I_1^B\left(t\right)\hfill \end{array}\right].(4.6)$

Furthermore, we can verify

$\begin{array}{c}\left|G\left(\tilde{\mathcal{X}}\right)-G\left(\mathcal{X}\right)\right|\le Q\left(\left|{\tilde{S}}_1-S_1\right|+\left|{\tilde{S}}_2-S_2\right|+\left|{\tilde{I}}_1^A-I_1^A\right|+\left|{\tilde{I}}_2^A-I_2^A\right|+\left|{\tilde{I}}_1^B-I_1^B\right|+\left|{\tilde{I}}_2^B-I_2^B\right|+\left|{\tilde{H}}_1-H_1\right|+\left|{\tilde{H}}_2-H_2\right|\right)\hfill \end{array}(4.7)$

where

$\begin{array}{c}\begin{array}{cc}\hfill Q=\max & \left\{2\left({\lambda }_1+{\lambda }_2\right)\left(⟨k_1⟩+⟨k_{12}⟩\kappa \right),2\left({\lambda }_1+{\lambda }_2\right)\left(⟨k_2⟩+⟨k_{21}⟩\kappa \right),2\left[⟨k_1⟩\left({\lambda }_1+{\theta }_1+{\theta }_2\right)+⟨k_{21}⟩\kappa \left({\lambda }_1+{\theta }_2\right)+⟨k_{12}⟩\kappa {\theta }_1\right],.\right.\hfill \\ \hfill & 2\left[⟨k_2⟩\left({\lambda }_1+{\theta }_1+{\theta }_2\right)+⟨k_{12}⟩\kappa \left({\lambda }_1+{\theta }_2\right)+⟨k_{21}⟩\kappa {\theta }_1\right],2\left[⟨k_1⟩\left({\lambda }_2+{\theta }_1+{\theta }_2\right)+⟨k_{21}⟩\kappa \left({\lambda }_2+{\theta }_1\right)+⟨k_{12}⟩\kappa {\theta }_2\right],\hfill \\ \hfill & \left.2\left[⟨k_2⟩\left({\lambda }_2+{\theta }_1+{\theta }_2\right)+⟨k_{12}⟩\kappa \left({\lambda }_2+{\theta }_2\right)+⟨k_{21}⟩\kappa {\theta }_2\right],3\max \left\{{\tilde{\epsilon }}_1^A+{\tilde{\epsilon }}_1^B,{\epsilon }_1^A+{\epsilon }_1^B\right\},3\max \left\{{\tilde{\epsilon }}_2^A+{\tilde{\epsilon }}_2^B,{\epsilon }_2^A+{\epsilon }_2^B\right\}\right\}.\hfill \end{array}\hfill \end{array}(4.8)$

Then we have

$\left|D\left(\tilde{\mathcal{X}}\right)-D\left(\mathcal{X}\right)\right|\le V\left|\tilde{\mathcal{X}}-\mathcal{X}\right|,(4.9)$

where

$V=\max \left\{Q,‖B‖\right\}<\infty .(4.10)$

Therefore, the function D is uniformly Lipschitz continuous and satisfies the required bound in Cesari theorem. The control set Q^C belongs to the closed set $\left[\mathrm{0,1}\right]$ and the objective function J lies in a compact interval $\left[J_{\min },J_{\max }\right]$. Consequently, the function $D(\mathcal{X})$ is linear in two controls v₁(t) and v₂(t), which means condition (3) is satisfied. As a result, we can draw the conclusion that the solution of the system exists.

Furthermore, we set C₁ = 2, $C_2=\frac{1}{2}\min \left\{d_2,d_3\right\}$, C₃ = Δ(0), then condition (5) is satisfied, which means the optimal solution exists. Based on the above discussion, the proof is completed.

4.2 The solution to optimal control problem

Here we employ Pontryagin minimum principle with fixed final time to analytically derive the optimal solution.

Theorem 4.2. Given an optimal control pair v₁(t) and v₂(t) and the corresponding solutions to the system (2.2) and (2.3), there exist adjoint functions φ₁(t), φ₂(t), φ₃(t), φ₄(t), φ₅(t), φ₆(t), φ₇(t), φ₈(t), satisfying

$\frac{d{\phi }_1\left(t\right)}{dt}=\left({\phi }_1\left(t\right)-{\phi }_2\left(t\right)\right)\left(⟨k_1⟩{\lambda }_1{I}_1^A\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_1{I}_2^A\left(t\right)\right)+\left({\phi }_1\left(t\right)-{\phi }_3\left(t\right)\right)\left(⟨k_1⟩{\lambda }_2{I}_1^B\left(t\right)+⟨k_{12}⟩\kappa {\lambda }_2{I}_2^B\left(t\right)\right)+\delta {\phi }_1\left(t\right),(4.11)$

$\begin{array}{c}\frac{d{\phi }_2\left(t\right)}{dt}=\left({\phi }_1\left(t\right)-{\phi }_2\left(t\right)\right)⟨k_1⟩{\lambda }_1{S}_1\left(t\right)+\left({\phi }_4\left(t\right)-{\phi }_2\left(t\right)\right)\left(\frac{1+{\omega }_1}{2}{H}_1\left(t\right)-⟨k_1⟩{\theta }_1{I}_1^B\left(t\right)-⟨k_{12}⟩\kappa {\theta }_1{I}_2^B\left(t\right)\right)+\left(\delta +\mu \right){\phi }_2\left(t\right)\hfill \\ +\left({\phi }_3\left(t\right)-{\phi }_4\left(t\right)\right)⟨k_1⟩{\theta }_2{I}_1^B\left(t\right)+\left({\phi }_5\left(t\right)-{\phi }_6\left(t\right)\right)⟨k_{21}⟩\kappa {\lambda }_1{S}_2\left(t\right)\hfill \\ +\left({\phi }_8\left(t\right)-{\phi }_6\left(t\right)\right)\frac{1-{\omega }_2}{2}{H}_2\left(t\right)+\left({\phi }_7\left(t\right)-{\phi }_8\left(t\right)\right)⟨k_{21}⟩\kappa {\theta }_2{I}_2^B\left(t\right),\hfill \end{array}(4.12)$

$\begin{array}{c}\frac{d{\phi }_3\left(t\right)}{dt}=\left({\phi }_1\left(t\right)-{\phi }_3\left(t\right)\right)⟨k_1⟩{\lambda }_2{S}_1\left(t\right)+\left({\phi }_4\left(t\right)-{\phi }_3\left(t\right)\right)\left(\frac{1+{\omega }_1}{2}{H}_1\left(t\right)-⟨k_1⟩{\theta }_2{I}_1^A\left(t\right)-⟨k_{12}⟩\kappa {\theta }_2{I}_2^A\left(t\right)\right)+\left(\delta +\mu \right){\phi }_3\left(t\right)\hfill \\ +\left({\phi }_2\left(t\right)-{\phi }_4\left(t\right)\right)⟨k_1⟩{\theta }_1{I}_1^A\left(t\right)+\left({\phi }_5\left(t\right)-{\phi }_7\left(t\right)\right)⟨k_{21}⟩\kappa {\lambda }_2{S}_2\left(t\right)+\left({\phi }_8\left(t\right)-{\phi }_7\left(t\right)\right)\frac{1-{\omega }_2}{2}{H}_2\left(t\right)\hfill \\ +\left({\phi }_6\left(t\right)-{\phi }_8\left(t\right)\right)⟨k_{21}⟩\kappa {\theta }_1{I}_2^A\left(t\right)-{\phi }_2\left(t\right)v_1\left(t\right)+{\phi }_3\left(t\right)v_1\left(t\right)-d_1,\hfill \end{array}(4.13)$

$\frac{d{\phi }_4\left(t\right)}{dt}=\left(\delta +\mu +v_2\left(t\right)\right){\phi }_4\left(t\right)+\left({\phi }_4\left(t\right)-{\phi }_2\left(t\right)\right){\epsilon }_1^A\left(t\right)+\left({\phi }_4\left(t\right)-{\phi }_3\left(t\right)\right){\epsilon }_1^B\left(t\right)-v_2\left(t\right){\phi }_2\left(t\right),(4.14)$

$\frac{d{\phi }_5\left(t\right)}{dt}=\left({\phi }_5\left(t\right)-{\phi }_6\left(t\right)\right)\left(⟨k_2⟩{\lambda }_1{I}_2^A\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_1{I}_1^A\left(t\right)\right)+\left({\phi }_5\left(t\right)-{\phi }_7\left(t\right)\right)\left(⟨k_2⟩{\lambda }_2{I}_2^B\left(t\right)+⟨k_{21}⟩\kappa {\lambda }_2{I}_1^B\left(t\right)\right)+\delta {\phi }_5\left(t\right),(4.15)$

$\begin{array}{c}\frac{d{\phi }_6\left(t\right)}{dt}=\left({\phi }_5\left(t\right)-{\phi }_6\left(t\right)\right)⟨k_2⟩{\lambda }_1{S}_2\left(t\right)+\left({\phi }_8\left(t\right)-{\phi }_6\left(t\right)\right)\left(\frac{1+{\omega }_2}{2}{H}_2\left(t\right)-⟨k_2⟩{\theta }_1{I}_2^B\left(t\right)-⟨k_{21}⟩\kappa {\theta }_1{I}_1^B\left(t\right)\right)+\left(\delta +\mu \right){\phi }_6\left(t\right)\hfill \\ +\left({\phi }_7\left(t\right)-{\phi }_8\left(t\right)\right)⟨k_2⟩{\theta }_2{I}_2^B\left(t\right)+\left({\phi }_1\left(t\right)-{\phi }_2\left(t\right)\right)⟨k_{12}⟩\kappa {\lambda }_1{S}_1\left(t\right)\hfill \\ +\left({\phi }_4\left(t\right)-{\phi }_2\left(t\right)\right)\frac{1-{\omega }_1}{2}{H}_1\left(t\right)+\left({\phi }_3\left(t\right)-{\phi }_4\left(t\right)\right)⟨k_{12}⟩\kappa {\theta }_2{I}_1^B\left(t\right),\hfill \end{array}(4.16)$

$\begin{array}{c}\frac{d{\phi }_7\left(t\right)}{dt}=\left({\phi }_5\left(t\right)-{\phi }_7\left(t\right)\right)⟨k_2⟩{\lambda }_2{S}_2\left(t\right)+\left({\phi }_8\left(t\right)-{\phi }_7\left(t\right)\right)\left(\frac{1+{\omega }_2}{2}{H}_2\left(t\right)-⟨k_2⟩{\theta }_2{I}_2^A\left(t\right)-⟨k_{21}⟩\kappa {\theta }_2{I}_1^A\left(t\right)\right)+\left(\delta +\mu \right){\phi }_7\left(t\right)\hfill \\ +\left({\phi }_6\left(t\right)-{\phi }_8\left(t\right)\right)⟨k_2⟩{\theta }_1{I}_2^A\left(t\right)+\left({\phi }_1\left(t\right)-{\phi }_3\left(t\right)\right)⟨k_{12}⟩\kappa {\lambda }_2{S}_1\left(t\right)+\left({\phi }_4\left(t\right)-{\phi }_3\left(t\right)\right)\frac{1-{\omega }_1}{2}{H}_1\left(t\right)\hfill \\ +\left({\phi }_2\left(t\right)-{\phi }_4\left(t\right)\right)⟨k_{12}⟩\kappa {\theta }_1{I}_1^A\left(t\right)-{\phi }_6\left(t\right)v_1\left(t\right)+{\phi }_7\left(t\right)v_1\left(t\right)-d_1,\hfill \end{array}(4.17)$

$\frac{d{\phi }_8\left(t\right)}{dt}=\left(\delta +\mu +v_2\left(t\right)\right){\phi }_8\left(t\right)+\left({\phi }_8\left(t\right)-{\phi }_6\left(t\right)\right){\epsilon }_2^A\left(t\right)+\left({\phi }_8\left(t\right)-{\phi }_7\left(t\right)\right){\epsilon }_2^B\left(t\right)-v_2\left(t\right){\phi }_6\left(t\right),(4.18)$

with boundary conditions

${\phi }_1\left(T\right)={\phi }_2\left(T\right)={\phi }_3\left(T\right)={\phi }_4\left(T\right)={\phi }_5\left(T\right)={\phi }_6\left(T\right)={\phi }_7\left(T\right)={\phi }_8\left(T\right)=0.(4.19)$

Furthermore, the optimal solutions of $v_1^{*}(t)$ and $v_2^{*}(t)$ are formulated as

$v_1^{*}\left(t\right)=\min \left\{\max \left\{\frac{1}{d_2}\left[\left({\phi }_3\left(t\right)-{\phi }_2\left(t\right)\right){\bar{I}}_1^B\left(t\right)+\left({\phi }_7\left(t\right)-{\phi }_6\left(t\right)\right){\bar{I}}_2^B\left(t\right)\right],v_1^{\min }\right\},v_1^{\max }\right\},(4.20)$

$v_2^{*}\left(t\right)=\min \left\{\max \left\{\frac{1}{d_3}\left[\left({\phi }_4\left(t\right)-{\phi }_2\left(t\right)\right){\bar{H}}_1\left(t\right)+\left({\phi }_7\left(t\right)-{\phi }_6\left(t\right)\right){\bar{H}}_2\left(t\right)\right],v_2^{\min }\right\},v_2^{\max }\right\}.(4.21)$

Proof: While characterizing the properties of the optimal solution, the costate conditions must be satisfied in the system of costate differential equations as

$\begin{array}{c}\frac{d{\phi }_1\left(t\right)}{dt}=-\frac{\partial H}{\partial S_1\left(t\right)},\frac{d{\phi }_2\left(t\right)}{dt}=-\frac{\partial H}{\partial I_1^A\left(t\right)},\frac{d{\phi }_3\left(t\right)}{dt}=-\frac{\partial H}{\partial I_1^B\left(t\right)},\frac{d{\phi }_4\left(t\right)}{dt}=-\frac{\partial H}{\partial H_1\left(t\right)},\hfill \\ \frac{d{\phi }_5\left(t\right)}{dt}=-\frac{\partial H}{\partial S_2\left(t\right)},\frac{d{\phi }_6\left(t\right)}{dt}=-\frac{\partial H}{\partial I_2^A\left(t\right)},\frac{d{\phi }_7\left(t\right)}{dt}=-\frac{\partial H}{\partial I_2^B\left(t\right)},\frac{d{\phi }_8\left(t\right)}{dt}=-\frac{\partial H}{\partial H_2\left(t\right)}.\hfill \end{array}(4.22)$

Then, by the optimal conditions, we have

$\begin{array}{c}\frac{\partial H}{\partial v_1\left(t\right)}=d_2{v}_1\left(t\right)+\left({\phi }_2\left(t\right)-{\phi }_3\left(t\right)\right)I_1^B\left(t\right)+\left({\phi }_6\left(t\right)-{\phi }_7\left(t\right)\right)I_2^B\left(t\right),\hfill \\ \frac{\partial H}{\partial v_2\left(t\right)}=d_3{v}_2\left(t\right)+\left({\phi }_2\left(t\right)-{\phi }_4\left(t\right)\right)H_1\left(t\right)+\left({\phi }_6\left(t\right)-{\phi }_8\left(t\right)\right)H_2\left(t\right).\hfill \end{array}(4.23)$

Let $\frac{\partial H}{\partial v_1(t)}=\frac{\partial H}{\partial v_2(t)}=0$ , so we can obtain the optimal control at time t satisfying

$\begin{array}{c}{v}_1^{*}\left(t\right)=\frac{1}{d_2}\left[\left({\phi }_3\left(t\right)-{\phi }_2\left(t\right)\right){\bar{I}}_1^B\left(t\right)+\left({\phi }_7\left(t\right)-{\phi }_6\left(t\right)\right){\bar{I}}_2^B\left(t\right)\right]\stackrel{\Delta }{=}{v}_1^{op}\left(t\right),\hfill \\ v_2^{*}\left(t\right)=\frac{1}{d_3}\left[\left({\phi }_4\left(t\right)-{\phi }_2\left(t\right)\right){\bar{H}}_1\left(t\right)+\left({\phi }_7\left(t\right)-{\phi }_6\left(t\right)\right){\bar{H}}_2\left(t\right)\right]\stackrel{\Delta }{=}{v}_2^{op}\left(t\right).\hfill \end{array}(4.24)$

Considering the property of the control space, we obtain

$v_1^{*}\left(t\right)=\left\{\begin{array}{c}{v}_1^{\min },\mathit{\text{if}}{v}_1^{op}\left(t\right)<v_1^{\min }\hfill \\ v_1^{op}\left(t\right),\mathit{\text{if}}{v}_1^{\min }\le v_1^{op}\left(t\right)\le v_1^{\max }\hfill \\ v_1^{\max },\mathit{\text{if}}{v}_1^{op}\left(t\right)>v_1^{\max }\hfill \end{array}\right.,v_2^{*}\left(t\right)=\left\{\begin{array}{c}{v}_2^{\min },\mathit{\text{if}}{v}_2^{op}\left(t\right)<v_2^{\min }\hfill \\ v_2^{op}\left(t\right),\mathit{\text{if}}{v}_2^{\min }\le v_2^{op}\left(t\right)\le v_2^{\max }\hfill \\ v_2^{\max },\mathit{\text{if}}{v}_2^{op}\left(t\right)>v_2^{\max }\hfill \end{array}\right.(4.25)$

Thus we have the optimal controls $v_1^{*}(t)$ and $v_2^{*}(t)$ in compact notation

$v_1^{*}\left(t\right)=\min \left\{\max \left\{\frac{1}{d_2}\left[\left({\phi }_3\left(t\right)-{\phi }_2\left(t\right)\right){\bar{I}}_1^B\left(t\right)+\left({\phi }_7\left(t\right)-{\phi }_6\left(t\right)\right){\bar{I}}_2^B\left(t\right)\right],v_1^{\min }\right\},v_1^{\max }\right\},(4.26)$

$v_2^{*}\left(t\right)=\min \left\{\max \left\{\frac{1}{d_3}\left[\left({\phi }_4\left(t\right)-{\phi }_2\left(t\right)\right){\bar{H}}_1\left(t\right)+\left({\phi }_8\left(t\right)-{\phi }_6\left(t\right)\right){\bar{H}}_2\left(t\right)\right],v_2^{\min }\right\},v_2^{\max }\right\}.(4.27)$

In summary, the proof of theorem 4.2 has been completed.

4.3 The uniqueness of optimal solution

Theorem 4.3. For a relatively short control time T, the states and the adjoint functions at the optimum and the optimal control strategies are unique.

Proof: Considering two different control states and their corresponding adjoint functions as

$\left(S_i,I_i^A,I_i^B,H_i,{\phi }_j\right),\left({\tilde{S}}_i,{\tilde{I}}_i^A,{\tilde{I}}_i^B,{\tilde{H}}_i,{\tilde{\phi }}_j\right),i=\mathrm{1,2},j=\mathrm{1,2},\dots ,8.$

Then we define S ₁ = e ^αt p ₁, $I_1^A=e^{\alpha t}{p}_2$ , $I_1^B=e^{\alpha t}{p}_3$ , H ₁ = e ^αt p ₄, S ₂ = e ^αt p ₅, $I_2^A=e^{\alpha t}{p}_6$ , $I_2^B=e^{\alpha t}{p}_7$ , H ₂ = e ^αt p ₈, and φ ₁ = e ^−αt h ₁, φ ₂ = e ^−αt h ₂, φ ₃ = e ^−αt h ₃, φ ₄ = e ^−αt h ₄, φ ₅ = e ^−αt h ₅, φ ₆ = e ^−αt h ₆, φ ₇ = e ^−αt h ₇, φ ₈ = e ^−αt h ₈. The same definitions holds for ${\tilde{S}}_1=e^{\alpha t}{\tilde{p}}_1$ , ${\tilde{I}}_1^A=e^{\alpha t}{\tilde{p}}_2$ , ${\tilde{I}}_1^B=e^{\alpha t}{\tilde{p}}_3$ , ${\tilde{H}}_1=e^{\alpha t}{\tilde{p}}_4$ , ${\tilde{S}}_2=e^{\alpha t}{\tilde{p}}_5$ , ${\tilde{I}}_2^A=e^{\alpha t}{\tilde{p}}_6$ , ${\tilde{I}}_2^B=e^{\alpha t}{\tilde{p}}_7$ , ${\tilde{H}}_2=e^{\alpha t}{\tilde{p}}_8$ , and ${\tilde{\phi }}_1=e^{-\alpha t}{\tilde{h}}_1$ , ${\tilde{\phi }}_2=e^{-\alpha t}{\tilde{h}}_2$ , ${\tilde{\phi }}_3=e^{-\alpha t}{\tilde{h}}_3$ , ${\tilde{\phi }}_4=e^{-\alpha t}{\tilde{h}}_4$ , ${\tilde{\phi }}_5=e^{-\alpha t}{\tilde{h}}_5$ , ${\phi }_6=e^{-\alpha t}{\tilde{h}}_6$ , ${\phi }_7=e^{-\alpha t}{\tilde{h}}_7$ , ${\phi }_8=e^{-\alpha t}{\tilde{h}}_8$ , where α > 0 is a constant to be chosen.

After substituting the above values into systems (2.2) and (2.3), we can obtain

$\alpha p_1+\frac{d{p}_1}{dt}=\xi e^{-\alpha t}-⟨k_1⟩{\lambda }_1{e}^{\alpha t}{p}_1{p}_2-⟨k_1⟩{\lambda }_2{e}^{\alpha t}{p}_1{p}_3-⟨k_{12}⟩\kappa {\lambda }_1{e}^{\alpha t}{p}_1{p}_6-⟨k_{12}⟩\kappa {\lambda }_2{e}^{\alpha t}{p}_1{p}_7-\delta p_1,(4.28)$

$\begin{array}{c}\begin{array}{cc}\hfill \alpha p_2+\frac{d{p}_2}{dt}& =⟨k_1⟩{\lambda }_1{e}^{\alpha t}{p}_1{p}_2+⟨k_{12}⟩\kappa {\lambda }_1{e}^{\alpha t}{p}_1{p}_6+\frac{1+{\omega }_1}{2}{e}^{\alpha t}{p}_2{p}_4+\frac{1-{\omega }_1}{2}{e}^{\alpha t}{p}_6{p}_4-⟨k_1⟩{\theta }_1{e}^{\alpha t}{p}_2{p}_3\hfill \\ \hfill & -⟨k_{12}⟩\kappa {\theta }_1{e}^{\alpha t}{p}_2{p}_7-\left(\delta +\mu \right)p_2+v_1^{*}{p}_3+v_2^{*}{p}_4,\hfill \end{array}\hfill \end{array}(4.29)$

$\begin{array}{c}\begin{array}{cc}\hfill \alpha p_3+\frac{d{p}_3}{dt}& =⟨k_1⟩{\lambda }_2{e}^{\alpha t}{p}_1{p}_3+⟨k_{12}⟩\kappa {\lambda }_2{e}^{\alpha t}{p}_1{p}_7+\frac{1+{\omega }_1}{2}{e}^{\alpha t}{p}_3{p}_4+\frac{1-{\omega }_1}{2}{e}^{\alpha t}{p}_7{p}_4-⟨k_1⟩{\theta }_2{e}^{\alpha t}{p}_3{p}_2\hfill \\ \hfill & -⟨k_{12}⟩\kappa {\theta }_2{e}^{\alpha t}{p}_3{p}_6-\left(\delta +\mu +v_1^{*}\right)p_3,\hfill \end{array}\hfill \end{array}(4.30)$

$\begin{array}{c}\begin{array}{c}\hfill \alpha p_4+\frac{d{p}_4}{dt}=⟨k_1⟩{\theta }_1{e}^{\alpha t}{p}_2{p}_3+⟨k_{12}⟩\kappa {\theta }_1{e}^{\alpha t}{p}_2{p}_7+⟨k_1⟩{\theta }_2{e}^{\alpha t}{p}_3{p}_2+⟨k_{12}⟩\kappa {\theta }_2{e}^{\alpha t}{p}_3{p}_6-\frac{1+{\omega }_1}{2}{e}^{\alpha t}{p}_2{p}_4\\ \hfill -\frac{1-{\omega }_1}{2}{e}^{\alpha t}{p}_6{p}_4-\frac{1+{\omega }_1}{2}{e}^{\alpha t}{p}_3{p}_4-\frac{1-{\omega }_1}{2}{e}^{\alpha t}{p}_7{p}_4-\left(\delta +\mu +v_2^{*}\right)p_4,\end{array}\hfill \end{array}(4.31)$

$\alpha p_5+\frac{d{p}_5}{dt}=\xi e^{-\alpha t}-⟨k_2⟩{\lambda }_1{e}^{\alpha t}{p}_5{p}_6-⟨k_2⟩{\lambda }_2{e}^{\alpha t}{p}_5{p}_7-⟨k_{21}⟩\kappa {\lambda }_1{e}^{\alpha t}{p}_5{p}_2-⟨k_{21}⟩\kappa {\lambda }_2{e}^{\alpha t}{p}_5{p}_3-\delta p_5,(4.32)$

$\begin{array}{c}\begin{array}{cc}\hfill \alpha p_6+\frac{d{p}_6}{dt}& =⟨k_2⟩{\lambda }_1{e}^{\alpha t}{p}_5{p}_6+⟨k_{21}⟩\kappa {\lambda }_1{e}^{\alpha t}{p}_5{p}_2+\frac{1+{\omega }_2}{2}{e}^{\alpha t}{p}_6{p}_8+\frac{1-{\omega }_2}{2}{e}^{\alpha t}{p}_2{p}_8-⟨k_2⟩{\theta }_1{e}^{\alpha t}{p}_6{p}_7\hfill \\ \hfill & -⟨k_{21}⟩\kappa {\theta }_1{e}^{\alpha t}{p}_6{p}_3-\left(\delta +\mu \right)p_6+v_1^{*}{p}_7+v_2^{*}{p}_8,\hfill \end{array}\hfill \end{array}(4.33)$

$\begin{array}{c}\begin{array}{cc}\hfill \alpha p_7+\frac{d{p}_7}{dt}& =⟨k_2⟩{\lambda }_2{e}^{\alpha t}{p}_5{p}_7+⟨k_{21}⟩\kappa {\lambda }_2{e}^{\alpha t}{p}_5{p}_3+\frac{1+{\omega }_2}{2}{e}^{\alpha t}{p}_7{p}_8+\frac{1-{\omega }_2}{2}{e}^{\alpha t}{p}_3{p}_8-⟨k_2⟩{\theta }_2{e}^{\alpha t}{p}_7{p}_6\hfill \\ \hfill & -⟨k_{21}⟩\kappa {\theta }_2{e}^{\alpha t}{p}_7{p}_2-\left(\delta +\mu +v_1^{*}\right)p_7,\hfill \end{array}\hfill \end{array}(4.34)$

$\begin{array}{c}\begin{array}{cc}\hfill \alpha p_8+\frac{d{p}_8}{dt}& =⟨k_2⟩{\theta }_1{e}^{\alpha t}{p}_6{p}_7+⟨k_{21}⟩\kappa {\theta }_1{e}^{\alpha t}{p}_6{p}_3+⟨k_2⟩{\theta }_2{e}^{\alpha t}{p}_7{p}_6+⟨k_{21}⟩\kappa {\theta }_2{e}^{\alpha t}{p}_7{p}_2-\frac{1+{\omega }_2}{2}{e}^{\alpha t}{p}_6{p}_8\hfill \\ \hfill & -\frac{1-{\omega }_2}{2}{e}^{\alpha t}{p}_2{p}_8-\frac{1+{\omega }_2}{2}{e}^{\alpha t}{p}_7{p}_8-\frac{1-{\omega }_2}{2}{e}^{\alpha t}{p}_3{p}_8-\left(\delta +\mu +v_2^{*}\right)p_8,\hfill \end{array}\hfill \end{array}(4.35)$

$\frac{d{h}_1}{dt}-\alpha h_1=e^{\alpha t}\left(h_1-h_2\right)\left(⟨k_1⟩{\lambda }_1{p}_2+⟨k_{12}⟩\kappa {\lambda }_1{p}_6\right)+e^{\alpha t}\left(h_1-h_3\right)\left(⟨k_1⟩{\lambda }_2{p}_3+⟨k_{12}⟩\kappa {\lambda }_2{p}_7\right)+\delta h_1,(4.36)$

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{h}_2}{dt}-\alpha h_2& =\left(h_1-h_2\right)⟨k_1⟩{\lambda }_1{e}^{\alpha t}{p}_1+e^{\alpha t}\left(h_4-h_2\right)\left(\frac{1+{\omega }_1}{2}{p}_4-⟨k_1⟩{\theta }_1{p}_3-⟨k_{12}⟩\kappa {\theta }_1{p}_7\right)+\left(\delta +\mu \right)h_2\hfill \\ \hfill & +\left(h_3-h_4\right)⟨k_1⟩{\theta }_2{e}^{\alpha t}{p}_3+\left(h_5-h_6\right)⟨k_{21}⟩\kappa {\lambda }_1{e}^{\alpha t}{p}_5+\left(h_8-h_6\right)\frac{1-{\omega }_2}{2}{e}^{\alpha t}{p}_8\hfill \\ \hfill & +\left(h_7-h_8\right)⟨k_{21}⟩\kappa {\theta }_2{e}^{\alpha t}{p}_7,\hfill \end{array}\hfill \end{array}(4.37)$

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{h}_3}{dt}-\alpha h_3& =\left(h_1-h_3\right)⟨k_1⟩{\lambda }_2{e}^{\alpha t}{p}_1+e^{\alpha t}\left(h_4-h_3\right)\left(\frac{1+{\omega }_1}{2}{p}_4-⟨k_1⟩{\theta }_2{p}_2-⟨k_{12}⟩\kappa {\theta }_2{p}_6\right)+\left(\delta +\mu -d_1\right)h_3\hfill \\ \hfill & +\left(h_2-h_4\right)⟨k_1⟩{\theta }_1{e}^{\alpha t}{p}_2+\left(h_5-h_7\right)⟨k_{21}⟩\kappa {\lambda }_2{e}^{\alpha t}{p}_5+\left(h_8-h_7\right)\frac{1-{\omega }_2}{2}{e}^{\alpha t}{p}_8\hfill \\ \hfill & +\left(h_6-h_8\right)⟨k_{21}⟩\kappa {\theta }_1{e}^{\alpha t}{p}_6+v_1^{*}{e}^{\alpha t},\hfill \end{array}\hfill \end{array}(4.38)$

$\frac{d{h}_4}{dt}-\alpha h_4=\left(\delta +\mu \right)h_4+e^{\alpha t}\left(h_4-h_2\right)\left(\frac{1+{\omega }_1}{2}{p}_2+\frac{1-{\omega }_1}{2}{p}_6\right)+e^{\alpha t}\left(h_4-h_3\right)\left(\frac{1+{\omega }_1}{2}{p}_3+\frac{1-{\omega }_1}{2}{p}_7\right)+v_2^{*}{e}^{\alpha t},(4.39)$

$\frac{d{h}_5}{dt}-\alpha h_5=e^{\alpha t}\left(h_5-h_6\right)\left(⟨k_2⟩{\lambda }_1{p}_6+⟨k_{21}⟩\kappa {\lambda }_1{p}_2\right)+e^{\alpha t}\left(h_5-h_7\right)\left(⟨k_2⟩{\lambda }_2{p}_7+⟨k_{21}⟩\kappa {\lambda }_2{p}_3\right)+\delta h_5,(4.40)$

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{h}_6}{dt}-\alpha h_6& =\left(h_5-h_6\right)⟨k_2⟩{\lambda }_1{e}^{\alpha t}{p}_5+e^{\alpha t}\left(h_8-h_6\right)\left(\frac{1+{\omega }_2}{2}{p}_8-⟨k_2⟩{\theta }_1{p}_7-⟨k_{21}⟩\kappa {\theta }_1{p}_3\right)+\left(\delta +\mu \right)h_6\hfill \\ \hfill & +\left(h_7-h_8\right)⟨k_2⟩{\theta }_2{e}^{\alpha t}{p}_7+\left(h_1-h_2\right)⟨k_{12}⟩\kappa {\lambda }_1{e}^{\alpha t}{p}_1+\left(h_4-h_2\right)\frac{1-{\omega }_1}{2}{e}^{\alpha t}{p}_4+\left(h_3-h_4\right)⟨k_{12}⟩\kappa {\theta }_2{e}^{\alpha t}{p}_3,\hfill \end{array}\hfill \end{array}(4.41)$

$\begin{array}{c}\begin{array}{cc}\hfill \frac{d{h}_7}{dt}-\alpha h_7& =\left(h_5-h_7\right)⟨k_2⟩{\lambda }_2{e}^{\alpha t}{p}_5+e^{\alpha t}\left(h_8-h_7\right)\left(\frac{1+{\omega }_2}{2}{p}_8-⟨k_2⟩{\theta }_2{p}_6-⟨k_{21}⟩\kappa {\theta }_2{p}_2\right)+\left(\delta +\mu -d_1\right)h_7\hfill \\ \hfill & +\left(h_6-h_8\right)⟨k_2⟩{\theta }_2{e}^{\alpha t}{p}_7+\left(h_1-h_2\right)⟨k_{12}⟩\kappa {\lambda }_2{e}^{\alpha t}{p}_1+\left(h_4-h_3\right)\frac{1-{\omega }_1}{2}{e}^{\alpha t}{p}_4+\left(h_2-h_4\right)⟨k_{12}⟩\kappa {\theta }_1{e}^{\alpha t}{p}_2+v_1^{*}{e}^{\alpha t},\hfill \end{array}\hfill \end{array}(4.42)$

$\frac{d{h}_8}{dt}-\alpha h_8=\left(\delta +\mu \right)h_8+e^{\alpha t}\left(h_8-h_6\right)\left(\frac{1+{\omega }_2}{2}{p}_6+\frac{1-{\omega }_2}{2}{p}_2\right)+e^{\alpha t}\left(h_8-h_7\right)\left(\frac{1+{\omega }_2}{2}{p}_7+\frac{1-{\omega }_2}{2}{p}_3\right)+v_2^{*}{e}^{\alpha t}.(4.43)$

Similarly, we can obtain other equations for ${\tilde{S}}_1$ , ${\tilde{I}}_1^A$ , ${\tilde{I}}_1^B$ , ${\tilde{H}}_1$ , ${\tilde{S}}_2$ , ${\tilde{I}}_2^A$ , ${\tilde{I}}_2^B$ , ${\tilde{H}}_2$ , ${\tilde{\phi }}_1$ , ${\tilde{\phi }}_2$ , ${\tilde{\phi }}_3$ , ${\tilde{\phi }}_4$ , ${\tilde{\phi }}_5$ , ${\tilde{\phi }}_6$ , ${\tilde{\phi }}_7$ , ${\tilde{\phi }}_8$ . Afterward, we subtract the equations for S ₁ and ${\tilde{S}}_1$ , $I_1^A$ and ${\tilde{I}}_1^A$ , $I_1^B$ and ${\tilde{I}}_1^B$ , H ₁ and ${\tilde{H}}_1$ , S ₂ and ${\tilde{S}}_2$ , $I_2^A$ and ${\tilde{I}}_2^A$ , $I_2^B$ and ${\tilde{I}}_2^B$ , H ₂ and ${\tilde{H}}_2$ , φ ₁ and ${\tilde{\phi }}_1$ , φ ₂ and ${\tilde{\phi }}_2$ , φ ₃ and ${\tilde{\phi }}_3$ , φ ₄ and ${\tilde{\phi }}_4$ , φ ₅ and ${\tilde{\phi }}_5$ , φ ₆ and ${\tilde{\phi }}_6$ , φ ₇ and ${\tilde{\phi }}_7$ , φ ₈ and ${\tilde{\phi }}_8$ respectively, then multiply each equation with appropriate difference subsequently, and integrate the obtained each equation from 0 to T. We take $I_1^A$ and ${\tilde{I}}_1^A$ , φ ₃ and ${\tilde{\phi }}_3$ as examples, thus

$\begin{array}{c}\frac{1}{2}{\left(p_2\left(T\right)-{\tilde{p}}_2\left(T\right)\right)}^2+\alpha {\int }_0^T{\left(p_2-{\tilde{p}}_2\right)}^{2}dt\hfill \\ =⟨k_1⟩{\lambda }_1{\int }_0^T{e}^{\alpha t}\left(p_1{p}_2-{\tilde{p}}_1{\tilde{p}}_2\right)\left(p_2-{\tilde{p}}_2\right)dt+⟨k_{12}⟩\kappa {\lambda }_1{\int }_0^T{e}^{\alpha t}\left(p_1{p}_6-{\tilde{p}}_1{\tilde{p}}_6\right)\left(p_2-{\tilde{p}}_2\right)dt\hfill \\ +\frac{1+{\omega }_1}{2}{\int }_0^T{e}^{\alpha t}\left(p_2{p}_4-{\tilde{p}}_2{\tilde{p}}_4\right)\left(p_2-{\tilde{p}}_2\right)dt+\frac{1-{\omega }_1}{2}{\int }_0^T{e}^{\alpha t}\left(p_6{p}_4-{\tilde{p}}_6{\tilde{p}}_4\right)\left(p_2-{\tilde{p}}_2\right)dt\hfill \\ -⟨k_1⟩{\theta }_1{\int }_0^T{e}^{\alpha t}\left(p_2{p}_3-{\tilde{p}}_2{\tilde{p}}_3\right)\left(p_2-{\tilde{p}}_2\right)dt-⟨k_{12}⟩\kappa {\theta }_1{\int }_0^T{e}^{\alpha t}\left(p_2{p}_7-{\tilde{p}}_2{\tilde{p}}_7\right)\left(p_2-{\tilde{p}}_2\right)dt\hfill \\ -\left(\delta +\mu \right){\int }_0^T{\left(p_2-{\tilde{p}}_2\right)}^{2}dt+{\int }_0^T\left(v_1^{*}{p}_3-{\tilde{v}}_1^{*}{\tilde{p}}_3\right)\left(p_2-{\tilde{p}}_2\right)dt+{\int }_0^T\left(v_2^{*}{p}_4-{\tilde{v}}_2^{*}{\tilde{p}}_4\right)\left(p_2-{\tilde{p}}_2\right)dt\hfill \\ \le {\tilde{C}}_1{e}^{\alpha T}{\int }_0^T\left[{\left(p_1-{\tilde{p}}_1\right)}^2+{\left(p_2-{\tilde{p}}_2\right)}^2+{\left(p_3-{\tilde{p}}_3\right)}^2+{\left(p_4-{\tilde{p}}_4\right)}^2+{\left(p_6-{\tilde{p}}_6\right)}^2+{\left(p_7-{\tilde{p}}_7\right)}^2\right]dt\hfill \\ +{\tilde{C}}_2{\int }_0^T\left[{\left(p_4-{\tilde{p}}_4\right)}^2+{\left(p_8-{\tilde{p}}_8\right)}^2+{\left(p_7-{\tilde{p}}_7\right)}^2+{\left(p_3-{\tilde{p}}_3\right)}^2+{\left(p_2-{\tilde{p}}_2\right)}^2+{\left(h_3-{\tilde{h}}_3\right)}^2+{\left(h_2-{\tilde{h}}_2\right)}^2\right.\hfill \\ \left.+{\left(h_6-{\tilde{h}}_6\right)}^2+{\left(h_4-{\tilde{h}}_4\right)}^2+{\left(h_7-{\tilde{h}}_7\right)}^2+{\left(h_8-{\tilde{h}}_8\right)}^2\right]dt\hfill \end{array}(4.44)$

Furthermore,

$\begin{array}{c}\frac{1}{2}{\left(h_3\left(0\right)-{\tilde{h}}_3\left(0\right)\right)}^2+\alpha {\int }_0^T{\left(h_3-{\tilde{h}}_3\right)}^{2}dt\hfill \\ =⟨k_1⟩{\lambda }_2{\int }_0^T{e}^{\alpha t}\left[\left(h_1-h_3\right)p_1-\left({\tilde{h}}_1-{\tilde{h}}_3\right){\tilde{p}}_1\right]\left(h_3-{\tilde{h}}_3\right)dt+\frac{1+{\omega }_1}{2}{\int }_0^T{e}^{\alpha t}\left[\left(h_4-h_3\right)p_4-\left({\tilde{h}}_4-{\tilde{h}}_3\right){\tilde{p}}_4\right]\left(h_3-{\tilde{h}}_3\right)dt\hfill \\ -⟨k_1⟩{\theta }_2{\int }_0^T{e}^{\alpha t}\left[\left(h_4-h_3\right)p_2-\left({\tilde{h}}_4-{\tilde{h}}_3\right){\tilde{p}}_2\right]\left(h_3-{\tilde{h}}_3\right)dt-⟨k_{12}⟩\kappa {\theta }_2{\int }_0^T{e}^{\alpha t}\left[\left(h_4-h_3\right)p_6-\left({\tilde{h}}_4-{\tilde{h}}_3\right){\tilde{p}}_6\right]\left(h_3-{\tilde{h}}_3\right)dt\hfill \\ +\left(\delta +\mu -d_1\right){\int }_0^T{\left(h_3-{\tilde{h}}_3\right)}^{2}dt+⟨k_1⟩{\theta }_1{\int }_0^T{e}^{\alpha t}\left[\left(h_2-h_4\right)p_2-\left({\tilde{h}}_2-{\tilde{h}}_4\right){\tilde{p}}_2\right]\left(h_3-{\tilde{h}}_3\right)dt\hfill \\ +⟨k_{21}⟩\kappa {\lambda }_2{\int }_0^T{e}^{\alpha t}\left[\left(h_5-h_7\right)p_5-\left({\tilde{h}}_5-{\tilde{h}}_7\right){\tilde{p}}_5\right]\left(h_3-{\tilde{h}}_3\right)dt+\frac{1-{\omega }_2}{2}{\int }_0^T{e}^{\alpha t}\left[\left(h_8-h_7\right)p_8-\left({\tilde{h}}_8-{\tilde{h}}_7\right){\tilde{p}}_8\right]\left(h_3-{\tilde{h}}_3\right)dt\hfill \\ +⟨k_{21}⟩\kappa {\theta }_1{\int }_0^T{e}^{\alpha t}\left[\left(h_6-h_8\right)p_6-\left({\tilde{h}}_6-{\tilde{h}}_8\right){\tilde{p}}_6\right]\left(h_3-{\tilde{h}}_3\right)dt+{\int }_0^T{e}^{\alpha t}\left(v_1^{*}-{\tilde{v}}_1^{*}\right)\left(h_3-{\tilde{h}}_3\right)dt\le {\tilde{C}}_2{\int }_0^T{\left(h_3-{\tilde{h}}_3\right)}^{2}dt\hfill \\ +{\tilde{C}}_1{e}^{\alpha T}{\int }_0^T\left[{\left(h_1-{\tilde{h}}_1\right)}^2+{\left(h_2-{\tilde{h}}_2\right)}^2+{\left(h_3-{\tilde{h}}_3\right)}^2+{\left(h_4-{\tilde{h}}_4\right)}^2+{\left(h_5-{\tilde{h}}_5\right)}^2+{\left(h_6-{\tilde{h}}_6\right)}^2+{\left(h_7-{\tilde{h}}_7\right)}^2+{\left(h_8-{\tilde{h}}_8\right)}^2\right]dt\hfill \\ +{\tilde{C}}_1{e}^{\alpha T}{\int }_0^T\left[{\left(p_1-{\tilde{p}}_1\right)}^2+{\left(p_2-{\tilde{p}}_2\right)}^2+{\left(p_3-{\tilde{p}}_3\right)}^2+{\left(p_4-{\tilde{p}}_4\right)}^2+{\left(p_5-{\tilde{p}}_5\right)}^2+{\left(p_6-{\tilde{p}}_6\right)}^2+{\left(p_7-{\tilde{p}}_7\right)}^2+{\left(p_8-{\tilde{p}}_8\right)}^2\right]dt\hfill \end{array}(4.45)$

Combining all of these equations, we can obtain

$\begin{array}{c}\frac{1}{2}\sum _{i=1}^8\left\{{\left(p_i-{\tilde{p}}_i\right)}^2\left(T\right)+\frac{1}{2}{\left(h_i-{\tilde{h}}_i\right)}^2\left(0\right)\right\}+\alpha \sum _{i=1}^8\left\{{\int }_0^T{\left(p_i-{\tilde{p}}_i\right)}^{2}dt+{\int }_0^T{\left(h_i-{\tilde{h}}_i\right)}^{2}dt\right\}\hfill \\ \le \left({\tilde{C}}_1+{\tilde{C}}_2{e}^{\alpha T}\right){\int }_0^T\sum _{i=1}^8\left\{{\left(p_i-{\tilde{p}}_i\right)}^2+{\left(h_i-{\tilde{h}}_i\right)}^2\right\}dt\hfill \end{array}(4.46)$

where ${\tilde{C}}_1$ and ${\tilde{C}}_2$ are constants depending on the coefficients and bounds of p ₁, p ₂, p ₃, p ₄, p ₅, p ₆, p ₇, p ₈, h ₁, h ₂, h ₃, h ₄, h ₅, h ₆, h ₇, h ₈. Therefore, we have

$\left[\alpha -\left({\tilde{C}}_1+{\tilde{C}}_2{e}^{\alpha T}\right)\right]{\int }_0^T\sum _{i=1}^8\left\{{\left(p_i-{\tilde{p}}_i\right)}^2+{\left(h_i-{\tilde{h}}_i\right)}^2\right\}dt\le 0(4.47)$

If α is chosen such that $\alpha >{\tilde{C}}_1+{\tilde{C}}_2$ and $T<\frac{1}{\alpha }\ln \left(\frac{\alpha -{\tilde{C}}_1}{{\tilde{C}}_2}\right)$ , then $p_i={\tilde{p}}_i$ , $h_i={\tilde{h}}_i$ , i = 1, 2, … , 8. As a result, based on the above proof, we can learn that the optimal control solution is unique.

5 Numerical experiments

In this section, we perform extensive numerical simulations to 1) corroborate the theoretical results of stability analysis towards information-free and information-endemic equilibria; 2) explore the influence of spreading parameters on dynamic trend and steady-state prevalence; 3) discuss the competition between two types of information; and 4) investigate the effectiveness of our optimal control strategies.

In order to verify the correctness of our theoretical modeling in characterize the competitive information propagation process on multi-layer interconnected networks, we first conduct the time evolution of each status according to Eqs 2.2, 2.3 and Monte Carlo (MC) simulations under different cases of spreading parameters. As shown in Figure 2, the MC simulation results are observed to match well with the theoretical results, which indicates that our formulations can accurately reflect the competitive spreading mechanism. Furthermore, we can calculate the basic reproduction number ${\mathcal{R}}_0$ under three cases, namely, (1) Case 1: ${\mathcal{R}}_0=2.6794>1$ , our system will converge to an information-endemic equilibrium point E* = (0.4398, 0, 0.3784, 0) when t → ∞; (2) Case 2: ${\mathcal{R}}_0=2.8133>1$ , our system will converge to an information-endemic equilibrium point E* = (0, 0.3383, 0, 0.2936) when t → ∞. (3) Case 3: ${\mathcal{R}}_0=0.8038<1$ , our system will converge to an information-free equilibrium point E ₀ = (0, 0, 0, 0) when t → ∞; These conclusions are consistent with our Theorems 3.1–3.3.

FIGURE 2

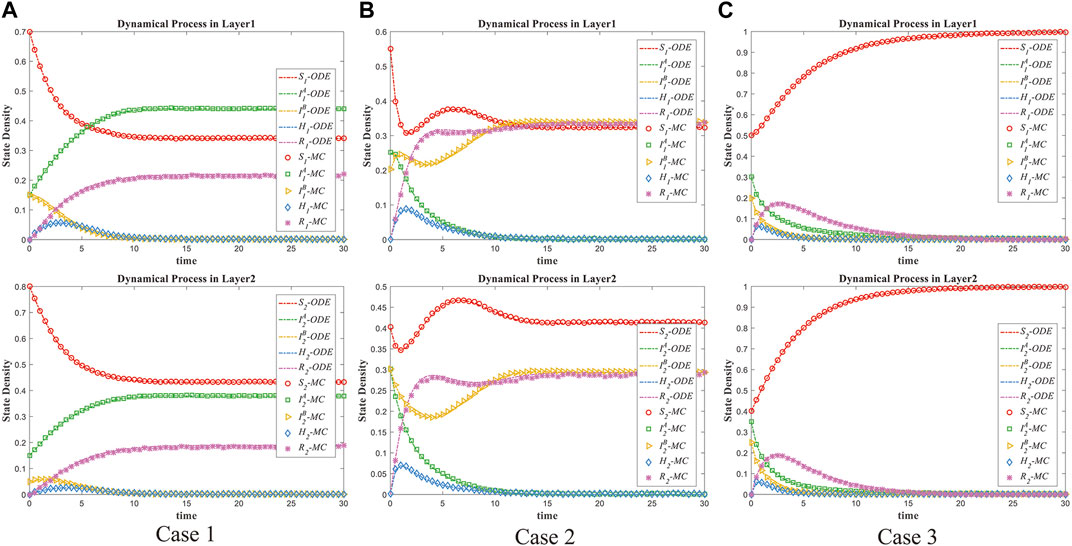
FIGURE 2. Time evolution of each state density via several combinations cases. The symbols correspond to Monte Carlo (MC) simulations and the dotted lines represent the theoretical modeling of dynamic equation (ODE). The shared parameter settings are $⟨k_1⟩$ = 4, $⟨k_2⟩$ = 3, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, θ ₁ = 0.2, θ ₂ = 0.15, ξ = δ = 0.3, κ = 0.5. (A) Case 1: S ₁ (0) = 0.7, $I_1^A(0)$ = 0.15, $I_1^B(0)$ = 0.15, S ₂ (0) = 0.8, $I_2^A(0)$ = 0.15, $I_2^B(0)$ = 0.05, λ ₁ = 0.25, λ ₂ = 0.15, μ = 0.15; (B) Case 2: S ₁ (0) = 0.55, $I_1^A(0)$ = 0.25, $I_1^B(0)$ = 0.2, S ₂ (0) = 0.4, $I_2^A(0)$ = 0.3, $I_2^B(0)$ = 0.3, λ ₁ = 0.25, λ ₂ = 0.35, μ = 0.30; (C) S ₁ (0) = 0.5, $I_1^A(0)$ = 0.3, $I_1^B(0)$ = 0.2, S ₂ (0) = 0.4, $I_2^A(0)$ = 0.35, $I_2^B(0)$ = 0.25, λ ₁ = 0.1, λ ₂ = 0.05, μ = 0.3.

It is well-acknowledged that spreading parameters are the key factors affecting the steady-state prevalence of information propagation, so it is necessary to explore the correlation between some important spreading parameters and the information prevalence. Note that the dynamic process of information in layer 1 is influenced by three aspects: 1) the interaction between individuals in layer 1 via intra-layer edges presented as $⟨k_1⟩$ ; 2) the interaction between individuals across layers 1 and 2 via inter-layer edges presented as $⟨k_{12}⟩$ ; 3) the weight ω ₁ between local and global information prevalence. Similarly, the dynamic process of information in layer 2 is also influenced by three aspects: 1) the interaction between individuals in layer 2 via intra-layer edges presented as $⟨k_2⟩$ ; 2) the interaction between individuals across layers 2 and 1 via inter-layer edges presented as $⟨k_{21}⟩$ ; 3) the weight ω ₂ between local and global information prevalence. We observe that the information propagation in layer 1 and 2 have similar mechanisms of state transition, leading to their similar evolution trend, and their differences are merely reflected in numerical results. Therefore, we only analyze the conclusions in layer 1, which are well generalized to layer 2. Here we provide the phase diagrams of five different experiments. For each diagram, the colormap adopts a JET mode, which starts with blue representing the minimum value, gradually transitions to cyan, green, yellow, orange, and ends with red representing the maximum value.

• Figure 3A describes the changing trend of steady-state density of $I_1^A$ and $I_1^B$ spreaders under heterogeneous combinations of λ ₁ and λ ₂. The color scale of $I_1^A(\infty )$ (left) ranges from $\left[\mathrm{0,0.3164}\right]$ , and the color scale of $I_1^B(\infty )$ (right) ranges from $\left[\mathrm{0,0.3183}\right]$ . We can observe that when both λ ₁ and λ ₂ are relatively small, the system converges to an information-free equilibrium, where two types of information will eventually die out. When λ ₁ and λ ₂ become larger, the infection density presents a coexistence of continuous and discontinuous phase transitions. Specifically, taking $I_1^A$ density as an example, when λ ₂ is very small, the steady-state density of $I_1^A$ gradually increases in a slow trend with the increase of λ ₁. This is because the small λ ₂ corresponds to the low-density $I_1^B$ spreaders, and the larger λ ₁ increases the probability that these small number of $I_1^B$ spreaders are infected with positive information. Although the infectivity of positive information is increased, the quantity of $I_1^B$ spreaders with potential infected possibility is low, thus the steady-state $I_1^A$ density will not increase dramatically. Besides, when λ ₂ is large, the steady-state density of $I_1^A$ spreaders will grow sharply with the increase of λ ₁. This is because the larger λ ₂ keeps the infected density of $I_1^B$ spreaders at a high level. The increase of λ ₁ will not only make these large number of $I_1^B$ spreaders change their opinions into $I_1^A$ state with a great probability, but also guide more S and H individuals to become $I_1^A$ spreaders. Both the large infectivity and potential population base contribute to a sharp increase in the steady-state density of $I_1^A$ spreader, which presents a transient process of discontinuous phase. The similar analysis also applies to the changing trend of $I_1^B$ spreader density influenced by $I_1^A$ and $I_1^B$ .

• Figure 3B illustrates how $I_1^A$ and $I_1^B$ are affected by the transmission rate θ ₁ and θ ₂. The color scale of $I_1^A(\infty )$ (left) ranges from $\left[\mathrm{0,0.2480}\right]$ , and the color scale of $I_1^B(\infty )$ (right) ranges from $\left[\mathrm{0,0.2930}\right]$ . It can be seen that the changing trends of $I_1^A$ and $I_1^B$ are completely complementary, which further verifies the competition between two kinds of information. With the increase of θ ₁, the probability of $I_1^A$ spreaders receiving negative information and turning into $I_1^B$ status may become larger significantly, thereby improving (decreasing) the density of $I_1^B$ $(I_1^A)$ spreaders. Similarly, the increase in θ ₂ will cause more $I_1^B$ individuals to change their opinions and become the $I_1^A$ spreaders.

• Figure 3C depicts the changing trend of $I_1^A$ and $I_1^B$ influenced by λ ₁ and μ. The color scale of $I_1^A(\infty )$ (left) ranges from $\left[\mathrm{0,0.5758}\right]$ , and the color scale of $I_1^B(\infty )$ (right) ranges from $\left[\mathrm{0,0.5176}\right]$ . When both λ ₁ and μ are small, the negative information propagation is dominant, and the system will converge to the information-endemic equilibrium with non-zero $I_1^B$ . However, when λ ₁ exceeds a certain threshold, the infectivity of positive information is stronger than that of negative information, thereby the system may converge to other equilibrium with non-zero $I_1^A$ . The transformation of equilibrium is a process of discontinuous phase transition. Further increases in λ ₁ will extend the prevalence of $I_1^A$ . No matter $I_1^A$ or $I_1^B$ is dominant, the increase in μ can significantly reduce the steady-state density of positive and negative information. And when μ is large enough, both kinds of information will eventually die out and the system will stabilize at the information-free equilibrium.

• Figure 3D provides the changing trend of steady-state $I_1^A$ under the influence of ξ and δ. The color scale of $I_1^A(\infty )$ ranges from $\left[\mathrm{0,0.9865}\right]$ . As ξ becomes larger, the number of S individuals may grow to participate in information propagation process, thus the individuals infected as $I_1^A$ spreaders will also increase correspondingly. On the contrary, the increase in δ not only directly removes more $I_1^A$ spreaders from information propagation, but also reduces the probability of individuals in other states being infected by positive information.

• Figure 3E shows the changing trend of steady-state $I_1^A$ under the influence of $⟨k_1⟩$ and $⟨k_2⟩$ . The color scale of $I_1^A(\infty )$ ranges from $\left[\mathrm{0,0.3156}\right]$ . We can see that the increase of both $⟨k_1⟩$ and $⟨k_2⟩$ can expand the steady-state density of $I_1^A$ spreaders. This is because larger $⟨k_1⟩$ will enhance the correlation between individuals in layer 1, making the probability of S and $I_1^B$ individuals receiving positive information larger, thus increasing the density of $I_1^A$ spreaders. Besides, a larger $⟨k_2⟩$ will also strengthen the interaction intensity of individuals in layer 2 and make more individuals become $I_2^A$ spreaders, thus increasing the density of individuals being infected as $I_1^A$ in layer 1 through the inter-layer edges.

FIGURE 3

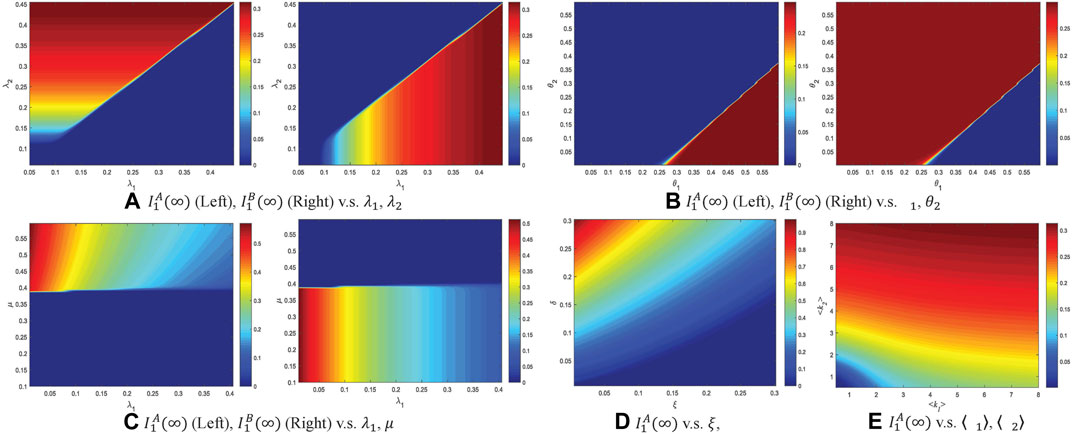
FIGURE 3. Phase diagram of correlation between spreading parameters and system steady-state characteristics. (A) $I_1^A(\infty )$ , $I_1^B(\infty )$ v.s. λ ₁, λ ₂; (B) $I_1^A(\infty )$ , $I_1^B(\infty )$ v.s. θ ₁, θ ₂; (C) $I_1^A(\infty )$ , $I_1^B(\infty )$ v.s. λ ₁, μ; (D) $I_1^A(\infty )$ v.s. ξ, δ; (E) $I_1^A(\infty )$ v.s. $⟨k_1⟩$ , $⟨k_2⟩$ .Parameter settings are listed as: (A) θ ₁ = 0.2, θ ₂ = 0.15, $⟨k_1⟩$ = 4, $⟨k_2⟩$ = 3, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, ω ₁ = 0.6, ω ₂ = 0.55, ξ = 0.2, δ = 0.2, κ = 0.5, μ = 0.3; (B) λ ₁ = 0.25, λ ₂ = 0.35, $⟨k_1⟩$ = 4, $⟨k_2⟩$ = 3, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, ω ₁ = 0.6, ω ₂ = 0.55, ξ = 0.2, δ = 0.2, κ = 0.5, μ = 0.3; (C) λ ₂ = 0.25, θ ₁ = 0.2, θ ₂ = 0.15, $⟨k_1⟩$ = 4, $⟨k_2⟩$ = 3, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, ω ₁ = 0.6, ω ₂ = 0.55, ξ = 0.2, δ = 0.2, κ = 0.5; (D) λ ₁ = 0.25, λ ₂ = 0.23, θ ₁ = 0.2, θ ₂ = 0.15, $⟨k_1⟩$ = 4, $⟨k_2⟩$ = 3, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, ω ₁ = 0.6, ω ₂ = 0.55, κ = 0.5, μ = 0.3; (E) λ ₁ = 0.25, λ ₂ = 0.23, θ ₁ = 0.2, θ ₂ = 0.15, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, ω ₁ = 0.6, ω ₂ = 0.55, ξ = 0.2, δ = 0.2, κ = 0.5, μ = 0.3.

In order to further verify the correctness of our Theorems 3.1–3.3 on the stability analysis of information-free and information-endemic equilibria, we construct the evolution trajectory of infection states $I_1^A,I_1^B,I_2^A,I_2^B$ under four settings of heterogeneous spreading parameters, which is shown in Figure 4. Each setting all covers 7 cases with different initial value conditions. Next, we separately discuss the results under four heterogeneous settings: (1) Setting 1: ${\mathcal{R}}_0=4.2182>1$ . No matter what the initial value condition is, the time-varying trajectory of infection states in all cases will converge to an information-endemic equilibrium E* = (0.3927, 0, 0.3377, 0), where positive information is dominant, and there is little difference between the trajectory evolution in layer 1 and layer 2. (2) Setting 2: ${\mathcal{R}}_0=2.8122>1$ , similarly, no matter what the initial value condition is, the infection states in all cases will converge to an information-endemic equilibrium E* = (0, 0.3363, 0, 0.2614), where negative information is dominant; (3) Setting 3: ${\mathcal{R}}_0=2.1091>1$ , the infection states in all cases will converge to an information-endemic equilibrium E* = (0.2784, 0, 0.1905, 0) where positive information is dominant; (4) Setting 4: ${\mathcal{R}}_0=0.9097<1$ , the infection states in all cases gradually die out and finally converge to an information-free equilibrium E ₀ = (0, 0, 0, 0). To sum up, the basic reproduction number ${\mathcal{R}}_0$ determines the stable state of the system. To be more precise, the propagation parameters associated with ${\mathcal{R}}_0$ significantly affect the evolution trend and steady-state conditions of the system, which are not related to the initial value conditions.

FIGURE 4

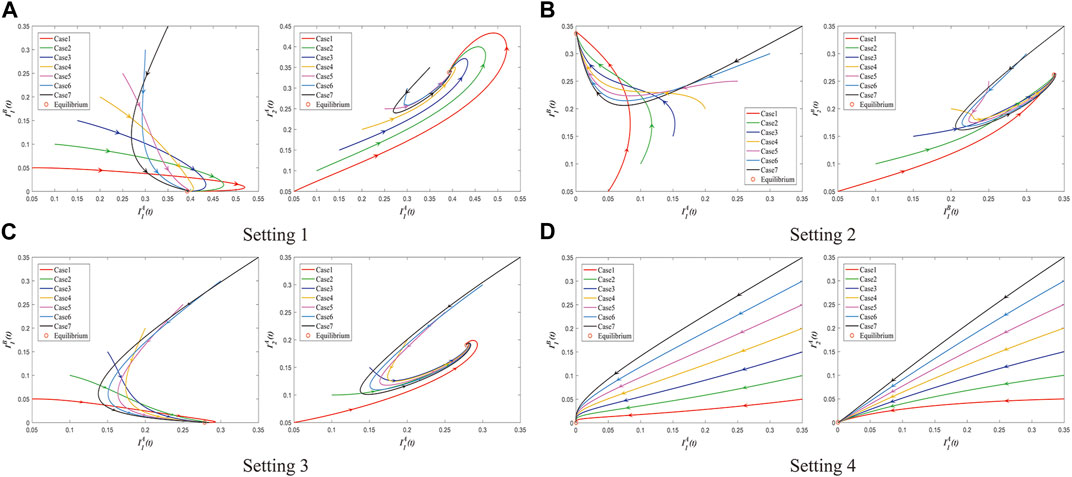
FIGURE 4. The evolution trajectory of infection states $I_1^A,I_1^B,I_2^A,I_2^B$ under four settings of heterogeneous spreading parameters. Homogeneous parameter settings are listed as: $⟨k_2⟩$ = 5, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, θ ₁ = 0.2, θ ₂ = 0.15, ξ = 0.3, δ = 0.3, κ = 0.5, μ = 0.3. And heterogeneous parameter settings are: (A) $⟨k_1⟩$ = 8, λ ₁ = 0.30, λ ₂ = 0.08; (B) $⟨k_1⟩$ = 8, λ ₁ = 0.15, λ ₂ = 0.20; (C) $⟨k_1⟩$ = 5, λ ₁ = 0.15, λ ₂ = 0.08; (D) $⟨k_1⟩$ = 6, λ ₁ = 0.05, λ ₂ = 0.08.

Furthermore, we explore the effects of weights ω ₁ and ω ₂ on the dynamical trend of positive and negative information. It is remarkable that larger ω ₁ and ω ₂ indicate that hesitant individuals consider the local information prevalence when deciding which information to believe, while smaller ω ₁ and ω ₂ imply that hesitant individuals consider the global information prevalence more. Figure 5 shows the evolution of $I_1^A$ (t), $I_1^B$ (t), $I_2^A$ (t) and $I_2^B$ (t) under different combinations of ω ₁ and ω ₂. From our parameter settings, it can be observed that: 1) the connection between nodes in layer 1 is tighter; 2) the spreading of negative information is more dominant that positive information. According to the comparison of Figures 5A,B, the spreading rate and prevalence of information in layer 1 are significantly higher than those in layer 2. This can be well-understood as: more edge relationships between nodes provide greater probability for information propagation. More interestingly, positive and negative information in layer 1 and 2 has the same evolution trend under different ω ₁ and ω ₂. Taking the spreading process of negative information as an example, the case where H ₁ individuals consider more local prevalence and H ₂ individuals consider more global prevalence corresponds to the fastest spreading rate and the highest prevalence of negative information. On the contrary, the case where H ₁ individuals consider more global prevalence and H ₂ individuals consider more local prevalence leads to the slowest spreading rate and the lowest prevalence of negative information. This can be interpreted as: the negative information in layer 1 has a larger propagation tendency due to a tighter network topology, while the negative information in layer 2 has a limited spreading prevalence due to sparse network connections. H ₁ individuals still have a strong tendency to become $I_1^B$ status if they consider more local prevalence, but their tendency to become $I_1^B$ status is weakened by the lower $I_2^B$ density if they consider more global prevalence. Similarly, if H ₂ individuals consider more local prevalence, their tendency to transform into $I_2^B$ status will be reduced because the lower $I_2^B$ density in their resident layer. But if H ₂ individuals consider more global prevalence, they are more willing to become $I_2^B$ status under the influence of a larger $I_1^B$ . In addition, when ω ₁ and ω ₂ are assigned the same settings, the larger ω ₁ and ω ₂ are, the more $I_1^B$ and $I_2^B$ will be. This is because a larger ω ₁ greatly promotes the transition from H ₁ to $I_1^B$ . Although H ₂ individuals takes more consideration of the prevalence in their resident layer, a larger $I_1^B$ can still significantly improve the transition probability from H ₂ to $I_2^B$ . On the contrary, a smaller ω ₁ means that the propagation of $I_1^B$ is limited by the smaller $I_2^B$ , and the probability of H ₁ becoming $I_1^B$ is significantly reduced, thus weakening the influence on H ₂. The conclusion of positive information can refer to the above analysis of negative information.

FIGURE 5

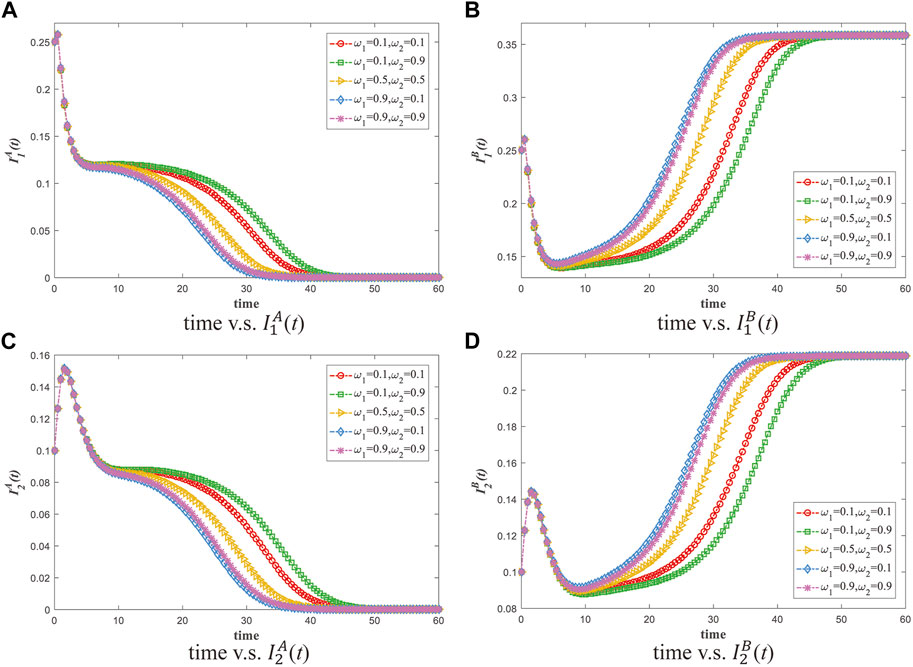
FIGURE 5. The infection states $I_1^A(t),I_1^B(t),I_2^A(t),I_2^B(t)$ under five different combinations of ω ₁ and ω ₂. (A) time v.s. $I_1^A(t)$ ; (B) time v.s. $I_1^B(t)$ ; (C) time v.s. $I_2^A(t)$ ; (D) time v.s. $I_2^B(t)$ . Parameter settings are listed as: S ₁ (0) = 0.5, $I_1^A(0)$ = $I_1^B(0)$ = 0.25, S ₂ (0) = 0.9, $I_2^A(0)$ = $I_2^B(0)$ = 0.1, λ ₁ = 0.08, λ ₂ = 0.05, θ ₁ = 0.2, θ ₂ = 0.15, $⟨k_2⟩$ = 8, $⟨k_2⟩$ = 3, $⟨k_{12}⟩$ = 4, $⟨k_{21}⟩$ = 2, ξ = δ = μ = 0.3, κ = 0.5.

To assess the performance of the proposed control mechanism, we introduce the following five control strategies, including our optimal control and other four baselines.

• No control: The system evolves naturally without implementing any control, namely, v ₁(t) = 0, v ₂(t) = 0;

• Constant control 1: The controls are time invariant, namely, v ₁(t) = 0.15, v ₂(t) = 0.15;

• Constant control 2: The controls are time invariant, namely, v ₁(t) = 0.25, v ₂(t) = 0.25;

• Heuristic control: The controls are referred as feedback mechanism based on $I_1^B$ , $I_2^B$ , H ₁ and H ₂ time-varying state density, namely,

     $v_1(t)=\alpha \left(I_1^B(t)+I_2^B(t)\right)/2$ ,

     $v_2(t)=\alpha \left(H_1(t)+H_2(t)\right)/2$ , α = 0.8;

• Optimal control: The controls follow Eqs 4.11—4.21.

Figure 6 illustrates the comparative results of cumulative costs under five strategies. As can be observed from Figure 6A, both the optimal and heuristic controls achieve the lower total cost in the control interval, while the total costs with no control and two constant controls are relatively high. Under no control strategy, even without the introduction of control cost, the corresponding infection cost will be very high because the current information prevalence is the largest. For the two constant controls, they merely focus on the control performance without any cost constraints. Therefore, although constant controls have significant suppression effect on the diffusion of negative information, their larger control intensity leads to the higher control costs. The results in Figures 6B, C also confirm these explanations. As the heuristic control strategy is a feedback mechanism to the time-varying infection prevalence, it can still inhibit the prevalence of negative information to a certain extent, but the control performance is worse than constant controls and optimal control. Another interesting phenomenon is that although our optimal control strategy can significantly inhibit the spread of negative information, the control intensity of the two heterogeneous costs is quite different. From Figures 6C,D, the intervention effect on the spreaders of negative information is significantly stronger than that on the hesitant individuals, which may be because hesitate status has no infectivity and does not significantly promote the spread of negative information. This also indicates that in order to achieve the ideal control performance, decision-makers should attach more importance on the direct restrictions towards the sources of negative information, instead of indirect control with little benefits towards hesitate individuals.

FIGURE 6

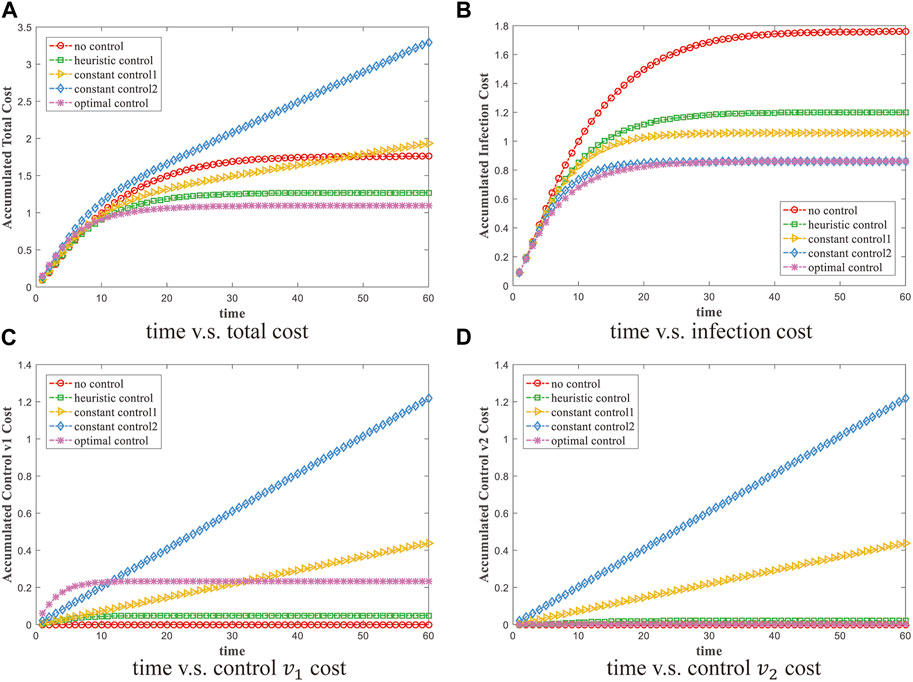
FIGURE 6. The total cost, infection cost, control cost1 and control cost2 under five different control strategies. (A) time v.s. total cost; (B) time v.s. infection cost; (C) time v.s. control $v_1$ cost; (D) time v.s. control ${\mathit{v}}_2$ cost. Parameter settings are listed as: S ₁ (0) = S ₂ (0) = 0.7, $I_1^A(0)$ = $I_1^B(0)$ = $I_2^A(0)$ = $I_2^B(0)$ = 0.15, λ ₁ = 0.35, λ ₂ = 0.25, θ ₁ = 0.2, θ ₂ = 0.15, $⟨k_2⟩$ = 8, $⟨k_2⟩$ = 5, $⟨k_{12}⟩$ = 3, $⟨k_{21}⟩$ = 2, ξ = δ = μ = 0.3, κ = 0.5, ω ₁ = 0.6, ω ₂ = 0.4, d ₁ = 0.3, d ₂ = d ₃ = 0.65.

Figure 7 presents the time-varying trend comparison of positive/negative information prevalence $I_1^A(t)$ , $I_1^B(t)$ , $I_2^A(t)$ , $I_2^B(t)$ under five control strategies. We can investigate that the evolution trends of positive/negative information in two different layers are almost consistent, but the information prevalence in layer 1 is larger than that in layer 2. Optimal, constant and heuristic controls can significantly reduce the real-time infection density of negative information and increase the density of positive information. Meanwhile, these controls also accelerate the spreading process to reach a steady state. In the initial propagation stage, our optimal control strategies play the most significant role in promoting the positive information propagation while suppressing the negative information propagation. And this control advantage will gradually weaken over time, because our controls will decline to 0 when approaching the control time terminal. Two constant control strategies have strong inhibition effects on negative information due that they always maintain high control intensity without cost constraint. Heuristic control is limited by the time-dependent density of negative information spreaders and hesitate individuals, and its control intensity is low, which makes its inhibition effect on negative information relatively poor.

FIGURE 7

FIGURE 7. The infection states $I_1^A,I_1^B,I_2^A,I_2^B$ under five different control strategies. (A) time v.s. $I_1^A(t)$ ; (B) time v.s. $I_1^B(t)$ ; (C) time v.s. $I_2^A(t)$ ; (D) time v.s. $I_2^B(t)$ . Parameter settings are the same as that in Figure 6.

6 Conclusion

In this paper, we have investigated the propagation dynamics of competitive information on multi-layer interconnected networks. On the one hand, we explored the correlation between information propagation and multi-layer network topology. On the other hand, we introduced individual adaptive behavior towards information propagation, i.e., the tendency of an infected individual to become a spreader of positive or negative information depends on the weighted consideration of local and global information prevalence. Under such propagation mechanism, the basic reproduction number ${\mathcal{R}}_0$ was theoretically calculated via next-generation matrix method. Based on the critical condition of ${\mathcal{R}}_0$ , the asymptotic stability of information-free and information-endemic equilibria was proven. That is, if ${\mathcal{R}}_0<1$ , the information-free equilibrium is globally stable, and if ${\mathcal{R}}_0>1$ , the information-endemic equilibrium is globally stable. Furthermore, we also designed two heterogeneous controls, which aims to maximize the spread of positive information and suppress the prevalence of negative information: 1) one is direct control mode, which persuades the spreaders of negative information to transform into the spreaders of positive information; 2) the other is indirect control mode, which guides hesitate individuals to become the spreaders of positive information. Then considering the cost constraints of the implementation of control strategies in reality, we developed an optimal control problem to solve the trade-off between the spreading prevalence of negative information and the control cost. Correspondingly, we provided the theoretical proof of the existence, analytical formulation and uniqueness of the optimal solution. Finally, the theoretical results of stability analysis and the performance of the optimal control were verified and discussed through numerical simulation. Extensive simulation experiments show that: 1) The different combinations of spreading parameters λ ₁, λ ₂, θ ₁, θ ₂, ω ₁, ω ₂, δ, μ, ξ not only affect the dynamic evolution process of information propagation, but also significant change the basic reproduction number and steady-state information prevalence. Driven by various spreading parameters, the steady-state behavior of our dynamic system may exhibit continuous or discontinuous phase transitions, which can serve as a theoretical guidance to regulate the steady-state system behavior via tuning spreading parameters. 2) Our optimal control strategy has achieved remarkable performance in both suppressing the spread of negative information and reducing total cost. Meanwhile, under the framework of optimal control, the direct control towards negative spreaders is significantly more dominant than the indirect control towards hesitant individuals. This theoretical result inspires decision-makers to attach more importance on the spreaders of negative information rather than hesitant individuals when conducting public opinion control in practice.

We provide two possible directions in the future: 1) our model assumes that the spreading parameters and the inter-layer average degree are time-invariant. However, in real life, information propagation is a rather complicated process associated with numerous social and cognitive psychology factors. Therefore, our model will be improved if the spreading parameters and topology settings are described as time-dependent variables driven by more social and psychological factors; 2) Our current control strategies are continuous within the specific time interval, however, in practical scenario, decision-makers can only intervene in the spreading processes at discrete time due to cost constraints. Therefore, we can introduce discrete controls to formulate the optimization problem, and discuss the optimal intensity and interval of these controls.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LC: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing–original draft, Writing–review and editing. HZ: Formal Analysis, Methodology, Software, Validation, Writing–original draft. XW: Formal Analysis, Methodology, Software, Validation, Writing–review and editing. XA: Formal Analysis, Methodology, Software, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Shandong Social Science Planning Fund Program under Grant No. 20CGLJ24.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lenormand M, Gonçalves B, Tugores A, Ramasco JJ. Human diffusion and city influence. J R Soc Interf (2015) 12:20150473. doi:10.1098/rsif.2015.0473

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Jin C, Li B, Jansen SJT, Boumeester HJFM, Boelhouwer PJ. What attracts young talents? Understanding the migration intention of university students to first-tier cities in China. Cities (2022) 128:103802. doi:10.1016/j.cities.2022.103802

CrossRef Full Text | Google Scholar

3. Jiang H, Jiang P, Wang D, Wu J. Can smart city construction facilitate green total factor productivity? A quasi-natural experiment based on China’s pilot smart city. Sustain Cities Soc (2021) 69:102809. doi:10.1016/j.scs.2021.102809

CrossRef Full Text | Google Scholar

4. Sardar T, Nadim SS, Rana S. Detection of multiple waves for COVID-19 and its optimal control through media awareness and vaccination: study based on some Indian states. Nonlinear Dyn (2023) 111:1903–20. doi:10.1007/s11071-022-07887-5

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Tiwari PK, Rai RK, Khajanchi S, Gupta RK, Misra AK. Dynamics of coronavirus pandemic: effects of community awareness and global information campaigns. Eur Phys J Plus (2021) 136:994. doi:10.1140/epjp/s13360-021-01997-6

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Rai RK, Khajanchi S, Tiwari PK, Venturino E, Misra AK. Impact of social media advertisements on the transmission dynamics of COVID-19 pandemic in India. J Appl Math Comput (2022) 68:19–44. doi:10.1007/s12190-021-01507-y

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yuan Y, Li N. Optimal control and cost-effectiveness analysis for a COVID-19 model with individual protection awareness. Phys A: Statist Mech Appl (2022) 603:127804. doi:10.1016/j.physa.2022.127804

CrossRef Full Text | Google Scholar

8. Pertwee E, Simas C, Larson HJ. An epidemic of uncertainty: rumors, conspiracy theories and vaccine hesitancy. Nat Med (2022) 28:456–9. doi:10.1038/s41591-022-01728-z

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Harper T, Attwell K. How vaccination rumours spread online: tracing the dissemination of information regarding adverse events of covid-19 vaccines. Int J Public Health (2022) 30:1604228. doi:10.3389/ijph.2022.1604228

CrossRef Full Text | Google Scholar

10. Islam MS, Kamal AHM, Kabir A, southern DL, Khan SH, Hasan SMM, et al. COVID-19 vaccine rumors and conspiracy theories: the need for cognitive inoculation against misinformation to improve vaccine adherence. Plos One (2021) 16(5):e0251605. doi:10.1371/journal.pone.0251605

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yu Z, Lu S, Wang D, Li Z. Modeling and analysis of rumor propagation in social networks. Inf Sci (2021) 580:857–73. doi:10.1016/j.ins.2021.09.012

CrossRef Full Text | Google Scholar

12. Yin F, Xia X, Zhang X, Zhang M, Lv J, Wu J. Modelling the dynamic emotional information propagation and guiding the public sentiment in the Chinese Sina-microblog. Appl Math Comput (2021) 396:125884. doi:10.1016/j.amc.2020.125884

CrossRef Full Text | Google Scholar

13. Zhu Q, Zhang G, Luo X, Gan C. An industrial virus propagation model based on SCADA system. Inf Sci (2023) 630:546–66. doi:10.1016/j.ins.2022.12.119

CrossRef Full Text | Google Scholar

14. Lucarelli A, Olof BP. City branding: a state-of-the-art review of the research domain. J Place Manage Dev (2011) 4(1):9–27. doi:10.1108/17538331111117133

CrossRef Full Text | Google Scholar

15. Perez-Cornejo C, Rodríguez-Gutierrez P, Quevedo-Puente E. City reputation and the role of sustainability in cities. Sustain Dev (2023) 31(3):1444–55. doi:10.1002/sd.2459

CrossRef Full Text | Google Scholar

16. Delgado-García JB, Quevedo-Puente E, Blanco-Mazagatos V. The impact of city reputation on city performance. Reg Stud (2018) 52(8):1098–110. doi:10.1080/00343404.2017.1364358

CrossRef Full Text | Google Scholar

17. Aloweidi A, Bsisu I, Suleiman A, Abu-Halaweh S, Almustafa M, Aqel M, et al. Hesitancy towards COVID-19 vaccines: an analytical cross–sectional study. Int J Environ Res Public Health (2021) 18(10):5111. doi:10.3390/ijerph18105111

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wu J, Tang B, Bragazzi NL, Nah K, McCarthy Z. Quantifying the role of social distancing, personal protection and case detection in mitigating covid-19 outbreak in Ontario, Canada. J Math Ind (2020) 10(1):15–2. doi:10.1186/s13362-020-00083-3

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Jarvis CI, Van Zandvoort K, Gimma A, Prem K, Klepac P, Rubin GJ, et al. Quantifying the impact of physical distance measures on the transmission of COVID-19 in the UK. BMC Med (2020) 18:124. doi:10.1186/s12916-020-01597-8

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Sharevski F, Huff A, Jachim P, Pieroni E. (Mis) perceptions and engagement on twitter: COVID-19 vaccine rumors on efficacy and mass immunization effort. Int J Inf Manag Data Insights (2022) 2(1):100059. doi:10.1016/j.jjimei.2022.100059

CrossRef Full Text | Google Scholar

21. Fan J, Wang X, Du S, Mao A, Du H, Qiu W. Discussion of the trust in vaccination against COVID-19. Vaccines (2022) 10(8):1214. doi:10.3390/vaccines10081214

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Antonopoulos CG, Shang Y. Opinion formation in multiplex networks with general initial distributions. Sci Rep (2018) 8:2852. doi:10.1038/s41598-018-21054-0

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yin F, Pan Y, Tang X, Wu C, Jin Z, Wu J. An information propagation network dynamic considering multi-platform influences. Appl Math Lett (2022) 133:108231. doi:10.1016/j.aml.2022.108231

CrossRef Full Text | Google Scholar

24. Wang J, Jiang H, Ma T, Hu C. Global dynamics of the multi-lingual SIR rumor spreading model with cross-transmitted mechanism. Chaos Sol Fract (2019) 126:148–57. doi:10.1016/j.chaos.2019.05.027

CrossRef Full Text | Google Scholar

25. Wang J, Wang YQ, Li M. Rumor spreading considering the herd mentality mechanism. In: 36th Chinese Control Conference; 26-28 July 2017; Dalian, China (2017). p. 1480–5.

CrossRef Full Text | Google Scholar

26. Xiao Y, Chen D, Wei S, Li Q, Wang H, Xu M. Rumor propagation dynamic model based on evolutionary game and anti-rumor. Nonlinear Dyn (2019) 95:523–39. doi:10.1007/s11071-018-4579-1

CrossRef Full Text | Google Scholar

27. Wang Q, Yang X, Xi W. Effects of group arguments on rumor belief and transmission in online communities: an information cascade and group polarization perspective. Inf Manage (2018) 55:441–9. doi:10.1016/j.im.2017.10.004

CrossRef Full Text | Google Scholar

28. Hosni AIE, Li K, Ahmad S. Minimizing rumor influence in multiplex online social networks based on human individual and social behaviors. Inf Sci (2020) 512:1458–80. doi:10.1016/j.ins.2019.10.063

CrossRef Full Text | Google Scholar

29. Zareie A, Sakellariou R. Minimizing the spread of misinformation in online social networks: a survey. J Netw Comput Appl (2021) 186:103094. doi:10.1016/j.jnca.2021.103094

CrossRef Full Text | Google Scholar

30. Yan R, Li Y, Wu W, Li D, Wang Y. Rumor blocking through online link deletion on social networks. ACM Trans Knowl Discov Data (2019) 13(2):1–26. doi:10.1145/3301302

CrossRef Full Text | Google Scholar

31. Wang B, Chen G, Fu L, Song L, Wang X. Drimux: dynamic rumor influence minimization with user experience in social networks. IEEE Trans Knowl Data Eng (2017) 29(10):2168–81. doi:10.1109/tkde.2017.2728064

CrossRef Full Text | Google Scholar

32. Cheng Y, Huo L, Zhao L. Stability analysis and optimal control of rumor spreading model under media coverage considering time delay and pulse vaccination. Chaos Sol Fract (2022) 157:111931. doi:10.1016/j.chaos.2022.111931

CrossRef Full Text | Google Scholar

33. Chen S, Jiang H, Li L, Li J. Dynamical behaviors and optimal control of rumor propagation model with saturation incidence on heterogeneous networks. Chaos Sol Fract (2020) 140:110206. doi:10.1016/j.chaos.2020.110206

CrossRef Full Text | Google Scholar

34. Lin Y, Wang X, Hao F, Jiang Y, Wu Y, Min G, et al. Dynamic control of fraud information spreading in mobile social networks. IEEE Trans Syst Man Cybern Syst (2021) 51(6):3725–38. doi:10.1109/tsmc.2019.2930908

CrossRef Full Text | Google Scholar

35. Li L, Liu Y, Zhou Q, Yang W, Yuan J. Targeted influence maximization under a multifactor-based information propagation model. Inf Sci (2020) 519:124–40. doi:10.1016/j.ins.2020.01.040

CrossRef Full Text | Google Scholar

36. Wang X, Wang X, Min G, Hao F, Chen CLP. An efficient feedback control mechanism for positive/negative information spread in online social networks. IEEE Trans Cybern (2022) 52(1):87–100. doi:10.1109/tcyb.2020.2977322

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci (2002) 180:29–48. doi:10.1016/s0025-5564(02)00108-6

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Shang Y. Lie algebraic discussion for affinity based information diffusion in social networks. Open Phys (2017) 15(1):705–11. doi:10.1515/phys-2017-0083

CrossRef Full Text | Google Scholar

39. Fleming WH, Rishel RW. Deterministic and stochastic optimal control. New York: Springer (1975).

Google Scholar