Challenges for dark matter direct search with SiPMs

Liquid xenon and liquid argon detectors are leading the direct dark matter search and are expected to be the candidate technology for the forthcoming generation of ultra-sensitive large-mass detectors. At present, scintillation light detection in those experiments is based on ultra-pure low-noise photo-multipliers. To overcome the issues in terms of the extreme radio-purity, costs, and technological feasibility of the future dark matter experiments, the novel silicon photomultiplier (SiPM)-based photodetector modules seem to be promising candidates, capable of replacing the present light detection technology. However, the intrinsic features of SiPMs may limit the present expectations. In particular, interfering phenomena, especially related to the optical correlated noise, can degrade the energy and pulse shape resolutions. As a consequence, the projected sensitivity of the future detectors has to be reconsidered accordingly.

1 Introduction

Indirect astrophysics observations from galactic to large structure scales imply the presence of a non-luminous and hidden mass, commonly named dark matter, accounting for approximately 85% of the matter content of the Universe (for a review, see, e.g., [1]). Although the nature of this missing ingredient is still unknown, many particle candidates have been proposed over the recent decades, with masses ranging from fractions of eV/c² to the grand unification mass scale. Weakly interacting massive particles (WIMPs), with mass in the range from 1 GeV/c² up to 1 TeV/c² [2, 3], have been considered promising candidates, as originating from natural high-energy extensions of the Standard Model of particle physics. However, the lack of observation in many direct and indirect searches has led to the questioning of their theoretical foundations recently [4].

Since the beginning of the new millennium, the direct dark matter search has been attracting a lot of interest in the astroparticle physics community, with a substantial effort in terms of engagement and funding. Since the majority of the experiments searching for WIMPs are providing null results, a quest is ongoing for the deployment of the ultimate hundred-ton-scale targets. The latter effort requires experimental technology that is easily scalable while preserving a very low level of background, high detection efficiency, and stable behavior over time exposures of tens of years.

One of the most successful and scalable detection technologies is based on liquid noble gas, in particular on xenon and argon. Both targets show clear pros and cons, and at the moment, the scientific community is split down the middle, and there is no clear choice for the ultimate experiment capable of reaching the so-called neutrino floor limit in the forthcoming decades [5, 6]. The experiments based on the xenon double-phase time projection chamber (TPC), as LZ [7], XENON1T [8], and PANDAX-4T [9], reported independently the strongest bound on the spin-independent (SI) WIMP–nucleon interaction (for a review of dark matter refer to [10]). DEAP-3600 [11], a single-phase liquid argon detector, reported an independent, even if less stringent, limit for the same interaction. Finally, DarkSide-50, using ultra-pure underground argon in a double-phase TPC, has set a corresponding limit, constraining especially the region down to a few GeV/c² [12, 13].

Recently, LZ has reported the strongest SI limit [7], and XENONnT has shown a very low background in the first physical data collection of its multi-ton target [14]. Meanwhile, DarkSide-20k [15], which will exploit approximately 20 ton (fiducial mass) of ultra-pure underground argon in a gigantic double-phase TPC, is under construction and should start data collection by the end of the present decade. The argon and xenon scientific communities are already designing the next iteration of experiments: the xenon community is converging on a future detector, called DARWIN, based on a target of 50 ton [6], while the argon community is planning a future detector, called ARGO-300, based on a target of 300 ton of ultra-pure argon naturally depleted in ³⁹Ar [5].

At present, the scintillation light of the aforementioned experiments is detected using ultra-pure low-noise photomultiplier tubes (PMTs) [7, 9, 11, 12, 14]. To overcome possible issues in terms of the extreme radio-purity, costs, and technological feasibility, many projects are planning to replace PMTs with novel photodetectors. In particular, the DarkSide-20k experiment, designed to reach 200 ton⋅y exposure, will install approximately 22 m² of silicon photomultiplier (SiPM) arrays [15–17].

In this work, extensive studies on the SiPM performances prove that the intrinsic features of the SiPM units, in addition to the well-known internal correlated noise, may limit the present expectations. In particular, interfering phenomena related to the optical correlated noise, i.e., the light emission of fired SiPMs triggering nearest SiPMs, produce an irreducible degradation of the resolution of the fundamental reconstructed observables as energy and pulse shape. As a consequence, the projected sensitivity on the dark matter parameter space of the future detectors, especially based on liquid argon, needs a corresponding revision.

The article is structured as follows: in Section 1, the main argon- and xenon-based characteristics concerning light detection are described; in Section 2, the main feature of the SiPM-based photodetector module at cryogenic temperature is reviewed, and the noise classification and the impact on the event reconstruction are largely discussed; in Section 3, a toy Monte Carlo simulation for a multi-ton liquid argon TPC is performed, and the impact of the correlated noise in the final dark matter analysis is outlined. Finally, in Section 4, the implication of the irreducible correlated noise on the dark matter sensitivity plots is discussed.

2 Liquid noble gas detectors

Noble liquid detectors can be designed to exploit either single- [11] or double-phase TPC [7, 9, 14, 15, 18]. The first type has a simpler design and shows fewer technological challenges. In those detectors, like DEAP-3600 [11], the liquid noble gas fills up a spherical vessel whose surface is instrumented with PMTs to detect the scintillation light. The reconstructed position is less accurate than in double-phase detectors, and it is, in principle, difficult to reject the pile-up events. In contrast, the second type shows a more complex design but features many advantages in terms of event reconstruction. A double-phase TPC is typically a cylindrical-shaped vessel filled with a noble liquid. On top of the liquid free surface, there is a thin gas pocket, separated by a conductive grid. On the bottom and on the top of the cylinder, there are a cathode and an anode, respectively, able to set the so-called drift and extraction fields. For each ionizing particle hitting the detector, two signals are produced: the first scintillation signal is originated in the liquid by the primary interaction and is typically called S1, whereas the second signal (S2) is produced by electro-luminescence of the gas pocket when ionization electrons, pulled upward by the drift fields, are accelerated in the gas pocket by the extraction field. The double signal allows to increase the spatial resolution and exploit the pulse shape discrimination between electron recoils (ERs) and nuclear recoils (NRs) using the ratio S2/S1.

Among the available noble gases in nature, at present, only argon and xenon have shown a reasonable feasibility in terms of costs and performances. Both technologies have proven to be easily scalable to multi-ton scales, with no insuperable obstacles and with reasonable economical effort. However, the two gases have very different physical properties being, to some extent, complementary. This is especially true as well for the design of PMT- and SiPM-based photodetectors.

The use of PMTs in liquid argon has experienced a very critical performance in terms of electronics stability, due to the very low cryogenic temperature of 87 K. In addition, the 128-nm scintillation light does not match the PMT photo-cathodic sensitive window, and therefore, a wavelength shifter-coated reflector is needed (typically made of tetraphenyl butadiene (TPB) at 420 nm [18]). On the contrary, in liquid argon, the use of SiPMs is encouraged by the low dark rate at 87 K and by the easy detection of visible shifted scintillation light that matches the high photon detection efficiency (PDE) of commercial SiPMs [19, 20].

For the xenon-based detector, instead, the use of PMTs is much convenient since they operate steadily at the xenon cryogenic temperature (165 K) and are highly sensitive to the scintillation light at 178 nm without the need for a wavelength shift. Concerning the use of SiPMs in xenon, in principle, photo-cathodic surfaces with a reasonable PDE to vacuum ultraviolet light are already available. However, the higher cryogenic temperature could not be sufficiently low to bring the dark rate down to an acceptable threshold.

3 SiPM-based photodetectors

SiPMs are solid-state devices based on single-photon avalanche diode (SPAD) micro-cells on silicon substrates [21]. The dimension of each single SPAD ranges between 10 and 100 µm. Each SPAD operates in the Geiger mode, coupled with the others by means of a quenching circuit. For analog SiPMs, the signal of the micro-cells is summed in parallel by appropriate quenching resistors; this results in a dynamic range spanning from one to thousands of photo-electrons (for mm²) with an intrinsic photon-counting resolution exceeding few percent [22]. SiPMs produce a signal proportional to the bias exceeding the breakdown voltage (typically between 20 and 50 V) with over-voltages (OV) in the range 2–10 V [23].

Since first measurements at cryogenic temperature [24], Fondazione Bruno Kessler intensified the effort for the development of SiPMs for cryogenic particle detectors. The current cryogenic near-ultraviolet high-density (NUV-HD-Cryo) family is capable of stable operation in liquid nitrogen/argon at over-voltages in excess of 10 V [25]. These devices are optimized for the detection of NUV and blue light with a peak photon detection efficiency close to 60% [19], measured at room temperature. The primary dark rate is lower than few counts per square centimeter per second at 77 K [26].

Beyond the dark rate, SiPMs exhibit correlated noises: after-pulsing (AP) occurs when, during an avalanche, a carrier is temporarily trapped by impurities in the medium. When released, a second avalanche is generated. If detrapping happens before SPAD is fully recharged, the after-pulse will have a charge lower than that of the single photo-electron. Optical cross-talk (oCT) is triggered by photons generated as the secondary process during the avalanche. These photons can interact with a neighbor micro-cell and generate internal cross-talk (iCT), or escape the silicon bulk and generate external cross-talk (eCT) in the nearest SiPMs. Figure 1 shows the optical-crosstalk cascade in case of high photo-detection coverage. Consider that in TPCs, due to the high reflectivity of the chosen materials, the collection efficiency for photons can typically exceed 90% [27]. Furthermore, the final signal is inevitably affected by electronic noise amplified and shaped by the read-out electronics.

FIGURE 1

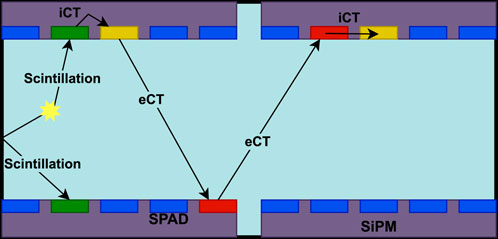
FIGURE 1. Photon detection in a high-coverage detector with SiPMs: scintillation photo-electron may be followed by a cascade of internal and external cross-talks. The SiPMs are drawn in gray with blue SPADs that become green/red/yellow when triggered, respectively, by a primary photon, eCT, and iCT (see text). All surfaces of the chamber are highly reflective; the scintillation medium is shown in cyan. For simplicity, after-pulsing is not shown.

At Laboratori Nazionali del Gran Sasso (LNGS), large integrated photodetectors for cryogenic applications have been developed [16, 22]. It is now possible to aggregate the signals of 96 SiPMs into a single analog output covering a surface of 100 cm² [17]. As a result, it is now possible to plan for large dark matter experiments using SiPMs for light detection [15].

3.1 Optical cross-talk models

The scientific literature reports many measurements of optical cross-talk for SiPMs (see, for example, [28–31]). In a highly reflective environment, the optical cross-talk cascade process leads to an information-less multiplication of the number photo-electron, defined here as detection noise gain ${\mathcal{G}}_{\text{oCT}}$ (not be confused with the charge gain of the SiPM avalanche). In other words, the apparent light yield of a particle detector can be significantly larger than the real one since for each real photo-electron associated with the scintillation photon, a number ${\mathcal{G}}_{\text{oCT}}(>1)$ is, in average, actually detected.

As described in [32], iCT follows a recursive process in which the primary avalanche is followed by secondaries, which, in turn, can produce other avalanches. The process is theoretically limited to the very large number of micro-cells in the detector (between millions and billions), but for mathematical convenience, the geometric progression is approximated with a series. Let λ_iCT be the mean number of secondaries for each primary avalanche (λ_iCT < 1); the noisy detection gain converges to ${\mathcal{G}}_{\text{iCT}}=1/(1-{\lambda }_{\text{iCT}})$ with an excess noise factor ${\mathcal{E}}_{\text{iCT}}\simeq 1+{\lambda }_{\text{iCT}}$ [32]. The fluctuations in the cascade have a strong impact on the resolution of a particle detector using SiPMs: it is possible to introduce a generalized Fano factor $({\mathcal{F}}_{\text{iCT}}={\mathcal{G}}_{\text{iCT}}{\mathcal{E}}_{\text{iCT}})$ that directly correlates the number of detected photons with its variance.

The modeling of iCT is further complicated by the neighbors effect, for which already triggered micro-cells reduce the acceptance for new photons; therefore, both the “Branching Poisson” and the “Geometric Chain” models introduced in [33] show inaccurate results.

For a simplified symmetric detector (where all SiPMs are identical and the optical acceptances for external cross-talk are uniform), using positive feedback theory, it is possible to write

$N_G^{\text{pe}}=N_N^{\text{pe}}+{\lambda }_{\text{iCT}}{N}_G^{\text{pe}}+{\lambda }_{\text{eCT}}{N}_G^{\text{pe}},(1)$

where $N_G^{\text{pe}}$ and $N_N^{\text{pe}}$ represent the detected (gross) and scintillation (net) number of photo-electrons, respectively. Equation 1 implies only the additive and independence properties of iCT and eCT photons. Under these assumptions, the oCT gain becomes by extension:

${\mathcal{G}}_{\text{oCT}}=\frac{1}{1-{\lambda }_{\text{iCT}}-{\lambda }_{\text{eCT}}}(2)$

that is valid for λ_oCT = λ_iCT + λ_eCT < 1; otherwise, the system diverges. It may be interesting to know how many eCT photo-electrons are generated in average for each physical scintillation photo-electron, discarding the contribution of iCT. The solution is simply

$\begin{array}{ll}\hfill N_{\text{iCT}}^{\text{pe}}& ={\mathcal{G}}_{\text{oCT}}{\lambda }_{\text{iCT}}{N}_N^{\text{pe}}\hfill \\ \hfill N_{\text{eCT}}^{\text{pe}}& ={\mathcal{G}}_{\text{oCT}}{\lambda }_{\text{eCT}}{N}_N^{\text{pe}}\hfill \end{array}(3)$

as the iCT and eCT probabilities are additive. Figure 2 reports a visual demonstration of these formulas for the geometric chain hypothesis. However, these are valid as well in the branching Poisson model, as application of the multinomial theorem.

FIGURE 2

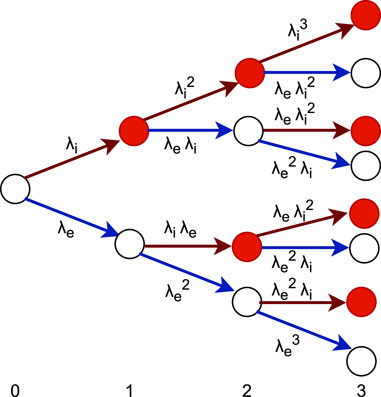
FIGURE 2. Optical cross-talk cascade in the presence of both internal and external processes. For level n of recursion, the average number of avalanches is $N^n={\left({\lambda }_{\text{iCT}}+{\lambda }_{\text{eCT}}\right)}^n$ (for brevity, the CT pedix has been removed in the figure), while the number of iCT-only photo-electrons (red circles) is $N_{\text{iCT}}^n=N^{n-1}{\lambda }_{\text{iCT}}$ (n > 0). The sum over i converges to ${\mathcal{G}}_{\text{oCT}}$, defined in Equation 2, and $N_{\text{iCT}}={\mathcal{G}}_{\text{oCT}}{\lambda }_{\text{iCT}}$.

For a highly reflective large-particle experiment, it is impossible to distinguish scintillation photo-electrons from the external cross-talk. The eCT emission happens with subnano-second timing [26] (significantly lower than the path spread in the detector), and photons are emitted isotropically from the surface of SiPM. As a matter of fact, eCT cannot be disentangled from scintillation photons reflected on the SiPM surface, whose reflectivity can reach 30% [34].

3.2 After-pulsing

AP adds another positive feedback contribution to the process, thus increasing the overall noise gain. Modifying Eq. 2 to include after-pulsing is not trivial because the charge gain of the avalanches depends on the delay from the primary photo-electron. At a leading order, one can write

${\mathcal{G}}_{\text{oCT}+\text{AP}}=\frac{1}{1-{\lambda }_{\text{iCT}}-{\lambda }_{\text{eCT}}-{\lambda }_{\text{AP}}^{*}},(4)$

where ${\lambda }_{\text{AP}}^{*}$ is an effective parameter.

The AP probability $(P_{\text{AP}}^T)$ in the literature is measured above a fixed signal amplitude, typically T = 50%. The amplitude of after-pulsing is proportional to the status of the recharge of the fired micro-cell. The signal half-life for the photodetectors in consideration is about T^(1/2) = 100 ns [17]. This means that for after-pulsing closer than T^(1/2), the charge of the avalanche is more than halved.

The probability of emitting oCT photons is proportional to the charge of the avalanche; therefore, after-pulsing with low amplitude will not contribute significantly to ${\mathcal{G}}_{\text{oCT}+\text{AP}}$. For NUV-HD-Cryo SiPM at the highest over-voltage, $P_{\text{AP}}^{(1/2)}$ is less than one-tenth of the combined oCT lambdas (see Table 1); therefore, (at a leading order) it can be assumed ${\lambda }_{\text{AP}}^{*}=P_{\text{AP}}^{(1/2)}$.

TABLE 1

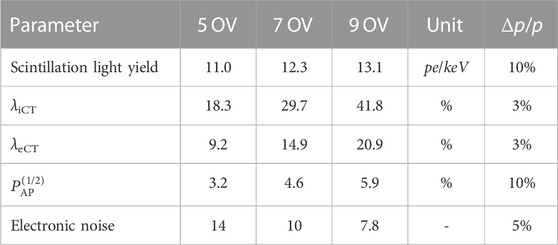
TABLE 1. Input parameters for the toy Monte Carlo simulation extracted from [27] at 5, 7, 9 over-voltages: the last column quantifies the relative uncertainty for each parameter at one sigma. eCT includes the contribution of the feedback cross-talk measured in STAR (see text). The light yield and the external cross-talk are rescaled by the light losses of the STAR chamber (13%).

3.3 Streamers

In addition to the correlated noises, SiPMs are subject to stability issues at cryogenic temperatures. The DUNE collaboration has recently reported for Hamamatsu SiPMs a burst of photo-electrons at a very high rate in liquid nitrogen [35]. In analogy to discharges in Geiger–Muller tubes, such events are called streamers. It is sensible to suppose that NUV-HD-Cryo SIPMs could be subjected to the same problem.

These events would represent a potential problem for highly reflective detectors equipped with many SiPMs. Although it is easy to identify and exclude a streamer in the analysis, all events during the burst may contain extraneous photo-electrons, indeed due to external cross-talk triggering other photodetectors. Assuming an incidence of one streamer event per SiPM per year with a duration of approximately 10 s, for a detector with 200,000 SiPMs, the probability of having a streamer for any event is approximately 7%.

4 Toy Monte Carlo simulations

To properly account for all noise contributions, a dedicated toy Monte Carlo (tMC) simulation was developed: the code is based on the simulation used in the STAR R&D facility at LNGS [27], i.e., a down-scaled liquid argon detector, instrumented with the aforementioned NUV-HD-Cryo SiPMs. The tMC was extended to a large homogeneous liquid argon detector with N_pd ≃ 2000 readout channels based on SiPM photodetectors. The SiPM parameters and scintillation light yield were extracted from STAR (Table 1).

The simulation does not include scintillation photon tracking (as for a full chain physical Monte Carlo simulation), and the light collection efficiency is considered uniform in the fiducial volume: all photodetectors have the same probability of being hit by scintillation or cross-talk photons. As a consequence of the simplification, the following results have to be considered a pure and ideal case, as just driven by the statistical features of the SiPM intrinsic noise. The real physical performances will further be reduced by the detector imperfections, such as detector reflectivity, scintillation light absorption, TPB re-emission, electronics flaws, and all other possible systematic effects.

For each detected photo-electron (from primary argon scintillation or from correlated noises), a recursive oCT + AP cascade is applied. This is implemented by a set of recursive functions, each describing one possible correlated noise. Each function generates the correlated noise using a binomial extraction (or two binomials for iCT, as in [27]). If an avalanche is generated, a recursion on all correlated noises is activated. In case of eCT, the avalanche is applied to another readout channel, randomly picked. All the oCT and AP components are accounted for individually. It is important to notice that tMC does not depend on the models described in the previous section that describe the average cascade behavior (Eq. 3, 4): tMC propagates each photo-electron independently.

tMC keeps track of photo-electrons (both primaries and secondaries) generated by the singlet and triplet argon states for electron and nuclear recoils (for a review of the scintillation in noble gasses, refer to [36]). The median values for the fast-to-total light yield (typically referred to as f₉₀ or f_prompt) are extracted from [37, 38]. As discussed above, after-pulsing closer than ${\tau }_{1/2}^{\text{AP}}$ has a smaller amplitude and reduced probability of triggering oCTs. It is safe to assume that after-pulsing, as well as its secondaries, does not contribute to the detected singlet photo-electrons with a timing of few nanoseconds. Note that, for large experiments, the propagation time of the photons in the liquid argon chamber can increase the spread of the singlet photo-electrons beyond ${\tau }_{1/2}^{\text{AP}}$. In such cases, after-pulsing can affect the singlet too. Since in any case the AP probability is very small for NUV-HD-Cryo, this case is not particularly interesting.

The region of interest (RoI) for the analysis is in the range 5–35 keVee; tMC simulates a wider window to avoid border effects due to statistical fluctuations of the simulated resolution.

4.1 Energy reconstruction

In the absence of correlated noises, it is possible to define three estimators for the net energy of the scintillation event. N_N is calculated as the total number of avalanches detected by photodetectors. B_N is the number of read-out channels with at least one avalanche. In the first approximation, B_N behaves as a binomial distribution with the success probability $1-e^{-N_N/N_{\text{pd}}}$ with N_pd extractions (i.e., the total number of read-out channels). Therefore,

$⟨B_{\text{N}}⟩=N_{\text{pd}}\left(1-e^{-N_N/N_{\text{pd}}}\right),(5)$

where the mean value is required because the binomial extraction introduces an irreducible spread in the data. To overcome the inherent non-linearity of B_N as a function of energy, the L_N (linearized binomial) variable is introduced with the following definition:

$L_N=-N_{\text{pd}}\ln \left(1-\frac{B_{\text{N}}}{N_{\text{pd}}}\right).(6)$

Figure 3 intuitively depicts the meaning of the binomial counting. For B_N, the information on piled-up photo-electrons in the same read-out channel is lost. The information loss leads inevitably to a spoiled resolution; however, the fluctuations introduced by the correlated noise are strongly reduced as it will be shown later. As hinted earlier, the binomial extraction is only an approximation because the number of photo-electrons is set to N_N, and only the pile-up can fluctuate. This is clearer for an event with N_N = 1; the binomial extraction allows non-physical events with B_N ≠ 1. The tMC simulation correctly simulates the pile-up, and the reported results are unaffected by the binomial approximation used to simplify the description.

FIGURE 3

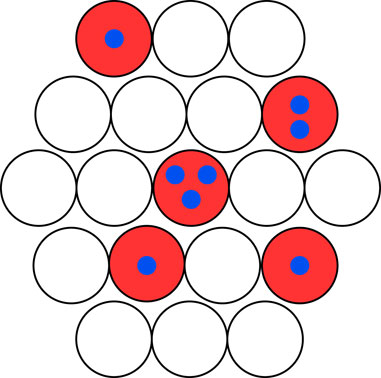
FIGURE 3. Example of an energy estimator during the event reconstruction. For both SiPM and PMTs, the energy of an event producing several photo-electrons can be estimated by counting the number of total photo-electrons (N, blue circles) or counting the number of total photodetectors (B, red circles).

For a real detector, the net estimators cannot be observed directly; similar quantities can be calculated in the presence of correlated noises (oCT and AP), obtaining N_G, B_G, and L_G for modeling the gross energy seen by the detector. Figure 4 reports the reconstructed values of N, B, and L (net and gross) as a function of the deposited energy for electron recoil events (E_e) in keVee. Both L and N provide a linear scale to measure the released energy (once a calibration is performed) and will hence be used as energy estimators. It is interesting to note that the L_G estimator is less affected by an internal cross-talk and after-pulsing than N_G since only the first photo-electron from scintillation (or from eCT) is accounted for by each photodetector. As a result, the noisy gain of the correlated processes (the slope of Figure 4) is unequivocally lower then N_G; from Eq. 3, ${\mathcal{G}}_{L_G}=1+{\mathcal{G}}_{\text{oCT}+\text{AP}}{\lambda }_{\text{eCT}}$.

FIGURE 4

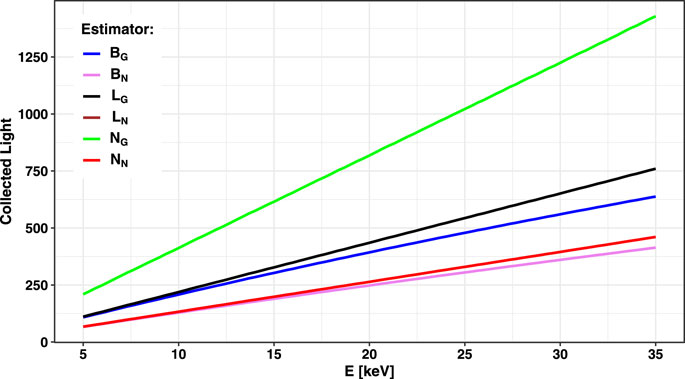
FIGURE 4. Average collected light for electron recoils for the different estimators described in the text. The L_N curve is completely overlapped by the N_N line. With the exception of the B* variables, the curves are a straight line with a slope defined by the light yield at 9 OV multiplied by the correlated noise gain (Eqs 4, 3). In the rest of the article, N_N, N_G, L_N, and L_G will be used as energy estimators by implicitly inverting this plot.

Figure 5 reports the generalized Fano factor (defined as the variance over mean of the collected number of photo-electrons) for different energy estimators. It is possible to express the energy resolution of the experiment as a function of the correlated noise gains. A non-linear regression analysis on the simulated data shows an exponential dependence of the Fano factors upon the noise gains, namely, ${\mathcal{F}}_{N_G}={({\mathcal{G}}_{\text{oCT}+\text{AP}})}^{-1.84\pm 0.02}$ and ${\mathcal{F}}_{L_G}={({\mathcal{G}}_{L_G})}^{-2.18\pm 0.04}$, with a standard deviation of the relative residuals of ∼3%.

FIGURE 5

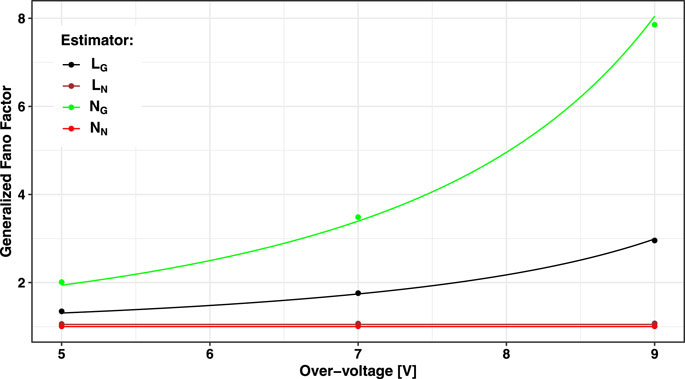
FIGURE 5. Average generalized Fano factor for electron recoil events versus SiPM over-voltages for the energy estimators described in the text. As expected, ${\mathcal{F}}_{N_N}$ has a unity value, the process being purely Poissonian. The generalized Fano factor for the L estimators (${\mathcal{F}}_{L_N}$ and ${\mathcal{F}}_{L_G}$) is inherently not constant as a function of the energy. Since in the region of interest it changes by less than 7%, the mean value is used. The lines for ${\mathcal{F}}_{N_G}$ and ${\mathcal{F}}_{L_G}$ represent the best-fit described in the text, while for ${\mathcal{F}}_{N_N}$ and ${\mathcal{F}}_{L_N}$, a constant line at 1 is drawn to guide the eye.

The lower generalized Fano factor for L_G with respect to N_G, and hence the better energy resolution in RoI, is directly linked to the lower noise gain of the oCT process, affecting the linearized binomial energy estimator. For example, at 9 OV, ${\mathcal{G}}_{L_G}\simeq 1/2{\mathcal{G}}_{\text{oCT}+\text{AP}}$.

4.2 Pulse shape

The tMC simulation keeps track of which photon corresponds to the singlet or triplet emission in liquid argon scintillation. The pulse discrimination parameter (PSD) is defined as the ratio between the number of singlet photo-electrons collected divided by the total number of photo-electrons. Figure 6 reports PSD as a function of the reconstructed energy for 3×10¹⁰ electron-like events for the energy estimators discussed earlier and with three SiPM over-voltages, namely, 5 V, 7 V, and 9 V. As expected, these plots are affected by the presence of correlated noise with a spread in PSD and by a lower resolution on the energy scale.

FIGURE 6

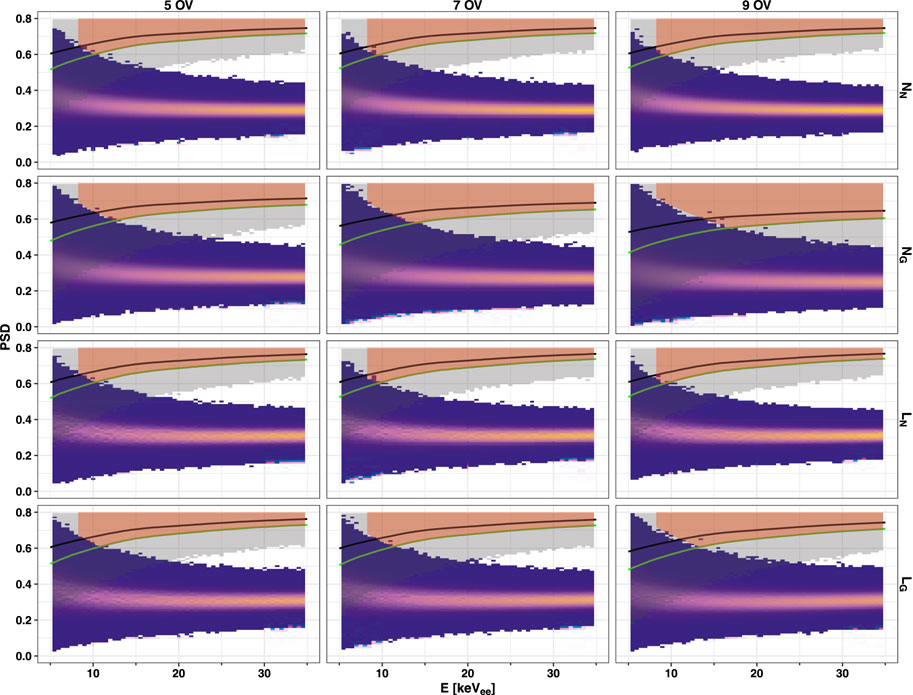
FIGURE 6. Pulse shape discrimination versus reconstructed energy for several SiPM over-voltages and different energy estimators. The blue–gold heatmaps correspond to 3×10¹⁰ electron-like events uniformly distributed between 5 and 35 keVee. The gray-shaded bands correspond to approximately 1×10⁹ nuclear recoil events: 50% (black) and 90% (green) quantiles are shown. The red ribbons identify the dark matter acceptance area with a leakage of about 10 electron-like events.

4.3 S2

As mentioned before, S2 plays a crucial role in the position and energy reconstruction of the double-phase argon TPCs and is fundamental for the pulse shape of the double-phase xenon TPC. Typically, S2 is much greater than S1 and depends on applied drift and extraction fields. For the reasons discussed above, S2 is indeed not free from all of the issues concerning the presence of oCTs. Furthermore, in S2, the scintillation photo-electrons are not uniformly distributed; only a few photo-detectors, just above the S2 position, will see the largest fraction of the emitted light. In these conditions, the use of binomial estimators is not possible. The full description of eCT effects on S2 would anyway require a detailed Monte Carlo analysis, e.g., for the position reconstruction algorithm, that goes beyond the scope of the present work.

5 Implications on the projected sensitivity

Assuming the SI WIMP–nucleon interaction, under the galactic Standard Halo model, it is possible to extract the projected sensitivity of the simulated experiment. The number of background events is considered zero; the suppression of nuclear recoil events is demanded to a proper detector design, including active neutron veto and low background materials. For a leaking electron recoil, this is obtained by tuning the NR acceptance regions. This process depends strongly on the correlated noise contribution and on the used energy estimator, as discussed in Section 3.

5.1 Acceptance regions

Based on the data shown in Figure 6, the acceptance regions are defined as the areas in which only approximately 10 ER leaking events are present over the aforementioned exposure. The acceptance regions are defined between 5 and 35 keV by the intersection of the 90% quantile for NR events and a segment of a rectangular hyperbola (1/(1 + ξE)) in the pulse shape parameter. The scale parameter (ξ) is tuned to satisfy the requirement of having 10 ER outliers in the acceptance for each SiPM OV and energy estimator. The resulting NR acceptance as a function of energy is shown in Figure 7.

FIGURE 7

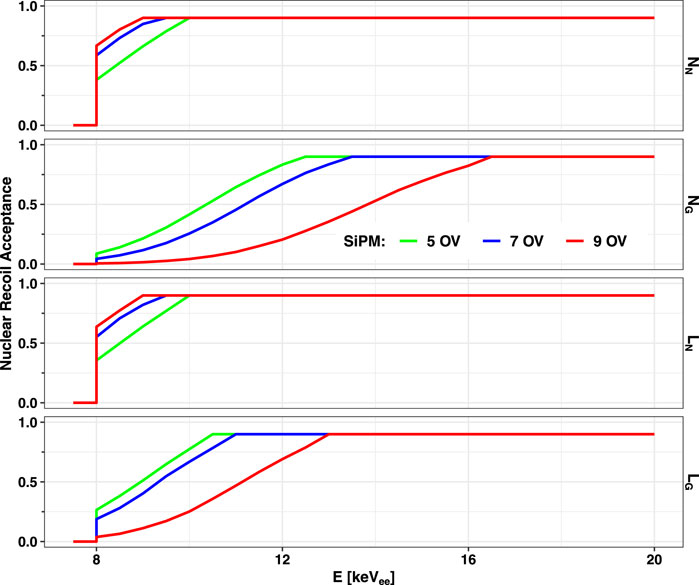
FIGURE 7. Nuclear recoil acceptances as a function of collected energy for the different estimators discussed in the text and at several over-voltages. Above 20 keVee, the acceptance remains at 90%. Below 8 keVee, it is set to zero.

This number of leaking events over the 200 ton⋅y exposure corresponds to 0.10 ± 0.01. Indeed, neglecting the contribution of all possible γ backgrounds in the detector fiducial volume, the only source of internal ER events is the ³⁹Ar β decay and amounts to

$N_{39_{\text{Ar}}}=3.15\cdot 10^{10}\times \frac{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}{\left[\mathrm{t}\mathrm{o}\mathrm{n}\right]}\times \frac{\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}}{\left[\mathrm{y}\right]}\times \frac{{\delta }_{\text{RoI}}}{\mu },(7)$

where μ is the ³⁹Ar depletion factor, reasonably assumed to be approximately 1/1,500 [38], with respect to the specific activity of atmospheric argon (1 Bq/kg); and δ_RoI is the fraction of the ³⁹Ar beta decays falling in RoI (calculated by integrating the normalized β–spectrum over RoI). For the chosen exposure, one obtains $N_{39_{\text{Ar}}}\simeq 3\times 10^8$ events.

5.2 Dark matter sensitivity plots

To calculate the dark matter sensitivity plot, the standard WIMP-halo model with v_esc = 544 km/s [40], v₀ = 220 km/s [40], v_earth = 232 km/s [41], and ρ_DM = 0.3 GeV/(c² cm³) [42] is assumed. The SI WIMP–nucleon differential interaction rate, as a function of the kinematic parameters and of the dark matter velocity distribution, is convoluted with the energy resolution for each energy estimator. The number of interactions is given by the exposure multiplied by the differential rate integrated over RoI, scaled by the acceptance of Figure 7 and by the exposure. NR quenching, as a function of the energy for liquid argon, is taken from [38]. Assuming the null result and neglecting the 0.1 ³⁹Ar background events, the 90% CL exclusion curves, corresponding to the observation of 2.3 events for the SI WIMP–nucleon interactions, are derived for each energy estimator.

Figure 8 shows the corresponding sensitivity curves for the energy estimators described earlier for different SiPM over-voltages. The figures show a progressive decrease in the sensitivity, depending on the operating over-voltage. In other words, the optical correlated noise produces a sizeable effect on the final analysis that may reduce the projected sensitivity even by a factor two, especially in case a large OV is used. This effect can be mildly reduced using the linearized binomial energy estimator but not completely removed.

FIGURE 8

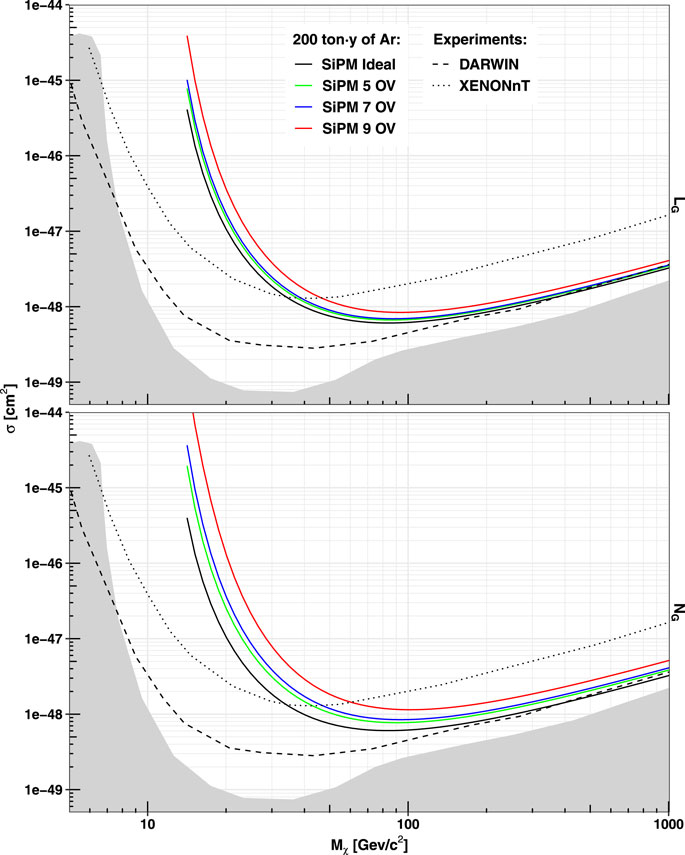
FIGURE 8. Sensitivity curve (90% CL) for a 200-ton⋅y exposure of a liquid argon detector using a SiPM-based photodetector module for different over-voltages and using two different energy estimators for S1: linearized binomial counting (top) and number of detected photo-electrons (bottom). The ideal curves refer to the absence of noises (oCT, AP, and electronic). As a reference, the projected sensitivity curves for XENONnT [39] and DARWIN [6] are added with dotted and dashed lines. The neutrino floor [1] with the gray area is also shown. As explained in the text, the projected sensitivity for the argon detector with SiPMs is overestimated by a factor 2 ÷ 3 with respect to a realistic experiment.

It should be noted that the ideal sensitivity curves are tangibly better than a realistic experimental situation because, as explained in Section 3, the tMC simulation does not take into account a further broadening of the energy and the pulse shape resolutions, due to the scintillation properties and detector geometry. Considering the acceptance of a real liquid argon detector as DarkSide-50 [12], one can easily estimate that sensitivity is overestimated by a factor 2 ÷ 3 or even more. For this reason, the distortion caused by the correlated noise with respect to the ideal Poisson baseline must be considered in a relative and not in an absolute way, and its real impact could be dramatically large, depending on how large is the difference between the reconstruction of the physical observables and their ideal expectations.

6 Conclusion

The direct dark matter search, especially concerning the WIMP-like detection in the mass interval 1 GeV–1 TeV, starts exploiting the multi-ton scale. For future detectors, scalable and reliable photodetectors are required. The argon community decided to use SiPMs, taking advantage of high PDE and low background. SiPMs have been developed at Fondazione Bruno Kessler for operation in liquid argon, and large photodetectors have been proven at LNGS, opening the path to the deployment of large experiments. However, as largely discussed in the present work, the presence of correlated noise can spoil the full scientific reach of future detectors if not properly managed.

We introduced a new energy estimator, based on the number of the fired module, which is capable of mitigating the noise caused by optical cross-talk and after-pulsing. Differently, the external optical cross-talk is irreducible and becomes dominant for high over-voltages. We have shown, as an example, a multi-ton liquid argon detector with 200-ton⋅y exposure. A dedicated simulation shows that the presence of the irreducible correlated noise can even divide the ideal projected sensitivity (Figure 8), basically doubling the needed experiment live time. A recent pre-print [43] demonstrates the effects of eCT for xenon-based detectors. In principle, with respect to argon, xenon-based detectors should be less affected by this issue as the sensitivity for an optical cross-talk of vacuum ultraviolet-sensitive SiPMs is lower.

Beyond analysis optimizations, it is possible to mitigate in the detectors the effects of correlated noise. A first solution could be the introduction of colored optical filters capable of attenuating wavelengths above 500 nm in front of the SiPM-based modules. More elaborate options require modifications to SiPM to reduce iCT, emission probability, and PDE above the green wavelength.

As we have shown in our toy Monte Carlo simulations, the correlated noise largely applies for high over-voltage settings, where the effect is strongly amplified. Therefore, a natural solution could be operating the detectors at very low over-voltage, to reduce the cascade gain down to some acceptable value. However, reducing the SiPM charge gain may require a very low electronic noise condition that cannot be easily achieved in very big detectors.

The dark matter search is entering a critical and challenging phase, in which old technological solutions may not be sufficient any longer, and novel and promising solutions have to be carefully tested and validated in dedicated prototypes. In addition, SiMP detectors are a clear example in this sense.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

AR: conceptualization, formal analysis, software, writing–original draft, and writing–review and editing. NR: investigation, software, validation, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors would like to thank the LNGS computing center and Dr. C. Pellegrino at CNAF for providing the CPU required to run the simulations. The authors acknowledge the support of Dr. G. Rannucci and Prof. V. Caracciolo, in the discussion of the statistical models and for proofreading.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zyla PA, Barnett RM, Beringer J, Dahl O, Dwyer DA, Groom DE, et al. Review of particle physics. PTEP (2020) 2020(8):083C01. doi:10.1093/ptep/ptaa104

CrossRef Full Text | Google Scholar

2. SteigmanTurner GMS. Cosmological constraints on the properties of weakly interacting massive particles. Nucl Phys B (1985) 253:375–86. doi:10.1016/0550-3213(85)90537-1

CrossRef Full Text | Google Scholar

3. Bertone G, Silk DHJ. Particle dark matter: evidence, candidates and constraints. Phys Rept (2005) 405:279–390. doi:10.1016/j.physrep.2004.08.031

CrossRef Full Text | Google Scholar

4. Tait GBT. A new era in the search for dark matter. Nature (2018) 562(7725):51–6. doi:10.1038/s41586-018-0542-z

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ajaj R. Low radioactivity argon for dark matter and Rare event searches, in Proc XXIX Int Symp Lepton Photon Interactions High Energies — PoS(LeptonPhoton2019) 367 (2019), 084. doi:10.22323/1.367.0084

CrossRef Full Text | Google Scholar

6. Aalbers , Agostini F, Alfonsi M, Amaro FD, Amsler C, Aprile E. JCAP (2016) 11:017. doi:10.1088/1475-7516/2016/11/017

CrossRef Full Text

7. Aalbers J, Akerib DS, Akerlof CW, Al Musalhi A, Alder F, Alqahtani A, et al. First dark matter search results from the LUX-ZEPLIN (LZ) experiment. Phys Rev Lett (2023) 131:041002. doi:10.1103/PhysRevLett.131.041002

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro F, et al. Constraining the spin-Dependent WIMP-nucleon cross sections with XENON1T. Phys Rev Lett (2019) 122(14):141301. doi:10.1103/PhysRevLett.122.141301

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Meng Y, Wang Z, Tao Y, Abdukerim A, Bo Z, Chen W, et al. Dark matter search results from the PandaX-4T Commissioning run. Phys Rev Lett (2021) 127(26):261802. doi:10.1103/PhysRevLett.127.261802

PubMed Abstract | CrossRef Full Text | Google Scholar

10. LewinSmith JDPF. Review of mathematics, numerical factors, and corrections for dark matter experiments based on elastic nuclear recoil. Astropart Phys (1996) 6:87–112. doi:10.1016/S0927-6505(96)00047-3

CrossRef Full Text | Google Scholar

11. Ajaj R, Amaudruz PA, Araujo GR, Baldwin M, Batygov M, Beltran B, et al. Search for dark matter with a 231-day exposure of liquid argon using DEAP-3600 at SNOLAB. Phys Rev D (2019) 100:022004. doi:10.1103/PhysRevD.100.022004

CrossRef Full Text | Google Scholar

12. Agnes P, Albuquerque IFM, Alexander T, Alton A, Araujo G, Ave M, et al. DarkSide-50 532-day dark matter search with low-radioactivity argon. Phys Rev D (2018) 98:102006. doi:10.1103/PhysRevD.98.102006

CrossRef Full Text | Google Scholar

13. Agnes P, Albuquerque IFM, Alexander T, Alton A, Ave M, Back H, et al. Search for low-mass dark matter WIMPs with 12 ton-day exposure of DarkSide-50. Phys Rev D (2023) 107:063001. doi:10.1103/PhysRevD.107.063001

CrossRef Full Text | Google Scholar

14. Aprile E, Abe K, Agostini F, Ahmed Maouloud S, Althueser L, Andrieu B, et al. First dark matter search with nuclear recoils from the XENONnT experiment. Phys Rev Lett (2023) 131:041003. doi:10.1103/PhysRevLett.131.041003

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Aalseth CE, Acerbi F, Agnes P, Albuquerque IFM, Alexander T, Alici A, et al. DarkSide-20k: a 20 tonne two-phase LAr TPC for direct dark matter detection at LNGS. Eur Phys J Plus (2018) 133(3):131. doi:10.1140/epjp/i2018-11973-4

CrossRef Full Text | Google Scholar

16. D’Incecco M, Galbiati C, Giovanetti GK, Korga G, Li X, Mandarano A, et al. Development of a novel single-channel, 24 cm², SiPM-based, cryogenic Photodetector. IEEE Trans Nucl Sci (2018) 65(1):591–6. doi:10.1109/TNS.2017.2774779

CrossRef Full Text | Google Scholar

17. Razeto A, Acerbi F, Camillo V, Carlini M, Consiglio L, Flammini A, et al. Very large SiPM arrays with aggregated output. J Instrumentation (2022) 17(05):P05038. doi:10.1088/1748-0221/17/05/p05038

CrossRef Full Text | Google Scholar

18. Agnes P, Alexander T, Alton A, Arisaka K, Back H, Baldin B, et al. First results from the DarkSide-50 dark matter experiment at Laboratori Nazionali del Gran Sasso. Phys Lett B (2015) 743:456–66. doi:10.1016/j.physletb.2015.03.012

CrossRef Full Text | Google Scholar

19. Gola A, Acerbi F, Capasso M, Marcante M, Mazzi A, Paternoster G, et al. NUV-sensitive silicon Photomultiplier technologies developed at Fondazione Bruno Kessler. Sensors (2019) 19(2):308. doi:10.3390/s19020308

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zappalà G, Acerbi F, Ferri A, Gola A, Paternoster G, Regazzoni V, et al. Study of the photo-detection efficiency of FBK High-Density silicon photomultipliers. J Instrumentation (2016) 11(11):P11010. doi:10.1088/1748-0221/11/11/p11010

CrossRef Full Text | Google Scholar

21. Buzhan P, Dolgoshein B, Ilyin A. Advanced Technology and Particle Physics (2002). doi:10.1142/9789812776464_0101

CrossRef Full Text | Google Scholar

22. D’Incecco M, Galbiati C, Giovanetti GK, Korga G, Li X, Mandarano A, et al. Development of a very low-noise cryogenic Preamplifier for large-area SiPM devices. IEEE Trans Nucl Sci (2018) 65(4):1005–11. doi:10.1109/TNS.2018.2799325

CrossRef Full Text | Google Scholar

23. Piemonte C. A new Silicon Photomultiplier structure for blue light detection. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2006) 568(1):224–32. doi:10.1016/j.nima.2006.07.018

CrossRef Full Text | Google Scholar

24. Collazuol G, Bisogni M, Marcatili S, Piemonte C, Del Guerra A. Studies of silicon photomultipliers at cryogenic temperatures. Nucl Instrum Methods Phys Res A (2011) 628(1):389–92. doi:10.1016/j.nima.2010.07.008

CrossRef Full Text | Google Scholar

25. Boulay MG, Camillo V, Canci N, Choudhary S, Consiglio L, Flammini A, et al. Direct comparison of PEN and TPB wavelength shifters in a liquid argon detector. Eur Phys J C (2021) 81(12):1099. doi:10.1140/epjc/s10052-021-09870-7

CrossRef Full Text | Google Scholar

26. Acerbi F, Davini S, Ferri A, Galbiati C, Giovanetti G, Gola A, et al. Cryogenic Characterization of FBK HD near-UV sensitive SiPMs. IEEE Trans Elec Dev (2017) 64(2):521–6. doi:10.1109/TED.2016.2641586

CrossRef Full Text | Google Scholar

27. Boulay MG, Camillo V, Canci N, Choudhary S, Consiglio L, Flammini A, et al. SiPM cross-talk in liquid argon detectors. Front Phys (2023) 11. doi:10.3389/fphy.2023.1181400

CrossRef Full Text | Google Scholar

28. Mirzoyan R, KosyraMoser RHG. Light emission in Si avalanches. Nucl Instrum Methods Phys Res A (2009) 610(1):98–100. doi:10.1016/j.nima.2009.05.081

CrossRef Full Text | Google Scholar

29. Nepomuk Otte A. On the efficiency of photon emission during electrical breakdown in silicon. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2009) 610(1):105–9. doi:10.1016/j.nima.2009.05.085

CrossRef Full Text | Google Scholar

30. Nagai A, Alispach C, Berghöfer T, Bonanno G, Coco V, della Volpe D, et al. SENSE: a comparison of photon detection efficiency and optical crosstalk of various SiPM devices. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2018) 912:182–5. doi:10.1016/j.nima.2017.11.018

CrossRef Full Text | Google Scholar

31. McLaughlin JB, Gallina G, Retière F, De St. Croix A, Giampa P, Mahtab M, et al. Characterisation of SiPM photon emission in the dark. Sensors (2021) 21(17):5947. doi:10.3390/s21175947

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Vinogradov S, Vinogradova T, Shubin V. In: 2009 IEEE nuclear science Symposium Conference Record (NSS/MIC) (2009). p. 1496–500. doi:10.1109/NSSMIC.2009.5402300

CrossRef Full Text | Google Scholar

33. Gallego L, Rosado J, Arqueros FBF. Modeling crosstalk in silicon photomultipliers. J Instrumentation (2013) 8(05):P05010. doi:10.1088/1748-0221/8/05/p05010

CrossRef Full Text | Google Scholar

34. Wagenpfeil M, Ziegler T, Schneider J, Fieguth A, Murra M, Schulte D, et al. Reflectivity of VUV-sensitive silicon photomultipliers in liquid Xenon. J Instrumentation (2021) 16(08):P08002. doi:10.1088/1748-0221/16/08/P08002

CrossRef Full Text | Google Scholar

35. Guarise M, Andreotti M, Calabrese R, Cotta Ramusino A, Cicero V, Fiorini M, et al. A newly observed phenomenon in the characterisation of SiPM at cryogenic temperature. J Instrumentation (2021) 16(10):T10006. doi:10.1088/1748-0221/16/10/t10006

CrossRef Full Text | Google Scholar

36. Lippincott WH, Coakley KJ, Gastler D, Hime A, Kearns E, McKinsey DN, et al. Scintillation time dependence and pulse shape discrimination in liquid argon. Phys Rev C (2008) 78:035801. doi:10.1103/physrevc.78.035801

CrossRef Full Text | Google Scholar

37. Cao H, Alexander T, Aprahamian A, Avetisyan R, Back H, Cocco A, et al. Measurement of scintillation and ionization yield and scintillation pulse shape from nuclear recoils in liquid argon. Phys Rev D (2015) 91:092007. doi:10.1103/PhysRevD.91.092007

CrossRef Full Text | Google Scholar

38. Agnes P, Addendum. Phys Rev D 93(8), 081101 (2016). DOI doi:10.1103/PhysRevD.93.081101

CrossRef Full Text | Google Scholar

39. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro F, et al. Projected WIMP sensitivity of the XENONnT dark matter experiment. J Cosmology Astroparticle Phys (2020) 2020(11):031. doi:10.1088/1475-7516/2020/11/031

CrossRef Full Text | Google Scholar

40. Smith MC, Ruchti GR, Helmi A, Wyse RFG, Fulbright JP, Freeman KC, et al. The RAVE survey: constraining the local Galactic escape speed. Mon Not Roy Astron Soc (2007) 379:755–72. doi:10.1111/j.1365-2966.2007.11964.x

CrossRef Full Text | Google Scholar

41. Savage C, Gelmini G, Freese PGK. JCAP (2009) 04:010. doi:10.1088/1475-7516/2009/04/010

CrossRef Full Text

42. Savage C, FreeseGondolo KP. Annual modulation of dark matter in the presence of streams. Phys Rev D (2006) 74:043531. doi:10.1103/PhysRevD.74.043531

CrossRef Full Text | Google Scholar

43. Gibbons R, Chen H, Haselschwardt SJ, Xia Q, Sorensen P e-print: 2309 (2023) 07913. doi:10.48550/arXiv.2309.07913

CrossRef Full Text | Google Scholar