3D digital holographic polarimetry of diffuse optically anisotropic biological tissue object fields

The experimental validation of methods for the digital holographic 3D layer-by-layer reconstruction of complex amplitude distributions in different phase planes of diffuse biological tissue histological section microscopic images with a subsequent reconstruction of azimuth and ellipticity polarization maps is presented. Polarization dependencies of the integral and layer-by-layer vector structure of the laser object field azimuth and ellipticity distributions in two types of biological layer samples—the fibrous myocardium and parenchymal liver—have been investigated. Scenarios and dynamics of changes in the values of statistical moments of the first to fourth orders, which characterize the integral and layer-by-layer polarization maps of diffuse biological tissue histological section microscopic images with different morphological structures, have been determined. Criteria for selecting the polarization components of the object field that are formed by acts of scattering of different multiplicities have been identified. An example of biomedical application in cancer detection of biological tissues is provided.

1 Introduction

Optical methods for diagnosing various biological tissues and visualizing their optically anisotropic structure (fibrillar networks and optically active molecular domains) occupy a prominent place due to their high informativeness and the possibility of multifunctional monitoring of the investigated environment (photometric, spectral, polarization, and correlation monitoring) [1–5]. However, currently, there is a lack of a unified methodological approach to diagnose such structures.

Polarimetric research [6] has emerged as a distinct direction in the field of optical analysis of biological tissues. Analyzing the polarization characteristics of scattered radiation allows obtaining qualitatively new insights into the morphological and physiological states of biological tissues, including cataracts in the lens, glucose concentration in tissues of diabetic patients, and malignant changes [7–12].

A significant advancement in the field of biomedical polarimetric diagnostics has been the development of Mueller matrix techniques, leading to the establishment of Mueller matrix microscopy (MMM) as a separate branch [13–18].

This direction of optical diagnostics is based on the synthesis of instrumental Mueller matrix imaging polarimetry with various theoretical models and methods of analysis (regression model of optical anisotropy [14], logarithmic Mueller matrix decomposition [15–18], Monte Carlo simulation of polarized radiation conversion [17], and statistical analysis of Mueller matrix images and optical anisotropy maps [14, 18]).

The fundamental results obtained within MMM [18] of biological tissues are also promising for applied clinical and preclinical studies of the polycrystalline structure of biological tissues. In particular, on account of the possibility of obtaining quantitative optical metrics to characterize the evolution of gastric tissues from a healthy state through inflammation to cancer by Mueller microscopy of gastric biopsies, a regression model of optical anisotropy and statistical analysis of the obtained images has been demonstrated [14].

Parallel to this, methods and systems of laser polarimetry for biological tissue and liquid samples have been intensively developed, utilizing a wide range of analytical algorithms (statistical, correlation, fractal, wavelet, and Fourier) for quantitative data processing [19–29].

The main informational limitation to polarimetric mapping has been the dependence of experimental data on the degree of depolarization of the laser radiation, which not only integrates the polarization distributions but also compromises the unambiguous relationships between polarization-inhomogeneous object fields and parameters of polycrystalline soft matter layers [7–18]. Therefore, the creation of new, well-reproducible, and more accurate laser polarimetry methods remains highly relevant.

A significant achievement in this field was the successful integration of polarimetric and interferometric mapping methods, which led to the development of various directions of 3D polarimetry of biological objects and environments.

Polarization-sensitive optical coherence tomography (PSOCT) techniques have become promising in this direction. The basic principles and achievements of PSOCT of biological objects over the past 25 years have been consistently set out in a series of review articles [30–32]. This laser polarization–interference technique makes it possible not only to obtain layered images from small depths (up to 2 mm) of biological tissues [33, 34] but also provides the possibility of obtaining coordinate distributions of elements of the Jones and Mueller matrices and anisotropy maps. This was demonstrated most effectively in studies of transparent eye tissues [35–37].

Studies of layered polarization and matrix images of scattering (depolarizing) biological tissues of various morphological structures and physiological states have become an extension of the functionality of PSOCT [33]. In particular, it was possible to accurately diagnose fibrosis and differentiate tumor sites with low fibrosis [38]. However, the sensitivity of such systems was limited by the distorting effect on the contrast of polarizing images of layers of such tissues of a high level of depolarized laser speckle background. In addition, PSOCT systems are expensive, have insignificant (8 microns–10 microns) resolution, and do not provide the possibility of quantitative analysis of optical parameters of biological tissues, including benign and malignant tumors [30–38].

At the same time, these studies have demonstrated new possibilities for three-dimensional polarimetric biomedical differential diagnosis of diffuse samples of benign and malignant tumors in human organs.

Nevertheless, the results obtained still remain somewhat empirical. Currently, there is no information about the possibilities of this method for tissue samples with different optical thicknesses, morphological structures, and various pathologies. From a physical point of view, the task is to establish scientific significance—to establish algorithmic relationships between the structure of polycrystalline grids in biological tissues and the layered distribution of polarization parameters (azimuth and ellipticity) of the scattered object field.

On account of this, a promising task in polarimetric biomedical optics is the development of a universal polarimetric description of scenarios for the formation of optical fields in anisotropic polycrystalline biological layers. This description should cover a more general case—the detection and selection of polarimetric components of the laser field of an object with varying degrees of light scattering by digital holographic reconstruction and high-resolution phase scanning [39–42]. It is expected that the combination of polarimetric and interferometric methods will allow a new look at the morphological and optically anisotropic structure of diffuse layers in biological tissues with various architectural anisotropic polycrystalline components.

Our work is focused on the development and experimental verification of methods for three-dimensional polarization–interference digital holographic polarimetry of repeatedly scattered object fields of biological tissues with two boundary types of morphological architecture—spatially organized fibrous networks of the myocardium and disordered structures of the liver parenchyma. The aim is to investigate the potential of layered phase selection of holographically reconstructed variously scattered components of the polarization-inhomogeneous field of a diffuse biological layer.

2 A brief theory

In this section of the article, we will briefly consider (without compromising the completeness of the analysis) the main theoretical relationships within the framework of the phase anisotropy approximation (linear $LB$ and circular $CB$ birefringence). These relationships describe the processes of forming polarization structures of singly and multiply scattered laser field components in the biological tissue diffuse layer.

2.1 Stokes polarimetry of the object field

The diffuse layer of the biological tissue is illuminated with a linearly polarized beam with an azimuth angle ${\alpha }_{0,}$ and the Stokes vector of the beam is given by the following equation [1, 6].

$S^0=\left(\begin{array}{c}1\\ \mathit{cos}2{\alpha }_0\\ \mathit{sin}2{\alpha }_0\\ 0\end{array}\right)(1)$

2.1.1 “Single interaction”

To each ($l=1$) optical anisotropic ($∆n$ and $∆\mu$—linear and circular birefringence indices, respectively) inhomogeneity with a geometric size $d$ and spatial orientation of the optical axis $\rho$ in the volume of a biological tissue sample, we associate a Mueller matrix operator.

${\left\{F\right\}}_l={\left(\begin{array}{ccc}{f}_{11}\left(\rho ;\delta ;\xi \right)& \cdots & f_{14}\left(\rho ;\delta ;\xi \right)\\ ⋮& \ddots & ⋮\\ f_{41}\left(\rho ;\delta ;\xi \right)& \cdots & f_{44}\left(\rho ;\delta ;\xi \right)\end{array}\right)}_l(2)$

where $f_{ik}$ is the set of matrix elements, $\delta =\left(\raisebox{1ex}{$2\pi $}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.\right)\Delta nd$, and $\xi =\left(\raisebox{1ex}{$2\pi $}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.\right)\Delta \mu d$ is the phase shift of linear $LB$ and circular $CB$ birefringence [11].

The process of local ($l=1$) single transformation of the polarization structure of the probing beam $S^0$ is described by the following matrix equation:

$S_{l=1}^{⨀}={\left\{F\right\}}_{l=1}{S}^0(3)$

Here, $⨀$ represents single scattering.

As a result, a partial laser wave is formed with the following azimuth ${\alpha }_{l=1}^{⨀}$ and ellipticity ${\beta }_{l=1}^{⨀}$ of polarization.

${\alpha }_{l=1}^{⨀}=0.5\mathit{arctan}\left(\raisebox{1ex}{$S_{3;l=1}^{⨀}$}\!\left/ \!\raisebox{-1ex}{$S_{2;l=1}^{⨀}$}\right.\right)(4)$

${\beta }_{l=1}^{⨀}=0.5arcin\left(\raisebox{1ex}{$S_{4;l=1}^{⨀}$}\!\left/ \!\raisebox{-1ex}{$S_{1;l=1}^{⨀}$}\right.\right)(5)$

Here, $S_{t=1;2;3;4}^{⨀}$ represents the parameters of the Stokes vector of a singly scattered ($l=1$) laser beam.

Thus, the singly scattered component of the object field of a diffuse biological layer is a polarization distribution of azimuths $A_{l=1}\left({\alpha }_{l=1}^{⨀}\right)$ and ellipticities $B_{l=1}\left({\beta }_{l=1}^{⨀}\right)$.

2.1.2 “n-fold” interaction

For a set of acts with different multiplicities $l=1,\dots ,n$ of interaction with the linearly polarized laser probe $S^0$, matrix Eq. 3 takes the following form:

$S_{l=1,\dots ,n}^{⨂}={\left\{F\right\}}_n{{\left\{F\right\}}_{n-1}\dots {\left\{F\right\}}_2{\left\{F\right\}}_{1}S}^0(6)$

Here, $⨂$ represents multiple scattering.

This optical scenario leads to the formation of the following random values of azimuth ${\alpha }_{l=1,\dots ,n}^{⨂}$ and ellipticity of polarization ${\beta }_{l=1,\dots ,n}^{⨂}$ at each point of the $n-$ times scattered object field.

${\alpha }_{l=1,\dots ,n}^{⨂}=0.5\mathit{arctan}\left(\raisebox{1ex}{$\sum _{l=1}^n{S}_{3;l}^{⨂}$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1}^n{S}_{2;l}^{⨂}$}\right.\right)(7)$

${\beta }_{l=1,\dots ,n}^{⨂}=0.5\mathit{arcsin}\left(\raisebox{1ex}{$\sum _{l=1}^n{S}_{4;l}^{⨂}$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1}^n{S}_{1;l}^{⨂}$}\right.\right)(8)$

As a result, a polarimetrically inhomogeneous component of the diffuse field is formed with different distributions of azimuth values ${\alpha }_{l=1,\dots ,n}^{⨂}$ and ellipticity values ${\beta }_{l=1,\dots ,n}^{⨂}$ of polarization. The probabilities of the realization of various multiplicities ($l=1,...,n$) of the light scattering of the probing laser beam in the volume of the diffuse layer of biological tissue are denoted $\left.A_l{\left(\alpha \right.}_l^{⨂}\right)$ and $\left.B_l{\left(\alpha \right.}_l^{⨂}\right)$.

Thus, the polarization structure of the multiply scattered laser field by a diffuse biological object can be represented as a next superposition.

$A_1\left({\alpha }_1^{⨀}\right)+A_2\left({\alpha }_2^{⨂}\right)+\dots +A_{n-1}\left({\alpha }_{n-1}^{⨂}\right)+A_n\left({\alpha }_n^{⨂}\right)=\sum _{l=1}^n\left.A_l{\left(\alpha \right.}_l^{⨂}\right)(9)$

$B_1\left({\beta }_1^{⨀}\right)+B_2\left({\beta }_2^{⨂}\right)+\dots +B_{n-1}\left({\beta }_{n-1}^{⨂}\right)+B_n\left({\beta }_n^{⨂}\right)=\sum _{l=1}^n\left.B_l{\left(\alpha \right.}_l^{⨂}\right)(10)$

The obtained expressions (1)–(10) are widely used within the framework of traditional polarimetry (or Stokes polarimetry) of the intensities of the biological objects' field.

On the other hand, the coherence of laser radiation enables a different (amplitude) analytical description of the processes forming the polarization structure of the object field in a diffuse biological layer.

2.1.3 Amplitude consideration

For coherent laser fields, there is a direct relationship between the parameters of the Stokes vector and the orthogonal components ($E_{x,l=1}^{⨀}$ and $E_{y,l=1}^{⨀}$) of complex amplitudes [27, 28, 39].

Based on this, the previously obtained expressions (4) and (5) for the polarization parameters can be rewritten as follows:

${\alpha }_{l=1}^{⨀}=0.5\mathit{arctan}\left(\raisebox{1ex}{$\left(E_{x,l=1}^{⨀}{\left(E_{y,l=1}^{⨀}\right)}^{\ast }+{\left(E_{x,l=1}^{⨀}\right)}^{\ast }{E}_{y,l=1}^{⨀}\right)$}\!\left/ \!\raisebox{-1ex}{$\left(E_{x,l=1}^{⨀}{\left(E_{x,l=1}^{⨀}\right)}^{\ast }-{E_{y,l=1}^{⨀}\left(E_{y,l=1}^{⨀}\right)}^{\ast }\right)$}\right.\right);(11)$

${\beta }_{l=1}^{⨀}=0.5arcin\left(\raisebox{1ex}{$j\left(E_{x,l=1}^{⨀}{\left(E_{y,l=1}^{⨀}\right)}^{\ast }-{\left(E_{x,l=1}^{⨀}\right)}^{\ast }{E}_{y,l=1}^{⨀}\right)$}\!\left/ \!\raisebox{-1ex}{$\left(E_{x,l=1}^{⨀}{\left(E_{x,l=1}^{⨀}\right)}^{\ast }-{E_{y,l=1}^{⨀}\left(E_{y,l=1}^{⨀}\right)}^{\ast }\right)$}\right.\right)(12)$

Here, $\ast$ is complex coupling and $j=\sqrt{-1}$.

In parallel with this scenario, another process occurs—the interference addition of differently polarized partial coherent waves, leading to the formation of another polarimetrically inhomogeneous component in the diffuse object field.

2.1.4 Interference interaction

For the orthogonal components $E_{x,l=1}^{⨀}$ and $E_{y,l=1}^{⨀}$ of the complex amplitudes of two ($q=1$ and $q=2$) partial singly scattered ($⨀$) coherent waves ${\left(E_{l=1}^{⨀}\right)}_{q=1}$ and ${\left(E_{l=1}^{⨀}\right)}_{q=2}$ at a local point of the object field, the following interference equations can be written.

${\left(E_{x,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}=\left({\left(E_{x,l=1}^{⨀}\right)}_{q=1}+{\left(E_{x,l=1}^{⨀}\right)}_{q=2}\right)=$

$=\left(\left|{\left(E_{x,l=1}^{⨀}\right)}_{q=1}\right|+\left|{\left(E_{x,l=1}^{⨀}\right)}_{q=2}\right|+2\sqrt{\left|{\left(E_{x,l=1}^{⨀}\right)}_{q=1}\right|\left|{\left(E_{x,l=1}^{⨀}\right)}_{q=2}\right|}\mathit{cos}{\left({\phi }_{x,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}\right);(13)$

${\left(E_{y,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}=\left({\left(E_{y,l=1}^{⨀}\right)}_{q=1}+{\left(E_{y,l=1}^{⨀}\right)}_{q=2}\right)=$

$=\left(\left|{\left(E_{y,l=1}^{⨀}\right)}_{q=1}\right|+\left|{\left(E_{y,l=1}^{⨀}\right)}_{q=2}\right|+2\sqrt{\left|{\left(E_{y,l=1}^{⨀}\right)}_{q=1}\right|\left|{\left(E_{y,l=1}^{⨀}\right)}_{q=2}\right|}\mathit{sin}{\left({\phi }_{y,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}\right)(14)$

Here, $\left|{\left(E_{x,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}\right|;\left|{\left(E_{y,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}\right|$—modules of complex amplitudes; ${\left({\phi }_{x,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}$ and ${\left({\phi }_{y,l=1}^{⨀}\right)}_{q=\mathrm{1,2}}$—phase shifts between ($\left.{\left(E_{x,l=1}^{⨀}\right)}_{q=1};{\left(E_{x,l=1}^{⨀}\right)}_{q=2}\right)$ and $\left.{\left(E_{y,l=1}^{⨀}\right)}_{q=1};{\left(E_{y,l=1}^{⨀}\right)}_{q=2}\right)$, respectively.

For the process of forming the orthogonal components of amplitudes $E_{x,l=1,\dots ,n}^{⨂}$ and $E_{y,l=1,\dots ,n}^{⨂}$ through $l=1,\dots ,n-$ fold interaction ($⨂$) of the laser probe with optical inhomogeneities, the following expressions can be written $\sum _{l=1}^n{E}_{x,l}^{⨂}$; $\sum _{l=1}^n{E}_{y,l}^{⨂}$; and $\left(\sum _{l=1}^n{\phi }_{x,l}^{⨂}-\sum _{l=1}^n{\phi }_{y,l}^{⨂}\right)$.

The interference addition of two orthogonal components $E_{x,l=1,\dots ,n}^{⨂}$ and $E_{y,l=1,\dots ,n}^{⨂}$ results in the formation of an elliptically polarized wave [40, 41]

$\frac{X^2}{{\left(\sum _{l=1}^n{E}_{x,l}^{⨂}\right)}^2}+\frac{Y^2}{{\left(\sum _{l=1}^n{E}_{y,l}^{⨂}\right)}^2}-\frac{2XY}{\left(\sum _{l=1}^n{E}_{x,l}^{⨂}\right)\left(\sum _{l=1}^n{E}_{y,l}^{⨂}\right)}\cos \left(\sum _{l=1}^n{\phi }_{x,l}^{⨂}-\sum _{l=1}^n{\phi }_{y,l}^{⨂}\right)=$

$={\mathit{sin}}^2\left(\sum _{l=1}^n{\phi }_{x,l}^{⨂}-\sum _{l=1}^n{\phi }_{y,l}^{⨂}\right)(15)$

with the following “interference” ($I$) values of azimuth ${\alpha \left(I\right)}_l$ and ellipticity ${\beta \left(I\right)}_l$:

${\alpha \left(I\right)}_l=0.5\mathit{arcsin}\left(\mathit{sin}2\left(\frac{{\sum }_{l=1}^n{E}_{y,l}^{⨂}}{{\sum }_{l=1}^n{E}_{x,l}^{⨂}}\right)/\sqrt{1+{{\mathit{tan}}^2{\phi }_{xyl}\mathit{cos}}^{2}2\left(\frac{{\sum }_{l=1}^n{E}_{y,l}^{⨂}}{{\sum }_{l=1}^n{E}_{x,l}^{⨂}}\right)}\right);(16)$

${\beta \left(I\right)}_l=0.5\mathit{arctan}\left(\mathit{tan}{\phi }_{xyl}\mathit{sin}2\left(\frac{\sum _{l=1}^n{E}_{y,l}^{⨂}}{{\displaystyle \sum _{l=1}^n}{E}_{x,l}^{⨂}}\right)/\sqrt{1+{{\mathit{tan}}^2{\phi }_{xyl}\mathit{cos}}^{2}2\left(\frac{{\displaystyle \sum _{l=1}^n}{E}_{y,l}^{⨂}}{{\displaystyle \sum _{l=1}^n}{E}_{x,l}^{⨂}}\right)}\right)(17)$

The probability of polarization parameters ${\alpha \left(I\right)}_l$ and ${\beta \left(I\right)}_l$ for different multiplicities ($l=1,\dots ,n$) of the secondary interference of the partial waves of laser radiation in the volume of the diffuse layer of biological tkanin denotes, respectively, $\left.C_l{\left(\alpha \left(I\right)\right.}_l\right)$ and $D_l\left({\beta \left(I\right)}_l\right)$.

As we can see, the secondary interference of differently polarized coherent partial waves also leads to the formation of a polarimetrically inhomogeneous component [expressed in relationships (16), (17)] of the object field in the diffuse biological layer$—\sum _{l=1}^n\left.C_l{\left(\alpha \left(I\right)\right.}_l\right)$ and $\sum _{l=1}^n{D}_l\left({\beta \left(I\right)}_l\right)$.

2.1.5 The resulting field

Thus, the object laser field in the biological tissues diffuse layers can be considered a superposition of the following polarimetric components:

$R_l\left({\alpha }_l,{\beta }_l\right)=\sum _{l=1}^n{A}_l\left({\alpha }_l^{⨂}\right)+\sum _{l=1}^n{B}_l\left({\beta }_l^{⨂}\right)+\sum _{l=1}^n{C}_l\left({\alpha \left(I\right)}_l\right)+\sum _{l=1}^n{D}_l\left({\beta \left(I\right)}_l\right).(18)$

3 The experimental setup and measurement methodology

A generalization of the polarization interferometry scheme [39, 40] is the Stokes-polarimetric mapping scheme on the base of the Mach–Zehnder interferometer, which is shown in Figure 1.

FIGURE 1

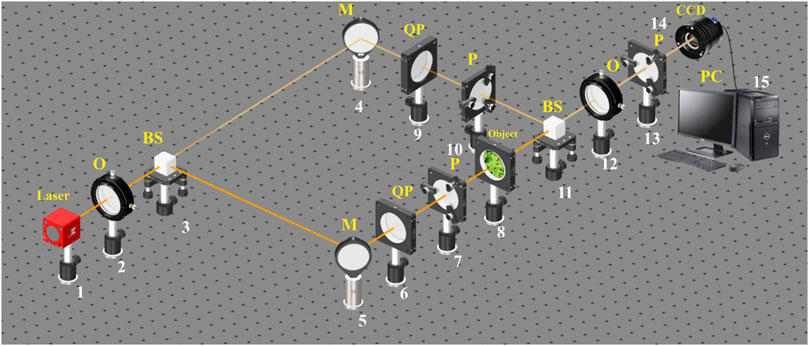
FIGURE 1. Optical scheme for polarization–interference mapping of the Stokes vector parameters. 1—He–Ne laser; 2—collimator—“O”; 3,11—beam splitters—“BS”; 4,5—mirrors—“M”; 6,9—quarter-wave plates—“QP”; 7,10,13—polarizers—“P”; 8—object; 12—polarization objective—“O”; 14—digital camera—“CCD”; 15—personal computer—“PC”.

The parallel ($Ø=2\times 10^3\mu m$) beam of He–Ne ($\lambda =0.6328\mu m$) laser 1 formed by spatial-frequency filter 2, with 50% beam splitter 3, is divided into “object” and “reference” ones.

The “object” beam with the help of a rotating mirror 5 is directed through the polarizing filters 6–7 in the direction of the biological layer 8 sample. The biological tissue histological Section 8 polarization-inhomogeneous image is projected by strain-free objective 12 into the plane of digital camera 14.

The “reference” beam is directed by mirror 4 through the polarization filters 9–10 into the biological tissue histological Section 8 polarization-inhomogeneous image plane.

As a result, an interference pattern is formed, the coordinate intensity distribution of which is recorded by a digital camera 14 through a polarizer 13.

To study the dependence of the diffuse biological tissue object field polarization structure on the incident radiation polarization state, plane-polarized illuminating and reference beams with different azimuths ${\alpha }_0=\begin{array}{ccc}{0}^0;& {45}^0;& {90}^0\end{array}$ are formed using the polarization filters 6–7 and 9–10, respectively

Before carrying out measurements of biological tissues, the experimental device passed metrological certification with the introduction of model objects (“clean air,” “linear polarizer,” “phase plates $0.25\lambda$,” and “$0.5\lambda$”). As a result of a 50 measurement series for each object, the polarization ellipticity errors were determined $\beta =0.0003rad$.

The methodology for determining the layer-by-layer measurement of the object field Stokes vector parameter (polarization maps $\alpha \left(m,n\right)$ and $\beta \left(m,n\right)$) distributions using complex amplitude $E_x$ and $E_y$ digital holographic reconstruction, followed by phase scanning ${\theta }_k$ of such a field, is presented in 39–41. However, detailed information is not provided in this work. For a better understanding of the further discussion, we will provide a brief overview of the 3D digital holographic scanning method.

4 The method of 3D polarimetry phase scanning of the object field

1. Three states of linear polarization are sequentially formed in the “irradiating” ($Ir$) and “reference” ($Re$) parallel laser beams$—Ir\left({\alpha }_0=\begin{array}{ccc}{0}^0;& {45}^0;& {90}^0\end{array}\right)-Re\left({\alpha }_0=\begin{array}{ccc}{0}^0;& {45}^0;& {90}^0\end{array}\right)$.

2. For each of the polarization states (${\alpha }_0$), two partial interference patterns are recorded through polarizer–analyzer 13 with the orientation of the transmission plane at angles $\begin{array}{cc}\mathrm{\Omega }=0^0;& \mathrm{\Omega }=90^0\end{array}$.

3. Analytical processing of microscopic interference images of biological samples was carried out using the digital Fourier transform $FT\left(\upsilon ,\nu \right)$ [26]

${FT}_{x;y}\left(\mathrm{\Omega }=0^0;90^0\right)\left(\upsilon ,\nu \right)=\frac{1}{M\times N}\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}{I}_{x,y}\left(\mathrm{\Omega }=0^0;90^0\right)\left(m,n\right)\mathit{exp}\left[-j2\pi \left(\frac{m\times \upsilon }{M}+\frac{n\times \nu }{N}\right)\right](19)$

where $\left\{\begin{array}{c}{I}_x^{{\alpha }_0}\left(\mathrm{\Omega }=0^0\right)\left(m,n\right)=E_{x,l}^{{\alpha }_0,⨂}\left(m,n\right){\left(E_{x,l}^{{\alpha }_0,⨂}\right)}^{\ast }\left(m,n\right);\\ I_y^{{\alpha }_0}\left(\mathrm{\Omega }={90}^0\right)\left(m,n\right)=E_{y,l}^{{\alpha }_0,⨂}\left(m,n\right){\left(E_{y,l}^{{\alpha }_0,⨂}\right)}^{\ast }\left(m,n\right);\end{array}\right.$ $E_{x,y,l}^{{\alpha }_0,⨂}$ are the orthogonal components of complex amplitude for different orientation $\begin{array}{cc}\mathrm{\Omega }=0^0;& \mathrm{\Omega }=90^0\end{array}$; $*$denotes the complex conjugation operation; $\left(\upsilon ,\nu \right)$ are the spatial frequencies, and $\left(m=1120,n=960\right)$ are the quantity of pixels of the CCD camera.

4. The results of the digital Fourier transform [relations (19)] are used to obtain distributions of complex amplitudes, according to the following algorithms:

$E_{0^0}\to \left|E_{x,l}^{{\alpha }_0,⨂}\left(\mathrm{\Omega }=0^0\right)\right|(20)$

$E_{90^0}\to \left|E_{y,l}^{{\alpha }_0,⨂}\left(\mathrm{\Omega }=90^0\right)\right|\mathit{exp}\left(i\left({\phi }_y^{{\alpha }_0}-{\phi }_x^{{\alpha }_0}\right)\right)(21)$

5. By means of stepwise ($\Delta \theta$) phase ($\theta$) scanning of the reconstructed field of complex amplitudes [relations (20), (21)] using algorithms (11)–(12), we obtain coordinate distributions of the polarization parameters $\alpha \left(\theta ,m,n\right)$ and $\beta \left(\theta ,m,n\right)$.

6. Distributions (20) and (21) are layered distributions of complex amplitudes and corresponding polarization maps $\alpha \left(\theta ,m,n\right)$ and $\beta \left(\theta ,m,n\right)$ of variously scattered components of the object field, respectively. Such phase-layered components correspond to different depths of the histological section of biological tissue. This is the meaning of layered digital holographic polarimetry of object fields of histological sections of biological tissues.

5 Statistical analysis of polarization maps

The morphological structure of optically anisotropic architectonics of various types of biological tissues is statistical and rather complex. This complexity is due to the presence in the volume of biological tissue of diverse scattering optical centers (cells, nuclei, and fibrils). The different spatial organization of such centers causes the formation of no less complex distributions of birefringence parameters and dichroism networks of biological crystals [1–12].

As a result of the passage of optical radiation through such spatially inhomogeneous structures, polarization maps with statistically distributed values of azimuth and ellipticity of polarization are formed [20, 21]. One of the most common quantitative methods for evaluating such maps is the calculation of a set of central statistical moments of first to fourth orders, which most fully characterize the histograms of polarization distributions.

Each of these moments provides different statistical information about the distributions (or changes) of the optical anisotropy parameters of the architectonics of biological tissues and the corresponding polarization maps. In other words, the first statistical moment characterizes the mean of the statistically distributed ensemble of random variables of birefringence and dichroism of the architectonics of biological tissue, as well as the azimuth and ellipticity of the polarization of the object field. The second central statistical moment determines the magnitude of the variance of fluctuations in the parameters of optical anisotropy and polarization states. Higher-order statistical moments characterize the asymmetry and kurtosis of probability distributions and turn out to be the most sensitive to “morphological” and “pathological” variations of optically anisotropic architectonics and polarization-inhomogeneous object fields [23–28].

This approach is universal and objective for assessing the probability distributions of optical and polarization distributions for a wide range of biological tissues, regardless of their morphological structure and physiological state.

The resulting set of polarization maps $p\equiv \left\{\begin{array}{c}\alpha \left(\theta ,m,n\right);\\ \beta \left(\theta ,m,n\right)\end{array}\right.$ was analyzed in a statistical approach using the following algorithms to calculate mean ($Z_1$), variance ($Z_2$), skewness ($Z_3$), and kurtosis ($Z_4$) [6]:

$\begin{array}{c}{Z}_1=\frac{1}{K}\sum _{j=1}^K{p}_j;\\ Z_2=\sqrt{\frac{1}{K}\sum _{j=1}^K{\left(p^2\right)}_j;}\\ Z_3=\frac{1}{Z_2^3}\frac{1}{K}\sum _{j=1}^K{\left(p^3\right)}_j;\\ Z_4=\frac{1}{Z_2^4}\frac{1}{K}\sum _{j=1}^K{\left(p^4\right)}_j,\end{array}(23)$

where $K$ represents CCD pixel quantity.

6 Objects of investigations

Our choice of research objects is based on the generalization of the following analytical and applied aspects that have been achieved in polarimetric studies of biological tissues:

• The optical properties of a layer of any biological tissue can be represented as a two-component “amorphous polycrystalline” matrix [2–7].

• The polarization properties of the architectonics of the polycrystalline component of biological tissue are formed by structural (dendritic, spatially supramolecular fibrillary networks of proteins) and chiral (clusters of optically active molecular domains) anisotropies.

The architectonics of real biological tissue simultaneously possess both structural (linear birefringence and dichroism) and chiral (circular birefringence and dichroism) anisotropies.

The processes of interaction of optical radiation with such ensembles of biological crystals and the formation of a set of polarization maps of the object field are described most fully and universally within the framework of the Mueller matrix formalism [8–10, 23–28].

Statistical parameters of azimuth and ellipticity maps of polarization are interrelated with the features of structural and chiral anisotropies of biological tissues.

Therefore, both analytical and experimental detailing of such interrelations by means of polarization study of some “boundary structures” of optically anisotropic architectonics of biological crystals turn out to be actual fundamental and applied tasks.

From a fundamental point of view, among the variety of architectonics of biological tissues, two “marginal” cases of polarization manifestations of structural and chiral anisotropies can be distinguished:

• Structural anisotropy of fibrillar tissues—spatially ordered networks of myocardial myosin fibrils.

• Chiral anisotropy of parenchymal tissues—clusters of optically active parenchymal molecules of biological tissues (in our case, the liver).

The obtained statistical characteristics of the corresponding polarization maps can also be used in applied detection studies within the framework of the universal Mueller matrix formalism of pathological changes in optical anisotropy of the widest class of biological tissues of human organs.

Morphologically, the myocardium is formed by well-organized myosin fibrous networks, while the liver’s structure consists of spatially disordered island-like clusters (Langerhans islets).

Optically, these biological tissues possess both common and distinct properties.

Common features—each layer of the mentioned biological tissues represents a two-component isotropic–anisotropic matrix [6].

The anisotropic component performs phase modulation ${\delta }_p$ and ${\xi }_p$ between the orthogonal components of the laser radiation amplitude propagating in the soft matter volume.

Distinct features—fibrous networks create a so-called structural anisotropy, resulting in the formation of linear birefringence ($LB$). This leads to the generation of an ensemble of polarized waves with individual azimuth and ellipticity values [expressed in relationships (4),(5),(7), and (8)]. For parenchymal structures, circular birefringence ($CB$) predominates, which forms coordinate-distributed regions of the laser field with different azimuth values of polarization [27, 28].

Histological sections were prepared using the conventional technique on a microtome with rapid freezing [6].

The optical geometric parameters of the histological section samples are presented in Table 1.

TABLE 1

TABLE 1. Optical geometric parameters of biological tissue samples.

The extinction coefficient ($\tau ,c{m}^{-1}$) of the biological tissues samples was measured according to the standard photometry method of the illuminating beam intensity attenuation of the sample [43, 44] using an integral light-scattering sphere [45].

The value of the integral degree of depolarization ($\mathrm{\Lambda },\%$) of the myocardium and liver samples was measured in the scheme of a standard Mueller matrix polarimeter [6, 28].

7 Experimental results and discussion

This part of the article contains a sequential presentation of research materials on the integral and layered statistical and polarization-inhomogeneous structure of diffuse biological tissue object field azimuths $\alpha \left(m,n\right)$ and ellipticity $\beta \left(m,n\right)$ polarization maps.

7.1 Myocardium histological section object field polarization azimuth maps

Figure 2 shows a series of fragments depicting integral maps of polarization azimuth [(1)–(3)] and histograms [(4)–(6)] representing the distributions of polarization azimuth values in microscopic images of the myocardial sample. Multi-channel irradiation was utilized with linearly polarized laser beams ${\alpha }_0=0^0$—fragments (1), (4); ${\alpha }_0={45}^0$—fragments (2), (5); and ${\alpha }_0={90}^0$—fragments (3), (6). From the analysis of the obtained results, it was observed that the polarization azimuth maps of the microscopic images in the diffuse histological section of the myocardium exhibit both coordinate and individual structural variations for each $\alpha \left({\alpha }_0,m\times n\right)$—[(1)–(3)].

FIGURE 2

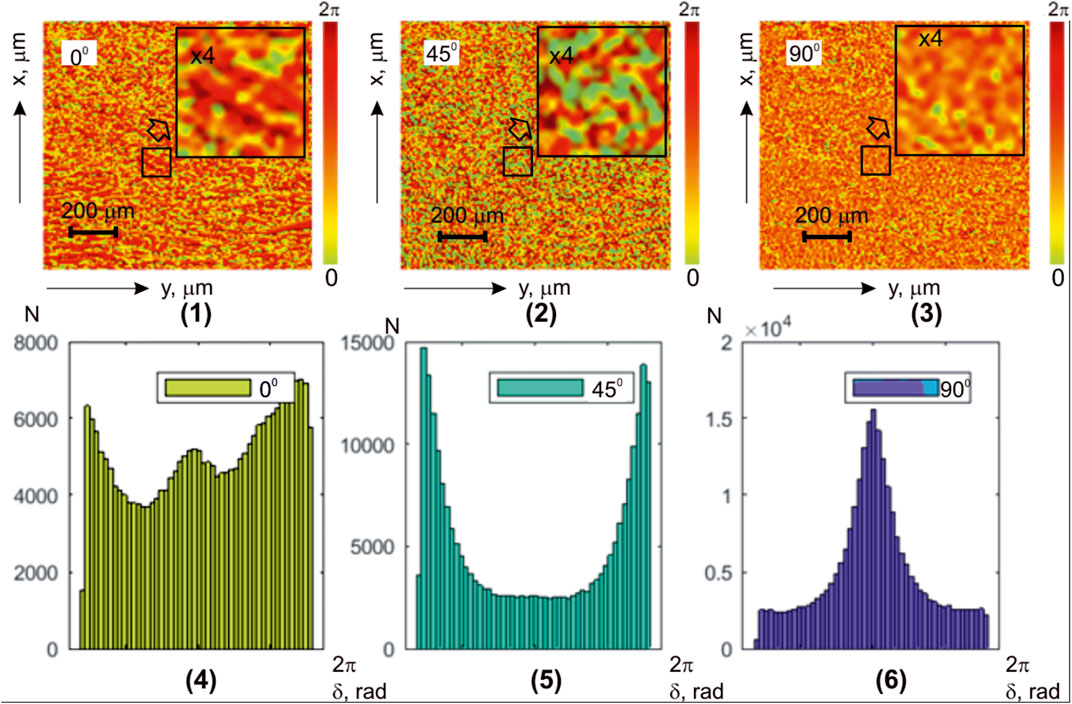
FIGURE 2. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the myocardium histological section microscopic image polarization azimuth maps.

Experimentally measured histograms $G\left(\alpha ,{\alpha }_0\right)$ representing the distribution of azimuth polarization values are found to be asymmetric with significant ranges of azimuth polarization variation—[(4)–(6)].

The quantitative statistical structure of the polarization maps $\alpha \left({\alpha }_0,m\times n\right)$ is characterized by a set of statistical moments of the first to fourth order denoted as $Z_{g=\mathrm{1,2,3,4}}$ (as shown in Eq. 23). The values of these statistical moments are provided in Table 2.

TABLE 2

TABLE 2. Statistical parameters of the myocardium histological section microscopic image polarization azimuth maps.

The comparison of the results from the statistical analysis of the integral azimuth polarization maps $\alpha \left({\alpha }_0,m\times n\right)$ revealed a deviation of all coordinate polarization distributions from normal or Gaussian—all statistical moments $Z_{g=\mathrm{1,2,3,4}}\ne 0$. Variations in the magnitude (from two to seven times) of all statistical moments $Z_{g=\mathrm{1,2,3,4}}$ were observed depending on the changes in the polarization state of the incident laser beam.

From a physical point of view, the obtained results can be attributed to the simultaneous influence of the following two factors:

1. Object-related: It arises due to the complex orientation (${\rho }_p$) structure of multi-scale ($d$) myocardial fibrous networks, which forms spatial phase distributions ${\delta }_p$. As a result of single and multiple interactions of laser radiation with such a polycrystalline component, an “object” polarization-inhomogeneous component (Eqs 4–10) emerges in the laser field. When the azimuth polarization ${\alpha }_0$ of the incident beam changes, the distribution of angles ${{\alpha }_0\pm \rho }_p\left(m,n\right)$ transforms, resulting in the formation of individual topographic maps $\alpha \left({\alpha }_0,m\times n\right)$.

2. Field-related: It is caused by the secondary interference of differently polarized partial laser waves, formed by optically anisotropic fibrous networks. As a consequence, an additional polarization-inhomogeneous “diffuse” component of the object’s laser radiation is formed (Eqs 11–16).

One of the challenges in solving inverse problems in diagnosing the polycrystalline structure of diffuse biological layers is to achieve conditions where the contribution of multiple scattering events to the formation of the vector structure of the object field is minimized.

One of the methods developed for this purpose is the phase scanning technique of holographically reconstructed distributions of complex amplitudes of laser radiation (Eqs 19–21).

The results of phase scanning and reconstruction of layered maps $\alpha \left(\theta ,m\times n\right)$ for $\theta =\pi /6$ and $\theta =\pi /8$ are presented in Figures 3, 4, respectively. A comparative analysis of the layered maps of the azimuth of polarization, reconstructed using the phase scanning method with digital holographic reconstruction of layered distributions of complex amplitudes of partially depolarizing optically thick histological sections of the myocardium, revealed that for all investigated phase planes ${\theta }_i$, the maps $\alpha \left({\theta }_i,m\times n\right)$ exhibit individual spatial heterogeneity, which depends on the changes in the polarization states of the incident laser beam ${\alpha }_0$—see Figures 3, 4, fragments (1)–(3) and (7)–(9).

FIGURE 3

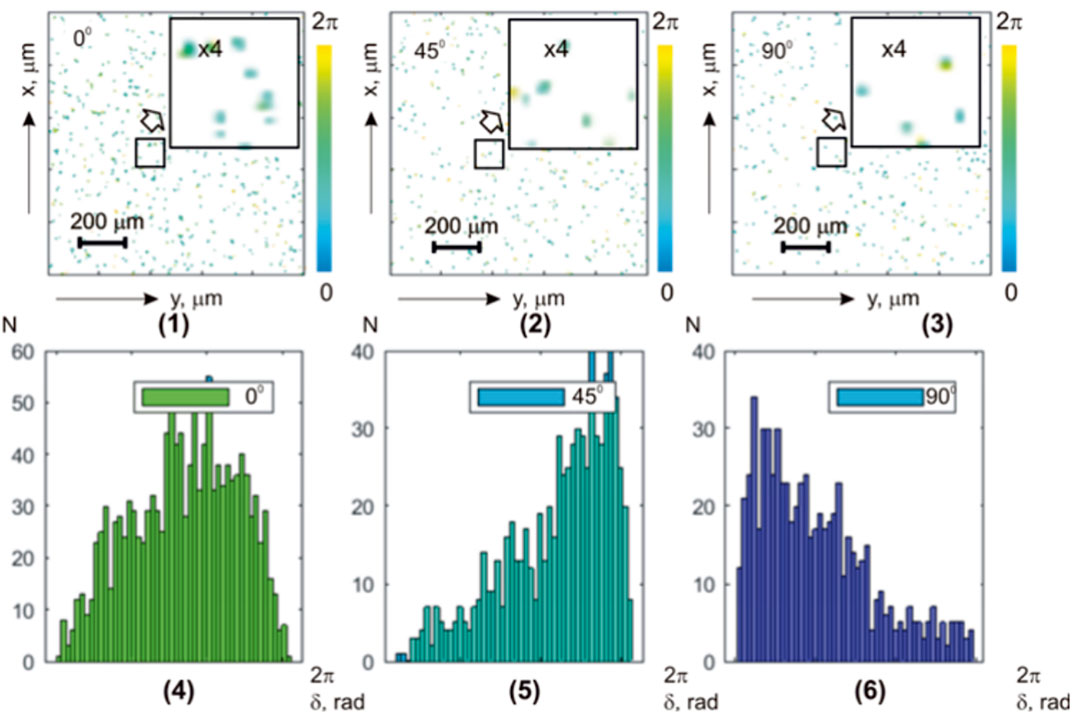
FIGURE 3. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the myocardium histological section microscopic image polarization azimuth maps in the phase plane $\theta =\pi /6$.

FIGURE 4

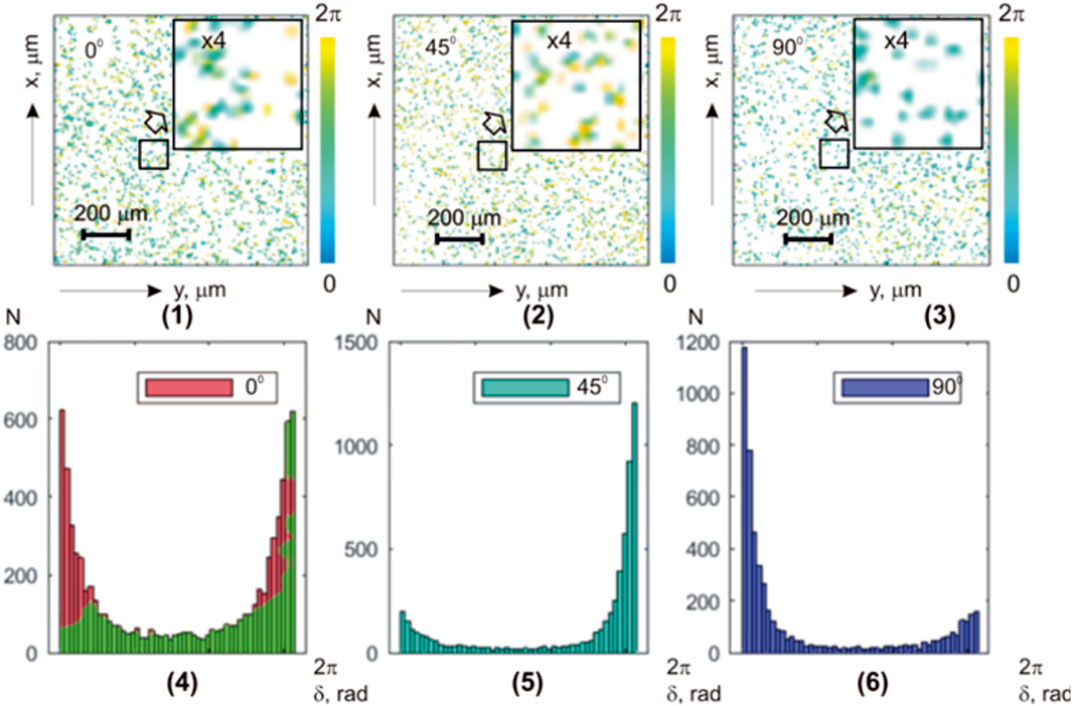
FIGURE 4. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the myocardium histological section microscopic image polarization azimuth maps in the phase plane $\theta =\pi /8$.

Table 3 presents the data on the statistical analysis of the layered maps of the azimuth of polarization in different phase planes of the myocardium histological section microscopic images.

TABLE 3

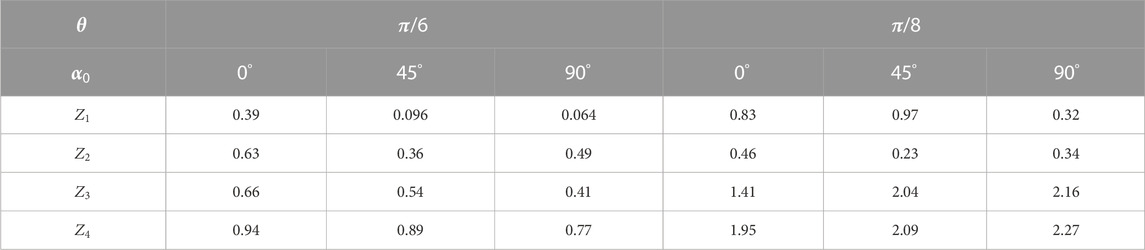
TABLE 3. Statistical parameters of the myocardium histological section microscopic image polarization azimuth maps.

It has been found that with a decrease in the value of $\theta$, there is a successive reduction (by 2–3 times) of the dispersion $Z_2\left(\theta ;\alpha \right)$, which represents the spread of random values of the azimuth of polarization in the phase planes of the object field.

On the contrary, higher-order statistical moments that characterize the asymmetry $Z_3\left(\theta ;\alpha \right)$ and kurtosis $Z_4\left(\theta ;\alpha \right)$ of the distributions $\sum _{l=1}^n\left.A_l{\left(\alpha \right.}_l^{⨂}\right)+\sum _{l=1}^n\left.C_l{\left(\alpha \left(I\right)\right.}_l\right)$ increase to the same order of magnitude—Table 2 and Table 3.

Further reduction of the parameter $\theta <\pi /8$ for the phase cross section of the object field practically does not lead to changes in the statistical structure of the polarization maps. This fact indicates that for such phase planes, a regime of single scattering in the volume of the myocardial diffuse layer is realized.

Thus, the application of the phase scanning method with digital holographic reconstruction of the microscopic image phase of polarization azimuth maps of the optically thick fibrous layer allows for the experimental selection of components of different multiplicities—isolating the “object” practically single-scattered component against the background of the overall “diffuse” background, which is formed by high-order interactions.

7.2 Parenchymal liver histological section object field azimuth polarization maps

Figure 5 shows a series of experimentally measured integral azimuth polarization maps [(1)–(3)] and histograms [(4)–(6)] of the liver histological section microscopic images.

FIGURE 5

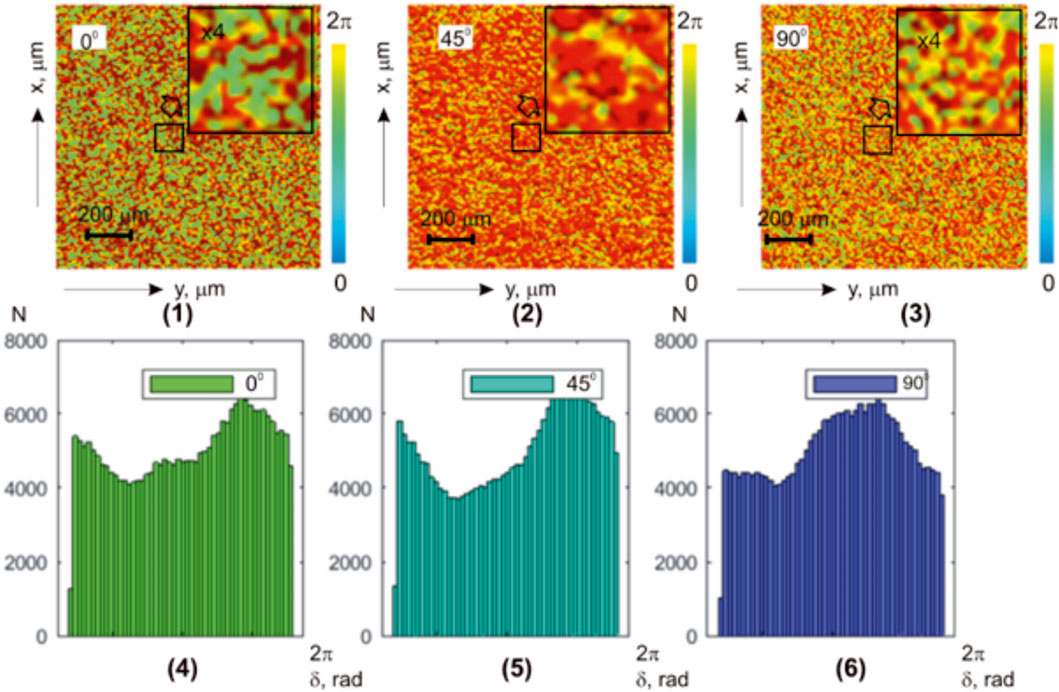
FIGURE 5. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the liver histological section microscopic image polarization azimuth maps.

Both coordinate and individual heterogeneities of the experimentally measured azimuth polarization maps $\alpha \left({\alpha }_0,m\times n\right)$ in the parenchymal liver tissues microscopic images are observed, similar to the findings in the case of the myocardium [Figure 5, fragments (1)–(3)].

The histograms $G\left(\alpha ,{\alpha }_0\right)$ of the azimuth values in the liver tissue exhibit significantly larger ranges of variation in random azimuth values than that of the fibrous myocardium [Figure 2; Figure 5, fragments (4)–(6)]. On the other hand, the “polarization” differences between $G\left(\alpha ,{\alpha }_0\right)$ are not as pronounced.

Quantitatively, the coordinate statistical structure of the parenchymal liver layer images maps $\alpha \left({\alpha }_0,m\times n\right)$ is characterized by the set of statistical moments $Z_{g=\mathrm{1,2,3,4}},$ which is listed in Table 4.

TABLE 4

TABLE 4. Statistical parameters of the liver histological section microscopic image polarization azimuth maps.

Statistical analysis of partially depolarizing hepatic parenchyma layer microscopic images integral polarization azimuth maps revealed a significant (up to three times) decrease in the higher-order statistical moments $Z_{\mathrm{3,4}}$ compared to asymmetry and excess, which characterize the coordinate distributions of myocardial microscopic image polarization azimuth maps. Conversely, the variance value $Z_2$ of the random variable $\alpha$ is larger by 1.5 times, as shown in Table 2 and Table 4.

From a physical point of view, the obtained results can be attributed to the predominant influence of the object factor—circular birefringence ($CB$) of hepatic parenchyma—combined with the secondary interference of linearly polarized partial laser waves. As a result, a polarization-inhomogeneous “diffuse” component of object laser radiation is formed, characterized by distributions of random values of azimuth, represented by the sum of individual components: $\sum _{l=1}^n\left.A_l{\left(\alpha \right.}_l^{⨂}\right)+\sum _{l=1}^n\left.C_l{\left(\alpha \left(I\right)\right.}_l\right)$.

Additionally, the spatial ordering of optically anisotropic domains (azimuthal symmetry) in the morphological structure of the liver is revealed in a relatively weak dependence of the distributions $\alpha \left({\alpha }_0,m\times n\right)$ on variations in the polarization azimuth ${\alpha }_0$ of the laser probe.

The results of phase scanning and reconstruction of layered maps $\alpha \left(\theta ,m\times n\right)$ for $\theta =\pi /6$ і $\theta =\pi /8$ are presented in Figures 6, 7, respectively.

FIGURE 6

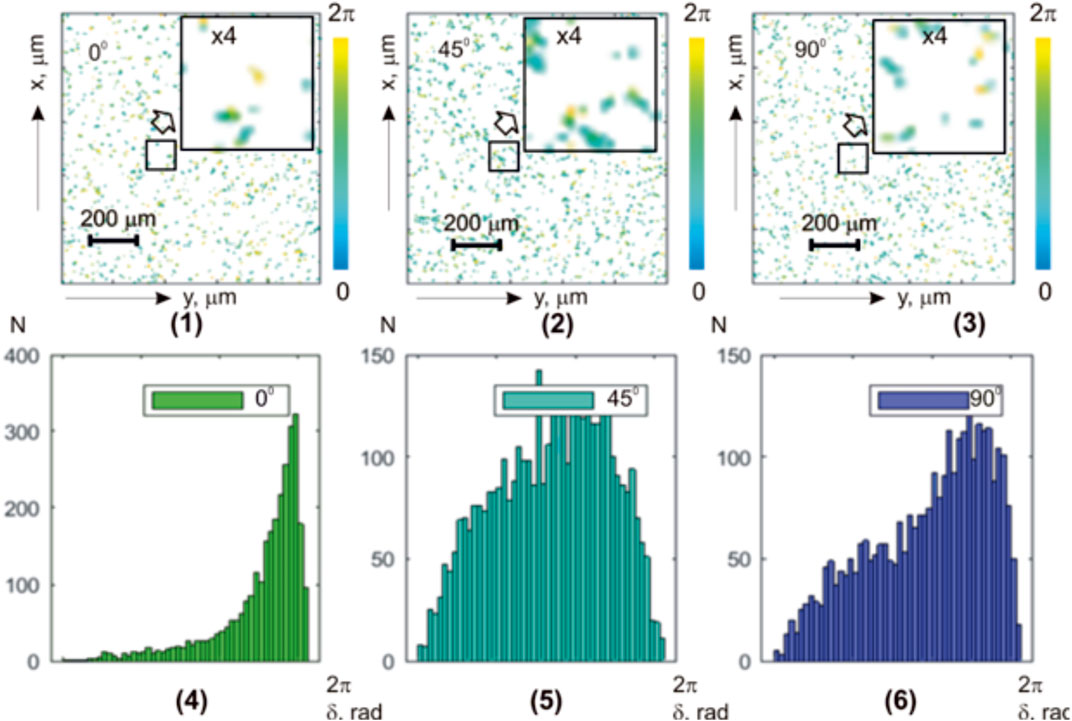
FIGURE 6. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the liver histological section microscopic image polarization azimuth maps in the phase cross section $\theta =\pi /6$.

FIGURE 7

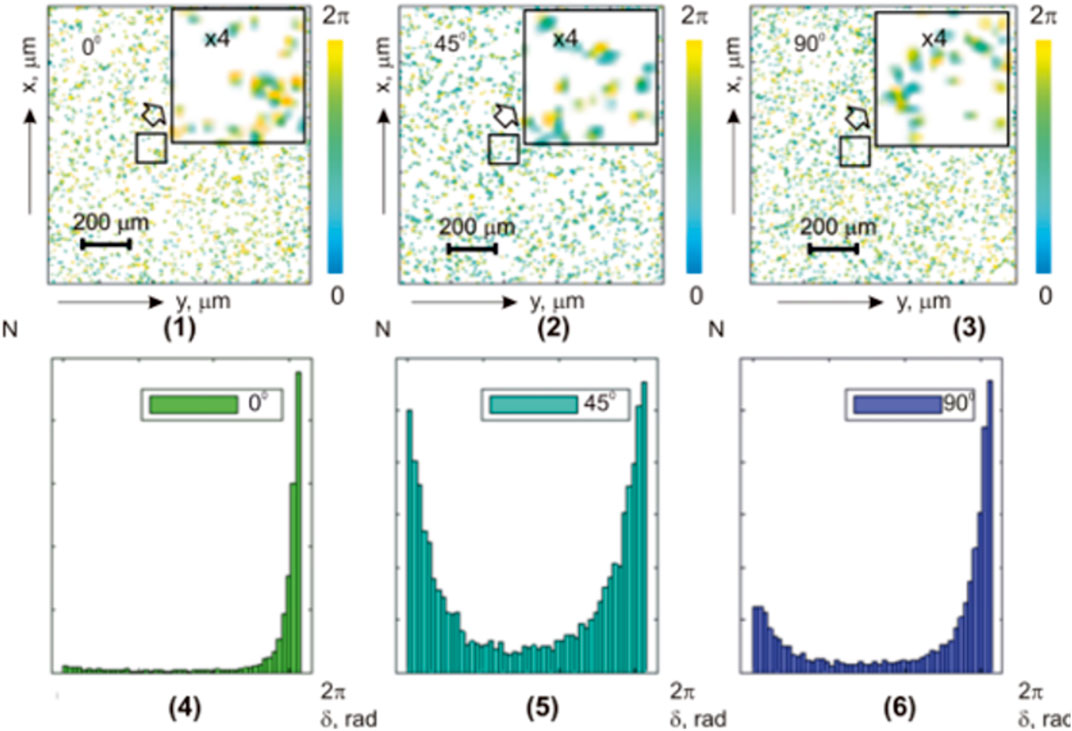
FIGURE 7. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the liver histological section microscopic image polarization azimuth maps in the phase section $\theta =\pi /8$.

The data from the statistical analysis of the optically thick liver histological section microscopic images layered polarization azimuth maps are presented in Table 5.

TABLE 5

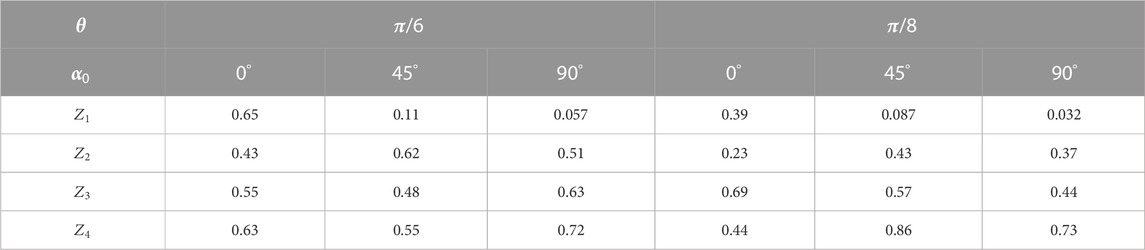
TABLE 5. Statistical parameters of the liver histological section microscopic image polarization azimuth maps.

Comparative analysis of a series of polarization azimuth $\alpha \left(\theta ,m\times n\right)$ layer-by-layer maps makes it possible (as in the case of studies of another biological tissue type—myocardium) to experimentally select the “object” single-scattered vector component of the laser field against the background of the general “diffuse” background, which is formed by interactions of high multiplicity.

This follows from the fact that when the phase parameter ${\theta }_k$ is reduced to the level of ${\theta }_k\le \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$8$}\right.$, there is a successive decrease in the variance of the spread of the random values of the polarization azimuths $Z_2\left(\alpha \right)$ by 3–4 times (Tables 4, 5) with the subsequent “stabilization” of the values of the set of statistical moments $Z_{g=1;2;3;4}\left(\alpha \right)$, which characterize the distributions $\sum _{l=1}^n\left.A_l{\left(\alpha \right.}_l^{⨂}\right)+\sum _{l=1}^n\left.C_l{\left(\alpha \left(I\right)\right.}_l\right)$.

In addition, the differences between the calculated values of $Z_3\left(\alpha \right)$ and $Z_4\left(\alpha \right)$ in the given phase plane of the object field of the myocardium (Table 7) and liver (Table 5) reach 2–2.5 times.

7.3 Myocardium histological section object field polarization map ellipticity

A series of fragments shown in Figure 8 presents integral maps $\beta \left({\alpha }_0;m,n\right)$ [(1)–(3)] and histograms [(4)–(6)] of myocardium histological section microscopic image polarization ellipticity distributions.

FIGURE 8

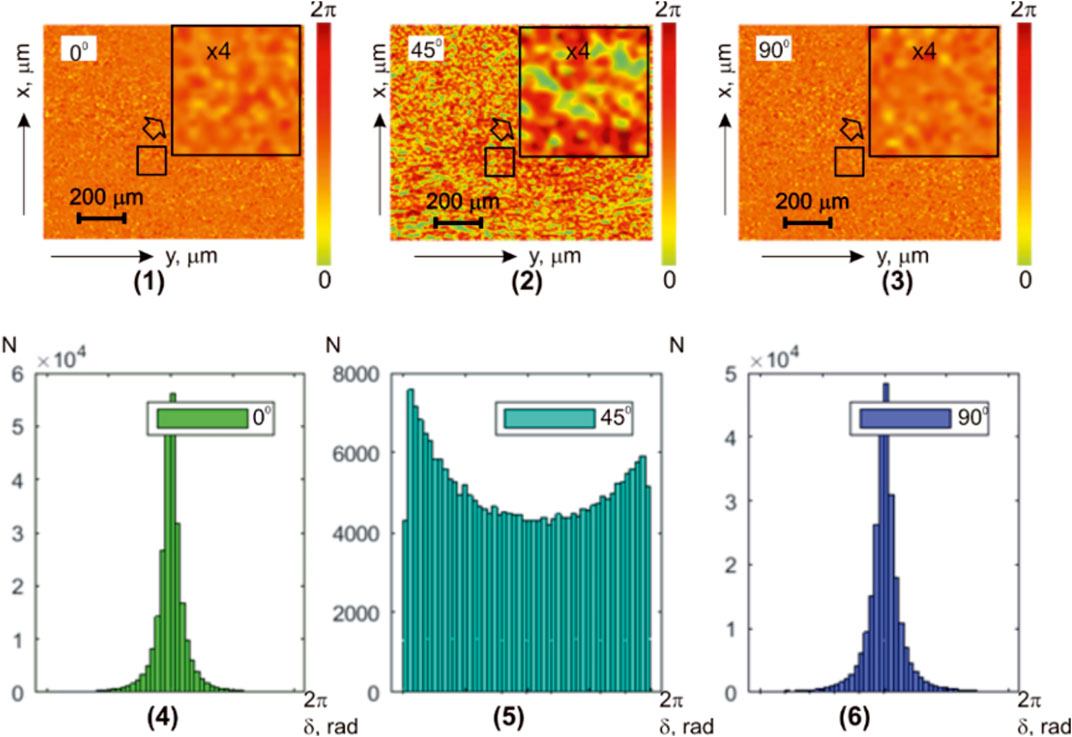
FIGURE 8. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the myocardium histological section microscopic image polarization ellipticity maps.

The obtained results (Figure 8) revealed the individual coordinate and statistical structure of the second object field polarization map parameter—polarization ellipticity $\beta \left({\alpha }_0,m,n\right)$. Quantitatively, this is indicated by different intervals of “polarization” change (within one order of magnitude) of the values of the set of statistical moments $Z_{g=1;2;3;4}$, which characterize the distributions $\sum _{l=1}^n\left.B_l{\left(\beta \right.}_l^{⨂}\right)+\sum _{l=1}^n{D}_l\left({\beta \left(I\right)}_l\right)$, as shown in Table 6.

TABLE 6

TABLE 6. Statistical parameters of the myocardium microscopic image polarization ellipticity maps.

From a physical point of view, the obtained results of polarimetry of $\beta \left({\alpha }_0;m,n\right)$ ellipticity maps can be associated with the complex influence of object [${\delta }_l$, ratios (2),(5)] and interference [${\phi }_l$, ratio (16),(18)] phase modulation between orthogonal components of complex amplitudes of partial coherent waves in volumes of the diffuse layer of the myocardium.

Possibilities of phase selection of components of the object field with different scattering multiplicities are illustrated by layer-by-layer maps $\beta \left(\theta ,m,n\right)$ for $\theta =\pi /8$ presented in Figure 9, and the results of their statistical analysis are shown in Table 7.

FIGURE 9

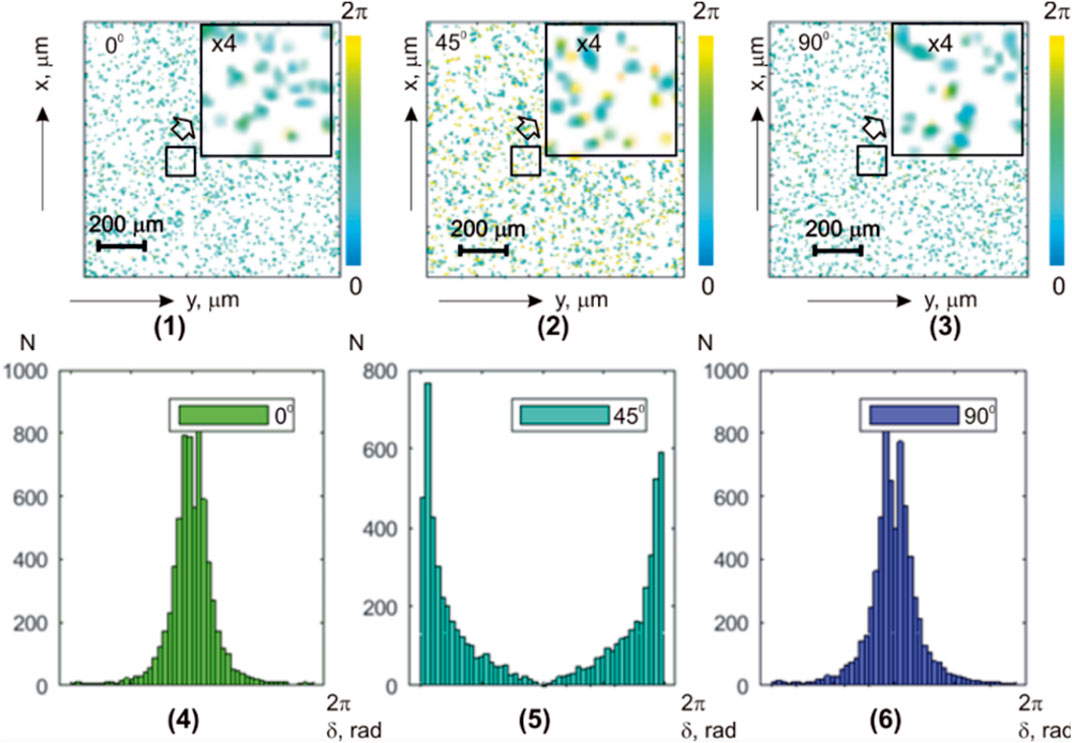
FIGURE 9. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the myocardium histological section microscopic image polarization ellipticity maps in the phase section $\theta =\pi /8$.

TABLE 7

TABLE 7. Statistical parameters of the myocardium histological section microscopic image polarization ellipticity maps in the phase section $\theta =\pi /8$.

The analysis of the layer-by-layer transformation in the statistical structure $\beta \left(\theta ,m,n\right)$ revealed the possibility of selection by the algorithm digital holographic reproduction [ratio (20)] and step-by-step phase scanning [ratios (20),(21)] of the single-scattered component in the diffuse myocardial sample polarization-inhomogeneous object field$—Z_{g=1;2;3;4}\left(\theta \le \pi /8\right)\approx const$.

7.4 Parenchymal liver histological section object field polarization ellipticity maps

Figure 10 presents integral maps [(1)–(3)] and histograms [(4)–(6)] of liver histological section microscopic image polarization ellipticity $\beta \left({\alpha }_0;m,n\right)$.

FIGURE 10

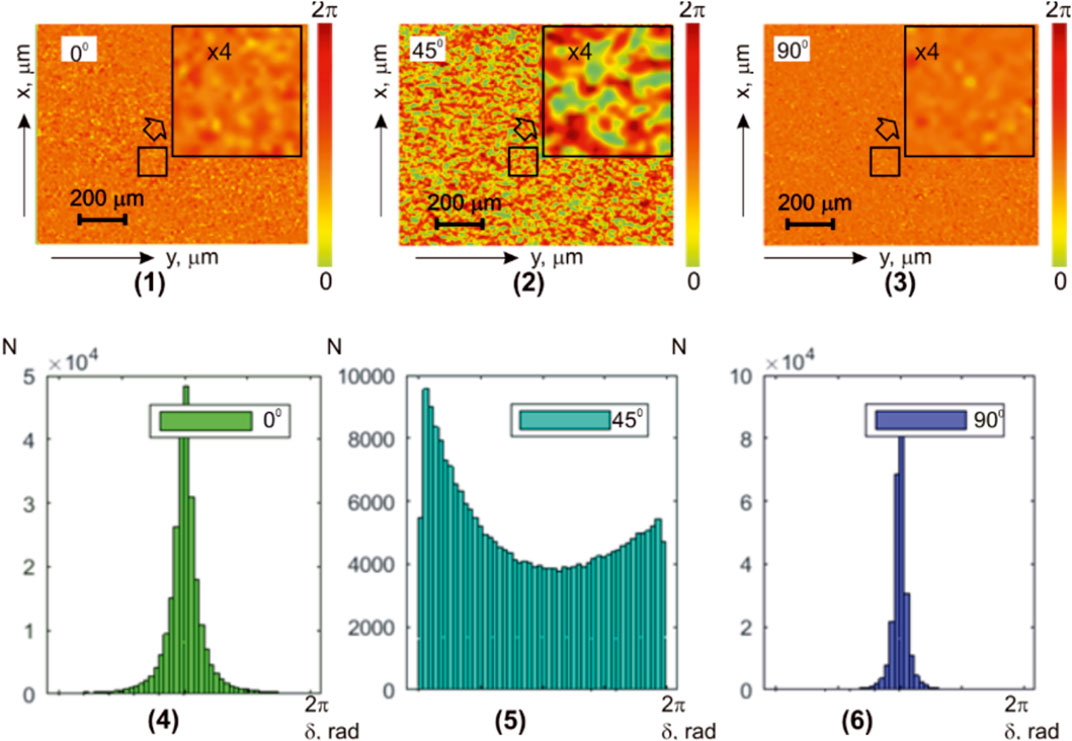
FIGURE 10. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the liver histological section microscopic image polarization ellipticity maps.

Quantitative statistical characteristics of distributions $\beta \left({\alpha }_0;m,n\right)$ are illustrated in Table 8.

TABLE 8

TABLE 8. Statistical parameters of the liver microscopic image polarization ellipticity maps.

Statistical analysis of integrated topographic microscopic image polarization ellipticity maps of the parenchymal liver layer revealed significantly (by 8–10 times) smaller values of dispersion of random values $\beta$ than maps of polarization distributions $\beta \left({\alpha }_0,m,n\right)$ of the myocardium object field (Table 8).

The established fact can be associated with the predominant influence of the liver parenchyma circular birefringence, $CB$, which forms the coordinate structure of the polarization azimuths of the object field.

An even more clearly revealed feature of the formation of the object field linearly polarized states’ distributions illustrated by the results of phase scanning and holographic reproduction of layer-by-layer maps $\beta \left(\theta ,m\times n\right)$ for $\theta =\pi /8$ presented in Figure 11 and Table 9, respectively.

FIGURE 11

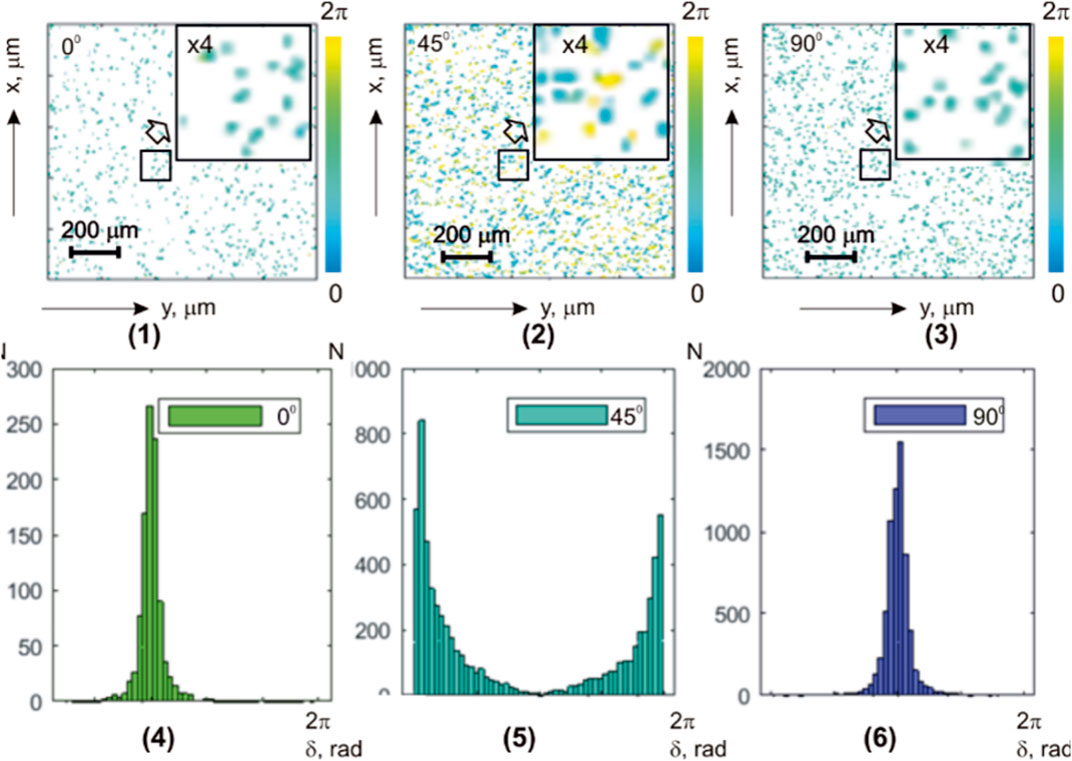
FIGURE 11. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of the liver histological section microscopic image polarization ellipticity maps in the phase section $\theta =\pi /8$.

TABLE 9

TABLE 9. Statistical parameters of the liver histological section microscopic image polarization ellipticity maps in the phase section $\theta =\pi /8$.

On the basis of a comparative analysis of a holographic reproduction of the liver diffuse histological section microscopic image set of layer-by-layer elliptical polarization maps, it was found that $Z_2\left(\beta \right)\to 0$. In accordance with this [ratio (23)], the value of the statistical moments of higher orders, which characterize the asymmetry $Z_3\left(\beta \right)$ and excess $Z_4\left(\beta \right)$ of the distributions $\beta \left(\theta ,m\times n\right)$ of the object field in comparison with the fibrillar myocardium, increases parenchymal tissue layer sharply (up to 10 times) (Table 7).

In addition, the differences between the calculated values of $Z_3\left(\beta \right)$ and $Z_4\left(\beta \right)$ in the given phase plane of the object field of the myocardium (Table 7) and liver (Table 9) reach 3–4 times.

8 An example of clinical application

Here, we will briefly give one example of the developed technique clinical application.

8.1 Information analysis

The information analysis of the results obtained from the methods of 3D polarization–interference-layered phase scanning of object fields of two groups' research on biological tissue samples involves the use of operational characteristics from evidence-based medicine [46]:

• Sensitivity ($Se$) is the proportion of true positive results ($A$) of the diagnostic method among all samples in group 2 (N).

$Se=\frac{A}{N}100\%(24)$

• Specificity ($Sp$) is the proportion of true negative results ($B$) of the method among all samples in group 1 ($H$).

$Sp=\frac{B}{H}100\%(25)$

• Accuracy ($Ac$) is the proportion of correct results ($A+B$) of the test among all samples (N + H).

$Ac=\frac{A+B}{N+H}100\%(26)$

If ($N+H$) = ($A+B$), $Ac$ is referred to as balanced accuracy.

8.2 Differential diagnosis of necrotic changes in myocardial fibrillar networks

Two groups of samples of the myocardium histological sections were formed:

• Coronary heart disease (CHD)—group 1 (12 samples).

• Ischemic heart disease (IHD)—group 2 (12 samples).

The optical geometric parameters of the samples are given in Table 10.

TABLE 10

TABLE 10. Optical geometric parameters of the samples.

From a morphological point of view, cases of CHD and IHD lead to various necrotic changes in myosin fibers and their spatial networks.

CHD—myosin fibers become thinner, and the spatial orderliness of fibrillar networks decreases.

IHD—myosin fibers in some areas are torn, while the spatial order of the myosin network remains unchanged.

Figure 12 presents the results of the myocardium polarization-inhomogeneous object field investigation of those who died as a result of CHD and IHD:

• integrated polarization ellipticity maps $\beta \left(m\times n\right)$ of the myocardium histological section microscopic images from both groups [fragments (1), (2)];

• layer-by-layer polarization of the myocardium histological section microscopic image phase polarization ellipticity $\beta \left(\theta ,m\times n\right)$ maps from both groups for the following steps of phase scanning $\theta =\pi /4$ [fragments (5), (6)] and $\theta =\pi /8$ [fragments (9), (10)];

• histograms of the magnitude [fragments (3), (4)] of polarization ellipticity $G\left(\beta \right)$ distributions; and

• histograms of layer-by-layer polarization ellipticity value $\left(\theta =\pi /4,\beta \right)$ distributions [fragments (7), (8)] and $G\left({\theta }_k=\pi /8,\beta \right)$ [fragments (11), (12)].

FIGURE 12

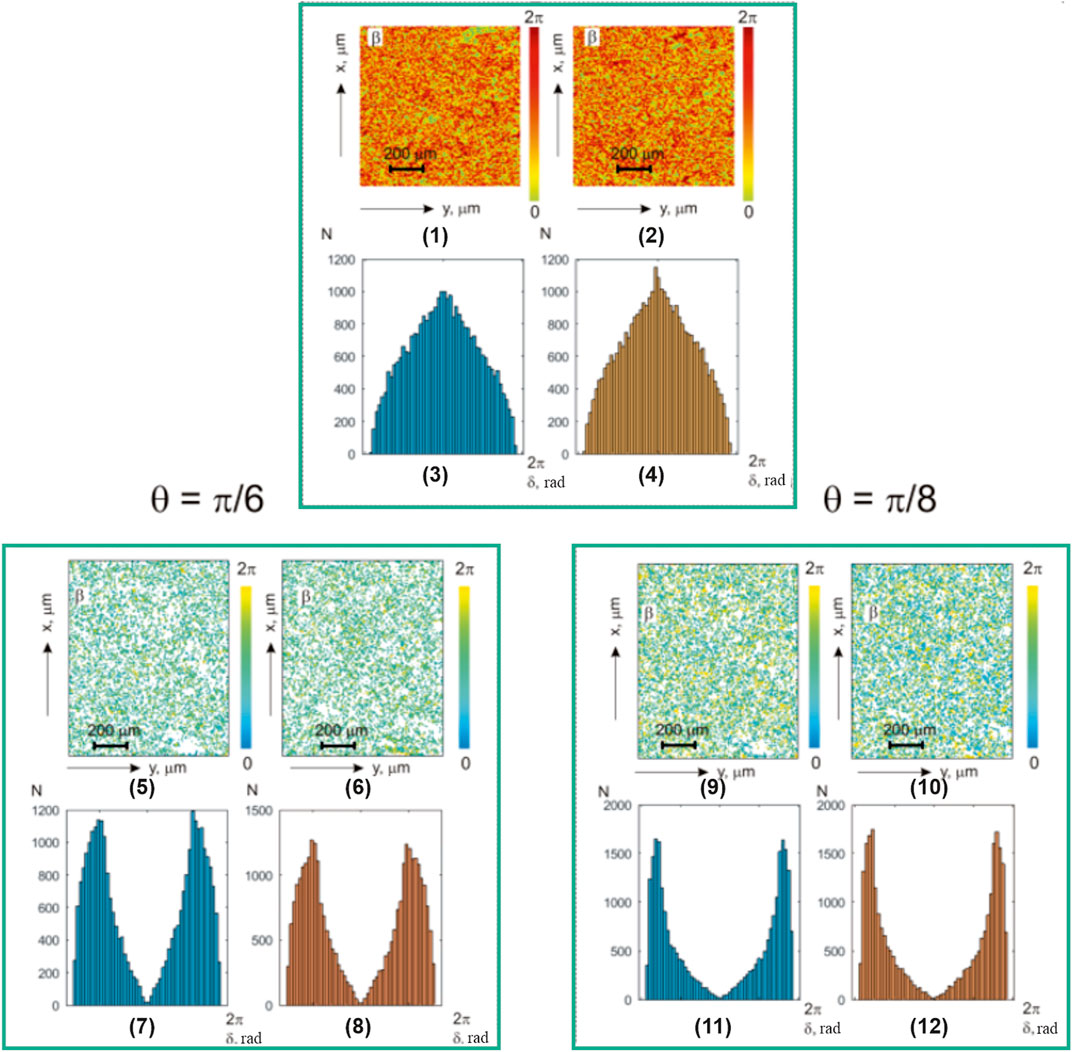
FIGURE 12. Coordinate ($x=0-1000\mu m;y=0-1000\mu m$) and statistical structure of layer-by-layer myocardium histological section microscopic image polarization ellipticity maps of the patients who died of CHD (left column) and IHD (right column).

Table 11 illustrates the results of the experimentally determined polarization ellipticity maps $\beta \left(m\times n\right)$ and $\beta \left(\theta ,m\times n\right)$ statistical analysis.

TABLE 11

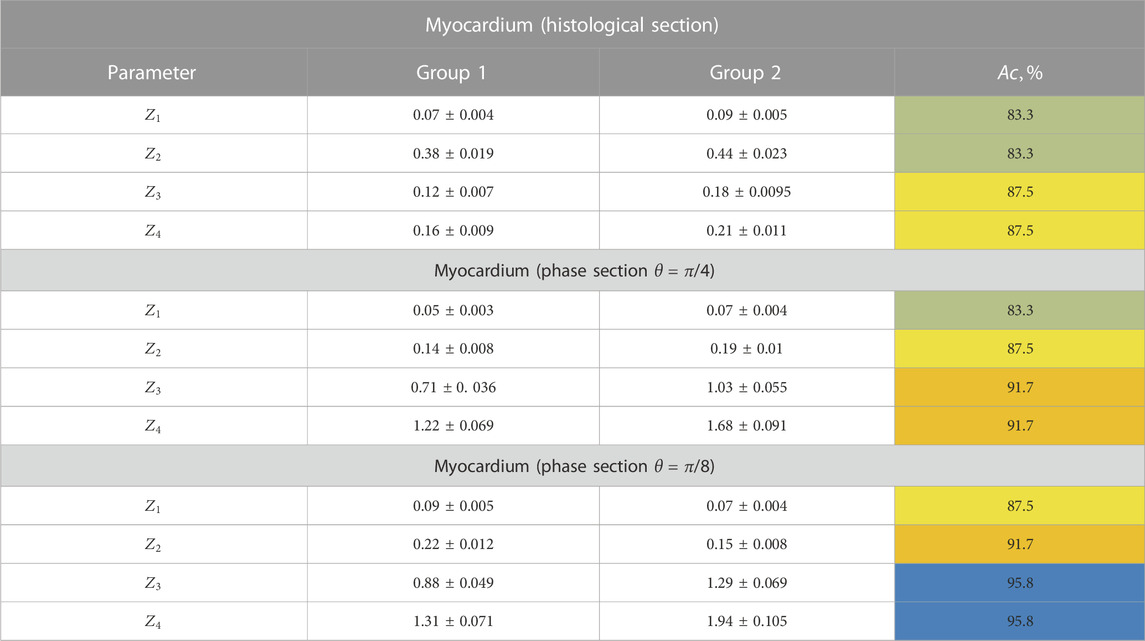
TABLE 11. Statistical moments of the first to fourth orders, which characterize the layer-by-layer polarization ellipticity maps.

The obtained results of integral and phase mapping can be associated with necrotic transformations of birefringent fibrous networks.

For the case of IHD, as a result of reducing the range of variations in the orientation of optical axes $∆\rho \left(m\times n\right)\to \mathit{min}$ in biological crystals and the magnitude of their phase-shifting capability, the mean $Z_1\left(\beta ,\rho ,\delta \right)\downarrow$ and the dispersion $Z_2\left(\beta ,\rho ,\delta \right)\downarrow$ of the polarization ellipticity random variables for the corresponding myocardial histological sections’ microscopic images decrease. At the same time, the value of statistical moments of the third and fourth orders, which characterize the asymmetry and excess of distributions of $\beta \left(m\times n\right)$, increases$Z_{\mathrm{3,4}}\left(\beta ,\rho ,\delta \right)\uparrow$.

In the case of CHD, the fast-paced morphological structures of myocardial fibrous networks due to acute coronary insufficiency show weak changes in the orientational and phase structures of optically anisotropic crystal networks$—∆\rho \left(m\times n\right)\approx const$ and $∆\delta \left(m\times n\right)\approx const$.

Therefore, the following statistical relationships are realized for such objects$:\left(\begin{array}{c}{Z}_{i=\mathrm{1,2}}\left(IHD,\left(\beta \right),\left(\theta \right)\right)<Z_{i=\mathrm{1,2}}\left(CHD,\left(\beta \right),\left(\theta \right)\right)\\ Z_{i=\mathrm{3,4}}\left(IHD,\left(\beta \right),\left(\theta \right)\right)>Z_{i=\mathrm{3,4}}\left(CHD,\left(\beta \right),\left(\theta \right)\right)\end{array}\right).$

It should be noted that the phenomenon of birefringence in optically uniaxial biological crystals predominantly generates various elliptically polarized states [6]. The probability of forming linearly polarized states in the object field points is insignificant.

Therefore, due to the advanced statistics of elliptically polarized states in the myocardial fibrous layer object field, the sensitivity of polarization ellipticity distributions to changes in the orientation and phase polycrystalline structure of the myocardium is significantly higher than when detecting histological section microscopic image polarization azimuth maps from samples in groups 1 and 2.

The given fact is supported by the results of the informational analysis, which revealed the following levels of balanced accuracy $\left(Ac,\%\right.$) for the diagnostic method [46]:

• integral maps of polarization ellipticity–a good level with $Ac\left(Z_{\mathrm{3,4}}\left(\beta \right)\right)=87.9\%$;

• layered polarization ellipticity phase maps–a good level with $Ac\left(Z_3\left(\beta ,\theta =\pi /4\right)\right)=87.5\%$, very good level with $Ac\left(Z_4\left(\beta ,\theta =\pi /8\right)\right)=91.7\%$, and excellent level with $Ac\left(Z_{\mathrm{3,4}}\left(\beta ,\theta =\pi /8\right)\right)=95.8\%$.

9 Conclusion

1. The proposed comprehensive Stokes polarimetric and interferometric analytical description allows for the formation of polarization-inhomogeneous components with different scattering multiplicities in the object laser field of diffuse layers in biological tissues with various types of optically anisotropic fibrous and parenchymal structures.

2. The methods of direct Stokes polarimetry and digital holographic 3D layered reconstruction of complex amplitudes in different phase planes of microscopic images of diffuse histological sections of biological tissues have been experimentally validated. This includes subsequent reconstruction of polarization azimuth and ellipticity maps.

3. The comparison of the results of statistical analysis of integral maps of polarization azimuth $\alpha \left({\alpha }_0,m,n\right)$ and ellipticity $\beta \left({\alpha }_0,m,n\right)$ revealed the following:

• difference of all coordinate polarization distributions from normal or Gaussian—all statistical moments $Z_{g=\mathrm{1,2,3,4}}\ne 0$;

• variations in the magnitude (from two to seven times) of all statistical moments $Z_{g=\mathrm{1,2,3,4}}$ depending on changes in the polarization state ${\alpha }_0$ of the incident laser beam.

4. The comparative analysis of layered maps of polarization azimuth and ellipticity, reconstructed using the phase scanning method with a digital holographic reconstruction of layered distributions of complex amplitude fields, revealed that with a decrease in the magnitude of ${\theta }_k$, there is a consecutive reduction (by 2–3 times) in the dispersion $Z_2\left({\theta }_k;\alpha \right)$ of the random values of polarization parameters in the phase cross-sectional planes of the object field.

5. It has been established that starting from a certain value of the phase parameter ${\theta }_k$, the statistical structure of the polarization azimuth and ellipticity maps “stabilizes” - $Z_{g=1;2;3;4}\left({\theta }_k\le \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$8$}\right.\right)\approx const$, which corresponds to a single-scattered object component of the laser field.

6. Biomedical validation of the method revealed an excellent level ($Ac\left(Z_{\mathrm{3,4}}\left(\beta ,{\theta }_k=\pi /8\right)\right)=95.8\%$) of diagnostic accuracy in differentiating diffuse samples of the myocardium from individuals who died due to ischemic heart disease and acute coronary insufficiency.

Therefore, we have demonstrated that the application of the 3D polarization–interference method by phase scanning with digital holographic reconstruction of biological diffuse tissue object field layered polarization azimuth and ellipticity maps with different architectural optical anisotropic components allows for the experimental selection of components with different scattering multiplicities. This enables the isolation of the “object” practically singly scattered component against the background of the overall “diffuse” background, which is formed by interactions with high multiplicities.

The significant differences (from two to four times) observed in the magnitudes of the statistical moments $Z_{g=1;2;3;4}\left({\theta }_k\le \pi /8\right)$ characterizing the polarization maps of azimuth and ellipticity of the singly scattered component of the object field in both tissue types indicate a high diagnostic sensitivity of the 3D polarization–interference method to changes in the optical anisotropic architecture of diffuse tissue layers. This makes it promising for a wide range of tasks in clinical differential diagnosis.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by the Bukovinian State Medical University, 3 Teatralna Sqr. Chernivtsi, Ukraine, 58005. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required from the participants or the participants’ legal guardians/next of kin because samples of histological sections of tissues of the myocardium and liver of the deceased were obtained from the Bureau of Forensic Medicine.

Author contributions

AU: conceptualization, data curation, resources, validation, and writing–original manuscript. JZ: validation, writing–original manuscript, investigation, and supervision. MG: writing–review and editing. AD: writing–review and editing, methodology, and software. YU: investigation, project administration, and writing–review and editing. IS: resources, visualization, and writing–review and editing. IM: data curation and writing–review and editing. ZC: formal analysis, methodology, and writing–review and editing. OW: resources and writing–review and editing. IG: formal analysis and writing–review and editing. CJ: visualization, investigation and writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. Authors acknowledge the support from the National Research Foundation of Ukraine, Project 2022.01/0034 and Scholarship of the Verkhovna Rada of Ukraine for Young Scientists-Doctors of Science 2023.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tuchin VV. Tissue optics and Photonics: light-tissue interaction. J Biomed Photon Eng (2015) 1(2):98–134. doi:10.18287/jbpe-2015-1-2-98

CrossRef Full Text | Google Scholar

2. Vo-Dinh T. Biomedical Photonics handbook. Florida, United States: CRC Press (2014).

Google Scholar

3. Boas DA, Pitris C, Ramanujam N. Handbook of biomedical optics. Florida, United States: CRC Press (2016).

Google Scholar

4. Tuchin VV. Tissue optics: light scattering methods and instruments for medical diagnosis. In: Society of photo-optical instrumentation engineers (SPIE) eBooks. Bellingham, Washington: Society of Photo-Optical Instrumentation Engineers SPIE (2015).

Google Scholar

5. Wang LV, Wu H. Biomedical optics. New Jersey, United States: John Wiley and Sons (2012).

Google Scholar

6. Ushenko AG, Pishak VP. Laser polarimetry of biological tissues: principles and applications. In: VV Tuchin, editor. Handbook of coherent domain optical methods. Cham: Springer US (2004). p. 93–138.

CrossRef Full Text | Google Scholar

7. Ghosh N Tissue polarimetry: concepts, challenges, applications, and outlook. J Biomed Opt (2011) 16(11):110801. doi:10.1117/1.3652896

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Jacques SL. Polarized light imaging of biological tissues. In: D Boas, C Pitris, and N Ramanujam, editors. Handbook of biomedical optics 2. Boca Raton: CRC Press (2011). p. 649–69.

Google Scholar

9. Ghosh N, Wood M, Vitkin A. Polarized light assessment of complex turbid media such as biological tissues using mueller matrix decomposition. In: VV Tuchin, editor. Handbook of Photonics for biomedical science. Boca Raton: CRC Press (2010). p. 253–82.

CrossRef Full Text | Google Scholar

10. Layden D, Ghosh N, Vitkin IA. Quantitative polarimetry for tissue characterization and diagnosis. In: RK Wang, and VV Tuchin, editors. Advanced biophotonics: tissue optical sectioning. Boca Raton: CRC Press (2013). p. 73–108.

CrossRef Full Text | Google Scholar

11. Vitkin A, Ghosh N, de Martino A. Tissue polarimetry. In: DL Andrews, editor. Photonics: scientific foundations, technology and applications. John Wiley & Sons, Ltd (2015). p. 239–321.

CrossRef Full Text | Google Scholar

12. Tuchin VV. Tissue optics and Photonics: biological tissue structures. J Biomed Photon Eng (2015) 1(1):3–21. doi:10.18287/jbpe-2015-1-1-3

CrossRef Full Text | Google Scholar

13. Bai X, Liang Z, Zhu Z, Schwing AG, Forsyth D, Gruev V. Polarization-based underwater geolocalization with deep learning. eLight (2023) 3(15):15. doi:10.1186/s43593-023-00050-6

CrossRef Full Text | Google Scholar

14. Lee HR, Lotz C, Groeber Becker FK, Dembski S, Novikova T. Digital histology of tissue with Mueller microscopy and FastDBSCAN. Appl Opt (2022) 61(32):9616. doi:10.1364/ao.473095

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Novikova T, Kim M, Lee HR, Ossikovski R, Malfait-Jobart A, Lamarque D. Optical diagnosis of gastric tissue biopsies with Mueller microscopy and statistical analysis. J Eur Opt Soc Rapid Publications (2022) 18(2):10. doi:10.1051/jeos/2022011

CrossRef Full Text | Google Scholar

16. Lee HR, Li P, Sang T, Lotz C, Groeber-Becker F, Dembski S, et al. Digital histology with Mueller microscopy: how to mitigate an impact of tissue cut thickness fluctuations. J Biomed Opt (2019) 24(07):1–11. doi:10.1117/1.jbo.24.7.076004

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li P, Lee HR, Chandel S, Lotz C, Groeber-Becker FK, Dembski S, et al. Analysis of tissue microstructure with Mueller microscopy: logarithmic decomposition and Monte Carlo modeling. J Biomed Opt (2020) 25(01):1. doi:10.1117/1.jbo.25.1.015002

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lee HR, Sang T, Li P, Lotz C, Groeber-Becker F, Dembski S, et al. Mueller microscopy of anisotropic scattering media: theory and experiments. India: HAL Le Centre pour la Communication Scientifique Directe (2018).

Google Scholar

19. Ma H, He H, Ramella-Roman JC. Mueller matrix microscopy. In: T Novikova, and JC Ramella-Roman, editors. Polarized light in biomedical imaging and sensing. Cham: Springer (2023). p. 281–321.

CrossRef Full Text | Google Scholar

20. Zabolotna N, Pavlov S, Ushenko A, Karachevtsev A, Savich V, Sobko O, et al. System of the phase tomography of optically anisotropic polycrystalline films of biological fluids. Proc SPIE (2014)(916616) 9166. doi:10.1117/12.2061116

CrossRef Full Text | Google Scholar

21. Ushenko O, Dubolazov A, Balanetska V, Karachevtsev A, Sydor M. Wavelet analysis for polarization inhomogeneous laser images of blood plasma. Proc SPIE (2011) 8338. 83381H. doi:10.1117/12.920169

CrossRef Full Text | Google Scholar

22. Angelsky O. Optical measurements: polarization and coherence of light fields. In: L Cocco, editor. Polarization and coherence of light fields. London, UK: INTECH Open Access Publisher (2012). p. 5–16.

Google Scholar

23. Garazdyuk M, Bachinskyi V, Vanchulyak O, Ushenko A, Dubolazov A, Gorsky M. Polarization-phase images of liquor polycrystalline films in determining time of death. Appl Opt (2016) 55(12):B67–71. doi:10.1364/ao.55.000b67

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ushenko Y, Sdobnov A, Dubolazov A, Grytsiuk M, Bykov A, Meglinski I, et al. Stokes-correlometry analysis of biological tissues with polycrystalline structure. IEEE J Selected Top Quan Elect (2019) 25(1):1–12. doi:10.1109/jstqe.2018.2865443

CrossRef Full Text | Google Scholar

25. Ushenko V, Sdobnov A, Mishalov W, Dubolazov A, Olar O, Bachinskyi V, et al. Biomedical applications of Jones-matrix tomography to polycrystalline films of biological fluids. J Innovative Opt Health Sci (2019) 12(06):12. doi:10.1142/s1793545819500172

CrossRef Full Text | Google Scholar

26. Ushenko AG, Dubolazov OV, Ushenko VA, Oyu N, Olar OV. Fourier polarimetry of human skin in the tasks of differentiation of benign and malignant formations. Appl Opt (2016) 55(12):B56–60. doi:10.1364/ao.55.000b56

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Peyvasteh M, Dubolazov A, Popov A, Ushenko A, Meglinski I. Two-point Stokes vector diagnostic approach for characterization of optically anisotropic biological tissues. J Phys D (2020) 53(39):395401–1. doi:10.1088/1361-6463/ab9571

CrossRef Full Text | Google Scholar

28. Ushenko A, Angelsky P, Sidor M, Marchuk Y, Andreychuk D, Pashkovska N. Spatial-frequency selection of complex degree of coherence of laser images of blood plasma in diagnostics and differentiation of pathological states of human organism of various nosology. Appl Opt (2014) 53(10):B172–80. doi:10.1364/ao.53.00b172

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ushenko V, Dubolazov A, Pidkamin L, Sakchnovsky M, Bodnar A, Ushenko Y, et al. Mapping of polycrystalline films of biological fluids utilizing the Jones-matrix formalism. Laser Phys (2018) 28(2):025602. doi:10.1088/1555-6611/aa8cd9

CrossRef Full Text | Google Scholar

30. de Boer JF, Milner TE. Review of polarization sensitive optical coherence tomography and Stokes vector determination. J Biomed Opt (2002) 7(3):359. doi:10.1117/1.1483879

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Spandana KU, Krishna KM, Mazumder N. Polarization-resolved Stokes-Mueller imaging: a review of technology and applications. Lasers Med Sci (2019) 34(7):1283–93. doi:10.1007/s10103-019-02752-1

PubMed Abstract | CrossRef Full Text | Google Scholar

32. He Y, Li K, Li W, Qiu Y, Li D, Wang C, et al. Polarization coherency matrix tomography. J Biophotonics (2023) 16(9):e202300093. doi:10.1002/jbio.202300093

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Yang D, Yuan Z, Hu M, Liang Y. Zebrafish brain and skull imaging based on polarization-sensitive optical coherence tomography. J Biophotonics (2022) 15(12):e202200112. doi:10.1002/jbio.202200112

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Park JE, Zhou X, Kwon DY, Kim SW, Lee H, Jung MJ, et al. Application of polarization sensitive-optical coherence tomography to the assessment of phase retardation in subpleural cancer in rabbits. Tissue Eng Regenerative Med (2021) 18(1):61–9. doi:10.1007/s13770-020-00318-9

CrossRef Full Text | Google Scholar

35. Willemse J, Maximilian Grafe GO, Verbraak FD, De Boer J. In vivo 3D determination of peripapillary scleral and retinal layer architecture using polarization-sensitive optical coherence tomography. Translational Vis Sci Tech (2020) 9(11):21–1. doi:10.1167/tvst.9.11.21

CrossRef Full Text | Google Scholar

36. Baumann B, Augustin M, Lichtenegger A, Harper DJ, Muck M, Eugui P, et al. Polarization-sensitive optical coherence tomography imaging of the anterior mouse eye. J Biomed Opt (2018) 23(08):1–12. doi:10.1117/1.jbo.23.8.086005

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Hariri LP, Adams DC, Applegate MB, Miller AJ, Roop BW, Villiger M, et al. Distinguishing tumor from associated fibrosis to increase diagnostic biopsy yield with polarization-sensitive optical coherence tomography. Clin Cancer Res (2019) 25(17):5242–9. doi:10.1158/1078-0432.ccr-19-0566

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Tao K, Sun K, Ding Z, Ma Y, Kuang H, Zhao H, et al. Catheter-based polarization sensitive optical coherence tomography using similar mueller matrix method. IEEE Trans Biomed Eng (2020) 67(1):60–8. doi:10.1109/tbme.2019.2908031

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Ushenko V, Sdobnov A, Syvokorovskaya A, Dubolazov A, Vanchulyak O, Ushenko A, et al. 3D mueller-matrix diffusive tomography of polycrystalline blood films for cancer diagnosis. Photonics (2018) 5(4):54. doi:10.3390/photonics5040054

CrossRef Full Text | Google Scholar

40. Peyvasteh M, Tryfonyuk L, Ushenko V, Syvokorovskaya A, Dubolazov A, Vanchulyak O, et al. 3D Mueller-matrix-based azimuthal invariant tomography of polycrystalline structure within benign and malignant soft-tissue tumours. Laser Phys Lett (2020) 17(11):115606. doi:10.1088/1612-202x/abbee0

CrossRef Full Text | Google Scholar

41. Ushenko A, Dubolazov A, Litvinenko O, Bachinskiy V, Lin B, Guo B, et al. 3D polarization correlometry of object fields of networks of biological crystals. Proc SPIE (2020):11369. 113691M. doi:10.1117/12.2553942

CrossRef Full Text | Google Scholar

42. Bodnar A, Dubolazov A, Pavlyukovich A, Pavlyukovich N, Ushenko A, Motrich A, et al. 3D Stokes correlometry of the polycrystalline structure of biological tissues. Proc SPIE (2020):11509. 115090V. doi:10.1117/12.2568451

CrossRef Full Text | Google Scholar

43. Ushenko VA, Hogan BT, Dubolazov A, Grechina AV, Boronikhina TV, Gorsky M, et al. Embossed topographic depolarisation maps of biological tissues with different morphological structures. Scientific Rep (2021) 11(1):3871. doi:10.1038/s41598-021-83017-2

CrossRef Full Text | Google Scholar

44. Marchesini R, Bertoni A, Andreola S, Melloni E, Sichirollo AE. Extinction and absorption coefficients and scattering phase functions of human tissues in vitro. Appl Opt (1989) 28(12):2318–24. doi:10.1364/ao.28.002318

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Edwards DK, Gier JT, Nelson KE, Roddick RD. Integrating sphere for imperfectly diffuse samples. J Opt Soc America (1961) 51(11):1279–88. doi:10.1364/josa.51.001279

CrossRef Full Text | Google Scholar

46. Robinson SP. Principles of forensic medicine. Cambridge; New York: Cambridge University Press (2008).

Google Scholar