- Department of Physics and Astronomy, University of Waterloo, Waterloo, ON, Canada
We consider a quantum Otto engine using an Unruh-DeWitt particle detector model which interacts with a quantum scalar field in curved spacetime. We express a generic condition for extracting positive work in terms of the effective temperature of the detector. This condition reduces to the well-known positive work condition in the literature under the circumstances where the detector reaches thermal equilibrium with the field. We then evaluate the amount of work extracted by the detector in two scenarios: an inertial detector in a thermal bath and a circulating detector in the Minkowski vacuum, which is inspired by the Unruh quantum Otto engine.
1 Introduction
Quantum thermodynamics is the study of thermodynamic phenomena from the perspective of quantum mechanics. Within this field, quantum heat engines, where the working substance is quantum matter that interacts with thermal baths, have emerged as a crucial area of research [1]. Notable among quantum heat engines are the quantum Carnot engine and the quantum Otto engine (QOE). The quantum Carnot engine operates through two isothermal processes and two quantum adiabatic processes. The QOE, on the other hand, is composed of two isochoric thermalization processes and two quantum adiabatic processes [1–7]. For a comprehensive review, see [8].
Our interest lies in the QOE using a two-level quantum system in the realm of relativistic quantum information (RQI), where relativity is taken into account. In particular, we consider a specific model for a qubit known as the Unruh-DeWitt (UDW) particle detector model [9, 10], which interacts with a quantum field in (curved) spacetime. The UDW detector model exhibits the essential features of the light–atom interaction as long as angular momenta are not exchanged [11, 12]. A UDW detector reveals interesting phenomena such as the Unruh effect [9], where a uniformly accelerating UDW detector perceives a thermal bath at the Unruh temperature TU = a/2π (where a is the magnitude of the acceleration), whilst an observer at rest sees a vacuum.
Investigations have been carried out previously on the QOE employing the UDW detector model. In [13], it was shown that a linearly accelerating UDW detector can be utilized to extract work in a QOE. This process is facilitated by the Unruh effect, which generates hot and cold thermal baths by varying the magnitude of acceleration a. Such an engine is commonly referred to as the Unruh QOE. The amount of work extracted is determined by a response function of the UDW detector, which is the probability of a transition from the ground state to the excited state and vice versa. Subsequent studies have further expanded on the Unruh QOE in various scenarios, including a fermionic field [14], a degenerate detector [15], entangled detectors [16, 17], and in the presence of a reflecting boundary [18]. However, these studies focus on a specific acceleration trajectory, the state of a field, and a switching function. A comprehensive investigation of the QOE in a more general setting still remains largely unexplored.
In this paper, we explore the QOE within the framework of RQI in a generalized setting. We consider a pointlike UDW detector following an arbitrary trajectory in curved spacetime, interacting with a quantum scalar field in a quasi-free state. Thus, the thermalization of the detector is not necessarily required. Employing a perturbative method, we derive general expressions (Eq. 3.15 and Eq. 3.20) for the work extracted through the quantum Otto cycle, which are written in terms of the response function of the detector. In addition, we identify conditions for extracting positive work in a generalized setting, given by Eq. 3.16 and Eq. 3.22. These conditions are expressed in terms of the effective temperature, an estimator for temperature, as perceived by the detector. Since thermality is not a prerequisite, the expressions for the work extracted and the positive work condition are applicable to any situation. Notably, when the field is in a thermal state, known as the Kubo–Martin–Schwinger (KMS) state and the interaction duration of a rapidly decreasing switching function is sufficiently long, the effective temperature becomes the KMS temperature. In such a case, the condition for positive work Eq. 3.22 becomes identical to the original condition found in [2, 3].
The derived expressions are demonstrated concretely within two scenarios: an inertial detector immersed in a KMS state of a quantum field in Minkowski spacetime and a detector in circular motion in the Minkowski vacuum. The first example is the most basic instance of thermality within QFT, for which we employ a Gaussian switching function and explore the effects of interaction duration.
The second example is inspired by the Unruh QOE previously examined in the literature, which has some challenges. A linearly accelerating detector requires an immense amount of acceleration to reach a temperature of 1 K. This can be observed from the expression of the Unruh temperature in SI units, TU = ℏa/2πkBc, where ℏ, kB, and c are the reduced Planck constant, Boltzmann constant, and speed of light, respectively. It is well known that an acceleration of a ∼ 1020 m/s2 is required to achieve TU ∼ 1 K. This implies that significant work must be performed on the detector to extract a small amount of work from the Unruh QOE. Moreover, the duration of interaction is almost instantaneous. Typically, the Unruh QOE assumes that the detector initially travels at a constant speed v and then accelerates until it attains the same speed in the opposite direction. The time interval in this process (in terms of the detector’s proper time τ) is given by Δτ = (2c/a)arctanh(v/c), and inserting a = 1020 m/s2, it requires v ≈ c to yield Δτ ∼ 1 s. Otherwise, if we demand a slower speed, say v = c/2, then the interaction duration amounts to Δτ ∼ 10−12 s, which is an extremely short period of time. The detector certainly cannot thermalize within such a time scale. Finally, executing such a protocol demands considerable space. The procedure in the Unruh QOE consists of linear acceleration and uniform motion at speed v. This means that it requires the detector to consistently move in one direction, which cannot be performed in a confined laboratory.
Instead, one can consider a UDW detector in circular motion, a concept that is motivated by [19–21], where an experimental setup is proposed to measure the circular Unruh effect (see also [22–25]). A circulating UDW detector overcomes the aforementioned shortcomings, although the temperature induced by the acceleration is no longer TU. In fact, the detector cannot be thermalized. Instead, one should define the effective temperature Tcirc as observed by the circulating detector [24, 26, 27]. This is where the proposed framework excels as our expressions remain valid even in the absence of thermality.
This paper is structured as follows. After we introduce the basic aspects of the UDW detector and thermality in quantum field theory in Section 2, we review the mechanism of QOE in Section 3.1. Our main results are shown in Section 3.2, followed by examples in Section 4.1 and Section 4.2.
Throughout this paper, we use ℏ = c = kB = 1 and the mostly positive signature convention (−+ ++).
2 Setup
2.1 Unruh-DeWitt detector model
Consider a pointlike UDW detector, which is a two-level quantum system with an energy gap Ω between ground |g⟩ and excited states |e⟩ locally interacting with the quantum Klein–Gordon field
In the Schrödinger picture, the total Hamiltonian
where
where λ is the coupling constant, τ is the proper time of the detector, and χ(τ/σ) is the switching function (with σ being the typical time scale of interaction), which determines the time dependence of coupling. In this paper, we assume that the L2 norm of χ(τ) is unity:
Let
where
Let us obtain the final state of the detector. The time-evolution operator in the interaction picture is given by
where
We consider the initial state of the total system
where ρϕ is the initial state of the field and ρD,0 is the initial state of the detector given by
The final total state ρtot can be obtained as
and by tracing out the field degree of freedom, we obtain the final state of the detector, ρD. In general, ρD contains n-point correlation functions
where
with
being the response function, i.e., the probability to excite the ground state |g⟩ to |e⟩. Similarly,
We note that ρD is the state of the detector after interacting with the field once, while in the QOE, the detector interacts with the field twice. Fortunately, Eq. 2.11 shows us that the density matrix ρD stays diagonal after the interaction, meaning the final density matrix also remains diagonal after the second interaction. Nevertheless, careful attention must be paid to the switching timings of these two interactions.
2.2 KMS condition
In quantum mechanics, a thermal state is given by the Gibbs state
We consider a Wightman function in a field state ρϕ:
It should be noted that the vacuum Wightman function
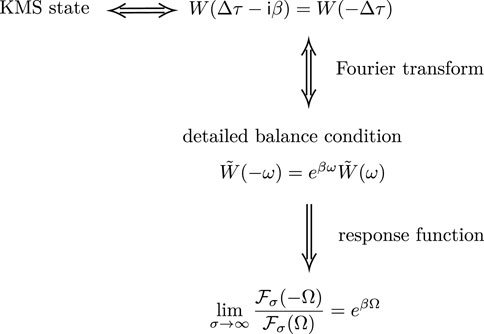
In addition, if the KMS condition is satisfied, then the Wightman function is stationary; i.e., it only depends on the difference in time: W(τ, τ′) = W(Δτ). We identify the KMS temperature TKMS as the temperature of the quantum field.
The KMS condition is related to the so-called detailed balance condition. For any function f(ω), the detailed balance condition at temperature β−1 is given by
It is known [31] that, assuming the Wightman function is stationary, the KMS condition with respect to τ at temperature
satisfies the detailed balance condition (Eq. 2.16).
The detailed balance condition can be implemented into the response function of a UDW detector. Suppose the Wightman function satisfies the KMS condition and the switching function χ(τ/σ) has a typical interaction duration time scale σ. The response function (Eq. 2.13) can be written as
where
Inspired by the detailed balance condition for the response function (Eq. 2.19), one may define the effective temperature Teff:
The effective temperature is an estimator for the KMS temperature of the field. In particular, if the Wightman function obeys the KMS condition and the long interaction limit (σ → ∞) is taken, then the effective temperature becomes the KMS temperature due to Eq. 2.19.
3 Relativistic quantum Otto engine
3.1 Review: quantum Otto engine
In this section, we review the QOE following [3]. It should be noted that the whole system is composed of a qubit and thermal baths in the Gibbs state. In the following section, we take the following protocol and apply it to the system composed of a UDW detector interacting with a quantum scalar field in a quasi-free state; i.e., we omit the assumption that the baths are in a thermal state.
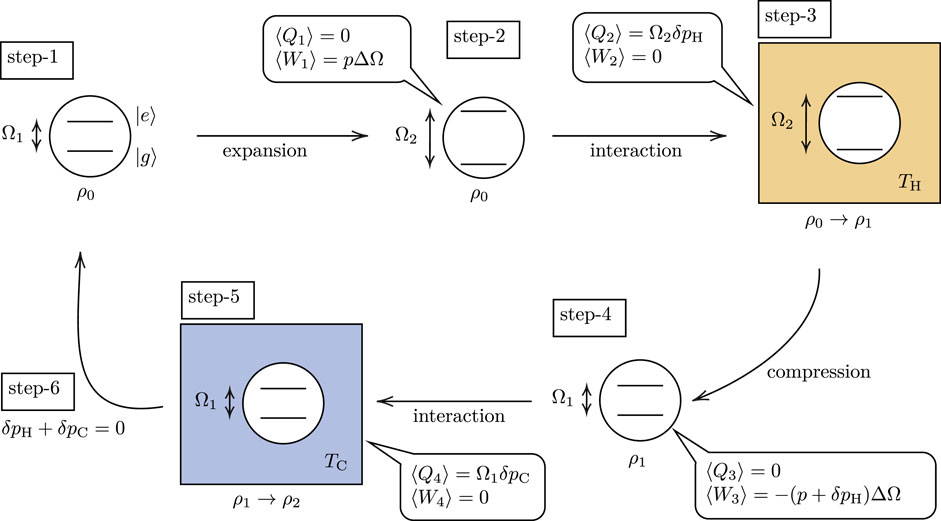
1. A qubit with energy gap Ω1 is prepared in an initial state ρ0 = p|e⟩⟨e| + (1 − p)|g⟩⟨g|, where p ∈ [0, 1], as shown in Figure 2.
2. The qubit undergoes an adiabatic expansion (zero heat exchange: ⟨Q1⟩ = 0) to enlarge the energy gap from Ω1 to Ω2, where Ω2 > Ω1. The Hamiltonian of the qubit is given by
where ΔΩ ≔ Ω2 − Ω1. The qubit’s state remains ρ0 due to the quantum adiabatic theorem.
3. The qubit interacts with a bath at temperature TH. The qubit’s Hamiltonian
This is an isochoric thermalization process.
4. After isolating the qubit from the bath, an adiabatic contraction of the energy gap from Ω2 to Ω1 is performed, while the state remains ρ1. From the same calculation as in step 2, we have
The work is extracted from the qubit in this process.
5. Next, another isochoric thermalization process is carried out: the qubit interacts with a bath at a colder temperature TC(<TH). At the end of the process, the state becomes ρ2 = (p + δpH + δpC)|e⟩⟨e| + (1 − p − δpH − δpC)|g⟩⟨g|, and so,
The total extracted work and dissipated heat read
Assuming that Ω2 > Ω1, the extracted work is positive if δpH > 0.
6. δpH + δpC = 0 is imposed to complete a thermodynamic cycle. From this condition, Eqs 3.7, 3.8 yield ⟨Q⟩ = ⟨Wext⟩, which obeys the first law of thermodynamics.
It is known that the positive work condition reads [2, 3] TC/Ω1 < TH/Ω2 and the efficiency of the QOE is ηO: = ⟨Wext⟩/Q2 = 1 − Ω1/Ω2.
3.2 Work extracted by a UDW detector
Now, let us employ a UDW detector as the qubit in this process. As mentioned previously, we do not assume that the baths are thermal. Instead, we only assume that the quantum field is in a quasi-free state, i.e., the one-point correlators
In this section, we consider a general scenario in which a UDW detector following an arbitrary path in spacetime interacts with a quantum field in a quasi-free state. Working perturbatively, we derive the extracted work and the condition for it to be positive.
3.2.1 Relativistic quantum Otto engine
We first describe our QOE in the relativistic setting, as shown in Figure 3.
• Step 1: Before the interaction, the detector with the energy gap Ω1 is prepared in ρD,0 in (2.9).
• Step 2: One performs a quantum adiabatic expansion Ω1 → Ω2 with Ω2 > Ω1. During this process, the detector does not interact with the field.
• Step 3: Isochoric process. The detector interacts with the field with a time dependence specified by a compactly supported switching function χH[(τ − τH)/σH], where τH is the center of interaction and σH(>0) is the interaction duration; its support is supp(χH) = [τH − σH/2, τH + σH/2]. The state changes from ρD,0 → ρD,1, where ρD,1 is given by Eqs 2.11–2.13, i.e.,
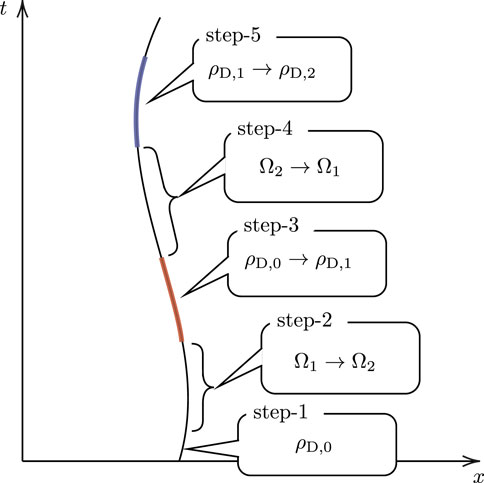
FIGURE 3. Each step in a relativistic QOE. The red and blue stripes indicate the isochoric process, i.e., the interaction between the detector and the field.
Although we identified the switching function as a compactly supported function, it is also possible to employ rapidly decreasing functions such as Gaussian or Lorentzian functions. These are not compactly supported, but the results remain unchanged when the exponentially decreasing tails of these functions are disregarded. We use these functions later in this section.
• Step 4: Adiabatic compression Ω2 → Ω1. Again, the detector does not interact during this process, and so, the state remains ρD,1.
• Step 5: Another isochoric process is implemented using χC[(τ − τC)/σC] for the switching function. To ensure that the interaction does not overlap with the previous isochoric process, we ensure that the supports of the two switching functions are disjoint by implementing τH + σH/2 < τC − σC/2. The state of the detector changes as ρD,1 → ρD,2, where ρD,2 = (p + δpH + δpC)|e⟩⟨e| + (1 − p − δpH − δpC)|g⟩⟨g|. The quantity δpC is
It should be noted that δpC contains λ4 terms since δpH is of the order λ2. As in the traditional QOE, the work extracted reads ⟨Wext⟩ = δpHΔΩ.
• Step 6: Finally, we impose the condition δpH + δpC = 0 to complete a thermodynamic cycle.
Since ⟨Wext⟩ only depends on δpH, it may appear that the cyclicity condition does not affect this value. However there is a subtlety. If we assume that an experimenter can freely choose a value of p ∈ [0, 1] at the beginning of the cycle, this means that the experimenter has to adjust the response functions
3.2.2 When p is free to choose
We first require the cyclicity condition, δpH + δpC = 0, to close the thermodynamic cycle. Since δpC contains terms of order
In particular, if the long interaction limit σH → ∞ is taken, we obtain
Thus, for long interaction duration,
Nevertheless, if the interaction duration is finite, then λ ≪ 1 is sufficient for our perturbative analysis.2
Under this restriction, the cyclicity condition for any p ∈ (0, 1] leads to
That is, one has to tune the response functions so that this equality is satisfied.
We then consider the positive work condition in the case where the value of p is chosen freely by an experimenter. The work extracted (Eq. 3.7) is
and the positive work condition is
It should be recalled that in the long interaction duration,
It should be noted that if the positive work is extracted while the cyclicity condition is satisfied, then
The opposite is not always true since the inequality does not necessarily imply the cyclicity condition (3.14). In addition, the statement (3.17) does not hold without the cyclicity condition. Nevertheless, by contraposition, if
The inequality
3.2.3 When p is adjusted
Let us focus on the case where p is initially adjusted and derive the work extracted. We again assume that p ≠ 0 and p ≫ δpH so that the terms higher than λ4 can be omitted in δpC. From the cyclicity condition, we can solve for p, which reads
By inserting p into Eq. 3.7, we obtain
The extracted work is positive if and only if
We find that the positive work condition (Eq. 3.21) can be written in terms of the effective temperature defined by Eq. 2.20 as
Again, we are not necessarily assuming that the field is in the KMS state, and so, the effective temperature is not necessarily the KMS temperature. If the field is in the KMS state and the detector with a rapidly decreasing switching function interacts with the field for a long time (σH, σC → ∞), the effective temperature becomes the KMS temperature, leading to
which is the condition found in [2, 3]. The extracted work in this case is
Therefore, Eq. 3.23 is a special case of Eq. 3.21 [and equivalently (Eq. 3.22)] when the response function obeys the detailed balance condition (Eq. 2.19). In other words, the condition (Eq. 3.21) [or alternatively (Eq. 3.22)] is applicable to any scenario, even when the detector is not thermalized.
In summary, we showed that within the perturbation theory, the positive work condition is associated with
4 Examples
We now demonstrate our results in (3 + 1)-dimensional Minkowski spacetime. Throughout this section, we use a Gaussian switching function
where τj is the center of the Gaussian and σ > 0 is the characteristic Gaussian width, which has the units of time.
4.1 Inertial detector in the thermal quantum field
Consider (3 + 1)-dimensional Minkowski spacetime. We aim to examine the extracted work (Eq. 3.20) by coupling an inertial UDW detector to a KMS state of the field to explore the basic properties of the work extraction.
The Wightman function in a thermal state of a massless field can be written as [34]
where WM is the Wightman function in the Minkowski vacuum and Wth is the contribution from the thermal state:
Here, ϵ is the UV cutoff and β = T−1 is the inverse KMS temperature of the field.
Assuming the Gaussian switching (Eq. 4.1), the response function
where
are the response functions for an inertial detector in the Minkowski vacuum and the thermal contribution, respectively. It should be noted that it does not depend on the center of the Gaussian switching since the Wightman function is time-translation invariant. We assume that the interaction durations are the same: σH = σC ≡ σ.
4.1.1 Case: free choice of p
We first consider the case where p is freely chosen, as discussed in Section 3.2.2. We plot ⟨Wext⟩/λ2σ defined in Eq. 3.15 as a function of interaction duration σ when TH = 2, Ω2 = 3, p = 0.315 and Ω1 = 1 in Figure 4Ai. The dashed line represents the asymptotic value, limσ→∞⟨Wext⟩/λ2σ, given by Eq. 3.18. We observe that the work can be extracted when the interaction duration is short, but as σ increases, extraction becomes exponentially difficult. This behavior can be explained by examining the positive work condition (Eq. 3.16) in Figure 4Aii. The figure shows that the positive work condition is satisfied when σ is small enough. When σ → ∞ is taken, the effective temperature becomes the KMS temperature:

FIGURE 4. Extracted work and conditions for a UDW detector in a KMS state of a thermal quantum field for (A) TH = 2 and (B) TH = 4. Here, Ω2 = 3, TC = 1, and p = 0.315 in units of Ω1. (Ai) and (Bi) depict ⟨Wext⟩/λ2σ as a function of the interaction duration σ in units of Ω1. The dashed line indicates the asymptotic value. The positive work condition is examined in (Aii) and (Bii), and the cyclicity condition is investigated in (Aiii) and (Biii). Negative values mean that work is carried out on the system (i.e., the UDW detector).
Although ⟨Wext⟩/λ2σ > 0 for some σ, the thermodynamic cycle is not closed. The cyclicity condition (Eq. 3.14) when σH = σC reads
We plot each side of this equation in Figure 4Aiii, fixing TC = 1 and other parameters (except σ) so as to find an optimal interaction duration σ such that the two curves cross. This point in the figure represents the scenario when the cyclicity condition is satisfied. As one can see, the positive work condition in Figure 4Aii and the cyclicity condition in 4Aiii are not satisfied at the same time; hence, the work extracted does not come from a genuine QOE. In fact, Figure 4Aii shows us that
Meanwhile, we can find a set of parameters that enables us to extract positive work from a closed QOE. This scenario is shown in Figure 4B, where TH = 4 is chosen. Figure 4Bi shows that the extracted work is positive for all σ, which is consistent with the positive work condition examined in Figure 4Bii. This time, from Figure 4Biii, there exists a value of σ that satisfies the cyclicity condition while ⟨Wext⟩/λ2σ > 0. Moreover, Figures 4Bii, iii exemplify the statement (Eq. 3.17): if positive work is extracted from a genuine QOE, then the effective temperatures satisfy
4.1.2 Case: adjusted p
We now consider the QOE described in Section 3.2.3. We first note that an inertial detector in the Minkowski vacuum (i.e., zero temperature: TH = TC = 0) cannot extract work from vacuum fluctuations since the condition (3.21) cannot be satisfied no matter what Ω and σ are. We then consider the KMS temperatures TH, TC ≠ 0 and compute the extracted work ⟨Wext⟩/λ2σ. The interaction duration σ is divided so that the perturbative analysis is valid—otherwise, the extracted work ⟨Wext⟩/λ2 monotonically increases with σ without an upper bound. In Figure 5A, we plot the extracted work ⟨Wext⟩/λ2σ as a function of σ with various TH. Here, quantities are in units of the energy gap Ω1 at the beginning of the cycle, and we fix Ω2/Ω1 = 3 and TC/Ω1 = 1. We observe that the detector cannot extract positive work when the interaction duration is too short (i.e., σΩ1 ≪ 1), while ⟨Wext⟩/λ2σ asymptotes to a number at σΩ1 ≫ 1. This is the opposite behavior of the result shown in Figure 4, and it can be attributed to the difference between the positive work conditions given by Eqs 3.16, 3.22. In the case of free p, as shown in Figure 4B,

FIGURE 5. (A) Extracted work ⟨Wext⟩/λ2σ as a function of the interaction duration σ in units of Ω1. Here, TC =1. The dashed lines are the work extracted (3.24) after the detailed balance condition is satisfied. (B) Effective temperature divided by the energy gap in the case of TH = 4 and Ω2 = 3 in (A). The positive work condition is satisfied when
The asymptotic value for each curve is depicted by the dashed line in Figure 5A, which is evaluated from (3.24). This confirms that, at the long interaction duration, the detailed balance condition for the response function (2.19) is satisfied. In addition, we observe that the work extracted when (TH/Ω1, Ω2/Ω1) = (2, 3) and (3,3) is always negative, whereas it is possible to extract positive work from the system with (TH/Ω1, Ω2/Ω1) = (4, 3). This can be understood from the condition (3.23); when the detailed balance condition (2.19) is satisfied (σΩ1 ≫ 1 in this case), the detector can extract positive work when the temperature of the baths and the energy gap obey (3.23).
4.2 UDW detector in circular motion
The Unruh QOE utilizes the thermality caused by the Unruh effect at the temperatures TH = aH/2π and TC = aC/2π with aH > aC in the protocol described in Section 3 [13]. However, as mentioned previously, a linearly accelerating UDW detector is not ideal for extracting thermodynamic work since it requires a tremendous amount of acceleration a as well as a huge space to let the detector travel long distances. Instead, we aim to employ a UDW detector in circular motion, which not only allows us to confine the detector in a compact space but also requires less space to acquire some temperatures compared to the linear acceleration case. Moreover, the Wightman function along a circulating detector’s trajectory does not satisfy the KMS condition. Our general expression for the extracted work (3.15) and (3.20) as well as the positive work condition (3.16) and (3.22) can still be applied to such a scenario.
We consider the circular trajectory of the UDW detector, which is given by
Here, R( > 0) is the radius of the circle, ω is the angular velocity of the detector, and
In order to calculate the response function (2.13), one needs to have an expression of the pullback of the Wightman function along the trajectory (4.7). We consider a minimally coupled, massless quantum scalar field in (3 + 1)-dimensional Minkowski spacetime. The Wightman function in the Minkowski vacuum is given by Eq. 4.3a. Inserting (4.7), we obtain the pullback of the Wightman function:
where Δτ ≔ τ − τ′. Since the Wightman function is a time-translation invariant, the response functions do not depend on the switching time.
4.2.1 Extracted work
From the aforementioned Wightman function, we can numerically calculate the response functions and the work extracted for the detector in circular motion. In Figure 6, we plot ⟨Wext⟩/λ2σ as a function of σ in units of the energy gap Ω1 in step 1. Figures 6A, B show the cases where p is freely chosen and tuned, respectively. In both figures, we set Ω2/Ω1 = 1.01, RΩ1 = 1, and aC/Ω1 = 1, and each figure includes the curves for aH/Ω1 = 2 and 3.
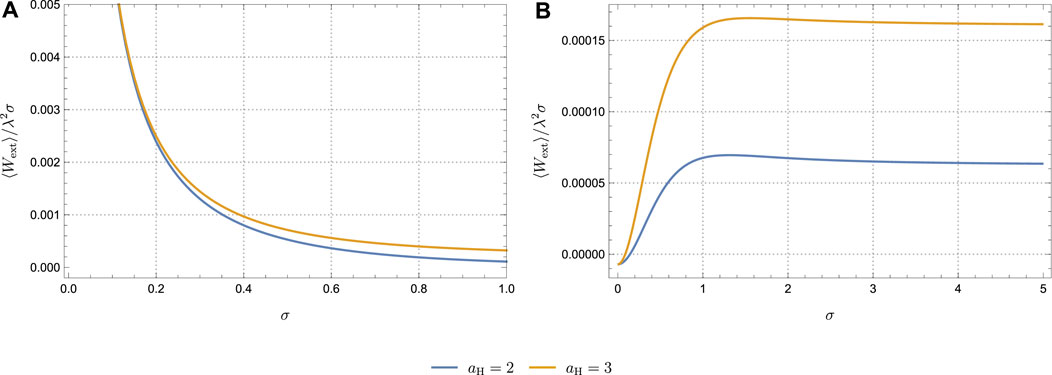
FIGURE 6. Extracted work ⟨Wext⟩/λ2σ by a detector in circular motion as a function of the interaction duration σ in units of Ω1. Here, Ω2 = 1.01 and aC = 1. (A) Case where p is adjustable and p = 1/20; (B) case where p is tuned to complete the cycle. Each figure contains aH = 2 and aH = 3.
As in the case of the inertial detector in a thermal bath, the QOE with a free p (here p = 1/20) extracts more work when the interaction duration is short [Figure 6A], whereas if p is tuned to close the cycle, the opposite behavior holds [Figure 6B]. However, we find that in the latter case, unlike in Section 2.2, the extracted work does not reach a maximum at large σ. Instead, there exists a maximum at σΩ1 ≈ 1. Nevertheless, we confirm that this behavior is contingent on the choice of parameters.
We then plot ⟨Wext⟩/λ2σ as a function of the radius of the circle, log10R, in units of Ω1 in Figure 7. Here, we set Ω2 = 2, σ = 1, aC = 1, and each figure includes curves for aH = 3, 4, and 5. As mentioned before, Figure 7A corresponds to the QOE with p = 1/20, while Figure 7B depicts the result with a tuned p. Both figures exhibit a similar pattern; a detector orbiting with a small radius R has difficulty extracting work, and ⟨Wext⟩/λ2σ is maximized as R increases, eventually asymptoting to some value at R → ∞. Thus, the radius R of the orbit must be optimized to extract the maximum amount of work.
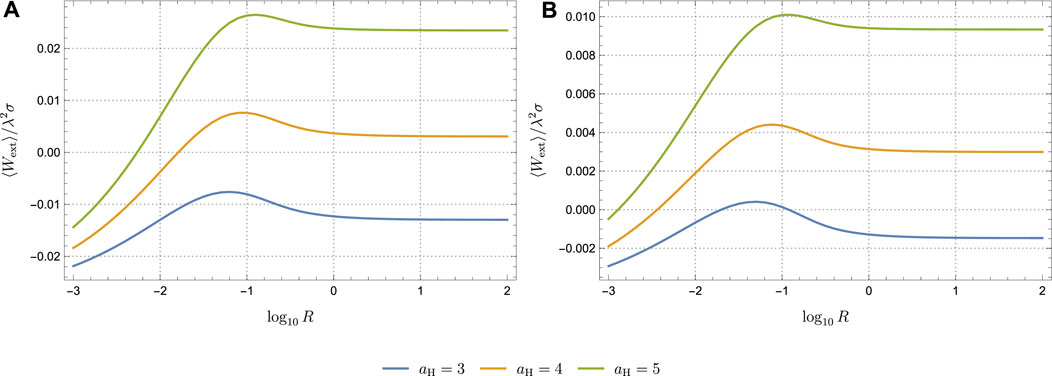
FIGURE 7. Work extracted by a circulating UDW detector as a function of the radius log10R when (A) p is adjustable (chosen to be p = 1/20) and (B) p is tuned to complete the cycle. Here, Ω2 = 2, σ = 1, and aC = 1 in units of Ω1. Each figure contains three cases of aH: aH = 3, 4, and 5. It should be noted that negative values correspond to work carried out on the system (i.e., the UDW detector).
4.2.2 Fixed acceleration
Although the analytic expression for the effective temperature for a circulating detector, Tcirc, cannot be obtained in general, one can impose an additional assumption to obtain the exact form of Tcirc. Suppose that the detector is circulating at high speed v ≈ 1 (i.e., ultrarelativistic regime), which can be realized by taking a large radius R. The effective temperature in this case is known to be [24, 27]
While the effective temperature Tcirc increases with a, it is also possible to enhance the temperature by enlarging the energy gap Ω with fixed acceleration. That is, for a given a, Tcirc(Ω2) > Tcirc(Ω1) if Ω2 > Ω1. We then ask if the detector circulating at high speed with a fixed acceleration a can extract positive work by manipulating the effective temperature by adjusting the energy gap.
The answer to this inquiry is negative. To see this, it is easy to check that, for a given a > 0, Ω2 > Ω1 ⇒ Tcirc(Ω2)/Ω2 < Tcirc(Ω1)/Ω1, which violates the necessary condition for positive work, (3.16) and (3.22). Thus, we find that, for any p ∈ (0, 1), it is impossible to extract positive work from a UDW detector in circular motion at v ≈ 1 by fixing a. This is one example of the feature of quantum heat engines: TC < TH does not necessarily guarantee the extraction of positive work in quantum heat engines, but rather, one should consider TC/Ω1 < TH/Ω2, where Ω1 < Ω2.
5 Conclusion
Inspired by the Unruh quantum Otto engines, we considered the QOE in a general setting utilizing a UDW detector interacting with a quantum scalar field. While the original QOE considered a qubit thermalized in thermal baths, we assumed that 1) the field is in a quasi-free state, not necessarily in a KMS thermal state and 2) the detector follows an arbitrary trajectory in curved spacetime. Using a perturbative method, we derived the extracted work (3.15 and 3.20) in terms of the response function of the UDW detector. In addition, we found that the condition for extracting positive work can be expressed in terms of the effective temperature perceived by the detector (3.16 and 3.22). These formulas are applicable to various scenarios outside (thermal) equilibrium. As a particular case, if the field is in the KMS state and the detector with a rapidly decreasing switching function interacts with it for a long time, the response function obeys the detailed balance condition, which makes the effective temperature identical to the KMS temperature. The condition (3.22) then becomes the positive work condition (3.23) originally found by [2, 3].
Using the formula for the extracted work, we explored two concrete examples: an inertial detector in the KMS state and a circulating detector in the Minkowski vacuum.
In the scenario of an inertial detector in thermal baths, we numerically examined the effect of the interaction duration. The relationship between the extracted work and the interaction duration is drastically changed by the choice of the detector’s initial state. Nevertheless, the extracted work asymptotes to the value that corresponds to thermal equilibrium as the interaction duration increases.
Another example involves a circulating detector in the Minkowski vacuum. The motivation for this scenario comes from the previously proposed Unruh QOE [13], in which the thermal baths are generated by the Unruh effect. However, utilizing a linearly accelerating UDW detector in the Unruh QOE is not practical for several reasons, such as the work necessary for acceleration and the requirement for a large space. The circulating detector, on the other hand, circumvents these issues. Moreover, the QOE with a circulating detector can be adequately examined only when our general framework is employed. The Wightman function pulled back along the circular trajectory does not satisfy the KMS condition, which suggests that the use of the effective temperature is necessary.
The work extracted by the circulating detector showed behavior similar to that of the inertial detector in a thermal bath. However, we found that there exist optimal values for the interaction duration and radius of the orbit to extract maximum work. Furthermore, we showed that the detector cannot extract work with a fixed acceleration due to the violation of the positive work condition.
An interesting extension to our work would involve exploring quantum heat engines using non-quasi-free states. In particular, coherent and squeezed states—which are not quasi-free—are of particular interest in a variety of settings. It would be interesting to see how a non-vanishing one-point correlator contributes to the cycle.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
KG-Y: conceptualization, formal Analysis, investigation, methodology, software, supervision, and writing–original draft and review and editing. VT: formal analysis, investigation, and writing–review and editing. RM: conceptualization, funding acquisition, investigation, methodology, supervision, and writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the Natural Sciences and Engineering Research Council of Canada.
Acknowledgments
KG-Y thanks Dr. Jorma Louko for the insightful discussion.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Sometimes, quasi-free states are called Gaussian states in the literature.
2To be precise, one has to make λ a dimensionless quantity since it has units of [Length](n−3)/2 in (n + 1) dimensions.
References
1. Scovil HED, Schulz-DuBois EO. Three-level masers as heat engines. Phys Rev Lett (1959) 2:262–3. doi:10.1103/physrevlett.2.262
2. Feldmann T, Kosloff R. Performance of discrete heat engines and heat pumps in finite time. Phys Rev E (2000) 61:4774–90. doi:10.1103/physreve.61.4774
3. Kieu TD. The second law, maxwell’s demon, and work derivable from quantum heat engines. Phys Rev Lett (2004) 93:140403. doi:10.1103/physrevlett.93.140403
4. Kieu TD. Quantum heat engines, the second law and Maxwell’s daemon. Eur Phys J D (2006) 39:115–28. doi:10.1140/epjd/e2006-00075-5
5. Rostovtsev YV, Matsko AB, Nayak N, Zubairy MS, Scully MO. Improving engine efficiency by extracting laser energy from hot exhaust gas. Phys Rev A (2003) 67:053811. doi:10.1103/physreva.67.053811
6. Quan HT, Zhang P, Sun CP. Quantum heat engine with multilevel quantum systems. Phys Rev E (2005) 72:056110. doi:10.1103/physreve.72.056110
7. Quan HT, Liu Y, Sun CP, Nori F. Quantum thermodynamic cycles and quantum heat engines. Phys Rev E (2007) 76:031105. doi:10.1103/physreve.76.031105
8. Myers NM, Abah O, Deffner S. Quantum thermodynamic devices: from theoretical proposals to experimental reality. AVS Quan Sci (2022) 4:027101. doi:10.1116/5.0083192
9. Unruh WG. Notes on black-hole evaporation. Phys Rev D (1976) 14:870–92. doi:10.1103/physrevd.14.870
10. DeWitt BS. Quantum gravity: the new synthesis. In: SW Hawking, and W Israel, editors. General relativity: an einstein centenary survey. Cambridge University Press (1979). 680–745.
11. Martín-Martínez E, Montero M, del Rey M. Wavepacket detection with the unruh-dewitt model. Phys Rev D (2013) 87:064038. doi:10.1103/physrevd.87.064038
12. Alhambra AM, Kempf A, Martín-Martínez E. Casimir forces on atoms in optical cavities. Phys Rev A (2014) 89:033835. doi:10.1103/physreva.89.033835
13. Arias E, de Oliveira TR, Sarandy MS. The Unruh quantum Otto engine. J High Energ Phys. (2018) 02:168. doi:10.1007/jhep02(2018)168
14. Gray F, Mann RB. Scalar and fermionic unruh Otto engines. J High Energ Phys. (2018) 11:174. doi:10.1007/jhep11(2018)174
15. Xu H, Yung MH. Unruh quantum Otto heat engine with level degeneracy. Phys Lett B (2020) 801:135201. doi:10.1016/j.physletb.2020.135201
16. Kane GR, Majhi BR. Entangled quantum Unruh Otto engine is more efficient. Phys Rev D (2021) 104:L041701. doi:10.1103/physrevd.104.l041701
17. Barman D, Majhi BR. Constructing an entangled Unruh Otto engine and its efficiency. J High Energ Phys. (2022) 05:046. doi:10.1007/jhep05(2022)046
18. Mukherjee A, Gangopadhyay S, Majumdar AS. Unruh quantum Otto engine in the presence of a reflecting boundary. J High Energ Phys. (2022) 09:105. doi:10.1007/jhep09(2022)105
19. Bell J, Leinaas J. Electrons as accelerated thermometers. Nu clear Phys B (1983) 212:131–50. doi:10.1016/0550-3213(83)90601-6
20. Bell J, Leinaas J. The Unruh effect and quantum fluctuations of electrons in storage rings. Nu clear Phys B (1987) 284:488–508. doi:10.1016/0550-3213(87)90047-2
21. Gooding C, Biermann S, Erne S, Louko J, Unruh WG, Schmiedmayer J, et al. Interferometric unruh detectors for bose-einstein condensates. Phys Rev Lett (2020) 125:213603. doi:10.1103/physrevlett.125.213603
22. Retzker A, Cirac JI, Plenio MB, Reznik B. Methods for detecting acceleration radiation in a bose-einstein condensate. Phys Rev Lett (2008) 101:110402. doi:10.1103/physrevlett.101.110402
23. Marino J, Menezes G, Carusotto I. Zero-point excitation of a circularly moving detector in an atomic condensate and phonon laser dynamical instabilities. Phys Rev Res (2020) 2:042009. doi:10.1103/physrevresearch.2.042009
24. Biermann S, Erne S, Gooding C, Louko J, Schmiedmayer J, Unruh WG, et al. Unruh and analogue Unruh temperatures for circular motion in 3 + 1 and 2 + 1 dimensions. Phys Rev D (2020) 102:085006. doi:10.1103/physrevd.102.085006
25. Bunney CRD, Biermann S, Barroso VS, Geelmuyden A, Gooding C, Ithier G, et al. Third sound detectors in accelerated motion (2023).
26. Good M, Juárez-Aubry BA, Moustos D, Temirkhan M. Unruh-like effects: effective temperatures along stationary worldlines. J High Energ Phys. (2020) 06:059. doi:10.1007/jhep06(2020)059
27. Unruh WG. Acceleration radiation for orbiting electrons (1998). Available from: https://arxiv.org/abs/hep-th/9804158 (Accessed October 27, 2023).
28. Kubo R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J Phys Soc Jpn (1957) 12:570–86. doi:10.1143/jpsj.12.570
29. Martin PC, Schwinger J. Theory of many-particle systems. I. Phys Rev (1959) 115:1342–73. doi:10.1103/physrev.115.1342
30. Haag R, Hugenholtz NM, Winnink M. On the equilibrium states in quantum statistical mechanics. Commun Math Phys (1967) 5:215–36. doi:10.1007/bf01646342
31. Fewster CJ, Juárez-Aubry BA, Louko J. Waiting for unruh. Class Quan Grav (2016) 33:165003. doi:10.1088/0264-9381/33/16/165003
32. Garay LJ, Martín-Martínez E, de Ramón J. Thermalization of particle detectors: the Unruh effect and its reverse. Phys Rev D (2016) 94:104048. doi:10.1103/physrevd.94.104048
33. Huang XL, Wang T, Yi XX. Effects of reservoir squeezing on quantum systems and work extraction. Phys Rev E (2012) 86:051105. doi:10.1103/physreve.86.051105
Keywords: Otto engine, Unruh effect, quantum thermodynamics, relativistic quantum information, quantum fields in curved space
Citation: Gallock-Yoshimura K, Thakur V and Mann RB (2023) Quantum Otto engine driven by quantum fields. Front. Phys. 11:1287860. doi: 10.3389/fphy.2023.1287860
Received: 02 September 2023; Accepted: 16 October 2023;
Published: 09 November 2023.
Edited by:
Yujun Zheng, Shandong University, ChinaReviewed by:
Subhashish Banerjee, Indian Institute of Technology Jodhpur, IndiaEkrem Aydiner, Istanbul University, Türkiye
Copyright © 2023 Gallock-Yoshimura, Thakur and Mann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Robert B. Mann, cmJtYW5uQHV3YXRlcmxvby5jYQ==
 Kensuke Gallock-Yoshimura
Kensuke Gallock-Yoshimura Vaishant Thakur
Vaishant Thakur Robert B. Mann
Robert B. Mann