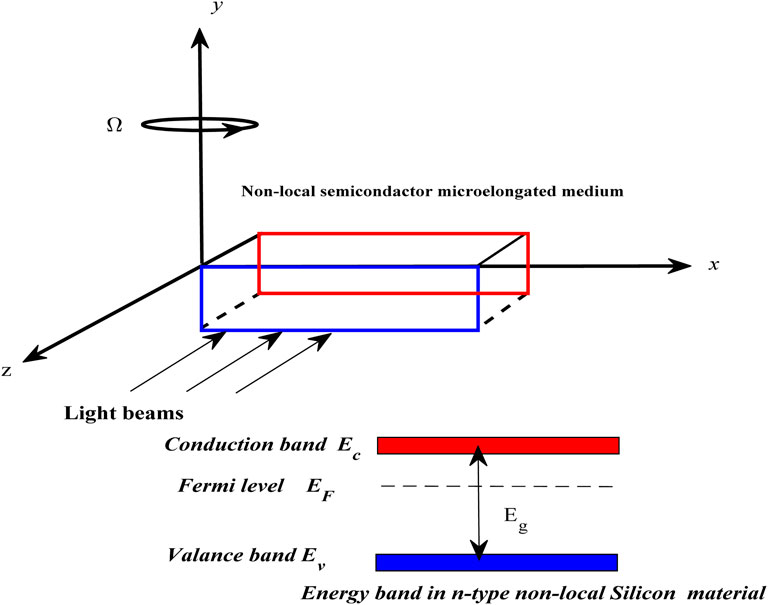
- 1Department of Mathematics, Faculty of Science, Islamic University of Madinah, Madinah, Saudi Arabia
- 2Department of Mathematical Sciences, College of Science, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
- 3Physics and Engineering Mathematics Department, Faculty of Engineering, Port Said University, Port Said, Egypt
- 4Arab Academy for Science, Technology and Maritime Transport, Alexandria, Egypt
- 5Council of Future Studies and Risk Management, Academy of Scientific Research and Technology, Cairo, Egypt
- 6Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
- 7Department of Mathematics, Faculty of Science, Taibah University, Madinah, Saudi Arabia
In this study, we investigate the effect of a rotation field on a homogeneous photo-thermoelastic nonlocal material and how its thermal conductivity changes as a result of a linearly distributed thermal load. The thermal conductivity of an interior particle is supposed to increase linearly with temperature. Microelastic, non-local semiconductors are used to model the problem in accordance with optoelectronic procedures, as proposed by the thermoelasticity theory. The micropolar-photo-thermoelasticity theory takes into account the medium’s microelongation properties in accordance with the microelement transport processes. This mathematical model is solved in two dimensions (2D) using harmonic wave analysis. Dimensionless components of displacement, temperature, microelongation, carrier density, and stresses are generated when the non-local semiconductor surface is subjected to the right boundary conditions. For silicon (Si) material, the wave propagation impact of the main physical fields is examined and graphically shown for various values of variable thermal conductivity, thermal relaxation durations, nonlocality, and rotation parameters.
1 Introduction
The classical theory of continuum mechanics, which regards matter as continuous, can only describe solids’ macroscale mechanical behavior since microstructures are microelements. Microinertia must be accounted for in continuum mechanics since macroscopic and microscopic scales must be considered. To conclude, thermoelasticity requires semiconductors to be elastic. Because thermoelastic and electrical deformations are linked. The ED is based on semiconductor crystal lattice photo-generation theory. Semiconductors microelongate because their internal resistance lowers with temperature. In light of the aforementioned, it is crucial to study how light’s thermal energy affects the material’s microelongation and microinertia. The photothermal (PT) theory states that transition phases promote free electrons on surfaces.
The idea of micro-elongation within the context of classical deformation posits that the micro-elongated medium can be classified into various typologies. The aforementioned examples encompass solid-liquid crystals, composite materials comprising elastic fibers, and porous media featuring pores filled with either gaseous or non-viscous fluids. The findings suggest that the expansion of material particles at the micro-scale exhibits volumetric characteristics. The material sites within the deformation medium undergo individual contraction and stretching. The semiconductor’s internal structure experiences various modifications in response to the thermal impact of light, as well as the shown microelongation parameters. Microelongation is dependent on thermal deformation, whereas the last one is dependent on electronic deformation based on electron rotation (micropolar) [1]. When studying the semiconductor materials in this scenario, the microstretch and micropolar theories are taken into account. When the directions of freedom of electrons are orthogonal and contraction, the microelongational theory arises as a specific instance of the microstretch theory. When considering the microstructure of the solid medium, Ref. [2, 3] introduced a unique microstretch-thermoelasticity model based on the micropolar theory. The generalized microstretch thermoelasticity theory [4–8] is used to investigate the many uses of elastic bodies. In the case of the Casson fluid flow of the porous medium, several applications of the microstretch theory are used for hydrodynamics [9, 10]. On the other hand, Ref. [11] investigated some viscoelastic conditions for the flow layer of a viscoelastic porous medium with a single relaxation period. To study the microelongated elastic media and determine wave propagation within an elastic medium, the impact of the internal heat source is applied [12, 13]. To understand the microelongated governing equations of an elastic material, The research conducted by Ref. [14–16] focused on analyzing the phenomenon of plane strain deformation along with the influence of an internal heat source. The micropolar theory of the elastic body is shown using the twofold porosity medium [17]. Reference [18–20] used the finite element analysis and eigenvalues approach to investigate the thermoelastic interactions in an initially stressed porous medium. Reference [21, 22] studied the responses of conductive semi-solid thermoelectric surface and thermomagnetic according to a heat transfer of Moore–Gibson–Thompson (MGT) model subjected to variable thermal shock.
The investigation of semiconductor materials using photoacoustic and photothermal theory (PT) has gained acceptance in recent years [1, 2]. Effective personification was examined by many authors in their examination of photoacoustic and photothermal technology [23–26]. This is made possible by using 2D deformation of the semiconductor material to examine how the photothermal and thermoelasticity theories interact [27]. According to ED, microcantilever methods are used to investigate the optical characteristics of semiconductor material [28, 54]. According to the photo-thermoelasticity theory of elastic semiconductor media, several researchers proposed some unique models with various applications that explain the interaction of mechanical, optical, thermal, and elastic waves [29–34]. In the framework of the two-temperature theory, Ref. [35, 36] conducted a study on a novel model that describes the excitation processes based on the theory of photo-thermoelasticity. This model takes into account variations in the thermal conductivity of the elastic media used in semiconductors. The dual-phase lags model under photothermal interaction processes was employed by Ref. [37]. To represent the photothermal excitation processes, Ref. [38] explored the revised multi-dual phase-lags model. When analyzing the semiconductor medium in the context of photothermal transport processes, Ref. [39] considered the microstretch theory under the impact of rotation. On the other hand, Ref. [40] investigated the photo-microstretch theory for a semiconductor elastic medium using the electro-magneto-thermoelasticity theory. Reference [41] investigated a cylindrical gap of semiconductor medium according to fractional MGT heat model of photothermal-induced due to laser pulse.
Reference [42] developed the nonlocal elasticity hypothesis by applying the principles of global balancing rules and the second law of thermodynamics. The theory of nonlocal elasticity initially focused on studying screw dislocation and surface waves in solids [43]. Reference [44] examined how the Hall current affected the nonlocality semiconductor media to obtain the optical, elastic, thermal, and diffusive waves. On the other hand, Ref. [45] investigated the thermos-diffusion waves for nonlocal semiconductors utilizing the fractional calculus and the laser short-pulse effect. When the thermal conductivity is variable (depends on the heat), previous works on non-local semiconductors ignored the impact of micro-elongation parameters and rotating fields.
In the present work, an examination of the ED and TE deformation in accordance with microelongated (microelements) excited medium was carried out. This examination looked at the impact of non-local, rotation field, and altering thermal conductivity, as well as photo-thermomechanical. When the primary physical fields are chosen in dimensionless form, the governing equations are stated in terms of the two-dimensional deformation of the space. Normal mode analysis is carried out to get the comprehensive analytical solutions of the primary variables under study under certain conditions that exist at the medium boundary. Several graphs are used in order to compare the waves that are propagated by the physical field variables in four distinct contexts. These contexts include the influence of rotational parameters, the effect of thermal memory, non-local contexts, and changing thermal conductivity.
2 Mathematical basic equations
The four basic quantities in this model: carrier density
1) The microelongated constitutive equations for non-local photo-thermoelasticity are [12, 54].
2) The coupled thermal-electronic equation is [28]:
3) The equation of motion and the microelongation equation for non-local medium, as determined by the processes involving microelements, may be expressed as [46]:
4) The non-local semiconductor medium’s microelongated heat conduction equation is [16]:
where
Certainly, in the context of a non-local microelongated semiconductor material, it is indeed possible to consider the thermal conductivity as a variable that depends on temperature. This relationship can be expressed mathematically as a linear function where the thermal conductivity is directly proportional to temperature. In this instance, the thermal conductivity may be expressed as follows by the thermal impact of light beams [35, 36]:
Where
The following quantities may be recast in space (xz-plane) and time
The basic Eqs. 2–4 in 2D can be reduced as:
The selected parameters
When applying map transform and differentiation affects, Eq. 2 may be rewritten as follows:
When the Taylor expansion was used to solve for the last component in the prior Eq. 13, the non-linear terms were ignored:
Integrating Eq. 12 and using Eq. 13, yields:
In this case, the non-local microelongated heat Eq. 5 can be reduced using the map transform (7) as:
Where
To further simplify things, the dimensionless quantities, have the form:
The basic equations may be rewritten as follows using the dimensionless Eq. 16 (with dropping the superscripts):
The potential scalar
Using Eq. 22, the main Eqs. 18–21 can be represented as:
The constitutive relations in 2D and dimensionless can be rewritten as [54]:
Where
3 Normal mode technique
Any function
Where
Using Eq. 29, the fundamental Eq. 17 and Eqs 23–27 take the following form:
Where,
Solving the system of Eqs. 30–34, yields:
Where the coefficients of Eq. 37 are:
Factorizing Eq. 37 with the roots
The solutions in linearity form for Eq. 37 are:
Where
The displacement components can be rewritten as:
The constitutive Eq. 35 can be represented as:
4 Boundary conditions
The arbitrary parameters may be assessed when certain boundary constraints are applied to the free non-local microelongated surface. The boundary conditions are selected at [45], and they may be introduced in the following ways:
Mechanical boundary conditions can be selected in the mechanical ramp type at
The other mechanical condition can be chosen for tangent stress freely at
When the converted temperature gradient has vanished, the thermal state may be considered. In the thermally insulated example, this is stated as [50]:
The scalar function’s elongation condition may be written as:
The carrier intensity condition of the microelongated non-local semiconducting may be shown following the diffusion transport mechanism. When the concentration of electrons
Where
5 Particular cases
1. The theory of rotational microelongation according to the non-local thermoelasticity is derived by considering the change in thermal conductivity while neglecting the impact of the photo-electronics plasma effect (i.e.,
2. The rotational non-local photo-thermoelasticity theory with the variable thermal conductivity is obtained under the effect of the photo-electronics plasma impact when the elongation parameters
3. The models of rotational photo-thermoelasticity with elongation and variation of the thermal conductivity are obtained when the non-local parameter is omitted (i.e.,
4. The elongation non-local photo-thermoelasticity theory according to the variable thermal conductivity is observed when the angular velocity is neglected (i.e.,
5. The elongation rotational non-local photo-thermoelasticity model is obtained when the thermal conductivity of the medium is independent of temperature (i.e.,
To depict the temperature previous to conversion using a map, it is possible to determine the connection between
6 Discussion and numerical results
A numerical analysis is carried out with the use of MATLAB (2022a) software to investigate the problem more closely and to explain the effects of relaxation times, rotation, the non-local parameter, and the thermal conductivity on the physical field variables according to the propagated waves. We have selected a polymer silicon (Si, n-type)-like semiconductor medium for numerical calculation. The SI units are selected for the physical constants of the Si media, which are represented as [52–54]:
In the current study, the dimensionless fields are used for numerical calculations to obtain wave propagations of the important physical variables in 2D according to a small value of time. The additional problem constants are used for numerical calculation as:
6.1 Impact of variable thermal conductivity
The effect of various non-positive parameters
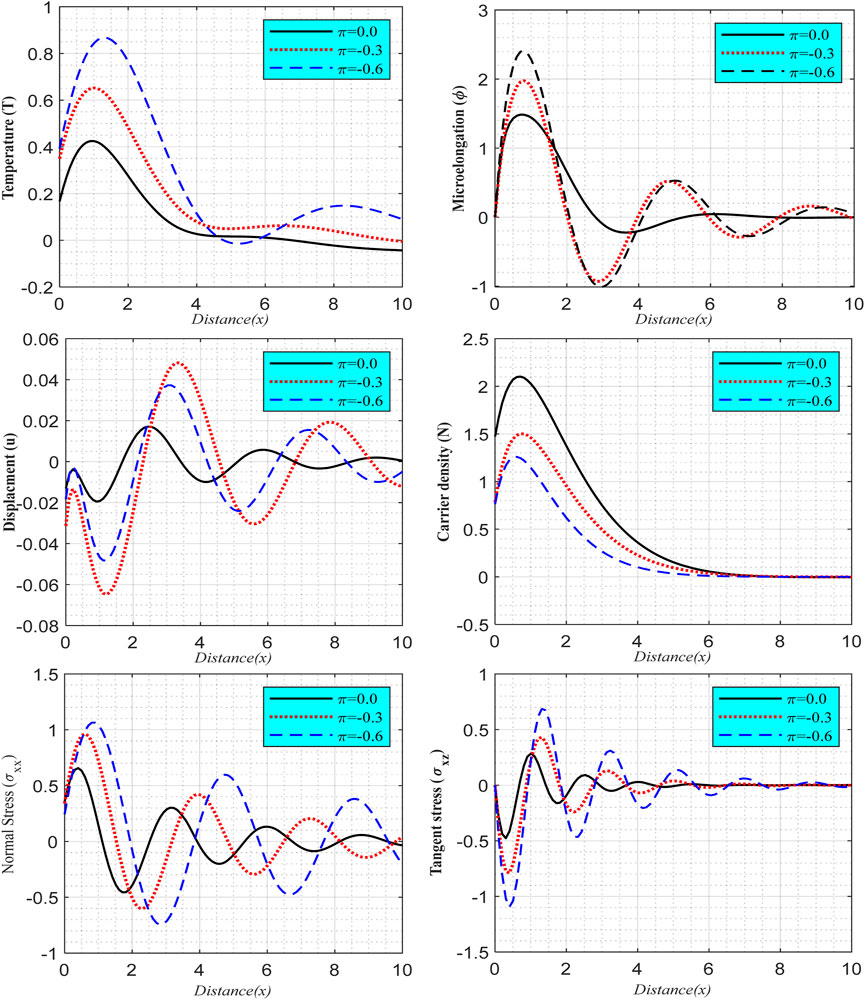
FIGURE 2. The effects of the rotating field in the non-local situation according to various values of variable thermal conductivity, as well as changes of the main physical field’s relative horizontal distance under the GL model.
6.2 Photo-thermoelasticity models
According to the photo-thermoelasticity models (
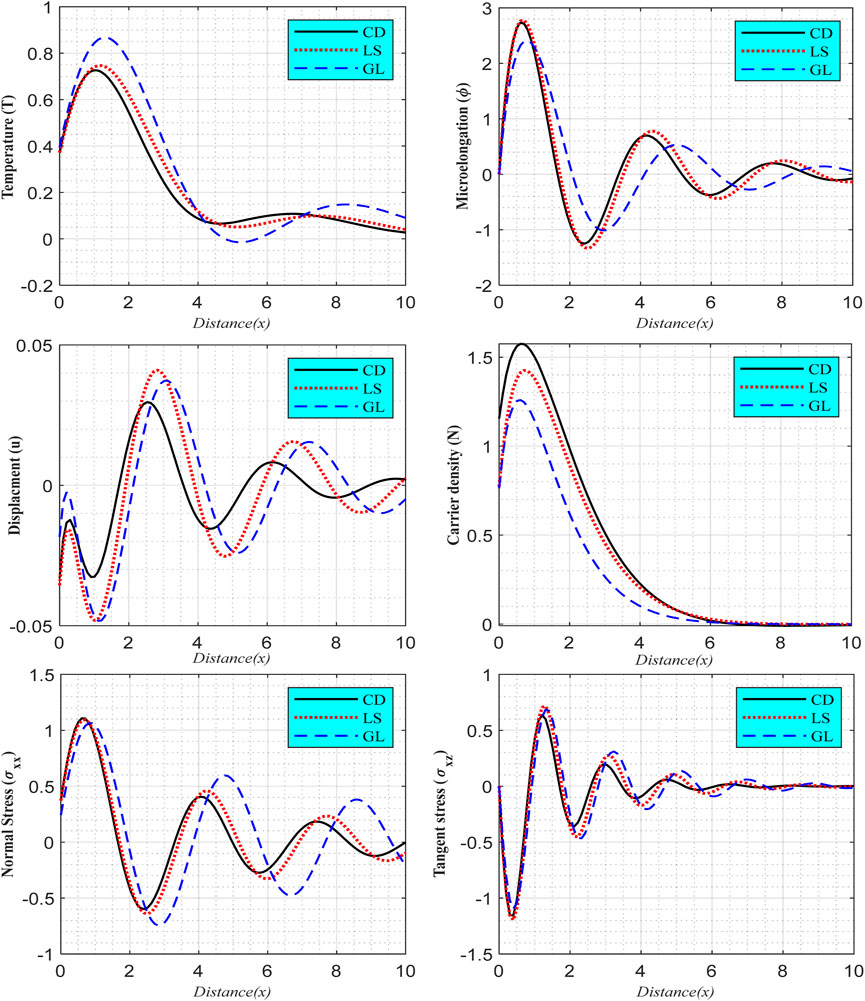
FIGURE 3. According to the variations in thermal relaxation times for non-local medium with varying thermal conductivity while
6.3 Impact of rotation parameter
The distribution of the basic physical fields in two different scenarios is shown in Figure 4 [presence and absence of rotation field (
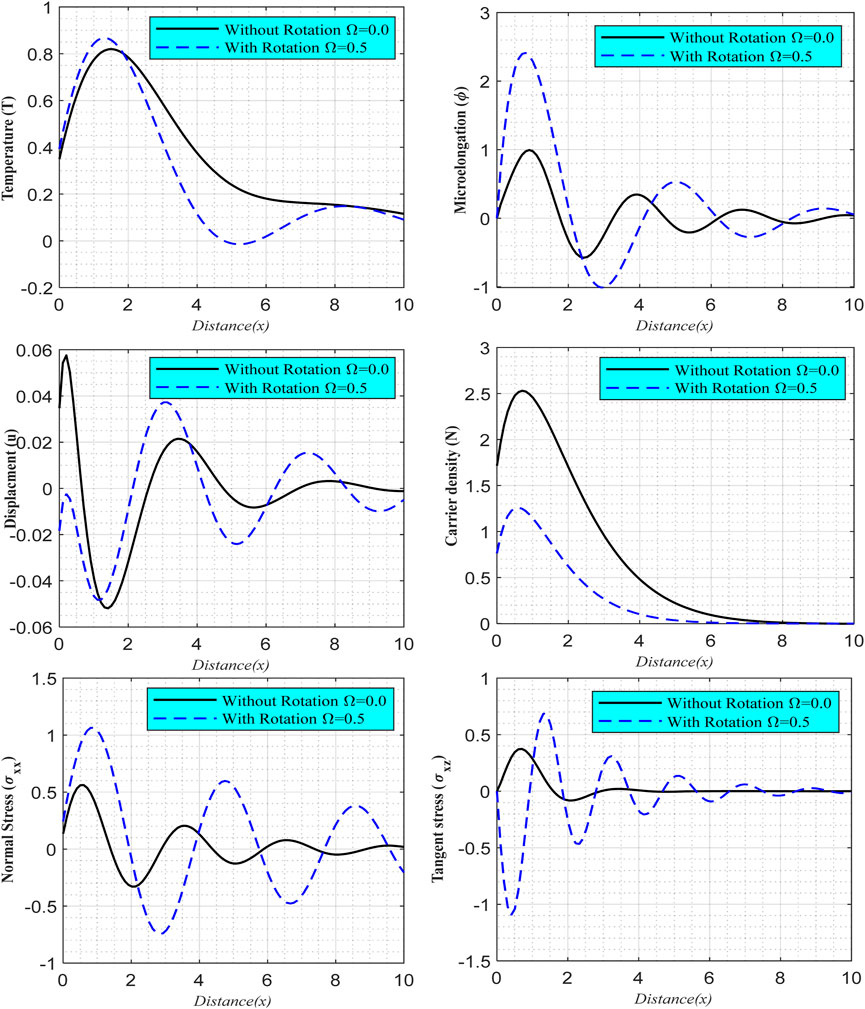
FIGURE 4. According to variable thermal conductivity (
6.4 Impact of the nonlocality parameter
To examine the impact of nonlocality in all of the distributions with the medium, Figure 5 has been plotted. At the small time according to the GL theory for rotational medium when
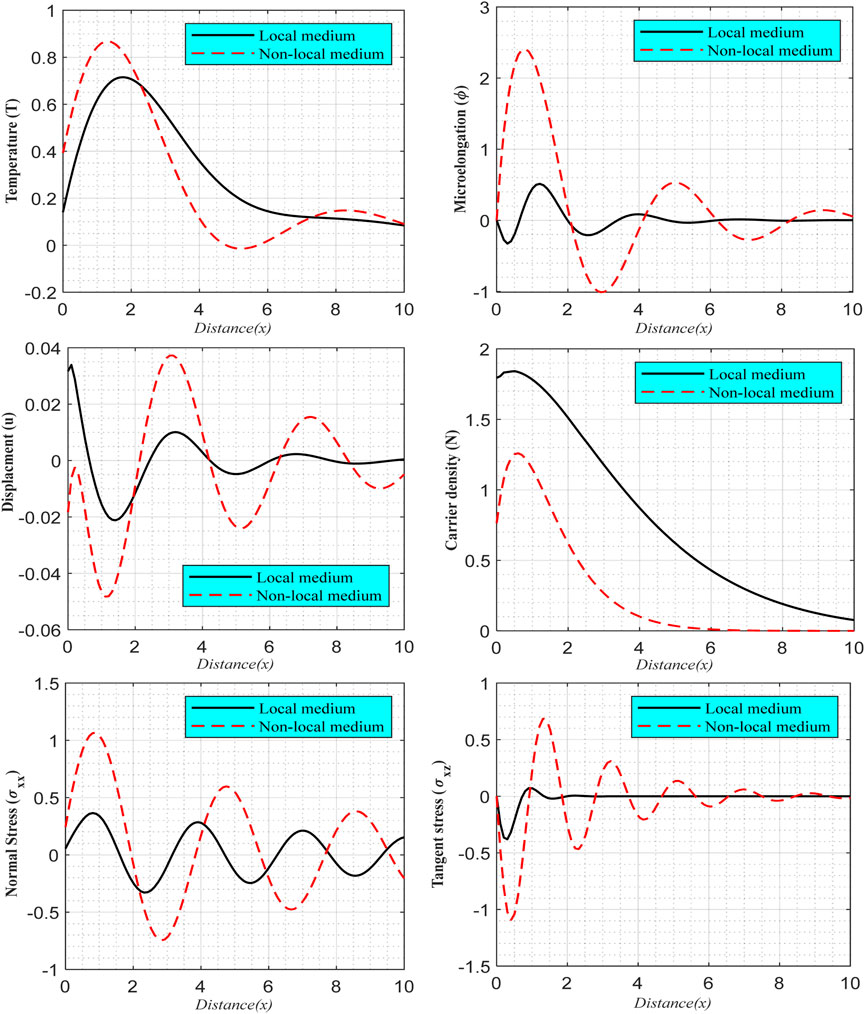
FIGURE 5. According to variable thermal conductivity (
6.5 The temporal influence
The present analysis pertains to the utilization of a time historical effect in accordance with the GL model for non-local rotating silicon (Si) material. Figure 6 illustrates the temporal variations of temperature, displacement, normal stress, and carrier density within the interval [0, 0.05] at three distinct distance values under the impact of the variable thermal conductivity. Based on the presented plot, it is evident that the distributions being examined exhibit an initial rise in amplitude, followed by a subsequent decline over time, ultimately penetrating further into the semiconductor material.
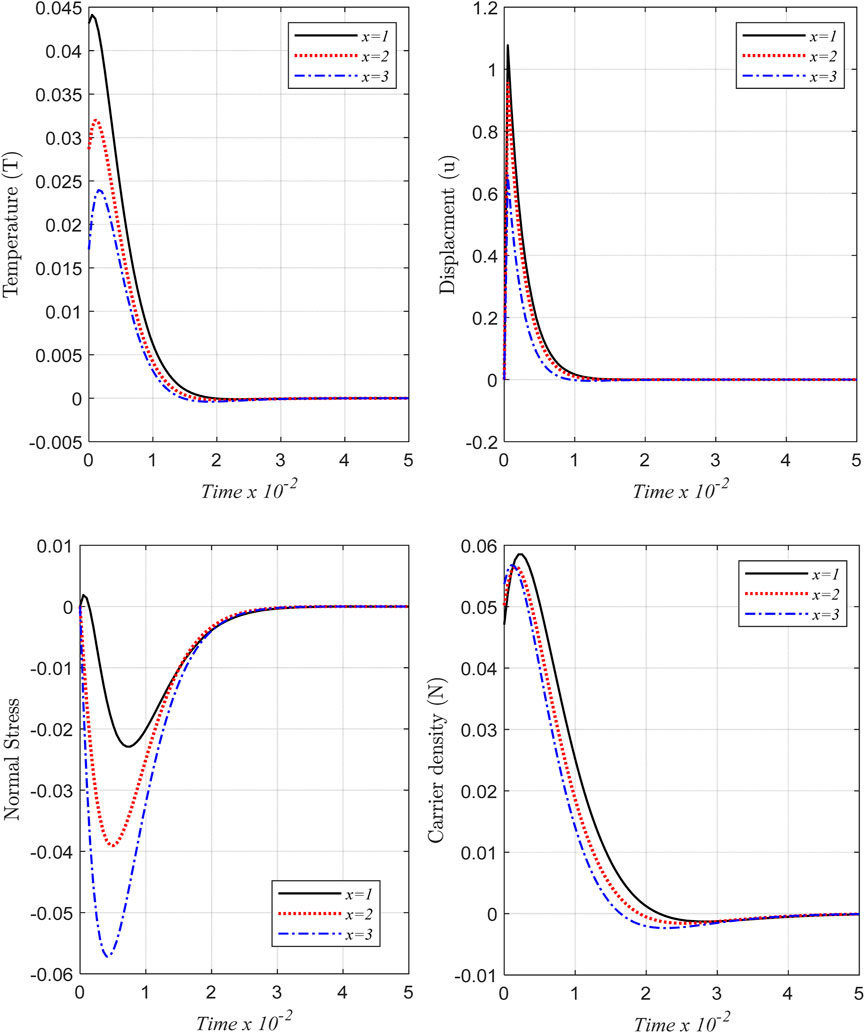
FIGURE 6. The temporal evolution of wave propagation in non-local rotating Si materials, as described by the GL model with variable thermal conductivity (
7 Conclusion
The research discussed focuses on investigating the two-dimensional deformation of a homogeneous, isotropic, microelongated semiconducting half-space within the framework of photo-thermoelasticity. The study incorporates variable thermal conductivity in its models and aims to explore the impact of this parameter, as well as thermal relaxation durations and rotation, on various physical fields. The numerical results obtained were approximated and visually represented. The findings suggest that the wave propagation behavior of the physical quantities is primarily influenced by the variable thermal conductivity parameter across a wide range. Using optoelectronics and thermoelastic processes, we are able to acquire and graphically illustrate the wave behavior of the primary fields in semiconductors. The magnitudes of the primary physical fields are observed to increase with different thermal relaxation time choices. Additionally, all waves propagating within the primary fields tend to approach equilibrium. The presence of angular velocity in the microelongated semiconductor medium, along with various relaxation time values, plays a crucial role in the distribution of the physical quantities within a nonlocality medium. Moreover, the rotation parameter is found to have a significant impact on the wave propagation of the studied physical variables. Research into microelongated semiconductor silicon is warranted because of its potential applications in modern electronic devices like cellphones, sensors, computer processors, medical equipment, diodes, accelerometers, inertial sensors, and electric circuits. It is also anticipated that it will be helpful in the design of structures in a wide range of engineering challenges, contemporary physics, mechanical material design, photo-thermal efficiency, and the solar cell. This article’s examination and findings will be invaluable to researchers interested in the applications of semiconductors like diodes, triodes, and other cutting-edge electrical devices.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
AK: Software, Data curation. WA: Writing–original draft. WH: Software, Writing–review and editing. AE-B: Software, Validation. KL: Supervision, Conceptualization, Methodology.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The researchers wish to extend their sincere gratitude to the Deanship of Scientific Research at the Islamic University of Madinah for the support provided to the Post-Publishing Program. The authors extend their appreciation to Princess Nourah bint Abdulrahman University for fund this research under Researchers Supporting Project number (PNURSP2023R229) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Eringen AC. Microcontinuum field theories, 1. New York: Foundations and Solids, Springer Verlag (1999).
2. Eringen AC. Linear theory of micropolar elasticity. J Math Mech (1966) 15(6) , 909–23. http://www.jstor.org/stable/24901442.
3. Eringen AC. Theory of thermo-microstretch elastic solids, Int J Eng Sci (1990) 28(12), 1291–301. doi:10.1016/0020-7225(90)90076-u
4. Singh B. Reflection and refraction of plane waves at a liquid/thermo-microstretch elastic solid interface, Int J Eng Sci (2001) 39(5). 583–98. doi:10.1016/s0020-7225(00)00051-3
5. Othman M, Lotfy K. The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation. J Comput Theor Nanoscience (2015) 12:2587–600. doi:10.1166/jctn.2015.4067
6. De Cicco , Nappa L. On the theory of thermomicrostretch elastic solids. J Therm Stress (1999) 22(6):565–80. doi:10.1080/014957399280751
7. Abouelregal A, Marin M. Response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry (2020) 12(8):Art. No. 1276. doi:10.3390/sym12081276
8. Marin M, Ellahi R, Vlase S, Bhatti M. On the decay of exponential type for the solutions in a dipolar elastic body. J Taibah Univ Sci (2020) 14(1):534–40. doi:10.1080/16583655.2020.1751963
9. Marin M, Chirila A, Othman M. Extension of Dafermos’s results for bodies with a dipolar structure. Appl Maths Comput (2019) 361:680–8. doi:10.1016/j.amc.2019.06.024
10. Ramesh G, Prasannakumara B, Gireesha B, Rashidi M. Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. J Appl Fluid Mech (2016) 9(3):1115–022. doi:10.18869/acadpub.jafm.68.228.24584
11. Ezzat M, Abd-Elaal M. Free convection effects on a viscoelastic boundary layer flow with one relaxation time through a porous medium. J Franklin Inst (1997) 334(4):685–706. doi:10.1016/s0016-0032(96)00095-6
12. Shaw S, Mukhopadhyay B. Periodically varying heat source response in a functionally graded microelongated medium. Appl Math Comput (2012) 218(11):6304–13. doi:10.1016/j.amc.2011.11.109
13. Shaw S, Mukhopadhyay B. Moving heat source response in a thermoelastic micro-elongated Solid. J Eng Phys Thermophys (2013) 86(3):716–22. doi:10.1007/s10891-013-0887-y
14. Ailawalia P, Sachdeva S, Pathania D. Plane strain deformation in a thermo-elastic microelongated solid with internal heat source. Int J Appl Mech Eng (2015) 20(4):717–31. doi:10.1515/ijame-2015-0047
15. Sachdeva S, Ailawalia P. Plane strain deformation in thermoelastic micro-elongated solid. Civil Environ Res (2015) 7(2):92–8.
16. Ailawalia P, Kumar S, Pathania D. Internal heat source in thermoelastic micro-elongated solid under Green Lindsay theory. J Theor Appl Mech (2016) 46(2):65–82. doi:10.1515/jtam-2016-0011
17. Marin M, Vlase S, Paun M. Considerations on double porosity structure for micropolar bodies. AIP Adv (2015) 5(3):037113. doi:10.1063/1.4914912
18. Abbas I. Finite element analysis of the thermoelastic interactions in an unbounded body with a cavity. Forsch Ingenieurwes (2007) 71:215–22. doi:10.1007/s10010-007-0060-x
19. Alzahrani F, Hobiny A, Abbas I, Marin M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry (2020) 12:848. doi:10.3390/sym12050848
20. Abbas I, Kumar R. 2D deformation in initially stressed thermoelastic half-space with voids. Steel Compos Struct (2016) 20:1103–17. doi:10.12989/scs.2016.20.5.1103
21. Megahid S, Abouelregal A, Askar S, Marin M. Study of thermoelectric responses of a conductive semi-solid surface to variable thermal shock in the context of the moore–gibson–thompson thermoelasticity. Axioms (2023) 12(7):659. doi:10.3390/axioms12070659
22. Megahid S, Abouelregal A, Ahmad H, Fahmy M, Abu-Zinadah H. A generalized More-Gibson-Thomson heat transfer model for the study of thermomagnetic responses in a solid half-space. Results Phys (2023) 51:106619. doi:10.1016/j.rinp.2023.106619
23. Gordon JP, Leite RCC, Moore RS, Porto SPS, Whinnery JR. Long-transient effects in lasers with inserted liquid samples. Bull Am Phys Soc (1964) 119:501–10. doi:10.1063/1.1713919
24. Kreuzer LB. Ultralow gas concentration infrared absorption spectroscopy. J Appl Phys (1971) 42:2934–43. doi:10.1063/1.1660651
26. Tam AC. Applications of photoacoustic sensing techniques. Rev Mod Phys (1986) 58:381–431. doi:10.1103/revmodphys.58.381
27. Tam AC. Photothermal investigations in solids and fluids. Boston: Academic Press (1989). p. 1–33.
28. Hobinya A, Abbas I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys (2019) 15:102588. doi:10.1016/j.rinp.2019.102588
29. Song YQ, Todorovic DM, Cretin B, Vairac P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int J Sol Struct. (2010) 47:1871–5. doi:10.1016/j.ijsolstr.2010.03.020
30. Lotfy K. The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field. Can J Phys (2016) 94:400–9. doi:10.1139/cjp-2015-0782
31. Lotfy K. A novel model of photothermal diffusion (PTD) for polymer nano-composite semiconducting of thin circular plate. Physica B- Condenced Matter (2018) 537:320–8. doi:10.1016/j.physb.2018.02.036
32. Lotfy K, Kumar R, Hassan W, Gabr M. Thermomagnetic effect with microtemperature in a semiconducting Photothermal excitation medium. Appl Math Mech Engl Ed (2018) 39(6):783–96. doi:10.1007/s10483-018-2339-9
33. Lotfy K, Gabr M. Response of a semiconducting infinite medium under two temperature theory with photothermal excitation due to laser pulses. Opt Laser Technol (2017) 97:198–208. doi:10.1016/j.optlastec.2017.06.021
34. Lotfy K. Photothermal waves for two temperature with a semiconducting medium under using a dual-phase-lag model and hydrostatic initial stress. Waves in Random and Complex Media (2017) 27(3):482–501. doi:10.1080/17455030.2016.1267416
35. Lotfy K. A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci Rep (2019) 9:3319. doi:10.1038/s41598-019-39955-z
36. Lotfy K. Effect of variable thermal conductivity during the photothermal diffusion process of semiconductor medium. Silicon (2019) 11:1863–73. doi:10.1007/s12633-018-0005-z
37. Abbas I, Alzahranib F, Elaiwb A. A DPL model of photothermal interaction in a semiconductor material. Waves in Random and Complex media (2019) 29:328–43. doi:10.1080/17455030.2018.1433901
38. Khamis A, El-Bary A, Lotfy K, Bakali A. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alex Eng J (2020) 59(1):1–9. doi:10.1016/j.aej.2019.11.016
39. Mahdy A, Lotfy K, El-Bary A, Alshehri H, Alshehri A. Thermal-microstretch elastic semiconductor medium with rotation field during photothermal transport processes. Mech Based Des Structures Machines (2021) 51:3176–93. doi:10.1080/15397734.2021.1919527
40. Lotfy K, El-Bary A. Magneto-photo-thermo-microstretch semiconductor elastic medium due to photothermal transport process. Silicon (2021) 14:4809–21. doi:10.1007/s12633-021-01205-1
41. Abouelregal A, Sedighi H, Megahid S. Photothermal-induced interactions in a semiconductor solid with a cylindrical gap due to laser pulse duration using a fractional MGT heat conduction model. Arch Appl Mech (2023) 93:2287–305. doi:10.1007/s00419-023-02383-7
42. Eringen A, Edelen D. On nonlocal elasticity. Int J Eng Sci (1972) 10:233–48. doi:10.1016/0020-7225(72)90039-0
43. Eringen A. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys (1983) 54:4703–10. doi:10.1063/1.332803
44. Chteoui R, Lotfy K, El-Bary A, Allan M. Hall current effect of magnetic-optical elastic-thermal-diffusive non-local semiconductor model during electrons-holes excitation processes. Crystals (2022) 12:1680. doi:10.3390/cryst12111680
45. Almoneef A, El-Sapa S, Lotfy K, El-Bary A, Saeed A. Laser short-pulse effect on thermodiffusion waves of fractional heat order for excited nonlocal semiconductor. Adv Condensed Matter Phys (2022) 2022:1–15. doi:10.1155/2022/1523059
46. Youssef H, El-Bary A. Two-temperature generalized thermoelasticity with variable thermal conductivity. J Therm Stresses (2010) 33:187–201. doi:10.1080/01495730903454793
47. Lord H, Shulman Y. A generalized dynamical theory of thermoelasticity. J Mech Phys Solid (1967) 15:299–309. doi:10.1016/0022-5096(67)90024-5
49. Biot M. Thermoelasticity and irreversible thermodynamics. J Appl Phys (1956) 27:240–53. doi:10.1063/1.1722351
50. Deresiewicz H. Plane waves in a thermoelastic solid. J Acoust Soc Am (1957) 29:204–9. doi:10.1121/1.1908832
51. Chadwick P, Sneddon IN. Plane waves in an elastic solid conducting heat. J Mech Phys Sol (1958) 6:223–30. doi:10.1016/0022-5096(58)90027-9
52. Chadwick P. Thermoelasticity: the dynamic theory. In: R Hill, and IN Sneddon, editors. Progress in solid mechanics, I. Amsterdam: North-Holland (1960). p. 263–328.
53. Todorović D, Nikolić P, Bojičic A. Photoacoustic frequency transmission technique: electronic deformation mechanism in semiconductors. J Appl Phys (1999) 85:7716–26. doi:10.1063/1.370576
54. Mandelis A, Nestoros M, Christofides C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt Eng (1997) 36(2):459–68. doi:10.1117/1.601217
55. Liu J, Han M, Wang R, Xu S, Wang X. Photothermal phenomenon: extended ideas for thermophysical properties characterization. J Appl Phys (2022) 131:065107. doi:10.1063/5.0082014
56. Abbas I, Hobiny A, Marin M. Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J Taibah Univ Sci (2020) 14:1369–76. doi:10.1080/16583655.2020.1824465
57. Marin M, Hobiny IA, Abbas I. The effects of fractional time derivatives in porothermoelastic materials using finite element method. Mathematics (2021) 9:1606. doi:10.3390/math9141606
58. Abouelregal A, Nasr M, Moaaz O, Sedighi H. Thermo-magnetic interaction in a viscoelastic micropolar medium by considering a higher-order two-phase-delay thermoelastic model. Acta Mech (2023) 234:2519–41. doi:10.1007/s00707-023-03513-6
59. Abouelregal A, Nasr M, Khalil K, Abouhawwash M, Moaaz O. Effect of the concept of memory-dependent derivatives on a nanoscale thermoelastic micropolar material under varying pulsed heating flow. Iran J Sci Technol Trans Mech Eng (2023). doi:10.1007/s40997-023-00606-4
Nomenclature
Keywords: semiconductor, photocarrier, micro-elongation, optoelectronic, rotation field, thermal conductivity
Citation: Kamel A, Alhejaili W, Hassan W, El-Bary AA and Lotfy K (2023) A changeable thermal conductivity and optoelectronic-mechanical wave behavior in a microelongated, non-locally rotating semiconductor media. Front. Phys. 11:1287381. doi: 10.3389/fphy.2023.1287381
Received: 01 September 2023; Accepted: 02 October 2023;
Published: 30 October 2023.
Edited by:
Gokhan Zengin, Selcuk University, TürkiyeReviewed by:
Katarzyna Jakimiuk, Medical University of Bialystok, PolandSengul Uysal, Erciyes University, Türkiye
Copyright © 2023 Kamel, Alhejaili, Hassan, El-Bary and Lotfy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Khaled Lotfy, a2hsb3RmXzF5QHlhaG9vLmNvbQ==
 Alwaleed Kamel1
Alwaleed Kamel1 Weaam Alhejaili
Weaam Alhejaili Alaa A. El-Bary
Alaa A. El-Bary Khaled Lotfy
Khaled Lotfy