- Department of Physics, University of Basel, Basel, Switzerland
A novel particle has been and still is an intriguing option to explain the strong evidence for dark matter in our universe. To quantitatively predict the dark matter energy density, two main ingredients are needed: interaction rates and the history of expansion of the universe. In this work, we explore the interplay between the recent progress in the determination of particle production rates and modified cosmological histories. For the freeze-out mechanism, we focus on Sommerfeld and bound-state effects, which boost and make dark matter pair annihilation more efficient. As regards the freeze-in option, we include thermal masses, which enter the decay processes that produce dark matter, and we find that they can suppress or enhance the dark matter yield. We consider a class of modified cosmological histories that induce a faster universe expansion, and we assess their effect in combination with improved particle interaction rates on the dark matter energy density.
1 Introduction
One of the major open challenges across cosmology and particle physics is to understand the content of our universe. There is mounting evidence that the fundamental building blocks of the Standard Model (SM) of Particle Physics account only for a small fraction of the matter in the cosmos, whereas the bulk appears to be some sort of non-luminous and non-baryonic particles. Complementary measurements of galaxy formation, gravitational lensing, large-scale structures, and the cosmic microwave background (CMB) point to the astounding conclusion that more than 80% of the matter consists of dark matter (DM). Nowadays, the DM energy density is very accurately determined by temperature anisotropies of the CMB, and it amounts to ΩDMh2 = 0.1200 ± 0.0012 [1], where h is the reduced Hubble constant.
Although this is not the only viable option, it is well possible for DM to be a new, yet undiscovered particle. The fervent interplay with particle physics-driven motivations for new physics has produced a plethora of models and rather different DM candidates (see, e.g., [2–3]) for extensive reviews. In order to establish whether a given DM model is cosmologically viable, one has to compare the corresponding prediction for the energy density and check its consistency with the Planck measurement. In practice, one needs to link the Lagrangian field content and parameters, most notably masses and couplings, with a production mechanism in the early universe. In this work, we consider the freeze-out [4–6] and freeze-in [7–9] mechanisms. In the former scenario, dark matter particles follow an equilibrium abundance when the temperature is larger than their mass and are kept in chemical equilibrium via pair annihilation, which is very efficient till T/M ≈ 1/25. Around this temperature, dark matter particles decouple from the thermal bath and their abundance is frozen ever since. The freeze-in mechanism entails the opposite situation: dark matter particles never reach equilibrium due to very small couplings with the plasma constituents. Typically, dark matter particles are generated through the decays of heavier accompanying states in the dark sector, as well as 2 → 1 annihilations and 2 → 2 scatterings that may involve SM particles. Dark matter particles only appear in the final state of the relevant processes, and their abundance increases over the thermal history. For renormalizable operators, the more important temperature window for freeze-in production is T ≳ M, which is complementary to that typical of the freeze-out scenario.
For both the freeze-out and freeze-in mechanisms, the interaction rates that are used for the prediction of the DM energy density are sometimes incomplete even at leading order. This is mainly due to a rather involved field content of realistic, and non-minimal, dark matter models, which triggers a series of compelling (thermal) phenomena. In this work, we consider two exemplary situations: (i) non-perturbative effects on non-relativistic annihilations for the freeze-out mechanism and (ii) the role of thermal masses in 1 → 2 decays driving the freeze-in production.
Around the freeze-out temperature, dark matter particles are non-relativistic and slowly moving objects in the early-universe thermal environment. Such a kinematical condition calls for a scrutiny and the inclusion of near-threshold (or non-perturbative) effects, that may be rather impactful depending on the details of the particle physics model. In many models, DM particles or accompanying states of the dark sector often interact with gauge bosons or scalar particles, which trigger self-interactions between dark sector particles. The typical manifestations of long-range interactions as induced by a repeated mediator exchange in the soft-momentum region are the Sommerfeld enhancement (for an attractive potential) [10, 11] and bound-state formation (BSF) [12–13]. The latter is caused due to transitions of DM pairs from a scattering state (or above-threshold state) into a bound state (or below-threshold state), and it can occur via different processes in a thermal environment [13–16]. In the non-relativistic regime, Sommerfeld factors and bound-state formation are formally a leading-order effect. Unless the coupling between the DM particles and force carriers is quite small, the inclusion of Sommerfeld and bound-state formation is crucial for a correct estimation of the DM energy density. Bound-state formation and decays especially work as an additional efficient channel to deplete the DM population. The effective annihilation cross-section is increased, and one typically finds larger DM masses that are compatible with the measurement of the Planck satellite for a fixed value of the DM couplings. Recent and ongoing efforts have shown that bound-state effects can substantially change the model parameter space that is compatible with the observed energy density. A research program that aims to reassess the reach of present and forthcoming experiments searching for DM, namely, direct and indirect detection, as well as collider searches, has been started only very recently (see, e.g., refs. [17–25] for exemplary studies).
As far as the less explored freeze-in mechanism is concerned, a systematic derivation of thermal cross-sections and widths is also being researched. Here, the relativistic (T ∼ M) and ultra-relativistic (T ≫ M) regimes are relevant, hence anticipating a prominent impact from plasma effects. Only recently has the use of a Maxwell–Boltzmann distribution been replaced by a more appropriate Fermi–Dirac/Bose–Einstein distribution for the decaying particle [26–28]. Despite the actual DM particle being feebly interacting, it is usually produced in multi-particle collisions or decays of equilibrated states in the thermal environment. This condition, which is largely model-independent, calls for a scrutiny of various thermal effects that are triggered by the interactions responsible for the equilibrium of such states, either SM gauge interactions or those of some hidden sector. Most notably, frequent interactions with a dense medium induce thermal masses and multiple soft scatterings. The latter, which is oftentimes called the Landau–Pomeranchuk–Migdal (LPM) effect, typically enhances the 1 → 2 decays and makes other effective 1 ↔ 2 processes possible [29–31]. At high temperature, 2 → 2 scatterings have to be treated with care when a soft-momentum region appears in the relevant processes [30, 32]. For all the mentioned processes, thermal masses have a significant role, which is the aspect we focus on in this work.
A thermal interaction rate on its own is almost meaningless unless it is compared with the expansion rate of the universe, namely, the Hubble rate. Irrespective of the production mechanism, either departing from thermal equilibrium (freeze-out) or never reaching it (freeze-in), the Hubble rate sets the clock that measures the efficiency of particle interactions. The main difficulty is that we do not know much about the expansion history of the universe at epochs prior to the Big Bang nucleosynthesis (BBN). Even though the early universe had to be radiation-dominated at the onset of the BBN, which occurred at
The paper is organized as follows. Section 2 describes near-threshold effects for DM pairs within the framework of potential non-relativistic effective field theories (pNREFTs). We discuss two exemplary models with a vector and scalar force carrier and highlight similarities and differences. Freeze-in via 1 → 2 decays is addressed in Section 3 for t-channel DM models, where we include thermal mass effects in the DM production rate. Section 4 presents a self-contained summary of modified cosmological histories that feature a faster expansion rate of the universe before the BBN epoch. Numerical results that show the interplay between improved thermal rates and modified cosmological histories are discussed in Section 5, whereas conclusions and outlook are offered in Section 6.
2 Near-threshold effects for DM freeze-out
Non-relativistic DM particles are susceptible to non-trivial dynamics whenever they interact through some force carrier. This happens in many ultraviolet completions of the SM, as well as in simplified DM models, where DM particles and/or co-annihilating partners interact via gauge bosons or scalar fields. If the mediator is sufficiently light to induce long-range interactions, DM pair annihilations can be severely affected. Typically, the Sommerfeld enhancement increases the annihilation cross-section for a pair in an attractive channel, which implies larger dark matter masses are compatible with the observed relic density. Moreover, there is yet another manifestation of multiple soft exchanges, namely, the existence of bound states: whenever they form in the early universe and are not efficiently dissociated, DM can also be depleted via bound-state decays. Hence, an additional efficient annihilation channel is active and, for a fixed value of the coupling strength, the corresponding dark matter energy density is further reduced.
In order to illustrate such effects, we consider the two following models: (i) Dirac dark matter fermion with a vector mediator in Section 2.2; (ii) Dirac dark matter fermion with a scalar mediator in Section 2.3. We first discuss some general features of non-relativistic dark matter pairs in a thermal environment within the framework of NREFTs and pNREFTs. Then, we specify the form of the low-energy theories for the two models and list the main observables that are necessary for the determination of the DM energy density.
2.1 pNREFTs for dark matter, Sommerfeld factors, and bound-state formation
The treatment of interacting non-relativistic particle pairs in a thermal environment is rather complicated because of the presence of many energy scales. To begin with, there are the dynamically generated scales by relative motion: (i) the momentum transfer, which is also proportional to the inverse of the typical size of the pair; (ii) the kinetic/binding energy of the pair. Such scales are hierarchically ordered with the DM mass for near-threshold states moving with relative non-relativistic velocities vrel, namely,
which we write specifically for the bound states.1
In this work, we exploit the framework of NREFTs [47, 48] and pNREFTs [49, 50] when dealing with interacting dark matter pairs and the observables of interest, namely, cross-sections and widths. We find convenient indicating pairs in a scattering state with
Since the ultimate goal is to address near-threshold effects at the ultrasoft scale, we integrate out the hard and soft energy modes in a two-step construction of the low-energy Lagrangian. The first step accounts for integrating out the hard energy/momentum modes of order M. The corresponding low-energy theory, which we generically indicate with NREFTDM, describes non-relativistic dark fermions and antifermions and low-energy mediators, and it is organized as an expansion in 1/M and α. The Lagrangian splits into a bilinear and a four-fermion sector. The former comprises interactions between non-relativistic fermion (and antifermions) with the force mediator. The four-fermion Lagrangian is especially relevant because the imaginary part of the corresponding matching coefficients originate from the particle–antiparticle annihilation diagrams [48]. In the so-obtained EFT, the soft scale (Mα) and ultrasoft scales (Mα2 and the temperature) are still intertwined.
The next step is to integrate out the typical relative distance among fermions and antifermions, which is induced by the soft-momentum exchange of the force mediator. As a result, the degrees of freedom are interacting dark matter pairs and ultrasoft mediators (see Figure 1 for a diagrammatic representation). The so-obtained low-energy theory is termed pNREFTDM. The potential between a fermion and an antifermion appears as a matching coefficient, and it is derived in a field theoretical fashion, namely, relativistic and quantum corrections can be computed. Moreover, there is a power counting that helps in estimating contributions to a given observable. Threshold phenomena affect fermion–antifermion pairs; hence, it is convenient to project the EFT on the fermion–antifermion space and express it in terms of a fermion–antifermion bilocal field φ(t, r, R),2 where r ≡x1 − x2 is the distance between a fermion at x1 and an antifermion at x2, which is typically of the order 1/(Mα), and R ≡ (x1 + x2)/2 is the center of the mass coordinate, which is of the order 1/(Mα2). In order to ensure that the mediators are ultrasoft, the corresponding fields are multipole expanded in r. Hence, a generic pNREFTDM Lagrangian density is organized as an expansion in 1/M and α(M), inherited from NREFTDM, and an expansion in r and α(1/r), and it reads schematically
where

FIGURE 1. One-loop self-energy diagrams of a scattering state
and S1 = σ1/2 and S2 = σ2/2 are the spin operators acting on the fermion and antifermion, respectively. Then, in the second line of Eq. 2, we display (i) the interaction Lagrangian that involves the bilocal field and the mediator Φ(t, R), where the latter does not depend on r; (ii) the Lagrangian term that comprises only mediator fields, which have been multipole expanded.
In the limit of the massless mediators considered in this study, the leading-order term V(0) in Eq. 4 is the Coulomb potential. The imaginary part of the potential terms V(2)/M2 and V(4)/M2 consists of local operators and describes the annihilation process
where S is the spin of the pair (S2 = 0 for spin singlets and S2 = 2 for spin triplets), while
The bound state formation process
2.2 Dark matter with a vector mediator
In this section, we consider a simple model where the dark sector consists of a dark Dirac fermion X that is charged under an abelian gauge group [59–63]. The Lagrangian density reads
where the covariant derivative is Dμ = ∂μ + igVμ, Vμ is the vector field, and Fμν = ∂μVν − ∂νVμ; we define the corresponding fine structure constant α ≡ g2/(4π). The term
The low-energy theory at the ultrasoft scale, which is obtained from the model Lagrangian (6), is expressed in the form of pNRQED [49, 66]. The scrutiny of the corresponding derivation in the context of dark matter is given in ref. [54]. By integrating out the hard and soft scales, one arrives at the following Lagrangian:
where we added the subscript in order to remind that the low-energy theory is for the abelian dark matter model in Eq. 6 and not for QED. We note that
We only display the non-vanishing matching coefficients. Depending on the two-particle states one projects onto, i.e., scattering and bound states, one obtains a cross-section or a decay width. The annihilation cross-section manifestly shows the factorization of hard and soft contributions, and it reads
where
where ζ = α/vrel. The corresponding observable for a bound state is a decay width. The expressions for nS and nP states exhibit the analogous hard versus soft factorization
and
where the bound-state wave functions and energy levels are taken at leading order, namely,
The ultrasoft vertex governs the transitions among dark matter pairs. For a vector mediator and in pNRQEDDM, the leading term is the electric dipole interaction of the dark fermion–antifermion pair with ultrasoft dark photons (see Eq. 7), which comprises thermal photons as well. The dipole interaction is needed to compute the bound-state formation process
The appearance of the Bose enhancement for the emitted mediator through the Bose–Einstein distribution comes naturally from pNRQEDDM at finite temperature. The subscript serves to distinguish the cross-section from the corresponding one in the case of a scalar mediator (cfr. Eq. 23). The energy splitting between a scattering state and a bound state, or equivalently the energy carried away from the emitted massless vector, is
which holds at the leading order. As a reference, and for later comparison with the scalar mediator case, we provide the explicit expression of the bound-state formation of the ground state, which reads
2.3 Dark matter with a scalar mediator
As in the previous model, we assume the DM particle to be a Dirac fermion that carries no charge under the SM gauge group. Dark matter fermions experience, however, an interaction that is mediated by a scalar particle of the hidden sector via Yukawa-type interactions. The Lagrangian density of the model reads [68–70]
where X is the DM Dirac field and ϕ is a real scalar. The scalar self-coupling is denoted by λϕ, whereas the scalar and pseudo-scalar couplings with the fermion are g and g5, respectively. For simplicity, we assume the scalar self-coupling to be negligible, playing no role in our analyses.3 The mass of the scalar mediator mϕ is assumed to be much smaller than the DM mass and, in order to compare the relevant observables with the gauge-invariant model where mγ = 0, we restrict to the situation mϕ ≪ Mα2. To a good approximation, we can then treat the corresponding bound states as Coulombic.
In this work, we consider the case where the scalar coupling is larger than the pseudo-scalar coupling, i.e.,
The low-energy theory that is obtained via a two-step matching from the model in Eq. 17, and with the hierarchy of scales (1), results in a pNREFT-like Lagrangian [73, 53]
where the square brackets in the second line of Eq. 18 indicate that the spatial derivatives act on the scalar field only, which is multipole expanded. It is worth mentioning the difference between the ultrasoft vertices of
The annihilation of heavy DM pairs into scalar particles is described by the universal Lagrangian in Eq. 5. One just has to obtain the specific matching coefficients for the model at hand. At leading order, the imaginary parts of the hard matching coefficients are [53]
They enable extracting the annihilation cross-section for scattering states and bound-state decay widths. The former observable reads
where the Sommerfeld factors are the same as the vector case (cfr. Eq. 11) because they are obtained from the wave function of dark matter pairs that satisfy the same Schrodinger equation with a Coulomb potential. We note that the pseudo-scalar interaction introduces a velocity-independent S-wave contribution for the annihilation cross-section in Eq. 21, which would be a pure P-wave in the limit α5 → 0. Projecting the operators of the Lagrangian in Eq. 5 onto bound states, one obtains, as counterparts of the decay widths in Eqs. 12, 13, the following decays into scalar pairs:
The bound-state formation
where three different matrix elements appear, at variance with the sole dipole matrix element in the vector case. Owing to the power counting offered by the pNREFT, and comparing the matrix elements, one can already note that the bound-state formation cross-section in Eq. 23 is α2-suppressed with respect to the case of a vector mediator. The bound-state formation for the ground state is
3 Thermal masses and dark matter freeze-in via decays
As mentioned in the Introduction, the production of dark matter via freeze-in involves temperatures larger than and of the order of the dark matter mass [8, 9] (see also [74] for a recent review). This calls for a careful scrutiny of thermal effects. A common modification for particles in a high-temperature environment is the appearance of thermal masses, which have only recently been addressed in the context of DM [75–80]. In these studies, the effect of thermal masses has been explored in decay processes, which would be forbidden at zero temperature and, instead, open up in a thermal plasma, and in combination with phase transitions in the early universe. In this paper, we consider a situation where thermal masses can either suppress or enhance the decay process that sources the DM production. At variance with the effects that we have discussed in Section 2, which increase particle interaction rates, here we focus on a situation where the particle production is less efficient due to thermal masses. We discuss an exemplary class of models where this situation occurs in the following section.
3.1 Majorana dark matter and t-channel mediators
Due to the increasing elusive characteristic of the dark matter particle, it is well-justified to assume it to be a SM gauge singlet. Of the different portal realizations, a quite rich phenomenology is offered by DM coupled to the visible sector via an accompanying component of the dark sector. The latter is taken to be charged under some (or all) gauge groups of the SM, and hence it triggers experimental prospects for direct and indirect detection, as well as collider searches. This class of models is often referred to as t-channel mediator models [81–83]. Here, the mediator stands for the particle of the dark sector that links the actual dark matter with SM fields, and it is not understood as a mediator of long-range interactions as in Section 2. The dark matter particle and the mediator carry a Z2 charge (they are odd under this symmetry), which makes the DM candidate stable in the first place upon assuming that it is the lightest state of the dark sector. Dark matter can be either a scalar or a fermion, and depending on the SM fermion it interacts with, the gauge quantum numbers for the mediator can be fixed (see [81] and [84]).
We consider two models where the DM is a Majorana fermion that interacts with (i) a right-handed up quark or (ii) a right-handed lepton. In both cases, the mediator is a scalar, either a triplet or a singlet under QCD, indicated by η. The Lagrangian can be written as follows:
where PL(R) are the chiral projectors, X is the Majorana fermion dark matter, f = q, ℓ is a SM fermion,
In the freeze-in scenario, the DM fermion only appears in the final state of the relevant processes. DM production occurs via 1 → 2 decays in this model, namely, η → Xf and its complex conjugate, as well as through 2 → 2 scatterings with SM particles. The latter are especially relevant for a compressed mass spectrum ΔM ≡ Mη − M ≪ M. We note that additional thermal phenomena can occur, which have been more carefully investigated for leptogenesis [29, 31, 32], such as multiple soft scatterings, namely, the LPM effect. The latter typically increases the production rate of a feeble interacting particle via effective 1 + n ↔ 2 + n processes (see [85] for their inclusion in the context of freeze-in DM). In this work, we aim to highlight the subset of thermal effects as restricted to thermal masses, which can make the production rate smaller. Such an approach already goes beyond the standard treatment in the present literature, where 1 → 2 decays are estimated with in-vacuum masses [86, 19, 84, 87, 88].
We derive the DM production rate in the formalism offered by the spectral function. For practical calculations, the spectral function of the produced particle can be related to the imaginary part of its retarded correlator at finite temperature ImΠR [89–91]. At leading order, one has to compute the imaginary part of the thermal one-loop self-energy of the dark matter particle (see Figure 2). The main advantage of such a formalism is that one can easily generalize a given process to a higher order and include thermal effects. The imaginary part of the retarded correlator enters the rate equation that governs the evolution of the DM particle. As we are in the freeze-in scenario, there is no loss term, and the rate equation is [85, 90]
where ∫k ≡∫d3k/(2π)3 and the factor of 2 counts the helicity states of the Majorana fermion. We consider only 1 → 2 decays as contributing to ImΠR; however, we assess the modification that may occur when including thermal masses.
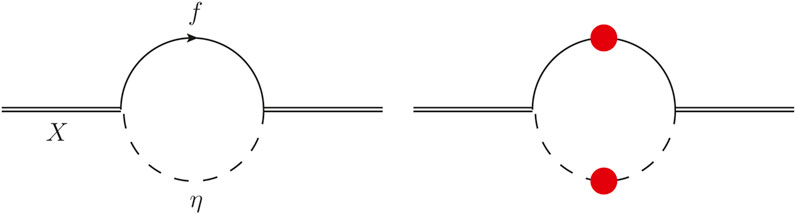
FIGURE 2. One-loop self-energy diagrams for the Majorana fermion dark matter X (solid double line). The scalar mediator and the SM fermion are displayed with dashed and solid lines, respectively. The left diagram shows a scalar mediator and SM with in-vacuum masses, whereas resummed propagators with thermal masses are shown in the right diagram.
In the high-temperature limit, which corresponds to temperatures larger than any in-vacuum mass scale, repeated interactions with the plasma constituents generate the so-called asymptotic masses. For the scalar mediator, SM right-handed quarks and leptons, they read [92, 93, 15]
where
We can now proceed with the calculation of the thermal process η → Xf, which is sometimes referred to as the Born approximation because it corresponds to the leading process that drives the freeze-in production. We present the result with finite thermal masses first, which corresponds to the right diagram in Figure 2 (red bubbles stand for resummed propagators with thermal masses). Then, we show the in-vacuum limit mi = 0, which originates from the left diagram in Figure 2. The production rate reads
where we have explicitly indicated that we single out the process η → Xf. Then,
It is useful to perform the in-vacuum mass limit, which yields an analytical expression for the Born rate, and serves as a reference for the corresponding result with thermal masses. It reads
where
The Born rate is our key factor to extract the DM energy density (cfr. Eq. 26) and to assess the interplay with modified cosmological histories. The corresponding numerical results are given in Section 5.2. Figure 3 shows the production rate ImΠR for the top-quark case (left panel) and a right-handed lepton (right panel). By choosing the top quark, we can inspect the impact of a finite Yukawa coupling hf in Eq. 27, which would be negligible for the other quarks and all the leptons. The in-vacuum masses of the dark sector particles, M = 2 TeV and Mη = 5 TeV, are chosen such that the freeze-in contribution to ΩDMh2 is largely dominant with respect to the one from the super-WIMP mechanism (see [19, 85]).6 For this choice of the masses, the 2 → 2 scatterings are also moderate with respect to the DM production from decays (see refs. [19, 85]). For a top-philic DM, the inclusion of thermal masses always suppresses the production rate with respect to the in-vacuum result (solid-blue line). Moreover, different values of the portal coupling λ3 ∈ [0, 1] have a rather marginal impact on ImΠR. A different effect due to thermal masses is instead found in the lepton case. Here, the outcome holds equally for each family since hℓ ≪ 1 for electrons, muons, and taus. The thermal correction to mη that is proportional to λ3 (see Eq. 28) plays a more important role, and it can make the production rate even larger than the in-vacuum limit (at high temperatures, the two-body phase space is increased by a large mη). For λ3 = 0, one finds again a suppressed rate with respect to the vacuum masses, although the Born rate with in-vacuum and thermal masses are closer with respect to the top-philic scenario. Section 5.2 focuses on scenarios where thermal masses inhibit DM production with respect to the in-vacuum mass limit. We then fix λ3 = 0, which reduces the number of free parameters of the models, while preserving their rich phenomenology.7
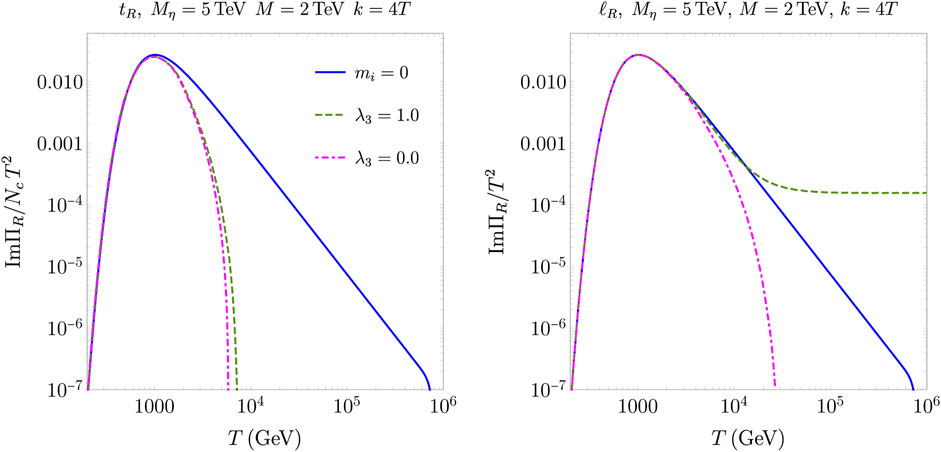
FIGURE 3. Production rate
4 Modified cosmological histories
The extraction of the DM energy density depends on the thermal history of the universe via the Hubble rate. This is the clock that measures the efficiency of a given particle rate in an expanding background. The standard procedure is to assume that the DM freeze-out and freeze-in occur in an epoch of radiation domination, where the SM is the dominant component at temperatures
4.1 A faster universe expansion
Following the approach given in ref. [100], a modification of the universe expansion history is achieved by introducing another species φ, that redshifts as φ ∝ a−(4+n), where a is the universe scale factor.8 For n > 0, the energy density of φ dominates the radiation component at early times, while it becomes completely negligible at later times. We label the corresponding energy densities as ρφ and ρrad, respectively. In order to be quantitative on the relative importance of the additional fluid during the thermal history, one has to choose some reference temperature. We use the prescription given in ref. [100], and we take the reference temperature Tref as the temperature at which ρφ = ρrad. On general grounds, the smaller Tref the longer and the faster the expansion takes place and modifies the standard picture. A variety of cosmological scenarios are accounted for by two parameters (Tref, n). For example, the case n = 2 describes the quintessential scenario [98, 99], which is also motivated by the discovery of the accelerated universe expansion. Such a case is also referred to as the kination regime, where the kinetic energy of the fluid is indeed dominant. Alternative realizations to the quintessence option, that still have the same redshift behavior, are described in refs. [101, 102]. Examples of cosmological scenarios with n > 2 are found in refs. [100, 103–105]. For the purpose of this study, the main point to be made is that, for temperature larger than Tref, the universe expands faster. Consequently, the predicted dark matter energy density may change because the particle interaction rates become less effective.9
In order to provide a self-contained discussion, we streamline the derivation of the main quantities that we need for the numerical extraction of the DM energy density. The steps for defining a modified effective number of relativistic degrees of freedom are as follows. First, one has to consider the conservation of the total entropy and assume that the standard radiation and additional specie φ dominate the universe energy budget, namely, ρ = ρrad + ρφ. This way, one can express the ratio of the energy density ρφ ∝ a−(4+n) at two different temperatures, which reads
and use this condition to express the energy density ρφ with the radiation temperature. The total energy density can be written as follows:
where we have used the definition ρφ(Tref) = ρrad(Tref) and geff(T) is the temperature-dependent number of relativistic degrees of freedom. From Eq. 34, one can define a generalized number of relativistic degrees of freedom for the modified cosmologies (Tref, n)
Let us remark that the limit to the standard cosmology is not recovered by setting n = 0. Rather, in this case, one has a double copy of a radiation-like fluid, which yields a factor of 2 for T = Tref in Eq. 35. The Hubble rate that is added to the relevant Boltzmann equations in Section 5 then reads
where MPl ≃ 1.22 × 1019 GeV is the Planck mass. Before concluding the section, let us briefly recall that an unavoidable constraint on the energy density of the additional field/fluid φ has to be imposed. Indeed, a faster expansion rate has to be limited at times (or temperatures) before the Big Bang nucleosynthesis, which occurs at TBBN ≃ 4 MeV [103, 106]. The remarkable agreement between the predictions and measurements of light-element abundances sets a cornerstone of particle cosmology. If the universe expands too fast at around the BBN epoch, then the light elements could not even form or, in any case, their abundance would sensibly change. The effect of the additional component φ is parameterized in terms of an effective number of relativistic degrees of freedom, more specifically adding up to the number of effective neutrinos, and we adopt a limit on the reference temperature, namely, Tref ≥ (15.4)1/n MeV [100]. We note that, by considering DM candidates with masses
5 DM energy density
In this section, we combine the improved interaction rates obtained in Sections 2, 3 with the modified cosmological histories of Section 4. Our aim is to quantitatively show the interplay of a faster expansion rate of the universe with (i) larger cross-sections from non-perturbative effects for the freeze-out scenario; (ii) a reduced particle production due to thermal masses in the case of freeze-in.
5.1 Freeze-out
In order to capture the DM annihilation in the form of bound states, we rely on an effective description, which is commonly adopted in the literature and was originally proposed in ref. [108]. In the most general case, the situation is rather complex because there is an equation for the DM particle number density, denoted by nX, and an equation for the number density of each bound state. A network of coupled Boltzmann equations would then need to be solved. However, whenever the reactions that drive the rate of change of the bound states are faster than the Hubble rate, the network of Boltzmann equations for the bound states significantly simplifies and turns into algebraic equations [108].10 The relevant particle rates are the bound-state dissociation rate and the bound-state decay width, which are both much larger than the Hubble rate for the mass parameters and couplings considered in this work. We have carefully checked that, even in the case of a faster universe expansion as discussed in Section 4, these conditions hold for the considered masses and couplings. As a result of such approximations, a single Boltzmann equation for nX is found, where the reprocessing of fermion–antifermion pairs into bound states and their decays is accounted for by an effective cross-section:
The factor of 1/2 on the right-hand side of Eq. 37 appears because we consider Dirac DM particles (hence not self-conjugated) [6]. For the Hubble rate, we will adopt the one in a standard cosmological history, i.e.,
where the sum runs over all bound states. The thermal averaging is carried out in the standard way, i.e., we take Maxwell–Boltzmann distributions for the incoming DM fermion and antifermion [6, 13]. The Sommerfeld-corrected annihilation cross-sections and the BSF cross-section are given in Eqs. 10, 14 for the vector mediator, whereas Eqs. 21, 23 give the scalar mediator. The decay widths
We present some numerical results where we aim to highlight the combination of larger particle rates and a modified cosmological history. The same version of each plot is presented for the two benchmark models, i.e., DM fermion with a vector and scalar mediator as discussed in Sections 2.2, 2.3. Figure 4 displays the DM energy density as a function of the reference temperature Tref. The DM mass and the couplings are indicated at the top label of each plot. The minimal reference temperature is well above the lower bounds
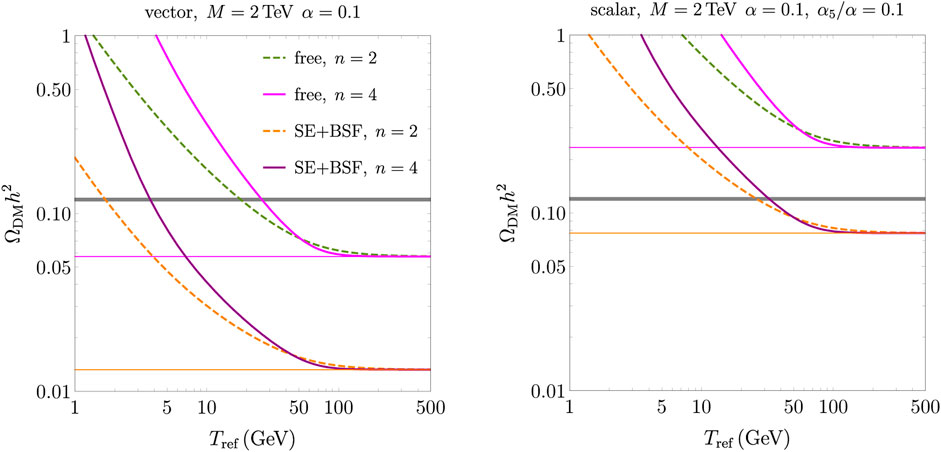
FIGURE 4. Dark matter energy density for the vector and scalar mediator models, (left and right panels, respectively) as a function of the reference temperature Tref. The coupling between the DM fermion and the mediator is set to α = 0.1 and M = 2 TeV (for the scalar mediator model α5/α = 0.1).
We next look at the contours that account for the Planck measurement of the DM energy density. Figure 5 shows the (M, Tref) plane for a fixed coupling strength (α = 0.1) and for two expansion histories (n = 2, 4). The DM mass that reproduces the experimental energy density within the standard cosmology can be inferred by looking at the vertical asymptotes for high enough Tref. The two sets of curves in each panel correspond to the DM relic density as obtained with a free annihilation cross-section, i.e., without non-perturbative effects, and with Sommerfeld and bound states, respectively. Bound-state effects are more prominent for the vector mediator case. For the vector model, the DM mass that is compatible with the observed energy density with the standard cosmology is M = 2.85 TeV (M = 5.90 TeV) for a free (non-perturbative) annihilation cross-section. As long as we consider Tref ≲ 200 GeV, a faster universe expansion demands larger cross-sections in order to agree with the observed DM energy density, and therefore smaller DM masses are needed. The effect of an increasingly longer and faster expansion is quite important, and the DM mass is progressively reduced up to approximately an order of magnitude for Tref = 154 MeV (we take the QCD phase transition as the minimal reference temperature in Figure 5). The faster expansion for n = 4 bends the contours further toward smaller values of the DM mass. Moreover, one can clearly observe how the non-perturbative effects move the contours to larger DM masses (free versus SE+BSF curves), whereas the faster expansion pushes toward smaller masses for Tref ≲ 200 GeV.
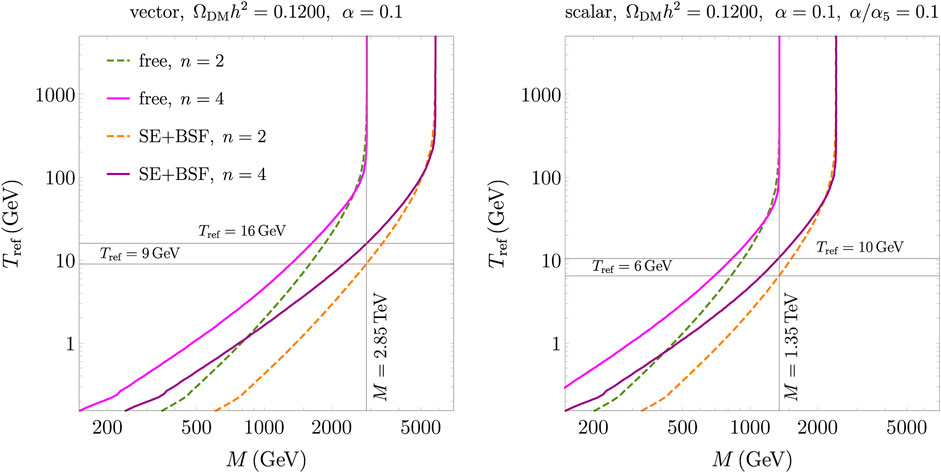
FIGURE 5. DM energy density contours for ΩDMh2 = 0.012 in the plane (M, Tref) for the vector (left panel) and scalar mediator models (right panels). Here, α = 0.1, α5/α = 0.1, and we show two options for the modified cosmologies (n = 2, 4).
There are two observations worth making about some degeneracy that is introduced when considering improved interaction rates and modified expansion histories. We refer to the vector mediator model for the specific values of the parameters. Similar statements hold for the scalar mediator model (mass and Tref benchmarks are indicated in Figure 5). First, the pair (M ≃ 800 GeV, Tref ≃ 1 GeV) is obtained when using the free annihilation cross-section and a modified cosmology with n = 2 or with non-perturbative effects and a modified cosmology with n = 4 (see intersecting dashed-green and solid-purple curves in Figure 5). Second, the dark matter mass M = 2.85 TeV, which provides the observed energy density for the standard cosmology and free cross-section, can be obtained with the inclusion of non-perturbative effects and modified cosmologies, respectively, for (Tref ≃ 9 GeV, n = 2) and (Tref ≃ 16 GeV, n = 4).
A final look at the interplay between particle rates and a faster universe expansion is explored in the parameter space (M, α) for different reference temperatures. The results are shown in Figure 6 for the vector and scalar mediator models. Here, we restrict to the case n = 2, which describes the case of kination domination or quintessence. As mentioned before, we extract the contours that account for the observed DM energy density; however, we use the annihilation cross-section with the inclusion of non-perturbative effects. The purple-dashed curve is the reference case for the standard cosmology; such a curve is also reproduced by modified cosmologies with Tref ≳ 103 GeV and for DM masses M ≲ 10 TeV. Then, for the vector model, the curves for Tref = 100 GeV and Tref = 20 GeV progressively deviate from the standard cosmology upon increasing the dark matter mass. This is because the freeze-out occurs more toward the epochs when the expansion is different from the standard setting (the freeze-out temperature is proportional to the DM mass). Smaller reference temperatures have a rather large impact, and the corresponding curves for Tref = 1 GeV and Tref = 0.154 GeV shift away from the standard scenario. Here, the observed energy density can only be maintained for large α and small DM masses. For example, for α = 0.1 in the vector model, modified cosmologies require a DM mass of M = 0.97 TeV and M = 0.43 TeV for Tref = 1 GeV and Tref = 0.154 GeV, respectively, instead of the standard cosmology case M = 4.9 TeV. Finally, we note a degeneracy of the predicted parameters (M, α) between the reference scenario given by the black-solid-thin line (standard cosmology and free annihilation cross-section) and modified cosmologies with Tref = 20 GeV and Tref = 10 GeV for the vector and scalar models, respectively (see dashed-orange lines overlapping with the black-solid-thin lines; for the vector case, the orange-dashed line gradually detaches at large couplings because of more relevant non-perturbative effects with respect to the scalar model).
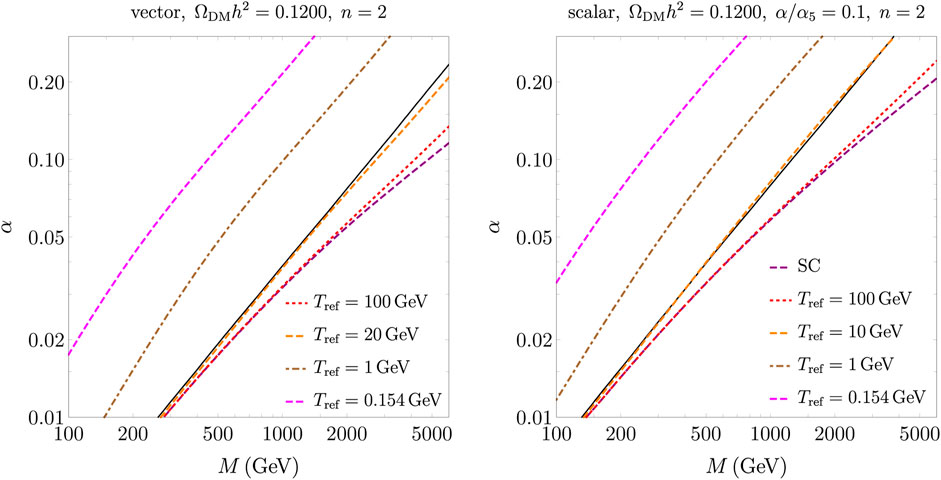
FIGURE 6. DM energy density contours for ΩDMh2 = 0.1200 in the parameter space (M, α) for the vector (left panel) and scalar mediator models (right panels). Here, we consider different reference temperatures, whereas we fix n = 2 to identify the kination/quintessence option for a modified expansion history.
5.2 Freeze-in
In this section, we present the numerical results for the DM energy density that are extracted with the Born rate with and without thermal masses (cfr. Eqs. 29, 31) and its interplay with a modified expansion history of the universe. The rate equation for the DM abundance has been given in Eq. 26. We further introduce (i) the yield variable YX = nX/s; (ii) the actual production rate, that has indeed the dimension of an energy and comprises the Yukawa coupling y, together with its thermal average as follows [89, 91]
Both Γ(k) and ⟨Γ⟩ inherit the temperature dependence of ImΠR as shown in Figure 3. Our integration variable is x ≡ ln(Tmax/T), with Tmax as the maximal temperature, and we start the evolution with vanishing DM abundance YX(x = 0) = 0. We present the numerical results for the top-quark and lepton options. For the SM couplings, we take them running at one loop (see [85] for the renormalization group equations).
Figure 7 shows the DM energy density as a function of the temperature. One may see how the DM abundance grows from a vanishing initial value and adjusts to a constant, i.e., freezes in, for T ≲ Mη/10, as indicated with the gray vertical line. As a reference to single out the impact of a faster universe expansion, the energy density is given for the standard cosmological scenario without and with the inclusion of thermal masses by solid-blue and dot-dashed magenta lines, respectively. The Yukawa coupling y is tuned to reproduce the observed ΩDMh2 for the in-vacuum mass case and with a standard cosmological history. Thermal mass effects change the final frozen-in density. The suppression of the production rate with thermal masses (dot-dashed magenta) is more important for the top-quark option, where a correction of approximately 25% is found, whereas in the lepton case, corrections are about few percentages for our choice of the parameters. When considering the effect of a faster expansion rate with Tref = Mη/10 and n = 2 (dashed-green lines) and thermal masses, the predicted energy density decreases quite visibly irrespective of the SM fermion–DM interaction. It is worth highlighting that the specific choice of the reference temperature Tref = Mη/10 makes the faster expansion relevant for the entire duration of the DM production. An important comment is in order. As noticed earlier in ref. [110], and at variance with the freeze-out scenario, a faster expansion rate induces a smaller DM energy density as a result of a less effective production rate over the thermal history. Thermal masses make this feature even more prominent.
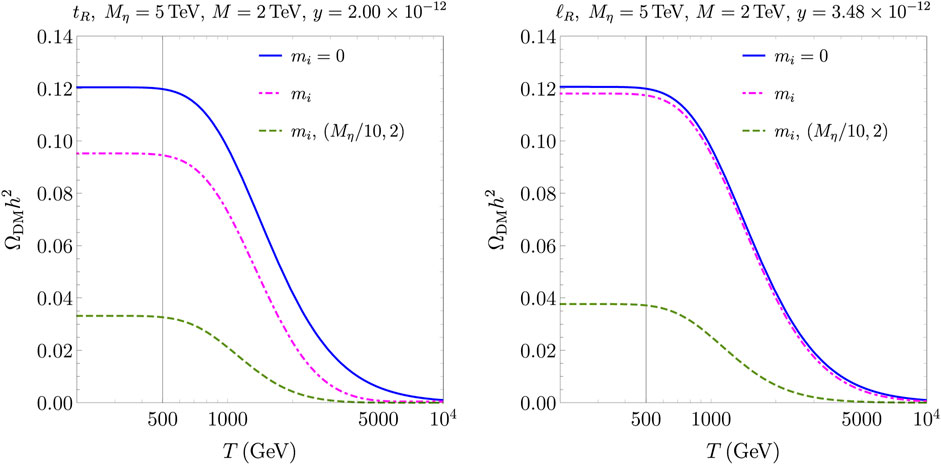
FIGURE 7. DM energy density as a function of the temperature. Thermal and in-vacuum masses are included in the production rate. The parameters of the modified cosmological history are Tref = Mη/10 and n = 2. The mediator–Higgs coupling is λ3 = 0.
Finally, in Figure 8, the DM energy density is given as a function of the reference temperature for two values of the modified cosmology parameter n = 2, 4. Dashed-green and dashed-orange lines stand for n = 2, whereas solid-magenta and solid-purple curves stand for n = 4. The observed DM energy density is attained with vacuum masses for Tref ≫ Mη, M. Indeed, the values of the Yukawa couplings have been set to obtain ΩDMh2 = 0.1200 with in-vacuum production rates and a standard cosmology (see solid-blue lines in Figure 7). By decreasing the reference temperature, the effect of a faster expansion becomes more important and reduces the DM energy density of about one order of magnitude for the smallest temperature that we consider, Tref = 200 GeV, and for n = 4. Moreover, one may see a rather different role of the thermal masses for the two DM–SM fermion interactions. Comparing the left and right panels of Figure 8, one may single out which effect is dominant for the colored or purely weak interacting mediator. First, the suppression of the production rate from thermal masses is more important for the interaction of the DM with a top quark, as one can note by looking at the relative separation of the green-dashed and orange-dashed (solid-magenta and solid-purple) lines for n = 2 (n = 4). Conversely, the curves are much closer in the case of a leptophilic DM particle. Second, for smaller Tref, there is a progressive approach of the DM energy density as obtained with in-vacuum or thermal masses. This feature is more visible in the top-quark scenario, and it originates from the shape of the thermal rates ImΠR (see Figure 3). More specifically, in the whole temperature window, which includes the region close to the peak of the particle production, ImΠR and
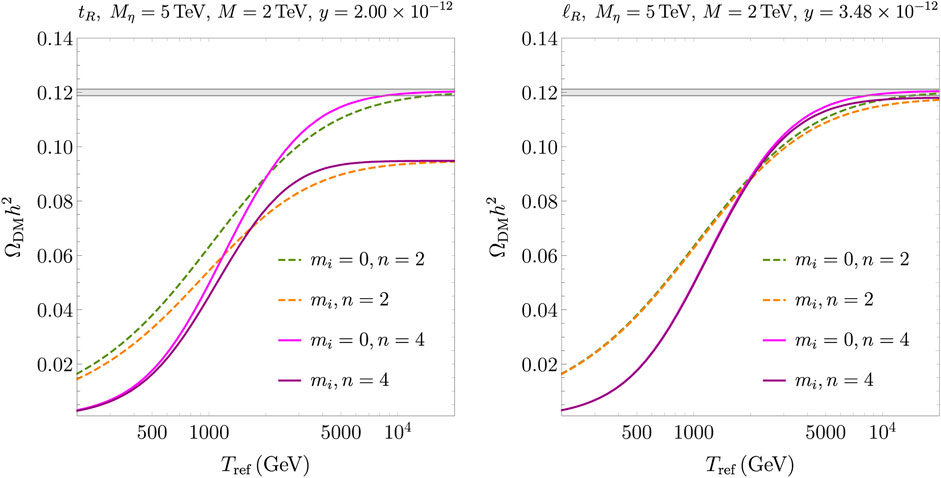
FIGURE 8. Dark matter energy density as a function of Tref, left panel for the top-quark scenario and right panel for leptophilic DM. Two cases of modified cosmologies are shown.
6 Conclusion
In view of recent advancements in particle interaction rates in the early universe, an update of the cosmologically viable parameter space for various dark matter models is underway. In most cases, this is done by assuming the rather conservative radiation-dominated scenario, which is extrapolated at temperatures much higher than in the Big Bang nucleosynthesis. In this paper, we considered the interplay between improved interaction rates, which are the particle physics input for extracting the DM energy density, and modified cosmological histories.
For realistic and next-to-minimal DM models, various phenomena can play a role and be relevant when computing the corresponding particle interaction rates. We considered non-perturbative effects for DM thermal freeze-out and the role of thermal masses for freeze-in-produced dark matter as triggered by 1 → 2 decays. The ameliorated rates can yield corrections as large as one order of magnitude to the predicted DM energy density. We have interfaced improved particle rates with modified cosmological histories in the extraction of the DM energy density. More specifically, we focused on a family of cosmological histories that feature a faster expansion and that make particle interactions in the early universe less efficient.
For dark matter freeze-out, we have included near-threshold effects on the annihilations of non-relativistic pairs. Here, Sommerfeld factors and bound-state formation and their decays boost DM annihilation and reduce the relic density for a given choice of the model parameters. We have considered fermionic dark matter with a vector or a scalar force mediator and summarized, in the framework of potential non-relativistic effective field theories, the cross-sections and widths that enter an effective Boltzmann equation. On one hand, non-perturbative effects tend to decrease the DM abundance. On the other hand, a faster expansion rate makes the annihilation process less efficient and triggers the opposite trend, namely, a larger DM abundance at the freeze-out. We have assessed the interplay between enhanced cross-sections and a faster universe expansion through complementary visualizations of the model parameter space. We found that modified cosmologies may open DM mass windows that are compatible with the observed DM energy density. Moreover, there is some degeneracy when extracting the DM energy density with the following two options: (i) standard particle rates and cosmology and (ii) improved annihilation cross-sections and modified cosmological histories (see Figures 5, 6). The latter observation may turn out useful when introducing experimental constraints for the parameter space that is compatible with the observed energy density, which may also apply to modified cosmological histories for a specific choice of the reference temperature. Improvements to the present treatment are in order, such as the inclusion of bound-state effects beyond the no-transition limit and a larger number of excited bound states.
As for the freeze-in scenario, we have picked one of the various effects that play a role in the ultra-relativistic and relativistic regime, namely, thermal masses. At high temperatures, higher than any in-vacuum mass scales, thermal masses modify the two-body phase space and the temperature dependence of the decay processes that produce DM particles. We have inspected the effects of thermal masses for t-channel mediator models that encompass a rich phenomenology even in the case of a feeble interaction between the DM and the visible sector. We found a qualitative difference between a top-philic and leptophilic DM candidate, which was not noticed in former studies, on the thermal production rate. Owing to rather different Yukawa couplings between SM fermions and the Higgs boson, thermal masses suppress the production rate in the top-quark case, whereas it can be enhanced for DM interacting with leptons. When comparing with modified cosmologies, we restrict to choices of the couplings that induce a suppressed production rate in both models. For freeze-in dark matter, a faster expansion history induces an opposite effect with respect to freeze-out. Since the DM abundance builds up over all the thermal history, which includes temperatures larger than the DM mass and accompanying states of the dark sector, a faster expansion inhibits the dark matter production and a smaller abundance is found. For the parameter choice of this work, thermal masses add up to a faster expansion in reducing the DM population. For a more rigorous assessment of the interplay with modified cosmologies within this class of models, we note that the complete set of high-temperature thermal effects, i.e., multiple-soft scattering 2 → 2 scatterings, should be included, especially when considering smaller mass splittings ΔM.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
SB: writing–original draft and writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work of SB was supported by the Swiss National Science Foundation (SNSF) under the Ambizione grant PZ00P2_185783.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Depending on the details and degrees of freedom of the DM model, T ≳ Mα2 may induce thermal masses and modify the Coulomb potential (see, e.g., [14, 15, 111] and [112, 113] for previous studies about heavy quarkonium).
2In order to clarify on the distinction between soft and ultrasoft mediators, and to introduce the degrees of freedom of pNREFTDM, we project onto the particle–antiparticle sector,
3Such an interaction would be responsible for the generation of a thermal mass for the scalar mediator in the early universe,
4It is worth mentioning that thermal masses have been considered in the production of heavy neutrinos from charged scalar decays in ref. and in the context of see-saw type I leptogenesis in refs. [29, 32]. Despite the models being different with respect to phenomenology, the topology of the relevant diagrams is indeed quite similar.
5For temperatures smaller than approximately Tc ≃ 150 GeV, the SM Higgs boson undergoes a crossover, and then, the top-quark and the mediator η thermal masses would acquire a more complicated form. Despite this aspect being interesting, it is not expected to qualitatively change the effect on the DM production, and we leave it for future investigations.
6In this class of modes, the super-WIMP mechanism comes along with the freeze-in. The former takes place at much smaller temperatures T ≪ Mη, and the relevant process is the freeze-out of the mediator η and its subsequent late decays into DM particles.
7An important and relevant consequence for
8The same symbol is also used to indicate the bilocal field of the low-energy pNREFTs in Section 2. Here, n enters the exponent of the scale factor, whereas it was used to label bound states in Section 2.
9In a recent work [118], the option where the universe expands slower than the standard cosmological history was considered, and its impact on the DM relic density is discussed.
10Such treatment has been very recently revisited in [22, 119] to include transitions among bound states, which make bound-state effects more prominent.
References
1. Aghanim N, Akrami Y, Arroja F, Ashdown M, Aumont J, Baccigalupi C, et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron Astrophys (2020) 641:A1. doi:10.1051/0004-6361/201833880
2. Bertone G, Hooper D, Silk J. Particle dark matter: evidence, candidates and constraints. Phys Rept (2005) 405:279–390. doi:10.1016/j.physrep.2004.08.031
3. Feng JL. Dark matter candidates from particle physics and methods of detection. Ann Rev Astron Astrophys (2010) 48:495–545. doi:10.1146/annurev-astro-082708-101659
4. Lee BW, Weinberg S. Cosmological lower bound on heavy neutrino masses. Phys Rev Lett (1977) 39:165–8. doi:10.1103/PhysRevLett.39.165
5. Griest K, Seckel D. Three exceptions in the calculation of relic abundances. Phys Rev (1991) D43:3191–203. doi:10.1103/PhysRevD.43.3191
6. Gondolo P, Gelmini G. Cosmic abundances of stable particles: improved analysis. Nucl Phys (1991) B360:145–79. doi:10.1016/0550-3213(91)90438-4
7. Moroi T, Murayama H, Yamaguchi M. Cosmological constraints on the light stable gravitino. Phys Lett B (1993) 303:289–94. doi:10.1016/0370-2693(93)91434-O
8. McDonald J. Thermally generated gauge singlet scalars as selfinteracting dark matter. Phys Rev Lett (2002) 88:091304. doi:10.1103/PhysRevLett.88.091304
9. Hall LJ, Jedamzik K, March-Russell J, West SM. Freeze-in production of FIMP dark matter. JHEP (2010) 03:080. doi:10.1007/JHEP03(2010)080
10. Sommerfeld A. Über die Beugung und Bremsung der Elektronen. Ann Phys (1931) 403, (3) 257–330. doi:10.1002/andp.19314030302
11. Hisano J, Matsumoto S, Nojiri MM, Saito O. Nonperturbative effect on dark matter annihilation and gamma ray signature from the galactic center. Phys Rev D (2005) 71:063528. doi:10.1103/PhysRevD.71.063528
12. Detmold W, McCullough M, Pochinsky A. Dark nuclei I: cosmology and indirect detection. Phys Rev D (2014) 90:115013. doi:10.1103/PhysRevD.90.115013
13. von Harling B, Petraki K. Bound-state formation for thermal relic dark matter and unitarity. JCAP (2014) 1412:033. doi:10.1088/1475-7516/2014/12/033
14. Kim S, Laine M. On thermal corrections to near-threshold annihilation. JCAP (2017) 1701:013. doi:10.1088/1475-7516/2017/01/013
15. Biondini S, Laine M. Thermal dark matter co-annihilating with a strongly interacting scalar. JHEP (2018) 04:072. doi:10.1007/JHEP04(2018)072
16. Binder T, Mukaida K, Petraki K. Rapid bound-state formation of dark matter in the early universe. Phys Rev Lett (2020) 124:161102. doi:10.1103/PhysRevLett.124.161102
17. Laha R. Directional detection of dark matter in universal bound states. Phys Rev D (2015) 92:083509. doi:10.1103/PhysRevD.92.083509
18. Asadi P, Baumgart M, Fitzpatrick PJ, Krupczak E, Slatyer TR. Capture and decay of electroweak WIMPonium. JCAP (2017) 02:005. doi:10.1088/1475-7516/2017/02/005
19. Garny M, Heisig J. Interplay of super-WIMP and freeze-in production of dark matter. Phys Rev (2018) D98:095031. doi:10.1103/PhysRevD.98.095031
20. Biondini S, Vogl S. Coloured coannihilations: dark matter phenomenology meets non-relativistic EFTs. JHEP (2019) 02:016. doi:10.1007/JHEP02(2019)016
21. Biondini S, Vogl S. Scalar dark matter coannihilating with a coloured fermion. JHEP (2019) 11:147. doi:10.1007/JHEP11(2019)147
22. Garny M, Heisig J. Bound-state effects on dark matter coannihilation: pushing the boundaries of conversion-driven freeze-out. Phys Rev D (2022) 105:055004. doi:10.1103/PhysRevD.105.055004
23. Bottaro S, Strumia A, Vignaroli N. Minimal Dark Matter bound states at future colliders. JHEP (2021) 06:143. doi:10.1007/JHEP06(2021)143
24. Becker M, Copello E, Harz J, Mohan KA, Sengupta D. Impact of Sommerfeld effect and bound state formation in simplified t-channel dark matter models. JHEP (2022) 08:145. doi:10.1007/JHEP08(2022)145
25. Biondini S, Bollig J, Vogl S. Indirect detection of dark matter with (pseudo)-scalar interactions (2023). [arXiv:2308.14594 [hep-ph]].
26. Bélanger G, Boudjema F, Goudelis A, Pukhov A, Zaldivar B. micrOMEGAs5.0: freeze-in. Comput Phys Commun (2018) 231:173–86. doi:10.1016/j.cpc.2018.04.027
27. Lebedev O, Toma T. Relativistic freeze-in. Phys Lett B (2019) 798:134961. doi:10.1016/j.physletb.2019.134961
28. Bandyopadhyay P, Mitra M, Roy A. Relativistic freeze-in with scalar dark matter in a gauged B − L model and electroweak symmetry breaking. JHEP (2021) 05:150. doi:10.1007/JHEP05(2021)150
29. Anisimov A, Besak D, Bodeker D. Thermal production of relativistic Majorana neutrinos: strong enhancement by multiple soft scattering. JCAP (2011) 1103:042. doi:10.1088/1475-7516/2011/03/042
30. Besak D, Bodeker D. Thermal production of ultrarelativistic right-handed neutrinos: complete leading-order results. JCAP (2012) 1203:029. doi:10.1088/1475-7516/2012/03/029
31. Ghisoiu I, Laine M. Interpolation of hard and soft dilepton rates. JHEP (2014) 10:083. doi:10.1007/JHEP10(2014)083
32. Ghiglieri J, Laine M. Neutrino dynamics below the electroweak crossover. JCAP (2016) 1607:015. doi:10.1088/1475-7516/2016/07/015
33. Tenkanen T, Vaskonen V. Reheating the standard model from a hidden sector. Phys Rev D (2016) 94:083516. doi:10.1103/PhysRevD.94.083516
34. Hardy E. Higgs portal dark matter in non-standard cosmological histories. JHEP (2018) 06:043. doi:10.1007/JHEP06(2018)043
35. Bernal N, Cosme C, Tenkanen T, Vaskonen V Scalar singlet dark matter in non-standard cosmologies. Eur Phys J C (2019) 79:30. doi:10.1140/epjc/s10052-019-6550-9
36. Bernal N, Cosme C, Tenkanen T. Phenomenology of self-interacting dark matter in a matter-dominated universe. Eur Phys J C (2019) 79:99. doi:10.1140/epjc/s10052-019-6608-8
37. Arias P, Karamitros D, Roszkowski L. Frozen-in fermionic singlet dark matter in non-standard cosmology with a decaying fluid. JCAP (2021) 05:041. doi:10.1088/1475-7516/2021/05/041
38. Chanda P, Hamdan S, Unwin J. Reviving Z and Higgs mediated dark matter models in matter dominated freeze-out. JCAP (2020) 01:034. doi:10.1088/1475-7516/2020/01/034
39. Bernal N, Elahi F, Maldonado C, Unwin J. Ultraviolet freeze-in and non-standard cosmologies. JCAP (2019) 11:026. doi:10.1088/1475-7516/2019/11/026
40. Chang Z-F, Chen Z-X, Xu J-S, Han Z-L. FIMP dark matter from leptogenesis in fast expanding universe. JCAP (2021) 06:006. doi:10.1088/1475-7516/2021/06/006
41. Barman B, Ghosh P, Queiroz FS, Saha AK. Scalar multiplet dark matter in a fast expanding Universe: resurrection of the desert region. Phys Rev D (2021) 104:015040. doi:10.1103/PhysRevD.104.015040
42. Han C. Higgsino dark matter in a non-standard history of the universe. Phys Lett B (2019) 798:134997. doi:10.1016/j.physletb.2019.134997
43. Salati P. Quintessence and the relic density of neutralinos. Phys Lett B (2003) 571:121–31. doi:10.1016/j.physletb.2003.07.073
44. Profumo S, Ullio P. SUSY dark matter and quintessence. JCAP (2003) 11:006. doi:10.1088/1475-7516/2003/11/006
45. Drees M, Hajkarim F. Neutralino dark matter in scenarios with early matter domination. JHEP (2018) 12:042. doi:10.1007/JHEP12(2018)042
46. Ghosh DK, Ghoshal A, Jeesun S. Axion-like particle (ALP) portal freeze-in dark matter confronting ALP search experiments (2023). [arXiv:2305.09188 [hep-ph]].
47. Caswell WE, Lepage GP. Effective Lagrangians for bound state problems in QED, QCD, and other field theories. Phys Lett (1986) 167B:437–42. doi:10.1016/0370-2693(86)91297-9
48. Bodwin GT, Braaten E, Lepage GP. Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys Rev (1995) D51:1125–71. [Erratum: Phys. Rev.D55,5853(1997)]. doi:10.1103/physrevd.51.1125
49. Pineda A, Soto J. Effective field theory for ultrasoft momenta in NRQCD and NRQED. Nucl Phys Proc Suppl (1998) 64:428–32. doi:10.1016/S0920-5632(97)01102-X
50. Brambilla N, Pineda A, Soto J, Vairo A. Potential NRQCD: an Effective theory for heavy quarkonium. Nucl Phys (2000) B566:275–310. doi:10.1016/S0550-3213(99)00693-8
51. Beneke M, Hellmann C, Ruiz-Femenia P. Non-relativistic pair annihilation of nearly mass degenerate neutralinos and charginos III. Computation of the Sommerfeld enhancements. JHEP (2015) 05:115. doi:10.1007/JHEP05(2015)115
52. Binder T, Blobel B, Harz J, Mukaida K. Dark matter bound-state formation at higher order: a non-equilibrium quantum field theory approach. JHEP (2020) 09:086. doi:10.1007/JHEP09(2020)086
53. Biondini S, Shtabovenko V. Bound-state formation, dissociation and decays of darkonium with potential non-relativistic Yukawa theory for scalar and pseudoscalar mediators. JHEP (2022) 03:172. doi:10.1007/JHEP03(2022)172
54. Biondini S, Brambilla N, Qerimi G, Vairo A. Effective field theories for dark matter pairs in the early universe: cross sections and widths. JHEP (2023) 07:006. doi:10.1007/JHEP07(2023)006
55. Brambilla N, Eiras D, Pineda A, Soto J, Vairo A. Inclusive decays of heavy quarkonium to light particles. Phys Rev D (2003) 67:034018. doi:10.1103/PhysRevD.67.034018
56. Brambilla N, Pineda A, Soto J, Vairo A. Effective field theories for heavy quarkonium. Rev Mod Phys (2005) 77:1423–96. doi:10.1103/RevModPhys.77.1423
57. Binder T, Mukaida K, Scheihing-Hitschfeld B, Yao X. Non-Abelian electric field correlator at NLO for dark matter relic abundance and quarkonium transport. JHEP (2022) 01:137. doi:10.1007/JHEP01(2022)137
58. Binder T, Garny M, Heisig J, Lederer S, Urban K. Excited bound states and their role in dark matter production (2023). [arXiv:2308.01336 [hep-ph]]
59. Feldman D, Kors B, Nath P. Extra-weakly interacting dark matter. Phys Rev D (2007) 75:023503. doi:10.1103/PhysRevD.75.023503
60. Fayet P U-boson production in e+ e-annihilations, psi and Upsilon decays, and Light Dark Matter. Phys Rev D (2007) 75:115017. doi:10.1103/PhysRevD.75.115017
61. Goodsell M, Jaeckel J, Redondo J, Ringwald A. Naturally light hidden photons in LARGE volume string compactifications. JHEP (2009) 11:027. doi:10.1088/1126-6708/2009/11/027
62. Morrissey DE, Poland D, Zurek KM. Abelian hidden sectors at a GeV. JHEP (2009) 07:050. doi:10.1088/1126-6708/2009/07/050
63. Andreas S, Goodsell MD, Ringwald A. Dark matter and dark forces from a supersymmetric hidden sector. Phys Rev D (2013) 87:025007. doi:10.1103/PhysRevD.87.025007
64. Holdom B. Two U(1)’s and epsilon charge shifts. Phys Lett B (1986) 166:196–8. doi:10.1016/0370-2693(86)91377-8
65. Foot R, He X-G. Comment on Z-Z′ mixing in extended gauge theories. Phys Lett B (1991) 267:509–12. doi:10.1016/0370-2693(91)90901-2
66. Pineda A, Soto J. The Lamb shift in dimensional regularisation. Phys Lett (1998) B420:391–6. doi:10.1016/S0370-2693(97)01537-2
67. Vairo A. A Theoretical review of heavy quarkonium inclusive decays. Mod Phys Lett A19 (2004) 19:253–69. doi:10.1142/S0217732304012927
68. Pospelov M, Ritz A, Voloshin MB. Secluded WIMP dark matter. Phys Lett B (2008) 662:53–61. doi:10.1016/j.physletb.2008.02.052
69. Kaplinghat M, Tulin S, Yu H-B. Direct detection portals for self-interacting dark matter. Phys Rev D (2014) 89:035009. doi:10.1103/PhysRevD.89.035009
70. Wise MB, Zhang Y. Stable bound states of asymmetric dark matter. Phys Rev D (2014) 90:055030. [Erratum: Phys.Rev.D 91, 039907 (2015)]. doi:10.1103/PhysRevD.90.055030
71. Kahlhoefer F, Schmidt-Hoberg K, Wild S. Dark matter self-interactions from a general spin-0 mediator. JCAP (2017) 08:003. doi:10.1088/1475-7516/2017/08/003
72. Arcadi G, Djouadi A, Raidal M. Dark matter through the Higgs portal. Phys Rept (2020) 842:1–180. doi:10.1016/j.physrep.2019.11.003
73. Biondini S, Shtabovenko V. Non-relativistic and potential non-relativistic effective field theories for scalar mediators. JHEP (2021) 08:114. doi:10.1007/JHEP08(2021)114
74. Bernal N, Heikinheimo M, Tenkanen T, Tuominen K, Vaskonen V. The dawn of fimp dark matter: a review of models and constraints. Int J Mod Phys A (2017) 32:1730023. doi:10.1142/S0217751X1730023X
75. Baker MJ, Kopp J. Dark matter decay between phase transitions at the weak scale. Phys Rev Lett (2017) 119:061801. doi:10.1103/PhysRevLett.119.061801
76. Baker MJ, Breitbach M, Kopp J, Mittnacht L. Dynamic freeze-in: impact of thermal masses and cosmological phase transitions on dark matter production. JHEP (2018) 03:114. doi:10.1007/JHEP03(2018)114
77. Dvorkin C, Lin T, Schutz K. Making dark matter out of light: freeze-in from plasma effects. Phys Rev (2019) D99:115009. doi:10.1103/PhysRevD.99.115009
78. Darmé L, Hryczuk A, Karamitros D, Roszkowski L. Forbidden frozen-in dark matter. JHEP (2019) 11:159. doi:10.1007/JHEP11(2019)159
79. Chakrabarty N, Konar P, Roshan and R, Show S. Thermally corrected masses and freeze-in dark matter: a case study. Phys Rev D (2023) 107:035021. doi:10.1103/PhysRevD.107.035021
80. Bringmann T, Heeba S, Kahlhoefer F, Vangsnes K. Freezing-in a hot bath: resonances, medium effects and phase transitions. JHEP (2022) 02:110. doi:10.1007/JHEP02(2022)110
81. Garny M, Ibarra A, Vogl S. Signatures of Majorana dark matter with t-channel mediators. Int J Mod Phys (2015) D24:1530019. doi:10.1142/S0218271815300190
82. De Simone A, Jacques T. Simplified models vs. effective field theory approaches in dark matter searches. Eur Phys J C (2016) 76:367. doi:10.1140/epjc/s10052-016-4208-4
83. Arina C, Fuks B, Mantani L. A universal framework for t-channel dark matter models. Eur Phys J C (2020) 80:409. doi:10.1140/epjc/s10052-020-7933-7
84. Bélanger G, Desai N, Goudelis A, Harz J, Lessa A, No JM, et al. LHC-friendly minimal freeze-in models. JHEP (2019) 02:186. doi:10.1007/JHEP02(2019)186
85. Biondini S, Ghiglieri J. Freeze-in produced dark matter in the ultra-relativistic regime. JCAP (2021) 03:075. doi:10.1088/1475-7516/2021/03/075
86. Garny M, Heisig J, Hufnagel M, Lülf B. Top-philic dark matter within and beyond the WIMP paradigm. Phys Rev (2018) D97:075002. doi:10.1103/PhysRevD.97.075002
87. Junius S, Lopez-Honorez L, Mariotti A. A feeble window on leptophilic dark matter. JHEP (2019) 07:136. doi:10.1007/JHEP07(2019)136
88. Bollig J, Vogl S. Impact of bound states on non-thermal dark matter production. JCAP (2022) 10:031. doi:10.1088/1475-7516/2022/10/031
89. Asaka T, Laine M, Shaposhnikov M. On the hadronic contribution to sterile neutrino production. JHEP (2006) 06:053. doi:10.1088/1126-6708/2006/06/053
90. Bödeker D, Sangel M, Wörmann M. Equilibration, particle production, and self-energy. Phys Rev D (2016) 93:045028. doi:10.1103/PhysRevD.93.045028
91. Laine M, Vuorinen A. Basics of thermal field theory, 925. Springer (2016). doi:10.1007/978-3-319-31933-9
92. Kajantie K, Laine M, Rummukainen K, Shaposhnikov ME. Generic rules for high temperature dimensional reduction and their application to the standard model. Nucl Phys B (1996) 458:90–136. doi:10.1016/0550-3213(95)00549-8
93. Giudice GF, Notari A, Raidal M, Riotto A, Strumia A. Towards a complete theory of thermal leptogenesis in the SM and MSSM. Nucl Phys B (2004) 685:89–149. doi:10.1016/j.nuclphysb.2004.02.019
94. Allahverdi R, Brandenberger R, Cyr-Racine F-Y, Mazumdar A. Reheating in inflationary cosmology: theory and applications. Ann Rev Nucl Part Sci (2010) 60:27–51. doi:10.1146/annurev.nucl.012809.104511
95. Berlin A, Hooper D, Krnjaic G. PeV-scale dark matter as a thermal relic of a decoupled sector. Phys Lett B (2016) 760:106–11. doi:10.1016/j.physletb.2016.06.037
96. Berlin A, Hooper D, Krnjaic G. Thermal dark matter from A highly decoupled sector. Phys Rev D (2016) 94:095019. doi:10.1103/PhysRevD.94.095019
97. Dine M, Randall L, Thomas SD. Supersymmetry breaking in the early universe. Phys Rev Lett (1995) 75:398–401. doi:10.1103/PhysRevLett.75.398
98. Caldwell RR, Dave R, Steinhardt PJ. Cosmological imprint of an energy component with general equation of state. Phys Rev Lett (1998) 80:1582–5. doi:10.1103/PhysRevLett.80.1582
99. Sahni V, Starobinsky AA. The Case for a positive cosmological Lambda term. Int J Mod Phys D (2000) 9:373–443. doi:10.1142/S0218271800000542
100. D’Eramo F, Fernandez N, Profumo S. When the universe expands too fast: relentless dark matter. JCAP (2017) 05:012. doi:10.1088/1475-7516/2017/05/012
101. Wetterich C. Cosmology and the fate of dilatation symmetry. Nucl Phys B (1988) 302:668–96. doi:10.1016/0550-3213(88)90193-9
102. Dimopoulos K, Owen C. Quintessential inflation with α-attractors. JCAP (2017) 06:027. doi:10.1088/1475-7516/2017/06/027
103. Kamenshchik AY, Moschella U, Pasquier V. An Alternative to quintessence. Phys Lett B (2001) 511:265–8. doi:10.1016/S0370-2693(01)00571-8
104. Chavanis P-H Cosmology with a stiff matter era. Phys Rev D (2015) 92:103004. doi:10.1103/PhysRevD.92.103004
105. Khoury J, Ovrut BA, Steinhardt PJ, Turok N. Ekpyrotic universe: colliding branes and the origin of the hot big bang. Phys Rev D (2001) 64:123522. doi:10.1103/PhysRevD.64.123522
106. Hannestad S. What is the lowest possible reheating temperature? Phys Rev D (2004) 70:043506. doi:10.1103/PhysRevD.70.043506
107. Bazavov A, Bhattacharya T, DeTar C, Ding HT, Gottlieb S, Gupta R, et al. Equation of state in (2+1)-flavor QCD. Phys Rev D (2014) 90:094503. doi:10.1103/PhysRevD.90.094503
108. Ellis J, Luo F, Olive KA. Gluino coannihilation revisited. JHEP (2015) 09:127. doi:10.1007/JHEP09(2015)127
109. Laine M, Meyer M. Standard Model thermodynamics across the electroweak crossover. JCAP (2015) 07:035. doi:10.1088/1475-7516/2015/07/035
110. D’Eramo F, Fernandez N, Profumo S. Dark matter freeze-in production in fast-expanding universes. JCAP (2018) 02:046. doi:10.1088/1475-7516/2018/02/046
111. Binder T, Covi L, Mukaida K. Dark Matter Sommerfeld-enhanced annihilation and Bound-state decay at finite temperature. Phys Rev (2018) D98:115023. doi:10.1103/PhysRevD.98.115023
112. Laine M, Philipsen O, Romatschke P, Tassler M. Real-time static potential in hot QCD. JHEP (2007) 03:054. doi:10.1088/1126-6708/2007/03/054
113. Brambilla N, Ghiglieri J, Vairo A, Petreczky P. Static quark-antiquark pairs at finite temperature. Phys Rev (2008) D78:014017. doi:10.1103/PhysRevD.78.014017
114. Oncala R, Petraki K. Dark matter bound states via emission of scalar mediators. JHEP (2019) 01:070. doi:10.1007/JHEP01(2019)070
115. Drewes M, Kang JU. Sterile neutrino Dark Matter production from scalar decay in a thermal bath. JHEP (2016) 05:051. doi:10.1007/JHEP05(2016)051
116. Liu J, Wang X-P, Xie K-P. Searching for lepton portal dark matter with colliders and gravitational waves. JHEP (2021) 06:149. doi:10.1007/JHEP06(2021)149
117. Biondini S, Schicho P, Tenkanen TVI. Strong electroweak phase transition in t-channel simplified dark matter models. JCAP (2022) 10:044. doi:10.1088/1475-7516/2022/10/044
Keywords: dark matter, freeze-out, freeze-in, effective field theories, thermal field theory, modified cosmologies
Citation: Biondini S (2023) Interplay between improved interaction rates and modified cosmological histories for dark matter. Front. Phys. 11:1285986. doi: 10.3389/fphy.2023.1285986
Received: 30 August 2023; Accepted: 09 October 2023;
Published: 02 November 2023.
Edited by:
Giorgio Arcadi, University of Messina, ItalyReviewed by:
Urjit Yajnik, Indian Institute of Technology Bombay, IndiaDavid Delepine, University of Guanajuato, Mexico
Copyright © 2023 Biondini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Simone Biondini, c2ltb25lLmJpb25kaW5pQHVuaWJhcy5jaA==
 Simone Biondini
Simone Biondini