- 1The Key Laboratory of Ministry of Education for Image Processing and Intelligent Control, School of Artificial Intelligence and Automation, Huazhong University of Science and Technology, Wuhan, Hubei, China
- 2Instrumentation Technology Economy Institute, Beijing, China
Social interaction, which is intricate and time-varying, has emerged as a pivotal consideration in epidemic spreading. In this paper, we devise a UAU–SIS model for simulating awareness diffusion and epidemic spreading on temporal multiplex networks. Drawing inspiration from individuals’ self-protection behaviors, a novel adaptive update mechanism is developed. To provide a more precise representation of the collective social interactions encompassing individuals, we introduce the higher-order network structure encompassing temporal variability. Building upon the established framework of the microscopic Markov chain approach (MMCA) for static networks, we extend its applicability to the condition of temporal networks and derive the threshold within the coupled dynamics. Our extensive simulations illuminate the dual role of awareness in epidemic mitigation. Beyond solely diminishing infection probabilities through self-protective measures, individual awareness additionally facilitates to change the network structure to separate them from the infected. By elucidating these fundamental characteristics, our research contributes to advancing more effective strategies for epidemic mitigation and containment.
1 Introduction
Numerous social scenarios can be described and analyzed through the complex network, including fields like e-mail [1], social systems [2], and brain networks [3, 4]. A good illustrative example is epidemic spreading, which can be described by the interaction of spreading dynamics and network structure [5-7]. By establishing an epidemic model and executing simulations, the internal mechanism of epidemic spreading can be explored in detail, thereby guiding epidemic prevention and control.
In order to describe the states of the individuals under the influence of the epidemic, diverse models and an array of simulation techniques have been established. Depending on whether the disease is immune-mediated, epidemic models are primarily categorized into SIS models [8] and SIR models [9], which delineate reversible and irreversible epidemic spreading processes, respectively. Drawing from these, many theoretical analysis methods have been proposed and advanced to study the dynamic process, thereby delving into the characteristics of epidemic outbreaks and evolution [10, 11]. The pivotal problem of epidemic spreading is to study the critical conditions of transmission activities, specifically the epidemic outbreak threshold [12]. When the infection rate is lower than the threshold, the epidemic will perish after only a small spread. Conversely, when the infection rate surpasses the threshold, the epidemic will break out in the network. In order to reflect the impact of human social behaviors on epidemic spreading, numerous researchers have extended the traditional network model to multi-layer networks and explored the coupled spread of awareness and epidemic alongside its influencing factors [13-15]. Li et al. introduced the individual protection degree into SIR models and developed an open Markov queueing network to explore the migration of individuals and transitions between states [16]. Zhang et al. developed a local and global information-controlled spreading model and explored the positive effect on inducing self-protection from local and global information [17]. Feng et al. discussed the different effects of individuals with different properties on epidemic spreading through awareness [18].
Conventional epidemic models typically assume a static network, where node connections remain fixed over time, resulting in uniformly distributed interactions. However, empirical investigations into various spreading processes, such as the Internet, social communications, and epidemic spreading, consistently reveal that the network in the real world often deviates from this model. Instead, they exhibit dynamic processes governed by specific temporal rules [19-23]. In recent years, an increasing focus within disciplines such as statistical physics and computer science has been directed toward the examination of evolving network models [24]. Addressing this context, Huang et al. formulated a coupled resource–epidemic dynamic model on the temporal network and analyzed the asymmetric interactions between the epidemic and the resource [25]. Guo et al. further enriched the understanding of temporal networks by introducing a two-layer network framework with partial mappings [26]. Investigating modular effects on the SIS and SIR models within a time-varying connectivity structure, Nadini et al. contributed to the comprehension of reciprocal influences between network modularity and disease dynamics [27].
In traditional static network models, the epidemic outbreak threshold can be calculated readily from the adjacency matrix that captures the network’s structural layout using the MMCA method [28]. In the temporal case, the dynamic transformation of network structures transpires at such a swift pace that we are compelled to rely upon temporally averaged attributes for the examination of awareness diffusion and epidemic proliferation. In addition, some empirical investigations into social interactions have shown that networks across different scales and environments usually show some non-Poissonian and non-Markovian evolutionary characteristics [29-31], which will generate many new theoretical research hotspots. Perra et al. and Miritello et al. modeled and investigated the spreading processes on time-varying networks, casting them as either discrete time series or as connected continuous-time dynamics [32, 33]. Several studies have been conducted to formulate methods building upon the foundations of traditional static networks. Extensive research has been devoted to adaptive temporal networks, revealing distinctive and innovative attributes, including oscillatory mechanisms and an increased number of mutation points [34, 35]. Nevertheless, the conventional models inherently portrayed interactions in a pairwise manner, failing to accurately depict the intricate architecture, particularly the collective interactions within social systems.
Recently, a series of inquiries into higher-order network structures have unveiled a novel panorama of dynamics [36-38]. Kuehn et al. expounded on the potential of abrupt transitions within epidemic dynamics stemming from higher-order interactions [39]. St-Onge et al. devised an approximate master equation grounded in group dynamics to delineate the mesoscopic localization regime influenced by the presence of higher-order network structures [40]. Peng et al. established a knowledge hypernetwork model with a hypernetwork-based approach, effectively capturing interrelationships among elements and addressing the multifaceted attributes of design knowledge [41].
Prior research on the domain of network modeling has established a robust groundwork for elucidating and deducing temporal dynamics inherent to networks. Furthermore, it has introduced an innovative avenue for scrutinizing the dissemination of network effects through the lens of temporal transformations. However, the intricate and multifaceted regulations governing alterations and revisions within temporal networks warrant a more comprehensive approach, which could transcend mere randomized selection rules and encompass a heightened emphasis on individual state transitions and social behaviors. Inspired by the behavior of people to protect themselves by keeping away from the infected, we propose a novel awareness-based adaptive network update mechanism, capturing individuals’ social behaviors aimed at curtailing infection risk and reducing the scope of outbreaks. At the same time, the network update mechanism also ensures the stability of the network scale to prevent extreme evolutionary results. To comprehensively study the characteristics of the coupled dynamics under it, we develop a temporal multiplex network with higher-order network structures and employ the UAU–SIS epidemic model. Through derivation of the MMCA method alongside extensive numerical simulations, we illustrate the nuanced manner by which individual awareness exerts a restraining influence on epidemic spreading and the evolution of the network.
2 Model description
In this section, we propose a model based on a temporal multiplex network with two layers to study the coupled dynamics and introduce an awareness-based adaptive mechanism.
2.1 UAU–SIS multiplex network model
In terms of the model describing the spreading process of the epidemic, we construct the UAU–SIS model with a two-way network. The spreading model is shown in Figure 1. In the upper layer of the network, we use the UAU model to describe the state of consciousness of the individual, which represents the information exchange and sharing between the individual and others in life or in the network. In the lower layer of the network, we adopt the SIS model to describe the physical state of the individual, which represents the individual’s close contact with others in life. Each individual participates in the interaction of the two-layer network at the same time, but the interaction objects are different, so the two layers of the two-way network have the same nodes and different edges. To simplify the model, we consider the entire network to be undirected and unweighted. In the virtual layer of the upper layer of the network, a single node is either in the U state or in the A state. In the physical layer of the lower network layer, the individual is either in the S state or in the I state. The transformation of the individual state is mainly realized through the two aspects of the transmission process and the restoration process.
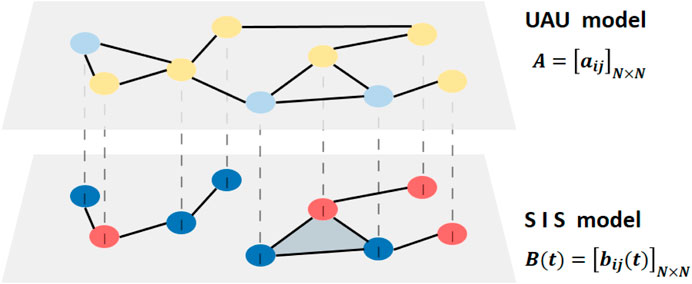
FIGURE 1. Diagrammatic sketch of the two-layer multiplex network in the proposed model. The upper layer representing the awareness diffusion is a static network, which contains U (light blue) and A (yellow). The lower layer representing the epidemic spreading is a temporal network, which contains S (dark blue) and I (red). Nodes are connected with edges in the upper layer and connected with edges and 2-simplex in the lower layer.
2.2 Dynamic process based on pairwise and group interactions
At each time step, nodes in our model will experience a dynamic process of awareness and epidemic, which could be summarized as a diffusion process and a recovery process, respectively.
In the diffusion process, we describe the interaction between two individuals based on edges and describe the group interaction behavior based on the hypergraph. In the propagation of the edges, the I individual in the physical layer transmits the disease to the S individual with the probability βU, and the A individual in the virtual layer transmits the consciousness to the U individual with the probability λ. As a reflection of taking preventive measures against diseases, we believe that the A individual can reduce the probability of being infected by the factor γ; that is to say, the infection probability decreases as βA = γβU(0 ≤ γ ≤ 1). In higher-order communication, group interaction is described by a 2-simplex composed of three nodes, which is specifically expressed as the influence of the 2-simplex on each individual. At the time of network initialization, a triplet composed of three nodes connected to each other forms a 2-simplex with the probability pΔ. If there is only one susceptible individual in the 2-simplex, then the probability that he is infected is βΔ. Group interactions tend to occur independently, so if an individual belongs to multiple hypergraphs, the infections of these hypergraphs are computed independently.
During the recovery process, individuals labeled as I in the physical layer have a probability δ to return to a susceptible state. Similarly, individuals labeled as A in the virtual layer have a probability σ to return to an unaware state. This process does not depend on any external factors and is only related to the model.
Therefore, considering the coupling effect of consciousness spread and disease spread, individuals in the model can be described as belonging to four states: unaware susceptible (US), unaware infected (UI), aware susceptible (AS), and aware infected (AI). We also assume that upon an individual transitioning into the infected state, an instantaneous realization of the disease’s presence and the imperative of its prevention ensues, leading to a prompt conversion from the UI state to the AI state. Therefore, individuals on the network have three states, and the conversion relationship between them is shown in Figure 2.
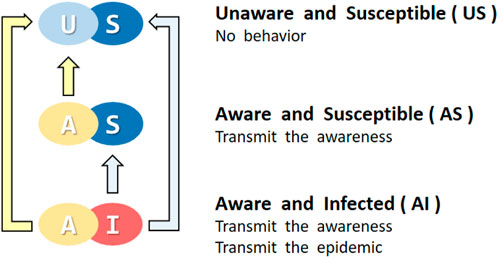
FIGURE 2. All possible individuals in the proposed model. Each individual maintains a certain state in both layers. In the upper layer, the individual is either U (light blue) or A (yellow). In the lower layer, the individual is either S (dark blue) or I (red). Among them, individuals in state A or I could propagate to others.
2.3 An awareness-based adaptive network update mechanism in temporal networks
In the process of social interaction, on the one hand, people will passively infect or recover, and on the other hand, they will actively seek a better environment for themselves to avoid infection. At the level of awareness, people will try to accept advanced and effective prevention and control concepts (A individuals). At the behavioral level, people try to avoid contact with infected people (I individuals) around them. The two abovementioned behaviors can be reflected by changes in the network structure.
Considering the time series T = t1, t2, …, tl, each time step t ∈ T uniquely corresponds to a two-layer network; that is, there will be l networks during the network evolution process. The social structure also exists for a certain period of time. For example, the family relationship can be considered constant, but the work collaboration relationship and living relationship keep changing. Only during the period when these relationships still exist can communication occur. In the network corresponding to two adjacent time steps, the nodes will not change, and the edges and higher-order structures will change with a certain probability. In other words, we believe that every adjacent edge and every 2-simplex has an existence time window τ belonging to [tb, te]. In order to describe the change process of the contact network normally, we update the edges and 2-simplex in the network at time h according to an awareness-based adaptive mechanism.
For edges, we design a time-varying rule for S–I edges based on the identification from individuals. When an S individual detects a new I individual around them, there is a probability α that they will take protective measures and disconnect the S–I connection. At the same time, this I individual has a probability α to avoid propagating the epidemic. We illustrate this process in Figure 3. This process could be expressed as follows:
• Select those nodes that are susceptible at time h − 1 and infected at time h, denoted as Ie. For every Iei, select the individual’s Se neighbors Sej. They will identify each other;
• On the part of Iei, the individual will cut off edges with the probability α. On the part of Sej, the individual will cut off with α;
• If an S–I edge is cut off exactly, the Sej will re-build an edge with one of the S neighbors.
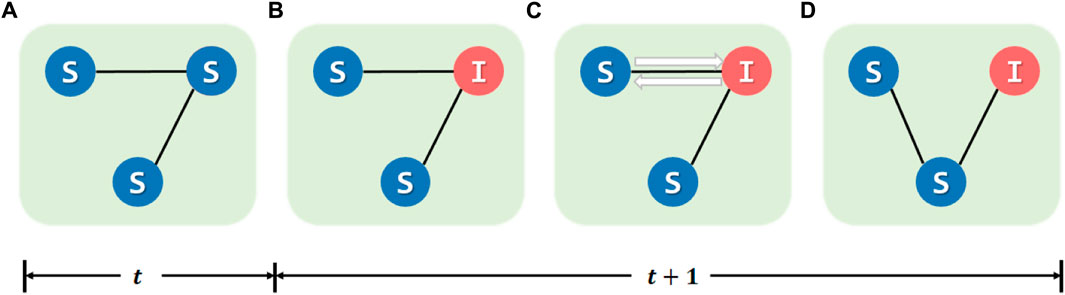
FIGURE 3. Awareness-based adaptive update mechanism for individuals in edges. (A) Node states at t time step. Between (A) and (B), state transition occurs, and some nodes will change the state. (C) All S individuals will identify the one who is infected in the last turn. Both S and I individuals will cut off the edge with the probability α. (D) Result after the mechanism takes effect.
For the 2-simplex, we design the update rule with two thresholds describing the risk of forming a 2-simplex. We assume that only the groups including three S individuals could form a 2-simplex, and the 2-simplex including more than half of those infected must be canceled. For example, a 2-simplex including two I individuals and one S individual will be canceled, but another 2-simplex including one I individual and two S individuals will not. Taking into account the complex factors and uncertainties in reality, the formation and canceling of the aforementioned 2-simplex also occur with the probability α. We illustrate this process in Figure 4. This process could be expressed as follows:
• Select those 2-simplex composed of two or more I individuals and denote them as IΔ. Select those triplets composed of three S individuals and denote them as SΔ.
• For IΔi, it will be canceled with the probability α. For SΔi, it will form a 2-simplex with the probability α.
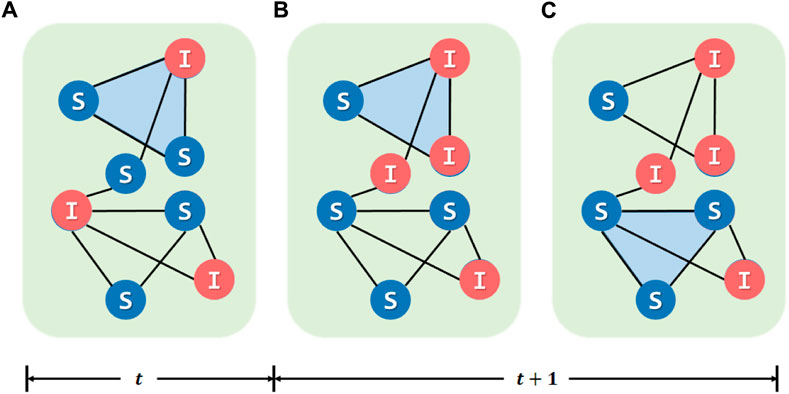
FIGURE 4. Awareness-based adaptive update mechanism for individuals in higher-order network structures. (A) Node states at t time step. Between (A) and (B), state transition occurs, and some nodes will change the state. (C) The cancellation or establishment of the 2-simplex. All 2-simplex composed of at least two I individuals and triplets composed of three S individuals will identify themselves. The former has a α probability to cancel the 2-simplex, and the latter has a α probability to form the 2-simplex.
All the aforementioned mechanisms could simulate the behavior of individuals seeking shelter and away from the infection. In addition, the number of edges will remain constant, which means that society will not excessively increase or decrease connections and activities due to the epidemic spreading.
3 Analytical results based on MMCA
In this section, we approximate the time-varying network by generalizing the MMCA method and provide an approximate solution for the global steady-state infection rate.
Based on the aforementioned model, we continue to deduce the epidemic outbreak threshold βc and explore the coupled dynamics of the network by applying MMCA. In an evolving temporal network, the process of network evolution is a series of static networks, so we first analyze the static network based on MMCA and then extend it to the temporal network. For the traditional UAU–SIS model in discrete time, an individual can be in one of three mutually exclusive states, US, AS, and AI, and can transition between states. In both the virtual layer and the physical layer, we set the adjacency matrix between N nodes, which are A and B, respectively:
With respect to representing and calculating the state transition process between individuals, we first define the following variables to simplify the expression: ri(t) is the probability that an unaware individual i is not changed into the aware state because of neighbors’ impact,
where
where
Subsequently, we will obtain the relationship between every state. In order to explain this relationship more intuitively, we introduce the transition probability trees showing conditions in every time step. The transition probability trees are shown in Figure 5.
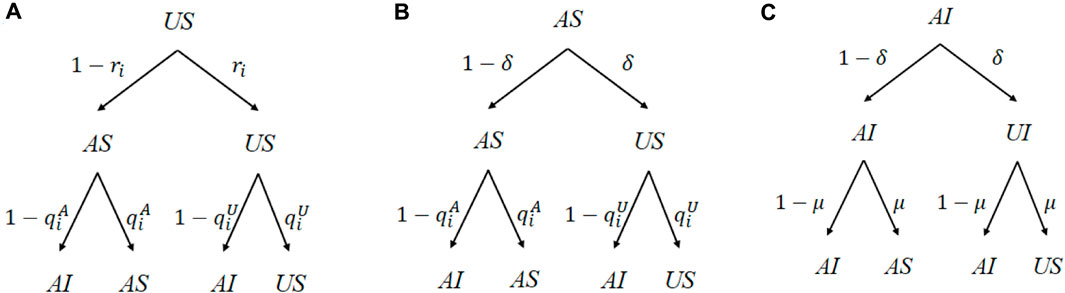
FIGURE 5. Probability transition trees of three states (US, AS, and AI). US individuals will not be turned into aware by neighbors with probability ri. AS or AI individuals will forget the disease with probability δ. US or AS individuals will not be turned into infected by neighbors with probability
Afterward, we could develop the MMCA equations to describe the coupled dynamics of every node in the network. The equation is specifically expressed as the full probability formula for nodes in various states at time t to change to a certain state at time t + 1:
Normally, we think that the model satisfies
In addition, we attempt to further simplify the third equation to solve the epidemic outbreak threshold by ignoring the high-order items and substituting
We rewrite Eq. 7 as
4 Numerical simulations
In this section, we will extensively apply the Monte Carlo (MC) simulations to conduct experiments under different configurations to verify the accuracy of MMCA and reveal the principle of the coupled dynamics.
Initially, some definitions and explanations are essential for our following discussion. The model mainly includes five parameters: β, λ, μ, δ, and pΔ. We set μ = 0.4 and δ = 0.8. While the experiment discusses some parameters, the others will be held constant. The disease is considered extinct when the epidemic scale is close to zero. Once the infected probability β is larger than βc, the epidemic will continue to circulate in the population. On the one hand, the focus of our experiments is on the epidemic scale representing the extent of the epidemic outbreak. Hence, we define that
First, we explore the impact of awareness and infection on the epidemic spreading on the WS network. As shown in Figure 6, the epidemic outbreak scale increases as β increases and decreases as λ increases. However, the preventive effect of awareness is relatively inconspicuous because of the limitation of the protective measure. By comparing the (a) and (b), (c) and (d), it is certain that the higher-order structure in the physical layer could exacerbate the outbreak of the epidemic and make the protective effect of awareness less pronounced. By comparing the (a), (b) and (c), (d), we find that the BA network tends to have a higher ρI.

FIGURE 6. Proportion reaching a stationary state of the infected individuals (ρI) as a function of β and λ. (A) ER network with pΔ = 0.7; (B) ER network with pΔ = 0; (C) BA network with pΔ = 0.7; (D) BA network with pΔ = 0. Each figure is drawn in the grid 50 × 50, and α = 0.3 remains constant.
Second, we consider the effect of the awareness-based adaptive mechanism on epidemic spreading. Specifically, the larger the value of α is, the more likely re-connection will occur. From the perspective of epidemic spreading, those re-connections contribute to cutting off the spreading route. From the perspective of network evolution, those re-connections facilitate the formation of distinct clusters including different individuals. The simulation results in Figure 7 reveal the relationship between ρI and β, α. The larger the α, the stronger the ability of network evolution to resist epidemic spreading. Under the conditions that α and the number of higher-order structures are both large, the resistance effect will be further strengthened. Moreover, the ER network could give a smoother figure, which indicates the adaptive mechanism is more stable in the ER network.

FIGURE 7. Proportion reaching a stationary state of the infected individuals (ρI) as a function of β and α. (A) ER network with pΔ = 0.7; (B) ER network with pΔ = 0; (C) BA network with pΔ = 0.7; (D) BA network with pΔ = 0. Each figure is drawn in the grid 50 × 50, and λ = 0.6 remains constant.
Next, we study the effect of the awareness-based adaptive mechanism on various types of networks from the view of network structure. We construct the ER network and the BA network with 1,000 nodes and 5,000 edges to simulate the evolution process. As shown in Figure 8, regardless of constructing the ER network or the BA network, the degree distribution of nodes tends to be a longtail distribution; that is to say, there will be more low-degree nodes and fewer high-level nodes. The process of network evolution will reduce the degree of most nodes and form many smaller clusters. A small number of nodes with relatively large degrees may play a role in connecting different clusters, and they are more dangerous after being infected.
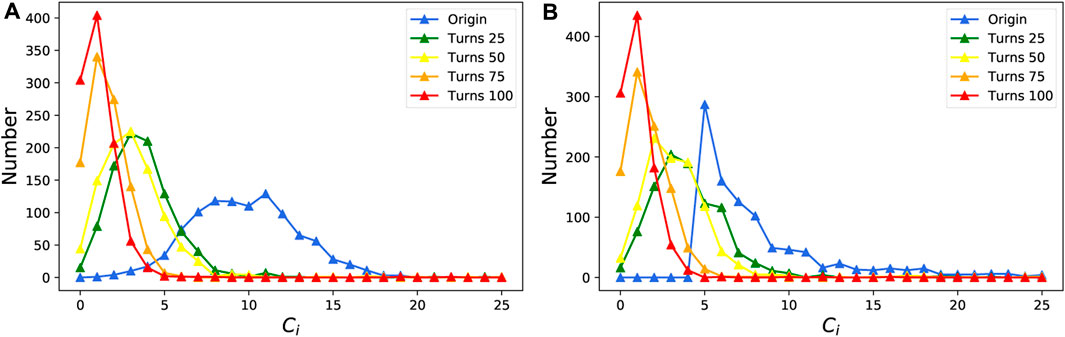
FIGURE 8. Evolution of node degree distribution over time. (A) ER network; (B) BA network. Each experiment is performed on the network including 1,000 nodes and 5,000 edges for 100 steps. We only draw nodes that have a degree less than 26. For each figure, α = 0.3, β = 0.6, and λ = 0.4. remain constant.
5 Conclusion and outlook
In this article, we improve a novel awareness-based adaptive mechanism into temporal networks and apply it to analyze the coupled dynamics between awareness diffusion and epidemic spreading. First, we establish a two-layer temporal multiplex network to symbolize the diffusion process. Then, we discuss the diffusion routes and adaptive update rules in both edges and higher-order network structures. Moreover, the expression of the epidemic threshold is derived through MMCA. Lastly, we study the effects of awareness, higher-order network structures, and the proposed adaptive mechanism through simulations. Our research comprehensively considers the behavior of network nodes in different structures and the role of network structure evolution, which provides some insights into the public sector’s future epidemic prevention and control measures. Moreover, we provide more realistic results, taking into account the needs of social operation, such as necessary social contact. In recent years, the fundamental advantages of hypergraphs and higher-order networks have attracted significant attention, which points toward the direction of exploring the novel characteristics in higher-order network propagation. We also hope to further explore the influence of this mechanism in future work and discuss it in depth. The temporal network will continue to be combined with higher-order network structures to achieve more scientific modeling.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
WX: Writing–original draft, Writing–review and editing. CZ: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Nature Science Foundation of China (No. 62127808).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ebel H, Mielsch L-I, Bornholdt S. Scale-free topology of e-mail networks. Phys Rev E (2002) 66:035103. doi:10.1103/physreve.66.035103
2. Benson AR, Gleich DF, Leskovec J. Higher-order organization of complex networks. Science (2016) 353:163–6. doi:10.1126/science.aad9029
3. Valencia M, Martinerie J, Dupont S, Chavez M. Dynamic small-world behavior in functional brain networks unveiled by an event-related networks approach. Phys Rev E (2008) 77:050905. doi:10.1103/physreve.77.050905
4. Panzeri S, Moroni M, Safaai H, Harvey CD. The structures and functions of correlations in neural population codes. Nat Rev Neurosci (2022) 23:551–67. doi:10.1038/s41583-022-00606-4
5. Gao S, Dai X, Wang L, Perra N, Wang Z. Epidemic spreading in metapopulation networks coupled with awareness propagation. IEEE Trans Cybernetics (2022) 1–13. doi:10.1109/tcyb.2022.3198732
6. Arenas A, Cota W, Gómez-Gardeñes J, Gómez S, Granell C, Matamalas JT, et al. Modeling the spatiotemporal epidemic spreading of covid-19 and the impact of mobility and social distancing interventions. Phys Rev X (2020) 10:041055. doi:10.1103/physrevx.10.041055
7. Paarporn K, Eksin C, Weitz JS, Shamma JS. Networked sis epidemics with awareness. IEEE Trans Comput Soc Syst (2017) 4:93–103. doi:10.1109/tcss.2017.2719585
8. Anderson RM, May RM. Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press (1991).
9. McCluskey CC. Complete global stability for an sir epidemic model with delay—distributed or discrete. Nonlinear Anal Real World Appl (2010) 11:55–9. doi:10.1016/j.nonrwa.2008.10.014
10. Li C, van de Bovenkamp R, Van Mieghem P. Susceptible-infected-susceptible model: a comparison of n-intertwined and heterogeneous mean-field approximations. Phys Rev E (2012) 86:026116. doi:10.1103/physreve.86.026116
11. Gómez S, Arenas A, Borge-Holthoefer J, Meloni S, Moreno Y. Discrete-time Markov chain approach to contact-based disease spreading in complex networks. Europhysics Lett (2010) 89:38009. doi:10.1209/0295-5075/89/38009
12. Funk S, Gilad E, Watkins C, Jansen VA. The spread of awareness and its impact on epidemic outbreaks. Proc Natl Acad Sci (2009) 106:6872–7. doi:10.1073/pnas.0810762106
14. Wang Z, Guo Q, Sun S, Xia C. The impact of awareness diffusion on sir-like epidemics in multiplex networks. Appl Math Comput (2019) 349:134–47. doi:10.1016/j.amc.2018.12.045
15. Granell C, Gómez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys Rev Lett (2013) 111:128701. doi:10.1103/physrevlett.111.128701
16. Li Y, Zeng Z, Feng M, Kurths J. Protection degree and migration in the stochastic sirs model: a queueing system perspective. IEEE Trans Circuits Syst Regular Pap (2021) 69:771–83. doi:10.1109/tcsi.2021.3119978
17. Zhang L, Guo C, Feng M. Effect of local and global information on the dynamical interplay between awareness and epidemic transmission in multiplex networks. Chaos: Interdiscip J Nonlinear Sci (2022) 32:083138. doi:10.1063/5.0092464
18. Feng M, Li X, Li Y, Li Q. The impact of nodes of information dissemination on epidemic spreading in dynamic multiplex networks. Chaos: Interdiscip J Nonlinear Sci (2023) 33:043112. doi:10.1063/5.0142386
19. Holme P, Saramäki J. Temporal networks. Phys Rep (2012) 519:97–125. doi:10.1016/j.physrep.2012.03.001
20. Starnini M, Baronchelli A, Pastor-Satorras R. Modeling human dynamics of face-to-face interaction networks. Phys Rev Lett (2013) 110:168701. doi:10.1103/physrevlett.110.168701
21. Cohen R, Erez K, Ben-Avraham D, Havlin S. Resilience of the internet to random breakdowns. Phys Rev Lett (2000) 85:4626–8. doi:10.1103/physrevlett.85.4626
22. Wu Y, Zhou C, Xiao J, Kurths J, Schellnhuber HJ. Evidence for a bimodal distribution in human communication. Proc Natl Acad Sci (2010) 107:18803–8. doi:10.1073/pnas.1013140107
23. Moody J. The importance of relationship timing for diffusion. Social forces (2002) 81:25–56. doi:10.1353/sof.2002.0056
24. Yang H, Gu C, Tang M, Cai S-M, Lai Y-C. Suppression of epidemic spreading in time-varying multiplex networks. Appl Math Model (2019) 75:806–18. doi:10.1016/j.apm.2019.07.011
25. Huang P, Chen X-L, Tang M, Cai S-M. Coupled dynamic model of resource diffusion and epidemic spreading in time-varying multiplex networks. Complexity (2021) 2021:1–11. doi:10.1155/2021/6629105
26. Guo H, Yin Q, Xia C, Dehmer M. Impact of information diffusion on epidemic spreading in partially mapping two-layered time-varying networks. Nonlinear Dyn (2021) 105:3819–33. doi:10.1007/s11071-021-06784-7
27. Nadini M, Sun K, Ubaldi E, Starnini M, Rizzo A, Perra N. Epidemic spreading in modular time-varying networks. Scientific Rep (2018) 8:2352. doi:10.1038/s41598-018-20908-x
28. Gómez S, Arenas A, Borge-Holthoefer J, Meloni S, Moreno Y. Discrete-time Markov chain approach to contact-based disease spreading in complex networks. Europhysics Lett (2010) 89:38009. doi:10.1209/0295-5075/89/38009
29. Karsai M, Kivelä M, Pan RK, Kaski K, Kertész J, Barabási A-L, et al. Small but slow world: how network topology and burstiness slow down spreading. Phys Rev E (2011) 83:025102. doi:10.1103/physreve.83.025102
30. Iribarren JL, Moro E. Impact of human activity patterns on the dynamics of information diffusion. Phys Rev Lett (2009) 103:038702. doi:10.1103/physrevlett.103.038702
31. Starnini M, Baronchelli A, Pastor-Satorras R. Modeling human dynamics of face-to-face interaction networks. Phys Rev Lett (2013) 110:168701. doi:10.1103/physrevlett.110.168701
32. Perra N, Gonçalves B, Pastor-Satorras R, Vespignani A. Activity driven modeling of time varying networks. Scientific Rep (2012) 2:469. doi:10.1038/srep00469
33. Miritello G, Moro E, Lara R. Dynamical strength of social ties in information spreading. Phys Rev E (2011) 83:045102. doi:10.1103/physreve.83.045102
34. Gross T, D’Lima CJD, Blasius B. Epidemic dynamics on an adaptive network. Phys Rev Lett (2006) 96:208701. doi:10.1103/physrevlett.96.208701
35. Sayama H, Pestov I, Schmidt J, Bush BJ, Wong C, Yamanoi J, et al. Modeling complex systems with adaptive networks. Comput Math Appl (2013) 65:1645–64. doi:10.1016/j.camwa.2012.12.005
36. Contisciani M, Battiston F, De Bacco C. Inference of hyperedges and overlapping communities in hypergraphs. Nat Commun (2022) 13:7229. doi:10.1038/s41467-022-34714-7
37. Iacopini I, Petri G, Barrat A, Latora V. Simplicial models of social contagion. Nat Commun (2019) 10:2485–9. doi:10.1038/s41467-019-10431-6
38. Battiston F, Amico E, Barrat A, Bianconi G, Ferraz de Arruda G, Franceschiello B, et al. The physics of higher-order interactions in complex systems. Nat Phys (2021) 17:1093–8. doi:10.1038/s41567-021-01371-4
39. Kuehn C, Bick C. A universal route to explosive phenomena. Sci Adv (2021) 7:eabe3824. doi:10.1126/sciadv.abe3824
40. St-Onge G, Thibeault V, Allard A, Dubé LJ, Hébert-Dufresne L. Master equation analysis of mesoscopic localization in contagion dynamics on higher-order networks. Phys Rev E (2021) 103:032301. doi:10.1103/physreve.103.032301
Keywords: multiplex network, temporal network, UAU–SIS model, epidemic outbreak threshold, adaptive mechanism, network evolution
Citation: Xiong W and Zhou C (2023) Epidemic spreading with an awareness-based adaptive mechanism in temporal multiplex networks. Front. Phys. 11:1285480. doi: 10.3389/fphy.2023.1285480
Received: 30 August 2023; Accepted: 09 October 2023;
Published: 12 December 2023.
Edited by:
Libo Zhang, Southwest University, ChinaReviewed by:
Tianxing Wang, Nanjing Audit University, ChinaYunlong Yu, Nanjing University of Information Science and Technology, China
Xue Yan, Nanjing Audit University, China
Copyright © 2023 Xiong and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chunjie Zhou, Y2ppZXpob3VAaHVzdC5lZHUuY24=
 Wenze Xiong
Wenze Xiong Chunjie Zhou1*
Chunjie Zhou1*