- 1State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Engineering Mechanics, Zhejiang University, Hangzhou, China
- 2Aircraft and Propulsion Laboratory, Ningbo Institute of Technology, Beihang University, Ningbo, China
- 3State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai, China
The study of microswimmers’ behavior, including their self-propulsion, interactions with the environment, and collective phenomena, has received significant attention over the past few decades due to its importance for various biological and medical applications. Microswimmers can easily access micro-fluidic channels and manipulate microscopic entities, enabling them to perform sophisticated tasks as untethered mobile microrobots inside the human body or microsize devices. Thanks to the advancements in micro/nano-technologies, a variety of synthetic and biohybrid microrobots have been designed and fabricated. Nevertheless, a key challenge arises: how to guide the microrobots to navigate through complex fluid environments and perform specific tasks. The model-free reinforcement learning (RL) technique appears to be a promising approach to address this problem. In this review article, we will first illustrate the complexities that microswimmers may face in realistic biological fluid environments. Subsequently, we will present recent experimental advancements in fabricating intelligent microswimmers using physical intelligence and biohybrid techniques. We then introduce several popular RL algorithms and summarize the recent progress for RL-powered microswimmers. Finally, the limitations and perspectives of the current studies in this field will be discussed.
1 Introduction
Microswimmers operate in the environment of low Reynolds number. Due to the dominant viscous force, they cannot propel themselves by imparting momentum. Through millions of years of evolution, biological microswimmers have developed many special propulsion mechanisms to overcome and even exploit the viscous force. Understanding these mechanisms is a key to shedding light on many biological and pathological problems. In the past few decades, there have been numerous studies focusing on the self-propelling behavior of biological microswimmers [1, 2]. With the help of advanced experimental techniques, such as light microscopy and atomic force microscopy, many biological and mechanical principles for natural microswimmers (e.g., the motility mechanisms of sperm cells [3, 4] and E. coli [5], the biological structures of the bacterial motors [6], and the eukaryotic flagellum undulation pattern [7–10]) have been elucidated. Theoretical advances in hydrodynamics at low Reynolds number also help clarify many basic mechanical rules of propelling microswimmers. For instance, the classical “scallop theorem” [11] summarizes the mobility condition for a microswimmer at low Reynolds number. The resistive force theory [12, 13] and the slender body theory [14–16] provide valuable simplification for the flagellar propulsion dynamics. The squirmer model, first proposed by Lighthill [17], can represent a large category of microswimmers ranging from Paramecium to Janus particles. It has been incorporated into computational fluid dynamics methods such as the lattice Boltzmann method (LBM) [18–20], boundary element method (BEM) [21, 22], immersed boundary method (IBM) [23], multi-particle collision dynamics (MPC) [24–26], Stokesian dynamics [27], and fictitious domain method (FD) [28] to illuminate the dynamics for a variety of microswimmers.
A microswimmer (synthetic or biohybrid) can be injected into the human body for non-invasive diagnosis and to act as a treatment agent. It is able to access very small fluidic channels and directly manipulate micro-/nanoscopic entities, thus having the potential to significantly improve the therapeutic level of medicine. Popular culture has envisaged this kind of technology decades ago (e.g., the 1966 sci-fi movie Fantastic Voyage). Microswimmers that are implantable and controlled through external magnetic [29] or ultrasonic field [30, 31] have already been successfully fabricated in recent years. However, there are still many tough challenges to be resolved before the Fantastic Voyage dream can be realized, such as the biocompatibility and biodegradability problem and the navigation problem in the complex biological fluid environments of dynamic nature. Constrained by the small dimension, a microswimmer usually has very limited on-board actuation, sensing, and computation ability. Therefore, it is very challenging to control and direct the microswimmer to swim through a complex fluidic system and perform specific cargo delivery or diagnosis tasks.
Driven by the need for understanding biological microswimmers and designing synthetic microrobots to operate in biological systems, in recent years, researchers have become more and more interested in the propulsion of microswimmers in complex fluids and environments as well as the clustering behavior of multiple microswimmers. The recent surge of advances in machine learning techniques has also prompted research studies to exploit the reinforcement learning (RL) algorithms to design intelligent microswimmers. In this article, we will first briefly review the current research status of microswimmers in complex environments and the attempts to produce intelligent microswimmers through physical intelligence and biohybrid techniques, and then we will introduce the recent advances in the incorporation of the RL technique into the microswimmer study. There is already an extensive review [32] summarizing advances on the application of general machine learning techniques to active matter, with the opportunities and challenges systematically discussed. Many recent advances in producing smart artificial microswimmers have also been timely reviewed by Tsang et al [33]. In this review, we will pay more attention to the application of RL techniques to the microswimmer study. We hope this article could help new researchers of the field get started.
2 Locomotion in complex environments
For healthcare and various other applications, synthetic or biohybrid microswimmers are often utilized in complex fluid environments which involve non-Newtonian effects, boundary confinements, and background flows. These factors significantly affect the hydrodynamics of the microswimmer, and therefore should be taken into account when training them for intelligent operations.
Biological materials and tissues can often be viewed as non-Newtonian fluids. For instance, the mucus in human gastrointestinal and cervical tracts constitutes viscoelastic fluids whose rheological properties are non-linear functions of the shear rate and stress [34]. The E. coli. and the sperm cells swim in these viscoelastic fluids and demonstrate different behaviors compared to that in Newtonian fluids. However, the influences of viscoelasticity on swimming are very complicated. Researchers have investigated intensively how the locomotion of a sperm-like microswimmer is affected by viscoelasticity through theoretical and numerical models. They found that viscoelasticity may either enhance or impede the locomotion when the different viscoelastic models (Oldroyd-B model [35–37], upper-convective Maxwell model [38], and Carreau model [39]) and swimmer models (Taylor sheet [35], cylindrical filament [38, 39], finite [36]/infinite length [35], and prescribing actuation force [35]/undulation wave [37, 38]) are used. Experiments have also shown that different combinations between viscoelastic fluids (Boger fluids [40, 41] or shear-thinning fluids [42]) and swimmer models can lead to contrasting results. More discussion on this topic can be found in a recent review [43]. Viscoelasticity also affects the synchronization/clustering behavior of multiple microswimmers. Elfring et al. [44] used the perturbation method to analyze the effects of viscoelasticity on two parallel infinitely long waving sheets (Taylor sheets), and they confirmed that viscoelasticity alone can induce synchronization of the two sheets in Stokes flow. Their work was later extended by Mo and Fedosov [45] to large beating amplitude using numerical simulations. Experiments by Tung et al. [46] demonstrated that in viscoelastic fluids of high viscosity, the clustering of bovine sperm cells is significantly enhanced. Through numerical simulations, Ishimoto and Gaffeney [47] suggested that it is the presence of cell yaw and swimmer pulling in low viscosity Newtonian fluids that inhibits clustering. Li and Ardekani [23] used the IBM to study the collective behavior of both the pusher and puller of rod shape. They found that for a suspension of pushers, viscoelasticity enhances the clustering and inhibits the large-scale flow structures and velocity fluctuations. However, viscoelasticity only has a small effect on the clustering of pullers and will also lead to further complicated phenomena when combined with the elasticity of microswimmers. It is known that a Taylor sheet swims slower in viscoelastic fluids than in Newtonian fluids [35], but Riley and Lauga [37] found that the combined effect of sheet elasticity and fluid elasticity could enhance the swimming of a Taylor sheet. Thomases et al. [48, 49] found that, as a result of the interplay of flagellum elastic force and viscoelastic force, a sperm cell model has a non-monotonic relationship between its swimming speed and the Deborah number. Furthermore, the coupling between flagellum elasticity and fluid elasticity will also affect the clustering of microswimmers. Mo and Fedosov [50] studied the clustering of two flagellated microswimmers in viscoelastic fluids and found that the elasticity of the flagellum (stiff versus soft) defines two qualitatively different regimes of clustering, where soft flagella exhibit a much less robust clustering than stiff flagella. In either case, clustering of two distinct microswimmers is most stable at Deborah numbers of approximately 1.
In most of the examples presented previously, the viscoelasticity is considered through continuum models, which is appropriate when the microswimmers are much larger than the bio-polymers or bio-colloids in the liquid. However, in some cases, the microswimmers may be of comparable size with the mesoscopic constituents. In these cases, the interactions between the microswimmers and the mesoscopic constituents (e.g., mucin [34] and blood cells [51–53]) may lead to further complex swimming behaviors. A prominent example of the significant influence of the interactions is the dramatic increase (up to two orders of magnitude) in rotational diffusivity of Janus particles in the polymer solution [54]. Qi et al. [24] have explained the origin of the increase through MPC simulation. They modelled a spherical squirmer in a solution of self-avoiding polymers whose sizes are comparable to those of the squirmer. Their simulation showed that the large enhancement of rotational diffusivity is a consequence of two effects: a decrease in the amount of absorbed polymers by active motion and an asymmetric encounter with polymers on the squirmer surface [24]. Further understanding on the interaction mechanism between many other kinds of microswimmers (e.g., flagellar microswimmers) and mesoscopic fluid structures is still in need.
Considering the significant effects of viscoelasticity (or of the macromelecules and colloidal particles) on the locomotion and clustering of many microswimmers, we anticipate that an intelligent microswimmer needs to mitigate or even exploit the effects of viscoelasticity by modifying its propulsion gait so that its navigation ability can be enhanced. However, to understand how the biological microswimmers adapt themselves to different complex fluidic structures and to discover smart gait-switching strategies for synthetic microswimmers are still open questions.
The presence of confinement is another important factor impacting the swimming behavior of microswimmers. An early study using Taylor’s swimming sheet model found that when the undulation pattern is fixed, the sheet swims faster near a solid wall [55]. Chrispell et al. [56] investigated the swimming of a Taylor sheet in viscoelastic fluids near an elastic membrane. They showed that the sheet can exploit the neighboring structures to enhance its swimming speed and efficiency. Bacteria propelling by rotation of helical flagella will experience an additional torque near a wall, causing their trajectories to become circular [57]. A freely moving microswimmer can be approximated as a pusher or puller. The dipolar flow field set up by the pusher tends to cause the swimmer to reorient parallel to the wall and is attracted toward the wall [58, 59]. For a puller, it tends to reorient perpendicular to the wall and swims toward/away from the wall [58]. Therefore, microswimmers swimming in confinement always tend to accumulate near the wall. Viscoelasticity of the fluid further enhances the wall attraction of the pusher swimmers [60]. Researchers have utilized these wall interaction mechanisms to direct and select microorganisms [61–63]. On the other hand, it is also possible to modulate the actuation of microswimmers to change their mobility in confinement. For instance, the beating pattern of a flagellum is known to significantly influence the wall attraction of a flagellated microswimmer [64]. For an E. coli swimming near a solid surface with a run-and-tumble motion pattern, it has been found that tumbling is the dominant escape mechanism [65]. Therefore, we anticipate that intelligent microswimmers should be designed to be able to navigate through complex confinements by modulating their actuation. However, discovering the right modulation strategies is still challenging.
External flows not only carry the microswimmers to move following the streamline, but they may also regulate the migration of the microswimmers. Miki and Clapham [66] demonstrated that sperm cells reorient and swim against the flow of the surrounding fluid in vitro and in vivo. Tung et al. [67] studied the upstream swimming behavior of bull sperm cells and showed that the near-wall resistive forces experienced by the microswimmer in shear flow are responsible for upstream swimming. They also found that the onset of upstream swimming can be described by a saddle-node bifurcation, and any microswimmers that possess front–back asymmetry and swim in circular trajectories near a surface will swim upstream above a critical shear rate. A novel micro-fluidic device that exploits the upstream swimming behavior to select sperm cells has also been designed and experimented [68, 69]. Even though the motion of microswimmers is usually inertialess, their background flow could still include vortical structures (e.g., plankton swimming in lakes and oceans) and cause non-trivial influences on swimming. Ardekani and Gore [70] studied the aggregation of self-propelled prolate spheroids in a Taylor–Green vortex. They found that the viscoelasticity-induced migration causes the microswimmers to aggregate in regions of low shear and rotate in a limit cycle. The viscoelasticity-induced migration is balanced by the motility; hence, their combined effects determine the shape and formation rate of the limit cycle. More discussions on this topic can be found in a recent review [71]. These discussions suggest that an intelligent microswimmer can implement smart navigation in different flows by not only controlling its swimming direction but also by exploiting the flow-induced regulation to facilitate its navigation. The discovery of the optimal path and optimal control strategy is a challenging problem that is being intensively explored by many researchers using machine learning techniques.
3 Synthetic microswimmers with physical intelligence
Intelligence can be incorporated into a microswimmer through physical intelligence or computational intelligence. According to Sitti [72], physical intelligence can be defined as “physically encoding sensing, actuation, control, memory, logic, computation, adaptation, learning, and decision-making into the body of an agent,” while computational intelligence utilizes a module functioning like a brain to control, memorize, learn, and make decisions. Many synthetic microswimmers are controlled by external fields (e.g., magnetic and ultrasonic field) and are localized with off-board techniques (e.g., fluorescence imaging or magnetic resonance imaging). Thus, they mainly adopt computational intelligence to accomplish complex tasks [73–75]. However, physical intelligence is also ubiquitous in the synthetic microswimmers.
Self-propulsion as a low-level physical intelligence: Autonomous self-propulsion implemented through physical/chemical interactions with the environment can be seen as a low-level physical intelligence [72]. The Janus particles are the most prominent examples. The surface of a Janus particle usually has two sides with distinct properties. One side of the particle is able to catalyze the surrounding fluid (e.g., hydrogen peroxide solution) to react and produce an asymmetric distribution of reaction products. A self-diffusiophoresis process will then propel the particles to move [81, 82]. Other Janus particles do not catalyze reactions but absorb different amounts of heat on the two sides. When it is immersed in a critical binary liquid mixture, it can create an asymmetric distribution of demixing products and propel itself through the process of self-diffusiophoresis (Figure 1A) [76]. Moreover, it is also possible for the particle to drive itself through the process of self-thermophoresis if the particle is in pure water [83]. In addition to diffusiophoresis and thermophoresis, other physical processes can also be utilized to drive a microswimmer. For instance, an oil droplet swimmer can propel itself by the Marangoni flow in an aqueous surfactant solution with a surfactant gradient [84]. Microswimmers can also be propelled by microjets. In the catalytic microrobots designed by Sanchez et al [85], the microswimmer is self-propelled by the release of oxygen bubbles generated in the cavity of the microtubes. Recently, significant efforts have been made to enhance the physical understanding of the linear and non-linear hydrodynamics of the self-propelled microparticles and droplets [86–89].
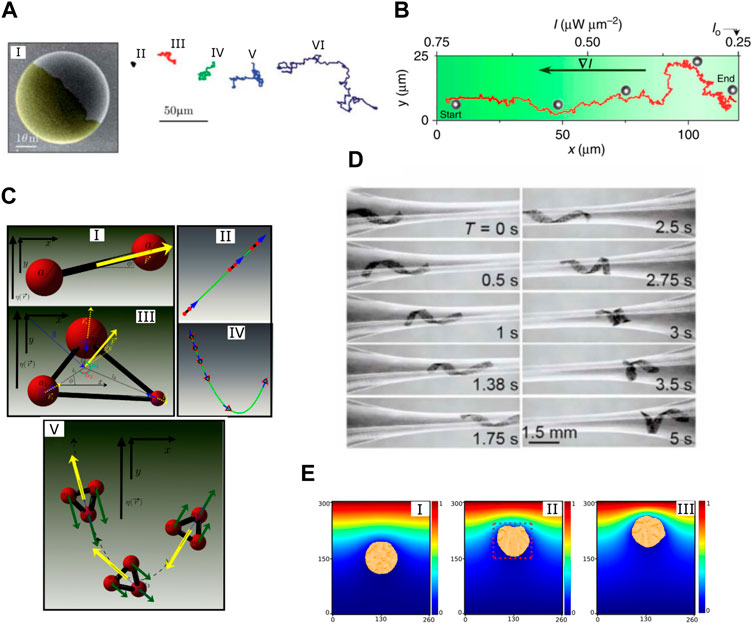
FIGURE 1. (A) A Janus particle propelled by demixing a critical mixture of water and 2,6-lutidine. 1) A scanning electron microscopy image of the Janus particle; (2–6) swimming trajectories of the Janus particle for different illumination intensities. Reproduced with permission [76]. Copyright The Royal Society of Chemistry 2011. (B) Chemotactic motion of a Janus particle in an illumination field with a linear gradient. Reproduced under a Creative Commons Attribution License (CC BY 4.0) [77]. Copyright 2016 The Authors. (C) Uniaxial swimmers do not show viscotaxis, while non-uniaxial swimmers generically show viscotaxis. 1) A uniaxial swimmer in which the propulsion force (the yellow arrow) is pointing to the direction of the symmetry axis. Its typical trajectory is shown in 2). 3) A non-uniaxial swimmer. 4) A typical swimming trajectory for the non-uniaxial swimmer with a1= a2= a3, l1= l2= l3, and ϕF =0. The swimmer initially swims toward lower viscosity, but it slowly turns the swimming direction toward higher viscosity. 5) Illustration of the viscotaxis mechanism. The green arrows represent the drag on the spheres. The viscous drag acting on body parts at high viscosity (sphere 1) is larger than the drag on spheres at low viscosity (sphere 2). The resultant torque turns the swimmer up the gradient. Reproduced with permission [78], Copyright 2018 American Physical Society. (D) A soft helical microswimmer undergoing shape adaption driven by velocity gradients in a conduit with a constriction. When the helical swimmer approaches the constriction, the front end experiences a higher flow rate; hence, the soft helical flagellum is elongated in the axial direction, and the helix radius is reduced. When the swimmer exits the constriction, the process is reversed, letting the swimmer to regain its original shape. This autonomous shape change process enables the swimmer to pass the constriction. Reproduced under CC BY-NC 4.0 [79]. Copyright 2019 The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. (E) Emergence of chemotactic motion as a collective behavior in a colony of active nematic droplets. 1) t =250000; 2) t =1000000; 3) t =2000000; the colony is depicted orange. The underlying color map represents the chemical concentration. Reproduced with permission [80], Copyright 2020 American Physical Society.
Klinotactic behavior powered by physical intelligence: Physical intelligence can lead to klinotactic behavior of microswimmers. Hagen et al. [90] studied the swimming of a fore–rear asymmetric microswimmer propelled by the catalytic process under gravity. They found that the shape anisotropy alone is enough to induce a gravitactic motion. The motion could be upward or downward, with straight or trochoid-like trajectories. The motional behavior depends sensitively on several geometric and propulsion parameters. It has been found by Lozano et al. [77] that phototaxis can be implemented for light-activated Janus particles through an inhomogeneous laser field. Under a non-uniform illumination, a reorientation torque is induced by symmetry-breaking of the slip velocity around the Janus particle and causes the particle to align in an anti-parallel manner to the gradient direction (Figure 1B). Furthermore, due to the saturation of the reorientation torque at a high light gradient, a periodic asymmetric light field can lead to a strongly rectified motion for the Janus particle. Popescu et al. [91] analyzed the forces and torques that an active spherical Janus nanoparticle experiences in a gradient of its fuel. They showed that the particle can reorient if there is a contrast in phoretic mobilities for the two halves of the particle. Depending on the sign of the average phoretic mobility (μcatal + μinert) and the sign of the difference in the phoretic mobility (μcatal − μinert), the Janus particle can show positive or negative chemotactic motion. Other researchers have studied the klinotactic motion from a more general perspective of microswimmers. Liebchen et al. [78] studied the propulsion of microswimmers in slowly varying viscosity fields. They found that viscotaxis generally emerges as a result of a systematic asymmetry of viscous forces on a non-uniaxial linear swimmer (Figure 1C).
Enabling adaptability through physical intelligence: Soft materials that respond to external stimuli can enable microswimmers with some adaptability for different environments and functionalities. For instance, the coupling between the flagellum elasticity and viscous force enables the flagellated microswimmers to adapt their undulation pattern automatically with change in the viscosity of the surrounding liquid. Moreover, as a result of the buckling instability, a planar undulation pattern may transit to a 3D undulation pattern when a critical sperm number (
Collective behavior as a physical intelligence: It has been known ever since Taylor’s [100] work that two undulating sheets tend to synchronize to be in-phase through purely hydrodynamic effects corresponding to the lowest energy dissipative phase. Passive cooperation among microswimmers is ubiquitous and can help the microswimmers swim faster and more efficiently and perform specific functionalities cooperatively. Samatas et al. [101] investigated the hydrodynamic synchronization of chiral microswimmers using a rotational squirmer model within the LBM. It was found that in an appropriate volume fraction and trajectory radius regime, the microswimmers swim in either circular or helical trajectories and synchronize their rotation spontaneously. The synchronization is manifested by velocity alignment with a high orientational order. In addition to the synchronization, collective locomotion can also emerge from many physically coupled stochastic microswimmers [102, 103]. In the work of Hughes and Yeomans [80], the emergence of chemotactic motion as a collective behavior in a colony of active nematic droplets (Figure 1E) was studied. It was found that the activity-driven alignment of cells on the cluster interface is responsible for the chemotactic response. These kinds of deterministic behaviors emerging from the coordination of many stochastic agents may be exploited to design some collective robotic systems. An active colloidal system has been reported to exhibit rich collective self-organization including clustering [104], flocking [105], and schooling [106]. In a recent work by Xie and coworkers [107], the authors investigated a microrobot system constituted by peanut-shaped hematite colloidal particles. The particles can be energized by an external magnetic field. It was found that different external signals cause the particles to exhibit rich dynamic modes including oscillating, rolling, tumbling, and spinning. These modes further lead to different self-organized formations: liquid, chains, ribbons, and vortex. The transformation among these formations can be well-controlled by the magnetic field signal and is fast and reversible. Therefore, it is possible to regulate the collective behavior of the microrobot system with an external signal and guide the microrobot system to implement complex tasks. However, further understanding on the mechanism of collective behavior of microswimmers is still in need. The readers are referred to a relevant review [2] for more information on this topic.
4 Biohybrid intelligent microswimmers
Biological organisms can be employed in the fabrication of biohybrid microswimmers to overcome the biocompatibility difficulties. This technique leverages the inherent intelligence of primitive life forms to achieve specific intelligent functions, often with the assistance of a control method. There are plenty of successful attempts to fabricate biohybrid intelligent microswimmers. Here, we mention several representative works that use different biological materials. Alapan et al. [75] constructed biohybrid microrobots with E. coli as the driver and red blood cells (RBCs) as the cargo carrier. The RBCs were loaded with not only drug molecules but also superparamagnetic nanoparticles, hence allowing the microrobot to be guided by an external magnetic field. Park et al. [108] fabricated microswimmers by attaching E. coli to the surface of drug-loaded polyelectrolyte multilayer (PEM) microparticles with embedded magnetic nanoparticles. As a result of bacteria chemotaxis, the microswimmer exhibits biased and directional motion in a chemo-attractant gradient field and can also be controlled through an external magnetic field to perform targeted drug delivery. Yan et al. [73] fabricated helical microrobots by dip-coating Fe3O4 nanoparticles onto the surfaces of microalgae (mainly Streptomyces platensis). The microrobot can be actuated and steered by an external rotating magnetic field. Requiring no surface modification, it can be tracked in vivo through either fluorescence imaging or magnetic resonance imaging. Moreover, the microrobot is biodegradable and exhibits selective cytotoxicity to cancer cell lines. This type of microrobot has the potential to be applied in vivo to imaging-guided therapy. Recently, the chemotactic motion of neutrophils has been utilized to design a biohybrid neutrophil-based microrobot (neutrobot) [109]. To fabricate a neutrobot, drug-loaded nanogels are first camouflaged with the E. coli membrane and then phagocytized by a neutrophil. Thereafter, the intravascular movement of the neutrobots can be controlled through an external magnetic actuation. Once the neutrobots reach the brain, they can cross the blood–brain barrier through active chemotactic motion and migrate toward the malignant glioma. The magnetotaxis and aerotaxis of bacteria have also been harnessed to direct the microswimmers to specific regions. In the work of Felfoul et al. [110], Magnetococcus marinus strain MC-1 was employed to transport drug-loaded nanoliposomes into hypoxic regions of the tumor. Guided by the magnetic field and facilitated by the aerotaxis of the MC-1, a high penetration rate was achieved into the hypoxic region. Microalgae (e.g., Chlamydomonas reinhardtii and Eudorina elegans) have also been utilized to fabricate biocompatible biohybrid microswimmers [111–113]. In the work of Weibel et al. [111], a surface chemical treatment is applied to attach loads to the Chlamydomonas reinhardtii. In addition, the phototaxis of the microalgae was exploited to steer the swimmers. When the swimmers reached the target, photochemistry was used to release loads, hence completing the targeted cargo delivery process.
5 Reinforcement learning
RL is a machine learning technique with which an intelligent agent learns to make sequential decisions to maximize a cumulative reward. The agent learns through continuous interactions with the environment, which can be described in the framework of a Markov decision process (MDP). An MDP can be represented by a tuple:
In addition to the explicit policy π(a|s), there are two other functions that are very useful for the decision-making of the agent: the state value function Vπ(s) and the action value function Qπ(s, a). The state value function estimates the expected future return at state s:
where
The two value functions are calculated on a specific policy π. Different policies can be evaluated using their corresponding value functions to decide which one is better. The two value functions can be determined recursively (Bellman expectation equation):
The Bellman expectation equation calculates the value functions recursively using the explicit forms of the reward function r and the state transition function P. However, in many realistic problems, the reward function and the state transition function are unknown, and the value functions have to be evaluated through a continuous interaction with the environment. In this case, the policy evaluation can be more conveniently achieved through a Monte Carlo method or a temporal difference (TD) method. We assume that the agent follows a policy π and produces many trajectories through interaction with the environment. In the Monte Carlo method, a value function (take V(s) as example) is updated incrementally by
where N(s) is a counter for the occurrence of the state s and G is the return. When N approaches infinity, the estimated value function V(s) will be the true value function. In the TD method, a value function is updated by
where α (0 < α ≤ 1) is the learning rate. The TD method uses the sum of the current reward rt and the discounted value at the next state γV(st+1) to estimate the return at the current state. Therefore, unlike the Monte Carlo method in which the value function can only be updated with a whole trajectory finished (so that the term G can be determined), in the TD method, we can update the value function at every step using the current reward rt.
When the action value function is updated with the TD method [115]
and the greedy (or ϵ-greedy) algorithm is used to select the action with the highest value at each state, a generalized policy iteration is properly implemented. This simple algorithm is already an effective RL algorithm and is known as the SARSA algorithm. The SARSA algorithm is an on-policy algorithm because all the values used in the TD method come from the current policy. In contrast, the famous Q-learning algorithm uses the following TD updating formula [116]:
where the term maxaQ(st+1, a) denotes that the maximum of action value Q is used out of all permitted actions. It is not necessary for the tuple ⟨s, a, r, s′⟩ to come from the current policy; hence, the Q-learning algorithm is an off-policy algorithm. As we will see later, the Q-learning is one of the most frequently used algorithms in intelligent microswimmer studies despite its simple form. However, the Q-learning algorithm requires the state and action space to be discrete and finite. The Q table will become extremely large in many realistic problems, leading to inefficient learning.
An important improvement for the Q-learning is the deep Q-network (DQN) algorithm, which employs a neural network to approximate the Q-value function. This method can be used to solve problems with a continuous state space and a discrete action space [117, 118]. In a typical Q-network, the input nodes take in the values of the continuous state parameters, the output nodes represent different actions, and their values are the Q values at the specific state and action. For a tuple
where ωi is the weight of the Q-network. The Q-value predicted by the Q-network is Qpredicted(si, ai; ωi). Therefore, the loss function can be defined as
Thereafter, the Q-network can be updated using the classical gradient descent method. In a DQN algorithm, the experience replay technique [118] is usually adopted to enhance the learning efficiency and remove correlations in the observation sequence. There are also many other techniques (e.g., target Q-network, double DQN, and dueling DQN) that can improve the performance of the DQN algorithm [114].
Another frequently used RL method in intelligent microswimmers is the actor–critic algorithm. The actor–critic algorithm employs two neural networks: policy network and value network. The policy network acts as an actor: it takes in the continuous values of the state parameters and outputs the probability of the actions or the Gaussian distribution parameters of the action parameters. Hence, the actor–critic is a stochastic algorithm and can be applied to problems with continuous state and action space. The value network acts as a critic: it takes in the values of the state parameters and outputs the estimation of the state value function (Eq. 1). In the actor–critic algorithm, the TD error of the value function: δt = rt + γV(st+1; ω) − V(st; ω) is used to guide the update of the policy. The weight of the policy network is updated following the policy gradient algorithm:
where δt has replaced the parameter that represents the return at t in the original policy gradient algorithm. The weight of the value network is updated through the following equation:
The actor–critic algorithm is quite simple and easy to understand, but it could be unstable for some problems. Many advanced RL algorithms have been proposed as improvement of the actor–critic algorithm, e.g., advantage actor–critic (A2C), trust region policy optimization (TRPO), proximal policy optimization (PPO), and soft actor–critic (SAC) [114, 119].
6 Intelligent microswimmers powered by RL
6.1 Self-learned propulsion
The RL technique is especially suitable for the purpose of discovering efficient propulsion strategies for various microswimmer models. Tsang et al. [120] used Q-learning to train the Najafi–Golestanian (N-G) swimmer (and its extension with more beads) to the self-learn propulsion strategy based on its interactions with the surrounding fluid. It is unsurprising that the RL approach can rediscover the known propulsion strategy in the simplest case, but it also discovered new efficient propulsion strategies when the structure of the swimmer becomes complex (Figure 2A). Zou et al. [121] used a DRL approach (PPO) to train a three-bead microswimmer to self-learn locomotory gaits for translation, rotation, and combined motions. They showed that the DRL enables the microswimmer to adopt efficient and robust locomotory strategies. These strategies guide the microswimmer to adaptively switch among various gaits and navigate toward target locations (Figure 2B) and even escape from a rotlet flow trap (Figure 2C). Qin et al. [122] also used Q-learning to study the swimming of the multi-link microswimmer (Purcell’s swimmer and its extension with more links). They showed that powered by RL, the swimmer can self-learn to swim. In addition, when the structure of the swimmer becomes complex, the RL algorithm can identify new classes of swimming gaits (Figure 2D). Note that all these research works studied only very simple microswimmer models. Even though the RL approach has been proven efficient, it has not been applied to derive a propulsion strategy for more complicated microswimmer models like flagellum-driven swimmers and cilium-driven swimmers. The major difficulty in extending this technique to more realistic and complicated models is that, for complicated models, the computation cost for both RL and computational fluid dynamics increases dramatically. For instance, if a flagellum-driven swimmer was used, the state space and action space for the swimmer would become extremely large, and the dynamics of the swimmer would need to be resolved by a direct numerical simulation (DNS) method due to the complex fluid–structure interaction. All these will lead to a dramatic increase in computation costs. Despite this challenge, applying the RL approach to a more realistic microswimmer model would still be beneficial. It will undoubtedly help us understand the propulsion strategy of many biological microswimmers and even discover novel propulsion strategies in complex dynamic environments.
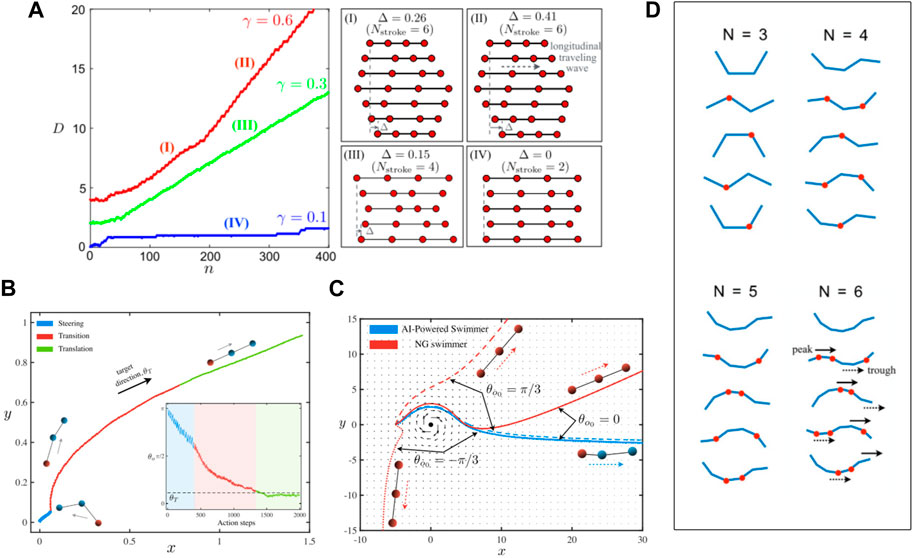
FIGURE 2. (A) Cumulative displacement of a four-bead swimmer at different discount factors γ. The right panels show the corresponding learned propulsion strategies. Reproduced with permission [120], Copyright 2020 American Physical Society. (B) A three-bead swimmer swims in 2D space using an RL-discovered strategy. The blue segment represents the steering stage, the red segment represents the transition stage, and the green segment represents the transition stage. Reproduced under a Creative Commons Attribution License (CC BY 4.0) [121]. Copyright 2022 The Authors. (C) The AI-powered swimmer escapes from a rotlet flow trap. The blue curves are trajectories of the AI-powered swimmer, and red curves are trajectories of a naïve Najafi–Golestanian swimmer. Solid, dashed, and dotted lines represent different initial orientations. Reproduced under a Creative Commons Attribution License (CC BY 4.0) [121]. Copyright 2022 The Authors. (D) Swimming gaits discovered by RL for multi-link microswimmers. The red dots mark the hinges that have been rotated relative to the previous action step. Reproduced with permission of AIP publishing [122]. Copyright 2023 The Authors.
6.2 Self-learned klinotactic motion
Klinotaxis is the directional movement of active agents toward a stimulus. With the RL technique, a microswimmer can self-learn to utilize the spatial or temporal stimulus information to determine the direction of the stimulus and steer toward it, hence leading to klinotactic motion. Colabrese et al. [123] used Q-learning to train active gyrotactic microswimmers to accomplish counter-gravity navigation through a 2D Taylor–Green vortex flow. A gyrotactic swimmer was considered using the trajectory equation:
where u is the velocity of the external flow field, vs is the swimming speed, p is the swimming direction, η is Gaussian white noise, and D0 is the translational diffusivity. The swimming direction p obeys
where ka is the preferred direction, B is the timescale of alignment, ω is the vorticity of the external flow field, DR is the rotational diffusivity, and ξ is Gaussian white noise. The state space constitutes the combinations of the coarse-grained vorticity
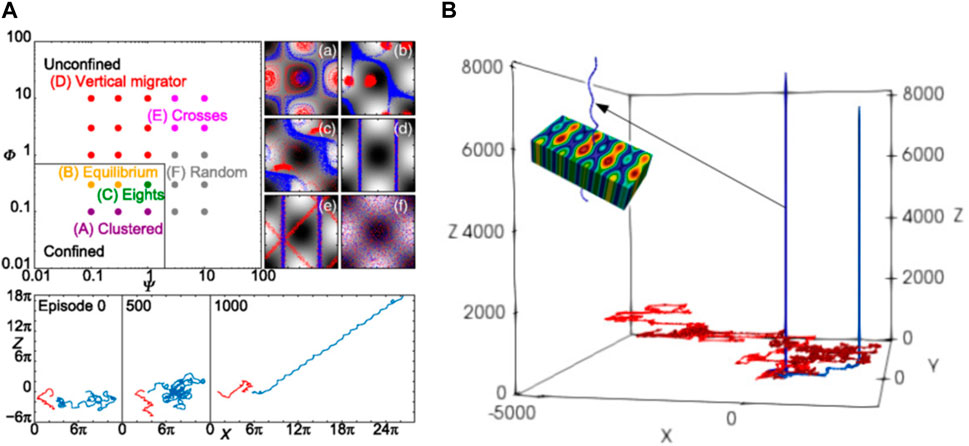
FIGURE 3. (A) Phase diagram of gyrotactic particles in a Taylor–Green vortex flow (top left); the trajectories for each of the six patterns (top right) and some representative trajectories at different learning episodes (bottom). Red trajectories: naive swimmers with ka fixed at ↑; blue trajectories: RL-powered swimmers. Reproduced with permission [123]. Copyright 2017 American Physical Society. (B) Representative trajectories of an RL-powered particle swimmer (blue) and a naïve particle swimmer swimming in a chaotic flow field. Reproduced with permission [124]. Copyright 2017 EDP Sciences, SIF, Springer-Verlag.
In the works of Colabrese et al. [123] and Gustavsson et al. [124], a point swimmer model was studied, which completely neglects the propulsion and steering mechanism of the swimmer. This reduced model is useful for preliminary research. However, more realistic models are needed to resolve the interaction between the swimmer and the fluid. Hartl et al. [125] studied the self-learned chemotaxis of an N-G swimmer in 1D space. The interaction between the beads and the fluid was modelled using Oseen approximation, and the propulsion of the swimmer was explicitly controlled by the stretching/contraction forces among the beads. They decoupled the task into two parts: first train the swimmer to learn to swim and then train the swimmer to determine the gradient direction of the chemo-attractant concentration field and steer itself toward that direction. The former was implemented with a swimmer action layer, while the latter was implemented with a concentration gradient block and two permutation control layers. The authors applied the neural evolution of augmenting topology (NEAT) to optimize both the weights and the topology of the neural network. Simple neural networks with only a few connections were found to be able to accomplish the chemotaxis task (Figure 4). These neural network models, which provide insights into how simple biological microswimmers are able to sense the environment and achieve chemotactic motion, have high feasibility to be implemented on synthetic microswimmers.
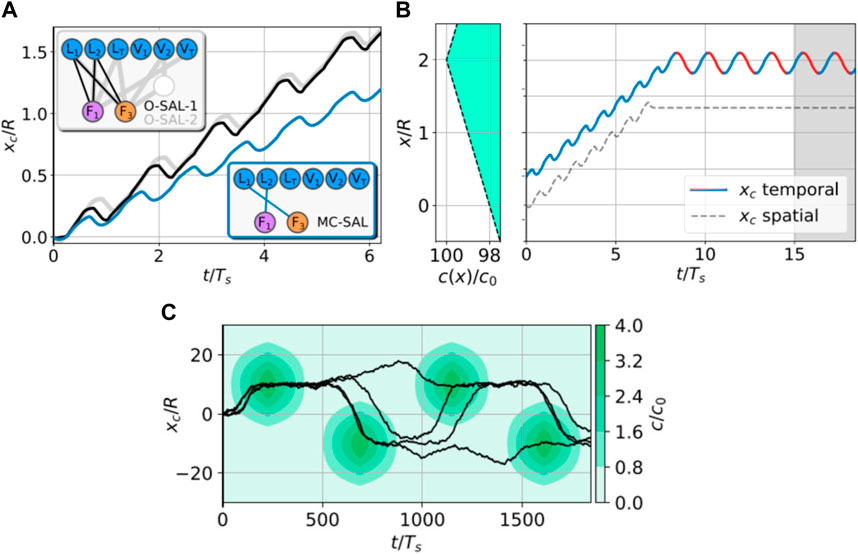
FIGURE 4. (A) Trajectories of the three-bead swimmer driven by several RL-discovered actuation strategies. The curves show the evolutions of the center of mass xc. The colors of the curves (black, blue, and gray) represent different neural network topologies, which are shown in the insets (only the swimmer action layer is presented). The O-SAL-1 layer is an optimal swimmer action layer, the O-SAL-2 layer is another optimal swimmer action layer, and the MC-SAL layer is the minimal complexity swimmer action layer. In the input nodes, L1 and L2 are the instantaneous arm lengths of the swimmer, and LT is the total length. V1 and V2 are the arm velocities Vi = dLi/dt, and VT is the sum of V1 and V2. The output nodes F1 and F2 are the stretching/contraction forces on the arms. (B) Chemotactic motion of the swimmer driven by the MC-SAL action layer in a linear chemical field (the left panel). Solid line: temporal sensing; dashed line: spatial sensing. (C) Sample trajectories in a time-dependent Gaussian chemical field c(x, t) (see the color bar). (A), (B) and (C) are reproduced from [125] under the PNAS license.
Mo and Bian [126] studied the RL-powered chemotactic motion in a more realistic situation: a sperm cell model swimming in a circular trajectory. They found that chemotactic behaviors can be achieved by the DQN, utilizing only a few environmental cues. In most cases, the DRL algorithm can discover strategies more efficient than those devised by the human. Furthermore, the DRL can utilize an external disturbance to facilitate the chemotactic motion if the extra flow information is also fed to the artificial neural network.
The RL method treats the interaction between the swimmer and the fluid as an environment and attempts to achieve the optimal policy through a Markov decision process. The algorithm is essentially a ‘trial-and-error’ process, and the learning data are collected online. However, if the biological dataset is available, supervised learning is also useful for the purpose of revealing the klinotactic mechanism of microswimmers and proposing efficient control policies to implement klinotactic motion. For instance, Ramakrishnan and Friedrich [127] employed support vector machines to a biologically motivated training dataset and discovered optimal decision filters for run-and-tumble chemotaxis under the influence of sensing and mobility noise. An empirical power law for the optimal measurement time
6.3 Point-to-point navigation through complex environments advised by RL
Synthetic or biohybrid microswimmers are usually designed to perform tasks like targeted delivery and microsurgery. For these purposes, the microswimmers should be able to navigate through some complex dynamic environments and reach a specific destination point. Many model-free RL approaches (e.g., Q-learning, DQN, PPO, and SAC) are highly efficient to discover the optimal trajectory for such a point-to-point navigation problem.
Schneider et al. [128] studied the optimal steering of an active particle. It was found that they can use Q-learning to rediscover the minimal travel-time path through a Mexican hat potential barrier. In addition, through Q-learning, the active particle can learn to rectify the effects of thermal fluctuations.
Alageshan et al. [75] studied the path-planning problem of an active particle through a complex turbulent flow field. The microswimmers were also modelled using Eqs 13 and 14 except that the noise terms are excluded. Similar to the work of Colabrese et al. [123], the state space constitutes the product of the coarse-grained vorticity set
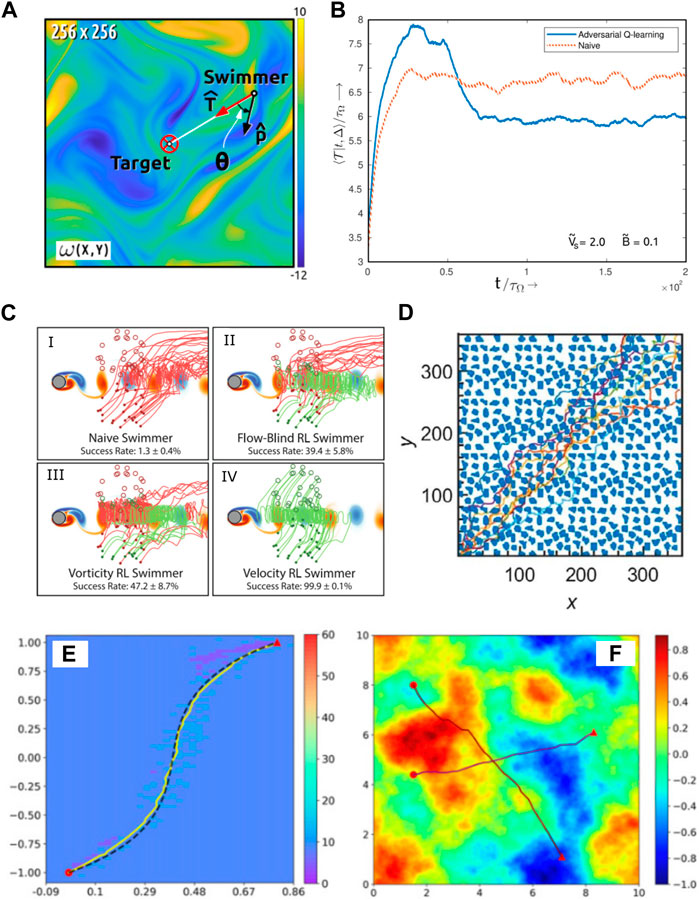
FIGURE 5. (A) Illustration of a microswimmer to swim through a turbulent flow field [75]. The background color map represents the vorticity. The red circle marks the target.
For the point-to-point navigation problem through time-dependent complex flow fields, environmental cues such as velocity and vorticity are usually necessary to be fed to the swimmer. This enables the swimmer to overcome or even exploit the external flow for its navigation. Gunnarson et al. [129] compared the vorticity sensing approach with the velocity sensing approach and found that the latter is significantly better. With velocity cues, the RL algorithm can discover strategies that have a near 100% success rate to guide the swimmer to reach the target through a cylinder wake region, while the success rate of a vorticity sensing approach is reduced by twofold (Figure 5C).
Nasiri and Liebchen [131] argued that on-policy algorithms are more robust to find the globally optimal solution in the navigation problem of an active particle than off-policy algorithms. They used the A2C algorithm and discovered the asymptotically optimal paths in different complex external potentials (Figures 5E,F). Unlike many other relevant research studies [129, 128, 121, 120, 75], where the relative distance and direction to the target are needed for the calculation of the reward function during learning, in this study, the reward depends mainly on the count of the actions; hence, heuristics is not required for the learning. It is the first time that asymptotic optimality is unified with the feasibility of handling generic complex environments.
It is worth noting that the RL approach has also been applied to the point-to-point navigation problem of macroscopic vessels. For instance, Buzzicotti et al. [132] used the actor–critic RL approach to find the optimal (minimum traveling time with/without energy consumption constraint) solution for a macroscopic vessel navigating through turbulent time-dependent flows. By comparing with the optimal navigation (ON) solution, it was shown that the RL approach is able to find quasi-optimal control solutions. While the deterministic ON solution is of little practical use due to the instability induced by the chaoticity of the environment, the RL stochastic strategies are able to overcome the instability problem. Moreover, the RL approach can discover non-trivial strategies where the vessel exploits the flows and navigates most of the time passively to minimize energy consumption. In this case, even though the dimension of the application is much larger than that of a microswimmer, the methodologies of simulating the swimmer and using RL as a decision-making agent are also applicable to a reduced point-like microswimmer model; hence, the solutions are also useful for the navigation problem of microswimmers.
Most of these studies consider complex flow fields for the microswimmer to navigate through, but it is also possible to investigate an environment with complex obstacles if we assume some vision ability for the microswimmer. Yang et al. [130] assumed that a Janus particle that keeps rotating in a Brownian way can perceive the obstacles around itself and used DRL to train the Janus particle to actively swim across a complex 2D environment full of obstacles of irregular shape. They showed that the Janus particle guided by the deep convolutional Q-network can act smartly to bypass those obstacles and swim toward its target (Figure 5D). Recently, Yang et al. [133] have extended their model using a hierarchical control scheme to guide an active particle to navigate 3D blood vessels filled with biconcave red blood cells. The new control scheme decomposes the point-to-point navigation task into many subtasks with short-ranged temporary targets. In addition, in each subtask, the swimmer is controlled by a DRL decision agent in a similar way as their previous model. Effective and robust navigation control was achieved within unseen, diverse complicated environments using the new control scheme.
It is also possible to use an RL approach to implement path-planning for multiple microswimmers at the same time. Amoudruz and Koumoutsakos [134] used the actor–critic RL method to realize independent control of two magnetic helical microswimmers using a uniform rotating magnetic field. Compared with a semi-analytical method, the RL approach works in not only quiescent flow but also complex flow background. Furthermore, it can reach lower travel time than the semi-analytical method.
The readers can also refer to a recent review [135] for in-depth discussions on this topic from a more general aspect of active particles.
6.4 Self-learned cooperation
In a recent work by Liu [136] et al., they employed the actor–critic DRL algorithm to train two N-G swimmers to learn to coordinate their motion and enhance the overall locomotory performance. The cooperation implemented by RL comprises two distinct states: the approach stage where the front swimmer waits, while the back swimmer propels with N-G strokes (Figure 6A), and the synchronization stage where the two swimmers both propel with N-G strokes but with a constant phase shift (Figure 6B). The transition between the two stages occurs when the distance between the two swimmers decreases to a specific value at which the hydrodynamic interaction can be effectively exploited. The specific phase shift discovered by the RL guarantees that hydrodynamic interaction is most efficiently exploited (Figure 6C).
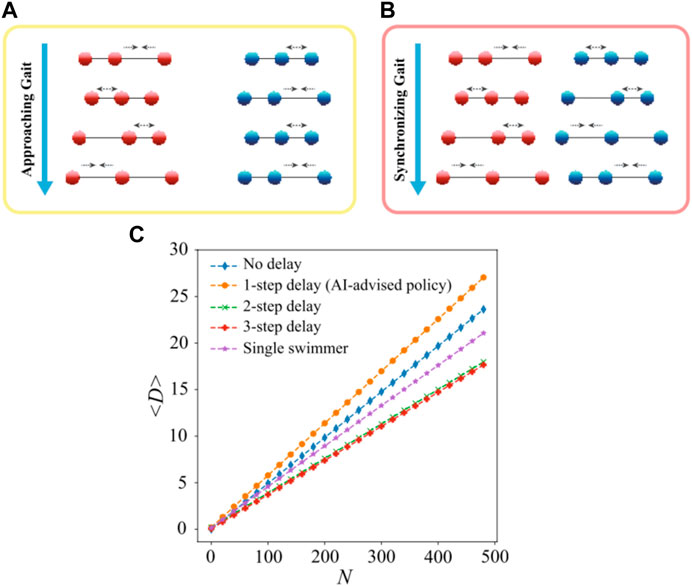
FIGURE 6. (A) Approaching gait discovered by the RL. The back swimmer propels with the N-G strokes, while the front swimmer waits. (B) Synchronizing gait discovered by the RL. Both the swimmers propel with the N-G strokes, but the back swimmer falls one action step behind. (C) Migration trajectories of the cooperating swimmer pairs with different step delays. Reproduced under a Creative Commons Attribution License (CC BY 4.0) [136]. Copyright 2023 The Authors.
In a low Reynolds number environment, the hydrodynamic interaction is long-ranged; hence, the movement of a microswimmer is easy to be detected when it is swimming alone. However, microswimmers can cooperate in cloaking each other. In a recent work by Mirzakhanloo and coworkers [137], the authors used a Q-learning algorithm to power swimming agents and train them to become smart cloaking agents. They found that when arranged properly, the cloaking agents cannot only cancel out the cloaked object’s induced flow disturbance in the far-field but also keep the object’s path unchanged. Powered by the RL technique, the cloaking agents can adjust their swimming actions to form optimal cloaking arrangements and robustly retain them in a dynamic crowded environment.
Compared with the very rare studies on the RL-powered cooperation of microswimmers, there are relatively more studies on the RL-powered cooperation of macroscopic swimmers [138, 139]. In a relatively recent work by Verma [140], they combined DNS of Navier–Stokes equations with DQN and investigated the cooperation among fish. It was found that a fish can improve its efficiency by intercepting the shed vortices of other fish and deforming its body to synchronize with the momentum of the vortices. The methodology of the macroscopic studies can also be transferred to the study of microswimmers, but due to the very different dynamics in the low Reynolds number environment, the cooperation mechanism is also expected to be very different from that of the macroscopic swimmers.
6.5 Implementation on the hardware platform
Most of the aforementioned studies are numerical simulations since it is usually more economical to discover efficient controlling schemes using numerical simulation before migrating the schemes to the practical hardware system. However, numerical simulations cannot capture all the complexity of the physical environment. Sometimes it could be beneficial to directly perform RL on physical systems. The work of Muiños-Landin et al. [141] was the first attempt to incorporate RL into active particles on a realistic hardware platform. They applied laser light to actuate a gold nanoparticle-coated microparticle through the self-thermophoretic effect. The direction of the laser light can be changed to steer the active particle. They employed the Q-learning algorithm to train the control agent, where the real-time coarse-grained position of the active particle was fed to the RL algorithm as the state parameter and meanwhile the coarse-grained directions of the heating laser constituted the action space. A steering policy was successfully learned to guide the swimmer to a target position. It was also revealed that noise also contributes to the learning process, and the learned strategy could be different at different levels of noise. Recently, Behrens and Ruder [142] made another attempt to implement RL on a realistic hardware platform to control microswimmers. They fabricated a helical magnetic hydrogel microswimmer and employed the SAC RL algorithm to autonomously derive a control policy to guide the microswimmer to swim through a circular fluidic channel (Figure 7A). The microswimmer was controlled through a three-axis array of electromagnets. The inputs for the decision-making machinery are either a state vector characterizing the system or the raw image of the system, while the action is the magnitudes and phases of the magnetic coils. It was found that in both cases, the RL-powered microswimmer learned successful actuation policies and the learned policies recapitulated the behavior of theoretically optimal physics-based approaches (Figures 7B,C). Since RL training usually requires thousands to millions of experiences, it is normally necessary to automatically reset the environment after every episode. In some cases, the system can be specially designed so that no mechanical resetting is needed. For example, in the case of Behrens and Ruder [142], a circular channel was used; hence, any point on the circle can be a new starting point, and no resetting of the position is required. Nevertheless, in some other cases, the requirement of automatic resetting may become a difficulty that needs to be resolved to perform RL on the hardware platform. Another difficulty is the possible system wear and tear caused by extended use in millions of training episodes. This wear and tear may lead to a distribution shift in the collected data and disrupt the learning process [142].
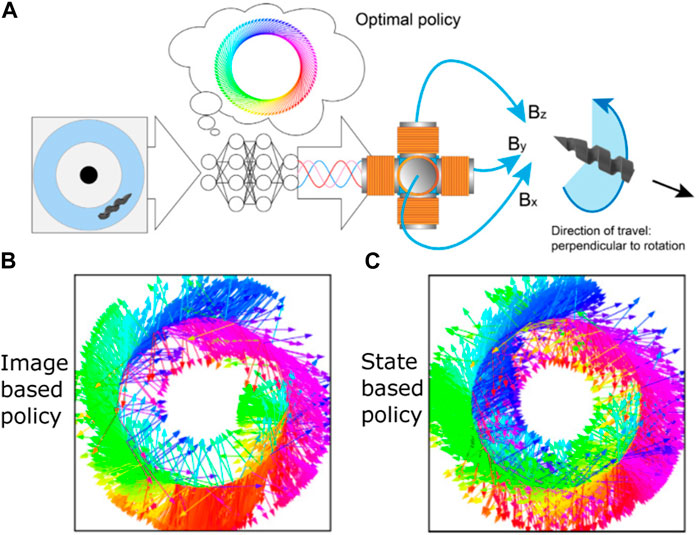
FIGURE 7. (A) Schematic of the RL control for a synthetic microswimmer. The magnetic helical microswimmer swims in a circular fluidic channel. The system image or state is captured to input to a neural network, which acts as a decision-making agent. The neural network outputs the magnitudes and phases of the magnetic coils to control the propulsion and steering of the magnetic microswimmer. The inset shows the optimal control policy, with the arrows depicting the direction of the rotating magnetic field when the swimmer is at the specific azimuthal angle. (B) RL-discovered policy with the system image as input for the neural network. (C) RL-discovered policy with the system state as input for the neural network. Reproduced under CC BY-NC 4.0 [142]. Copyright 2022 The Authors.
7 Summary and perspective
In this review, we first briefly illustrated the complexity that a microswimmer may face in a realistic biological fluid environment, and then we highlighted some recent attempts to enable intelligent microswimmers to swim through complex environments of dynamic nature autonomously. A biological fluid environment may contain non-Newtonian fluids, tortuous and flexible boundaries, and obstacles of irregular shapes. Microswimmers experience highly complicated interactions with the environment and with each other; hence, they are difficult to actively control. Physical intelligence which arises from the physical/chemical interactions between swimmers and the environment and from the inter-swimmer cooperation may provide some actuation/steering ability and adaptivity for the microswimmers. However, the ability obtained from physical intelligence is usually quite limited. Biohybrid microswimmers can utilize the inherited intelligence of the biological materials to overcome the biocompatibility and biodegradable problems and also possess some directional mobility. However, biohybrid microswimmers are usually used for specific purposes, and hence, they cannot adapt to various environments or perform general tasks. A model-free RL technique is a promising approach to address the challenges mentioned previously. We briefly introduced several popular RL algorithms (SARSA, Q-learning, DQN, and actor–critic) and further summarized the recent advances on RL-powered microswimmers. We categorized four application directions of the RL technique in the realization of intelligent microswimmers: 1) self-learned propulsion; 2) self-learned klinotactic motion; 3) point-to-point navigation advised by RL; 4) self-learned cooperation.
Many researchers have validated the effectiveness of the RL technique in guiding microswimmers. The RL technique can not only rediscover known optimal strategies in simplified cases but also find efficient strategies when the problems become intractable by other means. Moreover, the RL technique is able to propose strategies that mitigate the effect of noise. Nevertheless, there are still several limitations in most of the studies on RL-powered microswimmers: 1) simple reduced models (e.g., point swimmer, Najafi–Golestanian’s swimmer, and Purcell’s swimmer) are usually preferred, where the actuation and steering mechanisms are either not considered (for the point swimmer) or only conceptual (for the Najafi–Golestanian’s swimmer and Purcell’s swimmer). 2) The non-Newtonian feature of the biological fluids, the elasticity of the microswimmers, and the tortuous elastic boundaries are often not taken into account. These limitations are likely as a result of the resource-demanding feature of the RL algorithms. Since RL algorithms require substantial data, the computational cost would be very high if the fluid–solid interaction was fully resolved. However, accurately resolving the interactions between the flexible body and the complex environment is key to proposing an effective control strategy for realistic microswimmers. 3) Most of the studies are numerical simulations as a proof of concept, and migration to a realistic hardware platform is rare. In numerical simulations, the researchers are omnipotent observers and can feed any global or local information to the swimmers without worrying about how the swimmers can sense this information in reality. The researchers can also propose any control mechanism without worrying about how to implement the exact actuation/steering in reality. Therefore, the policies discovered by RL in numerical simulations may be infeasible for realistic microswimmers, impeding the practicality of the RL techniques. Resolving these problems is definitely necessary in the future.
Author contributions
CM: conceptualization, writing–review and editing, formal analysis, methodology, project administration, validation, and writing–original draft. GL: conceptualization, writing–review and editing, and supervision. XB: conceptualization, writing–review and editing, supervision, and funding acquisition.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors thank the financial support from National Natural Science Foundation of China (Grant Nos. 12302323, 12372264, 12172330) and Natural Science Foundation of Shanghai (Grant No. 23ZR1430800). XB received the starting grant from 100 talents program of Zhejiang University.
Acknowledgments
We are grateful for the referees for their critical suggestions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Lauga E, Thomas RP. The hydrodynamics of swimming microorganisms. Rep Prog Phys (2009) 72(9):096601. doi:10.1088/0034-4885/72/9/096601
2. Elgeti J, Winkler RG, Gompper G. Physics of microswimmers - single particle motion and collective behavior: A review. Rep Prog Phys (2015) 78(5):056601. doi:10.1088/0034-4885/78/5/056601
3. Hugh C. Crenshaw. A new look at locomotion in microorganisms: Rotating and translating. Am Zoologist (1996) 36(6):608–18.
4. Jikeli JF, Alvarez L, Friedrich BM, Wilson LG, Pascal R, Colin R, et al. Sperm navigation along helical paths in 3D chemoattractant landscapes. Nat Commun (2015) 6:7985. doi:10.1038/ncomms8985
5. Berg DA, Brown HC. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature (1972) 239:500–4. doi:10.1038/239500a0
6. Berg HC, Anderson RA. Bacteria swim by rotating their flagellar filaments. Nature (1973) 245:380–2. doi:10.1038/245380a0
7. Woolley DM. Motility of spermatozoa at surfaces. Reproduction (2003) 126(2):259–70. doi:10.1530/rep.0.1260259
8. Cosson J, Huitorel P, Gagnon C. How spermatozoa come to be confined to surfaces. Cell Motil Cytoskeleton (2003) 54(1):56–63. doi:10.1002/cm.10085
9. Saggiorato G, Alvarez L, Jikeli JF, Benjamin Kaupp U, Gompper G, Elgeti J. Human sperm steer with second harmonics of the flagellar beat. Nat Commun (2017) 8(1):1415. doi:10.1038/s41467-017-01462-y
10. Gong A, Rode S, Gompper G, Kaupp UB, Elgeti J, Friedrich BM, et al. Reconstruction of the three-dimensional beat pattern underlying swimming behaviors of sperm. Eur Phys J E (2021) 44(7):87–12. doi:10.1140/epje/s10189-021-00076-z
12. Hancock GJ. The self-propulsion of microscopic organisms through liquids. Proc R Soc Lond Ser A. Math Phys Sci (1953) 217(1128):96–121.
13. Gray J, Hancock GJ. The propulsion of sea-urchin spermatozoa. J Exp Biol (1955) 32(4):802–14. doi:10.1242/jeb.32.4.802
14. Keller JB, Rubinow SI. Slender-body theory for slow viscous flow. J Fluid Mech (1976) 75(4):705–14. doi:10.1017/s0022112076000475
15. Johnson R. An improved slender-body theory for Stokes flow. J Fluid Mech (1980) 99(2):411–31. doi:10.1017/s0022112080000687
16. Lighthill J. Reinterpreting the basic theorem of flagellar hydrodynamics. J Eng Math (1996) 30(25–34):25–34. doi:10.1007/bf00118822
17. Lighthill MJ. On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun Pure Appl Math (1952) 5(2):109–18. doi:10.1002/cpa.3160050201
18. Llopis I, Pagonabarraga I. Dynamic regimes of hydrodynamically coupled self-propelling particles. Europhysics Lett (2006) 75(6):999–1005. doi:10.1209/epl/i2006-10201-y
19. Kuron M, Philipp S, Burkard C, De Graaf J, Holm C. A lattice Boltzmann model for squirmers. J Chem Phys (2019) 150(14):1–9.
20. Ouyang Z, Lin J. The hydrodynamics of an inertial squirmer rod. Phys Fluids (2021) 33(7):1–11. doi:10.1063/5.0057974
21. Ishikawa T, Simmonds MP, Pedley TJ. Hydrodynamic interaction of two swimming model micro-organisms. J Fluid Mech (2006) 568:119–60. doi:10.1017/s0022112006002631
22. Kyoya K, Matsunaga D, Imai Y, Omori T, Ishikawa T. Shape matters: Near-field fluid mechanics dominate the collective motions of ellipsoidal squirmers. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2015) 92(6):063027–6. doi:10.1103/physreve.92.063027
23. Li G, Arezoo M. Ardekani. Collective motion of microorganisms in a viscoelastic fluid. Phys Rev Lett (2016) 117(11):1–5.
24. Qi K, Westphal E, Gompper G, Winkler RG. Enhanced rotational motion of spherical squirmer in polymer solutions. Phys Rev Lett (2020) 124(6):068001. doi:10.1103/physrevlett.124.068001
25. Clopés J, Gompper G, RolandWinkler G. Hydrodynamic interactions in squirmer dumbbells: Active stress-induced alignment and locomotion. Soft Matter (2020) 16(47):10676–87. doi:10.1039/d0sm01569e
26. Clopés J, Gompper G, Roland GW. Alignment and propulsion of squirmer pusher–puller dumbbells. J Chem Phys (2022) 156(19):05:194901.
27. Ishikawa T, Dang TN, Lauga E. Instability of an active fluid jet. Phys Rev Fluids (2022) 7(9):093102. doi:10.1103/physrevfluids.7.093102
28. Ouyang Z, Lin Z, Yu Z, Lin J, Phan-Thien N. Hydrodynamics of an inertial squirmer and squirmer dumbbell in a tube. J Fluid Mech (2022) 939:A32–23. doi:10.1017/jfm.2022.210
29. Martel S, Baptiste Mathieu J, Felfoul O, Arnaud C, Aboussouan E, Tamaz S, et al. Automatic navigation of an untethered device in the artery of a living animal using a conventional clinical magnetic resonance imaging system. Appl Phys Lett (2007) 90(11):24–7. doi:10.1063/1.2713229
30. Wang W, Li S, Mair L, Ahmed S, Huang TJ, Thomas EM. Acoustic propulsion of nanorod motors inside living cells. Angew Chem Int Edition (2014) 53(12):3201–4. doi:10.1002/anie.201309629
31. Schrage M, Medany M, Ahmed D. Ultrasound microrobots with reinforcement learning. Adv Mater Tech (2023) 8(10):2023. doi:10.1002/admt.202201702
32. Frank C, Gustavsson K, Mehlig B, Volpe G. Machine learning for active matter. Nat Machine Intelligence (2020) 2(2):94–103. doi:10.1038/s42256-020-0146-9
33. Tsang ACH, Demir E, Ding Y, Pak OS. Roads to smart artificial microswimmers. Adv Intell Syst (2020) 2(8):1900137.
34. Lai SK, Wang YY, Wirtz D, Hanes J. Micro- and macrorheology of mucus. Adv Drug Deliv Rev (2010) 61(2):86–100. doi:10.1016/j.addr.2008.09.012
36. Joseph T, Fauci L, Shelley M. Viscoelastic fluid response can increase the speed and efficiency of a free swimmer. Phys Rev Lett (2010) 104(3):1–4.
37. Riley EE, Lauga E. Enhanced active swimming in viscoelastic fluids. Epl (2014) 108(3):34003–6. doi:10.1209/0295-5075/108/34003
38. Fu HC, Powers TR, Wolgemuth CW. Theory of swimming filaments in viscoelastic media. Phys Rev Lett (2007) 99(25):258101–4. doi:10.1103/physrevlett.99.258101
39. Riley EE, Lauga E. Empirical resistive-force theory for slender biological filaments in shear-thinning fluids. Phys Rev E (2017) 95(6):062416–3. doi:10.1103/physreve.95.062416
40. Dasgupta M, Liu B, Fu HC, Berhanu M, Breuer KS, Powers TR, et al. Speed of a swimming sheet in Newtonian and viscoelastic fluids. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2013) 87(1):013015–7. doi:10.1103/physreve.87.013015
41. Espinosa-Garcia J, Lauga E, Zenit R. Fluid elasticity increases the locomotion of flexible swimmers. Phys Fluids (2013) 25(3). doi:10.1063/1.4795166
42. Shen XN, Arratia PE. Undulatory swimming in viscoelastic fluids. Phys Rev Lett (2011) 106(20):208101–4. doi:10.1103/physrevlett.106.208101
43. Li G, Lauga E, Arezoo M. Microswimming in viscoelastic fluids. J Non-Newtonian Fluid Mech (2021) 297(September):104655. doi:10.1016/j.jnnfm.2021.104655
44. Gwynn J. Elfring, on shun pak, and eric Lauga. Two-Dimensional flagellar synchronization in viscoelastic fluids. J Fluid Mech (2010) 646:505–15.
45. Mo C, Dmitry A. Fedosov. Competing effects of inertia, sheet elasticity, fluid compressibility, and viscoelasticity on the synchronization of two actuated sheets. Phys Fluids (2021) 33(4).
46. Tung CK, Lin C, Harvey B, Fiore AG, Ardon F, Wu M, et al. Fluid viscoelasticity promotes collective swimming of sperm. Scientific Rep (2017) 7(1):3152–9. doi:10.1038/s41598-017-03341-4
47. Ishimoto K, Gaffney EA. Hydrodynamic clustering of human sperm in viscoelastic fluids. Scientific Rep (2018) 8(1):15600–11. doi:10.1038/s41598-018-33584-8
48. Thomases B, Guy RD. Mechanisms of elastic enhancement and hindrance for finite-length undulatory swimmers in viscoelastic fluids. Phys Rev Lett (2014) 113(9):098102–5. doi:10.1103/physrevlett.113.098102
49. Thomases B, Guy RD. The role of body flexibility in stroke enhancements for finite-length undulatory swimmers in viscoelastic fluids. J Fluid Mech (2017) 825:109–32. doi:10.1017/jfm.2017.383
50. Mo C, Dmitry A. Hydrodynamic clustering of two finite-length flagellated swimmers in viscoelastic fluids. J R Soc Interf (2023) 20:20220667. 199. doi:10.1098/rsif.2022.0667
51. Amoudruz L, Economides A, Arampatzis G, Koumoutsakos P. The stress-free state of human erythrocytes: Data-driven inference of a transferable RBC model. Biophysical J (2023) 122(8):1517–25. doi:10.1016/j.bpj.2023.03.019
52. Qi X, Wang S, Ma S, Han K, Bian X, Li X. Quantitative prediction of rolling dynamics of leukocyte-inspired microroller in blood flow. Phys Fluids (2021) 33(12):12:121908. doi:10.1063/5.0072842
53. Venugopalan PL, Sai R, Chandorkar Y, Basu B, Shivashankar S, Ghosh A. Conformal cytocompatible ferrite coatings facilitate the realization of a nanovoyager in human blood. Nano Lett (2014) 14(4):1968–75. doi:10.1021/nl404815q
54. Gomez-Solano JR, Blokhuis A, Bechinger C. Dynamics of self-propelled Janus particles in viscoelastic fluids. Phys Rev Lett (2016) 116(13):138301–6. doi:10.1103/physrevlett.116.138301
55. Reynolds AJ. The swimming of minute organisms. J Fluid Mech (1965) 23(2):241–60. doi:10.1017/s0022112065001337
56. Chrispell JC, Fauci LJ, Shelley M. An actuated elastic sheet interacting with passive and active structures in a viscoelastic fluid. Phys Fluids (2013) 25(1). doi:10.1063/1.4789410
57. Lauga E, DiLuzio WR, Whitesides GM, Stone HA. Swimming in circles: Motion of bacteria near solid boundaries. Biophysical J (2006) 90(2):400–12. doi:10.1529/biophysj.105.069401
58. Berke AP, Turner L, Berg HC, Lauga E. Hydrodynamic attraction of swimming microorganisms by surfaces. Phys Rev Lett (2008) 101(3):038102–4. doi:10.1103/physrevlett.101.038102
59. Li G, Ardekani AM. Hydrodynamic interaction of microswimmers near a wall. Phys Rev E (2014) 90(1):013010. doi:10.1103/physreve.90.013010
60. Li G, Karimi A, Ardekani AM. Effect of solid boundaries on swimming dynamics of microorganisms in a viscoelastic fluid. Rheologica acta (2014) 53:911–26. doi:10.1007/s00397-014-0796-9
61. Denissenko P, Kantsler V, Smith DJ, Kirkman-Brown J. Human spermatozoa migration in microchannels reveals boundary-following navigation. Proc Natl Acad Sci USA (2012) 109(21):8007–10. doi:10.1073/pnas.1202934109
62. Nosrati R, Vollmer M, Eamer L, Maria C, Zeidan K, et al. Rapid selection of sperm with high DNA integrity. Lab A Chip (2014) 14(6):1142–50. doi:10.1039/c3lc51254a
63. Eamer L, Vollmer M, Nosrati R, Maria C, Zeidan K, et al. Turning the corner in fertility: High DNA integrity of boundary-following sperm. Lab A Chip (2016) 16(13):2418–22. doi:10.1039/c6lc00490c
64. Rode S, Elgeti J, Gompper G. Sperm motility in modulated microchannels. New J Phys (2019) 21(1):013016. doi:10.1088/1367-2630/aaf544
65. Junot G, Darnige T, Lindner A, Martinez VA, Arlt J, Dawson A, et al. Run-to-Tumble variability controls the surface residence times of E. coli bacteria. Phys Rev Lett (2022) 128(24):248101–6. doi:10.1103/physrevlett.128.248101
66. Miki K, David E. Rheotaxis guides mammalian sperm. Curr Biol (2013) 23(6):443–52. doi:10.1016/j.cub.2013.02.007
67. Tung CK, Ardon F, Roy A, Koch DL, Suarez SS, Wu. M. Emergence of upstream swimming via a hydrodynamic transition. Phys Rev Lett (2015) 114(10):108102–5. doi:10.1103/physrevlett.114.108102
68. Wu JK, Peng C, Chen Y, Nan L, Wang CW, Pan LC, et al. High-throughput flowing upstream sperm sorting in a retarding flow field for human semen analysis. Analyst (2017) 142(6):938–44. doi:10.1039/c6an02420c
69. Ali H, Targhi MZ, Halvaei I, Nosrati R. A novel microfluidic device with parallel channels for sperm separation using spermatozoa intrinsic behaviors. Scientific Rep (2023) 13(1):1–10.
70. Ardekani AM, Gore E. Emergence of a limit cycle for swimming microorganisms in a vortical flow of a viscoelastic fluid. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2012) 85(5):056309–5. doi:10.1103/physreve.85.056309
71. Ishimoto K. Jeffery’s orbits and microswimmers in flows: A theoretical review. J Phys Soc Jpn (2023) 92(6):1–20. doi:10.7566/jpsj.92.062001
72. Metin S. Physical intelligence as a new paradigm. Extreme Mech Lett (2021) 46:101340. doi:10.1016/j.eml.2021.101340
73. Yan X, Qi Z, Vincent M, Deng Y, Yu J, Xu J, et al. Multifunctional biohybrid magnetite microrobots for imaging-guided therapy. Sci Robotics (2017) 2(12):1–15.
74. Kei Cheang U, Kim H, Milutinović D, Choi J, Kim MJ. Feedback control of an achiral robotic microswimmer. J Bionic Eng (2017) 14(2):245–59. doi:10.1016/s1672-6529(16)60395-5
75. Alageshan JK, Verma AK, Bec J, Pandit R. Machine learning strategies for path-planning microswimmers in turbulent flows. Phys Rev E (2020) 101(4):043110. doi:10.1103/physreve.101.043110
76. Volpe G, Buttinoni I, Vogt D, Kümmerer HJ, Bechinger C. Microswimmers in patterned environments. Soft Matter (2011) 7(19):8810–5. doi:10.1039/c1sm05960b
77. Lozano C, Ten Hagen B, Löwen H, Bechinger C. Phototaxis of synthetic microswimmers in optical landscapes. Nat Commun (2016) 7:12828–10. doi:10.1038/ncomms12828
78. Liebchen B, Paul M, Ten Hagen B, Löwen H. Viscotaxis: Microswimmer navigation in viscosity gradients. Phys Rev Lett (2018) 120(20):208002. doi:10.1103/physrevlett.120.208002
79. Huang HW, Uslu FE, Katsamba P, Lauga E, Sakar MS, Nelson BJ. Adaptive locomotion of artificial microswimmers. Sci Adv (2019) 5(1):eaau1532–8. doi:10.1126/sciadv.aau1532
80. Hughes R, Yeomans JM. Collective chemotaxis of active nematic droplets. Phys Rev E (2020) 102(2):020601–5. doi:10.1103/physreve.102.020601
81. Paxton WF, Kistler KC, Olmeda CC, Sen A, SarahAngelo KST, Cao Y, et al. Catalytic nanomotors: Autonomous movement of striped nanorods. J Am Chem Soc (2004) 126(41):13424–31. doi:10.1021/ja047697z
82. Howse JR, Jones RAL, Ryan AJ, Gough T, Vafabakhsh R, Golestanian R. Self-Motile colloidal particles: From directed propulsion to random walk. Phys Rev Lett (2007) 99(4):048102–11. doi:10.1103/physrevlett.99.048102
83. Jiang HR, Yoshinaga N, Sano M. Active motion of a Janus particle by self-thermophoresis in a defocused laser beam. Phys Rev Lett (2010) 105(26):268302–4. doi:10.1103/physrevlett.105.268302
84. Jin C, Kru-ger C, CorinnaMaass C. Chemotaxis and autochemotaxis of self-propelling droplet swimmers. Proc Natl Acad Sci USA (2017) 114(20):5089–94. doi:10.1073/pnas.1619783114
85. Sanchez S, Solovev AA, Schulze S, Schmidt OG. Controlled manipulation of multiple cells using catalytic microbots. Chem Commun (2011) 47(2):698–700. doi:10.1039/c0cc04126b
86. Michelin S, Lauga E, Bartolo D. Spontaneous autophoretic motion of isotropic particles. Phys Fluids (2013) 25(6). doi:10.1063/1.4810749
87. Li G, Koch DL. Dynamics of a self-propelled compound droplet. J Fluid Mech (2022) 952:A16. doi:10.1017/jfm.2022.891
88. Li G. Swimming dynamics of a self-propelled droplet. J Fluid Mech (2022) 934(A20):A20. doi:10.1017/jfm.2021.1154
89. Schnitzer O. Weakly nonlinear dynamics of a chemically active particle near the threshold for spontaneous motion. i. adjoint method. Phys Rev Fluids (2023) 8(3):034201. doi:10.1103/physrevfluids.8.034201
90. Ten Hagen B, Kümmel F, Wittkowski R, Takagi D, Löwen H, Bechinger C. Gravitaxis of asymmetric self-propelled colloidal particles. Nat Commun (2014) 5:4829. doi:10.1038/ncomms5829
91. Popescu MN, Uspal WE, Bechinger C, Fischer P. Chemotaxis of active Janus nanoparticles. Nano Lett (2018) 18(9):5345–9. doi:10.1021/acs.nanolett.8b02572
92. Wei Huang H, Selman Sakar M, Petruska AJ, Salvador P, Nelson BJ. Soft micromachines with programmable motility and morphology. Nat Commun (2016) 7:12263–10. doi:10.1038/ncomms12263
93. Fu Z, Rong W, Wang L, Sun L. Magnetic actuated shape-memory helical microswimmers with programmable recovery behaviors. J Bionic Eng (2021) 18(4):799–811. doi:10.1007/s42235-021-0063-6
94. Leng J, Lan X, Liu Y, Du S. Shape-memory polymers and their composites: Stimulus methods and applications. Prog Mater Sci (2011) 56(7):1077–135. doi:10.1016/j.pmatsci.2011.03.001
95. Yoshida K, Onoe H. Soft spiral-shaped microswimmers for autonomous swimming control by detecting surrounding environments. Adv Intell Syst (2020) 2(9):2070090. doi:10.1002/aisy.202000095
96. Li H, Go G, Ko SY, Oh Park J, Park S. Magnetic actuated pH-responsive hydrogel-based soft micro-robot for targeted drug delivery. Smart Mater Structures (2016) 25(2):027001. doi:10.1088/0964-1726/25/2/027001
97. Go G, Nguyen VD, Jin Z, Oh Park J, Park S. A thermo-electromagnetically actuated microrobot for the targeted transport of therapeutic agents. Int J Control Automation Syst (2018) 16(3):1341–54. doi:10.1007/s12555-017-0060-z
98. Medina-Sánchez M, Magdanz V, Guix M, Fomin VM, Schmidt OG. Swimming microrobots: Soft, reconfigurable, and smart. Adv Funct Mater (2018) 28(25):1–27. doi:10.1002/adfm.201707228
99. Bunea A-I, Martella D, Nocentini S, Parmeggiani C, Taboryski R, Wiersma DS. Light-powered microrobots: Challenges and opportunities for hard and soft responsive microswimmers. Adv Intell Syst (2021) 3(4):2000256. doi:10.1002/aisy.202170041
100. Taylor G. Analysis of the swimming of microscopic organisms. Proc R Soc Lond A (1951) 209:447–61.
101. Samatas S, Lintuvuori J. Hydrodynamic synchronization of chiral microswimmers. Phys Rev Lett (2023) 130(2):024001. doi:10.1103/physrevlett.130.024001
102. Shamloo A. Cell-cell interactions mediate cytoskeleton organization and collective endothelial cell chemotaxis. Cytoskeleton (2014) 71(9):501–12. doi:10.1002/cm.21185
103. Adam S, Szabó A, Trepat X, Mayor R. Supracellular contraction at the rear of neural crest cell groups drives collective chemotaxis. Science (2018) 362(6412):339–43. doi:10.1126/science.aau3301
104. Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C, Speck T. Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys Rev Lett (2013) 110(23):238301–5. doi:10.1103/physrevlett.110.238301
106. Antoine B, Caussin JB, Desreumaux N, Dauchot O, Bartolo D. Emergence of macroscopic directed motion in populations of motile colloids. Nature (2013) 503(7474):95–8. doi:10.1038/nature12673
107. Xie H, Sun M, Fan X, Lin Z, Chen W, Wang L, et al. Reconfigurable magnetic microrobot swarm: Multimode transformation, locomotion, and manipulation. Sci Robotics (2019) 4(28):eaav8006–15. doi:10.1126/scirobotics.aav8006
108. Park BW, Jiang Z, Yasa O, Metin S. Multifunctional bacteria-driven microswimmers for targeted active drug delivery. ACS Nano (2017) 11(9):8910–23. doi:10.1021/acsnano.7b03207
109. Zhang H, Li Z, Gao C, Fan X, Pang Y, Li T, et al. Dual-responsive biohybrid neutrobots for active target delivery. Sci Robotics (2021) 6(52):eaaz9519. doi:10.1126/scirobotics.aaz9519
110. Felfoul O, Mohammadi M, Taherkhani S, De Lanauze D, Xu YZ, Dumitru L, et al. Magneto-aerotactic bacteria deliver drug-containing nanoliposomes to tumour hypoxic regions. Nat Nanotechnology (2016) 11(11):941–7. doi:10.1038/nnano.2016.137
111. Weibel DB, Garstecki P, Ryan D, DiLuzio WR, Mayer M, Seto JE, et al. Microoxen: Microorganisms to move microscale loads. Proc Natl Acad Sci USA (2005) 102(34):11963–7. doi:10.1073/pnas.0505481102
112. Xie S, Jiao N, Tung S, Liu L. Controlled regular locomotion of algae cell microrobots. Biomed Microdevices (2016) 18(3):47. doi:10.1007/s10544-016-0074-y
113. Yasa O, Erkoc P, Alapan Y, Metin S. Microalga-powered microswimmers toward active cargo delivery. Adv Mater (2018) 30(45):1804130–10. doi:10.1002/adma.201804130
115. Rummery GA, Niranjan M. On-line q-learning using connectionist systems. Cambridge University Engineering Department (1994). Technical report.
116. Jaakkola T, Jordan MI, Singh SP. On the convergence of stochastic iterative dynamic programming algorithms. Neural Comput (1994) 6(6):1185–201. doi:10.1162/neco.1994.6.6.1185
117. Mnih V, Kavukcuoglu K, Silver D, Graves A, Antonoglou I, Wierstra D, et al. (2013) Playing atari with deep reinforcement learning. arXiv:1312.5602v1. 1–9.
118. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level control through deep reinforcement learning. Nature (2015) 518(7540):529–33. doi:10.1038/nature14236
119. Graesser L, Keng WL. Foundations of deep reinforcement learning. Addison-Wesley Professional (2019).
120. Tsang ACH, Tong PW, Nallan S, Pak OS. Self-learning how to swim at low Reynolds number. Phys Rev Fluids (2020) 5(7):074101. doi:10.1103/physrevfluids.5.074101
121. Zou Z, Liu Y, Young YN, Pak OS, Tsang ACH. Gait switching and targeted navigation of microswimmers via deep reinforcement learning. Commun Phys (2022) 5(1):158–6. doi:10.1038/s42005-022-00935-x
122. Qin K, Zou Z, Zhu L, Pak OS. Reinforcement learning of a multi-link swimmer at low Reynolds numbers. Phys Fluids (2023) 35(3):2023. doi:10.1063/5.0140662
123. Colabrese S, Gustavsson K, Celani A, Biferale L. Flow navigation by smart microswimmers via reinforcement learning. Phys Rev Lett (2017) 118(15):158004–5. doi:10.1103/physrevlett.118.158004
124. Gustavsson K, Biferale L, Celani A, Colabrese S. Finding efficient swimming strategies in a three-dimensional chaotic flow by reinforcement learning. Eur Phys J E (2017) 40(12):110–6. doi:10.1140/epje/i2017-11602-9
125. Hartl B, Hübl M, Kahl G, Zöttl A. Microswimmers learning chemotaxis with genetic algorithms. Proc Natl Acad Sci USA (2021) 118(19):e2019683118–7. doi:10.1073/pnas.2019683118
126. Mo C, Bian X. Chemotaxis of sea urchin sperm cells through deep reinforcement learning (2022). arXiv preprint arXiv:2209.07407.
127. Ramakrishnan RO, Friedrich BM. Learning run-and-tumble chemotaxis with support vector machines. Epl (2023) 142(4):47001. doi:10.1209/0295-5075/acd0d3
128. Schneider E, Stark H. Optimal steering of a smart active particle. Epl (2019) 127(6):64003–7. doi:10.1209/0295-5075/127/64003
129. Gunnarson P, Mandralis I, Guido N, Koumoutsakos P, John OD. Learning efficient navigation in vortical flow fields. Nat Commun (2021) 12(1):1–7.
130. Yang Y, Bevan MA, Li B. Efficient navigation of colloidal robots in an unknown environment via deep reinforcement learning. Adv Intell Syst (2020) 2(1):1900106. doi:10.1002/aisy.201900106
131. Nasiri M, Liebchen B. Reinforcement learning of optimal active particle navigation. New J Phys (2022) 24(7):073042. doi:10.1088/1367-2630/ac8013
132. Buzzicotti M, Biferale L, Bonaccorso F, Clark di Leoni P, Gustavsson K. Optimal control of point-to-point navigation in turbulent time dependent flows using reinforcement learning. In: Matteo baldoni and randy goebel, 12414. AIxIA 2020 – Advances in Artificial Intelligence (2021). p. 223–34.
133. Yang Y, Bevan MA, Li B. Hierarchical planning with deep reinforcement learning for 3D navigation of microrobots in blood vessels. Adv Intell Syst (2022) 4(11):2200168. doi:10.1002/aisy.202200168
134. Amoudruz L, Koumoutsakos P. Independent control and path planning of microswimmers with a uniform magnetic field. Adv Intell Syst (2022) 4(3):2100183. doi:10.1002/aisy.202100183
135. Nasiri M, Löwen H, Liebchen B. Optimal active particle navigation meets machine learning. Epl (2023) 142(1).
136. Liu Y, Zou Z, Pak OS, Tsang ACH. Learning to cooperate for low - Reynolds - number swimming: A model problem for gait coordination. Scientific Rep (2023) 13:9397–10. doi:10.1038/s41598-023-36305-y
137. Mirzakhanloo M, Esmaeilzadeh S, Alam MR. Active cloaking in Stokes flows via reinforcement learning. J Fluid Mech (2020) 903(i):A34–25. doi:10.1017/jfm.2020.665
138. Gazzola M, Tchieu AA, Alexeev D, De Brauer A, Koumoutsakos P. Learning to school in the presence of hydrodynamic interactions. J Fluid Mech (2016) 789:726–49. doi:10.1017/jfm.2015.686
139. Guido N, Verma S, Alexeev D, Rossinelli D, WimRees MV, Koumoutsakos P. Synchronisation through learning for two self-propelled swimmers. Bioinspiration and Biomimetics (2017) 12(3):036001. doi:10.1088/1748-3190/aa6311
140. Verma S, Guido N, Koumoutsakos P. Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proc Natl Acad Sci USA (2018) 115(23):5849–54. doi:10.1073/pnas.1800923115
141. Muiños-Landin S, Ghazi-Zahedi K, Frank C, Cichos F. Reinforcement learning with artificial microswimmers. Sci Robotics (2021) 6(52):eabd9285. doi:10.1126/scirobotics.abd9285
Keywords: microswimmers, reinforcement learning, biological fluid, fluid–solid interaction, microrobot, low Reynolds
Citation: Mo C, Li G and Bian X (2023) Challenges and attempts to make intelligent microswimmers. Front. Phys. 11:1279883. doi: 10.3389/fphy.2023.1279883
Received: 18 August 2023; Accepted: 08 September 2023;
Published: 22 September 2023.
Edited by:
He Li, University of Georgia, United StatesReviewed by:
Lucas Amoudruz, Harvard University, United StatesOn Shun Pak, Santa Clara University, United States
Copyright © 2023 Mo, Li and Bian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gaojin Li, Z2FvamlubGlAc2p0dS5lZHUuY24=; Xin Bian, YmlhbnhAemp1LmVkdS5jbg==
 Chaojie Mo1,2
Chaojie Mo1,2 Gaojin Li
Gaojin Li Xin Bian
Xin Bian