Applications of neutron spin echo in soft matter

Soft matter systems exhibit diversity and intricacy in their structures and properties, with their dynamic behaviors and structural changes spanning wide time and length scales. Gaining insight into the internal structures and dynamics behaviors of soft matter systems, as well as the interactions among molecules and particles, contributes to a deeper comprehension of the microscopic behaviors of matter. Moreover, this endeavor has significant biomedical and materials engineering implications. This review focuses on the applications of spin-echo small-angle neutron scattering (SESANS) and high-resolution neutron spin echo (NSE) spectroscopy in soft matter science, particularly complex fluids and biomolecular systems. NSE spectroscopy has remarkable temporal resolution and sensitivity towards molecular-scale dynamic behaviors. Therefore, it provides comprehensive insights into microscale dynamic phenomena to soft matter systems, such as the rheological behaviors, stability, and aggregation dynamics of colloids; the domain dynamics and conformational changes of proteins; the collective dynamics of lipid membranes and interactions with other molecules, as well as the dynamic behaviors and interactions of surfactants within microemulsions. NSE technique helps reveal the complex nature of these systems, providing valuable insights into advances in materials science, biomedicine, and chemistry.

1 Introduction

Complex fluids, encompassing colloidal dispersions, microemulsions, lipid membranes, proteins, micellar polymers, and related systems, constitute a pivotal realm of investigation within soft matter physics. These complex molecular systems have broad applications across diverse fields, including biology, chemistry, and materials science. Nonetheless, their constituents frequently have intricate characteristics, and the spatial dimensions of the particles or molecules that make up their principal components lie in the mesoscopic range, between micro and macro scales, which results in long time scales for dynamic processes, typically on the order of 100 ns [1]. Traditionally, time-of-flight (TOF) spectroscopy with energy resolution ranging from about 3.5–4 µeV offers a dynamical window from about 10–600 ps [2]; while high resolution neutron backscattering (BS) spectroscopy allows to investigate diffusive motions up to several ns in the time domain (resolution around 0.7 µeV) [3]. Both of them have commonly served as a prominent tool for probing the dynamic characteristics of complex fluids. However, they are inadequate for characterizing the dynamics of larger structural domains for their limited scale of detection. The development of the neutron spin echo (NSE) technique has significantly increased the time-resolved neutron scattering techniques, thus making it possible to explore the dynamic characteristics of complex fluids. Since Mezei proposed the concept of neutron spin echo in 1972 [4], the first NSE spectrometer was constructed in Grenoble in 1978 [5]. This technique is used to quantify the energy and direction of neutron motions upon scattering, accomplished through calibration of neutron spin direction, i.e., measuring polarization and its detection time scales can reach up to several hundred nanoseconds. Therefore, the NSE technique operates on a fundamentally distinct principle compared with the other inelastic and quasi-elastic neutron scattering techniques, such as TOF and BS spectroscopy: the TOF and BS techniques primarily obtain the spectrum $S\left(Q,\omega \right)$ in the energy domain, whereas the NSE technique focuses on capturing correlations in the time domain, $F\left(Q,t\right)$.

The small angle neutron scattering (SANS) technique finds extensive applications in investigating the structures of complex fluids. However, limited by the design principles, the detection scale of SANS typically spans from a few to several hundred nanometers. In the experiments aimed at characterizing the structures of soft matter, sometimes, it is necessary to detect the space scale above the micron level. There are many upgraded techniques based on SANS technology, such as very small angle neutron scattering (VSANS), ultra small angle neutron scattering (USANS), and spin-echo small angle neutron scattering (SESANS), whose spatial detection ranges have significantly enhanced compared with that of traditional SANS techniques. Among them, the SESANS technique developed by Pynn [6], Gahler [7], Rekveldt [8], and coworkers is using the idea of neutron spin echo in analyzing elastic scattering for investigating the structural characteristics of various materials. The first SESANS spectrometer was built at the research reactor in Delft in 2005 [9, 10]. SESANS and traditional inelastic NSE are complementary in detecting the structure and dynamics of materials. In Section 2, we will describe the principles of these two neutron spin echo techniques.

Compared with the traditional SANS technique, SESANS has the following advantages: 1) SESANS directly measures the structural information of the sample in real space. In comparison, the conventional SANS technique can only make measurements in the reciprocal space. 2) Measuring at a larger scale and smaller scattering angle for reduced neutron flux. SESANS offers detection capabilities at the micron scale, which surpasses the conventional SANS technique by approximately one order of magnitude. In recent years, the development of the double-crystal diffraction USANS technique allows the resolution of extremely small scattering angles through highly collimated neutron beams [11]. However, in compromise, it loses most of the neutron flux simultaneously. Compared to this, the SESANS technique has notable advantages in guaranteeing the neutron flux. 3) Considering multiple scattering directly. The conventional SANS technique has specific requirements on the sample thickness to mitigate the effects of multiple scattering. In contrast, the SESANS technique can directly consider the multiple scattering to get more accurate measurements and has better adaptability to different samples. However, the SESANS technique faces the problems of expensive and difficult construction, and it cannot directly measure the information in different directions of each anisotropic sample [12].

This review article summarizes some of the applications of the NSE technique in the study of soft matter systems such as colloids, proteins, lipid membranes, and microemulsions, aiming to provide a comprehensive demonstration of the methodology of this technique in resolving the structural and dynamical behaviors of soft matter systems. Here we summarize the development of each research field in recent years. Firstly, we explain the fundamental principles of NSE and SESANS and show the design structures of these two most typical neutron spin echo spectrometers. Although the actual instrument design is much more complicated, it does not hinder our comprehension of their underlying principles. Indeed, the basic principles of NSE and SESANS are highly similar, as both techniques involve the movement of neutrons coupled with Lamor precession, with scattering information obtained through analysis of neutron polarization. Therefore, it is feasible to employ the same theoretical framework to describe the neutron motion in both types of spectrometers.

Subsequently, we deliberate upon the recent advancements in colloidal systems research. It is well known that colloids have consistently served as model systems for investigation. For instance, colloidal systems hold significant importance in probing the characteristics of globular proteins [13]. In the past decade, there has been a rapid proliferation of reports concerning the synthesis of anisotropic, non-uniformly distributed, and responsive synthetic colloids. These colloids are becoming analogous to complex biological counterparts. The experimental and theoretical toolkit of colloid science has considerably expanded, with the potential for the immense applicability of these concepts in protein solutions [14]. This review primarily focuses on the applications of NSE in colloidal research. For the simplest spherical colloidal particles, the interactions between particles can be explained using the hard sphere model. As the concentration of colloidal dispersions increases, the repulsive effects between particles gradually become prominent. Such interactions can be readily investigated by the SESANS technique. Studies on soft spherical colloidal particles suggest a correlation between interparticle interactions and their internal motion. Furthermore, more complex colloidal systems, such as those exhibiting short-range attraction and long-range repulsion (SALR), have become a hot topic in recent years. Such colloids have very complex phase diagrams. This review will introduce the research of the SALR system.

Proteins are generally characterized by structural complexity and functional diversity. Historically, NSE has been applied in protein research to characterize domain dynamics, elucidate protein cluster formation and equilibrium, and provide insights into local mobility within the glassy state. In this review, we offer a concise overview of the advantages of NSE for investigating protein solutions. We outline a general methodology for interpreting NSE data from protein solutions and underscore the pivotal role of establishing accurate and reliable models to comprehensively understand the dynamics of protein macromolecules. A significant emphasis is on exploring protein domain dynamics, a crucial factor governing the precise modulation of biological functions of proteins, including enzyme catalytic activity, signaling transduction, etc. Moreover, For the study of proteins, complementary combinations of techniques, including quasi-elastic neutron scattering (QENS), SANS, scattering length density (SLD) contrast match techniques, as well as molecular dynamics simulations (MDS) are also generally used to elucidate and understand the structure and dynamics of proteins in terms of static structures and dynamic behaviors, and in terms of broader temporal and spatial scales.

The lipid membrane is one of the most critical components of cells. The research on lipid membranes aims to better understand the structures and functions of biofilms and their pharmaceutical applications. Still, biofilms tend to be a much more complex system than the simple lipid membrane, incorporating interactions between proteins, sterols, and other small molecules and the membrane. A number of studies on lipid membranes using neutron scattering techniques have been reported in recent years [15, 16]. The structural and dynamic properties of membranes can be affected by bending fluctuations, thickness fluctuation, and other factors such as peptides, domains, and asymmetries. This review delves into NSE’s advancements and extensive applications in lipid membrane investigations. We mainly focus on how the shape and thickness fluctuations of lipid membranes can be characterized by the intermediate scattering function (ISF) of NSE and provide an in-depth introduction to the research of NSE in lipid membranes in recent years, which can help to deepen the understanding and knowledge of lipid membranes. Based on the basic theoretical models outlined earlier, we provide recent advances in research concerning more intricate structural and functional aspects of biological membranes through the NSE spectroscopy, which offers more ideas and possibilities for medical applications as they can give a great deal of substantial information on the interaction of lipid membranes with drug molecules.

Microemulsions and lipid membranes are self-assembled membranes, sharing similar properties yet possessing distinct characteristics. The dynamics and phase behavior of microemulsions can be elucidated through their effective curvature. Here we briefly review the methodological models and experimental studies of NSE describing the structure and dynamics of droplet microemulsions and bicontinuous microemulsions, respectively, and underscore the pivotal advantages of the NSE technique in studying microemulsion. Additionally, in recent years, the study of contrast variations in microemulsions involves adding polymers and copolymers to probe alterations in the properties of microemulsions, which is also a mainstream research direction in the study of microemulsions. Within microemulsion studies, the SESANS technique demonstrates its advantages in nanoscale structural probing, offering a valuable complement to the static SANS technique for structural investigations.

Finally, we summarized the significant applications of NSE in soft matter research and provided insights into potential future trends. The NSE technique offers a robust experimental tool for investigating soft materials’ structural and dynamic behaviors with its high resolution, wide dynamic range, and sensitivity to neutron-matter interactions. It is believed to be more prominent in future research endeavors. Through a comprehensive understanding of the properties of soft matter, we can unravel its crucial applications in fields such as biology, chemistry, and materials science, thereby fostering advancements and innovations in related fields.

2 Principles of NSE and SESANS

2.1 Larmor precession and manipulation of neutron spins

Equation of motion for neutron spin [17].

$\frac{d\mathit{S}}{dt}=\frac{2\gamma {\mu }_N}{\hslash }\mathit{S}\times \mathit{B}(1)$

where $\gamma =-1.91304273$. The angular velocity of spin precession is

${\omega }_L=\frac{2\left|\gamma \right|{\mu }_{N}B}{\hslash }(2)$

${\mu }_N$ is a nuclear magneton with a value of $5.051\times {10}^{-27}J·T^{-1}$. When the distance of the incident neutron with wavelength $\lambda$ in the magnetic field is $l$, the precession angle is:

$\varphi =c\lambda J(3)$

where $c=4\pi \left|\gamma \right|{\mu }_N{m}_n/h^2=4.6368\times {10}^{14}{T}^{-1}·m^{-2}$ [18]. It only has to do with fundamental physical constants, $m_n$ is the neutron mass, $J=\int Bdl$, is the magnetic field path.

2.2 The principles of NSE

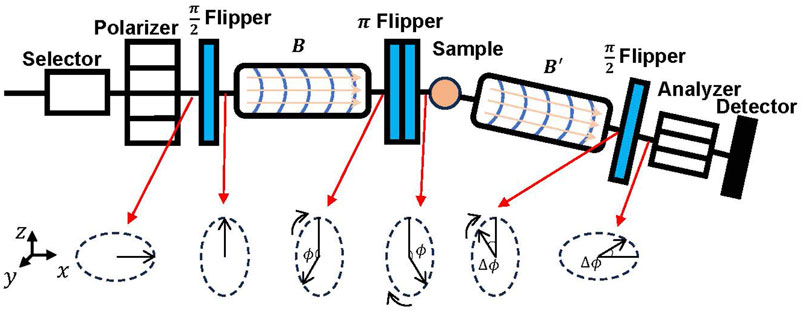
Figure 1 gives a schematic layout of a typical neutron spin spectrometer [1]. In the context of discourse, we establish the neutron trajectory direction as aligned with the x-axis. The focused neutron beam traverses an initial velocity selector to isolate incident neutrons with specific wavelengths. Subsequently, the neutron beam proceeds to the polarizer, inducing spin polarization within the neutron ensemble. After polarization, the neutron’s spin direction points in the $x$ direction. The polarized neutron beam first passes through a $\pi /2$ flipping device, which causes the neutron’s spin direction to change $\pi /2$. Here it adjusts the neutron’s spin direction from the $x$ direction to the $z$ direction. That is, the direction of the neutron’s spin is perpendicular to the direction in which the neutron is moving forward. Subsequently, the neutrons enter the first magnetic field, $\mathit{B}$, and begin precession. After exiting the first magnetic field, the precession angle of the neutron beam is denoted as $\varphi$. Before scattering with the sample, the neutron beam passes through a $\pi$-flipping device that causes the neutron spin precession angle to change from $\varphi$ to $-\varphi .$ The neutrons then scattered by the sample will enter the second magnetic field ${\mathit{B}}^{\prime }$. The scattered neutron beam will then be flipped by a second $\pi /2$ flipper, which will eventually be picked up by the analyzer and detector. Note that the sizes of $\varphi$ mentioned here result from modulo $2\pi$. To clarify the meaning of each device, Figure 1 shows the direction change of the neutron spin. In general, magnetic fields $\mathit{B}$ and ${\mathit{B}}^{\prime }$ are designed to be exactly the same. As depicted in Figure 1, the cumulative outcome of the procedural sequence results in the angular rotation $∆\varphi$ of the neutron’s spin orientation around the x-axis. In instances of elastic scattering, the angle of rotation $∆\varphi =0$, signifying the occurrence of a “spin echo”. When inelastic scattering occurs,

$\Delta \varphi =cJ\Delta \lambda (4)$

FIGURE 1

FIGURE 1. Schematic diagram of the NSE instrument.

In soft matter measurements, the energy transfer is generally very small, and in this case, the energy transfer is,

$\hslash \omega \approx \frac{\partial E}{\partial \lambda }\Delta \lambda =\frac{h^2\Delta \lambda }{m_n{\lambda }^3}(5)$

By simultaneous solution of the previous two equations, we obtain the following result:

$\Delta \varphi =\frac{cJ{m}_n{\lambda }^3}{2\pi h}\omega =\omega \tau (6)$

Hence, the determination of $∆\varphi$ enables the derivation of the energy transfer $\omega$. The coefficient $\tau$ in the equation above possesses temporal dimensions and is denoted as the “spin echo time.” For the scattered neutron beam, polarization is measured by counting for a given time spin up ($\pi$ flipper on) and spin down (π flipper off). As shown in Figure 2, the difference Up-Down is the maximum echo amplitude we can recover. Polarization is defined as

$P\left(Q,\mathrm{\tau }\right)=\frac{2A}{U-D}(7)$

where $A$ is amplitude, $U$ is spin up neutron counts and $D$ is spin down. The neutron polarization rate detected by the detector is the result of averaging the spectral distribution of incident neutrons, taking into account that incident neutrons of different energies have different effects on polarization. Here, a small additional magnetic field is varied which allows to determine the maximal polarization $P\left(Q,\mathrm{\tau }\right)$. This so-called Hahn echo allows to determine the amplitude of the polarized neutron beam at the specific time points $\mathrm{\tau }$. Finally, in the analyzer and detector, what we get is the polarization of the neutron in the x-direction [19],

$P\left(Q,\mathrm{\tau }\right)=〈\cos \left(\Delta \varphi \right)〉=〈\cos \left(\omega \mathrm{\tau }\right)〉(8)$

FIGURE 2

FIGURE 2. An illustration of the echo signal.

The probability distribution of $\omega$ is proportional to the double differential scattering cross section, so there is,

$P\left(Q,\mathrm{\tau }\right)=\frac{{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}}\frac{d^2\sigma }{d\mathrm{\Omega }d\omega }\cos \left(\omega \tau \right)d\mathrm{\omega }}{{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}}\frac{d^2\sigma }{d\mathrm{\Omega }d\omega }d\mathrm{\omega }}(9)$

Considering that the systems studied by NSE techniques are generally at high temperatures and large spatial scales, and $\frac{d^2\sigma }{d\mathrm{\Omega }d\omega }$ can be regarded as an even function of $\omega$, therefore

$P\left(Q,\mathrm{\tau }\right)=\frac{{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}}\frac{d^2\sigma }{d\mathrm{\Omega }d\omega }\exp \left(i\omega \tau \right)d\omega }{{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}}\frac{d^2\sigma }{d\mathrm{\Omega }d\omega }d\omega }=\frac{I\left(Q,\mathrm{\tau }\right)}{I\left(Q,0\right)}(10)$

Here the physical quantity measured by NSE is the ISF $I\left(Q,\tau \right)$. By changing the magnetic field or the wavelength of the incident neutron, a suitable $\tau$ can be selected to detect the sample.

2.3 The principles of SESANS

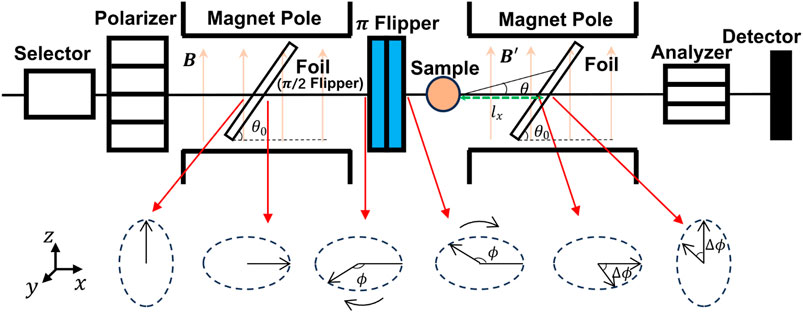
Figure 3 shows a schematic picture of a SESANS spectrometer [20]. The overall structure is similar to the traditional NSE spectrometer. However, it uses magnetic foils as flippers. Initially, the spin of the neutrons passing through the polarizer points in the $z$ direction. After entering the first magnetic field, Larmor precession does not occur at this time because its spin direction is parallel to the magnetic field direction. After passing the first magnetic foils, the spin is flipped to the direction of the x-axis. Before reaching the $\pi$ flipper, its precession angle is $\varphi$. Similarly, after passing through the π flipper, its precession angle becomes $-\varphi$. Suppose the neutrons are not scattered by the sample. In that case, they will directly enter the second magnetic field and subsequently be flipped by the magnetic foils before reaching the analyzer and detector. At this point, the precession angle $∆\varphi =0$, and the neutron returns to its initial polarization state. This process is known as the “spin echo” of SESANS [21, 22]. On the other hand, if the neutrons are scattered by the sample, they will not return to the initial polarization state due to the difference in the magnetic field path, and its precession angle is

$\Delta \varphi =c\lambda \Delta J(11)$

FIGURE 3

FIGURE 3. Schematic diagram of the SESANS instrument.

In the case of the scattering angle $\theta$ being very small, the precession angle can be approximated as [18],

$\Delta \varphi =c\lambda B{l}_x\theta \cot \left({\theta }_0\right)=Q_{z}z(12)$

where $Q_z=k_0\theta =2\pi \theta /\lambda$ is the component of the transfer vector in the $z$-direction and $l_x$ is the distance of the sample to the foil center. $z$ is a physical quantity with a dimension of length,

$z=\frac{c{\lambda }^{2}B\cot \left({\theta }_0\right)l_x}{2\pi }(13)$

which is called the “spin echo length”. The value of $z$ can be changed by changing the size of the magnetic field or the wavelength of the incident neutron. The detection range of a SESANS spectrometer $z$ is an important index to measure its detection performance. The final result of the analyzer and detector is the total neutron polarization for single scattering in the $z$ direction [23],

$P_1\left(z\right)=1-\sigma t+\sigma tG\left(z\right)(14)$

$1-\sigma t$ represents neutrons that have not been scattered. $\sigma tG\left(z\right)$ is the polarization of the scattered neutron. In small-angle scattering, the probability distribution of the transferred wave vector $Q_z$ is proportional to the differential scattering cross section, and $Q_x=0$ because the $x$-direction is the incident direction of the neutrons, so the polarization can be obtained by calculating all the scattering angles,

$G\left(z\right)=\frac{1}{\sigma k_0^2}\int \int \frac{d\sigma \left(\mathit{Q}\right)}{d\mathrm{\Omega }}\mathit{cos}\left(Q_{z}z\right)d{Q}_{z}d{Q}_y(15)$

where $\frac{d\sigma \left(\mathit{Q}\right)}{d\mathrm{\Omega }}$ is the differential scattering cross section, and $\sigma$ is the scattering probability per unit thickness,

$\sigma =\frac{1}{k_0^2}\int \int \frac{d\sigma \left(\mathit{Q}\right)}{d\mathrm{\Omega }}d{Q}_{z}d{Q}_y(16)$

Considering the effect of multiple scattering, the polarization can be written as

$P\left(z\right)=\exp \left[-\sigma t\left(1-G\left(z\right)\right)\right](17)$

It denoted that the Fourier transform of the differential scattering cross-section is a Deby correlation function,

$\gamma \left(r\right)=\int \frac{d\sigma \left(\mathit{Q}\right)}{d\mathrm{\Omega }}{e}^{i\mathit{Q}\cdot \mathit{r}}d\mathit{Q}(18)$

For an isotropic sample, $\frac{d\sigma \left(\mathit{Q}\right)}{d\mathrm{\Omega }}$ will be an even function of $Q_z$ in the $z$ direction, so Eq. 15 is essentially the two-dimensional Fourier transform of the differential scattering cross-section [12]. That is, SESNAS measures a projection of $\gamma \left(r\right)$ in the $z$ direction. We can express this projection relationship through the Abel transform [24],

$G\left(z\right)=2{\displaystyle \underset{z}{\overset{\infty }{\int }}}\frac{\mathrm{\gamma }\left(r\right)r}{\sqrt{r^2-z^2}}dr(19)$

In summary, SESANS can directly measure the structural characteristics of the sample in real space, omitting the Fourier transform step compared with the data processing process of SANS, which brings great convenience to data analysis.

This subsection gives a rough introduction of the principle of SESANS. The construction technology of SESANS spectrometer is also developing, according to the study of SESANS could be implemented as an add-on to NSE setups by Elisabeth Kadletz et al [25]. It is also worth mentioning that the spin echo modulated small-angle neutron scattering (SEMSANS) technology similar to the SESANS has also seen a new development [26].

3 Recent applications of NSE on soft matters

The dynamics of macromolecules in a solvent environment exhibit considerable intricacy. Neutron spin echo scattering emerges as a potent methodology for investigating macromolecular dynamics in solution. The coherent ISF measured by NSE gives internal, rotational, and translational dynamics of macromolecules in solution. To comprehensively understand macromolecular dynamics, it is imperative to discern and isolate the motion of the individual parts. In 2017, Liu introduced a theoretical framework that establishes a quantitative correlation between the various motion components encompassed within ISFs [27],

$\frac{I\left(Q,t\right)}{I\left(Q,0\right)}=\frac{S_{self}\left(Q,t\right)+\mathrm{\beta }\left(Q\right)\left[F\left(Q,t\right)-F_s\left(Q,t\right)\right]}{1+\mathrm{\beta }\left(Q\right)\left[S\left(Q\right)-1\right]}(20)$

where $F\left(Q,t\right)$ and $F_s\left(Q,t\right)$ are the coherent and incoherent ISFs of molecular translation, respectively. $\mathrm{\beta }\left(Q\right)$ is exclusively associated with the molecular shape, akin to the form factor. $S_{self}\left(Q,t\right)$ represents the intrinsic contribution of the molecule itself to translational, rotational, and internal motions. Based on the dynamic decoupling approximation, this theoretical framework provides valuable insights into the study of colloids, proteins, micelles, and other soft substances, enabling a comprehensive understanding of their behavior and properties.

The complexity of the components of macromolecular systems leads to the long-time scales involved in their dynamics, often reaching the order of 100 ns. However, even with the combination of backscattering technology, surpassing a time window of 10 ns remains challenging for traditional TOF spectrometers. The advent of neutron spin echo technology has enabled the investigation of dynamic characteristics in macromolecules.

The development of SESANS has brought a new perspective to studying the microstructure of complex fluids. The SESANS technique directly quantifies the correlation function in real space, which is very intuitive to reflect the microscopic information of the sample, and its detection range can extend to the order of microns. NSE and SESANS represent a potent approach for investigating the internal microstructure of soft matter.

3.1 Colloids

Colloids, or colloidal dispersion, is a special kind of homogeneous mixture. The colloidal system represents a specialized homogeneous mixture comprising two distinct phases: a dispersed phase with particle sizes ranging from 1 to 100 nm, a continuous phase in which the particles are immersed within a medium, and an apparent interface between colloidal particles and dispersive medium. Colloids, which have diverse morphologies and compositions, including micelles, proteins, star polymers, synthetic nanoparticles, and active colloids, pervade numerous materials in our daily lives. In-depth investigations into the structure and dynamics of colloidal systems are essential for comprehending, manipulating, and predicting the macroscopic properties of these materials.

Model colloidal systems have been an essential experimental platform to demonstrate the fundamental physical mechanisms for proving theories and showing many intriguing phenomena in complex systems. Typically, the model systems studied are spherical particles with isotropic interactions. Although this approach may oversimplify most real systems to some extent, the information obtained from these model systems has proven highly valuable for understanding the intricate interactions among various soft materials. Spherical systems with hard-sphere (HS) interactions are arguably the most studied colloidal systems. Traditional SANS has been widely applied to investigate such systems, and numerous reports have been published on this topic [28]. The SESANS technique has provided a more intuitive and precise approach to studying colloidal systems. The phase transition of a colloid containing silica spheres in a suspension of cyclohexane was first investigated with SESANS by Krouglov et al. showed that the correlation function $G\left(z\right)$ measured by SESANS is very sensitive to the shape and size of the particles [24, 29]. The experimental data are intuitively distinguishable for colloids at high and low concentrations. In real space, the state characteristics of a colloid can be directly split into three parts:

$\gamma \left(r\right)={\gamma }_{auto}\left(r\right)-\phi {\gamma }_{excl}\left(r\right)+\phi {\gamma }_{auto}*\left[g\left(r\right)-1\right](21)$

The $\phi$ represents the volume fraction of colloidal spheres. The first term is solely related to the particle’s shape and represents the real-space expression of the small-angle scattering form factor, known as the self-debye correlation function. The function ${\gamma }_{excl}\left(r\right)$ is negative correlations between particles due to repulsive volume. The correlation function related to the excluded volume effect is crucial for understanding scattering in dense systems of spherical particles. The third term accounts for the structural contribution between particles, involving the convolution of a pair distribution function and ${\gamma }_{auto}$ (Figure 4), and $*$ denotes a convolution integral. This decomposition approach decouples the particle shape from particle-particle correlations, allowing for separate investigations of the particle’s intrinsic properties and interactions among particles.

FIGURE 4

FIGURE 4. Correlation functions for a hard-sphere liquid at a volume fraction $\phi =0.5$.

We take the hardsphere model as an example for the data processing of SESANS. Figure 5A [30] shows the SESANS spectrum for dilute colloid suspension. In dilute suspension, the scattering data mainly provides information on the shape of the particles, and the structural information between the particles can be ignored in this case, thus $\gamma \left(r\right)={\gamma }_{auto}\left(r\right)$, which is the shape factor in real space for the hardsphere and can be expressed as [24],

${\gamma }_{auto}\left(r\right)=\left\{\begin{array}{c}\begin{array}{cc}1-\frac{3r}{4R}+\frac{r^3}{16R^3},& r\le 2R\end{array}\\ \begin{array}{cc}0,& r>2R\end{array}\end{array}\right.(22)$

where R is the radius of the hard sphere. It is sufficient to fit the data in the figure with Eqs. 17 and 19, 22 and obtain the radius of the sphere $R=149\text{nm}$. Notably, the fitted curve starts to flatten out just at $2R$, and the data points follow the same trend, so we can directly estimate the diameter of the spheres to be approximately $300\text{nm}$. In the example above, the radius of the spheres is homogeneous. For a polydisperse sample, it requires averaging the function $G\left(z\right)$ over all the radius distributions when fitting the data (specific methods can be found in [12]). As a result, the parameter R obtained is the average radius of all the spherical particles in the sample.

FIGURE 5

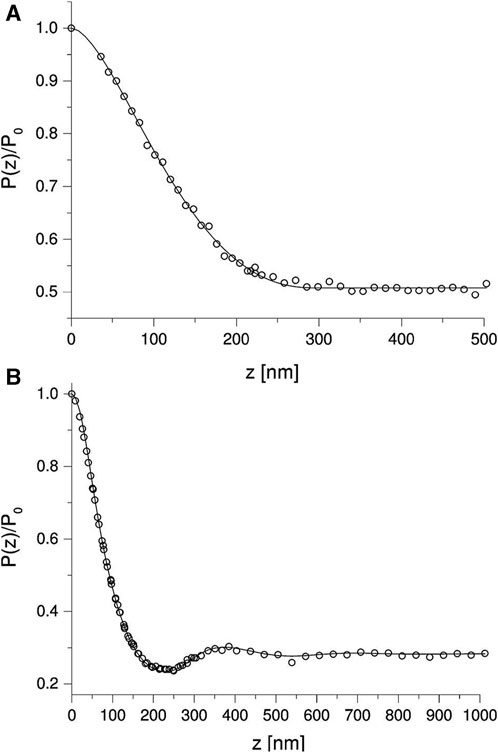
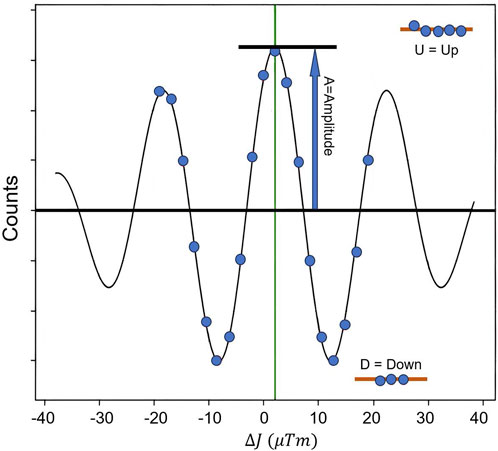
FIGURE 5. (A) Dilute suspension. The solid line is the fitted curve for isolated spherical particles using Eqs. 17, 19, 22 with $\phi =0.055$, $R=149\text{nm}$. (B) Semidilute suspension. The solid line represents the fitted curve using Eqs. 17, 19, 21 with $\phi =0.27$ and $R=149\text{nm}.$ The Percus–Yevick pair correlation function was used for $g\left(r\right)$ in Eq. 21. (Error bars are approximately equal to the size of the circles.) [24].

In semidilute colloid suspension, the interconnections between particles cannot be ignored. Figure 5B shows the SESANS data for colloid suspension with a volume fraction of $\phi =0.27$. It is necessary to fit these data by using Eqs. 17, 19, 21. For higher concentration colloid suspension systems, the internal structure will be more complex. In the following, we will introduce some applications of SESANS in the study of complex colloids.

The internal dynamics of colloidal particles can significantly influence their interactions. Neutral poly (amido amine) (PAMAM) dendrimers are an example of soft colloids (Figure 6) [31, 32]. Soft colloidal particles have flexibility and fluctuation properties that are important for the structure and dynamics of the colloid. Xin et al. revealed significant changes in the internal structure and internal dynamics with increasing concentrations of dendritic molecules, which were attributed to the competition between relaxation processes associated with inter-particle collisions and collective internal motion of dendritic molecules [33, 34]. The authors quantified the interactions between dendrimers and dendrimer internal dynamics by comparing their characteristic timescales, and they found that with increasing concentration, the physical contact frequency between neighboring dendritic molecules increased, leading to more significant restriction and slowing down of the internal dynamics of the dendritic molecules. In 2021, Huarui et al. gave more details on the particle dynamics of PAMAM [32]. Using SANS and NSE techniques, they revealed the size and shape fluctuations of generation 4 and 6 PAMAM dendritic polymers at finite concentrations. The results suggest that with an increase in the weight fraction of dendritic polymers, size fluctuations were suppressed while shape fluctuations increased. This transition was attributed to the competition between inter- and intra-particle dynamics. Additionally, low-generations dendritic polymers exhibited opposite results, indicating a mutual influence between the internal dynamics of soft colloidal particles and their interparticle structures.

FIGURE 6

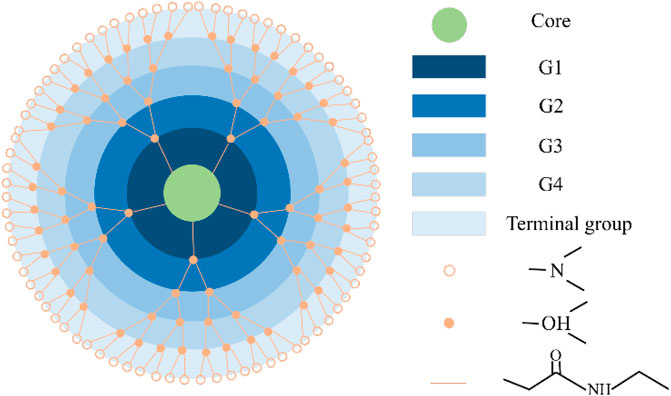
FIGURE 6. An illustration of the melocular form of the G4-OH. PAMAM dendrimer. As the generation grows, the number of branching units grows exponentially [31,32].

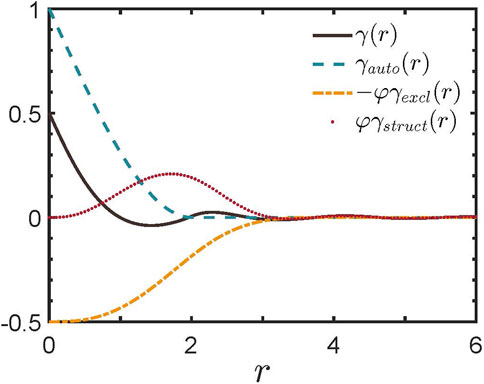
SESANS has been applied in investigating the microstructural features of soft colloidal systems. Xin et al. theoretically explored the prospects of using SESANS to study the structural characteristics of soft colloidal systems with non-uniform internal mass distribution [35], emphasizing that, compared to traditional SANS techniques, the unique sensitivity of SESANS is essential in studying effective interactions in colloidal systems. SESANS can accurately measure elastic neutron scattering in samples through the scattering angle of spin-encoded neutrons, thus providing a structural characterization method different from that of conventional SANS. SESANS can explore structures over a broader range of length scales, which bridges the gap in detection scales between confocal optical techniques and currently available SANS. Therefore, SESANS is of significant importance for investigating the large-scale structural properties of soft matter. By comparing the spatial autocorrelation function $G\left(z\right)$ and the scattering intensity $I\left(Q\right)$, derived from the same structural parameters obtained from SANS and SESANS, it has been found that SESANS exhibits unique sensitivity to effective colloidal interactions, while the sensitivity of traditional SANS techniques is relatively lower. Thus, SESANS provides a valuable alternative for the structural characterization of soft colloids, especially for understanding the relationship between macroscopic properties and microstructural features in colloidal systems.

The hard-sphere systems described above and sticky hard-sphere systems with short-range attractions are the two most commonly studied types of colloids. In recent years, there has been increasing interest in studying colloidal systems with short-range attractions and long-range repulsions (SALR). SALR colloidal systems exhibit rich phase diagrams and structures that are more complex than traditional hard-sphere or sticky hard-sphere systems. The 2019 review article by Liu et al. presented the latest advances in the structure, phase diagram, and dynamics of SALR colloidal systems [36]. One prominent feature of SALR colloidal systems is the appearance of intermediate-range order (IRO) peaks in the structure factor in SANS. Existing studies suggest that the competition between short-range attractive and long-range repulsive interactions among colloidal particles hinders phase separation, leading to the formation of intermediate-range structures and introducing new phases in the phase diagram as shown in Figure 7, such as clustered fluid, cluster percolated fluid, Wigner glass, and cluster glass. This article also briefly introduced some common mathematical forms of SALR interactions. The morphology and dynamic properties of these colloidal aggregates in solution are influenced and controlled by the SALR potential. Understanding SALR systems is essential in various aspects, including the gelation of protein solutions, the formation of colloidal aggregates, and the viscoelasticity of protein-drug formulations.

FIGURE 7

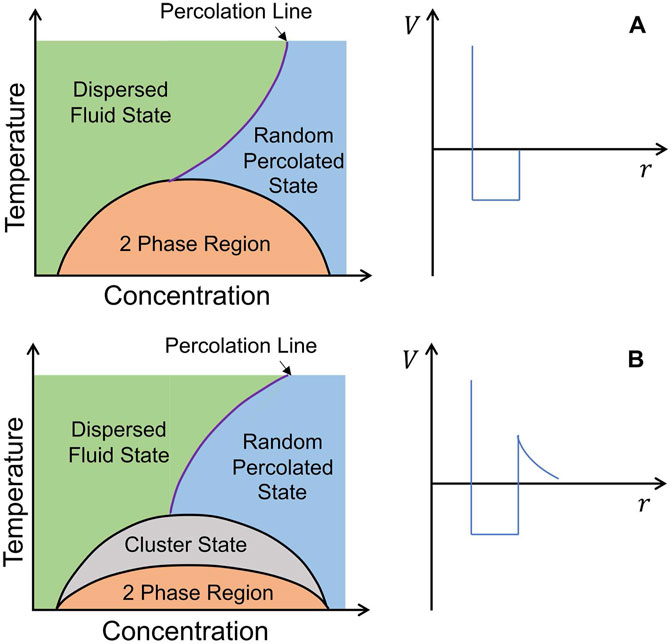
FIGURE 7. Schematic phase diagrams. (A) Systems with a short-range attraction. (B) Systems with a SALR interaction [36].

In 2014, Washington et al. used SESANS to investigate the inter-particle interactions between colloidal particles and polymer additives in a hard-sphere colloidal suspension. Such colloidal particles and additives combine to form a system of SALR [37]. The correlation functions between several sizes of poly (methyl-methacrylate) (PMMA) colloidal particles suspended in naphthalene were experimentally measured. SESANS provided precise information about the particle composition, including the solvent residing in the polymer interstices on the PMMA surface. They confirmed that for particles with radii ranging from 85 nm to 150 nm and colloid volume fractions between 30% and 50%, the particle correlations closely followed the Percus-Yevick hard-sphere model when the volume fraction was treated as a fitting parameter. Particle aggregation was not observed in these systems. However, when a small amount of polystyrene was added as a depletant to the concentrated PMMA particle suspension, short-range aggregation occurred among the particles, increasing the frequency of adjacent contacts. It can be concluded that SESANS effectively separated short-range and long-range correlations.

3.2 Proteins

Proteins undergo various conformational changes, which refer to alterations in their three-dimensional structure while retaining their primary sequence. These changes are critical for proteins to perform their diverse functions, such as enzymatic activity, signal transduction, and molecular recognition. Studying conformational changes in proteins is significant for understanding their functional versatility. The scale of protein dynamics can span from sub-nanoseconds of fast dynamics to seconds of long-time dynamics [38, 39]. Neutron spin echo spectroscopy covers a comprehensive time range from 0.1 nanoseconds to several hundred nanoseconds, making it highly suitable for investigating short-time protein dynamics.

Moreover, NSE can selectively probe specific chemical components in the system through deuterium labeling, offering a powerful tool to study and elucidate proteins’ dynamic behavior and functional mechanisms. The study of protein dynamics is essential for understanding the conformational and structural transitions of proteins, analyzing the interactions of proteins with other molecules, revealing the mechanisms of protein movement and functional regulation, and promoting drug development and targeted therapies. Employing the NSE technique, we can further unravel the complex interplay between protein structure and function and gain deeper insights into the underlying dynamics that govern their functional properties [40–42].

The ISF $I\left(Q,t\right)$ measured by neutron spin echo scattering provides a superposition of information about protein translational, rotational, and internal domain motions in solution. However, the challenge remains in separating the individual contributions of these different motion components and obtaining their respective characteristics. The general assumption is that rigid particles’ translational and rotational motions are independent and decoupled from the internal domain motions of the proteins. Under this circumstance, the effective diffusion coefficient $D_{eff}$ can be expressed as follows [43, 44]:

$D_{eff}=-\frac{1}{Q^2}\underset{t\to 0}{\lim }\frac{\partial }{\partial t}\frac{I\left(Q,t\right)}{I\left(Q,0\right)}(23)$

$D_{eff}$ can be accurately estimated using the first cumulant expression of the extended Akcasu-Gurol formula [45] for rotational motion,

$D_{eff}=\frac{k_{B}T}{Q^2}\frac{{\displaystyle \sum _{jl}}〈b_j{b}_l\left(Q{H}_{jl}^{T}Q+L_j{H}_{jl}^R{L}_l\right)\exp \left(iQ\left(r_j-r_l\right)\right)〉}{{\displaystyle \sum _{jl}}〈b_j{b}_l\exp \left(iQ\left(r_j-r_l\right)\right)〉}(24)$

where $k_B$ is the Boltzmann’s constant. $b_j$ is the scattering length of a subunit j. $H^T$ and $H^R$ are the translational and rotational mobility tensor respectively. The angular momentum vector $L_j=Q\times r_j$ for each coordinate and this model is widely applicable to rigid bodies and rigid bodies connected by soft springs [44]. Establishing a well-founded model is the foundation for characterizing inter-domain dynamic couplings [43, 46]. The accuracy of this method relies on the precise estimation of $D_{eff}\left(Q\right)$ for the rigid protein model.

Previous investigations have demonstrated that NSE spectroscopy is exceptionally well-suited for characterizing the domain dynamics of proteins. Many proteins consist of distinct domains that can move relative to each other. These movements are integral to protein function, allowing domains to interact with partners, bind ligands, or undergo allosteric regulation. In 1985, Alpert et al. studied the dynamic behavior of pig immunoglobulin G (IgG). In deuterium oxide solutions using NSE techniques [40]. Their findings revealed the involvement of mobile arms in the “y" shaped protein structure [47] (Figure 8A), which provide substantial segmental flexibility to IgG molecules, indicating the existence of domain motion and are the first neutron scattering evidence of internal motions of biomacromolecules. Later, Stingaciu et al. further elucidated that the flexible connecting region within the intermediate IgG molecules functions as a spring-like constraint on a time scale of 7 ns. NSE offers them distinctive insights into the internal dynamics of IgG, which remain unattainable through alternative methodologies [48]. In 2021, Gilelli et al. investigated the solutions of antibodies with poly (ethylene glycol). They unveiled the dynamic characteristics of antibodies within the dense phase, that is, a reduction in the diffusion behavior of antibodies but the persistent substantial internal flexibility and Y-shaped antibodies were lobes with domain dynamics [49].

FIGURE 8

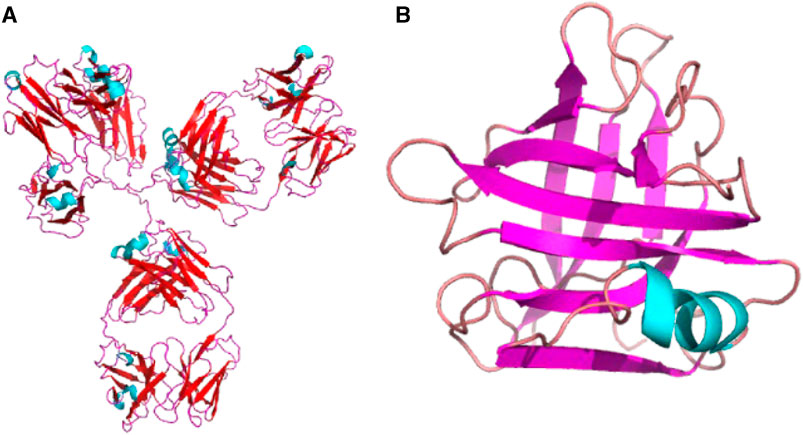
FIGURE 8. (A) Structure of immunoglobulin (Ig) (PDB 1IGY), a kind of “y” shape protein. (B) Structure of BLG (PDB 1CJ5). Cartoon diagram of a monomeric protein based on the PBD structure and generated by python. The two plots are not to scale.

In addition to classical antibody proteins, the NSE technique has revealed the relationship between protease domain dynamics and enzyme activity. In 2005, Bu et al. investigated the oscillatory behavior of the effective coefficient. $D_{eff}\left(Q\right)$ of Thermus aquaticus (Taq) polymerase, a dynamic behavior that differs markedly from the center-of-mass diffusion of macromolecules by NSE, and through different rigid protein models, it was shown how NSE could characterize dynamic interdomain coupling, which is considered to be an overdamped, creeping motion [43]. Figure 9 shows the effective diffusion coefficient $D$ of Taq polymerase as a function of $Q$ and the diffusion coefficient, $D_{t,DLS}$, for center-of-mass translation is measured by dynamic light scattering (DLS). The investigation conducted by Biehl et al. demonstrated that the movement of the external catalytic domain of protein alcohol dehydrogenase (ADH) leads to large-scale correlated domain motions [46]. These extensive fluctuations in domain structure have been confirmed to enhance the catalytic activity of phosphoglycerate kinase (PGK) [50]. Hong et al. achieved congruent outcomes through diverse methodologies, including SANS, NSE, and MD. By integrating information from static structural analyses and dynamic investigations, they elucidated the dynamics within the dense phase of mercury-ion reductase [51].

FIGURE 9

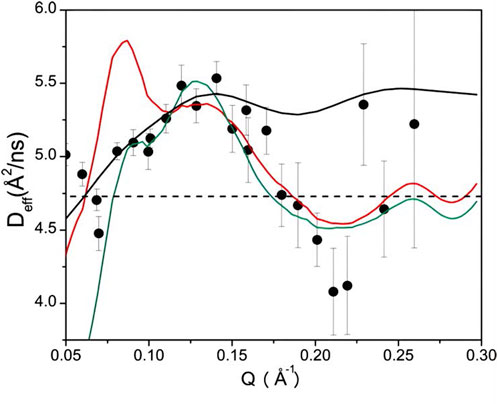
FIGURE 9. The $D_{eff}$ obtained from Eq. 23 of Taq polymerase by NSE with those from different dynamic models. The horizontal dotted line is $D_{t,DLS}$. The black, red and blue solid lines represent the results of the rigid-body model, the two-domain model and the three-domain model respectively. The figure is adapted from [43].

For some multi-domain proteins with critical physiological functions, the NSE technique reveals their domain motions. It offers a novel avenue to comprehend protein dynamics, elucidate functional implications, and unravel the mechanisms underlying protein information propagation. NHERF1 is a multi-domain scaffolding protein that plays an essential role in regulating ion balance, signal transduction, and biological processes in cells by interacting with various membrane proteins and signaling molecules. In 2010, Farago and colleagues investigated the interdomain dynamics of the NHERF1-ezrin complex by applying selective deuteration techniques. They described the interdomain motion of the multi-domain scaffold protein with a coarse-grained model. The findings unveiled that the interdomain motion was triggered by the interaction between NHERF1 and ezrin. Their study emphasized the mobility of PDZ1, PDZ2, and CT domains by employing selective deuterated ligands, offering an initial insight into the signaling mechanisms underpinning the interactions between NHERF1 and ezrin [44]. In 2021, Farago et al. again used NSE to investigate the nanoscale dynamics of protein domains within the 3-part cadherin-catenin complex through selective deuteration techniques. The mechanical adhesion coupling exhibited in this complex holds significant physiological implications. They devised six distinct component models, identified the most appropriate model via comparative analysis, and successfully delineated each constituent’s dynamic contributions, thus elucidating the interplay between protein complex domains and their role as force sensors [52].

Guanylate binding proteins (GBPs) are a class of soluble dynamin proteins associated with intracellular autoimmunity, which are immunologically active in mammals against a variety of intracellular pathogens, such as viruses and bacteria. In 2023, Peulen et al. applied a variety of experimental techniques to investigate the process of oligomerization of human GBP1 (hGBP1) in terms of conformational changes and mechanisms, this research study focused on mapping and characterizing the critical dynamics of hGBP1 [53]. They generated the structure of hGBP1 by SAXS, fixed-point spin-labeled electron magnetic resonance (EPR) spectroscopy [54], integrated and single-molecule fluorescence spectroscopy [55]. The spin-echo technique provided information on the conformational changes and assembly pathways of hGBP1, which, combined with filtered fluorescence correlation spectroscopy (fFCS), provided fundamental insight into the role of protein dynamics in signaling. This is then simulated by experimentally guided MD modeling, which integrates experimental data with simulations covering time scales of a few microseconds, and they generate integrated dynamic structures and insights into conformational changes and assembly pathways of hGBP1.

Intrinsically disordered proteins (IDPs) are proteins that lack a well-defined secondary structure, exhibit considerable structural flexibility, can undergo disordered-to-ordered transitions when interacting with specific binding partners, and are involved in a number of biological processes, including transcriptional regulation, cell signaling cascades, and protein degradation pathways. Studying IDPs poses a challenge due to the lack of a definitive structure. The current mechanical division of IDP binding to molecules is mainly divided into two relatively extreme views: induced folding[56] and conformational selection [57], so it is crucial to probe the large-scale conformational changes within IDPs. However, the superior ability of NSE technology to study the dynamics of protein structural domains in solution provides vital support to reveal the dynamic behavior and physiological mechanisms of IDPs. Disordered myelin basic protein (MBP) is analogous to Gaussian chains. It can be used as a model system for the properties of IDPs, whose dynamics are mainly described by flexible polymer models. In 2014, Stadler et al. showed that MBP reveals a dense dynamical behavior in solution, with a positive correlation between large-scale conformational motion and the accessible surface of the protein [58]. In 2019, Stringaciu et al. probed the internal dynamics of denatured MBP by adding urea to MBP solutions. The results indicate that urea-denatured MBP possesses greater amplitude and relaxation time of internal motion, and the internal friction parameter obtained based on the Zimm model with internal friction (ZIF) [59] is reduced by a factor of 6.5. And this difference is caused by the total disappearance of the MBP internal secondary structure [60].

Similarly, in 2022, Haris et al. investigated how the denaturant guanidinium chloride (GndCl) affected the dynamics and structure of MBP. They also found the same densification behavior of MBP. The difference was that at high concentrations of GndCl, MBP exhibited repulsive intra-chain interactions, with structure swelled and relaxation time increased [61]. The emerging field of intrinsically disordered proteins expands our understanding of protein structure-function relationships and emphasizes the importance of protein flexibility and conformational variability in cellular processes.

NSE has been effectively used to furnish insights into the formation and equilibrium of clusters, usually in combination with other structural techniques, particularly SANS. Short-term attraction and long-range repulsion describe interactions between molecules or particles through which molecules or particles in a system have been proven to form clusters, and such systems have garnered significant research attention in recent years. In 2010, the inter-cluster correlation peaks at small Q values in the SANS spectrum were interpreted by Porcar and Falus et al. as the formation of clusters [62]. They found a correspondence between concentration and system composition, i.e., at low concentrations, the system is dominated by monomers or dimers. In contrast, at high concentrations, it is dominated by large dynamic clusters.

Nevertheless, in 2010 Liu et al. contended that this peak originates from establishing a medium-range ordered structure governed by short-range attraction and long-range repulsion rather than a characteristic of cluster formations. In 2012, Porcar and Falus et al., in combination with SANS and NSE techniques, noted the finding that the formation of dynamic clusters in concentrated lysozyme solutions is regulated by a combination of short-term attraction and long-range repulsion in solution, and such dynamic clusters must be investigated through the assistance of dynamic measurements [63]. Cluster formation can also be observed in some concentrated monoclonal antibody solutions, which adds to our understanding of how antibody treatment can be used in practical applications. In 2014, Yearley et al. reported on the small-scale characteristics of clusters in concentrated monoclonal antibody solutions and the consistent relationship between the formation of reversible cluster phases and the increase in solution viscosity [64]. In 2017, Braun et al. investigated the cluster formation in β-lactoglobulin (BLG) protein (Figure 8B) solutions using static SAXS and neutron spectroscopy (NSE and NBS) techniques. The research unveiled that clusters emerged in BLG solutions due to the combined influence of short-range attraction and long-range repulsion. This particular amalgamation of interactions fosters the creation of clusters. According to their findings, BLGs form static, densely packed clusters over a temporal of several nanoseconds [65].

Additionally, NSE spectroscopy has provided insights into the localized motion within glassy states [66–68]. NSE effectively complements and extends the temporal and spatial coverage of QENS, encompassing broader ranges of time and length scales. Moreover, the enhanced resolution of NSE contributes to a heightened potential for protein research, thereby expanding the investigation possibilities in this domain.

3.3 Lipid membranes

Aqueous lipid molecules manifest an inherent inclination to undergo spontaneous self-organization, forming bilayers (Figure 10A) or other forms. This intrinsic self-assembly propensity allows lipid membranes to exhibit fluidic behavior and maintain structural integrity concurrently. This fluid nature of the membrane significantly influences the diffusion, motion, and spatial organization of molecules, proteins, and lipids within the membrane. It affects cellular processes, such as signal transduction, membrane trafficking, and lipid domain formation.

FIGURE 10

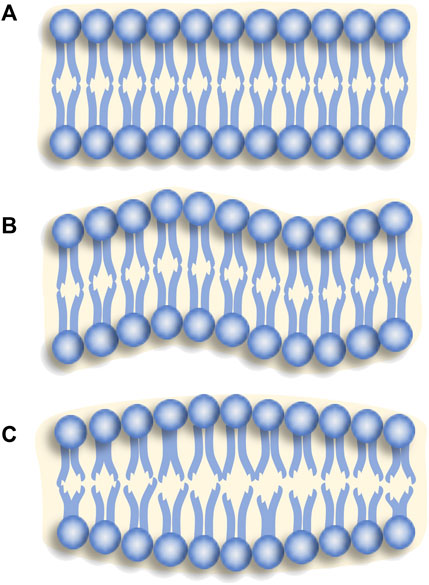
FIGURE 10. Lipid membranes with (A) a steady state, (B) bending fluctuation, (C) thickness fluctuation.

Lipid molecules exhibit collective motion, leading to membrane deformations, fusions, and undulations over extended distances and time scales. A comprehensive understanding of the dynamic properties of lipid membranes is crucial for elucidating their functional significance in cellular processes, biomolecular interactions, and overall cellular organization. Prior investigations have demonstrated the efficacy of neutron spectroscopy as a potent instrument for probing membrane dynamics [15, 16]. Integrating neutron spectroscopy with molecular dynamics simulations facilitates a molecular-level comprehension of lipid membranes [69–72].

The lipid membrane is a complex system characterized by fluidity and structural stability, with its motion characteristics exhibiting stratification, spatial heterogeneity, and temporal dependence. In 1973, Helfrich showed that curvature elasticity is the main factor controlling the non-spherical shape of vesicles, and the curvature elastic energy per unit area can be expressed as follows [73]:

$w_c=\frac{1}{2}\kappa {\left(C_1+C_2-C_0\right)}^2+{\kappa }_G{C}_1{C}_2(25)$

where $\kappa$ denotes the mean curvature modulus of elasticity, ${\kappa }_G$ represents the Gaussian curvature modulus of elasticity. $C_0$ is the spontaneous curvature, $C_1$ and $C_2$ correspond to the principal curvatures of the surfactant monolayer.

The NSE investigations concerning the bending fluctuations of lipid membranes (Figure 10B) primarily rely on the theoretical framework proposed by Zilman and Granek (ZG) model [74]. In 1996, Zilman and Granek employed Helfrich’s bending Hamiltonian [73], and incorporated the semi-flexible polymer model proposed by Farge and Maggs [75] to develop the theoretical framework for describing the fluctuations observed in two-dimensional single films [74]. They further elucidated the typical scaling behavior of the relaxation rate ${\mathrm{\Gamma }}_{bend}\propto {\kappa }^{-\frac{1}{2}}$. The ISF was deduced as the power-law function with an exponent of 2/3, represented as

$I\left(Q,t\right)=I\left(Q,0\right)\exp \left[-{\left({\mathrm{\Gamma }}_{bend}t\right)}^{\frac{2}{3}}\right](26)$

${\mathrm{\Gamma }}_{bend}=0.025{\gamma }_0\sqrt{\frac{k_{B}T}{\kappa }}\frac{k_{B}T}{\eta }{Q}^3(27)$

where $k_B$ represents the Boltzmann constant, T denotes the temperature, $\eta$ signifies the solvent viscosity coefficient, and ${\gamma }_0$ is a coefficient reliant on the bending modulus $\kappa$, where ${\gamma }_0=1$ when $\frac{\kappa }{k_{B}T}\gg 1$. The ZG model was employed for the kinetic analysis of membranes comprising surfactants or lipids, and its validity was subsequently corroborated [76, 77].

Nevertheless, in the research [78–81], it was observed that the bending modulus estimated through fitting the NSE data using the ZG model tended to be notably higher (about ten times) than the expected values. To address this discrepancy, researchers initially resorted to using an effective solvent viscosity coefficient, ${\eta }_{eff}$, approximately 3–4 times larger than the original $\eta$, to obtain a more reasonable value for the bending modulus. Indeed, the lipid membrane comprises a bilayer structure, a feature not captured in the ZG model. During the bending of the membrane, the outer lobe undergoes stretching while the inner lobe experiences compression, leading to a density gradient within a confined thickness. This gradient disrupts the uniformity of the lipid monolayer density, and the relative motion between the layers gives rise to viscous friction and augments the interlayer dissipation [82].

In 1993, Seifert and Langer (SL) introduced an additional density mode contribution to membrane fluctuations, leading to the prediction of the bend-stretch modulus [83]:

$\stackrel{\sim }{\kappa }=\kappa +2d^{2}k(28)$

where k represents the compressible modulus of the elastic area in the single layer, and d denotes the height of the neutral surface of the single layer relative to the mid-surface of the double layer. In 2010, Watson and Brown extended the ZG model by incorporating the SL dissipation mechanism in the bilayer context [84]. Concurrently, in the same year, Lee et al. experimentally validated the analytical predictions of this generalized model [81].

Lipid bilayer membrane thickness fluctuations (Figure 10C) are induced by the thermal motion of lipid molecules within the interior of the lipid bilayer membrane. The lipid bilayer membrane is composed of phospholipid molecules, which give rise to local changes in the membrane thickness when undergoing motion at various locations within the membrane, resulting in thickness fluctuations. In 2012, Woodka et al. first observed lipid membrane thickness fluctuations [85]. They employed the following expression to describe the observed relaxation rate [86, 87]:

$\frac{\mathrm{\Gamma }}{Q^3}=\frac{{\mathrm{\Gamma }}_{bend}}{Q^3}+\frac{{\mathrm{\Gamma }}_{TF}}{Q_0^3}\frac{1}{1+{\left(Q-Q_0\right)}^2{\xi }^{-2}}(29)$

The symbol ${\mathrm{\Gamma }}_{bend}$ represents the bending rate in the ZG theoretical framework. ${\mathrm{\Gamma }}_{TF}$ denotes the relaxation time of thickness fluctuations, with $Q_0$ determined by the form factor of the layered structure and correlated with the membrane thickness. ${\xi }^{-1}$ represents the half-width at half-maximum (HWHM) of the characteristic thickness fluctuation. The quantity $d_m{\xi }^{-1}/Q_0$ corresponds to the actual amplitude of the thickness fluctuations, where $d_m$ is the thickness of the lipid bilayer membrane. Figures 11B–D shows the $I\left(Q,t\right)/I\left(Q,0\right)$-$Q$ dependence of vesicles which are composed of dimyristoyl-, dipalmitoyl-, or distearoyl-phosphocholine (DMPC, DPPC, and DSPC), respectively. The clear peaks, indicating enhanced dynamics on the length scale of the film thickness in the relaxation rate are observed at a specific $Q$ corresponding to the film thickness. Their findings indicate that thickness fluctuations, similar to the bending rigidity, exhibit a significant variation as crossing the lipid transition temperature, becoming suppressed after the transition temperature. In 2015, Ashkar et al. introduced a second lipid component in a lipid bilayer system, investigating the modulation of membrane fluctuations by lipid tail mismatch, and the results represent the decoupling of the amplitude-temperature dependence and relaxation time [88].

FIGURE 11

FIGURE 11. (A) $I\left(Q,t\right)/I\left(Q,0\right)$ of the single lipid DPPC vesicles at $\mathrm{T}=50℃$ of five Q's, fits are to Eq. 26. Normalized relaxation rate $\mathrm{\Gamma }/Q^3$ for (B) DMPC (C) DPPC (D) DSPC vesicles. The solid lines are the results of fitting Eq. 29 above the melt transition temperature $T_m$. Variation of the bending modulus $\kappa$ calculated from Eq. 27 with reduce temperature, $T-T_m$. It is notable that $\kappa$ in Eq. 28 has been replaced with $\tilde{\kappa }$. The figure was adapted from [85].

Similar to the previously discussed membrane fluctuations, this model also does not account for internal dissipation within the membrane. In 2015, Bingham, Smye, and Olmsted (BSO) proposed a model for bilayer lipid membranes (BLMs) in a viscous solvent, revealing a dispersion relationship associated with inner surface motion, which includes three modes: 1) a pure shear mode describing fluctuations within the bilayer, 2) a coupled mode combining bilayer and inner surface motions, and 3) an internal mode related to inner surface motion [89]. Based on this theory, Nagao et al. incorporated the compressibility modulus $K_A$ into the expression for the relaxation rate [90], which accounts for the damping due to the viscosity of both the solvent and the membrane. They emphasized the interdependence between bilayer elasticity, viscosity, and collective membrane dynamics, demonstrating how the elastic and viscous properties of simple phospholipids with different tail lengths are influenced by lipid composition [91]. In 2020, Kelley et al. utilized this approach to study the dynamic characteristics of mixed membranes, and the results revealed that mixed membranes can be quantified in terms of reduced bending modulus, area compressibility modulus, and viscosity. Furthermore, the lipid composition can control the membrane’s properties [92].

In recent years, NSE spectroscopy has been widely used to study membrane interactions with other macromolecules such as nanoparticles, proteins, and sterols. These studies focus on the changes in the static structure and dynamic behavior of lipid membranes in a system, providing new perspectives and possibilities for studying biological membranes and elaborating their biological functions.

In 2018, Chakraborty et al. conducted a study revealing the modulation of the phospholipid bilayer structure by introducing hydrophobic gold nanoparticles (AuNPs) [93]. The primary focus of their research encompassed the synthesis and characterization of lipid nanoparticle assemblies (LNAs) formed by associating hexyl mercaptan functionalized AuNPs with dipalmitoyl phosphatidylglycerol (DPPG) lipids. They investigated the effect of AuNPs on the softening of the bilayer structure by adjusting the size and concentration of AuNPs using dynamic light scattering (DLS) and SANS techniques. The outcomes demonstrated the successful integration of AuNPs into the phospholipid bilayer with the observation of both small and large aggregates, and the presence of AuNPs affects the bending modulus of the phospholipid bilayer. The study underscored the necessity of considering diffusion and displacement motion in analyzing NSE measurement data. It evaluated the compressible modulus of the bilayer based on the thickness measurements from SANS and the bending modulus obtained from NSE.

Previous studies reveal that the timescale of conformational changes and spatial folding of membrane proteins aligns with the timescale of lipid membrane thickness fluctuations. Thus there may be potential mechanisms for membrane-protein interactions, which have consistently remained a prominent subject of investigation [86, 88, 94–96]. Antimicrobial peptides are one of the most promising antibiotic-resistant bacterial antibiotics, with strong interactions with cell membranes. Some research has indicated that antimicrobial peptides have profound effects on the dynamic properties of lipid molecules, especially their lateral motion or translocation, contingent on the bilayer phase state, and this influence has been demonstrated in various studies [97, 98]. NSE techniques offer a means to investigate the response mechanisms of antimicrobial membranes to membrane bending stiffness. In 2019, Yu et al. explored the use of end-phosphorylated polyethylene glycol (PEG) triblock copolymer (Pi-ABAPEG) as an antimicrobial agent to treat disease against microbial pathogens [99]. The unphosphorylated copolymer (ABAPEG) copolymer was found to interact with the lipid rafts of epithelial cell membranes, which is a critical structure in cell signal transduction and thus prevents dysregulation of barrier function and apoptosis. The study also sought to understand the protective effects of Pi-ABAPEG by studying the effects of PEG-polymerized polymers on the structure and dynamics of phospholipid bilayer films. Phospholipid bilayer membranes are highly flexible, self-assembled, and dynamic structures that can undergo different conformational transitions, and this flexibility is critical for many biological processes. They measured the thermal fluctuation and cavity motion of DMPC single-molecule vesicle membranes using NSE and characterized their structures in combination with DLS, SANS) and X-ray reflection (XRR) techniques. These findings contribute to a better understanding of the interactions between polymers and cell membranes, leading to the development of more effective disease treatments for microbial pathogens. In 2021, Kelley et al. investigated the impact of antimicrobial peptides (AMPs), alamethicin (Ala), and gramicidin on the collective dynamic properties of lipid membranes. Using NSE techniques, their findings indicated that the peptides exert opposing effects on the relaxation time of collective curvature fluctuations and the bending modulus of the membrane [95]—specifically, gramicidin-induced membrane stiffening, while Ala led to membrane softening. Furthermore, at low concentrations, gramicidin enhanced the dynamics of collective thickness fluctuations, while at higher concentrations, including those explored across the study, it attenuated such dynamics. The study underscored the synergistic interplay of lipids and proteins in determining collective membrane dynamics, emphasizing the importance of considering the influence of transmembrane peptides on lipid bilayer fluctuations.

Cholesterol is a fundamental constituent of eukaryotic cell membranes, exerting a crucial role in membrane properties and functions. Previous studies suggested cholesterol enhances the stiffness of saturated lipid membranes, yet its impact on unsaturated membranes remained unclear. In 2020, Chakraborty et al. investigated the influence of cholesterol on the bending stiffness of unsaturated lipid membranes [100]. Their research demonstrated that cholesterol, like its effect on saturated lipid membranes, locally increased the bending stiffness of DOPC membranes by augmenting the bilayer’s compressional density. These findings indicate the need to reassess the role of cholesterol in governing membrane bending stiffness, particularly at intermediate length and time scales relevant to essential biological functions such as virus budding and lipid-protein interactions. In 2023, Doole et al. utilized solid-state deuterium nuclear magnetic resonance (²H NMR) and NSE spectroscopy to reveal a synergistic modulation of lipid packing by cholesterol and PIP2, resulting in alterations in the bending stiffness of lipid membranes [101].

3.4 Microemulsion

The microemulsion is a thermodynamically stable, optically isotropic, and transparent dispersion system comprising two immiscible liquids, commonly oil and water phases, that are solubilized and stabilized by the presence of surfactant molecules. The dynamics and phase behavior of microemulsion systems can be elucidated by considering their favored curvature, leading to their classification into distinct types, including droplet microemulsions, lamellar microemulsions, and bicontinuous microemulsions. Recent research has demonstrated the effectiveness of NSE as a robust technique for evaluating the dynamic attributes of microemulsions, encompassing membrane dynamics, droplet diffusion, phase connectivity, and other related properties. Microemulsions find extensive and multifaceted applications across diverse domains, such as pharmaceuticals, cosmetics, food, and oil industries. They serve as efficacious drug delivery systems, constituents in personal care products, emulsifying agents in food formulations, and formulations employed in enhanced oil recovery. The distinctive properties and versatile characteristics of microemulsions render them highly desirable for a wide range of practical applications.

Common droplet microemulsions encompass both oil-in-water (O/W) and water-in-oil (W/O) microemulsions. In an O/W microemulsion, oil droplets are dispersed within a continuous water phase, while in a W/O microemulsion, water droplets are dispersed within a continuous oil phase. These droplet microemulsions are stabilized by surfactant molecules, exhibit remarkably low interfacial tension, and can be characterized by Helfrich bending free energy. In 1987, Milner and Safran used the spherical harmonic model to describe the droplet dynamics and derived the ISF of the thin shell approximation [102],

$I\left(Q,t\right)=\exp \left(-{\mathrm{\Gamma }}_{1}t\right)V_s^2{\left(\Delta \rho \right)}^2\left[f_0\left(QR\right)+{\displaystyle \sum _{l\ge 2}}\frac{2l+1}{4\pi R^2}{f}_1\left(QR\right)〈{\left|u_l\right|}^2〉\exp \left(-{\mathrm{\Gamma }}_{l}t\right)\right](30)$

where ${\mathrm{\Gamma }}_1$ is the attenuation coefficient of droplet centroid diffusion, $V_s$ is the droplet volume, $\Delta \rho$ is the scattering length density difference between the droplet and the solvent, and $R$ is the mean radius of the droplet. ${\mathrm{\Gamma }}_l$ is the relaxation rate of the corresponding mode, $〈{\left|u_l\right|}^2〉$ corresponds to the amplitude of the wave in the l th mode. The first term represents the translational motion of the particle, while the second term signifies the shape fluctuations of the particle. Farago et al. summarized the results of $l=0$ and $l=2$ models and combined SANS and NSE to obtain internal motion information such as curvature modulus, respectively [103, 104]. In 1999, Hellweg proposed that by neglecting the contribution of fluctuating modes with $l>2$ the ISF can be approximated as a double exponential function,

$\frac{I\left(Q,t\right)}{I\left(Q,0\right)}=a\exp \left(-D_0{Q}^{2}t\right)+\left(1-a\right)\exp \left(-\mathrm{\Gamma }t\right)(31)$

where the self-diffusion coefficient $D_0$ is derived from the DLS experiment, and $a$ is the amplitude factor. The relaxation rate $\mathrm{\Gamma }-D_0{Q}^2$ is related to the hydrodynamic factor and viscosity, and the bending modulus $\kappa$ and $\overline{\kappa }$ can be calculated by combining the polydispersity of the particles. Their investigation demonstrates a strong concurrence between the obtained results and the measured values of the systems ($oiln-decane/C_8{E}_3/C_{10}{E}_4$ ([105]; $C_{10}{E}_4/water$[106]; $dodecane/water/C_{10}{E}_5$[107])). In 2008, Nagao and Seto introduced the relative intermediate form factor method, decoupled shape and structure fluctuations, and simplified the normalized ISF [108]:

$\frac{I\left(Q,t\right)}{I\left(Q,0\right)}=\exp \left(-D_0\frac{H\left(Q\right)}{S\left(Q\right)}{Q}^{2}t\right)(32)$

where $H\left(Q\right)$ denotes the hydrodynamic function arising from the motion of proteins in solution and $S\left(Q\right)$ represents the interparticle structure factor associated with collective translational motion. They analyzed NSE data for concentrated W/O microemulsion systems, investigated shape fluctuations and bending elasticity changes with water concentration (dispersed phase), and found dynamic patterns of other structural fluctuations with non-centroid diffusion in regions of high momentum transfer and longer time.

Bicontinuous microemulsion represents a distinctive category of microemulsion wherein the dispersed and continuous phases create an interconnected continuous domain within the system. Unlike traditional microemulsions that exhibit distinct boundaries between dispersed and continuous phases, bicontinuous microemulsions possess a unique morphology where the two phases interpenetrate. The continuous domains of dispersed and continuous phases intertwine to establish an interconnected continuous structure. This distinctive morphological arrangement augments the interfacial area and enhances the solubilization and transport capabilities of bicontinuous microemulsions.

In high Q regimes ($Q\gg Q_0=2\pi /d$, where d is the distance between neighbor water–water or oil-oil domain), which primarily captures local membrane motion, researchers emphasize the investigation of layer displacement in impermeable amphiphilic films. The film dynamics characteristics predominantly arise from frictional dissipation resulting from the bending modulus (κ) and interlayer displacement. Bicontinuous microemulsions exhibit close resemblances to lipid films. In this context, the Zilman and Granek (ZG) model conceptualizes the amphiphilic film within the bicontinuous network as a collection of independent patches, each characterized by a scale similar to the relevant characteristic length (ξ). However, it is well-known that in the Zilman and Granek (ZG) model, the condition of ${\gamma }_0\approx 1-3\left(\frac{k_{B}T}{4\pi \kappa }\right)\ln \left(q\xi \right)\to 1$ is $\frac{\kappa }{k_{B}T}\gg 1$. Nevertheless, the SANS studies conducted by Grompper et al. suggest that the bicontinuous phase retains lower membrane rigidity, $\kappa \approx 0.9-1.3k_{B}T$ [109], potentially leading to a negative value of ${\gamma }_0$, which is obviously unreasonable. In 2001, Mihailescu et al. extended the ZG model through numerical complete integration [105]. Their investigation revealed that, besides polymer content, surfactant content plays a more substantial role in influencing the relaxation rate. In 2005, Monkenbusch et al. utilized the extended Zilman and Granek (ZG) model to map the relaxation frequency as a function of length scale and bending rigidity. By employing the characteristic length scale ($\xi$) obtained from SANS, they successfully determined the bending rigidity ($\kappa$) values for bicontinuous microemulsions [78].

In the intermediate q-range ($Q\approx Q_0$) it becomes considerably more intricate to describe the theoretical aspects of $S\left(Q,t\right)$ [110], and previous studies primarily involved qualitative descriptions and comparisons of experimental results [105]. The Ginzburg-Landau theories, along with parameters associated with $\xi$ and $d$, provide descriptions of the main features of relaxation rates [111–113]. Based on this theoretical framework, Nonomura and Ohta respectively presented the results for the volume and thin film dynamic structure factors as follows [113]:

$S_{11}\left(Q,t\right)=\left[\left(1-f\right)e^{-{\mathrm{\Gamma }}_{11}\left(Q\right)t}+f{e}^{-{\mathrm{\Gamma }}_{22}\left(Q\right)t}\right](33)$

$S_{22}\left(Q,t\right)=\left[f{e}^{-{\mathrm{\Gamma }}_{11}\left(Q\right)t}+\left(1-f\right)e^{-{\mathrm{\Gamma }}_{22}\left(Q\right)t}\right](34)$

where $S_{11}\left(Q,t\right)$ and $S_{22}\left(Q,t\right)$ represent the ISFs for bulk and thin film contrast microemulsions, respectively. The relaxation decay rates ${\mathrm{\Gamma }}_{11}$ and ${\mathrm{\Gamma }}_{22}$ are associated with bulk relaxation and thin film, respectively, and the weighted factor $f$ is determined as $f=\frac{{\mathrm{\Gamma }}_{12}{\mathrm{\Gamma }}_{21}}{{\left({\mathrm{\Gamma }}_{22}-{\mathrm{\Gamma }}_{11}\right)}^2}.$ The Q-dependent diffusion coefficient can be expressed as:

$D_Q=\frac{k_{B}T{k}_0}{6\pi \eta }N\left(\frac{Q}{k_0},\frac{u}{k_0}\right)(35)$

where $k_0=\sqrt{Q_0^2-{\xi }^{-2}}$ , $u=\sqrt{2Q_0/\xi }$ , N is the scaling function. It reveals the minimum value at $Q=k_0$ [110] and in Holderer et al.'s study, the hydrodynamic effect is observed only in ${\mathrm{\Gamma }}_{11}$, with a weighted factor $f\approx 0$. They systematically varied the sample contrast, elucidating two primary modes dominated by changes in the oil/water difference or surfactant concentration under the hydrodynamic condition. Subsequently, in 2013, Holderer et al. further enhanced the understanding of bicontinuous microemulsions by combining Neutron Spin Echo (NSE) experimental results for ${\kappa }_0$ and SANS experimental results for ${\kappa }_{R,SANS}$ to characterize the saddle-point bending modulus $\overline{\kappa }$ in the phase diagram [114].

Moreover, the dynamics of systems involving additives interacting with microemulsion membranes, such as microemulsion-block copolymers and microemulsion-proteins, have also sparked interest among soft matter scientists. The NSE technique has played a pivotal role in such research. The addition of hydrophobic polymers has been shown to increase the viscosity of the microemulsion by changing the droplet interaction, depending on the alkyl length of the hydrophobic polymer [115, 116]. In 2017, Klemmer et al. demonstrated that the addition of amphiphilic block copolymers to microemulsion systems composed of oil, water, and surfactants can significantly reduce the amount of surfactants required for microemulsion formation [117]. This observation aligns with the previously proposed enhancement effect mechanism [118, 119]. In 2020, Simon et al. used techniques including SANS, DLS, and NSE to elucidate the low-viscosity behavior of polyelectrolyte/microemulsion mixtures, which stands in stark contrast to the high-viscosity behavior exhibited by hydrophobic polymer-bound microemulsions. Their findings indicated that electrostatic interactions between microemulsion droplets and polyacrylate ions led to the formation of dynamically exchanging complexes with high exchange rates. At any given time, only a fraction of microemulsion droplets were encompassed within transient complexes [120].

Compared with the traditional emulsion as a carrier of bioactive nutrients, microemulsion has the advantages of easy preparation and scalability. It is widely used in pesticides, drugs, food, beverage, and cosmetics and is an excellent nano-extractor/nanoreactor carrier [121]. In 2019, Sharma et al. investigated the dynamics of melittin in a double-continuous microemulsion composed of water, dodecane (oil), 1-pentanol (cosurfactant), and sodium dodecyl sulfate (SDS). They observed that melittin constrained lateral and internal motions while enhancing long-range collective and fluctuation motions [122]. In 2021, Engelskirchen et al. investigated the flexural elasticity of surfactant monolayers in a bicontinuous microemulsion containing lipases (Figure 12). Using neutron scattering techniques, particularly SANS and NSE, they explored the effect of CalB, a lipase from Antarctic cryophilic fatty yeast, on the bending elasticity of the surfactant monolayer. The research findings revealed that as the concentration of CalB increased, its adsorption at the interface also increased, potentially leading to a stiffer interface—the mentioned experimental methods allowed for the determination of the bending elasticity constant. The study provided insights into the adsorption/desorption mechanism of CalB in surfactant monolayers and its influence on monolayer composition and curvature elasticity, offering potential applications in catalyzing organic reactions of non-naturally water-soluble substrates. Overall, this research focused on the structural and dynamic properties of lipase-containing microemulsions and their potential applications [123]. Moreover, they underscore the advantages of microemulsions as versatile systems for transdermal drug delivery, emphasizing their potential as multifunctional carriers [124].

FIGURE 12

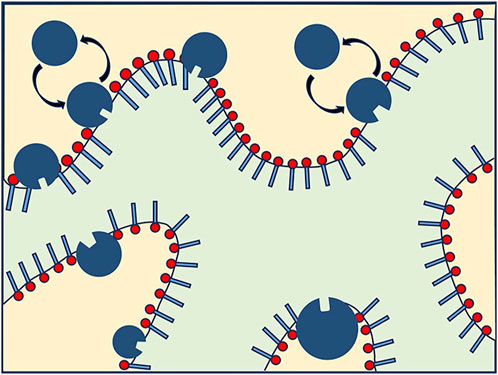
FIGURE 12. Schematic diagram of Candida antarctica B (CalB) exchange in a bicontinuous microemulsion surfactant layer, where the yellow part is the water phase and the light green part is the oil phase. There is no contain scale size information [123].

In addition, Maarten Mulder et al. systematically investigated oil-water microemulsion systems using SESANS. They mixed components n-decane ($C_{10}{H}_{22}$), n-dodecane ($C_{12}{H}_{26}$), n-pentadecane ($C_{15}{H}_{33}$) and deuterated water separately and subsequently introduced internal olefin sulfonate (IOS) surfactant ENORDET O242 ($C_{20-24}{H}_{39-47}S{O}_{3}Na$) to the mixed liquid to form the microemulsion. The research findings revealed that microemulsions exhibit the largest structural size in the bicontinuous state, representing the optimal condition. However, with increasing salt content, secondary butyl alcohol (SBA) content, and aliphatic carbon atom number, the structural size of the bicontinuous microemulsion rapidly decreases, transitioning to a non-optimal state where the bicontinuous phase folds into spherical droplets. This transition is attributed to reduced interfacial tension between the oil and water phases due to the increased salt content and aliphatic carbon number. In this study, SESANS demonstrated its advantage in probing structures at the nanoscale. It provided indirect information about the oil-water interface sharpness and the interfacial area occupied by each surfactant molecule [125]. Consequently, in microemulsions, SESANS measurements serve as a valuable supplement to SANS.

4 Summary and perspective

As our understanding of soft matter continues to advance, the findings from studies on soft matter are increasingly applied across various domains, particularly in biomedical sciences. For instance, unraveling the pathogenesis of neurodegenerative diseases, including Alzheimer’s disease, Parkinson’s disease, and amyotrophic lateral sclerosis, remains a significant challenge in medicine-related research. The intricate nature of their pathological mechanisms has led to many hypotheses, none of which have been definitively validated. One perspective posits that aberrant alterations in cell membranes are considered to be among the contributing factors to the onset of these diseases. For instance, in the context of Alzheimer’s disease, which is associated with memory and cognitive impairments, research suggests that alterations in the lipid composition of cell membranes may be closely linked to its development. Variations in lipid content, saturation levels of lipid components, and anomalous lipid distribution within cell membranes could lead to increased membrane rigidity and compromised membrane protein functionality, subsequently affecting regular neuronal communication and function [15]. Alternatively, another perspective proposes a connection between neurodegenerative diseases and the excessive aggregation of specific proteins, where liquid-liquid phase separation within biological cells may play a crucial role in the initial stages of protein aggregation [126]. However, the precise regulatory mechanisms governing these biological processes remain elusive, representing a pivotal research direction in current biological investigations. Indeed, the significance of lipid membrane research extends far beyond these instances. In the case of infectious diseases, cell membranes play crucial roles as well. For example, in viral infections, the interaction between membrane receptors on the cell surface and viral surface proteins is a critical initial step in infection. The structure and composition of the cell membrane dictate the specificity of binding between viruses and cells, thereby impacting infectivity and viral replication. Furthermore, certain studies have revealed that changes in the composition of specific membrane regions can enable viruses to evade immune system attacks, rendering infections more difficult to control [127]. Shortly, NSE techniques, in conjunction with molecular dynamics simulations, are poised to play pivotal roles in advancing these investigations.

Furthermore, NSE also finds application in investigating biological and medical systems such as lipid membranes and microemulsions for drug delivery. Lipid membranes constitute a fundamental component of cellular membranes within biological organisms and play a crucial role in drug delivery and cell signaling. NSE can be employed to probe the structure and interactions of lipid membranes, thereby unveiling their functional mechanisms and shedding light on drug delivery processes, which has implications for optimizing the design and application of microemulsions in the biomedical field.

Moreover, the significance of liquid-liquid phase separation (LLPS) within biological cells has gained widespread recognition. LLPS is a physicochemical process in which two or more compounds segregate from a homogeneous mixture into two or more phases under specific conditions such as temperature, pressure, and concentration. LLPS plays a pivotal role in various biological processes, particularly in forming diverse cellular structures. Within cells, numerous membrane-less organelles or structures exist, including nucleoli, stress granules, P-bodies, and centrosomes, the formation and function of which may be associated with LLPS [126]. These microenvironments or structural formations arising from LLPS can concentrate or segregate specific biomolecules, facilitating efficient processes such as cell signaling, gene regulation, and protein synthesis [128, 129]. The regulation of these biological processes relies on the interactions among various biomacromolecules, such as proteins and RNA. These interactions are highly intricate and remain incompletely understood to date. Recent research findings suggest that proteins prone to phase separation often possess intrinsically disordered regions (IDRs), leading to their classification as intrinsically disordered proteins (IDPs) [130]. IDPs are naturally unstructured proteins, lacking fixed conformations, which presents a challenging aspect in their study. Furthermore, as highlighted in our earlier discussion of SALR colloids, model systems featuring short-range attraction and long-range repulsion potentials could potentially contribute to understanding LLPS. Hence, the combined application of NSE and SESANS would provide a robust approach to investigate the dynamics of IDPs.

In conclusion, NSE technology has opened new frontiers in the research field of soft matter science. Nonetheless, the availability of inelastic NSE and SESANS spectrometers remains limited, falling significantly short of meeting the scientific community’s demands for diverse material explorations. Recently, two NSE spectrometers, both an inelastic LRNSE (longitudinal neutron resonance spin-echo) and a SESANS spectrometer, are commissioning at the China Mianyang Research Reactor (CMRR) [10, 131]. We expect a bright future of broad applications of NSE technology in soft matter sciences.

Author contributions

XL: Writing–original draft. TC: Writing–original draft. XC: Supervision, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This project was supported by the National Nature Science Foundation of China (No. U2230207), and grants from the City University of Hong Kong (Project Nos. 9610568, 7006132, and 9610490).

Acknowledgments

We acknowledge the valuable discussion and suggestions from Zhixin Wang, Dr. Jingjing Han, and Dr. Xin Jiang.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mezei F, Pappas C, Gutberlet T. Neutron spin echo spectroscopy: basics, trends and applications. Springer Science and Business Media (2002).

Google Scholar

2. Monkenbusch M, Stadler A, Biehl R, Ollivier J, Zamponi M, Richter D. Fast internal dynamics in alcohol dehydrogenase. J Chem Phys (2015) 143(7):075101. doi:10.1063/1.4928512

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hassani AN, Haris L, Appel M, Seydel T, Stadler AM, Kneller GR. Multiscale relaxation dynamics and diffusion of myelin basic protein in solution studied by quasielastic neutron scattering. J Chem Phys (2022) 156(2):025102. doi:10.1063/5.0077100

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Mezei F. Neutron spin echo: a new concept in polarized thermal neutron techniques. Z für Physik A Hadrons nuclei (1972) 255:146–60. doi:10.1007/bf01394523

CrossRef Full Text | Google Scholar

5. Dagleish P, Hayter J, Mezei F. The IN11 neutron spin echo spectrometer. In: Neutron spin echo: proceedings of a laue-Langevin institut workshop Grenoble. Springer (1980). p. 66–71. October 15–16, 1979.

Google Scholar

6. Pynn R. Neutron spin-echo and three-axis spectrometers. J Phys E: Scientific Instr (1978) 11(11):1133–40. doi:10.1088/0022-3735/11/11/015

CrossRef Full Text | Google Scholar

7. Gähler R, Golub R, Habicht K, Keller T, Felber J. Space-time description of neutron spin echo spectrometry. Physica B: Condensed Matter (1996) 229(1):1–17. doi:10.1016/s0921-4526(96)00509-1

CrossRef Full Text | Google Scholar

8. Rekveldt MT. Novel SANS instrument using neutron spin echo. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (1996) 114(3-4):366–70. doi:10.1016/0168-583x(96)00213-3

CrossRef Full Text | Google Scholar

9. Rekveldt MT, Plomp J, Bouwman WG, Kraan WH, Grigoriev S, Blaauw M. Spin-echo small angle neutron scattering in Delft. Rev Scientific Instr (2005) 76(3). doi:10.1063/1.1858579

CrossRef Full Text | Google Scholar

10. Wang T, Tu X, Wang Y, Li X, Gong J, Sun G. Design and simulations of spin-echo small angle neutron scattering spectrometer at CMRR. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2022) 1024:166041. doi:10.1016/j.nima.2021.166041

CrossRef Full Text | Google Scholar

11. Barker J, Glinka C, Moyer J, Kim M, Drews A, Agamalian M. Design and performance of a thermal-neutron double-crystal diffractometer for USANS at NIST. J Appl Crystallogr (2005) 38(6):1004–11. doi:10.1107/s0021889805032103

CrossRef Full Text | Google Scholar

12. Andersson R, Van Heijkamp LF, De Schepper IM, Bouwman WG. Analysis of spin-echo small-angle neutron scattering measurements. J Appl Crystallogr (2008) 41(5):868–85. doi:10.1107/s0021889808026770

CrossRef Full Text | Google Scholar

13. Stradner A, Sedgwick H, Cardinaux F, Poon WC, Egelhaaf SU, Schurtenberger P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature (2004) 432(7016):492–5. doi:10.1038/nature03109

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Stradner A, Schurtenberger P. Potential and limits of a colloid approach to protein solutions. Soft Matter (2020) 16(2):307–23. doi:10.1039/c9sm01953g

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sharma V, Mamontov E. Multiscale lipid membrane dynamics as revealed by neutron spectroscopy. Prog Lipid Res (2022) 87:101179. doi:10.1016/j.plipres.2022.101179

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nagao M, Seto H. Neutron scattering studies on dynamics of lipid membranes. Biophys Rev (2023) 4(2). doi:10.1063/5.0144544

CrossRef Full Text | Google Scholar

17. Longeville S, Doster W, Diehl M, Gähler R, Petry W. Neutron resonance spin echo: oxygen transport in crowded protein solutions. Neutron Spin Echo Spectroscopy: Basics, Trends Appl (2003) 325–35. doi:10.1007/3-540-45823-9_26

CrossRef Full Text | Google Scholar

18. Bouwman WG, Oossanen Mv., Uca O, Kraan WH, Rekveldt MT. Development of spin-echo small-angle neutron scattering. J Appl Crystallogr (2000) 33(3):767–70. doi:10.1107/S0021889800099829

CrossRef Full Text | Google Scholar

19. Mezei F. Fundamentals of neutron spin echo spectroscopy. In: Neutron spin echo spectroscopy: basics, trends and applications. Springer (2002). p. 5–14.

CrossRef Full Text | Google Scholar

20. Uca O. Spin-echo small-angle neutron scattering development (2003).

Google Scholar

21. Bouwman WG, Pynn R, Rekveldt MT. Comparison of the performance of SANS and SESANS. Physica B: Condensed Matter (2004) 350(1-3):E787–90. doi:10.1016/j.physb.2004.03.205

CrossRef Full Text | Google Scholar

22. Grigoriev SV, Kraan WH, Rekveldt MT, Kruglov T, Bouwman WG. Spin-echo small-angle neutron scattering for magnetic samples. J Appl Crystallogr (2006) 39(2):252–8. doi:10.1107/s002188980600481x

CrossRef Full Text | Google Scholar

23. Rekveldt MT, Bouwman WG, Kraan WH, Uca O, Grigoriev S, Habicht K, et al. Elastic neutron scattering measurements using Larmor precession of polarized neutrons. Neutron Spin Echo Spectroscopy: Basics, Trends Appl (2003) 87–99. doi:10.1007/3-540-45823-9_9

CrossRef Full Text | Google Scholar

24. Krouglov T, De Schepper IM, Bouwman WG, Rekveldt MT. Real-space interpretation of spin-echo small-angle neutron scattering. J Appl Crystallogr (2003) 36(1):117–24. doi:10.1107/s0021889802020368

CrossRef Full Text | Google Scholar

25. Kadletz E, Bouwman WG, Pappas C. Radial spin echo small-angle neutron scattering method: concept and performance. J Appl Crystallogr (2022) 55(5):1072–84. doi:10.1107/s1600576722007245

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Li F, Parnell SR, Bai H, Yang W, Hamilton WA, Maranville BB, et al. Spin echo modulated small-angle neutron scattering using superconducting magnetic Wollaston prisms. J Appl Crystallogr (2016) 49(1):55–63. doi:10.1107/s1600576715021573

CrossRef Full Text | Google Scholar

27. Liu Y. Intermediate scattering function for macromolecules in solutions probed by neutron spin echo. Phys Rev E (2017) 95(2):020501. doi:10.1103/physreve.95.020501

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Chen S-H, Tartaglia P. Scattering methods in complex fluids. Cambridge University Press (2015).

Google Scholar

29. Kruglov T. Correlation function of the excluded volume. J Appl Crystallogr (2005) 38(5):716–20. doi:10.1107/s0021889805017000

CrossRef Full Text | Google Scholar

30. Krouglov T, Bouwman WG, Plomp J, Rekveldt MT, Vroege GJ, Petukhov AV, et al. Structural transitions of hard-sphere colloids studied by spin-echo small-angle neutron scattering. J Appl Crystallogr (2003) 36(6):1417–23. doi:10.1107/s0021889803021216

CrossRef Full Text | Google Scholar

31. Meltzer AD, Tirrell DA, Jones AA, Inglefield PT. Chain dynamics in poly (amidoamine) dendrimers: a study of proton NMR relaxation parameters. Macromolecules (1992) 25(18):4549–52. doi:10.1021/ma00044a014

CrossRef Full Text | Google Scholar

32. Wu H, Song K, Chen W-R, Song J, Porcar L, Wang Z. Size and shape fluctuations of ultrasoft colloids. Phys Rev Res (2021) 3(3):033271. doi:10.1103/physrevresearch.3.033271

CrossRef Full Text | Google Scholar

33. Li X, Sánchez-Diáz LE, Wu B, Hamilton WA, Falus Pt., Porcar L, et al. Dynamical threshold of diluteness of soft colloids. ACS Macro Lett (2014) 3(12):1271–5. doi:10.1021/mz500500c

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Li X, Sánchez-Diáz LE, Wu B, Hamilton WA, Porcar L, Falus P, et al. Dynamical crossover in soft colloids below the overlap concentration (2014). arXiv preprint arXiv:1403.1812.

Google Scholar

35. Li X, Shew C-Y, Liu Y, Pynn R, Liu E, Herwig KW, et al. Prospect for characterizing interacting soft colloidal structures using spin-echo small angle neutron scattering. J Chem Phys (2011) 134(9):094504. doi:10.1063/1.3559451

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Liu Y, Xi Y. Colloidal systems with a short-range attraction and long-range repulsion: phase diagrams, structures, and dynamics. Curr Opin Colloid Interf Sci (2019) 39:123–36. doi:10.1016/j.cocis.2019.01.016

CrossRef Full Text | Google Scholar

37. Washington A, Li X, Schofield AB, Hong K, Fitzsimmons M, Dalgliesh R, et al. Inter-particle correlations in a hard-sphere colloidal suspension with polymer additives investigated by Spin Echo Small Angle Neutron Scattering (SESANS). Soft Matter (2014) 10(17):3016–26. doi:10.1039/c3sm53027b

PubMed Abstract | CrossRef Full Text | Google Scholar

38. McCammon J. Protein dynamics. Rep Prog Phys (1984) 47(1):1–46. doi:10.1088/0034-4885/47/1/001

CrossRef Full Text | Google Scholar

39. Parak FG, Achterhold K. Protein dynamics on different timescales. J Phys Chem Sol (2005) 66(12):2257–62. doi:10.1016/j.jpcs.2005.09.045

CrossRef Full Text | Google Scholar

40. Alpert Y, Cser L, Faragó B, Franěk F, Mezei F, Ostanevich YM. Segmental flexibility in pig immunoglobulin G studied by neutron spin-echo technique. Biopolymers: Original Res Biomolecules (1985) 24(9):1769–84. doi:10.1002/bip.360240908

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Biehl R, Richter D. Slow internal protein dynamics in solution. J Phys Condensed Matter (2014) 26(50):503103. doi:10.1088/0953-8984/26/50/503103

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Liu Y. Short-time dynamics of proteins in solutions studied by neutron spin echo. Curr Opin Colloid Interf Sci (2019) 42:147–56. doi:10.1016/j.cocis.2019.07.002

CrossRef Full Text | Google Scholar

43. Bu Z, Biehl R, Monkenbusch M, Richter D, Callaway DJ. Coupled protein domain motion in Taq polymerase revealed by neutron spin-echo spectroscopy. Proc Natl Acad Sci (2005) 102(49):17646–51. doi:10.1073/pnas.0503388102

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Farago B, Li J, Cornilescu G, Callaway DJ, Bu Z. Activation of nanoscale allosteric protein domain motion revealed by neutron spin echo spectroscopy. Biophysical J (2010) 99(10):3473–82. doi:10.1016/j.bpj.2010.09.058

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Kim Y, Eom SH, Wang J, Lee D-S, Suh SW, Steitz TA. Crystal structure of Thermus aquaticus DNA polymerase. Nature (1995) 376(6541):612–6. doi:10.1038/376612a0

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Biehl R, Hoffmann B, Monkenbusch M, Falus P, Préost S, Merkel R, et al. Direct observation of correlated interdomain motion in alcohol dehydrogenase. Phys Rev Lett (2008) 101(13):138102. doi:10.1103/physrevlett.101.138102

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Beck C. Protein dynamics studied with neutron spectroscopy. Universität Tübingen (2022). doi:10.15496/publikation-43961

CrossRef Full Text | Google Scholar

48. Stingaciu LR, Ivanova O, Ohl M, Biehl R, Richter D. Fast antibody fragment motion: flexible linkers act as entropic spring. Scientific Rep (2016) 6(1):22148. doi:10.1038/srep22148

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Girelli A, Beck C, Bauerle F, Matsarskaia O, Maier R, Zhang F, et al. Molecular flexibility of antibodies preserved even in the dense phase after macroscopic phase separation. Mol pharmaceutics (2021) 18(11):4162–9. doi:10.1021/acs.molpharmaceut.1c00555

CrossRef Full Text | Google Scholar

50. Inoue R, Biehl R, Rosenkranz T, Fitter J, Monkenbusch M, Radulescu A, et al. Large domain fluctuations on 50-ns timescale enable catalytic activity in phosphoglycerate kinase. Biophysical J (2010) 99(7):2309–17. doi:10.1016/j.bpj.2010.08.017

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Hong L, Sharp MA, Poblete S, Biehl R, Zamponi M, Szekely N, et al. Structure and dynamics of a compact state of a multidomain protein, the mercuric ion reductase. Biophysical J (2014) 107(2):393–400. doi:10.1016/j.bpj.2014.06.013

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Farago B, Nicholl ID, Wang S, Cheng X, Callaway DJ, Bu Z. Activated nanoscale actin-binding domain motion in the catenin–cadherin complex revealed by neutron spin echo spectroscopy. Proc Natl Acad Sci (2021) 118(13):e2025012118. doi:10.1073/pnas.2025012118

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Peulen T-O, Hengstenberg CS, Biehl R, Dimura M, Lorenz C, Valeri A, et al. Integrative dynamic structural biology unveils conformers essential for the oligomerization of a large GTPase. Elife (2023) 12:e79565. doi:10.7554/elife.79565

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Klare JP, Steinhoff H-J. Spin labeling EPR. Photosynthesis Res (2009) 102:377–90. doi:10.1007/s11120-009-9490-7

CrossRef Full Text | Google Scholar

55. Hellenkamp B, Schmid S, Doroshenko O, Opanasyuk O, Kühnemuth R, Rezaei Adariani S, et al. Precision and accuracy of single-molecule FRET measurements—a multi-laboratory benchmark study. Nat Methods (2018) 15(9):669–76. doi:10.1038/s41592-018-0085-0

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Sugase K, Dyson HJ, Wright PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature (2007) 447(7147):1021–5. doi:10.1038/nature05858

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Song J, Guo L-W, Muradov H, Artemyev NO, Ruoho AE, Markley JL. Intrinsically disordered γ-subunit of cGMP phosphodiesterase encodes functionally relevant transient secondary and tertiary structure. Proc Natl Acad Sci (2008) 105(5):1505–10. doi:10.1073/pnas.0709558105

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Stadler AM, Stingaciu L, Radulescu A, Holderer O, Monkenbusch M, Biehl R, et al. Internal nanosecond dynamics in the intrinsically disordered myelin basic protein. J Am Chem Soc (2014) 136(19):6987–94. doi:10.1021/ja502343b

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Ameseder F, Radulescu A, Khaneft M, Lohstroh W, Stadler AM. Homogeneous and heterogeneous dynamics in native and denatured bovine serum albumin. Phys Chem Chem Phys (2018) 20(7):5128–39. doi:10.1039/c7cp08292d

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Stingaciu LR, Biehl R, Changwoo D, Richter D, Stadler AM. Reduced internal friction by osmolyte interaction in intrinsically disordered myelin basic protein. J Phys Chem Lett (2019) 11(1):292–6. doi:10.1021/acs.jpclett.9b03001

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Haris L, Biehl R, Dulle M, Radulescu A, Holderer O, Hoffmann I, et al. Variation of structural and dynamical flexibility of myelin basic protein in response to guanidinium chloride. Int J Mol Sci (2022) 23(13):6969. doi:10.3390/ijms23136969

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Porcar L, Falus P, Chen W-R, Faraone A, Fratini E, Hong K, et al. Formation of the dynamic clusters in concentrated lysozyme protein solutions. J Phys Chem Lett (2010) 1(1):126–9. doi:10.1021/jz900127c

CrossRef Full Text | Google Scholar

63. Falus P, Porcar L, Fratini E, Chen W-R, Faraone A, Hong K, et al. Distinguishing the monomer to cluster phase transition in concentrated lysozyme solutions by studying the temperature dependence of the short-time dynamics. J Phys Condensed Matter (2012) 24(6):064114. doi:10.1088/0953-8984/24/6/064114

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Yearley EJ, Godfrin PD, Perevozchikova T, Zhang H, Falus P, Porcar L, et al. Observation of small cluster formation in concentrated monoclonal antibody solutions and its implications to solution viscosity. Biophysical J (2014) 106(8):1763–70. doi:10.1016/j.bpj.2014.02.036

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Braun MK, Grimaldo M, Roosen-Runge F, Hoffmann I, Czakkel O, Sztucki M, et al. Crowding-controlled cluster size in concentrated aqueous protein solutions: structure, self-and collective diffusion. J Phys Chem Lett (2017) 8(12):2590–6. doi:10.1021/acs.jpclett.7b00658

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Mezei F, Russina M, Chen G, Frauenfelder H, Fenimore P, Falus P, et al. Dynamic transition and glassy behaviour in hydrated proteins. In: Journal of Physics: conference series. Universitêtszentrum Obergurgl, Innsbruck, Austria: IOP Publishing (2009) 012011.

CrossRef Full Text | Google Scholar

67. Magazù S, Mezei F, Falus P, Farago B, Mamontov E, Russina M, et al. Protein dynamics as seen by (quasi) elastic neutron scattering. Biochim Biophys Acta (BBA)-General Subjects (2017) 1861(1):3504–12. doi:10.1016/j.bbagen.2016.07.030

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Godfrin PD, Falus P, Porcar L, Hong K, Hudson SD, Wagner NJ, et al. Dynamic properties of different liquid states in systems with competing interactions studied with lysozyme solutions. Soft Matter (2018) 14(42):8570–9. doi:10.1039/c8sm01678j

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Brannigan G, Brown FL. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophysical J (2006) 90(5):1501–20. doi:10.1529/biophysj.105.075838

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Brandt EG, Edholm O. Stretched exponential dynamics in lipid bilayer simulations. J Chem Phys (2010) 133(11):115101. doi:10.1063/1.3478998

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Carrillo J-MY, Katsaras J, Sumpter BG, Ashkar R. A computational approach for modeling neutron scattering data from lipid bilayers. J Chem Theor Comput (2017) 13(2):916–25. doi:10.1021/acs.jctc.6b00968

CrossRef Full Text | Google Scholar

72. Punia R, Goel G (2023). Free energy surface and molecular characterization of slow structural transitions in lipid bilayers. bioRxiv. doi:10.1101/2023.06.30.547217

CrossRef Full Text | Google Scholar

73. Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z für Naturforschung c (1973) 28(11-12):693–703. doi:10.1515/znc-1973-11-1209

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Zilman A, Granek R. Undulations and dynamic structure factor of membranes. Phys Rev Lett (1996) 77(23):4788–91. doi:10.1103/physrevlett.77.4788

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Farge E, Maggs AC. Dynamic scattering from semiflexible polymers. Macromolecules (1993) 26(19):5041–4. doi:10.1021/ma00071a009

CrossRef Full Text | Google Scholar

76. Takeda T, Kawabata Y, Seto H, Komura S, Ghosh S, Nagao M, et al. Neutron spin–echo investigations of membrane undulations in complex fluids involving amphiphiles. J Phys Chem Sol (1999) 60(8-9):1375–7. doi:10.1016/s0022-3697(99)00122-5

CrossRef Full Text | Google Scholar

77. Komura S, Takeda T, Kawabata Y, Ghosh SK, Seto H, Nagao M. Dynamical fluctuation of the mesoscopic structure in ternary C 12 E 5–water–n-octane amphiphilic system. Phys Rev E (2001) 63(4):041402. doi:10.1103/physreve.63.041402

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Monkenbusch M, Holderer O, Frielinghaus H, Byelov D, Allgaier J, Richter D. Bending moduli of microemulsions; comparison of results from small angle neutron scattering and neutron spin-echo spectroscopy. J Phys Condensed Matter (2005) 17(31):S2903–9. doi:10.1088/0953-8984/17/31/017

CrossRef Full Text | Google Scholar

79. Seto H, Yamada N, Nagao M, Hishida M, Takeda T. Bending modulus of lipid bilayers in a liquid-crystalline phase including an anomalous swelling regime estimated by neutron spin echo experiments. The Eur Phys J E (2008) 26:217–23. doi:10.1140/epje/i2007-10315-0

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Boggara MB, Faraone A, Krishnamoorti R. Effect of pH and ibuprofen on the phospholipid bilayer bending modulus. The J Phys Chem B (2010) 114(24):8061–6. doi:10.1021/jp100494n

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Lee J-H, Choi S-M, Doe C, Faraone A, Pincus PA, Kline SR. Thermal fluctuation and elasticity of lipid vesicles interacting with pore-forming peptides. Phys Rev Lett (2010) 105(3):038101. doi:10.1103/physrevlett.105.038101

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Evans E, Yeung A. Hidden dynamics in rapid changes of bilayer shape. Chem Phys Lipids (1994) 73(1-2):39–56. doi:10.1016/0009-3084(94)90173-2

CrossRef Full Text | Google Scholar

83. Seifert U, Langer SA. Viscous modes of fluid bilayer membranes. Europhysics Lett (1993) 23(1):71–6. doi:10.1209/0295-5075/23/1/012

CrossRef Full Text | Google Scholar

84. Watson MC, Brown FL. Interpreting membrane scattering experiments at the mesoscale: the contribution of dissipation within the bilayer. Biophysical J (2010) 98(6):L9–L11. doi:10.1016/j.bpj.2009.11.026

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Woodka AC, Butler PD, Porcar L, Farago B, Nagao M. Lipid bilayers and membrane dynamics: insight into thickness fluctuations. Phys Rev Lett (2012) 109(5):058102. doi:10.1103/physrevlett.109.058102

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Nagao M. Observation of local thickness fluctuations in surfactant membranes using neutron spin echo. Phys Rev E (2009) 80(3):031606. doi:10.1103/physreve.80.031606

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Nagao M, Chawang S, Hawa T. Interlayer distance dependence of thickness fluctuations in a swollen lamellar phase. Soft Matter (2011) 7(14):6598–605. doi:10.1039/c1sm05477e

CrossRef Full Text | Google Scholar

88. Ashkar R, Nagao M, Butler PD, Woodka AC, Sen MK, Koga T. Tuning membrane thickness fluctuations in model lipid bilayers. Biophysical J (2015) 109(1):106–12. doi:10.1016/j.bpj.2015.05.033

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Bingham R, Smye S, Olmsted P. Dynamics of an asymmetric bilayer lipid membrane in a viscous solvent. Europhysics Lett (2015) 111(1):18004. doi:10.1209/0295-5075/111/18004

CrossRef Full Text | Google Scholar

90. Lindahl E, Edholm O. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophysical J (2000) 79(1):426–33. doi:10.1016/s0006-3495(00)76304-1

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Nagao M, Kelley EG, Ashkar R, Bradbury R, Butler PD. Probing elastic and viscous properties of phospholipid bilayers using neutron spin echo spectroscopy. J Phys Chem Lett (2017) 8(19):4679–84. doi:10.1021/acs.jpclett.7b01830

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Kelley EG, Butler PD, Ashkar R, Bradbury R, Nagao M. Scaling relationships for the elastic moduli and viscosity of mixed lipid membranes. Proc Natl Acad Sci (2020) 117(38):23365–73. doi:10.1073/pnas.2008789117

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Chakraborty S, Abbasi A, Bothun GD, Nagao M, Kitchens CL. Phospholipid bilayer softening due to hydrophobic gold nanoparticle inclusions. Langmuir (2018) 34(44):13416–25. doi:10.1021/acs.langmuir.8b02553

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Scott HL (2018). Probing the complex interaction between the pH-low insertion peptide and membrane bilayers.

Google Scholar

95. Kelley EG, Butler PD, Nagao M. Collective dynamics in lipid membranes containing transmembrane peptides. Soft Matter (2021) 17(23):5671–81. doi:10.1039/d1sm00314c

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Nakao H, Nagao M, Yamada T, Imamura K, Nozaki K, Ikeda K, et al. Impact of transmembrane peptides on individual lipid motions and collective dynamics of lipid bilayers. Colloids Surf B: Biointerfaces (2023) 228:113396. doi:10.1016/j.colsurfb.2023.113396

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Sharma VK, Mamontov E, Anunciado DB, O'Neill H, Urban VS. Effect of antimicrobial peptide on the dynamics of phosphocholine membrane: role of cholesterol and physical state of bilayer. Soft matter (2015) 11(34):6755–67. doi:10.1039/c5sm01562f

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Sharma VK, Qian S. Effect of an antimicrobial peptide on lateral segregation of lipids: a structure and dynamics study by neutron scattering. Langmuir (2019) 35(11):4152–60. doi:10.1021/acs.langmuir.8b04158

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Yu J, Mao J, Nagao M, Bu W, Lin B, Hong K, et al. Structure and dynamics of lipid membranes interacting with antivirulence end-phosphorylated polyethylene glycol block copolymers. Soft Matter (2020) 16(4):983–9. doi:10.1039/c9sm01642b

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Chakraborty S, Doktorova M, Molugu TR, Heberle FA, Scott HL, Dzikovski B, et al. How cholesterol stiffens unsaturated lipid membranes. Proc Natl Acad Sci (2020) 117(36):21896–905. doi:10.1073/pnas.2004807117

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Doole FT, Gupta S, Kumarage T, Ashkar R, Brown MF. Biophysics of membrane stiffening by cholesterol and phosphatidylinositol 4, 5-bisphosphate (PIP2). In: Cholesterol and PI (4, 5) P2 in vital biological functions: from coexistence to crosstalk. Springer (2023). p. 61–85.

CrossRef Full Text | Google Scholar

102. Milner ST, Safran S. Dynamical fluctuations of droplet microemulsions and vesicles. Phys Rev A (1987) 36(9):4371–9. doi:10.1103/physreva.36.4371

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Farago B, Richter D, Huang J, Safran S, Milner ST. Shape and size fluctuations of microemulsion droplets: the role of cosurfactant. Phys Rev Lett (1990) 65(26):3348–51. doi:10.1103/physrevlett.65.3348

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Farago B, Monkenbusch M, Goecking K, Richter D, Huang J. Dynamics of microemulsions as seen by neutron spin echo. Physica B: Condensed Matter (1995) 213:712–7. doi:10.1016/0921-4526(95)00257-a

CrossRef Full Text | Google Scholar

105. Hellweg T, Gradzielski M, Farago B, Langevin D. Shape fluctuations of microemulsion droplets: a neutron spin–echo study. Colloids Surf A: Physicochemical Eng Aspects (2001) 183:159–69. doi:10.1016/s0927-7757(01)00567-2

CrossRef Full Text | Google Scholar

106. Hellweg T, Brûlet A, Sottmann T. Dynamics in an oil-continuous droplet microemulsion as seen by quasielastic scattering techniques. Phys Chem Chem Phys (2000) 2(22):5168–74. doi:10.1039/b005088l

CrossRef Full Text | Google Scholar

107. Hellweg T, Langevin D. The dynamics in dodecane/C10E5/water microemulsions determined by time resolved scattering techniques. Physica A: Stat Mech its Appl (1999) 264(3-4):370–87. doi:10.1016/s0378-4371(98)00461-0

CrossRef Full Text | Google Scholar

108. Nagao M, Seto H. Concentration dependence of shape and structure fluctuations of droplet microemulsions investigated by neutron spin echo spectroscopy. Phys Rev E (2008) 78(1):011507. doi:10.1103/physreve.78.011507

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Gompper G, Endo H, Mihailescu M, Allgaier J, Monkenbusch M, Richter D, et al. Measuring bending rigidity and spatial renormalization in bicontinuous microemulsions. Europhysics Lett (2001) 56(5):683–9. doi:10.1209/epl/i2001-00574-3

CrossRef Full Text | Google Scholar

110. Holderer O, Frielinghaus H, Monkenbusch M, Allgaier J, Richter D, Farago B. Hydrodynamic effects in bicontinuous microemulsions measured by inelastic neutron scattering. Eur Phys J E (2007) 22:157–61. doi:10.1140/epje/e2007-00021-2

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Gompper G, Hennes M. Dynamic structure factor of microemulsions. Phys Rev Lett (1994) 73(8):1114–7. doi:10.1103/physrevlett.73.1114

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Hennes M, Gompper G. Dynamical behavior of microemulsion and sponge phases in thermal equilibrium. Phys Rev E (1996) 54(4):3811–31. doi:10.1103/physreve.54.3811

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Nonomura M, Ohta T. Decay rate of concentration fluctuations in microemulsions. J Chem Phys (1999) 110(15):7516–23. doi:10.1063/1.478654

CrossRef Full Text | Google Scholar

114. Holderer O, Frielinghaus H, Monkenbusch M, Klostermann M, Sottmann T, Richter D. Experimental determination of bending rigidity and saddle splay modulus in bicontinuous microemulsions. Soft Matter (2013) 9(7):2308–13. doi:10.1039/c2sm27449c

CrossRef Full Text | Google Scholar

115. Malo de Molina P, Herfurth C, Laschewsky A, Gradzielski M. Structure and dynamics of networks in mixtures of hydrophobically modified telechelic multiarm polymers and oil in water microemulsions. Langmuir (2012) 28(45):15994–6006. doi:10.1021/la303673a

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Hoffmann I, de Molina PM, Farago B, Falus P, Herfurth C, Laschewsky A, et al. Dynamics of microemulsions bridged with hydrophobically end-capped star polymers studied by neutron spin-echo. J Chem Phys (2014) 140(3):034902. doi:10.1063/1.4861894

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Klemmer HF, Frielinghaus H, Allgaier J, Ohl M, Holderer O. The effect of amphiphilic polymers with a continuous amphiphilicity profile on the membrane properties in a bicontinuous microemulsions studied by neutron scattering. In: Journal of Physics: conference series. Munich (Freising), GermanyIOP Publishing (2017) 012014.

CrossRef Full Text | Google Scholar

118. Endo H, Allgaier J, Gompper G, Jakobs B, Monkenbusch M, Richter D, et al. Membrane decoration by amphiphilic block copolymers in bicontinuous microemulsions. Phys Rev Lett (2000) 85(1):102–5. doi:10.1103/physrevlett.85.102

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Endo H, Mihailescu M, Monkenbusch M, Allgaier J, Gompper G, Richter D, et al. Effect of amphiphilic block copolymers on the structure and phase behavior of oil–water-surfactant mixtures. J Chem Phys (2001) 115(1):580–600. doi:10.1063/1.1377881

CrossRef Full Text | Google Scholar

120. Simon M, Gradzielski M, Hoffmann I. Dynamics in polyelectrolyte/microemulsion complexes. Nanoscale Adv (2020) 2(10):4722–7. doi:10.1039/d0na00336k

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Jalali-Jivan M, Garavand F, Jafari SM. Microemulsions as nano-reactors for the solubilization, separation, purification and encapsulation of bioactive compounds. Adv Colloid Interf Sci (2020) 283:102227. doi:10.1016/j.cis.2020.102227

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Sharma V, Hayes D, Gupta S, Urban V, O’Neill H, Pingali S, et al. Incorporation of melittin enhances interfacial fluidity of bicontinuous microemulsions. The J Phys Chem C (2019) 123(17):11197–206. doi:10.1021/acs.jpcc.9b00103

CrossRef Full Text | Google Scholar

123. Engelskirchen S, Wellert S, Holderer O, Frielinghaus H, Laupheimer M, Richter S, et al. Surfactant monolayer bending elasticity in lipase containing bicontinuous microemulsions. Front Chem (2021) 8:613388. doi:10.3389/fchem.2020.613388

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Khatouri M, Ahfir R, Lemaalam M, El Khaoui S, Derouiche A, Filali M. Effect of hydrophobically modified PEO polymers (PEO-dodecyl) on oil/water microemulsion properties: in vitro and in silico investigations. RSC Adv (2021) 11(12):7059–69. doi:10.1039/d0ra09804c

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Mulder M, Li XX, Nazim MM, Dalgliesh RM, Tian B, Buijse M, et al. Systematically quantifying oil–water microemulsion structures using (spin-echo) small angle neutron scattering. Colloids Surf A: Physicochemical Eng Aspects (2019) 575:166–75. doi:10.1016/j.colsurfa.2019.04.045

CrossRef Full Text | Google Scholar

126. Boeynaems S, Alberti S, Fawzi NL, Mittag T, Polymenidou M, Rousseau F, et al. Protein phase separation: a new phase in cell biology. Trends Cell Biology (2018) 28(6):420–35. doi:10.1016/j.tcb.2018.02.004

CrossRef Full Text | Google Scholar

127. Gastaldo IP, Rheinstädter HV, Rheinstädter MC. Perspective on the role of the physical properties of membranes in neurodegenerative and infectious diseases. Appl Phys Lett (2020) 117(4). doi:10.1063/5.0018709

CrossRef Full Text | Google Scholar

128. Alberti S. Phase separation in biology. Curr Biol (2017) 27(20):R1097–102. doi:10.1016/j.cub.2017.08.069

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Alberti S, Gladfelter A, Mittag T. Considerations and challenges in studying liquid-liquid phase separation and biomolecular condensates. Cell (2019) 176(3):419–34. doi:10.1016/j.cell.2018.12.035

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Dignon GL, Best RB, Mittal J. Biomolecular phase separation: from molecular driving forces to macroscopic properties. Annu Rev Phys Chem (2020) 71:53–75. doi:10.1146/annurev-physchem-071819-113553

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Wang T, Pang B, Li X, Wang Y, Huang C, Gong J, et al. MyNeutronDAQ: a general program for data acquisition of neutron scattering spectrometers at China Mianyang Research Reactor and on-line data-analysis. Softw Pract Experience (2021) 51(2):438–48. doi:10.1002/spe.2912

CrossRef Full Text | Google Scholar