Implementing the edge enhancement with vortex filter in both linear and nonlinear optics

The edge enhancement technique, as an effective method to represent the boundary of objects, plays an important role in image processing. Among them, the vortex filtering, which is based on the radial Hilbert transformation, has been paid great attention due to its ability to achieve isotropic and anisotropic edge enhancement. Recent years have witnessed a growing interest in the nonlinear vortex filter to skillfully realize the visualization of the object edge under invisible light irradiation. In this paper, we start from reviewing the achievements have been made with the vortex filtering technique in linear optics, and then discussed the recent processes of the scalar and vector vortex filter in nonlinear optics. We hope that the nonlinear optical vortex filter can motivate some promising applications in biological edge imaging with visible light-sensitive specimens.

1 Introduction

With the development of optical information processing technology, the edge enhancement technology has been widely used in many fields such as optical imaging [1–3], fingerprint detection [4, 5], astronomical observation [6, 7] and so on. Although several new types of edge enhancement algorithms [8–11] and technologies [12–15] emerge in academic and industry, the disadvantages of poor sensitivity, low efficiency and high price in the information collection of infrared band are still existed. Thus methods for edge enhancement in the infrared band are urgently needed.

Since the Hilbert transform was proposed [16–18], it has been widely used in the optical information processing to realize the edge enhancement of images. Furthermore, the spiral phase plate, a new type of diffraction optical element, has quickly attracted wide attention [19–21]. The appearance of the helical phase plate expands the one-dimensional Hilbert transform to the radial space, ensuring that the phase difference in any radial direction is π, so the vortex filtering of the image on the spatial spectrum plane can obtain the isotropic edge enhancement effect. By classifying the vortex generation method, the vortex filtering method can be divided into scalar vortex filtering and vector vortex filtering.

Scalar vortex filtering is usually based on spiral phase plates, which usually requires spatial light modulation to achieve edge enhancement effects. However, the additional diffraction light from the central singularity and sharp edge of the spiral phase plate will lead to the formation of side lobes. The side lobes increase the background noise of the image and reduce the contrast of the out-put image [22–24]. To solve this problem, researchers have proposed many methods to suppress the vortex filter side lobes, and obtained the isotropic edge enhancement effect with high contrast [25–28]. In practical optical imaging, if some local features of the edges need to be emphasized, anisotropic edge enhancement techniques should be used to highlight the required edge information. Referring anisotropic vortex phase distribution in scalar vortex filtering can produce directed edge enhancement in the output image. The anisotropic enhancement of the edge can be achieved by the fraction or off-axis vortex filter [29–31] or by introducing image dispersion into the vortex filter [32]. However, due to the broken symmetry of the filter and the existence of the sharp edge, the diffraction light produced by it seriously affects the quality of the image, and the shadow effect begins to appear in the output image [33, 34]. In addition, in the anisotropic edge enhancement experiment, it is necessary to constantly replace the phase information diagram loaded on the spatial light modulator, and the convenience of the edge enhancement technology is greatly restricted.

Meanwhile, vectorial vortex filtering based on polarization of the vortex filter is proposed to realize directional and non-directional edge enhancement [35, 36] through the polarization sensitive element of vector vortex to realize radial Hilbert transformation. Anisotropic edge enhancement can be achieved by inserting a polarizer before the output plane, and edge enhancement in different directions can be obtained by rotating the polarizer. However, in the methods above, due to the influence of the vortex filter, the background noise is difficult to be suppressed and the contrast of the image is greatly reduced due to the influence of the shadow effect. In other words, the vector filtering would be able to greatly improve the convenience, but with high background noise.

Edge detection is usually performed in light source irradiation in the visible or infrared bands. In nonlinear optics, to improve the drawback of the traditional infrared image detector, which is usually considered as low efficiency, low resolution and complex equipment shortcomings, researchers skillfully convert infrared image information to visible band. And the visible light detector with high efficiency, high resolution, simple equipment and low price is then used for image acquisition. As a result, it extends this technology to the field of quantum imaging extremely weak light. This review details the basic principles and improvement scheme of optical edge detection technology, and also the achievements of scalar and vector vortex filtering technology in the field of linear optics, and then discusses about the application of scalar and vector vortex filters in the field of nonlinear optics, together with finally summarizes the latest relevant research progress.

2 Vortex filtering and the hilbert transformation principle

Vortex filtering is mainly based on the Fourier transform effect of the lens. And with the help of the 4f imaging system, the edge contour information of the object is enhanced by extracting useful higher-order information and eliminating irrelevant base frequency information, so as to realize the edge enhancement. As annotated in Figure 1, $o\left(r_0,{\theta }_0\right)$, $O\left(\rho ,\varphi \right)$, $o\prime \left(r_1,{\theta }_1\right)$ represent the object plane, Fourier plane and image plane, respectively. The object plane and the Fourier plane are located in the left and right focal plane of the lens L₁, respectively. And the image plane is located in the right focal plane of the lens L₂, while the designed vortex filter $H\left(\rho ,\varphi \right)$ is placed in the Fourier plane. After the Fourier transform of the input image information $o\left(r_0,{\theta }_0\right)$, whose spectral information in the Fourier plane is modulated by the vortex filter, the output light field can be obtained by the inverse Fourier transform of the modulated information. The relationship between object plane and image plane can be expressed as follows:

$o\prime \left(r_1,{\theta }_1\right)=o\left(r_0,{\theta }_0\right)\times h\left(\rho ,\varphi \right)(1)$

where the point spread function $h\left(\rho ,\varphi \right)$ is the Fourier transform of the vortex filter $H\left(\rho ,\varphi \right)$.

FIGURE 1

FIGURE 1. Schematic diagram of the spiral phase contrast filtering.

Using the imaging system above, the Hilbert transformation can be completed only by placing the vortex filter in the spectral plane of the input optical field. According to the definition of the one-dimensional Hilbert transform, the input light field $o\left(x\right)$ will be convolved with $h\left(x\right)=-1/\pi x$, and the Hilbert transform of the input light field $o\left(x\right)$ can be expressed as [37]:

$H\left[o\left(x\right)\right]=o\left(x\right)\ast \frac{1}{\pi x}(2)$

Comparing with Eq. 1, it is clear that the Hilbert transform can actually be considered as a filtering system with the point diffusion function −1/πx, and the corresponding one-dimensional Hilbert transform filter is shown in Figure 2A. After the Hilbert transformation of the input light field, the amplitude of each frequency component in the frequency domain remains unchanged, but the positive frequency part has a +π/2 phase shift, and the negative frequency part has a −π/2 phase shift. Thereby producing a phase difference of π between the positive and negative frequency parts, and with this property, the input information through the Hilbert transform produces the effect of one-dimensional image edge enhancement. The one-dimensional Hilbert transform can only satisfy the edge enhancement effect in one direction, but in many practical applications, it is usually necessary to observe all the edge information of the input light field information.

FIGURE 2

FIGURE 2. (A) One-dimensional Hilbert transform filter. (B) Radial Hilbert transform filter. Gray levels represent different phase values in both subgraphs. Reproduced from [19] with permission from Optica Publishing Group.

In 2000, Davis et al. proposed radial Hilbert transformation to further expand the effect of edge enhancement in the one-dimensional direction to isotropic edge enhancement [19]. The radial Hilbert transform filter is shown in Figure 2B, and the transmittance function of the filter is:

$H\left(\rho ,\varphi \right)=circ\left(\rho /R_0\right)\exp \left(il\varphi \right)(3)$

Where $\left(\rho ,\varphi \right)$ represents the polar frame of the spectral plane, $circ\left(\rho /R_0\right)$ represents the circular hole filter with radius R₀, and l represents the number of topological charges of the vortex phase. This is equivalent to adding a vortex phase to the spectral plane, which is also called vortex filtering. And the phase difference of the spectrum of the input light field is π in any radial direction, thus achieving isotropic edge enhancement. The point spread function of the vortex filter is:

$\begin{array}{cc}\hfill h\left(r_1,{\theta }_1\right)& =\frac{2\pi }{\lambda f}\exp \left(il{\theta }_1\right){\int }_0^{R_0}{J}_1\left(\frac{2\pi \rho r_1}{\lambda f_2}\right)d\rho \hfill \\ \hfill & =-i\frac{\pi R_0}{2r_1}\left[J_1\left(x\right)H_0\left(x\right)-J_0\left(x\right)H_1\left(x\right)\right]\exp \left(il{\theta }_1\right)\hfill \end{array}(4)$

where $\left(r_1,{\theta }_1\right)$ shows the coordinates of the image plane, while x = 2ρR₀/λf, λ is the wavelength of the incident light, and f represents the focal length of the Fourier lens. J₀ and J₁ are first class Bessel functions of zero and first order, respectively, while H₀ and H₁ are Struve functions of zero and first order, respectively. As can be seen from the point spread function, one can see that the amplitude of the central singularity is 0, so the low frequency information of the input light field can be effectively suppressed, and the distribution of the amplitude in all directions of the main lobe is relatively uniform, so the vortex filtering can produce isotropic edge enhancement. But the presence of many lateral lobes around the main lobe, which are the direct cause of edge-enhanced background noise, leading to a decrease in the contrast of the output image.

3 Image edge enhancement based on scalar vortex filtering

In optical imaging, the vortex filtering reduces the image contrast and increases the diffraction noise due to the presence of the side lobe. The idea of vortex filter side lobe inhibition was first proposed in 2004 by [38]. Further, through the designed annular spiral phase plate [39], the Laguerre Gaussian amplitude modulated spiral phase plate [40], the Bessel filter [41, 42] and the Airy vortex filter designed based on the Airy amplitude modulation spiral phase plate [43], the background diffraction noise is reduced and the image contrast is improved by suppressing the side lobes.

The methods above can be summarized as correcting the transmittance function of the filter to eliminate the background noise of the output image. Taking the Laguerre Gaussian vortex filter as an example [40], the transmittance function of the corresponding filter is:

$H\left(\rho ,\varphi \right)=\frac{\rho }{\omega }\exp \left[-{\left(\frac{\rho }{\omega }\right)}^2\right]circ\left(\frac{\rho }{R_0}\right)\exp \left(-il\varphi \right)(5)$

Where $\left(\rho /\omega \right)\cdot \exp \left[-{\left(\rho /\omega \right)}^2\right]$ is the Laguerre Gaussian term, the amplitude correction of the conventional vortex filter. Otherwise, ω represents the beam waist radius and R₀ represents the aperture size.

This vortex filter is applied, with the help of the Laguerre Gaussian amplitude modulation, to reduce the diffraction of the central singularity on the incident light. The holograms of the spiral phase plate vortex filter and the Laguerre Gaussian vortex filter are given in Figures 3A, B. Compared to Figure 3A, the filter center amplitude in Figure 3B is 0 and steps to 1 along the radial direction. The diffraction efficiency of this hologram in the positive level direction is reduced, which plays an important role in suppressing the side lobe of the traditional spiral phase plate vortex filter. Not only is the low frequency part of the input image is eliminated, but also the diffraction noise generated by the central singularity to the incident light is successfully reduced.

FIGURE 3

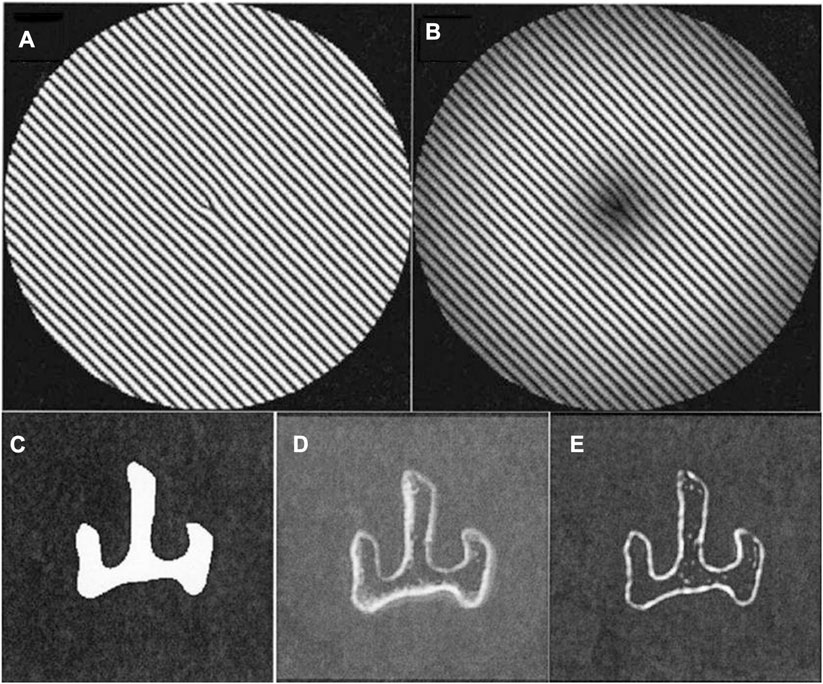
FIGURE 3. (A) Phase hologram of conventional vortex filters (B) Phase hologram of the vortex filters with Laguerre Gaussian amplitude modulation. (C) Image of the input object. (D) The output image after the spiral phase plate vortex filtering. (E) The output image after the Laguerre Gaussian vortex filtering. Reproduced from [40] with permission from Optica Publishing Group.

The edge enhancement effect of this filter and of the traditional vortex filter are shown in Figures 3C–E. Figure 3A shows the input image with the Chinese character “mountain,” Figure 3D is the edge-enhanced output image of the spiral phase plate vortex filter while Figure 3E is the edge-enhanced output image of the Laguerre Gaussian vortex filter. Comparing the two edge-enhanced output images, one can find that both of the filters can achieve edge enhancement, but Figure 3D has strong background noise and the enhanced edges are rough. While the image edge in Figure 3E is much more sharp, clearly successful in reducing the background noise and improving the contrast of the image.

However, in practice, when some local edge information needs to be highlighted, the anisotropic edge enhancement technique becomes urgently needed. To meet this need, fractional vortex filtering was implemented using fractional spiral phase plates by [44]. When the number of topological charges is fractional, the radial symmetry of the optical field is broken, resulting in a controllable edge dislocation. Thus the extent and direction of its edge enhancement can be changed by controlling the magnitude and initial phase of the fractional order. Moreover, by simulating the point spread function of the fractional vortex filtering, the direction of the anisotropic edge enhancement can be seen directly, as shown in Figure 4.

FIGURE 4

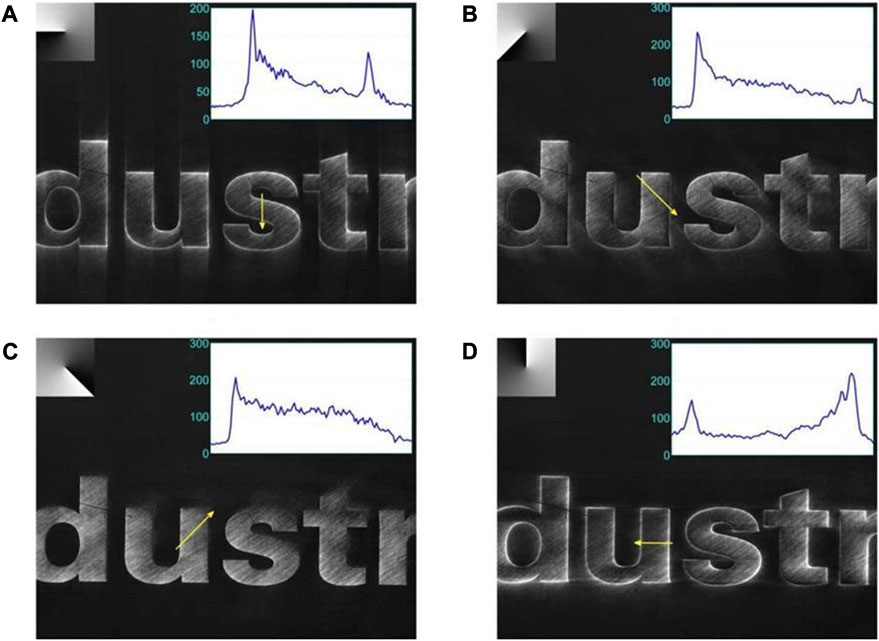
FIGURE 4. Experimental results for fractional vortex filtering [44]. The values of the parameter $\left(p,\theta \right)$ are (A) $\left(0.8,\pi \right)$. (B) $\left(0.6,5\pi /4\right)$. (C) $\left(0.4,7\pi /4\right)$. (D) $\left(0.9,\pi /2\right)$. The upper-left corners of the figures show the various stages of the spiral phase plate, while the upper-right corners show the cross-section view of the output patterns cross section along the direction of the arrow. Reproduced from [44] with permission from Optica Publishing Group

The transmittance function of the fractional vortex filter can be written as:

$H\left(\rho ,\varphi \right)=\exp \left[ip\left(\theta +\varphi \right)\right](6)$

In Figure 4, the left edge is enhanced when maintaining the initial phase p < 1, and when 1 < p < 2, the right edge is enhanced, but in most cases, the shadow effects emerge and the images are relief. By comparing the experimental results, it can be found that high contrast edge enhancement can be obtained when 0.5 < p < 1. In the same year, they further demonstrated that even by using incoherent LED light illumination of biological samples, fractional vortex filtering can still make the phase object present a relief effect [45]. Furthermore, fractional spiral wave bands were used to achieve anisotropic edge enhancement of phase-type objects under femto-second laser illumination by [46].

In 2015, Wang et al studied the gradually formed edge enhancement of pure phase objects by introducing fractional vortex phase plates [47]. In the experiment, two spatial light modulators are adopted, one for preparing pure phase objects while the other for loading a dynamic vortex filter with a fractional topological charge Q. As shown in Figures 5A–L, a complete reversal of the edge and background brightness is observed by gradually varying the value of the fraction Q. From the perspective of the orbital angular momentum eigenstates, the fractional vortex can be expressed as follows:

$\exp \left(iQ\phi \right)={\displaystyle \sum _l}{A}_l\exp \left(il\phi \right)(7)$

FIGURE 5

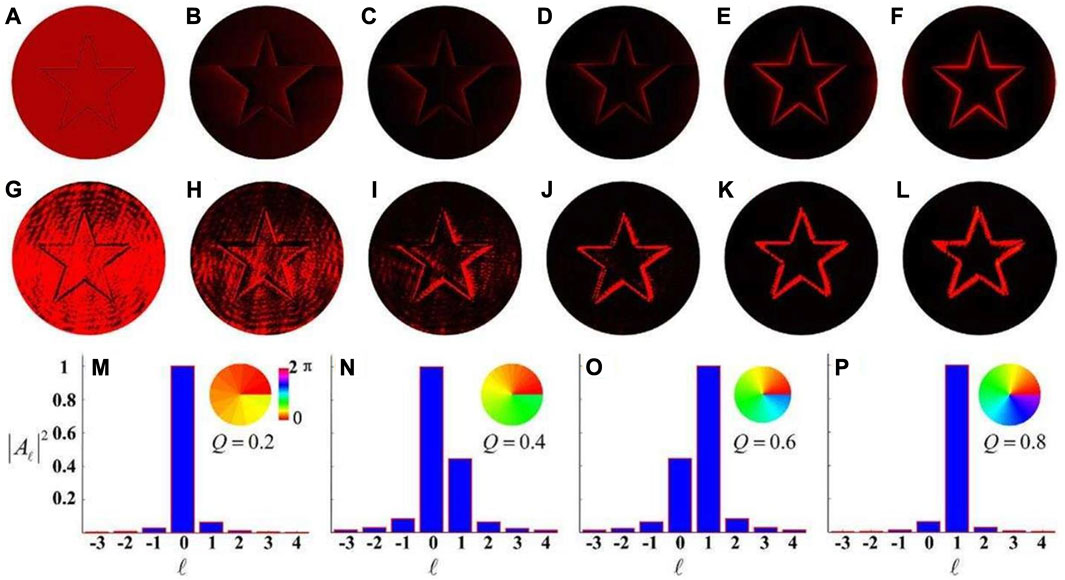
FIGURE 5. (A–L): Simulation and experimental results when topological charge values are (A, G): Q =0, (B, H): Q =0.2, (C, I): Q =0.4, (D, J): Q =0.6, (E, K): Q =0.8, (F, L): Q =1. (M–P): Orbital angular momentum spectra for spiral phase plate filters: (M) Q =0.2, (N) Q =0.4, (O) Q =0.6, (P) Q =0.8. Reproduced from [47] licensed CC-BY-4.0.

The equation above shows that the fractional vortices can represent a linear superposition of a limited number of different integer orders of vortices, where A_l represents the weight occupied by the topological charge of different integers. As shown in Figures 5M–P, based on the orbital angular momentum spectrum of the fractional spiral phase plate, the output image of the fractional vortex filtering can be seen as a coherent superposition of all possible images independently generated by integer order vortex filtering. This method is further extended to the field of partial coherent light by combining the partially coherent light source with vortex half-wave retarder, making it possible to produce gradual imaging system [48].

In addition to the fractional vortex being able to arbitrarily control the direction and amplitude of edge enhancement, another off-axis vortex filtering method was also proposed by [44]. The common point of both methods is breaking the symmetry of the traditional vortex filtering technique, the former via controllable edge dislocation and the latter via radial displacement. The transmitted function of the off-axis vortex filter is:

$H\left(\rho ,\varphi \right)=\frac{\rho \exp \left(i\varphi \right)+{\rho }_0\exp \left(i\theta \right)}{\sqrt{{\rho }^2+{\rho }_0^2+2\rho {\rho }_0\cos \left(\varphi -\theta \right)}}(8)$

where θ represents the direction of radial displacement and ρ₀ indicates the distance of the displacement.

As shown in Figure 6, the anisotropic edge enhancement effect in each direction can be obtained by setting different angle parameters θ and the displacement parameters ρ₀, respectively, among which it is noteworthy that the angle in the direction where the vortex is located needs to lag behind the displacement direction π/2. Similarly, in 2013, Sharma et al. successfully introduced a controllable shift into the traditional vortex filter by introducing anisotropic function [49]. In addition, edges of images under femtosecond laser illumination are also enhanced using off-axis spiral bands proposed by [46].

FIGURE 6

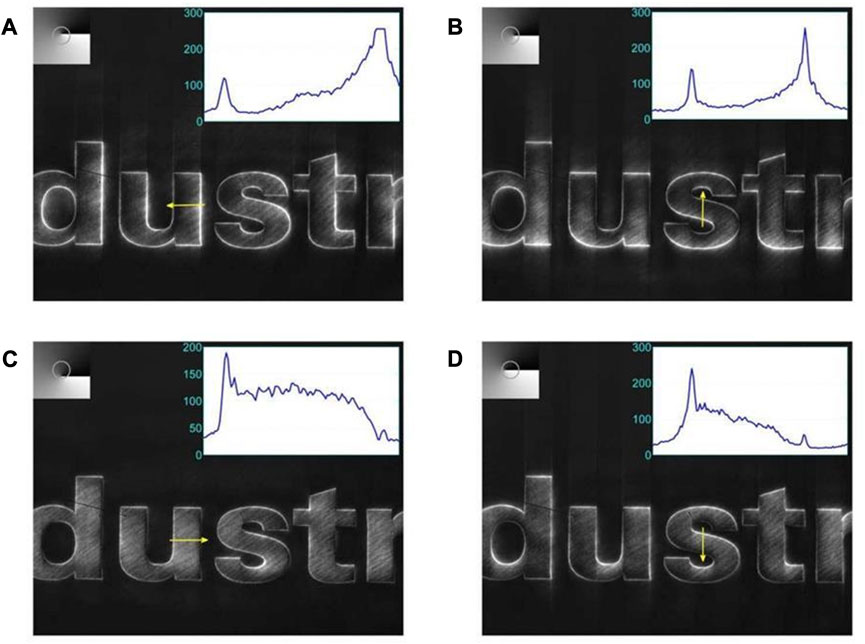
FIGURE 6. Experimental results for the off-axis vortex filtering [44]. The values of the parameter $\left({\rho }_0,\theta \right)$ are (A) $\left(3\delta ,\pi /2\right)$. (B) $\left(6\delta ,0\right)$. (C) $\left(11\delta ,3\pi /2\right)$. (D) $\left(10\delta ,\pi \right)$. The upper-left corners of the figures show the various stages of the spiral phase plate, while the upper-right corners show the cross-section view of the output patterns cross section along the direction of the arrow. Reproduced from [44] with permission from Optica Publishing Group.

However, the two anisotropic edge enhancement methods above break the symmetry of the traditional vortex filtering, and the output image will inevitably produce the shadow effect, and a part of the low-frequency information will reappear on the output image. Furthermore, the superposition filter proposed by Sharma et al. avoids this situation, achieving edge enhancement in different directions without breaking symmetry by combining positive and negative vortex filtering, [50]. This feature makes it have a broad application prospect in fingerprint recognition, with a better contrast than in the one-dimensional Hilbert transformation.

Further, this technology has been widely expanded and applied. For example, spiral phase filtering technology is combined with Fourier single-pixel phase imaging to extend optical edge detection to the single-pixel level [51]. In addition, this technology is combined with the metasurface to enable not only dynamic switching between edge-enhancd imaging and bright-field imaging [12, 13] but also differential high-contrast imaging across the whole visible spectrum [52]. At the same time, recent studies have also been conducted to achieve three-dimensional spiral imaging with high resolution and low background noise based on this method [53].

4 Image edge enhancement based on vector vortex filtering

Compared with the amplitude and phase modulation of the scalar vortex, the vector vortex adds a new modulation degree of freedom–polarization, which has a broader application prospect in information transmission [54–59], focal field regulation [60–67] and particle capture [68–71]. Similarly, on the image edge enhancement, achieving the anisotropic edge enhancement effect requires breaking the symmetry of the vortex filter, which will cause the shadow effect and thus affect the image quality. Compared to scalar vortex, vector vortex is more convenient to achieve isotropic and anisotropic conversion, and most importantly, part of the shadow can be eliminated through the polarizer. Vector light beams can be generated by orthogonal base vector superposition [72–77] or geometric phase devices [78–81]. In the edge enhancement, geometric devices such as Q-plate [82] and S wave plate [35] are usually used. Similar to the scalar vortex, the vector vortex with a topological charge of unit can realize the radial Hilbert transformation. Therefore, the geometric phase device can be filtered on the frequency spectrum plane of the 4f system. In 2013, Han et al. analyzed the point spread function as a spatial filter of the typical 4f optical image processing system, and found that the point diffusion function was vectorial. It is further shown that this optical system can be used for radially symmetric Hilbert transformation to achieve edge enhancement of images [83]. This indicates that the vector vortex can achieve isotropic and anisotropic edge enhancement in co-and off-axis, respectively.

In 2017, Sharma et al. adopted the S-wave plate as a filter in the object spectrum plane to achieve the effect of edge enhancement [35]. The S-wave plate is a polarization-sensitive element that can turn the linear polarized light into radial or angular polarized light, from which the isotropic edge enhancement can be realized. Furthermore, if it is combined with the polarizer in front of the charge-coupled device, the polarization state perpendicular to the direction of the polarizer can be eliminated, and thus the directional edge enhancement effect is obtained. In the same year, similar experimental results are also obtained with the help of Q-plate proposed by Ram et al [36]. In 2018, the negative Poincare Hoppford index filter was further proposed, which realized the negative index filtering effect for the first time, and obtained the anisotropic edge enhancement effect by making the vector vortex filter off-center [84].

When the incident light is linearly polarized, which can be written as $L_{in}={\left[\cos \theta ,\sin \theta \right]}^T$, the output light field is vector-selective, enabling isotropic edge enhancement. The Jones matrix of the S-wave plate can be expressed as:

$H\left(\rho ,\varphi \right)=\left[\begin{array}{cc}\hfill \cos \varphi \hfill & \hfill \sin \varphi \hfill \\ \hfill \sin \varphi \hfill & \hfill -\cos \varphi \hfill \end{array}\right](9)$

The S-wave plate as a filter provides the vector radial Hilbert transformation for the input light field, so the corresponding vector point spread function can be expressed as:

$h\left(r,\phi \right)=-\frac{2\pi A}{\lambda f}\left[\begin{array}{c}\hfill \cos \left(\phi -\theta \right)\hfill \\ \hfill \sin \left(\phi -\theta \right)\hfill \end{array}\right]{\int }_0^R{J}_1\left(\frac{2\pi }{\lambda f}r\rho \right)\rho d\rho (10)$

Where λ is the wavelength of the incident light, f is the focal length of the lens, A is the constant factor, R is the radius of the S-wave plate, and J₁ is the first order Bessel function of the first class. The ${\left[\cos \left(\phi -\theta \right),\sin \left(\phi -\theta \right)\right]}^T$ term fully shows that the point spread function is vector selective, that is, the spatially heterogeneous polarization distribution. As shown in Figure 7, an edge enhancement in any polarization direction is obtained by inserting and rotating the polarizer in front of the recording plane, which is currently impossible in scalar vortices.

FIGURE 7

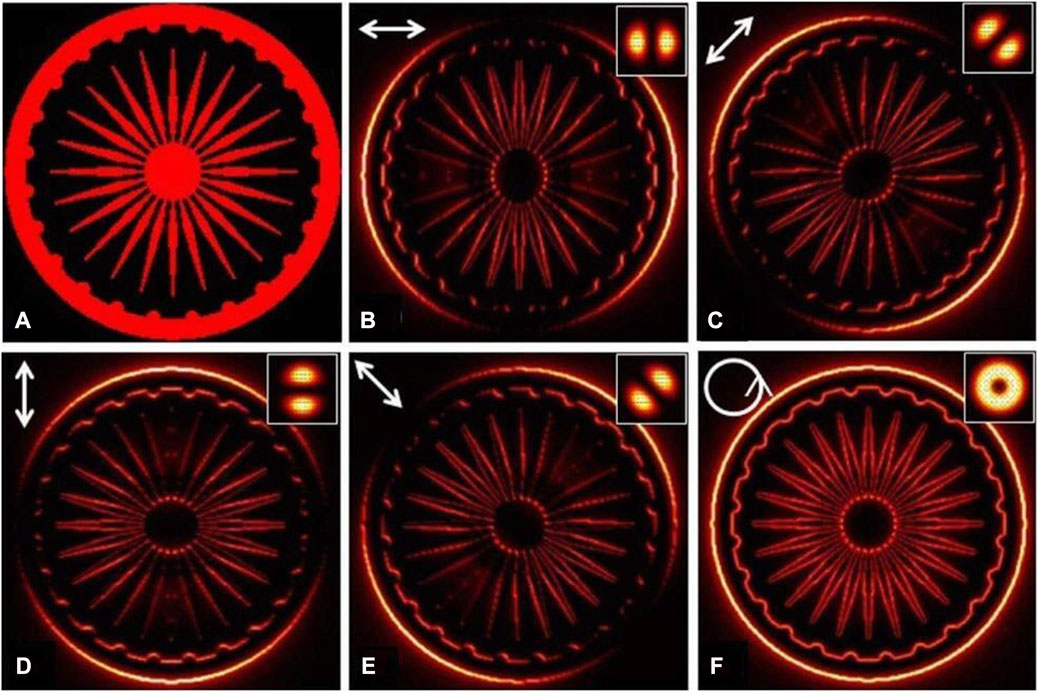
FIGURE 7. Simulation results for the input object shown in (A). The output edge-enhanced images are shown in (B–F). The input state of polarization, direction, and point spread function profiles are shown in each frame. Reproduced from [84] with permission from Optica Publishing Group.

When the incident beam is a circularly polarized light $L_{in}={\left[1,\pm i\right]}^T$, the two orthogonal components of the circularly polarized beam have equal magnitude as well as a phase difference of π/2. At this point, the point spread function of the filter optical system can be expressed as:

$h\left(r,\phi \right)=-\frac{2\pi A}{\lambda f}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill \mp i\hfill \end{array}\right]e^{\pm i\phi }{\int }_0^R{J}_1\left(\frac{2\pi }{\lambda f}r\rho \right)\rho d\rho (11)$

It shows from the above expression that the point spread function of this system has a scalar field distribution. For the polarization state of the incident light is circular polarization, the S-wave plate shows the scalar of the radial Hilbert transformation, namely, the scalar vortex filter. At this point, the polarizer is not selective for the output light field.

In 2016, Zhang et al. used the S-wave as off-axis filter to achieve anisotropic edge enhancement [85]. Off-axis vector vortex will produce serious shadow effect, but unlike off-axis scalar vortex, due to the existence of polarization selection. If the direction of the axis of the polarizer is orthogonal to the direction of the vector vortex offset, can eliminate most of the internal shadow, and realize the selective direction of high contrast edge enhancement effect. However, when the direction of the offset and the direction of the optical axis of the polarizer are consistent, the shadow effect will seriously affect the effect of the output image, and even the enhanced edge will become difficult to identify.

Similarly, the vector radial Hilbert transform can be completed when the linearly polarized light radiates the Q-plate with the value of Q is 0.5. If the central singularity of the vector vortex is off-axis, the anisotropic edge enhancement effect will thus occur, and the corresponding vector point diffusion function can be expressed as:

$\begin{array}{cc}\hfill h\left(r,\phi \right)& =-\frac{A}{\lambda f}\left[\begin{array}{c}\hfill \cos \left(2q\phi -\beta \right)\hfill \\ \hfill \sin \left(2q\phi -\beta \right)\hfill \end{array}\right]{\int }_0^R\rho J_1\left(\frac{2\pi \rho r}{\lambda f}\right)\hfill \\ \hfill & \times B\left(\rho ;{\rho }_0,{\theta }_0\right)\rho d\rho =-\frac{iA}{\lambda f}{\rho }_0\left[\begin{array}{c}\hfill \cos \left({\theta }_0-\beta \right)\hfill \\ \hfill \sin \left({\theta }_0-\beta \right)\hfill \end{array}\right]\hfill \\ \hfill & \times {\int }_0^R{J}_0\left(\frac{2\pi \rho r}{\lambda f}\right)B\left(\rho ;{\rho }_0,{\theta }_0\right)\rho d\rho \hfill \end{array}(12)$

where $h\left(r,\phi \right)$ is essentially a combination between the vector beam and linear polarized light, While the breaking of vector vortex symmetry is the main cause of non-edge shading. From the expression above, the non-edge shadow is a linear polarization field, whose direction is $\left(\theta -\beta \right)$ relative to the x-axis. Thus, the shading of the edge can be removed by using a polarizer with the polarization direction of $\left(\theta -\beta +\pi /2\right)$. Therefore, although edge enhancement can be performed very effectively with devices like silicon charge-coupled devices in the visible light field, due to the low detection efficiency and large dark current of existing infrared detection technologies, the application of the edge enhancement in direct infrared imaging is limited. Therefore, the introduction of nonlinear edge enhancement, that is, the conversion of infrared light into the visible light region solves this problem.

In addition to the methods above, several methods are also proposed to achieve anisotropic edge enhancement with shadow-effect-free and low background noise, such as Bessel-like composite vortex filter [86], specially designed superposed spiral phase plate filter [87]. Interestingly, in addition to the direction of enhancement, a recent study has used the higher-order spiral Fresnel incoherent correlation holography system to achieve the edge enhancement with tunable width and discovered double edge enhancement for the first time [88].

5 Image edge enhancement in nonlinear fields

In the field of nonlinear optics, the traditional infrared image detector is low efficiency, low resolution and the corresponding equipment is generally complex and expensive. Usually, the infrared image information is converted to the visible light band, and then the visible light detector with high efficiency, high resolution, simple equipment and low price is used for image acquisition. In 2018, Qiu et al. multiplied the frequency spectrum of the measured objects and a beam of OAM light based on the frequency doubling effect of nonlinear crystals in Fourier plane [29]. Thus, the traditional SPC technique was successfully extended to the field of nonlinear optics, which experimentally realizes the visualization of phase object edge enhancement under invisible light irradiation, as shown in Figures 8A, B. The expression for the output light field can be written as:

$E_{\mathit{out}}\left(r,\varphi ,{\lambda }_{\mathit{vis}}\right)\propto E_{in}\left(r,\varphi ,{\lambda }_{\mathit{invis}}\right)\ast \mathcal{F}\left[F\left(\rho ,\phi ,{\lambda }_{\mathit{invis}}\right)\right](13)$

FIGURE 8

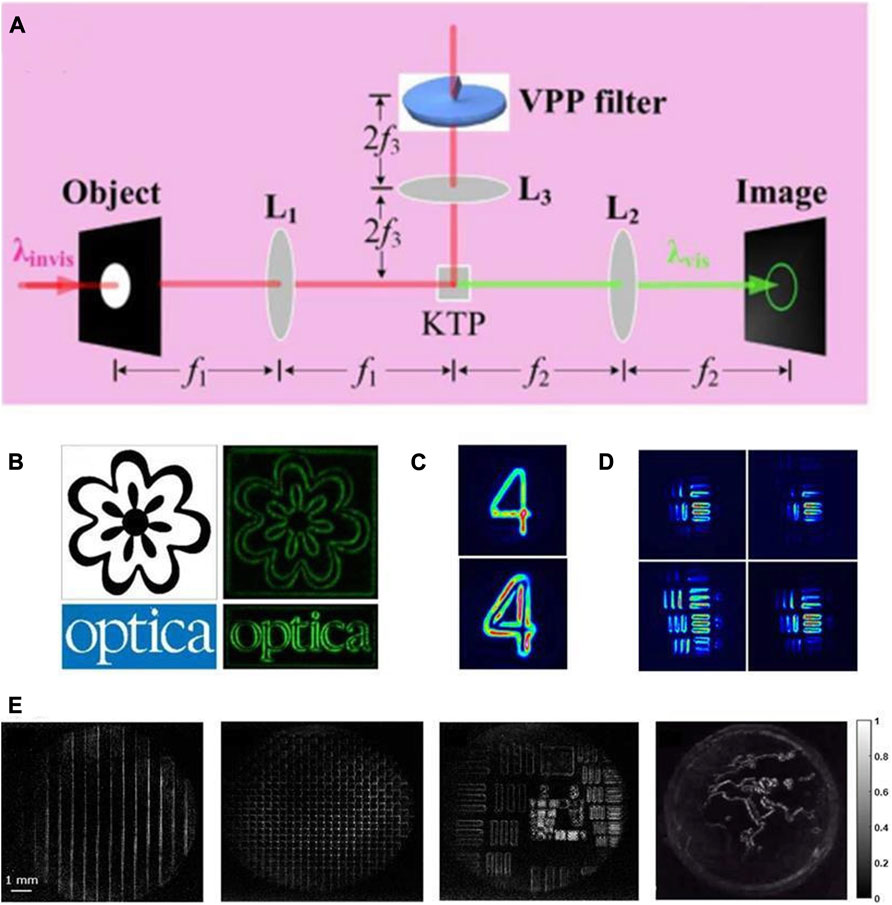
FIGURE 8. Spiral phase contrast up-conversion imaging based on second-order nonlinear processes. (A) Schematic diagram of the nonlinear spiral phase contrast imaging [29]; (B) experimental results of nonlinear edge enhancement of phase and intensity objects; (C) experimental results of nonlinear edge enhancement of intensity objects [95]; (D) different field of view changes of edge enhanced images by adjusting crystal temperature for changing phase mismatch [95]; (E) Large field of view upconverted images using a broadband illuminated SLM with binary 0-π phase objects [90]. (A,B) Reproduced from [29] with permission from Optica Publishing Group. (C,D) Reproduced from [95] with permission from American Physical Society. (E) Reproduced from [95] with permission from American Physical Society.

where with the constant coefficient trivially ignored, one can see from Eq. 13 that the invisible illumination has been apparently converted into a visible light signal. Later, in 2019, Liu et al. similarly combined quasi-phase matching with spiral phase filtering techniques [89]. Using a similar experimental setup, Liu et al. successfully extracted and converted the edge information of an infrared image with a wavelength of 1,559.5 nm into a visible 632.5 nm presentation with the help of a specific nonlinear crystal together with a near-infrared vortex beam of 1064 nm. This approach was further generalized, and in 2020, Junaid et al. achieved “video frame rate” (10 Hz in their demo) edge-enhanced imaging of a dynamic object [90], as shown in Figure 8E. In 2019, Liu et al. combined the previous quasi-phase matching regulation of the angle technology of spot field [91] and the nonlinear frequency change technology of structured light field [92–94] to realize the final image conversion to 525 nm edge detection under 1550 nm irradiation together with the vortex pump beam under 792 nm [95]. At the same time, by precisely regulating the crystal temperature, that is, changing the nonlinear phase matching condition, the maximum 2.1 times of the imaging field regulation range was achieved, as shown in Figure 8D. Compared with other nonlinear image field of view regulation, the regulation mode, such as the use of wide spectrum light source [96], double wavelength illumination [97], crystal temperature gradient [98], accurate rotation angle of the crystal [99], has the advantages of more simple and convenient operation and low requirements for light source. Consequently, with the help of these researches, this scheme was extended to the up-conversion edge enhancement.

Further in 2020, we further combined the nonlinear edge enhancement technology with the vector vortex filtering, realizing the direction-selective edge enhancement for the first time in the nonlinear field, as shown in Figure 9 [100]. In this case, the filtered image is expressed as follows:

$\begin{array}{c}\hfill E_{\mathit{out}}^H\left(r,\varphi ,{\lambda }_{\mathit{vis}}\right)\propto E_{in}^V\left(r,\varphi ,{\lambda }_{\mathit{invis}}\right)\otimes \mathcal{F}\left[T^V\left(r,\varphi ,{\lambda }_{\mathit{invis}}\right)\right]\\ \hfill E_{\mathit{out}}^V\left(r,\varphi ,{\lambda }_{\mathit{vis}}\right)\propto E_{in}^H\left(r,\varphi ,{\lambda }_{\mathit{invis}}\right)\otimes \mathcal{F}\left[T^H\left(r,\varphi ,{\lambda }_{\mathit{invis}}\right)\right]\end{array}(14)$

FIGURE 9

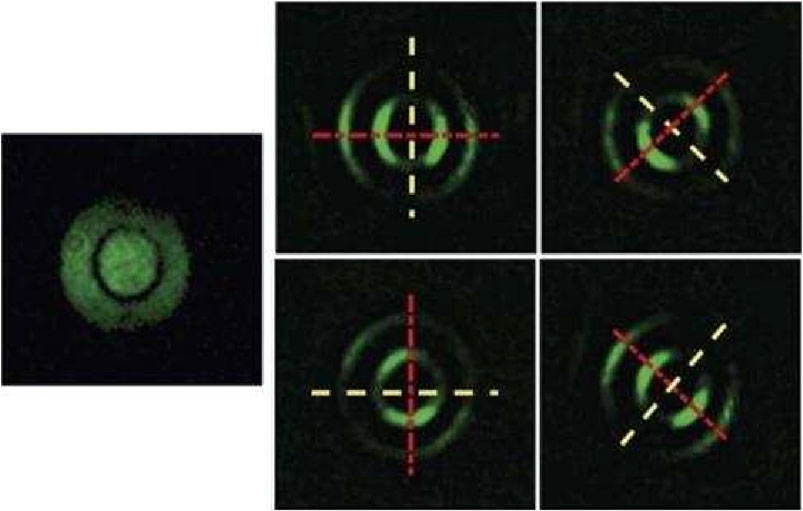
FIGURE 9. Experimental results of directional selective nonlinear edge enhancement of phase objects. Reproduced from [100] with permission from Optica Publishing Group.

From Eq. 13, one can see not only that the characteristics of the wavelength transformation of nonlinear vortex filtering, but also the output light field is vectorial, so the selectivity of the output light field edge can be realized by adjusting the polarization state of the input light field. This technology demonstrates the parallel image processing method of edge enhancement and field of view enhancement, which also has the advantages of low cost over conventional infrared detectors.

At the same time, the introduction of nonlinear crystals, in addition to promoting edge enhancement to the field of harmony frequency, in 2022, Zeng et al. combined it with optical parametric amplification [101]. They successfully realized the 1064 nm spiral phase-contrast idler imaging of biological tissues (frog egg cells and onion epidermis) with a spatial resolution at several microns level and a superior imaging contrast to both the traditional bright- or dark-field imaging under a weak illumination as shown in Figure 10A. Then, the edge augmentation technology is further promoted in the field of quantum imaging. In 2016, for the first time, edge enhancement is combined with ghost imaging, using position and orbital angular momentum (OAM) correlations between the signal and idler photons generated in the down-conversion process to obtain ghost images of a phase object. By using a non-local OAM phase filter, the image exhibits isotropic edge enhancement [102]. This imaging technique is the first to demonstrate a full-field phase contrast imaging system with non-local edge enhancement and allows phase objects to be imaged using fewer photons than standard phase contrast imaging techniques, which is shown in Figure 10B. Furthermore, in 2020, Liu et al. introduced and experimentally demonstrated a real-time (0.5 Hz) quantum edge-enhanced imaging method that combines helical phase contrast technology and predicted single-photon imaging [103]. Compared to direct ghost imaging, thry claim to achieve higher brightness and compact fiber optic delay instead of free space delay as shown in Figure 10C.

FIGURE 10

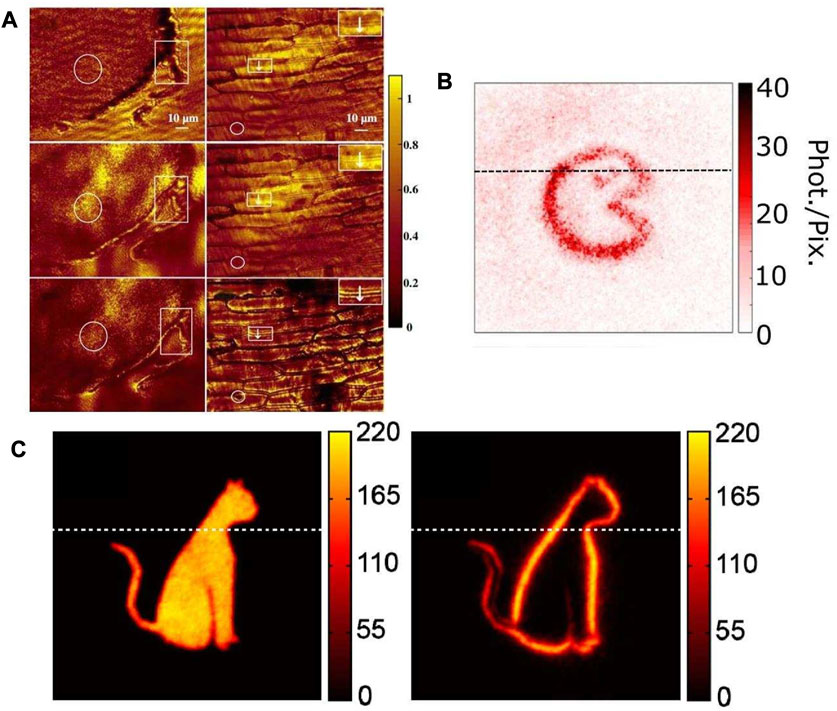
FIGURE 10. Application of edge enhancement in nonlinear areas. (A) Edge enhancement and parametric magnification are combined to achieve edge characterization on biological dark-field imaging [101]. (B) The results of edge enhancement under the ghost imaging framework [102]. (C) The results for the original image, the edge enhanced image captured by the ICCD in sequence [103]. (A) Reproduced from [101] with permission from Optica Publishing Group. (B) Reproduced from [102] licensed CC-BY-3.0. (C) Reproduced from [103] with permission from Optica Publishing Group.

In addition, metasurfaces still play an important role. Instead of focusing on the wavelength conversion, polarized entangled photon pairs are used as the light source, which are combined with high-efficiency metasurfaces to achieve switchable optical edge enhancement [104]. It is also confirmed that entangled photon illumination has a higher signal-to-noise ratio than direct single-photon illumination under low-light field illumination. In the same year, researchers also achieved non-local edge enhancement using incoherent thermal light, that is, the object and the spiral phase filter were placed non-locally in two separated light beams, achieving edge-enhanced ghost imaging through second-order intensity correlation measurement [105].

Therefore, this technology has important potential applications in the fields of biological imaging [106], microscopy with light-sensitive specimens [107], and pattern recognition and infrared remote sensing [108]. Achieving strong photon-photon interactions with more efficient protocols may even provide meaningful techniques for infrared SPC imaging at a minority photon level. It is believed that this technique can also be easily extended to other nonlinear optical processes, for example, sum frequency generation, difference frequency generation [95], and four-wave mixing to meet different needs.

6 Conclusion

With the development of image edge enhancement, the traditional vortex filter can not meet the needs, so numbers of new vortex filters have been applied in the edge enhancement technology in recent years. The scalar vortex achieves edge enhancement mainly through the modulation of amplitude and phase, while by introducing the polarization degree of freedom, the vector vortex can not only produce similar experimental results such as the scalar vortex, but also realize the directional edge enhancement effect combined with the polarizer because the polarization vector is selective. In addition, this technique is extended to the nonlinear field, realizing the wavelength transformation of the optical field and solving the shortcomings of infrared detectors. By adopting a more effective scheme to enable strong photon-photon interaction, the edge enhancement could provide a meaningful technique for infrared spatial filtering at the few-photon level, even the single photon level [109]. Moreover, this easy-to-implement filtering technique might also be integrated into the microscope to provide additional functions and can be readily extended to some barely mentioned nonlinear optical processes, such as four-wave mixing and so on, to meet different demands.

Author contributions

DX: Writing–review and editing, Writing–original draft, Data curation. WZ: Conceptualization, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (12374280), the Natural Science Foundation of Fujian Province of China (2023J01007), the Fundamental Research Funds for the Central Universities at Xiamen University (20720220030).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ferrari JA, Flores JL, Perciante CD, Frins E. Edge enhancement and image equalization by unsharp masking using self-adaptive photochromic filters. Appl Opt (2009) 48:3570–9. doi:10.1364/AO.48.003570

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Mazzaferri J, Ledesma S. Rotation invariant real-time optical edge detector. Opt Commun (2007) 272:367–76. doi:10.1016/j.optcom.2006.11.050

CrossRef Full Text | Google Scholar

3. Perciante CD, Ferrari JA. Visualization of two-dimensional phase gradients by subtraction of a reference periodic pattern. Appl Opt (2000) 39:2081–3. doi:10.1364/AO.39.002081

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Xue J, Liu J, guang Liu Z. An enhancement algorithm for low quality fingerprint image based on edge filter and Gabor filter. In: J Puschell, H mei Gong, Y Cai, J Lu, and J dong Fei, editors. International symposium on photoelectronic detection and imaging 2009: Advances in infrared imaging and applications. Bellingham, Washington: International Society for Optics and Photonics (2009). doi:10.1117/12.833498

CrossRef Full Text | Google Scholar

5. Jiang X. Research on the key technique of image preprocessing in the fingerprint identification. WRI World Congress Softw Eng (2009) 2:391–4. doi:10.1109/WCSE.2009.93

CrossRef Full Text | Google Scholar

6. Foo G, Palacios DM, Swartzlander GA. Optical vortex coronagraph. Opt Lett (2005) 30:3308–10. doi:10.1364/OL.30.003308

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mawet D, Serabyn E, Wallace JK, Pueyo L. Improved high-contrast imaging with on-axis telescopes using a multistage vortex coronagraph. Opt Lett (2011) 36:1506–8. doi:10.1364/OL.36.001506

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Muminov B, Vuong LT. Fourier optical preprocessing in lieu of deep learning. Optica (2020) 7:1079–88. doi:10.1364/OPTICA.397707

CrossRef Full Text | Google Scholar

9. Chung K-L, Pei S-C, Pan Y-L, Hsu W-L, Huang Y-H, Yang W-N, et al. A gradient-based adaptive error diffusion method with edge enhancement. Expert Syst Appl (2011) 38:1591–601. doi:10.1016/j.eswa.2010.07.079

CrossRef Full Text | Google Scholar

10. Rose RA, Govindaraju S. Hardware based algorithm for chaotic and edge enhanced error diffusion (2013).

Google Scholar

11. Lai JZ, Chen C-C. Algorithms of halftoning color images with edge enhancement. J Vis Commun Image Representation (2003) 14:389–404. doi:10.1016/S1047-3203(03)00041-5

CrossRef Full Text | Google Scholar

12. Yang H, Xie Z, He H, Zhang Q, Li J, Zhang Y, et al. Switchable imaging between edge-enhanced and bright-field based on a phase-change metasurface. Opt Lett (2021) 46:3741–4. doi:10.1364/OL.428870

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Huo P, Zhang C, Zhu W, Liu M, Zhang S, Zhang S, et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett (2020) 20:2791–8. doi:10.1021/acs.nanolett.0c00471

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ferrari JA, Flores JL, Ayubi GA, Di Martino JM, Perciante CD, Frins E. Orientation-selective edge enhancement of phase objects. Opt Commun (2019) 434:44–8. doi:10.1016/j.optcom.2018.10.031

CrossRef Full Text | Google Scholar

15. Chaira T. A rank ordered filter for medical image edge enhancement and detection using intuitionistic fuzzy set. Appl Soft Comput (2012) 12:1259–66. doi:10.1016/j.asoc.2011.12.011

CrossRef Full Text | Google Scholar

16. Lohmann AW, Mendlovic D, Zalevsky Z. Fractional hilbert transform. Opt Lett (1996) 21:281–3. doi:10.1364/OL.21.000281

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Davis JA, McNamara DE, Cottrell DM. Analysis of the fractional hilbert transform. Appl Opt (1998) 37:6911–3. doi:10.1364/AO.37.006911

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lohmann AW, Tepichín E, Ramírez JG. Optical implementation of the fractional hilbert transform for two-dimensional objects. Appl Opt (1997) 36:6620–6. doi:10.1364/AO.36.006620

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Davis JA, McNamara DE, Cottrell DM, Campos J. Image processing with the radial hilbert transform: Theory and experiments. Opt Lett (2000) 25:99–101. doi:10.1364/OL.25.000099

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Crabtree K, Davis JA, Moreno I. Optical processing with vortex-producing lenses. Appl Opt (2004) 43:1360–7. doi:10.1364/AO.43.001360

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Swartzlander GA. Peering into darkness with a vortex spatial filter. Opt Lett (2001) 26:497–9. doi:10.1364/OL.26.000497

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Maurer C, Jesacher A, Fürhapter S, Bernet S, Ritsch-Marte M. Upgrading a microscope with a spiral phase plate. J Microsc (2008) 230:134–42. doi:10.1111/j.1365-2818.2008.01968.x

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Fürhapter S, Jesacher A, Bernet S, Ritsch-Marte M. Spiral phase contrast imaging in microscopy. Opt Express (2005) 13:689–94. doi:10.1364/OPEX.13.000689

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bernet S, Jesacher A, Fürhapter S, Maurer C, Ritsch-Marte M. Quantitative imaging of complex samples by spiral phase contrast microscopy. Opt Express (2006) 14:3792–805. doi:10.1364/OE.14.003792

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kotlyar VV, Kovalev AA, Soifer VA, Tuvey CS, Davis JA. Sidelobe contrast reduction for optical vortex beams using a helical axicon. Opt Lett (2007) 32:921–3. doi:10.1364/OL.32.000921

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kotlyar VV, Kovalev AA, Skidanov RV, Moiseev OY, Soifer VA. Diffraction of a finite-radius plane wave and a Gaussian beam by a helical axicon and a spiral phase plate. J Opt Soc Am A (2007) 24:1955–64. doi:10.1364/JOSAA.24.001955

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lin J, Yuan X-C, Tao SH, Burge RE. Variable-radius focused optical vortex with suppressed sidelobes. Opt Lett (2006) 31:1600–2. doi:10.1364/OL.31.001600

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Bokor N, Iketaki Y. Laguerre-Gaussian radial hilbert transform for edge-enhancement fourier transform x-ray microscopy. Opt Express (2009) 17:5533–9. doi:10.1364/OE.17.005533

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Qiu X, Li F, Zhang W, Zhu Z, Chen L. Spiral phase contrast imaging in nonlinear optics: Seeing phase objects using invisible illumination. Optica (2018) 5:208–12. doi:10.1364/OPTICA.5.000208

CrossRef Full Text | Google Scholar

30. Wei S, Bu J, Zhu S, Yuan X. Image edge-enhancement in optical microscopy with a phase mismatched spiral phase plate. Chin Opt Lett (2011) 9:031001. doi:10.3788/col201109.031001

CrossRef Full Text | Google Scholar

31. Sharma MK, Joseph J, Senthilkumaran P. Selective edge enhancement using shifted anisotropic vortex filter. J Opt (2013) 42:1–7. doi:10.1007/s12596-012-0089-6

CrossRef Full Text | Google Scholar

32. Sharma MK, Joseph J, Senthilkumaran P. Effect of aberrations in vortex spatial filtering. Opt Lasers Eng (2012) 50:1501–7. doi:10.1016/j.optlaseng.2012.06.012

CrossRef Full Text | Google Scholar

33. Jesacher A, Fürhapter S, Bernet S, Ritsch-Marte M. Shadow effects in spiral phase contrast microscopy. Phys Rev Lett (2005) 94:233902. doi:10.1103/PhysRevLett.94.233902

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Teich M, Mattern M, Sturm J, Büttner L, Czarske JW. Spiral phase mask shadow-imaging for 3d-measurement of flow fields. Opt Express (2016) 24:27371–81. doi:10.1364/OE.24.027371

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gozali R, Nguyen T-A, Bendau E, Alfano RR. Compact oam microscope for edge enhancement of biomedical and object samples. Rev Scientific Instr (2017) 88:093701. doi:10.1063/1.5000508

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ram BSB, Senthilkumaran P, Sharma A. Polarization-based spatial filtering for directional and nondirectional edge enhancement using an s-waveplate. Appl Opt (2017) 56:3171–8. doi:10.1364/AO.56.003171

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bracewell RN, Bracewell RN. The Fourier transform and its applications. New York: McGraw-Hill (1986).

Google Scholar

38. Guo C-S, Liu X, He J-L, Wang H-T. Optimal annulus structures of optical vortices. Opt Express (2004) 12:4625–34. doi:10.1364/OPEX.12.004625

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Guo C-S, Liu X, Ren X-Y, Wang H-T. Optimal annular computer-generated holograms for the generation of optical vortices. J Opt Soc Am A (2005) 22:385–90. doi:10.1364/JOSAA.22.000385

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Guo C-S, Han Y-J, Xu J-B, Ding J. Radial hilbert transform with laguerre-Gaussian spatial filters. Opt Lett (2006) 31:1394–6. doi:10.1364/OL.31.001394

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Chen J, Yuan X-C, Zhao X, Fang ZL, Zhu SW. Generalized approach to modifying optical vortices with suppressed sidelobes using bessel-like functions. Opt Lett (2009) 34:3289–91. doi:10.1364/OL.34.003289

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wei SB, Zhu SW, Yuan X-C. Image edge enhancement in optical microscopy with a bessel-like amplitude modulated spiral phase filter. J Opt (2011) 13:105704. doi:10.1088/2040-8978/13/10/105704

CrossRef Full Text | Google Scholar

43. Zhou Y, Feng S, Nie S, Ma J, Yuan C. Image edge enhancement using airy spiral phase filter. Opt Express (2016) 24:25258–68. doi:10.1364/OE.24.025258

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Situ G, Pedrini G, Osten W. Spiral phase filtering and orientation-selective edge detection/enhancement. J Opt Soc Am A (2009) 26:1788–97. doi:10.1364/JOSAA.26.001788

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Joshi M, Shakher C, Singh K. Image encryption and decryption using fractional fourier transform and radial hilbert transform. Opt Lasers Eng (2008) 46:522–6. doi:10.1016/j.optlaseng.2008.03.001

CrossRef Full Text | Google Scholar

46. Zhou Y, Feng S, Nie S, Ma J, Yuan C. Anisotropic edge enhancement with spiral zone plate under femtosecond laser illumination. Appl Opt (2017) 56:2641–8. doi:10.1364/AO.56.002641

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wang J, Zhang W, Qi Q, Zheng S, Chen L. Gradual edge enhancement in spiral phase contrast imaging with fractional vortex filters. Scientific Rep (2015) 5:15826. doi:10.1038/srep15826

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Pérez-Aviñoa M, Martínez-Herrero R, Vallmitjana S, Latorre-Carmona P, Juvells I, Carnicer A. Partially-coherent spirally-polarized gradual-edge imaging. Opt Lasers Eng (2019) 112:53–8. doi:10.1016/j.optlaseng.2018.09.003

CrossRef Full Text | Google Scholar

49. Sharma MK, Joseph J, Senthilkumaran P. Selective edge enhancement using anisotropic vortex filter. Appl Opt (2011) 50:5279–86. doi:10.1364/AO.50.005279

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Sharma MK, Joseph J, Senthilkumaran P. Directional edge enhancement using superposed vortex filter. Opt Laser Tech (2014) 57:230–5. doi:10.1016/j.optlastec.2013.07.014

CrossRef Full Text | Google Scholar

51. Liu Y, Yu P, Hu X, Wang Z, Li Y, Gong L. Single-pixel spiral phase contrast imaging. Opt Lett (2020) 45:4028–31. doi:10.1364/OL.396903

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Zhou J, Qian H, Zhao J, Tang M, Wu Q, Lei M, et al. Two-dimensional optical spatial differentiation and high-contrast imaging. Natl Sci Rev (2020) 8:nwaa176. doi:10.1093/nsr/nwaa176

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Ma F, Shen P, Wang X, He J, Su J, Cheng L, et al. Enhanced resolution of edge enhancement in three-dimensional vortex imaging based on a modified michelson interferometer. Opt Lasers Eng (2023) 170:107785. doi:10.1016/j.optlaseng.2023.107785

CrossRef Full Text | Google Scholar

54. Li X, Cao Y, Gu M. Superresolution-focal-volume induced 3.0 tbytes/disk capacity by focusing a radially polarized beam. Opt Lett (2011) 36:2510–2. doi:10.1364/OL.36.002510

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Yu W, Ji Z, Dong D, Yang X, Xiao Y, Gong Q, et al. Super-resolution deep imaging with hollow bessel beam sted microscopy. Laser Photon Rev (2016) 10:147–52. doi:10.1002/lpor.201500151

CrossRef Full Text | Google Scholar

56. Gao X-Z, Pan Y, Zhao M-D, Zhang G-L, Zhang Y, Tu C, et al. Focusing behavior of the fractal vector optical fields designed by fractal lattice growth model. Opt Express (2018) 26:1597–614. doi:10.1364/OE.26.001597

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Pan Y, Li Y, Ren Z-C, Si Y, Tu C, Wang H-T. Parabolic-symmetry vector optical fields and their tightly focusing properties. Phys Rev A (2014) 89:035801. doi:10.1103/PhysRevA.89.035801

CrossRef Full Text | Google Scholar

58. Pan Y, Li Y, Li S-M, Ren Z-C, Si Y, Tu C, et al. Vector optical fields with bipolar symmetry of linear polarization. Opt Lett (2013) 38:3700–3. doi:10.1364/OL.38.003700

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Lerman GM, Levy U. Tight focusing of spatially variant vector optical fields with elliptical symmetry of linear polarization. Opt Lett (2007) 32:2194–6. doi:10.1364/OL.32.002194

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Lerman GM, Stern L, Levy U. Generation and tight focusing of hybridly polarized vector beams. Opt Express (2010) 18:27650–7. doi:10.1364/OE.18.027650

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Pan Y, Gao X-Z, Cai M-Q, Zhang G-L, Li Y, Tu C, et al. Fractal vector optical fields. Opt Lett (2016) 41:3161–4. doi:10.1364/OL.41.003161

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Han L, Liu S, Li P, Zhang Y, Cheng H, Gan X, et al. Managing focal fields of vector beams with multiple polarization singularities. Appl Opt (2016) 55:9049–53. doi:10.1364/AO.55.009049

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Pan Y, Li Y, Li S-M, Ren Z-C, Kong L-J, Tu C, et al. Elliptic-symmetry vector optical fields. Opt Express (2014) 22:19302–13. doi:10.1364/OE.22.019302

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Gao X-Z, Pan Y, Cai M-Q, Li Y, Tu C, Wang H-T. Hyperbolic-symmetry vector fields. Opt Express (2015) 23:32238–52. doi:10.1364/OE.23.032238

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Chen H, Zheng Z, Zhang B-F, Ding J, Wang H-T. Polarization structuring of focused field through polarization-only modulation of incident beam. Opt Lett (2010) 35:2825–7. doi:10.1364/OL.35.002825

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Chen Z, Zeng T, Ding J. Reverse engineering approach to focus shaping. Opt Lett (2016) 41:1929–32. doi:10.1364/OL.41.001929

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Lerman GM, Lilach Y, Levy U. Demonstration of spatially inhomogeneous vector beams with elliptical symmetry. Opt Lett (2009) 34:1669–71. doi:10.1364/OL.34.001669

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Kozawa Y, Sato S. Optical trapping of micrometer-sized dielectric particles by cylindrical vector beams. Opt Express (2010) 18:10828–33. doi:10.1364/OE.18.010828

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Kawauchi H, Yonezawa K, Kozawa Y, Sato S. Calculation of optical trapping forces on a dielectric sphere in the ray optics regime produced by a radially polarized laser beam. Opt Lett (2007) 32:1839–41. doi:10.1364/OL.32.001839

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Zhan Q. Trapping metallic Rayleigh particles with radial polarization. Opt Express (2004) 12:3377–82. doi:10.1364/OPEX.12.003377

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Wang X-L, Chen J, Li Y, Ding J, Guo C-S, Wang H-T. Optical orbital angular momentum from the curl of polarization. Phys Rev Lett (2010) 105:253602. doi:10.1103/PhysRevLett.105.253602

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Xu D, Gu B, Rui G, Zhan Q, Cui Y. Generation of arbitrary vector fields based on a pair of orthogonal elliptically polarized base vectors. Opt Express (2016) 24:4177–86. doi:10.1364/OE.24.004177

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Wang X-L, Li Y, Chen J, Guo C-S, Ding J, Wang H-T. A new type of vector fields with hybrid states of polarization. Opt Express (2010) 18:10786–95. doi:10.1364/OE.18.010786

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Li L, Chang C, Yuan X, Yuan C, Feng S, Nie S, et al. Generation of optical vortex array along arbitrary curvilinear arrangement. Opt Express (2018) 26:9798–812. doi:10.1364/OE.26.009798

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Li L, Chang C, Yuan C, Feng S, Nie S, Ren Z-C, et al. High efficiency generation of tunable ellipse perfect vector beams. Photon Res (2018) 6:1116–23. doi:10.1364/PRJ.6.001116

CrossRef Full Text | Google Scholar

76. Li D, Feng S, Nie S, Chang C, Ma J, Yuan C. Generation of arbitrary perfect poincaré beams. J Appl Phys (2019) 125:073105. doi:10.1063/1.5079850

CrossRef Full Text | Google Scholar

77. Gu F, Li L, Chang C, Yuan C, Feng S, Nie S, et al. Generation of fractional ellipse perfect vector beams. Opt Commun (2019) 443:44–7. doi:10.1016/j.optcom.2019.03.023

CrossRef Full Text | Google Scholar

78. Li D, Chang C, Nie S, Feng S, Ma J, Yuan C. Generation of elliptic perfect optical vortex and elliptic perfect vector beam by modulating the dynamic and geometric phase. Appl Phys Lett (2018) 113:121101. doi:10.1063/1.5048327

CrossRef Full Text | Google Scholar

79. Liu Y, Liu Z, Zhou J, Ling X, Shu W, Luo H, et al. Measurements of pancharatnam-berry phase in mode transformations on hybrid-order poincare sphere. Opt Lett (2017) 42:3447–50. doi:10.1364/OL.42.003447

PubMed Abstract | CrossRef Full Text | Google Scholar

80. He Y, Liu Z, Liu Y, Zhou J, Ke Y, Luo H, et al. Higher-order laser mode converters with dielectric metasurfaces. Opt Lett (2015) 40:5506–9. doi:10.1364/OL.40.005506

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Milione G, Evans S, Nolan DA, Alfano RR. Higher order pancharatnam-berry phase and the angular momentum of light. Phys Rev Lett (2012) 108:190401. doi:10.1103/PhysRevLett.108.190401

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Li D, Feng S, Nie S, Ma J, Yuan C. Scalar and vectorial vortex filtering based on geometric phase modulation with a q-plate. J Opt (2019) 21:065702. doi:10.1088/2040-8986/ab18e3

CrossRef Full Text | Google Scholar

83. Han Y-J, Guo C-S, Rong Z-Y, Chen L-M. Radial hilbert transform with the spatially variable half-wave plate. Opt Lett (2013) 38:5169–71. doi:10.1364/OL.38.005169

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Ram BSB, Senthilkumaran P. Edge enhancement by negative poincare–hopf index filters. Opt Lett (2018) 43:1830–3. doi:10.1364/OL.43.001830

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Zhang B, Chen Z, Sun H, Xia J, Ding J. Vectorial optical vortex filtering for edge enhancement. J Opt (2016) 18:035703. doi:10.1088/2040-8978/18/3/035703

CrossRef Full Text | Google Scholar

86. Gu Z, Yin D, Nie S, Feng S, Xing F, Ma J, et al. High-contrast anisotropic edge enhancement free of shadow effect. Appl Opt (2019) 58:G351–G357. doi:10.1364/AO.58.00G351

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Li Z, Zhao S, Wang L. Isotropic and anisotropic edge enhancement with a superposed-spiral phase filter. Opt Express (2021) 29:32591–602. doi:10.1364/OE.435927

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Bu Y, Wang X, Li Y, Du Y, Gong Q, Zheng G, et al. Tunable edge enhancement by higher-order spiral fresnel incoherent correlation holography system. J Phys D: Appl Phys (2021) 54:125103. doi:10.1088/1361-6463/abd12e

CrossRef Full Text | Google Scholar

89. Liu L, Wang H, Ning Y, Guo C, Ren G. Infrared upconverted image edge enhancement using spiral phase filter. Laser Phys (2018) 29:015401. doi:10.1088/1555-6611/aaed33

CrossRef Full Text | Google Scholar

90. Junaid S, Tidemand-Lichtenberg P, Pedersen C, Rodrigo PJ. Upconversion dark-field imaging with extended field of view at video frame rate. Appl Opt (2020) 59:2157–64. doi:10.1364/AO.384502

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Zhou Z, Li Y, Ding D, Jiang Y, Zhang W, Shi S, et al. Generation of light with controllable spatial patterns via the sum frequency in quasi-phase matching crystals. Scientific Rep (2014) 4:5650. doi:10.1038/srep05650

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Li Y, Zhou Z-Y, Ding D-S, Shi B-S. Sum frequency generation with two orbital angular momentum carrying laser beams. J Opt Soc Am B (2015) 32:407–11. doi:10.1364/JOSAB.32.000407

CrossRef Full Text | Google Scholar

93. Zhou Z-Y, Li Y, Ding D-S, Zhang W, Shi S, Shi B-S, et al. Highly efficient second harmonic generation of a light carrying orbital angular momentum in an external cavity. Opt Express (2014) 22:23673–8. doi:10.1364/OE.22.023673

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Zhou Z-Y, Liu S-L, Li Y, Ding D-S, Zhang W, Shi S, et al. Orbital angular momentum-entanglement frequency transducer. Phys Rev Lett (2016) 117:103601. doi:10.1103/PhysRevLett.117.103601

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Liu S-K, Yang C, Liu S-L, Zhou Z-Y, Li Y, Li Y-H, et al. Up-conversion imaging processing with field-of-view and edge enhancement. Phys Rev Appl (2019) 11:044013. doi:10.1103/PhysRevApplied.11.044013

CrossRef Full Text | Google Scholar

96. Demur R, Garioud R, Grisard A, Lallier E, Leviandier L, Morvan L, et al. Near-infrared to visible upconversion imaging using a broadband pump laser. Opt Express (2018) 26:13252–63. doi:10.1364/OE.26.013252

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Maestre H, Torregrosa AJ, Capmany J. Ir image upconversion under dual-wavelength laser illumination. IEEE Photon J (2016) 8:1–8. doi:10.1109/JPHOT.2016.2630852

CrossRef Full Text | Google Scholar

98. Maestre H, Torregrosa AJ, Fernández-Pousa CR, Capmany J. Ir-to-visible image upconverter under nonlinear crystal thermal gradient operation. Opt Express (2018) 26:1133–44. doi:10.1364/OE.26.001133

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Junaid S, Tomko J, Semtsiv MP, Kischkat J, Masselink WT, Pedersen C, et al. Mid-infrared upconversion based hyperspectral imaging. Opt Express (2018) 26:2203–11. doi:10.1364/OE.26.002203

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Xu D, Ma T, Qiu X, Zhang W, Chen L. Implementing selective edge enhancement in nonlinear optics. Opt Express (2020) 28:32377–85. doi:10.1364/OE.404594

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Zeng X, Wang C, Cai Y, Lin Q, Lu X, Lin J, et al. High spatial-resolution biological tissue imaging in the secondnear-infrared region via optical parametric amplification pumped by anultrafast vortex pulse [invited]. Chin Opt Lett (2022) 20:100003. doi:10.3788/col202220.100003

CrossRef Full Text | Google Scholar

102. Aspden RS, Morris PA, He R, Chen Q, Padgett MJ. Heralded phase-contrast imaging using an orbital angular momentum phase-filter. J Opt (2016) 18:055204. doi:10.1088/2040-8978/18/5/055204

CrossRef Full Text | Google Scholar

103. Liu S-K, Li Y-H, Liu S-L, Zhou Z-Y, Li Y, Yang C, et al. Real-time quantum edge enhanced imaging. Opt Express (2020) 28:35415–26. doi:10.1364/OE.395910

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Zhou J, Liu S, Qian H, Li Y, Luo H, Wen S, et al. Metasurface enabled quantum edge detection. Sci Adv (2020) 6:eabc4385. doi:10.1126/sciadv.abc4385

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Song H, Zhang Y, Ren Y, Yuan Z, Zhao D, Zheng Z, et al. Non-local edge enhanced imaging with incoherent thermal light. Appl Phys Lett (2020) 116:174001. doi:10.1063/5.0002069

CrossRef Full Text | Google Scholar

106. Kim Y, Lee G-Y, Sung J, Jang J, Lee B. Spiral metalens for phase contrast imaging. Adv Funct Mater (2022) 32:2106050. doi:10.1002/adfm.202106050

CrossRef Full Text | Google Scholar

107. Kato N. Optical second harmonic generation microscopy: Application to the sensitive detection of cell membrane damage. Biophysical Rev (2019) 11:399–408. doi:10.1007/s12551-019-00546-x

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Gibson GM, Sun B, Edgar MP, Phillips DB, Hempler N, Maker GT, et al. Real-time imaging of methane gas leaks using a single-pixel camera. Opt Express (2017) 25:2998–3005. doi:10.1364/OE.25.002998

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Wang Y, Fang J, Zheng T, Liang Y, Hao Q, Wu E, et al. Mid-infrared single-photon edge enhanced imaging based on nonlinear vortex filtering. Laser Photon Rev (2021) 15:2100189. doi:10.1002/lpor.202100189

CrossRef Full Text | Google Scholar