Modeling solar chromospheric spicules with intense lasers

Solar spicules are small-scale jet-like structures in the lower solar atmosphere. Currently, the formation of these widely distributed structures lacks a complete explanation. It is still unclear whether they play an essential role in corona heating. Here, based on the magnetohydrodynamic scaling transformation relation, we perform experiments with the interaction of a high power laser with a one-dimensional sinusoidal modulated target to model solar spicules. We observe several spicule-like structures with alternating polarity magnetic fields around them. Magnetohydrodynamic simulations with similar parameters show the detail information during the spicules’ formation. The results suggest that the so-called strong pulse model can lead to the formation of the solar spicules. The magnetic reconnection process may also play a part and lead to additional heating and brightening phenomena.

1 Introduction

Solar spicules are widely distributed in the lower solar atmosphere (chromosphere). The general length of the Type-I spicules is about 7,000–10,000 km, and most of them have widths of 300–500 km, and lifetimes of 1–10 min or even longer, the upward velocities of about 20–40 km s⁻¹, densities of about 3 × 10⁻¹³ g ⋅ cm⁻³ and temperatures of around 10,000 K, some spicules are heated to more than 100,000 K [1–7]. The spicules can carry 100 times the mass needed to sustain the solar wind [8]. Data from the Solar Dynamics Observatory showed the upper solar atmosphere had been heated subsequently when the spicules moved upwards [9]. There has been no conclusive explanation of the spicules since their discoveries in 1877. Many models have been proposed based on the source of energy driving the ejection of spicules from the chromosphere [10], including the strong pulse model [11,12], the rebound shock model [13], the Alfv$\acute{e}$n wave model [14–20] and the magnetic reconnection model [9,21]. Dey et al. discussed the similarities between spicules observed on the Sun and jets produced by polymeric fluids. They found that the nonlinear focusing of quasi-periodic waves in an-isotropic media can generate a forest of jets [22]. The strong pulse model depicts a scenario where a sudden pressure enhancement produces a strong pulse in the photosphere or lower atmosphere at the base of a vertical magnetic flux tube that drives local material into the corona and forms the spicules [11]. In this model, an initial pressure pulse generates a disturbance that nonlinearly steepens into a gas-dynamic shock. This shock can be considered as magnetohydrodynamic (MHD) slow-mode shock for low-beta plasma. This shock interacts with the transition region, thrusting it upward, and the material behind the uplifted transition region is identified as the spicules [2]. Similar to the above model, the rebound shock model has a weaker pulse, although it can explain the distribution of spicule-like structures everywhere in the chromosphere, it cannot account for the periodicity, evolution, and energetic of the spicules [10]. In addition to these hydrodynamic models, the magnetic field may also play an important role in the spicule generation process due to the complex field structure on the solar surface. Many numerical simulations including MHD simulations and two-fluid simulations indicate that Alfv$\acute{e}$n waves, magneto-sonic waves, and the magnetic reconnection process also contribute to the velocity, length and collimation of the spicules [23–26]. However, it is still uncertain which model is dominant due to the limitations in observational resolution. As an interdisciplinary subject, laboratory astrophysics provides one possible way for us to study solar chromospheric spicules. Current observations are often limited by resolution, atmospheric perturbations, and other factors, while in the laboratory, using the interaction of high energy density lasers with target materials, we can simulate astrophysical phenomena at close range, short timescales (nanosecond), small scales (millimeter) and controlled conditions [22,27,28], and eventually connect laboratory simulations with astrophysical phenomena through scaling laws and dimensionless parameters [29].

Based on the strong pulse model, we perform an experiment using a nanosecond long-pulse laser impinging on a one-dimensional sinusoidal modulated synthetic hydrocarbon (C₈H₈) target to simulate the spicule generation process. Results from nickel-silver-like 13.9 nm soft x-ray self-emission imaging system (SXIS) show several jet-like structures appear behind the target. Proton radiography reveals the magnetic field structure around the spicules, similar to the Biermann self-generated magnetic field. The results of a radiation MHD simulation program ‘FLASH’ show agreement with the experimental results. We reproduce the process of spicules generation through laser-target interaction experiments, and by applying scaling laws, we can show the relevance of the jet-like structures to solar spicules. This is a new approach to studying spicules. It may show great significance for further accurate magnetic field structure studies near the spicules’ footpoints and help the understanding of coronal heating and material transport.

The paper is organized as follows. Section 2 describes the setup of the experiment. In Section 3, we show the experimental results and analyses with the help of three-dimensional MHD simulations and discuss the applications in astrophysics. Section 4 summarizes the results, discusses some remaining problems, and describes future works concerning about experiments and simulations.

2 Experimental setup

We performed the experiments using the Shenguang-II laser facility (SG-II) firstly [30]. Figure 1 shows the setup of the experiment and the target configuration. The target was made of C₈H₈, and it was sinusoidally modulated with a period of 55 μm, a length of 2,200 μm, a width of 200 μm, a thickness of 18 ± 5 μm, and an amplitude of 3 μm (Figure 1B). A modulated target with varying thickness is used to imitate the tiny density disturbances and alternating magnetic fields in solar chromosphere or lower atmosphere (more details will be discussed in Section 3). The experiment employed a main laser with a wavelength of 527 nm, total energy of about 800 J and a pulse duration of 2 nanoseconds. The target’s modulated side was irradiated with a 450 μm × 450 μm square uniform illumination (with an intensity of $\sim 10^{14}W\cdot c{m}^{-2}$). The diameter of the laser spot size is 7–8 times larger than the target modulation period. Nickel-silver-like 13.9 nm soft x-ray self-emission imaging technology (SXIS) is a new approach to diagnosing the plasma self-emission intensity profile information. The SXIS system consists of two mirrors (M1 and M2) and an imaging unit (including a shielding cylinder, an aluminum film to shield stray light, and an imaging plane). These mirrors have been coated with multi-layer films that are only sensitive to wavelengths around 13.9 nm. As a result, the self-emission radiation from the plasma is reflected twice off these mirrors and then imaged on the imaging plane (IP), as depicted in Figure 1. The multi-layer spherical mirror M1 and multi-layer spherical imaging mirror M2 can filter out excessive radiation during laser-target interactions, which allow us to obtain clearer structures [31]. We used SXIS to diagnose the plasma self-emission profile after the main laser ablated the target, and we obtained several jet-like structures. However, the magnetic field was not obtained in this experiment, so we redesigned the experiment to investigate the formation of the jet-like structures and the role of the magnetic field in the plasma region.

FIGURE 1

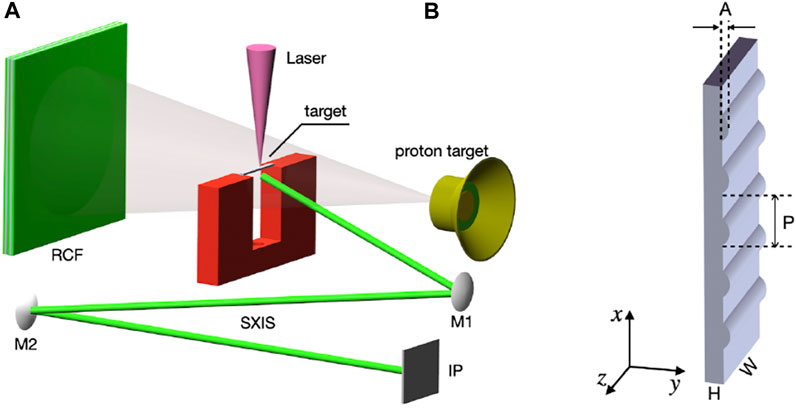
FIGURE 1. Schematic diagram of the experimental setup and sinusoidal modulated target. (A) The C₈H₈ target is located at the target chamber center (TCC). The main laser focuses on the target modulated side from the top, the proton target is located 1 cm to the right of TCC, and the proton detector (RCF) images are recorded at 15 cm to the left of TCC. Soft x-ray self-emission imaging system (SXIS) measures plasma parameters near TCC. (B) Sinusoidal modulated target parameters: width W = 200 μm, thickness H = 18 ± 5 μm, modulation period p = 55 μm, amplitude A = 3 μm or A = 10 μm, the material is synthetic hydrocarbon C₈H₈.

In order to map the magnetic field structure of the interaction region, a series of new experiments were performed on the Xingguang-III laser facility (XG-III) [32]. The target parameters were the same as before, but we increased the amplitude of the target to 10 microns in order to observe a clearer phenomenon. The experimental setup is shown in Figure 1A. The main laser (wavelength λ = 532 nm, energy about 120 J, pulse duration 2 ns, laser intensity $\sim 10^{14}W\cdot c{m}^{-2}$) focused on the modulated target with a focal spot diameter of 200 μm. We used proton radiography to diagnose the magnetic field [33]. The proton radiography is a common technique for diagnosing the structures of the magnetic fields. As the protons pass through the plasma, they are deflected by the Lorentz force and eventually imaged on the radiochromic film (RCF) stack. The protons on the RCF stack can form regions of evacuation and accumulation that correspond to regions of strong and weak magnetic fields, respectively [34]. Note that because the proton speed is much larger than the plasma velocity, the electric field has much less effect on the proton radiography. Therefore the deflection of the proton is mainly caused by the magnetic field [35]. In the experiment, we used a short pulse laser to drive a proton target to produce a proton beam. The proton target consists of a 10 μm Au foil, a 3 μm Ta foil and a shielding cylinder made of Ni. A picosecond laser (wavelength λ = 1,053 nm, energy about 100 J, pulse duration 0.86 ps, laser intensity $\sim 10^{19}W\cdot c{m}^{-2}$) is focused on the gold foil as soon as the nanosecond main laser ends (t = 2 ns), which will produce a beam of protons with an energy greater than 12 MeV. The proton source was 0.8 cm away from the target center. The RCF stack was 12 cm away from the proton target center. The protons passed through the plasma region in the direction of perpendicular to the nanosecond laser incidence direction, and were imaged on the multiple layers RCF stack. The protons with smaller energy will be imaged in the RCF layer closer to the proton target, and those with higher energy will be imaged in the RCF layer further to the proton target. The magnification factor in this experiment was about 15.

3 Results and discussions

Based on the high energy density experimental facilities described above, we use a modulated target to simulate the density fluctuations on the solar surface (or lower atmosphere). The high-power laser is like a sudden pressure enhancement in the photosphere or low chromosphere. When such a strong pulse hits the target, the laser drives a shock, which drives material jets from the opposite surface of the target, due to the interaction of the shocks and the ablative structures, which may mimic the pressure driven spicules on the surface of the sun. The magnetic Reynolds number is around 100 (Re_M ∼ L (cm)T (eV)²), according to the scaling law, if the magnetic Reynolds number in the experiment is at least an order of magnitude higher than 1, the process can be reasonably described by MHD [36,37]. Through a series of experiments and simulations, we can connect the results to the strong pulse model of solar spicules production with scale transformation criteria.

Figures 2A, B show the results of SXIS obtained in the ‘SG-II’ experiment. A 450 μm × 450 μm square focal spot laser is irradiated on a modulated target and a plain target, respectively. Darker color represents stronger x-ray emission. The modulated target is designed to imitate small density disturbances. A bush of spicules is often produced at the boundary between two adjacent supergranules [38,39]. In each supergranule, there are many granules on a much smaller scale. In the process of granules’ formation, the hot gas from the inner part rises to the surface and slides down again at the edge of a granule cell. As a result, the density will be non-uniform across a single granule cell. Observations also prove that the spicules originate from a small region near the boundary between two adjacent granules [9]. We are concerned about how each spicule in the spicule bush is produced. So we assume that there are some density inhomogeneities in the spicules production region, like ‘granules’ on a much smaller scale. As the distance between two spicules is about several hundred kilometers, we designed a modulated target with a thickness variation period of 55 μm to imitate the density inhomogeneities. After the scaling transformation, this period corresponds to the distance between two spicules in the solar environment. When the laser ablates the target and produces plasma, the density variation due to the different thicknesses of the target can correspond to the small density disturbances on the solar surface or lower atmosphere. The x-ray emission result (Figure 2A) shows that 10 jet-like structures with an interval of 55 μm are generated. The separation of those jets is consistent with the period of the modulated target. As shown in Figure 2A, the second to eighth spicules are longer because they are within the laser irradiation range. Their lengths range from 150 μm to 400 μm. On the other hand, laser irradiation of a plain target only causes the plasma to expand thermally without producing any multiple jet-like structures (Figure 2B). The experimental results verified our hypothesis that the disturbance of density is one of the necessary conditions for the generation of the spicules, while a surface with uniform density cannot produce such structures.

FIGURE 2

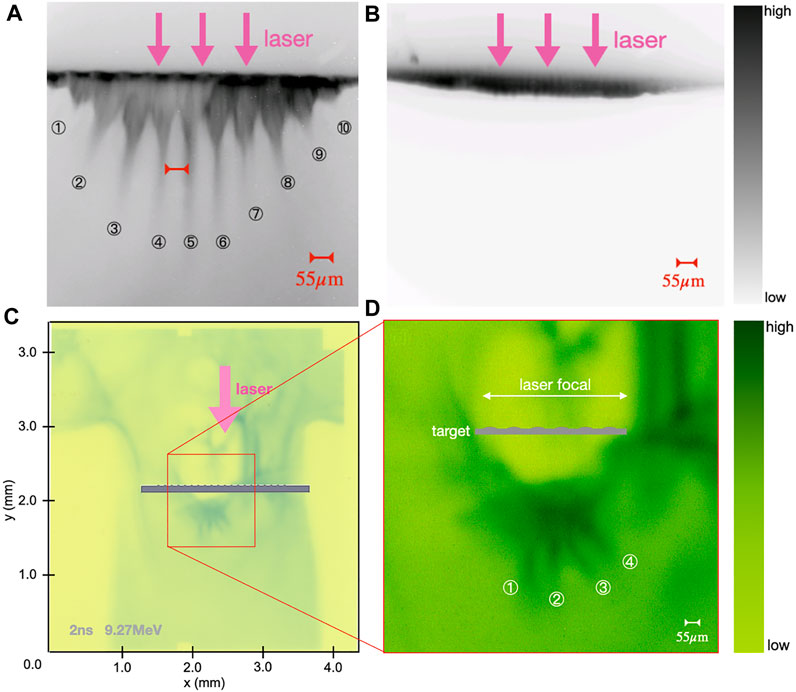
FIGURE 2. Soft x-ray self-emission imaging results in ‘SG-II’ experiments and proton radiography results obtained with 9.27 MeV protons at 2 ns. (A) Jet-like structures with an interval of 55 μm eject from the modulated target with the irradiation of a 450 μm × 450 μm square focal spot laser. (B) No jet-like structures show up when the laser irradiates the plain target. Darker color represents stronger X-ray emission. (C) Shows the position of the target and the direction of laser incidence; (D) is an enlarged view of the red box section in (C), four jet-like proton accumulation structures are visible. Darker green means more protons are accumulated.

Figure 2C shows one of the proton imaging results (an RCF layer that absorbs protons with a peak energy of 9.27 MeV) that is taken at t = 2 ns after the laser focuses on the target. The position of the target and the laser incidence direction are drawn in Figure 2C. The proton evacuation region in the middle is caused by the excessive strength of the laser magnetic field. Darker green means more protons are accumulated. Figure 2D is an enlarged view of the red box shown in Figure 2C, where we can clearly see the multiple jet-like structures. This implies that an alternating strong magnetic field appears behind the target. The separation between the jets is consistent with the period of the target (55 μm). When a thin solid target is ablated by an intense laser, a high-temperature and high-density plasma will be generated. Then the plasma expands forward in the laser direction. The temperature of the plasma is mainly determined by the heat conduction of electrons inside the target rather than the adiabatic expansion of the plasma. Therefore, the direction of the gradient of the plasma temperature is parallel to the target surface, while the gradient of the plasma density is perpendicular to the target surface. Such inconsistency of the temperature and density gradients will generate a thermoelectric potential, which in turn will induce a thermal current and finally generate a magnetic field. This is the so-called Biermann magnetic field [40–42].

Samanta et al. observed a magnetic network with positive polarity and negative polarity magnetic element around the spicule with a strength of about 10 Gauss [9]. This kind of magnetic field structure is similar to that produced in our experiments and simulations, and the strength of the magnetic field is close to the value scaled to solar spicule (Table 1). In our experiments, due to the periodic thickness variation of the modulated target, several plasma clusters are generated after the laser ablation. An alternating magnetic field is generated around each plasma cluster according to the Biermann battery effect. These alternating magnetic fields at the origin of the spicules are consistent with both the observed and experimentally obtained results. We can also estimate the magnetic field in the experiment by assuming that in the proton radiography the proton is deflected by a uniform magnetic field in the spicule region. The length of the magnetic field region can be considered the same as the thickness of the target. As a result, the magnetic field is around 1.8 × 10⁶ Gauss for a 9.27 MeV proton. According to the time delay and the length of spicule-like structures measured in Figure 2A, we can also estimate the maximum velocity of the jet, which is about 150 km s⁻¹.

TABLE 1

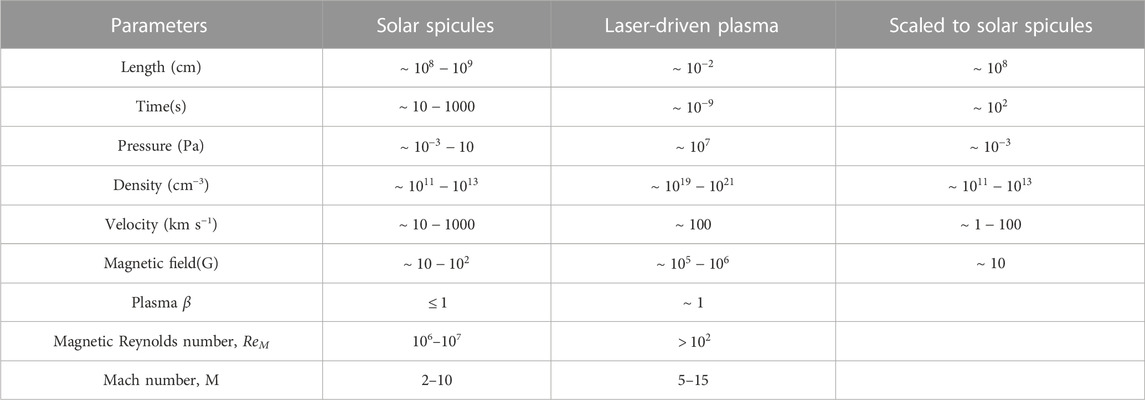
TABLE 1. The similarity of solar spicules and laser-driven plasma. The data of solar spicules referenced from [2–7,48,49].

To model the jet-like structures relevant to solar spicules in the laboratory, we should confirm that these two systems share some similar dimensionless parameters. Table 1 shows the comparison of the dimensionless parameters between the solar spicules and the laboratory jets. The Reynolds number (Re = Lv/ν) and the magnetic Reynolds number (Re_M ∼ L (cm)T (eV)²) for two systems are both much larger than 1, where L is the characteristic length, v is the jet speed, T is the jet temperature and ν is the viscosity. These values show that the viscosity is not important, and the plasma moves along the magnetic field lines. According to β = 4.03 × 10⁻¹¹n_eT_eB⁻², we can also obtain that the plasma has β ∼ 1 near the target surface, where n_e ∼ 10²⁰cm⁻³, T_e ∼ 10eV, B ∼ 10⁵G. It is similar to the β for the solar spicules generation region. We also calculate another important parameter -the density contrast η_ρ = ρ_j/ρ_a, where ρ_j and ρ_a represent for the densities of the jet and the surrounding environment. The η_ρ for these two systems are both larger than 1. The Mach numbers of the two systems are also close to each other, which indicates that the two systems are related to a large extent.

A radiation MHD simulation program ‘FLASH’ is used to help analyze the experimental results [43]. Based on the experimental parameters, we perform a three-dimensional MHD simulation using FLASH. The laser and the target parameters are consistent with ‘XG-III’ experiment except for the background plasma density, since the simulation requires the addition of a low density background plasma, while in the experiment is a high vacuum chamber. FLASH uses the generalized Ohm’s law [44,45] to calculate the magnetic field, which takes advection, diffusion, and Biermann battery terms into account:

$\frac{\partial \mathbf{B}}{\partial t}=\nabla \times \left(u\times \mathbf{B}\right)-c\nabla \times \left(\eta \mathbf{j}\right)+c\frac{\nabla P_{\mathrm{e}}\times \nabla n_{\mathrm{e}}}{e{n}_{\mathrm{e}}^2}(1)$

where u is the flow advection velocity, η is the electrical resistivity. Although the dissipation term is considered in our simulations, it can actually be neglected since the magnetic Reynolds number is large enough [37] $(>100)$.

Figure 3 shows the electron density, magnetic field along z-direction, and electric field along x-direction at 2 ns in the simulation results. The laser ablates the target from left to right. At the moment of the laser ends, it can be clearly seen that the multiple jet-like structures are moving toward the right, which is consistent with the x-ray self-emission result shown in Figure 2A. These jet-like structures have an interval of 55 μm, the maximum electron density of about 10²³ cm⁻³, the maximum length of about 120 μm, and the velocity of about 150 km s⁻¹, they are very similar to the parameters in Figure 2A. The full width at half maximum (FWHM) of the laser pulse is about 100 μm, which is 7–8 times larger than the modulation period of the target. With the generation and propagation of the jets, a temperature gradient and a density gradient are generated around each jet, and a magnetic field structure is formed by the Biermann battery effect. The magnetic field along the z-direction is shown in Figure 3B. A toroidal magnetic field surrounds each jet, which has a similar structure to proton radiography results shown in Figure 2D. However, the difference is that the proton accumulation jet-like structures from experiment are more divergent from each other, which may be caused by the power distribution of the laser. The magnetic field is interrupted at y = 0.012 cm because the continuity of the field is affected by the propagation of the plasma at the trough of the modulated target. During the propagation of the jet, it also expands laterally, which will cause the reverse magnetic field between the two neighboring jets are becoming closer and closer. From 1.5 ns, the reverse magnetic field annihilates, and the electric field in the vertical direction is significantly enhanced (Figure 3C), which is one of the evidence for the occurrence of magnetic reconnection [46]. We can obtain the averaged Lorentz force based on the simulation results along x-direction from the Maxwell stress tensor,

$F_x={\left(\nabla \cdot \mathbf{T}\right)}_x=\frac{\partial }{\partial x}\left(\frac{B_x{B}_x}{4\pi }\right)+\frac{\partial }{\partial y}\left(\frac{B_y{B}_x}{4\pi }\right)+\frac{\partial }{\partial z}\left(\frac{B_z{B}_x}{4\pi }\right)-\frac{\partial }{\partial x}\left(\frac{B^2}{8\pi }\right)(2)$

where $\mathbf{T}=\frac{\mathbf{B}\mathbf{B}}{4\pi }-\frac{|\mathbf{B}{|}^2}{8\pi }\mathbf{I}$ is the Maxwell stress tensor, where I is the identity tensor. We calculate the averaged ${\bar{F}}_x($which is $\frac{\int F_x\mathrm{d}x}{L_x})$ between x = 230 and x = 250 (i.e., the white rectangle shown in Figure 3A where the jets start to form). The ${\bar{F}}_x$ (the red curve shown in Figure 3D) has multiple spikes which have the same locations as those spicules (the blue curve of electron density shown in Figure 3D). It shows that the locations with strong magnetic force are consistent with the locations of the spicules. This indicates the Maxwell stress tensor does have contributions to the process of spicules formation.

FIGURE 3

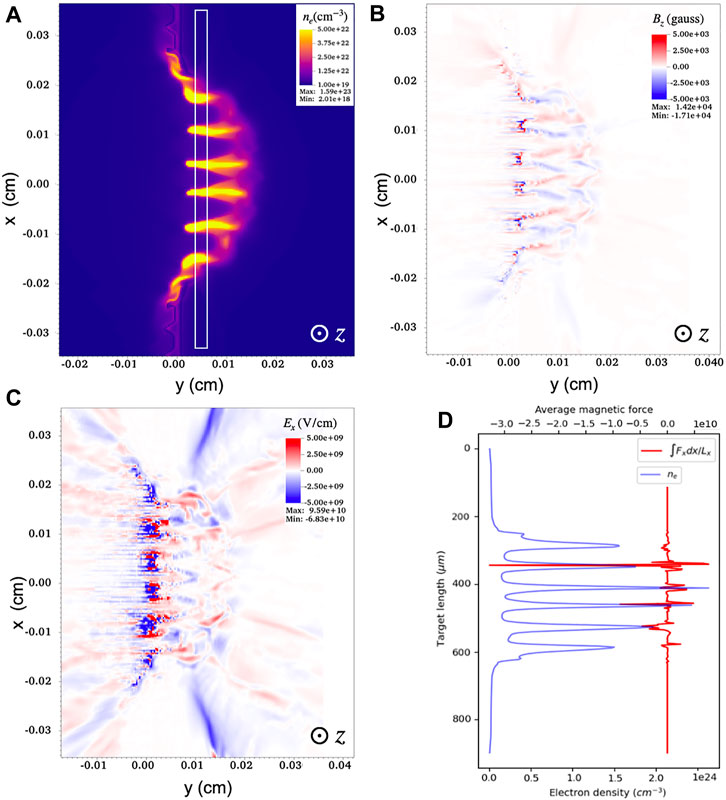
FIGURE 3. MHD simulation results of ‘XG-III’ experiment at 2 ns. (A) Electron density (cm⁻³) distribution map, several jet-like structures with an interval of 55 μm are found. (B) Magnetic field distribution in z-direction, alternating positive and negative magnetic fields surrounding the jets are found. (C) Electric field distribution in x-direction, the reconnection of reversed magnetic fields between adjacent jets leads to an increase in the local electric field strength. The z-direction is perpendicular to the x-y plane pointing to readers. (D). The red curve and the blue curve show the averaged magnetic force and the electron density along the length of the target, respectively. The data in (D) comes from the rectangle area in (A).

According to previous works ([29,37,47]), the two systems can behave as ideal compressible hydrodynamic fluids if the dimensionless numbers are much larger than 1, such as Reynolds number and magnetic Reynolds number. So the ideal MHD equations and the energy equation for the polytropic gas remain invariant when the following transformation conditions are satisfied: r₂ = ar₁, ρ₂ = bρ₁, p₂ = cp₁, $t_2=a\sqrt{b/c}{t}_1$, $v_2=\sqrt{c/b}{v}_1$, $B_2=\sqrt{c}{B}_1$, where r is the characteristic length, ρ is the number density, p is the pressure, t is the characteristic time, v is the velocity and B is the magnetic field. The subscript 1 represents parameters in the laboratory, and the subscript 2 represents parameters in the solar spicule system. The coefficients a, b, c are arbitrary positive numbers, which can be obtained directly by comparing the parameters from two systems. From our experimental results, we can obtained the transformation coefficients of a = 10¹⁰, b = 10⁻⁸, and c = 10⁻¹⁰. The scaled parameters (Table 1) are close to the parameters in the experiment, which indicates the experimental results can be applied to explore the formation mechanism of the solar spicules.

4 Conclusion

In this work, we used a high-power laser irradiating a sinusoidally modulated C₈H₈ target with a period of 55 μm and an MHD code ‘FLASH’ for simulation with similar setup parameters to experiments. We found several spicule-like structures with an interval of 55 μm emitting from the backside of the target and multipole magnetic fields around the spicules. These results are consistent with the description of the strong pulse model, which contributes to the generation of solar spicules. The alternating magnetic fields also correspond to the structures of the magnetic fields near the footpoints of the spicules. Magnetic reconnection between adjacent spicules may also be important for brightening and heating solar spicules.

This is a new way to study solar chromospheric spicules. We can change the amplitude and period of the modulated target to simulate the random density fluctuations on the solar surface, and also apply an external magnetic field to simulate the complex magnetic field on the solar surface. These ideas are easily implemented in the laboratory. In the simulations so far, we have only considered magnetic reconnection with low resistivity, which may underestimate the effect of the magnetic field on the spicules. However, both Alfv$\acute{e}$n waves and magnetic reconnection may play an important role during spicules’ generation and propagation. In the future, we will do more detailed studies regarding the heating effect of the spicules to the corona, the bright points in the chromospheric network, and the formation of micro-jets in the sunspot penumbra region. In addition, intrinsic oscillation is one of the important properties of the spicule. We will also study about this topic in the future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JW: Writing–original draft. JZ: Supervision, Writing–review and editing. WA: Supervision, Writing–review and editing. WZ: Conceptualization, Writing–review and editing. CW: Formal Analysis, Writing–review and editing. BZ: Data curation, Writing–review and editing. YP: Formal Analysis, Writing–review and editing. WS: Formal Analysis, Writing–review and editing. XY: Formal Analysis, Writing–review and editing. PT: Formal Analysis, Writing–review and editing. YZ: Formal Analysis, Writing–review and editing. QZ: Formal Analysis, Writing–review and editing. CX: Formal Analysis, Writing–review and editing. ZL: Formal Analysis, Writing–review and editing. JY: Formal Analysis, Writing–review and editing. JX: Formal Analysis, Writing–review and editing. SH: Data curation, Writing–review and editing. RH: Supervision, Writing–review and editing. YG: Supervision, Writing–review and editing. GZ: Funding acquisition, Writing–review and editing. JZ: Funding acquisition, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key R&D Program of China (grant Nos. 2022YFA1603200 and 2022YFA1603203) and the National Natural Science Foundation of China (grant Nos. 12325305, 12175018, 12135001, and 12075030), and the Strategic Priority Research Program of the Chinese Academy of Sciences (grant No. XDA25030700), Youth Interdisciplinary Team (JCTD-2022-05).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Beckers JM. Solar spicules. Solar Spicules (1972) 10:73–100. doi:10.1146/annurev.aa.10.090172.000445

CrossRef Full Text | Google Scholar

2. Sterling AC. Solar spicules: A review of recent models and targets for future observations - (invited review). Solar Phys (2000) 196:79–111. doi:10.1023/A:1005213923962

CrossRef Full Text | Google Scholar

3. de Pontieu B, McIntosh S, Hansteen VH, Carlsson M, Schrijver CJ, Tarbell TD, et al. A tale of two spicules: The impact of spicules on the magnetic chromosphere. The Impact Spicules Magn Chromosphere (2007) 59:S655–2. doi:10.1093/pasj/59.sp3.S655

CrossRef Full Text | Google Scholar

4. Tsiropoula G, Tziotziou K, Kontogiannis I, Madjarska MS, Doyle JG, Suematsu Y. Solar fine-scale structures. I. Spicules and other small-scale, jet-like events at the chromospheric level: Observations and physical parameters. Observations Phys Parameters (2012) 169:181–244. doi:10.1007/s11214-012-9920-2

CrossRef Full Text | Google Scholar

5. Pereira TMD, De Pontieu B, Carlsson M. Quantifying Spicules (2012) 759:18. doi:10.1088/0004-637X/759/1/18

CrossRef Full Text

6. Pereira TMD, De Pontieu B, Carlsson M, Hansteen V, Tarbell TD, Lemen J, et al. An interface region imaging spectrograph first view on solar spicules. AstroPhysical J Lett (2014) 792:L15. doi:10.1088/2041-8205/792/1/L15

CrossRef Full Text | Google Scholar

7. Skogsrud H, Rouppe van der Voort L, De Pontieu B, Pereira TMD. On the temporal evolution of spicules observed Withiris,Sdo, andhinode. AstroPhysical J Lett (2015) 806:170. doi:10.1088/0004-637X/806/2/170

CrossRef Full Text | Google Scholar

8. Withbroe GL. The role of spicules in heating the solar atmosphere Implications of EUV observations. Astrophys J (1983) 267:825–36. doi:10.1086/160917

CrossRef Full Text | Google Scholar

9. Samanta T, Tian H, Yurchyshyn V, Peter H, Cao W, Sterling A, et al. Generation of solar spicules and subsequent atmospheric heating. Science (2019) 366:890–4. doi:10.1126/science.aaw2796

PubMed Abstract | CrossRef Full Text | Google Scholar

10. De Pontieu B, Erdélyi R, James SP (2004). Solar chromospheric spicules from the leakage of photospheric oscillations and flows. Nature, 430, 536–9. doi:10.1038/nature02749

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Suematsu Y, Shibata K, Neshikawa T, Kitai R. Numerical hydrodynamics of the jet phenomena in the solar atmosphere: I. Spicules. Sol Phys (1982) 75:99–118. doi:10.1007/BF00153464

CrossRef Full Text | Google Scholar

12. Mackenzie Dover F, Sharma R, Erdélyi R. Magnetohydrodynamic simulations of spicular jet propagation applied to lower solar atmosphere model. Model (2021) 913:19. doi:10.3847/1538-4357/abefd1

CrossRef Full Text | Google Scholar

13. Hollweg JV. On the origin of solar spicules. Astrophys J (1982) 257:345–53. doi:10.1086/159993

CrossRef Full Text | Google Scholar

14. Cranmer SR, Woolsey LN. Driving solar spicules and jets with magnetohydrodynamic turbulence: Testing a persistent idea. Astrophys J (2015) 812:71. doi:10.1088/0004-637X/812/1/71

CrossRef Full Text | Google Scholar

15. Iijima H, Yokoyama T. A three-dimensional magnetohydrodynamic simulation of the formation of solar chromospheric jets with twisted magnetic field lines. Astrophys J (2017) 848:38. doi:10.3847/1538-4357/aa8ad1

CrossRef Full Text | Google Scholar

16. Martínez-Sykora J, De Pontieu B, Hansteen VH, Rouppe van der Voort L, Carlsson M, Pereira TMD. On the generation of solar spicules and Alfvénic waves. Science (2017) 356:1269–72. doi:10.1126/science.aah5412

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Liu J, Nelson CJ, Snow B, Wang Y, Erdélyi R. Evidence of ubiquitous Alfvén pulses transporting energy from the photosphere to the upper chromosphere. Nat Commun (2019) 10:3504. doi:10.1038/s41467-019-11495-0

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Oxley W, Scalisi J, Ruderman MS, Erdélyi R. Formation of chromospheric spicules in magnetic bright points: An analytical approach using cartesian slab geometry. Astrophys J (2020) 905:168. doi:10.3847/1538-4357/abcafe

CrossRef Full Text | Google Scholar

19. Scalisi J, Oxley W, Ruderman MS, Erdélyi R. Propagation of torsional alfvén pulses in zero-beta flux tubes. Astrophys J (2021) 911:39. doi:10.3847/1538-4357/abe8db

CrossRef Full Text | Google Scholar

20. Zaqarashvili TV, Lomineishvili S, Leitner P, Hanslmeier A, Gömöry P, Roth M. Kink instability of triangular jets in the solar atmosphere. Astron Astrophys (2021) 649:A179. doi:10.1051/0004-6361/202039381

CrossRef Full Text | Google Scholar

21. Ding JY, Madjarska MS, Doyle JG, Lu QM, Vanninathan K, Huang Z. Magnetic reconnection resulting from flux emergence: Implications for jet formation in the lower solar atmosphere? Astron Astrophys (2011) 535:A95. doi:10.1051/0004-6361/201117515

CrossRef Full Text | Google Scholar

22. Dey S, Chatterjee P, Korsós MB, Liu J, Nelson CJ Polymeric jets throw light on the origin and nature of the forest of solar spicules. Nat Phys (2022) 18:595–600. doi:10.1038/s41567-022-01522-1

CrossRef Full Text | Google Scholar

23. Heggland L, De Pontieu B, Hansteen VH. Numerical simulations of shock wave-driven chromospheric jets. Astrophys J (2007) 666:1277–83. doi:10.1086/518828

CrossRef Full Text | Google Scholar

24. James SP, Erdélyi R. Spicule formation by ion-neutral damping. Astron Astrophys (2002) 393:L11–4. –L14. doi:10.1051/0004-6361:20021126

CrossRef Full Text | Google Scholar

25. James SP, Erdélyi R, De Pontieu B. Can ion-neutral damping help to form spicules? Astron Astrophys (2003) 406:715–24. doi:10.1051/0004-6361:20030685

CrossRef Full Text | Google Scholar

26. Kuźma B, Murawski K, Kayshap P, Wójcik D, Srivastava AK, Dwivedi BN. Two-fluid numerical simulations of solar spicules. Astrophys J (2017) 849:78. doi:10.3847/1538-4357/aa8ea1

CrossRef Full Text | Google Scholar

27. Zhong J, Li Y, Wang X, Wang J, Dong Q, Xiao C, et al. Modelling loop-top X-ray source and reconnection outflows in solar flares with intense lasers. Nat Phys (2010) 6:984–7. doi:10.1038/nphys1790

CrossRef Full Text | Google Scholar

28. Ping Y, Zhong J, Wang X, Han B, Sun W, Zhang Y, et al. Turbulent magnetic reconnection generated by intense lasers. Nat Phys (2023) 19:263–70. doi:10.1038/s41567-022-01855-x

CrossRef Full Text | Google Scholar

29. Ryutov D, Drake RP, Kane J, Liang E, Remington BA, Wood-Vasey WM. Similarity criteria for the laboratory simulation of supernova hydrodynamics. AstroPhysical J Lett (1999) 518:821–32. doi:10.1086/307293

CrossRef Full Text | Google Scholar

30. He XT, Zhang WY. Inertial fusion research in China. Eur Phys J D (2007) 44:227–31. doi:10.1140/epjd/e2007-00005-1

CrossRef Full Text | Google Scholar

31. Wang C, An H, jia G, Fang Z, Wang W, Meng X, et al. Diagnosis of high-Z plasma with soft X-ray laser probe. Acta Physica Sinica (2014) 63:215203. doi:10.7498/aps.63.215203

CrossRef Full Text | Google Scholar

32. Zhu Q, Zhou K, Su J, Xie N, Huang X, Zeng X, et al. The xingguang-III laser facility: Precise synchronization with femtosecond, picosecond and nanosecond beams. Laser Phys Lett (2018) 15:015301. doi:10.1088/1612-202X/aa94e9

CrossRef Full Text | Google Scholar

33. Gao L, Ji H, Fiksel G, Fox W, Evans M, Alfonso N. Ultrafast proton radiography of the magnetic fields generated by a laser-driven coil current. Phys Plasmas (2016) 23:043106. doi:10.1063/1.4945643

CrossRef Full Text | Google Scholar

34. Kasim MF, Bott AFA, Tzeferacos P, Lamb DQ, Gregori G, Vinko SM. Retrieving fields from proton radiography without source profiles. Phys Rev E (2019) 100:033208. doi:10.1103/PhysRevE.100.033208

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Lu Y, Tzeferacos P, Liang E, Follett RK, Gao L, Birkel A, et al. Numerical simulation of magnetized jet creation using a hollow ring of laser beams. Phys Plasmas (2019) 26:022902. doi:10.1063/1.5050924

CrossRef Full Text | Google Scholar

36. Remington BA, Drake RP, Ryutov DD. Experimental astrophysics with high power lasers and Z pinches. Rev Mod Phys (2006) 78:755–807. doi:10.1103/RevModPhys.78.755

CrossRef Full Text | Google Scholar

37. Ryutov DD, Drake RP, Remington BA. Criteria for scaled laboratory simulations of astrophysical MHD phenomena. Astrophysical MHD Phenomena (2000) 127:465–8. doi:10.1086/313320

CrossRef Full Text | Google Scholar

38. Rutten RJ. The quiet-Sun photosphere and chromosphere. Philosophical Trans R Soc Lond Ser A (2012) 370:3129–50. doi:10.1098/rsta.2011.0537

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Goode PR, Yurchyshyn V, Cao W, Abramenko V, Andic A, Ahn K, et al. Highest resolution observations of the quietest Sun. Astrophysical J Lett (2010) 714:L31–5. doi:10.1088/2041-8205/714/1/L31

CrossRef Full Text | Google Scholar

40. Biermann L. Über den Ursprung der Magnetfelder auf Sternen und im interstellaren Raum (miteinem Anhang von A. Schlüter). Z Naturforschung Teil A (1950) 5:65.

Google Scholar

41. Stamper JA. Review on spontaneous magnetic fields in laser-produced plasmas: Phenomena and measurements. Laser Part Beams (1991) 9:841–62. doi:10.1017/S0263034600006595

CrossRef Full Text | Google Scholar

42. Gao L, Liang E, Lu Y, Follet RK, Sio H, Tzeferacos P, et al. Mega-gauss plasma jet creation using a ring of laser beams. Mega-Gauss Plasma Jet Creation Using a Ring of Laser Beams (2019) 873:L11. doi:10.3847/2041-8213/ab07bd

CrossRef Full Text | Google Scholar

43. Fryxell B, Olson K, Ricker P, Timmes FX, Zingale M, Lamb DQ, et al. FLASH: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophysical Thermonuclear Flashes (2000) 131:273–334. doi:10.1086/317361

CrossRef Full Text | Google Scholar

44. Epperlein EM. The accuracy of Braginskii’s transport coefficients for a Lorentz plasma. J Phys D Appl Phys (1984) 17:1823–7. doi:10.1088/0022-3727/17/9/007

CrossRef Full Text | Google Scholar

45. Epperlein EM, Haines MG. Plasma transport coefficients in a magnetic field by direct numerical solution of the Fokker-Planck equation. Phys Fluids (1986) 29:1029–41. doi:10.1063/1.865901

CrossRef Full Text | Google Scholar

46. Zhang K, Zhong J, Pei X, Li Y, Sakawa Y, Gang W, et al. Measurement of jet evolution and electron energy spectrum during the process of laser-driven magnetic reconnection. Acta Physica Sinica (2015) 64:165201. doi:10.7498/aps.64.165201

CrossRef Full Text | Google Scholar

47. Yuan D, Wu J, Li Y, Lu X, Zhong J, Yin C, et al. Modeling supersonic-jet deflection in the herbig-haro 110-270 system with high-power lasers. Astrophys J (2015) 815:46. doi:10.1088/0004-637X/815/1/46

CrossRef Full Text | Google Scholar

48. Orozco Suárez D, Asensio Ramos A, Trujillo Bueno J. Height variation of the vector magnetic field in solar spicules. Astrophysical J Lett (2015) 803:L18. doi:10.1088/2041-8205/803/2/L18

CrossRef Full Text | Google Scholar

49. Kriginsky M, Oliver R, Freij N, Kuridze D, Asensio Ramos A, Antolin P. Ubiquitous hundred-Gauss magnetic fields in solar spicules. Astron Astrophysics (2020) 642:A61. doi:10.1051/0004-6361/202038546

CrossRef Full Text | Google Scholar