Wei-Wang Yu1
Ying Liu
Yong Fang
Xianglin Ke
Xue Liu
Zhida Han
Xiaoming Zhang- 1School of Material Science and Engineering, Hebei University of Technology, Tianjin, China
- 2Changshu Institute of Technology, Suzhou, China
- 3Department of Physics and Astronomy, Michigan State University, East Lansing, MI, United States
- 4Institutes of Physical Science and Information Technology, Anhui University, Hefei, Anhui, China
Editorial on the Research Topic
Magnetotransport and electronic band structures of topological semimetals
Topological semimetals [1–5] have become a fascinating class of quantum materials that has captured the attention of researchers in recent years. Their unique band structure exhibits nontrivial band crossings near the Fermi level, which causes low-energy quasiparticles to behave differently than they would in topologically trivial materials. Many physical phenomena have been discovered that can be attributed to their unique electronic band structure, such as topological surface states, chiral anomaly, and giant magnetoresistance [6, 7].
The characterization and differentiation of topological phases is a critical area of research in investigating topological semimetals [8–10]. At present, magnetotransport has the potential to provide valuable information on the electronic band structures of topological semimetals [11–13]. Specifically, the study of magnetotransport in topological semimetals has revealed intriguing effects such as negative magnetoresistance, non-saturating magnetoresistance, and quantum oscillations, which are consequences of the nontrivial topology of their electronic band structures. Thus far, angle-resolved photoemission spectroscopy (ARPES) has been the most effective means of studying the electronic band structures of topological semimetals [3, 14, 15]. However, narrow band gaps, complex bands, and charge impurities can impede the detection of nontrivial band crossings.
It has been realized that the study of nontrivial band crossings can also be extended to bosonic and classical systems. Recently, there has been a surge of interest in exploring the topological quasiparticles in phonons, as the experimental detection of nontrivial phonons can be done throughout the full THz phonon spectrum with meV-resolution. For example, two-dimensional (2D) Weyl phonons have been systematically summarized in a recent review [Yang], and some typical material candidates have been identified, such as graphene, CrI3 [16] monolayer, SiH monolayer [17], TiB4 monolayer, Ti2P monolayer, and Cu2Si monolayer [18]. Interestingly, unlike 2D electronic systems, the highest order of a 2D Weyl phonon is quadratic rather than cubic. Naturally, three-dimensional topological phonons have also been identified in this bosonic system [19]. For instance, a Weyl complex of a double Weyl point and two linear Weyl points has been discovered in BaSi2 [Li], which belongs to P4332, as shown in Figure 1A. Moreover, as depicted in Figure 1B, one can observe that the Fermi arcs connect the linear and double Weyl points. Apart from the double degenerate Weyl points, a charge-2 point of threefold degeneracy has also been found in the dispersion spectrum of cubic Ca3I3P [Yang], as presented in Figure 1C. Given its topological charge, two Fermi arcs emerge from the projection of this charge-2 triple point.
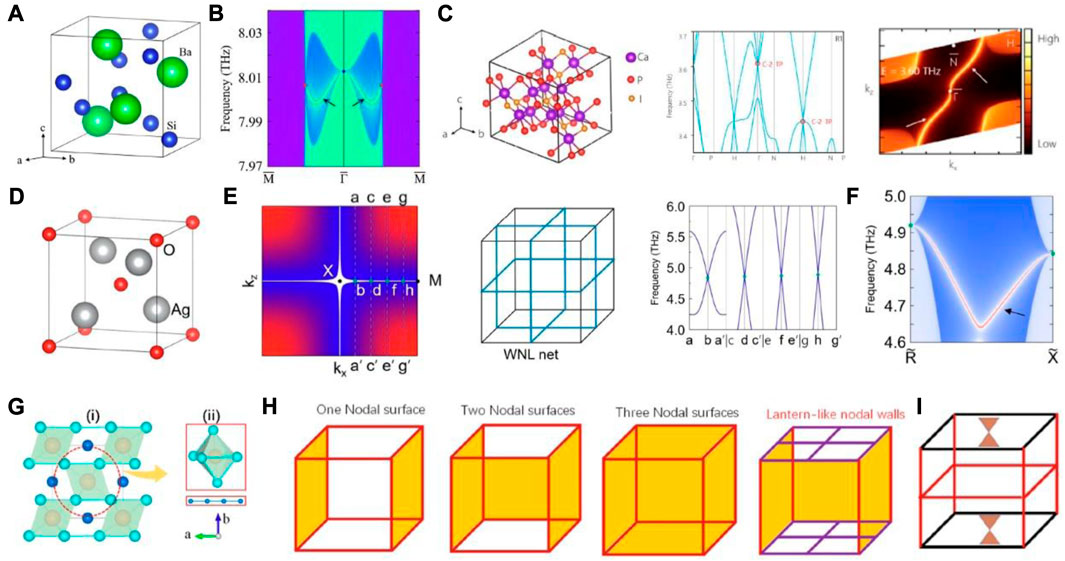
FIGURE 1. (A, B) the lattice structure for BaSi2 and its corresponding surface spectrum on (001) plane [2]. (C) the lattice structure, phonon spectrum and projected surface spectrum for Ca3I3P [3]. (D–F) the lattice structure, a map of energy gaps between the two crossing branches around 5 THz, schematic figures for a nodal frame, phonon dispersion along paths marked in the map and the surface states on (010) surface [4]. (G) the lattice structure for LiRuO2, (H) the nodal surfaces and the lantern-like nodal wall without SOC and (I) distribution of Dirac nodal lines and Dirac points with SOC in the Brillouin zone of LiRuO2.
Naturally, in the presence of certain symmetries, band crossings in phonon spectra may not be isolated, but instead belong to a nodal line. Most recently, an ideal nodal net of phonons, which is composed of several nodal lines, was identified in Pn-3m-type Ag2O [Li], as shown in Figure 1D. It was discovered that four nodal lines, which are sets of band crossings with the same energy, form a frame in Figure 1E. A clear drumhead surface state can be observed in its surface spectrum, as presented in Figure 1F. Moreover, nodal lines can also be a generic line for a nodal surface/wall.
Of course, several types of band crossings could simultaneously exist in the same material due to multiple symmetry protection. As demonstrated in the paper [Gao et al.], the lantern-like nodal wall is composed of two nodal networks and two nodal surfaces in Figure 1H. In the absence of spin-orbit coupling (SOC), lantern-like nodal walls protected by nonsymmorphic symmetries and time-reversal symmetry are discovered in the lithium-rich compound LiRuO2 (Figure 1G). On the other hand, when SOC is included, Dirac nodal points and nodal lines appear along high-symmetry paths and points, as shown in Figure 1I.
Recently, the most studies are mainly focusing on searching novel topological quantum phases or new material candidates, however, there is still much to be learned about the magnetotransport and electronic band structures of topological semimetals. Despite recent progress, many of the properties of these materials remain poorly understood, and new experimental and theoretical techniques are needed to fully explore their potential.
In conclusion, the study of magnetotransport and electronic band structures of topological semimetals is a rapidly developing field that holds great promise for advancing our understanding of the fundamental physics of quantum materials and for developing new technologies that exploit their unique properties. As researchers continue to explore the properties of these fascinating materials, we can expect to see many exciting discoveries and applications in the years ahead.
Author contributions
W-WY: Software, Writing–original draft, Writing–review and editing. YL: Methodology, Supervision, Writing–original draft, Writing–review and editing. YF: Funding acquisition, Supervision, Writing–original draft, Writing–review and editing. XK: Writing–original draft, Writing–review and editing. XL: Writing–original draft, Writing–review and editing. ZH: Writing–original draft, Writing–review and editing. XZ: Project administration, Supervision, Validation, Writing–original draft, Writing–review and editing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90(1):015001. doi:10.1103/revmodphys.90.015001
2. Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys Rev B (2011) 83(20):205101. doi:10.1103/physrevb.83.205101
3. Xu SY, Alidoust N, Belopolski I, Yuan Z, Bian G, Chang TR, et al. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nat Phys (2015) 11(9):748–54. doi:10.1038/nphys3437
4. Young SM, Zaheer S, Teo JCY, Kane CL, Mele EJ, Rappe AM. Dirac semimetal in three dimensions. Phys Rev Lett (2012) 108(14):140405. doi:10.1103/physrevlett.108.140405
5. Gorbar EV, Miransky VA, Shovkovy IA, Sukhachov PO. Dirac semimetals A3Bi (a= Na, K, Rb) as Z2 Weyl semimetals. Phys Rev B (2015) 91(12):121101. doi:10.1103/physrevb.91.121101
6. Huang X, Zhao L, Long Y, Wang P, Chen D, Yang Z, et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys Rev X (2015) 5(3):031023. doi:10.1103/physrevx.5.031023
7. Son DT, Spivak BZ. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys Rev B (2013) 88(10):104412. doi:10.1103/physrevb.88.104412
8. Zhang X, Meng W, Liu Y, Dai X, Kou L. Magnetic electrides: High-throughput material screening, intriguing properties, and applications. J Am Chem Soc (2023) 145(9):5523–35. doi:10.1021/jacs.3c00284
9. Meng W, Zhang X, Liu Y, Dai X, Gu Y, Liu G, et al. Multifold fermions and Fermi arcs boosted catalysis in nanoporous electride 12CaO·7Al2O3. Adv Sci (2023) 10(6):2205940. doi:10.1002/advs.202205940
10. Meng W, Zhang X, Liu Y, Dai X. Antiferromagnetism caused by excess electrons and multiple topological electronic states in the electride Ba4Al5⋅e-. Phys Rev B (2021) 104:195145. doi:10.1103/PhysRevB.104.195145
11. Tian L, Liu Y, Meng W, Zhang X, Dai X, Liu G. Spin-orbit coupling-determined topological phase: Topological insulator and quadratic Dirac semimetals. J Phys Chem Lett (2020) 11(24):10340–7. doi:10.1021/acs.jpclett.0c03103
12. Tian L, Liu Y, Yu WW, Zhang X, Liu G. Triple degenerate point in three dimensions: Theory and realization. Phys Rev B (2021) 104(4):045137. doi:10.1103/PhysRevB.104.045137
13. Jin L, Liu Y, Yu WW, Zhang X, Liu G, Dai X. Spin-polarized sextuple excitations in ferromagnetic materials. Phys Rev B (2022) 105(24):245141. doi:10.1103/PhysRevB.105.245141
14. Lv BQ, Xu N, Weng HM, Ma JZ, Richard P, Huang XC, et al. Observation of Weyl nodes in TaAs. Nat Phys (2015) 11(9):724–7. doi:10.1038/nphys3426
15. Yang LX, Liu ZK, Sun Y, Peng H, Yang HF, Zhang T, et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat Phys (2015) 11(9):728–32. doi:10.1038/nphys3425
16. Jin Y, Wang R, Xu H. Recipe for Dirac phonon states with a quantized valley berry phase in two-dimensional hexagonal lattices. Nano Lett (2018) 18(12):7755–60. doi:10.1021/acs.nanolett.8b03492
17. Yu WW, Liu Y, Tian L, He T, Zhang X, Liu G. Phononic linear and quadratic nodal points in monolayer XH (X= Si, Ge, Sn). J Phys Condens Matter (2022) 34(15):155703. doi:10.1088/1361-648X/ac4dbd
18. Yu WW, Liu Y, Meng W, Liu H, Gao J, Zhang X, et al. Phononic higher-order nodal point in two dimensions. Phys Rev B (2022) 105(3):035429. doi:10.1103/physrevb.105.035429
Keywords: topological semimetal, band structure, Dirac semimetal, Weyl semimetal, transport
Citation: Yu W-W, Liu Y, Fang Y, Ke X, Liu X, Han Z and Zhang X (2023) Editorial: Magnetotransport and electronic band structures of topological semimetals. Front. Phys. 11:1260872. doi: 10.3389/fphy.2023.1260872
Received: 18 July 2023; Accepted: 31 July 2023;
Published: 04 August 2023.
Edited and reviewed by:
Sung-Kwan Mo, Berkeley Lab (DOE), United StatesCopyright © 2023 Yu, Liu, Fang, Ke, Liu, Han and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ying Liu, eWluZ19saXVAaGVidXQuZWR1LmNu; Yong Fang, ZmFuZ3lvbmdAY3NsZy5lZHUuY24=; Xiaoming Zhang, emhhbmd4aWFvbWluZzg3QGhlYnV0LmVkdS5jbg==