ZrOsSi: a Z2 topological metal with a superconducting ground state

The silicide superconductors (Ta, Nb, Zr)OsSi are among the best candidate materials for investigating the interplay of topological order and superconductivity. Here, we investigate in detail the normal-state topological properties of (Ta, Nb, Zr)OsSi, focusing on ZrOsSi, by employing a combination of ²⁹Si nuclear magnetic resonance (NMR) measurements and first-principles band-structure calculations. We show that, while (Ta, Nb)OsSi behave as almost ideal metals, characterized by weak electronic correlations and a relatively low density of states, the replacement of Ta (or Nb) with Zr expands the crystal lattice and shifts ZrOsSi towards an insulator. Our ab initio calculations indicate that ZrOsSi is a Z₂ topological metal with clear surface Dirac cones and properties similar to a doped strong topological insulator.

1 Introduction

Topological metals (TMs) are special metallic materials characterized by a nontrivial topology, in particular, by their topologically-protected surface states [1, 2]. Depending on the presence of a “gap” at the Fermi level of their electronic band structure, they are broadly classified into two categories. i) TMs with a continuous direct band gap over all the k-points of the Brillouin zone, which exhibit also a nontrivial Z₂ topological invariant, are called Z₂ TMs [3, 4]. ii) TMs with topologically nontrivial band crossings near the Fermi level are called nodal semimetals. In turn, according to the dimensionality of the nodes, nodal semimetals are further classified into nodal-point, nodal-line and nodal-surface semimetals [1, 2]. Due to their novel quantum properties, that are of interest to both fundamental physics and technological applications [1, 2], TMs have been at the forefront of research on quantum materials.

Owing to their nontrivial band topology and the associated rich physical properties, TMs represent unique platforms for investigating the interplay between topology, strong correlation and superconductivity. In this regard, superconducting TMs are of particular interest. For instance, unconventional superconductivity with time-reversal symmetry (TRS) breaking [5] was recently discovered in the Weyl nodal-line semimetals La(Pt, Ni)Si and LaPtGe [6] and in the Dirac semimetal LaNiGa₂ [7, 8]. In particular, the recently discovered superconducting Z₂ TMs (Cs, Rb, K)V₃Sb₅ with a layered kagome crystal structure have generated a lot of interest in the community [9, 10]. However, due to the inherent geometric frustration, typical of the kagome lattice, these materials exhibit several competing orders. While their interplay leads to new and interesting phenomena [9, 10], at the same time it becomes difficult to grasp the underlying physics of the different phases.

In this respect, the silicide superconductors (Ta, Nb)OsSi are special since, despite being nonsymmorphic symmetry-protected semimetals [11–14] (with time-reversal symmetry-breaking superconducting ground states), their crystal structure does not have any geometric frustration. ZrOsSi, which is isostructural with (Ta,Nb)OsSi, is also superconducting, but with a superconducting transition temperature T_c ∼ 1.7 K [15] much lower than that of TaOsSi (5.5 K) and NbOsSi (3.1 K). This hints that possibly the physics of ZrOsSi is qualitatively different from that of its isostructural counterparts (Ta, Nb)OsSi, including some remarkably different topological properties. Motivated by these possibilities and by recent developments regarding topological metals, in this article, we investigate in detail the normal-state properties of ZrOsSi and contrast them with those of (Ta, Nb)OsSi.

Spin-orbit coupling (SOC) is a fundamental property of the electron motion, which lifts the spin degeneracy and renormalizes energy bands. Most importantly, it can lead to band inversions, which is the key to the physics of topological insulators and helical spin textures, as well as of their surface states [16]. Consequently, in quantum materials, SOC effects lie at the heart of topological properties and of phenomena related to the Berry curvature, such as quantum spin Hall effect [17], topological insulators [16], and Majorana fermions [18]. Since SOC grows larger in heavier elements, it typically does not play a role in 3d systems, but it becomes important in 4d, 5d and 5f systems [19]. In view of this, we devote special attention to SOC effects and their possible influence on the topological character of ZrOsSi.

Nuclear magnetic resonance (NMR) is a powerful bulk probe, which provides local resolution of the electronic properties, also in the case of topological materials [20]. Thus, modifications in the electronic band structure due to SOC can influence the nuclear magnetic shielding and, hence, be detected by NMR from the corresponding NMR frequency shift [20–23]. Further, in topological materials, the coherence time of nuclear spins is often reduced by their coupling to the surface states [24]. Hence, NMR can be used to probe both the surface metallic states and the bulk electronic structures [21, 22, 25, 26]. For instance, in large surface-to-volume samples, NMR has been successfully employed to detect and characterize nuclei in the proximity of the topologically protected surface states [27–29]. While an identification of the nuclei near the surface has been achieved in nanopowdered samples, a general characterization of the electronic surface states using NMR remains difficult. Nevertheless, NMR has been used to investigate the physical properties of surface metallic states in some semiconductor-based bulk- or low-dimensional systems [30, 31].

Recently, the combination of NMR and first principles band structure calculations has been used as a powerful tool to determine the topology of several quantum materials [22, 32–34]. For instance, NMR shift measurements in ZrTe₅ provide signatures of a topological phase transition and of band inversion [32]. Further, in Bi₂(Se,Te)₃, ²⁰⁹Bi NMR could show that its band inversion results from a charge redistribution between different crystal sites, in quantitative agreement with DFT calculations [22, 33]. Inspired by these examples, here we investigate the topological properties of ZrOsSi by combining band-structure calculations with NMR measurements. Using detailed first-principles calculations we show that ZrOsSi is a Z₂ topological metal with physical properties similar to a doped strong topological insulator [35]. This conclusion is further corroborated by our extensive NMR measurements, which clearly show that, while (Ta, Nb)OsSi are good metals, ZrOsSi exhibits distinct semimetallic features.

2 Results

Polycrystalline samples of (Ta, Nb, Zr)OsSi were synthesized via the arc-melting method [14, 15, 36]. 99.99% pure tantalum (niobium or zirconium) pellets, osmium ingots, and silicon pieces, all from Alfa Aesar, were used as starting materials. After preparing them in the prescribed 1:1:1 M ratio, the reagents were inserted into an arc furnace, which was purged multiple times and eventually filled with pure argon. The as-cast ingots were remelted more than ten times to ensure phase homogeneity. Finally the ingots were sealed under vacuum in a quartz tube and annealed at 1273 K for 9 days. In the whole process, the specimens lost very little weight (less than 1%) due to the non-volatile nature of the reactants. This ensured that the stoichiometry of the as-grown samples matched the nominal one. Note that, due to the toxicity of Os, it is generally difficult to grow Os-based materials, as they require special handling. The obtained (Ta, Nb, Zr)OsSi samples crystallize in a centrosymmetric orthorhombic TiNiSi-type structure, with space group Pnma (No. 62) [14, 15, 36]. The crystal structure of ZrOsSi and its corresponding Brillouin zone are shown in Figure 1. For the basic characterization of all the materials, we refer to our previous work [14, 36].

FIGURE 1

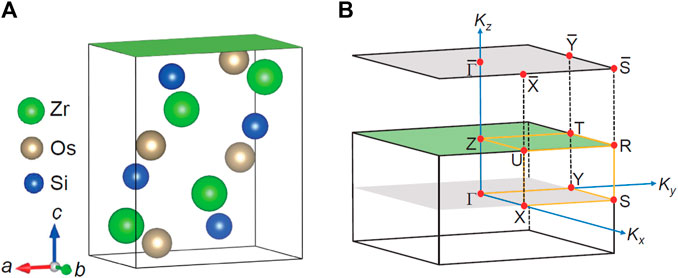
FIGURE 1. Crystal structure of ZrOsSi. (A) Unit cell of the centrosymmetric orthorhombic crystal structure. (B) First Brillouin zone, including the (001) surface-Brillouin zone and the high symmetry directions. The termination point of the slab calculation is indicated by the green-colored plane.

2.1 Electronic band structure

The electronic band structure of ZrOsSi was computed by first-principles calculations based on density functional theory using the full-potential linearized augmented plane wave (FP-LAPW) method, as implemented in the WIEN2k program suite [37]. Here, we use the exchange-correlation potential from the generalized gradient approximation (GGA) [38], with the plane-wave cutoff being defined by the condition rk_max = 7.0, with r being the minimum LAPW sphere radius and k_max being the plane-wave-vector cutoff. For ZrOsSi, the lattice parameters, optimized using DFT, are: a = 6.43 (9) Å, b = 4.08 (0) Å, and c = 7.50 (7) Å, consistent with previous reports [15]. The Wyckoff positions corresponding to the structure of ZrOsSi are: Zr 4c (0.01253, 0.25, 0.81533), Si 4c (0.21227, 0.75, 0.62165), Os 4c (0.16157, 0.25, 0.44187). The lattice parameters for TaOsSi [14] are: a = 6.26 (5) Å, b = 3.89 (3) Å, and c = 7.25 (9) Å; and for NbOsSi [14] are: a = 6.28 (1) Å, b = 3.89 (7) Å, and c = 7.27 (3) Å. Clearly, replacing Ta or Nb in (Ta, Nb)OsSi by Zr leads to an expansion of the unit cell.

The electronic band structure of ZrOsSi, with and without considering the effects of SOC, are shown in Figures 2A, B, respectively. We note that several bands cross the Fermi level, leading to the electron- and hole Fermi surfaces shown in Figure 3 (without SOC). Inside the Brillouin zone, one can identify extended regions where several Fermi-surface sheets are parallel and close to each other. This feature is also present in the Fermi surfaces of (Ta, Nb)OsSi, where it was argued to influence the nature of their superconducting ground states [14]. The reason for the closeness of the different Fermi surface sheets and the relatively small sizes of the Fermi surfaces of (Ta, Nb, Zr)OsSi can be traced back again to the nonsymmorphic symmetries of these materials, similar to that of others with the same space-group symmetry [13, 39].

FIGURE 2

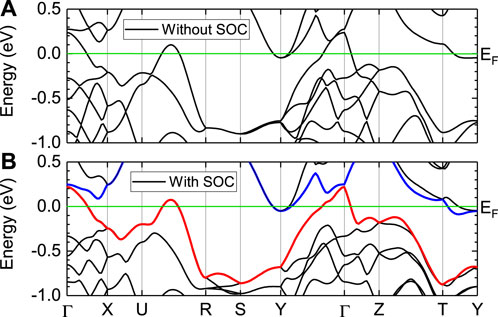
FIGURE 2. Electronic band structure of ZrOsSi: (A) without SOC and (B) with SOC. In (B), the highest occupied “valence” band and the lowest “conduction” band are marked in red and blue, respectively.

FIGURE 3

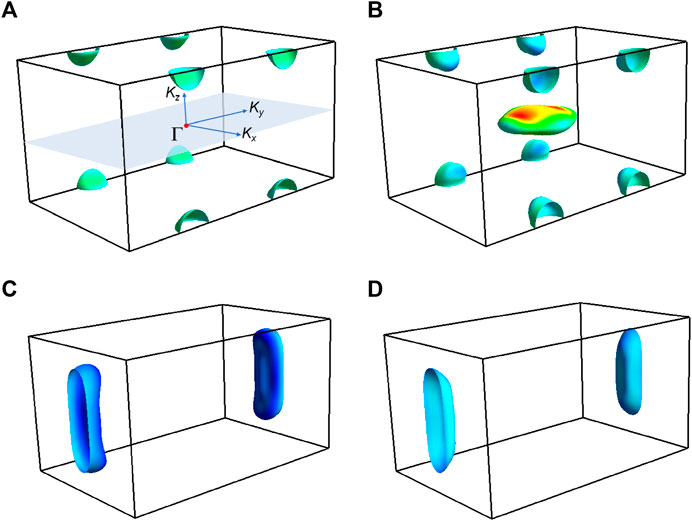
FIGURE 3. Fermi surfaces of ZrOsSi without SOC. The four Fermi-surface sheets are shown in (A), (B), (C) and (D). Note that between the Fermi surfaces shown in (A) and (B) and those in (C) and (D) there are several regions where two of the Fermi-surface sheets are parallel and close to each other. The color map denotes Fermi velocity.

From Figure 2, we note that SOC causes a significant band splitting. In particular, it results in a maximum band-splitting of $\sim 100$ meV along the TY direction, where an extra Fermi-surface sheet emerges due to SOC. Most importantly, from Figure 2B, we note that due to SOC there is a continuous direct energy gap throughout the Brillouin zone between the highest occupied “valence” band (shown in red) and the lowest unoccupied “conduction” band (shown in blue). As a result, ZrOsSi can be thought of as a semimetal, for which the classification of band insulators in three dimensions (3D), based on the Z₂ topological invariants (ν₀; ν₁ν₂ν₃), is also applicable [40]. From the topological point of view, such identification is possible since its bands can be continuously deformed into those of an insulating system, characterized by a full gap throughout the Brillouin zone. In general, the Z₂ topological invariants can be computed by calculating the evolution of the Wannier charge centers (WCCs) for the six time-reversal invariant planes: k_x = 0, π; k_y = 0, π; and k_z = 0, π [41, 42] as shown in Figure 4. In the ZrOsSi case, the Z₂ invariants are 1 for the k_x = 0, k_y = 0, and k_z = 0 planes, and 0 for the k_x = π, k_y = π, and k_z = π planes. This implies that, in ZrOsSi, the Z₂ topological invariants are (1; 000), thus indicating that ZrOsSi is a strong topological material.

FIGURE 4

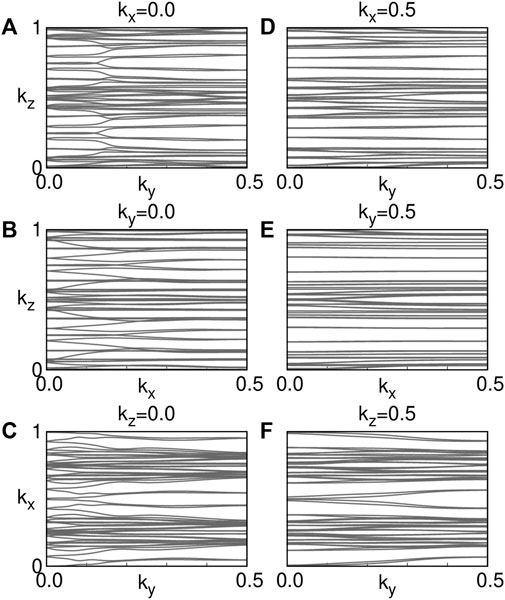
FIGURE 4. Wannier charge centres for ZrOsSi. The evolution of the Wannier charge centers in the six different time-reversal invariant planes is shown in the panels (A–F).

Since ZrOsSi has a centrosymmetric structure, we can confirm the above classification scheme by computing the Z₂ topological invariants from the product of the parity eigenvalues of the filled valence bands (up to the red band in Figure 2B) at the eight time-reversal invariant momentum (TRIM) points [40] with SOC. These parity products up to the red band in Figure 2B are −1 at the Γ point and +1 at all the other TRIM points. This leads to the Z₂ topological invariants (1; 000) for ZrOsSi, the same as those obtained by the WCC method described above. As a result, we conclude that ZrOsSi is a Z₂ topological metal, which can be continuously deformed into a strong Z₂ topological insulator. In this sense, the physics of ZrOsSi is expected to be similar to that of a doped topological insulator [35].

We show the orbital-decomposed band structure of ZrOsSi in Figure 5, where the p-d band inversions along the Γ − X, Γ − Y, and Γ − Z directions are clearly visible, thus supporting our identification of ZrOsSi with a strong topological material. Due to the bulk-boundary correspondence, there will be topologically protected metallic surface states in ZrOsSi. We investigate the surface states by computing the surface spectral function or the surface-state spectrum using surface Green’s function and maximum localized Wannier functions, as implemented in the WannierTools package [42]. In ZrOsSi, we compute the surface-state spectrum for a (001) slab, as well as the spectral function for the corresponding bulk. In both cases, we consider the SOC effects. The bulk spectral function is shown in Figure 6A and the corresponding surface-state spectral function for the slab is shown in Figure 6B on the (001) surface Brillouin zone. For clarity, here we focus on the high-symmetry $\bar{\mathrm{\Gamma }}-\bar{X}$ and $\bar{\mathrm{\Gamma }}-\bar{Y}$ directions (motivated also by the evidence of band inversion along these directions, as shown in Figure 5).

FIGURE 5

FIGURE 5. Orbital-resolved band structure of ZrOsSi. The Si-p orbitals are marked in red and the Zr-d orbitals are marked in blue. The orange boxes highlight the regions where band inversion occurs between the Si-p and Zr-d bands.

FIGURE 6

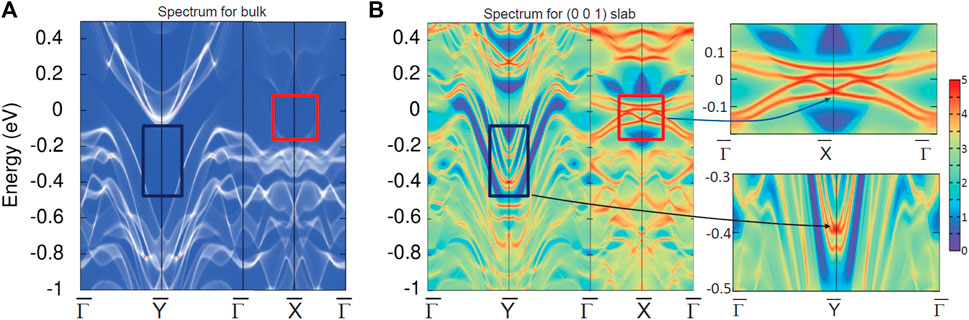
FIGURE 6. Surface states for ZrOsSi. The surface-state spectrum of ZrOsSi on the (001) surface Brillouin zone along the $\bar{\mathrm{\Gamma }}-\bar{X}-\bar{\mathrm{\Gamma }}$ and $\bar{\mathrm{\Gamma }}-\bar{Y}-\bar{\mathrm{\Gamma }}$ high-symmetry directions when including SOC. The spectral function for the bulk in (A) and for a slab with (001) surface in (B) are shown. Zoomed plots of the marked regions in (B) are shown in the rightmost panels. The color map denotes Fermi velocity.

Some key regions where the surface states are clearly visible are marked in Figure 6B, where we show also their zoomed versions. Note that, while in these regions the spectral function is nonzero for the slab, it is zero for the bulk [see Figure 6A]. This fact, together with the existence of nontrivial topological invariants and of band inversions described above, clearly indicate that, in ZrOsSi, the surface states are indeed due to its nontrivial bulk topology. The apparent asymmetry of the surface-state spectrum along the two high symmetry directions in Figure 6B is due to the direct gap moving up and down in energy, depending on the direction away from the Γ point, as shown in Figure 2B. We note that, just below the Fermi level, there are several topologically-protected surface Dirac cones. In our case, an odd number of them reflects the odd number of bulk band inversions, thus confirming the Z₂ topological-metal nature [3] of ZrOsSi, as highlighted by the zoomed images in the rightmost panels in Figure 6B. The surface states relevant to our discussion are most evident at $\sim 0.05$ eV below the Fermi level, at the $\bar{X}$ point, and at $\sim 0.4$ eV below the Fermi level, at the $\bar{Y}$ point. Hence, the normal state of ZrOsSi, which is like a strong topological insulator, is qualitatively different from that of its isostructural counterparts (Ta,Nb)OsSi, which are nonsymmorphic symmetry-protected semimetals [11–14]. The basic difference between insulating and metallic character of these materials can be probed, for instance, by NMR experiments. Therefore, in the following section, we report about and discuss our systematic investigation of these materials using NMR.

2.2 ²⁹Si NMR: ZrOSi vs. TaOsSi and NbOsSi

NMR investigations of AOsSi (A = Ta, Nb and Zr) are, in principle, very suitable, considering the presence of three NMR-active nuclei: A, Os and Si. However, the large spin and/or quadrupole moments of ⁹³Nb and ¹⁸¹Ta, and the low-frequency, low-abundance of ⁹¹Zr, make the A nuclei inapt for NMR experiments. Similarly, ¹⁸⁹Os has a low natural abundance and a low gyromagnetic ratio. These factors suggest the I = 1/2 ²⁹Si nucleus as the only viable microscopic probe for a systematic study of the AOsSi series. Since the magnetic field required for the NMR experiments suppresses an already low superconducting T_c (of only ∼ 1.7 K in the ZrOsSi case [15]), we had to limit our investigations to the normal-state electronic properties of ZrOsSi. Yet, this is not a major limitation, since we can still investigate the consequences of the nontrivial band topology of ZrOsSi, as compared with the conventional TaOsSi and NbOsSi metals. Note that, for ²⁹Si to be an effective probe, the Si 3p orbitals should contribute to the inverted bands responsible for the topological properties (here, the red band in Figure 2). As clearly evidenced from the orbital resolved DOS shown in Figure 5, this is indeed the case, further justifying the use of ²⁹Si NMR as a probe of the topological properties of ZrOsSi.

The ²⁹Si NMR spectra, collected at selected temperatures in a 7-T field, are shown in Figure 7. Since the NMR line shapes of TaOsSi and NbOsSi are quite similar, here we compare the representative line shapes of TaOsSi in Figure 7A with those of ZrOsSi in Figure 7B. In TaOsSi we observe a narrow main peak (at 59.785 MHz), followed by a secondary hump of negligible magnitude to the right. The latter is most likely due to impurities—probably arising from unreacted components—beyond the detection threshold of XRD. The unique crystallographic position of Si nuclei inside the Pnma structure of TaOsSi is reflected in the single main peak. Its position is almost independent of temperature and it shows only a smooth increase in width as the temperature is lowered. The shift from the ²⁹Si reference frequency decreases with temperature, to saturate below 100 K. Such trends are more clearly seen in Figure 8, where the evolution of both shifts and widths with temperature is quite smooth. In particular, the limited increase in width as the temperature is lowered is typical of nonmagnetic materials.

FIGURE 7

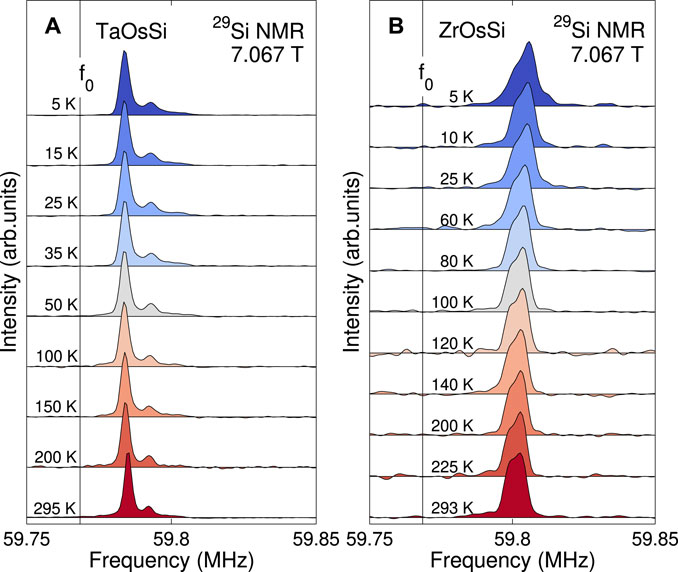
FIGURE 7. ²⁹Si NMR line shapes of powder samples measured at ∼ 7 T in TaOsSi (A) and ZrOsSi (B). The vertical lines at f₀ denote the reference Si-NMR signal. As the temperature is lowered, the lineshapes broaden and shift smoothly to higher frequencies. Note the much narrower lines and smaller shifts in TaOsSi vs. ZrOsSi, here highlighted by using the same frequency scale.

FIGURE 8

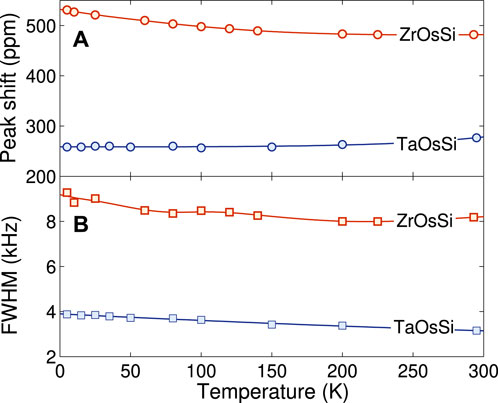
FIGURE 8. Temperature dependence of (A) ²⁹Si NMR line shifts and (B) ²⁹Si NMR line widths for ZrOsSi and TaOsSi. The full lines are guides to the eye. In ZrOsSi, the shift decreases by 9% in the investigated temperature range. The limited change in linewidth indicates the lack of a magnetic order. In TaOsSi, both shifts and widths are much smaller than in ZrOsSi.

Although normally silicon exhibits single narrow peaks, in ZrOsSi we observe a double NMR peak (centered at 59.8 MHz), compatible with its atomic coordination. Here, Si atoms reside in the 4c sites of the orthorhombic structure shown in Figure 1, bonded in a 10-coordinate geometry to 4-Os and 6-Zr atoms, on average 245 pm and 285 pm apart, respectively. Further, considering that Os is twice as electronegative as Zr, we expect a measurable line splitting into two groups with $\sim 2:3$ ratio, as experimentally observed. This assignment, however, should explain also the TaOsSi lines, since Ta and Zr have similar electronegativities and the two compounds have identical Pnma crystal structures (albeit with slightly different lattice parameters [15]). The different NMR lineshapes of TaOsSi and ZrOsSi (see Figure 7) might instead arise from the different topological character of ZrOsSi compared to that of the standard metal TaOsSi.

This hypothesis is indirectly confirmed by previous ⁷⁷Se NMR studies of the Bi₂Se₃ topological insulator, which also shows two distinct peaks in the NMR spectra, of which the shoulder was assigned to the topologically nontrivial surface effects [28]. These results suggest that NMR may be used as a sensitive and effective probe of the nontrivial surface states in topological insulators, although a detailed theoretical backing is still missing.

As shown in Figure 8, in the normal state, ZrOsSi exhibits a²⁹Si-NMR shift of ca. 500 ppm and a line width of ca. 8.5 kHz, both of which decrease smoothly with temperature, to saturate above 200 K. In contrast with metallic TaOsSi, where the electronic environment of Si nuclei is more homogeneous, the twofold larger line width of ZrOsSi reflects its insulating nature. In general, the total shift K, consists of an orbital- (chemical) K_orb and a spin part K_s. Considering the $\sim 200$ ppm chemical shift of sixfold coordinated Si [43], the shift we observe in ZrOsSi is essentially of chemical nature ($\sim 350$ ppm), with the spin contribution (arising from the conduction electrons) being marginal. This, too, is indicative of a poor metallic behavior, as confirmed also by electronic band-structure calculations, which indicate a deeply suppressed density of states at the Fermi level, here dominated by the Os- and Zr d-orbitals. We expect this to be reflected in very long spin-lattice relaxation times.

Indeed, this is confirmed by a comparison of the 1/T₁ relaxation rates of ZrOsSi with that of its isostructural counterparts NbOsSi and TaOsSi, as shown in Figure 9 (Ta, Nb)OsSi show fast relaxation rates (even at low temperature) and a practically linear dependence of 1/T₁ vs. T (Figure 9A). This is evident also from their almost constant Korringa product [44] 1/(T₁T) (=6.5 × 10⁻³ s⁻¹K⁻¹), shown in Figure 9B. The relatively small value of the Korringa product indicates a low electronic density of states at the Fermi level E_F of NbOsSi and TaOsSi, a result compatible with the electronic band-structure calculations [36], which suggest that, even in the presence of SOC, both compounds retain their metallic character. These results are in stark contrast with the relaxation rates and the 1/(T₁T) product of ZrOsSi, almost an order of magnitude smaller, typical of semimetals or insulating materials.

FIGURE 9

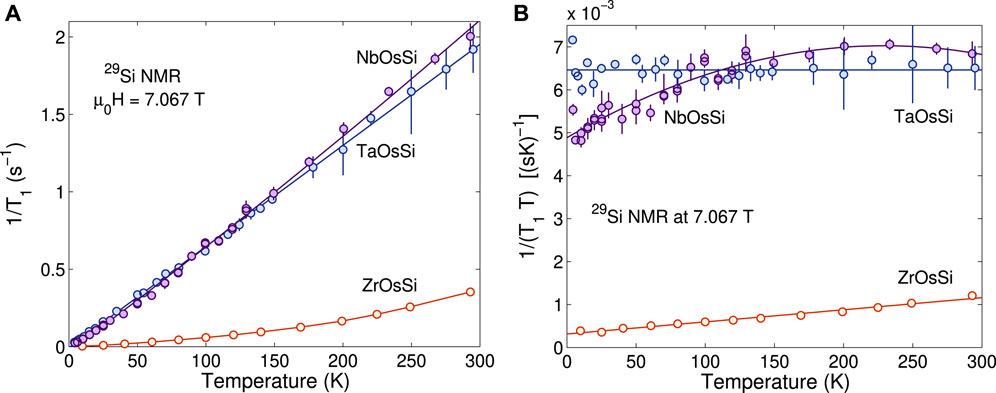
FIGURE 9. Comparison of the NMR relaxation rates. Comparison of (A) $\frac{1}{T_1}$ and (B) $\frac{1}{T_{1}T}$ vs. temperature for ZrOsSi, NbOsSi, and ZrOsSi. While the last two show a very similar (almost) linear behavior, ZrOsSi exhibits an almost quadratic dependence on T. In addition the density of states of ZrOsSi (see panel b) is a factor of ten lower, most likely reflecting its expanded lattice constants.

The NMR results in the normal state of (Ta, Nb)OsSi discussed above are in agreement with the resistivity measurements [14, 36], which show that the low-temperature resistivity follows a T²-law, i.e., these materials exhibit a good Fermi-liquid behavior. Recently, (Ta, Nb)OsSi were reported to be nonsymmorphic symmetry-protected semimetals [11–14], with the SOC effects playing a crucial role in determining their topological properties. Although NMR is not a direct probe of the topological properties, the lack of any anomalous behavior in the electronic properties of (Ta, Nb)OsSi as seen by NMR is a bit surprising, since one expects to see a change in the NMR shift if SOC changes the electronic band structure [20–23]. In view of the strikingly different electronic behavior of (Ta, Nb)OsSi vs. ZrOsSi (see Figure 9), one might wonder whether SOC has some role to play, which prompts for a closer comparison of the different SOC strengths of these materials.

The calculation of SOC is not straightforward. However, thanks to the early efforts of Herman [45, 46], based on the Hartree-Fock method, as well as to more recent results (see, e.g., Figure 1 in Ref. [47]), we have reliable estimates of SOC for all the elements. Considering the almost ∼ Z² dependence of SOC with the atomic number Z, we expect it to increase slightly from the 4d-element Zr (Z = 40) to the 4d-element Nb (Z = 41), and even more so to the 5d-element Ta (Z = 73). A similar trend is indeed found from band-structure calculations: while the SOC-induced maximum band splitting near the Fermi level is $\sim 100$ meV in both ZrOsSi (see Figure 2) and NbOsSi [14], it is $\sim 140$ meV in TaOsSi [36]. We note that since both Nb and Ta belong to group-5 of the periodic table, their comparison excludes the role of valence electrons and highlights that of SOC.

However, since the experimental results in Figure 9 show the NbOsSi and TaOsSi datasets to be basically clustered together, possibly the SOC effects are not the driving force for the observed phenomena. To justify these results we note that Zr exhibits a lower formal valency (+4), resulting in larger atomic and lattice parameters. Therefore, it does not come as a surprise that Zr acts as a lattice expander and moves the material towards the insulating side. Indeed, although the NbOsSi, TaOsSi, and ZrOsSi silicides share the same TiNiSi-type structure (space group Pnma, Z = 4), ZrOsSi is very different from the other two. (i) While NbOsSi and TaOsSi have practically the same cell parameters and unit-cell volume (differing by less than 0.5%), ZrOsSi shows an 8.6% increase in unit-cell volume, with a remarkable increase in all the cell parameters (a ∼ + 1.7%, b ∼ + 3.95%, c ∼ + 2.2%). (ii) The coordinates of Si (both relative and absolute) inside the unit cell change remarkably in ZrOsSi, implying an increase of ca. 3.5% in the interatomic distances [15].

The clear conjecture, therefore, is that the replacement of Nb (or Ta) with Zr corresponds to an expansion of the crystal lattice (i.e., to a negative chemical pressure) and consequently to a significant weakening of its metallic nature. These conclusions, are in good agreement with the atomic and covalent radii [48] of Nb and Ta (both being very similar and with the same formal valence of +5), to be contrasted with the 8% larger radius of Zr (with a formal valence +4 and here acting as lattice expander).

Incidentally, the negative chemical pressure occurring in ZrOsSi complements well our previous high-pressure study of TaOsSi [36], i.e., it allows us to understand how TaOsSi would have behaved under lattice expansion. As such, it would be interesting to investigate ZrOsSi further by means of other experimental techniques.

3 Discussion

Now we discuss critically some of our results, by comparing them with those of other topological materials. In principle, NMR is not the most suitable technique for studying topological phases of matter. Certainly, it is worth noting that while NMR is a local probe, the topological invariants however are nonlocal. Additionally, NMR primarily delves into the bulk properties, whereas topological invariants become apparent at the material’s boundaries. Nonetheless, these challenges have not discouraged a multitude of experimental endeavors [20–23] aimed at detecting direct or indirect signatures of topological invariants through NMR methods.

In particular, the use of nanoparticles allows for a more direct sampling of the surface states of a TI. The situation is similar to the NMR studies of superconductors which, in principle, would be very difficult, since RF fields cannot penetrate an ideal conductor. Surprisingly, with clever experiments, an ill-suited technique can still be made useful to provide the SC gap, the type of pairing, etc. [49–51].

Also in case of topological materials, the above experiments have been partly successful, although the results appear to offer conflicting responses (see, e.g., [22]). This is in part due to the lack of theoretical guidance and to the fact that calculations need to refer to the exact nucleus and compound under study. This is further complicated by the computationally difficult task of carrying DFT calculations of NMR shifts in conducting and strongly spin-orbit coupled crystals [24]. Finally, it is not easy to single out the orbital effects in NMR shifts (peculiar to each material), as opposed to the universal features expected for topological invariants. All the above facts suggest that further theoretical research is needed to enable the detection of genuine topological signatures via bulk NMR.

On the experimental side, large surface-to-volume samples (e.g., powders) are needed to detect and characterize the nuclei in the proximity of the topologically-protected surface states. While nanopowders are advantageous in this respect, their electronic band structures may be altered significantly due to quantum size effects. Consequently, standard powders (as in our case) might represent a good compromise for obtaining a suitable NMR signal from the topological phases despite a modest surface-to-volume ratio. In general, it has been shown that even the bulk NMR properties of these materials can provide crucial insight. For example, the real-space signature of band inversion can be seen as a charge re-distribution between different crystal sites. Hence, NMR together with DFT can be used to identify, e.g., Bi₂Se₃ as a topological insulator already from its bulk properties [22].

Unfortunately, for the time being it is difficult to find universal signatures, considering that the real NMR results depend crucially on the material under study and are often contradictory. For example, in our ZrOsSi case, T₁ values are longer and shifts are positive compared to their metallic counterparts, TaOsSi and NbOsSi. However, these are exactly opposite to the ²⁰⁹Bi NMR results in YPdBi and YPtBi, where the authors conclude that “it seems plausible that short T₁ values and negative shifts are universal features of the band inversion in topologically nontrivial materials” [21]. From the above discussion, it is clear that, while NMR is able to distinguish topological nontrivial materials from their standard counterparts, such signature is far from universal and of not an easy interpretation.

4 Conclusion

(Ta, Nb, Zr)OsSi are topological semimetals whose crystal structure has a very low degree of symmetry. As a result, they provide a unique opportunity to identify the nature of their different electronic phases based on symmetry considerations alone. For example, the time-reversal symmetry (TRS) breaking superconducting states stabilized in (Ta,Nb)OsSi can be identified as nonunitary triplet types. The nonsymmorphic glide mirror symmetries of the Pnma space group play an important role in determining the topological properties of (Ta, Nb)OsSi. While (Ta,Nb)OsSi are nonsymmorphic symmetry-protected semimetals [11–14], ZrOsSi is a Z₂ topological metal. As a result, ZrOsSi is expected to realize ordered phases that are qualitatively different from those of (Ta,Nb)OsSi. ZrOsSi also superconducts [15], but its transition temperature, T_c ∼ 1.7 K, is much lower than T_c ∼ 5.5 K of TaOsSi and T_c ∼ 3.1 K of NbOsSi [14]. Given that the superconducting ground states of (Ta,Nb)OsSi break TRS, it would be interesting to look for TRS-breaking superconductivity in ZrOsSi. Most importantly, since ZrOsSi is similar to a doped topological insulator [35], it could act as a platform for realizing a novel topological superconducting ground state. In addition, unlike (Cs,Rb,K)V₃Sb₅ [9], ZrOsSi does not bring the complications arising from inherent geometric frustration of crystal structure. This makes it a very attractive candidate for studying the interplay between topology and electronic correlations.

In summary, from detailed DFT band-structure calculations combined with extensive NMR measurements, we show that replacing Ta or Nb in (Ta, Nb)OsSi with Zr, modifies qualitatively the properties of the compound. We prove that, although all of them are superconductors, (Ta,Nb)OsSi are very good metals, while ZrOsSi exhibits features of a doped strong topological insulator. In general, since all the three materials are topologically nontrivial and superconduct at ambient pressure, they provide possible candidate platforms for realizing topological superconductivity in stoichiometric materials. Our results further confirm that the combination of DFT and NMR is a powerful tool to investigate the topological properties of quantum materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SKG: Conceptualization, Data-curation, Investigation, Writing–original draft, Writing–review and editing. BL: Data-curation, Investigation, Software, Writing–review and editing. CX: Data-curation, Investigation, Writing–review and editing. AH: Data-curation, Investigation, Writing–review and editing. PB: Investigation, Writing–review and editing. XX: Conceptualization, Data-curation, Investigation, Project-administration, Writing–review and editing. TS: Conceptualization, Data-curation, Investigation, Project-administration, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. SKG acknowledges the Indian Institute of Technology, Kanpur for financial support through the Initiation Grant (IITK/PHY/2022116). XX acknowledges the financial support from the National Natural Science Foundation of China under Grant nos. 11974061 and 12274369. This work was financially supported in part by the Schweizerische Nationalfonds zur Förderung der Wissenschaftlichen Forschung (SNF), Grant no. 200021-169455. Open access funding was provided by the PSI—Paul Scherrer Institute.

Acknowledgments

The authors acknowledge T. Tula and J. Quintanilla for enlightning discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90:015001. doi:10.1103/RevModPhys.90.015001

CrossRef Full Text | Google Scholar

2. Lv BQ, Qian T, Ding H. Experimental perspective on three-dimensional topological semimetals. Rev Mod Phys (2021) 93:025002. doi:10.1103/RevModPhys.93.025002

CrossRef Full Text | Google Scholar

3. Ortiz BR, Teicher SML, Hu Y, Zuo JL, Sarte PM, Schueller EC, et al. CsV₃Sb₅: a Z₂ topological kagome metal with a superconducting ground state. Phys Rev Lett (2020) 125:247002. doi:10.1103/PhysRevLett.125.247002

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sakano M, Okawa K, Kanou M, Sanjo H, Okuda T, Sasagawa T, et al. Topologically protected surface states in a centrosymmetric superconductor β-PdBi₂. Nat Commun (2015) 6:1–7. doi:10.1038/ncomms9595

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ghosh SK, Smidman M, Shang T, Annett JF, Hillier AD, Quintanilla J, et al. Recent progress on superconductors with time-reversal symmetry breaking. J Phys Condens Matter (2020) 33:033001. doi:10.1088/1361-648X/abaa06

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Shang T, Ghosh SK, Smidman M, Gawryluk DJ, Baines C, Wang A, et al. Spin-triplet superconductivity in Weyl nodal-line semimetals. Npj Quan Mater (2022) 7:1–9. doi:10.1038/s41535-022-00442-w

CrossRef Full Text | Google Scholar

7. Badger JR, Quan Y, Staab MC, Sumita S, Rossi A, Devlin KP, et al. Dirac lines and loop at the Fermi level in the time-reversal symmetry breaking superconductor LaNiGa₂. Commun Phys (2022) 5:22. doi:10.1038/s42005-021-00771-5

CrossRef Full Text | Google Scholar

8. Ghosh SK, Csire G, Whittlesea P, Annett JF, Gradhand M, Újfalussy B, et al. Quantitative theory of triplet pairing in the unconventional superconductor LaNiGa₂. Phys Rev B (2020) 101:100506. doi:10.1103/PhysRevB.101.100506

CrossRef Full Text | Google Scholar

9. Neupert T, Denner MM, Yin JX, Thomale R, Hasan MZ. Charge order and superconductivity in kagome materials. Nat Phys (2022) 18:137–43. doi:10.1038/s41567-021-01404-y

CrossRef Full Text | Google Scholar

10. Jiang K, Wu T, Yin JX, Wang Z, Hasan MZ, Wilson SD, et al. Kagome superconductors AV₃Sb₅ (A = K, Rb, Cs). Natl Sci Rev (2022) 9:nwac199. doi:10.1093/nsr/nwac199

CrossRef Full Text | Google Scholar

11. Wang Z, Alexandradinata A, Cava RJ, Bernevig BA. Hourglass fermions. Nature (2016) 532:189–94. doi:10.1038/nature17410

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li S, Liu Y, Wang SS, Yu ZM, Guan S, Sheng XL, et al. Nonsymmorphic-symmetry-protected hourglass Dirac loop, nodal line, and Dirac point in bulk and monolayer X₃SiTe₆ (X = Ta, Nb). Phys Rev B (2018) 97:045131. doi:10.1103/PhysRevB.97.045131

CrossRef Full Text | Google Scholar

13. Cuono G, Forte F, Cuoco M, Islam R, Luo J, Noce C, et al. Multiple band crossings and Fermi surface topology: role of double nonsymmorphic symmetries in MnP-type crystal structures. Phys Rev Mater (2019) 3:095004. doi:10.1103/PhysRevMaterials.3.095004

CrossRef Full Text | Google Scholar

14. Ghosh SK, Biswas PK, Xu C, Li B, Zhao JZ, Hillier AD, et al. Time-reversal symmetry breaking superconductivity in three-dimensional Dirac semimetallic silicides. Phys Rev Res (2022) 4:L012031. doi:10.1103/PhysRevResearch.4.L012031

CrossRef Full Text | Google Scholar

15. Benndorf C, Heletta L, Heymann G, Huppertz H, Eckert H, Pöttgen R. NbOsSi and TaOsSi — two new superconducting ternary osmium silicides. Solid State Sci (2017) 68:32–8. doi:10.1016/j.solidstatesciences.2017.04.002

CrossRef Full Text | Google Scholar

16. Hasan MZ, Kane CL. Colloquium: topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

17. Wu S, Fatemi V, Gibson QD, Watanabe K, Taniguchi T, Cava RJ, et al. Observation of the quantum spin Hall effect up to 100 kelvin in a monolayer crystal. Science (2018) 359:76–9. doi:10.1126/science.aan6003

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Frolov SM, Manfra MJ, Sau JD. Topological superconductivity in hybrid devices. Nat Phys (2020) 16:718–24. doi:10.1038/s41567-020-0925-6

CrossRef Full Text | Google Scholar

19. Browne AJ, Krajewska A, Gibbs AS. Quantum materials with strong spin-orbit coupling: challenges and opportunities for materials chemists. J Mater Chem C (2021) 9:11640–54. doi:10.1039/D1TC02070F

CrossRef Full Text | Google Scholar

20. Massiot D, Messinger RJ, Cadars S, Deschamps M, Montouillout V, Pellerin N, et al. Topological, geometric, and chemical order in materials: insights from solid-state NMR. Acc Chem Res (2013) 46:1975–84. doi:10.1021/ar3003255

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Nowak B, Kaczorowski D. NMR as a probe of band inversion in topologically nontrivial half-Heusler compounds. J Phys Chem C (2014) 118:18021–6. doi:10.1021/jp505320w

CrossRef Full Text | Google Scholar

22. Nachtigal J, Chong SV, Williams GVM, Isaeva A, Oeckler O, Haase J, et al. ¹²⁵Te NMR study of the bulk of topological insulators Bi₂Te₃ and Sb₂Te₃. Z Anorg Allg Chem (2022) 648:e202200208. doi:10.1002/zaac.202200208

CrossRef Full Text | Google Scholar

23. Nisson DM, Curro NJ. Nuclear magnetic resonance Knight shifts in the presence of strong spin-orbit and crystal-field potentials. New J Phys (2016) 18:073041. doi:10.1088/1367-2630/18/7/073041

CrossRef Full Text | Google Scholar

24. Boutin S, Ramírez-Ruiz J, Garate I. Tight-binding theory of NMR shifts in topological insulators Bi₂Se₃ and Bi₂Te₃. Phys Rev B (2016) 94:115204. doi:10.1103/PhysRevB.94.115204

CrossRef Full Text | Google Scholar

25. Zhang X, Hou Z, Wang Y, Xu G, Shi C, Liu E, et al. NMR evidence for the topologically nontrivial nature in a family of half-Heusler compounds. Sci Rep (2016) 6:1–7. doi:10.1038/srep23172

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Young BL, Lai ZY, Xu Z, Yang A, Gu GD, Pan ZH, et al. Probing the bulk electronic states of Bi₂Se₃ using nuclear magnetic resonance. Phys Rev B (2012) 86:075137. doi:10.1103/PhysRevB.86.075137

CrossRef Full Text | Google Scholar

27. Koumoulis D, Chasapis TC, Taylor RE, Lake MP, King D, Jarenwattananon NN, et al. NMR probe of metallic states in nanoscale topological insulators. Phys Rev Lett (2013) 110:026602. doi:10.1103/PhysRevLett.110.026602

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Choi DM, Lee CE. ⁷⁷Se nuclear magnetic resonance study of the surface effect in topological insulator Bi₂Se₃ nanoparticles. J Korean Phys Soc (2018) 72:835–7. doi:10.3938/jkps.72.835

CrossRef Full Text | Google Scholar

29. Papawassiliou W, Jaworski A, Pell AJ, Jang JH, Kim Y, Lee SC, et al. Resolving Dirac electrons with broadband high-resolution NMR. Nat Commun (2020) 11:1–7. doi:10.1038/s41467-020-14838-4

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Park JK, Kwon HJ, Lee CE. NMR observation of mobile protons in proton-implanted ZnO nanorods. Sci Rep (2016) 6:1–8. doi:10.1038/srep23378

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Hoch MJR, Holcomb DF. ³¹P Knight shifts and spin dynamics in Si:P at temperatures comparable to the Fermi temperature. Phys Rev B (2005) 71:035115. doi:10.1103/PhysRevB.71.035115

CrossRef Full Text | Google Scholar

32. Tian Y, Ghassemi N, Ross JH. Dirac electron behavior and NMR evidence for topological band inversion in ZrTe₅. Phys Rev B (2019) 100:165149. doi:10.1103/PhysRevB.100.165149

CrossRef Full Text | Google Scholar

33. Guehne R, Haase J, Shekhar C, Felser C. Field-induced charge symmetry revealed by nuclear magnetic resonance in the topological insulator Bi₂Te₃. Phys Rev Res (2021) 3:L012018. doi:10.1103/PhysRevResearch.3.L012018

CrossRef Full Text | Google Scholar

34. Dioguardi AP, Yasuoka H, Thomas SM, Sakai H, Cary SK, Kozimor SA, et al. ²³⁹Pu nuclear magnetic resonance in the candidate topological insulator PuB₄. Phys Rev B (2019) 99:035104. doi:10.1103/PhysRevB.99.035104

CrossRef Full Text | Google Scholar

35. Sato M, Ando Y. Topological superconductors: a review. Rep Prog Phys (2017) 80:076501. doi:10.1088/1361-6633/aa6ac7

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Xu CQ, Li B, Feng JJ, Jiao WH, Li YK, Liu SW, et al. Two-gap superconductivity and topological surface states in TaOsSi. Phys Rev B (2019) 100:134503. doi:10.1103/PhysRevB.100.134503

CrossRef Full Text | Google Scholar

37. Blaha P, Schwarz K, Tran F, Laskowski R, Madsen GKH, Marks LD. WIEN2k: an APW+lo program for calculating the properties of solids. J Chem Phys (2020) 152:074101. doi:10.1063/1.5143061

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Campbell D, Collini J, Sławińska J, Autieri C, Wang L, Wang K, et al. Topologically driven linear magnetoresistance in helimagnetic FeP. Npj Quan Mater (2021) 6:38. doi:10.1038/s41535-021-00337-2

CrossRef Full Text | Google Scholar

40. Fu L, Kane CL. Topological insulators with inversion symmetry. Phys Rev B (2007) 76:045302. doi:10.1103/PhysRevB.76.045302

CrossRef Full Text | Google Scholar

41. Soluyanov AA, Vanderbilt D. Computing topological invariants without inversion symmetry. Phys Rev B (2011) 83:235401. doi:10.1103/PhysRevB.83.235401

CrossRef Full Text | Google Scholar

42. Wu Q, Zhang S, Song HF, Troyer M, Soluyanov AA. WannierTools: an open-source software package for novel topological materials. Comput Phys Commun (2018) 224:405–16. doi:10.1016/j.cpc.2017.09.033

CrossRef Full Text | Google Scholar

43. Marsmann HC. ²⁹Si NMR. In: JC Lindon, editor. Encyclopedia of spectroscopy and spectrometry. Oxford: Elsevier (1999). p. 2031–42. doi:10.1006/rwsp.2000.0277

CrossRef Full Text | Google Scholar

44. Korringa J. Nuclear magnetic relaxation and resonnance line shift in metals. Physica (1950) 16:601–10. doi:10.1016/0031-8914(50)90105-4

CrossRef Full Text | Google Scholar

45. Herman F, Kuglin CD, Cuff KF, Kortum RL. Relativistic corrections to the band structure of tetrahedrally bonded semiconductors. Phys Rev Lett (1963) 11:541–5. doi:10.1103/PhysRevLett.11.541

CrossRef Full Text | Google Scholar

46. Herman F, Skillman S. Atomic structure calculations. Englewood Cliffs, NJ, USA: Prentice Hall (1963)

Google Scholar

47. Shanavas KV, Popović ZS, Satpathy S. Theoretical model for Rashba spin-orbit interaction in d electrons. Phys Rev B (2014) 90:165108. doi:10.1103/PhysRevB.90.165108

CrossRef Full Text | Google Scholar

48. Cordero B, Gómez V, Platero-Prats AE, Revcés M, Echeverría J, Cremades E, et al. Covalent radii revisited. Dalton Trans (2008) 21:2832. doi:10.1039/b801115j

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Hebel LC, Slichter CP. Nuclear spin relaxation in normal and superconducting aluminum. Phys Rev (1959) 113:1504–19. doi:10.1103/PhysRev.113.1504

CrossRef Full Text | Google Scholar

50. Weger M. NMR in superconductors. Pure Appl Chem (1972) 32:325–38. doi:10.1351/pac197232010325

CrossRef Full Text | Google Scholar

51. MacLaughlin DE. Magnetic resonance in the superconducting state. In: H Ehrenreich, F Seitz, and D Turnbull, editors. Solid state physics. San Diego, CA, USA: Academic Press (1976). p. 1–69. doi:10.1016/S0081-1947(08)60541-X

CrossRef Full Text | Google Scholar