A strong-field THz light source based on coherent transition radiation

Terahertz (THz) radiation is a powerful tool for exploring various scientific frontiers through THz pump–probe experiments. However, different experiments may require THz radiation with different spectral properties, such as broad-band or narrow-band, which are difficult to be generated by a single light source. In this paper, we propose a THz light source that can produce both types of THz radiation by manipulating the longitudinal profile of an electron beam and exploiting coherent transition radiation. We perform theoretical analysis and numerical simulations based on the parameters of the Shanghai soft X-ray Free-Electron Laser facility, and the results show that the proposed light source can generate broad-band THz radiation with a pulse energy of 342 µJ and narrow-band THz radiation with a pulse energy of 91 µJ. The proposed light source can offer more flexibility and versatility for free-electron laser (FEL) users to conduct THz pump–probe experiments.

1 Introduction

Terahertz (THz) radiation, which lies between 0.1 THz and tens of THz, is widely used in many industrial applications, such as medical imaging, quality testing, and wireless communication [1, 2]. In recent years, THz radiation has become increasingly important in many scientific frontiers with the development of strong-field THz, which can be used to conduct the so-called THz pump–probe experiments. THz users from different scientific fields need THz radiation with different spectral properties: narrow-band THz radiation can manipulate transient substances (lattice vibration, spin precession, and atomic photoionization emission) [3–7], be used to study the transition from insulators to metals or the ultrafast melting of metals [8], and achieve quantum control in information science [9]. However, broad-band THz is more suitable to do the time-domain spectral analysis of materials [10–12] and study nonlinear physical phenomena [13] because it has higher peak field strength and contains many characteristic fingerprints of materials between 0.1 and 5 THz.

Presently, strong-field THz radiation can be produced by ultrafast laser [14, 15], laser-produced plasma [16–21], and an electron accelerator [22, 23]. Among them, the electron accelerator-based THz light source has been treated as a reliable method to produce strong-field THz radiation with tunable frequency. In recent years, THz radiation in a high-gain free-electron laser (FEL) facility [24–29] has been one of the main choices for producing strong-field THz radiation, and the FEL facility can generate synchronized high-power X-ray pulse, which has been an excellent experimental platform for THz pump–probe experiments. In an FEL facility, THz radiation with a broad spectral bandwidth of about 10% can be obtained by compressing the duration of the electron beam into 1 THz period [24–26]. However, since it is difficult to compress beam length below 100 femtosecond (fs) and the spectral bandwidth is relative broad due to the single THz period, the THz frequency is limited to about 5 THz. On the contrary, the electron beam train, produced by direct laser pulse stacking [30], transverse and longitudinal phase space exchange [31], dielectric tube wakefield modulation [32, 33], and space-charge oscillation modulation [34, 35], can be used to obtain THz radiation with higher frequency and relative narrower bandwidth. However, it is hard to obtain both broad-band and narrow-band THz radiation with the same THz light source.

In this paper, a THz light source has been proposed to generate both broad-band and narrow-band THz pulses by manipulating the longitudinal profile of the electron beam. When the electron beam passes through the interface between media with different dielectric constants, it can produce THz radiation with different spectral properties: broad-band for the single-period beam and narrow-band for the bunch train. The paper is organized as follows: the principles of the method are introduced in Section 2. The simulation results using the parameters of the Shanghai soft X-ray free-electron laser facility (SXFEL) are presented in Section 3. Finally, some concluding comments are given in Section 4.

2 Principles and methods

The coherent transition radiation (CTR) is a dipole field radiation generated on both sides of two media due to the collapse and expansion of the dipole field [36, 37]. The radiation power can be expressed by Larmor’s formula $P=2e^2{a}^2{\gamma }^4/3c^3$, where e is the electron charge, a is the acceleration, c is the speed of light, and $\gamma$ is the relativistic factor [38]. According to Larmor’s formula, the coherent radiation power is proportional to the fourth power of the beam energy so that high-energy electron beams are generally required to produce strong-field THz pulses. The schematic layout of the proposed THz light source is shown in Figure 1. The proposed THz light source can produce both broad-band THz radiation and narrow-band strong-field THz radiation.

FIGURE 1

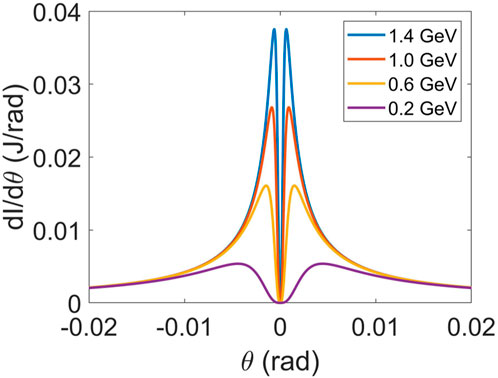
FIGURE 1. Schematic layout of the proposed THz light source based on the CTR. The modulation and dispersion sections (in the red box) are turned off and treated as drift sections for the broad-band radiation case.

2.1 Transition radiation of the compressed electron beam

In Figure 1, an electron beam with an energy chirp is first generated by Linac 1, and then the electron beam is compressed by the magnetic bunch compressor (BC), where the length of the electron beam can be controlled by adjusting the energy chirp and the intensity of the BC. Generally, the longitudinal structures of the electron beam can be expressed by the following equation:

$S\left(z,{\sigma }_z\right)=\frac{\mathit{exp}\left(-\frac{z^2}{2{\sigma }_z^2}\right)}{\sqrt{2\pi }{\sigma }_z},(1)$

where Z is the longitudinal coordinate of the electron beam and ${\sigma }_z$ is the length of the electron beam (rms). After that, the compressed electron beam passes through another accelerator section (Linac 2) to reach the final beam energy. The beam then produces transition radiation by passing through a metal foil directly, without the modulation and dispersion sections (chicane) in Figure 1, which are treated as drift sections (turning powers off). We use an aluminum (Al) foil as an example since the material of the foil has little effect on THz transition radiation [39, 40].

The transition radiation can be divided into forward radiation and backward radiation, which have different formation length L. Compared with forward radiation, backward radiation has a much shorter formation length [41, 42] and is easier to be collected. If only considering backward radiation, the transition radiation of a single electron can be expressed by the Ginzburg–Frank formula [36].

$\frac{d^2{P}_e}{d\mathrm{\Omega }dk}=\frac{r_{e}m{c}^2}{{\pi }^2}\frac{{\beta }^2{\mathit{sin}}^2\theta }{{\left(1-{\beta }^2{\mathit{cos}}^2\theta \right)}^2},(2)$

where $r_e$ is the classical electron radius, m is the rest mass of the electron, $\mathrm{\Omega }$ is the solid angle, k is the wave number of radiation, $\beta$ is the relative speed, and $\theta$ is the angle measured against the backward radiation. For an electron beam, the form factor of the electron beam $F\left(k,{\sigma }_z\right)={\left|\int e^{ikz}S\left(z,{\sigma }_z\right)dz\right|}^2$ is the square of the Fourier transform result for the normalized longitudinal particle distribution within the electron beam, which greatly affects the intensity of transition radiation. The form factor of the compressed electron beam can be expressed as follows:

$F_b\left(k,{\sigma }_z\right)=e^{{-\left(k{\sigma }_z\right)}^2}.(3)$

The transition radiation of an electron beam can be expressed by the Nodvick–Saxon formula [43].

$\frac{d^{2}P}{d\mathrm{\Omega }dk}=\frac{d^2{P}_e}{d\mathrm{\Omega }dk}\left[N+N\left(N-1\right)\times F\left(k,{\sigma }_z\right)\right],(4)$

where N is the number of the electrons. According to Eq. 4, the total radiation intensity can be simplified as $N\frac{d^2{P}_e}{d\mathrm{\Omega }dk}$ for $F\left(k,{\sigma }_z\right)=0$, which is called incoherent transition radiation. On the contrary, the total radiation intensity can be simplified as $N^2\frac{d^2{P}_e}{d\mathrm{\Omega }dk}$ for $F\left(k,{\sigma }_z\right)=$ 1, which is known as CTR. When substituting Eqs. 2, 3 into Eq. 4 and only considering CTR, the CTR intensity of the compressed electron beam can be obtained using the following equation:

$\frac{d^{2}P}{d\mathrm{\Omega }dk}=\frac{N^2{\beta }^2{r}_{e}m{c}^2}{{\pi }^2}\frac{{\mathit{sin}}^2\theta }{{\left(1-{\beta }^2{\mathit{cos}}^2\theta \right)}^2}\times e^{{-\left(k{\sigma }_z\right)}^2}.(5)$

Taking $d\mathrm{\Omega }=2\pi \mathit{sin}\theta d\theta$ and integrating wave number k of radiation, the angular distribution of the CTR can be expressed as follows:

$\frac{dP}{d\theta }=\frac{N^2{\beta }^2{r}_{e}m{c}^2}{\sqrt{\pi }{\sigma }_z}\times \frac{{\mathit{sin}}^3\theta }{{\left(1-{\beta }^2{\mathit{cos}}^2\theta \right)}^2}.(6)$

According to Eq. 6, the CTR has a conical distribution with the maximum intensity at angle $\theta ={\mathit{sin}}^{-1}\left(\sqrt{3}/\sqrt{{\gamma }^2-1}\right)$. When $\gamma$ is much greater than 1, the $\theta$ is approximately equal to $\sqrt{3}/\gamma$. In addition, taking $dk=-2\pi /{\lambda }^{2}d\lambda$ and integrating solid angle $\mathrm{\Omega }$, the energy spectrum of the CTR can be expressed as follows:

$\frac{dP}{d\lambda }=\frac{N^2{r}_{e}m{c}^2\left[2\mathit{ln}\left(2\gamma \right)-1\right]}{2\sqrt{\pi }{\sigma }_z}\times \mathit{Erf}\left(\frac{2\pi {\sigma }_z}{\lambda }\right),(7)$

where $\mathit{Erf}\left(x\right)=\left(2/\sqrt{\pi }\right){\int }_0^x{e}^{-{\eta }^2}d\eta$ is the error function. From Eq. 7, the CTR is a broad-band THz radiation with a center frequency related to length ${\sigma }_z$.

2.2 Transition radiation of the electron bunch train

To obtain narrow-band THz radiation, the CTR generated by an electron bunch train is also introduced. In Figure 1, an ultrafast laser is stretched by a parallel grating pair to introduce a linear chirp with chirp parameter $\left|\alpha \right|={1/\sigma }_0{\sigma }_{out}$, where ${\sigma }_0$ is the initial laser pulse length (rms) and ${\sigma }_{out}$ is the stretched laser pulse length. Furthermore, the stretched laser pulse is divided into two laser pulses by a beam splitter to introduce tunable time delay $\tau$ by a tunable optical delay line. Finally, the two laser pulses are recombined to obtain a frequency-beating laser pulse with a beating frequency [28, 29]

$f=\frac{\left|\alpha \right|\tau }{\pi }.(8)$

According to Eq. 8, the beating frequency can be continuously tuned by adjusting chirp parameter $\left|\alpha \right|$ and time delay $\tau$.

The electron beam at the exit of Linac 2 is sent into a modulation section together with the frequency-beating laser pulse to interact with each other. Due to the electron phase differences in the initial electron beam, some electrons obtain energy from the frequency-beating laser, while the other electrons transfer energy to the frequency-beating laser during the interaction. The energies of the electrons in the electron beam become different, resulting in periodic energy modulation over the wavelength of the frequency-beating laser [44, 45]. Then the modulated beam is sent to the chicane to convert the energy modulation into density modulation and obtain a pulse train structure with a THz period, which can be described as M Gaussian microbunches with a time interval of T. At the same time, the frequency-beating laser pulse is reflected out by an optical mirror. Finally, the electron bunch train passes through the Al foil to generate narrow-band THz radiation. Here, the form factor of the electron bunch train can be expressed as follows [46, 47]:

$F_t\left(k,{\sigma }_z\right)=e^{{-\left(k{\sigma }_s\right)}^2}\times {\left|\frac{\mathit{sin}\left(MkcT/2\right)}{Msin\left(kcT/2\right)}\right|}^2,(9)$

where ${\sigma }_s$ is the length of microbunch in the electron bunch train (rms). According to Eq. 9, the form factor has peaks at the resonance wavelength and its harmonics, which can be tuned by manipulating the frequency-beating laser pulse. Substituting Eqs 2, 9 into Eq. 4, the CTR intensity of the electron bunch train can be expressed as follows:

$\frac{d^{2}P}{d\mathrm{\Omega }dk}=\frac{N^2{\beta }^2{r}_{e}m{c}^2}{{\pi }^2}\frac{{\mathit{sin}}^2\theta }{{\left(1-{\beta }^2{\mathit{cos}}^2\theta \right)}^2}\times {\left|\frac{\mathit{sin}\left(MkcT/2\right)}{Msin\left(kcT/2\right)}\right|}^2\times e^{{-\left(k{\sigma }_s\right)}^2}.(10)$

Taking $dk=-2\pi /{\lambda }^{2}d\lambda$ and integrating solid angle $\mathrm{\Omega }$, the energy spectrum of the CTR can be expressed as follows:

$\frac{dP}{d\lambda }=\frac{4N^2{r}_{e}m{c}^2\left[-\beta +\left(1+{\beta }^2\right){\mathit{tanh}}^{-1}\beta \right]}{M^2{\lambda }^2\beta }\times \frac{-1+\mathit{cos}\left(\frac{2\pi cMT}{\lambda }\right)}{-1+\mathit{cos}\left(\frac{2\pi cT}{\lambda }\right)}\times e^{-\frac{4{\pi }^2{\sigma }_s^2}{{\lambda }^2}}.(11)$

3 Results

To illustrate the performance of the proposed method, simulations with the typical parameters of the SXFEL are performed; the detailed parameters are presented in Table 1. We use the ASTRA code [46] to simulate the beam dynamics in the photoinjector, and the ELEGANT code [48] to simulate the acceleration and compression processes in the LINAC. The beam dynamics in modulation and dispersion sections are simulated using the FALCON code [49].

TABLE 1

TABLE 1. Parameters of the electron beam and the laser system at the SXFEL.

3.1 Broad-band THz radiation generated by the compressed electron beam

In this simulation, an electron beam with a beam energy of 125 MeV, a pulse length of 1.7 ps, and a charge of 500 pC is produced at the entrance of the BC, and the bunch length can be easily adjusted with a minimum of 100 fs by tuning the current of the BC. The beam is then accelerated to 1.4 GeV by Linac 2. Finally, the beam passes through the Al foil with a thickness of several $\mu \mathrm{m}$ to produce the CTR. Here, an ideal longitudinal structure of the electron beam described in Eq. 1 is adopted, and then the form factors with different pulse lengths are shown in Figure 2.

FIGURE 2

FIGURE 2. Form factors of the compressed electron beams with different lengths.

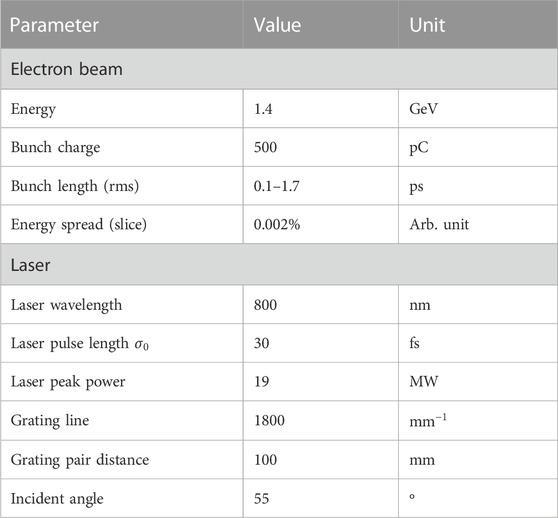
According to Figure 2, the form factor will decrease more slowly and have a relative wider bandwidth with the decrease of the beam length, and the CTR generated by the compressed electron beam will have a broad-band spectrum. Figure 3 shows the angular distributions of the CTR with a beam length of 100 fs and different energies.

FIGURE 3

FIGURE 3. Angular distributions of the CTR with a beam length of 100 fs and different energies.

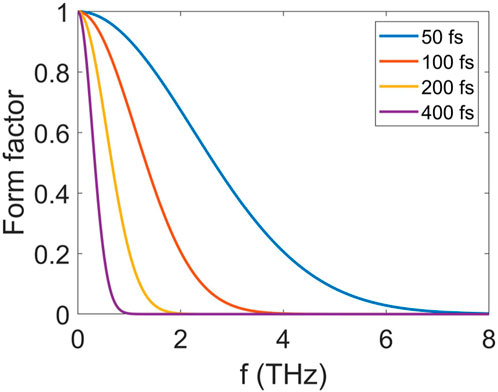
According to Figure 3, the angular distribution has a double-lobe distribution, which conforms to the conical distribution of the CTR. In addition, the intensity of the CTR will decrease and the divergence will increase with decrease in beam energy. For the electron beam with a beam energy of 1.4 GeV, the CTR has the maximal intensity at the angle of $6.28\times {10}^{-4}$ rad and has a good orientation, which is easy to be collected using an off-axis parabolic mirror. Figure 4 shows the CTR spectra generated by the electron beams with a beam energy of 1.4 GeV and different beam lengths.

FIGURE 4

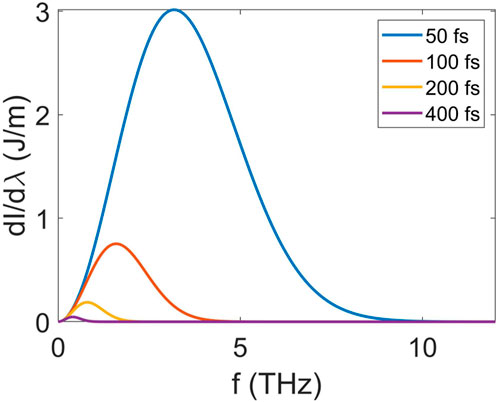
FIGURE 4. CTR spectra generated by the compressed electron beams with a beam energy of 1.4 GeV and different beam lengths.

From Figure 4, if f is less than $c/2.35{\sigma }_z$, the CTR intensity increases rapidly and has a maximum at $c/6{\sigma }_z$; otherwise, the enhancement effect disappears. The CTR intensity will increase with the decrease in the beam length and the center frequency is also proportional to the beam length; thus, an electron beam with a relative shorter beam length is beneficial to generate CTR radiation with a higher frequency and wider spectral bandwidth. However, compressing the length of the electron beam to below 100 fs generally is a significant challenge. The SXFEL can compress the electron beam to a final bunch length of 100 fs, and the beam can be used to generate CTR radiation with a pulse energy of 342 µJ and a frequency up to 5 THz. Moreover, the bunch length of the electron beam at SXFEL can easily be adjusted between 100 fs and 1.7 ps so the broad-band THz radiation can be produced from 0.1 to 5 THz.

3.2 Narrow-band THz radiation generated by the electron bunch train

To obtain THz radiation with a higher frequency and narrow spectral bandwidth, the CTR generated by a frequency-beating laser-modulated electron beam is also introduced. In this simulation, a laser pulse with the central wavelength of 800 nm and the initial pulse duration of 30 fs is adopted. The laser pulse is first stretched to 42 ps by the paralleled grating pair, and then a time delay of 40 ps is introduced to obtain the frequency-beating signal at the frequency of 10 THz (30 $\mu \mathrm{m}$). The longitudinal amplitude distributions and spectrum of the frequency-beating laser pulse are shown in Figures 5A, B, where one can observe that the fundamental wavelength is about 30 $\mu \mathrm{m}$.

FIGURE 5

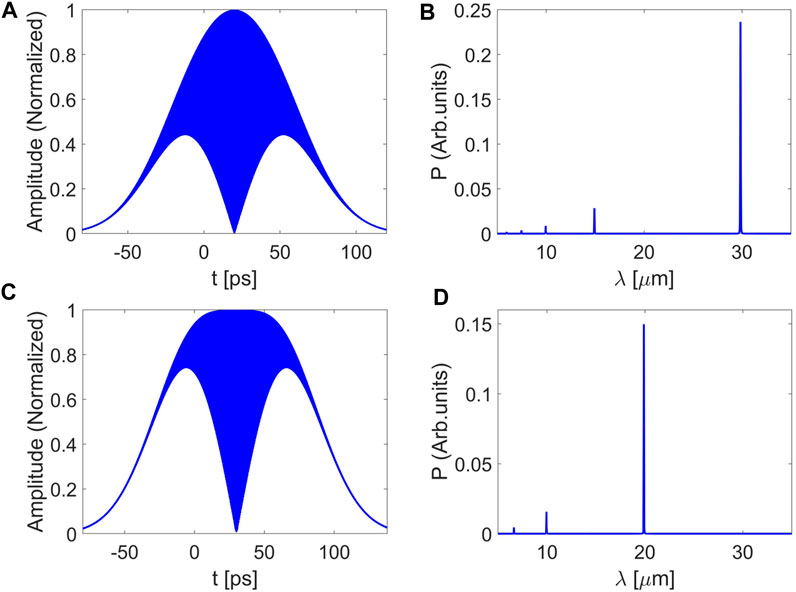
FIGURE 5. Longitudinal amplitude distributions of the seed laser at 10 THz (A) and 15 THz (C). Spectra of the seed laser at 10 THz (B) and 15 THz (D).

The beating frequency can be tuned by adjusting chirp parameter $\left|\alpha \right|$ and time delay $\tau$, which is limited by the initial laser power and pulse length. In theory, the beating frequency can be easily adjusted from 0.1 to 30 THz [29], while the number of modulation periods can decrease with the decrease in the beating frequency for limited electron bunch length, which may broaden the spectral bandwidth. In addition, the fundamental Fourier component decreases from 0.23 to 0.15 when the beating frequency is adjusted from 10 to 15 THz according to Figures 5C,D. For a larger beating frequency, a larger time delay τ will further decrease the fundamental Fourier component, which can decrease the final radiation power. To obtain a laser pulse with a larger beating frequency and sufficient fundamental Fourier component, higher initial laser power and shorter initial pulse length are required. Therefore, laser pulses with beating frequencies from 5 to 15 THz and sufficient fundamental Fourier component can be easily obtained by the frequency-beating technique. As an example, the frequency-beating laser pulse with a frequency of 10 THz is used as a seed in the following modulator.

Here, an electron beam with a full pulse length of 2 ps and a beam energy of 1.4 GeV at the exit of Linac 2 is adopted to simulate the performance. The frequency-beating laser pulse and the electron beam are sent into the modulation section to interact with each other and obtain the energy modulation with 20 periods at a frequency of 10 THz (100 fs). The electron beam passes through the modulator and the chicane with $R_{56}$ of 13.01 cm to convert the energy modulation into density modulation. The longitudinal phase spaces after the chicane and corresponding current profile of the electron bunch train are shown in Figure 6.

FIGURE 6

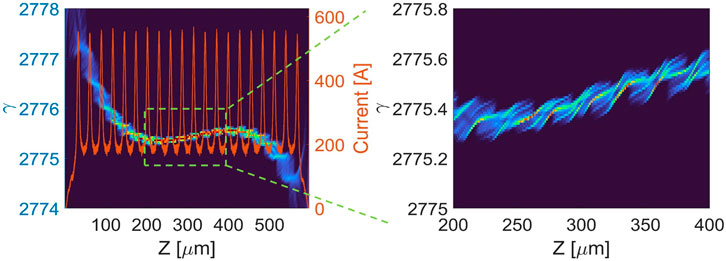
FIGURE 6. Longitudinal phase space and corresponding current profile of the electron bunch train (left) and local amplification in the phase space of the electron bunch train (right).

From Figure 6, one can find that the electron bunch train includes 20 microbunches, where the pulse length of each microbunch ${\sigma }_s$ is 19.2 fs and time interval T is 100 fs. Figure 7 shows the form factors of the electron bunch trains with different numbers of microbunches and the CTR spectrum generated by the electron bunch train with 20 microbunches.

FIGURE 7

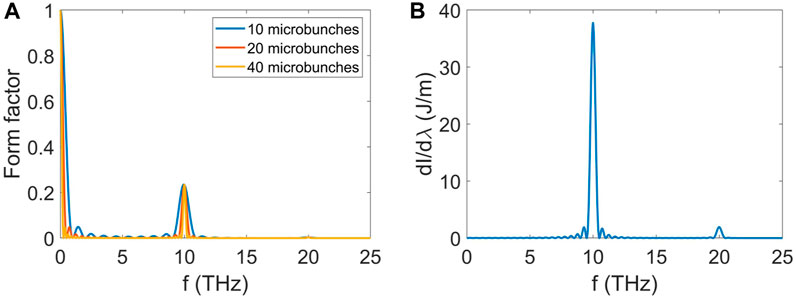
FIGURE 7. Form factors of the electron bunch with different numbers of microbunches (A) and the CTR spectrum generated by the electron bunch train with 20 microbunches (B).

From Figure 7, one can observe that the form factors have an apparent peak at 10 THz with a form factor of 0.23, and the CTR generated by the electron bunch train has a narrow spectral bandwidth. In addition, the spectral bandwidth decreases from 2.69 $\mu \mathrm{m}$ to 0.66 $\mu \mathrm{m}$ as the number of the microbunches increases; thus, a relative longer electron beam can also decrease the spectral bandwidth. The pulse energy of the CTR generated by the electron bunch train with 20 microbunches can reach 91 μJ at 10 THz. It is worth mentioning that the longitudinal space charge force has limited influence on the frequency-beating laser-modulated electron beam so the method can be adopted for a higher beam charge to generate THz radiation with higher pulse energy. Furthermore, the radiation frequency can be easily tuned from 5 to 15 THz by adjusting the beating frequency.

To compare the performance of the actual electron bunch train and the Gaussian microbunches, the form factors of the CTR generated by the actual electron bunch train and the 20 Gaussian microbunches are shown in Figure 8.

FIGURE 8

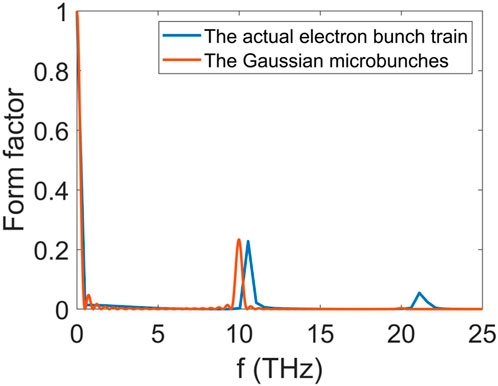
FIGURE 8. Form factors of the CTR generated by the actual electron bunch train and the 20 Gaussian microbunches.

Figure 8 shows that the form factor of the actual electron bunch train at the fundamental radiation is 0.22, which is close to the form factor of the Gaussian microbunches (0.23). However, the form factors of these two cases are quite different at the second harmonic. The form factor of the Gaussian microbunches is only 0.003 at the second harmonic, while the form factor of the actual electron bunch train is 0.05. Moreover, the form factor of the actual electron bunch train shifts from 10 to 10.6 THz compared with that of the Gaussian microbunches. These differences are caused by several reasons: the actual electron bunch train has a variable time interval, unlike the Gaussian microbunches, and the length of each microbunch of the actual electron bunch train is shorter than that of the Gaussian microbunches. Nevertheless, the CTR of the actual electron bunch train at the fundamental frequency can be estimated using the Gaussian microbunches.

4 Conclusion

In this paper, we propose a THz light source that can produce both broad-band and narrow-band THz radiation by manipulating the longitudinal profile of an electron beam and exploiting the CTR. Based on the theoretical analysis and numerical simulations using the typical parameters of the SXFEL, we have shown that the CTR generated by the compressed electron beam can provide broad-band strong-field THz radiation with frequencies from 0.1 to 5 THz and a pulse energy up to 342 μJ; the CTR generated by the electron bunch train obtained by modulating the electron beam with a frequency-beating laser pulse can provide narrow-band strong-field THz radiation from 5 to 15 THz, with a pulse energy of 91 μJ at 10 THz. Therefore, the proposed THz light source can generate THz radiation from 0.1 to 15 THz by combining beam compression and the frequency-beating laser-modulated electron beam. It is worth noting that the electron bunch train can suppress the influence of space charge force and can possibly carry more charge, resulting in a narrower bandwidth, stronger energy, and higher frequency of the CTR. This kind of a THz light source based on the CTR can effectively enhance the THz radiation capabilities of the SXFEL facility, and offer more flexibility and versatility for advanced THz pump–probe experiments.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YK, RW, KZ, and CF contributed to the conception and design of the study. YK, WC, and LT performed the statistical analysis. YK and KZ wrote the first draft of the manuscript. YK, KZ, and CF contributed to the proofreading and revised the article format. KZ and CF are the supervisors. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (grant numbers 12105347 and 12275340) and the Shanghai Science and Technology Commission project (grant number 20DZ2210300).

Acknowledgments

The authors would like to thank Hao Sun, Weijie Fan, Yaozong Xiao, Yiwen Liu, and Hanxiang Yang for their fruitful discussions on physics and simulations.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tonouchi M. Cutting-edge terahertz technology. Nat Photon (2007) 1(2):97–105. doi:10.1038/nphoton.2007.3

CrossRef Full Text | Google Scholar

2. Mittleman DM. Perspective: Terahertz science and technology. J Appl Phys (2017) 122(23):230901. doi:10.1063/1.5007683

CrossRef Full Text | Google Scholar

3. Leitenstorfer A, Moskalenko AS, Kampfrath T, Kono J, Castro-Camus E, Peng K, et al. The 2023 terahertz science and technology roadmap. J Phys D: Appl Phys (2023) 56(22):223001. doi:10.1088/1361-6463/acbe4c

CrossRef Full Text | Google Scholar

4. Zhang XC, Shkurinov A, Zhang Y. Extreme terahertz science. Nat Photon (2017) 11(1):16–8. doi:10.1038/nphoton.2016.249

CrossRef Full Text | Google Scholar

5. Salén P, Basini M, Bonetti S, Hebling J, Krasilnikov M, Nikitin AY, et al. Matter manipulation with extreme terahertz light: Progress in the enabling THz technology. Phys Rep (2019) 836:1–74. doi:10.1016/j.physrep.2019.09.002

CrossRef Full Text | Google Scholar

6. Kampfrath T, Tanaka K, Nelson KA. Resonant and nonresonant control over matter and light by intense terahertz transients. Nat Photon (2013) 7(9):680–90. doi:10.1038/nphoton.2013.184

CrossRef Full Text | Google Scholar

7. Schmid G, Schnorr K, Augustin S, Meister S, Lindenblatt H, Trost F, et al. Terahertz-field-induced time shifts in atomic photoemission. Phys Rev Lett (2019) 122(7):073001. doi:10.1103/physrevlett.122.073001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Liu M, Hwang HY, Tao H, Strikwerda AC, Fan K, Keiser GR, et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature (2012) 487(7407):345–8. doi:10.1038/nature11231

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Schlauderer S, Lange C, Baierl S, Ebnet T, Schmid CP, Valovcin DC, et al. Temporal and spectral fingerprints of ultrafast all-coherent spin switching. Nature (2019) 569(7756):383–7. doi:10.1038/s41586-019-1174-7

PubMed Abstract | CrossRef Full Text | Google Scholar

10. D’Angelo F, Mics Z, Bonn M, Turchinovich D. Ultra-broadband THz time-domain spectroscopy of common polymers using THz air photonics. Opt express (2014) 22(10):12475–85. doi:10.1364/oe.22.012475

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zouaghi W, Thomson MD, Rabia K, Hahn R, Blank V, Roskos HG. Broadband terahertz spectroscopy: Principles, fundamental research and potential for industrial applications. Eur J Phys (2013) 34(6):S179–99. doi:10.1088/0143-0807/34/6/s179

CrossRef Full Text | Google Scholar

12. Roskos HG, Thomson MD, Kreß M, Löffler AT. Broadband THz emission from gas plasmas induced by femtosecond optical pulses: From fundamentals to applications. Laser Photon Rev (2007) 1(4):349–68. doi:10.1002/lpor.200710025

CrossRef Full Text | Google Scholar

13. Shen Y, Watanabe T, Arena DA, Kao CC, Murphy JB, Tsang TY, et al. Nonlinear cross-phase modulation with intense single-cycle terahertz pulses. Phys Rev Lett (2007) 99(4):043901. doi:10.1103/physrevlett.99.043901

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Vicario C, Monoszlai B, Hauri CP. GV/m single-cycle terahertz fields from a laser-driven large-size partitioned organic crystal. Phys Rev Lett (2014) 112(21):213901. doi:10.1103/physrevlett.112.213901

CrossRef Full Text | Google Scholar

15. Vicario C, Ovchinnikov AV, Ashitkov SI, Agranat MB, Fortov VE, Hauri CP. Generation of 09-mJ THz pulses in DSTMS pumped by a Cr:Mg_2SiO_4 laser. Opt Lett (2014) 39(23):6632–5. doi:10.1364/ol.39.006632

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kim KY, Taylor AJ, Glownia JH, Rodriguez G. Coherent control of terahertz supercontinuum generation in ultrafast laser–gas interactions. Nat Photon (2008) 2(10):605–9. doi:10.1038/nphoton.2008.153

CrossRef Full Text | Google Scholar

17. Clerici M, Peccianti M, Schmidt BE, Caspani L, Shalaby M, Giguere M, et al. Wavelength scaling of terahertz generation by gas ionization. Phys Rev Lett (2013) 110(25):253901. doi:10.1103/physrevlett.110.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Malik HK, Malik AK. Tunable and collimated terahertz radiation generation by femtosecond laser pulses. Appl Phys Lett (2011) 99(25). doi:10.1063/1.3666855

CrossRef Full Text | Google Scholar

19. Manendra M, Singh KP, Singh BP, Malik AK. Bright terahertz (THz) generation by frequency mixing of dichromatic lasers in inhomogeneous cold plasma: Scaling of THz field. Phys Plasmas (2020) 27(6). doi:10.1063/5.0005643

CrossRef Full Text | Google Scholar

20. Manendra M, Singh KP, Bhati R, Malik AK. Efficient terahertz (THz) generation by nonlinear mixing of bicolor top-hat lasers in hot plasma. Phys Plasmas (2020) 27(2). doi:10.1063/1.5121913

CrossRef Full Text | Google Scholar

21. Singh KP, Jewariya M, Chaudhary P, Malik AK. Flexible control over polarization tuning using electric wiggler during terahertz generation. Opt Lasers Eng (2023) 167:107589. doi:10.1016/j.optlaseng.2023.107589

CrossRef Full Text | Google Scholar

22. Gopal A, Herzer S, Schmidt A, Singh P, Reinhard A, Ziegler W, et al. Observation of gigawatt-class THz pulses from a compact laser-driven particle accelerator. Phys Rev Lett (2013) 111(7):074802. doi:10.1103/physrevlett.111.074802

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Stojanovic N, Drescher M. Accelerator-and laser-based sources of high-field terahertz pulses. J Phys B: At Mol Opt Phys (2013) 46(19):192001. doi:10.1088/0953-4075/46/19/192001

CrossRef Full Text | Google Scholar

24. Zhang Z, Fisher AS, Hoffmann MC, Jacobson B, Kirchmann PS, Lee WS, et al. A high-power, high-repetition-rate THz source for pump–probe experiments at Linac Coherent Light Source II. J Synchrotron Radiat (2020) 27(4):890–901. doi:10.1107/s1600577520005147

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zapolnova E, Golz T, Pan R, Klose K, Schreiber S, Stojanovic N. THz pulse doubler at FLASH: Double pulses for pump–probe experiments at X-ray FELs. J synchrotron Radiat (2018) 25(1):39–43. doi:10.1107/s1600577517015442

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Pan R, Zapolnova E, Golz T, Krmpot AJ, Rabasovic MD, Petrovic J, et al. Photon diagnostics at the FLASH THz beamline. J synchrotron Radiat (2019) 26(3):700–7. doi:10.1107/s1600577519003412

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Patterson BD, Abela R, Braun HH, Flechsig U, Ganter R, Kim Y, et al. Coherent science at the SwissFEL x-ray laser. New J Phys (2010) 12(3):035012. doi:10.1088/1367-2630/12/3/035012

CrossRef Full Text | Google Scholar

28. Zhang K, Kang Y, Liu T, Wang Z, Feng C, Fang W, et al. A compact accelerator-based light source for high-power, full-bandwidth tunable coherent THz generation. Appl Sci (2021) 11(24):11850. doi:10.3390/app112411850

CrossRef Full Text | Google Scholar

29. Kang Y, Wang Z, Zhang K, Feng C. Generating high-power, frequency tunable coherent THz pulse in an X-ray free-electron laser for THz pump and X-ray probe experiments. Photon (2023) 10(2):133. doi:10.3390/photonics10020133

CrossRef Full Text | Google Scholar

30. Shen Y, Yang X, Carr GL, Hidaka Y, Murphy JB, Wang X. Tunable few-cycle and multicycle coherent terahertz radiation from relativistic electrons. Phys Rev Lett (2011) 107(20):204801. doi:10.1103/physrevlett.107.204801

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sun YE, Piot P, Johnson A, Lumpkin AH, Maxwell TJ, Ruan J, et al. Tunable subpicosecond electron-bunch-train generation using a transverse-to-longitudinal phase-space exchange technique. Phys Rev Lett (2010) 105(23):234801. doi:10.1103/physrevlett.105.234801

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Antipov S, Babzien M, Jing C, Fedurin M, Gai W, Kanareykin A, et al. Subpicosecond bunch train production for a tunable mJ level THz source. Phys Rev Lett (2013) 111(13):134802. doi:10.1103/physrevlett.111.134802

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lemery F, Piot P, Amatuni G, Boonpornprasert P, Chen Y, Good J, et al. Passive ballistic microbunching of nonultrarelativistic electron bunches using electromagnetic wakefields in dielectric-lined waveguides. Phys Rev Lett (2019) 122(4):044801. doi:10.1103/physrevlett.122.044801

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhang Z, Yan L, Du Y, Zhou Z, Su X, Zheng L, et al. Tunable high-intensity electron bunch train production based on nonlinear longitudinal space charge oscillation. Phys Rev Lett (2016) 116(18):184801. doi:10.1103/physrevlett.116.184801

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Liang Y, Liu Z, Tian Q, Li T, Lin X, Yan L, et al. Widely tunable electron bunch trains for the generation of high-power narrowband 1–10 THz radiation. Nat Photon (2023) 17:259–63. doi:10.1038/s41566-022-01131-7

CrossRef Full Text | Google Scholar

36. Ginzburg VL, Frank IM. Radiation of a uniformly moving electron due to its transition from one medium into another. J Phys (Ussr) (1945) 9:353–62.

Google Scholar

37. Garibian GM. Contribution to the theory of transition radiation. Sov Phys JETP (1958) 6(6):1079.

Google Scholar

38. Carr GL, Martin MC, McKinney WR, Jordan K, Neil GR, Williams GP. High-power terahertz radiation from relativistic electrons. Nature (2002) 420(6912):153–6. doi:10.1038/nature01175

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Shibata Y, Ishi K, Takahashi T, Kanai T, Ikezawa M, Takami K, et al. Observation of coherent transition radiation at millimeter and submillimeter wavelengths. Phys Rev A (1992) 45(12):R8340–3. doi:10.1103/physreva.45.r8340

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wen-Xin L, Wen-Hui H, Ying-Chao D, Li-Xin Y, Dai W, Chuan-Xiang T. Terahertz coherent transition radiation based on an ultrashort electron bunching beam. Chin Phys B (2011) 20(7):074102. doi:10.1088/1674-1056/20/7/074102

CrossRef Full Text | Google Scholar

41. Bass FG, Yakovenko VM. Theory of radiation from a charge passing through an electrically inhomogeneous medium. Soviet Phys Uspekhi (1965) 8(3):420–44. doi:10.1070/pu1965v008n03abeh003054

CrossRef Full Text | Google Scholar

42. Casalbuoni S, Schmidt B, Schmüser P, Arsov V, Wesch S. Ultrabroadband terahertz source and beamline based on coherent transition radiation. Phys Rev Spec Topics-Accelerators Beams (2009) 12(3):030705. doi:10.1103/physrevstab.12.030705

CrossRef Full Text | Google Scholar

43. Nodvick JS, Saxon DS. Suppression of coherent radiation by electrons in a synchrotron. Phys Rev (1954) 96(1):180–4. doi:10.1103/physrev.96.180

CrossRef Full Text | Google Scholar

44. Yu LH. Generation of intense uv radiation by subharmonically seeded single-pass free-electron lasers. Phys Rev A (1991) 44(8):5178–93. doi:10.1103/physreva.44.5178

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Yu LH, Babzien M, Ben-Zvi I, DiMauro LF, Doyuran A, Graves W, et al. High-gain harmonic-generation free-electron laser. Science (2000) 289(5481):932–4. doi:10.1126/science.289.5481.932

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Gover A. Superradiant and stimulated-superradiant emission in prebunched electron-beam radiators. I. Formulation. Phys Rev Spec Topics-Accelerators Beams (2005) 8(3):030701. doi:10.1103/physrevstab.8.030701

CrossRef Full Text | Google Scholar

47. Gover A, Dyunin E, Lurie Y, Pinhasi Y, Krongauz MV. Superradiant and stimulated-superradiant emission in prebunched electron-beam radiators. II. Radiation enhancement schemes. Phys Rev Spec Topics-Accelerators Beams (2005) 8(3):030702. doi:10.1103/physrevstab.8.030702

CrossRef Full Text | Google Scholar

48. Borland M. A flexible sdds-compliant code for accelerator simulation. Argonne, IL: ANL (2000).60439

Google Scholar

49. Zeng L, Feng C, Wang X, Zhang K, Qi Z, Zhao Z. A super-fast free-electron laser simulation code for online optimization. Photon (2020) 7(4):117. doi:10.3390/photonics7040117

CrossRef Full Text | Google Scholar

50. ASTRA. desy (2023). Available at: https://www.desy.de/∼mpyflo/ (Accessed June 28, 2023).

Google Scholar