Rough colloids at fluid interfaces: from fundamental science to applications

Colloidal particles pinned to fluid interfaces have applications ranging from Pickering emulsions and foams to the development of 2D materials via Langmuir-Blodgett deposition. While colloids come in virtually any size, shape, and chemistry, particle surface topography, or roughness, has recently found renewed interest as a design parameter for controlling interfacial pinning, capillary interactions, assembly, and mechanics of particulate monolayers. In this review, we highlight the fundamental science regarding rough colloidal particles at fluid interfaces and how manipulating roughness can be a tool for material design, rather than merely a characteristic needing to be dealt with. While existing work reveals the importance of roughness, the field is still rather nascent and therefore this review highlights both challenges and opportunities for future research.

1 Introduction

Colloidal particles are ubiquitous in a wide range of naturally existing and human-made substances. Their presence, whether suspended in liquids and gases, at the interfaces of immiscible fluids, or organized within solid materials, leads to a multitude of unique material properties that can be tailored towards a plethora of applications. Colloidal particles of varying size, shape, and chemistry are ubiquitous across industries, while also enabling advanced materials such as energy absorbing materials, medical devices, flexible body armors, paints, contrast fluid for MRI, and 3D printing of ceramic or conductive inks [1, 2]. Irreversible adsorption of colloidal particles to fluid interfaces allows them to stabilize Pickering emulsions and foams [3, 4] and be exploited to engineer the performance of interfacial materials and processes involving pharmaceuticals [5], foodstuffs, oil recovery [6], and personal care or household products [7, 8]. Moreover, self-assembly of particles at planar fluid interfaces enables the creation of functional structures and complex materials, such as development of colloidal lithography, colloidal photonic crystals, reversible plasmonic mirrors, and coatings with tailored wettability [9–12]. As a result, decades of research has been performed evaluating the structure-property relationships for model colloidal systems.

However, conventional studies of these phenomena often focus primarily on smooth, usually spherical, colloidal particles, and the influence of heterogenous surface topography and effects arising from the uneven surface structure have not been considered in as much depth. Recently, particle surface roughness has been found to lead to substantial variations in material properties, resulting in a surge of interest in studying the behavior of rough particle suspensions and interfaces. For instance, while surface roughness can induce attractive capillary interactions between isotropic spherical particles, causing 2D aggregation at fluid interfaces [13], it can cloak the same interaction between shape anisotropic particles and create well-dispersed monolayers [14]. Therefore, introducing tailored roughness to the particles’ surface leads to the emergence of unique and tunable behaviors across various materials. Due to advancement in particle synthesis techniques, researchers can now utilize model rough particles to incorporate surface roughness as a design parameter in both interfacial and bulk systems, enabling investigation of intriguing material properties that arise from the uneven surfaces of particles. Comprehensive discussion on synthesis and characterization of such model rough particles and their behavior in bulk suspensions can be found in literature [2, 15].

This review primarily examines the underlying scientific principles that give rise to distinct behaviors exhibited by rough particles at fluid interfaces and explores the connections between these behaviors and their applications in various fields. The review is organized by first considering the “life cycle” of a rough particle at a fluid interface, progressing through single particle interfacial adsorption, interparticle interactions, collective assembly, interfacial rheology, and, lastly, desorption. We then emphasize the connection between the aforementioned behavior exhibited by rough particles and their applicability across diverse application spaces followed by discussion of challenges and opportunities in the field.

2 Interfacial behavior of rough particles

2.1 Impact of roughness on interfacial adsorption and wetting

Solid micro and nanoparticles irreversibly adsorb to fluid interfaces since doing so minimizes the overall system energy. The decrease in surface energy during adsorption for a micrometer-sized particle can be several orders of magnitude higher than the thermal energy, $k_{B}T$, and is still significant for nanoparticles [16]. The magnitude of this decrease in energy relies on the interfacial tension between the two fluids in contact, the size of the particle, and its wetting behavior defined by three-phase contact angle ${\theta }_c$ as shown in Figure 1A. Commonly, ${\theta }_c$ is defined as the angle made by three-phase contact line at the particle surface measured through the aqueous phase; therefore, ${\theta }_c<90°$ and ${\theta }_c>90°$ corresponds to a hydrophilic and hydrophobic particle, respectively. The contact angle is a function of the chemistry of the particle and each fluid through their respective surface tensions and follows Young’s equation which takes the form [17]:

$\mathit{cos}{\mathit{\theta }}_{\mathit{c}}=\frac{{\mathit{\gamma }}_{\mathbf{2}\mathit{p}-}{\mathit{\gamma }}_{\mathbf{1}\mathit{p}}}{{\mathit{\gamma }}_{\mathbf{12}}}(1)$

FIGURE 1

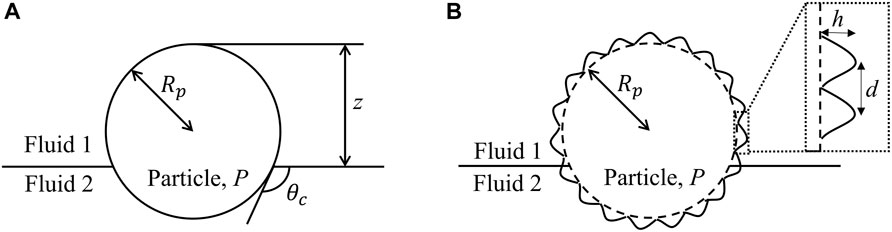
FIGURE 1. Schematic illustration of a (A) smooth and (B) rough spherical particle at a fluid-fluid interface.

Here, ${\gamma }_{1/2,p}$ is the surface tension of particle with fluid 1 and 2, and ${\gamma }_{12}$ is the surface tension between two immiscible fluid phases 1 and 2. For spherical particles with a homogeneous surface, both chemically and physically, the decrease in energy from the adsorption of a single particle can be described by the following relation [4, 18]:

$∆\mathit{E}=\mathit{\pi }{\mathit{R}}_{\mathit{p}}^{\mathbf{2}}{\mathit{\gamma }}_{\mathbf{12}}{\left(\mathbf{1}-\left|\mathit{cos}{\mathit{\theta }}_{\mathit{c}}\right|\right)}^{\mathbf{2}}+\mathit{\tau }{\mathit{l}}_{\mathit{c}}(2)$

Where $l_c$ is the length of contact line of which $\tau$ is the effective line tension. For micrometer sized smooth particles the contribution from line tension is often neglected [19].

The discussion regarding the mechanism of particle adsorption to fluid interfaces has largely focused on the interfacial energy argument alone, which is sufficient for smooth colloids [18]. In general, the particle’s radius, the portion of its surface area that interacts with the external fluid phases, and the interfacial tension between the solid and liquid phases all affect the adsorbed position as well as the interfacial energy. However, roughness, or more generally any anisotropy in surface topography and chemistry, also dictates the orientation of the particle at interface. The roughness of a particle can be characterized by the height, h, and distance, d, between asperities on the particle surface, as depicted in Figure 1B.

The adsorption and wetting of a rough colloid to a fluid interface can be considered in analogy to liquid spread on a nanostructured surface in either the Wenzel or Cassie-Baxter regime. For the Wenzel state, the particle becomes fully wet by whichever fluid it is suspended in. However, when fluid does not penetrate surface asperities, the wetting is considered to be in the Cassie-Baxter wetting regime [20]. For rough colloids adsorbing to fluid interfaces, this also encompasses the situation when particles are fully wet by one fluid, but not by the other. Experiments and simulations show that the transition from suspended (Cassie-Baxter regime) state to fully wetting (Wenzel regime) state occurs when the contact line retracts from the surface corrugations [21]. The same principles, such as contact line pinning, wetting transition, and contact angle hysteresis, applied to macroscopic rough surfaces are implicitly translated to rough particles trapped at fluid interfaces that helps in designing novel interfacial properties [22, 23].

Nonomura and Komura [24] reported that, in addition to the interfacial tensions and particle shape, the particle surface structure is a key factor in controlling their adsorption behavior. They theoretically studied the effect of roughness on adsorption and wetting behavior at liquid-liquid interfaces using a model spherical particle having many tube-like holes on the surface to replicate a highly rough texture, and considered a Cassie-Baxter-like condition where if a particle is allowed to adsorb at the liquid interface from liquid 1 having higher affinity with the particle which allows for imbibition of fluid into the pores, then after the particle is adsorbed to the interface the imbibed fluid will not be replaced by the second liquid 2. As a result, the equilibrium position of the spherical particle is determined not only by the interfacial tension between the particle surface and the fluids but also by the surface area of the particles. The interfacial energy, $F$ takes the following form [25]:

$\mathit{F}=\mathbf{4}\mathit{\pi }{\mathit{r}\mathit{R}}_{\mathit{p}}^{\mathbf{2}}{\mathit{\gamma }}_{\mathbf{2}\mathit{p}}-\mathbf{2}\mathit{\pi }{\mathit{R}}_{\mathit{p}}{\mathit{\gamma }}_{\mathbf{12}}\left(\mathbf{1}+\mathit{r}\mathit{c}\mathit{o}\mathit{s}{\mathit{\theta }}_{\mathit{c}}\right)\mathit{z}+\mathit{\pi }{\mathit{\gamma }}_{\mathbf{12}}{\mathit{z}}^{\mathbf{2}}(3)$

Where, $z$ is the immersion depth of the particle from liquid 1. The interfacial energy can be divided into two components: the first one represents the surface energy between the particle P and liquid 2, while the second one represents the energy change resulting from the elimination of the interface between liquids 1 and 2 due to particle adsorption. The increase in the particle surface area magnification ($r$) owing to rough microstructures influences the first factor directly, and also impacts the second factor. Therefore, the equilibrium position shifts to liquid 1, i.e., $z$ increases, if the particle has a relatively higher affinity to liquid 1. This theoretical equation can be experimentally tested if particles are spread from their preferred wetting phase. However, for neutrally wetting particles having same surface chemistry, the particles become more hydrophilic (hydrophobic) with increasing roughness when the particles are adsorbed to the interface from water (oil) phase, which is due to the surface-roughness-induced contact line pinning and arrested adsorption of the particles at metastable position [26]. Thus, rough surface structures influence the wetting properties of the particle; an initially hydrophilic smooth particle becomes more hydrophilic and vice versa [25].

Their results also suggest that the particles with extreme rough texture are more weakly held at the interface compared to the smooth particles [24], as was confirmed in AFM measurements of particle detachment energy discussed later. In addition, the adsorbed state of an extremely rough particle depends on the initial fluid from which the particle approaches the interface. As a result, this also becomes important in the preparation of emulsions stabilized by rough particles as the choice of the liquid to which the particles are initially added dictates the final emulsion stability. The above discussion assumes that the particle surface roughness produces pores on the surface that are filled by the liquid, but there can be other Cassie-Baxter like cases where neither fluid wets the particle and air remains trapped at the particle surface.

One can also consider a Wenzel-like model for rough particles where upon adsorption to the fluid interface liquid in the asperities of the particle surface is replaced by another liquid [25, 27]. In this regime, as the surface roughness increases, the particles’ equilibrium position shifts to the fluid with which they have higher affinity and eventually cannot be anchored at the interface and instead remain in dispersed in the preferential wetting fluid [27]. A spherical particle adsorbs at the interface when it meets the criteria of ${-r}^{-1}<-\mathit{cos}{\theta }_c<r^{-1}$ and is dispersed in liquid 1 (2) if ${-\mathit{cos}{\theta }_c<-r}^{-1}$ (${-\mathit{cos}{\theta }_c>-r}^{-1}$). The surface roughness also governs the orientation of the particle at the fluid interfaces if the microstructures are not homogeneously distributed. While the preceding considered spherical particles and neglected the contribution of line tension, it can influence the adsorption and wetting behavior if the particle is aspherical [28].

Reference [3] suggested that surface roughness appreciably lowers particle emulsifying power because a decrease in the adsorption energy coupled with a decrease in contact angle due to surface area enlargement, which is shown as an extension of Eq. 2:

$∆\mathit{E}=\mathit{\pi }{\mathit{R}}_{\mathit{p}}^{\mathbf{2}}{\mathit{\gamma }}_{\mathbf{12}}{\left(\mathbf{1}-\mathit{r}\left|\mathit{cos}{\mathit{\theta }}_{\mathit{c}}\right|\right)}^{\mathbf{2}}+\mathit{\tau }{\mathit{l}}_{\mathit{c}}(4)$

The above equation implies that the particles with contact angles closer to 90° are most efficiently trapped in the interface. Surface roughness enhances the inherent preference of the particle towards the preferential fluid, causing the contact angle to deviate from 90° and jeopardizing the emulsion stability. However, they reported that emulsions can be stabilized considerably even for very low particle trapping energy compared to smooth particles [3]. Modeling roughness as composed of cylindrical defects of radius $R_s$ and height $h_s$ on particle radius of $R_p$, Ref. [29] showed theoretically that with an increase in $r$, the energy minimum becomes shallower and may even disappear entirely as the asperity density approaches 40% of the particle surface (Figure 2A), which was later validated experimentally [21]. For raspberry-like rough silica particles with varying hydrophobic coating of Br-silanes, octadecyltrichlorosilane (OTS), and fluorosilanes, it has been shown that the surface roughness reduces the desorption force of hydrophobic particles trapped at water/oil interfaces through oil phase into the oil phase using colloidal-probe atomic force microscopy [21]. This indicates that the roughness decreases the particle adsorption energy to the fluid interfaces, which is also in line with the expectations of Eq. 4. Based on their experiment, a similar behavior is expected for the detachment of rough hydrophilic or neutrally wetting particles from water/oil (air) interface when the particles are trapped at the interface from the water phase.

FIGURE 2

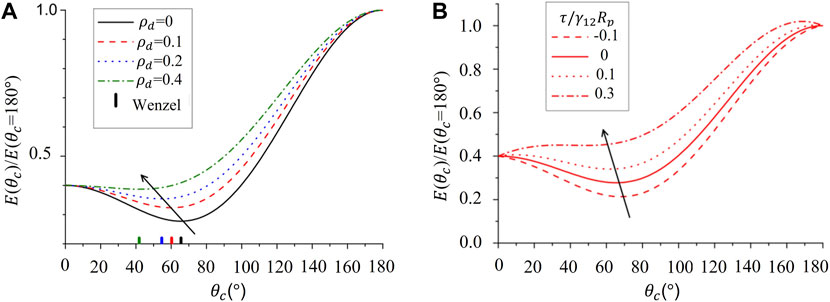
FIGURE 2. Free energy ratio $E$ (${\theta }_c$)/$E$ (${\theta }_c$ = 180 $°$) as a function of contact angle, ${\theta }_c$, for particles with (A) different asperity density concentration, ${\rho }_d$, and (B) different line tension values. Adapted from Stocco et al [23], with permission from Elsevier.

With increased roughness, the length of the contact line increases and the contribution from line tension ($\tau$) to the interfacial adsorption energy as described in Eq. 4 may no longer be negligible [14]. Stocco and Nobili [23] reported that a positive line tension means that an increases in the length of the contact line comes with an energy cost that decreases the colloidal stability at the interface as the energy minimum becomes less pronounced and even disappears (Figure 2B). The effect of positive line tension in decreasing the adsorption energy as well as the colloidal stability is more pronounced for nonspherical particles with high aspect ratios [28].

Nanoscale surface features can significantly influence the dynamics of wetting and binding of colloidal particles at fluid interfaces [16]. Observing rough polystyrene (PS) microspheres at an interface created between water/glycerol and oil using holographic microscopy, it has been shown that following a breach of the interface, the contact angle of the particle is much smaller than the expected equilibrium values and slowly relaxes over a longer timescale ($\sim$ 10 s) leading to particle protrusion evolving logarithmically [16]. If the interfacial energy gradient (driving force towards equilibrium) was mediated by the viscous drag, as in the case of smooth particles, particles would attain equilibrium in a fast exponential relaxation pattern with a time constant on the order of a microseconds [30]. However, for rough particles, a greater amount of energy is lost through pinning and depinning of the contact line at surface defects than through viscosity alone which leads to slow logarithmic relaxation to the equilibrium position [16]. To reach the equilibrium position, the particles might take months—which is much longer than typical experimental timescales, questioning the assumption of Young’s law driven equilibrium position of particles at interfaces used in most interfacial studies. This phenomenon is attributed to the surface heterogeneity that can pin the contact line with energy barriers up to ten times higher than those without heterogeneity. Wang et al also reported such contact line pinning on small-scale topographical features that perhaps associated with anchored charged groups in aqueous charge stabilized colloids [31]. As was the case with the thermodynamics of wetting, the pinning kinetics are also dependent on the fluid phase where the particles were first dispersed.

Hence, one unexplored field of inquiry is how precisely controlled chemical and/or physical heterogeneity affects contact line pinning and adsorption kinetics of colloidal particles at fluid interfaces. Careful design of the particle surface roughness can therefore control the nature of contact line pinning. At a sufficient roughness, the pinning sites can possess sufficiently high energy to arrest the particles at metastable positions during the adsorption process [26], which can result in interesting Pickering emulsions behavior described later. With increasing heterogeneity, the thermal energy required for the contact line to hop over surface heterogeneities or defects will no longer be able to overcome the increasing pinning energy, resulting in much slower lateral 2D diffusion of the particles compared to their 3D diffusion in the bulk. This could impact the collective dynamics, assembly, and mechanical properties at the interface in ways that have yet to be elucidated systematically. Even when the particle is at its equilibrium position, contact line fluctuations can have a strong influence on the viscous and line frictions, as evidenced by the decrease in diffusion coefficients for particles straddling at an interface [23]. However, we are not aware of any experimental studies on how the surface roughness of particles impacts the dynamics of adsorbed particles after equilibration at a 2D interface which is expected to decrease the diffusion coefficients even more.

Although the above thermodynamic consideration describes that the adsorption of rough colloidal particles to the fluid interfaces is energetically favorable, sometimes it is not spontaneous, especially when charged particles approach a fluid interface from the bulk. The electrostatic repulsion between the charged particle and the fluid interfaces acts as an adsorption barrier [32], which can be weakened by increasing the ionic strength of the bulk phase [33]. Electrostatic particle interactions with interface emanates from the “image charge” effect, a type of electrostatic interaction that arises when two fluids have a large difference in their dielectric constants ($\epsilon$), along with Coulombic contributions. With rough particles, the surface area as well as surface charge density may be much higher than their smooth counterparts and are expected to interact with the interface in complex ways. Therefore, if rough particles are allowed to adsorb to interface from a fluid with lower $\mathrm{\epsilon }$ (i.e., from oil phase), they could adsorb to the interface more readily. On the other hand, the repulsive barrier for adsorption to interface would increase if the rough particles are spread from the fluid having higher $\mathrm{\epsilon }$ (i.e., from aqueous phase).

2.2 Roughness induced interparticle capillary interactions

As mentioned above, the adsorption of colloidal particles at a fluid interface can result in an uneven particle meniscus due to the presence of surface roughness that causes uneven pinning of the interface (Figure 3A) [13]. The deviation of the meniscus local shape from planarity can be classified as convex and concave shape which can be described as positive and negative “capillary charges” that form “capillary multipoles”. The excess interfacial area caused by these distortions leads to an increased overall system energy, which can be minimized by the optimum orientation and separation of the particles that eliminates the most excess interfacial area. Typically, for spheres with diameter of 1 μm at an interparticle distance twice the particle diameter, deviations of as little as 50 nm from the ideal contact line may result in an interaction energy on the order of 10⁴ $k_{B}T$ [13].

FIGURE 3

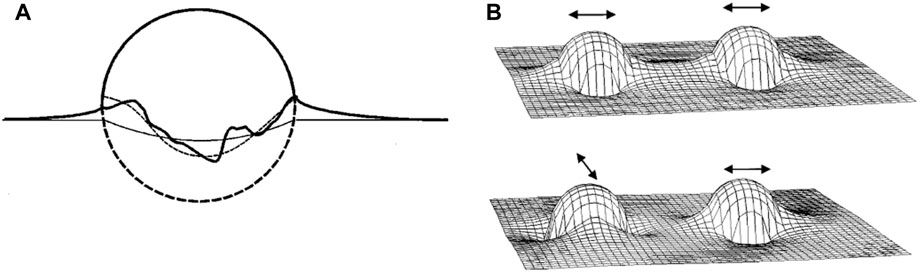
FIGURE 3. (A) Schematic description of an uneven meniscus at the particle surface due to pinning of the contact line at surface heterogeneities on the particle surface. The ideal contact line in the absence of pinning is represented by the thin straight line. The thin dashed line approximates the actual contact line, showing the quadrupolar nature of the meniscus. (B) Height of the interface surrounding two particles in close proximity. The top pair are oriented in parallel direction, meaning the sides with the rising meniscus face each other, which is attractive since the slope of the water level is reduced on particle approach. On the other hand, the bottom pair is oriented perpendicular to each other, resulting in an energy penalty upon approach. Reprinted from Stamou et al [13], with permission from American Physical Society.

Treating the interface surrounding the rough particle analogous to 2D electrostatics and applying the Young-Laplace equation that assumes that the mean curvature of the water surface vanishes everywhere, it can be shown that the height ($h\left(R_c,\phi \right)$) of the unevenly pinned interface around the particle follows a multipolar profile (Figure 3B) in cylindrical coordinate ($R,\phi$) according to the following equation [13]:

$\mathit{h}\left({\mathit{R}}_{\mathit{c}},\mathit{\phi }\right)={\displaystyle \sum _{\mathit{m}=\mathbf{2}}^{\mathit{\infty }}}{\mathit{H}}_{\mathit{m}}\mathbf{cos}\left[\mathbf{m}\left(\mathit{\phi }-{\mathit{\phi }}_{\mathit{m},\mathbf{0}}\right)\right](5)$

Here, $m$ is the multipole order, $H_m$ is the expansion coefficient, $R_c$ is the contact radius, and ${\phi }_{m,0}$ is the phase angles. For typical colloidal-scale particles, the effect of gravity is minimal, allowing for the monopole term to be neglected ($m$ = 0). The dipolar term ($m$ = 1) can also be neglected in the absence of external fields that would provide a torque on the particle. Higher order multipoles decay with an inverse power equal to the order of the multipole. The quadrupole order ($m$ = 2) is the lowest allowed order and decays as R^-2. While there is no explicit assumption for the shape of the contact line pinning due to roughness at the particle interface, the quadrupolar mode has been shown to be predominant in the far field. Therefore, the height profile of the distorted interface around the rough particle can be captured by the following equation [13]:

${\mathit{h}}^{\left(\mathbf{2}\right)}\left(\mathit{R},\mathit{\phi }\right)={\mathit{H}}_{\mathbf{2}}\mathbf{cos}\left[\mathbf{2}\left(\mathit{\phi }-{\mathit{\phi }}_{\mathbf{2,0}}\right)\right]{\left(\frac{{\mathit{R}}_{\mathit{c}}}{\mathit{L}}\right)}^{\mathbf{2}}(6)$

where the prefactor $H_2$ represents the height of the meniscus at the contact line. Translating this height of the interface around a single particle into an excess energy created by the interfacial deformation and applying superposition theorem on excess energy for such two particles A and B oriented at ${\phi }_A$ and ${\phi }_B$ relative to the line joining the particles at a center of mass separation distance of $L$, the capillary interaction between two adjacent rough particles can be described as:

${\mathit{U}}_{\mathit{c}\mathit{a}\mathit{p}}=-\mathbf{12}\mathit{\pi }{\mathit{\gamma }}_{\mathbf{12}}{\mathit{H}}_{\mathbf{2}}^{\mathbf{2}}\mathbf{cos}\left[\mathbf{2}\left({\mathit{\phi }}_{\mathit{A}}+{\mathit{\phi }}_{\mathit{B}}\right)\right]{\left(\frac{{\mathit{R}}_{\mathit{c}}}{\mathit{L}}\right)}^{\mathbf{4}}(7)$

As a result, the capillary quadrupole originated from the unevenly pinned meniscus results in an interparticle capillary attraction that follows a power law, decaying with distance as $L$⁻⁴. A detailed derivation of interfacial height profile and associated interaction potential can be found elsewhere [13, 19, 34]. This strong capillary attraction has a large influence on the interfacial assembly of rough particles, causing agglomerated structures instead of periodic arrangements shown by smooth spheres. Moreover, it influences the interfacial rheological behavior of rough particles as described later.

While roughness introduces capillary attraction between otherwise smooth spheres, the same can alleviate the capillary attraction coming from the distorted contact line around shape anisotropic particles. In a recent study, we showed that at least one order of magnitude reduction in capillary attraction at an air-water interface can be achieved via introducing roughness on otherwise smooth ellipsoids [14]. Interferometry measurements of the interfacial deformation surrounding a single ellipsoid shows that the meniscus around porous rough ellipsoids lack the characteristic quadrupolar symmetry of smooth ellipsoids (Figure 4), and quantitatively confirms the decrease in capillary interaction energy. On first glance, this result is somewhat paradoxical to the finding that roughness increases capillary attraction between spherical particles. However, the capillary attraction due to shape anisotropy in smooth particles is much greater, so in this case roughness serves to cloak shape effects. While there is still much to be learned about the exact mechanism of how roughness and particle shape couple, this study informs that tuning of nanoscale surface roughness holds the potential to manipulate interparticle interfacial interactions independent of the microparticle shape, allowing for the engineering of Pickering emulsion stability and the development of functional 2D metamaterials with novel material properties that have yet not been realized.

FIGURE 4

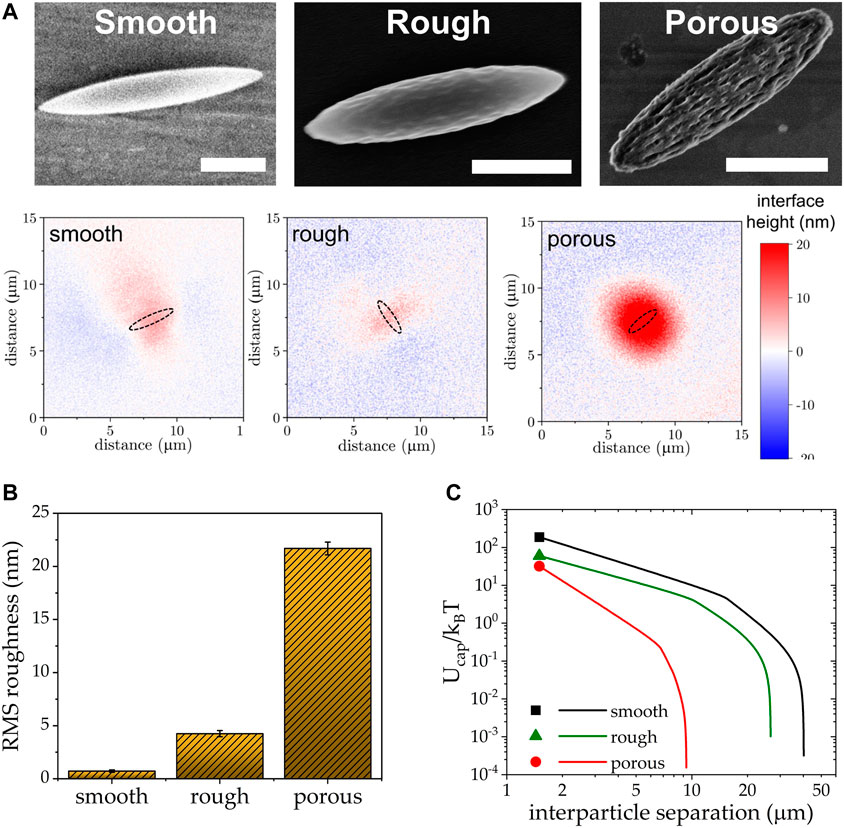
FIGURE 4. (A) SEM images of smooth, rough, and porous ellipsoids along with the relative height of the interface surrounding them. Scale bars = 1 μm. (B) Root-mean-square (RMS) roughness of the particle surface calculated from AFM. (C) Drastic reduction in capillary attraction energy as a result of changes in surface topography. Adapted with permission from Trevenen et al [14]. Copyright 2023 American Chemical Society.

2.3 Interfacial assembly

The pinning characteristics and interparticle capillary interactions dictate the subsequent monolayer microstructure at higher particle loadings, and therefore stabilized fluid interfacial systems are studied in a variety of contexts, including foams [35], emulsions [36], bijels [37] and liquid marbles [38]. As discussed in the previous section, spherical particles with a rough surface induce distortions at a liquid interface resulting in long range interparticle capillary attractions which are quadrupolar in nature [13, 39], changing the interfacial assembly and, as explained in the next section, interfacial mechanics, in comparison to smooth particles. The interaction between the quadrupolar deformation in the far field is expected to dominate the alignment and assembly of particles, however, if contact line pinning induces additional near-field deformations of the interface with higher order additional local particle arrangements may be observed [34, 40, 41].

Kato et al. [42] investigated how rough silica nanocolloids behave under compression at air-water interface using a Langmuir trough. They studied particles with four different surface roughnesses (smooth, SM; tiny rough, TR, medium rough, MR; very rough, VR) and compared the interfacial properties via surface pressure isotherm measurements upon a uniaxial compression. They concluded that in systems with sufficient roughness, a nontrivial intermediate state emerges which can be described by the formation of a percolated network before transitioning to a tightly packed jammed state. Formation of this intermediate state is attributed to the roughness induced capillary attraction. Figures 5A–D show the configurations of monolayers of SM, TR, MR, and VR particles at the starting point of jamming. With increasing roughness, the voids in the monolayer become more prominent. It is evident that the particle area fraction at jamming point ${\varnothing }_J$ (Figure 5E) diminishes as the roughness of the particles’ surface increases which is attributed to a combination of capillarity and interparticle friction. The disordered jammed structure becomes more pronounced as the surface roughness of the particles increases (as observed in Figures 5A–D) and can be quantified by relevant global order parameters. The rough silica particles can release the interfacial stress at high surface pressure via out-of-plane escaping to form disordered 3D structures. However, theoretical studies [43] show there is a possibility of achieving square packing for rough spheres due to the aligning of the quadrupole among the neighboring particles at high surface compression in Langmuir trough, i.e., at high concentration. Another possibility is hexagonal close packing with a vacancy to allow the angles between the line joining two particle centers and the orientation of the quadrupolar interface formed around the rough particles [43]. We hypothesize that rough polymeric particles having lower trapping energy (due to lower contact angle) would show either of the two crystalline ordering mentioned above since now the particles will release their interfacial stress by expulsing particles to the subphase.

FIGURE 5

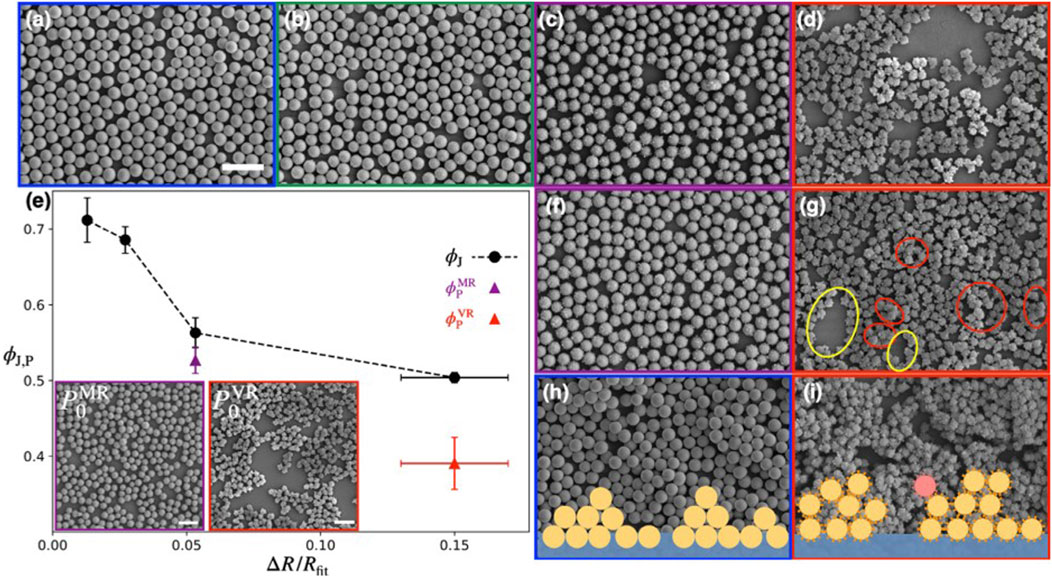
FIGURE 5. (A–D) SEM micrographs of (A) SM, (B) TR, (C) MR, and (D) VR particle configurations at the jamming point. (E) The particle area fraction at jamming point ${\varnothing }_J$ and percolation point ${\varnothing }_p$ as a function of roughness as defined by standard deviation of the radial length around the particle center ( $∆R/R_{fit}$). The insets represent micrographs at the percolation point $P_o$ for MR and VR. (F,G) Micrographs of the area surrounding the collapses. Red and yellow circles indicate the coexistence of escaped particles from the monolayer and voids, respectively. (H,I) Micrographs at the end of compression. All scale bars are 1 μm. Reprinted from Kato et al [42], with permission from Elsevier.

In both the MR and VR systems, a percolated network is formed at the onset surface pressure ($P_o$) (obtained from surface pressure-area (П-A) isotherm described in the next section) of the intermediate state (as shown in the inset of Figure 5E). Upon compression above jamming point, MR particles occupy the void spaces, forming denser and more ordered monolayer (Figure 5F). For VR systems, particles escape randomly from the monolayer in the solid-like state (Figure 5G), resulting in the formation of 3D aggregates at the interface (marked in red) coexisting with void regions (marked in yellow). At the end of the compression, VR particles create disordered 3D structures (Figure 5I), which differ greatly from the SM particles that form a multi-layer demonstrating a nearly hexagonal close packing (Figure 5H). The significant tangential contact force exhibited by rough particles might amplify the tendency of particles to escape out of the plane. The above experimental findings align with findings from numerical simulations considering different attractive forces ($U_{att}$) and friction values $\left(\mu \right)$. From numerical results, adding an interparticle attraction of $U_{att}$ = 20 $k_{B}T$ enables percolation at a much lower coverage (${\varnothing }_p=$ 0.2), while smooth, non-attractive particles percolate at ${\varnothing }_p$ = 0.9. The jamming point ${\varnothing }_J$ does depend on interparticle friction and decreases from about 0.9 to 0.6 as $\mu$ increases from 0 to 1. For attractive cases ($U_{att}$ > 0), the order parameter ${\mathrm{\Psi }}_6$ at percolation point ${\varnothing }_p$ and jamming point ${\varnothing }_J$ decrease with both $U_{att}$ and $\mu$, as shown in Figure 6.

FIGURE 6

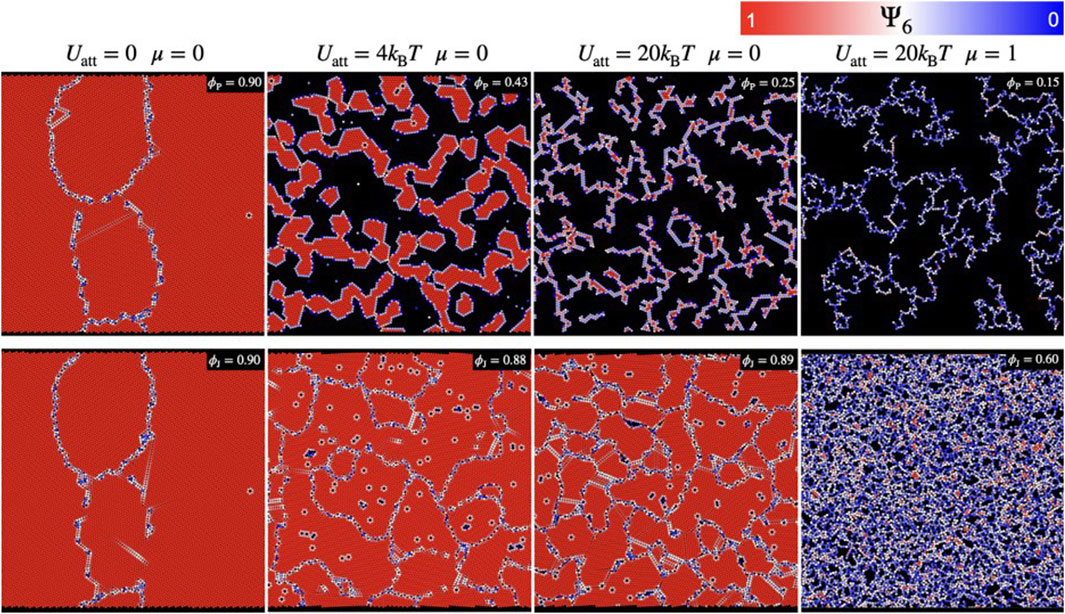
FIGURE 6. Snapshots of simulated monolayer of colloidal particles having different values of attractive forces ($U_{att}$) and friction ($\mathrm{\mu }$) using the Langevin Dynamics in Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS). The upper panel shows systems at percolation and lower panel shows system at jamming points. The size of each box is 100 $D_p\times$ 100 $D_p$, where $D_p$ is particle diameter. The color bar on the top indicates ${\mathrm{\Psi }}_6$ order parameter of each particle. Reprinted from Kato et al [42], with permission from Elsevier.

van Hooghten et al. [39] observed an immediate aggregation of carbon black (CB) rough nanoparticles with two different roughnesses [CB1 (higher) and CB2 (lower)] after spreading at n-octane-water interface, due to Marangoni flow driven particle collisions and subsequent lateral capillary attraction originating from particle surface roughness. Upon compression, the aggregates collide and densify to minimize the local compressional stress, resulting in localized wrinkles at the points of collision and indicating strong particle pinning at the interface. This finding is in contrast to what was obtained with rough silica where particles formed multilayers by sliding on top of each other. The estimated wavelength of the wrinkles parallel to the barriers is about 40 μm, suggesting that the interfacial layer possesses a high degree of elasticity. During a subsequent expansion, the monolayers break into smaller and more compact aggregates compared to the ones initially formed during spreading. Upon the second compression, these aggregates exhibit wrinkling with localized and smaller amplitude, indicating that the formed monolayer is highly elastic but behaves as a brittle solid. In comparison to CB2, CB1 monolayers forms wrinkle at lower compression levels that can be attributed to a more open structure upon spreading caused by the stronger attractions between the CB1 particles due to their higher roughness. Therefore, at an equal amount of surface loading, the open aggregates will percolate at lower degrees of compression, which is in line with the findings on rough silica nanocolloids discussed above. The interparticle interaction strength was quantified by fitting the $П$-A data to the Volmer equation of state for nanoparticles attached to an interface that takes the following form [44]:

$П=-\frac{k_{B}T}{a_0}\left[\ln \left(1-\frac{a}{A}\right)+\frac{a}{A}\right]-{П}_{coh}(8)$

in which $a_0$ is the area occupied by a single molecule of the subphase, $a$ is the total interfacial area covered by the particles and ${П}_{coh}$ is the cohesion surface pressure that accounts for the attraction between the nanoparticles at the interface. A higher value of ${П}_{coh}$ for CB1 (12 mN/m) than CB2 (4.4 mN/m) was found, indicating a stronger attraction between the CB1 particles which is consistent with the larger roughness induced stronger capillary interactions between these particles [39]. However, this equation does not consider the roughness characteristics (whether the roughness is due to dents or bulges and the degree of roughness) of the particle, which might change the interfacial interaction and assembly structure of the particle laden interface and the behavior of П-A isotherm. We view this as a key missing piece to the literature on rough colloids at fluid interfaces: the link between particle topography, interfacial pinning, and monolayer mechanics. Clearly, h and d are not sufficient to characterize the surface roughness as the shape, curvature, and even chemistry of the asperities can all potentially be manipulated with particle synthesis. Therefore, more rigorous theory and constitutive equations accounting for these factors needs to be developed to capture the П-A behavior of rough particle laden interfaces.

A similar gel state having a percolated network with a non-zero yield stress has been attributed to shape induced capillarity of shape anisotropic particles, such as ellipsoids [45, 46]. In general, ellipsoids with a sufficiently large aspect ratio demonstrate a gradual increase in the compression isotherms compared to their smooth spherical counterparts, which displays a rapid surge in surface pressure due to buckling [46]. After reaching a jammed state where in-plane rearrangements are no longer possible, the ellipsoids flip into an upright position releasing compressional stress and expelling particles from the monolayer that lead to a less abrupt increase of the pressure-area isotherms than in the case of the spherical particles. Moreover, jamming of anisotropic colloids may lead to monolayers containing void regions due to the anisotropic capillarity, which are distinguished from that of their spherical counterparts. In smooth ellipsoids, the percolation threshold varies as a monotonic decreasing (increasing) function of aspect ratio (capillary attraction) [46].

The overall potential between two particles, and the resultant collective assembly, is a result of combining both capillary forces and electrostatic forces, therefore it is important to note that combined with roughness induced control over interparticle capillary attraction, dipolar repulsion may also be tuned to control the interfacial arrangement. The dipolar repulsion energy can be calculated as:

$\frac{U_{dipole}}{k_{B}T}=\frac{a_{dipole}}{L^3}(9)$

Here, $a_{dipole}$ is a coefficient that measures the strength of the dipolar repulsive interaction and is a function of Debye screening length, $k^{-1}$ [47]. The part of the particles facing the aqueous phase creates this dipole due to a finite thickness condensed counterion layer. Apart from the long-range dipolar repulsion, the electrostatic interaction can originate from the short-range coulombic repulsion, which follows a screened exponential behavior according to the following relation [47, 48]:

$\frac{U_{coulomb}}{k_{B}T}=\frac{a_{coulomb}}{L}{e}^{-kL}(10)$

Here, $a_{coulomb}$ is a coefficient that measures the strength of the screened coulombic interaction and $k$ is the inverse Debye screening length. The total electrostatic interaction is an intricate balance between the long-range dipolar repulsion (Eq. 9) and short-range screened Coulombic repulsion (Eq. 10). For particles separated at long enough ($kL\gg$ 10) distances, the dipolar interaction is the predominant one [47, 48], and it has been shown that a smaller repulsive force leads to more elastic interfaces [49, 50].

The dipolar repulsion as well as coulombic interaction between the particles can be tweaked by modifying the chemical composition of the subphase (e.g., by adding salts and/or surfactants) that changes the Debye screening length [51–53]. This has been extensively investigated for smooth spheres, For example, changing monovalent salt (NaCl) or sodium dodecyl sulphate (SDS) concentration can induce a slow aggregation of particles from a sparse hexagonal crystal to a percolated network [51]. Here, changing ionic solution conditions altered electrostatic conditions in conjunction with the particle contact angle, so care must be taken to disentangle different contributions to particle assembly. Reference [13] studied the interfacial aggregation behavior of fluorescently labeled 1.06 μm diameter charged PS particles (charge density ∼8.5 mC/cm² of sulfate (SO₄^2-) surface charges) laden air-water interface under different subphase surfactant concentration on a Langmuir trough. By varying the neutral surfactant octylglocide from zero to 70 μM, they observed an increase in interparticle separation distance from 2 $\pm$ 0.5 μm to 10 $\pm$ 3 μm, changing the interfacial morphology form strongly clustered form to well dispersed form. When the subphase was purged with detergent free water, the cluster reappeared due to the capillary attraction emanating from surface roughness integrated during the synthesis. The detergent did not change the air-water interfacial tension, but rather changed the surface topography of the particles that was responsible for this long-ranged capillary interaction.

Little is known about how the combination of particle surface roughness and physical particle anisotropy dictates interfacial microstructure. As discussed above, roughness serves to weaken capillary interactions between ellipsoidal colloids [14]. As a result, it is possible the interfacial behavior will resemble that of smooth spheres up to reaching the jammed state since the capillary cloaked ellipsoids could align in the direction of compression and the surface pressure will increase only when the particles start to touch each other and form a percolating network like in hard spheres. Weakening capillary interactions increases the relative importance of dipolar repulsive interactions in the particle microstructure, allowing for the avoidance of kinetically trapped disordered arrangements and closer, more aligned packing upon compression. However, forming anisotropic long range ordered close packed 2D interfacial assemblies at the jamming point without having any voids (a highly desired arrangement for shape anisotropic particles) has not experimentally been realized yet.

Lastly, Janus particles may also be considered as a subtype of rough colloids due to the inhomogeneous interfacial contact angle and pinning between the different sides of the particle [7]. Qiao et al. [54] studied the effect of roughness on interfacial microstructure using binary distributions of smooth PS spheres and PS-Pt Janus spheres. Figures 7A–C illustrates the monolayer structure of a homogeneous PS particle along with the one obtained from 1:5 and 1:50 number ratio of PS-Pt Janus and PS particles spread over water-decane interface. Owing to high dipolar repulsion acting between the particles (Figure 7D), a hexagonal crystalline structure having a lattice constant approximately twice the diameter of the particle is obtained when the monolayer is occupied by charge-stabilized homogeneous PS particles. In contrast, the presence of Janus particles induces local particle clusters made of 3–5 PS particles bonded to each Janus particle, which is due to the roughness induced capillary attraction dominating the overall potential. Even with a very thin Pt coating of only 10 nm, the capillary attraction surpasses the dipolar repulsion, resulting in a substantial negative potential minimum of ∼ 1,200 $k_{B}T$ at the contact point between Janus and PS particles (Figure 7E). A comprehensive review of the behavior of Janus particles at fluid interfaces can be found elsewhere [7].

FIGURE 7

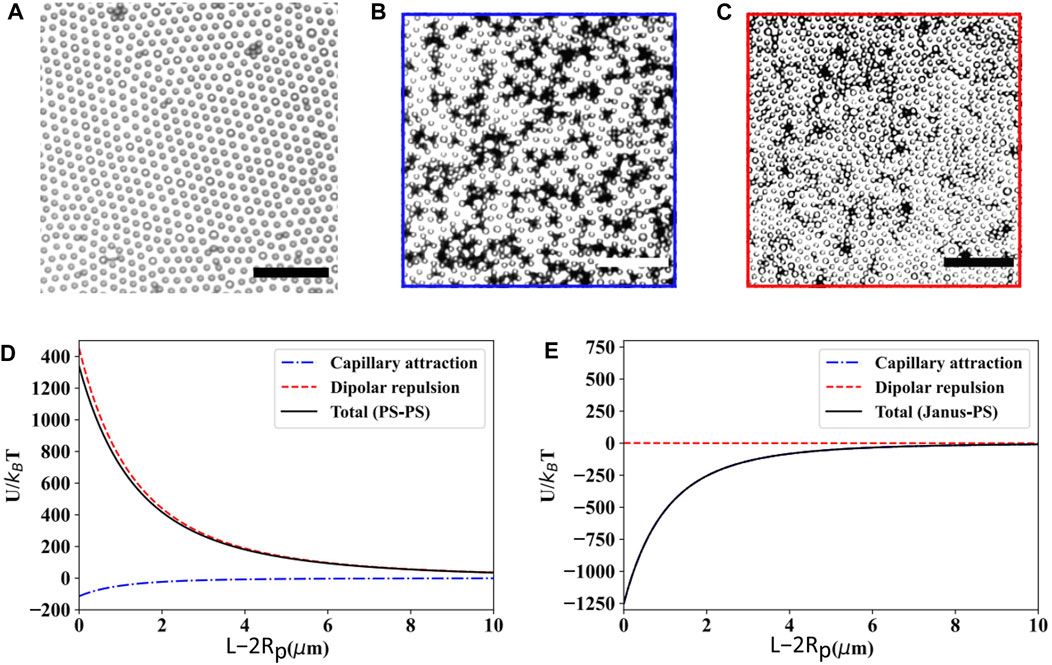
FIGURE 7. Bright-field microscopy images of particle monolayers at the water-decane interface: (A) homogeneous PS particles (area fraction of PS particles is $\sim$ 38%), (B) 1:5 number ratio of Pt-PS Janus and PS particles (area fraction of PS particles is $\sim$ 25%), and (C) 1:50 number ratio of Pt-PS Janus and PS particles (area fraction of PS particles is $\sim$ 40%). The dark particles in (B) and (C) are Janus particles with a20 nm thick Pt coating layers. The scale bars represent 50 μm. Interaction potentials between (D) two PS particles and (E) between a Janus particle and a PS particle. The potentials are calculated as a function of the surface-to-surface distance $L-2R_p$. Red dashed lines show electric dipolar repulsion and blue dash-dotted lines represent capillary attraction due to roughness caused by Pt cap. Black solid lines are the total potential. Adapted from Qiao et al. [54], with permission from Elsevier.

Based on all of these results, it is apparent that tuning dipolar repulsion along with the roughness induced capillary attraction has potential to produce monolayers with varying surface structures from percolating (high capillary, low dipolar) to non-close packed (low capillary, high dipolar). However, while several specific examples exist of qualitative changes to roughness impacting interfacial assembly, currently there are no design rules for engineering a specific particle topography (perhaps characterized by the RMS roughness or other, metrics) to attain a specific interaction energy necessary for a given interfacial microstructure. In addition, the equilibrium configuration of anisotropic particles will become more complex as there are now two knobs to control capillary interaction (shape and roughness), in addition to the dipolar interaction. Achieving this capability would provide an exciting pathway for creating novel microstructures controlled by particle shape and surface topography.

2.4 Interfacial rheology

Changes in interfacial microstructure naturally lead to changes in the mechanical properties of fluid interfaces. Understanding how to measure and control the interfacial rheology of particle monolayers are of great practical importance since the emulsions, foams and co-continuous blends that find enormous applications in many industrial products including food, cosmetics, oil recovery, and medicine [54–57] are dynamic systems that are subjected to mechanical disturbances either in their formation, destruction, or use. However, particle laden interfaces commonly possess viscoelasticity and nonlinear response to deformation, which makes the classical Boussinesq-Scriven constitutive equation inadequate. In addition to surface tension, particle laden interfaces are characterized by bending [58] and splay moduli [59], and shear and dilational viscosity [49, 60]. Roughness-induced interactions and assembly of particles can therefore impact all of these properties. While there are advanced constitutive models being developed for nonlinear viscoelastic [61, 62], smooth isotropic or anisotropic particle interfaces [63], we are not aware of a model that explicitly incorporates particle roughness.

Experimentally, several techniques including Langmuir trough, pendant drop, magnetic needle, bicone, double-walled ring (DWR) geometry, and microrheology are used to perform interfacial rheological measurements [7, 64].

Dilatational surface rheology measures the mechanical properties of particle laden interfaces under expansion and compression. The capability of interfaces to dampen external disturbances is often reported as surface elastic modulus (${ϵ}_{eq}$) which can be calculated from the surface pressure-area ($П$-A) isotherm obtained through Langmuir trough experiment using the following equation [65]:

${ϵ}_{eq}=-A\frac{\partial {П}_{eq}}{\partial A}(11)$

The dilatational rheology of colloidal particles at fluid interfaces is affected by aforementioned parameters such as wettability, particle surface charge density, subphase ionic strength, presence of surfactant in subphase, surface coverage, and shape anisotropy. Among these parameters, roughness has a direct impact on the wetting behavior and surface charge characteristics of particles. Improved mechanical performance of interfacial systems due to the enhanced dilational modulus of interface caused by increased particle wettability have been reported for isotropic spheres. For example, enhanced oil recovery (from $\sim$ 43% to $\sim$ 68%) has been reported when partially hydrophobic silica particles were introduced into foams [66]. The authors attributed this to the increased dilational viscoelasticity, measured via bubble/drop profile analysis tensiometer, of the gas-water interface by the introduced hydrophobic silica particles. With rough particles, the improved wettability to the preferred fluid phase has the potential to increase the dilatational elasticity of the interface. Moreover, the interlocking between asperities on rough particles, which have been found to facilitate the onset of discontinuous shear thickening in 3D suspensions [67], might also contribute to the increase in dilational elasticity of a 2D suspension, however, this needs to be experimentally verified. In addition, the mechanical behavior of particulate monolayers have been found to be dictated by the lateral capillary forces between interfacially adsorbed colloidal particles [34, 68]. Theoretically, it has been shown that, owing to the pronounced angular dependence of the quadrupolar interaction energy originated from the roughness induced interfacial deformation, an adsorbed monolayer of capillary multipoles exhibits a 2D elastic solid, rather than 2D fluid, character [34].

For smooth, rigid, spheres, $П$-A isotherms obtained from Langmuir trough experiments show a sharp surface pressure increase as the particles jam, indicating a direct transition from a gas-like state to the solid-like state [42]. Isotherms for spheres with increased roughness demonstrate an intermediate inflection point that corresponds to the aforementioned formation of a percolating network due to roughness induced capillary attraction. This results in an increase of the surface elastic modulus, ${ϵ}_{eq}$, at lower particle area fractions. However, once the solid-like state is reached, the surface elastic modulus is similar between spheres with varying roughness [46, 69] indicating jamming of sufficiently rough particles can be achieved after the intermediate state. However, in some cases for very rough particles the monolayers formed possess lower elasticities than the smoother systems, contradicting the theoretically predicted enhancement particle monolayers elasticity due to capillary attraction [34, 70]. Reference [42] proposed that the presence of frictional contact forces could potentially contribute to this contradictory outcome, which requires further investigation. Another plausible reason might be decreased trapping energy of rough particles owing to deviation from equilibrium contact angle that would be achieved by otherwise smooth particles.

If the wetting behavior of particles falls in Wenzel regime described above, which makes a hydrophilic particle sit at the interface in an even more hydrophilic configuration than its smooth counterpart, compressing a particle monolayer at an air/oil-water interface is expected to cause collapse via multilayer formation due to the high lateral capillary attraction energy induced by the surface roughness. However, at the same time, the increased surface area from increased roughness could also contribute to the increase in electrostatic repulsion at interface. Using smooth hydrophilic silica spheres at air-water interface, Ref. [71] showed that screening of electrostatic interaction via adding electrolyte to the subphase resulted in the collapse of the network through formation of multiple layers at the interface. However, in the absence of electrolyte, the particles with lower hydrophobicity resulted in a fluid-like monolayer owing to strong repulsive interparticle interactions that eventually collapsed as the particles were expelled into the sub-phase in contrast to the more hydrophobic ones that resulted in a solid-like network that collapsed via buckling. Therefore, the interfacial properties are highly dominated by wetting behavior and surface charge of particles that can be manipulated by tuning roughness. The compression properties highly depend on the particle contact angle between air and water and the maximum compression elastic moduli is obtained when the contact angle ${\theta }_c$ = 90 $°$ [72]. A decrease in hydrophilicity in silica particle by replacing the silanol groups with grafted alkyl chains via silanization process increased the 2D compression modulus from 40 mN/m (${\theta }_c$ = 40 $°$) to 100 mN/m (${\theta }_c$ = 90 $°$) [72]. Therefore, it is expected that spreading hydrophilic (hydrophobic) rough particles at air-oil (water) interface will improve the elasticity of the particle laden interface since now the contact angle will be larger compared to what would have been achieved from hydrophilic (hydrophobic) particle at polar (nonpolar) subphase.

When particle wetting is in the Cassie-Baxter regime, rough particles can trap some of the favored liquid phase, changing the contact angle as well as compression behavior compared to what have been achieved with smooth particles. As compression progresses, the contact line hopping over surface defects will increase as now the energy for depinning the contact line from the defect will be coming from the compression of the fluid interface, which will alter the interfacial elasticity compared to smooth spheres. The wetting behavior of particles can also be altered by adding surfactants in the subphase that have been found to impact the interfacial dilational elasticity [73]. The modulus of dilatational elasticity of a silica particle laden air-water interface, measured through oscillatory barrier method in custom made Langmuir trough, increased from ∼40 mN/m to ∼1,000 mN/m when the Cetyl Trimethyl Ammonium Bromide (CTAB) surfactant concentration was increased from 0.02 to 0.5 mM. The multilayer collapse of particles was attributed to surfactant adsorption onto the particle surface, which causes a decrease in dipolar repulsion via particle surface charge screening [73].

Shape anisotropy introduces an additional source of capillary interaction due to the deformed interface around them to maintain a constant three-phase contact angle. The role of shape anisotropy on the compressional modulus was studied by Ref. [60] using PS ellipsoids at different surface area fraction ($\varnothing$) and was compared to their smooth counterparts. The result shows PS ellipsoids form a percolated network at a low surface coverage ($\varnothing$ = 0.25), whereas spherical particles require higher surface coverage ($\varnothing$ = 0.5). Therefore, at intermediate surface coverages ($\varnothing$ = 0.4–0.6), ellipsoidal particles showed a higher elastic modulus (${ϵ}_{eq}$ ∼30 mN/m) compared to the spherical particles, which, however, yielded a much higher compressional modulus (${ϵ}_{eq}$ ∼ 300 mN/m) at higher coverages ($\varnothing$ > 0.7). The lower percolating threshold was attributed to the early formation of network by the shape anisotropic particles. Achieving maximum packing is important in controlling and predicting properties such as surface viscosity and surface moduli, which are pertinent to the stabilization of Pickering emulsions. With recently developed rough ellipsoids [74], the capillary attraction can be manipulated which, along with controlled dipolar repulsion via either particle surface charge or sub phase ionic strength, enables a possible transition from smooth ellipsoid-like behavior to smooth sphere-like behavior as a function of surface topography, irrespective of particle shape.

In addition to dilational rheology, shear rheology is also important for providing insights into the stability and mechanical properties of interfacial systems such as emulsions and foams. The shear rheological behavior of interfaces decorated with colloidal particles are influenced by the presence of subphase drag, effect of which can be estimated from the Boussinesq number, Bo, calculated as [39, 53].

$Bo=\frac{{\eta }_s}{\eta l}(12)$

Here, ${\eta }_s$ and $\eta$ are surface and subphase shear viscosity, respectively, and $l$ is a length scale related to the fluid motion which characterized by the ratio of particles’ contact area with the surrounding subphases and their perimeter with the interface. At a low value of $Bo$, more of the momentum from interface is transferred toward the subphase that can create significant torque on the measuring probe, overestimating the magnitude of the rheological properties [64, 75]. To avoid that overestimation from coupling of subphase with the interface, an iterative procedure to obtain the true value of $Bo$ and shear rate is required since the interfacial properties are a priori unknown [64, 76].

In order to determine the linear viscoelastic regime of carbon black (CB) nanoparticle laden interface, Ref. [39] performed strain sweep experiments using a DWR set up at a constant angular frequency ($\omega$) of 2 $\pi$ rad/s (Figure 8A). The result shows that for both type of rough particles (CB1 and CB2) the monolayer shows elastic response as confirmed by storage modulus $G^{\prime }$ is almost one order of magnitude larger than the loss modulus $G^{″}$ and both $G^{\prime }$ and $G^{″}$ increases with the increase in surface concentration of the nanoparticles. The highest value of $G^{\prime }$ (on the order of 1 Pa m) was obtained for CB1 particle, that is, two to three orders of magnitude higher than other types of particle laden interfaces in literature [77]. For both type of rough particles, a linear viscoelastic region is obtained up to a strain value on the order of 0.1%, above which the nonlinearity is due to the increased dissipation associated with the break-up of the surface structures, a behavior frequently observed in colloidal gels [78, 79]. The authors further characterized the linear viscoelastic properties via a frequency sweep (Figure 8B). Consistent with the result from strain sweep experiments, an elastic solid-like response is observed at all surface coverages investigated. At a fixed frequency, $G^{\prime }$ increases as the sample ages while $G^{″}$ decreases and the effect is particularly notable at lower frequencies. Both strain and frequency sweep experiment show a larger value $G^{\prime }$ and $G^{″}$ for CB1 (rougher) particles, which agrees well with theoretical predictions for more rough particles [34, 80] and is attributed to higher lateral capillary attraction.

FIGURE 8

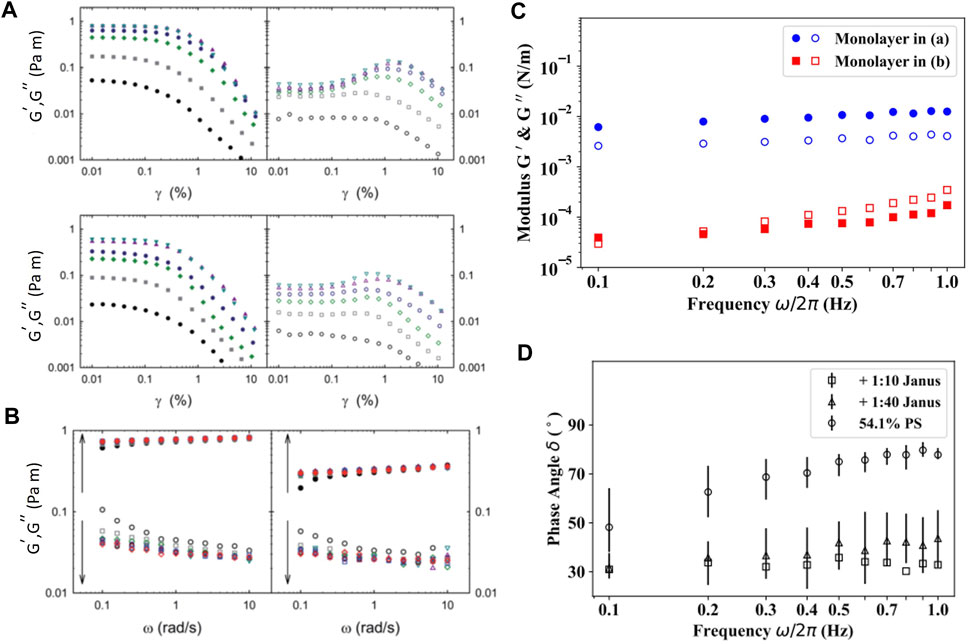
FIGURE 8. (A) Strain dependent response, $G^{\prime }$ (left) and $G^{″}$ (right), of CB1 (top) and CB2 (bottom) interfacial layers at an angular frequency of 2 $\mathrm{\pi }$ rad/s. The surface concentration is altered by spreading different amounts of particle containing mixture (from bottom to top: 150, 200, 250, 350, 450, and 550 μL). (B) Frequency dependent response of $G^{\prime }$ (filled symbols) and $G^{″}$ (open symbols) on CB1 (left) and CB2 (right) interfacial layers at a strain of 0.02% at different sample ages. The arrow indicates increasing time with an increment of 30 min. The particle concentration was set by spreading 200 μL of the spreading mixture. (C) A frequency sweep in the linear viscoelastic regime of $G^{\prime }$ and $G^{″}$ of the two particle monolayers: a) 1:5 number ratio of Pt-PS Janus and PS particles and b) 1:50 number ratio of Pt-PS Janus and PS particles. Closed symbols are for $G^{\prime }$ and open symbols are for $G^{″}$. (D) Phase angles $\delta$ of 1:10 and 1:40 number ratio of Pt-PS Janus and PS particles and homogeneous PS particles obtained from the frequency sweep data. Panels (A) and (B) reproduced from Van Hooghten et al [39] with permission from the Royal Society of Chemistry. Panels (C) and (D) adapted from Qiao et al [54], with permission from Elsevier.

As mentioned earlier, the introduction of Pt-PS Janus particles into otherwise pure PS monolayers caused capillary induced clustering of particles due to the roughness of the Pt cap [54]. Formation of these local clusters results in a significant enhancement in the surface moduli and elasticity. Using magnetic needle interfacial stress rheometer, the authors studied the storage and loss modulus, $G^{\prime }$ and $G^{″}$ of particle monolayers with PS particles and different amounts of Janus particles (1:40 and 1:10 Pt-PS Janus:PS) having a surface area fraction of 54.1%. Under frequency sweep (shearing frequencies in the range of 0.1 and 1.0 Hz at shear strains less than 0.1%) within the linear viscoelastic regime, drastic change in $G^{\prime }$ and $G^{″}$ was observed in the mixture of 1:40 Pt-PS Janus and PS particle monolayer compared to the one with only PS. Specifically, more than one order of magnitude increase was achieved with monolayers of 1:40 number ratio of Pt-PS Janus:PS particles, and it increased to more than two order of magnitude when the ratio increased to 1:10. However, the modulus values were found to be invariant with the thickness of Pt cap of Pt-PS Janus particles. Figure 8C shows that the surface moduli of a monolayer with 1:5 number ratio of Pt-PS Janus:PS particles is two orders of magnitude higher than a monolayer with 1:50 number ratio of Pt-PS Janus:PS particles, despite the former being at a lower area fraction. This demonstrates that the concentration of particle clusters, which is a function of the prevalence of Pt-PS Janus particles, i.e., roughness originating from the Pt cap, dominates over the total particle concentration in dictating the rheological response of particle-laden fluid interfaces. Moreover, the phase angle $\delta =\arctan \left(\frac{G^{\prime }}{G^{″}}\right)$ also decreased with the increase in number ratio of Janus particles in the monolayer (Figure 8D). Hence, the presence of Pt-PS Janus particles make the monolayer more elastic. Though the roughness of these particles is not well defined, overall, this result indicates the mechanical properties of particle laden fluid interfaces can be effectively manipulated via controlled roughness of the particles forming the monolayer.

While the interfacial shear elasticity behavior for both type of particles (CB and PS-Pt Janus) has been described based on the roughness induced capillary attraction, an additional consideration could be the competition between tangential frictional contact and lubrication hydrodynamic forces at different particle area fraction, shear rate, and roughness values as observed in shear rheology of 3D suspension of rough particles. For 3D suspension of rough particles, Ref. [81] reported that the shear behavior of moderately concentrated suspensions is dominated by lubrication hydrodynamics which gives way to roughness-induced tangential interactions at high shear rates, volume fractions, and surface roughness. This tangential interaction mediated load bearing contacts reduces the onset shear and particle volume fraction required for shear thickening and dilatancy [81]. In 2D monolayers, although not reported in literature, this tangential frictional contact between rough particles under shear might be responsible for enhancing the elasticity of the rough particle laden interface at high area fractions.

The existing studies of rough particles did not specifically address the impact of wettability on the viscoelastic behavior of the interface which is greatly influenced by the contact angle made by the particles at interface. For instance, Ref. [82] studied the effect of particle wetting behavior on the interfacial shear response of an air/water interface decorated by silica particles with varying hydrophobicity at a constant surface concentration (56 mg/m²). The hydrophobicity of the particle surface was increased by grafting hydrophobic methyl groups that decreased the % of hydrophilic SiOH on the particle surface. For lower to intermediate degrees of hydrophobicity (100<% of SiOH<51% or 20° < ${\theta }_c$ < 100°), both $G^{\prime }$ and $G^{″}$ were negligible. Increasing the hydrophobicity (36% SiOH or ${\theta }_c$ = 120°) led to equal value (0.2 mN/m) of $G^{\prime }$ and $G^{″}$ corresponding to a gel point. At even larger hydrophobicity (20% SiOH or ${\theta }_c$ = 135°), the elastic contribution $G^{\prime }$ was dominant and the layer became stiffer due to enhanced hydrophobic interactions between the particles. As the hydrophobicity increases, there is an augmentation of grafted hydrophobic methyl groups, resulting in increased particle heterogeneity and thus increases the capillary interactions leading to rigid particle laden interface. Therefore, the drastic change in wettability due to roughness, as described in previous sections, has potential to alter the viscoelastic behavior of particle laden interfaces that warrants further investigations.

As described in earlier sections, roughness can decrease the shape induced capillary interaction between shape anisotropic particles, e.g., ellipsoids. Therefore, the rheological behavior of interfaces occupied by rough ellipsoids are expected to show unique and different features compared to their smooth counterparts, however, rheological behavior of the former one under shear stress has not yet been investigated. Compared to spherical counterparts, shape anisotropic particles have been shown to be more effective in jamming at fluid interfaces [46, 83]. For instance, smooth ellipsoidal particles form a jammed network at lower surface coverages compared to the smooth spheres, with the threshold decreasing as the shape deviates from sphericity of 1 [84]. Moreover, they can undergo buckling transition at higher surface coverages [46] and show a greater yield stress for a comparable surface coverage compared to their spherical equivalent [85]. This high yield stress at even lower surface coverages was attributed to the prevention of gas dissolution from ellipsoidal particle-coated bubbles suspended in water, which has the potential to impede Ostwald ripening [60].

2.5 Detachment of rough particles from fluid interfaces

Although particle attachment to fluid interfaces reduces the free energy of the system in excess of thermal energy, leading to the colloquial term “irreversible adsorption”, particle detachment from the interface can still occur with sufficient external energy or bridging of emulsion droplets [86]. While the attachment of particles to an interface, on a microscopic level, involves the movement of the three-phase contact line across the surface features of the particle towards its equilibrium position, the detachment of particles follows an opposite trend and can occur in two ways: either moving the contact line back towards the phase from which the particle reached the interface, or going beyond its equilibrium position and entering the other phase. The detachment of the particle also comes with deformation of the surrounding interface that induces capillary forces on a single particle which results in lateral capillary interaction between neighboring particles. The receding motion of the contact line and the resulting capillary forces on a single particle can directly be measured using atomic force microscopy (AFM) [87]. The net capillary force acting on the spherical colloid has a vertical component only because of the axial symmetry of the system that can be described as:

$F=2\pi {R_p\gamma }_{12}\sin \left(\alpha \right)\sin \left({\theta }_c-\alpha \right)(13)$

Where, $\alpha$ is the central angle formed with the position of the contact line on the particle surface as shown in Figure 9A.

FIGURE 9

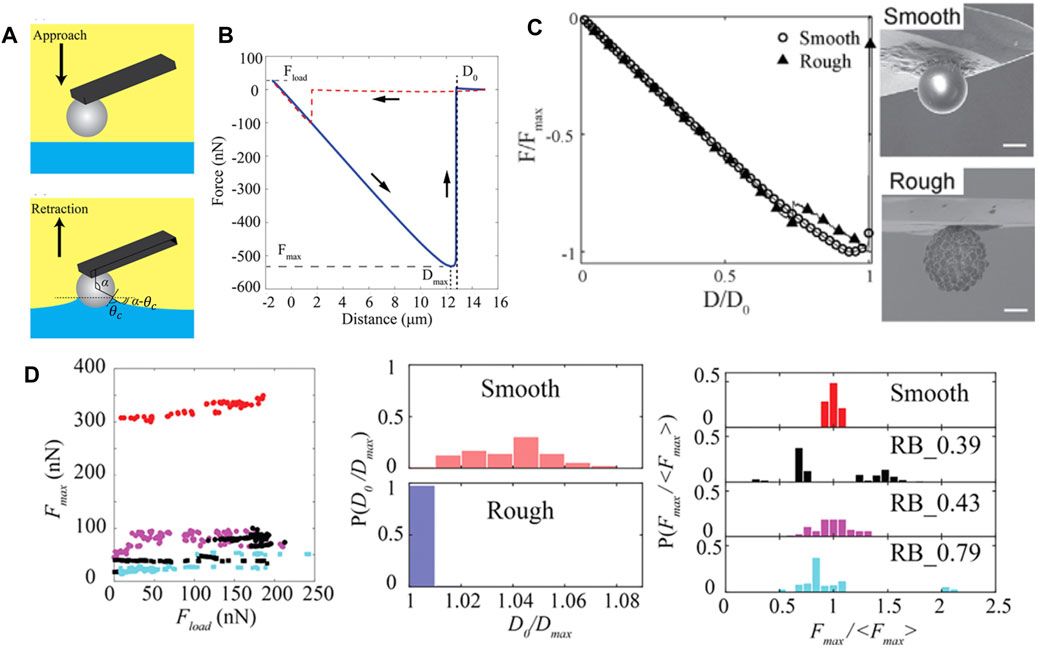
FIGURE 9. (A) Schematic illustration of the approach and retraction phases of colloidal probe during force measurement using colloidal-probe AFM technique at liquid-liquid interfaces. (B) Representative force-distance ($F-D$) curve obtained for a colloidal probe at a liquid-liquid interface. The maximum load applied on the interface during the approach is denoted as $F_{load}$ and the maximal adhesion force acting between the colloidal probe and the interface is denoted as $F_{\mathit{max}}$. $D_{\mathit{max}}$ is the distance that corresponds to $F_{\mathit{max}}$ and $D_0$ indicates the maximal detachment distance. (C) Retraction phase of $F-D$ curve of a smooth (open circles) and a rough silica particle (filled triangles) when pulled away from a hexadecane-water interface. For rough particle, pinning of contact line on surface heterogeneities leads to a rapid detachment along with earlier and smaller jumps associated with partial dewetting. On the right side, representative SEM images of smooth and rough colloidal probes has been shown. Scale bars: 3 μm [8]. (D) (Left) $F_{\mathit{max}}$ vs. $F_{load}$ applied on the interface during the approach of the OTS-modified probes with colloids having different roughness parameters $h/d$ = 0, 0.39, 0.43, and 0.79. The roughness parameter is a dimensionless quantity, calculated as the ratio between the average asperity height ($h$) and the average interasperity separation ($d$); (Middle) Probability distributions of $D_0$/$D_{\mathit{max}}$ for smooth and rough particles (all roughness categories are grouped together); (right) Probability distributions of the normalized detachment force $F_{\mathit{max}}$/⟨ $F_{\mathit{max}}$ ⟩ for particles with different roughness values. Panels (A), (B), and (D) adapted with permission from Zanini et al [21]. Copyright 2018 American Chemical Society.

While the gel-trapping technique (GTT) [26] and the freeze-fracture shadow-casting (FreSCa) [88] method offer measurements of contact angle distributions across multiple particles, colloidal-probe AFM assesses the dynamic wettability and detachment of an individual particle attached to an AFM cantilever. Using colloidal probe AFM, Ref. [87] obtained microparticle contact angles of both smooth and rough silica from the analysis of the force–distance relationship upon particle approach and retraction from the fluid interface. Three additional pieces of information can be extracted from each retraction curve (Figure 9B) regarding particle detachment form the interface: 1) the maximal capillary force ($F_{\mathit{max}}$) acting on the particle at the point of detachment, 2) the distance ($D_{\mathit{max}}$) at which particle detaches from the interface relative to the equilibrium position, and 3) the work required for quasistatic detachment, $W$. These parameters decrease as the contact angle increases, approaching zero for super-hydrophobic particles when ${\theta }_c$ = 180 $°$ [87]. During the process of detachment, the three-phase contact line can demonstrate two types of movement: either it smoothly moves across the particle surface while maintaining a constant contact angle (sliding contact line) or remains static until a threshold force is reached (pinned contact line). In general, with hydrophobic particles, a shift in the detachment mechanism from sliding contact-line in smooth particles to pinned contact-line in rough particles is observed. The force versus distance curve (Figure 9C) for rough particles deviates from the smooth one near the detachment point, where an abrupt change occurs due to the pinned contact-line. Numerous pinning sites arising from different asperities on the particle surface can cause a broad range of $F_{\mathit{max}}$ and $D_{\mathit{max}}$ values for particles from the same sample [21, 89].

The multi-step dewetting of the particle, i.e., the depinning of the contact line from several asperities can also be confirmed from the presence of noise in the retraction force curve of the rough particle. Zanini et al. [21] studied the impact of surface chemistry on the retraction behavior of the colloids from the interface via tuning the hydrophobicity of the silica particles, both smooth and rough, through the introduction of the bromosilane, chlorosilane, and fluorosilane chemistries on the particle surface. Figure 9D shows the data extracted from retraction curve for particles treated with chlorosilane (OTS). In general, the detachment forces for the rough colloids are lower than that of the smooth colloids, implying that the former one possesses a higher receding contact angle compared to the later. For smooth particles, irrespective of the chemical functionalization, the maximal detachment force, $F_{\mathit{max}}$, is narrowly distributed and is nearly independent of the maximum load exerted on the interface during the approach ($F_{load}$), however for rough particles, the dependence of $F_{\mathit{max}}$ with respect to $F_{load}$ is complex and widely distributed. In particular, for rough particles, the presence of multiple plateaus indicates a sudden change in the contact line position which undergoes several discrete arrangements over the surface defects until the particle is finally removed from the interface. While smooth particle retraction is characterized by contact line sliding, for rough particles, $D_0$/$D_{\mathit{max}}$ closer to 1 implies a contact line pinning regime (Figure 9D) [21]. In general, the energy required for particle detachment from the interface varies with its cross-sectional area at the interface. However, particles with surface heterogeneities may adsorb in metastable position, resulting in the cross-sectional area at the interface becoming dependent on the adsorption conditions.

3 Applications

As a result of the propensity of particle surface roughness to control interparticle interactions, microstructural assembly, and material properties at fluid interfaces, surface roughness is an important design parameter for a variety of applications. At the interface, this ranges from Pickering emulsions and foams to two-dimensional materials like superhydrophobic surfaces and photonic materials. In bulk, dense colloidal suspensions are used in shock-absorbing materials, energy-efficient batteries, oil and gas processing, agricultural and food sectors, as well as pharmaceutical and consumer formulations [90]. Here, we highlight just a few examples of the vast application space enabled and expanded by considering engineered rough particles.

Solid stabilized or Pickering emulsions and foams have immense potential in food and cosmetic industries, pharmaceuticals, ceramics processing, controlled release, and the manufacturing of microcapsules and porous materials [4, 91–98]. The wettability of the colloidal particles is a crucial property for the formulation and stability of Pickering emulsions [99]. Hydrophobic ($\theta$ >90 $°$) particles are more inclined to stabilize water droplets in oil (w/o), while hydrophilic colloids ($\theta$ <90 $°$) preferentially form oil-in-water emulsions (o/w), essentially requiring two kinds of particles to stabilize the two types of emulsion [100].

Similar to macroscopic surfaces, particles’ surface roughness can induce large contact angle hysteresis which is the difference between contact angle when adsorbing from the oil phase (advancing contact angle) or when adsorbing from water phase (receding contact angle) [23]. For a hysteresis large enough, the same rough particles can stabilize both w/o and o/w emulsion in a system called “universal emulsion” depending on the fluid phase from which they breach the interface, given the contact line is strongly pinned and thermally driven relaxations towards equilibrium are prevented owing to the high pinning energies greatly exceeding the thermal energy [26, 101, 102]. The uneven surface ensures that pinning sites have sufficient energy to arrest the particles at metastable positions during the adsorption process. By modifying the surface of the rough silica particles with almost neutrally wetting functional groups, Ref. [26] created “universal emulsifiers” by dispersing and stabilizing the colloids both in the aqueous and the non-polar phase. As the surface roughness increased, their adsorption to the interface from either phase was progressively arrested at earlier stages. Therefore, rougher particles when adsorbed from the water phase exhibited a greater hydrophilic behavior, whereas the same particles, when adsorbed from the oil phase, became effectively more hydrophobic. This behavior led to a wetting hysteresis that can be utilized to stabilize both o/w and w/o emulsions using the same batch of rough particles, depending on their initially wetting phase.

Roughness can be used as a dynamic tool to inverse the emulsion phase in situ under external triggers, such as mechanical energy. In this technique, when the energy input for emulsion formation is small enough, the rough particle breaching from a non-preferential fluid phase gets trapped at interface in a metastable position, preventing de-pinning and slow relaxation to the thermodynamic equilibrium position. This stabilization of an emulsion of preferential wetting fluid in non-preferential one (continuous phase) is known as “anti-Bancroft” emulsion. When, in the second emulsification step, the input mechanical energy is high enough to overcome the kinetic hurdle presented by the defects to transport the rough particles through the interface, the particles reach their thermodynamic equilibrium position with their preferential wetting fluid forming an emulsion of non-preferential wetting fluid in preferential one (continuous phase), switching metastable “anti-Bancroft” emulsion to stable “Bancroft” emulsion [102]. Therefore, the wettability changes from kinetically’’ hydrophobic to ‘‘thermodynamically’’ hydrophilic (and vice versa) leading to a mechanical phase inversion that might be attributed to the inversion of the local curvature of the droplets [59]. In case of equilibrium condition, the monolayers will curve in a way that the larger area of the particle surface remains with the preferential wetting fluid, giving rise to formation of emulsion of non-preferential wetting fluid in preferential one, i.e., stable “Bancroft” emulsion [59] after a sufficient mechanical energy is applied to overcome the kinetic hurdles offered by the surface defects. However, the spatiotemporal evolution of the emulsion droplet type and size, stability over long time storge, and the impact of the ratio of the two fluid phases and the concentration of particles with controlled roughness on the phase inversion need to be investigated.

The fact that the particle detachment force is a function of the force applied during the adsorption to the interface can be exploited to modulate the stability of Pickering emulsion stabilized by rough particles [8]. When high energy is applied to create an emulsion, more and more asperities encounter the interface, thus leading to greater detachment forces as well as enhanced stability of the emulsion. If a low stability emulsion is preferred, such as in oil separation, froth floatation, and particle recycling, the surface roughness can be tailored in such a way that a low emulsification energy is provided which in turn decreases the detachment energy [21]. However, experimental results in support of this phenomena are currently missing which opens a potential area of future work.

Superhydrophobic surfaces are water repellent surfaces that hold great prospects owing to their water repellence property in diverse applications, such as self-cleaning, anti-fogging, anti-bacterial surface, corrosion-resistant coatings, anti-icing surfaces, drag-reduction technologies, droplet transportation systems, energy conversion devices, electrochemical applications, biomedical applications, oil/water separation techniques, and water harvesting methods, and the list is still growing [103]. To realize superhydrophobicity, it is essential to have hierarchical surface topography where microscopic or nanoscopic surface features, i.e., a surface with a high degree of roughness, that can trap a large extent of air beneath the water [104]. The lotus leaf [105] is one of the most efficient examples of a superhydrophobic and self-cleaning surface due to its two-scale hierarchical structure that consist of microscale wax pillars decorated with nanoscale features [106]. This fascinating phenomenon is known as the lotus effect originating from the surface of its leaf featuring a large water contact angle (>150 $°$) and small sliding angle (<10 $°$), i.e., a large contact angle hysteresis [103, 105, 107]. Such a large contact angle hysteresis and hierarchical structure can be effectively created by controlling the size of colloidal particles with nanoscale surface heterogeneities present on the particle surface [23], and concentrated particles at fluid interfaces provide a facile way to fabricate solid monolayer materials via Langmuir-Blodget deposition. Using rough particles, the contact line of a fluid could be pinned to the defects, and a line displacement toward a new position won’t happen unless sufficient energy is introduced into the system, creating a large difference between advancing and retreating contact angles. Using polydopamine (PDA) coated rough PS ellipsoids, Ref. [104] created a two-scale hierarchical structure made of microscale interparticle packing of ellipsoids in the dried film, along with the nanoscale surface roughness of the constituent particle, fulfilling the requirements of superhydrophobic surfaces. Interestingly, while most of the superhydrophobic coatings obtained from rough spherical particles have a very low rolling-off angle of water, similar to lotus leaves [108–110], the one made with rough ellipsoids exhibits strong adhesion to water. This behavior is akin to some red rose pedals or peanut leaves that possess superhydrophobicity while also showing strong water adhesion behaviors [111].

The superhydrophobic behavior of rough particles can also be exploited to create liquid marbles which refers to isolated liquid droplets surrounded by solid particles and can be used for controllable transport and manipulation of small volumes of liquids immensely sought for miniaturized systems in many biological applications or in reactors for manipulation of inner liquid droplet with high positioning precision [112]. Using fluorinated PDA coated PS rough ellipsoids [104], Zhang et al created liquid marbles that possess reasonable mechanical strength and can be placed on many surfaces. Therefore, particles with controlled surface topologies can be employed as building blocks to construct superhydrophobic surfaces with strong water adhesion and liquid marbles with appropriate mechanics.

Surface-enhanced Raman scattering (SERS) is an optical spectroscopic analysis technique with potential for detecting highly sensitive molecules that can be used in biosensing and bioimaging. Colloidal lithography (CL) is a scalable nanofabrication technique and can produce various periodic nanostructures, such as multilayer, hierarchical, hollow, asymmetric, that can offer great performances in plasmonics at low cost and large scale by using fluid-interface deposited particles as an initial template [113]. On a single particle level, it has been shown that the nanometer-scale surface unevenness can provide several hot spots on a single particle, which significantly increases SERS enhancement [114]. For instance, flower-like silver particles with a nanometer-scale roughness on their surfaces have quite high and reproducible SERS enhancements on the order of 10⁷–10⁸ [115]. Therefore, textured periodic nanostructures obtained from CL of rough particles have immense potential to enhance the plasmonic response by providing additional hotspots, which has not experimentally been realized yet. Moreover, existing periodic nanostructures are mainly derived from non-close packed hexagonal assembly of spherical particles and cannot be extended to non-spherical particles due to their nonperiodic assembly driven by shape anisotropy induced high capillary attraction, limiting the achievable nanostructures. Owing to the roughness induced decrease in capillary attraction between shape anisotropic particles [14], it could now be possible to achieve long range ordered arrangement of such particles, which would open up possibilities for designing new plasmonic nanostructures.

4 Discussion and conclusion

In sum, all interfacial processes are impacted by the surface topography of colloids: initial adsorption, interfacial interactions, collective assembly, monolayer rheology, and finally desorption. Rationally designing the surface roughness and shape of particles via various synthesis techniques can therefore have important impacts. While excellent examples in the literature exist for understanding the qualitative impacts of roughness on some of these processes, a unifying, quantitative predictor of how surface roughness couples with particle size, shape, and chemistry is still lacking. Most notably, precise, quantitative, characterization of the rough topography of the particle surface is missing. In only some cases are traditional roughness metrics, like RMS roughness, reported and even fewer systematically manipulate them. With the advent of improved and more well-controlled synthesis techniques, coupled with the characterization techniques described in this review, this should be possible.

However, we caution that the standard methods of characterizing roughness may not be sufficient in all cases. Different particles may have the same RMS roughness, but varied surface topography based on the density and depth of asperities. More advanced roughness metrics will need to be taken into account, possibly such as waviness and “developed interfacial area ratio” [116]. Even these still assume a homogeneous distribution of rough features on the particle surface. Advanced synthesis combining Janus particle character, and/or shape anisotropy will create inhomogeneous, directional, rough features on the particle which could introduce new interfacial phenomena and more complex characterization and modeling.

We have attempted to highlight the state-of-the-art and emphasize the importance of surface roughness on the characteristics of colloidal particles at fluid interfaces that impart distinct qualities to various material properties, ranging from Pickering emulsions to dense suspensions. We discuss how the behavior of a single rough particle at fluid interface manipulates subsequent monolayer assembly structure and mechanical properties under compression and shear. While the impact of roughness on the particle adsorption to the interface has been extensively examined, the effect of the same on the dynamics of the interfacially absorbed particle, whether they are isotropic or anisotropic in shape, remains largely unexplored. Alongside the exploration of capillary interaction induced by the surface roughness, it is necessary to investigate the manipulation of other types of interactions, such as dipolar interactions, by altering factors like particle surface charge, ionic strength of subphase, and the addition of surfactant to the subphase. Coupling surface topography with shape anisotropy offers additional promise in combining shape and roughness to tune interfacial pinning, microstructure, and material properties. Carefully manipulating and fine-tuning these interactions has the potential to yield a diverse range of interfacial microstructures accompanied by distinctive mechanical properties.

Investigating the dynamics of rough particles, whether either at fluid interfaces or within bulk suspensions, can offer insights into various naturally occurring phenomena such as bacterial movement or the migration of microplastics. The incorporation of surface roughness in interfacial and bulk particulate systems has the potential to open doors for a more sustainable approach to formulating soft interfacial materials, based on the possibility of achieving the same functionality using lower area or volume fractions of particles. However, for this pathway to achieve success, it is imperative to maintain ongoing efforts in creating model systems that allow for precise tuning and characterization of single-particle properties. Additionally, the development of experiments and computational tools that establish the connection between single-particle properties and the corresponding macroscopic response is crucial in expanding current knowledge while bridging the existing gaps.

Author contributions

PB conceptualized the manuscript. MR wrote the first draft of the manuscript and both authors edited and finalized the manuscript. All authors contributed to the article and approved the submitted version.

Funding

Funding for this work was provided by the National Science Foundation under award no. CBET-2232579.

Acknowledgments

We acknowledge Prof. Nianqiang Wu and Dr. Samuel Trevenen for insightful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hsu CP, Mandal J, Ramakrishna SN, Spencer ND, Isa L Exploring the Roles of Roughness, Friction and Adhesion in Discontinuous Shear Thickening by Means of Thermo-Responsive Particles. Nat Commun (2021) 12(1):1477–10. doi:10.1038/s41467-021-21580-y

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hu M, Hsu CP, Isa L Particle Surface Roughness as a Design Tool for Colloidal Systems. Langmuir (2020) 36(38):11171–82. doi:10.1021/acs.langmuir.0c02050

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Vignati E, Piazza R, Lockhart TP Pickering Emulsions: Interfacial Tension, Colloidal Layer Morphology, and Trapped-Particle Motion. Langmuir (2003) 19(17):6650–6. doi:10.1021/la034264l

CrossRef Full Text | Google Scholar

4. Aveyard R, Binks BP, Clint JH Emulsions Stabilised Solely by Colloidal Particles. Adv Colloid Interf Sci (2003) 100–102:503–46. doi:10.1016/S0001-8686(02)00069-6

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rodzinski A, Guduru R, Liang P, Hadjikhani A, Stewart T, Stimphil E, et al. Targeted and Controlled Anticancer Drug Delivery and Release with Magnetoelectric Nanoparticles. Sci Rep (2016) 6(1):20867. doi:10.1038/srep20867

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Binks B, Horozov T Colloidal particles at liquid interfaces (2006).

Google Scholar

7. Correia EL, Brown N, Razavi S Janus Particles at Fluid Interfaces: Stability and Interfacial Rheology. Nanomaterials (2021) 11:374. mdpi.com2021. doi:10.3390/nano11020374

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Vialetto J, Zanini M, Isa L Attachment and Detachment of Particles to and from Fluid Interfaces. Curr Opin Colloid Interf Sci (2022) 58:101560. doi:10.1016/J.COCIS.2021.101560

CrossRef Full Text | Google Scholar

9. Böker A, He J, Emrick T, Russell TP Self-Assembly of Nanoparticles at Interfaces. Soft Matter (2007) 3(10):1231–48. doi:10.1039/B706609K

PubMed Abstract | CrossRef Full Text | Google Scholar

10. McGorty R, Fung J, Kaz D, Manoharan VN Colloidal Self-Assembly at an Interface. Mater Today (2010) 13(6):34–42. doi:10.1016/S1369-7021(10)70107-3

CrossRef Full Text | Google Scholar

11. Isa L, Kumar K, Müller M, Grolig J, Textor M, Reimhult E Particle Lithography from Colloidal Self-Assembly at Liquid-Liquid Interfaces. ACS Nano (2010) 4(10):5665–70. doi:10.1021/nn101260f

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Vogel N, Retsch M, Fustin CA, Del Campo A, Jonas U Advances in Colloidal Assembly: The Design of Structure and Hierarchy in Two and Three Dimensions. Chem Rev (2015) 8:6265–311. American Chemical Society July. doi:10.1021/cr400081d

CrossRef Full Text | Google Scholar

13. Stamou D, Duschl C, Johannsmann D Long-Range Attraction between Colloidal Spheres at the Air-Water Interface: The Consequence of an Irregular Meniscus. Phys Rev E (2000) 62(4):5263–72. doi:10.1103/PhysRevE.62.5263

CrossRef Full Text | Google Scholar

14. Trevenen S, Rahman MA, Hamilton HSC, Ribbe AE, Bradley LC, Beltramo PJ Nanoscale Porosity in Microellipsoids Cloaks Interparticle Capillary Attraction at Fluid Interfaces. ACS Nano (2023) 17(12):11892–904. doi:10.1021/ACSNANO.3C03301

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Hsiao LC, Pradeep S Experimental Synthesis and Characterization of Rough Particles for Colloidal and Granular Rheology. Curr Opin Colloid Interf Sci (2019) 43:94–112. doi:10.1016/J.COCIS.2019.04.003

CrossRef Full Text | Google Scholar

16. Kaz DM, McGorty R, Mani M, Brenner MP, Manoharan VN Physical ageing of the contact line on colloidal particles at liquid interfaces (2011). doi:10.1038/NMAT3190

CrossRef Full Text | Google Scholar

17. Young T An Essay on the Cohesion of Fluids. Philos Trans R Soc Lond (1805) 95:65–87. doi:10.1098/RSTL.1805.0005

CrossRef Full Text | Google Scholar

18. Levine S, Bowen BD, Partridge SJ Stabilization of Emulsions by Fine Particles I. Partitioning of Particles between Continuous Phase and Oil/Water Interface. Colloids Surf (1989) 38(2):325–43. doi:10.1016/0166-6622(89)80271-9

CrossRef Full Text | Google Scholar

19. Dasgupta S, Auth T, Gompper G Nano- and Microparticles at Fluid and Biological Interfaces. J Phys Condensed Matter (2017) 29(37):373003. doi:10.1088/1361-648X/aa7933

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cassie A, Baxter S Wettability of Porous Surfaces. Trans Faraday Soc (1944) 40:546–51. doi:10.1039/tf9444000546

CrossRef Full Text | Google Scholar

21. Zanini M, Lesov I, Marini E, Hsu CP, Marschelke C, Synytska A, et al. Detachment of Rough Colloids from Liquid-Liquid Interfaces. Langmuir (2018) 34(16):4861–73. doi:10.1021/ACS.LANGMUIR.8B00327

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Pieranski P Two-Dimensional Interfacial Colloidal Crystals. Phys Rev Lett (1980) 45(7):569–72. doi:10.1103/PhysRevLett.45.569

CrossRef Full Text | Google Scholar

23. Stocco A, Nobili M A Comparison between Liquid Drops and Solid Particles in Partial Wetting. Adv Colloid Interf Sci (2017) 247:223–33. doi:10.1016/J.CIS.2017.06.014

CrossRef Full Text | Google Scholar

24. Nonomura Y, Komura S Surface Activity of Solid Particles with Extremely Rough Surfaces. J Colloid Interf Sci (2008) 317(2):501–6. doi:10.1016/J.JCIS.2007.09.066

CrossRef Full Text | Google Scholar

25. Nonomura Y, Komura S, Tsujii K Adsorption of Microstructured Particles at Liquid-Liquid Interfaces. J Phys Chem B (2006) 110(26):13124–9. doi:10.1021/jp0617017

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zanini M, Marschelke C, Anachkov SE, Marini E, Synytska A, Isa L Universal Emulsion Stabilization from the Arrested Adsorption of Rough Particles at Liquid-Liquid Interfaces. Nat Commun (2017) 8(1):15701–9. doi:10.1038/ncomms15701

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Nonomura Y, Komura S, Tsujii K Surface-Active Particles with Microstructured Surfaces. Langmuir (2005) 21(21):9409–11. doi:10.1021/la051816m

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Dong L, Johnson DT Adsorption of Acicular Particles at Liquid-Fluid Interfaces and the Influence of the Line Tension. Langmuir (2005) 21(9):3838–49. doi:10.1021/la047851v

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang X, In M, Blanc C, Malgaretti P, Nobili M, Stocco A Wetting and Orientation of Catalytic Janus Colloids at the Surface of Water. Faraday Discuss (2016) 191(0):305–24. doi:10.1039/C6FD00025H

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Colosqui CE, Morris JF, Koplik J Colloidal adsorption at fluid interfaces: regime crossover from fast relaxation to physical aging (2013). doi:10.1103/PhysRevLett.111.028302

CrossRef Full Text | Google Scholar

31. Wang A, McGorty R, Kaz DM, Manoharan VN Contact-Line Pinning Controls How Quickly Colloidal Particles Equilibrate with Liquid Interfaces. Soft Matter (2016) 12(43):8958–67. doi:10.1039/C6SM01690A

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Vialetto J, Anyfantakis M Exploiting Additives for Directing the Adsorption and Organization of Colloid Particles at Fluid Interfaces. Langmuir (2021) 37(31):9302–35. doi:10.1021/acs.langmuir.1c01029

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Williams DF, Berg JC The Aggregation of Colloidal Particles at the Air—Water Interface. J Colloid Interf Sci (1992) 152(1):218–29. doi:10.1016/0021-9797(92)90021-D

CrossRef Full Text | Google Scholar

34. Danov KD, Kralchevsky PA, Naydenov BN, Brenn G Interactions between Particles with an Undulated Contact Line at a Fluid Interface: Capillary Multipoles of Arbitrary Order. J Colloid Interf Sci (2005) 287(1):121–34. doi:10.1016/j.jcis.2005.01.079

CrossRef Full Text | Google Scholar

35. Binks BP, Murakami R Phase Inversion of Particle-Stabilized Materials from Foams to Dry Water. Nat Mater (2006) 5:865–9. doi:10.1038/nmat1757

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tang J, Quinlan PJ, Tam KC Stimuli-Responsive Pickering Emulsions: Recent Advances and Potential Applications. Soft Matter (2015) 11(18):3512–29. doi:10.1039/C5SM00247H

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Cates ME, Clegg PS Bijels: A New Class of Soft Materials. Soft Matter (2008) 4(11):2132–8. doi:10.1039/B807312K

CrossRef Full Text | Google Scholar

38. Aussillous P, Quéré D Liquid Marbles. Nature (2001) 411(6840):924–7. doi:10.1038/35082026

PubMed Abstract | CrossRef Full Text | Google Scholar

39. van Hooghten R, Imperiali L, Boeckx V, Sharma R, Vermant J Rough Nanoparticles at the Oil–Water Interfaces: Their Structure, Rheology and Applications. Soft Matter (2013) 9(45):10791. doi:10.1039/c3sm52089g

CrossRef Full Text | Google Scholar

40. Liu IB, Sharifi-Mood N, Stebe KJ Capillary Assembly of Colloids: Interactions on Planar and Curved Interfaces. Annu Rev Condens Matter Phys (2017) 9:283–305. doi:10.1146/annurev-conmatphys-031016-025514

CrossRef Full Text | Google Scholar

41. Botto L, Lewandowski EP, Cavallaro M, Stebe KJ Capillary Interactions between Anisotropic Particles. Soft Matter (2012) 8(39):9957–71. doi:10.1039/C2SM25929J

CrossRef Full Text | Google Scholar

42. Kato AN, Jiang Y, Chen W, Seto R, Li T How Surface Roughness Affects the Interparticle Interactions at a Liquid Interface. J Colloid Interf Sci (2023) 641:492–8. doi:10.1016/J.JCIS.2023.03.041

CrossRef Full Text | Google Scholar

43. Brown ABD, Smith CG, Rennie AR Fabricating Colloidal Particles with Photolithography and Their Interactions at an Air-Water Interface. Phys Rev E (2000) 62(1):951–60. doi:10.1103/PhysRevE.62.951

CrossRef Full Text | Google Scholar

44. Fainerman VB, Kovalchuk VI, Grigoriev DO, Leser ME, Miller R Theoretical Analysis of Surface Pressure of Monolayers Formed by Nano-Particles. In: Surface chemistry in biomedical and environmental science vol. 228. Cham: Springer (2006). p. 79–90.

Google Scholar

45. Basavaraj MG, Fransaer J, Vermant J Self-Assembly and Rheology of Ellipsoidal Particles at Interfaces. Langmuir (2009) 25(5):2718–28. doi:10.1021/la803554u

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Basavaraj MG, Fuller GG, Fransaer J, Vermant J Packing, Flipping, and Buckling Transitions in Compressed Monolayers of Ellipsoidal Latex Particles. Langmuir (2006) 22(15):6605–12. doi:10.1021/la060465o

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Bresme F, Oettel M Nanoparticles at Fluid Interfaces. J Phys Condensed Matter (2007) 19(41):413101. doi:10.1088/0953-8984/19/41/413101

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Guzmán E, Martínez-Pedrero F, Calero C, Maestro A, Ortega F, Rubio RG A Broad Perspective to Particle-Laden Fluid Interfaces Systems: From Chemically Homogeneous Particles to Active Colloids. Adv Colloid Interf Sci (2022) 302:102620. doi:10.1016/J.CIS.2022.102620

CrossRef Full Text | Google Scholar

49. Barman S, Gordon , Christopher F, Christopher GF Role of Capillarity and Microstructure on Interfacial Viscoelasticity of Particle Laden Interfaces. J Rheol (2016) 60(1):35–45. doi:10.1122/1.4935128

CrossRef Full Text | Google Scholar

50. Barman S, Christopher GF Simultaneous Interfacial Rheology and Microstructure Measurement of Densely Aggregated Particle Laden Interfaces Using a Modified Double Wall Ring Interfacial Rheometer. AIChE Annu Meet Conf Proc (2021) 2021:9752–60. doi:10.1021/la502329s

CrossRef Full Text | Google Scholar

51. Park BJ, Pantina JP, Furst EM, Oettel M, Reynaert S, Vermant J Direct Measurements of the Effects of Salt and Surfactant on Interaction Forces between Colloidal Particles at Water-Oil Interfaces. Langmuir (2008) 24(5):1686–94. doi:10.1021/la7008804

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Reynaert S, Moldenaers P, Vermant J Control over Colloidal Aggregation in Monolayers of Latex Particles at the Oil-Water Interface. Langmuir (2006) 22(11):4936–45. doi:10.1021/la060052n

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Rahman SE, Laal-Dehghani N, Barman S, Christopher GF Modifying Interfacial Interparticle Forces to Alter Microstructure and Viscoelasticity of Densely Packed Particle Laden Interfaces. J Colloid Interf Sci (2019) 536:30–41. doi:10.1016/J.JCIS.2018.10.028

CrossRef Full Text | Google Scholar

54. Qiao Y, Ma X, Liu Z, Manno MA, Keim NC, Cheng X Tuning the Rheology and Microstructure of Particle-Laden Fluid Interfaces with Janus Particles. J Colloid Interf Sci (2022) 618:241–7. doi:10.1016/J.JCIS.2022.03.041

CrossRef Full Text | Google Scholar

55. Hunter TN, Pugh RJ, Franks GV, Jameson GJ The Role of Particles in Stabilising Foams and Emulsions. Adv Colloid Interf Sci (2008) 137(2):57–81. doi:10.1016/J.CIS.2007.07.007

CrossRef Full Text | Google Scholar

56. Bai Y, Zhang F, Xu K, Wang X, Wang C, Zhang H, et al. Pickering Emulsion Strategy to Control Surface Wettability of Polymer Microspheres for Oil–Water Separation. Appl Surf Sci (2021) 566:150742. doi:10.1016/J.APSUSC.2021.150742

CrossRef Full Text | Google Scholar

57. Anjali TG, Basavaraj MG Shape-Anisotropic Colloids at Interfaces. Langmuir (2019) 35(1):3–20. doi:10.1021/acs.langmuir.8b01139

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Yunker PJ, Gratale M, Lohr MA, Still T, Lubensky TC, Yodh AG Influence of Particle Shape on Bending Rigidity of Colloidal Monolayer Membranes and Particle Deposition during Droplet Evaporation in Confined Geometries. Phys Rev Lett (2012) 108(22):228303. doi:10.1103/physrevlett.108.228303

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Kralchevsky PA, Ivanov IB, Ananthapadmanabhan KP, Lips A On the Thermodynamics of Particle-Stabilized Emulsions: Curvature Effects and Catastrophic Phase Inversion. Langmuir (2005) 21(1):50–63. doi:10.1021/la047793d

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Beltramo PJ, Gupta M, Alicke A, Liascukiene I, Gunes DZ, Baroud CN, et al. Arresting Dissolution by Interfacial Rheology Design. Proc Natl Acad Sci (2017) 114(39):10373–8. doi:10.1073/pnas.1705181114

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Carrozza MA, Hütter M, Hulsen MA, Anderson PD Constitutive Framework for Rheologically Complex Interfaces with an Application to Elastoviscoplasticity. J Nonnewton Fluid Mech (2022) 301:104726. doi:10.1016/J.JNNFM.2021.104726

CrossRef Full Text | Google Scholar

62. Sagis LMC, Fischer P Nonlinear Rheology of Complex Fluid–Fluid Interfaces. Curr Opin Colloid Interf Sci (2014) 19(6):520–9. doi:10.1016/J.COCIS.2014.09.003

CrossRef Full Text | Google Scholar

63. Sagis LMC Rheology of Interfaces Stabilized by a 2D Suspension of Anisotropic Particles: A Classical Irreversible Thermodynamics Theory. Soft Matter (2011) 7(17):7727–36. doi:10.1039/C1SM05149K

CrossRef Full Text | Google Scholar

64. Fuller GG, Vermant J Complex Fluid-Fluid Interfaces: Rheology and Structure. Annu Rev Chem Biomol Eng (2012) 3:519–43. doi:10.1146/ANNUREV-CHEMBIOENG-061010-114202

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Cicuta P, Terentjev EM Viscoelasticity of a Protein Monolayer from Anisotropic Surface Pressure Measurements. The Eur Phys J E (2005) 16(2):147–58. doi:10.1140/EPJE/E2005-00016-Y

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Lu T, Li Z, Zhou Y Flow Behavior and Displacement Mechanisms of Nanoparticle Stabilized Foam Flooding for Enhanced Heavy Oil Recovery. Energies (2017) 10(4):560. doi:10.3390/EN10040560

CrossRef Full Text | Google Scholar

67. Hsu CP, Ramakrishna SN, Zanini M, Spencer ND, Isa L Roughness-Dependent Tribology Effects on Discontinuous Shear Thickening. Proc Natl Acad Sci U S A (2018) 115(20):5117–22. doi:10.1073/pnas.1801066115

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Boneva MP, Danov KD, Christov NC, Kralchevsky PA Attraction between Particles at a Liquid Interface Due to the Interplay of Gravity- And Electric-Field-Induced Interfacial Deformations. Langmuir (2009) 25(16):9129–39. doi:10.1021/la9006873

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Zang DY, Rio E, Langevin D, Wei B, Binks BP Viscoelastic Properties of Silica Nanoparticle Monolayers at the Air-Water Interface. Eur Phys J E (2010) 31(2):125–34. doi:10.1140/EPJE/I2010-10565-7

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Lucassen J Capillary Forces between Solid Particles in Fluid Interfaces. Colloids Surf (1992) 65(2–3):131–7. doi:10.1016/0166-6622(92)80268-7

CrossRef Full Text | Google Scholar

71. Razavi S, Cao KD, Lin B, Yee K, Lee C, Tu RS, et al. Collapse of Particle-Laden Interfaces under Compression: Buckling vs Particle Expulsion. Langmuir (2015) 16:7764–75. doi:10.1021/acs.langmuir.5b01652

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Zang DY, Rio E, Delon G, Langevin D, Wei B, Binks BP Influence of the Contact Angle of Silica Nanoparticles at the Air–Water Interface on the Mechanical Properties of the Layers Composed of These Particles. Mol Phys (2011) 109(7–10):1057–66. doi:10.1080/00268976.2010.542778

CrossRef Full Text | Google Scholar

73. Yazhgur PA, Noskov BA, Liggieri L, Lin SY, Loglio G, Miller R, et al. Dynamic Properties of Mixed Nanoparticle/Surfactant Adsorption Layers. Soft Matter (2013) 9(12):3305–14. doi:10.1039/C3SM27304K

CrossRef Full Text | Google Scholar

74. Rahman MA, Turner T, Hamilton HSC, Bradley LC, Beltramo PJ Engineering the Surface Patchiness and Topography of Polystyrene Colloids: From Spheres to Ellipsoids. J Colloid Interf Sci (2023) 652:82–94. doi:10.1016/J.JCIS.2023.08.083

CrossRef Full Text | Google Scholar

75. Vandebril S, Franck A, Fuller GG, Moldenaers P, Vermant J A Double Wall-Ring Geometry for Interfacial Shear Rheometry. Rheol Acta (2010) 49(2):131–44. doi:10.1007/s00397-009-0407-3

CrossRef Full Text | Google Scholar

76. Reynaert S, Brooks CF, Moldenaers P, Vermant J, Fuller GG Analysis of the Magnetic Rod Interfacial Stress Rheometer. J Rheol (N Y N Y) (2008) 52(1):261–85. doi:10.1122/1.2798238

CrossRef Full Text | Google Scholar

77. Reynaert S, Moldenaers P, Vermant J Interfacial Rheology of Stable and Weakly Aggregated Two-Dimensional Suspensions. Phys Chem Chem Phys (2007) 9(48):6463–75. doi:10.1039/B710825G

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Buscall R, Mills PDA, Goodwin JW, Lawson DW Scaling Behaviour of the Rheology of Aggregate Networks Formed from Colloidal Particles. J Chem Soc Faraday Trans 1: Phys Chem Condensed Phases (1988) 84(12):4249–60. doi:10.1039/F19888404249

CrossRef Full Text | Google Scholar

79. Mewis J, Wagner NJ Colloidal Suspension Rheology. Colloidal Suspension Rheology (2011) 1–393. 9780521515993. doi:10.1017/CBO9780511977978

CrossRef Full Text | Google Scholar

80. Danov KD, Kralchevsky PA Capillary Forces between Particles at a Liquid Interface: General Theoretical Approach and Interactions between Capillary Multipoles. Adv Colloid Interf Sci (2010) 154:91–103. doi:10.1016/j.cis.2010.01.010

CrossRef Full Text | Google Scholar

81. Hsiao LC, Jamali S, Glynos E, Green PF, Larson RG, Solomon MJ Rheological State Diagrams for Rough Colloids in Shear Flow. Phys Rev Lett (2017) 119(15):158001. doi:10.1103/physrevlett.119.158001

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Safouane M, Langevin D, Binks BP Effect of particle hydrophobicity on the properties of silica particle layers at the air-water interface (2007). doi:10.1021/la700800a

CrossRef Full Text | Google Scholar

83. Zang D, Langevin D, Binks BP, Wei B Shearing Particle Monolayers: Strain-Rate Frequency Superposition. Phys Rev E Stat Nonlin Soft Matter Phys (2010) 81(1):011604. doi:10.1103/physreve.81.011604

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Brown E, Zhang H, Forman NA, Maynor BW, Betts DE, Desimone JM, et al. Shear thickening and jamming in densely packed suspensions of different particle shapes (2011). doi:10.1103/PhysRevE.84.031408

CrossRef Full Text | Google Scholar

85. Stancik EJ, Gavranovic GT, Widenbrant MJO, Laschitsch AT, Vermant J, Fuller GG Structure and Dynamics of Particle Monolayers at a Liquid–Liquid Interface Subjected to Shear Flow. Faraday Discuss (2003) 123(0):145–56. doi:10.1039/B204382C

PubMed Abstract | CrossRef Full Text | Google Scholar

86. French DJ, Brown AT, Schofield AB, Fowler J, Taylor P, Clegg PS The Secret Life of Pickering Emulsions: Particle Exchange Revealed Using Two Colours of Particle. Scientific Rep (2016) 6(1):31401–9. doi:10.1038/srep31401

CrossRef Full Text | Google Scholar

87. Anachkov SE, Lesov I, Zanini M, Kralchevsky PA, Denkov ND, Isa L Particle Detachment from Fluid Interfaces: Theory vs. Experiments. Soft Matter (2016) 12(36):7632–43. doi:10.1039/C6SM01716A

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Isa L, Lucas F, Wepf R, Reimhult E Measuring Single-Nanoparticle Wetting Properties by Freeze-Fracture Shadow-Casting Cryo-Scanning Electron Microscopy. Nat Commun (2011) 2(1):438–9. doi:10.1038/ncomms1441

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Ye M, Deng X, Ally J, Papadopoulos P, Schellenberger F, Vollmer D, et al. Superamphiphobic Particles: How Small Can We Go? Phys Rev Lett (2014) 112(1):016101. doi:10.1103/physrevlett.112.016101

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Pradeep S, Wessel A, Hsiao LC Hydrodynamic Origin for the Suspension Viscoelasticity of Rough Colloids. J Rheol (N Y N Y) (2022) 66(5):895–906. doi:10.1122/8.0000424

CrossRef Full Text | Google Scholar

91. Dickinson E Food Emulsions and Foams: Stabilization by Particles. Curr Opin Colloid Interf Sci (2010) 15(1–2):40–9. doi:10.1016/J.COCIS.2009.11.001

CrossRef Full Text | Google Scholar

92. Rayner M, Marku D, Eriksson M, Sjöö M, Dejmek P, Wahlgren M Biomass-Based Particles for the Formulation of Pickering Type Emulsions in Food and Topical Applications. Colloids Surf A Physicochem Eng Asp (2014) 458(1):48–62. doi:10.1016/J.COLSURFA.2014.03.053

CrossRef Full Text | Google Scholar

93. Marto J, Ascenso A, Simoes S, Almeida AJ, Ribeiro HM Pickering Emulsions: Challenges and Opportunities in Topical Delivery. Expert Opin Drug Deliv (2016) 13(8):1093–107. doi:10.1080/17425247.2016.1182489

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Marquis M, Alix V, Capron I, Cuenot S, Zykwinska A Microfluidic Encapsulation of Pickering Oil Microdroplets into Alginate Microgels for Lipophilic Compound Delivery. ACS Biomater Sci Eng (2016) 2(4):535–43. doi:10.1021/acsbiomaterials.5b00522

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Silverstein MS PolyHIPEs: Recent advances in emulsion-templated porous polymers. Prog Polym Sci (2014) 39(1):199–234. doi:10.1016/J.PROGPOLYMSCI.2013.07.003

CrossRef Full Text | Google Scholar

96. Schrade A, Landfester K, Ziener U Pickering-Type Stabilized Nanoparticles by Heterophase Polymerization. Chem Soc Rev (2013) 42(16):6823–39. doi:10.1039/C3CS60100E

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Wu J, Ma GH Recent Studies of Pickering Emulsions: Particles Make the Difference. Small (2016) 12(34):4633–48. doi:10.1002/SMLL.201600877

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Gonzenbach UT, Studart AR, Tervoort E, Gauckler LJ Macroporous Ceramics from Particle-Stabilized Wet Foams. J Am Ceram Soc (2007) 90(1):16–22. doi:10.1111/J.1551-2916.2006.01328.X

CrossRef Full Text | Google Scholar

99. San-Miguel A, Behrens SH Influence of Nanoscale Particle Roughness on the Stability of Pickering Emulsions. Langmuir (2012) 28(33):12038–43. doi:10.1021/la302224v

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Xiao M, Xu A, Zhang T, Hong L Tailoring the Wettability of Colloidal Particles for Pickering Emulsions via Surface Modification and Roughness. Front Chem (2018) 6:225. doi:10.3389/fchem.2018.00225

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Binks BP, Rodrigues JA Types of Phase Inversion of Silica Particle Stabilized Emulsions Containing Triglyceride Oil. Langmuir (2003) 19(12):4905–12. doi:10.1021/la020960u

CrossRef Full Text | Google Scholar

102. Zanini M, Cingolani A, Hsu CP, Fernández-Rodríguez MÁ, Soligno G, Beltzung A, et al. Mechanical Phase Inversion of Pickering Emulsions via Metastable Wetting of Rough Colloids. Soft Matter (2019) 15(39):7888–900. doi:10.1039/C9SM01352K

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Feng L, Li S, Li Y, Li H, Zhang L, Zhai J, et al. Super-Hydrophobic Surfaces: From Natural to Artificial. Adv Mater (2002) 14(24):1857–60. doi:10.1002/ADMA.200290020

CrossRef Full Text | Google Scholar

104. Zhang P, Yang L, Li Q, Wu S, Jia S, Li Z, et al. Ellipsoidal Colloids with a Controlled Surface Roughness via Bioinspired Surface Engineering: Building Blocks for Liquid Marbles and Superhydrophobic Surfaces. ACS Appl Mater Inter (2017) 9(8):7648–57. doi:10.1021/acsami.6b16733

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Barthlott W, Neinhuis C Purity of the Sacred Lotus, or Escape from Contamination in Biological Surfaces. Planta (1997) 202(1):1–8. doi:10.1007/s004250050096

CrossRef Full Text | Google Scholar

106. Zhang X, Wang L, Levänen E Superhydrophobic Surfaces for the Reduction of Bacterial Adhesion. RSC Adv (2013) 3(30):12003–20. doi:10.1039/C3RA40497H

CrossRef Full Text | Google Scholar

107. de Gennes P-G, Brochard-Wyart F, Quéré D Capillarity and Wetting Phenomena. Capillarity and Wetting Phenomena (2004). doi:10.1007/978-0-387-21656-0

CrossRef Full Text | Google Scholar

108. Ming W, Wu D, Van Benthem R, De With G Superhydrophobic Films from Raspberry-like Particles. Nano Lett (2005) 5(11):2298–301. doi:10.1021/NL0517363

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Zhang L, Wu J, Wang Y, Long Y, Zhao N, Xu J Combination of Bioinspiration: A General Route to Superhydrophobic Particles. J Am Chem Soc (2012) 134(24):9879–81. doi:10.1021/ja303037j

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Maria D, Mammen L, Singh M, Deng X, Roth M, Auernhammer GK, et al. Superhydrophobic Surfaces by Hybrid Raspberry-like Particles. Faraday Discuss (2010) 146:35–48. doi:10.1039/b925676h

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Feng L, Zhang Y, Xi J, Zhu Y, Wang N, Xia F, et al. Petal Effect: A Superhydrophobic State with High Adhesive Force. Langmuir (2008) 24(8):4114–9. doi:10.1021/LA703821H

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Wang B, Liu Y, Zhang Y, Guo Z, Zhang H, Xin JH, et al. Bioinspired Superhydrophobic Fe3O4@Polydopamine@Ag Hybrid Nanoparticles for Liquid Marble and Oil Spill. Adv Mater Inter (2015) 2(13):1500234. doi:10.1002/ADMI.201500234

CrossRef Full Text | Google Scholar

113. Wang Z, Ai B, Möhwald H, Zhang G, Wang Z, Zhang G, et al. Colloidal Lithography Meets Plasmonic Nanochemistry. Adv Opt Mater (2018) 6(18):1800402. doi:10.1002/ADOM.201800402

CrossRef Full Text | Google Scholar

114. Lee JH, Oh JW, Nam SH, Cha YS, Kim GH, Rhim WK, et al. Synthesis, Optical Properties, and Multiplexed Raman Bio-Imaging of Surface Roughness-Controlled Nanobridged Nanogap Particles. Small (2016) 12(34):4726–34. doi:10.1002/SMLL.201600289

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Liang H, Li ZP, Wang W, Wu Y, Xu H Highly Surface-Roughened “Flower-like” Silver Nanoparticles for Extremely Sensitive Substrates of Surface-Enhanced Raman Scattering. Adv Mater (2009) 21(45):4614–8. doi:10.1002/ADMA.200901139

CrossRef Full Text | Google Scholar

116. İlhan B, Annink C, Nguyen DV, Mugele F, Siretanu I, Duits MHG A Method for Reversible Control over Nano-Roughness of Colloidal Particles. Colloids Surf A Physicochem Eng Asp (2019) 560:50–8. doi:10.1016/j.colsurfa.2018.09.071

CrossRef Full Text | Google Scholar