- Chemistry Department, Oregon State University, Corvallis, OR, United States
The total kinetic energy release and fission mass distributions for the fast neutron (En = 3–100 MeV) induced fission of 232Th, 233U, 235U, 237Np, 239Pu, 240Pu, and 242Pu have been measured using the LANSCE facility. The neutron energies were deduced from time-of- flight measurements. The fission fragments were detected using Si PIN diode detectors, giving us the fragment energies. The actinide targets were made by vapor deposition leading to high-quality targets, that were thin and uniform with reduced impurities. Corrections were made to the data for pulse height defect and the fragment energy loss in the target and its backing. The TKE distributions were Gaussian in shape and their mean value as a function of incoming neutron energy could be fitted with second order polynomials. In the case of 233U and 235U, our measurements agree with prior work. Our measurements for 232Th are unique. Our data agree with Viola scaling. The constant position of the heavy mass peak is interpreted as being due to the influence of the N = 88 and Z = 50 shells. The GEF model predictions agree with the data in general as do the CGMF model predictions.
1 Introduction
Most of the energy released in the fission of actinide nuclei appears in the form of the total kinetic energy (TKE) of the fragments. Because of this fact, it is important to understand the TKE release for its practical importance and the information gained about large scale nuclear collective motions. There are many books that describe the fission process. Some general books are P. Talou and R. Vogt [1],
W. Younes and W. Loveland [2], R. Vandenbosch and J.R. Huizenga “Nuclear Fission” Academic Press (1974) [3], C. Wagemans, “The Nuclear Fission Process”, CRC Press (1991) [4], and H.J. Krappe and K. Pomorski, “Theory of Nuclear Fission” Springer, (2011) [5].
From time to time there are important review articles on fission that influence the development of the field. Among the list of such articles that influenced the author are [6–8], and [9].
Viola et al. [10] have suggested a simple parameterization of the TKE release in the low energy and spontaneous fission of actinide nuclei in the form:
The first term in this equation represents the Coulomb energy of the deformed nascent fragments at scission while the second term represents an average estimate for the energy contributed to the TKE release from the conversion of the collective motion of the fissioning system into kinetic energy of the fragment during the saddle to scission descent. This simple notion of Viola scaling Eq. 1 can be used to parameterize the important and complex subject of fission total kinetic energy release.
In Table 1, we summarize the available data on the TKE release in the fission of actinide nuclei induced by neutrons and protons. Authoritative summaries of the data for the neutron induced fission of 235U, 238U and 239Pu are found in the work of Madland [11] and Lestone and Strother [12]. I omit discussion of the TKE release in transfer reactions and heavy ion induced reactions.
Materials and methods
All the targets used in this work were made by vapor deposition. Vapor deposition avoids the presence of impurities in the target. Actinide oxides are converted to actinide fluorides in a dual glove box system. The actinide fluorides are vapor deposited onto thin carbon foils. Typical actinide thicknesses are 100 ug/cm2. The preparation of the targets and their characterization are described in [33].
Experimental details
The experiments were carried out at the Weapons Neutron Research Facility (WNR) at the Los Alamos Neutron Science Center (LANSCE) at the Los Alamos National Laboratory (LANL) [34, 35]. “White spectrum” neutron beams were generated from an unmoderated tungsten spallation source using the 800 MeV proton beam from the LANSCE linear accelerator. The experiment was located on the 15R beam line (15° right with respect to the proton beam). The fast neutron beam intensities were ∼105–106/s for En = 2–100 MeV. The proton beam is pulsed allowing one to measure the time of flight (energy) of the neutrons arriving at the experimental area. The proton beam consists of a 625 us macro pulse containing about 340 micro pulses of width 250 ps that are spaced 1.8 us apart. The macro pulses had a repetition rate of 100 Hz. With neutron beam intensities of ∼105–106 n/s, one must use large solid angles for the detectors or long observation times or both to obtain statistically meaningful data.
The spallation neutrons from the LANSCE tungsten target traversed a 13.85 m flight path to the target position of our scattering chamber. The neutron beam was collimated to a 1 cm diameter at the entrance to the experimental area. At the entrance to the scattering chamber the beam diameter was measured to be 1.3 cm. A fission ionization chamber was used to continuously monitor the absolute neutron beam intensities. The targets and fission detectors were housed in an evacuated, thin-walled aluminum scattering chamber. The scattering chamber was located 55 cm from the collimator and ∼14 m from the neutron beam dump.
Fission products were detected by eight to nine pairs of Si PIN diode detectors (Hamamatsu S3590-09) arranged on opposite sides of the beam at angles of ∼60°–120° with respect to the incident beam. The area of the individual PIN diodes was 1 cm2. The distance of the detectors from the center of the target was ∼2.1 cm.
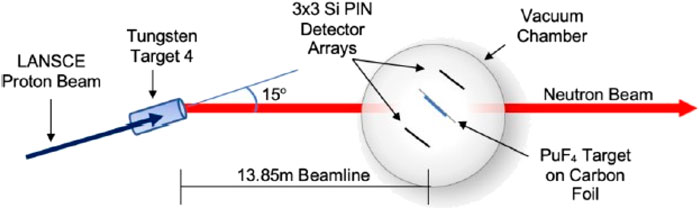
The time of flight of each interacting neutron was measured using a timing pulse from a silicon PIN diode and the accelerator RF signal. As stated previously, the distance from the spallation target to the actinide target was measured to be 1384.9 ± 1.1 cm. The position of the photofission peak in the time-of-flight spectrum was measured to have an uncertainty of 2.4%. The neutron energies were calculated using relativistic relationships, between the distance traveled by the neutrons, the mid-point of the photofission peak in the fission time of flight spectrum and the observed time difference between the neutron timing signal and the accelerator RF signal. The uncertainties from each of the components of the calculation of the neutron energy were added in quadrature as uncorrelated uncertainties to determine the final uncertainty in the measured neutron energy. The neutron energies were thus determined with an average uncertainty of 4.7%. The neutron energies were generally binned logarithmically to give bins of equal associated uncertainty in neutron energy. The widths of these bins give the relative neutron energy resolution of our measurements. Our experimental setup is shown schematically in Figure 1.
The actual detailed arrangement of the detectors and target are shown in Figure 2.

FIGURE 2. Picture of detector arrays and target. The dashed arrow shows the expected beam trajectory.
We measure, on an event-by-event basis, the pulse heights of the coincident fission fragments. To transform these pulse heights into energies, we must correct for the pulse height defect in our Si PIN diode detectors and the energy losses of the fragments in the target and backing foil. To make these corrections, we need to estimate the masses of the fragment. To do this we use an iterative procedure. The fragment masses and total kinetic energies were deduced using the 2E method.
In the 2E method that we are using, we must assume conservation of momentum.
We need to (iteratively), correct for: (a) pre-equilibrium neutron emission (b) pre-fission neutron emission (c) the dependence of the post-neutron emission on fragment mass and (d) the mean atomic number associated with each post-neutron emission fragment.
Predictions of the GEF and CGMF fission models for neutron multiplicity
The GEF (General Description of Fission Observables) model [36] is frequently used to estimate the pre-equilibrium, pre-fission, and post fission neutron emission.
GEF is a semiempirical code for predicting the outcomes of fast neutron induced fission reactions. It has ∼50 free parameters in the code allowing it to do quite well in its predictions. GEF can be used to treat reactions with Z = 80 to 112 and spontaneous and induced fission with excitation energies up to 100 MeV.
The CGMF (Cascade Gamma Multiplicities from Fission) model uses the ratio of the initial fragment temperatures to determine the partition of the excitation energy. The ratio of the fragment temperatures is correlated to the fragment deformation. The fragments near the Z = 50 and N = 82 closed shells are expected to be more spherical than the lighter fragments and as such to have lower excitation energies. Thus, their lighter partners will be more excited, resulting in higher associated neutron multiplicities. As shown in Table 2, the predicted total neutron multiplicities are similar in these models.
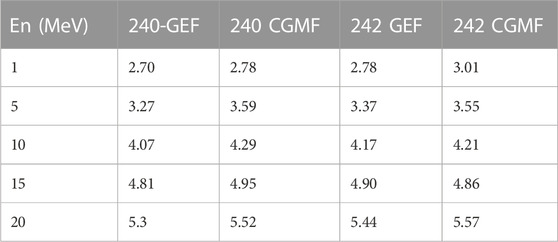
TABLE 2. Mean total neutron multiplicity predicted by the GEF [36] and CGMF models for 240,242Pu (n,f).
Corrections for pulse height defect
The pulse height defect is defined as the difference between the true energy of a fission fragment and its nominal energy based upon an energy calibration of the detector with alpha particles. This loss in energy is due to: (a) loss of energy of the fragment in the entrance window and dead layer of the detector (b) recombination of the electron-hole pairs created in the interaction of the fragment with the detector prior to charge collection and (c) loss of energy by nuclear stopping, an effect not that is not present in alpha particle interactions. For Si surface barrier detectors, the method of Schmitt et al. [37] is used to make the correction for pulse height defect which was 4.8–7.7 MeV. In measurements made with gas ionization detectors, a similar effect occurs but the magnitude of the energy loss is much less (pulse height defect = 2.5–4.5 MeV). All the measurements described in this work was made with silicon surface barrier detectors (SSB) or silicon pin diode detectors (PIN). The pulse height defect in Si PIN diode detectors is believed to be the same as that observed in Si surface barrier detectors [38]. Additional data on corrections for pulse height defect can be found in the work of Pleasanton (F. Pleasanton [31]) where the thermal neutron induced fission of 233U is studied and the work of [32]) where a scheme like the Schmitt method is proposed.
Corrections for the energy loss in the target and backing
Corrections for the energy loss of the fission products in the actinide deposits and the ∼100 ug/cm2 C target backing foils were made using the Northcliffe -Schilling tables [39]. These tables are used instead of the relations in the widely used SRIM] [40] code because it has been shown [41] that the dE/dx relations in SRIM mis-represent the correct dE/dx relations.
An important issue with respect to fragment energy losses in the target is the presence of “crud” in the target. “Crud” refers to the residues of solvent molecules that are frequently deposited when actinide targets are prepared by molecular plating. This “crud” material is of generally unknown composition. The best solution to this problem is to prepare the actinide deposits by vapor deposition. When that is not possible, one must use the well-known values of the TKE release for thermal neutron induced fission to make corrections for the presence of this “crud” material.
The effect of the target backing upon the measured TKE values is discussed in the work of A. Al-Adili et al., [42].
In Figure 3, I show the kinetic energy distributions for the fission fragments (after neutron emission) for the spontaneous fission of 252Cf and the thermal neutron induced fission of 235U. The point of this figure is to show that the fragment energies deduced in this work have proper corrections for energy losses in the target and backing materials.
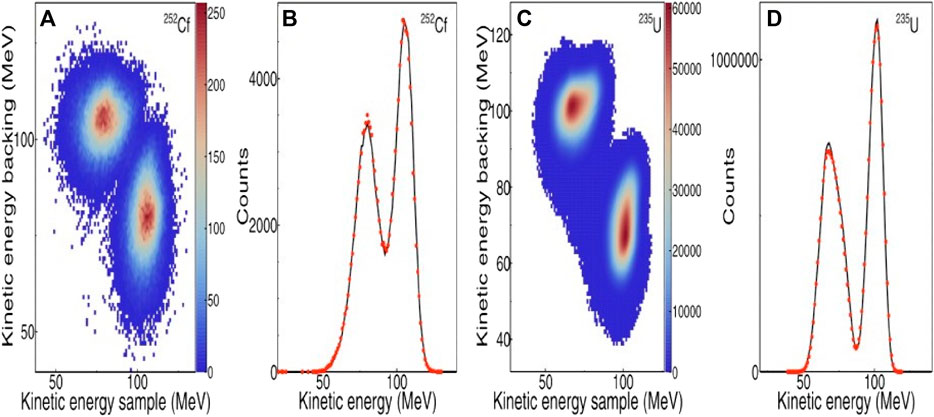
FIGURE 3. The kinetic energy distributions for 252Cf(sf) in (A), (B), and 235U(nth, f) in (C) and (D). The energies from the sample side are plotted versus the energies from the backing side. The projections of the two-dimensional distributions are plotted in (B,D). The energies from the sample and backing sides are in good agreement. The data is from [43].
Recent work on the preparation of targets for research on heavy and superheavy nuclei can be found in the review article of Lommel, Dullmann, Kindler and Renisch, [44].
Benchmarking
To benchmark the experimental method, the TKE release in the thermal neutron induced fission of 235U was measured/deduced. The measured/deduced value of the TKE release was 170.0 ± 0.15 MeV compared to the known value of 170.1 MeV for the 235U (n,f) reaction (16). Thus, no normalizations of the data were needed and thus our measurements are absolute measurements.
Results
General observations
The TKE distributions for each system studied, i.e., the fast neutron (En = 3–100 MeV) induced fission of 232Th, 233U, 235U, 237Np, 239Pu, 240Pu, and 242Pu, were Gaussian in shape. The words “TKE distributions” refer to the fragment energies after neutron emission, The words “TKE distributions” refer to the fragment energies after neutron emission.
TKE distributions
The measured TKE distributions in the fast neutron induced fission of 232Th (black squares) 235U (red triangles) 237Np (blue circles) and 239Pu (orange triangles) are shown in.
In general, the dependence of the mean TKE on neutron energy is similar for each of the reactions studied with the obvious point that the absolute values of the TKE increase with the Z of the fissioning system.
Earlier, I mentioned the role of Viola scaling in describing the general shape of the TKE distributions. The Viola systematics would predict TKE values of 170.1 and 163.8 MeV for the thermal neutron induced fission of 235U and 232Th, respectively. The Viola predictions are in remarkable agreement with the observed values (Figure 4). Thus, we can conclude that Viola scaling describes the essential physics of the scission point. (We can extend these calculations to include 237Np (which is not thermally fissionable) and 239Pu which is thermally fissionable and the predictive power of Viola scaling holds).
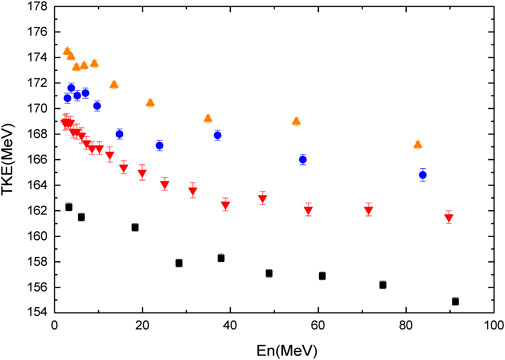
FIGURE 4. By the phrase “TKE distributions” we mean the mean value of the TKE distributions as a function of neutron energy. Average TKE measured by our group for the fast neutron induced fission of 232Th, 235U, 237Np, and 239Pu. See text for color code and further details.
Let’s pick “representative” values of the neutron energy like 10 and 20 MeV. Extrapolating in Figure 4, we deduce measured values of the TKE of 161, 166.5, 170, and 173.5 MeV for the case of En = 10 MeV for the fast neutron induced fission of 232Th, 235U, 237Np, and 239Pu and 160.5, 165, 167.5, and 171.5 MeV for En = 20 MeV for the fast neutron induced fission of 232Th, 235U, 237Np, and 239Pu. One can compare these measurements with the predictions of the Viola formula for spontaneous and thermal neutron induced fission to understand the effect of increasing the energy of the neutron inducing fission.
Other detailed models of TKE distributions (arranged chronologically) or “Works on TKE distributions over time.”
Among the earliest papers on the TKE release in the fast neutron induced fission of actinide nuclei was the paper of Bishop et al. [19]. In a study of the proton induced fission of 233U and 238U, [19] measured the energies and yields of the neutrons emitted from the fission fragments of known mass. They found a washing out of the sawtooth dependence of the emitted neutrons on fragment mass with increasing excitation energy with the effect being most pronounced for the heavy fragment. Bishop et al. presented data on the total fragment kinetic energy as a function of the proton energy.
A useful early compilation of the TKE release in the fission of 239Pu (n,f) in steps of 100 keV for neutron energies from 0 to 5.5 MeV is found in the work of N.I. Akimov et al. [45].
Bjornholm [46] related the fine structure of the mass yields and total kinetic energy of the even nuclides to the possibility of superfluid vs. a viscous descent from saddle to scission.
One of the most interesting and comprehensive early treatments of low energy fission of the actinides was the work of Wilkins, Steinberg and Chasman [47]. These authors proposed a static model that assumed statistical equilibrium among the collective degrees of freedom at the scission point. The general trends of the mass, charge, and kinetic energy distributions for a large range of nuclei from Po to Fm were correctly described. The role of deformed shell corrections for neutrons was emphasized.
Scheuter, Gregoire, Hofmann and Nix [48], calculated the fission total kinetic energy distributions for the fission of 213At, using a two-dimensional Fokker-Planck equation.
These authors showed how the effects of spreading in the stretching degree of freedom and fluctuations in the fission degree of freedom affected the TKE distributions. The Folker-Plank equation is also the basis of papers describing the mass-energy distributions of fission fragments and the dependences of the mean kinetic energy for a wide variety of heavy nuclei ranging from Hg to Pu [49]. A two-dimensional diffusion model is also used to describe the TKE release [50].
H.R. Faust [51] showed that a statistical model can reproduce the mean values of the fragment kinetic energy for compound systems ranging from 219Ac to 258Fm very accurately. The variances of the TKE distributions were also well reproduced. These calculations also gave the total excitation energy in the systems studied.
Wada, Abe and Carjan [52] studied the fission dynamics of hot nuclei using two dimensional Langevin equations. The pre-scission multiplicities of neutrons, protons and alpha particles were calculated. The average total kinetic energy of the fission fragments was correctly calculated when one body dissipation was assumed. They assumed a strong dissipation mechanism and a compact scission configuration.
[53] have made several important contributions to understand the total kinetic release in fission. Starting with the Los Alamos model of the TKE release, they were able to use semi-empirical models to correctly describe the TKE release in the fission of 232–226 Th, 233-224Pa, 238–229 U, 237–231 Np, 242–235 Pu and 245-240Am. Manea and Tudora proposed a simple approach for the calculation of the fission fragment total kinetic energy, TKE(A), based on the electrostatic repulsion between the fragments connected by a neck in the pre-scission configuration is described. The calculated TKE(A) is obtained in good agreement with the experimental data for many fissioning systems in the EXFOR library, such as 233,235U (nth, f), 239Pu(nth, f), 237Np(n, f), and 242Pu(SF), with minor adjustment of only one parameter, the neck length. This lack of a dependence of the TKE upon the excitation energy of the fissioning system is interesting.
V.M. Maslov has written several review articles that attempt to summarize the data on fast neutron induced fission of Th, Pa, U, Np, Pu and Am. Special attention is given to the role of symmetric and asymmetric fission in these systems [54].
Simenel and Umar [55] have studied the symmetric fission of 258, 264 Fm using a time dependent Hartree-Fock method. They showed that non-adiabatic evolution affects the kinetic and excitation energies of the fragments. Low-lying collective vibrations are more easily excited than giant resonances.
Sierk [43] used a Langevin model to calculate various features of fission at low to medium excitation energies. After benchmarking his calculational results to 235U (n,f), Sierk was able to reproduce the properties of the TKE release in a number of nuclei.
Chebbouhi et al. [56] made a theoretical investigation of the fission fragment kinetic energy distributions in the symmetric mass region for the 233U (nth, f) reaction. The Monte Carlo code FIFRELIN was used along with the Brosa model to get the kinetic energy distributions. The effect of energy losses in the measurements was considered.
The fission of the even-even isotopes of Hs to Og is studied in the work of Carjan, Ivanyuk and Oganessian [57]. For the isotopes of Hs, Ds, and Cn, a transition from symmetric to asymmetric fission is predicted for increasing neutron number.
Supersymmetric fission occurs at N ∼ 160. The mean vales of the TKE are predicted for Z = 108–118 along with the variances of the TKE distributions.
Randrup and Vogt [58] have made several important contributions to our understanding of the physics involved in the fast neutron induced fission of actinide nuclei using their code FREYA. In their FREYA calculations, they specified the A, Z, E* of the fissioning system and FREYA calculated the A and Z of both fission fragments and the total kinetic energies. Angular momentum was specifically accounted for in the calculations.
Specifically, FREYA does the calculation for the spontaneous fission of 238U, 238Pu, 240Pu, 242Pu,244Cm and 252Cf along with the neutron induced fission of 233U, 235U, 238U, 239Pu, and 241Pu at neutron energies up to 20 MeV. The rotational and statistical excitations of the fragments are considered. Angular momentum conservation is considered at pre-scission, scission, and post-scission stages. The nuclei are allowed to rotate and evaporate neutrons and then photons.
Three and four dimensional Langevin calculations of the TKE release in fission were made by Usang and co-workers [59]. Similar Langevin calculations were done by a Chinese group [60]. The paper by Ishizuka et al. focused on the low energy fission of 236U, while the work of Usang et al. treated a larger number of systems. The three-dimensional calculations do not describe the data as well as the four-dimensional calculations and the four-dimensional calculations do a better job of describing the Brosa modes.
Jaffke, Moller, Talou and Sierk [61] combined information from calculated macroscopic-microscopic calculations of the mass yields with a de-excitation model based on Hauser-Feshbach statistical decay theory. The authors restricted their attention to the thermal neutron induced fission of 235U and 239Pu where the experimental data is relatively well known. The uncertainties in the TKE release were estimated to be 0.3%–0.8% for 235U and 0.1%–0.2% for 239Pu.
Li-Le Liu et al. [62], used a Langevin approach to study the fission of 233,236, 239U and 239Pu at low excitation energies. Their calculations describe the details of the fast neutron reactions studied.
A fully microscopic scission-point model is used to predict the fission fragment observables in the thermal neutron induced fission of 235U, 239Pu and the spontaneous fission of 252Cf by Lemaitre, Goriely, Hilaire and Sida [63] The model, called the SPY2 model, is said to be fully microscopic and involves the properties of 7,000 nuclei. The use of this input of real data improves the predictive abilities of the model.
Kaldiani made a study [64] of the kinetic energy distribution the photofission of the light actinides. The deformation parameters of the fission fragments have a large change near the symmetric region. Kaldiani studied the TKE distributions for neutron-induced fission, spontaneous fission and photofission to predict the actinide TKE distributions. The TKE distributions are similar for all nuclei but the TKE distribution for spontaneous fission are different.
In a series of papers, Lovell and co-workers [Phys. Rev. C 100, 054610 (2019), Phys. Rev. C102, 024621 (2020), Phys. Rev. C 103, 014615 (2021)], used the fission event generator CGMF to study various aspects of the correlations between fission observables in fast neutron induced reactions. Among the reactions studied were 233,234,235,238U, 239, 241Pu, and 237Np (n,f).
Albertson and coworkers [Eur. Phys. J. A 56, 46 (2020); Phys. Rev C 103, 014609, (2021)] made a series of encyclopedic studies of fast neutron induced fission that involved the calculation of fission-fragment mass yields and average total kinetic energies for 896 e-e nuclei (74 < Z 126, 92 < N < 230) as well as the total kinetic energy and its uncertainty for 235U (n,f) for thermal and 5.5 MeV neutrons. In the latter studies, the correlation between the fragment properties and the TKE distributions are discussed in detail.
Bulgac [Phys. Rev. C 102, 044609 (2020)] points out that fission fragments share excitation energy long after they stop exchanging nucleons, leading to a lower total kinetic energy of the fission fragments.
An “improved” scission-point model is used by H. Pasca, A.V. Andreev, G.G. Adamian and N.V. Antonenko [Phys. Rev. C 104, 014604 (2021)] to provide a simultaneous description of the charge, mass, total kinetic energy and neutron multiplicities for the 222Th, 226Th, 230Th, 230U and 234U at 11 MeV. Detailed comparisons of theory and experiment are provided. For induced fission of 250Cf, the TKE distributions are calculated and found to agree with measurements.
L. Tong and S. Yan [Phys. Rev. C 106, 044611 (2022)] make time-dependent Hartree-Fock-Bogoliubov calculations of symmetric and asymmetric fission of 240Pu. The calculations agree with the measured data for 240Pu.
V. Yu Denisov and I. Yu. Sedykh describe the data on the average total kinetic energy of the fission fragments in the fission of 234,236, 239U and 240Pu using a simple expression. [Phys. Lett B 824, 136814 (2022)].
In a review article in this journal, D. Neudecker et al., Frontiers Phys. 10:1056324 (2023) reported the TKE values for the fast neutron induced fission of 239Pu and compared the measurements and the CGMF model for En = 0–20 MeV. The need for further experiments is clearly indicated.
Li et al. present time-dependent density functional theory calculations for the fast neutron induced fission of 240Pu, 234U, 244Cm and 250Cf. The partition of the initial energy of the system into the various components at scission is traced out. (Phys. Rev. C 107, 014303 (2023).)
GEF, CGMF and FREYA
There are certain omnibus approaches to predicting the outcome of fast neutron induced fission of heavy nuclei. Three such codes are GEF, FREYA and CGMF. As remarked earlier, GEF is a semiempirical code for predicting the outcomes of fast neutron induced fission reactions. It has ∼50 free parameters in the code allowing it to do quite well in its predictions. GEF can be used to treat reactions with Z = 80 to 112 and spontaneous and induced fission with excitation energies up to 100 MeV. A benchmark paper [C. Schmitt, K.-H. Schmidt and B Jurado, Phys. Rev. 98, 044605 (2018)] provides a summary description of the code and its use.
The CGMF code is a Monte Carlo implementation of the statistical Hauser-Feshbach nuclear reaction theory applied to the de-excitation of primary fission fragments. CGMF requires an input of fission fragment mass, charge, and kinetic energies. From these inputs, the code calculates the final cross sections. There is no statistical difference between the TKE values calculated by the CGMF and GEF codes.
FREYA is a more complete model that provides the full kinematic information on the two product nuclei and the emitted photons and neutrons. The input for FREYA is the fission mass distributions and the average total kinetic energy. FREYA treats spontaneous fission and neutron induced fission (up to 20 MeV). FREYA is described in J.M. Verbeke, J. Randrup and R. Vogt, LLNL-SM-705798, and M. Verbeke, J. Randrup and R. Vogt, Comp. Phys. Communication, 222, 263 (2018)
Contributions of the Oregon State group
I would be remiss if I did not specifically mention the contributions of the Oregon State group to the study of the fast fission of the actinide nuclei. The TKE release in the fast neutron induced fission of 232Th was studied by King et al. while similar studies of the TKE release in the fast fission of 235U were made by Yanez et al. The TKE release in the fast fission of 237Np was studied by Pica et al. The TKE release in the fast fission of 239Pu was studied by Chemey, Pica, Yao, Loveland, Lee and Kuvin. The TKE release in the fast fission of 240Pu and 242Pu were made by Pica, Chemey, and Loveland. Yao and co-workers studied the fast fission of 241Am. (See References for details).
Polynomial fits to the observed TKE distributions
The mean post neutron emission TKE release decreases non-linearly with increasing neutron energy. In Table 3, we give the results of fitting, using a quadratic equation, the observed TKE distributions as a function of energy of the neutron inducing fission for the systems we have studied.
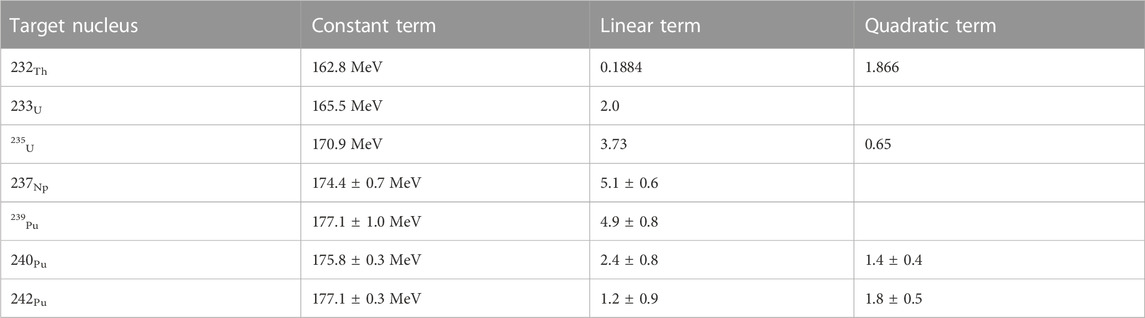
TABLE 3. The results of fitting the observed TKE release as a function of the energy of the neutron inducing fission for the systems we have studied.
While one can see the expected general increase in the TKE values with increasing Z and A of the fissioning system, there are some strange “bumps (errors??)” in the data such as the data for 240Pu. When an entry in Table 3 is blank, that means the term is not statistically significant in the fitting procedure. Also, the reader should not take the data described in Table 3 as an attempt to create an “energy dependent” Viola model.
Measurement of the 240,242Pu(n,f) mass and kinetic energy distributions
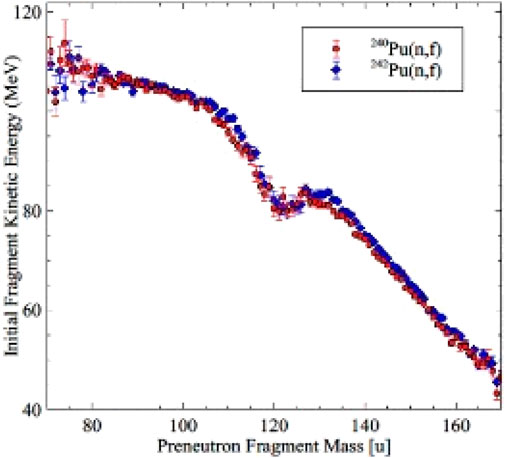
Our most recent work has involved measuring the total kinetic energy release in the fast neutron induced fission of 240,242Pu. Our measurements of the fission fragment mass distributions for the 240, 242Pu(n,f) reactions can be compared to previous work and some semiempirical models (Figures 5, 6). The agreement of the measured data and the semi-empirical models is excellent, suggesting we can correctly measure the fragment mass distributions in the fast neutron induced fission of 240, 242Pu and can understand the data in terms of accepted models for these reactions.
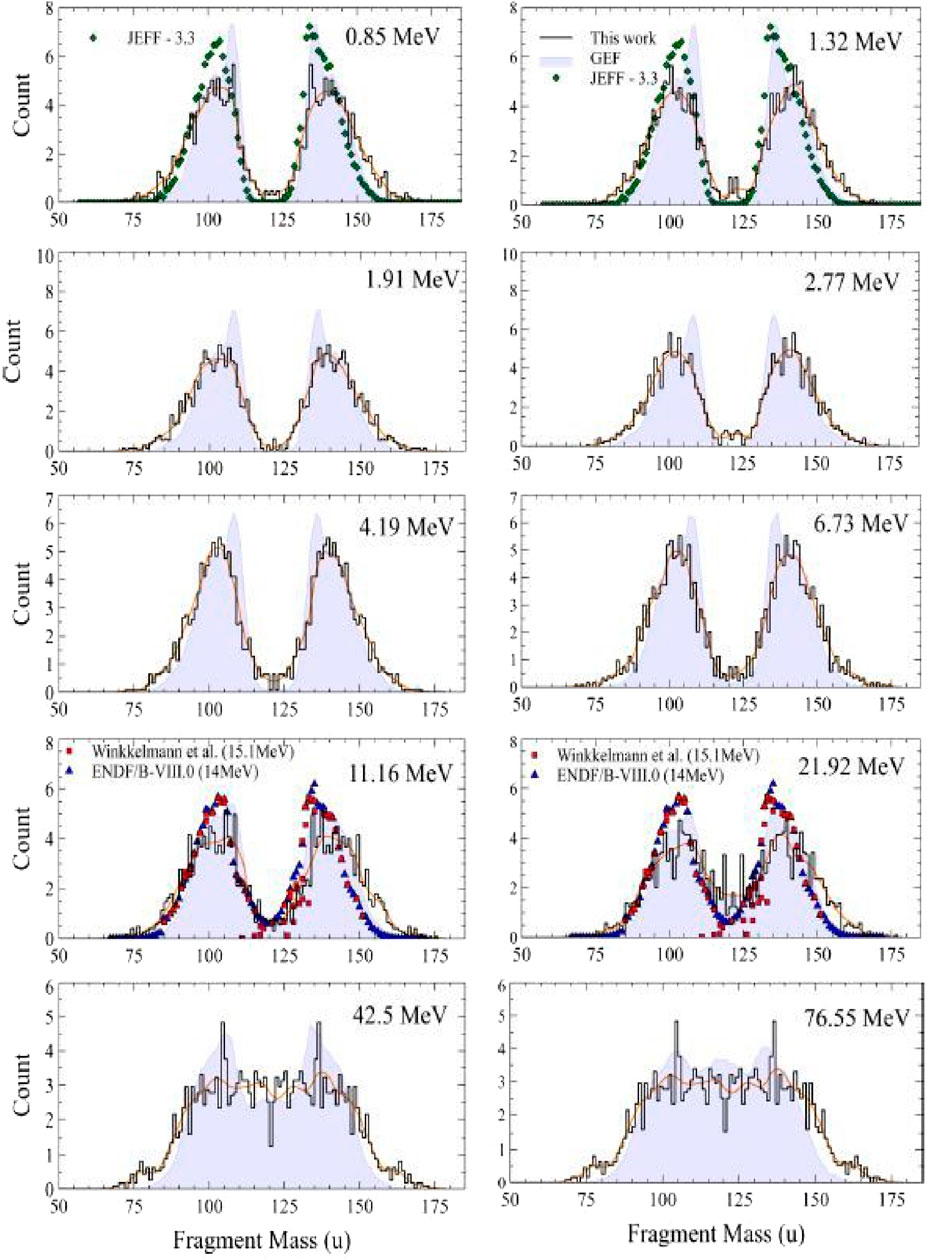
FIGURE 5. Comparison of the measured values of the mass distributions for the 240Pu (n,f) reaction with previous measurements (Winkelmann et al. [41]), the ENDF model (ENDF) [42] and the semiempirical JEFF 3.3 [45] and GEF [26] models.
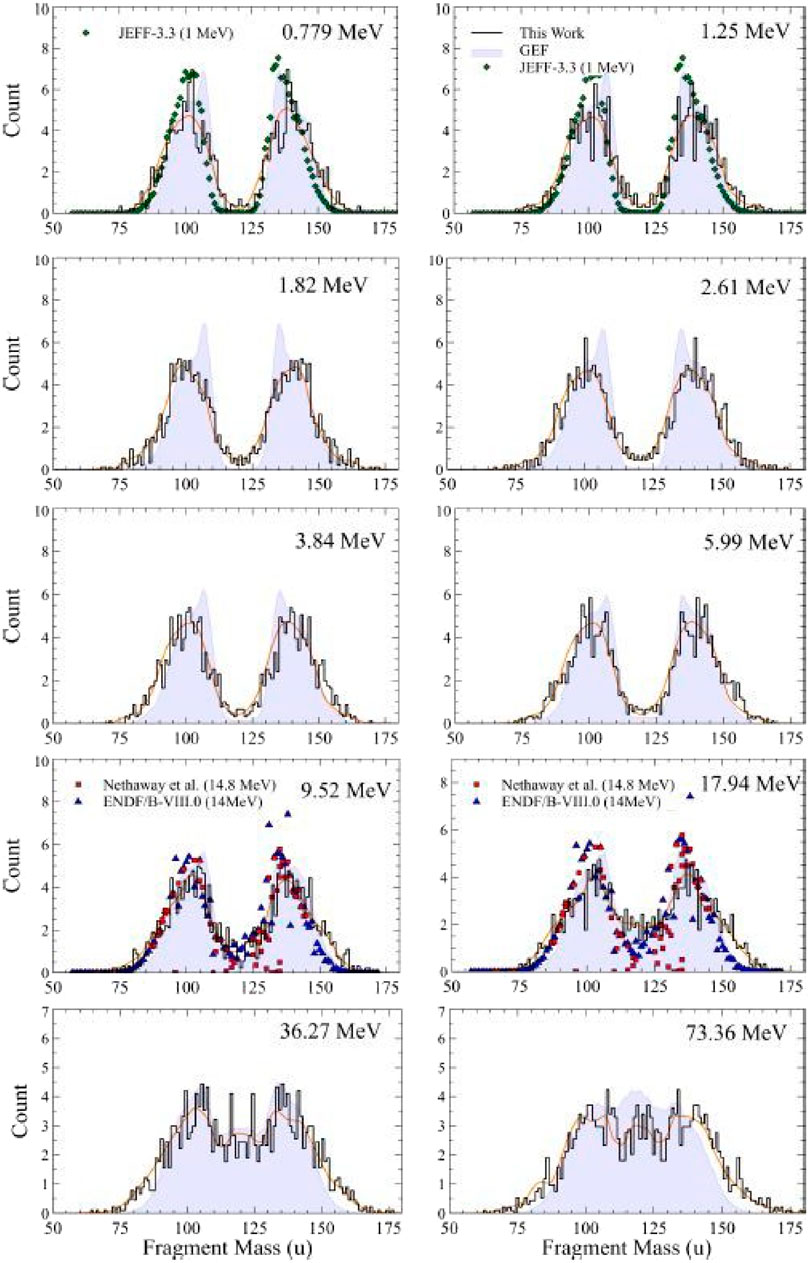
FIGURE 6. Measured fission mass distributions for 242Pu(n,f) reaction and comparisons with previous work (Nethaway [44]), ENDF [42] estimates and calculations of the GEF [26] and JEFF [45] codes.
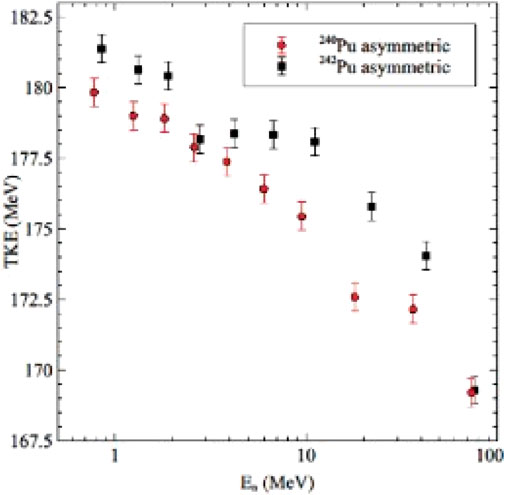
The fission mass distributions show the expected evolution from asymmetric fission at low neutron energies to symmetric fission at higher neutron energies. If we focus our attention on the events involving asymmetric fission, we get the results shown in Figure 7, where we show the TKE release in the asymmetric fission events.
The data clearly show the expected decrease in the TKE release with increasing neutron energy but there are some “bumps and wiggles” in the data. The observed TKE decrease with increasing En is a consequence of two factors: shell effects fade out at high excitation energies and the TKE associated with asymmetric fission decreases due to changes in the fragment shapes. (See Ref. [65]).
The data for low neutron energies is shown in Figure 8.
The data clearly show the importance of shell closures near A = 134 reflecting the extra stability of Z = 56, due to octupole deformation. The data are in general agreement with the predictions of the GEF model but with smaller jumps in the TKE release at nth chance fission energies. Similar agreement with the predictions of the CGMF model are observed. (See the work of Pica et al., Phys. Rev. C 106, 044603 (2022) for examples).
Variances of TKE distributions
One of the findings in our TKE data was the values of the variances of the TKE distributions. The features of the variances were:(a) the variances decrease as (Z, A) of the fissioning system increases(b) the variances are larger than expected from conventional models of scission (c) the variances show “bumps” at the onset of second chance, third chance, etc. fission.
Note the similarities between the measurements of Duke et al. and our data for the 235U (n,f) reaction (Figure 9). Also please note the relative insensibility of the variances to the large changes in the fission cross sections with increasing neutron energy. The variances, while important measures of the physics, are difficult to measure.
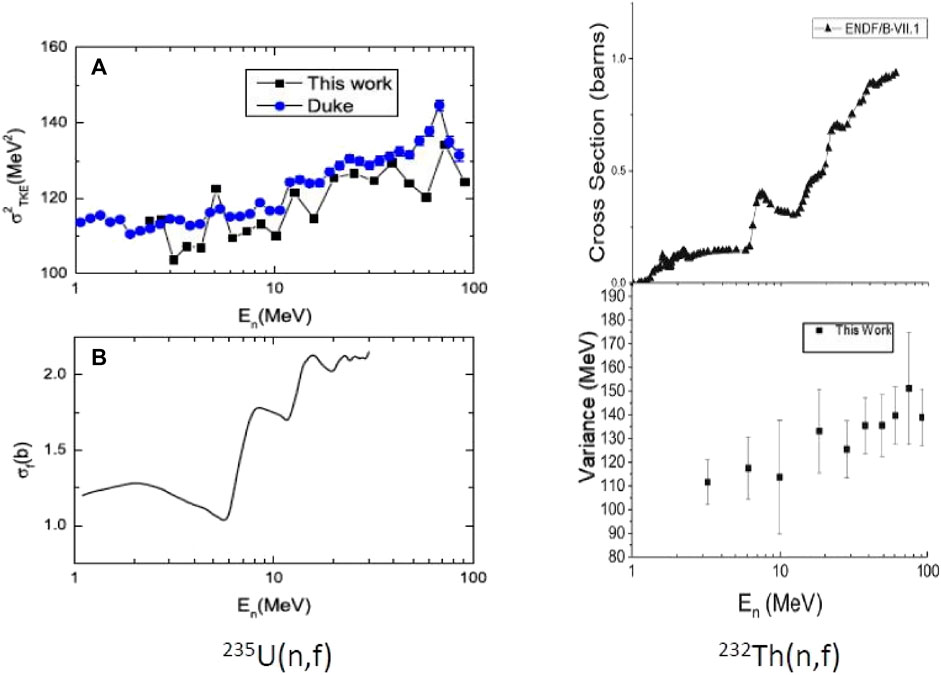
FIGURE 9. The variances of the TKE distributions and the fragment cross sections as a function of the initial neutron energy for the 235U (n,f) and 232Th (n,f) reactions. “This work” refers to refs. 15 and 30 and “Duke” refers to ref. 77.
In Figure 10, we observe a significant increase in the measured variance at the onset of second chance fission (∼7 MeV). For a detailed discussion of these trends in the variances, the reader is referred to the work of Pica et al. [28, 66].
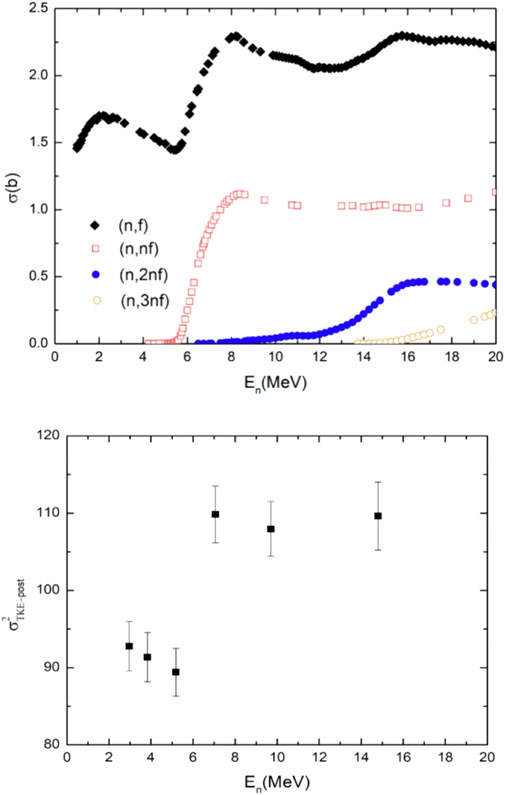
FIGURE 10. (A) The cross section for the 237Np(n,f) reaction from the evaluated nuclear data file (ENDF)/B=VIII and ENDF/B-VI. (B) Measured TKE variance vs. En for this reaction.
Fragment shapes at scission
We can transform the TKE distributions into representations of the shapes of the fragment at scission (Figure 11). The details of this analysis can be found in [66]. References 67–69, 70, 71, 72, 73, 74, 75–78 contain additional information about the fast neutron induced fission of actinide nuclei.
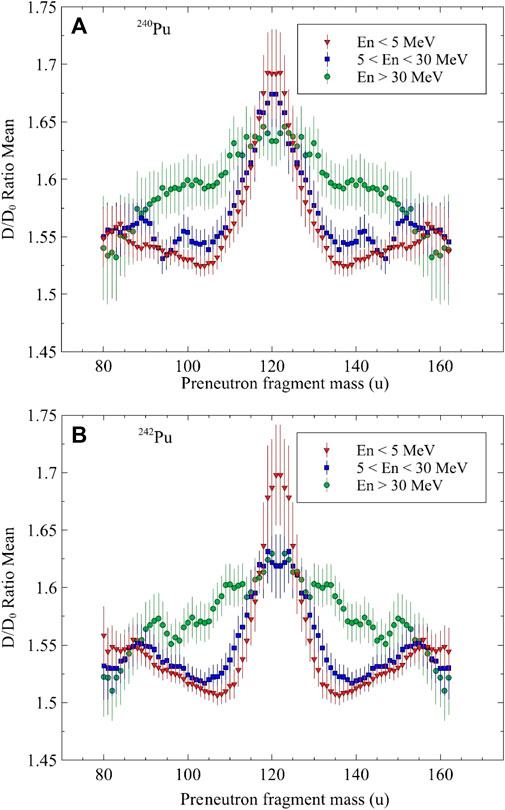
FIGURE 11. A rolling average ratio of the distance between the charge centers of the fragments at scission and that of spherical touching nuclei (D/D0) for 240Pu (n,f) (A) and 242Pu(n,f) (B).
Summary of paper
What have we learned from this review of the fast neutron induced fission of actinide nuclei? We begin with a summary of prior work (Materials and Methods). We discuss Experimental Details with separate discussions of Corrections for Pulse Height Defect and Corrections for Energy Loss in the Target and Backing. We interpose a discussion of the GEF and CGMF models. We then discuss Benchmarking of our data and our results (Experimental Observations, TKE distributions and Other detailed models of TKE distributions.) We then return to a more in-depth discussion of the GEF, CGMF and FREYA models. At this point, it seemed important to specifically call out the Contributions of the Oregon State Group. The most recent data is discussed in sections on the measurements of 240,242Pu, the variances of the TKE distributions and the fragment shapes at scission.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This manuscript is based upon work supported in part by the U.S. Dept. of Energy, Office of Science, Office of Nuclear Physics, under award number DEFG06-97ER41026.
Acknowledgments
The work described in this paper is the result of the efforts of several students and post-doctoral fellows in my research group. The principal contributors were J. S. Barrett, J. King, R. Yanez, A. Pica, A. Chemey, M. Silveira, and L. Yao. Financial support of the research was provided by the Stockpile Stewardship Academic Alliance, the U.S. Dept. of Energy, Office of Nuclear Physics, and the Lawrence Livermore National Laboratory.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Talou P, Vogt R. Nuclear fission theories. Experiments and Applications, Springer (2023).ISBN 978-3-031-14544-5
2. Younes W, Loveland W. An introduction to nuclear fission, springer (2021). ISSN 1868-4513. p. 1868–4513.
6. Hill DL, Wheeler JA. “Nuclear constitution and the interpretation of fission phenomena”. Phys Rev (1953) 89:1102–45. doi:10.1103/physrev.89.1102
7. Halpern I. “Nuclear fission”. Ann Rev Nucl Sci (1959) 9:245–342. doi:10.1146/annurev.ns.09.120159.001333
8. Leachman RB, Blumberg L. “Fragment anisotropies in neutron-deuteron-and alpha-particle-induced fission”. Phys Rev (1965) 137:B814–25. doi:10.1103/physrev.137.b814
9. Wilkins BD, Steinberg EP, Chasman RR. “Scission-point model of nuclear fission based on deformed-shell effects”. Phys Rev C (1976) 14:1832–63. doi:10.1103/physrevc.14.1832
10. Viola VE, Kwiatkowski K, Walker M. “Systematics of fission fragment total kinetic energy release”. Phys Rev C (1985) 31:1550–2. doi:10.1103/physrevc.31.1550
11. Madland DG. “Total prompt energy release in the neutron-induced fission of 235U, 238U, and 239Pu”. Nucl Phys A (2006) 772:113–37. doi:10.1016/j.nuclphysa.2006.03.013
12. Lestone JP, Strother T. “Energy dependence of plutonium and uranium average fragment total kinetic energies”. Nucl Data Sheets (2014) 118:208–10. doi:10.1016/j.nds.2014.04.038
13. Unik JP, Gindler JE, Glendenin LE, Flynn KF, Gorski A, Sjoblom RK. “Nuclear fission: A review of experimental advances”. Phys Chem Fission (1974) 1973:19. doi:10.1016/0022-1902(77)80149-8
14. Higgins D, Greife U, Tovesson F, Manning B, Majorov D, Mosby S, et al. “Fission fragment mass yields and total kinetic energy release in neutron-induced fission of 233U from thermal energies to 40 MeV”. Phys Rev C (2020) 104:014601. doi:10.1103/physrevc.101.014601
15. King J, Yanez R, Loveland W, Barrett JS, Oscar B, Fotiades N, et al. “The total kinetic energy release in the fast neutron-induced fission of 232Th”. Eur Phys J A (2017) 53:238. doi:10.1140/epja/i2017-12436-9
16. Gook A, Eckardt C, Enders J, Freudenberger M, Oberstedt A, Oberstedt S. “Correlated mass, energy, and angular distributions from bremsstrahlung-induced fission of 234U and 232Th in the energy region of the fission barrier”. Phys Rev C (2017) 96:044301. doi:10.1103/physrevc.96.044301
17. Geltenbort P, Gonnenwein F, Oed A. “Precision measurements of mean kinetic energy release in thermal-neutron-induced fission of 233U, 235U and 239Pu”. Radiat Effects (1986) 93:57–60. doi:10.1080/00337578608207429
18. Ferguson RL, Plasil F, Pleasanton F, Burnett SC, Schmitt HW. Systematics of fragment mass and energy distributions for proton-induced fission of 233U, 235U, and 238U. Phys Rev C (1973) 7:2510. doi:10.1103/PhysRevC.7.2510
19. Bishop CJ, Vandenbosch R, Aley R, Shaw RW, Halpern I. “Excitation energy dependence of neutron yields and fragment kinetic energy release in the proton induced fission of 233U and 238U”. Nucl Phys A (1970) 150:129–42. doi:10.1016/0375-9474(70)90462-8
20. Al-Adili A, Hambsch FJ, Pomp S, Oberstedt S. Impact of prompt-neutron corrections on final fission-fragment distributions. Phys Rev C (2012) 86:054601. doi:10.1103/physrevc.86.054601
21. Hambsch F-J, Oberstedt S, Al-Adili A, Brys T, Billnert R, Matei C, et al. “Fission fragment yield, cross section and prompt neutron and Gamma emission data from actinide isotopes”. Nucl Data Sheets (2014) 119:38–41. doi:10.1016/j.nds.2014.08.012
22. Al-Adili A, Hambsch F-J, Pomp S, Oberstedt S, Vidiela M. Fragment-mass, kinetic energy, and angular distributions for 234U(n, at incident neutron energies from En=0.2 MeV to 5.0 MeV. Phys Rev C (2016) 93:034603. doi:10.1103/physrevc.93.034603
23. Gook A, Hambsch F-J, Oberstedt S, Vidali M. Prompt neutrons in correlation with fission fragments from 235U(n,f). Phys Rev C (2018) 98:044615. doi:10.1103/physrevc.98.044615
24. Hambsch F -J, Knitter H-H, Budtz-Jorgensen C, Theobald JP. Fission mode fluctuations in the resonances of 235U(n,f)f). Nucl Phys A (1989) 941:56–90. doi:10.1016/0375-9474(89)90206-6
25. Muller R, Naqui AA, Kappeler F, Dickson F. “Fragment velocities, energies, and masses from fast neutron induced fission of 235U”. Phys Rev C (1984) 29:885–905. doi:10.1103/physrevc.29.885
26. Duke DL, Tovesson F, Brys T, Geppert-Kleinrath V, Hambsch FJ, Laptev A, et al. Fission-fragment total kinetic energy and mass yields for neutron-induced fission of 235U and 238U with En = 200 keV -30 MeV. EPJ Web of Conferences (2017) 146:04042. doi:10.1051/epjconf/201714604042
27. Naqvi AA, Kappeler F, Dickman FD, Muller R. “Fission fragment properties in fast-neutron-induced fission of 237Np”. Phys Rev C (1986) 34:218–25. doi:10.1103/physrevc.34.218
28. Pica A, Chemey AT, Yao L, Loveland W, Lee HY, Kuvin SA. EPJ Web of Conf 252 (2021) 07004. “Total kinetic energy release in the fast-neutron-induced fission of 237Np”. Phys Rev C (2020) 102:064612. doi:10.1103/physrevc.102.064612
29. Akimov NL, Vorob’eva VG, Kabenin NV. Effect of excitation energy on yields and kinetic energies of fragments in fission of Pu239 by neutrons. Sov J Nucl Phys (1971) 13:484.
30. Yanez R, Yao L, King J, Loveland W, Tovesson F, Fotiades N. Excitation energy dependence of the total kinetic energy release in 235U(n,. Phys Rev C (2014) 89:051604R. doi:10.1103/physrevc.89.051604
31. Pleasanton F. “Fission-Fragment energy-correlation measurements for the thermal-neutron fission of 233U”. Phys Rev (1968) 174:1500–8. doi:10.1103/physrev.174.1500
32. Kaufman SB, Steinberg EP, Wilkins BD, Unik J, Gorski AJ, Fluss MJ. “A calibration procedure for the response of silicon surface-barrier detectors to heavy ions”. Nucl Instr Meth (1974) 115:47–55. doi:10.1016/0029-554x(74)90423-6
33. Silveira MJ, Pica A, Loveland W. “The vapor deposition of high specific activity actinides”. Nucl Instru Meth Phys Res A (2020) 982:164570. doi:10.1016/j.nima.2020.164570
34. Lisowski PW, Bowman CD, Russell GJ, Wender SA. “The Los Alamos national laboratory spallation neutron sources”. Nucl Sci Eng (1980) 106:208–18. doi:10.13182/nse90-a27471
35. Lisowski PW, Schoenberg KF. “The Los Alamos neutron science center”. Nucl Instrum Methods (2006) 910:A562. doi:10.1016/j.nima.2006.02.178
36. Schmidt KH, Jurado B, Amouroux C, Schmitt C. “General description of fission observables: GEF model code”. Nucl Data Sheets (2016) 131:107–221. doi:10.1016/j.nds.2015.12.009
37. Schmitt HW, Neiler JH, Walter FJ. “Fragment energy correlation measurements for 252Cf spontaneous fission and 235U thermal-neutron fission”. Phys Rev (1966) 141:1146–60. doi:10.1103/physrev.141.1146
38. Gujrathi SC, Hetherington DW, Hinrichsen PR, Bentoiurkia M. “The detection of heavy ions with PIN diodes”. Nucl Instru Meth.Phys Res B (1990) 45:260–4. doi:10.1016/0168-583x(90)90831-e
39. Northcliffe LC, Schilling R. “Range and stopping-power tables for heavy ions”. Data Nucl Data Tables (1970) 7:233–463. doi:10.1016/s0092-640x(70)80016-x
40. Zeigler JF, Biersack JP, Zeigler MD SRIM—the stopping and range of ions in matter. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms (2010) 268:1818–1823. doi:10.1016/s0092-640x(70)80016-x
41. Knyazheva GN, Khlebnikov SV, Kozulin EM, Kuzmina TE, Lyapin VG, Mutterer M, et al. “Energy losses of 252Cf fission fragments in thin foils”. Nucl Instr Meth Phys Res Sect B (2006) 248:7–15. doi:10.1016/j.nimb.2006.04.071
42. Al-Adili A, Tarrío D, Jansson K, Rakopoulos V, Solders A, Pomp S, et al. “Prompt fission neutron yields in the thermal fission of 235U and spontaneous fission of 252Cf”. Phys Rev C (2023) 102:064610. doi:10.1103/PhysRevC.102.064610
43. Sierk AJ. “Langevin model of low-energy fission”. Phys Rev C (2017) 96:034603. doi:10.1103/physrevc.96.034603
44. Lommel B, Dullmann C, Kindler B, Renisch D, Eur. Phys. J. “Status and developments of target production for research on heavy and superheavy nuclei and elements”. A (2023) 59:14. doi:10.1140/epja/s10050-023-00919-7
45. Akimov NI, Vorob’eva VG, Kabenin VN “Effect of excitation energy on yields and kinetic energies of fragments in fission of Pu239 by neutrons”. Soviet J Nucl Phys (1971) 13:272.
46. Bjornholm S. “Superfluid versus viscous descent from saddle to scission”. Physica Scripta (1974) 10A:110–4. doi:10.1088/0031-8949/10/a/018
47. Wilkins BD, Steinberg EP, Chasman RR. Scission-point model of nuclear fission based on deformed-shell effects. Phys Rev C (1976) 14:1832–63. doi:10.1103/physrevc.14.1832
48. Scheuter F, Gregoire C, Hofmann H, Nix JR. Fission-Fragment kinetic-energy distributions from a two-dimensional fokker-planck equation. Phys Lett (1984) 149B:303–6. doi:10.1016/0370-2693(84)90411-8
49. Serdyuk OI, Adeev GD, Gontchar II, Pashkevich VV, Pischasov NI. Mass-energy distribution of fission fragments in the diffusion model. Sov J Nucl Phys (1987) 46:399.
50. Adeev GD, Gontchar II. A simplified two-dimensional diffusion model for calculating the fission-fragment kinetic-energy distribution. Phys. (1985) A322:479–86. doi:10.1007/bf01412083
51. Faust HR, Eur. Phys. J. “A model for fragment excitation and kinetic energy in nuclear fission”. A (2002) 14:459–68. doi:10.1140/epja/i2002-10028-6
52. Wada T, Abe Y, Carjan N. “One-body dissipation in agreement with prescission neutrons and fragment kinetic energies”. Phys Rev Lett (1993) 70:3538–41. doi:10.1103/physrevlett.70.3538
53. Tudora A. “Systematic behaviour of the average parameters required for the Los Alamos model of prompt neutron emission”. Rom Journ Phys (2014) 59:272–84. doi:10.1016/j.anucene.2008.10.004
54. Maslov VM, Kor J, Maslov VM. Prompt Fission Neutron Spectra of 238U(n,f) and 239Pu(n,f). AIP Conf Proc (2009) 1175:87.
55. Simenel C, Umar A. “Formation and dynamics of fission fragments”. Phys Rev C (2014) 89:031601. doi:10.1103/physrevc.89.031601
56. Chebbouhi A, Serot O, Kessedjian G, Litaize O, Blanc A, Bernard D, et al. Theoretical investigation of fission fragment kinetic energy distributions in the symmetric mass region for 233U(nth, f). EPJ Web of Conferences (2017) 146:04063. doi:10.1051/epjconf/201714604063
57. Carjan N, Ivanyuk FA, Yu TS. Fission of superheavy nuclei: Fragment mass distributions and their dependence on excitation energy. Phys Rev C (2019) 99:064606. doi:10.1103/physrevc.99.064606
58. Randrup J, Vogt R. Inclusion of angular momentum in FREYA. Phys Proced (2015) 64:19–27. doi:10.1016/j.phpro.2015.04.003
59. Usang MD, Ivanyuk FA, Ishizuka C, Chiba S, Ishizuka C, Usang MD, et al. Four-dimensional Langevin approach to low-energy nuclear fission of U236. Phys Rev C (2017) 96:064616. doi:10.1103/physrevc.96.064616
60. Huang Y, Feng Y, Erxi X, Lei X, Zhu L, Su J. Influence of pre-scission neutron emission on high-energy U238 fission studied by the Langevin approach. Phys Rev C (2022) 106:054606. doi:10.1103/physrevc.106.054606
61. JafAke P, Moller P, Talou P, Sierk AJ. Hauser-Feshbach fission fragment de-excitation with calculated macroscopic-microscopic mass yields. Phys.Rev C (2018) 97:034608. doi:10.1103/physrevc.97.034608
62. Lemaître J-F, Goriely S, Hilaire S, Sida J-L Influence of the neck parameter on the fission dynamics within the two-center shell model parametrization. Phys Rev C (2019) 99:044614. doi:10.1088/1674-1137/ac8867
63. LemaitreGorielyHilaire JFSS, Sida J-L. Fully microscopic scission-point model to predict fission fragment observables. Phys Rev C (2019) 99:034612. doi:10.1103/physrevc.99.034612
64. Kaldiani PM. Kinetic energy distribution for photofission of light actinides. Phys Rev C (2020) 102:044612. doi:10.1103/physrevc.102.044612
65. Shimada K., Chikako I, Fedir A. I, Chiba S., et al. Dependence of total kinetic energy of fission fragments on the excitation energy of fissioning systems. Phys Rev C 104, 054609 (2021). doi:10.1103/PhysRevC.104.054609
66. Pica A, Chemey AT, Loveland W. Fast-neutron-induced fission of 240Pu and 242Pu. Phys Rev C106 (2022) 044603. doi:10.1103/PhysRevC.106.044603
67. Naqvi AA, Kappeler F, Dickman FD, Muller R. “Fission fragment properties in fast-neutron-induced fission of 237Np”. Phys Rev C (1986) 34:218–25. doi:10.1103/physrevc.34.218
68. Pica A, Chemey AT, Yao L, Loveland W, Lee HY, Kuvin SA. “Total kinetic energy release in the fast-neutron-induced fission of 237Np”. Phys Rev C (2020) 102:064612. doi:10.1103/physrevc.102.064612
69. Vives F, Hambsch F-J, Bax H, Oberstedt S. Investigation of the fission fragment properties of the reaction 238U(n,f) at incident neutron energies up to 5.8 MeV. Nucl Phys A (2000) 662:63–92. doi:10.1016/s0375-9474(99)00413-3
70. Straede CH, Budtz-Jorgensen C, Knitter HH. 235U(n, f) Fragment mass-kinetic energy- and angular distributions for incident neutron energies between thermal and 6 MeV f) Fragment mass-kinetic energy- and angular distributions for incident neutron energies between thermal and 6 MeV. Nucl Phys A (1987) 462:85–108. doi:10.1016/0375-9474(87)90381-2
71. Yanez R, Yao L, King J, Loveland W, Tovesson F, Fotiades N. Excitation energy dependence of the total kinetic energy release in 235U(n,f). Phys Rev C (2014) 89:051604R. doi:10.1103/physrevc.89.051604
72. Vives F, Hambsch F-J, Bax H, Oberstedt S. Investigation of the fission fragment properties of the reaction 238U(n, f) at incident neutron energies up to 5.8 MeV. Nucl Phys A (2000) 662:63–92. doi:10.1016/s0375-9474(99)00413-3
73. Chemey AT, Pica A, Yao L, Loveland W, Lee HY, Kuvin SA. “Total kinetic energy and mass yields from the fast neutron-induced fission of 239Pu”. Eur Phys J A (2020) 56:297. doi:10.1140/epja/s10050-020-00295-6
74. Meierbachtol K, Tovesson F, Duke DL, Geppert-Kleinrath V, Manning B, Mecharchand R, et al. Total kinetic energy release in 239Pu(n, f) post-neutron emission from 0.5 to 50 MeV incident neutron energy. Phys Rev C (2016) 94:034611. doi:10.1103/physrevc.94.034611
75. Wagemans C, Allaert E, Deruyter A, K. Barthelemy , P. Schillebeeckx . Comparison of the energy and mass characteristics of the 239Pu(nth, f) and the 240Pu(sf) fragments. Phys Rev C (1984) 32:218–23. doi:10.1103/physrevc.30.218
76. Reisdorf W, Unik JP, Griffin HC, Glendenin LE. “Fission fragment K x-ray emission and nuclear charge distribution for thermal neutron fission of 233U, 235U, 239Pu and spontaneous fission of 252Cf”. Nucl Phys A (1971) 177:337–78. doi:10.1016/0375-9474(71)90297-1
77. Duke DL, Tovesson F, Laptev AS, Mosby S, Hambsch FJ, Brys T, et al. Fission-fragment properties in 238U(n, f) between 1 and 30 MeV. Phys Rev C (2016) 94:054604. doi:10.1103/physrevc.94.054604
Keywords: fission, kinetic energy, mass distributions, actinide targets, Viola scaling
Citation: Loveland W (2023) Total kinetic energy release in the fast neutron induced fission of actinide nuclei. Front. Phys. 11:1234198. doi: 10.3389/fphy.2023.1234198
Received: 03 June 2023; Accepted: 05 September 2023;
Published: 10 October 2023.
Edited by:
Olivier Serot, CEA Cadarache, FranceReviewed by:
Marina Barbui, Texas A and M University, United StatesChristelle Schmitt, UMR7178 Institut Pluridisciplinaire Hubert Curien (IPHC), France
Copyright © 2023 Loveland. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Walter Loveland, bG92ZWxhbndAb3JlZ29uc3RhdGUuZWR1
 Walter Loveland
Walter Loveland