
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys. , 08 December 2023
Sec. Nuclear Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1232691
This article is part of the Research Topic Exotic Aspects of Hadrons and Nuclei View all 5 articles
This study presents a solution to the Yakubovsky equations for four-body bound states in momentum space, bypassing the common use of two-body t − matrices. Typically, such solutions are dependent on the fully-off-shell two-body t − matrices, which are obtained from the Lippmann-Schwinger integral equation for two-body subsystem energies controlled by the second and third Jacobi momenta. Instead, we use a version of the Yakubovsky equations that does not require t − matrices, facilitating the direct use of two-body interactions. This approach streamlines the programming and reduces computational time. Numerically, we found that this direct approach to the Yakubovsky equations, using 2B interactions, produces four-body binding energy results consistent with those obtained from the conventional t − matrix dependent Yakubovsky equations, for both separable (Yamaguchi and Gaussian) and non-separable (Malfliet-Tjon) interactions.
The Yakubovsky equations provide a non-perturbative framework for investigating few-body bound and scattering systems in different sectors of physics, including atomic, nuclear, and particle physics. These equations have been utilized extensively in both momentum [1–24] and configuration [25–45] spaces. The Yakubovsky equations fundamentally rely on two-body (2B) transition matrices, denoted as t(ϵ), which are derived from the solution of the Lippmann-Schwinger (LS) equation, considering either positive (scattering states) or negative (bound states) 2B subsystem energies ϵ. Notably, solving the LS equation for positive energies can prove to be a numerically demanding task due to the presence of singularities. Contrarily, for negative energies, the LS equation must be computed for the 2B subsystem energies, which are determined by the Jacobi momenta of the third and fourth particles.
In this study, we utilize a version of the Yakubovsky equations for four-body (4B) bound states that directly incorporates 2B interactions, eliminating the need for 2B t − matrices. This t − matrix-free approach to the Yakubovsky equations has been previously solved in configuration space by Lazauskas et al. [29, 39, 40, 44]. In our work, we present the t − matrix-free coupled Yakubovsky equations in momentum space. Here, the Yakubovsky components linked to the 3 + 1 and 2 + 2 chains are derived as a function of the Jacobi momentum vectors, directly including 2B interactions. To determine the 4B binding energies, we solve the coupled Yakubovsky integral equations using separable potentials with Yamaguchi and Gaussian form factors, as well as the non-separable Malfliet-Tjon potential, with all potentials projected into the s − wave channel. Our numerical findings highlight that the t − matrix-free version of the Yakubovsky integral equations, when utilizing 2B interactions, aligns perfectly with results derived from the conventional Yakubovsky integral equations that employ 2B t − matrices. In a related research, this t − matrix-free approach is successfully employed for relativistic three-body (3B) bound states [46]. This led to a version of the relativistic Faddeev equation that directly employs 2B boosted interactions [47, 48], eliminating the need for 2B boosted t − matrices [19, 20, 24].
This paper has been structured into several sections. Section 2. provides a brief overview of the Yakubovsky equations for 4B bound states, bypassing the use of 2B t − matrices. Herein, we formulate the coupled Yakubovsky equations in momentum space, considering Jacobi momentum vectors and presenting a simplified form for s − wave interactions. Section 3. Outlines our numerical results for 4B binding energies as calculated from the t − matrix-free Yakubovsky equations, alongside a comparison with results obtained from conventional t − matrix-dependent Yakubovsky equations. Lastly, Section 4. presents our conclusion and discusses prospects for succeeding studies.
The conventional form of Yakubovsky equations that describe the bound state of four identical particles interacting through pairwise interactions reads as follows [4].
where ψ1 and ψ2 denote Yakubovsky components of the 4B wave function, corresponding to 3 + 1 and 2 + 2 type chains, respectively.
The coupled Yakubovsky Eq. 1 can be restructured to yield another form of Yakubovsky equations as follows
where the 2B interactions V are being directly utilized as input to the Yakubovsky equations, consequently eliminating the need for the 2B t − matrices. The representation of the t − matrix-free form of the coupled Yakubovsky Eq. 3 in momentum space leads to the following coupled 3D integral equations
with the symmetrized 2B interaction defined as Vs(a, b) = V(a, b) + V(a, − b) and 4B free propagators characterized through the following expressions
The Jacobi momenta ui and vi (i = 1, 2, 3) correspond to 3 + 1 and 2 + 2 chains, respectively [11]. The coupled Yakubovsky Eq. 4 can be simplified for the s − wave interactions as
where the shifted momentum arguments are defined as [49].
For comparison purposes, the representation of the conventional t − matrix-dependent form of the coupled Yakubovsky Eq. 1 in momentum space can be found in Appendix A. Upon comparing the t − matrix-free and conventional t − matrix-dependent forms of the Yakubovsky equations - specifically, Eqs. 4 and (A1) - it is evident that the t − matrix-free form incorporates an extra term. This term involves integration over the 2B interaction and the Yakubovsky components without interpolations on momenta or angles. Despite this, its numerical solution proves to be more straightforward and cost-effective than that of the conventional t − matrix-dependent that necessitates solving the LS equation to compute the 2B t − matrices for all required 2B subsystem energies, which depend on the magnitude of the second and third Jacobi momenta.
The numerical solution of the coupled Yakubovsky integral Eq. 6 for the calculation of 4B binding energy demands solving an eigenvalue equation, where the physical binding energy corresponds to an eigenvalue equal to one. The Lanczos iterative method is implemented for solving such eigenvalue equation [24, 49–52]. We employ Gauss-Legendre quadratures to discretize the continuous momentum and angular variables with a hyperbolic mapping for Jacobi momenta and a linear mapping for angle variables [53]. This allows us to properly capture the behavior of the Yakubovsky components of the 4B wave function at both small and large momenta. In each iteration step of solving the coupled Yakubovsky integral equations, to accurately perform multi-dimensional interpolations on the shifted momentum arguments given in Eq. 7, we employ the Cubic-Hermite spline method due to its combination of high accuracy and computational speed [54].
Our numerical analysis presents a comparison between 4B binding energy obtained from the t − matrix-free approach and the conventional t − matrix-dependent formulation of the coupled Yakubovsky equations, namely, Eqs. 6 and A4. For our numerical analysis, we employ two models of one-term separable potential with the following general form
where λ represents the potential strength. The potential form factor g(p) for the Yamaguchi-type potential is defined as g(p) = 1/(p2 + β2) [55], while for the Gaussian potential, it takes the form g(p) = exp(−p2/Λ2) [56]. Furthermore, to provide a comprehensive validation of our formalism and code, we also incorporate an s-wave non-separable Malfliet-Tjon (MT) potential, comprises two attractive and repulsive terms [57].
In Table 1, we provide the parameters for the potentials employed in our calculations, which include MT model V (MT-V), Yamaguchi potential model IV (Y-IV), and a Gaussian potential. The strength of the Gaussian potential was adjusted to reproduce the deuteron binding energy of −2.225 MeV, with a form factor parameter Λ = 0.7 fm−1.
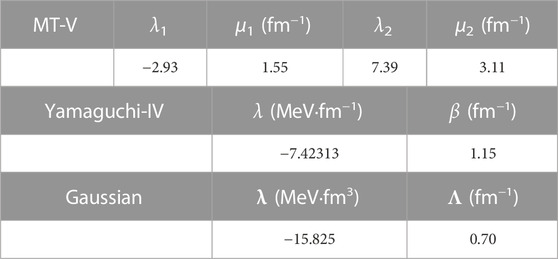
TABLE 1. The parameters for the Malfliet-Tjon (MT-V), Yamaguchi (Y-IV), and Gaussian potentials utilized in this study.
Table 2 presents the convergence of the 4B binding energy as a function of the number of mesh points for the Jacobi momenta magnitudes ui and vi. The table provides a side-by-side comparison of results obtained using both the t-matrix-free and conventional t-matrix-dependent forms of the coupled Yakubovsky equations. Specifically, our results show that the t − matrix-free Yakubovsky equations yield a 4B binding energy of −30.08 MeV for the MT-V potential and −36.27 MeV for the Yamaguchi-IV potential. These values closely align with the −30.07 MeV [58] and −36.3 MeV [59] obtained by other groups using the t − matrix-dependent Yakubovsky calculations. The comparison validates the potential of the t − matrix-free adoption of Yakubovsky formulation to solve 4B bound state problems efficiently, matching the precision of the conventional method but potentially offering more straightforward computational requirements. Moreover, the convergence behavior remains consistent across different numbers of mesh points for the magnitude of Jacobi momenta, emphasizing the computational robustness of the t − matrix-free formulation.
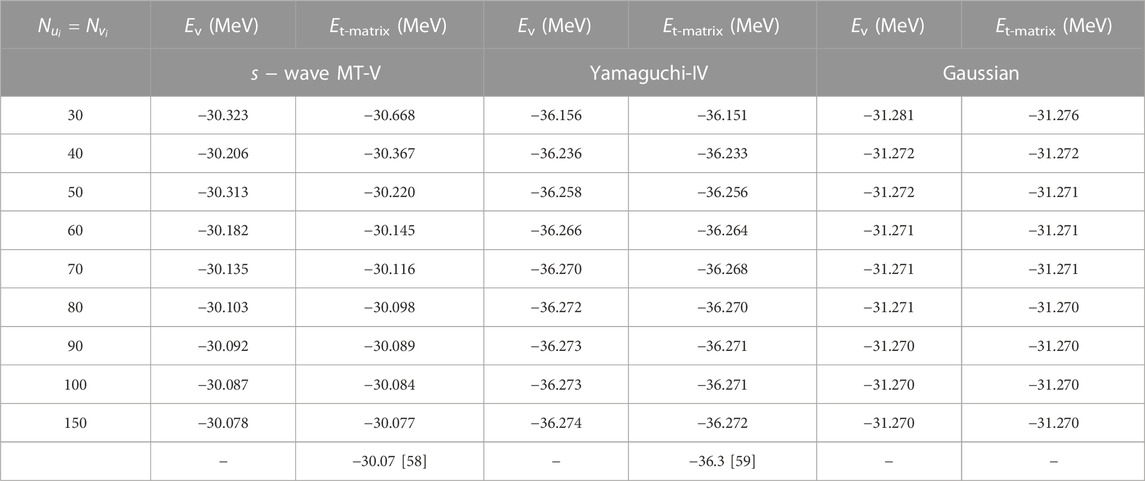
TABLE 2. Convergence of the 4B binding energy obtained from the t −matrix-free (Ev), Eq. 6, and the conventional t −matrix-dependent (Et-matrix), Eq. (A4), versions of the coupled Yakubovsky equations. The convergence is shown as a function of the number of mesh points for the magnitude of Jacobi momenta ui and vi, denoted as
The Yakubovsky approach is a powerful method to study few-body bound and scattering systems. However, the solution of these equations can be computationally demanding due to inherent singularities in 2B t − matrices when dealing with scattering problems and the need to calculate them for 2B subsystem energies dictated by second and third Jacobi momenta when 4B bound state problems are considered. This study utilizes a version of the coupled Yakubovsky equations for 4B bound states that directly incorporates 2B interactions in momentum space, avoiding the use of the 2B t − matrices. The efficacy of this approach is validated through the calculation of 4B binding energies in momentum space using, both the separable potentials with Yamaguchi and Gaussian form factors, and the non-separable Malfliet-Tjon potential. Our findings align well with results from the conventional form of the coupled Yakubovsky integral equations incorporating 2B t − matrices. The extension of calculations to include more general interactions, beyond just the s − wave, is currently in progress.
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
MR took the lead in project design, while MR and MRH collaborated on developing the theoretical formalism and computer codes. MM and KM calculated the four-body binding energies. MRH, MR, and KM engaged in the result discussion and contributed to the final manuscript. All authors contributed to the article and approved the submitted version.
The work of MRH was supported by the National Science Foundation under Grant No. NSF-PHY-2000029 with Central State University. KM was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) Grant No. 400789/2019-0.
KM acknowledges a Ph.D. scholarship from the Brazilian agency CNPq.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Kamada H, Glöckle W. Solutions of the four-body Yakubovsky equations for the α-particle using realistic 2N interactions. Phys Lett B (1992) 292:1–4. doi:10.1016/0370-2693(92)90598-x
2. Glöckle W, Kamada H. On the inclusion of 3N-forces into the 4N-Yakubovsky equations. Nucl Phys A (1993) 560:541–7. doi:10.1016/0375-9474(93)90113-c
3. Nogga A, Kamada H, Glöckle W. Modern nuclear force predictions for the α particle. Phys Rev Lett (2000) 85:944–7. doi:10.1103/physrevlett.85.944
4. Nogga A, Kamada H, Glöckle W, Barrett BR. The α particle based on modern nuclear forces. Phys Rev C (2002) 65:054003. doi:10.1103/physrevc.65.054003
5. Uzu E, Kamada H, Koike Y. Complex energy method in four-body Faddeev-Yakubovsky equations. Phys Rev C (2003) 68:061001. doi:10.1103/physrevc.68.061001
6. Platter L, Hammer H-W, Meißner U-G. Four-boson system with short-range interactions. Phys Rev A (2004) 70:052101. doi:10.1103/physreva.70.052101
7. Nogga A. Faddeev-Yakubovsky calculations for A = 4 hypernuclear systems. Nucl Phys A (2005) 754:36–42. doi:10.1016/j.nuclphysa.2005.01.013
8. Nogga A. Application of chiral nuclear forces to light nuclei. In: Chiral dynamics 2006. Singapore: World Scientific (2007). p. 182–93.
9. Bayegan S, Hadizadeh M, Harzchi M. A realistic three-dimensional calculation of 3H binding energy. Few-body Syst (2008) 44:65–7. doi:10.1007/s00601-008-0258-y
10. Deltuva A, Fonseca AC. Four-nucleon scattering: ab initio calculations in momentum space. Phys Rev C (2007) 75:014005. doi:10.1103/physrevc.75.014005
11. Hadizadeh M, Bayegan S. Four-body bound-state calculations in three-dimensional approach. Few-Body Syst (2007) 40:171–91. doi:10.1007/s00601-006-0169-8
12. Bayegan S, Hadizadeh MR, Harzchi M. Three-nucleon bound state in a spin-isospin dependent three dimensional approach. Phys Rev C (2008) 77:064005. doi:10.1103/physrevc.77.064005
13. Bayegan S, Hadizadeh MR, Glöckle W. A realistic formalism for 4N bound state in a three-dimensional Yakubovsky scheme. Prog Theor Phys (2008) 120:887–916. doi:10.1143/ptp.120.887
14. Hadizadeh M, Bayegan S. Towards a three-dimensional solution for 3N bound states with 3NFs. Mod Phys Lett A (2009) 24:816–22. doi:10.1142/s0217732309000073
15. Hadizadeh MR, Tomio L, Bayegan S. Solutions of the bound-state Faddeev-Yakubovsky equations in three dimensions by using NN and 3N potential models. Phys Rev C (2011) 83:054004. doi:10.1103/physrevc.83.054004
16. Frederico T, Delfino A, Hadizadeh M, Tomio L, Yamashita MT. Universality in four-boson systems. Few-Body Syst (2013) 54:559–68. doi:10.1007/s00601-012-0463-6
17. Tomio L, Hadizadeh M, Yamashita MT, Delfino A, Frederico T. Four-Boson systems close to a universal regime. Few-Body Syst (2013) 54:1543–6. doi:10.1007/s00601-012-0588-7
18. Kamada H. Four-body scattering equations including a three-body force in the Faddeev-Yakubovsky theory. Few-Body Syst (2019) 60:33. doi:10.1007/s00601-019-1501-4
19. Hadizadeh MR, Elster C, Polyzou WN. Relativistic three-body bound state in a 3D formulation. Phys Rev C (2014) 90:054002. doi:10.1103/physrevc.90.054002
20. Hadizadeh M, Elster C, Polyzou W. The relativistic three-body bound state in three-dimensions. EPJ Web of Conferences (2016) 113:03011. doi:10.1051/epjconf/201611303011
21. Radin M, Mohseni H, Nazari F, Hadizadeh M. Four-body bound state calculations using three-dimensional low-momentum effective interaction Vlow−k. Int J Mod Phys E (2017) 26:1750083. doi:10.1142/s0218301317500835
22. Bazak B, Petrov DS. Energy of N two-dimensional bosons with zero-range interactions. New J Phys (2018) 20:023045. doi:10.1088/1367-2630/aaa64f
23. Bazak B, Kirscher J, König S, Valderrama MP, Barnea N, van Kolck U. Four-body scale in universal few-boson systems. Phys Rev Lett (2019) 122:143001. doi:10.1103/physrevlett.122.143001
24. Hadizadeh M, Radin M, Mohseni K. A three-dimensional momentum-space calculation of three-body bound state in a relativistic Faddeev scheme. Scientific Rep (2020) 10:1949. doi:10.1038/s41598-020-58577-4
25. Barnea N, Viviani M. Projected Faddeev-Yakubovsky equations for the N-body problem. Phys Rev C (2000) 61:034003. doi:10.1103/physrevc.61.034003
26. Filikhin I, Yakovlev S. 16O nucleus in the 4α cluster model. Phys At Nuclei (2000) 63:343–52. doi:10.1134/1.855641
27. Kezerashvili RY. Elastic N-body to N-body scattering in the hyperspherical representation. In: 150 Years of quantum many-body theory. Singapore: World Scientific (2001). p. 89–95.
28. Filikhin I, Yakovlev S, Roudnev V, Vlahovic B. The 4He tetramer ground state in the Faddeev-Yakubovsky differential equations formalism. J Phys B: At Mol Opt Phys (2002) 35:501–8. doi:10.1088/0953-4075/35/3/305
29. Lazauskas R, Carbonell J. Ab-initio calculations of four-nucleon elastic scattering. Few-Body Syst (2004) 34:105. doi:10.1007/s00601-004-0049-z
30. Uzu E, Koike Y. Four-body Faddeev-Yakubovsky calculation using the finite range expansion method. Prog Theor Phys (2006) 115:309–23. doi:10.1143/ptp.115.309
31. Lekala ML, Masita DF (2010). Four-body reactions of light nuclei. AIP Conf. Proc. 1265 (1):88–91. doi:10.1063/1.3480268
32. Schellingerhout NW. Numerical methods in configuration-space a = 3, 4 bound-state and scattering calculations. In: BLG Bakker, and R van Dantzig, editors. Few-body problems in physics ’93. Vienna: Springer (1994). p. 361–70.
33. Filikhin I, Suslov V, Vlahovic B. Modeling of 6ΛHe hypernucleus within configuration space Faddeev approach (2014). Available at: https://arxiv.org/abs/1401.2189.
34. Lazauskas R. Modern nuclear force predictions for n −3H scattering above the three- and four-nucleon breakup thresholds. Phys Rev C (2015) 91:041001. doi:10.1103/physrevc.91.041001
35. Hiyama E, Lazauskas R, Carbonell J, Kamimura M. Possibility of generating a 4-neutron resonance with a T = 3/2 isospin 3-neutron force. Phys Rev C (2016) 93:044004. doi:10.1103/physrevc.93.044004
36. Kezerashvili RY. Few-body neutron and kaonic clusters. Phys Sci Tech (2017) 3:63–72. doi:10.26577/phst-2016-1-95
37. Kezerashvili RY. Strange dibaryonic and tribaryonic clusters, Physics, properties and dynamics (2017) 227.
38. Ferrari Ruffino F, Lonardoni D, Barnea N, Deflorian S, Leidemann W, Orlandini G, et al. Benchmark results for few-body hypernuclei. Few-Body Syst (2017) 58:113. doi:10.1007/s00601-017-1273-7
39. Lazauskas R. Solution of the n −4He elastic scattering problem using the Faddeev-Yakubovsky equations. Phys Rev C (2018) 97:044002. doi:10.1103/physrevc.97.044002
40. Lazauskas R, Carbonell J. The faddeev-yakubovsky symphony. Few-Body Syst (2019) 60:62. doi:10.1007/s00601-019-1529-5
41. Lazauskas R, Song Y-H. Parity-violating neutron spin rotation in 4He. Phys Rev C (2019) 99:054002. doi:10.1103/physrevc.99.054002
42. Kezerashvili RY. Few-body systems in condensed matter physics. Few-Body Syst (2019) 60:52. doi:10.1007/s00601-019-1520-1
43. Filikhin I, Kezerashvili RY, Suslov VM, Tsiklauri SM, Vlahovic B. Three-body model for K(1460) resonance. Phys Rev D (2020) 102:094027. doi:10.1103/physrevd.102.094027
44. Lazauskas R, Carbonell J. Description of four- and five-nucleon systems by solving Faddeev-Yakubovsky equations in configuration space. Front Phys (2020) 7:251. doi:10.3389/fphy.2019.00251
45. Kezerashvili RY, Tsiklauri SM, Takibayev NZ. Search and research of K-NNN and K-K-NN antikaonic clusters. Prog Part Nucl Phys (2021) 121:103909. doi:10.1016/j.ppnp.2021.103909
46. Mohammadzadeh M, Radin M, Hadizadeh M. Relativistic Faddeev equations for three-body bound states without 2B T − matrices, submitted for publication (2023).
47. Hadizadeh M, Radin M. Calculation of relativistic nucleon-nucleon potentials in three dimensions. The Eur Phys J A (2017) 53:18. doi:10.1140/epja/i2017-12209-6
48. Hadizadeh M, Radin M, Nazari F. Relativistic nucleon-nucleon potentials in a spin-dependent three-dimensional approach. Scientific Rep (2021) 11:17550. doi:10.1038/s41598-021-96924-1
49. Hadizadeh MR, Yamashita MT, Tomio L, Delfino A, Frederico T. Binding and structure of tetramers in the scaling limit. Phys Rev A (2012) 85:023610. doi:10.1103/physreva.85.023610
50. Ahmadi M, Hadizadeh MR, Radin M, Bayegan S. Novel regularization scheme for nucleon-nucleon lattice simulations with effective field theory. Phys Rev C (2020) 102:044001. doi:10.1103/physrevc.102.044001
51. Mohseni K, Chaves A, da Costa D, Frederico T, Hadizadeh M. Three-boson stability for boosted interactions towards the zero-range limit. Phys Lett B (2021) 823:136773. doi:10.1016/j.physletb.2021.136773
52. Hadizadeh MR, Yamashita MT, Tomio L, Delfino A, Frederico T. Scaling properties of universal tetramers. Phys Rev Lett (2011) 107:135304. doi:10.1103/physrevlett.107.135304
53. Mohseni K, Hadizadeh MR, Frederico T, da Costa DR, Chaves AJ. Trion clustering structure and binding energy in two-dimensional semiconductor materials: Faddeev equations approach. Phys Rev B (2023) 107:165427. doi:10.1103/physrevb.107.165427
54. Hüber D, Witała H, Nogga A, Glöckle W, Kamada H. A new look into the partial-wave decomposition of three-nucleon forces. Few-Body Syst (1997) 22:107–35. doi:10.1007/s006010050057
55. Yamaguchi Y. Two-Nucleon problem when the potential is nonlocal but separable. I. Phys Rev (1954) 95:1628–34. doi:10.1103/physrev.95.1628
56. Deltuva A, Lazauskas R, Platter L. Universality in four-body scattering. Few-Body Syst (2011) 51:235–47. doi:10.1007/s00601-011-0227-8
57. Kessler B, Payne GL, Polyzou W. Scattering calculations with wavelets. Few-body Syst (2003) 33:1–26. doi:10.1007/s00601-003-0008-0
58. Kamada H, Glöckle W. Solutions of the yakubovsky equations for four-body model systems. Nucl Phys A (1992) 548:205–26. doi:10.1016/0375-9474(92)90009-9
59. Gibson BF, Lehman DR. Erratum: four-body bound states from the Schrödinger equation with separable potentials. Phys Rev C (1977) 15:2257. doi:10.1103/physrevc.15.2257.2
The conventional form of the coupled Yakubovsky Eq. 1 in momentum space is represented as follows [11].
with the symmetrized 2B t − matrices defined as
The matrix elements of 2B t − matrices t(a, b; ϵ) needs to be calculated from the solution of the LS Eq. 2 for the 2B subsystem energies associated with the 3 + 1 and 2 + 2 chains, given by
The coupled Yakubovsky equations (A1) can be simplified for the s − wave interactions as
Keywords: Yakubovsky equations, four-body bound state, momentum space, Malfliet-Tjon potential, Yamaguchi potential, Gaussian potential
Citation: Mohammadzadeh M, Radin M, Mohseni K and Hadizadeh MR (2023) Four-body bound states in momentum space: the Yakubovsky approach without two-body t − matrices. Front. Phys. 11:1232691. doi: 10.3389/fphy.2023.1232691
Received: 01 June 2023; Accepted: 06 November 2023;
Published: 08 December 2023.
Edited by:
Alberto Martinez Torres, University of São Paulo, BrazilReviewed by:
Gaotsiwe Joel Rampho, University of South Africa, South AfricaCopyright © 2023 Mohammadzadeh, Radin, Mohseni and Hadizadeh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. R. Hadizadeh, bWhhZGl6YWRlaEBjZW50cmFsc3RhdGUuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.