
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys., 28 September 2023
Sec. High-Energy and Astroparticle Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1230737
The discovery of the Higgs boson, a fundamental particle of the Standard Model, at the Large Hadron Collider (LHC) in 2012, marked a monumental milestone in the field of particle physics. Since then, extensive research has been conducted to understand the properties and interactions of the Higgs boson, particularly its couplings with other known particles. This article provides a review of the past, present, and future measurements of the Higgs boson couplings, with a focus on the most recent experimental developments. It discusses the experimental techniques and methods used to study the Higgs boson couplings, including the production and decay channels employed in various experiments. The article highlights the important relationships between the Higgs boson and other known particles, including the gauge bosons (W and Z bosons), quarks, and leptons and the Higgs boson itself, through its self-interaction. After discussing the channels used by ATLAS and CMS collaborations to measure the Higgs boson coupling to the other standard model particles, the article will present an overview of the latest results obtained at the LHC, commenting on how various measurements have evolved over time along with a better comprehension of the detectors and ever more refined analysis techniques. Future collider developments and expectation for the measurement of the Higgs boson couplings and double-Higgs boson production with increased precision and accuracy will be discussed along with the main challenges faced by future experiments.
The Standard Model (SM) of particle physics is one of the most successful scientific theories ever developed, with confirmed predictions spanning many orders of magnitude at great precision, and the Higgs boson plays a pivotal role in it. According to the SM, as particles interact with the Higgs field, they acquire mass through a mechanism called electroweak symmetry breaking (EWSB). The Higgs boson is the quantum excitation associated with fluctuations in the Higgs field, and its presence is a necessary consequence of this mechanism. The Higgs boson is, therefore, essential for explaining the origin of mass and maintaining the internal consistency of the theory, and its existence was one of the most important predictions of the theory.
Given its importance in the SM, one of the main goals of the CERN Large Hadron Collider (LHC) was indeed to produce, observe, and study the Higgs boson. The LHC started colliding protons in 2010, for the first period of data collection at a center of mass energy of
At hadron colliders, such as the LHC, the Higgs boson can be produced via several different mechanisms and can decay in several different final states. The cross sections (branching ratios) of the different production (decay) modes are shown in Figures 1A, B for a Higgs boson of about 125 GeV/c2. The most common production mode is the gluon fusion (g g H) production, occurring when two gluons from the colliding protons interact by exchanging quarks. The quarks themselves can then emit a Higgs boson. A Feynman diagram of this process is shown in Figure 2A [9]. This process has a cross section of 48.58 pb for a Higgs boson with a mass of 125 GeV/c2 [10]. At 3.78 pb, the vector boson fusion (VBF) is more than 10 times rarer than g g H, but it is extremely relevant for the study of the Higgs boson coupling. In this process, as shown in Figure 2B, a pair of quarks from the two incoming protons exchange a vector boson (W or Z), emitting a Higgs boson in the process. Even rarer production modes are VH (Figure 2C, 2.25 pb), t
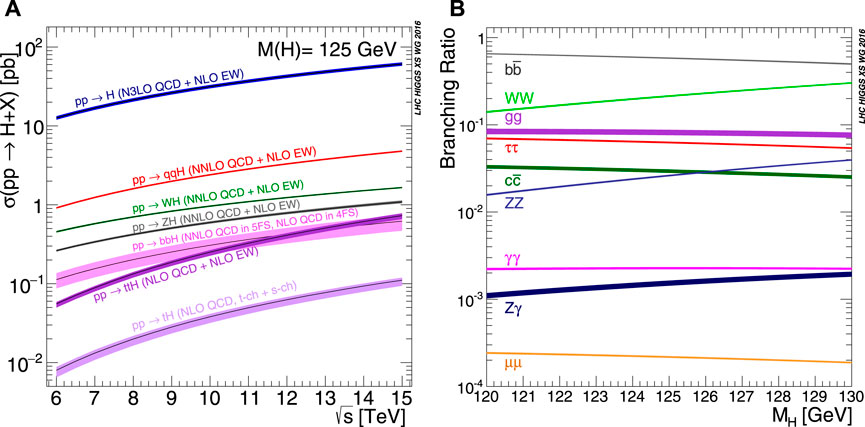
FIGURE 1. (A) Standard Model Higgs boson production cross sections through the proton–proton interaction as a function of the center-of-mass energies for different production modes. The t H production mode does not include t H W production. Assuming mH =125 GeV/c2. (B) Standard Model Higgs boson decay branching ratios for a Higgs boson mass between 120 and 130 GeV/c2 [10].
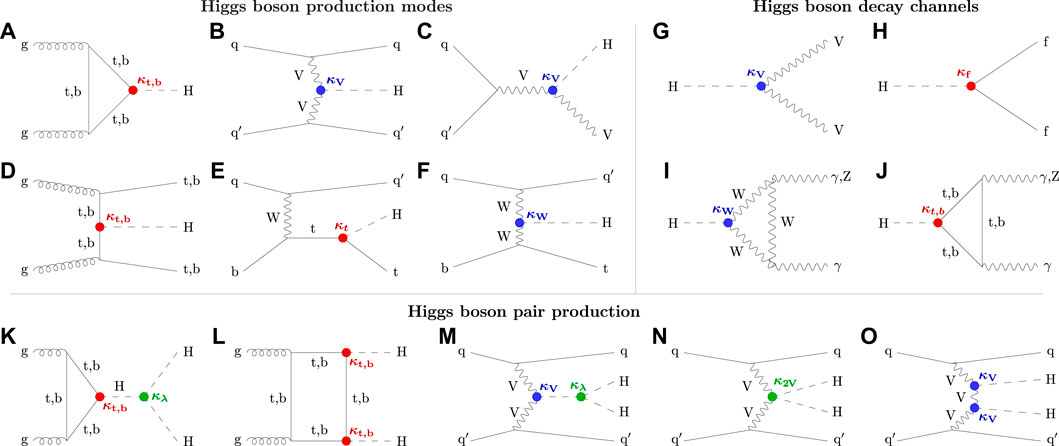
FIGURE 2. Feynman diagrams of the Higgs boson production (top left) and decay (top right) modes at the LHC. From (A–F) are shown g g H, VBF, VH, t
The Higgs boson generated in the collision can then decay in several final states, as shown in Figures 2G–J. Decays to heavier particles (up to a pair of b-quarks) are generally preferred according to the SM. Thus, the generation of each Higgs boson in a proton–proton collision at the LHC involves its coupling to different SM particles, whether in production (quarks and vector bosons) or in decay (leptons, quarks, and vector bosons). Thanks to the small predicted width of the Higgs boson, the production and decay mechanism can be considered independent and can be factorized. The number of Higgs bosons produced in any given production (ii) and decay (ff) combination can, therefore, be computed according to the following formula:
where Γf represents the partial decay width of the Higgs boson to a pair of f particles, and Γtot represents the total Higgs boson decay width. To simplify the notation, one can introduce the signal strength modifiers as
This paper will focus on the determination of the k parameters. It is nevertheless important to mention that the high-energy physics community is exploring frameworks that are not only able to evaluate the (dis)agreement between the current results and the SM, such as with the signal strengths and the k-framework, but also to explore possible new physics signals hiding in the data collected by the ATLAS and CMS experiments. To this scope, the STXS [13] framework has been developed to provide a common definition for the measurements’ phase space. This allows for an easier comparison between the experiment and the reinterpretation of the results within an effective field theory (EFT) framework.
Experimental signatures in the final states are exploited by the CMS and ATLAS collaborations in order to categorize the events according to their most likely production and decay mechanisms. Careful simulations of the experimental apparatus and precise predictions of the Higgs boson production cross sections [10] are used to predict the exact component, in terms of production processes, of each category, and with this knowledge, as we will discuss in the following sections, it is possible to perform a multidimensional statistical analysis to extract the couplings of the Higgs boson to each SM particle.
Given its very short lifetime (τH ∼ 1.58 ⋅ 10−22s), experiments cannot directly observe the Higgs boson but must reconstruct it from its decay products. It is, thus, convenient to classify the observed events according to the particles involved in the Higgs boson decay and target each decay with a dedicated strategy.
The first very broad classification that can be made is whether the Higgs boson decays into a pair of bosons (W, Z, or photons via a quark loop) or into fermions (leptons and quarks). When it was first devised [14–19], the main goal of the EWSB mechanism was to provide mass to the weak interaction gauge bosons, i.e., W and Z, which was necessary to explain the short interaction range of the weak force. The measurement of the coupling of the Higgs boson to other gauge bosons is, therefore, a crucial test of the most fundamental aspects of the EWSB mechanism.
Experimentally, this is carried out at the LHC by measuring the Higgs boson decaying in pairs of bosons, either W + W − or Z Z. The final state where a Higgs boson decays into a pair of photon is also discussed in this section for convenience, although in the SM, the Higgs boson does not couple directly to massless photons, but can generate two photons in the final state via loops (Figures 2I, J).
The Higgs boson decay in a final state with two photons is among the most precise tools available to the experimental collaborations for assessing the properties of the Higgs boson, such as its mass and couplings. Due to the detector resolution effects, the distribution of the invariant mass of the photon pair mγγ shows a Gaussian-like peak centered at the Higgs boson mass over a falling combinatorial background due to the QCD production of two photons that follows a power-law distribution, as shown in Figure 3. The large number of events available in this channel allows measuring the properties of the signal peak with high precision. Multivariate analyses (MVAs) and machine learning techniques based on information related to photon quality, resolution, kinematics of the decay, and quality of the reconstructed system are used in order to classify events in different categories of signal-to-background ratio. In this way, the categories with low S/B will help constrain the background from the actual data, without having to rely on MC simulation. Although the strategy has remained the same, the increase in the number of collected events and a better understanding of the detectors obtained through years of data taking allowed the experiments to develop even more refined categorizations, from the original 5 (CMS) to 10 (ATLAS) used at the time of the discovery [20, 21] to the current 80 used in CMS or 101 used by ATLAS [22, 23], which are specifically designed to target the STXS measurement and are shown in Figure 4.
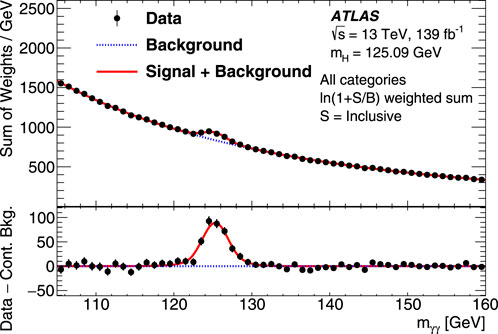
FIGURE 3. Inclusive diphoton invariant mass distribution of events from all analysis categories considered in the ATLAS H → γ γ analysis [23]. The data events (dots) in each category are weighted by ln (1+ S/B), where S and B are the expected signal and background yields in this category within the smallest mγγ window containing 90% of the signal events. The solid line shows the fitted signal-plus-background pdfs from all categories. The blue dotted line represents the weighted sum of the fitted background functions from all categories.
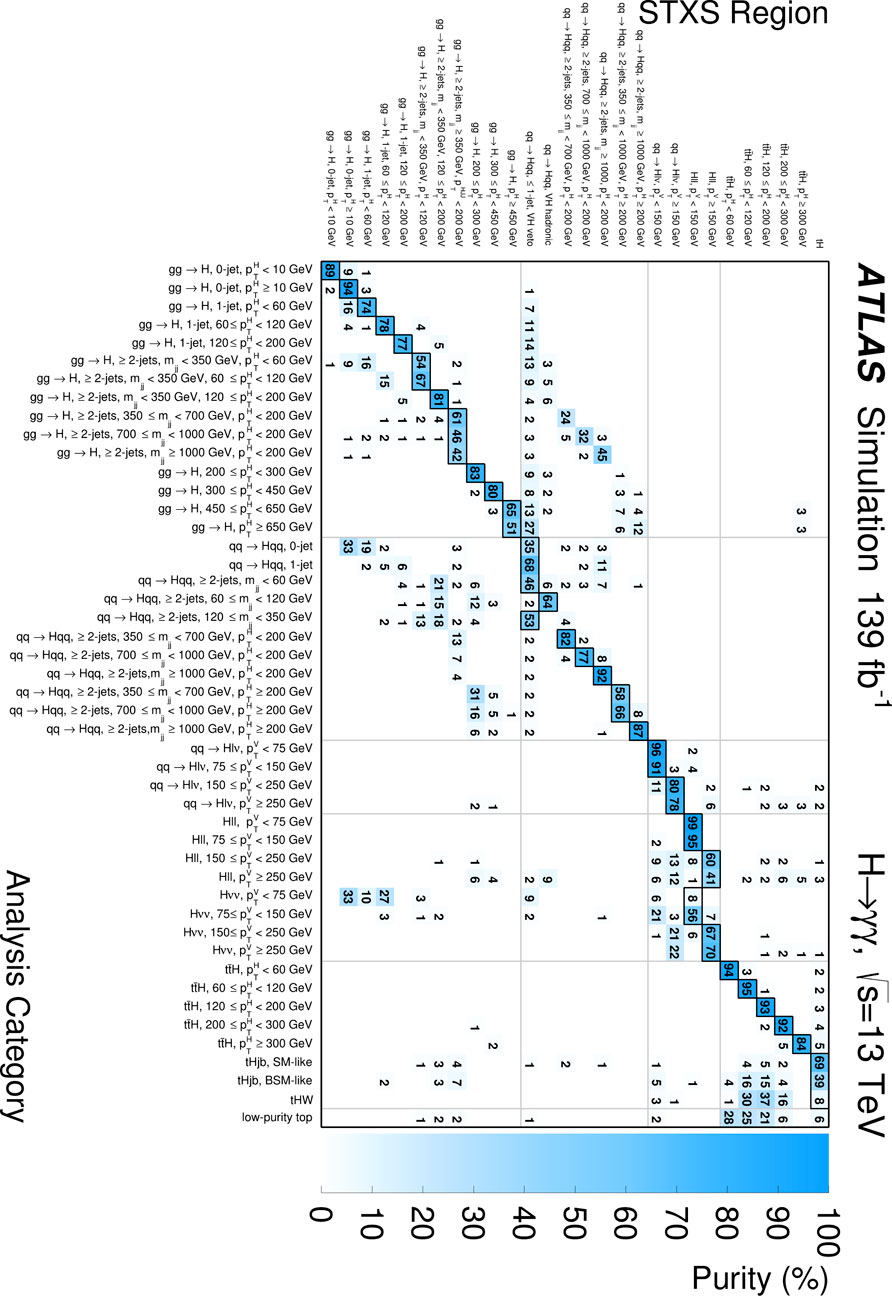
FIGURE 4. Contributions of STXS regions to the expected event yields in groups of analysis categories in the ATLAS H → γ γ analysis [23]. The vertical axis lists 28 merged STXS regions measured in the analysis, while the horizontal axis lists groups of analysis categories that target the same STXS region, weighted by their relative importance. Entries correspond to the percentage of the signal yield in each group of analysis categories (on the x-axis) that is contributed by a given STXS region (on the y-axis). Entries with a value below 1% are not shown.
The main systematic uncertainties in the H → γ γ channel come from the uncertainties on the modeling of the background function and on photon measurement and identification. On the theory side, uncertainties on the renormalization and factorization scales and on the parton shower mechanism are also relevant, although overall statistical uncertainties still dominate this measurement.
Together with H → γ γ, the ZZ decay channel of the Higgs boson was dubbed the golden channel due to its importance for the Higgs boson discovery and its precision, especially in the final state with four leptons (either muons or electrons). In the H → γ γ channel, there is an important number of signal events produced on top of a very large combinatorial background; the situation is the opposite in the case of H → Z Z* → 4ℓ. This is a relatively rare process, with a branching ratio of just 0.003% for a 125 GeV/c2 Higgs boson. On the other hand, the presence of four well-identified leptons in the final state with the right masses and charges makes this a very clean channel, resulting in a large peak over a small and flat background in the invariant mass distribution of the four leptons and a very high signal-over-background ratio, as shown in Figure 5A.
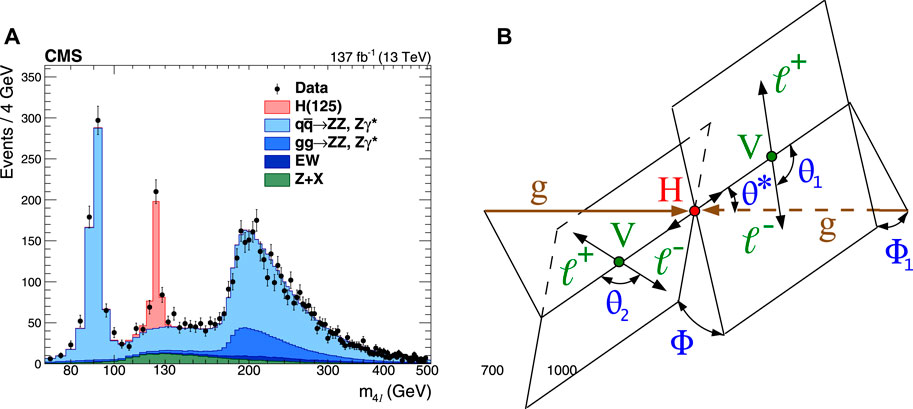
FIGURE 5. (A) Four-lepton mass distribution obtained by the CMS collaboration on the full Run 2 dataset, up to 500 GeV with 4-GeV bin size. Points with error bars represent the data, and stacked histograms represent the expected distributions for the signal and background processes. The SM Higgs boson signal with mH =125 GeV/c2, the ZZ, and electroweak backgrounds are normalized to SM expectation; the Z + X background is estimated from data. (B) Illustration of a generic boson X production from gluon fusion and its subsequent decay in a pair of leptons and a pair of fermions, gg → X → ZZ → ℓ+ℓ−ℓ+ℓ−. The production and decay chains are fully characterized by the five angles shown in blue, and the invariant masses of the two vector bosons are shown in green.
The kinematics of the H → ZZ* → 4ℓ decay is fully described by the invariant mass of the four-lepton system, five of the decay angles, and the invariant masses of the two lepton pairs (mZ1, mZ2), as shown in Figure 5B. These variables hold a significant discriminant power to differentiate between the signal and background. Additional variables related to jets and extra leptons in the event can also be used to target specific production mechanisms. It is thus possible to achieve a large separation between the signal and background or between different signal hypotheses either by training machine learning algorithms on them [24] or by computing the ratio of the probabilities with a kinematic discriminant defined as follows:
Due to the low branching ratio of this channel, only the most common production modes were accessible to this channel in Run 1. CMS measured g g H and VBF [27], while ATLAS developed four categories, targeting VH as well [28]. Since then, thanks to the increase in the collected luminosity and to improvements in the analysis techniques, a more refined categorization was developed, with events classified in 12 categories targeting STXS1.1 by the ATLAS collaboration [24] and 22 categories closely following the STXS1.2 scheme [13] by the CMS collaboration [29]. This way, the two collaborations were able to measure the four main Higgs boson production modes (g g H, VBF, VH, and t
The statistical uncertainty is still the largest component for the H → ZZ* → 4ℓ results, although in Run 2 is now very close to the systematic component. Among the main sources of systematic uncertainties, on the experimental side, there are uncertainties on lepton reconstruction and efficiency, and on the determination of the luminosity. The theoretical uncertainties are at least as important as the experimental uncertainties, with the most important uncertainties due to the QCD factorization and renormalization scales and uncertainties on the most important production modes’ cross sections [24, 29].
The precision measurements in the H → Z Z decay channel are dominated by the 4ℓ final state, but it should be mentioned that the final states with two leptons and two neutrinos or two leptons and two jets are also investigated by the experimental collaborations, providing useful insights into the searches for anomalous couplings, off-shell ZZ production, or massive scalar resonances.
The H → W W channel is extremely sensitive for Higgs boson masses above the W W threshold of ≈160 GeV/c2. For a mass of 125 GeV/c2, its branching fraction is almost 10 times larger than that for H → ZZ and enjoys a relatively large signal-over-background ratio. Despite this, the reconstruction of the W decay is experimentally much more challenging than the Z decay. The fully hadronic final state is affected by an overwhelming background at the LHC, so the most sensitive final state is the leptonic state, where the presence of two opposite sign leptons can be used to identify signal events with the discrimination being even more effective when both an electron and a muon are present in the final state (H → WW* → μνeν). However, the W leptonic decays have undetectable neutrinos in the final state. The H → WW has, therefore. a worse mass resolution on the Higgs boson peak than the more precise H → ZZ* → 4ℓ and H → γ γ, resulting in a diminished sensitivity. The presence of neutrinos in the final state means that the analysis relies heavily on the reconstruction of missing energy in the analyzed event, under the assumption that most of that energy originates from the neutrinos produced in the W decay. To further complicate the analysis, there are many different background sources present in the final state, with the most important sources being non-resonant WW production, Drell–Yan, tW, and t
The large number of events allows separating them in several categories according to the transverse momentum pT of the Higgs boson and extra objects in the events to distinguish between the g g H, and VBF, and, owing to the LHC Run 2, also the VH production mechanisms. The reconstructed invariant mass of the Higgs boson mH is not a particularly discriminant variable for this decay due to its low resolution. The first instances of these analyses were, therefore, relying on variables with stronger discriminant power between the signal and background, such as the invariant mass of the visible leptons pair or the transverse mass
Systematic uncertainties mostly originate from theoretical uncertainties on the renormalization and factorization scales and, less importantly, from experimental uncertainties on lepton identification. The systematic uncertainties are the most relevant in the g g H production mode, which is the most common process, providing a 10% uncertainty against a 6% statistical uncertainty. The statistical uncertainty is roughly at the same level as the systematic uncertainty in the VBF production mode and dominates the rarer VH production.
In the SM, the Higgs boson couples to fermions through the Yukawa interaction. These couplings are generally more difficult to measure at the LHC than the bosonic ones. τ leptons present some unique challenges due to the presence of neutrinos and, in the case of their hadronic decays, jets in the final state. In the case of muons and electrons, their lighter masses result in very small branching ratios. In the case of quarks, they hadronize into jets and their identification is difficult against the large QCD background at the LHC. Nevertheless, the effort to measure the Yukawa couplings of the Higgs boson started as soon as the particle was discovered in 2012 with the third-generation particles (τ, t-quarks, and b-quarks) and it is now expanding to the second generation (H → μ μ and H → c
When considering all the possible decay modes of the τ lepton, the branching ratio of H → ττ is about 6.3%, competitive or even larger than bosonic channels. Nevertheless, this is somehow counterbalanced by a complex final state with the presence of neutrinos, light jets, or both. For this reasons, the actual observation of the Higgs boson decay in τ leptons was only achieved at the beginning of LHC Run 2 with the data collected in 2016 [32, 33]. Events are classified according to the different decays of the τ pair: eμ, μμ, μτh, eτh, and τhτh and according to the number of jets in the event in order to boost sensitivity to production modes beyond gluon fusion. The ee final state is generally ignored as it is affected by a very large DY background and usually provides very little sensitivity. Much effort has been dedicated to improve the reconstruction and identification of the τ coming from the Higgs boson decays. This resulted in the development of likelihood-based estimators that greatly improved these searches [34, 35] and helped this channel to reach a sensitivity to the couplings close to that of the bosonic channels. This is especially true in subdominant production modes such as VBF, where the extra candle of the two jets from the VBF mechanism helps reduce the background, mostly DY, while at the same time profiting from the relative large branching ratio of this final state.
At the face value, the strategy of the H → μμ analysis looks relatively simple. The analysis is focused at the distribution of the reconstructed invariant mass of pairs of opposite-sign muons. The well-reconstructed Z → μμ peak can be used to normalize the background component, and CMS and ATLAS excel in the reconstruction of muons. The main issue is given by the fact that the process is extremely rare with a branching ratio of just 0.02% on top of a large combinatorial background and with an S/B ratio of
The Higgs boson decay into a pair of bottom quarks enjoys the largest decay branching ratio of the SM at 58.2% and a fair resolution on the Higgs boson peak of about 15%. The main challenge in measuring this decay is thus not the availability of candidates but, at first, separating jets originating from the decay of a b-quark from other jets originated from lighter quarks, and then further identifying which of those truly originate from a Higgs boson decay. This is one of the most important applications of machine learning techniques to high-energy physics. Several algorithms have been developed to this scope over the years, and some of them are now applied even when triggering on jets to quickly identify possible candidates. At the start of the LHC physics program, most of the effort was dedicated to identify b-jets coming from the main interaction vertex or from top quark decays. With the increase in energy and pile-up obtained between Run 1 and Run 2, these algorithms needed to be even more refined in order to keep up with the more challenging conditions. An illustration of these algorithms’ capabilities is shown in Figure 6A from the CMS collaboration. Since the larger amount of data in Run 2 now allows the collaboration to target the Higgs boson decay to charm quarks, the latest developments of these algorithms are focusing on developing neural networks [37, 38] that are able to separate not only heavy from light flavors but also c-quarks from b-quarks [39, 40], as shown in Figure 6B. ATLAS has shown a light (charm) jets rejection power of 600 (11) for a 70% efficiency in identifying b-jets and a rejection power of 70 for light jets and 9 for b-jets at a 30% efficiency on c-tagged jets [40]. CMS rejection power is 500 at 70% b-jet efficiency and approximately 40 for 30% efficiency on c-tagged jets [39, 41].
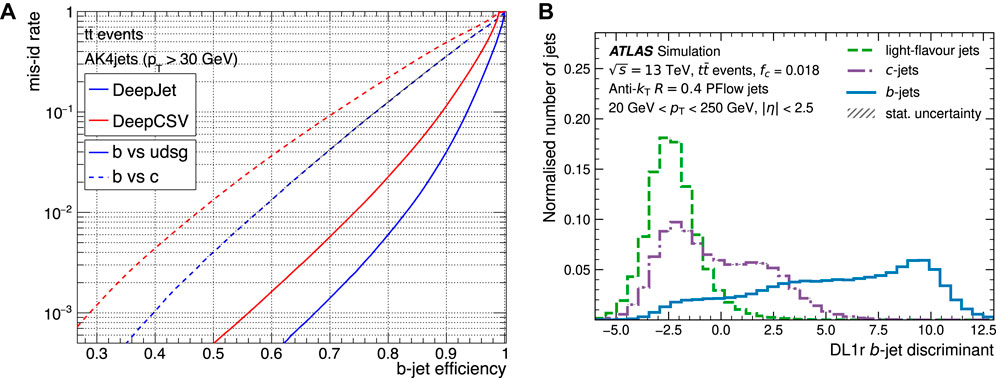
FIGURE 6. (A) B-tagging efficiency and misidentification rates for two different algorithms employed by the CMS collaboration. Both algorithms use a deep neural network to discriminate. Solid line: discrimination of b-quark jets against light (u, d, s, and (g) jets. Dashed line: b-quark jets against c jets. (B) Distribution of the deep learning DL1r algorithm by the ATLAS collaboration in differentiating between light (green), charm (purple), and bottom (blue) jets.
Armed with these tools, it is possible to tackle the measurement of the Higgs boson decay into b-quarks. Given the very large background of 2-jet events at the LHC, the observation was made possible in Run 2 by looking for events where the Higgs boson was produced in association with a vector boson [31, 42], where this measurement can provide a tight constraint on the Higgs boson couplings to vector bosons. By using the whole LHC Run 2 data and advanced machine learning techniques such as adversarial neural networks, it was finally possible to see evidence of VBF and g g H productions in this channel [43]. Another strategy to enhance the signal-over-background ratio is instead to look at highly boosted events, where the b-tagged jets are very collinear and almost merged together [44].
The search for the Higgs boson decay into a pair of c-quarks works similarly to the b-quarks but is made more challenging by a branching ratio 20 times smaller (2.9%), larger background, and c-jets that are harder to distinguish from the overwhelmingly large QCD background. Given these premises, it is hardly a surprise that this decay channel has not been observed yet. Nevertheless, the first promising results have been obtained with the Run 2 dataset in the VH → Vc
Among the couplings to different quark species, the top quark holds a special place. The top quark is the heaviest particle in the SM, and the top quark Yukawa coupling is, therefore, extremely important both for the stability of the SM and for the exploration of BSM models. Indeed, before the discovery of the Higgs boson in 2012, the best indirect estimate of its mass (at about 90 GeV/c2) was obtained through global electro-weak fits, where among the most important components were the top quark and W masses [48]. Since the top quark is heavier than the Higgs boson, the H → t
Whenever a sufficient amount of data are available, all the decay channels discussed so far try to develop categories especially designed to target top quark associated production. In addition to the measurements from the different decay channels [49, 50], comprehensive analyses primarily dedicated to the measurement of the t
These analyses were able to observe the t
Each of the decay channels discussed so far is sensitive only to those couplings that enter the Higgs boson production and the decay mode of that channel. The best way to assess the Higgs boson couplings in a comprehensive way is, therefore, to perform a combined measurement of all the channels together. This is a challenging task since one must take into account not only correlations between the Higgs boson couplings across different channels, whose determination is the goal of this exercise, but also among different background processes and systematic uncertainties. To avoid the possible double-counting effects, the final states should be mutually exclusive whenever possible. Excluding channels for which the actual sensitivity is too low to provide a meaningful constraint, such as b
The procedure used to perform the combined fit and to estimate the parameters of interest was established by a common agreement before the Higgs boson discovery [52], and it is still used today. It is based on a profile likelihood technique with asymptotic approximation, where the systematic uncertainties are the nuisance parameters. The full correlation of the nuisance parameters across years and channels is taken into account when performing the fit, and systematic uncertainties are considered correlated when they are related to the same underlying effect. The fit is an extremely onerous and complex task. It includes O (104) nuisance parameters for each experiment, and in the end is a summary of most of our knowledge of the Higgs boson. The results of the combined likelihood fit by the CMS collaboration [9, 53] are shown in Figure 7. The same results from the ATLAS collaboration are very similar [54]. It can be observed that the measurements obtained at the LHC are in remarkable agreement with the SM predictions. To appreciate the extent of the work performed in these years by the experimental collaborations, it is possible, for example, to look at the improvements obtained on the precision on some of these couplings, as shown in Figure 7B. At the discovery of the Higgs boson, even the couplings accessible to the most precise channels contributing to the discovery, such as κZ, κγ, κg, and κW, were measured with less than 50% accuracy. By the end of Run 1, it was possible to measure κt and most couplings were known with an accuracy close to 10%. Moreover, in some cases such as κt, κb, and κg, the statistical uncertainty was already subdominant with respect to the systematic uncertainty. By the end of Run 2, which is our current knowledge, we passed the 10% threshold for most couplings. Systematic and statistical uncertainties are roughly the same size. Further reducing these uncertainties significantly will be very challenging at the LHC, and future machines will be better suited for this task, as discussed in Section 5. It is also possible to look for more specific BSM effects by imposing symmetries on the fit. For example, assuming that there is a universal coupling modifier for all couplings to vector bosons and a different one for all the couplings to fermions so that κV = κZ = κW and κf = κt = κτ = κb = κμ. The effective couplings corresponding to loops in the gluon fusion and H → γ γ vertices are resolved in terms of their fundamental SM couplings. Figure 8 from the ATLAS collaboration (a similar result can be seen from the CMS collaboration in [9]) shows the two-dimensional fit on the κV and κf parameters, along with the contribution of each decay channel to it.
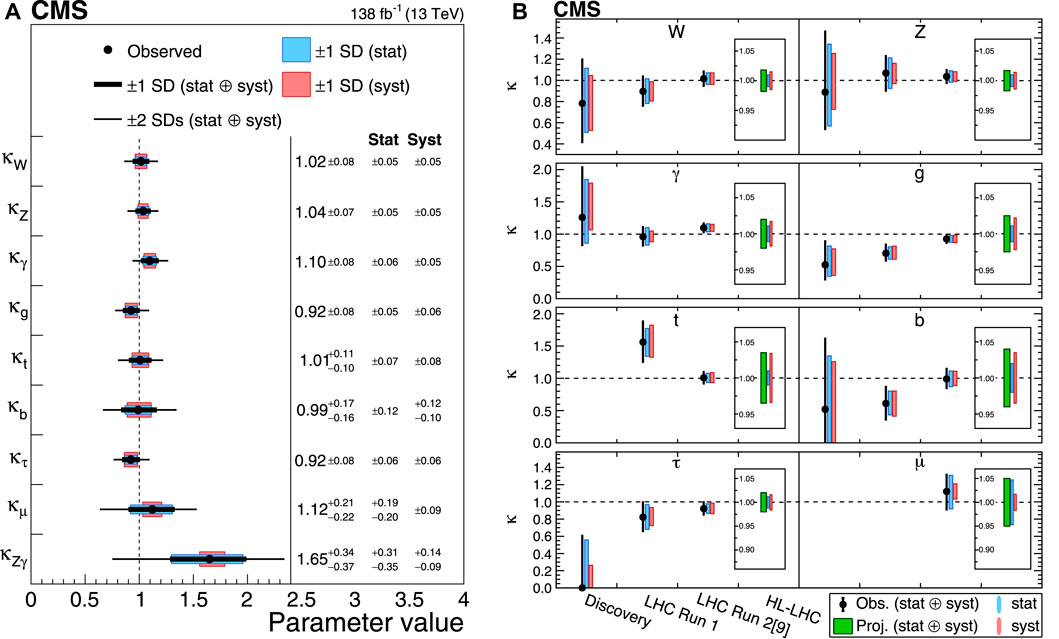
FIGURE 7. (A) Measurement from the CMS collaboration of different coupling modifiers for the Higgs boson using the whole Run 2 dataset. The blue (red) band represents the 68% CL uncertainty due to the statistical (systematic) component. The wide (thin) black bar represents the full 68% (95%) CL uncertainty. (B) Evolution over time of the measurement of the different coupling modifiers, as performed by the CMS collaboration. The boxed estimates on the right are projections for the HL-LHC (in green) with their corresponding statistical and systematic uncertainty break down in blue and red, respectively.
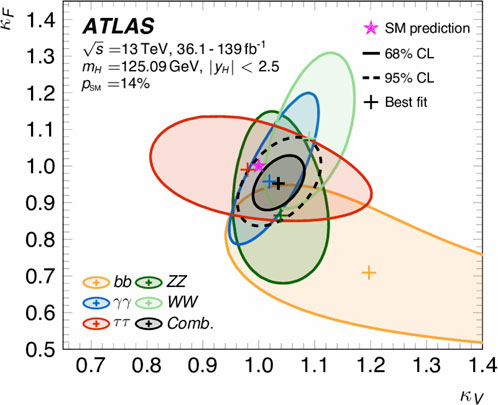
FIGURE 8. Negative log-likelihood contours at 68% CL in the (κV, κF) plane for the individual Higgs boson decay modes (colors) and their combination (black). The 95% CL contour of the combined measurement is also shown (black dashes). They are obtained assuming positive coupling strengths to fermions and bosons, and no contributions from invisible or undetected non-SM Higgs boson decays. The best-fit value for each measurement is indicated by a cross, while the SM hypothesis is indicated by a star. The probability of compatibility between the combined measurement and the SM prediction corresponds to a p-value of pSM =14% with two degrees of freedom.
Since a combination, even within a single experiment, is an extremely challenging task, only a pair of cross-experiment Higgs physics combinations between ATLAS and CMS have been performed so far, both of them based on Run 1 data. They were aimed at measuring as precisely as possible the Higgs boson mass [55] and its couplings [56]. Further efforts on Run 2 are being discussed between the collaborations, also targeting some rarer channels such as double-Higgs boson and Z γ productions. The STXS scheme was developed to implement a compatible binning between the experiment and ease future combinations.
For a given value of the Higgs boson mass, the relationship between the mass of a SM particle and its coupling to the Higgs boson is well known in the SM. For bosons, it is represented as
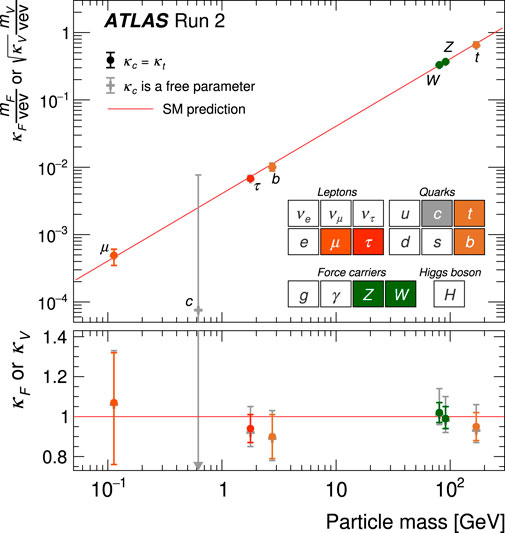
FIGURE 9. Scaling of the reduced Higgs boson coupling modifiers and their uncertainties to fermions (F = t, b, τ, μ) and vector bosons as a function of their masses, as measured by the ATLAS collaboration using the full Run 2 dataset. Colored circle markers: fit scenario with κc = κt. Gray cross markers: fit scenario with κc floating freely. Loop-induced processes are assumed to have the SM structure, and Higgs boson decays to non-SM particles are not allowed. The vertical bar on each point denotes the 68% confidence interval. The p-values for compatibility of the combined measurement and the SM prediction are 56% and 65% for the respective scenarios. The lower panel shows the values of the coupling modifiers. The gray arrow points in the direction of the best-fit value, and the corresponding gray uncertainty bar extends beyond the lower panel range.
The potential of the Higgs field φ is given by
At the LHC, it is possible to obtain a more direct measurement of this coupling by studying events where a pair of Higgs boson is produced. The study of double-Higgs events, where a pair of Higgs bosons is produced, was first suggested in the late 80s [59]. At the LHC, the most common production mode for Higgs boson pairs is via gluon fusion to H H. This can happen either through the production of an off-shell Higgs boson that subsequently decays into a pair of Higgs boson at their nominal mass or through the emission of a pair of Higgs bosons via a quark loop, as shown in the Feynman diagrams in Figures 2K, L. The two diagrams of Figures 2K, L produce a destructive interference among them, so the production cross section of double-Higgs events at the LHC is very small. For a center of mass energy of
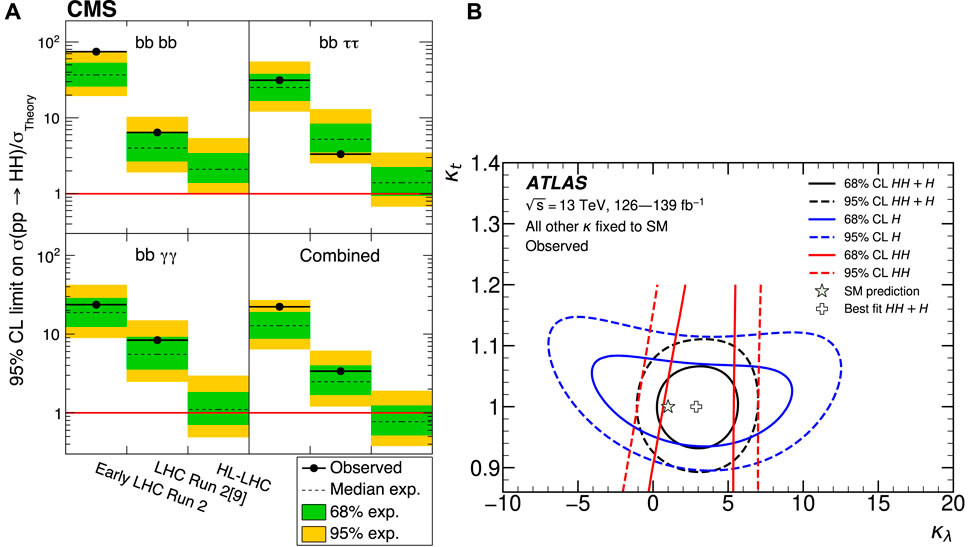
FIGURE 10. (A) Expected (dashed line) and observed (solid line) limits on double Higgs boson production as measured by the CMS collaboration in different datasets: early LHC Run 2 data (35.9 fb−1), full LHC Run 2 data [9], (138 fb−1), and projections for the HL-LHC (3,000 fb−1). (B) Constraints observed by ATLAS in the (κλ, κt) plane from single-Higgs (blue) and double-Higgs (red) analyses, and their combination (black). The solid lines show the 68% (95%) CL contours. The double-Higgs contour is only shown for κt <1.2.
In order to obtain a significant number of events, the collaborations resort to explore as many final states as possible. The most sensitive channels, and the first ones to have been explored, are those where one of the Higgs bosons decays into a b
The combined results from the collaborations were able to put a constraint on the Higgs boson trilinear coupling at −0.6 < κλ < 6.6 (ATLAS) and −1.2 < κλ < 6.5 (CMS) using the double-Higgs events alone. It must be noted that since it is not possible to distinguish between events coming from the Higgs boson trilinear interaction (Figure 2K) or from the quark loop (Figure 2L), these measurements rely on the assumption that κt = 1 and that all possible deviations are only due to effects from κλ. To overcome this limitation and to increase the sensitivity on κλ, the collaborations and the theory community are working on the combination of double- and single-Higgs measurements, where it would be possible to constrain separately the two couplings. Such an effort was recently shown by the ATLAS collaboration [57]. The final result is still dominated by the double-Higgs boson production sensitivity, with a final constraint of −0.4 < κλ < 6.3. The importance of the single Higgs measurement contribution in breaking the degeneracy between κλ and κt can be observed in Figure 10B, showing the constraints obtained in the κλ − κt plane by single- and double-Higgs measurements and their combination.
The LHC plans to continue to collect data at
After 2025, the LHC will undergo a major overhaul, with the goal of reopening in 2029 with a new machine capable of running at an instantaneous luminosity 3–4 times higher than the LHC. The resulting machine has been named high-luminosity LHC (HL-LHC), and it is planned to deliver between 3,000 and 4,000 fb−1 at a center of mass energy of 14 TeV by 2041. Both the ATLAS and CMS experiments will need substantial upgrades in order to be able to collect data at the HL-LHC, with the major challenge being posed by the pile-up, which will rise up to an average of 200 pile-up collisions for each hard proton–proton scattering. Timing detectors, ultrafast triggers, and much more granular trackers will be among the strategies deployed in order to maintain, if not improve, the current experiment performances. This amount of luminosity will allow constraining the Higgs boson coupling to most SM particles at around 2%–4%, including the Higgs boson coupling to muons, as shown in Figure 11A. To appreciate the improvement with respect to the LHC measurement, it is possible to compare the current LHC measurements with the projected HL-LHC performances in Figure 7B, where the small inset on the right shows the HL-LHC projections. At these sensitivities, even relatively small deviations from the SM should start to be visible [71]. Among the most important targets for the Higgs boson couplings at the HL-LHC, there will be precise measurements of the Higgs boson decay into muons. On the double-Higgs side, it will be possible to obtain evidence of the existence of double-Higgs boson production, with an expected significance of approximately 4.0 and a projected precision on the double-Higgs boson production of roughly 50% [71]. It could be possible to measure the first hints of ttHH production [72]. Figure 10A shows the expected evolution for the limit on the double-Higgs boson production cross section, with the combined limit going below the threshold of 1, meaning that the sensitivity is sufficient to establish the existence of the Higgs boson pair production. It is expected that in the absence of new physics and by combining results from both CMS and ATLAS, the constraints on the Higgs boson trilinear coupling will be set in the region 0.52 < κλ < 1.5 [71], as shown in Figure 11B.
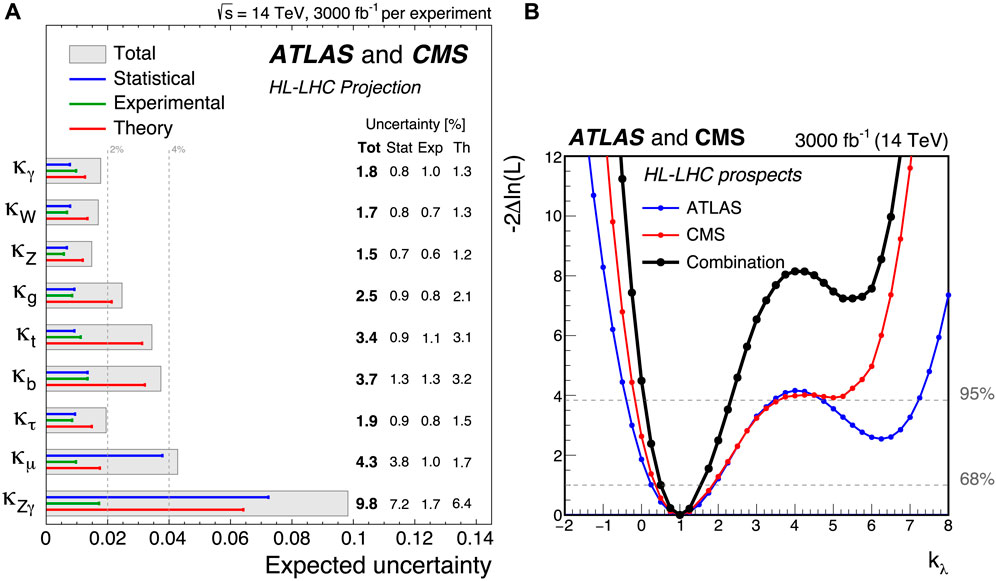
FIGURE 11. (A) Summary plot showing the total expected ±1σ uncertainties on the coupling modifier parameters for the combination of ATLAS and CMS extrapolations to the HL-LHC. For each measurement, the total uncertainty is indicated by a gray box, while the statistical, experimental, and theory uncertainties are indicated by a blue, green, and red line, respectively. The projections assume reduced experimental systematic uncertainties, according to the expectations for HL-LHC. (B) Expected likelihood scan as a function of κλ = λHHH/λSM for HL-LHC. The blue (red) line corresponds to the combined ATLAS (CMS) projection, with the black line being the combination of the two experiments.
In order to reach even tighter constraints on the couplings and to observe the Higgs boson coupling to light particles such as the c-quark, completely new machines will be needed, which are currently in their exploratory phases. A couple of the most promising proposals that are being circulated will be briefly discussed here.
The Future Circular Collider (FCC) is a collider with a circumference of 90–100 km capable of running both as a lepton–lepton (FCC-ee) [73], lepton–hadron (FCC-eh), and hadron–hadron (FCC-hh) [74] collider, which should be built in the area of CERN. The FCC-hh will deliver 30 ab−1 of proton–proton collisions at the center-of-mass energy of
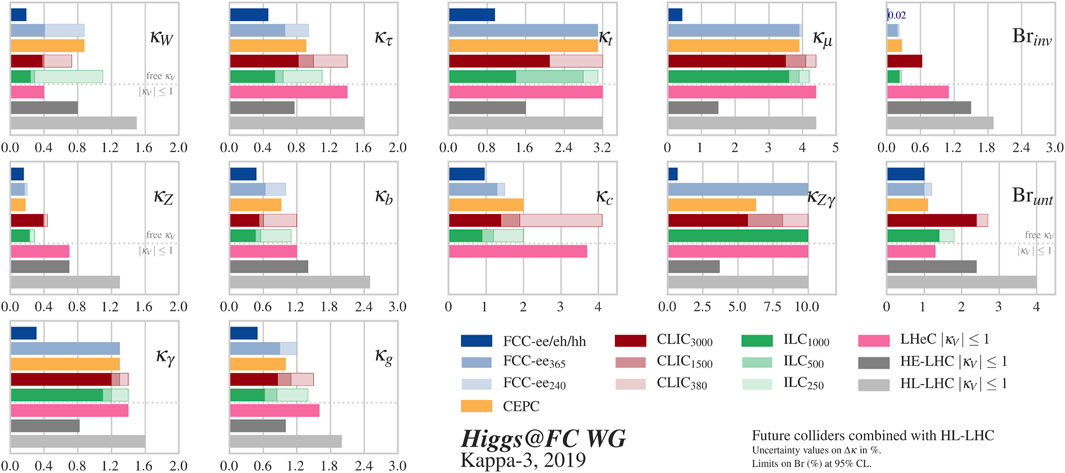
FIGURE 12. Expected relative precision (in %) for the coupling modifier parameters at the FCC in combination with HL-LHC (blue) and other proposed colliders: CEPC (yellow), CLIC (red) ILC (green), and LHeC (pink). HE-LHC- and HL-LHC-projected sensitivities are shown in gray. Higgs boson decays into untagged and invisible particles are both possible in these scenarios, with their branching ratios being free parameters in the fit.
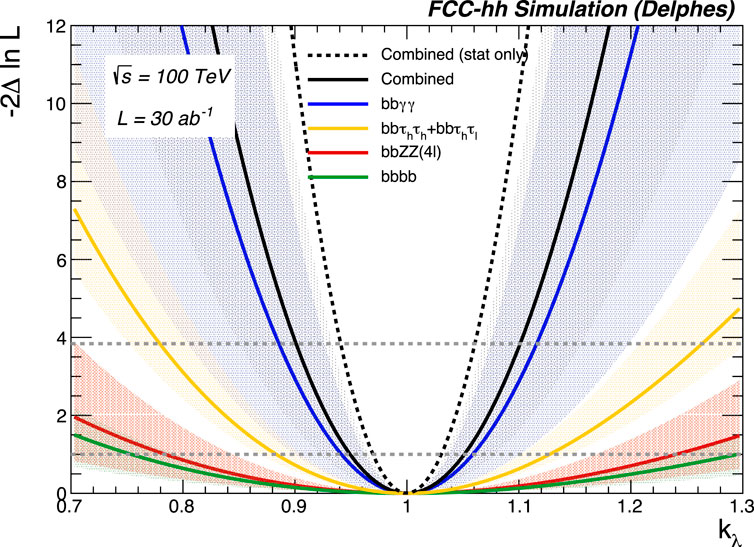
FIGURE 13. Expected negative log-likelihood scans as a function of the Higgs boson trilinear self-coupling for FCC-hh. The colored band represents different systematic scenarios. Each color represents a different decay channel, and black is the combined result.
FCC will be a monumental task to complete, and it is difficult to imagine even larger colliders to be built in the future. To reach energies higher than what FCC would be capable of, new technologies must be deployed. One such proposal is the Muon Collider. Collisions between leptons provide a much cleaner environment with respect to proton–proton collision, but it is difficult to reach high energies colliding particles as light as electrons. One solution is to operate a lepton collider, but colliding muons instead of electrons and thus exploiting the much larger mass of the muon to reach higher center-of-mass energies. The idea is not new. The possibility of building muon storage rings was first mentioned in the 60s [77], and the idea of using heavy leptons, such as muons instead of electrons, has been floating around since the 70s, although building one such machine was technically impractical until now. The main technical issues for a Muon Collider, which we are now managing to address, are that the muons must be accelerated very quickly in order to boost their lifetime in the laboratory frame before they decay since their proper lifetime is only 2.2 μs. Moreover, the decay of muons inside the beam will generate a large beam-induced background that must be controlled. Nevertheless, the first estimation for the physics reach of the Muon Collider is very promising. The current proposal suggests operating a Muon Collider at
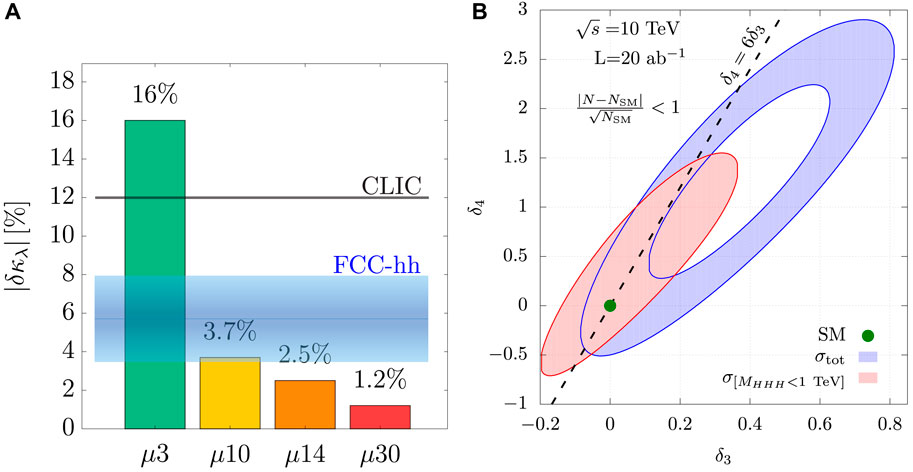
FIGURE 14. (A) Expected precision on the Higgs boson trilinear coupling at the Muon Collider, for different center-of-mass energy scenarios: 3 TeV (green), 10 TeV (yellow), 14 TeV (orange), and 30 TeV (red). The black line is the expected sensitivity at CLIC, and the blue band is the expectation for FCC-hh. (B) Expected 1σ exclusion for the anomalous Higgs boson self-coupling in the (δ3, δ4) plane, where the deviation from the SM is parameterized as 1+ δi, δ3 is the deviation from the SM Higgs boson trilinear coupling, and δ4 is the deviation from the SM quartic coupling. The pink region represents the same results with a cut on mH H H <1 TeV.
The discovery of the Higgs boson at the CERN LHC by the ATLAS and CMS collaborations unleashed a new era of measurements of the Higgs sector. Among the studies of the properties of the Higgs boson are its couplings with the particles of the SM, which are a direct test of the electroweak symmetry breaking.
In the 10 years since the discovery, the LHC made huge improvements in luminosity delivered and in energy available in the center of mass. The experiments on their side adapted to these evolving conditions by developing ever more refined analysis tools and strategies. This allowed progressing from testing the more common production modes such as g g H and VBF, and the decay modes with the best signal-over-background ratio such as H → γ γ, H → Z Z, and H → W W to ever more comprehensive measurements. The latest combined fits address all the main production and decay mechanisms of the Higgs boson, including the first exploration of the Higgs boson self-coupling. The results obtained by the experiments running at the LHC show a remarkable agreement with the SM prediction, spanning three orders in magnitude in mass and four in the coupling values, with no significant deviations observed so far.
Nevertheless, there still is plenty of phase space available for possible deviations from the SM, in what could be an indication of higher-energy BSM effects. To tackle these effects and to narrow the uncertainties on the couplings, the HL-LHC upgrade planned for 2029 will deliver 10 times the luminosity of the LHC. This will allow reducing the uncertainty on the couplings down to the 2% level and will make channels such as μ μ and Z γ accessible for precision studies, as well as providing a definite observation of HH production.
Even at the HL-LHC, coupling to first- and second-generation fermions will remain elusive. Constraints below the 1% level and measurement of processes such as H → c c can be obtained at future facilities, such as the FCC and the Muon Collider, which are also projected to obtain a few percentage-level precision on the H H production.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Aad G, Abat E, Abdallah J, Abdelalim AA, Abdesselam A, et al. The ATLAS experiment at the CERN large hadron collider. JINST (2008) 3:S08003. doi:10.1088/1748-0221/3/08/S08003
2. Chatrchyan S, Hmayakyan G, Khachatryan V, Sirunyan AM, Adam W, et al. The CMS experiment at the CERN LHC. JINST (2008) 3:S08004. doi:10.1088/1748-0221/3/08/S08004
3. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdelalim AA, et al. Improved luminosity determination in pp collisions at $\sqrt {s} = 7\ \mathrm{TeV}$ using the ATLAS detector at the LHC. Eur Phys J C (2013) 73:2518. doi:10.1140/epjc/s10052-013-2518-3
4. ATLAS Collaboration. Luminosity determination in pp collisions at √s =13$ √s=13 TeV using the ATLAS detector at the LHC (2022). arXiv [preprint].
5. ATLAS Collaboration. Preliminary analysis of the luminosity calibration of the ATLAS 13.6 TeV data recorded in 2022 (2023). CERN Document Server [preprint].
6. CMS Collaboration. CMS luminosity based on pixel cluster counting—summer 2013 update (2013). CERN Document Server [preprint].
7. Sirunyan AM, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Precision luminosity measurement in proton–proton collisions at $$\sqrt{s} = 13\,\hbox {TeV}$$ in 2015 and 2016 at CMS. Eur Phys J C (2021) 81:800. doi:10.1140/epjc/s10052-021-09538-2
8. CMS Collaboration. Luminosity monitoring with Z counting in early 2022 data (2023). CERN Document Server [preprint].
9. CMS Collaboration. A portrait of the Higgs boson by the CMS experiment ten years after the discovery. Nature (2022) 607:60–8. doi:10.1038/s41586-022-04892-x
10. de Florian D. Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector. CERN Yellow Rep Monogr (2016) 2017. doi:10.23731/CYRM-2017-002
11. David A, Denner A, Duehrssen M, Grazzini M, Grojean C, Passarino G, et al. LHC HXSWG interim recommendations to explore the coupling structure of a Higgs-like particle (2012). arXiv [preprint].
12. Andersen JR, Artoisenet P, Bagnaschi EA, Banfi A, Becher T, Bernlochner FU, et al. Handbook of LHC Higgs cross sections: 3. Higgs properties. CERN Yellow Rep Monogr (2013) 2013. doi:10.5170/CERN-2013-004
13. Monti F, Pandini CE, Lucio Alves FL, Yang H, Huang Y, Wang J, et al. Modelling of the single-Higgs simplified template cross-sections (STXS 1.2) for the determination of the Higgs boson trilinear self-coupling (2022). CERN Document Server [preprint].
14. Englert F, Brout R. Broken symmetry and the mass of gauge vector mesons. Phys Rev Lett (1964) 13:321–3. doi:10.1103/PhysRevLett.13.321
15. Higgs PW. Broken symmetries, massless particles and gauge fields. Phys Lett (1964) 12:132–3. doi:10.1016/0031-9163(64)91136-9
16. Higgs PW. Broken symmetries and the masses of gauge bosons. Phys Rev Lett (1964) 13:508–9. doi:10.1103/PhysRevLett.13.508
17. Guralnik GS, Hagen CR, Kibble TWB. Global conservation laws and massless particles. Phys Rev Lett (1964) 13:585–7. doi:10.1103/PhysRevLett.13.585
18. Higgs PW. Spontaneous symmetry breakdown without massless bosons. Phys Rev (1966) 145:1156–63. doi:10.1103/PhysRev.145.1156
19. Kibble TWB. Symmetry breaking in nonAbelian gauge theories. Phys Rev (1967) 155:1554–61. doi:10.1103/PhysRev.155.1554
20. Chatrchyan S, Khachatryan V, Sirunyan A, Tumasyan A, Adam W, Aguilo E, et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys Lett B (2012) 716:30–61. doi:10.1016/j.physletb.2012.08.021
21. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdelalim A, et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys Lett B (2012) 716:1–29. doi:10.1016/j.physletb.2012.08.020
22. Sirunyan AM, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Measurements of Higgs boson production cross sections and couplings in the diphoton decay channel at $$ \sqrt{\mathrm{s}} $$ = 13 TeV. JHEP (2021) 07:027. doi:10.1007/JHEP07(2021)027
23. ATLAS, Aad G, Abbott B, Abbott DC, Abeling K, Abidi SH, et al. Measurement of the properties of Higgs boson production at √s=13 TeV in the H → γγ channel using 139 fb−1 of pp collision data with the ATLAS experiment. JHEP. arXiv (2023) 07:088. doi:10.1007/JHEP07(2023)088
24. Aad G, Abbott B, Abbott DC, Abud AA, Abeling K, Abhayasinghe DK, et al. Higgs boson production cross-section measurements and their EFT interpretation in the 4ℓ decay channel at √s=13 TeV with the ATLAS detector. Eur Phys J C (2020) 80 957. doi:10.1140/epjc/s10052-020-8227-9
25. De Rujula A, Lykken J, Pierini M, Rogan C, Spiropulu M. Higgs boson look-alikes at the LHC. Phys Rev D (2010) 82:013003. doi:10.1103/PhysRevD.82.013003
26. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, et al. Search for a Higgs boson in the decay channel H to ZZ(*) to q qbar ℓ− l+ in pp collisions at √s=7 TeV. JHEP (2012) 04:036. doi:10.1007/JHEP04(2012)036
27. Chatrchyan S, Khachatryan V, Sirunyan A, Tumasyan A, Adam W, Bergauer T, et al. Measurement of the properties of a Higgs boson in the four-lepton final state. Phys Rev D (2014) 89:092007. doi:10.1103/PhysRevD.89.092007
28. Aad G, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, Aben R, et al. Measurements of Higgs boson production and couplings in the four-lepton channel in pp collisions at center-of-mass energies of 7 and 8 TeV with the ATLAS detector. Phys Rev D (2015) 91:012006. doi:10.1103/PhysRevD.91.012006
29. Sirunyan AM, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, et al. Measurements of production cross sections of the Higgs boson in the four-lepton final state in proton–proton collisions at $$\sqrt{s} = 13\,\text {TeV} $$. Eur Phys J C (2021) 81:488. doi:10.1140/epjc/s10052-021-09200-x
30. ATLAS. Measurements of Higgs boson production by gluon−gluon fusion and vector-boson fusion using H → WW* → eνμν decays in pp collisions at √s=13 TeV with the ATLAS detector (2022). arXiv.
31. CMS, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Measurements of the Higgs boson production cross section and couplings in the W boson pair decay channel in proton-proton collisions at √s=13 TeV. Eur Phys J C (2023) 83 (7):667. arXiv. doi:10.1140/epjc/s10052-023-11632-6
32. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Observation of the Higgs boson decay to a pair of τ leptons with the CMS detector. Phys Lett B (2018) 779:283–316. doi:10.1016/j.physletb.2018.02.004
33. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abhayasinghe D, et al. Cross-section measurements of the Higgs boson decaying into a pair of τ-leptons in proton-proton collisions at √s=13 TeV with the ATLAS detector. Phys Rev D (2019) 99:072001. doi:10.1103/PhysRevD.99.072001
34. Elagin A, Murat P, Pranko A, Safonov A. A new mass reconstruction technique for resonances decaying to. Nucl Instrum Meth A (2011) 654:481–9. doi:10.1016/j.nima.2011.07.009
35. Bianchini L, Conway J, Friis EK, Veelken C. Reconstruction of the Higgs mass in H → ττ events by dynamical likelihood techniques. J Phys Conf Ser (2014) 513:022035. doi:10.1088/1742-6596/513/2/022035
36. Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, Erö J, et al. Evidence for Higgs boson decay to a pair of muons. JHEP (2021) 01:148. doi:10.1007/JHEP01(2021)148
37. Qu H, Gouskos L. ParticleNet: Jet tagging via particle clouds. Phys Rev D (2020) 101:056019. doi:10.1103/PhysRevD.101.056019
38. Bols E, Kieseler J, Verzetti M, Stoye M, Stakia A. Jet flavour classification using DeepJet. JINST (2020) 15:P12012. doi:10.1088/1748-0221/15/12/P12012
39. Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, Dragicevic M, et al. A new calibration method for charm jet identification validated with proton-proton collision events at √s = 13 TeV. JINST (2022) 17:P03014. doi:10.1088/1748-0221/17/03/P03014
40. ATLAS, Aad G, Abbott B, Abbott DC, Abeling K, Abidi SH, et al. (2023). arXiv 83 (7):681. doi:10.1140/epjc/s10052-023-11699-1
41. CMS Collaboration. Performance of the ParticleNet tagger on small and large-radius jets at high level trigger in run 3 (2023). CERN Document Server [preprint].
42. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abhayasinghe D, et al. Observation of H→bb decays and VH production with the ATLAS detector. Phys Lett B (2018) 786:59–86. doi:10.1016/j.physletb.2018.09.013
43. Aad G, Abbott B, Abbott DC, Abud AA, Abeling K, et al. Measurements of Higgs bosons decaying to bottom quarks from vector boson fusion production with the ATLAS experiment at $$\sqrt{s}=13\,\text {TeV}$$. Eur Phys J C (2021) 81:537. doi:10.1140/epjc/s10052-021-09192-8
44. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, Dragicevic M, et al. Inclusive search for highly boosted Higgs bosons decaying to bottom quark-antiquark pairs in proton-proton collisions at $$ \sqrt{s} $$ = 13 TeV. JHEP (2020) 12:085. doi:10.1007/JHEP12(2020)085
45. CMS, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Search for Higgs boson decay to a charm quark-antiquark pair in proton-proton collisions at √s=13 TeV. Phys Rev Lett (2023). arXiv 131 (6):061801. doi:10.1103/PhysRevLett.131.061801
46. Aad G, Abbott B, Abbott DC, Abud AA, Abeling K, Abhayasinghe DK, et al. Direct constraint on the Higgs-charm coupling from a search for Higgs boson decays into charm quarks with the ATLAS detector. Eur Phys J C (2022) 82:717. doi:10.1140/epjc/s10052-022-10588-3
47. CMS, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Search for boosted Higgs boson decay to a charm quark-antiquark √s=13 TeV. Phys Rev Lett (2023). arXiv 131 (4):041801. doi:10.1103/PhysRevLett.131.041801
48. The SLD Electroweak. A Combination of preliminary electroweak measurements and constraints on the standard model (2003). arXiv [preprint].
49. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abhayasinghe D, et al. Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector. Phys Lett B (2018) 784:173–91. doi:10.1016/j.physletb.2018.07.035
50. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Observation of tṫH production. Phys Rev Lett (2018) 120:231801. doi:10.1103/PhysRevLett.120.231801
51. Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. CMS Collaboration Measurement of the Higgs boson production rate in association with top quarks in final states with electrons, muons, and hadronically decaying tau leptons at √s=13 TeV. Eur Phys J C (2021) 81:378. doi:10.1140/epjc/s10052-021-09014-x
52. ATLAS, CMSLHC Higgs Combination Group. Procedure for the LHC Higgs boson search combination in Summer 2011 (2011). CERN Document Server [preprint].
53. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Combined measurements of Higgs boson couplings in proton–proton collisions at $$\sqrt{s}=13\,\text {Te}\text {V} $$. Eur Phys J C (2019) 79:421. doi:10.1140/epjc/s10052-019-6909-y
54. ATLAS Collaboration. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature (2022) 607:52–9. doi:10.1038/s41586-022-04893-w
55. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Combined measurement of the Higgs boson mass in pp collisions at √s=7 and 8 TeV with the ATLAS and CMS experiments. Phys Rev Lett (2015) 114:191803. doi:10.1103/PhysRevLett.114.191803
56. Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, Aben R, et al. Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at s = 7 $$ \sqrt{s}=7 $$ and 8 TeV. JHEP (2016) 08:045. doi:10.1007/JHEP08(2016)045
57. Barrow JD, Turner MS. Baryosynthesis and the origin of galaxies. Nature (1981) 291:469–72. doi:10.1038/291469a0
58. ATLAS Collaboration Abbott B, Abbott D, Abeling K, Abidi S, Aboulhorma A, et al. Constraints on the Higgs boson self-coupling from single- and double-Higgs production with the ATLAS detector using pp collisions at s=13 TeV. Phys Lett B (2023) 843:137745. doi:10.1016/j.physletb.2023.137745
59. Eboli OJP, Marques GC, Novaes SF, Natale AA. Twin Higgs boson production. Phys Lett B (1987) 197:269–72. doi:10.1016/0370-2693(87)90381-9
60. Grazzini M, Heinrich G, Jones S, Kallweit S, Kerner M, Lindert JM, et al. Higgs boson pair production at NNLO with top quark mass effects. JHEP (2018) 05:059. doi:10.1007/JHEP05(2018)059
61. Baglio J, Campanario F, Glaus S, Mühlleitner M, Ronca J. Spira mgg → HH: Combined uncertainties. Phys Rev D (2021) 103:056002. doi:10.1103/PhysRevD.103.056002
62. Dreyer FA, Karlberg A. Vector-boson fusion Higgs pair production at N3LO. Phys Rev D (2018) 98:114016. doi:10.1103/PhysRevD.98.114016
63. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Combination of searches for Higgs boson pair production in proton-proton collisions at √s= 13 TeV. Phys Rev Lett (2019) 122:121803. doi:10.1103/PhysRevLett.122.121803
64. Tumasyan A, Adam W, Andrejkovic J, Bergauer T, Chatterjee S, Damanakis K, et al. Search for Higgs boson pair production in the four b quark final state in proton-proton collisions at s=13 TeV. Phys Rev Lett (2022) 129:081802. doi:10.1103/PhysRevLett.129.081802
65. CMS, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Search for nonresonant pair production of highly energetic Higgs bosons decaying to bottom quarks. Phys Rev Lett (2023). arXiv 131 (4):041803. doi:10.1103/PhysRevLett.131.041803
66. Tumasyan A, Adam W, Andrejkovic J, Bergauer T, Chatterjee S, Damanakis K, et al. Search for nonresonant Higgs boson pair production in final state with two bottom quarks and two tau leptons in proton-proton collisions at s=13 TeV. Phys Lett B (2023) 842:137531. doi:10.1016/j.physletb.2022.137531
65. Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, Escalante Del Valle A, et al. Search for nonresonant Higgs boson pair production in final states with two bottom quarks and two photons in proton-proton collisions at $$ \sqrt{s} $$ = 13 TeV. JHEP (2021) 03:257. doi:10.1007/JHEP03(2021)257
68. Aad G, Abbott B, Abbott D, Abed Abud A, Abeling K, Abhayasinghe D, et al. Combination of searches for Higgs boson pairs in pp collisions at √s=13 TeV with the ATLAS detector. Phys Lett B (2020) 800:135103. doi:10.1016/j.physletb.2019.135103
69. CMS, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Search for nonresonant Higgs boson pair production in the four leptons plus two b jets final state in proton-proton collisions at √s= 13 TeV. JHEP (2023). arXiv 06:130. doi:10.1007/JHEP06(2023)130
70. CMS, Tumasyan A, Adam W, Andrejkovic JW, Bergauer T, Chatterjee S, et al. Search for Higgs boson pairs decaying to WWWW, WWττ, and ττττ in proton-proton collisions at √s= = 13 Te. JHEP (2023). arXiv 07:095. doi:10.1007/JHEP07(2023)095
71. Cepeda M. Report from working group 2: Higgs physics at the HL-LHC and HE-LHC. CERN Yellow Rep Monogr (2019) 7:221–584. doi:10.23731/CYRM-2019-007.221
72. CMS Collaboration. Prospects for non-resonant Higgs boson pair production measurement in bbγγ final states in proton-proton collisions at √s=14 TeV at the High-Luminosity LHC (2022). CERN Document Server [preprint].
73. Abada A, Abbrescia M, AbdusSalam SS, Abdyukhanov I, Abelleira Fernandez J, Abramov A, et al. FCC-ee: The lepton collider: Future circular collider conceptual design report volume 2. Eur Phys J ST (2019) 228:261–623. doi:10.1140/epjst/e2019-900045-4
74. Abada A, Abbrescia M, AbdusSalam SS, Abdyukhanov I, Abelleira Fernandez J, Abramov A, et al. FCC-hh: The hadron collider: Future circular collider conceptual design report volume 3. Eur Phys J ST (2019) 228:755–1107. doi:10.1140/epjst/e2019-900087-0
75. de Blas J, Cepeda M, D’Hondt J, Ellis R, Grojean C, Heinemann B, et al. Higgs boson studies at future particle colliders. JHEP (2020) 01 139. doi:10.1007/jhep01(2020)139
76. Mangano ML, Ortona G, Selvaggi M. Measuring the Higgs self-coupling via Higgs-pair production at a 100 TeV p-p collider. Eur Phys J C (2020) 80:1030. doi:10.1140/epjc/s10052-020-08595-3
77. Tinlot J, Green DR. A storage ring for 10 BeV muons. IEEE Trans Nucl Sci (1965) 12:470–5. doi:10.1109/TNS.1965.4323677
Keywords: Higgs-boson, EWSB, LHC, CMS, ATLAS, frontiers
Citation: Ortona G (2023) The Higgs boson couplings: past, present, and future. The relationships between Higgs boson and other known particles as measured by current and future experiments. Front. Phys. 11:1230737. doi: 10.3389/fphy.2023.1230737
Received: 29 May 2023; Accepted: 18 August 2023;
Published: 28 September 2023.
Edited by:
J. W. F. Valle, Spanish National Research Council (CSIC), SpainReviewed by:
Hua-Sheng Shao, UMR7589 Laboratoire de Physique Théorique et Hautes Énergies (LPTHE), FranceCopyright © 2023 Ortona. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giacomo Ortona, Z29ydG9uYUBjZXJuLmNo
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.