Research on far-field spot search and centre location algorithms

The energy distribution of the far-field spot is uneven, and the background is complex. Therefore, the identification of far-field points and the positioning of the centre are difficult. This article proposes an algorithm for multi-scale Gaussian cyclic convolution for locating the centre of far-field spots. First, wavelet denoising is performed on the image of multiple far-field spots, and the images of adjacent frames are subtracted. Then, the absolute values of the differences are added. Due to the large size of the far-field spot, the Gaussian distribution of the laser energy is not obvious. Therefore, a multi-scale Gaussian convolution kernel is used to perform circular convolution on these images. To preserve low-scale Gaussian features, features are spliced between two convolutions. In this article, we also design multi-angle combination filters to filter the enhanced Gaussian distribution features. Finally, curved polynomials are fitted to the reconstructed Gaussian energy distribution to obtain the maximum value; at this point, the position where the maximum value lies is the centre of the far-field spot. The experiments showed that this method has better robustness.

1 Introduction

The classic laser spot centre positioning methods include the Hough transform method [1], the circular fitting method [2], and the grey-scale centroid [3]. The aforementioned methods have some shortcomings in terms of positioning accuracy, computational complexity, and robustness. The Hough transform method requires a large amount of computation. The circular fitting method requires high integrity of far-field spots. The grey-scale centroid method is susceptible to the uniformity of the digital number (DN) value. Therefore, there is a need to devise more advanced algorithms for laser spot centre localisation.

To be specific, Zhou et al. used iterative thresholding for coarse localisation, followed by interpolation, to achieve the positioning of sub-pixels in the centre of the spot [4]. Liu et al. proposed a curve-fitting algorithm that was introduced to improve the positioning accuracy of the laser spot centre based on the centroid method, but the algorithm is only suitable for images that conform to the Gaussian distribution. Liu, Z. R., et al. proposed laser spot centre localisation accuracy, but the algorithm is only suitable for the case where the grey scale of the spot image conforms to a Gaussian distribution [5]. Zhang et al. proposed an algorithm for laser spot localisation based on a weighted interpolation algorithm; the principle is to use weighted processing for spot positioning, which not only improves the accuracy and stability of the positioning but also provides accurate positioning to the edge of the spot. However, the algorithm is computationally complex and susceptible to saturated image elements within the speckle [6]. Thomas et al. propose a simple approach for the estimation of the circular arc centre and its radius [7], which can be used for laser spot centring. The aforementioned algorithm relies on the image of the ideal spots.

In our study, we found that the far-field spot has a weak Gaussian distribution at multiple scales but not at other locations in the image [8]. To enhance this feature, a multi-scale convolution kernel is used to perform cyclic convolution on the image. Then, features are spliced between two convolutions. The presence of low-scale Gaussian features results in the high-scale convolutions. Finally, the binomials of the results are fitted to the Gaussian distribution; at this point, the position where the global maximum value lies is the coordinate of the centre point.

2 Theoretical analysis

2.1 Model for the energy distribution of laser beams

The energy distribution of laser beams has multiple stable modes, including fundamental and higher-order modes. The fundamental mode is the ideal Gaussian beam, which is usually represented as a plane wave, denoted by $I_0$. As shown in Figure 1A, red indicates the distribution points with high intensity, and blue indicates the spatial distribution of weak intensity; most of the energy is concentrated near the propagation axis to form an Airy spot [9]. The Gaussian beam is represented as the plane wave when $z$ is equal to a constant. As shown in Figure 1B, the amplitude of the light field decreases gradually from the propagation axis to the edge as a Gaussian function $\exp \left(-r2/r20\right)$. When the amplitude is reduced to a central value of $1/e$, $r$ is defined as the radius of the spot. Therefore, the amplitude of the optical field A of a Gaussian beam at a certain cross section is expressed as follows:

$A\left(\mathrm{r}\right)=A_0\exp \left(-\frac{r^2}{{r_0}^2}\right).(1)$

FIGURE 1

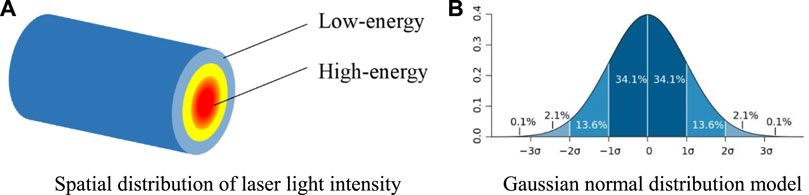
FIGURE 1. Light intensity distribution of an ideal Gaussian beam. (A) Spatial distribution of laser light intensity. (B) Gaussian normal distribution model.

In the formula, $r_0$ is the distance from the centre of the spot. The energy of the laser, $I$, is expressed as

$I\left(\mathrm{r}\right)=I_0\exp \left(-\frac{2r^2}{{r_0}^2}\right).(2)$

Due to the long distance of the far-field spot, the following effects can occur.

2.1.1 Light spot drift

Due to the long distance of the far-field spot, there is an effect on the beam propagation, resulting in a certain change in the direction of propagation and a consequent change in the position of the spot. The effect on the beam is manifested in several ways, and the spot drift effect refers to the change in the spatial position of the spot. Furthermore, with time, the spot drift exhibits a certain superposition effect, which is the beam expansion. The effects of this phenomenon must be taken into account in applications such as optical tracking systems and targeted designs should be created.

2.1.2 Beam extension

Based on the previous analysis, it is clear that the superposition effect of spot drift over time creates a beam expansion. This results in a beam drift phenomenon, which means that the beam after passing through the medium has changed, resulting in an increase in the spot size trend. When beam expansion occurs, the spot size increases and the light intensity at the centre is reduced [10].

2.1.3 Intensity fluctuations of the laser

The transmission of the laser light over long distances is subjected to laser undulation, which is the random undulation of the laser. Affected by the light beam, scattering and other phenomena occur in the medium, resulting in continuous changes in the intensity of the receiving surface. This is known as the intensity fluctuations of the laser [11].

The aforementioned effects weaken the Gaussian characteristics of the laser spot, as shown in Figure 2.

FIGURE 2

FIGURE 2. Effect of the unprocessed far-field spot image.

2.2 Image pre-processing

2.2.1 Wavelet denoising

In this article, wavelet denoising is used to denoise the captured images to eliminate the effect of noise on positioning accuracy [12]. We believe that suppressing the high-frequency noise of the speckle helps resolve the inhomogeneity of the far-field spot and improve the accuracy of speckle image segmentation [13, 14]. The process can be expressed as shown in Figure 3. After image wavelet decomposition, the image noise is reflected in the high-frequency components, and the absolute value of the wavelet coefficient is small; however, the part with uniform laser energy is reflected in the high-frequency component, and the wavelet coefficient is large [15]. According to the idea of wavelet threshold denoising proposed by Johnstone, when the wavelet coefficient is less than a certain threshold, it is considered to be mainly noise components, and the part larger than the threshold is retained.

FIGURE 3

FIGURE 3. Diagrams of the orthogonal wavelet transform.

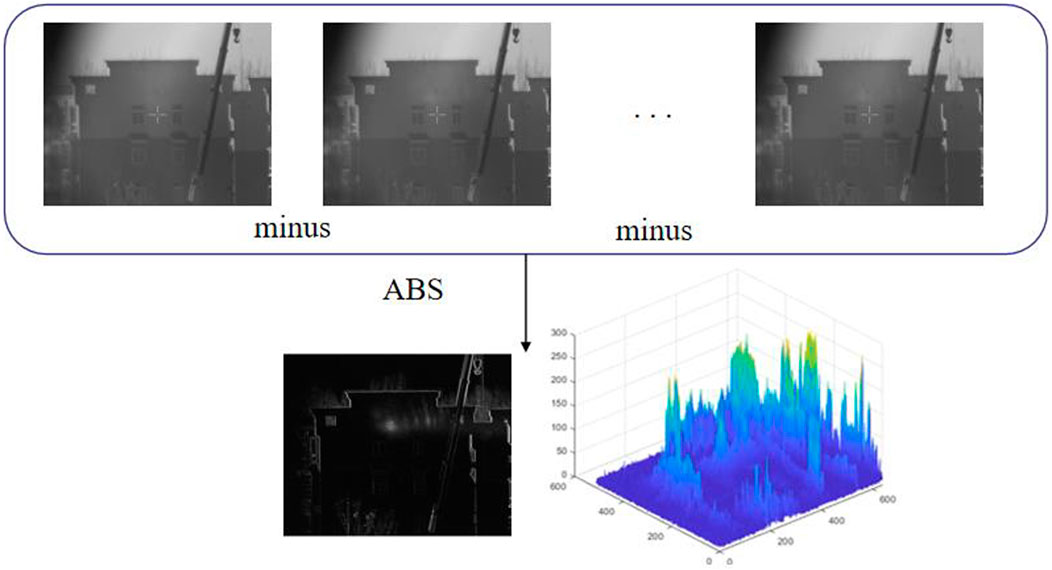
2.2.2 Background removal

Background removal is required for far-field spot images after wavelet denoising. Figure 4 represents the background removal process. Two adjacent frame images are subtracted, and the absolute value is calculated. Due to the frequency of the laser, there are four cases of adjacent frames: no laser spot in both frames; a laser spot in both preceding and following frames; a laser spot in the preceding frame and no laser spot in the following frame; and no laser spot in the preceding frame and a laser spot in the following frame. In the first and second cases, image subtraction results in zero, while in the third and fourth cases, image subtraction of the laser spot energy can be retained; however, the former has positive laser spot pixels and the latter has negative laser spot pixels. Finally, the spot pixels are unified to obtain a positive value by calculating the absolute value.

FIGURE 4

FIGURE 4. Background removal results.

2.3 Gaussian kernel

Due to the Gaussian nature of the laser, a two-dimensional Gaussian kernel needs to be selected to convolve the image. A one-dimensional Gaussian kernel can be obtained by solving the following equation.

The one-dimensional Gaussian kernel function is defined by

$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-{\left(x-\mu \right)}^2/2{\sigma }^2},(3)$

where $\mu$ is the mean of $x$ and $\sigma$ is the variance of $x$. Because when calculating the average, the centre point is the origin and $\mu$ is equal to 0 by default, which then provides the following equation:

$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-x^2/2{\sigma }^2}.(4)$

A two-dimensional Gaussian can then be derived as follows:

$G\left(x,y\right)=\frac{1}{2\pi {\sigma }^2}{e}^{-\left(x^2+y^2\right)/2{\sigma }^2}.(5)$

The value of $\sigma$ in the formula determines the width of the resulting Gaussian convolution kernel. The larger the value of $\sigma$, the wider the graph, the smaller the spikes, and the flatter the graph; the smaller the value of $\sigma$, the narrower and more concentrated the graph, the larger the spikes, and the more dramatic the graph changes. To ensure consistency in the transformation of images at different sizes in the Gaussian kernel, the value of $\sigma$ can be calculated using the following formula:

$\sigma =0.3\times \left(\left(ksize-1\right)\times 0.5-1\right)+0.8.(6)$

Figure 5 shows images of Gaussian kernels of different sizes according to the function.

FIGURE 5

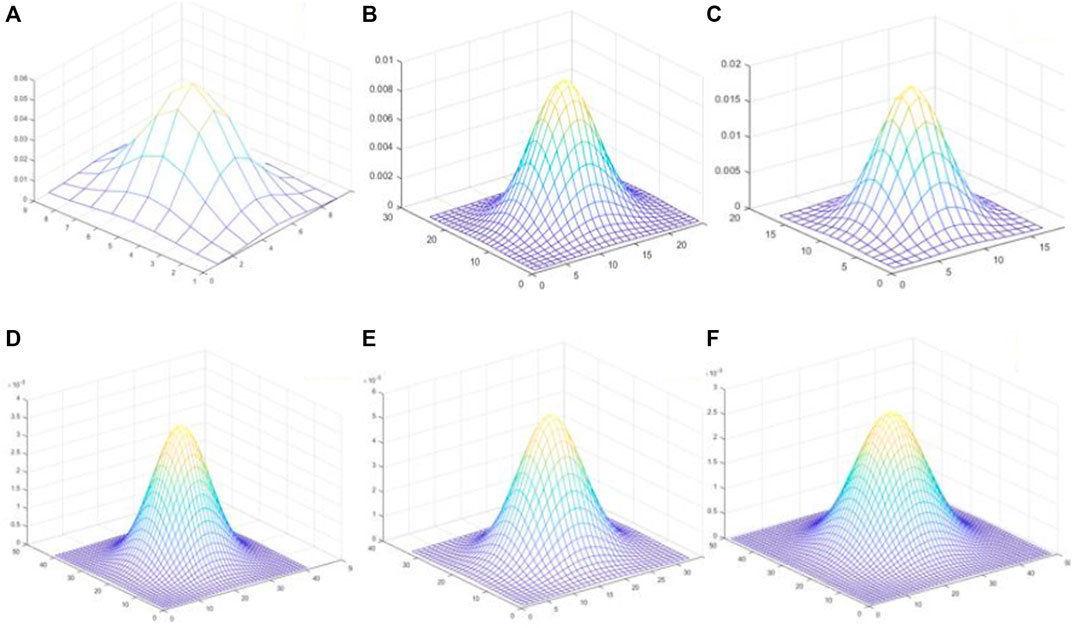
FIGURE 5. Gaussian kernels of different sizes. (A) shows the Gaussian kernel generated by ksize/2, (B) shows the Gaussian kernel generated by ksize/4, (C) shows the Gaussian kernel generated by ksize/6, (D) shows the Gaussian kernel generated by ksize/8, (E) shows the Gaussian kernel generated by ksize/10, and (F) shows the Gaussian kernel generated by the function, which is the Gaussian kernel that best meets the algorithm’s needs.

2.4 Multi-scale Gaussian cyclic convolution

Deeper features in images rely heavily on convolution for extraction [16, 17]. The laser spot features in the pre-processed image are submerged in the background, which are still not extracted and localised, so a multi-scale Gaussian convolution is designed to suppress the background features and highlight the laser spot features. The structure diagram is as follows:

In this article, the Gaussian characteristics of the laser are combined with the choice of using multiple Gaussian convolution kernels of different sizes, i.e., weight matrices, to obtain the convolution feature results at different scales, and then all the feature results are normalised to finally extract the Gaussian features of the light spot image.

Figure 6 shows the effect of the image after multi-scale circular convolution. From the figure, it can be seen that the original image has no obvious spot features; the spot features are enhanced by 3 times of circular convolution, but the difference in the surrounding background is small; the Gaussian features in the spot area are more obvious by 6 times of circular convolution; and the difference between the Gaussian features of the spot and the surrounding Gaussian distribution can be clearly observed by 8 times of circular convolution and above. More detail of the source image is retained in the high-frequency features [18]. The multi-scale cyclic convolution method can effectively enhance the Gaussian characteristics of the spot and improve its distinctness.

FIGURE 6

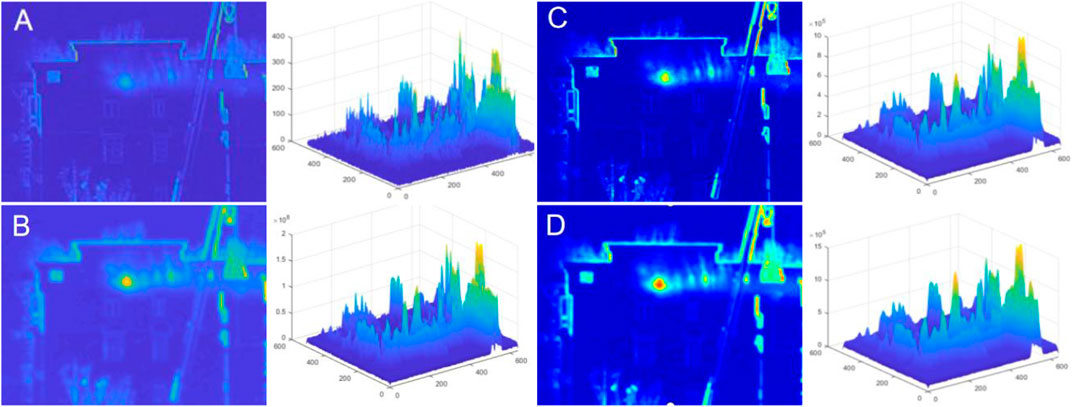
FIGURE 6. Multi-scale Gaussian convolution before and after comparison and its histogram. Plot (A) represents the result of looping the convolution 1 time, plot (B) represents the result of looping 3 times, plot (C) represents the result of looping 5 times 5 times, and plot (D) represents the result of looping 7 times.

Gaussian features in the spot region are significantly improved after multi-scale cyclic convolution, and the background detail information in the darker regions of the spot image is improved, but the search for locating the centre of the spot requires the removal of information such as background detail that interferes with the experimental results. To solve this problem, a multi-angle-based combination filter is proposed to extract contour information and that information is subtracted from each iteration of the cycle. The rotation matrix ${\gamma }_i$ is used to construct the kernel function for the $i$th angle. Let ${\theta }_i$ be the rotation angle of the kernel function; then, the rotation matrix A for the $i$ th angle is as follows:

${\gamma }_i=\left[\begin{array}{cc}\cos {\theta }_i& -\sin {\theta }_i\\ \sin {\theta }_i& \cos {\theta }_i\end{array}\right].(7)$

If $P\left(x,y\right)$ is a point on the kernel function under the coordinate system, the point $\breve{P}$ at the $i$th angle $U-V$ coordinate after the rotation process is as follows:

$\breve{P}\left(u,v\right)=P{\gamma }_i=\left[\begin{array}{cc}x& y\end{array}\right]\left[\begin{array}{cc}\cos {\theta }_i& -\sin {\theta }_i\\ \sin {\theta }_i& \cos {\theta }_i\end{array}\right].(8)$

In order to uniformly filter the spot background while extracting contour and detail information from the image, i.e., if the response of the background region (i.e., non-contour and detail information) after stencil filtering is zero, the filter kernel function $\breve{G}\left(x,y\right)$ for the $i$th angle is defined as follows:

$\breve{G}\left(x,y\right)=\lceil \lambda \cdot \exp \left(-\frac{x^2+y^2}{{\sigma }^2}\right)-{\displaystyle \sum _{\breve{P}\in \mathbb{Q}}}K/N\rceil +{\gamma }_{i}Lap\cdot \left(x,y\right),(9)$

where a is the weight and b belongs to the neighbourhood. $\mathbb{Q}=\left\{\left|u\right|\le 3\epsilon ,\left|v\right|\le L/2\right\}$; $K$ is the number of grey values in the neighbourhood $\mathbb{Q}$ at the $i$th angle; $\lceil \rceil$ is rounded; $Lap$ is the $Laplace$ operator, which is used to extract the background detail information of each angle of the image [19].

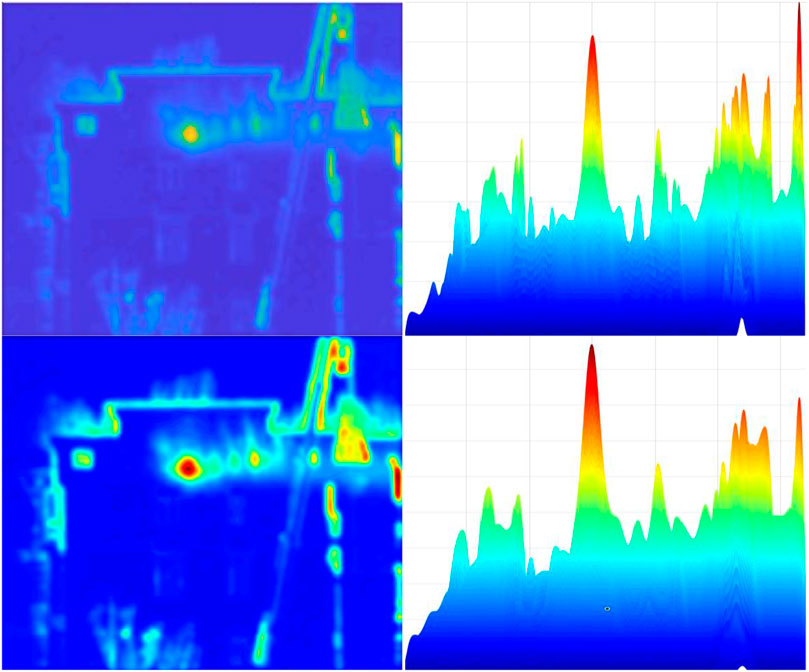
Figure 7 shows the images and feature histograms before and after the multi-angle-based filter combined with multi-scale circular convolution processing. The comparison shows that the spot features are more pronounced after processing than before processing.

FIGURE 7

FIGURE 7. Image histograms and features before and after multi-angle combination filter processing.

The contrast of the laser spot image is significantly improved by comparison with the multi-angle-based combination filter. The background of the image is filtered out, while the Gaussian characteristics of the laser spot are enhanced.

3 Verification of the accuracy of the central positioning algorithm

3.1 Selection of evaluation indicators

Commonly evaluated metrics for laser spot-centring algorithms are repeatability verification and accuracy verification. Repeatability means that the spot is photographed and measured several times in the same position with a stable far-field spot, and the individual measurements are analysed in comparison with the maximum difference between the average values of the measurements. Accuracy is the difference between the measured value of the laser position coordinates and the true value [20]. In practice, however, it is not possible to know the definitive true value of the laser position coordinates, so straightness is used to evaluate the accuracy of the positioning algorithm. When the laser beam moves along a certain straight line, the movement of the spot centre coordinates must be a straight line, and the straightness of the fitted line is chosen as the evaluation index. The smaller the straightness, the better the accuracy of the positioning algorithm.

3.2 Repetitive experimental results

Eight randomly selected far-field spot images with different noises added were taken at the same location, and the spot centre should remain the same. The effect of the spot after the algorithm is shown in Figure 8.

FIGURE 8

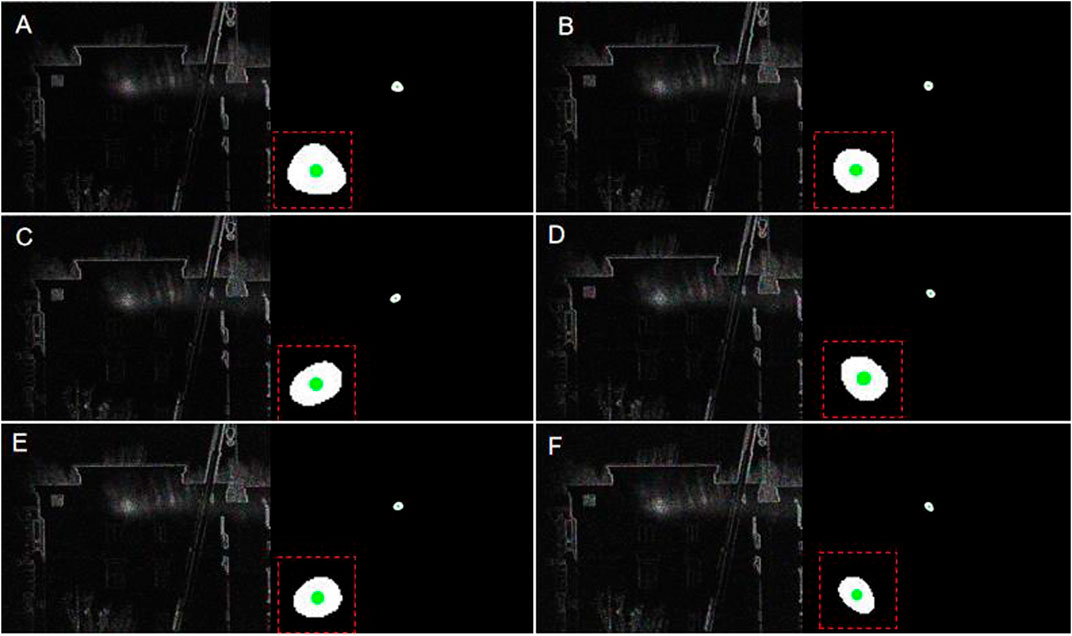
FIGURE 8. Corresponding light spot effect after adding different noise images and algorithm processing, (A–F) images with speckle noise added for (0.02, 0.04, 0.06, 0.08, 0.1, 0.12 noise parameters, respectively).

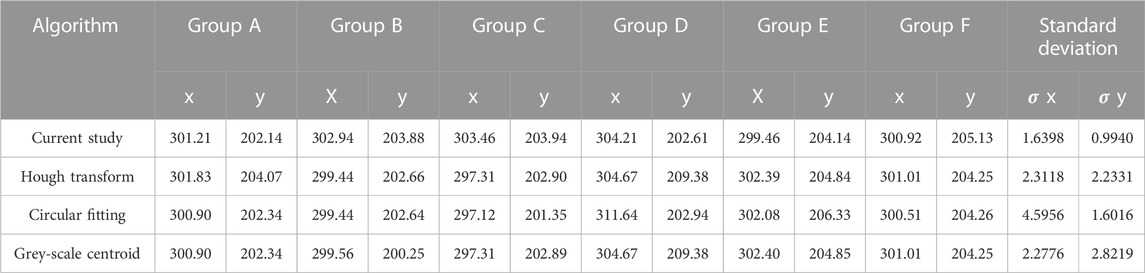
The coordinates of the spot centres calculated by several positioning algorithms are shown in Table 1.

TABLE 1

TABLE 1. Coordinates of spot centres calculated by several positioning algorithms.

The comparison results show that the standard deviation of the algorithm proposed in this paper is smaller, and its stability and accuracy are higher than those of other classical algorithms.

3.3 Accuracy experiment results

The far-field spot image is panned to obtain five frames, and the same level of noise is added. As only horizontal panning is performed, the spot centre coordinates should only change on the y-axis. The results of the far-field spot panning and positioning are shown in Figure 9.

When moving in the horizontal direction, the centre of the extracted spot must also be a straight line in the vertical direction, and the straightness of this line is used as a criterion to evaluate the accuracy of the localisation algorithm. Figure 9 shows the straightness results for several localisation algorithms at different step sizes.

FIGURE 9

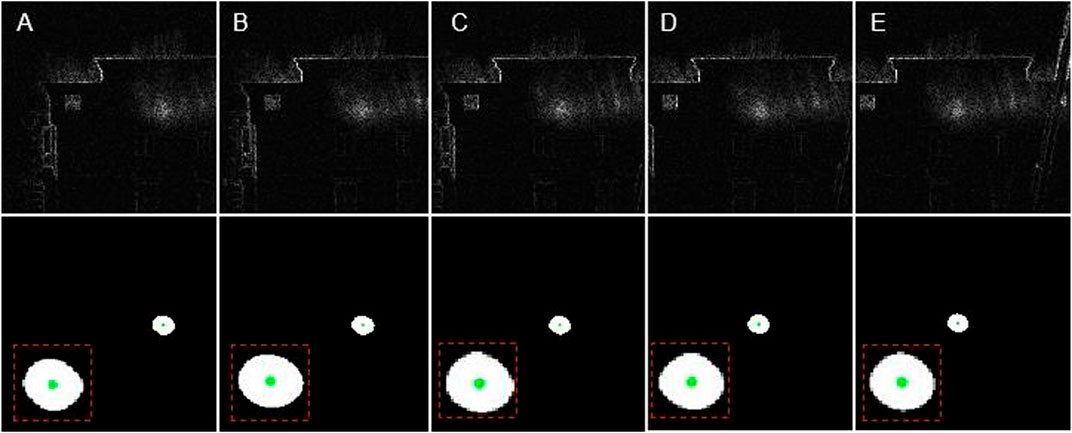
FIGURE 9. Far-field spot translation and positioning results. The (A–E) image represents the image after moving 20, 40, 60, 80, 100 units to the X-axis respectively.

The results of each algorithm were linearly fitted, and the results of the fit are shown in Figure 10A. The three coloured lines in the figure indicate the fitting results for several algorithms in the horizontal direction. Figure 10B shows the fit results for several algorithms in the horizontal direction.

FIGURE 10

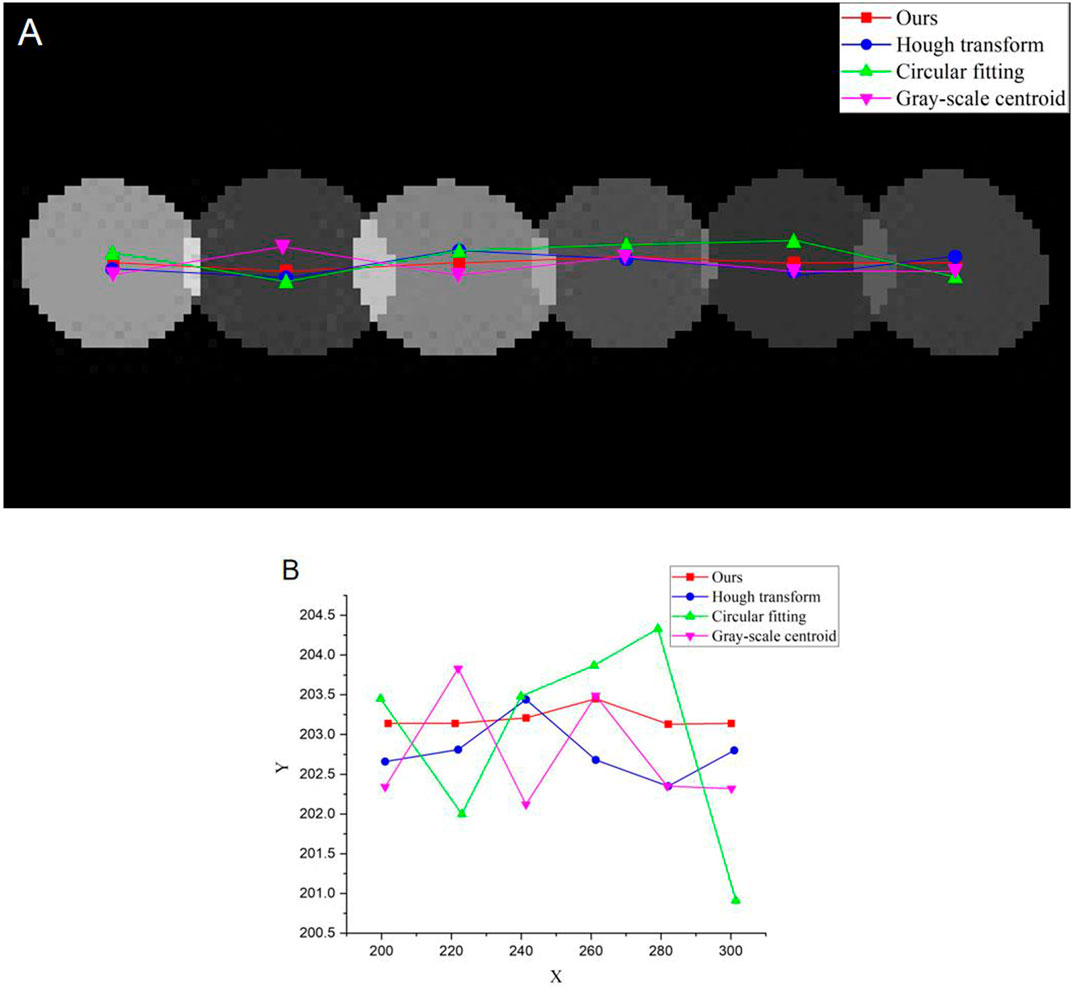
FIGURE 10. Centre coordinate connections calculated by several algorithms. (A) represents a graph of the effect of several light-point localisation algorithms after panning the image, (B) represents a line graph of the variation of several light-point localisation algorithms on the Y-axis after panning the image.

From the aforementioned data, it is intuitively clear that our method is the best fit, meaning that each coordinate is very close to the trajectory of the motion, which matches the trajectory of the laser. The Hough transform method is the second most effective method, with coordinates that are essentially identical to the trajectory of the motion, and the residual sum of squares in the circular fitting method transformation is the largest.

4 Conclusion

The main research in this paper is an algorithm based on multi-scale Gaussian convolution for locating the centre of the far-field spot. To improve the accuracy of the segmentation, several methods are proposed in this paper. First, wavelet denoising is performed on images of multiple far-field spots, and the images of adjacent frames are subtracted. Second, due to the large size of the far-field spots, the Gaussian distribution of the laser energy is not obvious, so a multi-scale Gaussian convolution kernel is used to perform circular convolution on the denoised images. We also designed a multi-angle-based combination filter to filter the enhanced Gaussian distribution features. Finally, a bending polynomial is fitted to the reconstructed Gaussian energy distribution to obtain the maximum value; i.e., the location where the maximum value lies is the centre of the far-field point. In this article, three classical algorithms are chosen for comparison, and the proposed algorithm is more stable and accurate than the other three classical algorithms. Thus, the algorithm in this paper demonstrates that a laser point centre localisation algorithm based on multi-scale Gaussian convolution can be applied to the detection of far-field spot centres.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XM proposed the idea and wrote the original manuscript. XM and HS performed the simulation work. HS helped collect the data. ZL helped in revising the original manuscript. JH and ZL supervised the research work and helped complete the experiment. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yang YQ, Shi R. An algorithm to improve the accuracy of laser spot centre positioning by Hough transform[J]. J Opt (1999) 19(12): 6. doi:10.3321/j.issn:0253-2239.1999.12.013

CrossRef Full Text | Google Scholar

2. Wu ZK, Li GQ, Wang WT, Ma C. Laser spot center detection based on improved circle fitting algorithm. Laser & Infrared (2016) 46(3):346–50. doi:10.3969/j.issn.1001-5078.2016.03.021

CrossRef Full Text | Google Scholar

3. Xi JH, Bao H. Laser stripe center extraction algorithm based on improved centroid method. Fire Control & Command Control (2019) 44(5):149–53. doi:10.3969/j.issn.1002-0640.2019.05.032

CrossRef Full Text | Google Scholar

4. Zhou HF, Ailing G. Research on sub-pixel localization of CCD spot centres in images. Metrology Tech (2007) (11) 21–3. doi:10.3969/j.issn.1000-0771.2007.11.007

CrossRef Full Text | Google Scholar

5. Liu ZR, Wang ZQ, Liu SJ, Shen CW. Research on algorithm for accurate positioning of laser spot centre[J]. Comput Simul (2011) 28(5): 399–401. doi:10.3969/j.issn.1006-9348.2011.05.097

CrossRef Full Text | Google Scholar

6. Zhang J. Research on the measurement accuracy of different laser spot center location. In: Proceedings Volume 11052, Third International Conference on Photonics and Optical Engineering; 110520K; 2019 Jan 24 (2019). doi:10.1117/12.2521709

CrossRef Full Text | Google Scholar

7. Thomassamuel M, Chany T. A simple approach for the estimation of circular arc center and its radius. Comp Vis Graphics Image Process (1989) 45:362–70. doi:10.1016/0734-189x(89)90088-1

CrossRef Full Text | Google Scholar

8. Liu K, Zhiping J, Fang H. Laser spot effective area detection technology[J]. Comput Modernization (2011) 8(10):70–3. doi:10.3969/j.issn.1006-2475.2011.10.020

CrossRef Full Text | Google Scholar

9. Bai Z, Zhao Z, Tian M, Jin D, Pang Y, Li S, et al. A comprehensive review on the development and applications of narrow-linewidth lasers. Microwave Opt Tech Lett (2022) 64(12):2244–55. doi:10.1002/mop.33046

CrossRef Full Text | Google Scholar

10. Andrews LC, Al-Habash MA, Hopen CY, Phillips RL. Theory of optical scintillation: Gaussian-Beam wave model. Waves Random Media (2001) 11:271–91. doi:10.1080/13616670109409785

CrossRef Full Text | Google Scholar

11. Yang C, Goguen J. The Mars exploration rovers descent image motion estimation system. IEEE Intell Syst (2004) 3(19):13–21. doi:10.1109/MIS.2004.18

CrossRef Full Text | Google Scholar

12. Tosellia I, Andrews LC, Phillips RL, Ferrero L. Angle of arrival fluctuations for free space laser beam propagation through non Kolmogorov turbulence. SPIE (2007) 6551:65510E-1–65510E-12. doi:10.1117/12.719033

CrossRef Full Text | Google Scholar

13. Chen H, Bai Z, Yang X, Ding J, Qi Y, Yan B, et al. Enhanced stimulated Brillouin scattering utilizing Raman conversion in diamond. Appl Phys Lett (2022) 120(18):181103. doi:10.1063/5.0087092

CrossRef Full Text | Google Scholar

14. Bai Z, Williams RJ, Kitzler O, Sarang S, Spence DJ, Wang Y, et al. Diamond Brillouin laser in the visible. APL Photon (2020) 5(3):031301. doi:10.1063/1.5134907

CrossRef Full Text | Google Scholar

15. Guo XC, Ma PG, Pang DD, Sun J, Jin Q, Wei H. Research on laser center positioning under CV model segmentation[J]. Front Phys (2022): 104–5. doi:10.3389/fphy.2022.1021950

CrossRef Full Text | Google Scholar

16. Luo W, Xue Q, Zhang Y, Shen J, Cao X. Enhancing sketch-based image retrieval by CNN semantic Re-ranking. IEEE Trans Cybernetics (2019) 50(7):3330–42. doi:10.1109/TCYB.2019.2894498

CrossRef Full Text | Google Scholar

17. Tu Z, Xie W, Dauwels J. Semantic cues enhanced multi-modality multi-stream CNN for action recognition[J]. IEEE Trans Circuits Syst Video Tech (2018) 29(99):1423–37. doi:10.1109/TCSVT.2018.2830102

CrossRef Full Text | Google Scholar

18. Zhang ZH, Wu X, Xu T. Combining multi-scale decomposition and octave convolution for infrared and visible image fusion[J]. Chin J Image Graphics (2023) 28(1):181. doi:10.11834/jig.220517

CrossRef Full Text | Google Scholar

19. Lu HX, Liu ZB, Zhang J. Infrared image enhancement combining multiscale circular convolution and multiclustering space[J]. J Elect (2022)(2) 419. doi:10.12263/DZXB.2021017

CrossRef Full Text | Google Scholar

20. Jiang JW, Kang JH, Wu B. Research on high-precision positioning compensation algorithm for laser spot centre[J]. Adv Laser Optoelectronics (2021) 58(14):141202–5.

Google Scholar