- 1Faculty of Science, Al Balqa Applied University, Al-Salt, Jordan
- 2Faculty of Science, Zarqa University, Zarqa, Jordan
A novel analytical solution to the neutron diffusion equation is proposed in this study using the residual power series approach for both spherical and hemispherical fissile material reactors. Various boundary conditions are investigated, including zero flux on the boundary, zero flux on the extrapolated boundary distance, and the radiation boundary condition (RBC). The study also shows how two hemispheres with opposing flat faces interact. We give numerical results for the same energy neutrons diffused in pure
1 Introduction
Modern physics is taken into consideration after classical physics failed to explain various phenomena, and many branches of modern physics developed, including nuclear physics. To perform nuclear fission in a nuclear reactor, it is essential to have a neutron in the thermal state to break through the nucleus, as each fission produces more than one neutron, leading to a new reaction where a chain reaction is created [1].
The continuity equation, known as the time-dependent transfer equation, expresses the distribution of neutrons in the reactor, which is given as
where
The continuity equation involves both neutron current
where
By applying Fick’s law, the time-dependent transport equation can be simplified to the following time-dependent neutron diffusion equation:
whose solution is considered very important in studying the behavior of neutrons in reactors [2, 3].
The stability of the nuclear reactor has been studied in detail in the past [4]. The condition of criticality in a nuclear reactor is essential to ensure its stability, as the number of neutrons in the reactor must be constant at any time. The flow in the critical state must be time-independent, which can be mathematically expressed using a time-independent diffusion equation as follows:
Various techniques, analytical and numerical, have been employed to solve the neutron diffusion equation throughout the past few decades, such as the homotopy perturbation method, the Laplace transform process, and the Galerkin method with B-splines [5–21]. To the best of our knowledge, the residual power series method (RPSM) [21–29], an analytical technique, has never been used to handle issues relating to the neutron diffusion equation.
RPSM is a relatively new technique that provides exact and approximate analytical solutions in the series form to many differential and integrodifferential equations of integer and fractional orders [21–29]. The idea of the RPSM is based on using the residual function and the derivative operator concepts in determining the coefficients of the solution, which is assumed to be in a power series form. In RPSM, it is usual to use a classical derivative operator to determine the coefficients of a power series solution if the differential equation is of integer order. However, a fractional derivative operator is used to determine the coefficients if the differential equation is of fractional order.
Later, we will rewrite Eq. 1 using spherical coordinates in spherical and hemispherical reactors, which gives rise to single equations. This work aims to adapt and modify RPSM to solve Eq. 1 after being formulated in spherical coordinates. This modification is a regeneration of RPSM and is presented for the first time in this work. This modification relies on using a fractional derivative operator, such as the Caputo fractional derivative (CFD) [30, 31] or the conformable fractional derivative [21, 32], in differential equations of the integer order. Since the equations to be solved are singular, we impose the solution in a Frobenius series form. Therefore, the new modified method can be considered an alternative method to the Frobenius method in determining the power series solution coefficients.
In fact, several types of fractional derivative operators can be used in our hypothetical modification of the RPSM, such as the CFD operator, the Riemann–Liouville fractional derivative operator [33], and the conformable fractional derivative operator. The CFD is employed in the modified method without bias or preference to determine the Frobenius series coefficients. The CFD operator is defined using the following formula:
where
Moreover, the numerical results in this study are contrasted using pure
The following section presents the methodology of the RPSM and its application to spheres and hemispheres. The radiation boundary condition is also covered in depth to set the stage for the computations. Section 3 presents numerical results for the flux distribution in the studied nuclear reactors and critical radius calculations. The associated technical problems encountered throughout the computations are presented, along with the corresponding solutions.
2 Theory
2.1 The basic idea of the RPSM
RPSM is a technique to find the power series solution coefficients without having a recurrence relation. Indeed, the coefficients of the power series are calculated by the concept of residual error through a sequence of algebraic equations, and in the end, a truncated series solution (approximate solution) is obtained. The major merit of RPSM is that it can be implemented to the problem directly without linearization, perturbation, or discretization and without any transformation by selecting appropriate initial conditions.
Most of the problems resolved using RPSM were to provide series solutions about regular points and did not address situations where there are singular points. In this work, we introduce a simple modification to the construction of the RPSM to be able to solve issues containing these types of points.
The basic definition in addition to the basic theories of RPSM and its applicability to different types of differential equations is given in [21–29]. For the convenience of the reader, we will introduce a review of the RPSM by clarifying the following algorithm on an ordinary differential equation:
(1) Express the
subject to the initial conditions
where
(2) If
whereas if
(3) Define the residual functions as follows:
Indeed,
(4) Substitute the expansions (5) and (6) of
where
(5) In the singular point case, we need to find the value of
where
(6) Since the CFD of a constant is 0, the value of
Since
(7) If
whereas if
(8) Replace the values obtained for
(9) If there is a pattern in the coefficients of the series in terms of some well-known elementary functions, then we have the exact solution
2.2 Bare sphere
First, the application of RPSM in spherical reactors is studied. We consider first the rather simple example of a bare spherical reactor of radius
where
is the buckling of the reactor. Substituting the Laplacian in spherical coordinates and using
To solve Eq. 18 using RPSM, we assume that the solution has a fractional power series representation at
Define the residual function of Eq. 18 as
Substitute Eq. 19 into the residual function (20), we obtain the following series:
According to Eq. 10, the CFD of the residual function in Eq. 21 will be as
The solution of the indicial equations
Thus, the
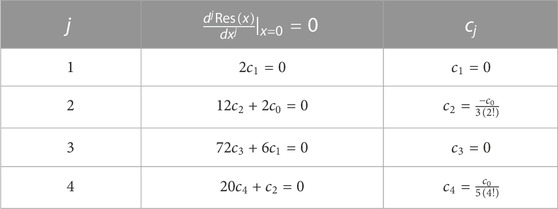
According to step (9) in Subsection 2.1, the solution of the algebraic equations
can be summarized in Table 1.
If we continue in the same manner, then we conclude that the general form of the coefficients in series (19) will be in the following form:
Therefore, the solution for Eq. 18 has the following exact solution:
Consequently, the final solution for Eq. 16, in a closed form, is given by
This flux must satisfy the relevant boundary conditions.
2.3 Hemispherical reactor
In this subsection, we will consider the hemispherical reactor. This case is more complicated because the flux is a function in two variables
where the buckling
2.3.1 Solution by the separation of variables and residual power series method
Applying the separation of variables, we obtain
We obtain the eigenvalue equations as follows:
To solve the radial part using RPSM, we first, for simplicity, consider
and we assume the solution has a power series representation at
The residual function of Eq. 33 has the following form:
If we substitute Eq. 34 into the residual function (35), then we obtain the following series function:
and so, the CFD of the residual function of order
Substituting
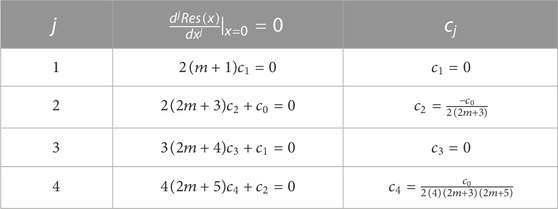
Following the same manner as in Section 2.2, if we apply the sequential operator
Consequently, the first few coefficients of the series in Eq. 34 are given in Table 2.
It is clear that there is a pattern in the coefficients of our series. So, the
which can be reformulated as follows:
Therefore, the eigensolutions to the Sturm–Liouville equation in Eq. 31 appear in the following series:
Now, to solve the angular part, which is a Legendre equation, we construct the residual function of Eq. 32 as
and since
Substitute Eq. 44 into Eq. 43, and we obtain
Applying the differential operator
Thus, the first few coefficients of the series in Eq. 44 are given in Table 3.
Note that there are two linearly independent solutions one of them is an infinite series and the other is a polynomial of degree m. If m is an even number, then the solution that contains terms of even exponents will be the polynomial whereas the solution that contains terms of odd exponents will be infinite series and vice versa if m is an odd number. Anyway, we can keep track of the pattern in the coefficients and write the solutions as follows:
Legendre was able to combine both solutions in a single format, regardless of whether the number
By using Rodrigues’s formula for the Legendre polynomials, the solution can be expressed as follows:
Therefore, the general solution for Eq. 29 can be expressed as
2.4 The radiation boundary condition
Although the choice of suitable boundary conditions in solving the neutron diffusion equation is at the core of the nuclear reactor physicist mission, here, we will apply three boundary conditions, namely, zero flux boundary condition (ZFBC), extrapolated boundary condition (EBC), and radiation boundary condition (RBC). These boundary conditions will be applied on both spherical and hemispherical reactors.
ZFBC cures about the point at the surface of the reactor
The use of the application of RBC on the solution of the hemispherical reactor using RPSM based on the separation of variable techniques can be performed as follows:
where
The RBC on the curved surface where
However, RBC on the flat surface will be
where
Applying RBC on the flat surface in Eq. 50 yields
Using the following recurrence relationships of
and some Legendre polynomials properties, we obtain the following relationship:
We can use the previous result to write the odd term amplitude in terms of the even term amplitude as
where
as reported in [ 36].
Similarly, applying the RBC on the curved surface, we obtain
or it can be written as
where
Following [35], we obtain
where
and
The alternating method of
where
3 Numerical results
The numerical data of neutrons diffusing in pure
The important diffusion constant and buckling are
Depending on these data, to calculate the flux, applying different boundary conditions, to find the critical radii, and to study the flux distribution for both spherical and hemispherical reactors,, this work has been compared with benchmark calculations [34].
3.1 Critical radius calculations
The critical radius
The first case we will study is the spherical reactor. Here, the critical radius using ZFBC and EBC is considered, and the results are compared with RBC. A
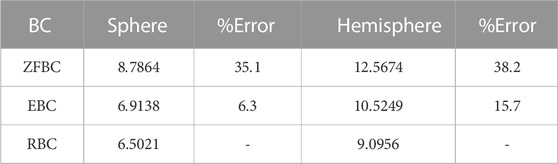
TABLE 5. Critical radius
After taking the bare sphere, the hemispherical reactor is considered, and the neutron flux using ZFBC will vanish on the flat surface (µ = 0). Using the Legendre polynomial properties, the even amplitudes must be equal to 0, and on the curved surface, we need to find the first zero of the solution
The critical radii in pure
Unlike the spherical reactor, applying RBC is essential for the hemispherical reactor.
The calculation of the critical dimension using RBC is illustrated in the following equation, and the infinite summation in Eq. 62 will be cut off to the value N, where the dimension of the matrix is finite, and rewritten as
where
This simplification is an important numerical calculation to make cut-off limit value N. Then, the flux in Eq. 50 will be simplified to
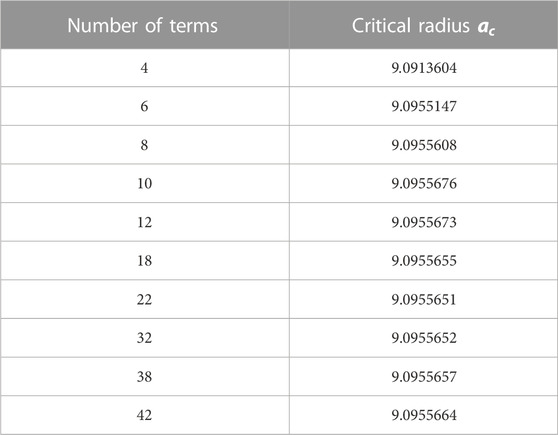
A third computer code has been used to calculate the critical radius using RBC. The code calculates the determinant of
The determination of the critical dimension depends on the cut-off value N, where the number of terms will be
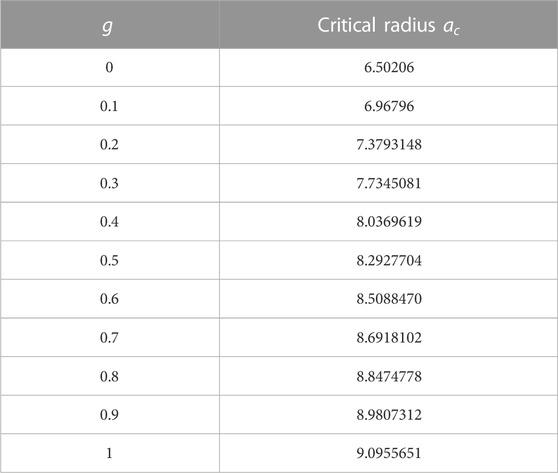
The effect of the number of terms is clear; the value of the critical radius is converged by increasing the number of terms. Now, the effect of changing the interaction parameter
The reactor is a sphere when the interaction parameter
3.2 Flux distribution
Now, the flux destruction inside the hemispherical reactor will be considered. It is straightforward that the symmetry of the spherical reactor makes the flux distribution a simple case study in [35], so the flux in Eq. 69 will be written as
For computational calculation purpose, this equation can be expressed as
The amplitudes
where
The value of the average flux is
Based on these data, the averaged flux calculated using the
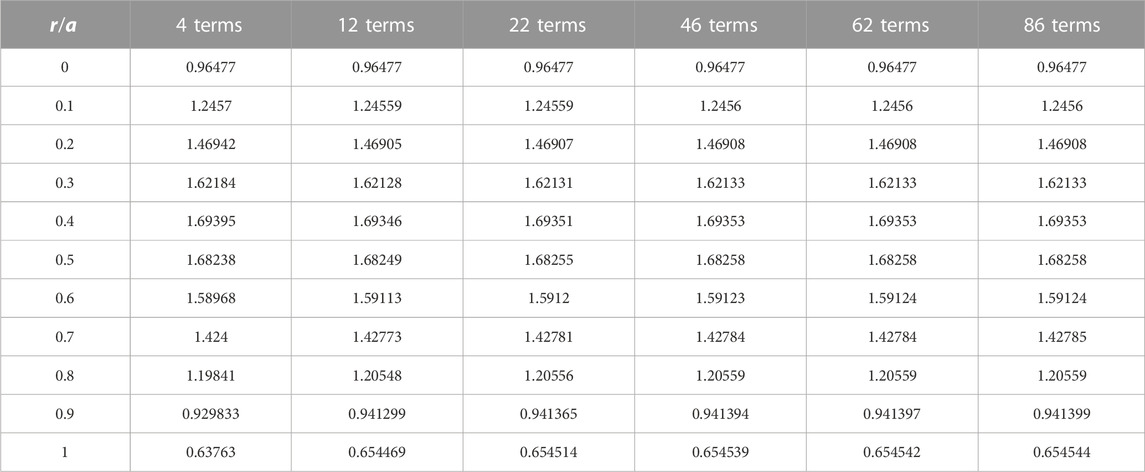
The convergence of the flux values is clearly given in Table 8.
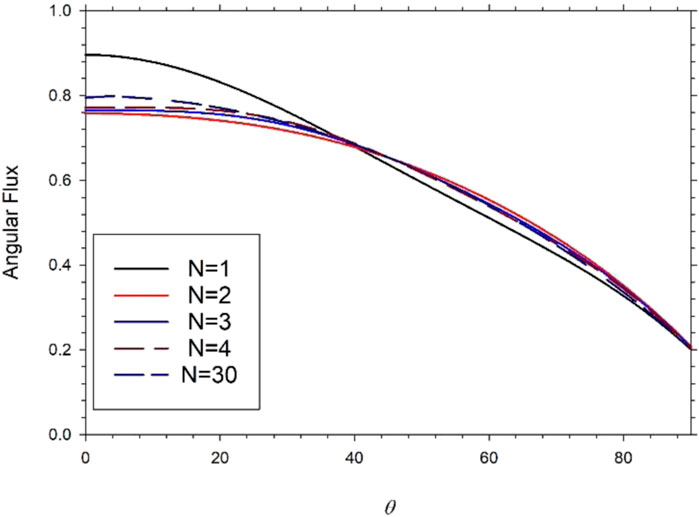
As shown in Figure 1, the fast convergence of the flux on the curved surface is obtained with the increasing number of terms (for
It is important to clarify, from Figure 1, that the convergence is stable and acceptable, and when the number of terms is 30, the angular flux, which expresses the behavior of neutrons when they are diffusing in pure
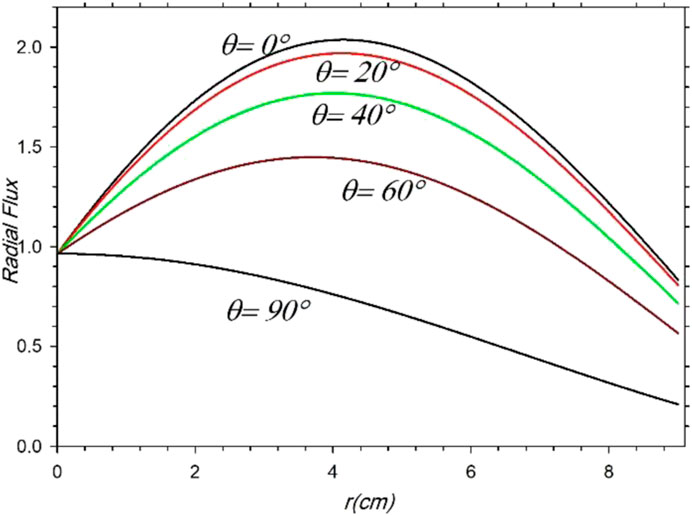
After studying the effect of the number of terms on the flux, it is taken into consideration at a wide range of angle values in Figure 2.
As shown in Figure 2, it is noted that the radial flux does not decrease when
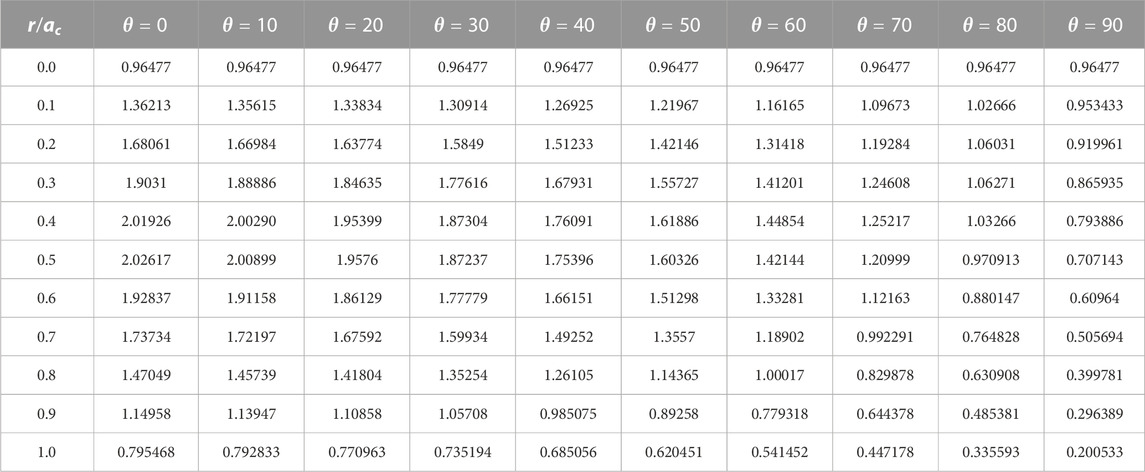
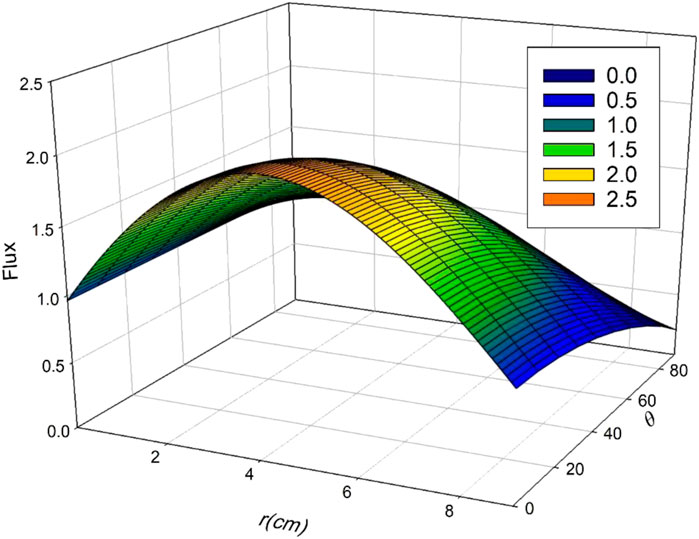
To clarify the flux behavior in more detail, the flux values for different angles and radii are tabulated in Table 9 and depicted in Figure 3.
Furthermore, a three-dimensional plot of the flux distribution across the core of a bare hemisphere as a function of
The flux in Table 6 is represented graphically in Figure 3. The data in Figure 1 and Figure 2 are merged in the same figure, where the full neutron behavior is represented; however, this three-dimensional flux representation is not figured out previously for the hemispherical reactor.
Although the neutrons diffusing in pure
4 Conclusion
In this article, we introduced the application of RPSM in solving the neutron diffusion equation in hemispherical symmetry. The method is efficient and can present the solution in the form of a rapid series that converge to the exact solution. Two important cases are discussed: the spherical reactor and hemispherical reactor. The results are presented in tables and illustrative figures using
In future work, we attend to solve more partial differential equations with physical applications, using the proposed method that showed its accuracy in handling similar problems, and further investigation of the convergence-produced series should be the goal of future specialized research [37–41].
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
4. Kochenov AS. The stability of a nuclear power plant. J Nucl Energ A. Reactor Sci (1960) 12(4):194–200. doi:10.1016/0368-3265(60)90103-1
5. Dababneh S, Khasawneh K, Odibat Z. An alternative solution of the neutron diffusion equation in cylindrical symmetry. Ann Nucl Energ (2011) 38(5):1140–3. doi:10.1016/j.anucene.2010.12.011
6. Nairat M, Shqair M, Alhalholy T. Cylindrically symmetric fractional Helmholtz equation. Appl Math E-notes (2019) 19:708–17.
7. Shqair M. Developing a new approaching technique of homotopy perturbation method to solve two-group reflected cylindrical reactor. Results Phys (2019) 12:1880–7. doi:10.1016/j.rinp.2019.01.063
8. Shqair M, Farrag EA, Al-Smadi M. Solving multi-group reflected spherical reactor system of equations using the homotopy perturbation method. Mathematics (2022) 10(10):1784. doi:10.3390/math10101784
9. Ala’yed O, Saadeh R, Qazza A. Numerical solution for the system of Lane-Emden type equations using cubic B-spline method arising in engineering. AIMS Maths (2023) 8(6):14747–66. doi:10.3934/math.2023754
10. Edwan R, Saadeh R, Hadid S, Al-Smadi M, Momani S. Solving time-space-fractional Cauchy problem with constant coefficients by finite-difference method. Comput Math Appl (2020) 25–46.
11. Shqair M, Ghabar I, Burqan A. Using Laplace residual power series method in solving coupled fractional neutron diffusion equations with delayed neutrons system. Fractal Fract (2023) 7:219. doi:10.3390/fractalfract7030219
12. Aboanber AE, Nahla AA, Aljawazneh SM. Fractional two energy groups matrix representation for nuclear reactor dynamics with an external source. Ann Nucl Energ (2021) 153:108062. doi:10.1016/j.anucene.2020.108062
13. Sardar T, Saha Ray S, Bera RK, Biswas BB, Das S. The solution of coupled fractional neutron diffusion equations with delayed neutrons. Int J Nucl Energ Sci Technol (2010) 5(2):105–13. doi:10.1504/ijnest.2010.030552
14. El-Nabulsi RA. Fractal neutrons diffusion equation: Uniformization of heat and fuel burn-up in nuclear reactor. Nucl Eng Des (2021) 380:111312. doi:10.1016/j.nucengdes.2021.111312
15. El-Nabulsi RA. Nonlocal effects to neutron diffusion equation in a nuclear reactor. J Comput Theor Transport (2020) 49(6):267–81. doi:10.1080/23324309.2020.1816551
16. El-Nabulsi RA. Neutrons diffusion variable coefficient advection in nuclear reactors. Int J Adv Nucl Reactor Des Technol (2021) 3:102–7. doi:10.1016/j.jandt.2021.06.005
17. Patra A, Shone TT, Mishra BB. Natural decomposition approximation solution for first order nonlinear differential equations. Int J Eng Technol (2018) 7(4):442–5. doi:10.14419/ijet.v7i4.5.20202
18. Nahla AA, Al-Malki FA, Rokaya M. Numerical techniques for the neutron diffusion equations in the nuclear reactors. Adv Stud Theor Phys (2012) 6(14):649–64.
19. Tumelero F, Lapa CM, Bodmann BE, Vilhena MT. Analytical representation of the solution of the space kinetic diffusion equation in a one-dimensional and homogeneous domain. Braz J Radiat Sci (2019) 7(2B):7. doi:10.15392/bjrs.v7i2b.389
20. Khaled SM. Exact solution of the one-dimensional neutron diffusion kinetic equation with one delayed precursor concentration in Cartesian geometry. AIMS Math (2022) 7:12364–73. doi:10.3934/math.2022686
21. El-Ajou A, Al-Smadi M, Oqielat MN, Momani S, Hadid S. Smooth expansion to solve high-order linear conformable fractional PDEs via residual power series method: Applications to physical and engineering equations. Ain Shams Eng J (2020) 11(4):1243–54. doi:10.1016/j.asej.2020.03.016
22. El-Ajou A. Taylor’s expansion for fractional matrix functions: Theory and applications. J Math Comput Sci (2020) 21(1):1–17. doi:10.22436/jmcs.021.01.01
23. Oqielat MN, Eriqat T, Al-Zhour Z, Ogilat MN, El-Ajou A, Hashim I. Construction of fractional series solutions to nonlinear fractional reaction–diffusion for bacteria growth model via Laplace residual power series method. Int J Dyn Control (2023) 11(2):520–7. doi:10.1007/s40435-022-01001-8
24. Oqielat MN, Eriqat T, Ogilat O, El-Ajou A, Alhazmi SE, Al-Omari S. Laplace-residual power series method for solving time-fractional reaction–diffusion model. Fractal and Fractional (2023) 7(4):309. doi:10.3390/fractalfract7040309
25. Saadeh R, Burqan A, El-Ajou A. Reliable solutions to fractional Lane-Emden equations via Laplace transform and residual error function. Alexandria Eng J (2022) 61(12):10551–62. doi:10.1016/j.aej.2022.04.004
26. Saadeh R. A reliable algorithm for solving system of multi-pantograph equations. WSEAS Trans Math (2022) 21:792–800. doi:10.37394/23206.2022.21.91
27. Khresat H, El-Ajou A, Al-Omari S, Alhazmi SE, Oqielat MA. Exact and approximate solutions for linear and nonlinear partial differential equations via Laplace residual power series method. Axioms (2023) 12(7):694. doi:10.3390/axioms12070694
28. Korpinar Z, Baleanu D, İnç M, Almohsen B. Some applications of the least squares-residual power series method for fractional generalized long wave equations. J Ocean Eng Sci (2021). doi:10.1016/j.joes.2021.09.001
29. Salah E, Qazza A, Saadeh R, El-Ajou A. A hybrid analytical technique for solving multi-dimensional time-fractional Navier-Stokes system. AIMS Maths (2023) 8(1):1713–36. doi:10.3934/math.2023088
30. El-Ajou A, Al-Zhour Z. A vector series solution for a class of hyperbolic system of Caputo-time-fractional partial differential equations with variable coefficients. Front Phys (2021) 9:276. doi:10.3389/fphy.2021.525250
31. Burqan A, El-Ajou A, Saadeh R, Al-Smadi M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alexandria Eng J (2022) 61(2):1069–77. doi:10.1016/j.aej.2021.07.020
32. El-Ajou A. A modification to the conformable fractional calculus with some applications. Alexandria Eng J (2020) 59(4):2239–49. doi:10.1016/j.aej.2020.02.003
33. El-Nabulsi RA, Torres DF. Necessary optimality conditions for fractional action-like integrals of variational calculus with Riemann–Liouville derivatives of order (α, β). Math Methods Appl Sci (2007) 30(15):1931–9. doi:10.1002/mma.879
34. Cassell JS, Williams MM. A solution of the neutron diffusion equation for a hemisphere with mixed boundary conditions. Ann Nucl Energ (2004) 31(17):1987–2004. doi:10.1016/j.anucene.2004.04.008
35. Khasawneh K, Dababneh S, Odibat Z. A solution of the neutron diffusion equation in hemispherical symmetry using the homotopy perturbation method. Ann Nucl Energ (2009) 36(11-12):1711–7. doi:10.1016/j.anucene.2009.09.001
36. Sood A, Forster RA, Parsons DK. Analytical benchmark test set for criticality code verification. Prog Nucl Energ (2003) 42(1):55–106. doi:10.1016/s0149-1970(02)00098-7
37. Yang L, Su H, Zhong C, Meng Z, Luo H, Li X, et al. Hyperspectral image classification using wavelet transform-based smooth ordering. Int J Wavelets, Multiresolution Inf Process (2019) 17(06):1950050. doi:10.1142/s0219691319500504
38. Guariglia E. Harmonic Sierpinski gasket and applications. Entropy (2018) 20(9):714. doi:10.3390/e20090714
39. Zheng X, Tang YY, Zhou J. A framework of adaptive multiscale wavelet decomposition for signals on undirected graphs. IEEE Trans Signal Process (2019) 67(7):1696–711. doi:10.1109/tsp.2019.2896246
40. Guariglia E, Silvestrov S. Fractional-Wavelet Analysis of Positive definite Distributions and Wavelets on D'(C) D′(C). In Engineering mathematics II: Algebraic, stochastic and analysis structures for networks, data classification and optimization 2016. Springer International Publishing (2017). p. 337–53.
Keywords: neutron diffusion, power series, radial flux, radiation boundary condition, nuclear reactor physics
Citation: El-Ajou A, Shqair M, Ghabar I, Burqan A and Saadeh R (2023) A solution for the neutron diffusion equation in the spherical and hemispherical reactors using the residual power series. Front. Phys. 11:1229142. doi: 10.3389/fphy.2023.1229142
Received: 25 May 2023; Accepted: 23 August 2023;
Published: 11 September 2023.
Edited by:
Rami Ahmad El-Nabulsi, Chiang Mai University, ThailandReviewed by:
Marwan Alquran, Jordan University of Science and Technology, JordanYusif Gasimov, Azerbaijan University, Azerbaijan
Copyright © 2023 El-Ajou, Shqair, Ghabar, Burqan and Saadeh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rania Saadeh, cnNhYWRlaEB6dS5lZHUuam8=
 Ahmad El-Ajou
Ahmad El-Ajou Mohammed Shqair
Mohammed Shqair Ibrahim Ghabar
Ibrahim Ghabar Aliaa Burqan
Aliaa Burqan Rania Saadeh
Rania Saadeh