
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 26 July 2023
Sec. Interdisciplinary Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1227917
This article is part of the Research Topic Lost Circulation Control During Drilling and Completion in Complex Formations View all 10 articles
 Xuesong Xing1
Xuesong Xing1 Guangai Wu1
Guangai Wu1 Jun Zhou1
Jun Zhou1 Anshun Zhang1
Anshun Zhang1 Yanan Hou1
Yanan Hou1 Xin Xie1
Xin Xie1 Jianshu Wu1
Jianshu Wu1 Xiangwei Kong2,3*
Xiangwei Kong2,3* Song Li2
Song Li2Hydraulic fracturing technology is an important means to efficiently exploit unconventional oil and gas reservoirs. As the development of oil and gas fields continues at a high rate, the life cycle of oil and gas wells has been significantly shortened. Fracture sealing is often used to transform oil and gas reservoirs, maintaining long-term economic development benefits. Multiple high-conductivity channels were created between the borehole and the reservoir through temporary sealing of fractures near the contaminated zone. This extended the recovery range and further improved the recovery of oil and gas. A mathematical model was developed to predict the distribution of stress around the artificial fracture prior to the rupture of the seal. Finite element software was used to model the stress distribution around a reservoir containing natural and artificial fractures. We discuss the mechanical conditions for the initiation of a new fracture and the optimal timing for fracture sealing. The prediction of the propagation and propagation trajectories of the new fracture is revealed, and the behavior rules for the initiation and steering propagation of the new fracture are clarified. These results can facilitate theoretical studies and on-site technical optimization of fracture sealing.
Hydraulic fracturing technology is one of the important means to efficiently exploit unconventional oil and gas reservoirs. It plays a crucial role in reducing costs and maximizing production efficiency in the development of unconventional oil and gas reservoirs. With the continuous and high-speed development of oil and gas fields, the life cycle of oil and gas wells has been significantly shortened. Therefore, it is essential to utilize temporary plug fracturing to transform oil and gas reservoirs and maintain long-term economic development benefits. Temporary plug fracturing technology is designed to increase the reconstruction effort of the target layer, reduce the difficulty of fracture construction, and increase the efficiency of unit well section reconstruction. The creation of multiple high-conductivity channels between the wellbore and the reservoir through the temporary plug of the fracture extends the recovery range and further improves oil and gas recovery. This approach not only reduces the cost of fracturing but also ensures production maximization in the efficient development of tight oil and gas [1–6].
Research and field testing on temporary plugging fracturing technology began in the 1950s and 1960s, leading to significant progress in understanding the mechanisms, materials, numerical simulation, design, and construction of temporary plugging fracturing [1–3, 7, 8]. Field experiments have shown that several factors, such as initial artificial fractures, changes in reservoir pore pressure and temperature fields due to long-term production, artificial fractures in adjacent wells, and production/injection activities, can affect the size and direction of the in situ stress field [5, 9–11]. According to the theory of rock and fracture mechanics, artificial fractures are always perpendicular to the direction of minimum horizontal stress. Therefore, performing temporary plug fracturing on a reservoir where stress reorientation has already occurred may result in a new fracture reorientation, which is fracturing and extending in a different direction from the initial fracture.
Refracturing old wells in low permeability oil fields has been established, mainly through intra-fracture diversion fracturing, which has become a leading technology for tapping potential and stabilizing production in many blocks [11–16]. By developing numerical models of the stress field and fracture propagation, we obtain new fracture propagation behaviors and optimal fracture timing based on different geological features and fracture design parameters generated by temporary plug fracturing [17–19]. Compared to theoretical calculations and numerical simulation methods, indoor fracture propagation experiments are more realistic and intuitive. The use of true triaxle fracturing experiments to study fracture propagation behavior reveals geological and engineering factors that affect changes in fracture morphology. Zhang et al. [20] used large-scale true triaxle simulation experiments to believe that perforations change the distribution of ground stress around the well, thereby affecting the initiation and propagation of fracturing fractures. Wu et al. [21] studied the impact of perforating parameters on the initiation and propagation of fracturing fractures under different ground stress differences through true triaxle physical model experiments, thereby optimizing perforating parameters that improve reconstruction efficiency. Yuanqing et al. [22] simulated matrix acidification in a fractured porous medium using the CF model and DBF framework and validated it by comparing it with the simulations of Khoei. In addition, the thermal DBF framework was utilized to investigate the impact of temperature on the acidification of the matrix. Yue et al. [23] used CT scanning technology to describe large physical model experiments to simulate the fracture morphology after primary fracturing and temporary plugging fracturing; analyzed the effects of ground stress difference, natural fractures, and fracturing fluid viscosity on the fracture morphology; and discussed the theory of temporary plugging and fracturing. Liu et al. [24] improved the commonly used model of fracture–hole duality scaling by proposing a pseudo-fracture model in which the cavity consists of a cluster of anomalous matrices with high porosity. They proposed a new method for generating stochastic pore-breaking models. The finite volume method was used to obtain the sensitivity of the solution dynamics to the fracture and hole parameters. The aforementioned studies have gained much understanding in terms of fracture formation mechanisms, fracture simulation, and process techniques, effectively guiding the field testing of temporary plug fracture techniques. However, due to the “complexity” of temporary plugging fracturing technology in creating new fractures and the diversity of factors affecting the initiation and diversion of fractures, the consideration of factors affecting the initiation and diversion of new fractures is not perfect.
The aforementioned studies have given us a better understanding of the experimental procedures and other aspects of TCEF, which have effectively guided the field testing of the technique. However, due to the complexity of creating new fractures and the diversity of factors that influence the initiation and diversion of such fractures in the technique of temporary plug fracturing, a more comprehensive consideration of these factors is required. Therefore, a mathematical model for the distribution of the stress field around the artificial fracture prior to the rupture of the temporary plug was developed. The stress distribution around a reservoir containing both natural and artificial fractures is accurately modeled using finite element software. Therefore, we discuss the mechanical conditions sufficient for the initiation of new fractures and the optimal timing of temporary plug fracturing. The propagation and propagation trajectories of the new fracture are predicted, and the mechanism of initiation and diversion of the new fracture in the temporary stop fracture is revealed.
Temporary plug fracturing is the refracking of wells and formations that have undergone one or more fracturing measures. From a fracture and formation perspective, there are currently one or more mechanisms for temporarily plugging and fracturing a well:
① Reopen the fractures that were originally opened: after fracturing, the water injected into the fracture during the previous fracturing process failed to keep up, resulting in a decrease in the formation pressure, which significantly increased the closing pressure. The fracture was closed, and the fracture failed. During temporary plug fracturing, enhanced water injection into the corresponding formation during fracturing and re-energization will effectively open the fracture that was originally opened.
② Effectively extend the original fracture system, increase the contact surface between the fracture and the oil-bearing layer, expand the oil drainage area, and increase the oil flow channel of the original fracture system: this requires applying a high sand ratio and large sand volume fracturing techniques in the temporary plug fracturing of old wells to operate in the original fracture system and effectively extend the original fracture system.
③ Flush the fracture surface: on the fracture surface that was originally fractured due to being blocked by insoluble substances (residues) of the fracturing fluid or the filter cake formed by the fracturing fluid being too thick or too strong, which affects the seepage of the fracture surface, it should be effectively cleaned, and the blocked substances should be returned to the oil well. Due to the current presence of certain residues in the fracturing fluid used for fracturing, the study of the mechanism and measures for flushing the fracture surface is still at an exploratory stage and requires further in-depth investigation.
④ Refill with proppant: fracking and proppant embedding in hydraulically fractured wells will continue to increase over time, requiring temporary plug fracturing, refilling with high-conductivity proppants, and improved sand addition methods to increase production in temporary plug fracturing wells.
⑤ Press open new fractures: the new fracture generated by temporary plugging fracturing starts and extends in a different direction from the previous artificial fracture, which can open new oil and gas flow channels in the oil and gas reservoir, communicate with the unused oil and gas reservoir of the old fracture in a wider range, and greatly increase production.
According to the theory of elastic mechanics and the rock fracture criterion, the fracture always starts along the direction perpendicular to the minimum horizontal principal stress. Therefore, the distribution of stress fields in temporary plugging fracturing wells determines whether temporary plugging fracturing will expand along old fractures or generate new fractures, as well as the optimal time to generate new fractures, the location and orientation of the initiation of new fractures, the direction and trajectory of the extension of new fractures, and the length of new fractures. Therefore, the distribution of the stress field around the fracture prior to temporary plug fracturing is very important for studying the mechanism of temporary plug fracturing.
A large number of field and indoor experimental studies have shown that the existence of previous artificial fractures in oil and gas wells, changes in pore pressure caused by long-term production activities in oil and gas wells, and changes in temperature fields will lead to changes in the size and direction of the in situ stress field in the reservoir, resulting in stress redirection. After fracturing an oil and gas well, the presence of artificial fractures can alter the magnitude and direction of the ground stress near the borehole, as confirmed by field and laboratory tests. Operations such as production and water injection in oil and gas wells can cause changes in the formation pore pressure, and if such changes are not uniform, then so are changes in the stress field, resulting in a redistribution of stress. The prolonged injection of cold water inevitably leads to a decrease in the temperature inside the reservoir, which also induces a change in the stress field. These induced stresses alter the distribution of the reservoir stress field in wells with hydraulic fracturing fractures and may cause stress reorientation, making it possible for temporary plug fracturing to generate new fractures with different orientations from the initial fracture, achieving the goal of reforming the reservoir and improving oil recovery.
The total stress field in the borehole and in the vicinity of the fracture prior to temporary plug fracturing can be viewed as a superposition of the following four stress fields: 1) the in situ stress field, which is the unperturbed far-field in situ stress field; 2) the stress field induced by the first artificial fracture: the stress field is induced by the variation of the pore pressure; 3) variation of the stress field induced by the temperature field: for a well, it is necessary to calculate the aforementioned three stress fields separately and then add them together to obtain the total stress field; and 4) the stress field induced by the initial artificial break: the direction of fracture resulting from temporary plug fracturing still depends on the stress state, and its geometry is still controlled by the mechanical properties of the strata and the parameters of the construction. Therefore, it is important to investigate the mechanism of temporary plug fracturing by studying the variation of the in situ stress field after the initial fracturing. The magnitude of the initial artificial fracture-induced stress decreases as the distance from the fracture surface increases. The pressure field is induced by the pore pressure change. During the exploitation of oil and gas reservoirs, changes in the pressure of the pore fluid, on the one hand, cause changes in the stress of the rock skeleton, which in turn cause changes in the rock properties. On the other hand, these variations affect the flow and pressure profiles of the pore fluid. As oil and gas production progresses, the distribution of the pore pressure around the fracture becomes very inhomogeneous, which changes the pore pressure gradient around the fracture in the formation, leading to a redistribution of the in situ stress throughout the reservoir. The stress field is induced by the change in the formation temperature. During the exploitation of oil and gas reservoirs, water injection is commonly used to maintain formation energy. The injection of water into the injection well also causes changes in the ground stress, which are mainly reflected in two ways: one is that the injection well enters the reservoir and generates pore elastic stress; conversely, due to the temperature difference between the injected water and the reservoir rock, long-term cold water injection is necessary to lead to a decrease in the temperature in the reservoir, causing rock shrinkage. Thermal elastic tensile stress is generated, which can also lead to changes in the geostress field.
The total stress field in the borehole and the vicinity of the fracture prior to temporary plug fracturing can be viewed as a superposition of the following four stress fields. First, a small deformation is assumed under the assumption of a planar strain state inside the reservoir. This satisfies the superposition principle and results in an in situ stress field representing the unperturbed long-range force exerted on the region. Second, the stress field induced by the first artificial break is considered. In addition, the pressure field induced by the pressure change at the pore is calculated, and finally, the variation of the stress field induced by the temperature field is noted. The aforementioned four stress fields are calculated individually and then added together to obtain the total stress field.
When studying the induced stress field in temporary plugging fracturing wells, for ease of expression, the coordinate system shown in Figure 1 is used: the fracture length direction of the initial artificial fracture is the x-axis, and the direction perpendicular to the initial fracture through the wellbore is the y-axis. Obviously, the x-axis is parallel to the initial maximum horizontal principal stress
If the stress variation values induced by the aforementioned factors are known, it is feasible to calculate the stress distribution in time and space before fracturing of the well plug, which can determine whether new fractures will be generated during the temporary plugging fracturing operation, as well as the direction in which new fractures initiate and extend. In the following, the stress field induced by temperature variations is neglected, and only the stress field induced by hydraulic fracture and formation pore pressure is considered. In addition, the mechanical mechanism by which the temporary plug breaks to produce a new fracture was investigated.
In order to analyze the stresses induced by artificial fractures, it is necessary to first develop mathematical and mechanical models. These models rely on an understanding of the rock medium and the mechanical environment surrounding the fracture. In real reservoirs, the rock surrounding a fracture may undergo plastic deformation under complex stress conditions during fracturing. The presence of heterogeneity and anisotropy in the formation, coupled with natural micro-fractures, voids, and other factors in the reservoir, makes mathematical analysis quite challenging. The following assumptions are made to simplify the analysis of the stress field around artificial fractures: 1) the fractures are vertical; 2) the reservoir is homogeneous and isotropic; 3) the reservoir is in a linear elastic state; and 4) the interaction between the reservoir and proppant is not considered.
A vertical fracture containing a symmetric double wing in an infinite reservoir can be simplified to the physical model shown in Figure 2: a linear fracture in the center of an infinite flat plate (which can be regarded as the limit case of an ellipse with a short half axis), with a length of
Clearly, the horizontal hydraulic fracture-induced in situ stress field, the formation pore pressure-induced stress field, and the stress field plate problem induced by the change of the formation temperature in the physical model described previously belong to the plane strain problem. According to the theory of elasticity, the equilibrium differential equation of the plane strain problem (excluding physical force) is as follows:
The geometric equations for planar problems are as follows:
where
The physical equation for plane strain problems is the stress–strain equation:
where
The boundary conditions of the aforementioned physical model are shown in the Figure 2:
Equations 1–6 are the equilibrium equations, geometric equations, physical equations, and boundary conditions that describe the aforementioned physical model. These six equations constitute a mathematical model that facilitates quantitative analysis of this physical problem.
Long-term production and water injection in an oil well can decrease or increase the formation pore pressure, resulting in a change in the in situ stress state. There is some gradient in the pore pressure around the hydraulic fracture. As oil and gas production progresses, the distribution of the pore pressure around the fracture becomes very inhomogeneous, which changes the pore pressure gradient around the fracture in the formation, resulting in a redistribution of the in situ stress throughout the reservoir.
The production process of oil and gas reservoirs is a dynamic coupling process of multiphase fluid (oil, gas, and water) seepage and deformation of porous media in reservoir rock and soil, which is mainly manifested as follows: 1) with the development of oil and gas fields, production and injection will cause changes in pore pressure; 2) changes in pore pressure lead to changes in rock and soil deformation and effective stress field Changes in situ stress and rock deformation will lead to changes in reservoir physical properties, such as porosity, permeability, rock and soil density, and pore compression coefficient, affecting pore fluid seepage and production. As a result, oil, gas, water seepage, and rock and soil deformation are mutually affected and constrained during the exploitation of oil and gas reservoirs, with strong coupling effects between them. Therefore, when studying the changes in geostress caused by changes in pore pressure during the production of oil and gas reservoirs, it is necessary to consider the flow laws of fluids, including liquids (oil or water) and gases (e.g., natural gas) in porous media and their impact on the deformation or strength of the rock mass itself, as well as the interaction between the stress field and the seepage field within the rock mass.
The following assumptions are made: 1) assume that the thickness of the reservoir does not vary with space, that the height of the fracture is equal to the thickness of the reservoir, and that the rock is in a plane strain state; 2) it is assumed that rock deformation during mining can be linear, nonlinear, elastic, and elastic–plastic small deformations, but no fracturing occurs; 3) the seepage flow in a reservoir is planar, two-dimensional, and isothermal, and the fluid is compressible; 4) the flow of each phase in the matrix obeys Darcy’s law relative to the rock particle, and the flow in the fracturing support fracture obeys Forcheimer’s high-speed non-Darcy flow; and 5) consider the effects of gravity and capillary forces.
(1) The equation of motion is as follows:
(2) The continuity equation is as follows:
(3) The partial equation of seepage flow is as follows:
Equation 9 is multiphase and multicomponent fluid–solid coupling in a fracturing fracture system.
The in situ stress around the borehole is redistributed due to the phenomenon of stress concentration around the borehole. In order to better analyze the stress distribution in boreholes with artificial fractures, the phenomenon of stress concentration around boreholes was first studied. The in situ stress field distribution around the borehole was modeled by a finite element analytical model using Abaqus software.
The geological parameters used in the numerical model are based on the reservoir parameters of tight oil and gas reservoirs in the Ordos Basin, China, as shown in Table 1 and Table 2.
This is sufficient to establish a small reservoir boundary region due to the main studies on the distribution of in situ stress fields in the vicinity of boreholes and the fact that the induced stress due to boreholes generally vanishes within a few times the extent of the borehole. The boundary of a 100 × 100-cm square oil reservoir is centered on an oil well with a hole diameter of 21.59 cm.
The maximum principal stress loaded in the X direction is 60 MPa, that in the Y direction is 55 MPa, and that in the formation pore pressure is 40 MPa. The purpose is to study the phenomenon of stress diversion near boreholes caused by boreholes without considering the effect of changes in borehole pressure during production. Figure 3 shows the Abaqus finite element analytical model for the near-well bore geostress field. A quadrilateral free mesh is used for mesh partitioning, with the element type being pore fluid/stress element. A total of 9,260 elements and 9,490 nodes are partitioned. Figure 3 shows the scheme for the in situ stress field around the bore. Figure 3 shows that a significant stress concentration is formed around the borehole due to the compression of the largest principal stress in the formation, with the X direction being the direction of the largest principal stress.
The condition of the well before temporary plugging and fracturing can be simplified as a straight fracture with a length of 2a penetrating the plate thickness in the center of a plate, which can be regarded as the limit case of an ellipse with a short half-axis tending to 0. According to the theory of elasticity, calculating the induced stress field in the presence of fractures belongs to a plane strain problem. Based on the stress–strain equation and boundary conditions, the integration formula of the Fourier transform, inverse transform, and Bessel function is introduced. The fracture-induced stress is as follows:
where P is the fluid pressure in fractures, MPa, and h is the fracture height, m.
c = h/2,
This software is used to construct finite element analytical models of in situ stresses in artificial fracture wells. A rectangular stratum boundary with a semi-length of 80 m, a width of 1.0 cm, and a borehole diameter of 10.0 cm was used. The maximum and minimum principal stresses in the horizontal direction of the formation were taken to be 40 and 25 MPa, respectively. The cloud pattern of the artificial fracture-induced stress field is shown in Figure 4, which shows that a distinct induced stress field is formed around the artificial fracture, with the maximum principal stress in this region being much higher than in the other regions. The maximum principal stress is in the x-axis direction, with a significant increase in the in situ stress in the y-axis direction, which is much larger than the maximum principal stress value around the borehole in the absence of fracture. The occurrence of this phenomenon provides a basis for the diversion of new fractures in the temporary plug fracture.
Figure 5 shows the maximum principal stress scheme for near-well formation, with a large maximum principal stress value in the y-axis direction. The maximum principal stress in the borehole is generated in the Y direction of the borehole. Figure 5shows a significant stress shift near the bore, with the stress direction generally following the tangential direction of the bore. In the x-axis direction, the stress deviates most from the direction of the initial maximum principal stress. In the y-axis direction, the stress hardly changes direction.
In order to study the effect of in situ stress difference on the size of the stress diversion region near the wellbore, a user-defined field variable Smax-S11 was established, which is the difference between the maximum principal stress and the X direction stress. As the initial maximum principal stress is in the X direction, when the difference between the maximum principal stress in the vicinity of the well and the X direction is zero, the maximum principal stress can be considered to have recovered to the X direction. Figure 6 shows the nephogram of the difference between the maximum principal stress and the stress in the X direction. The difference is large in the X direction of the wellbore, and the stress steering angle is the largest.
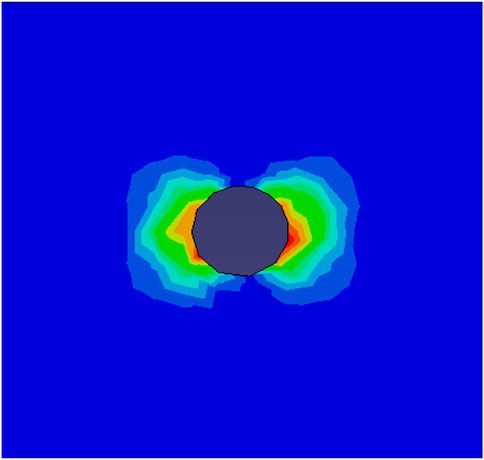
FIGURE 6. Cloud chart of the difference between the maximum principal and the principal stress in the X direction (S.max-S11).
By customizing the field variable Smax-S11 and changing the stress difference, the impact of the stress difference on the size of the stress steering region can be analyzed. Figure 7 shows the relationship curve between the length of the steering area and the stress difference in the x-axis direction. With the increase in the stress difference, the stress turning area shows a significant decrease trend. It can be restored to the original stress field direction within the range of 3–5 times the diameter of the borehole.
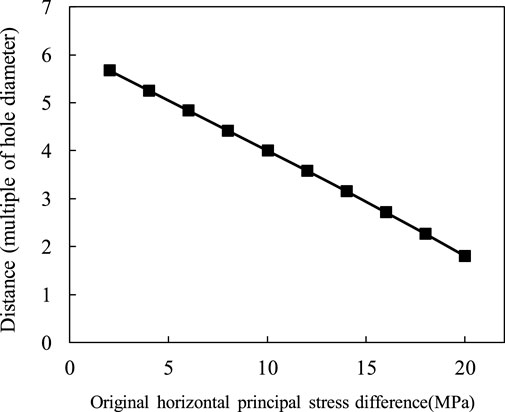
FIGURE 7. Relationship curve between stress steering area length and stress difference in the x-axis direction.
For initial fracturing, the direction of fracture initiation may not necessarily follow the direction of the maximum principal stress in the original formation due to changes in the direction of the in situ stress near the borehole. As the fracture is extended and the direction of the stress field is restored, it gradually transitions to the original maximum principal stress direction. Due to the generally small stress-turning region near the borehole, the process of fracture turning and extending along the direction of the original maximum principal stress will be completed quickly.
A zone of 640 m × 640 m was constructed with a 0.15 m diameter borehole in the center. A symmetric artificial fracture was established in the X direction of the borehole. The fracture has a half-length of 80 m and a width of 1.0 cm. Divide a rectangular area around the fracture for subsequent mesh generation. The maximum principal stress loaded in the X direction is 60, that in the Y direction is 55 MPa, and that in the formation pore pressure is 40 MPa. Because the permeability in the artificial fracture is far greater than the formation permeability, the fluid pressure drop in the artificial fracture is ignored, and the production flow rate of the fluid is loaded on the fracture wall. For the artificial fracture-induced stress field, the impact of pore pressure changes during production will not be considered temporarily.
The induced stress field due to a single artificial fracture is shown in Figure 8, without considering the effect of the pore pressure change on the ground stress during the production process. The induced stress field forms around the fracture, and the stress concentration are pronounced at the fracture tip. The induced stress field due to a single artificial fracture is shown in Figure 9. The induced stress field forms around the fracture, and the stress concentration is evident at the fracture tip.

FIGURE 9. Maximum principal stress vector diagram around fractures. (A) the maximum principal stress vector diagram of the whole model. (B) the maximum principal stress vector diagram near the fracture.
Figure 9A shows the maximum principal stress vector diagram of the whole model, and Figure 9B shows the maximum principal stress vector diagram near the fracture displayed in magnification. Perpendicular to the fracture wall, the principal stress direction changes little and essentially remains the same as the original maximum principal stress direction. At the tip of the fracture, the principal stress changes considerably, and the direction of the maximum principal stress is almost perpendicular to the original stress direction. The direction of the maximum principal stress does not change much in the direction of the vertical fracture wall, but the change in the direction of the maximum principal stress outside the fracture tip is very pronounced. The shift in the ground stress prior to temporary plug fracturing is mainly caused by the production of multiple wells in a local area, and the effect of the artificial fracture-induced stress field on the shift toward the new fracture is limited.
With the progress of production, the formation pore pressure will change, and there is a certain gradient of pore pressure around hydraulic fractures (its graph is shown in Figure 10). Based on the finite element analysis model of artificial fracture, the formation pore pressure was loaded with 40 MPa, and a certain production rate was assigned to the fracture wall to simulate the effect of pore pressure on the stress field in the production process. Figure 10 compares the program of the maximum principal stress distribution around the borehole before and after production. It shows that after a production period, the maximum principal stress value decreases to a certain extent, and the decrease is the largest in the direction of the maximum principal stress.
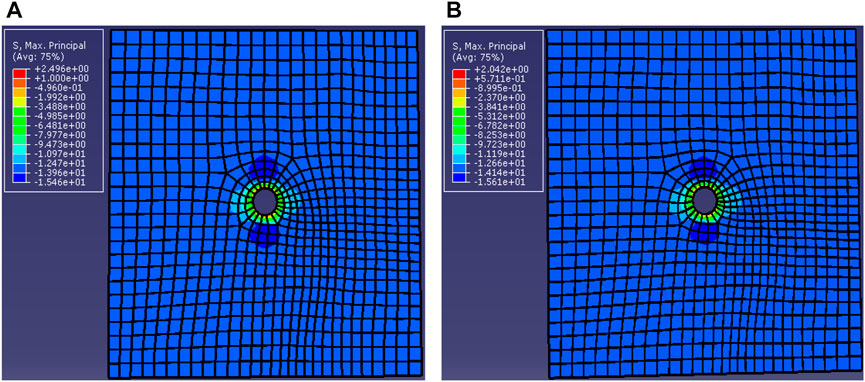
FIGURE 10. Comparison of the maximum principal stress nephogram around wellbore (A) before production and (B) after production.
Considering the effect of a change in the pore pressure due to production on the stress field around the artificial fracture, the pore pressure is applied at the formation boundary, and the production rate is set at the fracture wall. Figure 11 shows that the maximum principal stress around the artificial fracture is distributed along the x-axis before production. After a period of production, the maximum principal stress around the artificial fracture significantly decreases, the direction of the maximum principal stress is not clearly located in the x-axis direction, and there is a tendency for the principal stress to turn. This opens up the possibility of refracturing fracture diversion.
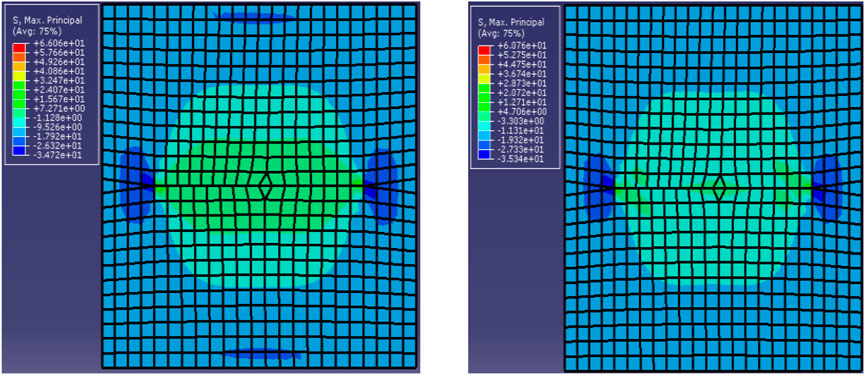
FIGURE 11. Comparison of maximum principal stress nephograms around artificial fractures (A) before production and (B) after production.
Figure 12A shows the maximum principal stress vector diagram of the whole model, and Figure 12B shows the maximum principal stress vector diagram near the fracture displayed in magnification. As shown in Figure 12B, when the pore pressure of the local layer is sufficiently reduced, the maximum principal stress undergoes a sharp turn, which occurs over a large area, making it possible for temporary plug fracturing to generate new turn fractures.
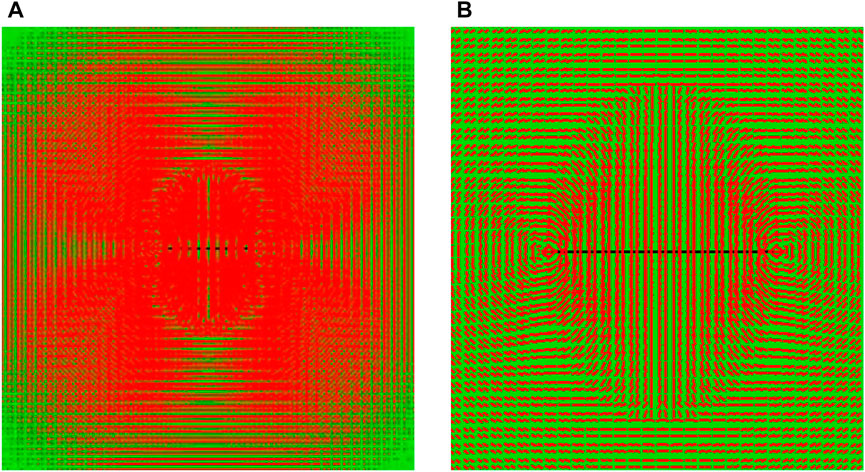
FIGURE 12. Vector diagram of the maximum principal stress field around artificial fractures. (A) the maximum principal stress vector diagram of the whole model. (B) the maximum principal stress vector diagram near the fracture.
Before temporarily plugging a vertically fractured well, the initial artificial fracture can cause induced stress, and the pore pressure decrease caused by the production of oil and gas wells can lead to stress direction changes in and around the wellbore. If a temporary fracture is created perpendicular to the initial fracture at this time, it may be possible to temporarily plug and break the new fractures. However, this effect is valid only within a finite distance from the wellhead. As the new fracture extends during temporary plugging, the stress distribution in the reservoir constantly changes and directly affects the direction of the fracture extension. When the stress steering vanishes due to certain conditions, such as the influence of adjacent wells, the new fracture may continue to extend in the direction parallel to the primary fracture length under heavy pressure. If the stress direction is not reoriented, the new fracture may acquire a longer twist fracture as temporary plugging fracturing extends.
Suppose a vertically fractured well with an initial fracture half-length
In the vicinity of the initial artificial fracture of a vertically fractured well, tensile stresses are induced by factors such as hydraulic fractures and changes in pore pressure in both parallel and vertical directions along the length of the initial hydraulic fracture. However, they are balanced by the compressive stresses induced at locations far away from the fracture. The induced tensile stress perpendicular to the fracture surface is initially larger than the tensile stress in the direction parallel to the fracture length. If the stress difference induced by factors, such as hydraulic fracture and pore pressure change, is greater than the initial horizontal stress difference, the initial maximum horizontal stress direction becomes the current minimum horizontal stress direction.
According to fracture mechanics in rocks, fractures always start and extend perpendicular to the direction of the minimum horizontal principal stress. If a temporary plug fracture is performed at this time, the new fracture will start and extend perpendicular to the direction of the initial fracture length. Thus, the mechanical conditions for the generation of new fractures in a vertically fractured well by temporary plug fracturing are stress reorientation in the pretemporary plug stress profile at and near the borehole.
If the initial maximum horizontal stress direction at the wellbore changes to the current minimum horizontal stress direction, and the initial minimum horizontal stress direction changes to the current maximum horizontal stress direction, then temporary plugging fracturing will generate a new fracture perpendicular to the length direction of the primary fracture. The mechanical conditions for generating new fractures at the wellbore are as follows:
If stress redirection does not occur at the wellbore but occurs at a point
Shear stress may be induced by a variety of factors affecting stress changes in a temporarily capped fracking well, resulting in an increase in the maximum shear stress. If the maximum shear stress causes a shear fracture of the formation, new fractures in temporary plugging fracturing may start and extend along the shear plane, and the direction of the new fracture may not be perpendicular to the direction of the initial fracture length, but there may be a certain angle with it.
In order to quantitatively determine the optimal time for a temporary plug fracture to generate a new fracture, it is necessary to consider the length of the fracture before it changes direction and the pore pressure distribution at that time. Tests showed that the longer the interval between temporary plug fracturing, the longer the time before the fracture turned. Although the pore pressure of oil and gas wells continues to decrease after a few years of production, the length of the fracture before turning increases slowly. The best time to break a temporary plug is when the fracture length can reach a very long length or when the pore pressure in the area where the fracture will extend is still high. When the local layer stress profile and other factors governing the pressure profile, such as porosity, permeability, geostress, and reservoir properties, are known, the optimal time to perform temporary plug fracturing can be determined. When the distribution of the pore pressure cannot be accurately determined, the stress distribution can still be used to better estimate the optimal timing of temporary plug fracturing.
Stress reorientation must occur at a point in the borehole or in the direction of the initial fracture length to generate new fractures during temporary plug fracturing. The optimal time for temporary plug fracturing can initially be determined using the time at which stress reorientation occurs at a point in the borehole or in the direction of the initial fracture length. According to Eqs 12, 13 and the stress calculation model, the optimal timing of temporary plugging fracturing can be accurately calculated. The optimal time t to initiate a new fracture at the borehole is as follows:
The best time
where
During the extension of a new fracture during temporary plugging fracturing, the induced stress gradually changes as it moves away from the wellbore and gradually enters an isotropic point on the regional boundary along the expected direction of fracture extension under heavy pressure (equal horizontal stress point: the maximum horizontal stress equals the minimum horizontal stress). After the temporary plugging fracturing new fracture exceeds the isotropic point (the distance from the wellbore is
Numerous studies and numerical calculations have shown that the stress isotropic point is generally located within half of the initial fracture length. The distance between the stress isotropic point and the borehole depends on parameters such as the magnitude of the initial horizontal stress difference, the initial fracture penetration depth, the production speed, the reservoir permeability, and the difference in the elastic modulus between the production layer and the interlayer.
Dimensionless time
Dimensionless stress deflection tensor
Dimensionless fracture toughness
The dimensionless fracture height ratio
The dimensionless shear modulus ratio
where
According to Eq. 16, the distance
The distance
The distance
As the time in Eqs 22, 23 has been determined, it is convenient to calculate the vertical penetration distance of a new fracture under heavy pressure, that is, the length
A mathematical model of the stress field around the artificial fracture prior to the temporary plug fracture was developed, and the stress distribution around the reservoir containing the artificial fracture was simulated using finite element software. The results indicate that the maximum horizontal principal stress in the induced stress field around artificial fractures is much higher than that in other regions, with its x-axis direction, and the horizontal principal stress in the y-axis direction significantly increases, which is greater than the maximum horizontal principal stress value around the wellbore without fractures.
In situ stress simulations before and after the production of artificial fracture wells show that the magnitude of the induced stress in the initial artificial fracture decreases with increasing distance from the fracture surface. The artificial fracture tip exhibits a concentration of stress, while the area in the direction perpendicular to the fracture wall where the stress direction changes is relatively small and insufficient to generate a new kink fracture. When the production time is sufficiently long and the pore pressure around the fracture is significantly reduced, the maximum stress is shifted perpendicular to the fracture wall and the turning area is large. Repeated fracturing can create new artificial fractures. Changes in the pore pressure are the main effect in the occurrence of directional fractures during repeated fracturing.
We calculated the mechanical conditions for the initiation of new fractures and the optimal timing of temporary plug fracturing and predicted the propagation of new fractures. The longer the interval between the temporary plug and the break, the longer the fracture length before turning. The initial maximum horizontal stress direction at the bore changes to the current minimum horizontal stress direction, and the initial minimum horizontal stress direction changes to the current maximum horizontal stress direction. At this point, repeated fracturing generates new fractures perpendicular to the direction of the initial fracture length.
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
GW and XuX: Conceptualization, funding acquisition, project administration, resources, writing—original draft and software. YH: Data curation, formal analysis, methodology. GW and SL: writing—original draft, and writing—review and editing. XK: Project administration, resources. JZ: Investigation, methodology, software, and visualization. XiX and JW: Conceptualization, funding acquisition, methodology. XK: Investigation, methodology, project administration. All authors have read and agreed to the published version of the manuscript.
This research was funded by “Research on Offshore Large-Scale Fracturing Engineering Technology (KJGG2022-0704), Key Parameter Characterization and Dessert Area Evaluation Technology of Coalbed Methane Geological Engineering (KJGG2022-1001), and Research on Inter-Well Disturbance Integral Fracturing Technology of Coalbed Gas (2021-YXKJ-010).”
The authors are grateful to the reviewers and editors for their careful review of this manuscript.
XX, GW, JZ, AZ, YH, XX, and JW were employed by CNOOC Research Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Lindsay GJ, White DJ, Miller GA, et al. Understanding the applicability and economic viability of refracturing horizontal wells in unconventional plays. In: Proceedings of the SPE hydraulic fracturing technology conference; February 2016; The Woodlands, Texas, USA (2016).
2. Barree RD, Miskimins JL, Svatek KJ. Reservoir and completion considerations for the refracturing of horizontal wells. SPE Prod Operations (2018) 33(01):1–11. doi:10.2118/184837-pa
3. Goehtz F, Evers SC, Prommersberger KJ. Re-fracture of the distal radius with lying palmar plate Handchirurgie, Mikrochirurgie, plastische Chirurgie: Organ der Deutschsprachigen Arbeitsgemeinschaft Fur Handchirurgie: Organ der Deutschsprachigen Arbeitsgemeinschaft Fur Mikrochirurgie der Peripheren Nerven und Gefasse. Organ der V (2020) 52(3):218–9. doi:10.1055/a-1170-8515
4. Nolan EK, Chen HY. A comparison of the cox model to the Fine-Gray model for survival analyses of re-fracture rates [J]. Arch Osteoporos (2020) 15:1–8. doi:10.1007/s11657-020-00748-x
5. Artun E, Kulga B. Selection of candidate wells for re-fracturing in tight gas sand reservoirs using fuzzy inference. Pet Exploration Develop (2020) 47(2):413–20. doi:10.1016/s1876-3804(20)60058-1
6. Singh A, Bierrum WRN, Wormald JCR, Eastwood D. Non-operative versus operative management of open fractures in the paediatric population: A systematic review and meta-analysis of the adverse outcomes. Injury (2020) 51(7):1477–88. doi:10.1016/j.injury.2020.03.055
7. Zhao L, Chen Y, Du J, Liu P, Luo Z, et al. Experimental Study on a new type of self-propping fracturing technology. Energy (2019) 183:249–61. doi:10.1016/j.energy.2019.06.137
8. Xu CY, Zhang HL, Kang YL, Zhang J, Bai Y, Zhang J, et al. Physical plugging of lost circulation fractures at microscopic level. Fuel (2022) 317:123477. doi:10.1016/j.fuel.2022.123477
9. Zhao H, Li W, Wang L, et al. A novel numerical simulation method for predicting the initiation position of refracturing technology using temporary plugging for fluid diversion. FREsENIUs ENVIRONMENTAL BULLETIN (2020).
10. Shammam FO, Alkinani HH, Al-Hameedi AT, et al. Assessment of the production gain from refractured wells in the major shale plays in the United States. In: Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium; June 2021; Santa Fe, New Mexico, USA. (2021).
11. Zhang J, White M, McEwen J, Schroeder S, Cramer DD. Investigating near-wellbore diversion methods for refracturing horizontal wells. SPE Prod Operations (2020) 35(04):836–51. doi:10.2118/199703-pa
12. Zhang G, Chen M. Study on optimal re-fracturing timing in anisotropic formation and its influencing factors [J]. Acta Petrolei Sinica (2008) 29(6):885–93.
13. Jiang X, Cheng M, Zhang G, et al. Effect of directional perforation on the initiation and extension of hydraulic fractures [J]. J Rock Mech Eng (2009) 28(7):1321–6.
14. Zhu H, Deng J, Liu S, et al. Prediction model for fracturing initiation pressure in directional perforation hydraulic fracturing [J]. Acta Petrolei Sinica (2013) 34(3):556–62.
15. Guo TK, Liu BY, Qu ZQ, Gong DG, Lei X. Study on initiation mechanisms of hydraulic fracture guided by vertical multi-radial boreholes. Rock Mech Rock Eng (2017) 50(7):1767–85. doi:10.1007/s00603-017-1205-3
16. Huang L, Liu J, Zhang F, Donstov E, Damjanac B. Exploring the influence of rock inherent heterogeneity and grain size on hydraulic fracturing using discrete element modeling. Int J Sol Struct. (2019) 176:207–20. doi:10.1016/j.ijsolstr.2019.06.018
17. Zhu X, Cheng F, Shi C, Chen K. Mechanical plugging—Solid expandable tubular refracturing technology. J Mech Sci Technol (2020) 34:2357–64. doi:10.1007/s12206-020-0512-x
18. Lei Y, Wang H, Wu X, et al. Analysis of fracture geometry for refractured vertical wells in tight conglomerate reservoir. Pet Reservoir Eval Develop (2021) 11(5):782–92. doi:10.13809/j.cnki.cn32-1825/te.2021.05.017
19. Hou B, Chen M, Cheng W, et al. Fracture mechanism on shale gas reservoir fracturing with variable pump rate. Chin J Geotechnical Eng (2014) 36(11):2149–52.
20. Zhang X, Jiang T, Jia C, Zhang B, Zhou J. Physical simulation of hydraulic fracturing of shale gas reservoir. Pet Drilling Tech (2013) 41(2):70–4.
21. Wu Y, Hou B, Han H, et al. Study on the optimization of helical perforation parameters for horizontal wells in the condition of high horizontal stress difference. Chin J Underground Space (2019) 15(1):226–31.
22. WuKouSun YJS. Matrix acidization in fractured porous media with the continuum fracture model and thermal Darcy-Brinkman-Forchheimer framework. J Pet Sci Eng (2022) 211:110210. doi:10.1016/j.petrol.2022.110210
23. Yue L, Mou J, Qiong J, et al. Experimental study on fracture propagation during in-fracture temporary plugging and diverting fracturing in carbonate rock. Oil Drilling Prod Technol (2022) 44(2):204–10. doi:10.13639/j.odpt.2022.02.011
Keywords: temporarily block the steering, fracture initiation and expansion, geostress reconstruction, fracture diversion, temporary plugging
Citation: Xing X, Wu G, Zhou J, Zhang A, Hou Y, Xie X, Wu J, Kong X and Li S (2023) Finite element study on the initiation of new fractures in temporary plugging fracturing. Front. Phys. 11:1227917. doi: 10.3389/fphy.2023.1227917
Received: 24 May 2023; Accepted: 10 July 2023;
Published: 26 July 2023.
Edited by:
Chong Lin, CCDC Drilling & Production Technology Research Institute, ChinaReviewed by:
Yuanqing Wu, Shenzhen University, ChinaCopyright © 2023 Xing, Wu, Zhou, Zhang, Hou, Xie, Wu, Kong and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiangwei Kong, a29uZ3h3X3lhbmd0emVAMTYzLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.