Thermometric absorption spectroscopy through active locking of microbubble resonators

We implemented a Microbubble Resonator (MBRs) as an opto-thermal transducer to reconstruct the absorption spectrum of a nanoparticle suspension through its temperature increase. The experimental configuration features the MBR as both the vial containing the suspension and the optical transducer, allowing for a sensitive ultra-compact system with a straightforward microfluidic integration. With respect to a previous publication, the active lock of the MBR resonance produced an order-of-magnitude improvement in the system performance and a smooth absorption reconstruction. Additionally, since the detection process is temperature-based, the measurement is intrinsically insensitive towards scattering spectrum, both of the particles and of the host liquid. These features make the MBR system an interesting candidate for the characterisation of extremely small samples in the context of medical diagnosis from whole biological samples, quality controls for food safety or chemical production processes, and, in general, for the measurement of absorption in opaque mediums.

1 Introduction

In the last decades Whispering gallery mode microresonators (WGMRs) have demonstrated to be interesting and reliable platforms for studies in fundamental physics and for the development of technological applications. They can be fabricated in different materials and different geometries (e.g., microspheres, microdisks, microtoroids, microbottle and microbubbles), but they all share the presence of sharp optical resonances with small modal volumes. These two features allowed them to be implemented, for example, for laser stabilization and line narrowing [1, 2], as compact cavities in non-linear optics [3–6], as interrogation platforms for single-molecules properties [7–11], and as optical transducers for the measurement of physical perturbations [12, 13].

A shared aspect between all kinds of WGMRs is their important thermal response, which is based on the thermo-optical coefficient of the resonator material. In practise, two main circumstances can occur. If the optical power injected into the resonator is high, there is a strong interplay between field intensity, resonator temperature and effective refractive index, which produces strong non-linear responses such as thermal locking [14, 15] and optomechanical oscillations [16, 17]. If, instead, injection power is low, this interplay is not triggered, the response is linear and the thermo-optical coefficient can be exploited to use the resonator as an optical thermometer. When using WGMRs for temperature detection, it is important to ensure the best thermal contact between the resonator and the sample. In particular, in the case of bulk WGMRs, the thermal contact is implemented through the external surface of the resonator and this implies some attentions to avoid to compromise the surface through contamination or mechanical damage. For hollow WGMRs, instead, the internal surface can be exploited for thermal contact and the external one for detection, preserving the optical quality of the latter. This approach is particularly useful for liquid samples, where the hollow resonator allows to confine the liquid in a well-defined volume and to integrate the resonator in a microfluidic circuit.

In this context, microbubble resonators (MBRs) made from glass capillaries [18, 19] represent an interesting platform since they combine many of the previously discussed features. These resonators are produced by heating a pressurized silica capillary and therefore forming a spherical bulge by isotropic expansion: this bulge is the resonator itself. We heat the silica capillary using an arc discharge technique [19] featuring four electrodes in a square arrangement, with the capillary at the center of the square. Sequential discharges connecting the square sides allow to produce the MBR, while keeping the capillary pressurized at about 1 bar. In practise, MBRs can be easily filled through their capillary stem, have a sharp optical spectrum (Q ≥ 10⁶ at 1,550 nm, after being filled with water) and the physical contact between the liquid sample and the silica walls guarantees a good thermal exchange, allowing a sensitive temperature read-out [20]. Since these resonators have a very small volume $(<100\text{nL})$, a minute volume of liquid sample is necessary to perform the detection and this makes them particularly promising for the development of ultra-compact (or even on-chip) devices in the context of cytometric-like applications. In addition to thermal sensitivity, MBRs also allow for sensitive mechanical detection due to their thin silica walls $(<4\text{μ\hspace{0.17em}m})$ [21–24], effectively making them a multi-purpose transducer.

In a previous publication [25], we exploited the MBRs thermal sensitivity to implement them as ultra-compact spectrometers. In particular, we probed the absorption spectrum of nanoparticles dispersed in real-scenario liquids, such as milk at room temperature, by measuring the MBRs temperature response. In that system, the MBR is filled with the nanoparticles suspension and a supercontinuum source is filtered to illuminate the sample with selected wavelengths. Upon absorption, the nanoparticles release heat into the suspension and the temperature of the system increases. In turn, this produces a shift of the MBR optical spectrum, which is monitored through a narrow-line CW laser. This thermal shift, ultimately, represents an indirect measurement of the nanoparticles absorption coefficient, since all the transduction processes involved are linear. Since the MBR system reads the temperature variation of the nanoparticle sample and light scattering does not change the temperature of the sample, it is intrinsically insensitive towards the scattering spectrum of the nanoparticles and of the host liquid. This aspect is key feature of the system and is at variance with spectrophotometers. These instruments, in fact, measure the overall light extinction of the sampe and some hypothesis or additional measurements have to be done to separate the absorption contribution from the scattering contribution. Due to this different detection principle, the MBR spectrometer appears particularly promising when the nanoparticles are dispersed in highly scattering and highly opaque samples (e.g., biological ones), since the scattering spectrum could hide the absorption spectrum in a typical spectrophotometer measurement.

Here we propose a revision of the setup and of the experimental procedure discussed in [25], focusing on the active locking of the MBR resonance used for the detection. This new approach improved significantly the system performance, allowing to read-out a 15-fold dilution in nanoparticles concentration, while keeping a signal-to-noise ratio above 10. Active locking, in fact, allowed to reliably read-out fractions of the resonance width (therefore enhancing detection sensitivity) and also to constantly compensates for unwanted fluctuations (therefore producing a more stable read-out). These improvements represent key steps towards the implementation of the MBR spectrometers in real-case applications, such as the characterisation of extremely small samples in the context of medical diagnosis, food safety and molecular/nanoparticles identification.

2 Experimental setup

Figure 1 shows the experimental setup using the active resonance-locking technique to improve the performance of the MBR spectrometer. The system can be conceptually divided into three parts aimed at different functions, with the MBR being the common connecting element.

FIGURE 1

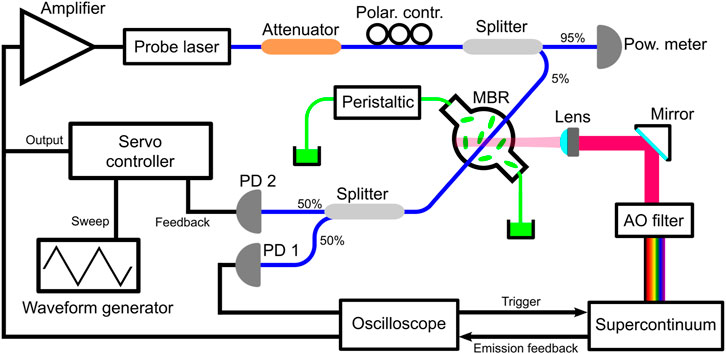
FIGURE 1. Sketch of the experimental setup implementing thermometric spectroscopy using the active lock of the MBR resonance. Abbreviations used: PD, photodiode; AO, acousto-optic. Black lines represent electrical connections, blue lines represent optical fibers and green lines represent the microfluidic circuit.

The first part is a simple microfluidic circuit comprising polymer tubings (Tygon R-3607, Saint-Gobain, La Défense, Courbevoie, France) connected to the MBR and a peristaltic pump (Minipuls 3, Gilson, Middleton, WI, United States) and it was used to fill the MBR with the absorber under study (green lines in Figure 1). Here, we used as benchmark a water suspension of PEGylated gold nanorods (GNRs) synthesised with the seed-mediated approach [26, 27]: this particles, in fact, represent a well-known standard and allow a like-for-like comparison of the results of this experiment with the ones of our previous works [21, 22, 25]. In particular, here we use a 15-fold dilution of GNRs with respect to [25] (i.e. 0.2 mM Au vs. 3 mM Au), showing the potential of the active locking detection.

The second part of the setup is aimed at illuminating the GNRs with a series of selected wavelengths to test their different thermal response. This was achieved by using a supercontinuum source (SuperK COMPACT, NKT Photonics, Birkerød, Denmark; spectral range 400–2,400 nm) in combination with a dedicated acousto-optic modulator (SuperK SELECT, NKT Photonics, Birkerød, Denmark; spectral range 680–1,100 nm), which allowed to crop Lorentzian-like lines with 4 nm bandwidth from the supercontinuum emission. The MBR was illuminated with an inverted microscope configuration using a 45° mirror and an aspherical lens (C110TME-B, Thorlabs, Newton, NJ, United States; focal length 6.24 mm) focused the beam to a 40 µm waist. The repetition rate of the supercontinuum source was set at 20 kHz to simulate the emission of a low-power CW laser (≈20 µW), while the emission of the source was triggered and gated through a square pulse generated by the oscilloscope (MDO4000C, Tektronix, Beaverton, OR, United States). For this experiment the square wave was set to produce an exposition of 1.2 s.

Finally, the third part of the setup is aimed at reading out the temperature shift produced by the GNRs absorption by monitoring the WGM resonances of the MBR. In particular, this was achieved by exciting the MBR resonances with a low-noise CW fiber laser (Koheras ADJUSTICK, NKT Photonics, Birkerød, Denmark; spectral range 1,532–1,533 nm, linewidth 0.1 kHz) through an home-made tapered fiber and reading the MBR transmission through an InGaAs photodiode (New Focus 1623, MKS Newport, Andover, MA, United States). At variance with the previous configurations [21, 22, 25], a second photodiode (PDA400, Thorlabs, Newton, NJ, United States) is added to provide a servo controller (New Focus LB1005, MKS Newport, Andover, MA, United States) with a feedback signal for the active lock of the resonance. While not locking the resonance, the servo controller feeds to the laser source a triangular wave generated by a waveform generator (Keysight 33220A, Agilent Technologies, Santa Clara, CA, United States) to perform wavelength scans up to 8 pm. An electric amplifier (E-501.00, Physik Instrumente GmbH and Co. KG, Karlsruhe, Germany) is necessary for both performing scans or actively locking the resonance, since the wavelength drive coefficient is 0.12 pm/V. An optical attenuator and a 95/5 splitter were introduced to limit the power launched into the tapered fiber (≈10 µW) and avoid unwanted thermal effects in the resonator, while a polarisation controller allowed to optimise the contrast of the WGM resonances.

The MBR used in this experiment was fabricated from a fused silica capillary (Z-FSS-100-165, Postnova Analytics GmbH, Landsberg, Germany) with an arc-discharge technique [19] and had a diameter of 435 μm, corresponding to a 43 nL volume. The area surrounding the MBR was shielded with transparent PMMA walls to minimize perturbations from air currents. As a general note, due to the high number of datafiles recorded during the experiment, the oscilloscope was interfaced to a PC for programmatic control and acquisition.

3 Experiment description and data discussion

After filling the MBR with the water suspension of GNRs, a WGM resonance with a narrow FWHM (full width at half maximum) was searched by scanning the probe laser wavelength, and the resonance contrast was optimised through the polarisation controller. In this phase the servo controller does not operate any locking action and simply feeds the triangular wave to the probe laser. Figure 2A shows in blue the resonance selected for this experiment (λ_probe = 1532.559 nm, Q = 0.97 ⋅ 10⁶, FWHM = 200 MHz, contrast = 42%) and in red the voltage driving the wavelength scan. After this initial phase, the servo controller was used to modify the wavelength scan and actively lock the laser wavelength to a specific point of the resonance fringe. For this experiment the lock point was set at 28% of the resonance fringe, corresponding to a laser detuning of −27 MHz and an MBR transmission of 11 mV (cfr. Figure 2A).

FIGURE 2

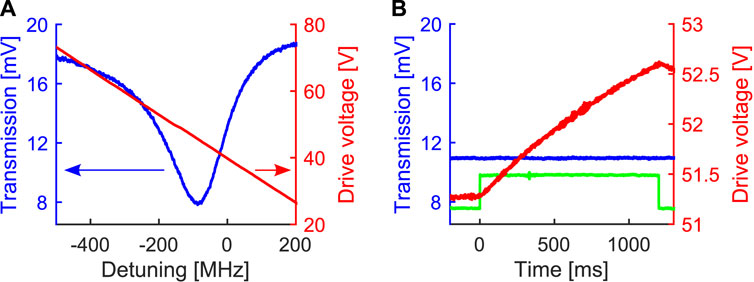
FIGURE 2. (A) WGM resonance used for the thermometric sensing (blue curve, left vertical axis) and voltage ramp driving the laser wavelength (red curve, right vertical axis). (B) Data collected while illuminating the GNRs with 800 nm. As in the previous panel, the blue curve is the MBR transmission (left vertical axis) and the red curve is the voltage driving the laser wavelength (right vertical axis). The illumination window is shown though the emission feedback from the supercontinuum source (green curve, arbitrary units).

After this step, the MBR was illuminated with a series of user-defined wavelengths selected by the acousto-optic filter and for each illumination the oscilloscope acquisition was triggered to record the system response. More in detail, we covered the 680–1,070 nm range with 10 nm steps, for a total of 40 wavelengths, and 4 illuminations were performed for each wavelength to characterise the reproducibility of the measurement. As an example, Figure 2B shows the data collected for a single illumination at 800 nm. In particular, one can observe that, during the illumination (which is marked by the emission feedback from the supercontinuum source, green curve in Figure 2B), the servo controller changes the probe wavelength (red curve in Figure 2B) to compensate the thermal shift of the WGM resonance and keep the MBR transmission at the same level (blue curve in Figure 2B). Since silica has a positive thermo-optic coefficient [28], the heating of the nanoparticles shifts the WGM resonance towards longer wavelengths (i.e., red shift) and therefore the voltage compensation is positive (cfr. Figure 2A).

In practise, the compensation voltage is an indirect measurement of the WGM shift, and the actual optical shift can be obtained by applying the wavelength drive coefficient (0.12 pm/V) and considering that 8 pm correspond to 1 GHz at 1,532 nm. The signals resulting from this conversion are shown in Figure 3A for two groups of 4 different illuminations at 800 nm. In particular, the first group (top part) was recorded while the MBR was filled with the GNRs suspension, while the second group (bottom part) was recorded while the MBR was filled only with plain water. Each acquisition is marked with a different color in Figure 3A and the data demonstrate a very good reproducibility of the measurement for both configurations. As expected, at 800 nm the thermal shift is dominated by the GNRs presence, since water absorption is very low at this wavelength [29]. We highlight that, at variance with our previous experiment [25], here the optical shift is just a small fraction of the resonance FWHM ($\approx 1/10$ for the peak value at 1,200 ms) and that the signal-to-background contrast is still very good (19 vs. 1.4 MHz at 1,200 ms). Measuring such small shifts would be very challenging through the method discussed in [25], which focused on the difference between the resonance positions during a wavelength scan. Here, instead, the task is accomplished reliably by exploiting the compensation signal produced by the servo controller. In the end, the active-locking approach brings a significant improvement in detection sensitivity.

FIGURE 3

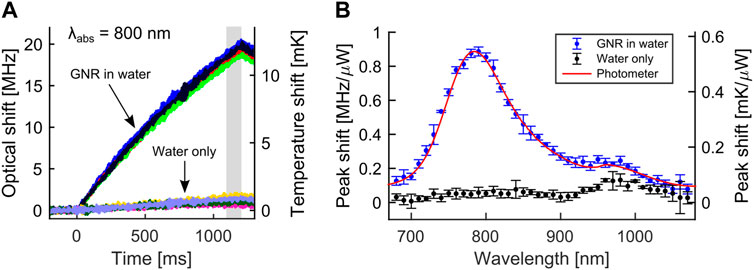
FIGURE 3. (A) Optical shifts (left vertical axis) and associated temperature shifts (right vertical axis) resulting from the absorption at 800 nm, for both an MBR filled with the GNRs suspension and plain water. Each acquisition is marked with a different color. (B) Normalised peak shifts against excitation wavelength for both the GNRs suspension (blue curve) and the plain water (black curve). A rescaled spectrophotometer profile (red curve) is added for comparison.

Before making further considerations on Figure 3A, we comment on our choice in terms of exposure time (1.2 s). From Figure 3A, where the excitation wavelength is 800 nm, one can notice that using a 500 ms exposure time or even a 250 ms exposure time would have produced clearly measurable shifts and also a faster experiment overall. However, a very short exposure time would have decreased the measurement quality for wavelengths outside the GNRs maximum (for example, 900 nm), since the thermal response is lower for these wavelengths. In the end, to preserve a good readability for all the excitation wavelengths used in the experiment and to keep a reasonable overall experiment time (more on this later), we have chosen 1.2 s as the exposure time.

In addition to sensitivity, active locking also improves the stability and the reproducibility of the measurements. In fact, residual fluctuations in the resonance position (e.g., due to air currents or temperature fluctuations in proximity of the MBR) are more impactful for an unlocked system (as in [25]), since no compensation is possible during a wavelength scan. Active locking, instead, compensates these unwanted fluctuations by continuously adjusting the laser wavelength to the selected lock point and therefore does not lose the resonance position. In particular, when the GNRs were not illuminated, the residual instability of the resonance position was up to ±0.4 MHz over a time-scale equal to the illumination time (1.2 s). In practical terms, this error was deduced by acquiring data for a long interval while the supercontinnum laser was disabled (1 min, not shown in Figure 3) and then averaging the optical shifts over the various 1.2 s intervals. We highlight that this error is consistent with the difference between the 4 repetitions in Figure 3A and therefore it represents the reproducibility limit of the measurement.

Using the silica thermo-optic coefficient α_sili = 12 ⋅ 10⁻⁶ K⁻¹ (Δn = αΔT) [28] and a simple resonance expression 2πRn = ℓλ (where R is MBR radius, n is silica refractive index, ℓ is the WGM modal number, and λ the resonance wavelength), it was also possible to convert the optical shift Δν into a thermal shift ΔT using

$\mathrm{\Delta }T=\frac{n\lambda }{{\alpha }_{\text{sili}}c}\mathrm{\Delta }\nu (1)$

where c is the speed of light in vacuum. We add that this conversion is the most straightforward, since it takes into account only the silica thermo-optic coefficient, implicitly assuming the WGM field to be totally confined in the MBR walls. Indeed, the WGM partially enters the MBR core with this evanescent tail, and one can envisage a more refined computational method to take into account also the thermo-optic coefficient of the GNRs suspension. In particular, the thermo-optic coefficient of water is negative and much larger than that of silica (α_wat = −1.103 ⋅ 10⁻⁴ K⁻¹ at room temperature [30]), and this would imply a smaller effective thermo-optic coefficient α_eff to be used in Eq. 1. This, in turn, means that using only the silica thermo-optic coefficient brings to an underestimation of the temperature shift ΔT. However, due to the small field fraction in the evanescent tail (cfr. [31] for a detailed discussion for MBRs), we assume this effect to be secondary and keep Eq. 1 (with only α_sili) for the temperature conversion.

The right vertical axis in Figure 3A is deduced by applying Eq. 1 to the optical shifts: in practice, the right axis is a rescaling of the left axis that performs the conversion shown in Eq. 1. In this way, one can observe the optical shift by looking at the left axis (for example, 10 MHz at 500 ms) and quickly check its temperature conversion by looking at the right axis (6 mK for this example). For the illumination at 800 nm shown in Figure 3A, one notices temperature shifts close to 10 mK. This shift is indeed a small fraction of the room temperature (4 ⋅ 10⁻⁵) and highlights the sensitivity of the MBR transducer. We also add that the previously discussed fluctuation error of ±0.4 MHz translates to a ±0.25 mK fluctuation in temperature units, which appears remarkable considering that no active temperature control is applied to the MBR.

As previously discussed, we collected datasets like the one shown in Figure 3A for other 39 wavelengths, spanning the 680–1,070 nm range with 10 nm steps. To compare the various datasets and characterise the absorption, we applied the following procedure for each dataset. First, we estimated the maximum shift for each trace through a mean value integral in the 1,100–1,200 ms range (grey-shadow area in Figure 3A). We have preferred the integration with respect to just taking the value at 1,200 ms to compensate for electric noise. Second, we computed the average and the standard deviation using the 4 repeated illuminations. Third, we normalized these results to the optical power illuminating the MBR, which was measured while assembling the setup.

The analysis procedure leads to Figure 3B, where we show the results for both the GNRs suspension (blue dots) and the plain water (black dots). We also added as a red curve the rescaled spectrophotometer (V-770, JASCO, Tokyo, Japan) profile of the GNRs suspension to compare the MBRs results with the ones from standard equipment. The normalized MBR shifts follow smoothly the GNRs absorption profile over the entire wavelength range, reproducing correctly both the bell-shaped absorption of the GNRs at 790 nm and the secondary peak at 960 nm, which is mostly associated with water absorption (cfr. water-only data). This reconstruction is a significant improvement with respect to the one obtained in [25], where some MBR datapoints show a misalignment with respect to the spectrophotometer data, resulting in a less smooth profile. We ascribe this improvement to the fluctuation compensation produced by the resonance locking, as discussed while commenting Figure 3. We also highlight that this improved reconstruction is obtained while using a 15-fold dilution in GNRs concentration with respect to [25] (0.2 vs. 3 mM), and that the GNRs concentration used for the MBR measurement and the spectrophotometer measurement is the same.

Figure 3B also allows to estimate the limit-of-detection (LOD) of the system by comparing the responses of the GNRs suspension and the plain water. In particular, focusing on the 800 nm reading, we have 0.87 MHz/μW for the GNRs suspension and 0.053 MHz/μW for the plain water, leading to a signal-to-background ratio equal to 16. By diluting the GNRs suspension by a factor 5.5, one would obtain a 0.158 MHz/μW reading and therefore a signal-to-background ratio equal to 3, which is the typical limit for quantitative detection. Since the GNRs suspension here used is 0.2 mM Au, then the previous argument gives 36 µM Au as the LOD. Assuming a 15 nm diameter and a 60 nm length for the GNRs, as well as a face-centred cubic structure for the gold lattice making up each GNR, the 36 µM Au concentration translates into a 62 pM GNRs concentration (equivalent to 3.7 ⋅ 10¹⁰ nanoparticle/cm³), which is an alternative formulation of the LOD.

Considering the repeated acquisitions and the number of excitation wavelengths, a total of 160 datafiles were collected to produce each spectrum in Figure 3B. Since the illumination time is 1.2 s, one could ideally perform the entire acquisition in 160 ⋅ 1.2 s = 3.2 min. However, the save-time of the acquisition system and the thermal relaxation of the resonance increase this ideal time. For this proof-of-concept experiment, we purposely used a very long wait-time of 10 s between acquisitions (leading to a spectrum time of roughly 27 min) to be certain of the resonance relaxation. Indeed, the optimisation of the system in terms of acquisition speed represents an interesting activity that links to the application of the MBR spectrometer in a real scenario.

Finally, we apply a simple absorption model described in [31] to estimate the absorption coefficient μ of the GNRs suspension in absolute units, rather than arbitrary units as in Figure 3B. In short, the model computes the energy absorbed by the GNRs suspension based on the Lambert-Beer law, the optical power impinging on the MBR (P_opt) and the exposition time (δt). This energy is then used to compute the temperature increase of the suspension, assuming that its heat capacity is the same as water. The temperature increase is computed via water specific heat capacity (c_wat), water density (ρ_wat) and the MBR volume (V_MBR = 4/3 πR³ with R being the MBR radius). Since the modelling neglects heat dissipation in the environment, it has to be applied for very limited exposition times (i.e., δt → 0) and, in the end, the key quantity for the computation is the temperature rate dT/dt at t = 0. This quantity is experimentally retrieved by the dataset shown in Figure 3A (and equivalently for the other excitation wavelengths) by fitting the temperature shift with the function $f(t)=\mathrm{\Delta }{T}_{\infty }\left(1-\exp (-t/\tau )\right)$ and then computing dT/dt(t = 0) as ΔT_∞/τ. In the end, the absorption coefficient is computed as [31].

$\mu =-\frac{\log \left(1-\frac{\mathrm{d}T}{\mathrm{d}t}\frac{c_{\text{wat}}{\rho }_{\text{wat}}{V}_{\text{MBR}}}{P_{\text{opt}}}\right)}{2R\log \left(e\right)}(2)$

where log is the base-10 logarithm and e is the Euler number.

Figure 4 shows the absorption coefficient μ of the GNRs suspension resulting from Eq. 2 and the MBR data (blue dots), as well as its spectrophotometer profile (red curve). Indeed, there is a mismatch in absolute value between the two datasets, but the general trend is well reconstructed, since a rescaling (blue crosses) by a factor of 2 produces overlapping profiles. We ascribe this mismatch to an oversimplification of the model, which does not take into account the details of the experimental configuration, such as the thermal propagation inside of the MBR (and possibly through the capillary) and the spatial distribution of the focused beam. In the end, the model here resumed represents a starting point for more elaborate computational models, such as FEM simulations. We also add that another possible cause for the absorption coefficient mismatch may lay in the temperature conversion previously discussed. Indeed, if the WGM used for the detection is not a fundamental one, it has a greater field fraction in the evanescent tail [31] and Eq. 1 may underestimate the temperature shift, producing, in turn, a lower μ. For completeness, we also repeated the μ computation for the water-only configuration, resulting in the black dots dataset shown in Figure 4. The trend is mostly flat and shows a little bump at around 950 nm, which corresponds to a known increase in water absorption [29]. Even in this case, there is a mismatch between the estimated value (0.18 cm⁻¹) and the tabulated value (0.45 cm⁻¹) [29].

FIGURE 4

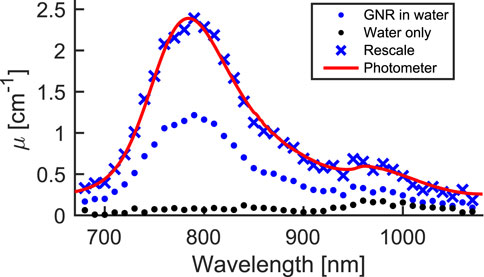
FIGURE 4. Absorption coefficient μ computed through the MBR measurements for the GNRs suspension (blue dots) and for plain water (black dots). The spectrophotometer absorption profile for the GNRs suspension (red curve) is added for comparison. The blue crosses are a rescaling of the experimental data (blue dots) producing a good match with the spectrophotometer data.

4 Conclusion

In this article we have shown that MBRs can be implemented as absorption spectrometers for nanoparticles suspensions, exploiting the high MBR sensitivity towards temperature variations. With respect to a previous publication [25], we have shown that active locking of the MBR resonances produces a significant improvement in both detection and system stability. In particular, our revised approach allowed to reconstruct the absorption profile of a 15-fold diluted suspension, while keeping a signal-to-background ratio above 10. The absorption profile from the MBR measurements has been compared to the one obtained with a standard spectrophotometer, and a smooth match between the two was found. We have also discussed a simple model to estimate the absorption coefficient μ of the nanoparticle suspension in absolute units (cm⁻¹), rather than in arbitrary ones. The model produces the correct order of magnitude for μ, but does not hit the correct value, highlighting the necessity of a more complex and detailed computational model.

Since the MBR system is based on a thermal read-out of the nanoparticle absorption, its spectra are intrinsically scattering-free and this is at variance with standard spectrophotometers. Spectrophotometers, in fact, are based on overall light extinciton from the sample and therefore measure a combination of both absorption and scattering. This means that the MBR spectrometer promises to be more efficient in absoprtion measurements in the case of highly opaque samples (for example, whole biological samples, food, chemical preparations) since it intrinsically remove scattering contributions. The advanced resonance-lock detection scheme here presented further increases this advantage, by enhancing the system sensitivity and allowing a low concentration of absorber to be revealed. In the end, this is a key step for the implementation of the MBR spectrometers in real-case scenarios, such as the characterisation of extremely small samples in the context of medical diagnosis from whole biological samples, and quality controls in food safety and chemical production processes.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

GF build the setup and run the experiment, GF and GV collected the data, SC prepared the nanoparticles suspensions, FR and GN designed the experiment, SP and DF analysed the data, TM contributed to data interpretation, SS directed the experiment. GF wrote the main draft. All authors contributed to the article and approved the submitted version.

Funding

GF, SS, and TM acknowledge fundings from bilateral project CNR-RFBR “Active Resonant Tunable Dielectric Microstructures for Ultrafast Photonics” (RFBR number: 20-52-7819). GF, SS, SC, and FR wish to acknowledge partial support of Tuscany Region under Project Therminator (Bando Ricerca Salute 2018).

Acknowledgments

The authors thank Mr. Franco Cosi from Istituto di Fisica Applicata Nello Carrara for the preparation of the tapered fibers. The authors thank Prof. Marco Marangoni and Prof. Davide Gatti from Politecnico di Milano for sharing equipment.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Liang W, Ilchenko VS, Savchenkov AA, Matsko AB, Seidel D, Maleki L. Whispering-gallery-mode-resonator-based ultranarrow linewidth external-cavity semiconductor laser. Opt Lett (2010) 35:2822–4. doi:10.1364/OL.35.002822

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Siciliani de Cumis M, Borri S, Insero G, Galli I, Savchenkov A, Eliyahu D, et al. Microcavity-stabilized quantum cascade laser. Laser Photon Rev (2016) 10:153–7. doi:10.1002/lpor.201500214

CrossRef Full Text | Google Scholar

3. Lin G, Coillet A, Chembo YK. Nonlinear photonics with high-q whispering-gallery-mode resonators. Adv Opt Photon (2017) 9:828–90. doi:10.1364/AOP.9.000828

CrossRef Full Text | Google Scholar

4. Ilchenko VS, Savchenkov AA, Matsko AB, Maleki L. Nonlinear optics and crystalline whispering gallery mode cavities. Phys Rev Lett (2004) 92:043903. doi:10.1103/PhysRevLett.92.043903

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Venkatakrishnarao D, Mamonov EA, Murzina TV, Chandrasekar R. Advanced organic and polymer whispering-gallery-mode microresonators for enhanced nonlinear optical light. Adv Opt Mater (2018) 6:1800343. doi:10.1002/adom.201800343

CrossRef Full Text | Google Scholar

6. Strekalov DV, Marquardt C, Matsko AB, Schwefel HGL, Leuchs G. Nonlinear and quantum optics with whispering gallery resonators. J Opt (2016) 18:123002. doi:10.1088/2040-8978/18/12/123002

CrossRef Full Text | Google Scholar

7. Hogan LT, Horak EH, Ward JM, Knapper KA, Nic Chormaic S, Goldsmith RH. Toward real-time monitoring and control of single nanoparticle properties with a microbubble resonator spectrometer. ACS Nano (2019) 13:12743–57. doi:10.1021/acsnano.9b04702

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Heylman KD, Knapper KA, Goldsmith RH. Photothermal microscopy of nonluminescent single particles enabled by optical microresonators. J Phys Chem Lett (2014) 5:1917–23. doi:10.1021/jz500781g

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Heylman KD, Thakkar N, Horak EH, Quillin SC, Cherqui C, Knapper KA, et al. Optical microresonators as single-particle absorption spectrometers. Nat Photon (2016) 10:788–95. doi:10.1038/nphoton.2016.217

CrossRef Full Text | Google Scholar

10. Ward JM, Yang Y, Lei F, Yu XC, Xiao YF, Nic Chormaic S. Nanoparticle sensing beyond evanescent field interaction with a quasi-droplet microcavity. Optica (2018) 5:674–7. doi:10.1364/OPTICA.5.000674

CrossRef Full Text | Google Scholar

11. Arnold S, Shopova SI, Holler S. Whispering gallery mode bio-sensor for label-free detection of single molecules: Thermo-optic vs. reactive mechanism. Opt Express (2010) 18:281–7. doi:10.1364/OE.18.000281

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Foreman MR, Swaim JD, Vollmer F. Whispering gallery mode sensors. Adv Opt Photon (2015) 7:168–240. doi:10.1364/AOP.7.000168

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ward JM, Dhasmana N, Nic Chormaic S. Hollow core, whispering gallery resonator sensors. Eur Phys J Spec Top (2014) 223:1917–35. doi:10.1140/epjst/e2014-02236-5

CrossRef Full Text | Google Scholar

14. Jiang X, Yang L. Optothermal dynamics in whispering-gallery microresonators. Light: Sci Appl (2020) 9:24. doi:10.1038/s41377-019-0239-6

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Carmon T, Yang L, Vahala KJ. Dynamical thermal behavior and thermal self-stability of microcavities. Opt Express (2004) 12:4742–50. doi:10.1364/OPEX.12.004742

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kippenberg T, Vahala K. Cavity opto-mechanics. Opt Express (2007) 15:17172–205. doi:10.1364/OE.15.017172

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/RevModPhys.86.1391

CrossRef Full Text | Google Scholar

18. Sumetsky M, Dulashko Y, Windeler RS. Optical microbubble resonator. Opt Lett (2010) 35:898–900. doi:10.1364/OL.35.000898

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Berneschi S, Farnesi D, Cosi F, Nunzi Conti G, Pelli S, Righini GC, et al. High q silica microbubble resonators fabricated by arc discharge. Opt Lett (2011) 36:3521–3. doi:10.1364/OL.36.003521

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liao J, Yang L. Optical whispering-gallery mode barcodes for high-precision and wide-range temperature measurements. Light: Sci Appl (2021) 10:32. doi:10.1038/s41377-021-00472-2

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Frigenti G, Cavigli L, Fernández-Bienes A, Ratto F, Centi S, García-Fernández T, et al. Resonant microbubble as a microfluidic stage for all-optical photoacoustic sensing. Phys Rev Appl (2019) 12:014062. doi:10.1103/PhysRevApplied.12.014062

CrossRef Full Text | Google Scholar

22. Frigenti G, Cavigli L, Fernández-Bienes A, Ratto F, Centi S, García-Fernández T, et al. Microbubble resonators for all-optical photoacoustics of flowing contrast agents. Sensors (2020) 20:1696. doi:10.3390/s20061696

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Kim KH, Luo W, Zhang C, Tian C, Guo LJ, Wang X, et al. Air-coupled ultrasound detection using capillary-based optical ring resonators. Scientific Rep (2017) 7:109. doi:10.1038/s41598-017-00134-7

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Tu X, Wang Y, Guo Z, Chen Z, Huang T, Wu X, et al. Underwater acoustic wave detection based on packaged optical microbubble resonator. J Lightwave Tech (2022) 40:6272–9. doi:10.1109/JLT.2022.3187960

CrossRef Full Text | Google Scholar

25. Frigenti G, Cavigli L, Ratto F, Centi S, Murzina TV, Farnesi D, et al. Microbubble resonators for scattering-free absorption spectroscopy of nanoparticles. Opt Express (2021) 29:31130. doi:10.1364/OE.434868

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Vigderman L, Zubarev ER. High-yield synthesis of gold nanorods with longitudinal SPR peak greater than 1200 nm using hydroquinone as a reducing agent. Chem Mater (2013) 25:1450–7. doi:10.1021/cm303661d

CrossRef Full Text | Google Scholar

27. Ye X, Zheng C, Chen J, Gao Y, Murray CB. Using binary surfactant mixtures to simultaneously improve the dimensional tunability and monodispersity in the seeded growth of gold nanorods. Nano Lett (2013) 13:765–71. doi:10.1021/nl304478h

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Toyoda T, Yabe M. The temperature dependence of the refractive indices of fused silica and crystal quartz. J Phys D: Appl Phys (1983) 16:L97–L100. doi:10.1088/0022-3727/16/5/002

CrossRef Full Text | Google Scholar

29. Curcio JA, Petty CC. The near infrared absorption spectrum of liquid water. J Opt Soc America (1951) 41:302. doi:10.1364/JOSA.41.000302

CrossRef Full Text | Google Scholar

30. Kim YH, Park SJ, Jeon SW, Ju S, Park CS, Han WT, et al. Thermo-optic coefficient measurement of liquids based on simultaneous temperature and refractive index sensing capability of a two-mode fiber interferometric probe. Opt Express (2012) 20:23744–54. doi:10.1364/OE.20.023744

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Frigenti G. Microbubble resonators for sensing and light generation applications. Ph.D. thesis. University of Florence (2021).

Google Scholar