Photonic quantum chromodynamics

Twisted photons with finite orbital angular momentum have a distinct mode profile with topological charge at the center of the mode while propagating in a certain direction. Each mode with different topological charges of m is orthogonal, in the sense that the overlap integral vanishes among modes with different values of m. Here, we theoretically consider a superposition state among three different modes with left and right vortices and a Gaussian mode without a vortex. These three states are considered to be assigned to different quantum states; thus, we employed the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra and the associated SU(3) Lie group to classify the photonic states. We calculated expectation values of eight generators of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, which should be observable, since the generators are Hermite matrices. We proposed to call these parameters Gell-Mann parameters, named after the theoretical physicist Murray Gell-Mann, who established quantum chromodynamics (QCD) for quarks. The Gell-Mann parameters are represented on the eight-dimensional hypersphere with its radius fixed due to the conservation law of the Casimir operator. Thus, we discussed a possibility of exploring photonic QCD in experiments and classified SU(3) states to embed the parameters in SO(6) and SO(5).

1 Introduction

The Lie algebra and Lie group [1–6] were developed mathematically much earlier than the discoveries of quantum mechanics [5, 7–10]. The theory formulates general principles on how to classify various matrices with complex numbers $(\mathbb{C})$ and provides deep insights into the topological structure underlying matrix calculations. The theory covers quite wide areas and thus applicable to many fields in quantum physics, including various two-level systems, described by the special unitary group of two dimensions, SU(2), to understand polarization [8, 9, 11–27]. Historically, however, the powerful mathematical features are not widely recognized for SU(2) states since it is not so much complicated to deal with, even if we do not employ the knowledge of Lie algebra. The situation completely changed once Murray Gell-Mann identified the underlying symmetries for composite elementary particles of baryons and mesons, establishing the quantum chromodynamics (QCD) [4, 5, 10, 28–31]. The Lie algebra is now an indispensable tool in physics on elementary particles. Here, we propose to introduce the framework of the Lie algebra and Lie group to photonics, especially for exploring the photonic analog of QCD by utilizing photonic orbital angular momentum (Figures 1A–D).

FIGURE 1

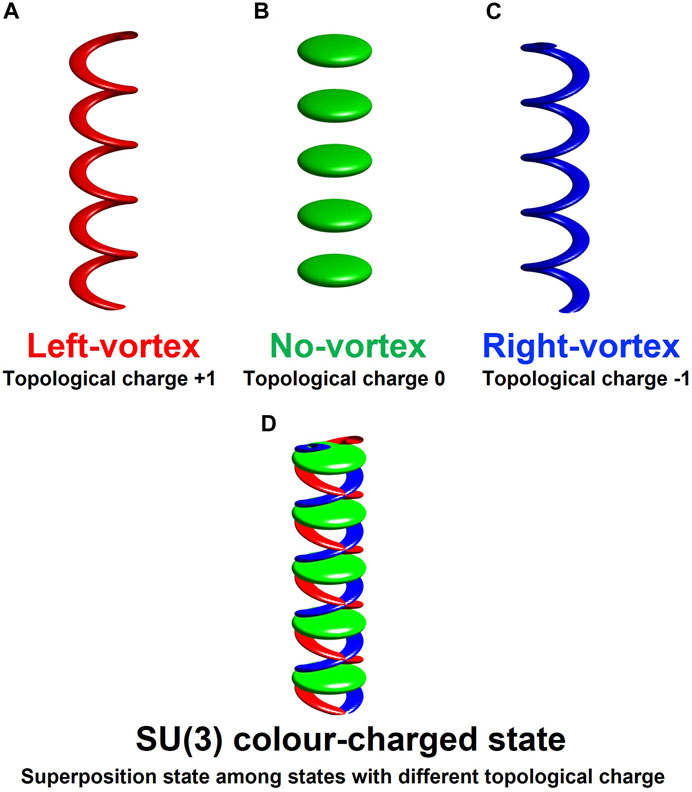
FIGURE 1. Concept of photonic QCD. Trajectories of a constant phase for photons with (A) left vortex, (B) no vortex, and (C) right vortex are schematically shown. These three states have different topological charges, characterized by orbital angular momentum, and thus, they are orthogonal to each other. We assign three different colors for different charges, red, green, and blue, for these states, as SU(3) states. We consider (D) an arbitrary superposition state among states with different topological charges for variable amplitudes and phases.

Photons are elementary particles of light [32, 33], which have both spin [11, 13, 14] angular momentum and orbital angular momentum [23, 34–51] as internal degrees of freedom. The nature of spin is known as polarization [11, 13, 14, 52], which is widely used in sunglasses, liquid-crystal displays, and digital coherent communications [53–56], while orbital angular momentum is used in optical tweezers, laser-patterning, and quantum optics [57–65]. Previously, spin angular momentum and orbital angular momentum of photons were considered to be impossible for splitting into two independent degrees of freedom [66] in a free space [41, 42, 67, 68]. However, it was recently reported that these degrees of freedom could be successfully separated in a proper gauge invariant way by plane wave expansions [69]. We also confirmed that both spin angular momentum and orbital angular momentum are well-defined quantum observables for photons in a waveguide and a free space as far as the propagation mode is sufficiently confined in the core [26]. Therefore, we can measure quantum mechanical averages of the angular momentum, which could be macroscopic values for coherent photons.

2 Summary of the Lie algebra

First, we summarize theoretically minimum knowledge on fundamental properties of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra in order to make our discussions self-contained and clarify our notations. This study would help photonic researchers, who are not familiar with the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, understand the idea to treat three orthogonal quantum states in an equal fashion. It is far from a comprehensive summary, such that interested readers should refer to excellent textbooks [1–5, 7]. Those who are familiar with the $\mathfrak{s}\mathfrak{u}(3)$ algebra may skip this section.

The Lie algebra and Lie group were mathematically developed as early as the 1870s, without specific applications in physics [1–4, 6]. The first serious applications in physics was found in elementary physics, leading to the discoveries of quarks [5]. Obviously, the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra and more general representation theories are robust, and they will be applicable to various cases. On the other hand, here, we focus on applications in photonics, and we use this example to review fundamental characteristics of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra. Thus, we lose the generality in our construction of the logic, but it is easier to understand the concept, and applications in higher dimensions will be straightforward.

2.1 Generators of the $\mathfrak{s}\mathfrak{u}(3)$ algebra

We consider three orthogonal quantum states, namely, left- and right-twisted states and the no-vortex state, which are described in the Hilbert space with three complex numbers, ${\mathbb{C}}^3$. We allow arbitrary mixing of these three states, realized by the superposition principle, and the wavefunction could be considered to be normalized to 1 or to the fixed number of photons, N, such that the radius of the complex sphere is fixed. Consequently, the number of freedom is 2 × 3–1 = 5, and the Hilbert space is equivalent to the sphere of five dimensions, S⁵. In order to describe arbitrary rotational operations of the wavefunction in the Hilbert space, we need complex matrices of 3 × 3 for the SU(3) Lie group, which is realized by the exponential mapping form of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra. The SU(3) forms a group, whose determinant must be unity, which corresponds to the traceless condition for the Lie algebra. Therefore, we need 3 × 3–1 = 8 bases, defined by Gell-Mann [4, 5, 10, 28–31] as

${\widehat{\lambda }}_1=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(1)$

${\widehat{\lambda }}_2=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -i\hfill & \hfill 0\hfill \\ \hfill i\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(2)$

${\widehat{\lambda }}_3=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(3)$

${\widehat{\lambda }}_4=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(4)$

${\widehat{\lambda }}_5=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -i\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill i\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(5)$

${\widehat{\lambda }}_6=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right),(6)$

${\widehat{\lambda }}_7=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -i\hfill \\ \hfill 0\hfill & \hfill i\hfill & \hfill 0\hfill \end{array}\right),(7)$

${\widehat{\lambda }}_8=\frac{1}{\sqrt{3}}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -2\hfill \end{array}\right),(8)$

which are all Hermite matrices, ${\widehat{\lambda }}_i^{†}={\widehat{\lambda }}_i$ (i = 1, …, 8), implying that their expectation values must be real and observable. We can also use the bases, ${\widehat{e}}_i={\widehat{\lambda }}_i/2$, reflecting the underlying $\mathfrak{s}\mathfrak{u}(2)$ symmetry between two orthogonal states. The bases satisfy the normalization relationship for the trace, $\mathrm{Tr}\left({\widehat{\lambda }}_i\cdot {\widehat{\lambda }}_j\right)=2{\delta }_{ij},$ where δ_ij is the Kronecker delta function.

2.2 Commutation relationship

The commutation relationship is obtained by the straightforward calculation of basis matrices, which is derived as:

$\left[{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right]=2i{\displaystyle \sum _k}{C}_{\mathit{ijk}}{\widehat{\lambda }}_k,(9)$

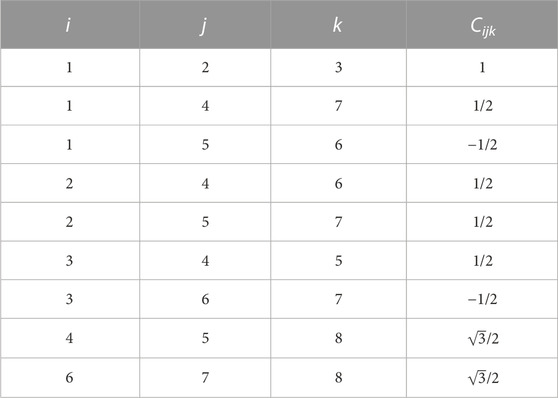
where the structure constants, C_ijk, are listed in Table 1. C_ijk is an asymmetric tensor, such that odd permutation of indices changes its sign. Most commutation relationships involve only one term in the summation on the right-hand side of the equation, similar to the $\mathfrak{s}\mathfrak{u}(2)$ commutation relationship for spin. On the other hand, we must account for two terms involved in equations

$\left[{\widehat{\lambda }}_4,{\widehat{\lambda }}_5\right]=2i\left(\frac{1}{2}{\widehat{\lambda }}_3+\frac{\sqrt{3}}{2}{\widehat{\lambda }}_8\right),(10)$

$\left[{\widehat{\lambda }}_6,{\widehat{\lambda }}_7\right]=2i\left(-\frac{1}{2}{\widehat{\lambda }}_3+\frac{\sqrt{3}}{2}{\widehat{\lambda }}_8\right).(11)$

TABLE 1

TABLE 1. Structure constant of the commutation relationship, $\left[{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right]=2i{\sum }_k{C}_{\mathit{ijk}}{\widehat{\lambda }}_k$, in the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

We also confirm that there are two mutually commutable operators,

$\left[{\widehat{\lambda }}_1,{\widehat{\lambda }}_8\right]=\left[{\widehat{\lambda }}_2,{\widehat{\lambda }}_8\right]=\left[{\widehat{\lambda }}_3,{\widehat{\lambda }}_8\right]=0(12)$

while we see

$\left[{\widehat{\lambda }}_1,{\widehat{\lambda }}_2\right]\ne 0,\left[{\widehat{\lambda }}_1,{\widehat{\lambda }}_3\right]\ne 0,\left[{\widehat{\lambda }}_2,{\widehat{\lambda }}_3\right]\ne 0.(13)$

Therefore, the rank-2 character of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra is confirmed. It is also evident that ${\widehat{\lambda }}_3$ and ${\widehat{\lambda }}_8$ are already diagonalized in our representation for the basis.

2.3 Basis operators for the $\mathfrak{s}\mathfrak{u}(2)$ algebra within the $\mathfrak{s}\mathfrak{u}(3)$ algebra

We consider three orthogonal states for the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, and we select two states among three available states. There are three ways to choose two states, and each of the pairs of states will form the $\mathfrak{s}\mathfrak{u}(2)$ Lie algebra.

For example, if we choose the first and second states, corresponding to the left- and right-twisted states, respectively, we use bases

${\widehat{e}}_1^{\left(t\right)}=\frac{1}{2}{\widehat{\lambda }}_1,(14)$

${\widehat{e}}_2^{\left(t\right)}=\frac{1}{2}{\widehat{\lambda }}_2,(15)$

${\widehat{e}}_3^{\left(t\right)}=\frac{1}{2}{\widehat{\lambda }}_3,(16)$

for describing the SU(2) states since they are equivalent to Pauli matrices,

${\widehat{\sigma }}_1=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right),(17)$

${\widehat{\sigma }}_2=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -i\hfill \\ \hfill i\hfill & \hfill 0\hfill \end{array}\right),(18)$

${\widehat{\sigma }}_3=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right),(19)$

if we neglect the third quantum state for the no-vortex state. These operators, ${\widehat{e}}_i^{(t)}$, were originally used for describing isospin for quarks [5]. For our applications, they will be useful to describe the rotation between the left- and right-twisted states. The rotation corresponds to mixing the left- and right-twisted states, which are described in the Poincaré sphere for vortices.

The introduction of the coupling between the left- and right-twisted states corresponds to allowing the direct SU(2) coupling between states with ℓ = −1 and ℓ = +1, as shown in Figure 2B. In standard quantum mechanics for orbital angular momentum [5, 8, 31], this coupling is not considered since it changes to the topological charge of ± 2, such that the ladder operations of SU(2) cannot directly transfer states to each other. On the other hand, we allow this coupling for photons simply by mixing states with certain amplitudes and phases [23, 25, 35, 47, 48, 50, 51, 70], which allows us to extend photonic states to obtain an SU(3) symmetry.

FIGURE 2

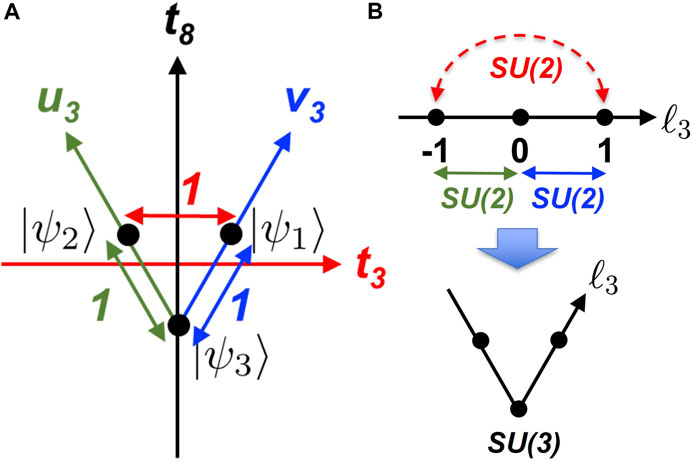
FIGURE 2. SU(3) states with photonic orbital angular momentum. (A) Fundamental multiplet of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra. Fundamental basis states of |ψ₁⟩, |ψ₂⟩, and |ψ₃⟩ are shown on the (t₃, t₈) plane, characterized by their quantum numbers. t₃ is known as isospin for quarks. The states are shown by points, given by the eigenvalues, which are separated by the same distance and form an equilateral triangle as their topology, implying the states are treated in an equal footing in the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra. We can use u₃, v₃, or hypercharge of y = 2 (u₃ + v₃)/3 instead of t₈, but only two vectors are required to span the t₃–t₈ plane due to the rank-2 character of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra. (B) Bending of the quantization axis of SU(2) to form SU(3) states. The quantum number (ℓ₃) of orbital angular momentum along the quantization axis is usually characterized by SU(2) states, as shown in the upper diagram. By allowing SU(2) rotation between left- and right-twisted states, we effectively bend the ℓ₃ to realize the superposition state. By combining superposition states with the no-vortex state, we mix the three orthogonal states to realize SU(3) states.

Another pair of states is made of the right-twisted state and the no-vortex state, whose bases are

${\widehat{e}}_1^{\left(u\right)}=\frac{1}{2}{\widehat{\lambda }}_6,(20)$

${\widehat{e}}_2^{\left(u\right)}=\frac{1}{2}{\widehat{\lambda }}_7,(21)$

${\widehat{e}}_3^{\left(u\right)}=\frac{1}{2}\left(-\frac{1}{2}{\widehat{\lambda }}_3+\frac{\sqrt{3}}{2}{\widehat{\lambda }}_8\right),(22)$

$=\frac{1}{2}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right).(23)$

Here, it is noteworthy that we can define a new vector operator of ${\widehat{e}}_3^{(u)}$, for example, from ${\widehat{\lambda }}_3$ and ${\widehat{\lambda }}_8$, since they are basis vector operators in the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, which forms a vector space. We cannot simply add components in the SU(3) Lie group since the SU(3) Lie group is not a vector space. We observe that ${\widehat{e}}_3^{(u)}$ is normalized to be similar to ${\widehat{e}}_3^{(t)}$, such that it is useful to consider SU(2) rotations by ${\widehat{e}}_1^{(u)}$, ${\widehat{e}}_2^{(u)}$, and ${\widehat{e}}_3^{(u)}$.

Similarly, we consider the pair of states consisting of left-vortex state and the no-vortex state, whose bases are

${\widehat{e}}_1^{\left(v\right)}=\frac{1}{2}{\widehat{\lambda }}_4,(24)$

${\widehat{e}}_2^{\left(v\right)}=\frac{1}{2}{\widehat{\lambda }}_5,(25)$

${\widehat{e}}_3^{\left(v\right)}=\frac{1}{2}\left(\frac{1}{2}{\widehat{\lambda }}_3+\frac{\sqrt{3}}{2}{\widehat{\lambda }}_8\right),(26)$

$=\frac{1}{2}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right).(27)$

These $\mathfrak{s}\mathfrak{u}(2)$ commutation relationships are summarized as

$\left[{\widehat{e}}_1^{\left(x\right)},{\widehat{e}}_2^{\left(x\right)}\right]=i{\widehat{e}}_3^{\left(x\right)},(28)$

where x = t, u, or v. We used lower-case letters (x = t, u, or v) for operators describing a single quanta such as a quark or a photon, and we used upper-case letters for coherent states of photons (X = T, U, or V) under Bose–Einstein condensation, where a macroscopic number, N, of photons are occupying the same state, as discussed further in this paper.

The $\mathfrak{s}\mathfrak{u}(3)$ algebra does not contain a non-trivial invariant group. For example, we see that

$\left[{\widehat{e}}_1^{\left(t\right)},{\widehat{e}}_4\right]=-\frac{1}{4}\left[{\widehat{\lambda }}_1,{\widehat{\lambda }}_4\right]=-\frac{1}{4}i{\widehat{\lambda }}_7=-\frac{1}{2}{\widehat{e}}_7,(29)$

such that the internal SU(2) groups are connected by commutation relationships, and the $\mathfrak{s}\mathfrak{u}(2)$ Lie algebra is not closed.

2.4 Ladder operators

We utilize the Cartan–Dynkin formulation [5] for describing the SU(3) states. In the formalism, we consider to fix the quantization axis, rather than isotropic to all directions in the $\mathfrak{s}\mathfrak{u}(2)$ Lie algebra, and consider ladder operators for increasing and decreasing the quantum number along the quantization axis [5, 9]. More specifically, we define

${\widehat{t}}_{\pm }=\frac{1}{2}\left({\widehat{\lambda }}_1\pm i{\widehat{\lambda }}_2\right),(30)$

${\widehat{t}}_3=\frac{1}{2}{\widehat{\lambda }}_3,(31)$

where ${\widehat{t}}_3$ stands for the operator of the z component of the rotationally symmetric $\mathfrak{s}\mathfrak{u}(2)$ operator $\widehat{\mathbf{t}}=({\widehat{t}}_1,{\widehat{t}}_2,{\widehat{t}}_3)$ and ${\widehat{t}}_{+}$ and ${\widehat{t}}_{-}$ represent the rising and the lowering operators, respectively, to increase and decrease the quantum number for ${\widehat{t}}_3$. We use ${\widehat{t}}_3$ and ${\widehat{t}}_{\pm }$ instead of ${\widehat{e}}_i^{(t)}$ (i = 1, 2, 3), and their commutation relationships become

$\left[{\widehat{t}}_3,{\widehat{t}}_{\pm }\right]=\pm {\widehat{t}}_{\pm },(32)$

$\left[{\widehat{t}}_{+},{\widehat{t}}_{-}\right]=2{\widehat{t}}_3.(33)$

For applications in isospin, ${\widehat{t}}_3$ provides the fixed isospin value (t₃) for each elementary particle, such as a proton (t₃ = 1/2) and a neutron (t₃ = −1/2), a deuterium (D, t₃ = 0), and a tritium (T, t₃ = 1/2). In elementary particle physics, a superposition state between a proton and a neutron, for example, is not realized due to the superselection rule [5] since the superposition state between different charged states is prohibited. On the other hand, for applications in vortices, we can safely consider the superposition state between the left- and right-twisted states [35, 63], such that we can consider arbitrary mixing of left- and right-twisted states with an arbitrary phase between them. The ladder operators ${\widehat{t}}_{\pm }$ correspond to changing the topological charge at the center of the vortices for changing its orbital angular momentum from the left to the right circulation or vice versa.

Similarly, we consider the rising and lowering ladder operators, ${\widehat{u}}_{+}$ and ${\widehat{u}}_{-}$, respectively, for the superposition state between the right-twisted and no-vortex states, and the z component of the rotationally symmetric $\mathfrak{s}\mathfrak{u}(2)$ operator $\widehat{\mathbf{u}}=({\widehat{u}}_1,{\widehat{u}}_2,{\widehat{u}}_3)$:

${\widehat{u}}_{\pm }=\frac{1}{2}\left({\widehat{\lambda }}_6\pm i{\widehat{\lambda }}_7\right),(34)$

${\widehat{u}}_3=\frac{1}{4}\left(-{\widehat{\lambda }}_3+\sqrt{3}{\widehat{\lambda }}_8\right),(35)$

whose commutation relationships become

$\left[{\widehat{u}}_3,{\widehat{u}}_{\pm }\right]=\pm {\widehat{u}}_{\pm },(36)$

$\left[{\widehat{u}}_{+},{\widehat{u}}_{-}\right]=2{\widehat{u}}_3.(37)$

For the mixing of the left-twisted and no-vortex states, the corresponding ladder operators, ${\widehat{v}}_{+}$ and ${\widehat{v}}_{-}$, and the z component of the rotationally symmetric $\mathfrak{s}\mathfrak{u}(2)$ operator $\widehat{\mathbf{v}}=({\widehat{v}}_1,{\widehat{v}}_2,{\widehat{v}}_3)$ become

${\widehat{v}}_{\pm }=\frac{1}{2}\left({\widehat{\lambda }}_4\pm i{\widehat{\lambda }}_5\right),(38)$

${\widehat{v}}_3=\frac{1}{4}\left({\widehat{\lambda }}_3+\sqrt{3}{\widehat{\lambda }}_8\right),(39)$

whose commutation relationships become

$\left[{\widehat{v}}_3,{\widehat{v}}_{\pm }\right]=\pm {\widehat{v}}_{\pm },(40)$

$\left[{\widehat{v}}_{+},{\widehat{v}}_{-}\right]=2{\widehat{v}}_3.(41)$

Here, we defined nine operators for ladders and the quantization components of the three sets of $\mathfrak{s}\mathfrak{u}(2)$ operators $(\widehat{\mathbf{t}},\widehat{\mathbf{u}},\widehat{\mathbf{v}})$, while only eight bases are required for the $\mathfrak{s}\mathfrak{u}(3)$ algebra due to the traceless requirement. Consequently, we obtained one identity,

${\widehat{v}}_3={\widehat{u}}_3+{\widehat{t}}_3,(42)$

which must be met for all states. This means that only two quantum numbers are independently chosen, regardless of apparent three sets of SU(2) states, which is, in fact, consistent with the rank-2 nature of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

2.5 Hypercharge and topological charge

As discussed previously, we select two quantum operators from three operators, ${\widehat{t}}_3$, ${\widehat{u}}_3$, and ${\widehat{v}}_3$, for describing the SU(3) quantum states. If we choose ${\widehat{t}}_3$, we can choose ${\widehat{u}}_3$ or ${\widehat{v}}_3$. Alternatively, we can consider the superposition state, made of both ${\widehat{u}}_3$ and${\widehat{v}}_3$, whose z component becomes

${\widehat{\lambda }}_8=\frac{2}{\sqrt{3}}\left({\widehat{u}}_3+{\widehat{v}}_3\right).(43)$

Equivalently, we define the hypercharge operator [5] as

$\widehat{y}=\frac{1}{\sqrt{3}}{\widehat{\lambda }}_8,(44)$

$=\frac{2}{3}\left({\widehat{u}}_3+{\widehat{v}}_3\right)=\frac{4}{3}{\widehat{u}}_3+\frac{2}{3}{\widehat{t}}_3=\frac{4}{3}{\widehat{v}}_3-\frac{2}{3}{\widehat{t}}_3,(45)$

which was indispensable to understand quarks, their 2-body (3-body) compounds of meson, and the 3-body compounds of baryons. They are commutative with the other three operators,

$\left[\widehat{y},{\widehat{t}}_3\right]=\left[\widehat{y},{\widehat{u}}_3\right]=\left[\widehat{y},{\widehat{v}}_3\right]=0,(46)$

meaning that hypercharge could be the simultaneous quantum number with the other parameter. Therefore, we expect that the eigenstate is labeled by the quantum numbers, t₃, u₃, and v₃ with y = (u₃ + v₃)/3, to satisfy

$\widehat{y}\left|t_3,u_3,v_3\right.⟩=y\left|t_3,u_3,v_3\right.⟩=y\left|t_3,y\right.⟩.(47)$

We also confirm the identity

$\left[\widehat{y},{\widehat{t}}_{\pm }\right]=\frac{2}{3}\left[{\widehat{u}}_3,{\widehat{t}}_{\pm }\right]+\frac{2}{3}\left[{\widehat{v}}_3,{\widehat{t}}_{\pm }\right]=0,(48)$

which ensures that

$\widehat{y}\left({\widehat{t}}_{\pm }\left|t_3,y\right.⟩\right)=y\left({\widehat{t}}_{\pm }\left|t_3,y\right.⟩\right),(49)$

meaning that the application of ladder operations by ${\widehat{t}}_{\pm }$ preserves the hypercharge, y.

On the other hand, we find that

$\left[\widehat{y},{\widehat{u}}_{\pm }\right]=\frac{2}{3}\left[{\widehat{u}}_3+{\widehat{v}}_3,{\widehat{u}}_{\pm }\right]=\pm {\widehat{u}}_{\pm },(50)$

which leads to

$\widehat{y}\left({\widehat{u}}_{\pm }\left|t_3,y\right.⟩\right)=\left(y\pm 1\right)\left({\widehat{u}}_{\pm }\left|t_3,y\right.⟩\right),(51)$

which means ${\widehat{u}}_{+}$ increments y and ${\widehat{u}}_{-}$ decrements y, respectively. We also confirm the same rule for ${\widehat{v}}_{\pm }$ as

$\left[\widehat{y},{\widehat{v}}_{\pm }\right]=\frac{2}{3}\left[{\widehat{u}}_3+{\widehat{v}}_3,{\widehat{v}}_{\pm }\right]=\pm {\widehat{v}}_{\pm },(52)$

which corresponds to

$\widehat{y}\left({\widehat{v}}_{\pm }\left|t_3,y\right.⟩\right)=\left(y\pm 1\right)\left({\widehat{v}}_{\pm }\left|t_3,y\right.⟩\right).(53)$

Finally, we obtain the fundamental multiplets (Figures 2A, B), given by three states,

$|{\psi }_1\rangle =\left|t_3=\frac{1}{2},t_8=\frac{1}{3}\frac{\sqrt{3}}{2}\right.⟩=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),(54)$

$|{\psi }_2\rangle =\left|t_3=-\frac{1}{2},t_8=\frac{1}{3}\frac{\sqrt{3}}{2}\right.⟩=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),(55)$

$|{\psi }_3\rangle =\left|t_3=0,t_8=-\frac{2}{3}\frac{\sqrt{3}}{2}\right.⟩=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right).(56)$

An arbitrary quantum state can be generated by mixing these three states using the superposition principle: multiplying complex numbers to fundamental ket states and adding up. In a standard matrix formulation of quantum mechanics, a general state is given by a row of three complex numbers.

For quarks, there exists an identity relationship between hypercharge and charge, q, as

$q=t_3+\frac{1}{2}y.(57)$

Therefore, one can use charge instead of hypercharge for an alternative quantum number.

For our applications to photonic orbital angular momentum, we consider superposition states between left- and right-twisted states and no-vortex state. We use the orbital angular momentum along the quantization axis, z, which is the direction of the propagation, as the first quantum number, instead of the isospin of t₃. For the second quantum number, instead of hypercharge, we choose the topological charge, defined by

$q_{\mathrm{t}}=y+\frac{2}{3},(58)$

which becomes 0 for the no-vortex state and 1 for both left- and right-twisted states. The topological charge corresponds to the winding number of the mode at the core, propagating along a certain z direction. It is also linked to the magnitude of photonic orbital angular momentum. In this paper, we only consider vortices with a winding number of 1 or 0, but it will be straightforward to extend our discussions to higher-order states.

2.6 Casimir operators

There are other conservative properties in the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra. We define a Casimir operator as

${\widehat{C}}_1=\frac{1}{4}{\displaystyle \sum _{i=1}^n}{\widehat{\lambda }}_i^2={\displaystyle \sum _{i=1}^n}{\widehat{e}}_i^2.(59)$

We calculate the commutation relationship as follows:

$\left[{\widehat{C}}_1,{\widehat{\lambda }}_j\right]=\frac{1}{4}{\displaystyle \sum _{i=1}^n}\left[{\widehat{\lambda }}_i^2,{\widehat{\lambda }}_j\right],(60)$

$=\frac{1}{4}{\displaystyle \sum _{i=1}^n}\left({\widehat{\lambda }}_i^2{\widehat{\lambda }}_j-{\widehat{\lambda }}_j{\widehat{\lambda }}_i^2\right),(61)$

$=\frac{1}{4}{\displaystyle \sum _{i=1}^n}\left({\widehat{\lambda }}_i\left({\widehat{\lambda }}_i{\widehat{\lambda }}_j\right)-\left({\widehat{\lambda }}_j-{\widehat{\lambda }}_i\right){\widehat{\lambda }}_i\right),(62)$

$=\frac{1}{4}{\displaystyle \sum _{i=1}^n}\left({\widehat{\lambda }}_i\left[{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right]-\left[{\widehat{\lambda }}_j,{\widehat{\lambda }}_i\right]{\widehat{\lambda }}_i\right),(63)$

$=\frac{2i}{4}{\displaystyle \sum _{ik}}\left(C_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_k-C_{\mathit{jik}}{\widehat{\lambda }}_k{\widehat{\lambda }}_i\right),(64)$

$=0,(65)$

where we changed the dummy indices in the last line as ${\sum }_{ik}{C}_{\mathit{jik}}{\widehat{\lambda }}_k{\widehat{\lambda }}_i={\sum }_{ki}{C}_{\mathit{jki}}{\widehat{\lambda }}_i{\widehat{\lambda }}_k={\sum }_{ik}{C}_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_k$. Therefore, the Casimir operator, ${\widehat{C}}_1$, obtains the simultaneous eigenstate with the rank-2 states for ${\widehat{\lambda }}_i$. In fact, we observe, from direct calculations, that

${\widehat{C}}_1=\left(\begin{array}{ccc}\hfill 1+\frac{1}{3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1+\frac{1}{3}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1+\frac{1}{3}\hfill \end{array}\right)=\frac{4}{3},(66)$

which means that ${\widehat{C}}_1$ is constant for SU(3) states. Here, it is obvious that we abbreviated the unit matrix of 3 × 3, 1₃, multiplied with $\frac{4}{3}=\frac{4}{3}{\mathbf{1}}_3$, for simplicity.

There is another Casimir operator, defined by

${\widehat{C}}_2={\displaystyle \sum _{\mathit{ijk}}}{D}_{\mathit{ijk}}{\widehat{t}}_i{\widehat{t}}_j{\widehat{t}}_k=\frac{1}{8}{\displaystyle \sum _{\mathit{ijk}}}{D}_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k,(67)$

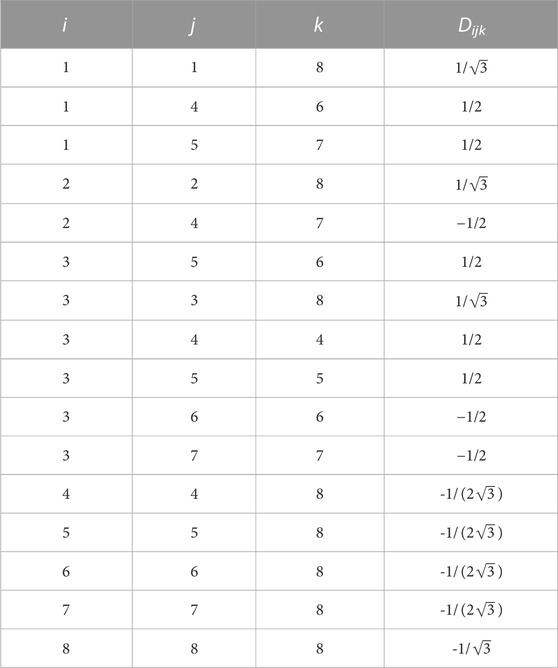
where D_ijk is a symmetric tensor as defined in the anti-commutation relationship given as follows. We observe that ${\widehat{C}}_2$ is also constant in the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, such that the commutation relationship

$\left[{\widehat{C}}_2,{\widehat{\lambda }}_i\right]=0,(68)$

vanishes.

2.7 Anti-commutation relation

We also obtain the anti-commutation relationship as

$\left\{{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right\}=\frac{4}{3}{\delta }_{ij}+2{\displaystyle \sum _{k=1}^8}{D}_{\mathit{ijk}}{\widehat{\lambda }}_k,(69)$

which is equivalent to

$\left\{{\widehat{e}}_i,{\widehat{e}}_j\right\}=\frac{1}{3}{\delta }_{ij}+{\displaystyle \sum _{k=1}^8}{D}_{\mathit{ijk}}{\widehat{e}}_k,(70)$

where $\frac{4}{3}{\delta }_{ij}$ should be considered as $\frac{4}{3}{\delta }_{ij}{\mathbf{1}}_3$, as before. The symmetric tensor, D_ijk, is shown in Table 2.

TABLE 2

TABLE 2. Structure constant of the anti-commutation relationship, $\left\{{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right\}=4{\delta }_{ij}/3+2{\sum }_k{D}_{\mathit{ijk}}{\widehat{\lambda }}_k$, in the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

By multiplying ${\widehat{\lambda }}_k$ with the anti-commutation relationship, we obtain

$\left\{{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right\}{\widehat{\lambda }}_k=\frac{4}{3}{\delta }_{ij}{\widehat{\lambda }}_k+2D_{ij{k}^{\prime }}{\widehat{\lambda }}_{k^{\prime }}{\widehat{\lambda }}_k.(71)$

We take the trace of the equation, while using $\mathrm{Tr}({\widehat{\lambda }}_i)=0$ and $\mathrm{Tr}({\widehat{\lambda }}_i{\widehat{\lambda }}_j)=2{\delta }_{ij}$, and we obtain

$D_{\mathit{ijk}}=\frac{1}{4}\mathrm{Tr}\left(\left\{{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right\}{\widehat{\lambda }}_k\right).(72)$

Similarly, we also obtain

$C_{\mathit{ijk}}=\frac{1}{4i}\mathrm{Tr}\left(\left[{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right]{\widehat{\lambda }}_k\right)(73)$

from the commutation relationship.

Finally, we show that

${\widehat{C}}_2={\widehat{C}}_1\left(2{\widehat{C}}_1-\frac{11}{6}\right)=\frac{10}{9}.(74)$

To prove the identity, we use

$\left\{{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right\}={\widehat{\lambda }}_i{\widehat{\lambda }}_j+{\widehat{\lambda }}_j{\widehat{\lambda }}_i(75)$

and

$\left[{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right]={\widehat{\lambda }}_i{\widehat{\lambda }}_j-{\widehat{\lambda }}_j{\widehat{\lambda }}_i.(76)$

By adding these equations, we obtain

$\left\{{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right\}+\left[{\widehat{\lambda }}_i,{\widehat{\lambda }}_j\right]=2{\widehat{\lambda }}_i{\widehat{\lambda }}_j,(77)$

which becomes

$\frac{4}{3}{\delta }_{ij}+2D_{\mathit{ijk}}{\widehat{\lambda }}_k+2i{C}_{\mathit{ijk}}{\widehat{\lambda }}_k=2{\widehat{\lambda }}_i{\widehat{\lambda }}_j(78)$

from commutation and anti-commutation relationships. Then, we multiply a factor of ${\widehat{\lambda }}_i{\widehat{\lambda }}_j$ and sum up to obtain

${\displaystyle \sum _{ij}}{\widehat{\lambda }}_i^2{\widehat{\lambda }}_j^2=\frac{2}{3}{\displaystyle \sum _i}{\widehat{\lambda }}_i^2+{\displaystyle \sum _{\mathit{ijk}}}{D}_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k-i{\displaystyle \sum _{\mathit{ijk}}}{C}_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k,(79)$

where the last term becomes

$\begin{array}{ccc}\hfill {\displaystyle \sum _{\mathit{ijk}}}{C}_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k=\frac{1}{2}{\displaystyle \sum _{\mathit{ijk}}}\left(C_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k+C_{\mathit{ikj}}{\widehat{\lambda }}_i{\widehat{\lambda }}_k{\widehat{\lambda }}_j\right)& \hfill & \hfill \\ \hfill =\frac{1}{2}{\displaystyle \sum _{\mathit{ijk}}}\left(C_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k-C_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_k{\widehat{\lambda }}_j\right)& \hfill & \hfill \\ \hfill =\frac{1}{2}{\displaystyle \sum _{\mathit{ijk}}}{C}_{\mathit{ijk}}{\widehat{\lambda }}_i\left({\widehat{\lambda }}_j{\widehat{\lambda }}_k-{\widehat{\lambda }}_k{\widehat{\lambda }}_j\right)& \hfill & \hfill \\ \hfill =\frac{1}{2}{\displaystyle \sum _{\mathit{ijk}}}{C}_{\mathit{ijk}}{\widehat{\lambda }}_i\left[{\widehat{\lambda }}_j,{\widehat{\lambda }}_k\right]& \hfill & \hfill \\ \hfill =i{\displaystyle \sum _{\mathit{ijk}}}{C}_{\mathit{ijk}}{C}_{\mathit{jkl}}{\widehat{\lambda }}_i{\widehat{\lambda }}_l& \hfill & \hfill \\ \hfill =i{\displaystyle \sum _{\mathit{ijk}}}{C}_{\mathit{jki}}{C}_{\mathit{jkl}}{\widehat{\lambda }}_i{\widehat{\lambda }}_l& \hfill & \hfill \\ \hfill =3i{\displaystyle \sum _i}{\widehat{\lambda }}_i^2,& \hfill & \hfill \end{array}(80)$

which leads to

${\displaystyle \sum _{ij}}{\widehat{\lambda }}_i^2{\widehat{\lambda }}_j^2={\displaystyle \sum _{\mathit{ijk}}}{D}_{\mathit{ijk}}{\widehat{\lambda }}_i{\widehat{\lambda }}_j{\widehat{\lambda }}_k+\left(\frac{2}{3}+3\right){\displaystyle \sum _i}{\widehat{\lambda }}_i^2.(81)$

Therefore, we obtain

${\widehat{C}}_2={\widehat{C}}_1\left(2{\widehat{C}}_1-\frac{11}{6}\right)=\frac{10}{9},(82)$

which is in fact constant under the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

3 SU(3) state for twisted modes

3.1 Gell-Mann hypersphere

Now, we discuss how to classify the superposition state between left- and right-twisted states and no-vortex state using the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra and the SU(3) Lie group. We assume Laguerre–Gauss modes with a topological charge of q_t = 1 for both left- and right-twisted states [23, 34, 35, 39, 40, 47–51, 63, 65, 71–73] for simplicity.

Here, our main idea is to assign the three states of twisted modes and no-vortex mode to orthogonal states of the SU(3) states (Figures 1, 2). The most important part of the twisted modes for orbital angular momentum is its azimuthal (ϕ) dependence [34]; i.e., the wavefunction of the ray with orbital angular momentum of m is given by

$⟨\varphi |m⟩={\mathrm{e}}^{im\varphi },(83)$

which is orthogonal to each other for states with different charges of m in a sense,

$⟨m^{\prime }|m⟩={\int }_0^{2\pi }\frac{d\varphi }{2\pi }{\mathrm{e}}^{i(m-m^{\prime }\varphi }={\delta }_{m,m^{\prime }}.(84)$

This means that the modes with different orbital angular momentum could be treated as orthogonal quantum mechanical states. For our consideration and notation [24–27, 63, 70, 74–76], we assign left- and right-twisted states as |L⟩ = |1⟩ = |ψ₁⟩ and |R⟩ = | − 1⟩ = |ψ₂⟩, respectively, and the no-vortex Gaussian state as |O⟩ = |0⟩ = |ψ₃⟩. These states are also considered to have different topological charge, such as red, blue, and green (Figure 1).

We also assume that all modes have the same polarization state, such that our SU(3) state is polarized. Then, we consider the polarization degree of freedom, which comes from the SU(2) spin of photons [8, 9, 11–21, 24–27], such that we explore the photonic states with the SU(2) × SU(3) symmetry.

We consider a coherent ray of photons emitted from a laser source [17–19, 24, 63, 70, 75], such that a macroscopic number of photons per second, N, pass through the cross section of the ray. We use upper-case letters to describe macroscopic observables and expectation values, such as photonic orbital angular momentum [23, 34, 35, 39, 40, 47–51, 63, 65, 71–73],

${\widehat{L}}_i=\hslash N{\widehat{\ell }}_i=\hslash N{\widehat{\lambda }}_i,(85)$

where ℏ = h/(2π) is the Dirac constant, defined by the Plank constant (h), divided by 2π, while lower-case letters are used for a single-quantum operator or a normalized parameter, such as a normalized orbital angular momentum operator,

${\widehat{\ell }}_i={\widehat{\lambda }}_i,(86)$

for i = 1, 2, and 3.

There is a difference of factor of 2 in the definition between the orbital angular momentum operator ${\widehat{\ell }}_i$ and the isospin operator of ${\widehat{t}}_3$, but it would be more appropriate to use ${\widehat{\ell }}_i$ for photonic vortices since the orbital angular momentum is quantized in the unit of ℏ [24–26, 34, 35, 63].

First, let us review the SU(2) coupling between left- and right-twisted states [35, 63]. For this, we consider the following state:

$|{\theta }_l,{\varphi }_l\rangle =\left(\begin{array}{c}\hfill {\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill {\mathrm{e}}^{+i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill 0\hfill \end{array}\right),(87)$

where the amplitudes of left- and right-vortex states are controlled by the polar angle of θ_l and the phase is defined by ϕ_l. We can realize this state using an exponential map from the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra to the SU(3) Lie group:

${\widehat{\mathcal{D}}}_2\left({\theta }_l\right)=\exp \left(-\frac{i{\widehat{\lambda }}_2{\theta }_l}{2}\right),(88)$

$=\left(\begin{array}{ccc}\hfill \cos \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill -\sin \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill 0\hfill \\ \hfill \sin \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill \cos \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(89)$

which is a phase-shifter with its fast axis rotated for π/4 from the horizontal axis [24], together with another exponential map of

${\widehat{\mathcal{D}}}_3\left({\varphi }_l\right)=\exp \left(-\frac{i{\widehat{\lambda }}_3{\varphi }_l}{2}\right),(90)$

$=\left(\begin{array}{ccc}\hfill \exp \left(-i\frac{{\varphi }_l}{2}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \exp \left(i\frac{{\varphi }_l}{2}\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(91)$

which is a rotator. We apply these operators to a unit vector, |ψ₁⟩, to confirm the SU(2) state,

$|{\theta }_l,{\varphi }_l\rangle ={\widehat{\mathcal{D}}}_3\left({\varphi }_l\right){\widehat{\mathcal{D}}}_2\left({\theta }_l\right)|{\psi }_1\rangle ,(92)$

made of left- and right-twisted states.

By calculating a standard quantum mechanical average from |θ_l, ϕ_l⟩, such that

${\ell }_i={\lambda }_i=⟨{\widehat{\ell }}_i⟩=⟨{\widehat{\lambda }}_i⟩=⟨{\theta }_l,{\varphi }_l|{\widehat{\lambda }}_i|{\theta }_l,{\varphi }_l⟩(93)$

for i = 1, 2, and 3, respectively, we obtain

${\lambda }_1=\sin \left({\theta }_l\right)\cos \left({\varphi }_l\right),(94)$

${\lambda }_2=\sin \left({\theta }_l\right)\sin \left({\varphi }_l\right),(95)$

${\lambda }_3=\cos \left({\theta }_l\right).(96)$

Thus, the SU(2) states between left- and right-twisted states could be shown on the Poincaré sphere for orbital angular momentum [35, 39, 40, 63, 72]. Usually, the rotational symmetry and the corresponding orbital angular momentum are considered by the SU(2) symmetry since the states between |L⟩ = |1⟩ and |R⟩ = | − 1⟩ cannot be transferred by the change in Δm = ±1, and instead, Δm = ±2 is required. This could be achieved by using a spiral phase plate [37] with a topological charge of m = 2. Alternatively, it is possible to create a superposition state between |L⟩ = |1⟩ and |R⟩ = | − 1⟩, and SU(2) states could be realized by controlling the amplitudes and phases [35, 63]. For our considerations in the SU(3) states, this corresponds to bending the quantization axis, ${\widehat{\ell }}_3$, for allowing three states to couple among each other (Figures 2A, B).

Next, we consider coupling between the no-vortex state and left- or right-vortex states. This corresponds to changing the hypercharge and topological charge. We call these SU(2) couplings hyperspin since they exhibit spin-like SU(2) behaviors, yet they are different from spin. For elementary particles, such as quarks, states with different charged particles cannot be realized at all due to the superselection rule, such that composite particles, such as a neutron and a proton, cannot be in their superposition state [5]. However, for coherent photons, we consider a superposition state among different topologically charged states, such that we can mix the no-vortex state and twisted state at an arbitrary ratio in amplitudes with a certain definite phase. Topologically, the vortex is well known to be equivalent to a shape of a doughnut, which cannot be continuously changed to a shape of a ball. Our challenge could be considered to realize a superposition state between a doughnut and a ball, which is impossible classically, while we would have a chance since photons are elementary particles with a wave character allowing a superposition state of orthogonal states.

Here, we consider the hyperspin coupling, which means that we explore mixing between twisted states and no-vortex state. In order to achieve this, the easiest option is to follow the previous approach of the SU(2) state between left and right vortices. We simply need to change from ${\widehat{\lambda }}_2/2={\widehat{e}}_2^{(t)}$ and ${\widehat{\lambda }}_3/2={\widehat{e}}_3^{(t)}$ to ${\widehat{\lambda }}_5/2={\widehat{e}}_2^{(v)}$ and ${\widehat{e}}_3^{(v)}$, respectively, and we define

${\widehat{\mathcal{D}}}_2^{\left(v\right)}\left({\theta }_y\right)=\exp \left(-i{\widehat{e}}_2^{\left(v\right)}{\theta }_y\right),(97)$

$=\left(\begin{array}{ccc}\hfill \cos \left(\frac{{\theta }_y}{2}\right)\hfill & \hfill 0\hfill & \hfill -\sin \left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \sin \left(\frac{{\theta }_y}{2}\right)\hfill & \hfill 0\hfill & \hfill \cos \left(\frac{{\theta }_y}{2}\right)\hfill \end{array}\right),(98)$

and

${\widehat{\mathcal{D}}}_3^{\left(v\right)}\left({\varphi }_y\right)=\exp \left(-i{\widehat{e}}_3^{\left(v\right)}{\varphi }_y\right),(99)$

$=\left(\begin{array}{ccc}\hfill \exp \left(-i\frac{{\varphi }_y}{2}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \exp \left(i\frac{{\varphi }_y}{2}\right)\hfill \end{array}\right).(100)$

We obtain a general SU(3) state,

$\begin{array}{ccc}\hfill |{\theta }_l,{\varphi }_l;{\theta }_y,{\varphi }_y\rangle & =\hfill & {\widehat{\mathcal{D}}}_3\left({\varphi }_l\right){\widehat{\mathcal{D}}}_2\left({\theta }_l\right){\widehat{\mathcal{D}}}_3^{\left(v\right)}\left({\varphi }_y\right){\widehat{\mathcal{D}}}_2^{\left(v\right)}\left({\theta }_y\right)|{\psi }_1\rangle \hfill \\ \hfill & =\hfill & \left(\begin{array}{c}\hfill {\mathrm{e}}^{-i\frac{{\varphi }_y}{2}}{\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\cos \left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill {\mathrm{e}}^{-i\frac{{\varphi }_y}{2}}{\mathrm{e}}^{+i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\cos \left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill {\mathrm{e}}^{+i\frac{{\varphi }_y}{2}}\sin \left(\frac{{\theta }_y}{2}\right)\hfill \end{array}\right).\hfill \end{array}(101)$

Finally, we can calculate the expectation values for all generators of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, which becomes a vector in an eight-dimensional space, given by

$\vec{\lambda }=\left(\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4\hfill \\ \hfill {\lambda }_5\hfill \\ \hfill {\lambda }_6\hfill \\ \hfill {\lambda }_7\hfill \\ \hfill {\lambda }_8\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\varphi }_y+\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \sin \left({\varphi }_y+\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \cos \left({\varphi }_y-\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \sin \left({\varphi }_y-\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right).(102)$

An arbitrary state of SU(3) is characterized by this vector, which is similar to the Stokes parameters [11] on the Poincaré sphere [12]. The higher-dimensional vector of $\vec{\lambda }$ satisfies the norm conservation

${\displaystyle \sum _{i=1}^8}{\lambda }_i^2=\frac{4}{3},(103)$

upon rotations in the eight-dimensional space, which is guaranteed from the constant Casimir operator of ${\widehat{C}}_1=4/3$, as shown previously. Therefore, an SU(3) state is represented as a point on the hypersphere with the radius of

$\sqrt{{\displaystyle \sum _{i=1}^8}{\lambda }_i^2}=\frac{2}{\sqrt{3}}.(104)$

We propose this hypersphere as the Gell-Mann hypersphere, named after Gell-Mann who found the SU(3) symmetry of baryons and mesons, leading to the discovery of quarks [28–30]. In fact, we have the eightfold way [28–30] to allow the SU(3) superposition state by changing the amplitudes and the phases of the wavefunction. We can attribute color charge of red, green, and blue to three fundamental states of |ψ₁⟩, |ψ₂⟩, and |ψ₃⟩, respectively, similar to QCD [4, 10, 28–30]. In QCD for quarks, only certain sets of multiplets, such as baryons and mesons, are observed as stable bound states of quarks, due to the spontaneous symmetry breaking of the universe [77–81]. In our photonic QCD, on the other hand, we can discuss an arbitrary superposition state by mixing three orthogonal states of left- and right-vortices and no-twisted rays. Therefore, we can discuss the SU(3) state before the symmetry is broken; in other words, the symmetry can be recovered without injecting additional energies to the system, similar to the Nambu–Goldstone bosons [77–81]. This corresponds to the rotation of the hyperspin of $\vec{\lambda }$ in the eight-dimensional Gell-Mann space by using eight generators of rotation ${\widehat{\lambda }}_i$ (i = 1, ⋯, 8) to change the amplitudes and phases. In experiments, this is achieved by using rotators and phase-shifters of SU(2) [24–27, 63, 70, 74–76] since we can realize arbitrary rotations of the SU(3) state by using three sets of SU(2) rotations, as shown previously.

Among the eight Gell-Mann parameters, ${\widehat{\lambda }}_i$, two are especially important since the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra is of rank-2 nature. One of them is ℓ₃ = λ₃, which determines the average orbital angular momentum along the direction of propagation, z. The other important parameter is

$y_3=\frac{1}{\sqrt{3}}{\lambda }_8=-\frac{1}{6}+\frac{1}{2}\cos \left({\theta }_y\right),(105)$

which determines the average hypercharge. We confirm the expected maximum and minimum hypercharge of $\max \left(y_3\right)=1/3$ and $\min \left(y_3\right)=-2/3$, respectively. Hypercharge is simply converted to the topological charge, q_t = y₃ + 2/3, and we confirm $\max \left(q_{\mathrm{t}}\right)=1$ and $\min \left(q_{\mathrm{t}}\right)=0$ as expected maximum and minimum hypercharge for vortices and no-twisted state, respectively.

The Gell-Mann parameters are composed of eight real parameters, and the vector, $\vec{\lambda }$, has a unit length, $|\vec{\lambda }|=1$. Therefore, the rotation of the vector $\vec{\lambda }$ is achieved by the special orthogonal group of eight dimensions, SO(8). The corresponding generators of the $\mathfrak{s}\mathfrak{o}(8)$ Lie algebra are adjoint representations of the $\mathfrak{s}\mathfrak{u}(3)$ generators (${\widehat{\lambda }}_i$, i = 1, …, 8), which become the structure constants of C_ijk (i, j, k = 1, …, 8).

3.2 Hyperspin with the left/right vortex

The Gell-Mann hypersphere contains all practical information about the SU(3) states in terms of amplitudes and phases. Unfortunately, it is impossible to recognize the eight-dimensional hypersphere in the three-dimensional space and time. In the previous sub-section, we showed that the coupling between left and right vortices could be represented by the Poincaré sphere for the twisted photons [35, 63], which corresponds to the coupling controlled by the $\mathfrak{s}\mathfrak{u}(2)$ generators of ${\widehat{e}}_1^{(t)}$, ${\widehat{e}}_2^{(t)}$, and ${\widehat{e}}_3^{(t)}$. Here, we consider other $\mathfrak{s}\mathfrak{u}(2)$ generators and discuss how hyperspin is represented in a similar way to the Poincaré sphere.

First, we consider the coupling between the left-twisted state and no-vortex state. This corresponds to the limit (θ_l, ϕ_l) → (0, 0), and the Gell-Mann parameters become

$\vec{\lambda }=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \frac{1}{2}\left(1+\cos \left({\theta }_y\right)\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\cos \left({\varphi }_y\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\sin \left({\varphi }_y\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right).(106)$

In this case, the parameter λ₃ can take a value between 1 and 0 since the left vortex has a topological charge of 1 due to $\widehat{{\lambda }_3}|\mathrm{L}\rangle =|\mathrm{L}\rangle$, while the no-vortex state, (|O⟩), does not have a topological charge, as $\widehat{{\lambda }_3}|\mathrm{O}\rangle =0$. The superposition state is characterized to be the non-zero average of λ₃, and if the amount of the right-vortex component is less than that of the left-vortex component, λ₃ becomes positive. This corresponds to the net left circulation of orbital angular momentum. The other Gell-Mann parameters are given by θ_y and ϕ_y. In the limit of the zero right-vortex component, it is convenient to consider the average of the $\mathfrak{s}\mathfrak{u}(2)$-generating vector,

$\mathbf{v}=\left(v_1,v_2,v_3\right)=⟨\widehat{\mathbf{v}}⟩,(107)$

$=\left({\lambda }_4/2,{\lambda }_5/2,v_3\right),(108)$

$=\frac{1}{2}\left(\begin{array}{c}\hfill \sin \left({\theta }_y\right)\cos \left({\varphi }_y\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\sin \left({\varphi }_y\right)\hfill \\ \hfill \cos \left({\theta }_y\right)\hfill \end{array}\right),(109)$

which corresponds to introducing $v_3=({\lambda }_3+\sqrt{3}{\lambda }_8)/4$, instead of λ₈ or t_q, since only two parameters are independent among (t₃, u₃, v₃) due to the rank-2 character of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

Similarly, we also check the coupling between the right-vortex state and the no-vortex state, which corresponds to take the limit of (θ_l, ϕ_l) → (π, 0), and we obtain the Gell-Mann parameters,

$\vec{\lambda }=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -\frac{1}{2}\left(1+\cos \left({\theta }_y\right)\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \sin \left({\theta }_y\right)\cos \left({\varphi }_y\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\sin \left({\varphi }_y\right)\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right).(110)$

In this case, the sign of λ₃ changed compared with the coupling with the left vortex since we assigned a negative sign for $\widehat{{\lambda }_3}|\mathrm{R}\rangle =-|\mathrm{R}\rangle$ to the right vortex, which is observed from the observer side against the light coming to the detector [24, 63]. Therefore, λ₃ can take a value between −1 and 0, which corresponds to the average right circulation of orbital angular momentum. For the right circulation, it is useful to calculate the average of the $\mathfrak{s}\mathfrak{u}(2)$-generating vector, $\widehat{\mathbf{u}}$ as

$\mathbf{u}=\left(u_1,u_2,u_3\right)=⟨\widehat{\mathbf{u}}⟩,(111)$

$=\left({\lambda }_6/2,{\lambda }_7/2,u_3\right),(112)$

$=\frac{1}{2}\left(\begin{array}{c}\hfill \sin \left({\theta }_y\right)\cos \left({\varphi }_y\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\sin \left({\varphi }_y\right)\hfill \\ \hfill \cos \left({\theta }_y\right)\hfill \end{array}\right),(113)$

which becomes the same formula for v, when only one chirality (i.e., left or right vortex) is involved. In fact, the parameters θ_y and ϕ_y account for the relative phase and the amplitudes, respectively, between the state with |m| = 1 and the state with m = 0 without including the difference in chiralities. Here, u₃ is introduced by $u_3=(-{\lambda }_3+\sqrt{3}{\lambda }_8)/4$, and it satisfies the conservation law of v₃ − u₃ = t₃.

Consequently, we obtained three vectors, (t, u, v), where t = (ℓ₁, ℓ₂, ℓ₃)/2 is obtained from the average orbital angular momentum. Each vector of t, u, or v is three-dimensional, such that they are represented by the Poincaré spheres. However, care must be taken when dealing with the radiuses of the Poincaré spheres since they depend on the relative amplitudes determined by θ_l and θ_y. This comes from the mutual dependence among three sets of the $\mathfrak{s}\mathfrak{u}(2)$ Lie algebra since the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra does not contain the non-trivial invariant group, as confirmed previously. As a result, we obtained three mutually dependent spheres, which have 3 × 3 = 9 parameters, with one identity of v₃ = u₃ + t₃. For visualization purposes, the three Poincaré spheres with variable radiuses might be practically more useful for humans living in three spatial dimensions, rather than an eight-dimensional Gell-Mann hypersphere of the constant radius of $2/\sqrt{3}$, whose surface is equivalent to a seven-dimensional spherical surface of ${\mathbb{S}}^7$, given by real numbers, with a fixed radius in the eight-dimensional space.

3.3 Hyperspin embedded in SO(6)

Gell-Mann parameters in SO(8) are useful for understanding the coupling among |L⟩, |R⟩, and |O⟩. However, we can easily recognize that the generators of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra cannot span the whole hypersurface of SO(8). For example, parameters λ_i (i = 1, …, 7), except for λ₈, cannot take values above 1 or below −1, while the radius of $2/\sqrt{3}$ is larger than 1. This clearly shows that a point like $(2/\sqrt{3},0,\dots ,0)$ cannot be covered at all, such that SO(8) is much larger than the parameter space required to represent the photonic states, composed of three orthogonal states.

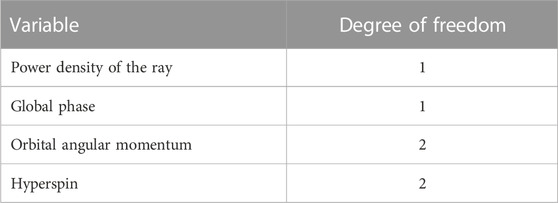
Then, let us consider the number of freedom required for mixing |L⟩, |R⟩, and |O⟩. In general, we should consider the variable density of photons since the radius of the Poincaré sphere depends on the output power of the ray [8, 9, 11–21, 24–27, 63, 70, 75]. Then, photons in the coherent state are represented by one complex number per orthogonal degree of freedom for the component of the wavefunction. We consider this for a fixed polarization state while we have three orthogonal states for vortices, and therefore, we have six degrees of freedom (Table 3).

TABLE 3

TABLE 3. Degrees of freedom for photons with three orthogonal states.

These six degrees of freedom are attributed to corresponding physical parameters (Table 3). One degree of freedom is assigned to the power density of the ray, and another is used for the global U(1) phase, which will not play a role in the expectation values of the Gell-Mann hypersphere. Two degrees of freedom are required for describing the superposition state for orbital angular momentum, which is shown in the Poincaré sphere with variable radiuses (Figure 3A). Therefore, the remaining two parameters should be assigned to hyperspin to account for the mixing of |L⟩ and/or |R⟩ with |O⟩. This picture is consistent with the wavefunction of |θ_l, ϕ_l; θ_y, ϕ_y⟩, where θ_y and ϕ_y account for hyperspin. On the other hand, we used eight Gell-Mann parameters for describing the superposition state from the expectation values. All eight parameters are required to understand the full rotational ways on the Gell-Mann hypersphere; however, fewer parameters are required to scan the full wavefunction over the expected Hilbert space of ${\mathbb{S}}^5$. Here, we try to reduce the number of Gell-Mann parameters to embed hyperspin in SO(6). The aim is to represent the hyperspin

$y_1=\frac{1}{2}\sin \left({\theta }_y\right)\cos \left({\varphi }_y\right),(114)$

$y_2=\frac{1}{2}\sin \left({\theta }_y\right)\sin \left({\varphi }_y\right),(115)$

$y_3=-\frac{1}{6}+\frac{1}{2}\cos \left({\theta }_y\right),(116)$

as shown on the Poincaré sphere (Figure 3B), which should be enough for representing θ_y and ϕ_y topologically.

FIGURE 3

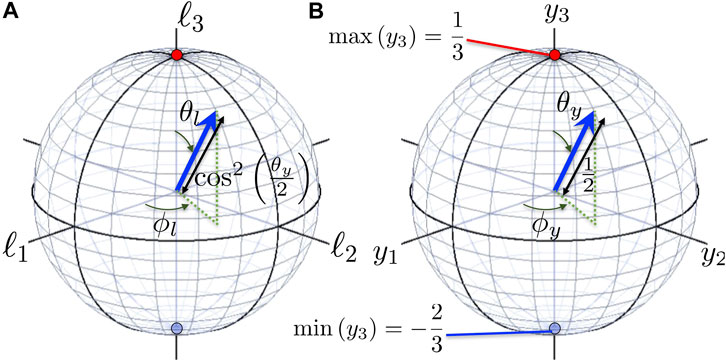
FIGURE 3. Renormalization of Gell-Mann parameters. The eight-dimensional Gell-Mann hypersphere was reduced to two Poincaré spheres for (A) photonic orbital angular momentum and (B) hyperspin. The radius of the Poincaré sphere for orbital angular momentum is cos² (θ_y/2), while it is 1/2 for hyperspin. The maximum and minimum y₃ correspond to a hypercharge of 1/3 and −2/3, respectively, which are equivalent to a topological charge of 1 (pure vortex of |L⟩ or |R⟩) and 0 (no vortex, |O⟩).

A hint is found in Gell-Mann parameters, λ₄, ⋯, λ₇, which has the magnitude

${\left({\lambda }_4\right)}^2+{\left({\lambda }_5\right)}^2+{\left({\lambda }_6\right)}^2+{\left({\lambda }_7\right)}^2={\sin }^2\left({\theta }_y\right)(117)$

upon changing the other parameters θ_l, ϕ_l, and ϕ_y. Therefore, we can eliminate λ₆ and λ₇ by renormalizing the operators for the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

By inspecting λ₄, ⋯, λ₇, we realize that the phases of ϕ_y and ϕ_l are coupled in a mixed form. If we convert ϕ_y ± ϕ_l/2 → ϕ_y, the rest of parameters are easily converted upon rotations. This could be achieved if we remember the rotation matrices of

$\mathcal{R}\left(\theta \right)=\left(\begin{array}{cc}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill \\ \hfill \sin \theta \hfill & \hfill \cos \theta \hfill \end{array}\right)(118)$

from a group to satisfy the associative requirement

$\mathcal{R}\left({\varphi }_y+\frac{{\varphi }_l}{2}\right)=\mathcal{R}\left(\frac{{\varphi }_l}{2}\right)\mathcal{R}\left({\varphi }_y\right).(119)$

Then, we obtain

$\left(\begin{array}{c}\hfill \cos \left({\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \\ \hfill \sin \left({\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \end{array}\right)=\mathcal{R}\left(\frac{{\varphi }_l}{2}\right)\left(\begin{array}{c}\hfill \cos \left({\varphi }_y\right)\hfill \\ \hfill \sin \left({\varphi }_y\right)\hfill \end{array}\right),(120)$

whose reverse relationship becomes

$\left(\begin{array}{c}\hfill \cos \left({\varphi }_y\right)\hfill \\ \hfill \sin \left({\varphi }_y\right)\hfill \end{array}\right)=\mathcal{R}\left(-\frac{{\varphi }_l}{2}\right)\left(\begin{array}{c}\hfill \cos \left({\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \\ \hfill \sin \left({\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \end{array}\right).(121)$

Using these formulas, we define

$\left(\begin{array}{c}\hfill {\lambda }_4^{\prime }\hfill \\ \hfill {\lambda }_5^{\prime }\hfill \end{array}\right)=\mathcal{R}\left(-\frac{{\varphi }_l}{2}\right)\left(\begin{array}{c}\hfill {\lambda }_4\hfill \\ \hfill {\lambda }_5\hfill \end{array}\right),(122)$

$=\left(\begin{array}{cc}\hfill \cos \left(\frac{{\varphi }_l}{2}\right)\hfill & \hfill \sin \left(\frac{{\varphi }_l}{2}\right)\hfill \\ \hfill -\sin \left(\frac{{\varphi }_l}{2}\right)\hfill & \hfill \cos \left(\frac{{\varphi }_l}{2}\right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\lambda }_4\hfill \\ \hfill {\lambda }_5\hfill \end{array}\right),(123)$

$=\left(\begin{array}{c}\hfill \cos \left({\varphi }_y\right)\sin \left({\theta }_y\right)\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \sin \left({\varphi }_y\right)\sin \left({\theta }_y\right)\cos \left(\frac{{\theta }_l}{2}\right)\hfill \end{array}\right),(124)$

and

$\left(\begin{array}{c}\hfill {\lambda }_6^{\prime }\hfill \\ \hfill {\lambda }_7^{\prime }\hfill \end{array}\right)=\mathcal{R}\left(\frac{{\varphi }_l}{2}\right)\left(\begin{array}{c}\hfill {\lambda }_6\hfill \\ \hfill {\lambda }_7\hfill \end{array}\right),(125)$

$=\left(\begin{array}{cc}\hfill \cos \left(\frac{{\varphi }_l}{2}\right)\hfill & \hfill -\sin \left(\frac{{\varphi }_l}{2}\right)\hfill \\ \hfill \sin \left(\frac{{\varphi }_l}{2}\right)\hfill & \hfill \cos \left(\frac{{\varphi }_l}{2}\right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\lambda }_6\hfill \\ \hfill {\lambda }_7\hfill \end{array}\right),(126)$

$=\left(\begin{array}{c}\hfill \cos \left({\varphi }_y\right)\sin \left({\theta }_y\right)\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \sin \left({\varphi }_y\right)\sin \left({\theta }_y\right)\sin \left(\frac{{\theta }_l}{2}\right)\hfill \end{array}\right).(127)$

Then, we successfully converted ϕ_y ± ϕ_l/2 → ϕ_y, as intended. Finally, we can rotate between λ₄ and λ₆ to eliminate λ₆ by defining

$\left(\begin{array}{c}\hfill {\lambda }_4^{\prime \prime }\hfill \\ \hfill {\lambda }_6^{\prime \prime }\hfill \end{array}\right)=\mathcal{R}\left(-\frac{{\theta }_l}{2}\right)\left(\begin{array}{c}\hfill {\lambda }_4^{\prime }\hfill \\ \hfill {\lambda }_6^{\prime }\hfill \end{array}\right),(128)$

$=\left(\begin{array}{c}\hfill \cos \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill 0\hfill \end{array}\right).(129)$

Similarly, we define

$\left(\begin{array}{c}\hfill {\lambda }_5^{\prime \prime }\hfill \\ \hfill {\lambda }_7^{\prime \prime }\hfill \end{array}\right)=\mathcal{R}\left(-\frac{{\theta }_l}{2}\right)\left(\begin{array}{c}\hfill {\lambda }_5^{\prime }\hfill \\ \hfill {\lambda }_7^{\prime }\hfill \end{array}\right),(130)$

$=\left(\begin{array}{c}\hfill \sin \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill 0\hfill \end{array}\right).(131)$

In order to obtain these expectation values for Gell-Mann parameters, we should renormalize the original basis operators of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra to define

${\widehat{\lambda }}_4^{\prime \prime }=\cos \left(\frac{{\theta }_l}{2}\right){\widehat{\lambda }}_4^{\prime }+\sin \left(\frac{{\theta }_l}{2}\right){\widehat{\lambda }}_6^{\prime },(132)$

$\begin{array}{cc}\hfill & =\cos \left(\frac{{\theta }_l}{2}\right)\left(\cos \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_4+\sin \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_5\right)\hfill \\ \hfill & \hfill & +\sin \left(\frac{{\theta }_l}{2}\right)\left(\cos \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_6-\sin \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_7,\right)\hfill \end{array}(133)$

$=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{e}}^{i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill {\mathrm{e}}^{i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill {\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill 0\hfill \end{array}\right)(134)$

and

${\widehat{\lambda }}_5^{\prime \prime }=\cos \left(\frac{{\theta }_l}{2}\right){\widehat{\lambda }}_5^{\prime }+\sin \left(\frac{{\theta }_l}{2}\right){\widehat{\lambda }}_7^{\prime },(135)$

$\begin{array}{cc}\hfill & =\cos \left(\frac{{\theta }_l}{2}\right)\left(-\sin \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_4+\cos \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_5\right)+\sin \left(\frac{{\theta }_l}{2}\right)\left(\sin \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_6+\cos \left(\frac{{\varphi }_l}{2}\right){\widehat{\lambda }}_7\right),\hfill \end{array}(136)$

$=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -i{\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -i{\mathrm{e}}^{i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill i{\mathrm{e}}^{i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill i{\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\hfill & \hfill 0\hfill \end{array}\right).(137)$

If we use these operators, the Gell-Mann parameters become

${\vec{\lambda }}^{\prime \prime }=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill \sin \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right),(138)$

such that we successfully removed λ₆ and λ₇. These parameters are equivalent to using photonic orbital angular momentum

$\vec{\ell }=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \end{array}\right)(139)$

and hyperspin

$\vec{y}=\left(\begin{array}{c}\hfill \frac{1}{2}\sin \left({\theta }_y\right)\cos \left({\varphi }_y\right)\hfill \\ \hfill \frac{1}{2}\sin \left({\theta }_y\right)\sin \left({\varphi }_y\right)\hfill \\ \hfill -\frac{1}{6}+\frac{1}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right),(140)$

which can be shown on two Poincaré spheres with the radiuses of cos² (θ_y/2) and 1/2, respectively, instead of the original three spheres. This is consistent with the four degrees of freedom for orbital angular momentum and hyperspin, as confirmed previously (Table 3), and it is also expected from the rank-2 nature of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra, which requires only two sets of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra among three sets of $(\widehat{\mathbf{t}},\widehat{\mathbf{u}},\widehat{\mathbf{v}})$. In practice, we do not know the angles of θ_l and ϕ_l, a priori, such that the angles are obtained from expectation values or experimental results.

Finally, we successfully embedded Gell-Mann parameters in SO(6) to renormalize

$\vec{S}=\left(\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill S_3\hfill \\ \hfill S_4\hfill \\ \hfill S_5\hfill \\ \hfill S_6\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4^{\prime \prime }\hfill \\ \hfill {\lambda }_5^{\prime \prime }\hfill \\ \hfill {\lambda }_8\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill \sin \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right),(141)$

which satisfies the conservation law of the norm,

${\displaystyle \sum _{i=1}^6}{\left(S_i\right)}^2=\frac{4}{3},(142)$

which was derived from the constant Casimir operator of ${\widehat{C}}_1$.

3.4 Alternative coherent states

We used ${\widehat{\mathcal{D}}}_2^{(v)}\left({\theta }_y\right)$ and ${\widehat{\mathcal{D}}}_3^{(v)}\left({\varphi }_y\right)$ to define an arbitrary state, but we can define an alternative coherent state using original bases of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra by the expression

${\widehat{\mathcal{D}}}_8\left({\varphi }_y\right)=\exp \left(-i{\widehat{\lambda }}_8\frac{{\varphi }_y}{2}\right),(143)$

$=\left(\begin{array}{ccc}\hfill \exp \left(-i\frac{1}{\sqrt{3}}\frac{{\varphi }_y}{2}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \exp \left(-i\frac{1}{\sqrt{3}}\frac{{\varphi }_y}{2}\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \exp \left(i\frac{2}{\sqrt{3}}\frac{{\varphi }_y}{2}\right)\hfill \end{array}\right)(144)$

and ${\widehat{\mathcal{D}}}_5\left({\theta }_y\right)={\widehat{\mathcal{D}}}_2^{(v)}\left({\theta }_y\right)$, as

$\begin{array}{ccc}\hfill |{\theta }_l,{\varphi }_l;{\theta }_y,{\varphi }_y\rangle & =\hfill & {\widehat{\mathcal{D}}}_8\left({\varphi }_y\right){\widehat{\mathcal{D}}}_3\left({\varphi }_l\right){\widehat{\mathcal{D}}}_2\left({\theta }_l\right){\widehat{\mathcal{D}}}_5\left({\theta }_y\right)|{\psi }_1\rangle \hfill \\ \hfill & =\hfill & \left(\begin{array}{c}\hfill {\mathrm{e}}^{-i\frac{1}{\sqrt{3}}\frac{{\varphi }_y}{2}}{\mathrm{e}}^{-i\frac{{\varphi }_l}{2}}\cos \left(\frac{{\theta }_l}{2}\right)\cos \left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill {\mathrm{e}}^{-i\frac{1}{\sqrt{3}}\frac{{\varphi }_y}{2}}{\mathrm{e}}^{+i\frac{{\varphi }_l}{2}}\sin \left(\frac{{\theta }_l}{2}\right)\cos \left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill {\mathrm{e}}^{+i\frac{2}{\sqrt{3}}\frac{{\varphi }_y}{2}}\sin \left(\frac{{\theta }_y}{2}\right)\hfill \end{array}\right).\hfill \end{array}(145)$

Using this coherent state, we obtain the Gell-Mann parameters as expectation values:

$\vec{\lambda }=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left(\frac{\sqrt{3}}{2}{\varphi }_y+\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \sin \left(\frac{\sqrt{3}}{2}{\varphi }_y+\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\cos \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \cos \left(\frac{\sqrt{3}}{2}{\varphi }_y-\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill \sin \left(\frac{\sqrt{3}}{2}{\varphi }_y-\frac{{\varphi }_l}{2}\right)\sin \left({\theta }_y\right)\sin \left(\frac{{\theta }_l}{2}\right)\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right).(146)$

We embedded Gell-Mann parameters into SO(6) for this coherent state as shown previously. To achieve such a conversion, we need to transfer $\sqrt{3}{\varphi }_y/2\pm {\varphi }_l/2\to \sqrt{3}{\varphi }_y/2$, which appeared in λ₄, ⋯, λ₇, by confirming

$\left(\begin{array}{c}\hfill \cos \left(\frac{\sqrt{3}}{2}{\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \\ \hfill \sin \left(\frac{\sqrt{3}}{2}{\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \end{array}\right)=\mathcal{R}\left(\frac{{\varphi }_l}{2}\right)\left(\begin{array}{c}\hfill \cos \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill \sin \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \end{array}\right),(147)$

whose inverse becomes

$\left(\begin{array}{c}\hfill \cos \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill \sin \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \end{array}\right)=\mathcal{R}\left(-\frac{{\varphi }_l}{2}\right)\left(\begin{array}{c}\hfill \cos \left(\frac{\sqrt{3}}{2}{\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \\ \hfill \sin \left(\frac{\sqrt{3}}{2}{\varphi }_y+\frac{{\varphi }_l}{2}\right)\hfill \end{array}\right).(148)$

The rest of the calculations are exactly the same as those shown in the previous subsection. We can use the same renormalized operators of ${\widehat{{\lambda }_4}}^{\prime \prime }{\widehat{{\lambda }_5}}^{\prime \prime }$, while we remove ${\widehat{{\lambda }_6}}^{\prime \prime }=0$ and ${\widehat{{\lambda }_7}}^{\prime \prime }=0$. Then, the renormalized Gell-Mann parameters become

${\vec{\lambda }}^{\prime \prime }=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\cos \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\sin \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right),(149)$

which keep $\vec{\ell }$ remain unchanged, while hyperspin becomes

$\vec{y}=\left(\begin{array}{c}\hfill \frac{1}{2}\sin \left({\theta }_y\right)\cos \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill \frac{1}{2}\sin \left({\theta }_y\right)\sin \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill -\frac{1}{6}+\frac{1}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right).(150)$

This equation just corresponds to the change in the azimuthal angle, ${\varphi }_y\to \sqrt{3}{\varphi }_y/2$, in the Poincaré sphere shown in Figure 3B. Consequently, we embedded Gell-Mann parameters in SO(6) as

$\vec{S}=\left(\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill S_3\hfill \\ \hfill S_4\hfill \\ \hfill S_5\hfill \\ \hfill S_6\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4^{\prime \prime }\hfill \\ \hfill {\lambda }_5^{\prime \prime }\hfill \\ \hfill {\lambda }_8\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\cos \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill \sin \left({\theta }_y\right)\sin \left(\frac{\sqrt{3}}{2}{\varphi }_y\right)\hfill \\ \hfill -\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}\cos \left({\theta }_y\right)\hfill \end{array}\right),(151)$

which also keeps the norm

${\displaystyle \sum _{i=1}^6}{\left(S_i\right)}^2=\frac{4}{3},(152)$

upon arbitrary rotations in the six-dimensional space in SO(6). In practical experiments, however, it is more complex, if we set up a rotator for ${\widehat{\mathcal{D}}}_8\left({\varphi }_y\right)$, since three waves are involved rather than two waves. In conventional optical experiments, various splitters and combiners are prepared for two waves such that it is much easier to rely on SU(2) rotations, including ${\widehat{\mathcal{D}}}_3^{(v)}\left({\varphi }_y\right)$ and ${\widehat{\mathcal{D}}}_3^{(u)}\left({\varphi }_y\right)=\exp \left(-i{\widehat{e}}_3^{(u)}{\varphi }_y\right)$, such that we do not have to use the original bases of ${\widehat{\lambda }}_i$ for SU(3) states.

4 Embedding in SO(5)

For the complete description of the eightfold way to rotate the SU(3) states, Gell-Mann parameters in SO(8) are more useful for understanding the differences in phases and amplitudes among |L⟩, |R⟩, and |O⟩. On the other hand, SO(8) is larger to show the nature of the wavefunction, made of three complex numbers $({\mathbb{C}}^3)$ with its norm conserved to cover ${\mathbb{S}}^5$ in the Hilbert space.

We could successfully reduce the dimension of Gell-Mann parameters from SO(8) to SO(6) or SO(3) × SO(3) to represent SU(3) states, in terms of orbital angular momentum and hyperspin, as expectation values. On the other hand, we have only four parameters (θ_l, ϕ_l, θ_y, and ϕ_y), such that we can reduce one more dimension to represent ${\mathbb{S}}^4$ in SO(5).

Before proceeding further, we review the relationship between SU(2) and SO(3) for describing spin states or polarization states for photons [8, 9, 11–21, 24–27]. For polarization, we have two orthogonal states, such that a ray of coherent photons are described by SU(2) states, which require two complex numbers $({\mathbb{C}}^2)$. The SU(2) wavefunction was normalized for a fixed power density, such that one degree of freedom disappeared and the wavefunction covered ${\mathbb{S}}^3$ in the Hilbert space. In fact, according to the fundamental theorem of homomorphism [1–6], $\mathrm{S}\mathrm{U}(\mathrm{2})/\mathrm{S}\mathrm{U}(\mathrm{1})\cong \mathrm{S}\mathrm{U}(\mathrm{2})/\mathrm{U}(\mathrm{1})\cong {\mathbb{S}}^3$, which means that the SU(2) wavefunction is equivalent to ${\mathbb{S}}^3$, except for the global phase factor of U(1). On the other hand, it is also well known that $\mathrm{S}\mathrm{U}(\mathrm{2})/{\mathbb{S}}^0\cong \mathrm{S}\mathrm{U}(\mathrm{2})/{\mathbb{Z}}_2\cong \mathrm{S}\mathrm{O}(\mathrm{3})$, where ${\mathbb{S}}^0=\{-\mathrm{1,1}\}$ and ${\mathbb{Z}}_2=\{\mathrm{0,1}\}$. This means that if we neglect the impact of the global phase factor, such as those expected from the geometrical Pancharatnam–Berry phases [82, 83] in closed loops, the expectation values of SU(2) states are indicated on the sphere, represented by the SO(3) group. Consequently, the original topology of the wavefunction on ${\mathbb{S}}^3$ is reduced to the Poincaré sphere of ${\mathbb{S}}^2$ in expectation values.

Similarly, in SU(3), the fundamental theorem of homomorphism [1–5] leads to $\mathrm{S}\mathrm{U}(\mathrm{3})/\mathrm{S}\mathrm{U}(\mathrm{2})\cong {\mathbb{S}}^5$. This means that we obtain a degree of freedom of SU(2) symmetry within SU(3) states, which maintains the states essentially equivalent to ${\mathbb{S}}^5$, as confirmed from the identity of v₃ = u₃ + t₃ to allow two arbitrary choices of SU(2) states from three sets of SU(2) bases, $(\widehat{\mathbf{t}},\widehat{\mathbf{u}},\widehat{\mathbf{v}})$. Similar to the SU(2) states, one of the degrees of freedom in ${\mathbb{S}}^5$ would be obtained from the global phase, such that we can represent the expectation values on ${\mathbb{S}}^4$ in SO(5).

However, we could not establish surjective mapping from SO(6) to SO(5) purely upon rotations using our bases of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra because the expectation values of λ_i (i = 1, …, 7) cannot be larger than 1, while we needed to renormalize λ₈ to combine with ${\lambda }_4^{\prime \prime }$ and ${\lambda }_5^{\prime \prime }$. Then, we focused on the conservation relationships of

${\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2={\cos }^2\left(\frac{{\theta }_y}{2}\right),(153)$

${\left({\lambda }_4^{\prime \prime }\right)}^2+{\left({\lambda }_5^{\prime \prime }\right)}^2+{\left({\lambda }_8\right)}^2=\frac{4}{3}-{\cos }^2\left(\frac{{\theta }_y}{2}\right)(154)$

and considered the following non-surjective mapping from SO(6) to SO(5) while we renormalize:

$\vec{S}=\left(\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill S_3\hfill \\ \hfill S_4\hfill \\ \hfill S_5\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4^{\prime \prime \prime }\hfill \\ \hfill {\lambda }_5^{\prime \prime \prime }\hfill \end{array}\right),(155)$

$=\left(\begin{array}{c}\hfill \sin \left({\theta }_l\right)\cos \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sin \left({\theta }_l\right)\sin \left({\varphi }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \cos \left({\theta }_l\right){\cos }^2\left(\frac{{\theta }_y}{2}\right)\hfill \\ \hfill \sqrt{\frac{4}{3}-{\cos }^2\left(\frac{{\theta }_y}{2}\right)}\cos \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \\ \hfill \sqrt{\frac{4}{3}-{\cos }^2\left(\frac{{\theta }_y}{2}\right)}\sin \left({\varphi }_y\right)\sin \left({\theta }_y\right)\hfill \end{array}\right),(156)$

which preserve

${\left({\lambda }_4^{\prime \prime \prime }\right)}^2+{\left({\lambda }_5^{\prime \prime \prime }\right)}^2=\frac{4}{3}-{\cos }^2\left(\frac{{\theta }_y}{2}\right).(157)$

We also confirm that the renormalized Gell-Mann parameters conserve the norm

${\displaystyle \sum _{i=1}^5}{\left(S_i\right)}^2=\frac{4}{3},(158)$

which is consistent with the constant Casimir operator. Consequently, expectation values are embedded on a compact Gell-Mann hypersphere of ${\mathbb{S}}^4$ in SO(5).

5 Discussion

5.1 SU(2) × SU(3) and higher-dimensional systems

However, we assumed that the ray is polarized such that the polarization state is fixed. We can control the polarization state using a phase-shifter and a rotator. We recently proposed a Poincaré rotator, which allows an arbitrary rotation of the polarization state by realizing SU(2) rotations in a combination of half- and quarter-wave plates and phase-shifters [63, 70, 75, 76]. If we use the Poincaré rotator for the ray with SU(3) states of vortices under certain polarization, we can realize SU(2) × SU(3), since spin angular momentum and orbital angular momentum are different quantum observables, such that a general state is made of a direct product state for spin and orbital angular momentum. We can also realize a state created by a sum of these states with different spin and orbital angular momentum states. For example, if we realize the SU(2) state of left and right vortices and assign horizontally and vertically polarized states, respectively, we can realize both singlet and triplet states by controlling the phase among two different many-body states.

Recently, the relationships between topology and polarization are being extensively studied in various forms of structured lights [6, 49, 76, 84–88]. Three-dimensional polarization states [84–86] are novel structured lights to realize knots and links in intensity profiles. It is also exciting that skyrmions were realized by combining spin and orbital angular momentum of photons [89, 90]. Our results suggest that photons have a higher order SU(N) symmetry by allowing various superposition states among orthogonal basis states of spin and orbital angular momentum.

5.2 Cavity QCD and photonic mesons

It is well established that a photonic crystal is an excellent test bed to explore a cavity quantum electro-dynamics (QED) in an artificial environment [91]. Here, we consider an analog to a cavity QED as a cavity QCD. We construct a one-dimensional cavity, for example, a Fabry–Perot interferometer, where |L⟩, |R⟩, and |O⟩ states are realized. The ray propagates in the cavity along z and is reflected back to propagate along the opposite direction of −z. The chiralities of spin and orbital angular momentum are reversed upon reflections [15–21, 24–27], such that the state along −z would be a conjugate state to the state along z. Consequently, we can construct multiplets, similar to mesons, made of quarks and anti-quarks [4, 5, 9, 10]. For quarks, an individual quark is very difficult to observe in experiments due to the strong confinements in composite materials of mesons and baryons. On the other hand, we expect an opposite behavior since photons trapped inside the cavity are difficult to observe as is, while photons escaping from the cavity are observed and analyzed using detectors. This corresponds to observing an individual quark, which is a ray of photons propagating at either z or −z. It is quite hard to observe the composite meson analog, which is realized inside the cavity, and it would be difficult to allocate detectors to observe photons propagating in the opposite directions at the same time, which would require a transparent detector. However, it is not essential to observe within the cavity since we can examine the state inside the cavity from the photons escaping from both ends. The cavity QCD experiments will allows us to explore SU(3) and SU(2) × SU(3) multiplets in a standard photonic experimental setup. If we distinguish each polarization state with different orbital angular momentum states as an individual orthogonal state, we can also explore SU(6) states, for example, and it will also be possible to investigate how symmetry breaking from SU(6) to SU(2) × SU(3) affects the photonic states by observing the corresponding expectation values of generators of rotations in a higher-dimensional space. Another remarkable difference in the proposed photonic systems with quarks is quantum statistics; quarks are fermions, and photons are bosons. Our analysis is quite primitive, such that some of our ideas could be applicable to fermionic systems. However, coherent photons out of lasers are quite easy to treat due to technological advances, while a macroscopic number of photons are coherently degenerate, which would be ideal for experiments that require coherent interference. As mentioned previously, phases and amplitudes of a wavefunction determine the crucial Gell-Mann parameters, similar to Stokes parameters for polarization. Polarization is a macroscopic manifestation of the nature of spin for photons, represented on the Poincaré sphere. A similar argument will hold for orbital angular momentum of coherent photons, and the Gell-Mann hypersphere can play a similar role in clarifying the SU(3) states for photons.

5.3 Correlation between SU(n) and SO(n² − 1)

Finally, we discuss the relationship between SU(n) wavefunctions and expectation values in SO(n² − 1). It is well known that the SU(2) wavefunction for spin is related to spin average values in SO(3), and therefore, the rotation in SU(2) is linked to the corresponding rotation in SO(3). This fact is also explained by the relationship SU(2)/${\mathbb{Z}}_2\cong$SO(3), claiming that the SU(2) is the twofold coverage of SO(3). In this paper, we discussed the relationship between SU(3) and SO(8). More generally, we show that a quantum mechanical average of an generator in SU(n) is related to a rotation in SO(n² − 1) using an adjoint representation of the $\mathfrak{s}\mathfrak{u}(n)$ Lie algebra.

We assume that a generator of rotation in SU(n) is ${\widehat{X}}_a$ and the commutation relationship is $[{\widehat{X}}_a,{\widehat{X}}_b]=i{\sum }_c{f}_{\mathit{abc}}{\widehat{X}}_c$ [5]. In the aforementioned example of SU(3), this corresponds to ${\widehat{X}}_a={\widehat{\lambda }}_a$. We consider that an initial SU(n) state of |I⟩ will be rotated by an exponential map of $\exp (-i{\widehat{X}}_a\theta )$ with an angle of θ to be the final state:

$|\mathrm{F}\rangle ={\mathrm{e}}^{-i{\widehat{X}}_a\theta }|\mathrm{I}\rangle .(159)$

Then, we consider how an average expectation value of ${\widehat{X}}_b$ in the initial state ${⟨{\widehat{X}}_b⟩}_{\mathrm{I}}=⟨\mathrm{I}|{\widehat{X}}_b|\mathrm{I}⟩$ is transferred to the final state:

${⟨{\widehat{X}}_b⟩}_{\mathrm{F}}=⟨\mathrm{F}|{\widehat{X}}_b|\mathrm{F}⟩,(160)$

$=⟨\mathrm{I}|{\mathrm{e}}^{i{\widehat{X}}_a\theta }{\widehat{X}}_b{\mathrm{e}}^{-i{\widehat{X}}_a\theta }|\mathrm{I}⟩,(161)$

$\approx ⟨\mathrm{I}|\left(1+i{\widehat{X}}_a\theta \right){\widehat{X}}_b\left(1-i{\widehat{X}}_a\theta \right)|\mathrm{I}⟩+\mathcal{O}\left({\theta }^2\right),(162)$

$\approx ⟨\mathrm{I}|\left({\widehat{X}}_b+i\theta \left[{\widehat{X}}_a,{\widehat{X}}_b\right]\right)|\mathrm{I}⟩+\mathcal{O}\left({\theta }^2\right),(163)$

$\approx \left({\delta }_{bc}-{\displaystyle \sum _c}{f}_{\mathit{abc}}\theta \right){⟨{\widehat{X}}_c⟩}_{\mathrm{I}}+\mathcal{O}\left({\theta }^2\right),(164)$

$\approx {\displaystyle \sum _c}{\left({\mathrm{e}}^{-{\widehat{F}}_a\theta }\right)}_{bc}{⟨{\widehat{X}}_c⟩}_{\mathrm{I}}+\mathcal{O}\left({\theta }^2\right),(165)$

where we assumed that θ is infinitesimally small and considered only the first order in the expansion, and ${\widehat{F}}_a$ is an adjoint operator, whose matrix element becomes ${({\widehat{F}}_a)}_{bc}=f_{\mathit{abc}}$, which is a matrix of (n² − 1) × (n² − 1). Therefore, the rotation of the wavefunction in SU(n) becomes the rotation of the corresponding expectation value in SO(n² − 1), as expected.

We also checked its validity in the second order of θ as

$\begin{array}{ccc}\hfill \mathcal{O}\left({\theta }^2\right)& =\hfill & -\frac{{\theta }^2}{2}\langle \mathrm{I}|{\widehat{X}}_a^2{\widehat{X}}_b|\mathrm{I}\rangle +{\theta }^2\langle \mathrm{I}|{\widehat{X}}_a{\widehat{X}}_b{\widehat{X}}_a|\mathrm{I}\rangle \hfill \\ \hfill & \hfill & -\frac{{\theta }^2}{2}\langle \mathrm{I}|{\widehat{X}}_b^2{\widehat{X}}_a|\mathrm{I}\rangle ,\hfill \end{array}(166)$

$\begin{array}{c}=-\frac{{\theta }^2}{2}\langle \mathrm{I}|\left({\widehat{X}}_a^2{\widehat{X}}_b-2{\widehat{X}}_a{\widehat{X}}_b{\widehat{X}}_a+{\widehat{X}}_b^2{\widehat{X}}_a|\mathrm{I}\rangle \right.\hfill \\ =-\frac{{\theta }^2}{2}\langle \mathrm{I}|\left({\widehat{X}}_a^2{\widehat{X}}_b\right.-2{\widehat{X}}_a\left({\widehat{X}}_a{\widehat{X}}_b-i{\displaystyle \sum _c}{f}_{\mathit{abc}}{\widehat{X}}_c\right)\hfill \\ +\left.{\widehat{X}}_a^2{\widehat{X}}_b-i{\displaystyle \sum _c}{f}_{\mathit{abc}}\left({\widehat{X}}_a{\widehat{X}}_c+{\widehat{X}}_c{\widehat{X}}_a\right)\right)|\mathrm{I}\rangle \hfill \\ =-\left.\frac{{\theta }^2}{2}\langle \mathrm{I}|\left(2i{\displaystyle \sum _c}{f}_{\mathit{abc}}{\widehat{X}}_a{\widehat{X}}_c\right)\right)|\mathrm{I}\rangle ,\hfill \end{array}(167)$

$\begin{array}{cc}\hfill & =-\left.i\frac{{\theta }^2}{2}{\displaystyle \sum _c}\langle \mathrm{I}|\left(f_{\mathit{abc}}{\widehat{X}}_a{\widehat{X}}_c+f_{\mathit{cba}}{\widehat{X}}_c{\widehat{X}}_a\right)\right)|\mathrm{I}\rangle \hfill \\ \hfill & =-i\frac{{\theta }^2}{2}{\displaystyle \sum _c}{f}_{\mathit{abc}}\langle \mathrm{I}|\left[{\widehat{X}}_a,{\widehat{X}}_c\right]|\mathrm{I}\rangle ,\hfill \end{array}(168)$

$=\frac{{\theta }^2}{2}{\displaystyle \sum _{cd}}{f}_{\mathit{abc}}{f}_{\mathit{acd}}\langle \mathrm{I}|{\widehat{X}}_d|\mathrm{I}\rangle ,(169)$

$=\frac{{\theta }^2}{2}{\displaystyle \sum _c}{\left({\widehat{F}}_a^2\right)}_{bc}\langle \mathrm{I}|{\widehat{X}}_c|\mathrm{I}\rangle ,(170)$

and therefore, the aforementioned formula is also valid in the second order. Actually, this is a reflection of the differentiability of the Lie group, which was originally called an infinitesimal group. Once a formula is derived in an infinitesimal small value, it is straightforward to extend it to the finite value. In our case, we can repeat the infinitesimal amount of rotation with an angle of θ/N, while we can repeat N times, and we take the limit N → ∞ as

${⟨{\widehat{X}}_b⟩}_{\mathrm{F}}=\underset{N\to \infty }{\lim }{\displaystyle \sum _c}{\left(1-{\widehat{F}}_a\frac{\theta }{N}\right)}_{bc}^N{⟨{\widehat{X}}_c⟩}_{\mathrm{I}},(171)$

$={\displaystyle \sum _c}{\left({\mathrm{e}}^{-{\widehat{F}}_a\theta }\right)}_{bc}{⟨{\widehat{X}}_c⟩}_{\mathrm{I}}.(172)$

Therefore, we proved that the quantum mechanical rotation of the wavefunction in SU(N), which is given by ${\mathbb{C}}^n$ on ${\mathbb{S}}^{(n-1)}$ upon the normalization, will rotate the expectation value of the generator, which is a vector of ${\mathbb{R}}^{n^2-1}$ in SO(n² − 1), using the adjoint operator of the $\mathfrak{s}\mathfrak{u}(3)$ Lie algebra.

6 Conclusion

In this study, we proposed to use photonic orbital angular momentum for exploring the SU(3) states as a photonic analog of QCD. We showed that the eight-dimensional Gell-Mann hypersphere in SO(8) characterizes the SU(3) state, made of left- and right-twisted photons and no-twisted photons. There are several ways to visualize the Gell-Mann hypersphere, and we calculated expectation values for the orbital angular momentum and defined hyperspin to represent the coupling between twisted and no-twisted states, which could be shown on two Poincaré spheres or one hypersphere in SO(6) or SO(5). We believe that the proposed superposition state of photons is useful for exploring photonic many-body states to gain some insights into the nature of the symmetries in photonic states.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by JSPS KAKENHI (grant number: JP 18K19958).

Acknowledgments

The author thanks Prof I. Tomita for continuous discussions and encouragements.

Conflict of interest

Author SS is employed by Hitachi, Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Stubhaug A. The mathematician sophus Lie - it was the audacity of my thinking. Berlin: Springer-Verlag (2002).

Google Scholar

2. Fulton W, Harris J. Representation theory: A first course. New York: Springer (2004).

Google Scholar

3. Hall BC. Lie groups, Lie algebras, and representations; an elementary introduction. Switzerland: Springer (2003).

Google Scholar

4. Pfeifer W. The Lie Algebras su(N) An Introduction. Berlin: Springer Basel AG (2003).

Google Scholar

5. Georgi H. Lie algebras in particle physics: From isospin to unified theories (Frontiers in physics). Massachusetts: Westview Press (1999).

Google Scholar

6. Cisowski C, Götte JB, Franke-Arnold S. Colloquium: Geometric phases of light: Insights from fiber bundle theory. Rev Mod Phys (2022) 94:031001. doi:10.1103/RevModPhys.94.0310015

CrossRef Full Text | Google Scholar

7. Dirac PAM. The principle of quantum mechanics. Oxford: Oxford University Press (1930).

Google Scholar

8. Baym G. Lectures on quantum mechanics. New York: Westview Press (1969).

Google Scholar

9. Sakurai JJ, Napolitano JJ. Modern quantum mechanics. Edinburgh: Pearson (2014).

Google Scholar

10. Weinberg S. The quantum theory of fields: Foundations volume 1. Cambridge: Cambridge University Press (2005).

Google Scholar

11. Stokes GG. On the composition and resolution of streams of polarized light from different sources. Trans Cambridge Phil Soc (1851) 9:399–416. doi:10.1017/CBO9780511702266.010

CrossRef Full Text | Google Scholar

12. Poincaré JH. Théorie mathématique de la lumière, Tome 2. Paris: Georges Carré (1892). Available at: https://gallica.bnf.fr/ark:/12148/bpt6k5462651m Accessed August 23, 2023.

Google Scholar

13. Jones RC. A new calculus for the treatment of optical systems i. description and discussion of the calculus. J Opt Soc Am (1941) 31:488–93. doi:10.1364/JOSA.31.000488

CrossRef Full Text | Google Scholar

14. Fano U. A Stokes-parameter technique for the treatment of polarization in quantum mechanics. Phy Rev (1954) 93:121–3. doi:10.1103/PhysRev.93.121

CrossRef Full Text | Google Scholar

15. Born M, Wolf E. Principles of optics. Cambridge: Cambridge University Press (1999). doi:10.1017/9781108769914

CrossRef Full Text | Google Scholar

16. Jackson JD. Classical electrodynamics. New York: John Wiley and Sons (1999).

Google Scholar

17. Yariv Y, Yeh P. Photonics: Optical electronics in modern communications. Oxford: Oxford University Press (1997).

Google Scholar

18. Gil JJ, Ossikovski R. Polarized light and the mueller matrix approach. London: CRC Press (2016). doi:10.1201/b19711

CrossRef Full Text | Google Scholar

19. Goldstein DH. Polarized light. London: CRC Press (2011). doi:10.1201/b10436

CrossRef Full Text | Google Scholar

20. Hecht E. Optics. Essex: Pearson Education (2017).

Google Scholar

21. Pedrotti FL, Pedrotti LM, Pedrotti LS. Introduction to optics. New York: Pearson Education (2007).

Google Scholar

22. Spreeuw BJC. A classical analogy of entanglement. Found Phys (1998) 28:361–74. doi:10.1023/A:1018703709245

CrossRef Full Text | Google Scholar

23. Shen Y. Rays, waves, su(2) symmetry and geometry: Toolkits for structured light. J Opt (2021) 23:124004. doi:10.1088/2040-8986/ac3676

CrossRef Full Text | Google Scholar

24. Saito S. Spin of photons: Nature of polarisation (2023). arXiv 2303 17112. doi:10.48550/arXiv.2303.17112

CrossRef Full Text | Google Scholar

25. Saito S. Quantum commutation relationship for photonic orbital angular momentum. Front Phys Sec Opt Photon (2023) 11. doi:10.3389/fphy.2023.1225346

CrossRef Full Text | Google Scholar

26. Saito S. Spin and orbital angular momentum of coherent photons in a waveguide. Front Phys (2023) 11:1225360. doi:10.3389/fphy.2023.1225360

CrossRef Full Text | Google Scholar

27. Saito S. Dirac equation for photons: Origin of polarisation (2023). arXiv 2303 18196. doi:10.48550/arXiv.2303.18196

CrossRef Full Text | Google Scholar

28. Gell-Mann M. The eightfold way: A theory of strong interaction symmetry (1961). doi:10.2172/4008239

CrossRef Full Text | Google Scholar

29. Gell-Mann M. A schematic model of baryons and mesons. Phys Lett (1964) 8:214–5. doi:10.1016/S0031-9163(64)92001-3

CrossRef Full Text | Google Scholar

30. Ne’eman Y. Derivation of strong interactions from a gauge invariance. Nuc Phys (1961) 26:222–9. doi:10.1016/0029-5582(61)90134-1

CrossRef Full Text | Google Scholar

31. Sakurai JJ. Advanced quantum mechanics. New York: Addison-Wesley Publishing Company (1967).

Google Scholar

32. Plank M. On the theory of the energy distribution law of the normal spectrum. Verhandl Dtsch Phys Ges (1900) 2:237–45. doi:10.1016/B978-0-08-012102-4.50013-9

CrossRef Full Text | Google Scholar

33. Einstein A. Concerning an heuristic point of view toward the emission and transformation of light. Ann Phys (1905) 17:132. Available at: https://einsteinpapers.press.princeton.edu/papers Accessed August 23, 2023.

Google Scholar

34. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Padgett MJ, Courtial J. Poincaré-sphere equivalent for light beams containing orbital angular momentum. Opt Lett (1999) 24:430–2. doi:10.1364/OL.24.000430

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Allen L, Padgett MJ. The poynting vector in Laguerre-Gaussian beams and the interpretation of their angular momentum density. Opt Comm (2000) 184:67–71. doi:10.1016/S0030-4018(00)00960-3

CrossRef Full Text | Google Scholar

37. Golub MA, Shimshi L, Davidson N, Friesem AA. Mode-matched phase diffractive optical element for detecting laser modes with spiral phases. Appl Opt (2007) 46:7823–8. doi:10.1364/AO.46.007823

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Bliokh K. Geometrodynamics of polarized light: Berry phase and spin Hall effect in a gradient-index medium. J Opt A: Pure Appl Opt (2009) 11:094009. doi:10.1088/1464-4258/11/9/094009

CrossRef Full Text | Google Scholar

39. Holleczek A, Aiello A, Gabriel C, Marquardt C, Leuchs G. Classical and quantum properties of cylindrically polarized states of light. Opt Exp (2011) 19:9714–36. doi:10.1364/OE.19.009714

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-order poincaré sphere, Stokes parameters, and the angular momentum of light. Phys Rev Lett (2011) 107:053601. doi:10.1103/PhysRevLett.107.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Bliokh KY, Rodríguez-Fortuño FJ, Nori F, Zayats AV. Spin-orbit interactions of light. Nat Photon (2015) 9:796–808. doi:10.1038/NPHOTON.2015.201

CrossRef Full Text | Google Scholar

42. Barnett SM, Allen L, Cameron RP, Gilson CR, Padgett MJ, Speirits FC, et al. On the natures of the spin and orbital parts of optical angular momentum. J Opt (2016) 18:064004. doi:10.1088/2040-8978/18/6/064004

CrossRef Full Text | Google Scholar

43. Barnett SM, Babiker M, Padgett MJ. Optical orbital angular momentum. Phil Trans R Soc A (2016) 375:20150444. doi:10.1098/rsta.2015.0444

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Bliokh KY, Bekshaev AY, Nori F. Optical momentum and angular momentum in complex media: From the abraham-minkowski debate to unusual properties of surface plasmon-polaritons. New J Phys (2017) 19:123014. doi:10.1088/1367-2630/aa8913

CrossRef Full Text | Google Scholar

45. Moreau PA, Toninelli E, Gregory T, Aspden RS, Morris PA, Padgett MJ. Imaging Bell-type nonlocal behavior. Sci Adv (2019) 5:eaaw2563. doi:10.1126/sciadv.aaw2563

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Shen Y, Yang X, Naidoo D, Fu X, Forbes A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. Optica (2020) 7:820–31. doi:10.1364/OPTICA.382994

CrossRef Full Text | Google Scholar

47. Shen Y, Wang Z, Fu X, Naidoo D, Forbes A. Su(2) poincar’e sphere: A generalised representation for multidimensional structured light. Phys Rev A (2020) 102:031501. doi:10.1103/PhysRevA.102.031501

CrossRef Full Text | Google Scholar

48. Shen Y, Nape I, Yang X, Fu X, Gong M, Naidoo D, et al. Creation and control of high-dimensional multi-particle classically entangled light. Light Sci Appl (2021) 10:50. doi:10.1038/s41377-021-00493-x

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Zdagkas A, McDonnell C, Deng J, Shen Y, Li G, Ellenbogen T, et al. Observation of toroidal pulses of light. Nat Photon (2022) 16:523–8. doi:10.1038/s41566-022-01028-5

CrossRef Full Text | Google Scholar

50. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical vortices 30 years on: Oam manipulation from topological charge to multiple singularities. Light Sci Appl (2019) 8:90. doi:10.1038/s41377-019-0194-2

PubMed Abstract | CrossRef Full Text | Google Scholar

51. He C, Shen Y, Forbes A. Towards higher-dimensional structured light. Light Sci Appl (2022) 11:205. doi:10.1038/s41377-022-00897-3

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Sotto M, Tomita I, Debnath K, Saito S. Polarization rotation and mode splitting in photonic crystal line-defect waveguides. Front Phys (2018) 6:85. doi:10.3389/fphy.2018.00085

CrossRef Full Text | Google Scholar

53. Bull JD, Jaeger NAF, Kato H, Fairburn M, Reid A, Ghanipour P. 40 GHz electro-optic polarization modulator for fiber optic communications systems. Proc Spie, Photon North (Spie) (2004) 5577:133–43. doi:10.1117/12.567640

CrossRef Full Text | Google Scholar

54. Goi K, Kusaka H, Oka A, Ogawa K, Liow TY, Tu X, et al. 128-Gb/s DP-QPSK using low-loss monolithic silicon IQ modulator integrated with partial-rib polarization rotator. In: Optical fiber communication conference (OFC). San Francisco: Optica Publishing Group (2014). p. W1I–2. doi:10.1364/OFC.2014.W1I.2

CrossRef Full Text | Google Scholar

55. Doerr CR. Silicon photonic integration in telecommunications. Front Phys (2015) 3:37. doi:10.3389/fphy.2015.00037

CrossRef Full Text | Google Scholar

56. Kikuchi K. Fundamentals of coherent optical fiber communications. J Light Technol (2016) 34:157–79. doi:10.1109/JLT.2015.2463719

CrossRef Full Text | Google Scholar

57. Guan B, Scott RP, Qin C, Fontaine NK, Su T, Ferrari C, et al. Free-space coherent optical communication with orbital angular, momentum multiplexing/demultiplexing using a hybrid 3d photonic integrated circuit. Opt Exp (2013) 22:145–56. doi:10.1364/OE.22.000145

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Sotto M, Debnath K, Khokhar AZ, Tomita I, Thomson D, Saito S. Anomalous zero-group-velocity photonic bonding states with local chirality. J Opt Soc Am B (2018) 35:2356–63. doi:10.1364/JOSAB.35.002356

CrossRef Full Text | Google Scholar

59. Sotto M, Debnath K, Tomita I, Saito S. Spin-orbit coupling of light in photonic crystal waveguides. Phys Rev A (2019) 99:053845. doi:10.1103/PhysRevA.99.053845

CrossRef Full Text | Google Scholar

60. Al-Attili AZ, Kako S, Husain MK, Gardes FY, Higashitarumizu N, Iwamoto S, et al. Whispering gallery mode resonances from ge micro-disks on suspended beams. Front Mat (2015) 2:43. doi:10.3389/fmats.2015.00043

CrossRef Full Text | Google Scholar

61. Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, Capasso F. Arbitrary spin-to-orbital angular momentum conversion of light. Science (2018) 358:896–901. doi:10.1126/science.aao5392

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Saito S, Tomita I, Sotto M, Debnath K, Byers J, Al-Attili AZ, et al. Si photonic waveguides with broken symmetries: Applications from modulators to quantum simulations. Jpn J Appl Phys (2020) 59:SO0801. doi:10.35848/1347-4065/ab85ad

CrossRef Full Text | Google Scholar

63. Saito S. Poincaré rotator for vortexed photons. Front Phys (2021) 9:646228. doi:10.3389/fphy.2021.646228

CrossRef Full Text | Google Scholar

64. Angelsky OV, Bekshaev AY, Dragan GS, Maksimyak PP, Zenkova CY, Zheng J. Structured light control and diagnostics using optical crystals. Front Phys (2021) 9:715045. doi:10.3389/fphy.2021.715045

CrossRef Full Text | Google Scholar

65. Andrews DL. Symmetry and quantum features in optical vortices. Symmetry (2021) 13:1368. doi:10.3390/sym.13081368

CrossRef Full Text | Google Scholar

66. v Enk SJ, Nienhuis G. Commutation rules and eigenvalues of spin and orbital angular momentum of radiation fields. J Mod Opt (1994) 41:963–77. doi:10.1080/09500349414550911

CrossRef Full Text | Google Scholar

67. Chen XS, Lü XF, Sun WM, Wang F, Goldman T. Spin and orbital angular momentum in gauge theories: Nucleon spin structure and multipole radiation revisited. Phys Rev Lett (2008) 100:232002. doi:10.1103/PhysRevLett.100.232002

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Leader E, Lorcé C. The angular momentum controversy: What’s it all about and does it matter? Phys Rep (2014) 541:163–248. doi:10.1016/j.physrep.2014.02.010

CrossRef Full Text | Google Scholar

69. Yang LP, Khosravi F, Jacob Z. Quantum field theory for spin operator of the photon. Phys Rev Res (2022) 4:023165. doi:10.1103/PhysRevResearch.4.023165

CrossRef Full Text | Google Scholar

70. Saito S. SU(2) symmetry of coherent photons and application to poincaré rotator. Front Phys (2023) 11:1225419. doi:10.3389/fphy.2023.1225419

CrossRef Full Text | Google Scholar

71. Naidoo D, Roux FS, Dudley A, Litvin I, Piccirillo B, Marrucci L, et al. Controlled generation of higher-order poincaré sphere beams from a laser. Nat Photon (2016) 10:327–32. doi:10.1038/NPHOTON.2016.37

CrossRef Full Text | Google Scholar

72. Liu Z, Liu Y, Ke Y, Liu Y, Shu W, Luo H, et al. Generation of arbitrary vector vortex beams on hybrid-order poincaré sphere. Photon Res (2017) 5:15–21. doi:10.1364/PRJ.5.000015

CrossRef Full Text | Google Scholar

73. Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted photons: New quantum perspectives in high dimensions. Light: Sci Appl (2018) 7. doi:10.1038/lsa.2017.146

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Saito S. Special theory of relativity for a graded index fibre. Front Phys (2023) 11:1225387. doi:10.3389/fphy.2023.1225387

CrossRef Full Text | Google Scholar

75. Saito S. Macroscopic single-qubit operation for coherent photons (2023). arXiv 2304 00013. doi:10.48550/arXiv.2304.00013

CrossRef Full Text | Google Scholar

76. Saito S. Topological polarisation states (2023). arXiv 2304.00014. doi:10.48550/arXiv.2304.00014

CrossRef Full Text | Google Scholar

77. Nambu Y. Quasi-particles and gauge invariance in the theory of superconductivity. Phys Rev (1960) 117:648–63. doi:10.1103/PhysRev.117.648

CrossRef Full Text | Google Scholar

78. Goldstone J, Salam A, Weinberg S. Broken symmetries. Phy Rev (1962) 127:965–70. doi:10.1103/PhysRev.127.965

CrossRef Full Text | Google Scholar

79. Higgs PW. Broken symmetries, massless particles and gauge fields. Phys Lett (1962) 12:132–3. doi:10.1103/PhysRevLett.13.508

CrossRef Full Text | Google Scholar

80. Anderson PW. Random-phase approximation in the theory of superconductivity. Phys Rev (1958) 112:1900–16. doi:10.1103/PhysRev.112.1900

CrossRef Full Text | Google Scholar

81. Schrieffer JR. Theory of superconductivity. Boca Raton: CRC Press (1971). doi:10.1201/9780429495700

CrossRef Full Text | Google Scholar

82. Pancharatnam S. Generalized theory of interference, and its applications. Proc Indian Acad Sci Sect A (1956) XLIV:398–417. doi:10.1007/BF03046050

CrossRef Full Text | Google Scholar

83. Berry MV. Quantual phase factors accompanying adiabatic changes. Proc R Sco Lond A (1984) 392:45–57. doi:10.1098/rspa.1984.0023

CrossRef Full Text | Google Scholar

84. Bauer T, Neugebauer M, Leuchs G, Banzer P. Optical polarization Möbius strips and points and purely transverse spin density. Phys Rev Lett (2016) 117:013601. doi:10.1103/PhysRevLett.117.013601

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Kuznetsov NY, Grigoriev KS, Vladimirova YV, Makarov VA. Three-dimensional structure of polarization singularities of a light field near a dielectric spherical nanoparticle. Opt Exp (2020) 28:27293–9. doi:10.1364/OE.398602

CrossRef Full Text | Google Scholar

86. Intaravanne Y, Wang R, Ahmed H, Ming Y, Zheng Y, Zhou ZK, et al. Color-selective three-dimensional polarization structures. Light Sci Appl (2022) 11:302. doi:10.1038/s41377-022-00961-y

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Forbes A, d Oliveira M, Dennis MR. Structured light. Nat Photon (2021) 15:253–62. doi:10.1038/s41566-021-00780-4

CrossRef Full Text | Google Scholar

88. Nape I, Sephton B, Ornelas P, Moodley C, Forbes A. Quantum structured light in high dimensions. APL Photon (2023) 8:051101. doi:10.1063/5.0138224

CrossRef Full Text | Google Scholar

89. Beckley AM, Brown TG, Alonso MA. Full poincaré beams. Optica (2010) 10:10777–85. doi:10.1364/OE.18.010777

CrossRef Full Text | Google Scholar

90. Shen Y, Martinez EC, Rosales-Guzmán C. Generation of optical Skyrmions with tunable toplogical textures. ACS Photon (2022) 9:296–303. doi:10.1021/acsphotonics.1c01703

CrossRef Full Text | Google Scholar

91. Joannopoulos JD, Johnson SG, Winn JN, Meade RD. Photonic crystals: Molding the flow og light. New York: Princeton Univ. Press (2008).

Google Scholar