The spin angular momentum (SAM) and orbital angular momentum (OAM) are unique properties of vortex beams and widely used in optical communication and sensing, wherein unambiguous detection of them is of significance. However, the existing methodologies mostly require complicated optical setups, bulky devices, multiple measurements and suffer from limited detection range and ability. Here, we propose a novel angular momentum (AM) detection mechanism that based on optical symmetry transformation for single-shot AM detection within a large mode space. We first give a detailed theoretical derivation and then carry numerical verification. Subsequently, an ultra-compact metasurface is designed so that an OAM mode high up to 150 orders can be determined with a single-shot measurement. Finally, a spin-decoupled metasurface combining the propagation and geometric phase is constructed, which allows simultaneous discrimination of SAM and OAM. Our proposed method may be promising for a wide range of applications in AM measurements and polarization singularity detection.

1 Introduction

In the field of optics, vortex beam can carry both spin angular momentum (SAM) parallel to the wave vector direction and orbital angular momentum (OAM) associated with free space, SAM is related to the circular polarization state of light, and each photon carries a SAM of ± h/2π, where h is Planck’s constant and ± signs indicate the direction of rotation of light. The OAM is related to the spiral phase exp (ilφ), where φ is the azimuthal angle, and l is the topological charge. The spatial orthogonality between different OAM modes ensures that each mode can be encoded and transmitted as an independent information channel, and thus can play an essential role in various fields such as high-capacity optical communication [1–4] and high-dimensional quantum information systems [5–7]. Therefore, SAM and OAM detection [8–10] is of great research importance.

There are many different methods for vortex beam detection [11–19], but most of them require complex optical setups and bulky devices, which are contrary to the development trend of device miniaturization and system integration [20–24]. Most importantly, multiple repeated projection measurements were inefficient for the detection of various possible OAM modes, especially for high-order OAMs [25]. Therefore, SAM and OAM mode identification still face significant challenges. With the development of nanofabrication techniques, compact schemes utilizing on-chip plasmonic nanostructures, metasurfaces, and liquid crystals [9, 10] have been proposed in sequence to achieve the identification of both SAM and OAM. Based on plasmonic devices, alignment-free near-field OAM detection has been demonstrated, but restricted by complex optical systems for surface plasmon polariton (SPP) beam observation [17]. Although recent efforts have been made to achieve far-field detection, there remain challenges in limited detectable OAM modes and low energy efficiency [21, 22] Additionally, they suffer from the limitations of narrow operating bandwidth and strict focusing conditions or wavevector-matching condition. Metasurface devices, on the other hand, have emerged as a versatile wavefront shaping platform [26–36], which is an artificial optical surface composed of a subwavelength scale two-dimensional array. Metasurface has the advantages of being ultra-light, ultra-thin, and highly integrated, which provides novel modulation of amplitude [37, 38], phase [39, 40], polarization [41, 42], and OAM [43] of the optical field. Therefore, it provides an opportunity to solve the above problems. However, existing metasurfaces typically detect no more than ten OAM modes. In addition, optical transformation systems have been investigated for converting different OAMs to separate different intensity modes in the horizontal plane. However, optical transformation usually requires two or more optical elements separated by a specific distance and precisely aligned. Recently, excellent progresses have been made in mitigating mode overlap by helical transformation [44] and in reducing the number of optical elements used by single-angle lenses [45]. However, the above optical transformations rely mainly on bulky refractive elements or large diffractive elements, which cannot distinguish between SAM and OAM at the same time. Recently, metasurface devices have been proposed for detecting both SAM and OAM, and the superimposed OAM modes can be sorted in certain interval steps [46, 47].

In this paper, inspired by the optical symmetry transformation based wide-angle imaging and OAM sorting proposed by our group before [42, 46, 48], an optical symmetry transformation method for OAM mode recognition is proposed through detailed mathematical derivation and theoretical analysis. OAM beams with different modes are converted to focus points with different horizontal displacements in the focal plane. Different modes of OAM beams correspond to different horizontal coordinate so that a single measurement can achieve OAM mode discrimination. Numerical simulation shows that a single OAM mode up to ±150 orders can be detected with a single-shot measurement. In addition, a spin-decoupled metasurface device combining propagation phase and geometric phase was designed to achieve simultaneous identification of SAMs and OAMs by probing the position of the focal point in the focal plane. The proposed metasurface device has a wide range of applications in the measurement of full AM as well as phase and polarization singularity detection.

2 Principle of optical symmetry transformation for OAM detection

As shown in Figure 1A, we assume that there is a wavefront coding metasurface normally illumined by a vortex beam can produces an OAM mode dependent transversal shift, so that we can determine the OAM mode according to the mapping relationship between the topology charge and transversal shift. In mathematical, the optical symmetry transformation above can be expressed as follows:

$\begin{array}{c}\mathrm{\Phi }\left(\mathit{x},\mathit{y}\right)+\mathit{l}\mathit{\phi }=\mathrm{\Phi }\left(\mathit{x}-\Delta \mathit{x},\mathit{y}\right)\end{array}(1)$

where φ = arctan (y/x), denotes the azimuthal angle of the metasurface, l denotes the topological charge of the OAM, Φ(x, y) denotes the phase of the metasurface, and Δx is the displacement. After a simple mathematical variation, it is obtained that

$\begin{array}{c}\frac{\mathrm{\Phi }\left(\mathit{x},\mathit{y}\right)-\mathrm{\Phi }\left(\mathit{x}-\Delta \mathit{x},\mathit{y}\right)}{\Delta \mathit{x}}=\frac{-\mathit{l}\mathit{\phi }}{\Delta \mathit{x}}\end{array}(2)$

when Δx tends to be infinitely small, we can approximate the difference operation as a differential operation as follows:

$\begin{array}{c}\frac{\partial \mathrm{\Phi }\left(\mathit{x},\mathit{y}\right)}{\partial \mathit{x}}=\frac{-\mathit{l}\mathit{\phi }}{\Delta \mathit{x}}\end{array}(3)$

FIGURE 1

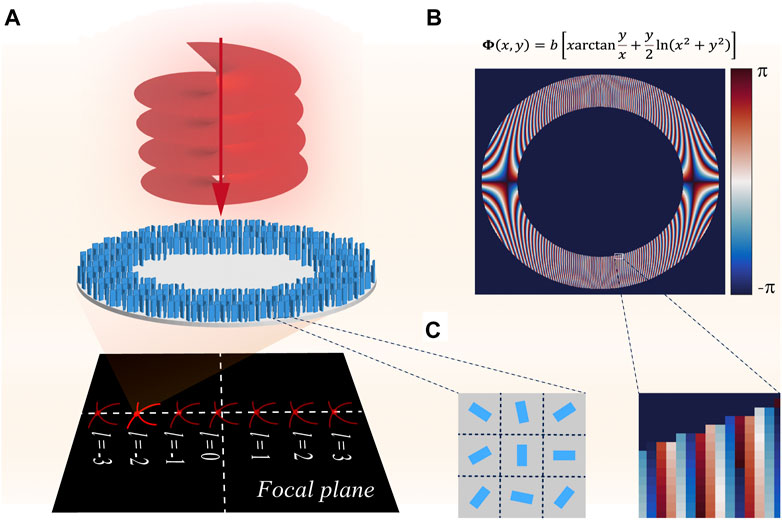
FIGURE 1. Principle of optical symmetry transformation for OAM detection and the phase distribution of the metasurface (A) Translation of the different OAM modes into transverse displacement of the focal point in the plane of focus (B) Phase distribution of the metasurface (C) Enlarged view of the local area in (A, B).

Since the displacement Δx is related to the topological charge of the OAM, we assume that

$\begin{array}{c}\mathit{b}=\frac{-\mathit{l}}{\Delta \mathit{x}}\end{array}(4)$

Then Eq. 3 can be expressed as follows:

$\begin{array}{c}\frac{\partial \mathrm{\Phi }\left(\mathit{x},\mathit{y}\right)}{\partial \mathit{x}}=\mathit{b}\mathit{\phi }=\mathit{b}\arctan \left(\frac{\mathit{y}}{\mathit{x}}\right)\end{array}(5)$

By integrating Eq. 5, we obtain the phase distribution of the metasurface as

$\begin{array}{c}\mathrm{\Phi }\left(x,y\right)=b\left[x\arctan \left(\frac{y}{x}\right)+\frac{y}{2}\ln \left(x^2+y^2\right)\right]\end{array}(6)$

where b is the phase coefficient, and for an OAM beam with topological charge l, the phase accumulated after passing through the metasurface can be expressed as

$\begin{array}{c}\mathrm{\Phi }\left(x,y\right)+l\phi =b\left\{\left(x+\frac{l}{b}\right)\arctan \left(\frac{y}{x+\frac{l}{b}}\right)+\frac{y}{2}\ln \left[{\left(x+\frac{l}{b}\right)}^2+y^2\right]\right\}-\frac{y{l}^2}{2b}=\mathrm{\Phi }\left(x^{\prime },y^{\prime }\right)-\frac{y{l}^2}{2b}\end{array}(7)$

where x denotes the new horizontal coordinate. If we ignore the last terms on the right-hand side of the equation that are not related to the horizontal coordinates, we find that the OAM has only mode-related displacements after passing through the metasurface, where the displacements are

$\begin{array}{c}{x}_l=-\frac{l}{b}\end{array}(8)$

Consequently, the rotational symmetry of the OAM beam could be transformed into the translational symmetry of the focused spots, as shown in Figure 1A. The phase distribution of the metasurface implementing the optical symmetry change function is illustrated in Figure 1B, C shows a partial enlargement of Figure 1A, B. Once the horizontal coordinates of the focusing pattern have been recorded, the OAM can be unambiguous measured. According to Eq. 8, the relative vortices are focused symmetrically about the y-axis. As the topological charge increases from negative to positive, the focus point shifts horizontally at intervals of 1/b. Intuitively, if we can record the horizontal coordinates of the focus pattern through such a phase distribution, the received OAM mode can be determined as

$\begin{array}{c}l=-b{x}_l\end{array}(9)$

3 OAM detection based on geometric metasurface

Compared with conventional refractive or diffractive optical devices, metasurfaces can easily achieve the desired phase distribution with higher spatial sampling resolution. In general, the phase delay introduced by optical subwavelength structures can be divided mainly into propagation and geometric phases (also known as Pancharatnam-Berry phases). The geometric phase carried by the spin reversal circular polarization (CP) component depends only on the direction of the spin and anisotropic unit cell of the incident CP light. It is therefore inherent dispersionless and can operate in a broadband range [29]. However, the diffraction efficiency of the geometric phase is related to the polarization conversion efficiency and depends on the wavelength, so the unit cell has to be optimized parametrically. Here, we have designed an all-dielectric geometric metasurface. We show a schematic diagram of a metasurface unit cell. The desired phase is obtained by using Computer Simulation Technology Microwave Studio (CST) electromagnetic simulation software to optimize the period, height, length, and width of a rectangular structure, as shown in Figure 2A. The unit cell is designed with a substrate square structure of 300 nm period. The phase modulation of our designed metasurface is achieved by using Si nanopillars rotated at different azimuthal angles on the sapphire substrate (Al₂O₃). To make the unit cell close to the ideal half-wave sheet near 633 nm, the unit cell parameters were optimized to a rectangular cell structure with length (L) 160 nm, width (W) 95 nm, and height (H) 400 nm, and the transmission efficiency at 633 nm was 88%, as shown in Figure 2B.

FIGURE 2

FIGURE 2. Schematic diagram of metasurface unit cell and polarization conversion ratio (PCR), as well as numerical simulation results of vortex beams incident on metasurfaces with different inner and outer radii (A) Schematic diagram of metasurface unit cell (B) Polarization conversion ration of the unit cell around a wavelength of 550 nm–850 nm (C–I) Focusing results of the vortex beam with l = 15 after passing through the metasurface with different inner radii (J) Compared with (F), the focusing result of the vortex light through the metasurface after equal amplification of the inner and outer radii.

According to the Pancharatnam-Berry (P-B) phase principle, using an anisotropic rectangular structure, the rotation angle θ of the nanopillar has a minimal effect on the propagation efficiency, and for the incident circularly polarized light, the phase response has a 2-fold relationship with the azimuthal angle of rotation, i.e., Φ(x, y) = 2θ. Therefore, the rotation angle θ of the nanopillar is

$\begin{array}{c}\theta =\frac{\mathrm{\Phi }\left(x,y\right)}{2}=\frac{b}{2}\left[x\arctan \left(\frac{y}{x}\right)+\frac{y}{2}\ln \left(x^2+y^2\right)\right]\end{array}(10)$

Usually, in order not to waste computational resources and to improve the computational speed, the electric field distribution in the target plane is not directly calculated by the simulation software in practical simulations. In this paper, the vector angular spectrum (VAS) theory is used to calculate the light intensity distribution of light diffracted into the target plane after passing through the metasurface. We design a simulation area of 800 × 800 μm² for the whole mode of the metasurface, and the number of grids in the horizontal plane is set to 2048 × 2048. For any point (x, y) in the Cartesian coordinate system, its corresponding polar coordinates can be expressed as:

$\begin{array}{c}r={\left(x^2+y^2\right)}^{\frac{1}{2}}\\ \phi =\arctan \left(\frac{y}{x}\right)\end{array}(11)$

An metasurface based amplitude and phase mask is utilized

$\begin{array}{c}E\left(r,\phi \right)=g\left(r\right)\exp \left\{b\left[x\arctan \left(\frac{y}{x}\right)+\frac{y}{2}\ln \left(x^2+y^2\right)\right]\right\}\end{array}(12)$

where,

$\begin{array}{c}\left\{\begin{array}{c}\begin{array}{cc}g\left(r\right)=1,& r_i\le r\le r_o\end{array}\\ \begin{array}{cc}g\left(r\right)=0,& otherwise\end{array}\end{array}\right.\end{array}(13)$

When the vortex light carrying OAM mode passes normally through the metasurface, the output electric field can be expressed as:

$\begin{array}{c}{E}_{out}\left(r,\phi \right)=g\left(r\right)\exp \left\{b\left[x\arctan \left(\frac{y}{x}\right)+\frac{y}{2}\ln \left(x^2+y^2\right)\right]+l\phi \right\}\end{array}(14)$

Then, the electric field at any transverse plane behind the metasurface is calculated by VAS:

$\begin{array}{c}E\left(r_{\perp },z\right)=\int d^2{k}_{\perp }{e}^{i{k}_{\perp }\bullet r_{\perp }+i{k}_{z}z}\left\{A_{\perp }\left(k_{\perp }\right)-\left[k_{\perp }\bullet \frac{A_{\perp }\left(k_{\perp }\right)}{k_{\perp }}\right]{\mathit{e}}_{\mathit{z}}\right\}\end{array}(15)$

where:

$\begin{array}{c}\left\{\begin{array}{c}{r}_{\perp }=x{\mathit{e}}_{\mathit{x}}+y{\mathit{e}}_{\mathit{y}}\\ k_{\perp }={\mathit{k}}_{\mathit{x}}{\mathit{e}}_{\mathit{x}}+{\mathit{k}}_{\mathit{y}}{\mathit{e}}_{\mathit{y}}\\ A_{\perp }\left(k_{\perp }\right)=A_x\left(k_{\perp }\right){\mathit{e}}_{\mathit{x}}+A_y\left(k_{\perp }\right){\mathit{e}}_{\mathit{y}}\\ A_{\perp }\left(k_{\perp }\right)=\left[\int d^2{r}_{\perp }{e}^{-i{k}_{\perp }\bullet r_{\perp }}{E}_{out}\left(r,\phi \right)\right]/{\left(2\pi \right)}^2\\ {\mathit{k}}_{\mathit{z}}=\sqrt{{\mathit{k}}_{\mathbf{0}}^{\mathbf{2}}-{\mathit{k}}_{\mathit{x}}^{\mathbf{2}}-{\mathit{k}}_{\mathit{y}}^{\mathbf{2}}}\end{array}\right.\end{array}(16)$

In order to obtain a better focus in the focal plane, we optimize the radius of the metasurface. Taking the LCP OAM with topological charge of l = 15 as an example, numerical simulations are performed using VAS, and the simulations are uniformly set with the same coefficient b = 3. We can see that when the inner radius is 0 μm (i.e., the ordinary circular phase distribution), many streaks appear at the two arms of the focusing pattern, as shown in Figure 2C. In Figure 2D–F, we increase the inner radius to 60 μm in turn, and we can find that the streaks near the two arms gradually become less. Although the streaks near the two arms gradually become less as the inner radius is further increased, the energy gradually expands toward the two arms of the focusing pattern and is no longer concentrated at the position where the two arms intersect, as shown in Figure 2G–I.

Furthermore, in Figure 2F–J, we simulated the results for b = 3 for inner radii r_i of 60 μm and 90 μm, and outer radii r_o of 200 μm and 300 μm, respectively. When both the inner and outer radii are enlarged, it is found that the focusing pattern is only scaled proportionally. Moreover, it was found that when the inner and outer radii were scaled equally, the focusing pattern showed many streaks, which required finer sampling points. Therefore, the inner radius was chosen to be 60 μm when the outer radius was 200 μm in order to obtain a better focusing pattern and to improve the intensity utilization.

To make the focus pattern as good as possible, we choose the inner radius r_i and outer radius r_o of the metasurface to be 60 μm and 200 μm, respectively. When the wavelength is 633 nm and b is 3 and 6, after numerical simulation, it is found that good focusing effect can be seen when the focal lengths of the metasurface are 430.12 μm and 215.06 μm, respectively. We give the focusing effects of the OAM topological charges on the focusing surface for −6, −3, 0, 3, and 6 in Figure 3A and Figure 3B, respectively, where Figure 3A, B correspond to 430.12 μm and 215.06 μm focal planes, respectively. The results of the numerical simulation show that the OAMs of different modes are focused in one plane without any relationship with the topological charge values, and the displacement corresponding to each OAM topological charge is fixed. The focal point is moved from right to left when the topological charge is shifted from negative to positive. The focal points produced by the negative-valued topological charge OAM and the positive-valued topological charge OAM passing through the metasurface are symmetrically distributed about the y-axis. When b is set to 3 and 6, respectively, and the OAM topological charges are the same, the displacement is clearly seen to be related to b by the intensity distribution curve under the horizontal white dashed line. When the value of b is doubled, the displacement of the adjacent mode OAM is halved and the focusing focal length is also halved, as shown in Figure 3C, D. The results show that the numerical simulations are consistent with our theoretical analyses. And the topological charge can be predicted explicitly as

$\begin{array}{c}{l}_{predict}=\left[-b{x}_l\right]\end{array}(17)$

where [.] is defined to take the closest integer value. For b of 3, when the topological charge of the OAM pattern increases from 0 to 150, the shape change of the focusing pattern is negligible, and only the lateral translation along the white dashed line is observed, as shown in Figure 4A. The simulation results shown in Figure 4B agree well with the theoretical results, both of which show that the displacement of the focal point increases linearly with the increase of the topological charge. We show the predicted results of the topological charges in Figure 4C based on the lateral coordinates obtained in the simulation results in Figure 4B, and it is found to match well with the topological charge of the vortex received at the focal plane.

FIGURE 3

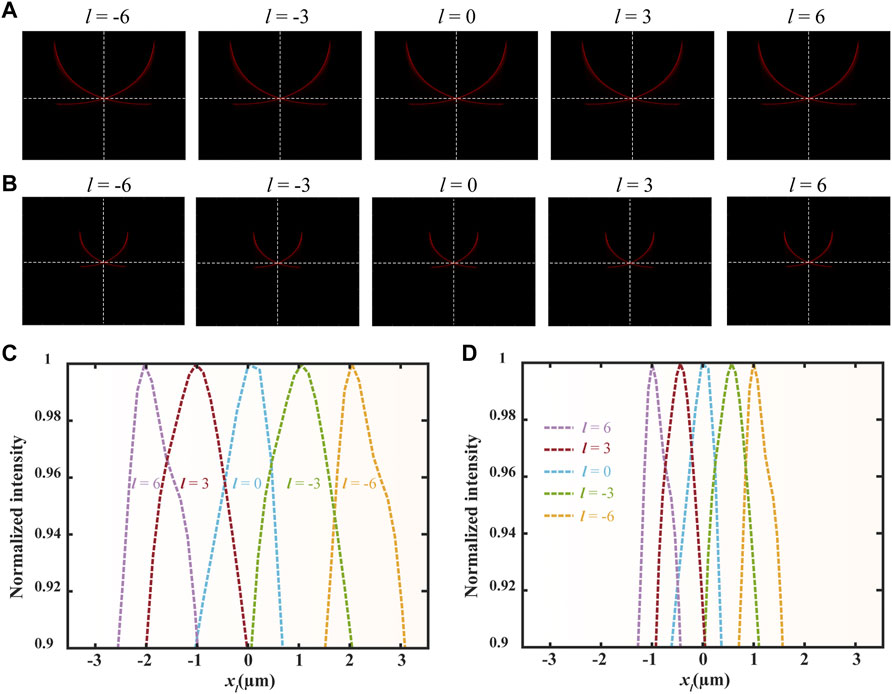
FIGURE 3. Numerical mode fruits of the vortex beam incident on the metasurface when b is 3 and 6, respectively (A) The focusing results of the vortex beams with different topological charges passing through the metasurface at b = 3 (B) The focusing results of the vortex beams with different topological charges passing through the metasurface at b = 6 (C) The normalized intensity distribution curves under the transverse white dashed line in (A–D) The normalized intensity distribution curves under the transverse white dashed line in (B).

FIGURE 4

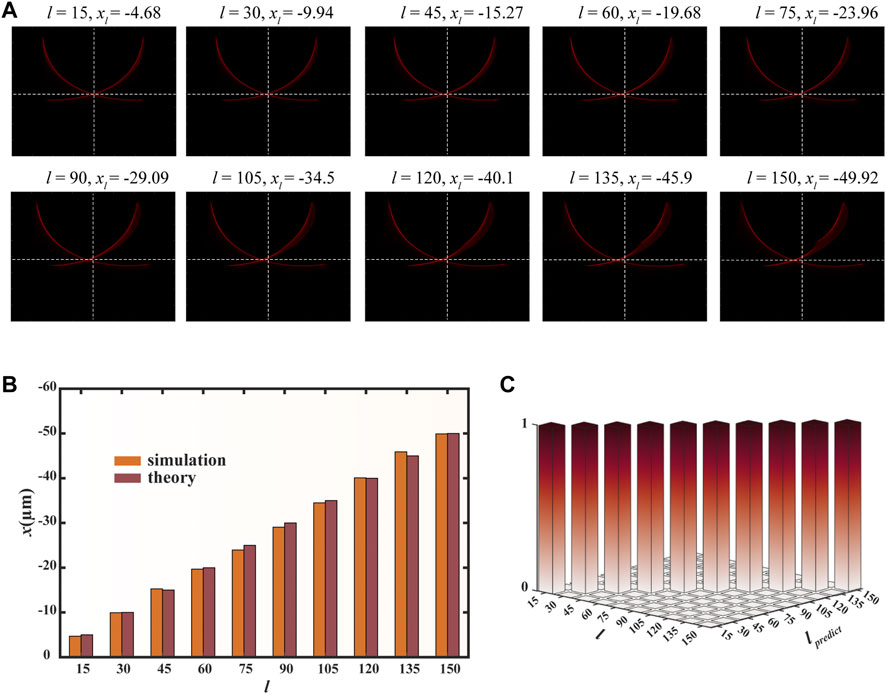
FIGURE 4. LCP OAM sorting at a wavelength of 633 nm (A) Simulated focusing patterns for different OAM modes with the topological charge increasing from 15 to 150 with a step of 15 (B) Theoretical and simulated radial coordinates of the focus peak versus the topological charge (C) OAM prediction results based on the simulated radial coordinates in (B).

4 Simultaneous detection of SAM and OAM based on spin-decoupled metasurface

Light waves carry not only OAMs but also SAMs at the same time. Due to the inherent orthogonality of light waves, SAMs and OAMs have been used to extend the dimensionality of quantum information, optical communication, and signal processing, where explicit identification of SAMs and OAMs is one of the essential research elements. Since the geometric phase is only associated with a single spin, the focused state of the far-field diffraction of the phase distribution of the original geometric metasurface becomes divergent when the spin direction is reversed, so that the geometric phase-based metasurface can work under only one spin direction. Here, we designed a spin-decoupled metasurface combining the propagation and geometric phase, so that we can identify both SAM and OAM. Vortex beams with different spin states are converted into focused patterns in the horizontal and vertical axes. The SAM of the vortex beam is determined by the axis where the focused pattern is located, and the OAM is discriminated by the displacement of the focused pattern.

The metasurface devices are composed of Si rectangular nanopillars with different orientations and geometries. On the one hand, the propagation phase along the central axis of the cell structure can be adjusted by changing the length L and width W of the unit cell. On the other hand, arbitrary angular geometrical phases can be achieved by controlling the local orientation of the unit cell’s fast axis by rotating it between 0 and π. The polarization-independent propagation phase is introduced to break the conjugate limitation of the spin-orbit interaction, so that the polarization multiplexing metasurface can be realized. Unlike the multifunctional metasurface constructed by the aperture division multiplexing method, each spin can share the entire aperture in the spin-decoupled metasurface.

Figure 5A is a schematic diagram of the spin-decoupled metasurface implementation for simultaneous SAM and OAM detection, where the phase distribution of the spin-decoupled metasurface is divided into the following two parts:

$\begin{array}{c}{\mathrm{\Phi }}_{LCP}\left(x,y\right)=b\left[x\arctan \left(\frac{y}{x}\right)+\frac{y}{2}\ln \left(x^2+y^2\right)\right]\\ {\mathrm{\Phi }}_{RCP}\left(x,y\right)=b\left[y\arctan \left(\frac{x}{y}\right)+\frac{x}{2}\ln \left(y^2+x^2\right)\right]\end{array}(18)$

FIGURE 5

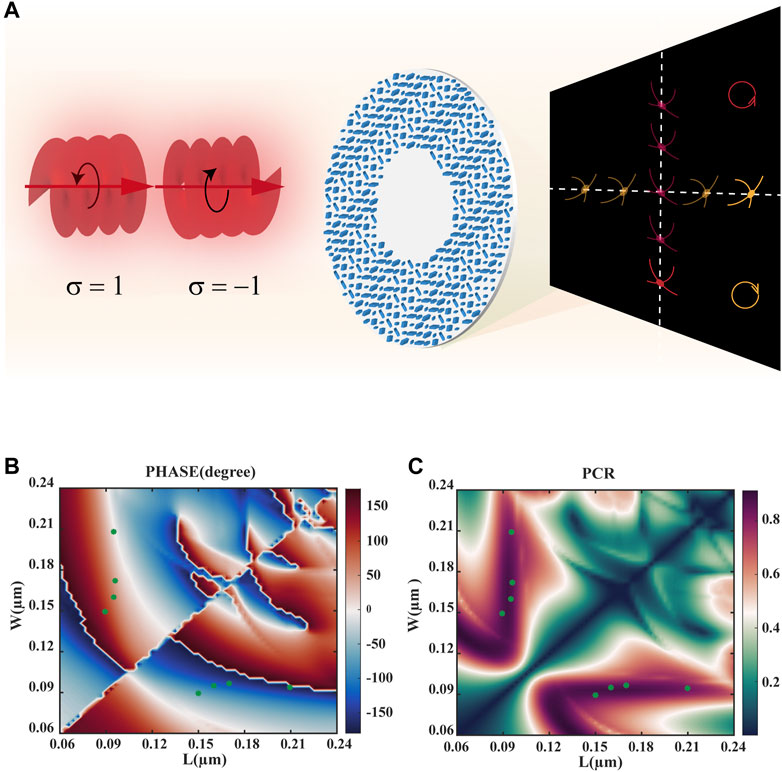
FIGURE 5. Spin-decoupled metasurface based PMTs for simultaneous SAM and OAM sorting (A) Working principle of a spin-decoupled metasurface (B) The phase distribution of unit cells with different L and W was obtained by scanning at 633 nm band and eight unit-cells were selected (green solid dots) (C) Polarization Conversion Ratio (PCR) of unit cells with different L and W was obtained by scanning at 633 nm band and eight groups were selected (green solid dots).

After passing through the spin-decoupled metasurface, the vortices of different spins are focused on the horizontal and vertical axes, so the SAM can be easily classified by detecting the axes where the focal point is located. The OAM can be identified by determining the horizontal and vertical coordinates of the focal point, similar to the demonstration of a geometric metasurface.

To construct the spin-decoupled metasurface, the anisotropic phase shifts (δx and δy) and the orientation θ of the nanopillar should have to satisfy:

$\begin{array}{c}\left\{\begin{array}{c}{\delta }_x=\frac{1}{2}\left({\mathrm{\Phi }}_{LCP}+{\mathrm{\Phi }}_{RCP}\right)\\ {\delta }_y=\frac{1}{2}\left({\mathrm{\Phi }}_{LCP}+{\mathrm{\Phi }}_{RCP}\right)+\pi \\ \theta =\frac{1}{4}\left({\mathrm{\Phi }}_{LCP}-{\mathrm{\Phi }}_{RCP}\right)\end{array}\right.\end{array}(19)$

By scanning the parameters L and W of the unit cell, we selected eight groups of unit cells with the same height H = 400 nm and period p = 300 nm, including four basic nanopillars with different lengths and widths and their orthogonal systems, to provide eight phases in steps of π/4, as shown in Figure 5B. Since the latter four unitary systems are obtained by rotating the first four by π/2, the rotation does not affect the polarization conversion efficiency, which reaches more than 84% at the 633 nm wavelength, as shown in Figure 5C.

We have simulated in Figure 6A the focusing focus on the focal plane for incident light with LCP and RCP ± 150th order OAM modes spaced by 30 orders at b of 3. The results show that all methods of OAM focus on the x-axis or y-axis, in agreement with our theoretical derivation. The focusing results of LCP are on the x-axis of the focusing plane, and the focusing results of RCP are on the y-axis. The theoretical results calculated according to Eq. 9 are in good agreement with the results of the simulation, proving the effectiveness of the proposed method, as shown in Figure 6B, C.

FIGURE 6

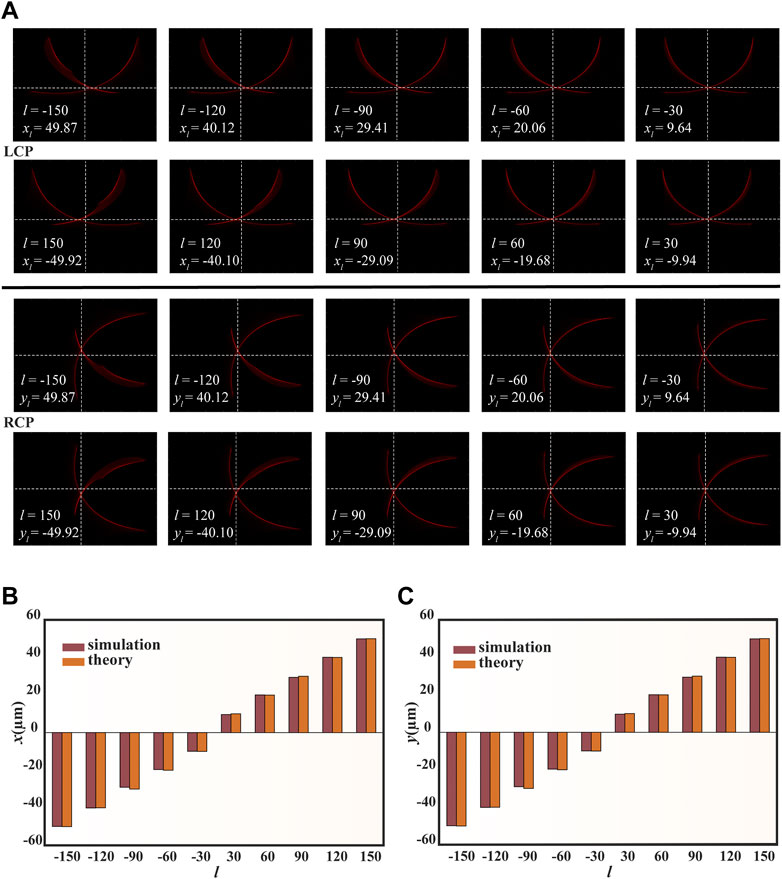
FIGURE 6. SAM and OAM sorting at a wavelength of 633 nm (A) Simulated focusing patterns for different SAMs and OAMs with the topological charge changing from −150 to +150 (B) Radial coordinates of the theoretical and simulated focal peaks under LCP incidence versus topological charge (C) Radial coordinates of the theoretical and simulated focal peaks under RCP incidence versus topological charge.

5 Conclusion

In summary, a general theory of optical symmetry transformation AM detection is proposed for single-shot AM detection within a large mode space. Both detailed theoretical derivation and solid numerical verifications have been presented to illustrate and verify our proposal. An ultra-compact metasurface was designed so that an OAM mode high up to 150 orders can be determined with a single-shot measurement. The angular momentum can be detected as long as the vortex beam is superimposed with the ring-shaped metasurface. For a vortex beam that not matches the ring area, the beam expansion/reduction can be implemented by using the lens build 4f system, which allows it to match the ring detection area. Therefore, it can also be applied to the detection of special OAM modes including Laguerre–Gaussian modes. Furthermore, a spin-decoupled metasurface allows simultaneous discrimination of SAM and OAM has been constructed. With the merits of ultracompact device size, simple optical configuration, and prominent vortex recognition ability, our proposed method may be promising for a wide range of applications in AM measurements and polarization singularity detection.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YL, RnZ, and YG conceived the principle, YL and RnZ performed the simulations. YL analyzed the simulation data and wrote the manuscript. YL, XLi, and QZ plotted the figures. YL, YG, and MP revised the manuscript. All authors discussed and analyzed the data and results. MP and XLu co-supervised the project. All authors contributed to the article and approved the submitted version.

Funding

This work was partially supported by the National Natural Science Foundation of China (62222513 and U20A20217), National Key Research and Development Program of China (2021YFA1401000), Sichuan Science and Technology Program (2021ZYCD001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang J, Yang J-Y, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat Photon (2012) 6(7):488–96. doi:10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

2. Wen Y, Chremmos I, Chen Y, Zhu G, Zhang J, Zhu J, et al. Compact and high-performance vortex mode sorter for multi-dimensional multiplexed fiber communication systems. Optica (2020) 7(3):254–62. doi:10.1364/OPTICA.385590

CrossRef Full Text | Google Scholar

3. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical communications using orbital angular momentum beams. Adv Opt Photon (2015) 7(1):66–106. doi:10.1364/AOP.7.000066

CrossRef Full Text | Google Scholar

4. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical vortices 30 Years on: Oam manipulation from topological charge to multiple singularities. Light: Sci Appl (2019) 8(1):90. doi:10.1038/s41377-019-0194-2

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature (2001) 412(6844):313–6. doi:10.1038/35085529

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhou H, Sain B, Wang Y, Schlickriede C, Zhao R, Zhang X, et al. Polarization-encrypted orbital angular momentum multiplexed metasurface holography. ACS Nano (2020) 14(5):5553–9. doi:10.1021/acsnano.9b09814

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Molina-Terriza G, Torres JP, Torner L. Twisted photons. Nat Phys (2007) 3(5):305–10. doi:10.1038/nphys607

CrossRef Full Text | Google Scholar

8. Liu S, Chen S, Wen S, Luo H. Photonic spin Hall effect: Fundamentals and emergent applications. Opto-Electronic Sci (2022) 1(7):220007-1–32. doi:10.29026/oes.2022.220007

CrossRef Full Text | Google Scholar

9. Chen P, Ma L, Duan W, Chen J, Ge S, Zhu Z, et al. Digitalizing self-assembled chiral superstructures for optical vortex processing. Adv Mater (2018) 30(10):1705865. doi:10.1002/adma.201705865

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhu L, Xu C, Chen P, Zhang Y, Liu S, Chen Q, et al. Pancharatnam–Berry phase reversal via opposite-chirality-coexisted superstructures. Light: Sci Appl (2022) 11(1):135. doi:10.1038/s41377-022-00835-3

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Heckenberg NR, Mcduff RG, Smith CP, White A. Generation of optical phase singularities by computer-generated holograms. Opt Lett (1992) 17 3:221. doi:10.1364/OL.17.000221

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Beijersbergen MW, Coerwinkel RPC, Kristensen M, Woerdman JP. Helical-wavefront laser beams produced with a spiral phaseplate. Opt Commun (1994) 112(5):321–7. doi:10.1016/0030-4018(94)90638-6

CrossRef Full Text | Google Scholar

13. Ma H, Li X, Tai Y, Li H, Wang J, Tang M, et al. In situ measurement of the topological charge of a perfect vortex using the phase shift method. Opt Lett (2017) 42:135–8. doi:10.1364/OL.42.000135

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Leach J, Courtial J, Skeldon K, Barnett SM, Franke-Arnold S, Padgett MJ. Interferometric methods to measure orbital and spin, or the total angular momentum of a single photon. Phys Rev Lett (2004) 92(1):013601. doi:10.1103/PhysRevLett.92.013601

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Fu S, Zhang S, Wang T, Gao C. Measurement of orbital angular momentum spectra of multiplexing optical vortices. Opt Express (2016) 24 6:6240–8. doi:10.1364/OE.24.006240

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Leach J, Padgett MJ, Barnett SM, Franke-Arnold S, Courtial J. Measuring the orbital angular momentum of a single photon. Phys Rev Lett (2002) 88(25):257901. doi:10.1103/PhysRevLett.88.257901

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett (2006) 96(16):163905. doi:10.1103/PhysRevLett.96.163905

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hickmann JM, Fonseca EJS, Soares WC, Chávez-Cerda S. Unveiling a truncated optical lattice associated with a triangular aperture using light's orbital angular momentum. Phys Rev Lett (2010) 105(5):053904. doi:10.1103/PhysRevLett.105.053904

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Cai X, Wang J, Strain MJ, Johnson-Morris B, Zhu J, Sorel M, et al. Integrated compact optical vortex beam emitters. Science (2012) 338(6105):363–6. doi:10.1126/science.1226528

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Mirhosseini M, Malik M, Shi Z, Boyd RW. Efficient separation of the orbital angular momentum eigenstates of light. Nat Commun (2013) 4(1):2781. doi:10.1038/ncomms3781

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Berkhout GCG, Lavery M, Courtial J, Beijersbergen MW, Padgett MJ. Efficient sorting of orbital angular momentum states of light. Phys Rev Lett (2010) 105(15):153601. doi:10.1103/PhysRevLett.105.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lightman S, Hurvitz G, Gvishi R, Arie A. Miniature wide-spectrum mode sorter for vortex beams produced by 3d laser printing. Optica (2017) 4(6):605–10. doi:10.1364/OPTICA.4.000605

CrossRef Full Text | Google Scholar

23. O’Sullivan MN, Mirhosseini M, Malik M, Boyd RW. Near-perfect sorting of orbital angular momentum and angular position states of light. Opt Express (2012) 20 22:24444–9. doi:10.1364/OE.20.024444

CrossRef Full Text | Google Scholar

24. Wen Y, Chremmos I, Chen Y, Zhu J, Zhang Y, Yu S. Spiral transformation for high-resolution and efficient sorting of optical vortex modes. Phys Rev Lett (2018) 120(19):193904. doi:10.1103/PhysRevLett.120.193904

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Liu Z, Gao S, Xiao W, Yang J, Huang X, Feng Y, et al. Measuring high-order optical orbital angular momentum with a hyperbolic gradually changing period pure-phase grating. Opt Lett (2018) 43:3076–9. doi:10.1364/OL.43.003076

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jahani S, Jacob Z. All-dielectric metamaterials. Nat Nanotechnology (2016) 11(1):23–36. doi:10.1038/nnano.2015.304

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang Y-H, Chen P, Xu C-T, Zhu L, Wang X-Y, Ge S-J, et al. Dynamically selective and simultaneous detection of spin and orbital angular momenta of light with thermoresponsive self-assembled chiral superstructures. ACS Photon (2022) 9(3):1050–7. doi:10.1021/acsphotonics.1c02017

CrossRef Full Text | Google Scholar

28. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science (2011) 334(6054):333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kuznetsov AI, Miroshnichenko AE, Brongersma ML, Kivshar YS, Luk’yanchuk B. Optically resonant dielectric nanostructures. Science (2016) 354(6314):aag2472. doi:10.1126/science.aag2472

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Soukoulis CM, Wegener M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat Photon (2011) 5(9):523–30. doi:10.1038/nphoton.2011.154

CrossRef Full Text | Google Scholar

31. Meinzer N, Barnes WL, Hooper IR. Plasmonic meta-atoms and metasurfaces. Nat Photon (2014) 8(12):889–98. doi:10.1038/nphoton.2014.247

CrossRef Full Text | Google Scholar

32. Paul D, Sharma DK, Kumar GVP. Simultaneous detection of spin and orbital angular momentum of light through scattering from a single silver nanowire. Laser Photon Rev (2022) 16(7):2200049. doi:10.1002/lpor.202200049

CrossRef Full Text | Google Scholar

33. Zhang F, Pu M, Li X, Ma X, Guo Y, Gao P, et al. Extreme-angle silicon infrared optics enabled by streamlined surfaces. Adv Mater (2021) 33(11):2008157. doi:10.1002/adma.202008157

CrossRef Full Text | Google Scholar

34. Fang X, Ren H, Gu M. Orbital angular momentum holography for high-security encryption. Nat Photon (2020) 14(2):102–8. doi:10.1038/s41566-019-0560-x

CrossRef Full Text | Google Scholar

35. Ren H, Fang X, Jang J, Bürger J, Rho J, Maier SA. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat Nanotechnology (2020) 15(11):948–55. doi:10.1038/s41565-020-0768-4

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ruffato G. Oam-inspired new optics: The angular metalens. Light: Sci Appl (2021) 10(1):96. doi:10.1038/s41377-021-00541-6

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Huang K, Liu H, Garcia-Vidal FJ, Hong M, Luk’yanchuk B, Teng J, et al. Ultrahigh-capacity non-periodic photon sieves operating in visible light. Nat Commun (2015) 6(1):7059. doi:10.1038/ncomms8059

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Park J, Lee K, Park Y. Ultrathin wide-angle large-area digital 3d holographic display using a non-periodic photon sieve. Nat Commun (2019) 10(1):1304. doi:10.1038/s41467-019-09126-9

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Huang L, Chen X, Mühlenbernd H, Zhang H, Chen S, Bai B, et al. Three-dimensional optical holography using a plasmonic metasurface. Nat Commun (2013) 4(1):2808. doi:10.1038/ncomms3808

CrossRef Full Text | Google Scholar

40. Wang H, He Y-M, Chung TH, Hu H, Yu Y, Chen S, et al. Towards optimal single-photon sources from polarized microcavities. Nat Photon (2019) 13(11):770–5. doi:10.1038/s41566-019-0494-3

CrossRef Full Text | Google Scholar

41. Zhang Y, Pu M, Jin J, Lu X, Guo Y, Cai J, et al. Crosstalk-free achromatic full Stokes imaging polarimetry metasurface enabled by polarization-dependent phase optimization. Opto-Electronic Adv (2022) 5(11):220058-1–13. doi:10.29026/oea.2022.220058

CrossRef Full Text | Google Scholar

42. Zhang F, Guo Y, Pu M, Chen L, Xu M, Liao M, et al. Meta-optics empowered vector visual cryptography for high security and rapid decryption. Nat Commun (2023) 14(1):1946. doi:10.1038/s41467-023-37510-z

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photon (2021) 15(4):253–62. doi:10.1038/s41566-021-00780-4

CrossRef Full Text | Google Scholar

44. Wen Y, Chremmos I, Chen Y, Yu S. Arbitrary Multiplication and Division of the Orbital Angular Momentum of Light. Physical Review Letters (2020) 124(21):213901. doi:10.1103/PhysRevLett.124.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Sahu R, Chaudhary S, Khare K, Bhattacharya M, Wanare H, Jha A K. Angular lens. Opt Express (2018) 26:8709–18. doi:10.1364/OE.26.008709

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Guo Y, Zhang S, Pu M, He Q, Jin J, Xu M, et al. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light: Sci Appl (2021) 10(1):63. doi:10.1038/s41377-021-00497-7

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Zhang R, Guo Y, Li X, He Q, Zhang Q, Zhang F, et al. Angular superoscillatory metalens empowers single-shot measurement of oam modes with finer intervals. Adv Opt Mater (2023) 2300009. doi:10.1002/adom.202300009

CrossRef Full Text | Google Scholar

48. Pu M, Li X, Guo Y, Ma X, Luo X. Nanoapertures with ordered rotations: Symmetry transformation and wide-angle flat lensing. Opt Express (2017) 25:31471–7. doi:10.1364/OE.25.031471

PubMed Abstract | CrossRef Full Text | Google Scholar