Amplitude and phase noise in two-membrane cavity optomechanics

Cavity optomechanics is a suitable field to explore quantum effects on macroscopic objects and develop quantum technology applications. A perfect control of the laser noise is required to operate the system in such extreme conditions necessary to reach the quantum regime. In this paper, we consider a Fabry–Perót cavity, driven by two laser fields, with two partially reflective SiN membranes inside it. We describe the effects of amplitude and phase noise on the laser introducing two additional noise terms in the Langevin equations of the system’s dynamics. Experimentally, we add an artificial source of noise on the laser. We calibrate the intensity of the noise, inject it into the system, and check the validity of the theoretical model. This procedure provides an accurate description of the effects of a noisy laser in the optomechanical setup and allows for quantifying the amount of noise.

1 Introduction

In cavity optomechanics, a number of mechanical degrees of freedom is coupled by a dispersive parametric coupling, typically due to the radiation pressure interaction, to one or more driven modes of an optical cavity [1]. Such a configuration can be realized on a large variety of platforms, with different cavity geometries, as well as very different kinds of mechanical modes, ranging from vibrational modes of 1D, 2D, or 3D systems to the center-of-mass motion of trapped nanoparticles and to bulk and surface acoustic waves of properly designed materials. Despite their macroscopic nature, these devices can now be operated in a quantum regime for a number of relevant applications in quantum technologies and for answering fundamental physics questions. For example, entangled states of radiation modes [2, 3] and mechanical modes [4, 5] and hybrid optomechanical entanglement [6], as well as squeezed states of optical [7–9] and mechanical [10] modes, have been generated. Detection of displacements and forces below the standard quantum limit (SQL) has been demonstrated [11], and also, microwave-optical transduction with added noise very close to the quantum limit has been demonstrated [12, 13].

In all these experiments, the required effective interaction between the mechanical and the cavity modes is obtained by engineering the amplitudes and the frequencies of the driving sources, which have to be phase-locked and stabilized as much as possible. In fact, as can be easily expected, both the amplitude and phase noise of the laser driving are detrimental for any quantum effects, as it has already been theoretically suggested [14, 15] and experimentally verified. In fact, analyses of the effect of the laser phase noise on the cooling of the mechanical mode appeared in [16–18], while its effect on squeezing was analyzed in [19]. On the one hand, one has to minimize these technical noise sources as much as possible, for example, by using filter cavities or moving to higher mechanical resonance frequencies where these noises become less relevant; on the other hand, it would be useful to develop a procedure for modeling and quantifying the effect of these noises in a simple way. Here, we provide such a procedure by considering a multimode cavity optomechanical system in which two silicon nitride (SiN) membranes are placed within a Fabry–Perót cavity and driven by two laser fields, which has been considered for a large number of physical processes, such as synchronization of mechanical modes [20, 21], mechanical state swapping [22], heat transfer [23], cooperativity competition [24], and enhancement of single-photon optomechanical coupling [25, 26]. Here, we artificially add amplitude and phase noise to one of the driving fields, the pump beam controlling the interaction in the linearized regime of cavity optomechanics [1], and show how one can calibrate and quantify the corresponding noise spectra and describe it in terms of the size of the noise spectra of additional amplitude and phase noise terms in the Langevin equations describing the dynamics.

The calibration and modelization of the laser noise presented here is general and can be applied to a generic optomechanical system. For its experimental verification, we consider here the so-called “membrane-in-the-middle” [27, 28] configuration of cavity optomechanics, which has been employed by many groups since 2008 [17, 20–23, 27, 28] and presents many advantages. In fact, thin semitransparent Si₃N₄ membranes are commercially available and present a very high mechanical quality factor due their intrinsic high stress [29]. Moreover, they are characterized by a negligible absorption at optical wavelengths [30] so that if they are placed near the waist of an optical Fabry–Perót cavity, losses due to scattering are negligible, and the cavity decay rate is mostly determined by the empty cavity finesse only [17, 27, 28, 30]. Furthermore, the single-photon optomechanical coupling with a given optical cavity mode can be fine-tuned by controlling the longitudinal and transversal positions of the membrane within the cavity [27, 28, 31]. These facts make membrane-in-the-middle optomechanical setups particularly suitable for operating in the resolved sideband regime and for reaching a very large optomechanical cooperativity, which are fundamental conditions for the realization and manipulation of quantum states of the cavity mode and of the mechanical resonator [1] and witnessed, for example, by the results of [3, 9, 11, 12]. Recent advances have shown that SiN membranes are particularly suitable for further engineering and suppression of clamping losses, either via the use of the on-chip seismic filtering stage [32] or phononic bandgap crystal designs [33], which have allowed very large mechanical quality factors, even at room temperature [33, 34].

This paper is organized as follows. In Section 2, we present the model Hamiltonian and show how one can modify the standard QLE treatment in order to include the effects of laser noise. In Section 3, we describe the experimental setup and show the detected noise spectra, either the output spectrum in transmission and the homodyne detection of the mechanical motion of the two membranes. In addition, we show how one can reconstruct and model the effect of the amplitude and phase noise of the driving fields. Section 4 presents the concluding remarks.

2 The model

The system is composed of two mechanical resonators which are effectively coupled through two driven optical cavity modes, as described in Figure 1, namely, the pump mode that is responsible for the optomechanical interaction and the probe mode to perform the spectral analysis. The Hamiltonian, hence, includes several components as follows:

$\begin{array}{ll}\hfill \widehat{H}/\hslash & ={\displaystyle \sum _{k=\mathrm{1,2}}}\left\{{\omega }_{c,k}{{\widehat{a}}_k}^{†}{\widehat{a}}_k+{\displaystyle \sum _{j=\mathrm{1,2}}}\left[{\omega }_{m,j}{\widehat{b}}_j^{†}{\widehat{b}}_j-g_{jk}^{\left(0\right)}{{\widehat{a}}_k}^{†}{\widehat{a}}_k\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right)\right]\right.\hfill \\ \hfill & +i{E}_k\left(t\right)\left({{\widehat{a}}_k}^{†}{e}^{-i\left[{\omega }_{L,k}t+{\varphi }_k\left(t\right)\right]}-{\widehat{a}}_k{e}^{i\left[{\omega }_{L,k}t+{\varphi }_k\left(t\right)\right]}\right)\},\hfill \end{array}(1)$

where the first term describes the energy of the cavity modes represented by the bosonic annihilation operator ${\widehat{a}}_k([{\widehat{a}}_k,{{\widehat{a}}_k}^{†}]=1)$ at frequency ω_c,k, where we consider ${\widehat{a}}_1$ the operator related to the probe mode and ${\widehat{a}}_2$ to the pump mode; the second term takes into account the energies of the two mechanical resonators with annihilation operators ${\widehat{b}}_j([{\widehat{b}}_j,{\widehat{b}}_j^{†}]=1)$ at frequency ω_m,j for the j-th membrane and the optomechanical interactions that appear from the dependence of the optical mode frequencies on the positions of the mechanical resonators and characterized by a single-photon coupling rate $g_{jk}^{(0)}=-\sqrt{\hslash /2m_j{\omega }_{m,j}}\cdot {\partial }_{x_j}{\omega }_{c,k}(x_j)$. The third and last describes the laser driving fields at frequencies ω_L,k. We consider general driving fields which are affected by fluctuations, both in amplitude and phase. The amplitude is related to the number of photons that enter into the cavity every second and can be written as $E_k(t)=\overline{E_k}+{ϵ}_k(t)$. The mean value corresponds to $\overline{E_k}=\sqrt{P_k{\kappa }_{1k}/\hslash {\omega }_{L,k}}$, where P_k is the laser power of the k-th optical mode and κ_1k is the cavity decay rate for the input mirror, while the time-dependent term ϵ_k(t) represents the real, zero-mean amplitude fluctuations of the k-th driving field.

FIGURE 1

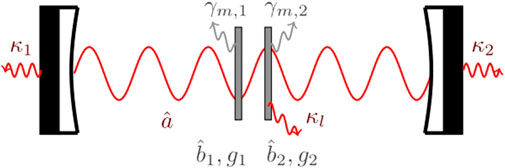
FIGURE 1. Two SiN membranes within a Fabry–Perót cavity. The two mechanical resonators ${\widehat{b}}_1$ and ${\widehat{b}}_2$, having masses m₁ and m₂, resonance frequencies ω_m,1 and ω_m,2, and damping rates γ_m,1 and γ_m,2, interact with an optical mode $\widehat{a}$. The cavity is characterized by decay rate κ₁ for the input port, κ₂ for the output port, and κ_l that takes into account losses due to absorption or scattering.

We considered $\overline{E_k}$ real, which means that we are choosing the laser driving field as a phase reference for the k-th optical field. Similarly, we call ω_L,k the average laser frequency, and ϕ_k(t) denotes the zero mean fluctuating phase. In order to remove the explicit time dependence from the Hamiltonian and consequently from the Langevin equations, one can choose the frame rotating at the laser frequency. Our case involves the exploitation of a fluctuating-frequency laser, so we pose in the randomly rotating frame at instantaneous frequency ${\omega }_{L,k}+{\dot{\varphi }}_k(t)$. One obtains a new form for the Hamiltonian devoid of the time-dependent exponentials of the laser driving term:

$\widehat{H}/\hslash ={\displaystyle \sum _{k=\mathrm{1,2}}}\left\{\left({\mathrm{\Delta }}_k^{\left(0\right)}-{\dot{\varphi }}_k\right){{\widehat{a}}_k}^{†}{\widehat{a}}_k+{\displaystyle \sum _{j=\mathrm{1,2}}}\left[{\omega }_{m,j}{\widehat{b}}_j^{†}{\widehat{b}}_j-g_{jk}^{\left(0\right)}{{\widehat{a}}_k}^{†}{\widehat{a}}_k\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right)\right]+i{E}_k\left(t\right)\left({{\widehat{a}}_k}^{†}-{\widehat{a}}_k\right)\right\},(2)$

where we defined the detuning ${\mathrm{\Delta }}_k^{(0)}={\omega }_{c,k}-{\omega }_{L,k}$. From the latter expression for the Hamiltonian, we are able to derive the quantum Langevin equations for the optical and mechanical modes as follows:

${\dot{\widehat{a}}}_k=-\left[\frac{{\kappa }_k}{2}+i\left({\mathrm{\Delta }}_k^{\left(0\right)}-{\dot{\varphi }}_k\right)\right]{\widehat{a}}_k+i{\displaystyle \sum _{j=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right){\widehat{a}}_k+E_k+\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}+{ϵ}_k\right)+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k},(3)$

${\dot{\widehat{b}}}_j=-\left(\frac{{\gamma }_{m,j}}{2}+i{\omega }_{m,j}\right){\widehat{b}}_j+i{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}{{\widehat{a}}_k}^{†}{\widehat{a}}_k+\sqrt{{\gamma }_{m,j}}{\widehat{b}}_{in,j}.(4)$

The Langevin equation for the optical mode takes into account the optical noise operators related to the input mirror ${\widehat{a}}_{in,1k}$, characterized by decay rate κ_1k, and the output mirror ${\widehat{a}}_{in,2k}$, which loses photons at rate κ_2k, meaning that the whole cavity has a total decay rate κ_k = κ_1k + κ_2k + κ_l, where κ_l takes into account the other loss mechanisms. Note that the laser amplitude noise is added to the optical noise; the system is indeed affected by the vacuum optical noise as well as the laser amplitude fluctuations. Differently, the phase frequency noise affects the optical mode acting as a multiplicative noise, similar to the position fluctuations of the mechanical resonators that appear because of the optomechanical interaction. Technical noise effects can be negligible or relevant depending on the quality of the laser itself. In fact, as will be shortly outlined, the features of the laser in connection with the frequency region of interest determine the significance of the laser noises. The Langevin equation for the j-th mechanical mode is governed by thermal noise ${\widehat{b}}_{in,j}$ and damping rate γ_m,j and shows an optomechanical interaction proportional to the number of intracavity photons. We consider the following Markovian correlation functions for the optical and mechanical input noise operators:

$⟨{\widehat{a}}_{in,lk}\left(t\right){\widehat{a}}_{in,l{k}^{\prime }}^{†}\left(t^{\prime }\right)⟩={\delta }_{k{k}^{\prime }}\delta \left(t-t^{\prime }\right),(5)$

$⟨{\widehat{b}}_{in,j}^{†}\left(t\right){\widehat{b}}_{in,j^{\prime }}\left(t^{\prime }\right)⟩=n_j^{th}{\delta }_{j{j}^{\prime }}\delta \left(t-t^{\prime }\right),(6)$

$⟨{\widehat{b}}_{in,j}\left(t\right){\widehat{b}}_{in,j^{\prime }}^{†}\left(t^{\prime }\right)⟩=\left(n_j^{th}+1\right){\delta }_{j{j}^{\prime }}\delta \left(t-t^{\prime }\right),(7)$

where the l index refers to the input or output port of interest. Both optical and mechanical noises are thermal and, hence, proportional to the thermal boson number given by the Bose–Einstein statistics $n^{th}={(e^{\hslash \omega /K_{B}T}-1)}^{-1}$. Specifically, at room temperature and at the cavity frequency ℏω_c,k/K_BT ≫ 1, the optical noise can be treated as vacuum noise, and the only relevant correlation is Eq. 5; differently, at the mechanical resonant frequencies, one can consider $n_j^{th}\simeq K_B{T}_j/\hslash {\omega }_j$. The correlation functions for the amplitude and phase noises have the following expressions:

$\langle {ϵ}_k\left(t\right){ϵ}_k\left(t^{\prime }\right)\rangle ={\mathrm{\Gamma }}_{ϵ,k}{\gamma }_{ϵ,k}{e}^{-{\gamma }_{ϵ,k}|t-t^{\prime }|},(8)$

$\langle {\dot{\varphi }}_k\left(t\right){\dot{\varphi }}_k\left(t^{\prime }\right)\rangle ={\mathrm{\Gamma }}_{L,k}{\gamma }_{\varphi ,k}{e}^{-{\gamma }_{\varphi ,k}|t-t^{\prime }|},(9)$

where Γ_ϵ,k is a dimensionless parameter that quantifies the intensity of the laser amplitude fluctuations and γ_ϵ,k corresponds to the bandwidth of the amplitude noise spectrum; analogously, Γ_L,k denotes the strength of the laser phase noise but has the dimension of a frequency, and γ_ϕ,k represents the bandwidth of the phase noise. More precisely, Γ_L,k stands for the linewidth of the laser that characterizes the laser spectrum itself, and typical values span in the range ∼ (1–100) kHz [15]. Performing the Fourier transform of such correlations, one obtains the following spectra for the noises:

$S_{ϵ,k}\left(\omega \right)={\mathrm{\Gamma }}_{ϵ,k}\frac{2{\gamma }_{ϵ,k}^2}{{\gamma }_{ϵ,k}^2+{\omega }^2},(10)$

$S_{\varphi ,k}\left(\omega \right)={\mathrm{\Gamma }}_{L,k}\frac{2{\gamma }_{\varphi ,k}^2}{{\gamma }_{\varphi ,k}^2+{\omega }^2}.(11)$

Therefore, we consider the amplitude and phase noises as colored noises with a Lorentzian spectrum that are different from the Markovian vacuum optical and thermal mechanical noises, which have a flat frequency noise spectrum. Indeed, a flat spectrum tends to overestimate the effect of laser noises [14]. However, we note that when γ_ϵ ≫ ω_m,j or γ_ϕ ≫ ω_m,j, we recover a flat frequency spectrum situation.

2.1 Linearized quantum Langevin equations

We focus on the stationary state of the system, and our purpose is to investigate the dynamics of the membranes around the equilibrium positions due to several noise sources. Hence, we consider the annihilation operators of the quantum Langevin equations as composed by a mean amplitude term and a fluctuation term around that value, so that the optical annihilation operator can be written as $\widehat{a}=\alpha +\delta \widehat{a}$ and the mechanical one results in $\widehat{b}=\beta +\delta \widehat{b}$. Disregarding the noises, by inserting this decomposition for the operators into Eqs 3, 4 and retaining the zero-th order terms, we obtain the steady-state values as follows:

${\alpha }_k=\frac{E_k}{{\kappa }_k/2+i{\mathrm{\Delta }}_k},(12)$

${\bar{x}}_j={\beta }_j+{\beta }_j^{\ast }=\frac{2{\sum }_k{g}_{jk}^{\left(0\right)}|\alpha {|}^2{\omega }_{m,j}}{{\gamma }_{m,j}^2/4+{\omega }_{m,j}^2}\simeq \frac{2{\sum }_k{g}_{jk}^{\left(0\right)}|\alpha {|}^2}{{\omega }_{m,j}}.(13)$

Here, we introduced a new detuning ${\mathrm{\Delta }}_k={\mathrm{\Delta }}_k^{(0)}-{\sum }_j{g}_{jk}^{(0)}{\bar{x}}_j$ which is influenced by the stationary position of both mechanical resonators and an effective coupling rate $g_{jk}=g_{jk}^{(0)}{\alpha }_k$. The final expression for the mean position of each mechanical resonator is valid in the case of the damping rate being much lower than the resonant frequency γ_m,j ≪ ω_m,j, a condition satisfied in optomechanical devices. Now, taking into account the first-order fluctuation terms, we obtain the linearized quantum Langevin equations for the annihilation operators as follows:

$\delta {\dot{\widehat{a}}}_k=-\left(\frac{{\kappa }_k}{2}+i{\mathrm{\Delta }}_k\right)\delta {\widehat{a}}_k+i{\displaystyle \sum _{j=\mathrm{1,2}}}{g}_{jk}\left(\delta {\widehat{b}}_j+\delta {\widehat{b}}_j^{†}\right)+\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}+{ϵ}_k\right)+i{\alpha }_k{\dot{\varphi }}_k+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k},(14)$

$\delta {\dot{\widehat{b}}}_j=-\left(\frac{{\gamma }_{m,j}}{2}+i{\omega }_{m,j}\right)\delta {\widehat{b}}_j+i{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}\left({\alpha }_k^{*}\delta {\widehat{a}}_k+{\alpha }_k\delta {\widehat{a}}_k^{†}\right)+\sqrt{{\gamma }_{m,j}}{\widehat{b}}_{in,j}.(15)$

We have omitted all the second-order terms, which are negligible when |α|≫ 1. From these equations, it is evident that in the linearized regime, the effect of the laser phase noise can be more relevant than that of the amplitude noise, since it is multiplied by the intracavity amplitude α. By switching to the frequency domain by performing the Fourier transform of Eqs 14, 15, we obtain

${\left[{\chi }_{c,k}\left(\omega \right)\right]}^{-1}{\widehat{a}}_k=i{\displaystyle \sum _{j=\mathrm{1,2}}}{g}_{jk}\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right)+\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}+{ϵ}_k\right)+i{\alpha }_k{\dot{\varphi }}_k+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k},(16)$

${\left[{\chi }_{c,k}^{*}\left(-\omega \right)\right]}^{-1}{\widehat{a}}_k^{†}=-i{\displaystyle \sum _{j=\mathrm{1,2}}}{g}_{jk}^{*}\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right)+\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}^{†}+{ϵ}_k\right)-i{\alpha }_k^{*}{\dot{\varphi }}_k+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k}^{†},(17)$

${\left[{\chi }_{m,j}\left(\omega \right)\right]}^{-1}{\widehat{b}}_j=i{\displaystyle \sum _{k=\mathrm{1,2}}}\left(g_{jk}^{*}{\widehat{a}}_k+g_{jk}{\widehat{a}}_k^{†}\right)+\sqrt{{\gamma }_{m,j}}{\widehat{b}}_{in,j},(18)$

${\left[{\chi }_{m,k}^{*}\left(-\omega \right)\right]}^{-1}{\widehat{b}}_j^{†}=-i{\displaystyle \sum _{k=\mathrm{1,2}}}\left(g_{jk}^{*}{\widehat{a}}_k+g_{jk}{\widehat{a}}_k^{†}\right)+\sqrt{{\gamma }_{m,j}}{\widehat{b}}_{in,j}^{†}.(19)$

The previous equations refer to the fluctuation operators, and we dropped out the fluctuation symbol δ for convenience. We introduced the optical and mechanical bare susceptibilities which are

${\left[{\chi }_{c,k}\left(\omega \right)\right]}^{-1}=\frac{{\kappa }_k}{2}-i\left(\omega -{\mathrm{\Delta }}_k\right),(20)$

${\left[{\chi }_{m,j}\left(\omega \right)\right]}^{-1}=\frac{{\gamma }_{m,j}}{2}-i\left(\omega -{\omega }_{m,j}\right).(21)$

In particular, for the probe field, we consider from now on a detuning Δ₁ = 0. By inserting Eqs 16, 17 into Eq. 18, one obtains the equation for one mechanical annihilation operator as a function of the other mechanical operators and noises:

$\begin{array}{ll}\hfill {\left[{\chi }_{m,j}^{\prime }\left(\omega \right)\right]}^{-1}{\widehat{b}}_j& =-i{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}{\sigma }_k\left(\omega \right)\left[g_{jk}^{\left(0\right)}{\widehat{b}}_j^{†}+g_{3-jk}^{\left(0\right)}\left({\widehat{b}}_{3-j}+{\widehat{b}}_{3-j}^{†}\right)+{\dot{\varphi }}_k\right]\hfill \\ \hfill & +i{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}\left\{{\alpha }_k^{*}{\chi }_{c,k}\left(\omega \right)\left[\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}+{ϵ}_k\right)+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k}\right]\right.\hfill \\ \hfill & \left.+{\alpha }_k{\chi }_{c,k}^{*}\left(-\omega \right)\left[\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}^{†}+{ϵ}_k\right)+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k}^{†}\right]\right\}+\sqrt{{\gamma }_{m,j}}{\widehat{b}}_{in,j},\hfill \end{array}(22)$

where we have defined ${\sigma }_k(\omega )=i|{\alpha }_k{|}^2\left[{\chi }_{c,k}^{*}(-\omega )-{\chi }_{c,k}(\omega )\right]$ and ${\left[{\chi }_{m,j}^{\prime }(\omega )\right]}^{-1}={\left[{\chi }_{m,j}(\omega )\right]}^{-1}+i{\sum }_k{\sigma }_{jk}(\omega )$ with ${\sigma }_{jk}(\omega )=g_{jk}^{(0)2}{\sigma }_k(\omega )$. We now choose to work in a rotating-wave approximation, valid in the red detuned regime (Δ > 0), weak coupling, and resolved sideband limit (g_j < κ ≤ ω_m,j); hence, we neglect the counter-rotating mechanical term ${\widehat{b}}^{†}$ and obtain the following equation for the j-th mechanical annihilation operator, which depends solely on the noise terms:

$\begin{array}{ll}\hfill & {\left[{\chi }_{m,j}^{\mathit{rwa}}\left(\omega \right)\right]}^{-1}{\widehat{b}}_j=-i{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}{\sigma }_k\left(\omega \right)\left[-i{\displaystyle \sum _{k^{\prime }=\mathrm{1,2}}}{g}_{3-jk}^{\left(0\right)}{g}_{3-j{k}^{\prime }}^{\left(0\right)}{\sigma }_{k^{\prime }}\left(\omega \right){\chi }_{m,3-j}^{\prime }\left(\omega \right){\dot{\varphi }}_{k^{\prime }}+{\dot{\varphi }}_k\right]\hfill \\ \hfill & +{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}\left\{{\displaystyle \sum _{k^{\prime }=\mathrm{1,2}}}{\sigma }_k\left(\omega \right)g_{3-jk}^{\left(0\right)}{g}_{3-j{k}^{\prime }}^{\left(0\right)}{\chi }_{m,3-j}^{\prime }\left(\omega \right)\left[{\alpha }_{k^{\prime }}^{*}{\chi }_{c,k^{\prime }}\left(\omega \right)\left(\sqrt{{\kappa }_{1k^{\prime }}}\left({\widehat{a}}_{in,1k^{\prime }}+{ϵ}_{k^{\prime }}\right)+\sqrt{{\kappa }_{2k^{\prime }}}{\widehat{a}}_{in,2k^{\prime }}\right)\right.\right.\hfill \\ \hfill & \left.+{\alpha }_{k^{\prime }}{\chi }_{c,k^{\prime }}^{*}\left(-\omega \right)\left(\sqrt{{\kappa }_{1k^{\prime }}}\left({\widehat{a}}_{in,1k^{\prime }}^{†}+{ϵ}_{k^{\prime }}\right)+\sqrt{{\kappa }_{2k^{\prime }}}{\widehat{a}}_{in,2k^{\prime }}^{†}\right)\right]+i\left[{\alpha }_k^{*}{\chi }_{c,k}\left(\omega \right)\left(\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}+{ϵ}_k\right)+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k}\right)\right.\hfill \\ \hfill & \left.\left.+{\alpha }_k{\chi }_{c,k}^{*}\left(-\omega \right)\left(\sqrt{{\kappa }_{1k}}\left({\widehat{a}}_{in,1k}^{†}+{ϵ}_k\right)+\sqrt{{\kappa }_{2k}}{\widehat{a}}_{in,2k}^{†}\right)\right]\right\}\hfill \\ \hfill & -i{\displaystyle \sum _{k=\mathrm{1,2}}}{g}_{jk}^{\left(0\right)}{g}_{3-jk}^{\left(0\right)}{\sigma }_k\left(\omega \right){\chi }_{m,3-j}^{\prime }\left(\omega \right)\sqrt{{\gamma }_{m,3-j}}{\widehat{b}}_{in,3-j}+\sqrt{{\gamma }_{m,j}}{\widehat{b}}_{in,j},\hfill \end{array}(23)$

where the effective susceptibility in rotating-wave approximation is

${\left[{\chi }_{m,j}^{\mathit{rwa}}\left(\omega \right)\right]}^{-1}={\left[{\chi }_{m,j}^{\prime }\left(\omega \right)\right]}^{-1}+{\displaystyle \sum _{k,k^{\prime }=\mathrm{1,2}}}{g}_{j,k}^{\left(0\right)}{g}_{j,k^{\prime }}^{\left(0\right)}{\sigma }_k{\sigma }_{k^{\prime }}{g}_{3-j,k}^{\left(0\right)}{g}_{3-j,k^{\prime }}^{\left(0\right)}{\chi }_{3-j}\left(\omega \right).(24)$

The first term of Eq. 23 takes into account the phase noise contributions for both the probe and pump laser beams, and the second one refers to the vacuum optical and amplitude laser noises for the input and output ports, while the latter term is related to the mechanical thermal noise.

2.2 Output quadrature spectrum

We detect the noise spectrum of the general amplitude quadrature ${\widehat{X}}_k=i({\widehat{a}}_k^{†}{e}^{i\phi }+{\widehat{a}}_k{e}^{-i\phi })/\sqrt{2}$. In particular, if we are interested in monitoring the pump field signal (which we denoted as optical mode 2) in transmission (hence measured from the output port 2), using the input–output relation, we obtain ${\widehat{X}}_{\mathit{out,22}}=\sqrt{{\kappa }_{22}}{\widehat{X}}_2-{\widehat{X}}_{in,22}$, where ${\widehat{X}}_{in,22}=({\widehat{a}}_{in,22}^{†}{e}^{i\phi }+{\widehat{a}}_{in,22}{e}^{-i\phi })/\sqrt{2}$. The expression for the output amplitude quadrature is

$\begin{array}{ll}\hfill {\widehat{X}}_{\mathit{out,22}}& =\sqrt{\frac{{\kappa }_{22}}{2}}\{-i\left({\alpha }_2^{*}{\chi }_{c,2}^{*}\left(-\omega \right)e^{i\phi }-{\alpha }_2{\chi }_{c,2}\left(\omega \right)e^{-i\phi }\right)\left({\displaystyle \sum _{j=\mathrm{1,2}}}{g}_{j2}^{\left(0\right)}\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right)+{\dot{\varphi }}_2\right)\hfill \\ \hfill & +\sqrt{{\kappa }_{12}}\left[{\chi }_{c,2}^{*}\left(-\omega \right)e^{i\phi }\left({\widehat{a}}_{in,12}^{†}+{ϵ}_2\right)+{\chi }_{c,2}\left(\omega \right)e^{-i\phi }\left({\widehat{a}}_{in,12}+{ϵ}_2\right)\right]\hfill \\ \hfill & +\sqrt{{\kappa }_{22}}\left[\left({\chi }_{c,2}^{*}\left(-\omega \right)-\frac{1}{{\kappa }_{22}}\right)e^{i\phi }{\widehat{a}}_{in,22}^{†}+\left({\chi }_{c,2}\left(\omega \right)-\frac{1}{{\kappa }_{22}}\right)e^{-i\phi }{\widehat{a}}_{in,22}\right]\}\hfill \end{array}(25)$

so that inserting Eq. 23 for the mechanical annihilation and creation operators in Eq. 25, one gets the full, but cumbersome, expression in terms of the noises. The related spectrum can be calculated as $S_{X_{\mathit{out}}}(\omega )={\int }_{-\infty }^{\infty }⟨{\widehat{X}}_{\mathit{out}}(\omega ){\widehat{X}}_{\mathit{out}}({\omega }^{\prime })⟩d{\omega }^{\prime }$ (see [1]). Hence, in order to derive the expression for the auto-correlation of the output optical quadrature, one needs to insert in the calculation the auto-correlation for each noise source, which is reported in Eqs 5–9 in the time domain. However, since we are working in the frequency domain, it is necessary to perform the Fourier transform of such quantities.

Similarly, the general phase quadrature ${\widehat{Y}}_k=i({\widehat{a}}_k^{†}{e}^{i\phi }-{\widehat{a}}_k{e}^{-i\phi })/\sqrt{2}$ can be obtained for the probe field signal (which we denoted as optical mode 1) in reflection (hence measured from the output port 1). From the input–output relation, we have ${\widehat{Y}}_{\mathit{out,11}}=\sqrt{{\kappa }_{11}}{\widehat{Y}}_1-{\widehat{Y}}_{in,11}$, where ${\widehat{Y}}_{in,11}=i\left[({\widehat{a}}_{in,11}^{†}+{ϵ}_1)e^{i\phi }-({\widehat{a}}_{in,11}+{ϵ}_1)e^{-i\phi }\right]/\sqrt{2}$. The expression is

$\begin{array}{ll}\hfill {\widehat{Y}}_{\mathit{out,11}}& =i\sqrt{\frac{{\kappa }_{11}}{2}}\{-i\left({\alpha }_1^{\ast }{\chi }_{c,1}^{*}\left(-\omega \right)e^{i\phi }+{\alpha }_1{\chi }_{c,1}\left(\omega \right)e^{-i\phi }\right)\left({\displaystyle \sum _{j=\mathrm{1,2}}}{g}_{j1}^{\left(0\right)}\left({\widehat{b}}_j+{\widehat{b}}_j^{†}\right)+{\dot{\varphi }}_1\right)\hfill \\ \hfill & +\sqrt{{\kappa }_{11}}\left[\left({\chi }_{c,1}^{*}\left(-\omega \right)-\frac{1}{{\kappa }_{11}}\right)e^{i\phi }\left({\widehat{a}}_{in,11}^{†}+{ϵ}_1\right)-\left({\chi }_{c,1}\left(\omega \right)-\frac{1}{{\kappa }_{11}}\right)e^{-i\phi }\left({\widehat{a}}_{in,11}+{ϵ}_1\right)\right]\hfill \\ \hfill & +\sqrt{{\kappa }_{21}}\left({\chi }_{c,1}^{*}\left(-\omega \right)e^{i\phi }{\widehat{a}}_{in,21}^{†}-{\chi }_{c,1}\left(\omega \right)e^{-i\phi }{\widehat{a}}_{in,21}\right)\}\hfill \end{array}(26)$

One can derive the expression in terms of the noises and the related spectrum through the aforementioned method.

3 Materials and methods

3.1 Description of the experimental setup

The optomechanical setup is constituted by two Si₃N₄ square membranes within an optical cavity [21, 25, 35, 36]. A laser beam at wavelength λ = 1064 nm is split into a probe beam and a pump beam. The first one has power P_pr = 3.8 µW, and it is modulated by using an electro-optical modulator (EOM). It is locked to the cavity resonance frequency by means of the Pound–Drever–Hall (PDH) technique. The fraction of the beam reflected by the cavity is revealed by homodyne detection, yielding an effective measurement of the motion of the membranes. The pump beam is more intense, and its power can be controlled. It is employed to realize the optomechanical interaction. The pump beam is also suitable to inject the amplitude and phase noise into the system and scan the cavity linewidth.

Amplitude and phase noise can be controlled by adding a modulation to the pump beam. The light modulation is implemented through an acousto-optic modulator (AOM), which is driven by a voltage-controlled oscillator (VCO). We control the frequency and the amplitude of the modulation feeding the VCO with DC signals. The frequency modulation (FM) is useful to detune the pump beam with respect to the cavity. The amplitude and phase modulation is used to introduce a seed beam into the cavity. We can evaluate the response function of the system to the amplitude and phase noise modulation, respectively, by measuring the light transmitted by the cavity at different frequencies of the seed. A schematic view of the experimental setup is depicted in Figure 2. The light transmitted by the cavity is collected on a PIN photodiode. The photocurrent is then amplified by using a FEMTO DHPCA-100 transimpedance amplifier with 1 × 10⁶ V/A gain and 3.5 MHz bandwidth.

FIGURE 2

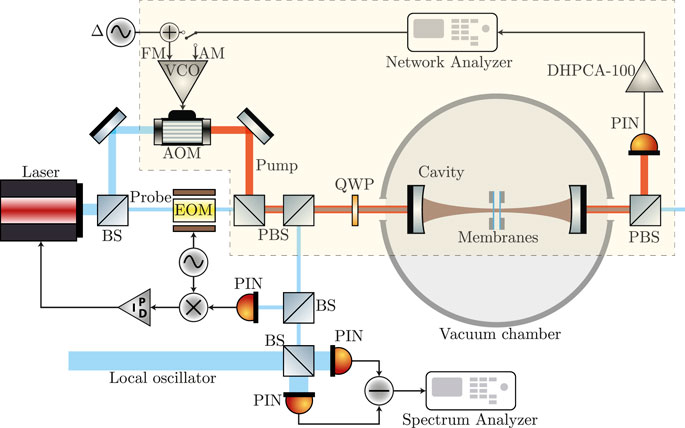
FIGURE 2. Schematic of the experimental setup. The laser is split into a probe beam and a pump beam. The probe is modulated by an EOM. A fraction of the reflected component is measured to implement the PDH technique. The remaining field is mixed with a local oscillator to obtain the homodyne signal. The pump beam, whose path is highlighted by the yellow-dashed poligon, is modulated through an AOM. The AOM is driven by a VCO. The frequency modulation allows the pump to be detuned in a controlled way from the cavity resonance frequency. The input ports of the VCO allow injecting amplitude and phase noise into the system. The cavity-transmitted light is detected directly by a PIN photodiode. The photocurrent is amplified using a FEMTO DHPCA-100 transimpedance amplifier.

3.2 Experimental parameters

The two membranes form themselves an inner cavity L_c = 53.571(9) μm long, the thickness of the Si₃N₄ layer is L_m = 106(1) nm, and the transverse dimensions were estimated from the normal mode spectrum to be $L_x^{(1)}=1.519(6)\mathrm{m}\mathrm{m}$, $L_y^{(1)}=1.536(6)\mathrm{m}\mathrm{m}$, $L_x^{(2)}=1.522(6)\mathrm{m}\mathrm{m}$, and $L_y^{(2)}=1.525(6)\mathrm{m}\mathrm{m}$. A complete description of the characterization method allowing to derive the aforementioned membrane parameters is presented in [25]. We have studied the fundamental vibration mode of the two membranes by measuring the voltage spectral noise of the reflected cavity field, revealed by homodyne detection, as shown in Figure 3.

FIGURE 3

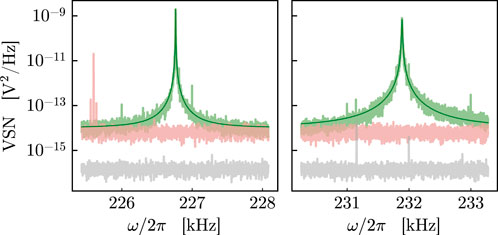
FIGURE 3. Homodyne voltage spectral noise (VSN) around mechanical fundamental mode frequencies. The light green curve shows the thermal noise of the mechanical oscillators. The mechanical parameters are estimated using the Lorentzian functions represented in green. The red curve indicates the shot noise level, and the black one is the electronic noise of the device.

The effective mass of the fundamental mode for both membranes is m_eff = 174 ng. The first oscillator is centered around ω_m,1 = 2π × 226.764581(1) kHz, with a bandwidth (i.e., the mechanical damping rate) γ_m,1 = 2π × 1.44(1) Hz, yielding a mechanical quality factor ${\mathcal{Q}}_{m,1}=$1.57×10⁵. For the second membrane, we have found ω_m,2 = 2π × 231.88732(2) kHz, γ_m,2 = 2π × 8.8(1) Hz, and ${\mathcal{Q}}_{m,2}=$2.63×10⁴. We evaluated the cavity decay rate by measuring its linewidth, and we extracted an amplitude decay rate κ = 2π × 119(1) kHz. The detuning is fixed to Δ = 2π × 240 kHz. The experimental parameters are presented in Table 1.

TABLE 1

TABLE 1. Optical and mechanical parameters.

3.3 Amplitude and phase noise calibration

We have experimentally verified the theoretical model by measuring the response of the optomechanical system to amplitude noise modulations on the pump beam. The pump beam transmitted by the cavity, around the mechanical frequencies, is detected with the schematic presented in Figure 2. To calibrate the quadrature spectrum, we have to point out the relationship between the theoretical spectrum, i.e., the spectrum of Eq. 25, and the measured data. Experimentally, a lock-in amplifier (LIA) is used to probe the response of the system at the modulation frequency Ω_m. We can calibrate the noise impinging on the cavity by measuring the ratio between the amplitude of the field sidebands, generated by the AOM modulation at frequency ±Ω_m, and the amplitude of the field at the carrier frequency. A heterodyne scheme can be easily obtained by mixing the pump beam and the probe beam polarizations. The amplitude of the pump field modulated by the AOM is written as

${ϵ}_{pu}\left(t\right)=\sqrt{{ϵ}_a^2+{ϵ}_m^2\cos \left({\mathrm{\Omega }}_{m}t\right)}{e}^{i\left({\omega }_L-\mathrm{\Delta }\right)t},(27)$

where ${ϵ}_a=\sqrt{P_{pu}/\hslash {\omega }_L}$, with P_pu = 67 µW. Instead, we do not add any artificial noise to the probe beam, and we can safely neglect the noise due to the laser (Coherent, Mephisto 500). The field of the probe is

${ϵ}_{pr}\left(t\right)={ϵ}_b{e}^{i{\omega }_{L}t}.(28)$

The intensity of the light impinging on the photodiode is given by

$\begin{array}{ll}\hfill |{ϵ}_{pu}+{ϵ}_{pr}{|}^2& \simeq \mathrm{D}\mathrm{C}+{ϵ}_m^2\cos \left({\mathrm{\Omega }}_{m}t\right)+2{ϵ}_a{ϵ}_b\left[1+\frac{1}{2}\frac{{ϵ}_m^2}{{ϵ}_a^2}\cos \left({\mathrm{\Omega }}_{m}t\right)\right]\cos \left(\mathrm{\Delta }t\right)\hfill \\ \hfill & =\mathrm{D}\mathrm{C}+{ϵ}_m^2\cos \left({\mathrm{\Omega }}_{m}t\right)+2{ϵ}_a{ϵ}_b\cos \left(\mathrm{\Delta }t\right)+2{ϵ}_a{ϵ}_b\frac{{ϵ}_m^2}{4{ϵ}_a^2}\left\{\cos \left[\left({\mathrm{\Omega }}_m+\mathrm{\Delta }\right)t\right]+\cos \left[\left({\mathrm{\Omega }}_m-\mathrm{\Delta }\right)t\right]\right\},\hfill \end{array}(29)$

assuming a small modulation ϵ_m ≪ϵ_a. This form clearly reveals a DC signal and oscillating components at Ω_m, Δ, and Ω_m ±Δ, respectively. We can measure the amplitude of the signal at different frequencies by means of an LIA. After the demodulation, the signal is passed through a fourth-order band-pass filter with 19 Hz bandwidth. We perform the demodulation at frequencies Δ, Ω_m + Δ, and Ω_m, to measure V_car, V_sb, and $V_{{\mathrm{\Omega }}_m}$, respectively. Eventually, we can calculate the amplitude of the modulation as

${ϵ}_m^2=4{ϵ}_a^2\frac{V_{sb}}{V_{\mathit{car}}}=4\frac{P_{pu}}{\hslash {\omega }_L}\frac{V_{sb}}{V_{\mathit{car}}}.(30)$

The calibration for different values of the modulation input voltage is presented in Figure 4A. The interference between the modulated pump and the probe also contains a component at frequency Ω_m, which is proportional to ${ϵ}_m^2$. The amplitude $V_{{\mathrm{\Omega }}_m}$ is related to ${ϵ}_m^2$ by

$V_{{\mathrm{\Omega }}_m}=\mathcal{A}{ϵ}_m^2,(31)$

where $\mathcal{A}$ takes into account the detection apparatus. We emphasize that V_sb and V_car contain the detection term too. When we divide them to determine the ratio ${ϵ}_m^2/{ϵ}_a^2$, the factor $\mathcal{A}$ cancels out, but, nonetheless, it can be calculated from $V_{{\mathrm{\Omega }}_m}$, V_sb, and V_car as follows:

$\mathcal{A}=\frac{V_{{\mathrm{\Omega }}_m}{V}_{\mathit{car}}}{4{ϵ}_a^2{V}_{sb}}.(32)$

FIGURE 4

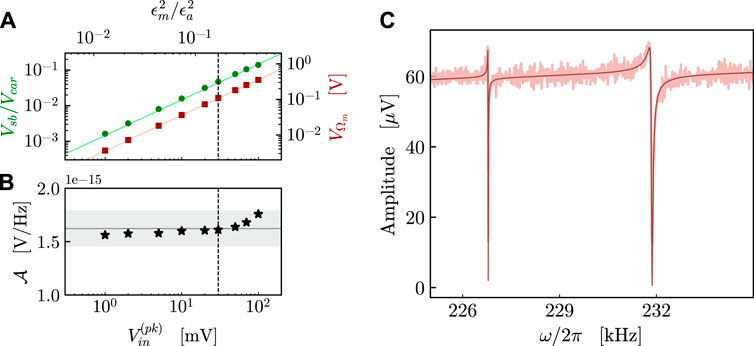
FIGURE 4. Calibration of the noise and transmitted seed spectrum around the mechanical frequency. (A) The green dots represent the measured ratio between sideband and carrier amplitudes, while the red squares are the amplitude of the signal at frequency Ω_m. The calibration is performed for different input voltages. (B) Calculated detection factors for different seed amplitudes. The horizontal line indicates the average of the points, with the shadow area representing ± 10% of variation from the mean value. (C) The seed is injected as the amplitude modulation of the pump beam, using an input voltage $V_{in}^{(pk)}=$30 mV, highlighted by the vertical dashed line in (A,B). The component transmitted by the cavity is detected. The interference between the seed directly transmitted by the cavity and the pump photons scattered by the oscillators gives rise to cancellations at the mechanical frequencies. The theoretical model, shown as a darker line on the experimental data, is calculated using the calibrated parameters. The single-photon optomechanical couplings $g_{12}^{(0)}=2\pi \times$0.13 Hz and $g_{22}^{(0)}=2\pi \times$0.39 Hz, respectively, optimize the fitting.

The measured points for $V_{{\mathrm{\Omega }}_m}$ at different modulation voltages are shown in Figure 4A, and the estimated $\mathcal{A}$ in Figure 4B. Moreover, we measured the seed transmitted by the cavity around the mechanical frequencies, injecting noise with voltage modulation $V_{in}^{(pk)}=$30 mV. The measured data are shown in Figure 4C and compared to the theoretical model given in Eq. 25. The theoretical curves reproduce the measured data accurately using a noise amplitude ϵ_m = 8.2 × 10⁶ Hz^1/2 and a detection factor $\mathcal{A}=$ 1.6 × 10⁻¹⁵ V Hz⁻¹, both given by the calibration. Experimentally, each point of the spectrum is obtained by simulating the effect of white noise within the bandwidth of the measurement BW = 10 Hz, and the equivalent amplitude noise spectral density Γ_ϵ, defined in Eq. 10 of the model, can be linked to ϵ_m through $2{\mathrm{\Gamma }}_{ϵ}={ϵ}_m^2/\mathrm{B}\mathrm{W}\simeq$6.7 × 10¹² Hz/Hz. The estimated value of the detection factor is valid for the measurement in Figure 4C. In fact, the detection system used for the calibration and the one employed to measure the light transmitted by the cavity are analogous. The best-fitting optomechanical couplings are comparable to what can be evaluated using the method in [35] and are given by $g_{12}^{(0)}=2\pi \times$0.13 Hz and $g_{22}^{(0)}=2\pi \times$0.39 Hz.

The spectrum in Figure 4C shows two Fano resonances with an asymmetric shape, which is a typical manifestation of interference, and its possible occurrence in optomechanical systems has been described, for example, in [37, 38]. In this case, the two dips in correspondence to the mechanical resonance frequencies of the membranes are due to the destructive interference between the amplitude noise of the driving pump directly transmitted by the cavity and the optical output associated with the effective response of each mechanical resonator to the same amplitude noise. In the experiment, the two oscillators have different bare mechanical quality factors and optomechanical couplings, resulting in two distinct effective responses, which appear in the spectrum as different shapes of the two dips. This output field cancellation is similar to optomechanically induced transparency (OMIT) [39, 40], stimulated in this case by the amplitude noise term.

Alternatively, we can inject noise on the phase of the pump beam. We have described previously a method to evaluate the amount of amplitude noise on the beam and introduced the factor $\mathcal{A}$ to take into account the detection. Using the experimental apparatus represented in Figure 2, we also measured the cavity output when the phase noise is injected into the system. In Figure 5, we show the spectrum of the light intensity transmitted by the cavity, near the mechanical resonances. In this case, the single-photon optomechanical couplings are $g_{12}^{(0)}=2\pi \times$0.42 Hz and $g_{22}^{(0)}=2\pi \times$0.51 Hz. The value of the detection factor is already determined, and it is given by $\mathcal{A}=$1.6 × 10⁻¹⁵ V Hz⁻¹. We can estimate the intensity of the phase noise seed by fitting the amplitude of the experimental data and obtain $\dot{\varphi }=$5.6 × 10⁵ Hz. This result yields the equivalent phase noise spectral density $2{\mathrm{\Gamma }}_L={\dot{\varphi }}^2/BW\simeq$3.1 × 10¹⁰ Hz²/Hz, which can be intended as the linewidth of the noisy simulated laser.

FIGURE 5

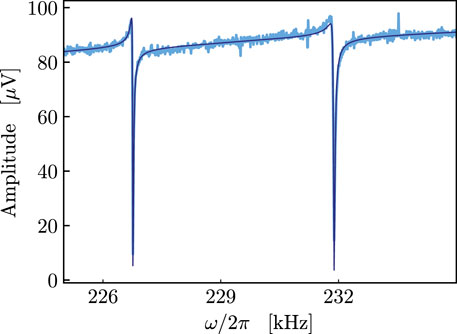
FIGURE 5. Seed is injected as phase modulation of the pump beam, and the output of the optical cavity is detected. The lighter curve represents the experimental data, with the darker one representing the best-fitting function. Knowing the detection factor $\mathcal{A}=$1.6 × 10⁻¹⁵ V Hz⁻¹, we can estimate the noise amplitude $\dot{\varphi }=$5.6 × 10⁵ Hz. The single-photon optomechanical couplings $g_{12}^{(0)}=2\pi \times$0.42 Hz and $g_{22}^{(0)}=2\pi \times$0.51 Hz, respectively, optimize the fitting. The values of single-photon optomechanical couplings are different from those of the amplitude noise case of the previous figure because the membranes have been displaced along the cavity axis from the previous positions, yielding a different coupling situation, as illustrated in [25].

The two dips in Figure 5 are again addressed to an OMIT-like behavior, here stimulated by the phase noise seed.

3.4 Noise cancellation

Eventually, we can detect the mechanical displacement noise by means of homodyne detection of the reflected probe beam while injecting amplitude noise in the system through the pump beam. The detection reveals the phase quadrature of the probe field in the presence of amplitude noise on the pump. The same detection can be carried out also by adding phase noise, obtaining almost identical results for the detected spectra. The noise calibration described in the previous section remains valid. The first excited modes of one membrane, labeled as (12) and (21), have resonance frequencies ${\omega }_m^{(12)}=366.8525(2)\mathrm{k}\mathrm{H}\mathrm{z}$ and ${\omega }_m^{(21)}=367.3389(2)\mathrm{k}\mathrm{H}\mathrm{z}$ and mechanical damping rates ${\gamma }_m^{(12)}=11.9(5)\mathrm{H}\mathrm{z}$ and ${\gamma }_m^{(21)}=8.6(4)\mathrm{H}\mathrm{z}$, respectively. The characterization of the mechanical parameters has been performed by fitting the mechanical displacement spectrum with Lorentzian peaks, as shown in Figure 6. Closer resonance frequencies, compared to the previous case of the fundamental modes of two distinct membranes, facilitate the observation of a cancellation window within them. Amplitude noise cancellation in a bandwidth between the two resonances is observed, and the theoretical result in Eq. 26 describes the measured data with an excellent agreement.

FIGURE 6

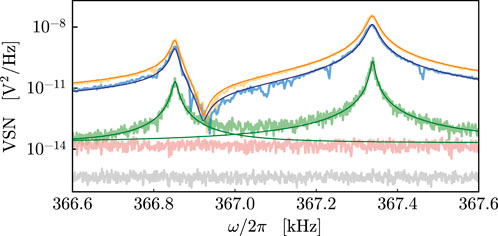
FIGURE 6. Homodyne voltage spectral noise around the first excited mechanical mode frequencies of one membrane. The lighter curves represent the measured data, and the solid darker lines represent the theoretical best-fitting functions. The green curve represents the thermal noise of the membrane, i.e., the homodyne signal spectrum when the pump beam is switched off. We estimate the mechanical parameters by fitting it with Lorentzian peaks. The orange and blue lines are measured injecting a seed of intensity ${ϵ}_m^2=$6.7 × 10¹³ Hz and ${ϵ}_m^2=$1.1 × 10¹⁴ Hz, respectively, through the pump beam amplitude. By sweeping the frequency of the seed, we obtain the spectra. A noise cancellation window can be noted within the two thermal peak frequencies. The shot noise is presented in red, and the electronic noise is presented in gray.

The orange and blue curves in Figure 6 refer to the case when amplitude noise is much larger than the other noise sources. As a consequence, the two mechanical modes are excited via radiation pressure by the same fluctuating force. In the spectral region between the resonances, the two mechanical responses are out of phase and destructively interfere, yielding visible noise cancellation. Similar noise cancellation phenomena have been observed in different experimental setups, and these features can be engineered to improve the sensitivity of the measurement within the cancellation’s bandwidth [41, 42].

4 Conclusion

In this work, we considered a multimode cavity optomechanical system in which two SiN membranes are placed within a Fabry–Perót cavity and driven by two laser fields. We provided a description of the effects of the laser’s amplitude and phase noises, which are introduced in the system’s equations of motion as an additive term and a multiplicative term, respectively. Moreover, we have used an artificial source of white noise to prove experimentally the validity of the model. We evaluated the equivalent noise spectral density when the artificial noises overwhelm the other sources of noise. Finally, the effective displacement spectral noise of the membranes in the presence of amplitude noise has been measured; a cancellation window within the mechanical resonance frequencies arises due to the opposite sign of the phases in the mechanical response. The theoretical model with the calibrated value of the noise provided an accurate description in this case as well.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors conceived the experiment. FM, RN, PP, and GDG performed the experiment. FR, FM, PP, GDG, and DV analyzed the data, and all authors wrote the paper. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors acknowledge financial support from the NQSTI within PNRR MUR project PE0000023-NQSTI.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/revmodphys.86.1391

CrossRef Full Text | Google Scholar

2. Barzanjeh S, Redchenko ES, Peruzzo M, Wulf M, Lewis DP, Arnold G, et al. Stationary entangled radiation from micromechanical motion. Nature (London) (2019) 570:480–3. doi:10.1038/s41586-019-1320-2

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chen J, Rossi M, Mason D, Schliesser A. Entanglement of propagating optical modes via a mechanical interface. Nat Commun (2020) 11:943. doi:10.1038/s41467-020-14768-1

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ockeloen-Korppi CF, Damskägg E, Pirkkalainen JM, Asjad M, Clerk AA, Massel F, et al. Stabilized entanglement of massive mechanicaloscillators. Nature (London) (2018) 556:478–82. doi:10.1038/s41586-018-0038-x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kotler S, Peterson GA, Shojaee E, Lecocq F, Cicak K, Kwiatkowski A, et al. Direct observation of deterministic macroscopic entanglement. Science (2021) 372:622–5. doi:10.1126/science.abf2998

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Palomaki TA, Teufel JD, Simmonds RW, Lehnert KW. Entangling mechanical motion with microwave fields. Science (2013) 342:710–3. doi:10.1126/science.1244563

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Brooks DWC, Botter T, Schreppler S, Purdy TP, Brahms N, Stamper-Kurn DM. Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature (2012) 488:476–80. doi:10.1038/nature11325

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Safavi-Naeini AH, Gröblacher S, Hill JT, Chan J, Aspelmeyer M, Painter O. Squeezed light from a silicon micromechanical resonator. Nature (2013) 500:185–9. doi:10.1038/nature12307

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Purdy TP, Yu PL, Peterson RW, Kampel NS, Regal CA. Strong optomechanical squeezing of light. Phys Rev X (2013) 3:031012. doi:10.1103/PhysRevX.3.031012

CrossRef Full Text | Google Scholar

10. Pirkkalainen JM, Damskägg E, Brandt M, Massel F, Sillanpää MA. Squeezing of quantum noise of motion in a micromechanical resonator. Phys Rev Lett (2015) 115:243601. doi:10.1103/PhysRevLett.115.243601

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Mason D, Chen J, Rossi M, Tsaturyan Y, Schliesser A. Continuous force and displacement measurement below the standard quantum limit. Nat Phys (2019) 15:745–9. doi:10.1038/s41567-019-0533-5

CrossRef Full Text | Google Scholar

12. Brubaker BM, Kindem JM, Urmey MD, Mittal S, Delaney RD, Burns PS, et al. Optomechanical ground-state cooling in a continuous and efficient electro-optic transducer. Phys Rev X (2022) 12:021062. doi:10.1103/PhysRevX.12.021062

CrossRef Full Text | Google Scholar

13. Seis Y, Capelle T, Langman E, Saarinen S, Planz E, Schliesser A. Ground state cooling of an ultracoherent electromechanical system. Nat Commun (2022) 13:1507. doi:10.1038/s41467-022-29115-9

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Rabl P, Genes C, Hammerer K, Aspelmeyer M. Phase-noise induced limitations on cooling and coherent evolution in optomechanical systems. Phys Rev A (2009) 80:063819. doi:10.1103/PhysRevA.80.063819

CrossRef Full Text | Google Scholar

15. Abdi M, Barzanjeh S, Tombesi P, Vitali D. Effect of phase noise on the generation of stationary entanglement in cavity optomechanics. Phys Rev A (2011) 84:032325. doi:10.1103/PhysRevA.84.032325

CrossRef Full Text | Google Scholar

16. Schliesser A, Riviere R, Anetsberger G, Arcizet O, Kippenberg TJ. Resolved-sideband cooling of a micromechanical oscillator. Nat Phys (2008) 4:415–9. doi:10.1038/nphys939

CrossRef Full Text | Google Scholar

17. Jayich AM, Sankey JC, Børkje K, Lee D, Yang C, Underwood M, et al. Cryogenic optomechanics with a si₃n₄ membrane and classical laser noise. New J Phys (2012) 14:115018. doi:10.1088/1367-2630/14/11/115018

CrossRef Full Text | Google Scholar

18. Meyer N, de Los Rios Sommer A, Mestres P, Gieseler J, Jain V, Novotny L, et al. Resolved-sideband cooling of a levitated nanoparticle in the presence of laser phase noise. Phys Rev Lett (2019) 123:153601. doi:10.1103/physrevlett.123.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Pontin A, Biancofiore C, Serra E, Borrielli A, Cataliotti FS, Marino F, et al. Frequency-noise cancellation in optomechanical systems for ponderomotive squeezing. Phys Rev A (2014) 89:033810. doi:10.1103/physreva.89.033810

CrossRef Full Text | Google Scholar

20. Sheng J, Wei X, Yang C, Wu H. Self-organized synchronization of phonon lasers. Phys Rev Lett (2020) 124:053604. doi:10.1103/physrevlett.124.053604

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Piergentili P, Li W, Natali R, Malossi N, Vitali D, Di Giuseppe G. Two-membrane cavity optomechanics: Nonlinear dynamics. New J Phys (2020) 23:073013. doi:10.1088/1367-2630/abdd6a

CrossRef Full Text | Google Scholar

22. Weaver MJ, Buters F, Luna F, Eerkens H, Heeck K, de Man S, et al. Coherent optomechanical state transfer between disparate mechanical resonators. Nat Commun (2017) 8:824. doi:10.1038/s41467-017-00968-9

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yang C, Wei X, Sheng J, Wu H. Phonon heat transport in cavity-mediated optomechanical nanoresonators. Nat Commun (2020) 11:4656–6. doi:10.1038/s41467-020-18426-4

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jong MD, Li J, Gärtner C, Norte R, Gröblacher S. Coherent mechanical noise cancellation and cooperativity competition in optomechanical arrays. Optica (2022) 9:170–6. doi:10.1364/optica.446434

CrossRef Full Text | Google Scholar

25. Piergentili P, Catalini L, Bawaj M, Zippilli S, Malossi N, Natali R, et al. Two-membrane cavity optomechanics. New J Phys (2018) 20:083024. doi:10.1088/1367-2630/aad85f

CrossRef Full Text | Google Scholar

26. Li J, Xuereb A, Malossi N, Vitali D. Cavity mode frequencies and strong optomechanical coupling in two-membrane cavity optomechanics. J Opt (2016) 18:084001. doi:10.1088/2040-8978/18/8/084001

CrossRef Full Text | Google Scholar

27. Thompson JD, Zwickl BM, Jayich AM, Marquardt F, Girvin SM, Harris JGE. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature (London) (2008) 452:72–5. doi:10.1038/nature06715

CrossRef Full Text | Google Scholar

28. Wilson DJ, Regal CA, Papp SB, Kimble HJ. Cavity optomechanics with stoichiometric sin films. Phys Rev Lett (2009) 103:207204. doi:10.1103/PhysRevLett.103.207204

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Southworth DR, Barton RA, Verbridge SS, Ilic B, Fefferman AD, Craighead HG, et al. Stress and silicon nitride: A crack in the universal dissipation of glasses. Phys Rev Lett (2009) 102:225503. doi:10.1103/PhysRevLett.102.225503

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Serra E, Bawaj M, Borrielli A, Di Giuseppe G, Forte S, Kralj N, et al. Microfabrication of large-area circular high-stress silicon nitride membranes for optomechanical applications. AIP Adv (2016) 6. doi:10.1063/1.4953805

CrossRef Full Text | Google Scholar

31. Biancofiore C, Karuza M, Galassi M, Natali R, Tombesi P, Di Giuseppe G, et al. Quantum dynamics of an optical cavity coupled to a thin semitransparent membrane: Effect of membrane absorption. Phys Rev A (2011) 84:033814. doi:10.1103/PhysRevA.84.033814

CrossRef Full Text | Google Scholar

32. Borrielli A, Marconi L, Marin F, Marino F, Morana B, Pandraud G, et al. Control of recoil losses in nanomechanical sin membrane resonators. Phys Rev B (2016) 94:121403. doi:10.1103/PhysRevB.94.121403

CrossRef Full Text | Google Scholar

33. Tsaturyan Y, Barg A, Polzik ES, Schliesser A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat Nanotechnology (2017) 12:776–83. doi:10.1038/nnano.2017.101

CrossRef Full Text | Google Scholar

34. Serra E, Borrielli A, Marin F, Marino F, Malossi N, Morana B, et al. Silicon-nitride nanosensors toward room temperature quantum optomechanics. J Appl Phys (2021) 130:064503. doi:10.1063/5.0055954

CrossRef Full Text | Google Scholar

35. Piergentili P, Li W, Natali R, Vitali D, Di Giuseppe G. Absolute determination of the single-photon optomechanical coupling rate via a hopf bifurcation. Phys Rev Appl (2021) 15:034012. doi:10.1103/PhysRevApplied.15.034012

CrossRef Full Text | Google Scholar

36. Piergentili P, Natali R, Vitali D, Di Giuseppe G. Two-membrane cavity optomechanics: Linear and non-linear dynamics. Photonics (2022) 9:99. doi:10.3390/photonics9020099

CrossRef Full Text | Google Scholar

37. Elste F, Girvin SM, Clerk AA. Quantum noise interference and backaction cooling in cavity nanomechanics. Phys Rev Lett (2009) 102:207209. doi:10.1103/PhysRevLett.102.207209

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Qu K, Agarwal GS. Fano resonances and their control in optomechanics. Phys Rev A (2013) 87:063813. doi:10.1103/PhysRevA.87.063813

CrossRef Full Text | Google Scholar

39. Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, et al. Optomechanically induced transparency. Science (2010) 330:1520–3. doi:10.1126/science.1195596

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Karuza M, Biancofiore C, Bawaj M, Molinelli C, Galassi M, Natali R, et al. Optomechanically induced transparency in a membrane-in-the-middle setup at room temperature. Phys Rev A (2013) 88:013804. doi:10.1103/PhysRevA.88.013804

CrossRef Full Text | Google Scholar

41. Caniard T, Verlot P, Briant T, Cohadon PF, Heidmann A. Observation of back-action noise cancellation in interferometric and weak force measurements. Phys Rev Lett (2007) 99:110801. doi:10.1103/PhysRevLett.99.110801

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Moaddel Haghighi I, Malossi N, Natali R, Di Giuseppe G, Vitali D. Sensitivity-bandwidth limit in a multimode optoelectromechanical transducer. Phys Rev Appl (2018) 9:034031. doi:10.1103/PhysRevApplied.9.034031

CrossRef Full Text | Google Scholar