- Multi-Scale Mechanics (MSM), Department of Thermal and Fluids Engineering (TFE), Faculty of Engineering Technology (ET), University of Twente, Enschede, Netherlands
How do soft granular materials (or dense amorphous systems) respond to externally applied deformations at different rates and for different system sizes? This long-standing question was intensively studied for shear deformations but only more recently for isotropic deformations, like compression–decompression cycles. For moderate strain rates, in the solid-like state, above jamming, the system appears to evolve more or less smoothly in time/strain, whereas for slow enough deformations, the material flips intermittently between the elastic, reversible base state and plastic, dynamic “events.” Only during the latter events, the microstructure re-arranges irreversibly. The reversible base state involves both affine and non-affine deformations, while the events are purely non-affine. The system size and rate dependence of the events are studied, providing reference data for comparison in future studies evaluating materials like hydrogel particles.
1 Introduction
In non-Newtonian fluids [1], colloidal suspensions [2], or granular matter [3, 4], the transport properties depend on various state variables, such as the density and granular temperature [5], but also on the deformation rate [6] and system size, which is a main focus of this study.
This interdependence and the presence of energy dissipation are at the origin of many interesting phenomena, like clustering [7], shear band formation [8], jamming/unjamming [9, 10], dilatancy [11], shear thickening [2, 12, 13], or shear jamming [10, 14, 15]. While granular gases are better described by kinetic theory [5], dense granular fluids and granular solids are much harder to understand, in particular since they can transit from fluid-like flowing states to static, reversibly elastic states, dependent on the inflow and dissipation of energy. How and why they achieve this transition is still under debate, e.g., by irreversible plastic deformations [16–25], related also to creep/relaxation [11, 26–28], and many other studies, see Ref. [29] and references therein.
Related experiments on systems other than granular matter are presented in Ref. [30] on creep and aging of hard-sphere glasses under constant stress [31], on rheological signatures of aging in hard-sphere colloidal glasses, or [32] rheology and relation to microstructure in colloids and metallic glasses. More recently, different further flow situations were studied in Ref. [33] for colloids under shear and extensional flow, and in Ref. [34] for yielding and resolidification of colloidal gels under constant stress, both related to rheology and aging, where the latter study is displaying intermittent, discrete “events” under very low shear stress conditions—possibly quite similar to the present results.
While slow shear shows evident stress drops due to meso-scale re-arrangements and deformations, see Refs. [21, 23–25], it was reported that there is only much weaker action under isotropic deformations in a small density window [21] for non-spherical, frictional particles. However, for frictionless spheres, a lot of re-arrangements are possible [4, 6] and visible if only the compression rate is slow enough. Therefore, we look closer to isotropic compression—over a wide density window, as relevant for soft particles—for moderate-to-very-slow compression rates and for various system sizes. A complementing study involved network analysis by persistence diagrams [35], and related results for frictional spheres are (to be) published elsewhere [29].
To the best of the author’s knowledge, it is not clear if and how the re-arrangements that occur during shear are related to the present “events” during (isotropic) compression. Both show similar characteristics, but the analysis and understanding of isotropic events lag behind, e.g., concerning questions about their avalanche type [20, 36–38], statistics, or the nature and shape of the minimal local events, as reported in Refs. [21, 23–25].
The remainder of the article is organized as follows: in Section 2, the system, the particle model, and the affine as well as non-affine deformation modes are discussed. In Section 3, particle simulations from isotropic loading cycles at highly different rates and system sizes are compared, and Section 4 concludes the study with the summary, conclusion, and outlook.
2 DEM particle simulations
The discrete element method (DEM) particle simulations presented here are a simple element test in a periodic cubical cell, in three dimensions, with only diagonal components of the strain rate tensor active. Only isotropic loading is presented here, from many different alternative loading paths (e.g., unloading, pure shear in plane strain, or axial strain modes). Deformations are applied to all particles in each time-step, while at the same time, the periodic cell size also changes accordingly. The reference system contains N = 3371 particles, with various additional simulations with 999 < N < 85184. The particle diameters are drawn randomly from a homogeneous size distribution with maximum to minimum width,
2.1 Non-dimensionalization of DEM
In this paper, parameters given with a prime, e.g.,
For working with units, there are two alternatives: one can read either the numbers in chosen, typical units (e.g., length,
2.2 Affine, non-affine, and event displacements
One basic idea of continuum theories—and relevant to granular packings—is that the macroscopic elastic work (per volume) needed to deform a system is equal to the sum of the work performed at the level of all grain–grain contacts:
where V is the system volume, kc is the contact stiffness, and δc is the overlap of all M contacts. Δq signifies the change in any quantity q, during a finite but small deformation during time Δt, without change in the contact network, ignoring dynamics/inertia (for simplification, without loss of generality). On the contact scale—not detailed further here—and on the particle scale, deformations can be split into global/average (affine) and local/fluctuating (non-affine) contributions.
The displacement of particle i during Δt is
where xi = xi(t) is the position of particle i at time t in a coordinate system with the origin relative to which deformations are applied2. The subscripts indicate (a) affine and (na) non-affine deformations, both reversible, and (ev) non-affine, irreversible displacements (during plastic events), with a velocity gradient ∇v or displacements Δx evaluated at the position of the particles. As introduced in Ref. [35] and shown in the following paragraph, for some of the present cases, the “events” are characterized by much higher displacement, velocity, or granular temperature (several orders of magnitude) than the system features during the smooth, reversible deformation phases.
In this study, the affine velocity gradient is homogeneous, i.e., for isotropic decompression/compression,
This desirable homogeneity is actively taken care of in the DEM simulations by a strain-control step that, first, computes the forces fi(t) at time t; second, integrates the equations of motion with a simple Verlet integrator:
third, computes the non-affine velocities:
fourth, updates the present velocity to the previous; and finally applies the affine displacement ∇ va ⋅xiΔt to every particle position at both3 times t + Δt and t (which will be t and t − Δt in the next iteration); finally, the time is increased by Δt before the next iteration.
This choice of step-sequence results in uniformly driven particle trajectories; their positions homogeneously follow the applied strain rate. On top of these (affine) displacements, the particles respond to their interaction forces, while the affine velocity (and thus inertia/momentum) is not active 4. In other words, the particle motion is integrated with a “moving” or deforming reference frame, where the affine velocity of particles,
If the total velocity
which enter the total affine kinetic energy5:
Note that while the first two terms (a and na) in Eq. 2 are reversible, only the first term is affine. The last two terms (na and ev) provide qualitatively different contributions to non-affine deformations. The former is reversible, due to the disordered structure of the packing, while the latter is irreversible, due to re-arrangements of the packing. Whether the granular temperature is isotropic or not can be checked by comparing the non-affine contributions in the three spatial directions, α (not discussed further here).
The first two terms in Eq. 2 provide the smooth, elastic, reversible total displacements of particles, both affine and non-affine, as will be detailed further in the following sections. However, the last term accounts for the much more violent dynamics during non-reversible deformations (events); it is intermittent, i.e., neither smooth in time nor in space (density); it reveals the plastic, irreversible system response to finite strain deformations and the subsequent relaxation dynamics toward a new, different elastic state.
Note the different system size and rate dependencies of the three different energies:
In this study without friction, dissipation is caused by normal contact dissipation only and leads to an exponential decay of kinetic energy Ek(t) ∝ exp (−t/tdiss), with a characteristic decay time tdiss ∝ (1 − r2), with a coefficient of restitution r (data not shown). Note the qualitative difference between the homogeneous cooling state of a (dilute or dense) granular gas Ek(t) ∝ t−2 and the solid Ek(t) ∝ exp (−t)—below and above jamming, respectively—as highlighted in Ref. [4].
In Figure 1, the affine, non-affine, and event displacements are visualized for one characteristic example, from before to after an event, while in Figure 2, a series of non-affine displacements is shown during compression, covering static steps, dynamic, local events, and system-spanning, global events.

FIGURE 1. Snapshots (2D projections) of the (left) affine, (middle) non-affine, and (right) total displacements, from data with very slow strain rate

FIGURE 2. Snapshots of the non-affine displacements at various volume fractions during compression, from the same simulation as in Figure 1. The first eight panels are taken at ϕ = 0.68731, relative to ϕ − Δϕ, with steps Δϕ = 0.00036, while the last four panels are taken from ϕ = 0.69202, with the same Δϕ. Counting from top, left to right, and then to bottom, panels 1, 2, 4, and 8 are from elastic situations, where Δxna is active, while Δxev ≈ 0. The black arrows are the upscaled displacement vectors, where the sixth panel, at ϕ = 0.68912—corresponding to the largest peak in Figure 4 (right)—has a much reduced scaling factor, 100 times smaller than others; particles are plotted as colored circles only if their non-affine displacement is higher than a certain threshold, where blue, green, and orange indicate increasing magnitudes of order 1, 100, and 104 higher than the threshold.
From Figure 1, we conclude that neither the affine nor the total displacements are relevant since they contain size-dependent affine motion contributions; we rather consider the non-affine displacements, which are either homogeneous in elastic, stable situations or quantify the event activity in the system, where the highlighted particles indicate the location of an event. During events, reversible, non-affine displacements are typically much smaller than irreversible, non-affine displacements, so we do not attempt to separate them but rather display in Figure 2, both non-affine contributions together as Δxnon-affine. In order to visualize the evolution during compression, the non-affine displacements of all particles (from ϕ = 0.682 to 0.693) are plotted as thin lines with a given stretch factor in Figure 2. The figure shows a smooth, almost (not perfectly) homogeneous non-affine deformation field for a few steps (panels 1, 2, and 4), disrupted by events of strongly varying magnitudes, where particles with displacements higher than a certain threshold are plotted in color, whereas the particles with less displacement amplitude are omitted. Some events are local when only a few particles are involved (panels 5, 7, 8, 10, and 12), while in one case, events are global where the whole system is violently involved (panel 6), and a few other cases (panels 3, 9, and 11) indicate events approaching system size and thus possible finite size effects.
3 Results
3.1 Rate- and size-dependent loading
In this subsection, various simulations are compared with different system sizes, and thus particle numbers N, and with different applied (constant) isotropic strain rates:
Next, physical quantities are reported for initial loading, from a density slightly below jamming, for different system sizes, complementing a previous study in Ref. [6], where the focus was on different rates.
The dimensionless pressure p = p′dp/kn is plotted against the volume fraction (density) in Figure 3 for a few different system sizes and for one system, N = 3375, as well as for different rates, as indicated in the legend. The fastest deformation rate (S) results in a smooth, nonlinear increase in pressure with ϕ, see Refs. [4, 14], while much slower rates result in much more discontinuous pressure increases at slightly lower magnitudes, see Ref. [6], where the pressure drops are perfectly sharp only for the very slow rate (XXXS). The pressure is not much different for different system sizes, for the compression rate (XXS), but the pressure drops (events) are somewhat less pronounced when the larger the system gets, as can be seen best in the right zoom-in panel. The slow and very slow simulation data support the picture illustrated in Refs. [4, 14], where each event means an increase in the jamming density ϕJ, with corresponding shift of the state-line p = p0 (ϕ − ϕJ) to the right in Figure 3; given a system with certain N and
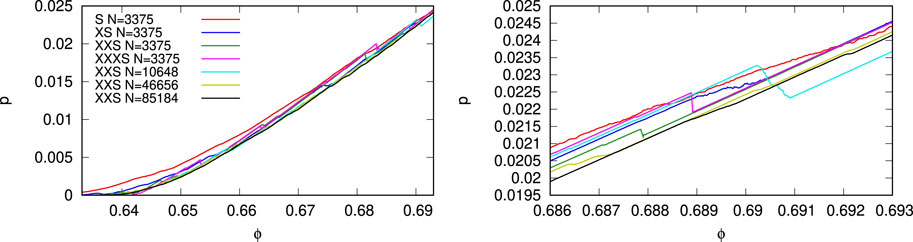
FIGURE 3. Dimensionless pressure p = p′d/kn plotted against the volume fraction for initial loading (left) and zoom-in (right) for different particle numbers N and strain rates, as indicated in the legend (every X means 10 times slower than the reference “S”), see main text for details. The data almost collapse for different slow strain rates [6], and the pressure magnitude is also almost independent of the system size. The reference simulation “S” features a systematically higher pressure than most of the other data due to the dynamic stress invoked by its comparatively large compression rate.
In Figure 4, the energy ratio K = Ek/Ep plotted against the volume fraction is strongly rate-dependent, as discussed previously in Ref. [6], with approximately two orders of magnitude difference between simulations that feature different rates with factors X (= 10) between each other. The largest strain rate (S) is comparatively smooth with K ≈ 10−3, while decreasing rates lead to smaller K, with more and more non-smooth, irregular, violent variations over many orders of magnitude. The slow (XXS) and very slow (XXXS) cases, feature baselines of the order of K ≈ 10−10 and K ≈ 10−12, respectively, approximately 20% lower than the affine kinetic energy ratio. The events, pressure drops, are associated with a very rapid increase in K by orders of magnitude and a subsequent exponential decay with time because ϕ ∝ t; this can be seen in zoom-in picture in Figure 4, where the cases XS, XXS, and XXXS decay slowly, rapidly, and very sharply, respectively; each drop is exponential, see Ref. [4], from a large K level, established during an event, back to the baseline. Note that (data not shown) the exponential rate of decrease is practically constant in time, given the same material properties (dissipation), even though the pressure drops appear with different negative slopes when plotted against ϕ—see also Ref. [29]. Only the very slow case (XXXS) shows perfectly separated peaks (events) due to the rapid decay of the kinetic energy ratio K, with ϕ, while the rather fast compression S does not show much fluctuation at all.
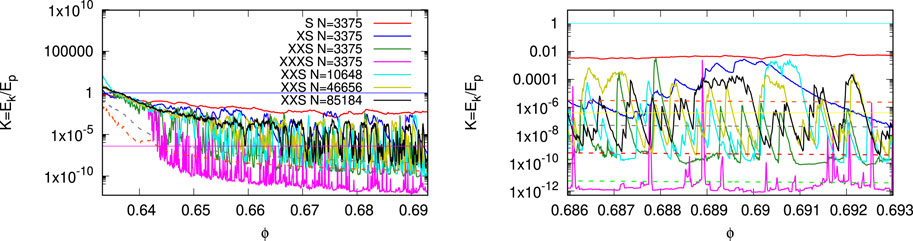
FIGURE 4. Kinetic-to-potential energy ratio Ek/Ep plotted against the volume fraction (density), for initial loading (left) and zoom-in (right), from the same simulations as in Figure 3 with the same colors. The horizontal lines are the ratio of unity (1), indicating the dynamic jamming/unjamming transition point, and K0 = 4 × 10−7, an arbitrary threshold below which the systems with rate XXS can be considered static, elastic, or reversible, almost in mechanical equilibrium. The two dashed lines in the left panel give the affine kinetic energy ratio Ek,a/Ep from the slow (XXS) small N = 3375 (lower) and large N = 85184 (upper) simulations; the four dashed lines in the right panel give Ek,a/Ep from the small N = 3375 simulation, with decaying rates S, XS, XXS, and XXXS, from top to bottom.
The zoom-in picture in Figure 4 (right) also shows the affine kinetic energy (dashed lines) at various rates from the small system. For the fastest compression case S, we observe Ek,na ≫ Ek,a; for the case XS, the non-affine energy varies considerably and reaches the affine case in its minimum only,
Considering the rate of case XXS only, the small system N = 3375 features clearly separated events, whereas the larger systems suffer more and more events with increasing N. For a given compression rate, more events mean that those are also overlapping in time (density). However, this can only be appreciated if the deformation rate is small enough, i.e., larger systems require even smaller rates than small systems if events are to be observed in isolation from each other. As a consequence, if K is used to identify the jamming density ϕJ, then care has to be taken to apply slow enough compression, like case XXXS; if events are too likely, too frequent, an artificially increased jamming density might be the consequence. From our more complete data, all system sizes 999 < N < 85184 consistently have their first, initial jamming at approximately ϕJ ≈ 0.641 ± 0.001. There is no systematic size dependence in ϕJ for these exemplary cases where particle number was varied by two orders of magnitude. A detailed statistical analysis of events (sizes, numbers, intervals, etc.) is in progress; however, data are not shown here since this is beyond the scope of this study.
3.2 Micro- and macro-mechanics observables
In Figure 5, the coordination numbers C* are also very similar for different system sizes N and for various slow compression rates. Only the faster simulation S is somewhat less than the other simulations, i.e., the coordination number is slightly smaller for more dynamic, faster compression. The slower the compression, the more localized the events in ϕ. Furthermore, like for pressure, events are associated with drops in C* that, if strong enough, can undershoot the continuous increase in coordination numbers due to compression. Note that for a few events, one can also observe an increase in C* after an event.
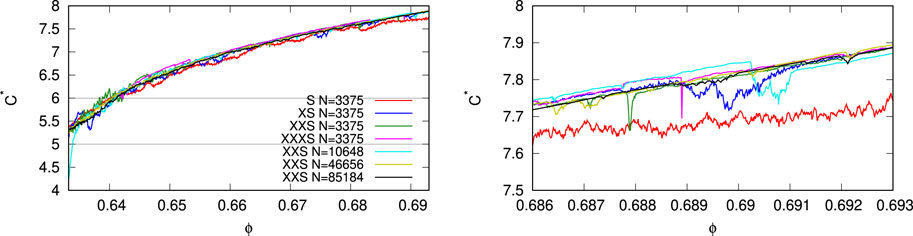
FIGURE 5. Coordination number, C* (without rattlers), plotted against the volume fraction (density), for initial loading (left) and zoom-in (right), from the same simulations as in Figure 3 with the same colors. The three horizontal lines indicate the levels C = 4, 5, and 6, respectively, where the jamming/unjamming, here, occurs at
In Figure 6, the bulk (tangent) modulus B is computed by discrete differentiation at density ϕ(t), such that B = dp/dɛV ≈ Δp/(−ΔV/V), where Δp = p (t + Δt) − p(t) and −ΔV/V = 1 − V (t + Δt)/V(t), only if K < K0 ≪ 1, with an arbitrary, small threshold K0 = 4 × 10−7. The modulus B appears to be independent of system size and rate (for small enough compression rates); only the negative peaks that indicate plastic, irreversible re-arrangement events are different. Note that B only shows up for the two slowest simulations, when the system is in an elastic state, with K < K0 ≪ 1.
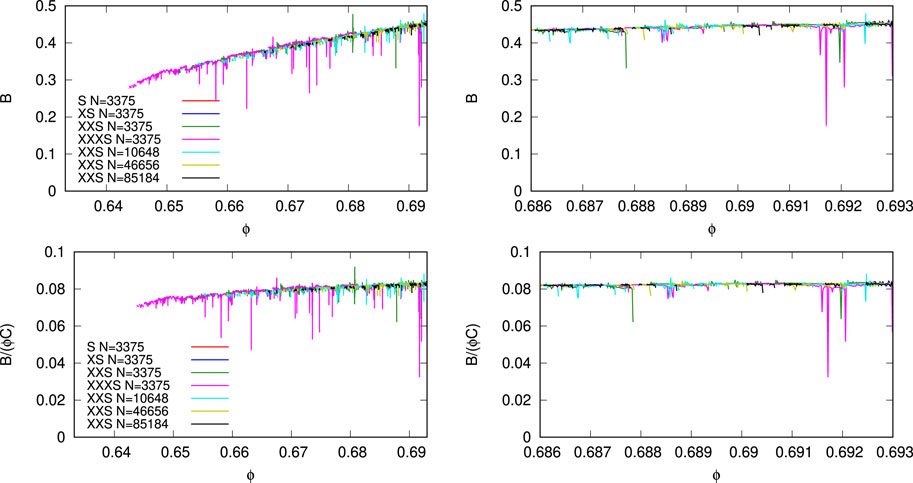
FIGURE 6. Bulk modulus B = dp/dɛV plotted (only for Ek/Ep < K0) against the volume fraction (density), from the same simulations as in Figure 3 with the same colors. Due to the rather low threshold K0, see Figure 4, the faster simulations (S and XS) do not show up here. Due to the discrete differentiation, the vertical peaks do not indicate B but the beginning/ending of a plastic, reorganization event with considerable dynamics. The cases (XXS) display a bulk modulus only higher than ϕ > 0.65, while the very slow case (XXXS) displays a bulk modulus much closer to ϕJ ≈ 0.641.
4 Conclusion and outlook
In summary, “microscopic” DEM particle simulations were used to track the system response at granular jamming and slightly above, in order to obtain some novel insights on the strain rate dependence and completely new results from different system sizes during initial isotropic loading. Another new observation concerns the affine and non-affine deformations and more details on the system evolution slightly above jamming during over-compression. For moderately fast compression, the system state variables, pressure, kinetic energy ratio, and coordination number, develop rather smoothly. However, for slower and slower compression rates, the system rather features elastic (base) states interrupted by discontinuous, irreversible re-arrangement “events.” During compression, the elastic states are reversible, mechanically stable configurations, with smooth minor changes (in pressure and coordination number) and very small kinetic energy; from those states, the bulk modulus can be deduced consistently for different rates and different system sizes. Every event is characterized by (i) a drop in pressure, mostly, (ii) a drop in coordination, and always (iii) a peak in kinetic energy; events are associated with a change in the jamming density, increasing during loading, as described in detail in Refs. [4, 14]. For different rates, if slow enough, the evolution becomes rate-independent and events occur after a certain strain step—where the frequency of events increases with increasing system size.
During isotropic compression, with a constant strain rate, the elastic (base) states deform affinely, due to the imposed strain field, as well as non-affinely, due to their disordered structure. The affine field leads to an artificial, system size-dependent kinetic energy Ek,a, which is ignored in objective, intensive analysis but seems to be comparable to, somewhat larger than the non-affine, fluctuation kinetic energy Ek,na, which is caused by the disorder in the contact network. During events, the non-affine deformation increases by orders of magnitude, featuring a dynamic, granular temperature. Events can be isolated only if the compression rate is small enough and if the system is not too large. The larger the system gets, the slower the compression rate needed to isolate events.
The “mesoscopic” system re-arrangement events can be local, involving only a few particles, or global, re-arranging most of the system; they can be tracked and identified from macroscopic information such as stress (drops) or kinetic energy (peaks)—if the deformation rate is small enough. For larger pressures, well above jamming, the system is much less sensible to the rate, and—except for too fast simulations—the system has more time between events (discrete in time) to relax back to hyper-elastic, mechanically stable, elastic states that also have a well-defined elastic bulk modulus.
However, even the smallest rate used here could not separate events very close to jamming, since their relaxation times are still too long, i.e., events are interfering with each other due to the comparatively fast compression rate. Therefore, in the future, even much slower compressions have to be performed. The slower the compression, the closer to jamming one gets in order to allow for a clean separation, identification, and statistical analysis of the events. The following questions remain unanswered: whether events can trigger each other if global events are a superposition of many local events and whether there are temporal/spatial interrelations between those.
Work in progress concerns more realistic contact models like frictional [29] or cohesive particles. The question of how the re-arrangement events look like and whether global events are possibly a superposition of many local events remains unanswered.
The present work also intends to include this into a macroscopic continuum-level theory as given in Eq. (84) in Ref. [4] but considering a more complete statistical analysis of event probabilities, waiting time (strain) distributions, and event magnitudes.
Finally, the relationship between this granular model system and other hard-sphere systems, such as dense colloidal suspensions or even metallic glasses, is still an open question for modern research.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Acknowledgments
The author thanks R. Basak, C. Cheng, K. Taghizadeh, and L. Kondic for their collaboration and valuable discussions on this research study during the last years. Thanks also to the referees for their helpful comments and constructive criticism that helped me to improve the paper.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1211394/full#supplementary-material
Supplementary Videos 1–5 | In the supplementary material of this paper, the velocity fields of the XXXS data set for N = 3375 are animated during the first five events (peaks in magenta curve in Fig. 4, right) at the volume fractions: ϕ1 = 0.68610, ϕ2 = 0.68775, ϕ3 = 0.68854, ϕ4 = 0.68883, and ϕ5 = 0.68931. The time-step used for the animations corresponds to Δϕ ≈ 0.69 × 10−7 with a static color code (blue, green, red corresponds to velocities of order of 10−4, 10−3, 10−2). Due to the strongly different intensities of event velocities, the movies involve different scaling factors v → δvv, for the lengths of the vectors, with
Footnotes
1The alternative dimensionless stress:
2In our systems, all deformations are applied symmetrically to the center, equally from all sides.
3The sequence of steps can be changed, such that the velocity contains the affine motion, but this is not detailed further here.
4An alternative way of driving compression/decompression in each direction is wall-driven, where the affine strain-control step is just left out (works for both wall and periodic boundary conditions). This works well for frictionless particles, if the deformation is slow; however, it is strongly discouraged for frictional and cohesive particles since it causes strong inhomogeneities due to inertia effects (data not shown). For isotropic deformations, there is an alternative to changing the system size, namely growing or shrinking particles such that their size distribution is conserved, like in experiments with swelling hydrogel particles. This procedure leads to identical results like the strain-driven method used here, even for frictional/cohesive materials since inertia is not active and the system remains homogeneous (work in progress, data not shown).
5The affine kinetic energy is valid for isotropic deformations, summing up
6Note that the factor (1/5), which connects the non-affine baseline minimum kinetic energy with the artificial affine kinetic energy, is both density- and system size-dependent and thus cannot be used as a constant, in general. Without more details, an approximation for the density dependence of the base non-affine kinetic energy is
References
2. Nicolas A, Ferrero EE, Martens K. Deformation and flow of amorphous solids: Insights from elastoplastic models. J.L Barrat, Rev Mod Phys (2018) 90:045006. doi:10.1103/revmodphys.90.045006
3. Jaeger HM, Nagel SR, Behringer RP. Granular solids, liquids, and gases. Rev Mod Phys (1996) 68:1259–73. doi:10.1103/revmodphys.68.1259
4. Luding S, Jiang Y, Liu M. Un-jamming due to energetic instability: Statics to dynamics. Granular Matter (2021) 23:80. doi:10.1007/s10035-021-01119-0
6. Luding S. How does static granular matter re-arrange for different isotropic strain rate? Powders and Grains 2021 – EPJ Web of Conferences (2021) 249:10001. doi:10.1051/epjconf/202124910001
7. Luding S. Towards dense, realistic granular media in 2D. Nonlinearity (2009) 22:R101–46. doi:10.1088/0951-7715/22/12/r01
8. Lätzel M, Luding S, Herrmann HJ, Howell DW, Behringer RP. Comparing simulation and experiment of a 2D granular Couette shear device. Eur Phys J E (2003) 11:325–33. doi:10.1140/epje/i2002-10160-7
9. Göncü F, Durán O, Luding S. Jamming in frictionless packings of spheres: Determination of the critical volume fraction. AIP Conf Procs Powders Grains (2009) 1145:531–4. doi:10.1063/1.3179980
10. Bi D, Zhang J, Chakraborty B, Behringer RP. Jamming by shear. Nature (2011) 480:355–8. doi:10.1038/nature10667
11. Ren J, Dijksman JA, Behringer RP. Reynolds pressure and relaxation in a sheared granular system. Phys Rev Lett (2013) 110:018302. doi:10.1103/PhysRevLett.110.018302
12. Mari R, Seto R, Morris JF, Denn MM. Discontinuous shear thickening in Brownian suspensions by dynamic simulation. Proc Natl Acad Sci (2015) 112:15326–30. doi:10.1073/pnas.1515477112
13. Singh A, Mari R, Denn MM, Morris JF. A constitutive model for simple shear of dense frictional suspensions. J Rheology (2018) 62:457–68. doi:10.1122/1.4999237
14. Kumar N, Luding S. Memory of jamming–multiscale models for soft and granular matter. Granular matter (2016) 18:58. doi:10.1007/s10035-016-0624-2
15. Wang D, Ren J, Dijksman JA, Zheng H, Behringer RP. Microscopic origins of shear jamming for 2D frictional grains. Phys Rev Lett (2019) 120:208004. doi:10.1103/physrevlett.120.208004
16. Einav I, Puzrin AM. Pressure-dependent elasticity and energy conservation in elastoplastic models for soils. J Geotechnical Geoenvironmental Eng (2004) 130:81–92. doi:10.1061/(asce)1090-0241(2004)130:1(81)
17. Wan RG, Pinheiro M, Guo PJ. Elastoplastic modelling of diffuse instability response of geomaterials. Int J Numer Anal Meth Geomech (2011) 35:140–60. doi:10.1002/nag.921
18. Manning ML, Liu AJ. Vibrational modes identify soft spots in a sheared disordered packing. Phys Rev Lett (2011) 107:108302. doi:10.1103/physrevlett.107.108302
19. Zhang Q, Kamrin K. Microscopic description of the granular fluidity field in nonlocal flow modeling. Phys Rev Lett (2017) 118:058001. doi:10.1103/physrevlett.118.058001
20. Long AA, Denisov DV, Schall P, Hufnagel TC, Gu X, Wright WJ, et al. From critical behavior to catastrophic runaways: Comparing sheared granular materials with bulk metallic glasses. Granular Matter (2019) 21:99. doi:10.1007/s10035-019-0946-y
21. Kuhn MR, Daouadij A. Stress fluctuations during monotonic loading of dense three-dimensional granular materials. Granular Matter (2019) 21:10. doi:10.1007/s10035-018-0861-7
22. Alaei E, Marks B, Einav I. A hydrodynamic-plastic formulation for modelling sand using a minimal set of parameters. Mech Phys Sol (2021) 151:104388. doi:10.1016/j.jmps.2021.104388
23. Clerc A, Wautier A, Bonelli S, Nicot F. Meso-scale signatures of inertial transitions in granular materials. Granular Matter (2021) 23:28. doi:10.1007/s10035-021-01087-5
24. Clerc A, Wautier A, Bonelli S, Nicot F. Mesoscale inertial transition in granular materials. EPJ Web of Conferences (2021) 249:10004. doi:10.1051/epjconf/202124910004
26. Brujić J, Song C, Wang P, Briscoe C, Marty G, Makse HA. Measuring the coordination number and entropy of a 3D jammed emulsion packing by confocal microscopy. Phys Rev Lett (2007) 98:248001. doi:10.1103/physrevlett.98.248001
27. Imole OI, Paulick M, Magnanimo V, Morgeneyer M, Montes BE, Ramaioli M, et al. Slow stress relaxation behavior of cohesive powders. Powder Technol (2016) 293:82–93. doi:10.1016/j.powtec.2015.12.023
28. Ando E, Dijkstra J, Roubin E, Dano C, Boller E. A peek into the origin of creep in sand. Granular Matter (2019) 21:11. doi:10.1007/s10035-018-0863-5
30. Ballesta P, Petekidis G. Creep and aging of hard-sphere glasses under constant stress. Phys Rev E (2016) 93:042613. doi:10.1103/physreve.93.042613
31. Jacob AR, Moghimi E, Petekidis G. Rheological signatures of aging in hard sphere colloidal glasses. Phys Fluids (2019) 31:087103. doi:10.1063/1.5113500
32. Voigtmann T, Siebenbürger M, Amann CP, Egelhaaf SU, Fritschi S, Krüger M, et al. Rheology of colloidal and metallic glass formers. Colloid Polym Sci (2020) 298:681–96. doi:10.1007/s00396-020-04654-z
33. Andrade RJE, Jacob AR, Galindo-Rosales FJ, Campo-Deano L, Huang Q, Hassager O, et al. Dilatancy in dense suspensions of model hard-sphere-like colloids under shear and extensional flow. J Rheology (2020) 64:1179–96. doi:10.1122/1.5143653
34. Moghimi E, Schofield AB, Petekidis G. Yielding and resolidification of colloidal gels under constant stress. J Phys Condens Matter (2021) 33:284002. doi:10.1088/1361-648x/abfb8d
35. Luding S, Taghizadeh K, Cheng C, Kondic L. Understanding slow compression and decompression of frictionless soft granular matter by network analysis. Soft Matter (2022) 18:1868–84. doi:10.1039/d1sm01689j
36. Dahmen KA, Ben-Zion Y, Uhl JT. Micromechanical model for deformation in solids with universal predictions for stress-strain curves and slip avalanches. Phys Rev Lett (2009) 102:175501. doi:10.1103/physrevlett.102.175501
37. Casals B, Dahmen KA, Gou B, Rooke S, Salje EKH. The duration-energy-size enigma for acoustic emission. Scientific Rep (2021) 11:5590. doi:10.1038/s41598-021-84688-7
38. Regev I, Attia I, Dahmen K, Sastry S, Mungan M. Topology of the energy landscape of sheared amorphous solids and the irreversibility transition. Phys Rev E (2021) 103:062614. doi:10.1103/physreve.103.062614
39. Ogarko V, Luding S. Prediction of polydisperse hard-sphere mixture behavior using tridisperse systems. Soft Matter (2013) 9:9530. doi:10.1039/c3sm50964h
40. Vescovi D, Luding S. Merging fluid and solid granular behavior. Soft Matter (2016) 12:8616–28. doi:10.1039/c6sm01444e
Keywords: granular matter, elastic–plastic behavior, force network re-arrangement, very slow compression, particle simulation
Citation: Luding S (2023) Elastic–plastic intermittent re-arrangements of frictionless, soft granular matter under very slow isotropic deformations. Front. Phys. 11:1211394. doi: 10.3389/fphy.2023.1211394
Received: 24 April 2023; Accepted: 07 September 2023;
Published: 25 October 2023.
Edited by:
Andrew Lyon, Chapman University, United StatesReviewed by:
Paul Umbanhowar, Northwestern University, United StatesGeorge Petekidis, University of Crete, Greece
Copyright © 2023 Luding. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Luding, cy5sdWRpbmdAdXR3ZW50ZS5ubA==
 Stefan Luding
Stefan Luding