- School of Mathematics and Statistics, Shaanxi Normal University, Xi’an, China
This paper deals with an unstirred competitive chemostat model with the Beddington–DeAngelis functional response. With the help of the linear eigenvalue theory and the monotone dynamical system theory, we establish a relatively clear dynamic classification of this system in terms of the growth rates of two species. The results indicate that there exist several critical curves, which may classify the dynamics of this system into three scenarios: 1) extinction; 2) competitive exclusion; and 3) coexistence. Comparing with the classical chemostat model [26], our theoretical results reveal that under the weak–strong competition cases, the role of intraspecific competition can lead to species coexistence. Moreover, the simulations suggest that under different competitive cases, coexistence can occur for suitably small diffusion rates and some intermediate diffusion rates. These new phenomena indicate that the intraspecific competition and diffusion have a great influence on the dynamics of the unstirred chemostat model of two species competing with the Beddington–DeAngelis functional response.
1 Introduction
It is well known that the chemostat is a laboratory apparatus used for the continuous culture of microorganisms, while the chemostat models are extensively applied in ecology to simulate the growth of single-celled algal plankton in oceans and lakes [1–4]. Most of the earlier chemostat models assume the well-stirring of culture, which leads to chemostat models generally described by ordinary differential equation models (see, e.g., [2, 4, 5]). However, this idealized mixing is quite different from the real environment in which microbial populations live. Since the ability of microorganisms to move in a random fashion plays an important role in determining the survival and extinction of populations, many unstirred chemostat models have sprung up in which populations and resources are distributed in spatially variable habitats; please refer to [6–10] for small sampling of such works.
There are various types of response functions; among them, Holling types I–IV [11] are usually introduced to model the growth of microorganisms. Particularly, the various chemostat models with Holling type II functional response have been extensively studied (see, e.g., [4, 10, 12, 13]). As far as we know, for the unstirred competitive chemostat models with Holling type II functional response, So and Waltman [14] first obtained the local coexistence by standard bifurcation theorems. Later, Hsu and Waltman [6] obtained the asymptotic behavior of solutions by the theory of uniform persistence in an infinite-dimensional dynamical system and the theory of strongly order-preserving semi-dynamical system. To explore the effect of diffusion, Shi et al. [8] further studied this model and confirmed that stable coexistence solutions only occur at the intermediate diffusion rates. In addition, a diffusive predator–prey chemostat model with Holling type II functional response was studied by Nie et al. [7], and their analytical and numerical results show that a relatively small diffusion is conducive to the coexistence of species.
However, in nature, it is known that there is not only competition between two species but also mutual interference in species. Therefore, it is necessary to consider mutual interference in species. To this end, Beddington [15] and DeAngelis et al. [16] (simplified as B.–D.) proposed the following B.–D. functional response:
where ki > 0 (i = 1, 2) are the Michaelis–Menten constants, S represents the density of the resources, u and v represent the density of two species, respectively, and βi > 0 (i = 1, 2) model the mutual interference between two species.
As illustrated by Harrision [17], the B.–D. functional response with intraspecific interference competition was superior to well-known Holling type II functional response in modeling the resource uptake of species. Therefore, there appear successively many works to describe the population dynamics by using the B.–D. functional response. For instance, Jiang et al. [18] discussed a competition model with the B.–D. functional response, and they applied the fixed-point index theory to obtain the sufficient conditions for the existence of positive solutions. In addition, a predator–prey model with a heterogeneous environment and the B.–D. functional response was constructed by Zhang and Wang [19], and the existence of positive stationary solutions was obtained by using the fixed-point index theory. We also refer the recent works [20–22] about population models with the B.–D. functional response.
Particularly, the unstirred chemostat models with the B.–D. functional response have also received considerable attention in the past decades. Wang et al. [23] obtained the sufficient conditions for the existence of positive steady-state solutions and studied the effect of parameter β1 on coexistence states by the fixed-point index theory, the perturbation technique, and the bifurcation theory. Meanwhile, Nie and Wu [24] studied the unstirred chemostat model with the B.–D. functional response and inhibitor, and the uniqueness, multiplicity, and stability of the coexistence solutions were obtained by the degree theory in cones, bifurcation theory, and perturbation technique. More works on chemostat models with the B.–D. functional response can be found in [25–27] and the references therein.
Mathematically speaking, these sufficient conditions for the existence of coexistence solutions are usually established in terms of the principal eigenvalues of the corresponding linearized eigenvalue problems at trivial or semi-trivial steady states (see, e.g., [18, 19, 23, 24]). It is worth noting that these principal eigenvalues depend heavily on the model parameters, which motivates us to explore how these model parameters affect the existence of coexistence solutions and establish the dynamics classification of this system in terms of these model parameters. Moreover, it should be noted that studying the asymptotic analysis of steady states of chemostat models is non-trivial, and some new techniques need to be introduced. Overall, for the unstirred chemostat system with the B.–D. functional response, we are concerned with the following questions:
(1) How do parameters such as diffusion rates, growth rates, and intraspecific competition parameters affect the dynamics of the unstirred chemostat system with the B.–D. functional response?
(2) Can we establish a clear dynamic classification of the unstirred chemostat system with the B.–D. functional response in terms of these parameters?
(3) Will there arise a new phenomenon if one introduces the B.–D. functional response into the unstirred chemostat model?
The purpose of this paper is to address these problems. We hope that the approaches in this paper might provide some new insights on the dynamical behavior of the unstirred chemostat models.
This paper is organized as follows. In Section 2, we introduce an unstirred chemostat model with the B.–D. functional response and its corresponding limiting system. In Section 3, some preliminary results are given. In Section 4, we aim to investigate the dynamics of this limiting system and obtain a relatively clear dynamic classification of this limiting system in the m1 − m2 plane. In Section 5, the coexistence solution for this limiting system is established by a bifurcation argument. In Section 6, we study the effect of diffusion on system dynamics by numerical approaches. In Section 7, a discussion is presented from the opinion of analytic and numerical results. Finally, the proofs of some theoretical results are deferred to the Supplementary Appendix in Supplementary Section S8.
2 The model
In this paper, we consider following the unstirred chemostat system with the B.–D. functional response:
where S(x, t) is the concentration of the nutrient and u(x, t) and v(x, t) represent the population density for the two competing microorganisms with location x and time t, respectively. The positive constants m1 and m2 are corresponding to the growth rates of species u and v with nutrient concentration S. d > 0 is the diffusion rate of the nutrient and microorganisms. The initial data S0(x), u0(x), and v0(x) are non-negative non-trivial continuous functions. In the reactor, the nutrients are pumped with the rate of S0 > 0 at position x = 0, and the mixed cultures containing nutrients and microorganisms are pumped out with the rate of γ > 0 at the position x = 1, which results in the Robin boundary conditions at x = 1 [6]. Here, f1(S, u), f2(S, v) satisfying Eq. 1.1 are the nutrient uptake of species u and v at nutrient concentration S. Moreover, we redefine f1(S, u), f2(S, v) as follows [10]:
For convenience, we still denote
It is worth pointing out that system (2.1) satisfies the conservation law [4]. In other words, the total biomass concentration S + u + v in the chemostat approaches asymptotically a steady state
Hence, we apply the classical internal chain transitive theory [[28], Lemma 2.1] to reduce system (2.1) into the following limiting system:
In this paper, we are mainly concerned with the dynamics classification of system (2.2). Based on the competition relationship of two species, system (2.2) generates a strictly monotone dynamical system in the partial competitive order induced by the cone K = {(u, v) ∈ C[0, 1] × C[0, 1]: u ≥ 0, v ≤ 0} (see [27], Proposition 1.3 in Chapter 8). Since the dynamics of Eq. 2.2 are related to the stability of non-negative steady states [29], we also focus on the following steady-state system:
The contribution of this paper is to explore the effect of these model parameters on the dynamics of system (2.2). Precisely, we first apply the linear eigenvalue theory and the monotone dynamical system theory to establish the threshold dynamics of system (2.2) in terms of growth rates and intraspecific competition parameters (see Theorems 4.1, 4.2). Moreover, we give a relatively clear dynamic classification of system (2.2) in the m1 − m2 plane (Figure 2). Finally, by numerical simulations, we further investigate the effect of diffusion on the dynamics of system (2.2) (Figures 3–5). Particularly, the numerical results show that under the different competitive cases, coexistence occurs for suitably small diffusion rates and some intermediate diffusion rates, which reveals that the dynamics of system (2.2) are relatively complicated.
3 Preliminaries
In this section, some preliminary results are presented, which are helpful in the following analysis.
We first consider a linear eigenvalue problem
where γ is a positive constant and q(x) ∈ C[0, 1]. For fixed d > 0, it is well known that problem (3.1) admits a principal eigenvalue μ1(q(x)) [29], which corresponds to a positive eigenfunction φ1(⋅, q(x)) normalized by
Moreover, the principal eigenvalue μ1(q(x)) has the following properties.
Lemma 3.1 (See [21], Lemma 2.1). The following statements on the principal eigenvalue μ1(q(x)) are true:
(i) μ1(q(x)) depends continuously and differentially on parameter d in (0, + ∞), and it is strictly decreasing with respect to d in (0, + ∞).
(ii) qn(x) → q(x) in C[0, 1] implies μ1(qn(x)) → μ1(q(x)).
(iii) q1(x) ≥ q2(x) implies that μ1(q1(x)) ≥ μ1(q2(x)), and the equality holds only if q1(x) ≡ q2(x). Particularly, μ1(0) < 0.
We consider the following single-species model:
where d, m > 0 are constants and
where
To stress the dependence of the unique positive steady state of system (3.3) on m and β, let us denote it by ω∗(⋅; m, β).
Lemma 3.2 Suppose d, m, β, k > 0. Let ω(x, t) be the solution of system (3.3). Then,
(i) if m > m∗, system (3.3) admits a unique positive steady state 0 < ω∗(⋅; m, β) < ϕ(x) for x ∈ [0, 1], and
(ii) if m ≤ m∗, system (3.3) has no positive steady state and
The proof of Lemma 3.2 is similar to the arguments in [6], Theorem 3.2. So, we omit it here.
We next give some asymptotic properties of the unique positive steady state ω∗(⋅; m, β) of system (3.3) by taking m and β as the variable parameters.
Lemma 3.3 suppose that m > m∗ holds. The following statements about the positive solution ω∗(; m, β) will hold.
(i) For fixed d, k, β > 0, there exists positive solution ω∗(; m, β), which is continuously differentiable with respect to m in (m∗, + ∞), and it is point-wise strictly increasing in m ∈ (m∗, + ∞). Moreover,
(ii) For fixed d, k > 0 and m > m∗, there exists positive solution ω∗(⋅; m, β), which is continuously differentiable with respect to β in (0, + ∞), and it is point-wise strictly decreasing in β ∈ (0, + ∞). Moreover,
Proof For (i), it follows from Lemma 3.2 that ω∗(⋅; m, β) exists if and only if m > m∗. Moreover, ω∗(⋅; m, β) is continuously differentiable with respect to m in (m∗, + ∞) refering to the arguments in [30], Lemma 5.4(ii). Differentiating the equation of ω∗(⋅; m, β) with respect to m and denoting Pm(x) = ∂ω∗(⋅; m, β)/∂m, Pm(x) satisfies
We define
Since 0 < ω∗(⋅; m, β) < ϕ and
To prove ω1 = 0 on [0,1], we assume by contradiction that ω1≢0 on [0,1]. Since 0 < f(ϕ − ω∗, ω∗) < 1, the standard Lp-estimate implies that ω∗(⋅; m, β) is uniformly bounded in W2,p(0, 1) with p ∈ (1, ∞) for m ∈ (m∗, M], where M is a fixed constant larger than m∗. Therefore,
Since ω1≢0 on [0,1], we have ω1 > 0 on [0,1] by the strong maximum principle. It is easy to see that μ1(m∗f(ϕ, 0)) > μ1(m∗f(ϕ − ω1, ω1)) = 0 by Lemma 3.1(iii), a contradiction to the definition of m∗ (Eq. 3.4). Thus, ω1 = 0.
We next prove ω2 = ϕ(x) on [0,1]. We recall that ω∗(⋅; m, β) satisfies
Dividing the first equation of Eq. 3.9 by mω∗ and integrating over (0,1),
which implies
Note
(ii) The monotonicity of ω∗(⋅; m, β) with respect to β in (0, + ∞) can be proved by the similar arguments as in the proof of (i) and
It is clear that system (2.2) generates a monotone dynamical system in the partial competitive order induced by the cone K = {(u, v) ∈ C[0, 1] × C[0, 1]: u ≥ 0, v ≤ 0} (see [27], Proposition 1.3 in Chapter 8). Hence, we can recall the well-known results on the monotone dynamical system as follows.
Lemma 3.4 [9]. For the monotone dynamical system,
(i) if two semi-trivial steady states are asymptotically stable, then it has at least one unstable coexistence steady state.
(ii) if two semi-trivial steady states are unstable, then it has at least one stable coexistence steady state. Furthermore, if its coexistence steady states are all linearly stable, then there is a unique coexistence steady state that is globally asymptotically stable.
(iii) if there is no coexistence steady state and if one semi-trivial solution is linearly unstable, the other semi-trivial solution is globally asymptotically stable.
4 The dynamics analysis of system (2.2)
As we already know, the local dynamics of system (2.2) are related to the stability of semi-trivial solutions [29]. Hence, we next establish the stability of semi-trivial solutions, including local and some global stability results. Recalling
Clearly,
Proposition 4.1 For fixed d > 0, the following statements hold:
Proof (i) Since
it is easy to check that
As the consequence of Lemma 3.2, system (2.2) admits the following trivial and semi-trivial solutions: trivial solution (0,0); semi-trivial solution (ω∗(⋅; m1, β1), 0) exists if and only if
Lemma 4.1 Suppose that (u(x), v(x)) is a non-negative solution of system (2.2) with u≢0 and v≢0 on [0,1]. Then,
(i)
(ii) 0 < u(x) + v(x) < ϕ(x) for x ∈ [0, 1]
The proof of Lemma 4.1 is exactly similar to that in [10], Lemma 4.2; hence, it is omitted here.
We next establish the linear stability of
where
subject to the corresponding boundary conditions. It follows from Lemma 3.1 (iii) that
The linearized operator of system (2.3) at
where
Similarly,
Theorem 4.1 We consider d, k1, k2 > 0 fixed. Let (u(x, t), v(x, t)) be the solution of (2.2) with any non-negative non-trivial initial condition. The following statements hold:
(i) We consider β1, β2 > 0 fixed.
(i.1) If
(i.2) If
(i.3) If
(ii) We consider
(ii.1) (4.8) holds provided
(ii.2) there exists a unique
(iii) We consider
(iii.1) Eq. 4.9 holds provided
(iii.2) there exists a unique
Proof (i) can be proved by the similar arguments as in [6], Theorems 3.5, 3.6, and we omit it here. Next, we only prove (ii), since (iii) can be proved by similar arguments.
Claim 1. For
Note that
which implies
which means that
Claim 2. (1) For
(2) There exists a unique
For (1), we recall that
provided
For (2), since
based on
which means that
Claim 3. For
We assume by contradiction that system (2.2) admits a positive steady state
Multiplying the first equation of (4.13) by
Since
In conclusion, we can deduce that (ii.1) holds from Claim 1, Claim 2(1), Claim 3, and Lemma 3.4(iii). In addition, (ii.2) is the direct result of Claim 1, Claim 2(2), and Lemma 3.4(ii). The proof is completed.
Remark 4.1 Theorem 4.1(i) implies that both species with sufficiently small growth rates are washed out, while competition exclusion occurs and the species with a sufficiently faster growth rate will finally win the competition. In particular, when both species admit sufficient fast growth rates, Theorem 4.1(ii.1) suggests that the species v with stronger growth ability (
We next investigate the local dynamics of system (2.2). Note that the stability of
Lemma 4.2 The principal eigenvalues σ1(m1, m2, β1) and τ1(m1, m2, β2) have the following properties:
(i) For fixed d, k1, k2 > 0 and
(i.1) σ1(m1, m2, β1) is strictly decreasing with respect to m1 in
(i.2) σ1(m1, m2, β1) is strictly increasing with respect to β1 in (0, + ∞),
(i.3) σ1(m1, m2, β1) is strictly increasing with respect to m2 in
(ii) For fixed d, k1, k2 > 0 and
(ii.1) τ1(m1, m2, β2) is strictly increasing with respect to m1 in
(ii.2) τ1(m1, m2, β2) is strictly increasing with respect to β2 in (0, + ∞),
(ii.3) τ1(m1, m2, β2) is strictly decreasing with respect to m2 in
Proof For (i), (i.1) can be obtained by Lemma 3.1(iii) and Lemma 3.3(i). Similarly, (i.2) is followed by Lemma 3.1(iii) and Lemma 3.3(ii). To prove (i.3), it is obvious that σ1(m1, m2, β1) is strictly increasing with respect to m2 in
For (ii), (ii.1) can be obtained by Lemma 3.1(iii), and (ii.2) can be proved by Lemma 3.1(iii) and Lemma 3.3(ii). We then prove (ii.3). Since
based on
The proof is completed.
Clearly, both σ1(m1, m2, β1) and τ1(m1, m2, β2) depend on m1 and m2. To investigate the local dynamics of system (2.2) in the m1 − m2 plane, we fix β1, β2 > 0 and denote them by σ1(m1, m2) and τ1(m1, m2).
Lemma 4.3 Suppose
where
respectively. Then,
(i) the semi-trivial steady state
(ii) the semi-trivial steady state
Proof (i) By Lemma 4.2(i), we conclude that for any
Therefore,
(ii) Similarly, we can conclude from Lemma 4.2(ii) that for any
Therefore,
Combining with Lemma 3.4 and Lemma 4.3, we obtain the following results.
Theorem 4.2 Suppose
(i) Suppose
(ii) Suppose
(iii) Suppose
For fixed d, k1, k2, β1, β2 > 0, Lemma 4.3 and Theorem 4.2 imply that there exist two critical curves Γ1 and Γ2 in the m1 − m2 plane, which divide the local dynamics of Eq. 2.2 into competitive exclusion, bi-stability, and coexistence. To further characterize classification on the dynamics of system (2.2) in the m1 − m2 plane, we next give some properties of critical curves Γ1 and Γ2. We recall
Clearly,
Proposition 4.2 We consider d, k1, k2 > 0 fixed. The critical curve
(i) For any β1 > 0 given,
(ii) For any
Particularly,
(iii) For any
where
Proof (i) For any β1 > 0 given, we can conclude from Lemma 4.2(i.1) (i.3) that
(ii) For any
Substituting β1 → 0+ in
Then, we can deduce from [26], Theorem 2.1 that
Finally, when
(iii) Let ψ1 > 0 with ‖ψ1‖∞ = 1 be the corresponding principal eigenfunction of
By differentiating Eq. 4.19 with respect to m1, denoting
where
We next show that
where
Since
Proposition 4.3 We consider d, k1, k2 > 0 fixed. The critical curve
(i) For any β2 > 0 given,
(ii) For any
Particularly,
(iii) For any
where
Proof (i) For any β2 > 0 given, we can conclude from Lemma 4.2(ii.1) (ii.3) that
(ii) For any
Similarly, substituting β2 → 0+ in
When
(iii) Let φ1 with ‖φ1‖∞ = 1 be the corresponding principal eigenfunction of
By differentiating Eq. 4.27 with respect to m1 and denoting
where
Similar to Proposition 4.2(iii), we can show
We assume k1 > k2 > 0 without loss of generality. Then, there exist six critical curves:
in the m1 − m2 plane (Figure 2), which classify the dynamics of system (2.2) into extinction of both species, competitive exclusion and coexistence. Clearly, it follows from Proposition 4.1(i) that line
Now, we are ready to illustrate the dynamical classification of system (2.2) in the m1 − m2 plane under the assumption k1 > k2 > 0, by dividing the following four cases.
Case I:
Case II:
Next, we illustrate two-fold that Γ2 will first intersect L2 and then lie above L2 as m1 increases (Figure 2B). On one hand, Theorem 4.1(ii) indicates that when
Case III:
Similarly, we next illustrate that Γ1 will first intersect L1 and then lie below L1 as m1 increases (see Figure 2C). On one hand, Theorem 4.1(iii) suggests that when
On the other hand, Proposition 4.2(iii) gives
Case IV:
We next make a comparison with the results in [8]. When the intraspecific competition is relatively weak (i.e., for the case of
However, when the intraspecific competition becomes strong, some new phenomena may occur. For instance, for the standard unstirred chemostat models, competition exclusion always happens for the weak–strong competition of two species (see [26], Theorem 2.1), while coexistence may occur in the unstirred chemostat model with B.–D. functional response with the increase of intraspecific competition, under the weak–strong competition cases (see Theorem 4.1 and Figures 2B–D). More precisely, under the weak–strong competition case
In summary, these theoretical results indicate that for the weak–strong competition cases, if the intraspecific competition parameter of the species with stronger growth ability is suitably large, we can observe different results from [8] that coexistence may occur. This new phenomenon suggests that the intraspecific competition parameters β1 and β2 have a great influence on the competitive outcomes of two species.
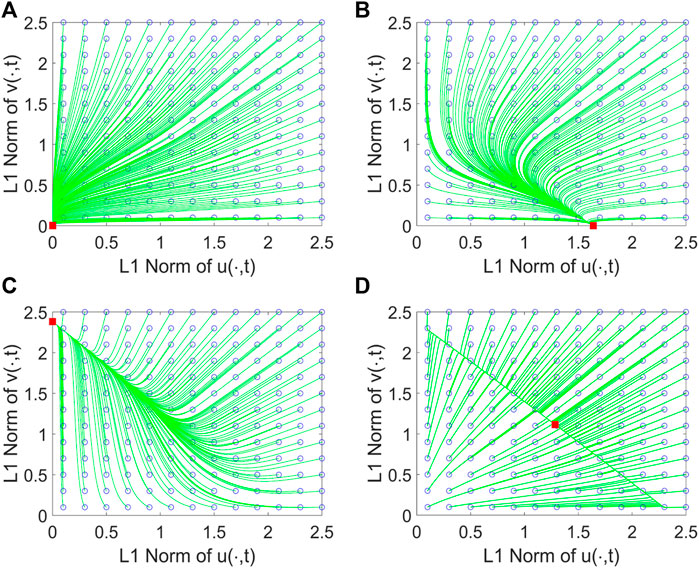
FIGURE 1. Phase portrait graphs of system (2.2) for different growth rates m1 and m2. Here, we take β1 = 0.01, β2 = 0.01, L = 1, S0 = 1, d = 0.5, γ = 0.5, k1 = 1, and k2 = 0.4. As shown, (0,0) is globally asymptotically stable (simplified as g.a.s) in (A) with m1 = 0.2, m2 = 0.1;
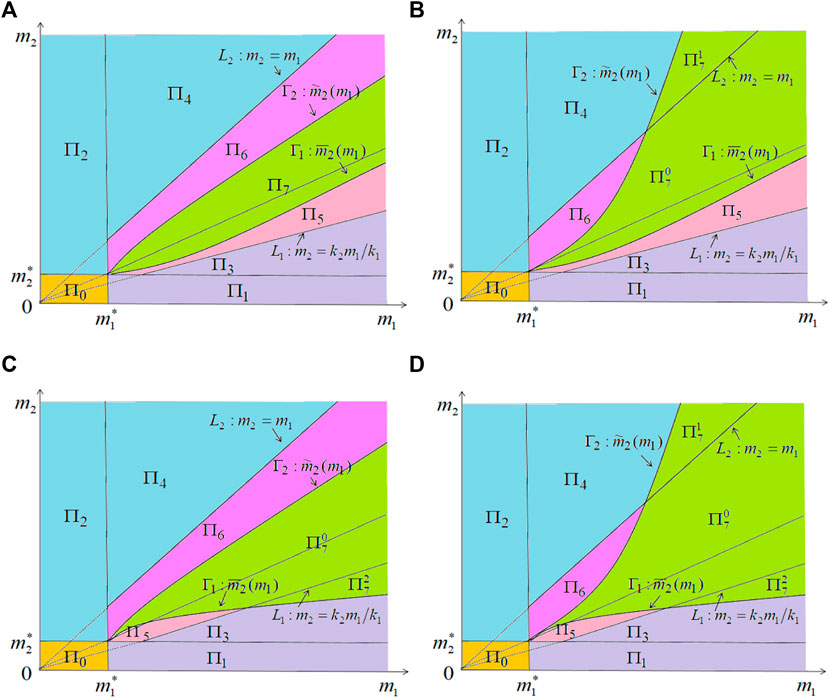
FIGURE 2. Illustration of the dynamics of system (2.2) in the m1 − m2 plane for the case of k1 > k2 > 0. More precisely, (A)
5 Positive solution branches of system (2.2)
We define X = W2,p(0, 1) × W2,p(0, 1) and Y = Lp(0, 1) × Lp(0, 1), where p > 1. For fixed d, k1, k2, β1, β2 > 0 and
We first show that there exists a positive solution branch that bifurcates from the semi-trivial solution
Theorem 5.1 For fixed d, k1, k2, β1, β2 > 0 and
and φ0 < 0 satisfies
Moreover,
where
Theorem 5.1. can be proved by the similar arguments as in [35], Theorem 6.2. For completeness, we defer the proof of Theorem 5.1 to the Supplementary Appendix.
Theorem 5.2 For fixed d, k1, k2, β1, β2 > 0 and
and
Moreover,
where
The proof of Theorem 5.2 is similar to the arguments in Theorem 5.1, and we omit it here.
We define
Theorem 5.3 We consider d, k1, k2, β1, β2 > 0 and
The proof is motivated by the methods in [13], Theorem 6.4 (see also [8], Theorem 4.10]). For readability, the proof is given in Supplementary Appendix.
6 Numerical descriptions
In this section, we will study the effect of diffusion rates d on the dynamics of system (2.2). It follows from Eqs 4.1, 4.15 that the threshold values
Case I:
First, if β1 = 0.01, β2 = 0.01, there is no coexistence and the competitive exclusion principle holds (species v with a stronger growth ability will win the competition) when d is sufficiently small (Figure 3A). As d increases, both species go extinct, which is consistent with our biological intuition that the sufficiently large diffusion rates will put species at a disadvantage. These numerical observations in Figure 3A coincide with [26], Theorem 5.4.
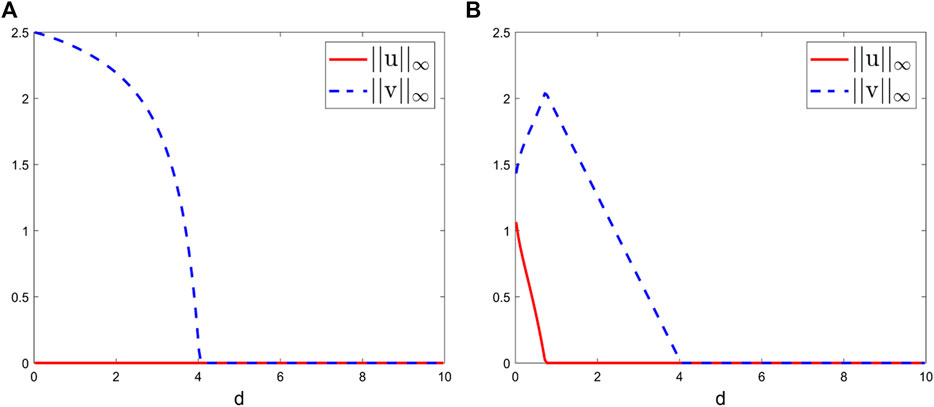
FIGURE 3. Bifurcation diagrams of the positive steady-state solutions to system (2.2) at t = 2000 with the bifurcation parameter d ranging from 0.01 to 10. Here, we take L = 1, S0 = 1, γ = 0.5, k1 = 1, k2 = 0.4, m1 = 1, and m2 = 2 and (A) β1 = 0.01, β2 = 0.01 and (B) β1 = 0.01, β2 = 1.
Second, if β1 = 0.01, β2 = 1. Clearly, under this weak–strong competition case, though species v has stronger growth ability compared to species u, the increase of β2 makes the competitive ability of v weaker. This is consistent with our biological intuition that the stronger intraspecific competition will put species at a disadvantage. Moreover, coexistence may occur when d is sufficiently small (Figure 3B), which is different from [8], Theorem 5.4. As d increases, species v wins the competition. As d further increases, the sufficiently large diffusion rates drive both species to extinction.
Case II:
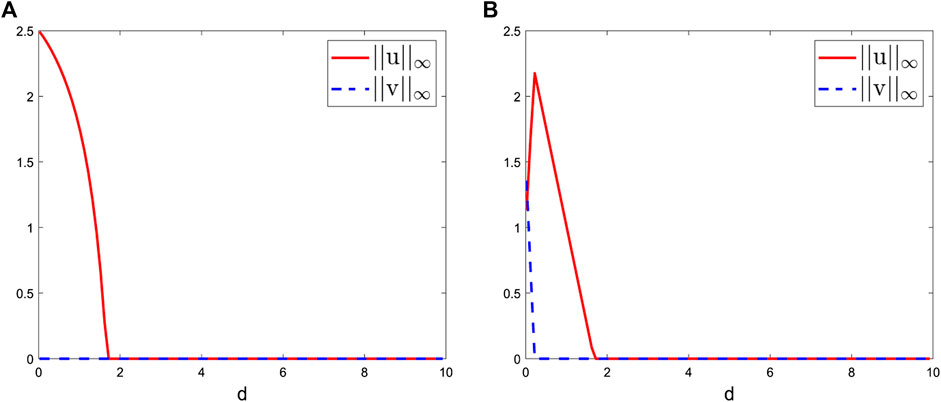
FIGURE 4. Bifurcation diagrams of the positive steady-state solutions to system (2.2) at t = 2000 with the bifurcation parameter d ranging from 0.01 to 10. Here, we take L = 1, S0 = 1, γ = 0.5, k1 = 1, k2 = 0.4, m1 = 1, and m2 = 0.2 and (A) β1 = 0.01, β2 = 0.01 and (B) β1 = 1, β2 = 0.01.
Case III:
For β1 = 0.01, β2 = 0.01, as shown in Figure 5A, the diffusion rates have a significant effect on the dynamics of system (2.2). More precisely, the dynamics of system (2.2) shift between four scenarios with the bifurcation parameter d increasing; that is, 1) competitive exclusion occurs and species v wins the competition, when d is sufficiently small; 2) coexistence occurs as d increases; 3) competitive exclusion occurs again and species u wins the competition, as d further increases; and 4) both species are washed out as d continues to increase. These suggest that system (2.2) may show a trade-off among extinction, exclusion, and coexistence as d increases. Particularly, coexistence occurs at the intermediate diffusion rates, which is in line with the theoretical results in [8].
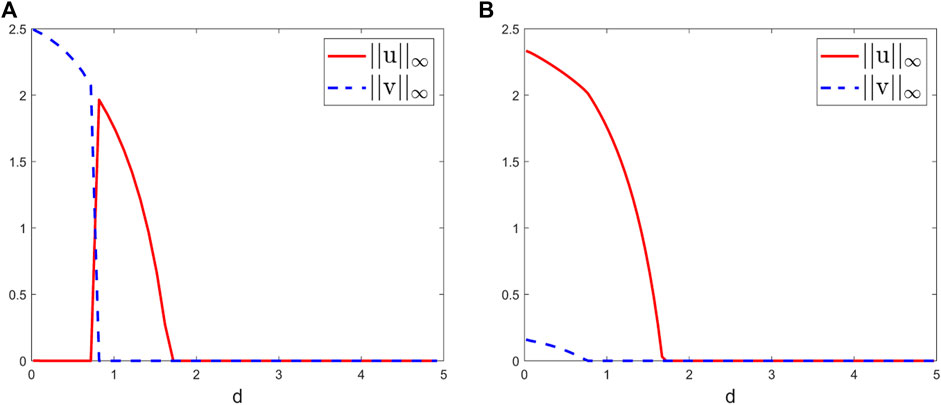
FIGURE 5. Bifurcation diagrams of the positive steady state solutions to system (2.2) at t = 2000 with the bifurcation parameter d ranging from 0.01 to 5. Here we take L = 1, S0 = 1, γ = 0.5, k1 = 1, k2 = 0.4, m1 = 1, and m2 = 0.6 and (A) β1 = 0.01, β2 = 0.01 and (B) β1 = 0.01, β2 = 1.
For β1 = 0.01, β2 = 1, as stated before, the increase of β2 will make the competitive ability of v weaker. Then, we can observe from Figure 5B that both species can coexist when d is sufficiently small. As d increases, competitive exclusion happens and species u wins the competition. As d further increases, the large diffusion rates drive two species to extinction.
In shorts, for different competition Cases (I)–(III), we investigate the effect of diffusion on the dynamics of system (2.2) by taking different intraspecific competition parameters β1, β2. As shown in Figures 3–5, the impacts of diffusion and intraspecific competition on the competitive outcomes of species are complex, which further suggests that diffusion and intraspecific competition play a key role in determining the dynamics of system (2.2).
7 Discussion
In this paper, we investigate an unstirred chemostat model with the Beddington–DeAngelis functional response (see system (2.2)). The analytical and numerical results show that the intraspecific competition and diffusion have an important biological effect on the dynamics of system (2.2).
Theoretically, we first adopt a basic strategy regarding the growth rates as variable/bifurcation parameters to study the effect of growth rates on system (2.2). The results show that there exist six critical curves
in the m1 − m2 plane, which may classify the dynamics of system (2.2) into extinction of both species, competitive exclusion and coexistence (see Theorems 4.1, 4.2). To further understand the effect of βi, (i = 1, 2) on the dynamics of (2.2), we explore the properties of critical curves Γ1 and Γ2 (see Propositions 4.2 and 4.3) and get a relatively clear dynamics classification of system (2.2) in the m1 − m2 plane (Figure 2).
Numerically, since diffusion plays a key role in determining the competition outcomes of two species, we study the effect of diffusion on the dynamics of system (2.2). More precisely, for two weak–strong competition cases, due to the effect of intraspecific competition parameters β1 and β2, the coexistence may occur at sufficiently small diffusion rates (Figures 3B, 4B), while for the evenly matched competition case, the dynamics of system (2.2) shift between different scenarios (competitive exclusion, coexistence, and extinction) when β1 and β2 are small and the coexistence only occurs at the intermediate diffusion rates (Figure 5A). When β2 is larger than β1, we observe from Figure 5B that coexistence may occur at sufficiently small diffusion rates.
In conclusion, in this paper, the dynamics classification of system (2.2) in the m1 − m2 plane is established by the linear eigenvalue theory and the monotone dynamical system theory (Figure 2). Due to the effect of intraspecific competition parameters β1 and β2, the dynamics of system (2.2) are more complex than that of the unstirred chemostat model with Holling type II functional response (see Figure 1 of [8]). Numerically, we study the effect of diffusion on system (2.2) and obtain rich numerical results (Figures 3–5). These numerical observations reveal that, under different competition cases, the effects of diffusion and intraspecific competition on the dynamics of system (2.2) are complex. This, in turn, suggests that the B.–D. functional response is more biologically realistic and superior to the well-known Holling type II functional response in modeling the resource uptake of species.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
The theory part and simulation were obtained by the first author WZ. The second and third authors HN and ZW guided the work. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (12071270 and 12171296) and the Natural Science Basic Research Program of Shaanxi (No. 2023-JC-JQ-03).
Acknowledgments
The authors are very grateful to the referees and the handling co editor-in-chief for their kind and valuable suggestions leading to a substantial improvement of the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1205571/full#supplementary-material
References
1. Bayen T, Cazenave-Lacroutz H, Coville J. Stability of the chemostat system including a linear coupling between species. Discrete Contin Dyn Syst Ser B (2023) 28(2023):2104–29. doi:10.3934/dcdsb.2022160
2. Hsu SB, Jin Y. The dynamics of a two host-two virus system in a chemostat environment. Discrete Contin Dyn Syst Ser B (2021) 26:415–41. doi:10.3934/dcdsb.2020298
3. Nie H, Hsu SB, Grover JP. Algal competition in a water column with excessive dioxide in the atmosphere. J Math Biol (2016) 72:1845–92. doi:10.1007/s00285-015-0926-8
5. Dellal M, Bar B. Global analysis of a model of competition in the chemostat with internal inhibitor. Discrete Contin Dyn Syst Ser B (2021) 26:1129–48. doi:10.3934/dcdsb.2020156
6. Hsu SB, Waltman P. On a system of reaction-diffusion equations arising from competition in an unstirred chemostat. SIAM J Appl Math (1993) 53:1026–44. doi:10.1137/0153051
7. Nie H, Shi Y, Wu JH. The effect of diffusion on the dynamics of a predator-prey chemostat model. SIAM J Appl Math (2022) 3:821–48. doi:10.1137/21m1432090
8. Shi JP, Wu YX, Zou XF. Coexistence of competing species for intermediate dispersal rates in a reaction-diffusion chemostat model. J Dynam Differential Equations (2020) 32:1085–112. doi:10.1007/s10884-019-09763-0
9. Smith HL. Monotone dynamical systems: An introduction to the theory of competitive and cooperative systems. In: Mathematical surveys and monographs. Providence, RI: American Mathematical Society (1995).
10. Wu JH. Global bifurcation of coexistence state for the competition model in the chemostat. Nonlinear Anal (2000) 39:817–35. doi:10.1016/s0362-546x(98)00250-8
11. Holling CS. The functional response of predator to prey density and its role in mimicry and population regulation. Mem Entonmol Soc Can (1965) 45:1–60.
12. Zhang W, Nie H, Wu JH. A reaction-diffusion-advection chemostat model in a flowing habitat: Mathematical analysis and numerical simulations. Internat J Bifur Chaos Appl Sci Engrg (2023) 33:1245–74. doi:10.1142/s0218127423500736
13. Zhang W, Nie H, Wu JH. Dynamics of a reaction-diffusion-advection model with two species competing in a flow reactor. Discrete Contin Dyn Syst Ser B (2023) 28:3453–86. doi:10.3934/dcdsb.2022226
14. So WH, Waltman P. A nonlinear boundary value problem arising from competition in the chemostat. Appl Math Comput (1989) 32:169–83. doi:10.1016/0096-3003(89)90092-1
15. Beddington JR. Mutual interference between parasites or predators and its effect on searching efficiency. J Anim Ecol (1975) 44:331–40. doi:10.2307/3866
16. DeAngelis DL, Goldstein RA, O’Neill RV. A model for trophic interaction. Ecology (1975) 56:661–892.
17. Harrision GW. Comparing predator-prey models to Luckinbill’s experiment with didinium and paramecium. Ecology (1995) 76:357–69.
18. Jiang HL, Wu JH, Wang LJ, Guo GH. Qualitative analysis for a competition model with B-D functional response and numerical simulation. Numer Methods Partial Differential Equations (2014) 30:1575–94. doi:10.1002/num.21848
19. Zhang GH, Wang XL. Extinction and coexistence of species for a diffusive intraguild predation model with B-D functional response. Discrete Contin Dyn Syst Ser B (2018) 23:3755–86. doi:10.3934/dcdsb.2018076
20. Meng Q, Yang L. Steady state in a cross-diffusion predator-prey model with the Beddington-DeAngelis functional response. Nonlinear Anal Real World Appl (2019) 45:401–13. doi:10.1016/j.nonrwa.2018.07.012
21. He X, Zheng SN. Protection zone in a diffusive predator-prey model with Beddington-DeAngelis functional response. J Math Biol (2017) 75:239–57. doi:10.1007/s00285-016-1082-5
22. Feng XZ, Sun C, Yang WB, Li CT. Dynamics of a predator-prey model with nonlinear growth rate and B-D functional response. Nonlinear Anal Real World Appl (2023) 70:103766. in press. doi:10.1016/j.nonrwa.2022.103766
23. Wang YE, Wu JH, Guo GH. Coexistence and stability of an unstirred chemostat model with Beddington-DeAngelis function. Comput Math Appl (2010) 60:2497–507. doi:10.1016/j.camwa.2010.08.057
24. Nie H, Wu JH. Coexistence of an unstirred chemostat model with Beddington-DeAngelis functional response and inhibitor. Nonlinear Anal Real World Appl (2010) 11:3639–52. doi:10.1016/j.nonrwa.2010.01.010
25. Feng XZ, Sun SP, Zhang TQ, An XM. The effect of parameters on positive solutions and asymptotic behavior of an unstirred chemostat model with B-D functional response. Adv Difference Equ (2018) 23:181–204. doi:10.1186/s13662-018-1587-x
26. Zhang S, Tan D, Chen LS. Chaotic behavior of a chemostat model with Beddington-DeAngelis functional response and periodically impulsive invasion. Chaos Solitons Fractals (2006) 29:474–82. doi:10.1016/j.chaos.2005.08.026
27. Zhou X, Song X, Shi X. Analysis of competitive chemostat models with the Beddington-DeAngelis functional response and impulsive effect. Appl Math Model (2007) 31:2299–312. doi:10.1016/j.apm.2006.08.010
28. Hirsch MW, Smith HL, Zhao XQ. Chain transitivity, attractivity, and strong repellors for semidynamical systems. J Dynam Differential Equations (2001) 13:107–31. doi:10.1023/a:1009044515567
29. Cantrell R, Cosner C. Spatial ecology via reaction-diffusion equations. Chester, UK: John Wiley and Sons Ltd (2003).
30. Lou Y, Nie H, Wang YE. Coexistence and bistability of a competition model in open advective environments. Math Biosci (2018) 306:10–9. doi:10.1016/j.mbs.2018.09.013
31. Crandall MG, Rabinowitz PH. Bifurcation from simple eigenvalues. J Funct Anal (1971) 8:321–40. doi:10.1016/0022-1236(71)90015-2
32. Protter MH, Weinberger HF. Maximum principles in differential equations. New York: Springer-Verlag (1984).
33. Shi JP. Persistence and bifurcation of degenerate solutions. J Funct Anal (1999) 169:494–531. doi:10.1006/jfan.1999.3483
34. Shi JP, Wang XF. On global bifurcation for quasilinear elliptic systems on bounded domains. J Differential Equations (2009) 246:2788–812. doi:10.1016/j.jde.2008.09.009
Keywords: unstirred chemostat model, coexistence, competitive exclusion, bifurcation, numerical simulation
Citation: Zhang W, Nie H and Wang Z (2023) Dynamics of an unstirred chemostat model with Beddington–DeAngelis functional response. Front. Phys. 11:1205571. doi: 10.3389/fphy.2023.1205571
Received: 14 April 2023; Accepted: 06 July 2023;
Published: 27 July 2023.
Edited by:
Xiaoming Zheng, Central Michigan University, United StatesCopyright © 2023 Zhang, Nie and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhiguo Wang, emd3YW5nQHNubnUuZWR1LmNu
 Wang Zhang
Wang Zhang Hua Nie
Hua Nie Zhiguo Wang
Zhiguo Wang