- 1School of Ocean Information Engineering, Jimei University, Fujian, China
- 2School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, China
- 3School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen, China
- 4Department of Automation, School of Aerospace Engineering, Xiamen University, Xiamen, China
An image encryption and decryption method of fractional order chaotic systems (FOCS) with predefined time synchronization is proposed in this article. Compared with the existing integer order chaotic systems (IOCS), fractional order chaotic systems has the advantage of increasing the complexity of the ciphertext. At the same time, by using the predefined synchronization time, the key space is expanded, the complexity of the key is increased, and the security of the algorithm is improved. To further improve the security of encryption and decryption process, this article uses a combination of DNA encoding, row/column cyclic shift and XOR diffusion, position scrambling and Arnold scrambling. The simulation tests of image encryption and decryption are carried out, and the effectiveness and advantages of the proposed encryption/decryption method are verified by histogram analysis, correlation analysis, entropy analysis, key sensitivity analysis and plaintext sensitivity analysis.
1 Introduction
Chaos is a kind of irregular and complex movement in nature [1]. Chaotic phenomena are seemingly random, irregular movements that occur in a deterministic system. The development of chaotic systems originated from the discovery of the Lorentz system [2]. Information encryption through chaotic signals or direct communication using chaotic systems is the future direction of chaotic applications [3]. In the past 2 decades, the algorithms combining chaotic systems with image encryption [4]; [5]; [6]; [7]; [8]; [9]; [10]; [11]; [12]; [13]; [14]; [15] have been investigated. Chaotic systems can generate extensive chaotic sequences (chaotic signal) by using different initial conditions and parameter settings [9]. Moreover, the signal is extremely sensitive to the change of system parameters and the disturbance of initial conditions [9]; [10]. Thus, chaotic systems provide a less consumption and higher speed means of implementing encryption tasks for large-scale data such as images [16]; [17]; [18], video and audio [11]; [19]. In order to combine chaotic systems with encryption algorithms, many properties of chaotic systems have been studied and developed [20]; [21]; [22]; [23]; [24]; [25]; [26]. In [20], the synchronization of two chaotic systems is studied, and the chaotic synchronization system is applied to the encryption algorithm. The synchronization technique of generalized chaotic systems, which excellently eliminates the negative effects of channel noise, are studied in [24]. The combination of analog chaotic system and digital chaotic system can effectively weaken the time delay of analog chaotic system and the periodicity of digital chaotic system, then improving the security of chaotic system [25]. To deal with the degradation of the dynamics leading to quantization, digital chaotic systems with higher dimensions than universal chaotic systems are constructed [27]. However, most of the existing encryption algorithms are based on IOCS. The description of many phenomena by IOCS is flawed. FOCS is proposed to overcome the deficiency of description ability of IOCS. Compared with the dynamic system described by integer order calculus, fractional order system contains more complex dynamic characteristics and genetic characteristics, and its memory function is nearly infinite. Classical fractional order systems include FOCS of Duffing Lu [28], FOCS of Rossler [29], FOCS of Chua [30]. Information security has always been a major issue in secure communications and related applications of information science. Achieving information security relies on reliable information encryption techniques. Research [31]; [32] has shown that using fractional order systems for information encryption has better performance. An image cryptosystem using fractional order chaotic systems is scrutinized for security applications [33]. An integral analysis framework based on a comprehensive security analysis with the aim to establish a basis in security analysis for chaos-based image cryptosystems were presented in [34].
The key to secure communication is to realize chaotic synchronization. The encryption process corresponds to the drive system and the decryption process corresponds to the response system. Under different initial conditions, the drive system and the response system often present completely different motion states, which is extremely unfavorable to the encryption algorithm. Therefore, how to design the synchronization method of chaotic systems is very important. The synchronization process of chaotic system includes asynchronous stage and synchronous stage. As mentioned before, once the chaotic signal is used in the asynchronous phase, the decryption of the final information cannot be achieved. Therefore, we need to accurately estimate the synchronization time of chaotic systems. We can predefined the synchronization time (i.e., adjusting the synchronization time) to enhance the effect of confidentiality. The definition of predefined time stability was proposed in [35], and the upper limit of its stability time can be acquired by adjusting system parameters [36]; [37]. In addition, a number synchronization methods of chaotic systems [38,39]; [37] within predefined time are proposed. In [37], an active controller with predefined time sliding mode synchronization was designed. To realize the predefined time sliding mode synchronization, a new formula was proposed in [39] and a series of controllers were designed.
To realize synchronization of the FOCS within a predefined time, the correction function of the hyperchaotic system was studied and a near sliding synchronization controller was designed in [40]. Inspired by the above work, this article proposes adaptive predefined time synchronization for time-delayed FOCS, and tests the performance of this system by applying it to image encryption/decryption. The novelties of the proposed encryption/decryption method in this article are as follows.
(1) The adjustable synchronization time process is used for generating the key, which increases the complexity of the key by expanding the key space. Compared to most previous image encryption algorithms, this one does not require that the sender transmits the key to the receiver over the channel, which may put the risk of the key being intercepted and cracked.
(2) A new encryption algorithm is carefully designed, and the scrambling and diffusion algorithm which is highly correlated with the plaintext is introduced. The encryption algorithm has a strong ability to resist attacks.
(3) To improve the security of the communication process, IOCS is replaced by FOCS in the proposed encryption/decryption method.
2 Preliminary
2.1 Definitions and lemmas
Some definitions and lemmas related to FOCS are introduced [41].
Definition 1. Arslan et al. [42] The fractional integral of h(t) is defined as
where q > 0 is the order of integral; t0 is the initial time and t > t0; h(t): (0, + ∞) → R and Γ(⋅) is the generalized Euler’s Gamma function
Definition 2. Petráš [43]; Song et al. [44] The Caputo definition derivative for h(t) is described by
where β > 0 is the order of derivative, t0 is the initial time and t ≥ t0; n is integer and n − 1 < β ≤ n.
Lemma 1. Song et al. [45] An equation describes the Caputo fractional derivative and Riemann–Liouville fractional derivative, that is:
where m ∈ N and n − 1 < α < n ∈ N+.
Lemma 2. Arslan et al. [42] If f(t) ∈ Cm[0, ∞), n − 1 < q < n ∈ N+, then
Lemma 3. Li et al. [46] For constant γ and δ, the linear characteristic of Caputo fractional order derivatives describes as:
Definition 3. Jiménez-Rodríguez et al. [47] Tc is an important parameter in the process of predefined time stability. The value of the stable time T(x0) for fixed-time synchronization has a functional relationship with the value of Tc, that is, the stable time Tx can be set by adjusting the parameter Tc,
Remark 1. Obviously, when the dynamic error system achieves convergence within predefined time, predefined time synchronization of the drive-response chaotic systems can be realized. Therefore, a controller ui(t) will be designed to force the error system to converge within the predefined time.
Lemma 4. Lin [48] If there exists a continuous radially unbounded and positive definite function V: Rn → R such that satisfies
where α, λ, q, k > 0, qk > 1 and
where B(σ, θ) is the complete beta function. Then, the formula (1) is globally predefined time stable, and the predefined time is Tc.
Lemma 5. Zuo [49] For constants ηj ∈ R+(j = 1, 2, …, n) and ϵ ∈ R+, the following inequalities is satisfied:
2.2 Secure hash algorithm (SHA-256)
Hash function [50] is a way to convert the information we want to encrypt into a short string. The hash function maps the input information into a unique string digest, which significantly reduces the space occupied by the information and unifies the information storage format. The information mapped by the hash function becomes a string digest that no longer has any characteristics of the original information. This string digest is called a hash value. Secure hash algorithm is a family of cryptographic hash functions. It is designed by the National Security Agency (NSA) and published by the National Institute of standards and Technology (NIST) and is widely used [14]; [51]. Including SHA-0 series, SHA-1 series, SHA-2 series and ShA-3 series. SHA-256 is one of SHA-2 series functions. SHA-256 has two features: 1. No matter how long the input is, it outputs 64 characters, a total of 32 bytes and 256 bits; 2. The output contains only the number 0 through 9 and the letters A through F, which are not case-sensitive.
3 Predefined time synchronization of fractional order systems with different structures
3.1 System introduction
The FOCS has more complex dynamic behaviors and mathematical explanations than the IOCS, so they have higher degrees of nonlinearity. The fractional order time delay drive system is described as [52].
where xi(i = 1, 2, 3, 4) is the state variable, 0 < α < 1 is the order of system (3), and
where yi(i = 1, 2, 3, 4) is the state variable and
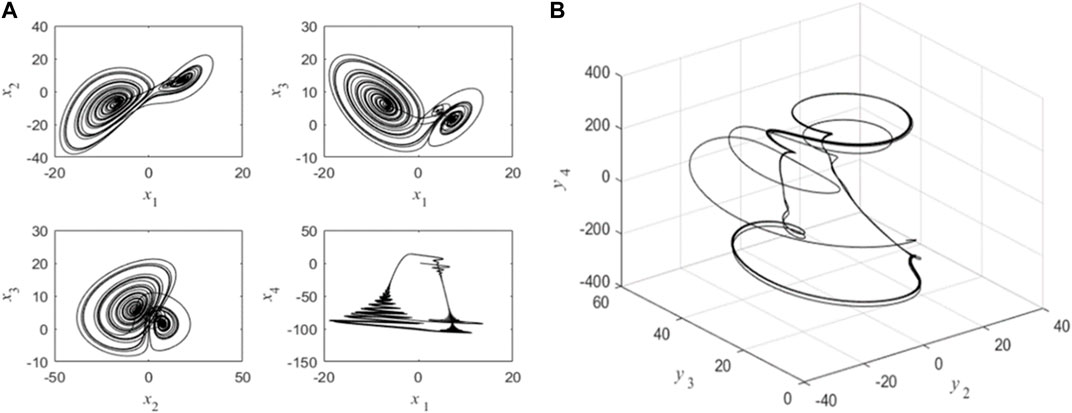
FIGURE 1. Chaotic images of driving and response system: (A) driving system (3); (B) response system (4) without ui(t).
Theorem 1. The response fractional order delay system (4) can achieve predefined time synchronization with the drive fractional order delay system (3) via the following control law:
where α1, λ1, q and k meet the requirements of Lemma 4 and L ≥ 0.2.
Proof. According to the definition of errors, ei(t) is described as
Supposing that
Substituted formula (3) and (4) into (6), one can obtain that:
Continuous function ‖e(t)‖1 is chosen as Lyapunov function
Taking the derivative of V2(t), one can obtain that
According to Lemma 5, the following inequality holds
Substitute the above formula into
Since N1−qk > 1 and N > 1. formula (9) has
According to Lemma 5, the following inequality holds
Then substitute (10) into
where α2 and λ2 are positive parameters. If
It can be obtained by combining Lemma 4 that
Based on the above discussion, for any t ≥ Tc, there are V2(t) = 0. That is, the system can achieve synchronization within a predefined time Tc.
Remark 2. The complexity of the FOCS can be fully utilized to increase the complexity of the encrypted text and improve the security of the encryption/decryption algorithm. The predefined time synchronization of the FOCSs is used to generate the decrypted text. By using the predefined time as the key, the key space is expanded and the complexity of the key is increased.
Remark 3. Here, the delay function is designed as
3.2 Synchronization performance analysis
The variation of state variables for systems (3) and (4) with and without controller input (5) are shown in Figures 2A, B; Figure 2A shows the time response curves of the state variables of the drive system and the response system without controller input (5). At this time, the change amplitude of the state variable yi is obviously greater than that of xi, and there is no relationship between them. Figure 2B shows the time response of xi and yi under the controller input (5). Among the four state variables, the state variable yi of the response system (4) quickly approaches the state variable xi of the drive system (3) from a larger fluctuation amplitude, thereby showing good tracking performance of yi on xi. The parameters of systems (3) and (4) are completely the same, but due to the change of the initial values of the system, the state variables in Figure 2A are significantly different from those in Figure 1, especially in response to the change amplitude of yi in the system. This also reflects the sensitivity of the proposed FOCSs (3) and (4) to the initial values. To illustrate the validity of the predefined time synchronization method, the controller ui(t) (i = 1,2,3,4) is designed with setting parameter Tc = 1 and Tc = 1.5, α = 0.82, k = 5.2, λ2 = 11, q = 12.9, α2 = 0.5, L = 0.2. The simulation performances are shown in Figure 2C with predefined time Tc = 1s; Figure 2B with predefined time Tc = 1.5s. When Tc = 1 (Figure 2C), the errors of drive system (3) and response system (4) gradually tends to 0 in the synchronization time period 0–1s. Whereas, when Tc = 1.5 (Figure 2D) the errors converge to 0 in the synchronization time period 0–1.5s. The results show that, by setting the controller and variables xi and yi, the realized predefined time synchronization system is effective under different Tc conditions.
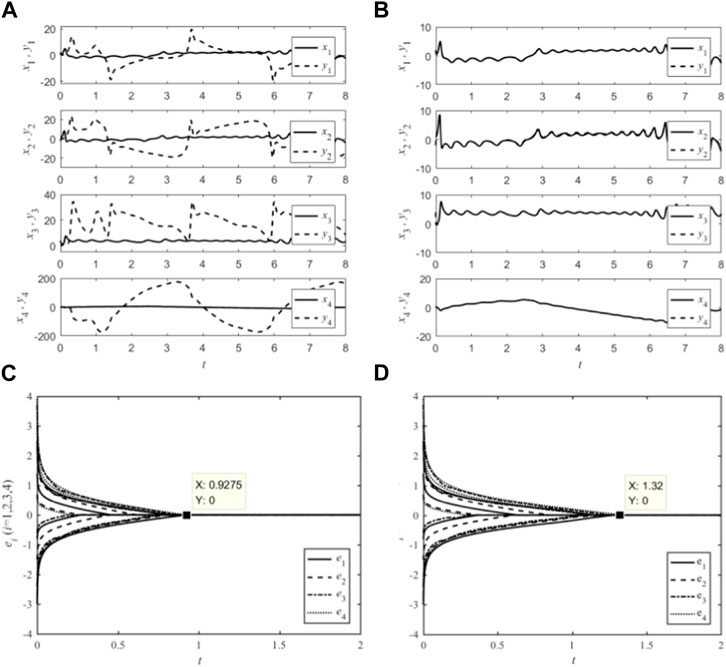
FIGURE 2. State behaviors and synchronization error: (A) without controller input; (B) with controller input; (C) with q = 0.5, Tc = 1; (D) with q = 0.5, Tc = 1.5.
3.3 Randomness performance analysis
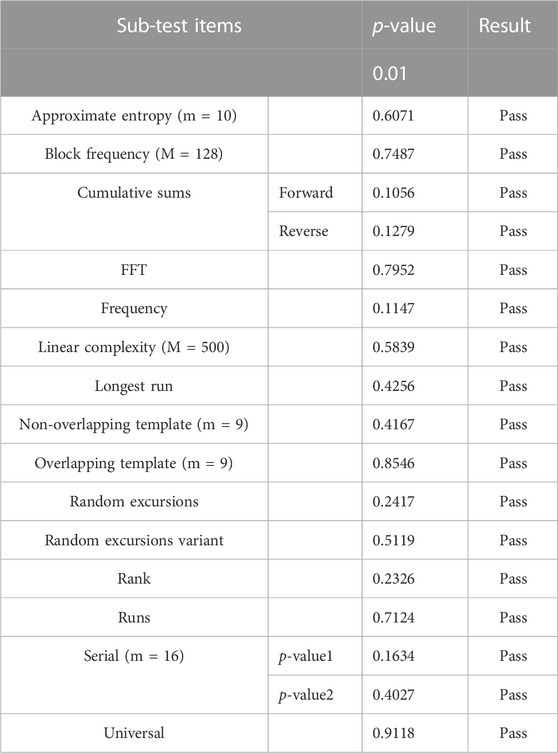
To further illustrate the proposed chaotic system is suitable for image encryption algorithm, the National Institute of Standards and Technology (NIST) SP800-22 is adopted to test the randomness of the output sequences. The NIST SP800-22 has 15 sub-tests and a p-value may be generated by every sub-test. According to the suggestion of [53], 100 binary streams with 1000000 bits are used as input data and the corresponding p-value is expected to fall into the range of 0.01 and 1 to pass the test. Table 1 lists the test results. It is clear that the binary streams of the four-wing FOCS can pass all the sub-tests, which indicates that FOCS is very suitable for image encryption.
4 Encryption/decryption algorithm and process
The encryption algorithm designed in this article includes four steps: chaotic sequence generation, image DNA coding, image scrambling, diffusion encryption and Arnold scrambling. In order to achieve the effect of diffusion, at least two rounds of encryption are required.
4.1 Generating initial value of chaotic system and chaotic sequence
In the key generating step, SHA-256 hash function is used for generating the initial key. The image information represented as matrix in plaintext form is input into SHA-256 function to form a string of 64-bit hexadecimal summaries with a length of 256 bits. The 64-bit hexadecimal digest is firstly converted to decimal then divided into 8 sequences:
4.2 DNA coding encryption rules
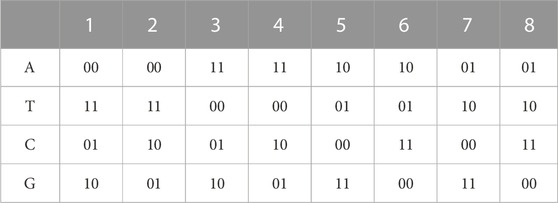
The aim of DNA coding is to scramble and diffuse the information of the origin image and generate a new image. DNA coding follows the principle of base complementary pairing, which is composed of Adenine (A), Thymine (T), Cytosine (C) and Guanine (G). The principle is similar to the complementary principle of binary numbers. For binary numbers, 00 and 11 are complementary, 01 and 10 are complementary. While, A and T are complementary and G and C are complementary. Thus, there are 24 coding combinations, but only eight meet the principle of base complementary pairing, by using four bases A, T, C and G to encode 00, 01, 10 and 11, which are listed in Table 2. According to DNA coding rules, image pixels value can be encoded. For example, if the binary number of a pixel value is [01100100] (decimal nuber 100), it can be encoded as [CGCA] according to DNA coding rule 1 from Table 2. Whereas, DNA decoding is the opposite process of DNA coding, which can recover the pixel value from the DNA sequence. If the DNA sequence is [CGCA], it can be decoded as binary number [01100100] (decimal number 100) according to rule 1 or as binary number [10011000] (decimal number 152) according to rule 2. In view of the above example, pixel value of original image can be changed by firstly encoding its binary sequence with rule R1 and then decoding the output DNA sequence with rule R2 to convert the original image pixel value and hide the original image information, where the rule R2 and R2 are two different coding rules in Table 2. The details of the above process are as follows:
Step 1. get the pixel value from the original image, assuming the pixel value is 100;
Step 2. convert pixel values into binary sequences and use the coding rule R1 to encode the pixel value. For example, the binary expression of pixel value 100 is [01100100], if R1 = 3, then the output DNA code is [ATAC];
Step 3. using coding rule R2 to decode the encoded pixel value to obtain a new pixel value. For example, it is encoded as [ATAC], when R2 = 5, the decoded binary sequence is [10011000], which is 152 in decimal nubler. That is, the original pixel value 100 is converted to a new value 152.Determination of Rule R1,R2: randomly take M × N × 3 × 2 groups of data in chaotic sequence X to obtain chaotic sequence:
Thus, a new image hiding the original image information is obtained, and the new image is scrambled and diffused.
4.3 Scrambling based on circular shifting
Scrambling based on circular shifting is aim to disrupt the order of the DNA-encoding image information and change it into a cluttered image. Scrambling based on circular shifting only operates on the orders of columns (M) and rows(N) of the image matrix. As the output new image in subsection 4.2 consists of three channels: R,G,B, so M + 3N groups of data in chaotic sequence x are arbitrarily taken to obtain chaotic sequence:
where a is from the sequence in S1. The sequence
where Sr is the sequence required for row cyclic shift and Sc is the sequence required for column cyclic shift. Then, the image matrix is scrambled with the results Sr, Sc as follows:
where i = 1, 2, …, m; j = 1, 2, …, 3N, the function circshift (a, b) means to circularly shift matrix a by b bits. Finally, the scrambled matrix Ip is obtained.
4.4 Diffusion algorithm
The pixels in each channel of color need to be diffused. The aim is to hide image information. Randomly take M × N groups of data from chaotic sequence X and get the sequence:
Then conduct diffusion operation according to the following
Matrix Ic is the output diffused matrix. After Arnold replacement of Ic,
The proposed encryption algorithm is a symmetric password, that is, the inverse of the encryption process is the decryption process. The encrypted image can be obtained by reverse Arnold scrambling, reverse diffusion, reverse cyclic scrambling and reverse DNA decoding. Because the chaotic system proposed in this article is completely synchronization, the chaotic sequence used in the decryption system is completely consistent with that used in the encryption system. The decryption performance of the algorithm will be given in the numerical simulation in Section 5.
4.5 Encryption and decryption transmission system
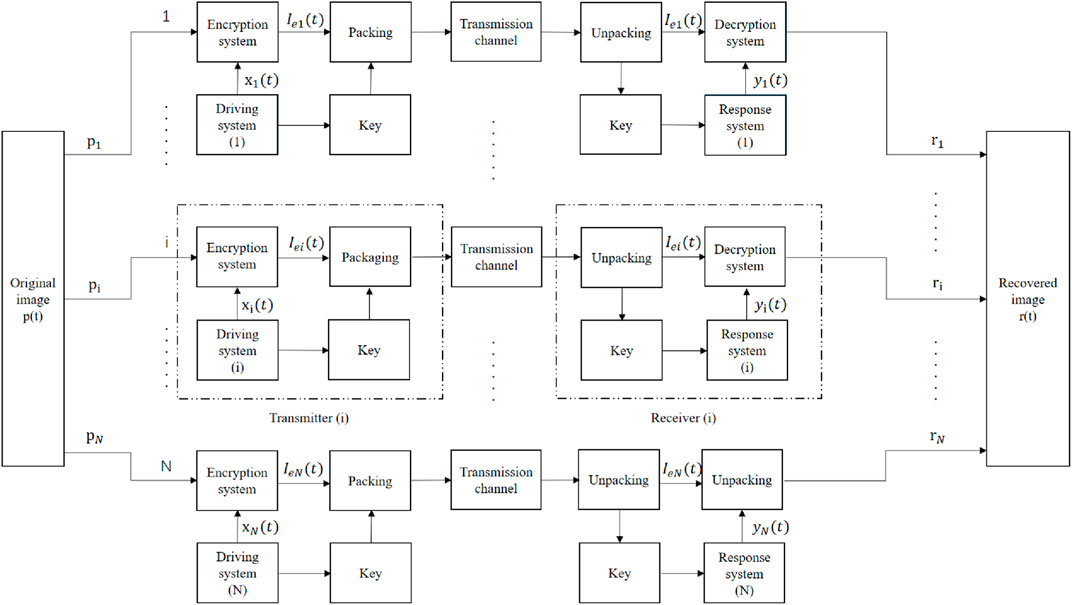
The proposed encryption/decryption system consists of three components. They are the transmitter, the receiver and the transmission channel, where the transmitter consists of N encryptors and the receiver consists of N decryptors. Chaotic sequences can be generated by N predefined time chaotic driving systems in the encryptor, and then chaotic sequences can be generated by the synchronization system in the decryptor. Let p(t) represent the plaintext encrypted by the hash function to be transmitted. The block diagram of the system is shown in Figure 3.
5 Simulation and performance analysis
5.1 Performance analysis of encryption and decryption
To evaluate the performance of the proposed encryption/decryption algorithm, simulation experiments are conducted. Firstly, the encryption algorithm given in Section 4 is applied to encrypt the original images. Figure 4 shows the original plain-images. The original images are Lena (256 × 256) (from Figure 5A in [54]), Panda (256 × 256) (from Figure 5C in [54]), All white (512 × 512) and All black (512 × 512). After the plaintext images are encrypted, the ciphertext images as shown in Figure 5 is formed. The ciphertext images present a noise state and cannot recognize the original image information. Then, the decryption algorithm given in Section 4 is applied to the encrypted image. The decrypted images are shown in Figure 6. Additionally, the proposed encryption has no limit for image size, and it can be applied for color images of various sizes. To accurately evaluate the consistency of the decrypted images with the original images, an image-subtraction is performed with the decrypted image and the original image. As shown in Figure 7, some images with all pixel values of 0 (a black image) are obtained, which proves that the decrypted images are completely consistent with the original images, so the proposed encryption and decryption algorithm is valid and can achieve a lossless encryption and decryption result.

FIGURE 4. The original images: (A) Lena plain-image; (B) Panda plain-image; (C) All black plain-image; (D) All white plain-image. Reproduced from “A Color Image Encryption Algorithm Based on One Time Key, Chaos Theory, and Concept of Rotor Machine” by Aqeel Ur Rehman, Amnah Firdous, Salman Iqbal, Zahid Abbas, Malik M. Ali Shahid, Huiwei Wang, and Farman Ullah, licensed under [https://creativecommons.org/licenses/by/4.0/], [54]”.

FIGURE 5. The cipher-images: (A) Lena cipher-image; (B) Panda cipher-image; (C) All black cipher-image; (D) All white cipher-image.

FIGURE 6. The decrypted images: (A) Decrypted image of Lena; (B) Decrypted image of Panda; (C) Decrypted image of All black; (D) Decrypted image of All white.

FIGURE 7. The difference images: (A) Difference image of Lena; (B) Difference image of Panda; (C) Difference image of all black; (D) Difference image of All white.
5.2 Key space analysis
The key space is an important indicator to measure the security performance of an encryption system. The larger the key space, the more difficult it is to brute force. In this algorithm, the key space is composed of the proposed chaotic system. The eight initial values
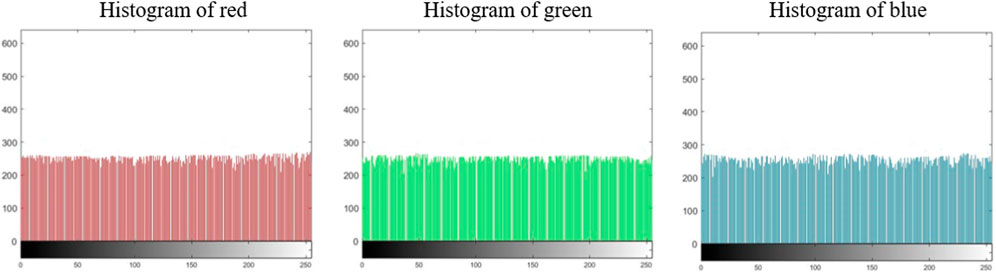
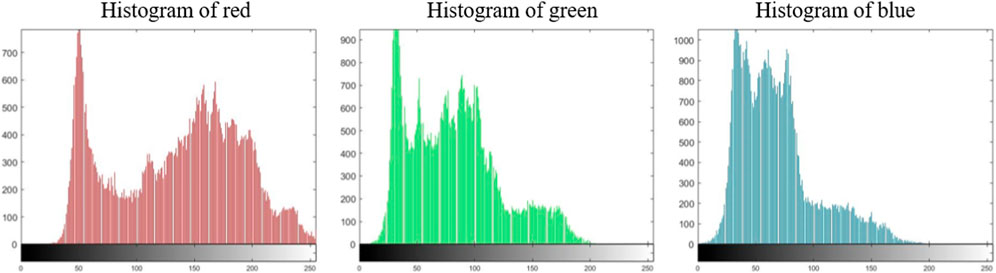
5.3 Histogram analysis
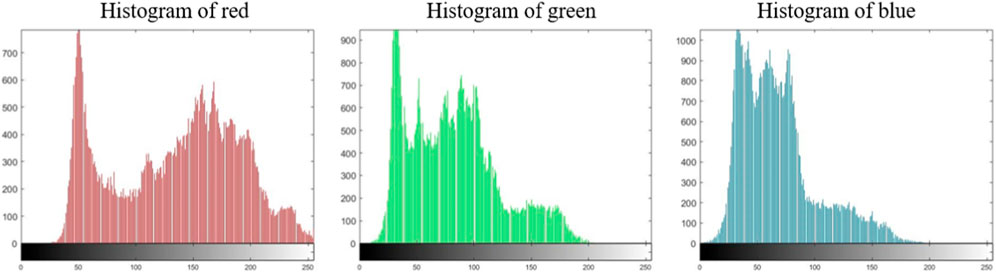
The image histogram describes the statistical characteristics of each gray level of the image and counts the number or frequency of each gray level in the image, so intruders can attack encrypted images through histogram analysis even the original image information is hidden in a encrypted image. For a reliable encryption strategy, the histogram of the encrypted image should be smooth and uniform thus no characteristics of original gray-level distribution is reflected. Figures 8, 9 indicates the histogram of the original image and the encrypted image respectively. It can be seen intuitively that the histogram of the plaintext image fluctuates obviously, while the histogram of the ciphertext is evenly and stably distributed. That is to say, through applying the proposed encryption method, the gray value in each channel is close to the uniform distribution, which effectively hides the original plaintext information, and makes it difficult for the attackers to crack the ciphertext image through statistical analysis. Figure 10 indicates the histogram of the decrypted image. It has exactly the same statistical features as the original image histogram, which indicates that the proposed algorithm has excellent decryption.
5.4 Correlation analysis
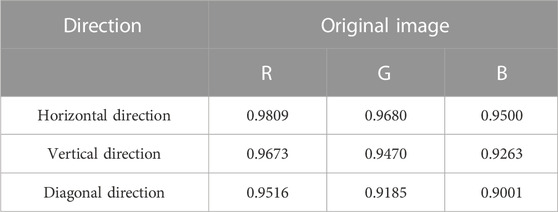
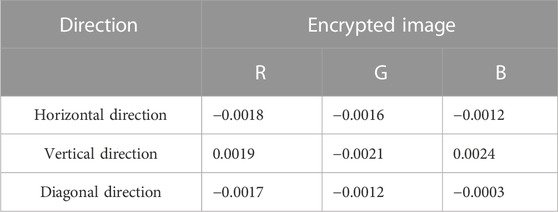
Data correlation can reflect the characteristics of the original data in terms of organization structure, and an attacker can analyze the data correlation to parse out the original data and cause data leakage. And a reliable encryption algorithm should hide the correlation reflected by the original data. Therefore, data correlation can be used as an indicator to evaluate encryption algorithms. The correlation coefficients of two data sets X and Y with length n are calculated according to equation:
In the simulation, 8,000 couples of adjacent pixels in the horizontal, vertical and diagonal directions of plaintext image and ciphertext image are randomly selected, and the correlation coefficient of the adjacent pixel values is calculated, as shown in Tables 3, 4. For all three directions, the ((absolute value of)) adjacent pixels correlation of the original image is higher (which are greater than 0.9) than that of the encrypted image (which approximate to 0). For a more intuitive description, the adjacent pixels correlation of original image and encrypted image in horizontal direction is shown in Figures 11A, B. The scattered points of original image are concentrated on a straight line, which is close to linear correlation, while the scattered points of encrypted image are evenly distributed without obvious aggregation. The above results indicates that the correlation of adjacent pixels in ciphertext image is reduced to a lower level by applying the proposed encryption algorithm, which proofs the encryption effectiveness of the propose method. Figure 11C shows the correlation of the decrypted image, and its statistical features are consistent with the statistical features of the original image correlation, which indicates that the proposed algorithm has excellent decryption results.
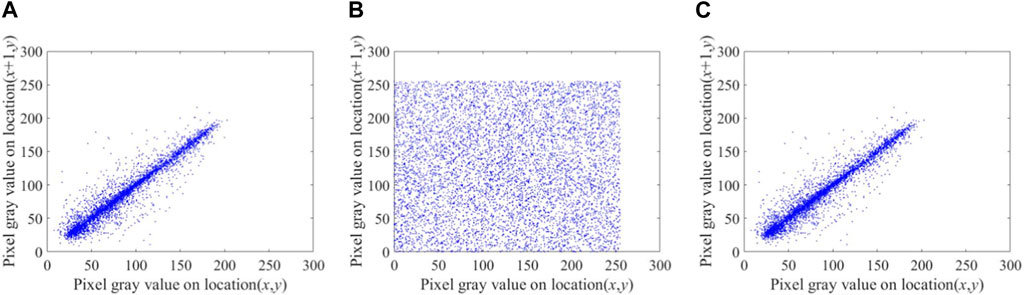
FIGURE 11. Correlation scatter of adjacent pixels: (A) the original image; (B) the encrypted image; (C) the decrypted image.
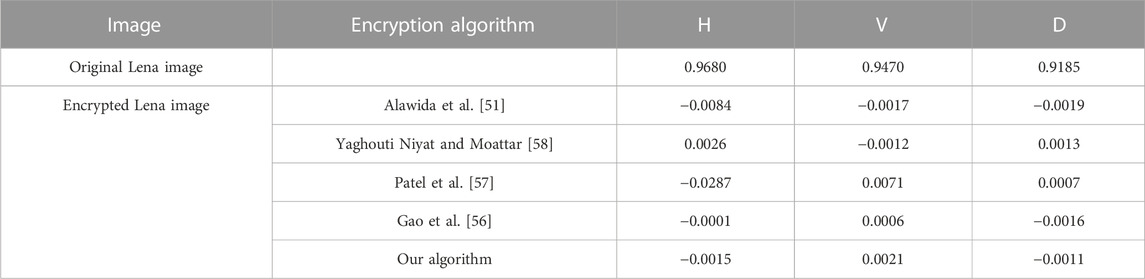
Table 5 compares the correlation between the original Lena image and its encrypted version generated using different encryption algorithms (Alawida et al. [51], Gao et al. [56], Patel et al. [57], Yaghouti Niyat and Moattar [58]). The last row of Table 5 shows the correlation coefficient values for this paper. It is clear that the correlation values of the Lena image cipher implemented using the algorithm of this paper are close to the advanced level in the field in the horizontal, vertical and diagonal directions.
5.5 Information entropy analysis
Information entropy indicates the degree of chaos of a chaotic system. The higher the information entropy, the more chaotic the system. The information entropy H of the image with gray level L is:
where P(si) is the probability that the pixel belongs to gray level si.
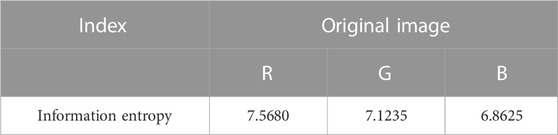
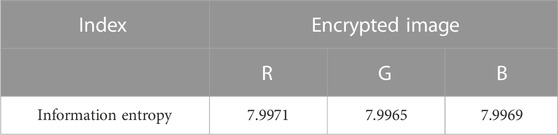
The maximum value of information entropy of a 256 gray level image is 8. Tables 6, 7 respectively shows the information entropy in each channel of original image and encrypted image. It can be seen that the information entropy of original image is lower than that of encrypted image, which shows that the proposed encryption algorithm can improve the complexity of image and increase the difficulty of cracking.
5.6 Plaintext sensitivity and key sensitivity analysis
Differential attack is a means for the attacker to decipher the encrypted messages, which obtains the original information (image) by comparing and analyzing the propagation of plaintext with specific differences after encryption. A secure image encryption algorithm should be highly sensitive to changes in pixels of ordinary images, which will change the encrypted image. Plaintext sensitivity and key sensitivity indicate the performance of an encryption algorithm against differential attack, whereas these two sensitivities can be evaluated with two indexes which are pixel number change rate (NPCR) and unified average change intensity (UACI). For each channel of a color image, NPCR and UACI values can be calculated by the following formula
As for plaintext sensitivity analysis, it refers to encrypt two plaintext images with slight difference by image encryption system with the same key, then compare the differences between the two encrypted images. If the two ciphertext images are very different, the image encryption system has strong plaintext sensitivity. On the contrary, the image encryption system has weak plaintext sensitivity, which can not resist selective plaintext attack or known plaintext attack.
In the simulation, SHA-256 hash function is used to generate the initial key sequence associated with plaintext, which is highly sensitive to the input image data. The original plaintext image and a changed plaintext image is used as inputs for encryption system. The changed plaintext image is generated by randomly changing one pixel value of the original plaintext image. Through the calculation of Equations 19, 20, the NPCR and UACI (%) of two encrypted images are listed in Table 8.
The theoretical value of NPCR is 99.6094% and the theoretical value of UACI is 33.4635%. The result of the proposed encryption algorithm approximates to the theoretical value. Table 9 provides the comparison of the NPCR and UACI results on the Lena image using our proposed algorithm and some other schemes. As can be clearly seen, [54] and our algorithm have the closest results to the ideal values of NPCR and UACI. The results indicate that the algorithm has excellent performance against differential attack.
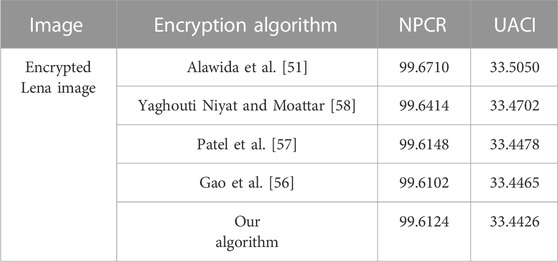
TABLE 9. Comparison of the average NPCR and UACI (%) on the Lena image by different Encryption algorithm.
As for Key sensitivity analysis, it refers to compute NPCR and UACI of the two ciphertext images after the key is slightly changed. As for plaintext sensitivity analysis, it refers to compute NPCR and UACI of the two ciphertext images after the plaintext image is slightly changed. When NPCR and UACI are close to the theoretical value, it indicates that the encryption method has a strong key sensitivity. Through the calculation of Eqs. 19, 20, the NPCR and UACI of two encrypted images are listed in Table 10.
It can be seen that the experimental values of NPCR and UACI are close to the theoretical values, which proves that the algorithm has strong key sensitivity.
5.7 Application of the algorithm
QR code as a technology to store and identify information has been widely used in many fields. However, QR code encoding algorithm is public and does not implement information encryption, so there are information security problems in some fields. In order to evaluate the performance of the proposed encryption and decryption algorithm, this section applies the encryption algorithm to the QR code image encryption scheme. Firstly, a QR code containing information about the title of this paper (Encryption algorithm based on fractional order chaotic system combined with adaptive predefined time synchronization) is generated as shown in Figure 12A. Then, the QR code is encrypted to get a noisy image that does not contain any information of the original QR code as shown in Figure 12B. Finally, the encrypted QR code is decrypted, and the decrypted image is obtained as shown in Figure 12C. After scanning and recognition, the identical text information is obtained. Therefore, the encryption algorithm can be applied to the process of QR code encryption, and at the same time, it can enhance the security of the process of using QR code.
6 Conclusion
In this article, a new encryption/decription method based on fractional order time-delay chaotic systems is proposed. Compared with the existing method based on IOCS, the proposed encryption method expands the key space and, furthermore, adopts cyclic shift, position disorder and row column XOR diffusion thus obtains higher security. Simulation results show that the proposed algorithm can achieve lossless encryption/decryption for image information. In addition, the proposed method possesses the advantages such as, low histogram distribution, low correlation of adjacent pixels, strong plaintext sensitivity and strong key sensitivity. These characteristics make the proposed method resistant to various attacks such as statistical attack, differential attack. In future research, we will make efforts in the following aspects.
(1) More attention will be paid to the characteristics of fractional order chaotic systems, including bifurcation diagrams and the Lyapunov spectrum [53].
(2) Different attack factors are added, such as noise, cropping, occlusion and so on, and the influence of these factors on the image encryption/decryption process is analyzed in depth.
(3) We will implement the proposed systems and predefined time controller in digital hardware such as FPGAs, DSP, ARMs.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
The authors declare that the study was realized in collaboration with the same responsibility. Writing—review and editing, LL, YZ, ZX, DY, and DW. All authors contributed to the article and approved the submitted version.
Funding
This research was funded by the Startup Research Project of Jimei University (No. ZQ2022002), the Natural Science Foundation of Fujian Province, China (No. 2019J05024), Xiamen Ocean and Fishery Development Special Fund Project (No. 21CZB013HJ15), Xiamen Key Laboratory of Marine Intelligent Terminal R&D and Application (No. B18208), Jimei University (No. ZP2022042).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Lorenz EN. Deterministic nonperiodic flow. J Atmos Sci (1963) 20:130–41. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2
3. Tsafack N, Iliyasu AM, De Dieu NJ, Zeric NT, Kengne J, Abd-El-Atty B, et al. A memristive rlc oscillator dynamics applied to image encryption. J Inf Security Appl (2021) 61:102944. doi:10.1016/j.jisa.2021.102944
4. Cuomo KM, Oppenheim AV, Strogatz SH. Synchronization of lorenz-based chaotic circuits with applications to communications. IEEE Trans circuits Syst Analog digital signal Process (1993) 40:626–33. doi:10.1109/82.246163
5. Yang T, Chua LO. Impulsive stabilization for control and synchronization of chaotic systems: Theory and application to secure communication. IEEE Trans Circuits Syst Fundam Theor Appl (1997) 44:976–88. doi:10.1109/81.633887
6. He Z, Li K, Yang L, Shi Y. A robust digital secure communication scheme based on sporadic coupling chaos synchronization. IEEE Trans Circuits Syst Fundam Theor Appl (2000) 47:397–403. doi:10.1109/81.841923
7. Li K-Z, Zhao M-C, Fu XC. Projective synchronization of driving–response systems and its application to secure communication. IEEE Trans Circuits Syst Regular Pap (2009) 56:2280–91. doi:10.1109/tcsi.2008.2012208
8. Jiang Z-P. A note on chaotic secure communication systems. IEEE Trans Circuits Syst Fundam Theor Appl (2002) 49:92–6. doi:10.1109/81.974882
9. Tse C, Lau F. Chaos-based digital communication systems. In: Operating principles, analysis methods and performance evaluation (2003).
10. Jovic B. Synchronization techniques for chaotic communication systems. Springer Science & Business Media (2011).
11. Lin Z, Yu S, Lü J, Cai S, Chen G. Design and arm-embedded implementation of a chaotic map-based real-time secure video communication system. IEEE Trans circuits Syst video Technol (2014) 25:1203–16.
12. Daldoul I, Tlili AS. Secured transmission design schemes based on chaotic synchronization and optimal high gain observers. Simulation Model Pract Theor (2022) 120:102625. doi:10.1016/j.simpat.2022.102625
13. Jithin K, Sankar S. Colour image encryption algorithm combining arnold map, dna sequence operation, and a mandelbrot set. J Inf Security Appl (2020) 50:102428. doi:10.1016/j.jisa.2019.102428
14. Murillo-Escobar D, Murillo-Escobar MÁ, Cruz-Hernández C, Arellano-Delgado A, López-Gutiérrez RM. Pseudorandom number generator based on novel 2d hénon-sine hyperchaotic map with microcontroller implementation. Nonlinear Dyn (2022) 111:6773–89. doi:10.1007/s11071-022-08101-2
15. Meranza-Castillón MO, Murillo-Escobar MA, López-Gutiérrez RM, Cruz-Hernandez C. Pseudorandom number generator based on enhanced hénon map and its implementation - sciencedirect. AEU - Int J Elect Commun (2019) 107:239–51.
16. Jirjees SW, Alkalid FF, Shareef WF. Image encryption using dynamic image as a key based on multilayers of chaotic permutation. Symmetry (2023) 15:409. doi:10.3390/sym15020409
17. Luo Z, Pei Z, Yang C, Liu Z, Chen H. Secure image signal transmission scheme using poly-polarization filtering and orthogonal matrix. Appl Sci (2023) 13:2513. doi:10.3390/app13042513
18. Abusham E, Ibrahim B, Zia K, Rehman M. Facial image encryption for secure face recognition system. Electronics (2023) 12:774. doi:10.3390/electronics12030774
19. Volos CK, Kyprianidis IM, Stouboulos IN. Image encryption process based on chaotic synchronization phenomena. Signal Process. (2013) 93:1328–40. doi:10.1016/j.sigpro.2012.11.008
20. Lu J, Wu X, Lü J. Synchronization of a unified chaotic system and the application in secure communication. Phys Lett A (2002) 305:365–70. doi:10.1016/s0375-9601(02)01497-4
21. Li Z, Li K, Wen C, Soh YC. A new chaotic secure communication system. IEEE Trans Commun (2003) 51:1306–12. doi:10.1109/tcomm.2003.815058
22. Alvarez G, Hernández L, Muñoz J, Montoya F, Li S. Security analysis of communication system based on the synchronization of different order chaotic systems. Phys Lett A (2005) 345:245–50. doi:10.1016/j.physleta.2005.07.083
23. Huang S-I, Shieh S, Tygar J. Secure encrypted-data aggregation for wireless sensor networks. Wireless Networks (2010) 16:915–27. doi:10.1007/s11276-009-0177-y
24. Moskalenko OI, Koronovskii AA, Hramov AE. Generalized synchronization of chaos for secure communication: Remarkable stability to noise. Phys Lett A (2010) 374:2925–31. doi:10.1016/j.physleta.2010.05.024
25. Cheng M, Deng L, Gao X, Li H, Tang M, Fu S, et al. Security-enhanced ofdm-pon using hybrid chaotic system. IEEE Photon Tech Lett (2014) 27:326–9. doi:10.1109/lpt.2014.2370757
26. Chatzinakos C, Tsouros C. Estimation of the dimension of chaotic dynamical systems using neural networks and robust location estimate. Simulation Model Pract Theor (2015) 51:149–56. doi:10.1016/j.simpat.2014.11.005
27. Wang Q, Yu S, Li C, Lü J, Fang X, Guyeux C, et al. Theoretical design and fpga-based implementation of higher-dimensional digital chaotic systems. IEEE Trans Circuits Syst Regular Pap (2016) 63:401–12. doi:10.1109/tcsi.2016.2515398
28. Fan Z. A new six-dimensional duffing-lu chaotic system and its circuit implementation. Sci Tech Eng (2013).
29. Qian Z, Zeng-Qiang C, Zhu-Zhi Y. Generation of on–off intermittency based on rössler chaotic system. Chin Phys (2007) 16:2616–26. doi:10.1088/1009-1963/16/9/020
30. Wang Y, Guan Z-H, Wen X. Adaptive synchronization for chen chaotic system with fully unknown parameters. Chaos, Solitons & Fractals (2004) 19:899–903. doi:10.1016/s0960-0779(03)00256-x
31. Xue H, Peng J, An X, Zhang L, Wang Z, Hu P. Full state hybrid projective synchronization of fractional-order chaotic systems and its application to secure communication. Inf Control (2013) 42:229–35.
32. Wang Z, Sun W. Synchronization of fractional chaotic systems and secure communication. Appl Res Comput (2012) 29:2221–3.
33. Ahmad M, Shamsi U, Khan IR. An enhanced image encryption algorithm using fractional chaotic systems. Proced Comp Sci (2015) 57:852–9. doi:10.1016/j.procs.2015.07.494
34. Murillo-Escobar MA, Meranza-Castillón MO, López-Gutiérrez RM, Cruz-Hernández C. Suggested integral analysis for chaos-based image cryptosystems. Entropy (2019) 21:815. doi:10.3390/e21080815
35. Sánchez-Torres JD, Sanchez EN, Loukianov AG. A discontinuous recurrent neural network with predefined time convergence for solution of linear programming. In: Procedding of the 2014 IEEE symposium on swarm intelligence; December 2014; Orlando, FL, USA. IEEE (2014). p. 1–5.
36. Sánchez-Torres JD, Sanchez EN, Loukianov AG. Predefined-time stability of dynamical systems with sliding modes. In: Procedding of the 2015 American control conference (ACC); July 2015; Chicago, IL, USA. IEEE (2015). p. 5842–6.
37. Anguiano-Gijón CA, Muñoz-Vázquez AJ, Sánchez-Torres JD, Romero-Galván G, Martínez-Reyes F. On predefined-time synchronisation of chaotic systems. Chaos, Solitons & Fractals (2019) 122:172–8. doi:10.1016/j.chaos.2019.03.015
38. Sánchez-Torres JD, Gómez-Gutiérrez D, López E, Loukianov AG. A class of predefined-time stable dynamical systems. IMA J Math Control Inf (2018) 35:i1–i29. doi:10.1093/imamci/dnx004
39. Sánchez-Torres JD, Muñoz-Vázquez AJ, Defoort M, Jiménez-Rodríguez E, Loukianov AG. A class of predefined-time controllers for uncertain second-order systems. Eur J Control (2020) 53:52–8. doi:10.1016/j.ejcon.2019.10.003
40. Li Q, Yue C. Predefined-time modified function projective synchronization for multiscroll chaotic systems via sliding mode control technology. Complexity (2020) 2020:1–11. doi:10.1155/2020/6590502
41. Lin L, Wang Q, He B, Chen Y, Peng X, Mei R. Adaptive predefined-time synchronization of two different fractional-order chaotic systems with time-delay. IEEE Access (2021) 9:31908–20. doi:10.1109/access.2021.3059324
42. Arslan E, Narayanan G, Ali MS, Arik S, Saroha S. Controller design for finite-time and fixed-time stabilization of fractional-order memristive complex-valued bam neural networks with uncertain parameters and time-varying delays. Neural Networks (2020) 130:60–74. doi:10.1016/j.neunet.2020.06.021
43. Petráš I. Chaos in the fractional-order volta’s system: Modeling and simulation. Nonlinear Dyn (2009) 57:157–70. doi:10.1007/s11071-008-9429-0
44. Song X, Song S, Li B. Adaptive synchronization of two time-delayed fractional-order chaotic systems with different structure and different order. Optik (2016) 127:11860–70. doi:10.1016/j.ijleo.2016.09.077
45. Song S, Song X-N, Pathak N, Balsera IT. Multi-switching adaptive synchronization of two fractional-order chaotic systems with different structure and different order. Int J Control Automation Syst (2017) 15:1524–35. doi:10.1007/s12555-016-0097-4
46. Li H-L, Cao J, Jiang H, Alsaedi A. Finite-time synchronization and parameter identification of uncertain fractional-order complex networks. Physica A: Stat Mech its Appl (2019) 533:122027. doi:10.1016/j.physa.2019.122027
47. Jiménez-Rodríguez E, Sánchez-Torres JD, Loukianov AG. On optimal predefined-time stabilization. Int J Robust Nonlinear Control (2017) 27:3620–42. doi:10.1002/rnc.3757
48. Lin L. Predefined-time synchronization of 5d hindmarsh–rose neuron networks via backstepping design and application in secure communication. Nonlinear Anal Model Control (2022) 27:1–20. doi:10.15388/namc.2022.27.26557
49. Zuo Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica (2015) 54:305–9. doi:10.1016/j.automatica.2015.01.021
50. Tran TH, Pham HL, Nakashima Y. A high-performance multimem sha-256 accelerator for society 5.0. IEEE Access (2021) 9:39182–92. doi:10.1109/access.2021.3063485
51. Alawida M, Samsudin A, Teh JS, Alkhawaldeh RS. A new hybrid digital chaotic system with applications in image encryption. Signal Process. (2019) 160:45–58. doi:10.1016/j.sigpro.2019.02.016
52. Wang Q. Fixed-time/predefined-time synchronization of fractional-order chaotic systems and their implementation on FPGA. Ph.D. thesis. Fuzhou, Fujian: Fuzhou University (2022).
53. Bassham LE, Rukhin AL, Soto J, Nechvatal JR, Smid ME, Barker EB, et al. Sp 800-22 rev 1a a statistical test suite for random and pseudorandom number generators for cryptographic applications. Gaithersburg, MD: National Institute of Standards & Technology (2010).
54. Rehman AU, Firdous A, Iqbal S, Abbas Z, Shahid MMA, Wang H, et al. A color image encryption algorithm based on one time key, chaos theory, and concept of rotor machine. IEEE Access (2020) 8:172275-172295. doi:10.1109/ACCESS.2020.3024994
55. Montero-Canela R, Zambrano-Serrano E, Tamariz-Flores EI, Muñoz-Pacheco JM, Torrealba-Meléndez R. Fractional chaos based-cryptosystem for generating encryption keys in ad hoc networks. Ad Hoc Networks (2020) 97:102005. doi:10.1016/j.adhoc.2019.102005
56. Gao S, Wu R, Wang X, Liu J, Li Q, Wang C, et al. Asynchronous updating boolean network encryption algorithm. IEEE Trans Circuits Syst Video Tech (2023) 1. doi:10.1109/tcsvt.2023.3237136
57. Patel S, Thanikaiselvan V, Pelusi D, Nagaraj B, Arunkumar R, Amirtharajan R. Colour image encryption based on customized neural network and dna encoding. Neural Comput Appl (2021) 33:14533–50. doi:10.1007/s00521-021-06096-2
Keywords: fractional hyperchaotic system, predefined time stability, image encryption, image decryption, adaptive predefined time synchronization
Citation: Lin L, Zhuang Y, Xu Z, Yang D and Wu D (2023) Encryption algorithm based on fractional order chaotic system combined with adaptive predefined time synchronization. Front. Phys. 11:1202871. doi: 10.3389/fphy.2023.1202871
Received: 09 April 2023; Accepted: 01 June 2023;
Published: 15 June 2023.
Edited by:
Yifei Sun, Hohai University, ChinaReviewed by:
Cesar Cruz-Hernandez, Center for Scientific Research and Higher Education in Ensenada (CICESE), MexicoShaobo He, Central South University, China
Copyright © 2023 Lin, Zhuang, Xu, Yang and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dongjie Wu, d3Vkb25namllY2huQG91dGxvb2suY29t
†These authors have contributed equally to this work
 Lixiong Lin
Lixiong Lin Yufu Zhuang
Yufu Zhuang Zhiping Xu
Zhiping Xu Disai Yang
Disai Yang Dongjie Wu
Dongjie Wu