Comprehensive analysis on the magnetic field error of a K–Rb–21Ne comagnetometer with low-frequency bias magnetic field sensitivity

The spin-exchange relaxation-free comagnetometer (SERFC) is of important research value compared to existing high-precision gyroscopes because of its extremely high theoretical limit sensitivity and long-term stability, in which one significant limiting factor is the magnetic field error. First, the relationship between the magnetic field gradient and the nuclear spin relaxation mechanism is introduced into the frequency response and steady-state response models of SERFC. Then, a novel method for suppression of the low-frequency magnetic field error based on the modified bias magnetic field sensitivity model is proposed. Finally, the effectiveness of the proposed suppression methods is demonstrated by optimizing the cell temperature, pump light power, and compensation magnetic field gradient to increase the suppression factor by 72.19%, 20.24%, and 69.86%, and the corresponding bias instability increased by 55.41%, 20.84%, and 27.63%, respectively. This study contributes to improving the long-term zero bias stability of the SERFC.

1 Introduction

In recent years, quantum sensing has been used in various applications, including fundamental physics research, such as Lorentz test and charge-parity-time (CPT) symmetry research [1, 2], long-range spin correlation search [3, 4] and high-precision rotary sensing gyroscopes [5], and controllability analysis of the atomic spin ensemble system [6]. Among them, the comagnetometer working in the no spin-exchange relaxation-free (SERF) state has proven to be of significant research value in ultra-high-precision inertial measurement instruments [7]. In all applications, the comagnetometer of alkali noble gases working under the SERF regime is considered one of the promising quantum spin gyroscopes due to its extremely high theoretical limit accuracy [8]. However, the magnetic field error caused by the magnetic field gradient is the main error source in the rotation measurement of the SERF comagnetometer [10, 11]. The main reason for the low-frequency magnetic field error is that the values of nuclear spin relaxation rate $R_{\mathit{tot}}^n$ and nuclear spin exchange rate $R_{se}^{en}$ cannot be ignored [11, 12]. In addition, the effect of magnetic field on the bias stability of SERFC based on K–Rb–²¹Ne is analyzed, and the experiment shows that the bias drift caused by magnetic field fluctuation is 0.02 deg/h in SERFC in [13]. Afterward, Ref. [14] carried out research on the magnetic field response of Rb–¹²⁹Xe, and the simulation results show that a larger nuclear magnetic field can shift the hybrid resonance frequency to the right, while a larger electronic magnetic field can reduce the magnetic field suppression factor.

In atomic sensor systems, the non-orthogonality of the triaxial coils and the non-overlapping of the laser direction and the magnetic field direction can cause the central position of the vapor cell not to coincide with the center position of the magnetic compensation system [15]. The coupling effect between the magnetic shielding system that shields the external ambient magnetic field and the active magnetic compensation coil results in a non-uniform magnetic field distribution [16, 17]. In addition, magnetic shielding, heating film magnetic fields, and coil inhomogeneities can all lead to inhomogeneous field distribution in SERF comagnetometers, resulting in the magnetic field gradient [18]. In addition, although the hybrid pumping technique was applied to K–Rb–²¹Ne to solve the problem of lower atomic density and smaller optical depth of K atoms resulting in worse atomic coherence of the pumped optical path, the SERFC atomic spin polarization distribution was still experimentally demonstrated to be inhomogeneous [19, 20]. Therefore, both the coregulator components themselves and the atomic relaxation mechanism in SERFC introduce the magnetic field gradient and thus affect the coherence of the atoms.

In previous studies, the effect of magnetic field inhomogeneity on spin relaxation has been investigated. [21] conducted systematic theoretical and experimental studies on the effect of magnetic field gradients on the spin relaxation of atoms. Afterward, [22] derived the theoretical expression for the transverse relaxation rate of the spin-polarized gas due to the magnetic field gradient by combining Redfield theory. Consequently, all the aforementioned studies show that the magnetic field gradient brings about an equivalent gradient relaxation of the nuclear spins, which is a non-negligible factor to increase the atomic decoherence time [23, 24]. For various experiments on polarized nucleon spins aimed at increasing atomic coherence, it is important to develop a study of the compensation of magnetic field gradients based on the relationship between the atomic relaxation mechanism and the magnetic field inhomogeneity [25]. However, it is rare and valuable to comprehensively and quantitatively analyze the influence of magnetic field gradients on $R_{\mathit{tot}}^n$ based on the bias magnetic field sensitivity model method for K–Rb ²¹Ne comagnetometers.

In this study, the low-frequency bias magnetic field sensitivity (LFBMS) model of SERFC is modified, and the influence of magnetic field gradients on the low-frequency magnetic error is considered. The research shows that the magnetic field gradient affects the LFBMS of the system by reducing the atomic decoherence time. An effective method to suppress the low-frequency magnetic field error based on the modified bias magnetic field sensitivity model is proposed. The SERFC prototype of K–Rb–²¹Ne is used to verify our theory and method. This paper contributes to further studies on the magnetic field gradient-based compensation of the K–Rb–²¹Ne comagnetometer to suppress magnetic field errors, thus increasing the atomic decoherence time to eventually improve the long-term stability of the SERFC.

2 Methodology

The Bloch equations of the K–Rb–²¹Ne comagnetometer can be expressed as follows:

$\begin{array}{cc}\hfill \frac{\partial {\mathbf{P}}^e}{\partial t}=& \frac{{\gamma }^e}{Q\left(P^e\right)}\left(\mathbf{B}+\lambda M^n{\mathbf{P}}^n+\mathbf{L}\right)\times {\mathbf{P}}^e\hfill \\ \hfill -& \mathbf{\Omega }\times {\mathbf{P}}^e+\frac{\left(R_p{\mathbf{s}}_p+R_{se}^{en}{\mathbf{P}}^n-R_{tot}^e{\mathbf{P}}^e\right)}{Q\left(P^e\right)},\hfill \\ \hfill \frac{\partial {\mathbf{P}}^n}{\partial t}=& {\gamma }^n\left(\mathbf{B}+\lambda M^e{\mathbf{P}}^e\right)\times {\mathbf{P}}^n\hfill \\ \hfill -& \mathbf{\Omega }\times {\mathbf{P}}^n+R_{se}^n{\mathbf{P}}^e-\mathbf{R}\cdot {\mathbf{P}}^n\hfill \end{array}(1)$

where P^e and Pⁿ are the Rb spin polarization vector and ²¹Ne spin polarization vector, respectively; Ω is the inertial rotation vector; γ_e = 2π × 28 Hz/nT and γ_n = 2π × 0.00336 Hz/nT are the gyromagnetic ratios of the electron spin and nuclear spin, respectively; Q is the deceleration factor of the nucleon, which is related to the longitudinal polarizability of the electron [26]; B is the ambient magnetic field vector; $R_{\text{se}}^{\text{en\hspace{0.17em}}}$ and $R_{\text{se}}^{\text{ne}}$ are the spin exchange rates of the nuclear and the electron with each other; L is the light shift (AC-Stark shift) field arising from the pump and probe lasers; $R_{\text{tot\hspace{0.17em}}}^e$ is the total relaxation rate for electrons, defined as $R_{\text{tot}}^e=R_{\mathrm{p}}+R_m+R_{\text{se}}^{\text{en}}+R_{\text{sd}}^e$, where $R_{\text{sd}}^e$ is the electron spin-destruction rate, and $R_{\text{sd}}^n$ is the nuclear spin-destruction rate, R_p is pumping rate, R_m is the pumping rate from the probe laser; and M^e and Mⁿ are the magnetizations of electron spin and nuclear spin, respectively. Finally, we define the vector $\mathbf{R}=\left\{R_{\text{tot\hspace{0.17em}}}^n,R_{\text{tot\hspace{0.17em}}}^n,R_1^n\right\}$, where $R_1^n$ and $R_{\mathit{tot}}^n$ are the longitudinal relaxation rate and the transverse relaxation rate of the nuclear spin, respectively; B^e = λM^eP^e and Bⁿ = λMⁿPⁿ are the magnetic fields produced by electron spin and nuclear spin, respectively.

The SERFC can be linearized into the following equation of state:

$\dot{\mathbf{X}}=\mathbf{A}\mathbf{X}+\mathbf{W}\mathbf{U},(2)$

where the state vector $\mathbf{X}={\left[P_x^e,P_y^e,P_x^n,P_y^n\right]}^T$ is composed of electron polarization transverse components $P_x^e$, $P_y^e$ and nuclear polarization transverse components $P_x^n$, $P_y^n$; $\mathbf{U}={\left[{\mathrm{\Omega }}_x,{\mathrm{\Omega }}_y,B_x,B_y\right]}^T$ is the input vector; Ω_x and Ω_y are the transverse angular rate inputs; and B_x and B_y are the transverse magnetic field inputs. The matrix A can be written as

$\mathbf{A}=\left[\begin{array}{cccc}\hfill -\frac{R_{\text{tot}}^{\mathrm{e}}}{Q}\hfill & \hfill \frac{{\gamma }^{\mathrm{e}}{B}_{\mathrm{z}}^{\mathrm{e}}}{Q}\hfill & \hfill \frac{R_{\text{se}}^{\text{en}}}{Q}\hfill & \hfill \frac{{\gamma }^{\mathrm{e}}{B}_{\mathrm{z}}^{\mathrm{n}}{P}_{\mathrm{z}}^{\mathrm{e}}}{Q{P}^{\mathrm{n}}}\hfill \\ \hfill -\frac{{\gamma }^{\mathrm{e}}{B}_{\mathrm{z}}^{\mathrm{e}}}{Q}\hfill & \hfill -\frac{R_{\text{tot}}}{Q}\hfill & \hfill -\frac{{\gamma }^{\mathrm{e}}{B}_{\mathrm{z}}^{\mathrm{n}}{P}_{\mathrm{z}}^{\mathrm{e}}}{Q}\hfill & \hfill \frac{R_{\text{se}}^{\mathrm{e}}}{Q}\hfill \\ \hfill R_{\text{se}}^{\text{ne}}\hfill & \hfill \frac{{\gamma }^{\mathrm{n}}{P}_{\mathrm{z}}^{\mathrm{n}}{B}_{\mathrm{z}}^{\mathrm{e}}}{P_{\mathrm{z}}^{\mathrm{e}}}\hfill & \hfill -R_{\text{tot}}^{\mathrm{n}}\hfill & \hfill {\gamma }^{\mathrm{n}}{B}_{\mathrm{z}}^{\mathrm{n}}\hfill \\ \hfill -\frac{{\gamma }^{\mathrm{n}}{B}_{\mathrm{z}}^{\mathrm{e}}{P}_{\mathrm{z}}^{\mathrm{n}}}{P_{\mathrm{z}}^{\mathrm{n}}}\hfill & \hfill R_{\text{se}}^{\text{ne}}\hfill & \hfill -{\gamma }^{\mathrm{n}}{B}_{\mathrm{z}}^{\mathrm{n}}\hfill & \hfill -R_{\text{tot}}^{\mathrm{n}},\hfill \end{array}\right].(3)$

The matrix W can be written as

$\mathbf{W}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill -P_z^{\mathrm{e}}\hfill & \hfill 0\hfill & \hfill \frac{P_z^{\mathrm{e}}{\gamma }^{\mathrm{e}}}{Q}\hfill \\ \hfill P_z^{\mathrm{e}}\hfill & \hfill 0\hfill & \hfill -\frac{P_z^{\mathrm{e}}{\gamma }^{\mathrm{e}}}{Q}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -P_z^{\mathrm{n}}\hfill & \hfill 0\hfill & \hfill P_z^{\mathrm{n}}{\gamma }^{\mathrm{n}}\hfill \\ \hfill P_z^{\mathrm{n}}\hfill & \hfill 0\hfill & \hfill -P_z^{\mathrm{n}}{\gamma }^{\mathrm{n}}\hfill & \hfill 0\hfill \end{array}\right],(4)$

$\begin{array}{c}\hfill {\lambda }_{\mathrm{1,2}}={\phi }_1\pm i{\omega }_1=\left(\alpha +\frac{\sqrt{\sqrt{a^2+b^2}+a}}{2\sqrt{2}}\right)\pm i\left(\beta -\frac{\sqrt{\sqrt{a^2+b^2}-a}}{2\sqrt{2}}\right)\end{array},(5)$

$\begin{array}{c}\hfill {\lambda }_{\mathrm{3,4}}={\phi }_2\pm i{\omega }_2=\left(\alpha -\frac{\sqrt{\sqrt{a^2+b^2}+a}}{2\sqrt{2}}\right)\pm i\left(\beta +\frac{\sqrt{\sqrt{a^2+b^2}-a}}{2\sqrt{2}}\right)\end{array}.(6)$

The intermediate equations in Eq. (5) and Eq. (6) are

$\alpha =-\frac{R_{\text{tot\hspace{0.17em}}}^{\mathrm{e}}+R_{\text{tot\hspace{0.17em}}}^{\mathrm{n}}}{2Q},\beta =\frac{\lambda M^{\mathrm{e}}{P}_z^{\mathrm{e}}{\gamma }^{\mathrm{e}}+\lambda M^{\mathrm{n}}{P}_z^{\mathrm{n}}Q{\gamma }^{\mathrm{n}}}{2Q},(7)$

$a=\frac{{\left(R_{\text{tot}}^{\mathrm{e}}-R_{\text{tot}}^{\mathrm{n}}\right)}^2-{\left(\lambda M^{\mathrm{e}}{P}_z^{\mathrm{e}}{\gamma }^{\mathrm{e}}+Q\lambda M^{\mathrm{n}}{P}_z^{\mathrm{n}}{\gamma }^{\mathrm{n}}\right)}^2}{Q^2},(8)$

$b=\frac{2\left(R_{\text{tot}}^{\mathrm{e}}-R_{\text{tot}}^{\mathrm{n}}\right)\left(Q\lambda M^{\mathrm{n}}{P}_z^{\mathrm{n}}{\gamma }^{\mathrm{n}}-\lambda M^{\mathrm{e}}{P}_z^{\mathrm{e}}{\gamma }^{\mathrm{e}}\right)}{Q^2}.(9)$

The transfer function of the SERFC in the Laplace domain is

$\mathbf{H}\left(s\right)={\left(s\mathbf{I}-\mathbf{A}\right)}^{-1}\mathbf{W}=\mathbf{N}\left(s\right)/D\left(s\right),(10)$

where I is the identity matrix of 4 × 4. The molecular matrix ψ(s) of the transfer function is simply expressed here as

$\psi \left(s\right)=\left[\begin{array}{cccc}\hfill {\psi }_{11}\left(s\right)\hfill & \hfill {\psi }_{12}\left(s\right)\hfill & \hfill {\psi }_{13}\left(s\right)\hfill & \hfill {\psi }_{14}\left(s\right)\hfill \\ \hfill {\psi }_{21}\left(s\right)\hfill & \hfill {\psi }_{22}\left(s\right)\hfill & \hfill {\psi }_{23}\left(s\right)\hfill & \hfill {\psi }_{24}\left(s\right)\hfill \\ \hfill {\psi }_{31}\left(s\right)\hfill & \hfill {\psi }_{32}\left(s\right)\hfill & \hfill {\psi }_{33}\left(s\right)\hfill & \hfill {\psi }_{34}\left(s\right)\hfill \\ \hfill {\psi }_{41}\left(s\right)\hfill & \hfill {\psi }_{42}\left(s\right)\hfill & \hfill {\psi }_{43}\left(s\right)\hfill & \hfill {\psi }_{44}\left(s\right)\hfill \end{array}\right].(11)$

The denominator of the transfer function is as follows:

$D\left(s\right)=\left[{\left(s-{\phi }_1\right)}^2+{\omega }_1^2\right]\left[{\left(s-{\phi }_2\right)}^2+{\omega }_2^2\right].(12)$

The transfer function expressions for output $P_x^e$ and input [Ω_x, Ω_y, B_x, B_y] are as follows:

$\begin{array}{cc}\hfill & H_{\mathrm{\Omega }x}\left(s\right)=P_x^e\left(s\right)/{\mathrm{\Omega }}_x\left(s\right)={\psi }_{11}\left(s\right)/D\left(s\right),\hfill \\ \hfill & H_{\mathrm{\Omega }y}\left(s\right)=P_x^e\left(s\right)/{\mathrm{\Omega }}_y\left(s\right)={\psi }_{12}\left(s\right)/D\left(s\right),\hfill \\ \hfill & H_{Bx}\left(s\right)=P_x^e\left(s\right)/B_x\left(s\right)={\psi }_{13}\left(s\right)/D\left(s\right),\hfill \\ \hfill & H_{By}\left(s\right)=P_x^e\left(s\right)/B_y\left(s\right)={\psi }_{14}\left(s\right)/D\left(s\right).\hfill \end{array}(13)$

Next, the effect of the magnetic field gradient on $R_{\text{tot}}^{\mathrm{n}}$, resulting in the change of the system output, is analyzed.

2.1 Responses in steady-state and frequency

2.1.1 Steady-state response

Setting s = 0 in Eq. 13 would result in the steady-state input and output solutions for the system.

$P_x^e=K_{\mathrm{\Omega }x}{\mathrm{\Omega }}_x+K_{\mathrm{\Omega }y}{\mathrm{\Omega }}_y+K_{Bx}{B}_x+K_{By}{B}_y,(14)$

where K_Ωx, K_Ωy, K_Bx, and K_By are the scale factors. The principle of steady-state response of a gyroscope to B_x and B_y is shown in Figure 1. By compensating the magnetic compensation point to zero and considering only the input angular velocity in the y-axis direction, the main component term representing the gyroscope response can be determined as

$\begin{array}{cc}\hfill P_x^e& =\frac{P_z^e{R}_{\text{tot\hspace{0.17em}}}^e{\gamma }^e{\gamma }^n{\left(B_z^n\right)}^2{\mathrm{\Omega }}_y}{{\left({\gamma }^e{B}_z^e{R}_{\text{tot\hspace{0.17em}}}^n+{\gamma }^n{B}_z^n{R}_{\text{tot\hspace{0.17em}}}^e\right)}^2+{\left(R_{\text{tot\hspace{0.17em}}}^n{R}_{\text{tot\hspace{0.17em}}}^e\right)}^2}\hfill \\ \hfill & +\frac{\left(P_z^e{R}_{\text{tot}}^n{\gamma }^e+{\gamma }^n{P}_z^n{R}_{se}^{en}\right)\left({\gamma }^e{R}_{\text{tot}}^n{B}_z^e+{\gamma }^n{R}_{\text{tot}}^e{B}_z^n\right)B_x}{{\left({\gamma }^e{B}_z^e{R}_{\text{tot\hspace{0.17em}}}^n+{\gamma }^n{B}_z^n{R}_{\text{tot\hspace{0.17em}}}^e\right)}^2+{\left(R_{\text{tot\hspace{0.17em}}}^n{R}_{\text{tot\hspace{0.17em}}}^e\right)}^2}.\hfill \end{array}(15)$

From Eq. 15, since the values of $R_{se}^{en}$, $R_{\text{tot\hspace{0.17em}}}^n$, and $R_{\text{tot\hspace{0.17em}}}^e$ cannot be ignored, the input of the system to the transverse magnetic field B_x is affected by these terms. Therefore, the magnetic field error must be suppressed in order to increase the accuracy of inertial measurements, and a method using amplitude frequency response analysis is next proposed to suppress the B_x magnetic field error.

FIGURE 1

FIGURE 1. (A) Steady-state response of B_y. (B) Steady-state response of B_x.

2.1.2 Frequency response

The amplitude frequency response of B_x is composed of one proportional link, two second-order oscillation links, and two first-order differential links, and the following equation can be used to define the conversion relationship between B_x and $P_x^e$:

$\begin{array}{cc}\hfill H_{Bx}\left(s\right)& =P_x^{\mathrm{e}}\left(s\right)/B_x\left(s\right)\hfill \\ \hfill & =\frac{k_{Bx}\left(s-{\omega }_{Bx1}\right)\left(s-{\omega }_{Bx2}\right)}{\left[{\left(s-{\phi }_1\right)}^2+{\omega }_1^2\right]\left[{\left(s-{\phi }_2\right)}^2+{\omega }_2^2\right]}\hfill \end{array}.(16)$

The two zeros are

${\omega }_{Bx1}=-\frac{P_z^e{R}_{\text{tot\hspace{0.17em}}}^n{\gamma }^e+P_z^n{R}_{se}^{en}{\gamma }^n}{P_z^e{\gamma }^e},(17)$

${\omega }_{Bx2}=-\frac{M^e{P}_z^e{R}_{\text{tot\hspace{0.17em}}}^n{\gamma }^e+M^e{P}_z^n{R}_{se}^{en}{\gamma }^n+M^n{P}_z^n{R}_{\text{tot\hspace{0.17em}}}^e{\gamma }^n}{M^e{P}_z^e{\gamma }^e+M^n{P}_z^{n}Q{\gamma }^n}.(18)$

$k_{Bx}=-\frac{P_z^{\mathrm{e}}{\gamma }^{\mathrm{e}}\left(B_z^e{\gamma }^{\mathrm{e}}+B_z^{n}Q{\gamma }^{\mathrm{n}}\right)}{Q^2}$ is the coefficient in the proportional link. Frequency ω and amplitude A of the low-frequency platform section can be expressed as

$\omega =-\frac{P_z^e{R}_{\text{tot\hspace{0.17em}}}^n{\gamma }^e+P_z^n{R}_{se}^{en}{\gamma }^n}{P_z^e{\gamma }^e},(19)$

$A=\frac{\left(P_z^e{R}_{\text{tot}}^n{\gamma }^e+{\gamma }^n{P}_z^n{R}_{se}^{en}\right)\left({\gamma }^e{R}_{\text{tot}}^n{B}_z^e+{\gamma }^n{R}_{\text{tot}}^e{B}_z^n\right)}{{\left({\gamma }^e{B}_z^e{R}_{\text{tot\hspace{0.17em}}}^n+{\gamma }^n{B}_z^n{R}_{\text{tot\hspace{0.17em}}}^e\right)}^2+{\left(R_{\text{tot\hspace{0.17em}}}^n{R}_{\text{tot\hspace{0.17em}}}^e\right)}^2}.(20)$

The response of B_x with respect to the AC magnetic field signal of frequency ω is expressed as

$\begin{array}{c}\hfill \left|H_{Bx}\left(j\omega \right)\right|=\left|k_{Bx}\right|\sqrt{\frac{\left({\omega }^2+{\omega }_{Bx1}^2\right)\left({\omega }^2+{\omega }_{Bx2}^2\right)}{\left(4{\phi }_1^2{\omega }^2+{\left({\omega }^2-{ϵ}_1^2\right)}^2\right)\left(4{\phi }_2^2{\omega }^2+{\left({\omega }^2-{ϵ}_2^2\right)}^2\right)}}\end{array},(21)$

where ${ϵ}_1^2={\phi }_1^2+{\omega }_1^2$ and ${ϵ}_2^2={\phi }_2^2+{\omega }_2^2$.

2.2 Magnetic field gradient effects on A_MFER

In this study, the SERFC pump laser direction is strictly aligned with the z-axis main magnetic field direction, the detection laser direction is consistent with the x-axis magnetic field compensation direction and is orthogonal to the pump laser direction, and the inertial sensitive axis is the y-axis. In Liu et al. (2022c); Fan et al. [16], the influence of the B_x magnetic field error on the system is analyzed using the magnetic field equivalent velocity sensitivity A_MFVS. Based on the previous research, we carried out a more complete derivation and concluded that the expression of the low-frequency bias magnetic field sensitivity (LFBMS) (the low-frequency band studied in SERFC is the spectrum below 10⁻³ Hz) A_MFVS can be expressed as

$A_{MFVS}=\left|\frac{K_{Bx}\left(0\right)}{K_{\mathrm{\Omega }y}\left(0\right)}\right|=\frac{\left(P_z^e{R}_{\text{tot}}^n{\gamma }_e+P_z^n{R}_{\text{se}}^{en}{\gamma }_n\right)\left(Q{R}_{\text{tot}}^n{\omega }_e+R_{\text{tot}}^e{\omega }_n\right)}{\lambda M_n{\omega }_n{\gamma }_e{P}_z^e{P}_z^n{R}_{\text{tot}}^e},(22)$

where ω_e = γ_eB^e/Q and ω_n = γ_nBⁿ. The representative measurement parameters in the experiment are shown in Table 2. Since $R_{\text{tot}}^e{\omega }_n$ is 2–3 orders of magnitude larger than $Q{R}_{\text{tot}}^n{\omega }_e$, Eq. 22 can be simplified as

$A_{MFVS}=\left|\frac{K_{Bx}\left(0\right)}{K_{\mathrm{\Omega }y}\left(0\right)}\right|=\frac{1}{\lambda M_n}\left(\frac{R_{\text{tot}}^n}{P_z^n}+\frac{{\gamma }_n}{{\gamma }_e}\frac{R_{se}^{en}}{P_z^e}\right).(23)$

Obviously, $R_{\text{tot\hspace{0.17em}}}^n$, $R_{se}^{en}$, $P_z^n$, and $P_z^e$ play an important role in Eq. 22. In addition, if we ignore $P_z^n{R}_{\text{se}}^{en}{\gamma }_n$ by considering the magnitude of $P_z^e{R}_{\text{tot}}^n{\gamma }_e$ over $P_z^n{R}_{\text{se}}^{en}{\gamma }_n$ in Eq. 22, the conclusion of the model is the same as in [5], thus proving the correctness of the aforementioned derivation. In the SERFC with the atomic source as K–Rb–²¹Ne, the influence term of the transverse decoherence time of ²¹Ne can be expressed as [27]

$R_{\mathit{tot}}^n=R_{\text{quad\hspace{0.17em}}}^n+R_{\text{sd}}^n+R_{\text{se}}^{\text{en}}+R_{\text{MG}1}^n,(24)$

$R_1^n=R_{\text{quad\hspace{0.17em}}}^n+R_{\text{sd}}^n+R_{\text{se}}^{\text{en}}+R_{\text{MG}2}^n,(25)$

where $R_{\text{quad\hspace{0.17em}}}^n$is the relaxation of electric quadrupole moment; $R_{\text{sd}}^n$ is the relaxation of spin destruction; $R_{\text{se}}^{\text{en}}$ is the spin exchange rate of ²¹Ne spin polarized by alkali-metal electrons through spin exchange collision; and $R_{\text{MG}}^n$ is the relaxation term affected by the inhomogeneity of the magnetic field distribution, and its relationship items are as follows [22]:

$R_{\text{MG}1}^n=\frac{1}{V}{\int }_{\text{Volume\hspace{0.17em}}}\frac{8{\gamma }_n^2{R}^4{\left|\vec{\nabla }{B}_z\right|}^2}{175D_{\text{Ne}-\mathrm{N}\mathrm{e}}}dV,(26)$

$R_{\text{MG}2}^n=\frac{1}{V}{\int }_{\text{Vollame\hspace{0.17em}}}{D}_{\text{Ne}-\mathrm{N}\mathrm{e}}\frac{{\left|\vec{\nabla }{B}_x\right|}^2+{\left|\vec{\nabla }{B}_y\right|}^2}{{B_0}^2}dV,(27)$

where R is the radius of the vapor cell; D_Ne−Ne is the diffusion constant of ²¹Ne in the atomic cell; $B_0=-B{x}_z^e-B_z^n$; $\vec{\nabla }{B}_x$ and $\vec{\nabla }{B}_y$ represent the first-order transverse magnetic field gradient along the x-axis and y-axis, respectively; and $\vec{\nabla }{B}_z$ represents the first-order longitudinal magnetic field gradient along the z-axis [28, 29].

2.3 Magnetic field gradient caused by pump optical power density and temperature

On the one hand, the pump light power density affects the magnetic field gradient. From Eq. 27, it is shown that for the decay of the pump rate with the propagation distance z, the D1 line pump light of K atoms propagates in the vapor cell. The strong absorption of pump light by dense alkali-metal atoms in the atomic vapor cell leads to a significant electron spin polarization gradient.

$R_{\mathrm{p}}\left(z\right)=R_{\text{rel}}W\left[\frac{R_{\mathrm{p}}\left(0\right)}{R_{\text{rel}}}{e}^{\left(-n_K{\sigma }_L\left(v\right)z+\frac{R_{\mathrm{p}}\left(0\right)}{R_{\text{rel}}}\right)}\right]e^{-2{\left(\rho /r\right)}^2},(28)$

where R_rel is the relaxation rate of the electron spin of the K atom except for the pumping rate; R_p(0) is the initial pump rate when the pump light is incident into the vapor cell; ρ is the distance from the center of the spot; r is the radius of the spot; W is the Lambert-W function; n_K is the K-atomic density; and σ_L(v) is the absorption cross-sectional area of the K-atomic absorption pump light.

The expression for the decay of the alkali-metal polarizability with propagation distance z is

$\begin{array}{cc}\hfill & P_z^e\left(z\right)=\frac{R_{\mathrm{p}}\left(z\right)}{R_{\mathrm{p}}\left(z\right)+R_{\text{rel}}},\hfill \\ \hfill & P_z^n=\frac{P_z^e\left(z\right)R_{\text{se}}^{\text{en}}}{R_1^n},\hfill \end{array}(29)$

where $R_{se}^{en}$ is the equivalent spin exchange rate between the mixed alkali-metal atom and ²¹Ne atom. The equivalent magnetic field expressions of electron spin and nuclear spin in the atomic polarization state are as follows [30]:

$\begin{array}{cc}\hfill {\mathbf{B}}^{\mathrm{e}}& =\frac{2}{3}{k}_0{\mu }_0{\mu }_B{n}_e{\mathbf{P}}^{\mathbf{e}},\hfill \\ \hfill {\mathbf{B}}^{\mathbf{n}}& =\frac{2}{3}{k}_0{\mu }_0{\mu }_B{n}_n{\mathbf{P}}^{\mathbf{n}},\hfill \end{array}(30)$

where k₀ is the Fermi-contact-shift enhancement factor; μ₀ is the permeability of vacuum; μ_B is the Bohr magneton; and n_e and n_n are the densities of alkali-metal atoms and noble gas, respectively. The distribution simulation of electron and nucleon polarizability under different pump light power densities is shown in Figure 2. Increasing the pump light power density can produce a uniform and saturated spin polarization, but too high pump light power density will reduce the sensitivity of SERFC, so the pump light power density value needs to be set at the corresponding specific polarization rate value [31].

FIGURE 2

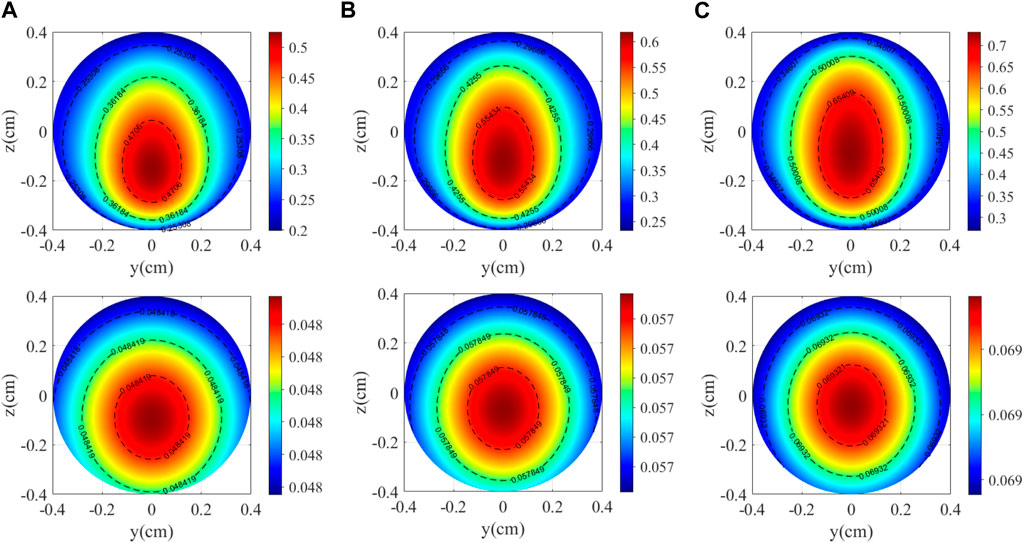
FIGURE 2. Electron and nucleon polarizability distributions at different pump power densities. (A) 84.92 mW/cm²; (B) 127.39 mW/cm²; and (C) 205.34 mW/cm².

On the other hand, the temperature also affects the magnetic field gradient. The empirical formula of alkali-metal atom density n and temperature of alkali-metal is [32]

$n\left(T\right)=\frac{10^{21.866+n_A-n_B/T}}{T},(31)$

where n_A and n_B are constants related to the type of alkali-metal atom and T is the temperature of the steam cell expressed on the thermodynamic temperature scale. The expression of $R_{se}^{en}$ is as follows:

$R_{\text{se}}^{\text{en}}=n_{\text{Rb}}{\kappa }_{\text{se}}^{\text{Rb}-\mathrm{N}\mathrm{e}}+n_K{\kappa }_{\text{se}}^{\mathrm{K}-\mathrm{N}\mathrm{e}},(32)$

where ${\kappa }_{\text{se}}^{\text{Rb}-\mathrm{N}\mathrm{e}}$ and ${\kappa }_{\text{se}}^{\mathrm{K}-\mathrm{N}\mathrm{e}}$ are the spin exchange rate constants between Rb −²¹Ne and K −²¹Ne atom pairs, respectively.

$R_{sd}={\sigma }_{sd}\bar{v}{n}_x,(33)$

where σ_sd is the collision cross-sectional area; $\bar{v}$ is the relative thermal movement speed, and the influence of the vapor cell temperature on the relative thermal movement speed is ignored because the amplitude of its change with temperature is small [33]; and n_x represents the number density of atoms or molecules colliding with alkali-metal atoms. The distribution simulations of electron polarizability and nuclear polarizability at different temperatures are shown in Figure 3. It can be seen that both $R_{\text{se}}^{\text{en}}$ and R_sd are temperature-dependent, thus affecting the A_MFVS.

FIGURE 3

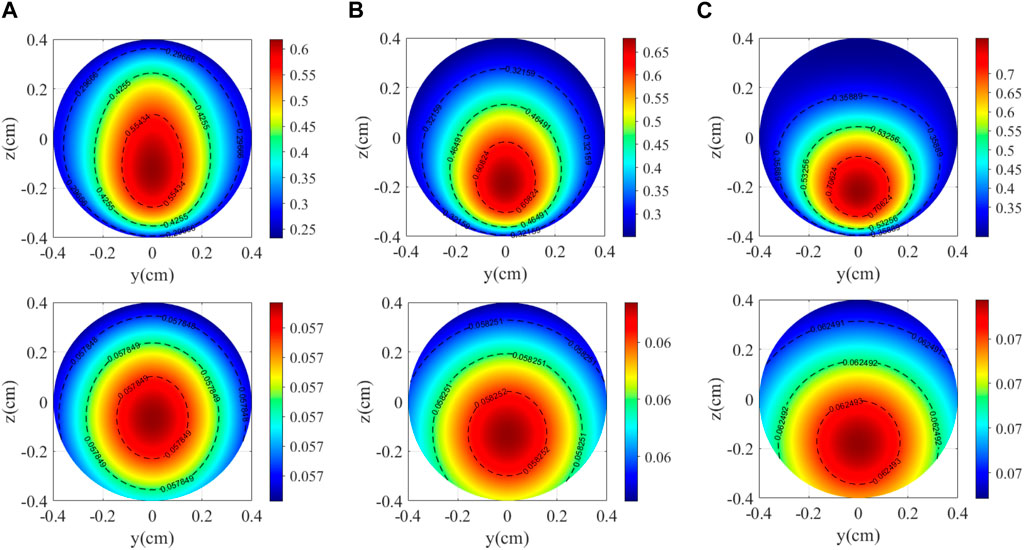
FIGURE 3. Electron and nucleon polarizability distributions at different temperatures. (A) 170°C; (B) 190°C; and (C) 210°C.

3 Experimental setup

The schematic diagram of the SERFC based on K–Rb–²¹Ne is shown in Figure 4. A spherical vapor cell with a diameter R of 8 mm made of GE180 aluminosilicate glass was placed in a boron nitride ceramic oven. The vapor cell contained 2 amagats of ²¹Ne (70% isotope-enriched) gas, a natural abundance K and Rb alkali-metal mixture with a density ratio of 1: 94, and 50 torrs of N₂. Three layers of μ-metal magnetic shielding cylinder with high permeability are used to shield the external magnetic field, and the innermost layer is MnZn ferrite magnetic shielding cylinder to suppress low-frequency magnetic errors [8]. The pump light is generated by a distributed Bragg reflector (DBR) laser with a center frequency of 770.108 nm (K D1 resonant line), a quarter wave plate in the pump path converts a linearly polarized state to a circularly polarized state, and a pair of planoconvex lenses is used to expand the beam of pump light. The probe beam is generated by a distributed feedback (DFB) laser with a center frequency of 795.311 nm (approximately 0.3 nm to the blue side of the Rb D1 resonance line), and the Glan–Taylor polarizer (GT-5, Thorlabs) can purify the laser to a better linearly polarized laser. The power stability control system of the pump laser and laser consists of a polarizing beam splitter (PBS), liquid crystal variable retarder (LCVR), Glan–Taylor polarizer, half-wave plate, photodetector (PD), and electronic controller.

FIGURE 4

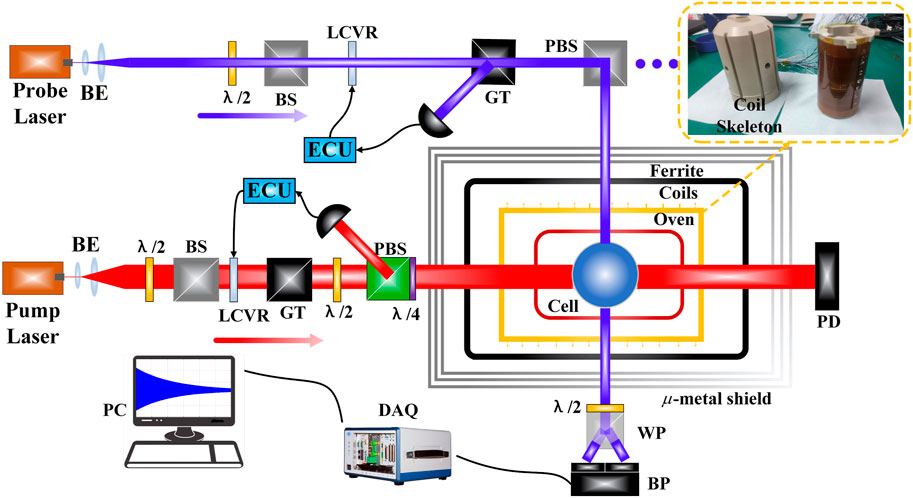
FIGURE 4. Schematic of the K–Rb–²¹Ne comagnetometer. BE, beam expander; P, linear polarizer; LCVR, liquid crystal variable retarder; GT, Glan–Taylor polarizer; PD, photodiode; PBS, polarizing beam splitter; ECU, electronic control unit; WP, Wollaston prism; BP, balanced photodiode; λ/2, half-wave plate; λ/4, quarter-wave plate.

The three-axis magnetic compensation coils and gradient magnetic coils are used to compensate the residual magnetic field and generate the magnetic field gradient, respectively. According to the magnetic flux continuity principle ∇ ⋅ B = 0, it shows that the magnetic field is a passive field, the magnetic line of force is always a closed curve, and the divergence calculation formula is

$\mathrm{d}\mathrm{i}\mathrm{v}\mathrm{A}=\nabla \cdot B=\frac{d{B}_{\mathrm{x}}}{dx}+\frac{d{B}_{\mathrm{y}}}{dy}+\frac{d{B}_{\mathrm{z}}}{dz}=0,(34)$

so the $\frac{d{B}_{\mathrm{z}}}{dz}$ coil can also generate magnetic field gradients along the $\frac{d{B}_{\mathrm{x}}}{dx}$ and $\frac{d{B}_{\mathrm{y}}}{dy}$ directions, as shown in Figure 5A and Figure 5B, the magnetic field gradient coil constants corresponding to the three-axis directions obtained through finite element simulation. In this paper, the designed coil parameters are shown in Table 1. First, according to the size of the atomic vapor cell (the outer diameter R is 8 mm), the coil radius is chosen to be 24.9 mm so that the magnetic field uniformity zone is greater than 0.25 R. The coil is designed using the forward method: the transverse magnetic field coils Bx and By adopt the saddle coil configuration, and the Maxwell coil generates magnetic fields of Bz and dBz/dz by changing the current spin direction, respectively. Afterward, the magnetic field magnitude can be calculated according to the Biot–Savart law. Finally, the homogeneous field coils and gradient coils are fabricated by the flexible printed circuit (FPC) technique, as shown in Figure 5C and Figure 5D, respectively. After the FPC coil is fixed on the coil skeleton, the coil is mounted on the SERFC in the position shown in Figure 4.

FIGURE 5

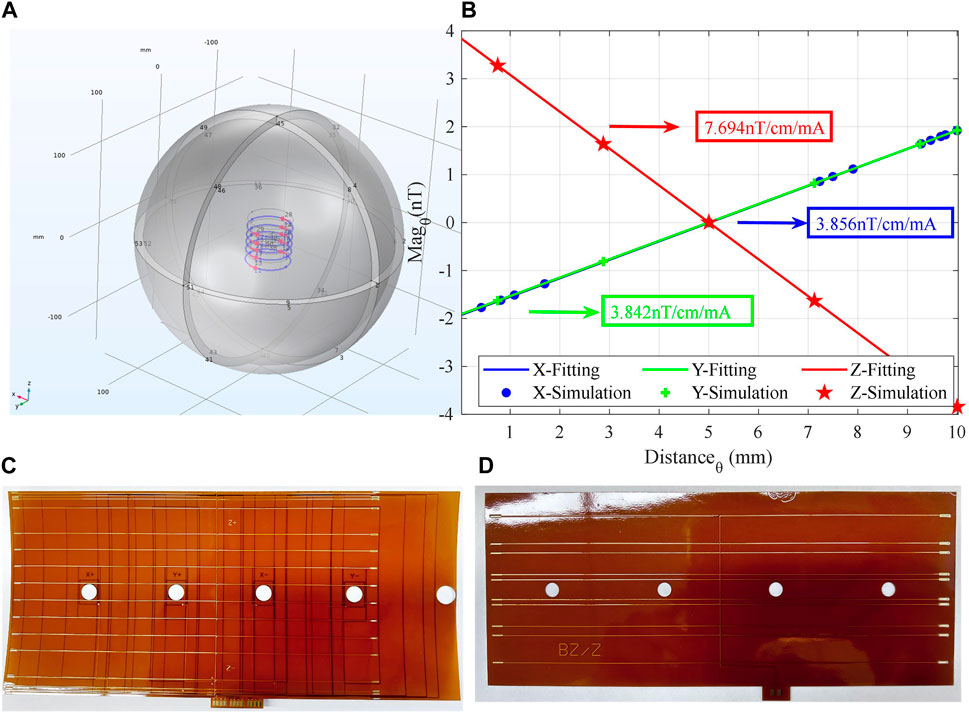
FIGURE 5. (A) Overall model of finite element simulation. (B) Triaxial magnetic field coil constant. (C) Bx, By, and Bz three-in-one uniform magnetic field coil. (D) dBz/dz magnetic field gradient coil.

TABLE 1

TABLE 1. Design parameters of the magnetic field coil.

TABLE 2

TABLE 2. Summary of the measured parameters.

4 Results and discussion

In this experiment, the spin coupling between electron spin and nuclear spin is decoupled by applying a magnetic field of approximately 1,500 nT, but it does not affect the measurement and fitting of free induction decay (FID) signals [34]. As shown in Figure 6, the relaxation times are obtained by measuring the output of the system at different times and fitting the relationship between the pump time and the precession signal.After measuring T₁ and T₂ at different magnetic field gradients by the aforementioned method, Eqs 24–25 are verified by fitting the relationship between the relaxation rate of ²¹Ne and the magnetic field gradient. According to Eqs 26–27, it can be seen that $R_{\mathit{tot}}^n$ is mainly affected by the longitudinal magnetic field gradient and temperature, while $R_1^n$ is mainly affected by the transverse magnetic field gradient. Figure 7 shows the relationship between the experimental transverse and longitudinal relaxation rates of ²¹Ne with different magnetic field gradients under different temperature conditions. Therefore, the inhomogeneity of the total magnetic field distribution of the system can be compensated by applying an appropriate magnetic field gradient, that is, the gradient value corresponding to the lowest point of the quadratic fitting parabola or the minimum value of the ²¹Ne relaxation rate.

FIGURE 6

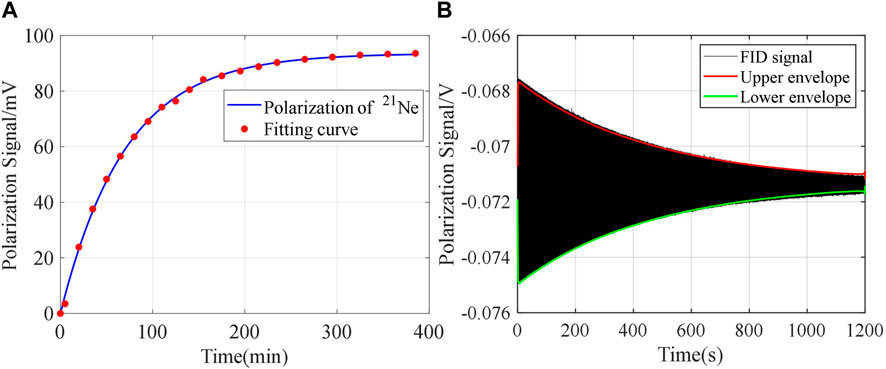
FIGURE 6. (A) Longitudinal relaxation time of nucleon spin. (B) Transverse relaxation time of nucleon spin.

FIGURE 7

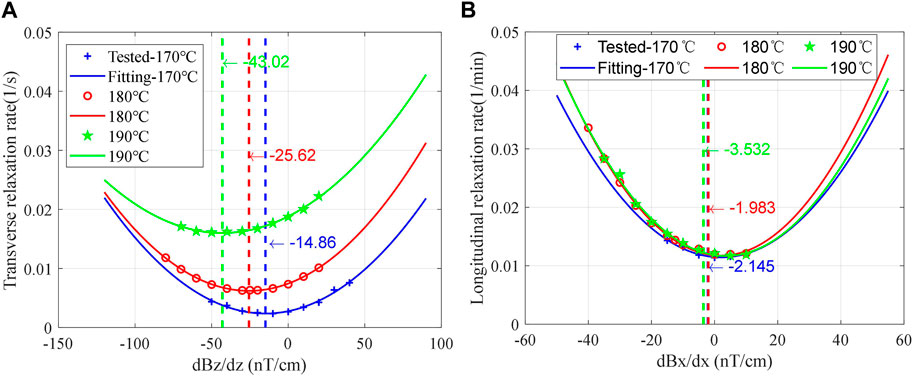
FIGURE 7. Measured at different temperatures: (A) relationship between $R_{\mathit{tot}}^n$ and longitudinal magnetic field gradient and (B) relationship between $R_1^n$ and transverse magnetic field gradient.

The frequency response of the K–Rb–²¹Ne comagnetometer was obtained by applying 0.5542 nTpp sine waves with a frequency range of 0.01–600 Hz along the x-axis, and the results were fitted with Eq. 21. It can be seen from Figure 8A that both the electronic and nuclear resonance peaks shift to the right with the increase in the vapor cell temperature, indicating that the electron spin polarizability and the nuclear spin polarizability are proportional to the vapor cell temperature. However, according to Eqs 31–33, the LFBMS can be suppressed in two ways: one is by reducing the temperature of the vapor cell to reduce the atomic density n_K (in order to improve the polarization of ²¹Ne and reduce the polarization magnetic field gradient, a hybrid pumping technique is adopted. The density ratio of K and Rb atoms determines the uniformity of polarization, so it is necessary to choose an appropriate atomic density ratio to make SERFC work in the optimal state), and finally $R_{\text{se}}^{\text{en}}$ is reduced. The other is by reducing $\bar{v}$ determined by temperature, and finally $R_{\mathit{tot}}^n$ is reduced affected by R_sd. The relaxation caused by other temperature-related factors (such as $R_{\text{quad\hspace{0.17em}}}^n$ and $R_{\text{sd}}^n$) are smaller than that caused by the magnetic field gradient when the vapor cell temperature is low, so the LFBMS is mainly determined by the variation in $R_{\text{MG}}^n$. The Allan deviation analysis method is introduced to evaluate the influence of the low-frequency magnetic field error on the long-term stability. After the SERFC system is stabilized, the output signals for 2 h are collected under different vapor cell temperatures, and then the Allen deviation diagram is drawn in Figure 8B. The bias instability improves with the vapor cell temperature, and a bias instability of 0.012 deg/h is achieved at 170°C. In addition, the suppression factor is defined as the ratio of the scale factor to the amplitude of the magnetic response [5], which is used to characterize the influence on the suppression of low-frequency magnetic field errors. It can be seen from Figure 8C that the suppression factor decreases with the increase in temperature, indicating that the magnetic field error suppression capability decreases with the increase in temperature.

FIGURE 8

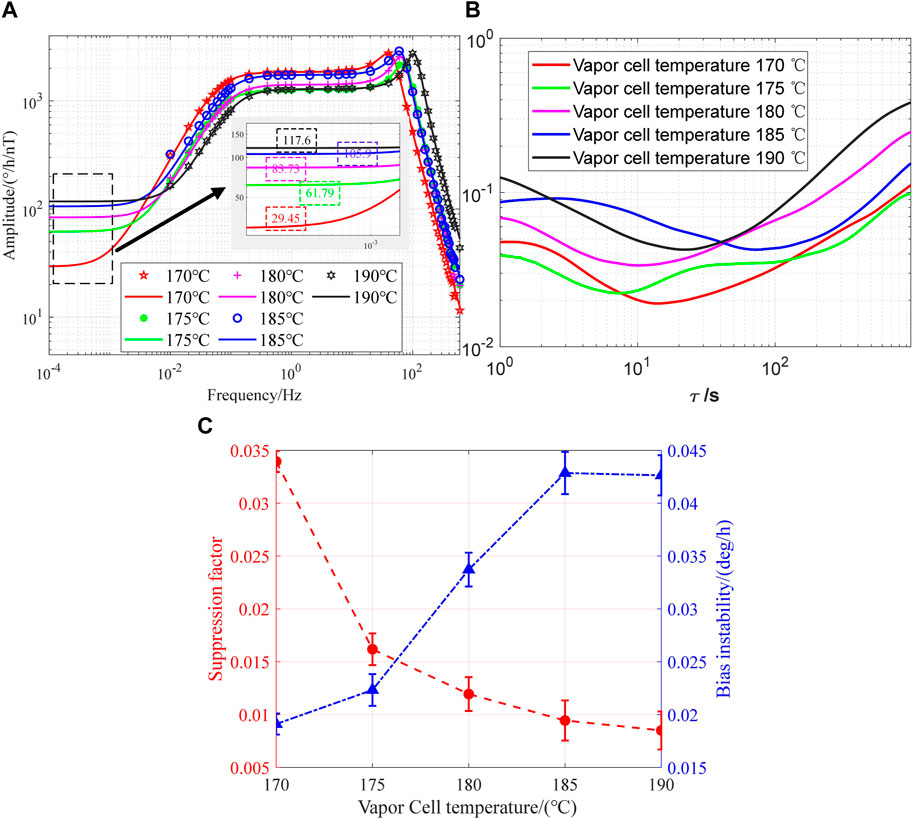
FIGURE 8. (A) Amplitude–frequency response B_x at different cell temperatures. (B) Corresponding Allan deviation at different cell temperatures. (C) Suppression factor and bias instability.

According to Eqs 28–30, increasing the pump light power density can produce a uniform and saturated spin polarization magnetic field gradient. It can be seen from Figure 9A that LFBMS is suppressed with the increase in pump light power density, and the experimental results show that the LFBMS can be suppressed by increasing the pump light power density to improve $P_z^e$ and $P_z^n$. However, when the pump power density increases to a certain value, the LFBMS will also increase. It is speculated that the reason for the increase in LFBMS is that the absorption rate of K atoms is oversaturated when the power density of the pump light increases to a certain extent. With the increase in pump light power density, the frequency ω_e = γ_eB^e/Q corresponding to the electron resonance peak shifts to the right, proving the increase in electron spin polarizability. However, the frequency ω_n = γ_nBⁿ corresponding to the nucleon resonance peak does not shift significantly to the right, which may be caused by the low nucleon spin polarizability. From the Allan deviation analysis at different pump light power densities in Figure 9B, the bias instability is reduced to 0.011 deg/h by suppressing the system response to B_x at low frequencies. Figure 9C shows the relationship between low-frequency magnetic field suppression factor and bias instability at different pump light power densities. This further proves that the bias instability is enhanced due to the suppression of the magnetic field suppression factor.

FIGURE 9

FIGURE 9. (A) Amplitude–frequency response B_x at different pump laser power densities. (B) Corresponding Allan deviation at different pump laser power densities. (C) Suppression factor and bias instability.

In addition, the magnetic field gradient is applied to reduce LFBMS by changing the influence of $R_{\mathit{tot}}^n$ on the low-frequency magnetic field error. Figure 10A shows the comparison results of the fitting curves of the B_x amplitude–frequency response under different longitudinal magnetic field gradients. It can be seen from Figure 10A that the measured low-frequency magnetic field error is the smallest when the magnetic field gradient is set to −10 nT/cm, and the bias instability measured in Figure 10B is 0.021 deg/h. Therefore, it can be stated that low-frequency magnetic field errors can also be suppressed by actively applying magnetic field gradients. Similarly, it can be seen from Figure 10C that the bias instability is improved by suppressing the magnetic field inhibitory factor B_x. However, the bias instability is not completely improved because the applied longitudinal magnetic field gradient dBz/dz increases the transverse relaxation rate but affects the longitudinal relaxation rate. Subsequent research can compensate for the low-frequency magnetic field error by designing a three-axis magnetic field gradient coil.

FIGURE 10

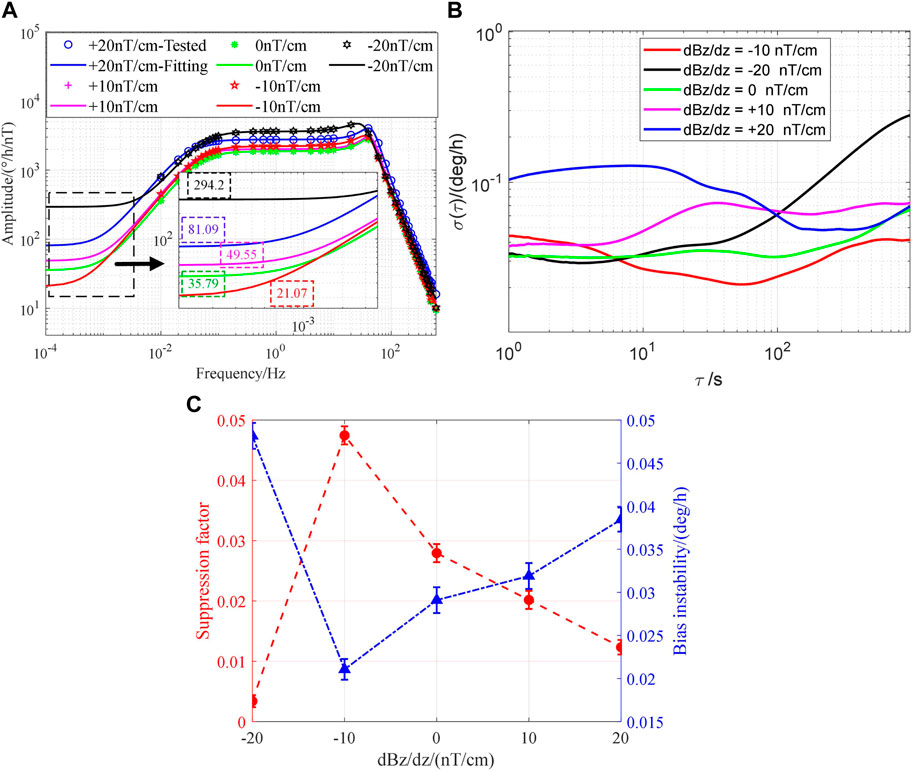
FIGURE 10. (A) Amplitude–frequency response B_x at different magnetic field gradients. (B) Corresponding Allan deviation at different magnetic field gradients. (C) Suppression factor and bias instability.

The K–Rb–²¹Ne comagnetometer sensitivity to B_x in our research conclusions is comparable to the magnetic field suppression factor of the K–³He comagnetometer reported by [5]. Ref. [14] believes that increasing the electronic magnetic field can suppress the magnetic noise and reduce the magnetic field suppression factor, which is similar to the conclusion of increasing the pump light power density in this study. In Ref. [23], the magnetic field gradient leads to atomic decoherence of the K–Rb–²¹Ne comagnetometer, which is complementary to the conclusion in this study that low-frequency magnetic field errors are suppressed by active magnetic field gradient compensation.

5 Conclusion

In conclusion, this paper analyzes the influence of magnetic field gradients on the steady-state response and frequency response of the K–Rb–²¹Ne comagnetometer. The bias magnetic field sensitivity model of SERFC is modified, and the influence of magnetic field gradients on low-frequency magnetic errors is considered. We experimentally verify that the magnetic field gradient of the K–Rb–²¹Ne comagnetometer can be measured in situ through the relationship between the relaxation rate and magnetic field gradient. In addition, the LFBMS can be suppressed by optimizing the vapor cell temperature and the pump light power density and using the magnetic field gradient coil to actively compensate for the magnetic field gradient, and it is verified that the magnetic error suppression method proposed in this paper can reduce the LFBMS of SERFC. After the vapor cell temperature is optimized from 170°C to 190°C, the suppression factor and bias instability are optimized by 72.19% and 55.41%, respectively. After the pump power density is optimized from 85 mW/cm² to 149 mW/cm², the suppression factor and bias instability are optimized by 20.24% and 20.84%, respectively. After the magnetic field gradient is compensated from −10 nT/cm to 0 nT/cm, the suppression factor and bias instability are optimized by 69.86% and 27.63%, respectively. This work provides an experimental and theoretical basis for measuring the magnetic field gradient of the K–Rb–²¹Ne comagnetometer and suppressing the low-frequency magnetic field error.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Methodology: ZWu, FL, ZWa, WQ, and WF; formal analysis: ZWu and FL; investigation: ZWu and HP; data curation: ZWu and HP; validation: ZWu and HP; writing—original draft preparation: ZWu. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the Key Area Research and Development Program of Guangdong Province (Grant No. 2021B0101410005), in part by the National Natural Science Foundation of China (Grant Nos 61673041 and 62103026), and by the China Postdoctoral Science Foundation (Grant No. 2022M720362).

Acknowledgments

This is a short text to acknowledge the contributions of specific colleagues, institutions, or agencies that aided the efforts of the authors.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Schmidt U, Heil W, Allmendinger F. Comment on new limit on lorentz-invariance- and cpt-violating neutron spin interactions using a free-spin-precession ³He-¹²⁹Xe comagnetometer reply. Phys Rev Lett (2014) 112.

CrossRef Full Text | Google Scholar

2. Bear D, Stoner RE, Walsworth RL, Kostelecky VA, Lane CD. Limit on lorentz and cpt violation of the neutron using a two-species noble-gas maser. Phys Rev Lett (2000) 85:5038–41. doi:10.1103/physrevlett.85.5038

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Vasilakis G, Brown JM, Kornack TW, Romalis MV. Limits on new long range nuclear spin-dependent forces set with a k-3 he comagnetometer. Phys Rev Lett (2009) 103:261801. doi:10.1103/physrevlett.103.261801

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Hunter L, Gordon J, Peck S, Lin JF. Using the Earth as a polarized electron source to search for long-range spin-spin interactions. Science (2013) 339:928–32. doi:10.1126/science.1227460

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kornack TW, Ghosh RK, Romalis MV. Nuclear spin gyroscope based on an atomic co-magnetometer. Phys Rev Lett (2005) 95:230801. doi:10.1103/physrevlett.95.230801

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wang Z, Liu S, Wang R, Yuan L, Huang J, Zhai Y, et al. Atomic spin polarization controllability analysis: A novel controllability determination method for spin-exchange relaxation-free co-magnetometers. IEEE/CAA J Automatica Sinica (2022) 9:699–708. doi:10.1109/jas.2021.1004383

CrossRef Full Text | Google Scholar

7. Zhang C, Yuan H, Tang Z, Quan W, Fang JC. Inertial rotation measurement with atomic spins: From angular momentum conservation to quantum phase theory. Appl Phys Rev (2016) 3:041305. doi:10.1063/1.4972187

CrossRef Full Text | Google Scholar

8. Dang HB, Maloof AC, Romalis MV. Ultra-high sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl Phys Lett (2010) 97:151110. doi:10.1063/1.3491215

CrossRef Full Text | Google Scholar

9. Lee SK, Romalis MV. Calculation of magnetic field noise from high-permeability magnetic shields and conducting objects with simple geometry. J Appl Phys (2008) 103:084904–190. doi:10.1063/1.2885711

CrossRef Full Text | Google Scholar

10. Clem J. Johnson noise from normal metal near a superconducting squid gradiometer circuit. IEEE Trans Magnetics (1987) 23:1093–6. doi:10.1109/tmag.1987.1065127

CrossRef Full Text | Google Scholar

11. Fan W, Quan W, Liu F, Xing L, Liu G. Suppression of the bias error induced by magnetic noise in a spin-exchange relaxation-free gyroscope. IEEE Sensors J (2019) 19:9712–21. doi:10.1109/jsen.2019.2929505

CrossRef Full Text | Google Scholar

12. Liu Y, Fan W, Fu Y, Pang H, Pei H, Quan W. Suppression of low-frequency magnetic drift based on magnetic field sensitivity in K-Rb-21Ne atomic spin comagnetometer. IEEE Trans Instrumentation Meas (2022) 71:1–8. doi:10.1109/tim.2022.3169541

CrossRef Full Text | Google Scholar

13. Li R, Quan W, Fan W, Xing L, Fang J. Influence of magnetic fields on the bias stability of atomic gyroscope operated in spin-exchange relaxation-free regime. Sensors Actuators A Phys (2017) 266:130–4. doi:10.1016/j.sna.2017.09.023

CrossRef Full Text | Google Scholar

14. Shi M. Investigation on magnetic field response of a 87rb-129xe atomic spin comagnetometer. Opt Express (2020) 28:32033–41. doi:10.1364/oe.404809

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xing L, Quan W, Fan W, Zhang W, Fu Y, Song T. The method for measuring the non-orthogonal angle of the magnetic field coils of a K-Rb-21Ne co-magnetometer. IEEE Access (2019) 7:63892–9. doi:10.1109/access.2019.2916160

CrossRef Full Text | Google Scholar

16. Fan W, Quan W, Liu F, Pang H, Xing L, Liu G. Performance of low-noise ferrite shield in a K-Rb-21Ne co-magnetometer. IEEE Sensors J (2020) 20:2543–9. doi:10.1109/jsen.2019.2952121

CrossRef Full Text | Google Scholar

17. Ma D, Lu J, Fang X, Yang K, Wang K, Zhang N, et al. Parameter modeling analysis of a cylindrical ferrite magnetic shield to reduce magnetic noise. IEEE Trans Ind Elect (2022) 69:991–8. doi:10.1109/tie.2021.3050351

CrossRef Full Text | Google Scholar

18. Fang X, Wei K, Zhai Y, Zhao T, Chen X, Zhou M, et al. Analysis of effects of magnetic field gradient on atomic spin polarization and relaxation in optically pumped atomic magnetometers. Opt Express (2022) 30:3926–40. doi:10.1364/oe.447041

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Liu S, Wang R, Yuan L, Wu J, Yuan Q, Zhu J, et al. Transverse light-shift in a spin-exchange relaxation-free co-magnetometer: Measurement, decoupling, and suppression. Opt Express (2022) 30:15310. doi:10.1364/oe.456937

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Huang J, Wang Z, Fan W, Xing L, Quan W, Duan L, et al. Analysis and suppression of the polarization error for the optical rotation detection system in an atomic comagnetometer. Opt Express (2020) 28:35748. doi:10.1364/oe.406073

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Cates G, White D, Chien T-R, Schaefer S, Happer W. Spin relaxation in gases due to inhomogeneous static and oscillating magnetic fields. Phys Rev A (1988) 38:5092–106. doi:10.1103/physreva.38.5092

PubMed Abstract | CrossRef Full Text | Google Scholar

22. McGregor DD. Transverse relaxation of spin-polarized he 3 gas due to a magnetic field gradient. Phys Rev A (1990) 41:2631–5. doi:10.1103/physreva.41.2631

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Fu Y, Wang Z, Xing L, Fan W, Ruan J, Pang H. Suppression of nonuniform magnetic fields in magnetic shielding system for serf co-magnetometer. IEEE Trans Instrumentation Meas (2022) 71:1–8. doi:10.1109/tim.2022.3178738

CrossRef Full Text | Google Scholar

24. Pang H, Fan W, Huang J, Liu F, Liu S, Quan W. A highly sensitive in situ magnetic field fluctuation measurement method based on nuclear-spin depolarization in an atomic comagnetometer. IEEE Trans Instrumentation Meas (2022) 71:1–8. doi:10.1109/tim.2022.3166169

CrossRef Full Text | Google Scholar

25. Liu X, Chen C, Qu T, Yang K, Luo H. Transverse spin relaxation and diffusion-constant measurements of spin-polarized 129xe nuclei in the presence of a magnetic field gradient. Scientific Rep (2016) 6:24122. doi:10.1038/srep24122

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zhao J, Ding M, Lu J, Yang K, Ma D, Yao H, et al. Determination of spin polarization in spin-exchange relaxation-free atomic magnetometer using transient response. IEEE Trans Instrumentation Meas (2020) 69:845–52. doi:10.1109/tim.2019.2905308

CrossRef Full Text | Google Scholar

27. Zhan X, Chen C, Wang Z, Jiang Q, Luo H. Improved compensation and measurement of the magnetic gradients in an atomic vapor cell. AIP Adv (2020) 10:045002. doi:10.1063/1.5127032

CrossRef Full Text | Google Scholar

28. Huang J, Wang Z, Fan W, Pang H, Zhang K, Yuan L, et al. In-situ evaluation of low-frequency magnetic field fluctuation in an atomic comagnetometer. IEEE Sensors J (2021) 21:22846–52. doi:10.1109/jsen.2021.3106899

CrossRef Full Text | Google Scholar

29. Vasilakis G. Precision measurements of spin interactions with high density atomic vapors. Princeton, NJ, USA: Princeton Univ. (2011). Ph.D. thesis.

Google Scholar

30. Wei K, Zhao T, Fang X, Li H, Quan W, Han B, et al. Simultaneous determination of the spin polarizations of noble-gas and alkali-metal atoms based on the dynamics of the spin ensembles. Phys Rev Appl (2020) 13:044027. doi:10.1103/physrevapplied.13.044027

CrossRef Full Text | Google Scholar

31. Liwei J, Wei Q, Yixiang L, Liu J, Duan L, Fang J. Effects of pump laser power density on the hybrid optically pumped comagnetometer for rotation sensing. Opt express (2019) 27:27420–30. doi:10.1364/OE.27.027420

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Alcock CB, Itkin VP, Horrigan MK. Vapour pressure equations for the metallic elements: 298–2500K. Can Metallurgical Q (1984) 23:309–13. doi:10.1179/cmq.1984.23.3.309

CrossRef Full Text | Google Scholar

33. Liu F, Duan L, Fan W, Pang H, Liu S, Quan W. Suppression of the bias error induced by vapor cell temperature in a spin-exchange relaxation-free gyroscope. IEEE Sensors J (2022) 22:1990–7. doi:10.1109/jsen.2021.3138831

CrossRef Full Text | Google Scholar

34. Cates GD, Schaefer SR, Happer W. Relaxation of spins due to field inhomogeneities in gaseous samples at low magnetic fields and low pressures. Phys Rev A (1988) 37:2877–85. doi:10.1103/physreva.37.2877

PubMed Abstract | CrossRef Full Text | Google Scholar