- 1Centre for Quantum Physics, Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement (MOE), School of Physics, Beijing Institute of Technology, Beijing, China
- 2Beijing Key Laboratory of Nanophotonics and Ultrafine Optoelectronic Systems, School of Physics, Beijing Institute of Technology, Beijing, China
The study of topological semimetals has been extended to more general topological nodal systems such as metamaterials and artificial periodic structures. Among various nodal structures, triply degenerate nodal line (TDNL) is rare and, hence, has received little attention. In this work, we have proposed a simple tight-binding (TB) model, which hosts a topological non-trivial TDNL. This TDNL not only has the drumhead surface states (DSSs) as usual nodal line systems but also has surface states that form a contracted-drumhead shape. The shape and area of this contracted drumhead can be tuned by the hopping parameters of the model. This provides an effective way to modulate surface states and their density of states, which can be important in future applications of topological nodal systems.
1 Introduction
In recent years, topological semimetals have become a frontier topic in condensed matter physics because of their promising applications in electronics, spintronics, and optics [1–9]. According to the dimensions of the degenerate manifolds in k-space formed by band crossings, topological semimetals are divided into nodal point semimetals, such as Weyl [9–12], Dirac [13–17], or triple-point semimetals [18, 19]; nodal line semimetals [20–23]; and nodal surface semimetals [24–27]. Due to the non-trivial topological band structure, Weyl (Dirac) semimetals can exhibit Fermi arc surface states [5, 9, 10] connecting different Weyl node (Dirac node) projections on a two-dimensional (2D) surface Brillouin zone (BZ). Nodal line semimetals can exhibit another special surface state—drumhead surface state (DSS) [21, 22, 28–31] on a 2D surface BZ. These non-trivial topological properties are not limited to being present in semimetals because they originate from the nodal band structures and exist in other systems, such as metals [32–35], optical crystals [36–38], phononic crystals [39, 40], mechanical systems [41], and circuit systems [42–44].
For topological nodal line materials, the doubly degenerate Weyl nodal line [23, 45–47] and quadruply degenerate Dirac nodal line [48–51] have been broadly studied, and the DSS has been observed in these two types of materials. However, there is little research on the triply degenerate nodal line (TDNL). The only such research we can find is [52] by Liu et al. in 2021. Liu et al. [52] proposed two TDNL models, of which one is non-topological and the other is topological, according to the existence of Fermi arc topological surface states. However, Liu et al. did not report any DSS for the TDNL models. Accordingly, in this work, we aim to construct a tight-binding (TB) model with TDNL and investigate its DSS.
However, it is almost impossible to construct a TDNL model based on real crystalline materials because real crystalline materials are constrained by the symmetries of (magnetic) space groups, and systematic studies on the possible emergent particles from band crossings have shown that no TDNL exists under various (magnetic) space groups [53–55]. Subsequently, to construct a TDNL model, one has to get rid of the constraints by (magnetic) space groups. This can be achieved in artificial systems, such as metamaterials, circuit systems, and mechanical systems, because when described by TB models, the effective hoppings in these systems can be tuned at will, for example, adjusting the connection mode among circuit components or changing the coupling strength through springs [41, 43, 56].
In this work, we first constructed a three-band TB model hosting TDNL by designing the hoppings. Subsequently, we calculated the Berry phase and Zak phase to check the topological non-triviality of the TDNL. Surface states on two different surfaces (i.e., (010) and
2 Model and method
The model is constructed based on a simple cubic lattice whose basis vectors
where
where λ1, λ2, and λ3 are the following three matrices, respectively:
One can easily see that when ky = 0, Eq. 4 becomes a diagonal matrix whose diagonal elements can be null simultaneously. This implies that a TDNL can exist in the plane ky = 0 under suitable values of t0 and t1. The key feature of the hoppings that results in this TDNL is that hii (0)/hii (±α) keeps constant for i = 1, 2, 3. This is a special request that cannot be derived from symmetries of the (magnetic) space group.
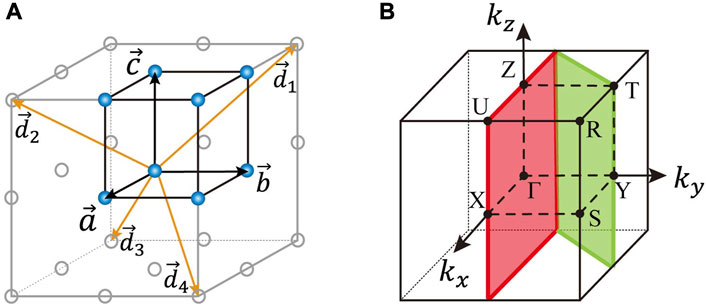
FIGURE 1. (A) Unit cell (black frame and blue balls) and hopping vectors [
The surface density of state (SDOS) was obtained by calculating the surface Green’s function of the semi-infinite system using the WannierTools package [57]. The input data for WannierTools were prepared using the MagneticTB package [58]. To investigate the surface states, we also constructed TB slab models of 80 layers using the PythTB package [59]. To judge whether a state is a surface state, we first define the topmost five layers on each side, A or B, of the slab model as “surface layers” and then define the following quantity η to characterize the degree to which a state is a surface state:
where wA∕B represents the wavefunction weight within the surface layers of side A/B of the slab. A bulk state wavefunction is periodic, and its weights are equally distributed within all the 80 layers, in which case wA = wB = 5/80 and η = 0. For a perfect surface state, the wavefunction is totally localized within the surface layers, leading to wA = wB = 1/2 and η = 1. By means of η, a state can be determined as a strong (or typical) surface state if its η is greater than a critical value ηc, and in this paper, ηc = 0.5 is adopted.
3 Results
If not otherwise stated, the parameters t0 = 2, t1 = −1, and t2 = t3 = 1 are used for the model, and the unit is eV for all energies. The bulk energy bands are shown in Figure 2A, in which the k-points are defined in Figure 1B. In this model, the TDNL is actually an approximately circular nodal ring in the ky = 0 plane, as shown in Figure 2B. To check the topological properties of the TDNL, we first calculated the Berry phase defined on a closed k-point loop enclosing the TDNL, with fully gapped energies, as shown by the small orange loop in Figure 2B. The Berry phase is calculated using the Wilson loop approach [60], and the result is π, which shows the topological non-triviality of the TDNL.
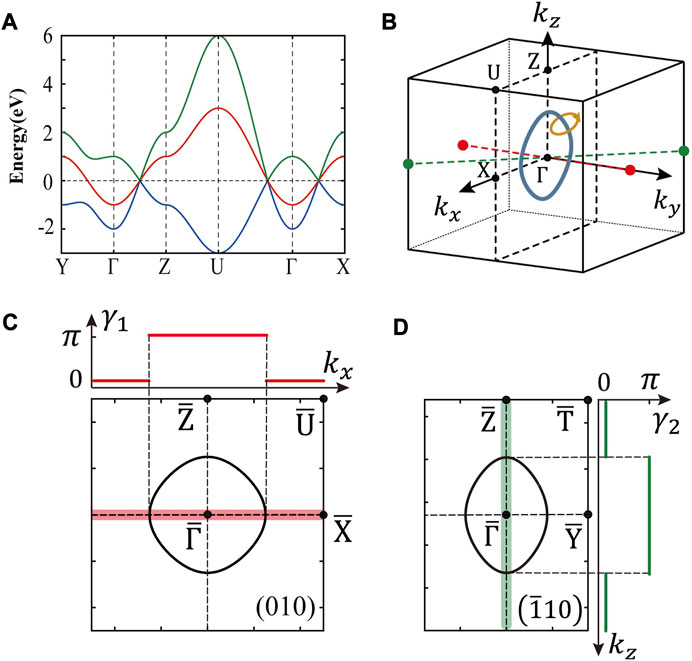
FIGURE 2. (A) Bulk band structure of the model. (B) TDNL (thick blue nodal ring) and the k-point path (small orange loop) for calculating the Berry phase. The red (green) dashed line is the integral path for Zak phase γ1 at kx = 0 (γ2 at kz = 0). (C, D) TDNL projections onto (C) (010) and (D)
Furthermore, we calculated the Zak phase [61, 62], which is the Berry phase defined in a one-dimensional BZ along a certain direction. Two Zak phases are investigated here. The first one γ1 (kx) is defined along the line from
The semi-infinite system terminated with that surface should be constructed to explore the topological surface states of a certain surface. Two surfaces (010) and
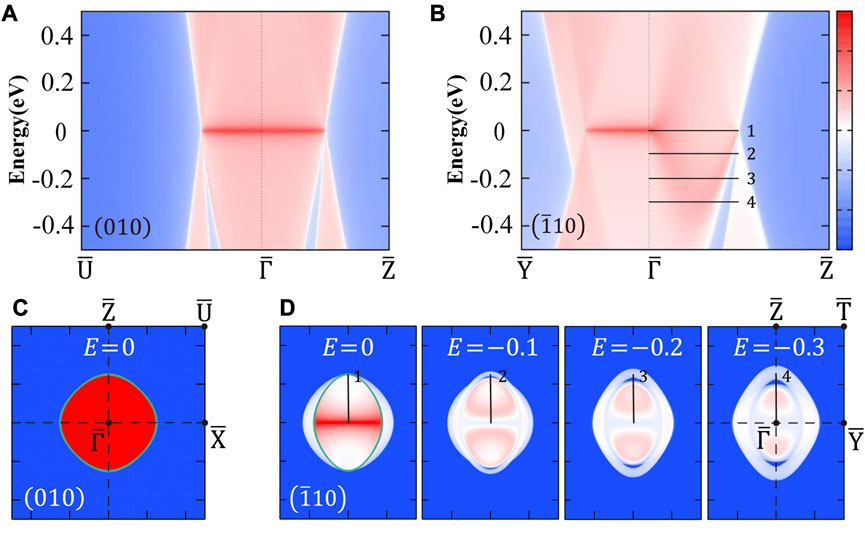
FIGURE 3. Topological surface states given by SDOS for the semi-infinite systems terminated with (A, C) (010) and (B, D)
In order to further explore the CDSS in the
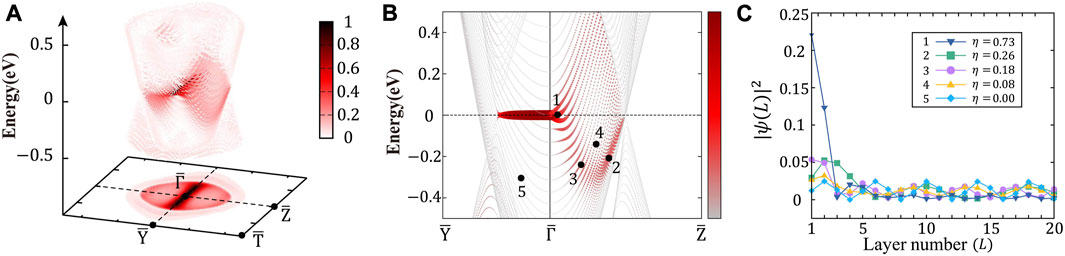
FIGURE 4.
Because the weak surface states are much like bulk states, they are not efficient in most applications, which require large SDOS. Thus, only strong surface states need to be considered, and the shape of the CDSS can be revealed by the distribution of the k-points at which strong surface states exist. Figure 5 shows the distribution of the k-points of strong surface states (i.e., the shape of CDSS) under different model parameters. We can see that the shape of CDSS for the
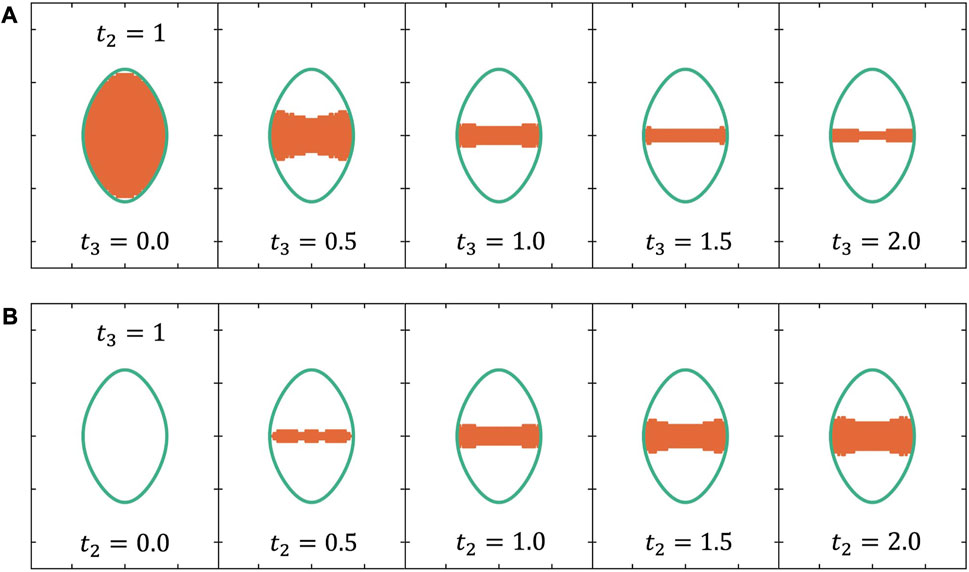
FIGURE 5. k-point distribution (orange area) of the CDSS for the
4 Conclusion
We have proposed a simple TB model hosting TDNL and studied its topological properties. Both the Berry phase and Zak phase demonstrate that the TDNL is topological non-trivial. This TDNL model not only has a full DSS as usual topological nodal line systems, but also has a CDSS, which we first noticed. The CDSS exists on the
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author contributions
G-BL supervised the project and guided the work. Y-RW performed the calculations and wrote the manuscript. G-BL revised the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China with Grant Nos 12274028, 52161135108, and 12234003 and the National Key R&D Program of China with Grant No. 2022YFA1402603.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bansil A, Lin H, Das T. Colloquium: topological band theory. Rev Mod Phys (2016) 88:021004. doi:10.1103/RevModPhys.88.021004
2. Weng HM, Dai X, Fang Z. Topological semimetals predicted from first-principles calculations. J Phys Condens Matter (2016) 28:303001. doi:10.1088/0953-8984/28/30/303001
3. Burkov AA, Hook MD, Balents L. Topological nodal semimetals. Phys Rev B (2011) 84:235126. doi:10.1103/PhysRevB.84.235126
4. Yan BH, Felser C. Topological materials: Weyl semimetals. Annu Rev Conden Matter Phys (2017) 8:337–54. doi:10.1146/annurev-conmatphys-031016-025458
5. Hasan MZ, Xu SY, Belopolski I, Huang SM. Discovery of weyl fermion semimetals and topological fermi arc states. Annu Rev Conden Matter Phys (2017) 8:289–309. doi:10.1146/annurev-conmatphys-031016-025225
6. Witczak-Krempa W, Chen G, Kim YB, Balents L. Correlated quantum phenomena in the strong spin-orbit regime. Annu Rev Conden Matter Phys (2014) 5:57–82. doi:10.1146/annurev-conmatphys-020911-125138
7. Bernevig BA, Felser C, Beidenkopf H. Progress and prospects in magnetic topological materials. Nature (2022) 603:41–51. doi:10.1038/s41586-021-04105-x
8. Lv BQ, Qian T, Ding H. Experimental perspective on three-dimensional topological semimetals. Rev Mod Phys (2021) 93:025002. doi:10.1103/RevModPhys.93.025002
9. Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological semimetal and fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys Rev B (2011) 83:205101. doi:10.1103/PhysRevB.83.205101
10. Weng HM, Fang C, Fang Z, Bernevig BA, Dai X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys Rev X (2015) 5:011029. doi:10.1103/PhysRevX.5.011029
11. Xu SY, Belopolski I, Alidoust N, Neupane M, Bian G, Zhang C, et al. Discovery of a weyl fermion semimetal and topological fermi arcs. Science (2015) 349:613–7. doi:10.1126/science.aaa9297
12. Xu SY, Alidoust N, Belopolski I, Yuan Z, Bian G, Chang TR, et al. Discovery of a weyl fermion state with fermi arcs in niobium arsenide. Nat Phys (2015) 11:748–54. doi:10.1038/nphys3437
13. Wang Z, Sun Y, Chen XQ, Franchini C, Xu G, Weng H, et al. Dirac semimetal and topological phase transitions in A3Bi(A=Na, K, Rb). Phys Rev B (2012) 85:195320. doi:10.1103/physrevb.85.195320
14. Wang Z, Weng H, Wu Q, Dai X, Fang Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys Rev B (2013) 88:125427. doi:10.1103/physrevb.88.125427
15. Liu ZK, Zhou B, Zhang Y, Wang ZJ, Weng HM, Prabhakaran D, et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science (2014) 343:864–7. doi:10.1126/science.1245085
16. Liu ZK, Jiang J, Zhou B, Wang ZJ, Zhang Y, Weng HM, et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat Mater (2014) 13:677–81. doi:10.1038/nmat3990
17. Neupane M, Xu SY, Sankar R, Alidoust N, Bian G, Liu C, et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat Comms (2014) 5:3786. doi:10.1038/ncomms4786
18. Lv BQ, Feng ZL, Xu QN, Gao X, Ma JZ, Kong LY, et al. Observation of three-component fermions in the topological semimetal molybdenum phosphide. Nature (2017) 546:627–31. doi:10.1038/nature22390
19. Ma JZ, He JB, Xu YF, Lv BQ, Chen D, Zhu WL, et al. Three-component fermions with surface fermi arcs in tungsten carbide. Nat Phys (2018) 14:349–54. doi:10.1038/s41567-017-0021-8
20. Fang C, Chen Y, Kee HY, Fu L. Topological nodal line semimetals with and without spin-orbital coupling. Phys Rev B (2015) 92:081201. doi:10.1103/PhysRevB.92.081201
21. Huang H, Liu J, Vanderbilt D, Duan W. Topological nodal-line semimetals in alkaline-earth stannides, germanides, and silicides. Phys Rev B (2016) 93:201114. doi:10.1103/physrevb.93.201114
22. Xu Q, Yu R, Fang Z, Dai X, Weng H. Topological nodal line semimetals in the CaP3 family of materials. Phys Rev B (2017) 95:045136. doi:10.1103/PhysRevB.95.045136
23. Chen W, Lu HZ, Hou JM. Topological semimetals with a double-helix nodal link. Phys Rev B (2017) 96:041102. doi:10.1103/PhysRevB.96.041102
24. Wu W, Liu Y, Li S, Zhong C, Yu ZM, Sheng XL, et al. Nodal surface semimetals: theory and material realization. Phys Rev B (2018) 97:115125. doi:10.1103/physrevb.97.115125
25. Fu BB, Yi CJ, Zhang TT, Caputo M, Ma JZ, Gao X, et al. Dirac nodal surfaces and nodal lines in ZrSiS. Sci Adv (2019) 5:eaau6459. doi:10.1126/sciadv.aau6459
26. Yang Y, ping Xia J, xiang Sun H, Ge Y, Jia D, qi Yuan S, et al. Observation of a topological nodal surface and its surface-state arcs in an artificial acoustic crystal. Nat Commun (2019) 10:5185. doi:10.1038/s41467-019-13258-3
27. Chen SZ, Li S, Chen Y, Duan W. Nodal flexible-surface semimetals: case of carbon nanotube networks. Nano Lett (2020) 20:5400–7. doi:10.1021/acs.nanolett.0c01786
28. Weng HM, Liang YY, Xu QN, Yu R, Fang Z, Dai X, et al. Topological node-line semimetal in three-dimensional graphene networks. Phys Rev B (2015) 92:045108. doi:10.1103/PhysRevB.92.045108
29. Chan YH, Chiu CK, Chou MY, Schnyder AP. Ca3P2 and other topological semimetals with line nodes and drumhead surface states. Phys Rev B (2016) 93:205132. doi:10.1103/PhysRevB.93.205132
30. Bian G, Chang TR, Zheng H, Velury S, Xu SY, Neupert T, et al. Drumhead surface states and topological nodal-line fermions inTlTaSe2. Phys Rev B (2016) 93:121113. doi:10.1103/physrevb.93.121113
31. Belopolski I, Manna K, Sanchez DS, Chang G, Ernst B, Yin J, et al. Discovery of topological weyl fermion lines and drumhead surface states in a room temperature magnet. Science (2019) 365:1278–81. doi:10.1126/science.aav2327
32. Xu SY, Liu C, Kushwaha SK, Sankar R, Krizan JW, Belopolski I, et al. Observation of fermi arc surface states in a topological metal. Science (2015) 347:294–8. doi:10.1126/science.1256742
33. Wang Z, Gresch D, Soluyanov AA, Xie W, Kushwaha S, Dai X, et al. MoTe2: A type-II weyl topological metal. Phys Rev Lett (2016) 117:056805. doi:10.1103/physrevlett.117.056805
34. Zhu Z, Winkler GW, Wu Q, Li J, Soluyanov AA. Triple point topological metals. Phys Rev X (2016) 6:031003. doi:10.1103/physrevx.6.031003
35. Sun JP, Zhang D, Chang K. Coexistence of topological nodal lines, weyl points, and triply degenerate points in TaS. Phys Rev B (2017) 96:045121. doi:10.1103/physrevb.96.045121
36. Gao W, Yang B, Tremain B, Liu H, Guo Q, Xia L, et al. Experimental observation of photonic nodal line degeneracies in metacrystals. Nat Commun (2018) 9:950. doi:10.1038/s41467-018-03407-5
37. Yang B, Guo Q, Tremain B, Liu R, Barr LE, Yan Q, et al. Ideal weyl points and helicoid surface states in artificial photonic crystal structures. Science (2018) 359:1013–6. doi:10.1126/science.aaq1221
38. Wang L, Jian SK, Yao H. Topological photonic crystal with equifrequency weyl points. Phys Rev A (2016) 93:061801. doi:10.1103/physreva.93.061801
39. Li F, Huang X, Lu J, Ma J, Liu Z. Weyl points and fermi arcs in a chiral phononic crystal. Nat Phys (2017) 14:30–4. doi:10.1038/nphys4275
40. Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120:016401. doi:10.1103/physrevlett.120.016401
41. Ma GC, Xiao M, Chan CT. Topological phases in acoustic and mechanical systems. Nat Rev Phys (2019) 1:281–94. doi:10.1038/s42254-019-0030-x
42. Lu YH, Jia NY, Su L, Owens C, Juzeliunas G, Schuster DI, et al. Probing the berry curvature and fermi arcs of a weyl circuit. Phys Rev B (2019) 99:020302. doi:10.1103/PhysRevB.99.020302
43. Lee CH, Imhof S, Berger C, Bayer F, Brehm J, Molenkamp LW, et al. Topolectrical circuits. Commun Phys (2018) 1:39. doi:10.1038/s42005-018-0035-2
44. Luo K, Yu R, Weng H. Topological nodal states in circuit lattice. Research (2018) 2018:6793752. doi:10.1155/2018/6793752
45. Feng BJ, Zhang RW, Feng Y, Fu BT, Wu SL, Miyamoto K, et al. Discovery of weyl nodal lines in a single-layer ferromagnet. Phys Rev Lett (2019) 123:116401. doi:10.1103/PhysRevLett.123.116401
46. Liu LL, Wang CZ, Li JX, Chen XQ, Jia Y, Cho JH. Two-dimensional topological semimetal states in monolayer Cu2Ge, Fe2Ge, and Fe2Sn. Phys Rev B (2020) 101:165403. doi:10.1103/PhysRevB.101.165403
47. Chen C, Yu ZM, Li S, Chen ZY, Sheng XL, Yang SA. Weyl-loop half-metal in Li3(FeO3)2. Phys Rev B (2019) 99:075131. doi:10.1103/PhysRevB.99.075131
48. Kim Y, Wieder BJ, Kane CL, Rappe AM. Dirac line nodes in inversion-symmetric crystals. Phys Rev Lett (2015) 115:036806. doi:10.1103/PhysRevLett.115.036806
49. Nakhaee M, Ketabi SA, Peeters FM. Dirac nodal line in bilayer borophene: tight-binding model and low-energy effective Hamiltonian. Phys Rev B (2018) 98:115413. doi:10.1103/PhysRevB.98.115413
50. Li RH, Ma H, Cheng XY, Wang SL, Li DZ, Zhang ZY, et al. Dirac node lines in pure alkali earth metals. Phys Rev Lett (2016) 117:096401. doi:10.1103/PhysRevLett.117.096401
51. Mullen K, Uchoa B, Glatzhofer DT. Line of Dirac nodes in hyperhoneycomb lattices. Phys Rev Lett (2015) 115:026403. doi:10.1103/PhysRevLett.115.026403
52. Liu ZH, Wang LY, Yao DX. Triply degenerate nodal lines in topological and nontopological metals. Phys Rev B (2021) 103:205145. doi:10.1103/PhysRevB.103.205145
53. Yu ZM, Zhang Z, Liu GB, Wu W, Li XP, Zhang RW, et al. Encyclopedia of emergent particles in three-dimensional crystals. Sci Bull (2022) 67:375–80. doi:10.1016/j.scib.2021.10.023
54. Liu GB, Zhang Z, Yu ZM, Yang SA, Yao Y. Systematic investigation of emergent particles in type-III magnetic space groups. Phys Rev B (2022) 105:085117. doi:10.1103/PhysRevB.105.085117
55. Zhang Z, Liu GB, Yu ZM, Yang SA, Yao Y. Encyclopedia of emergent particles in type-IV magnetic space groups. Phys Rev B (2022) 105:104426. doi:10.1103/physrevb.105.104426
56. Luo KF, Yu R. Topological states in electric circuit. Acta Phys Sin (2019) 68:220305. doi:10.7498/aps.68.20191398
57. Wu QS, Zhang SN, Song HF, Troyer M, Soluyanov AA. Wanniertools: an open-source software package for novel topological materials. Comput Phys Commun (2018) 224:405–16. doi:10.1016/j.cpc.2017.09.033
58. Zhang ZY, Yu ZM, Liu GB, Yao YG. Magnetictb: A package for tight-binding model of magnetic and non-magnetic materials. Comput Phys Commun (2022) 270:108153. doi:10.1016/j.cpc.2021.108153
59. Coh S, Vanderbilt D. Python tight binding (PythTB) (2012). Available from: http://www.physics.rutgers.edu/pythtb.
60. Wang HX, Guo GY, Jiang JH. Band topology in classical waves: Wilson-loop approach to topological numbers and fragile topology. New J Phys (2019) 21:093029. doi:10.1088/1367-2630/ab3f71
61. Zak J. Berry’s phase for energy bands in solids. Phys Rev Lett (1989) 62:2747–50. doi:10.1103/PhysRevLett.62.2747
62. Xiao D, Chang MC, Niu Q. Berry phase effects on electronic properties. Rev Mod Phys (2010) 82:1959–2007. doi:10.1103/RevModPhys.82.1959
Keywords: triply degenerate nodal line, tight-binding model, drumhead surface states, Berry phase, Zak phase
Citation: Wang Y-R and Liu G-B (2023) Triply degenerate nodal line and tunable contracted-drumhead surface state in a tight-binding model. Front. Phys. 11:1200601. doi: 10.3389/fphy.2023.1200601
Received: 05 April 2023; Accepted: 02 August 2023;
Published: 17 August 2023.
Edited by:
Sung-Kwan Mo, Berkeley Lab (DOE), United StatesReviewed by:
Wenlong Gao, University of Paderborn, GermanyBotao Fu, Sichuan Normal University, China
Copyright © 2023 Wang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gui-Bin Liu, Z2JsaXVAYml0LmVkdS5jbg==
 Yi-Ru Wang
Yi-Ru Wang Gui-Bin Liu1,2*
Gui-Bin Liu1,2*