The two-body collision controlled by the magnetic field and laser field near magnetic Feshbach resonance

It is crucial to control the collision between ultracold atoms by applying external fields. We developed a theoretical model for investigating the s-wave scattering of ultracold atoms controlled by the magnetic field and laser field. The calculation is performed by using the close-coupling method and mapped Fourier grid method. Due to the interference between the photoassociation and bound-to-bound transitions, the bound state in the continuum, which is a resonance with a vanishing width, occurs at the magnetic field position near the magnetic Feshbach resonance. The widths of resonances in the neighborhood of the bound state in the continuum are narrow. Changing the laser intensity can shift the magnetic field position where the bound state in the continuum occurs through modifying the ground molecular state to induce wide resonances at desired magnetic field positions. By increasing the resonance width, the tunability of the real part of the scattering length at resonances can be significantly improved. Changing the laser intensity can also adjust the coupling between the ground and excited molecular states. When the coupling between the ground and excited molecular states approaches zero, a resonance is induced, and the photoassociation and bound-to-bound transitions are both significantly suppressed at this resonance. Therefore, the atomic loss peak due to spontaneous emission does not appear at this resonance. The magnetic field position of this resonance is stable against the change in laser frequency.

1 Introduction

The manipulation of ultracold atoms by external fields has attracted a lot of interest from researchers in recent years. Among various technologies, magnetic Feshbach resonances have been widely studied and detected in many systems [1–5]. Taking advantage of magnetic Feshbach resonances, researchers can modulate the scattering length of ultracold atoms [6, 7] and prepare the Bose–Einstein condensate (BEC) [8]. Feshbach resonances can also be used to realize the 3D or quasi-2D BEC-BCS crossover with atomic Fermi gases [9–11]. Laser can be used to induce photoassociation resonances and regulate the interaction between ultracold atoms as well [12]. Photoassociation resonances are also widely applied to prepare ultracold molecules [13, 14]. Ultracold atoms can be excited by laser to the excited molecular state during the collision, but this will cause atomic spontaneous emission losses.

In order to control the collision of ultracold atoms effectively, both the magnetic field and laser field are usually applied [15–17]. The frequency and intensity of the laser field are two adjustable parameters, offering more flexibility for researchers in experiments. In the mixture experiments of BECs of two different species [18, 19] or BECs in different internal states of the same isotope [20], several scattering lengths need to be modulated independently. In an optical lattice, the scattering length can be modulated in specific lattice sites [21–25]. The fine spatial modulation of the scattering length can be realized by laser, and this offers experimental feasibility for spatial modulation of the interatomic interaction [26, 27].

A traveling-wave laser beam has been applied to control the magnetic Feshbach resonance [28]. Under the co-action of the magnetic field and laser field, the magnetic Feshbach resonance splits into two resonances, and an Autler–Townes doublet in the particle loss has been observed. Compared with tuning the scattering length with an optically induced Feshbach resonance [29], the loss rate coefficient can be reduced by one order of magnitude. Bauer and co-workers used one specific excited molecular state in this experiment, where the photoassociation coupling between this specific excited molecular state and the continuum state of the incoming atom pair is negligible [28]. Thus, laser only induces the molecular bound-to-bound transition between ground and excited molecular states [30–32]. With the photoassociation coupling not being considered, the resonance width is proportional to $|\frac{E_{\text{col}}-{ϵ}_3}{E_{\text{col}}-{ϵ}_2+E_{\text{col}}-{ϵ}_3}|$, where ϵ₂ and ϵ₃ are the energies of the ground and excited molecular states. The energy E_col is the collision energy between two colliding atoms. The probability of being trapped in the excited molecular state is proportional to $\frac{1}{{(E_{\text{col}}-{ϵ}_3)}^2}$. Therefore, tuning the laser frequency to shift ϵ₃ far away from E_col suppresses spontaneous emission losses. The “dark-state” optical method is proposed to tune the scattering length and suppress spontaneous emission losses, in which two lasers with different frequencies are applied to couple one excited molecular state to two ground molecular states [33–36]. In this method, the photoassociation coupling was not taken into account.

Friedrich and co-workers demonstrated that when two ultracold atoms are trapped in the bound states of two different closed channels during the collision, the resonance position and width can be altered by changing the external field [37, 38]. However, the particle loss caused by the external field is not considered. The modification of the ground molecular state by laser is not considered either. The external field can induce a resonance with vanishing width. Such a resonance is also called the bound state in the continuum, which has been observed in various systems such as quantum billiard and quantum dot [39, 40]. The bound state in the continuum can be prepared by lasers near a magnetic Feshbach resonance in ultracold atoms but decays fast due to the spontaneous emission loss [41, 42].

In the present work, we investigated the collision property between two ultracold atoms under the co-action of the magnetic field and laser field. The magnetic field is adjusted to the neighborhood of a magnetic Feshbach resonance. Laser can induce the photoassociation process and bound-to-bound transition. With the photoassociation coupling being considered, the resonance width is dependent on the three coupling terms among the ground molecular state, the excited molecular state, and the continuum state of the incoming atom pair. The resonance width can be increased by adjusting the laser intensity. Compared with a narrow resonance, the tunability of the scattering length at a wide resonance is significantly improved and the spontaneous emission loss is reduced. The coupling between the ground and excited molecular states is composed of the direct bound-to-bound coupling and the indirect coupling induced by the photoassociation coupling and Feshbach coupling via the continuum states of the incoming atom pair. The coupling can be almost completely canceled by adjusting the laser intensity. We found that in this case, the spontaneous emission loss at the resonance is significantly suppressed and that the magnetic field position of this resonance is stable against the change in laser frequency. We found that the interference between the bound-to-bound transition and photoassociation transition can be used to prepare the bound state in the continuum, a resonance with a vanishing width. The magnetic field position of the bound state in the continuum can be shifted by changing the laser intensity. At the magnetic field position where the bound state in the continuum occurs, when laser frequency is detuned with respect to the resonant frequency, the scattering length is almost unchanged with laser frequency and the spontaneous emission loss is significantly suppressed.

This paper is organized as follows: in Section 2, we present the solution to the coupled equations for the three-radial channel wave functions in the magnetic field and laser field. The resonance width is given, which depends on the three coupling terms among the ground, excited molecular states, and the continuum state of the incoming atom pair. It is explained why the scattering length is frequency-independent at the magnetic field position where the bound state in the continuum occurs when the frequency is detuned away from the resonance condition. We give the amplitude factors of the ground and excited molecular states in the condition that the open-channel wavefunction remains normalized in energy, which are related to the resonance width. In Section 3, we calculate the magnetic field positions of resonances and the loss rate coefficients at different laser frequencies and intensities. We also investigate the modulation of the real part of the s-wave scattering length at the magnetic field positions near the original magnetic Feshbach resonance. Finally, a conclusion is drawn in Section 4.

2 Theory

The scattering process of two ultracold atoms controlled by the magnetic field and laser field is shown in Figure 1. In the absence of the laser field, channel 1 is only coupled with channel 2. Two colliding atoms are trapped in the bound states of channel 2, and the magnetic field induces a magnetic Feshbach resonance. After laser is applied, two colliding atoms are either directly excited to the bound states of channel 3 by photoassociation coupling or first trapped in the bound states of channel 2 and then excited to the bound states of channel 3 by bound-to-bound coupling. When the two atoms are trapped in the bound states of channel 3, the spontaneous emission may take place and induce atomic losses. In our close-coupling calculations, an open-channel coupled with channel 3 is used to describe atomic losses [43–45]. Under the rotating-wave approximation, the coupled equation of radial channel wavefunctions for the three-channel system is given by the following:

$\left[-\frac{{\hslash }^2}{2\mu }\frac{d^2}{d{r}^2}+V_i+E_i\right]u_i\left(r\right)+{\displaystyle \sum _{i\ne j}}{V}_{i,j}{u}_j\left(r\right)=E_{\text{col}}{u}_i\left(r\right),(1)$

where ℏ is the reduced Planck constant, μ the reduced mass, and r the internuclear separation. E_i and V_i (i = 1,2,3) are the channel energy and interaction potential, respectively. V_i (i = 1,2,3) approaches zero as r → ∞. The threshold energy E₁ of channel 1 is taken to be zero. Channels 2 and 3 are closed channels with E₂ and E₃ > 0. The energy E₃ of channel 3 is obtained by reducing the energy of one photon ℏω from the original channel energy. E₃ can be adjusted by changing the laser frequency. V_i,j (i ≠ j) are the coupling potentials between the channels. The coupling potential V_1,2 (V_2,1) between channels 1 and 2 does not vary with the laser frequency and intensity. V_1,3 (V_3,1) and V_2,3 (V_3,2) can be modulated by changing the laser intensity and are independent of the laser frequency. E_col is the collision energy between two ultracold atoms. E_col = 1 μK × k_B in our close-coupling calculations, where k_B is the Boltzmann constant. Here, only the s-wave scattering is considered. The interaction potentials V_i (i = 1,2,3) and coupling potentials V_i,j (i ≠ j) used in our calculation are taken from [46], which change with the magnetic field. In the appendix, V_i (i = 1,2,3) and V_i,j (i ≠ j) are shown in Figure A1 at the magnetic field having the original magnetic Feshbach resonance. Figures A1E, F show the laser-induced coupling potentials V_1,3 and V_2,3 when laser amplitude is set to 10E_s. The minimal laser amplitude in our calculation is taken to be E_s, where the coupling potentials V_1,3 (V_3,1) and V_2,3 (V_3,2) are much weaker than the coupling potential V_1,2 (V_2,1).

FIGURE 1

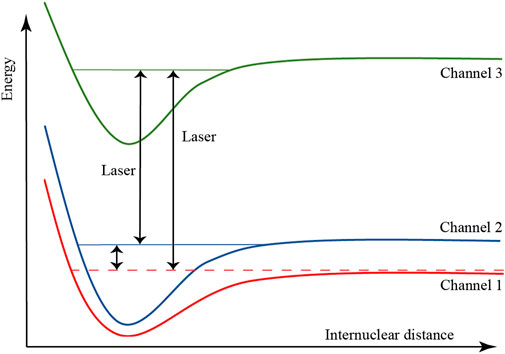
FIGURE 1. (Color online) Schematic illustration of the three-channel system. The ground molecular state in channel 2 is coupled to the incoming continuum state in channel 1, which induces the magnetic Feshbach resonance. The laser induces the bound-to-bound transition between the ground and excited molecular states and the photoassociation from the incoming continuum state to the excited molecular state in channel 3.

By using the mapped Fourier grid method [47, 48], we calculate the wavefunctions of several stationary s-wave continuum states with the lowest eigenenergies in the three-channel system. We find that the wavefunctions in channels 2 and 3 are both superpositions of bound-state wavefunctions of corresponding closed channels. In the absence of the laser field, the wavefunctions in channel 2 in the neighborhood of the magnetic Feshbach resonance are also superpositions of bound-state wavefunctions. Therefore, when obtaining the solution of Eq. 1 by using the Feshbach theory, we cannot think that the wavefunction in channel 2 or 3 is composed of a single bound-state wavefunction.

The solution of Eq. 1 can be written as follows:

$U=\left(\begin{array}{c}\hfill u_1\left(r\right)\hfill \\ \hfill A_2{u}_2^0\left(r\right)\hfill \\ \hfill A_3{u}_3^0\left(r\right)\hfill \end{array}\right),(2)$

where $u_2^0(r)$ and $u_3^0(r)$ are normalized superpositions of bound-state wavefunctions in channels 2 and 3, respectively. The wavefunction u₁(r) in channel 1 is given by the following:

$u_1\left(r\right)=u_1^{\mathrm{r}\mathrm{e}\mathrm{g}}\left(r\right)+{\int }_0^{\infty }\mathcal{G}\left(r,r^{\prime }\right)+\left[A_2{V}_{\mathrm{1,2}}\left(r^{\prime }\right)u_2^0\left(r^{\prime }\right)+A_3{V}_{\mathrm{1,3}}\left(r^{\prime }\right)u_3^0\left(r^{\prime }\right)\right]d{r}^{\prime },(3)$

where $u_1^{\mathrm{r}\mathrm{e}\mathrm{g}}(r)$ is the solution of the radial equation in channel 1 without the coupling with channel 2 or 3. The asymptotic behavior of $u_1^{\mathrm{r}\mathrm{e}\mathrm{g}}(r)$ is given by the following:

$u_1^{\text{reg}}\left(r\right)\stackrel{r\to \infty }{\sim }\sqrt{\frac{2\mu }{\pi {\hslash }^{2}k}}\sin \left(kr+{\delta }_{\text{bg}}\right),(4)$

where k is the magnitude of the incoming wave vector and δ_bg the s-wave background phase shift in channel 1. In Eq. 3, $\mathcal{G}(r,r^{\prime })$ is the radial Green’s function.

We then obtain two equations about A₂ and A₃,

$A_2\left[E_{\text{col}}-⟨u_2^0|{\widehat{H}}_2|u_2^0⟩-⟨u_2^0|V_{\mathrm{2,1}}\widehat{G}{V}_{\mathrm{1,2}}|u_2^0⟩\right]=⟨u_2^0|V_{\mathrm{2,1}}|u_1^{\text{reg}}⟩+A_3\left[⟨u_2^0|V_{\mathrm{2,3}}|u_3^0⟩+⟨u_2^0|V_{\mathrm{2,1}}\widehat{G}{V}_{\mathrm{1,3}}|u_3^0⟩\right],(5)$

$A_3\left[E_{\text{col}}-⟨u_3^0|{\widehat{H}}_3|u_3^0⟩-⟨u_3^0|V_{\mathrm{3,1}}\widehat{G}{V}_{\mathrm{1,3}}|u_3^0⟩\right]=⟨u_3^0|V_{\mathrm{3,1}}|u_1^{\text{reg}}⟩+A_2\left[⟨u_3^0|V_{\mathrm{3,2}}|u_2^0⟩+⟨u_3^0|V_{\mathrm{3,1}}\widehat{G}{V}_{\mathrm{1,2}}|u_2^0⟩\right],(6)$

where

${\widehat{H}}_i=-\frac{{\hslash }^2}{2\mu }\frac{d^2}{d{r}^2}+V_i+E_i,i=\mathrm{2,3}.(7)$

By using the abbreviations,

${ϵ}_i=⟨u_i^0|{\widehat{H}}_i|u_i^0⟩+⟨u_i^0|V_{i,1}\widehat{G}{V}_{1,i}|u_i^0⟩,W_{i,1}=⟨u_i^0|V_{i,1}|u_1^{\text{reg}}⟩=W_{1,i}^{*},i=\mathrm{2,3}(8)$

and

$W_{\mathrm{2,3}}=\langle u_2^0|V_{\mathrm{2,3}}|u_3^0\rangle +\langle u_2^0|V_{\mathrm{2,1}}\widehat{G}{V}_{\mathrm{1,3}}|u_3^0\rangle =W_{\mathrm{3,2}}^{*},(9)$

the solutions of Eqs 5–6 are expressed as

$A_2=\frac{\left(E_{\text{col}}-{ϵ}_3\right)W_{\mathrm{2,1}}+W_{\mathrm{2,3}}{W}_{\mathrm{3,1}}}{\left(E_{\text{col}}-{ϵ}_2\right)\left(E_{\text{col}}-{ϵ}_3\right)-|W_{\mathrm{2,3}}{|}^2},(10)$

$A_3=\frac{\left(E_{\text{col}}-{ϵ}_2\right)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}}{\left(E_{\text{col}}-{ϵ}_2\right)\left(E_{\text{col}}-{ϵ}_3\right)-|W_{\mathrm{2,3}}{|}^2}.(11)$

With the photoassociation coupling V_1,3 being considered, the coupling W_3,2 between the ground and excited molecular states $|u_2^0\rangle$, $|u_3^0\rangle$ is induced by the direct bound-to-bound coupling V_2,3 and the indirect coupling induced by the Feshbach coupling V_2,1 and photoassociation coupling V_1,3 via $\widehat{G}$ in channel 1.

The s-wave scattering phase shift δ_res caused by the resonance is given by the following [37]:

$\tan {\delta }_{\text{res}}=-\pi \frac{\left(E_{\text{col}}-{ϵ}_3\right)|W_{\mathrm{2,1}}{|}^2+W_{\mathrm{1,2}}{W}_{\mathrm{2,3}}{W}_{\mathrm{3,1}}+\left(E_{\text{col}}-{ϵ}_2\right)|W_{\mathrm{3,1}}{|}^2+W_{\mathrm{1,3}}{W}_{\mathrm{3,2}}{W}_{\mathrm{2,1}}}{\left(E_{\text{col}}-{ϵ}_2\right)\left(E_{\text{col}}-{ϵ}_3\right)-|W_{\mathrm{2,3}}{|}^2}.(12)$

When (E_col − ϵ₂)(E_col − ϵ₃) − |W_2,3|² = 0, the resonance takes place under the co-action of the magnetic field and laser field. The resonance width Γ is given by the following:

$\mathrm{\Gamma }=2{\left[\frac{d{\delta }_{\text{res}}}{d{E}_{\text{col}}}\right]}^{-1}.(13)$

When W_i,j (i, j = 1, 2, 3) does not change with E_col, we obtain the following:

$\mathrm{\Gamma }{|}_{D=0}=2\left(1+\frac{N^2}{D^2}\right)\frac{D^2}{D^{\prime }N-N^{\prime }D}=\frac{2N}{D^{\prime }},(14)$

where

$N\left(E_{\text{col}}\right)=\pi \left[\left(E_{\text{col}}-{ϵ}_3\right)|W_{\mathrm{2,1}}{|}^2+W_{\mathrm{1,2}}{W}_{\mathrm{2,3}}{W}_{\mathrm{3,1}}+\left(E_{\text{col}}-{ϵ}_2\right)|W_{\mathrm{3,1}}{|}^2+W_{\mathrm{1,3}}{W}_{\mathrm{3,2}}{W}_{\mathrm{2,1}}\right],(15)$

$D\left(E_{\text{col}}\right)=\left(E_{\text{col}}-{ϵ}_2\right)\left(E_{\text{col}}-{ϵ}_3\right)-|W_{\mathrm{2,3}}{|}^2,(16)$

and

$N^{\prime }=\frac{dN}{d{E}_{\text{col}}},(17)$

$D^{\prime }=\frac{dD}{d{E}_{\text{col}}}.(18)$

When (E_col − ϵ₂)W_3,1 + W_3,2W_2,1 = 0 at a specific magnetic field position B₁ and the resonance condition D = 0 is met, we obtain the following:

$\begin{array}{ll}\hfill \left(E_{\text{col}}-{ϵ}_3\right)W_{\mathrm{2,1}}+W_{\mathrm{2,3}}{W}_{\mathrm{3,1}}& =\frac{|W_{\mathrm{2,3}}{|}^2}{E_{\text{col}}-{ϵ}_2}{W}_{\mathrm{2,1}}+W_{\mathrm{2,3}}{W}_{\mathrm{3,1}}\hfill \\ \hfill & =\frac{W_{\mathrm{2,3}}}{E_{\text{col}}-{ϵ}_2}\left[\left(E_{\text{col}}-{ϵ}_2\right)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}\right]\hfill \\ \hfill & =0.\hfill \end{array}(19)$

From Eqs 14, 15, it is shown that N (E_col) = 0, and hence, the resonance width is zero. Thus, due to the interference between the photoassociation transition induced by W_3,1 and the bound-to-bound transition induced by W_3,2, (E_col − ϵ₂)W_3,1 + W_3,2W_2,1 = 0 at B₁ and the bound state in the continuum occurs when D = 0.

When the energy ϵ₃ of the excited molecular state is detuned away from the resonance condition by changing the laser frequency, at B₁ where (E_col − ϵ₂)W_3,1 + W_3,2W_2,1 = 0, we obtain

$A_2=-\frac{W_{\mathrm{3,1}}}{W_{\mathrm{3,2}}}=\frac{W_{\mathrm{2,1}}}{E_{\text{col}}-{ϵ}_2},A_3=0.(20)$

In this case, two colliding atoms will be almost free from being trapped in the bound states of channel 3 during the collision. The spontaneous emission loss is negligible. The phase shift δ_res is entirely dominated by channel 2, that is,

$\tan {\delta }_{\text{res}}=-\pi W_{\mathrm{1,2}}{A}_2=-\pi \frac{|W_{\mathrm{1,2}}{|}^2}{E_{\text{col}}-{ϵ}_2}.(21)$

Tuning the laser frequency does not change the scattering length at B₁.

In order to let the wavefunction $u_1^{\prime }(r)$ in channel 1 to be normalized in energy, the asymptotic behavior of $u_1^{\prime }(r)$ should be expressed as

$u_1^{\prime }\left(r\right)\stackrel{r\to \infty }{\sim }\sqrt{\frac{2\mu }{\pi {\hslash }^{2}k}}\sin \left(kr+{\delta }_{\text{bg}}+{\delta }_{\text{res}}\right).(22)$

To meet this requirement, we multiplied U by cos δ_res,

$U^{\prime }=\left(\begin{array}{c}\hfill u_1^{\prime }\left(r\right)\hfill \\ \hfill A_2^{\prime }{u}_2^0\left(r\right)\hfill \\ \hfill A_3^{\prime }{u}_3^0\left(r\right)\hfill \end{array}\right)=\cos {\delta }_{\text{res}}U,(23)$

where

$\begin{array}{ll}\hfill A_2^{\prime }& =-\sin {\delta }_{\text{res}}\frac{\left(E_{\text{col}}-{ϵ}_3\right)W_{\mathrm{2,1}}+W_{\mathrm{2,3}}{W}_{\mathrm{3,1}}}{N\left(E_{\text{col}}\right)}\hfill \\ \hfill & =-2\sin {\delta }_{\text{res}}\frac{\left(E_{\text{col}}-{ϵ}_3\right)W_{\mathrm{2,1}}+W_{\mathrm{2,3}}{W}_{\mathrm{3,1}}}{D^{\prime }\mathrm{\Gamma }}\hfill \end{array}(24)$

and

$\begin{array}{ll}\hfill A_3^{\prime }& =-\sin {\delta }_{\text{res}}\frac{\left(E_{\text{col}}-{ϵ}_2\right)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}}{N\left(E_{\text{col}}\right)}\hfill \\ \hfill & =-2\sin {\delta }_{\text{res}}\frac{\left(E_{\text{col}}-{ϵ}_2\right)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}}{D^{\prime }\mathrm{\Gamma }}.\hfill \end{array}(25)$

When the resonance condition D = 0 is fulfilled, we obtain $|A_3^{\prime }{|}^2=\frac{8}{\pi \mathrm{\Gamma }}|\frac{E_{\text{col}}-{ϵ}_2}{E_{\text{col}}-{ϵ}_2+E_{\text{col}}-{ϵ}_3}|$. The probability of being trapped in the excited molecular state increases as the resonance width decreases.

3 Results and discussion

In our model, there is a magnetic Feshbach resonance at B = B₀ in the absence of laser, and B₀ is given in the appendix. With laser applied, the two colliding atoms are excited to the bound states of channel 3 during the collision. We calculate the real part Re(a) of the scattering length and loss rate coefficient at different magnetic field positions and laser frequencies using the close-coupling method. For the minimal laser amplitude E₀ = E_s of the electric field E = E₀ cos (ωt), we find that the bound state in the continuum occurs at the magnetic field position $B_1^{E_0=E_{\mathrm{s}}}=B_{\mathrm{0}}-2.49$ G. With laser frequency detuned away from the resonance condition, according to Eq. 21, tan δ_res is independent of the energy ϵ₃ of the excited molecular state at $B_1^{E_0=E_{\mathrm{s}}}$ so that the tuning laser frequency does not change Re(a) at $B_1^{E_0=E_{\mathrm{s}}}$ and Re(a) = −130.15 a₀. As shown in Eq. 20, when the resonance condition is not met, the probability of being trapped in the excited molecular state at $B_1^{E_0=E_{\mathrm{s}}}$ is significantly suppressed and the loss rate coefficient is lower than 10^–18 cm³s⁻¹.

We then calculate the wavefunction $u_2^0{(r)}_{|E_0=E_{\mathrm{s}}}$ in channel 2 at $B=B_1^{E_0=E_{\mathrm{s}}}$ using the mapped Fourier grid method. We find that $u_2^0{(r)}_{|E_0=E_{\mathrm{s}}}$ is almost invariant with the laser frequency. By comparing $u_2^0{(r)}_{|E_0=E_{\mathrm{s}}}$ with the wavefunction $u_2^0{(r)}_{|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}$ in channel 2 at $B=B_1^{E_0=E_{\mathrm{s}}}$ in the absence of the laser field, we obtain

$1-|⟨u_{2|E_0=E_{\mathrm{s}}}^0|u_{2|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}^0⟩{|}^2<10^{-10}.(26)$

It can be seen that the two wavefunctions $u_2^0{(r)}_{|E_0=E_{\mathrm{s}}}$ and $u_2^0{(r)}_{|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}$ are almost the same, and hence, W_1,2 and ϵ₂ are also almost unchanged. Therefore, the scattering length at $B_1^{E_0=E_{\mathrm{s}}}$ in the absence of the laser field should be very close to the real part Re(a) of the scattering length under the action of laser according to Eq. 20. The calculated scattering length at $B_1^{E_0=E_{\mathrm{s}}}$ in the absence of the laser field is −130.31 a₀. The difference between the scattering length without laser and Re(a) under the action of laser is less than 0.16 a₀. This shows that when the amplitude E₀ = E_s, the laser-induced bound-to-bound coupling and photoassociation coupling are much weaker than the Feshbach coupling between the ground molecular state and the incoming continuum state so that the wavefunction in channel 2 is slightly changed by the laser field.

When the amplitude E₀ increases to 5E_s, the bound state in the continuum occurs at the magnetic field position $B_1^{E_0=5E_{\mathrm{s}}}=B_{\mathrm{0}}-2.49$ G. With laser frequency detuned, Re(a) = −126.45 a₀ at $B_1^{E_0=5E_{\mathrm{s}}}$ and the loss rate coefficient is lower than 10^–16 cm³s⁻¹. Comparing $u_2^0{(r)}_{|E_0=5E_{\mathrm{s}}}$ with $u_2^0{(r)}_{|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}$ at $B_1^{E_0=5E_{\mathrm{s}}}$, we obtain

$1-|⟨u_{2|E_0=5E_{\mathrm{s}}}^0|u_{2|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}^0⟩{|}^2<10^{-8}.(27)$

It can be seen that when E₀ = 5E_s, the wavefunction $u_2^0{(r)}_{|E_0=5E_{\mathrm{s}}}$ is changed more. Although the magnetic field position where the bound state in the continuum occurs is not shifted, the difference between the scattering length in the absence of laser and Re(a) under the action of laser is more than 3.85 a₀.

When the amplitude E₀ increases to 10E_s, the bound state in the continuum occurs at $B_1^{E_0=10E_{\mathrm{s}}}=B_{\mathrm{0}}-2.47$ G. With laser frequency detuned, Re(a) = −119.52 a₀ at $B_1^{E_0=10E_{\mathrm{s}}}$ and the loss rate coefficient is lower than 10^–15 cm³s⁻¹. Comparing $u_2^0{(r)}_{|E_0=10E_{\mathrm{s}}}$ with $u_2^0{(r)}_{|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}$ at $B_1^{E_0=10E_{\mathrm{s}}}$, we obtain

$1-|⟨u_{2|E_0=10E_{\mathrm{s}}}^0|u_{2|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}^0⟩{|}^2<10^{-6}.(28)$

It can be seen from the aforementioned results that the wavefunction in channel 2 will be more significantly changed as laser intensity increases. As a result, the magnetic field position B₁ where the bound state in the continuum occurs is shifted and the real part Re(a) of the scattering length is changed.

According to Eq. 12, the s-wave resonance takes place under the co-action of the magnetic field and laser field when (E_col − ϵ₂)(E_col − ϵ₃) − |W_2,3|² = 0. The energy ϵ₃ can be modulated by changing laser frequency, and hence, the magnetic field position of the resonance shifts with laser frequency. Figure 2 shows the magnetic field positions of resonances at different laser frequencies ω when the amplitude E₀ = 10E_s. When $\omega ={\omega }_0^{E_0=10E_{\mathrm{s}}}$, the two resonances are located at the magnetic field positions B₀ ± 1.08 G. It can be seen that as ω is changed, one of the resonances is obviously shifted, while the other resonance is just located near B₀. For the resonance located far away from B₀, |E_col − ϵ₃|≪|E_col − ϵ₂|. For the resonance located close to B₀, |E_col − ϵ₃|≫|E_col − ϵ₂|. When ω is tuned to ${\omega }_0^{E_0=10E_{\mathrm{s}}}$, ϵ₂ and ϵ₃ are close to each other, and hence, the magnetic field positions of the two resonances deviate from B₀, and the deviation is about 1 G.

FIGURE 2

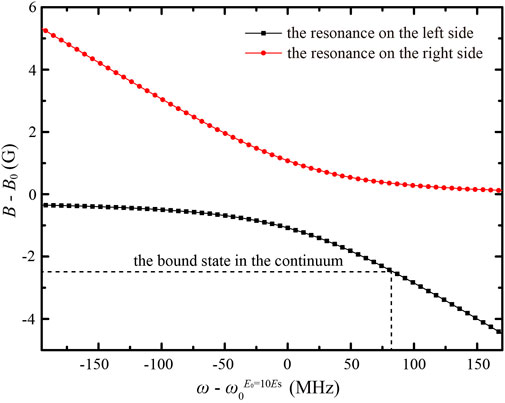
FIGURE 2. (Color online) The magnetic field positions of the two resonances split from the original magnetic Feshbach resonance versus laser frequency when E₀ =10E_s. When laser frequency at $\omega ={\omega }_0^{E_0=10E_{\mathrm{s}}}+80.5$ MHz, the bound state in the continuum occurs at $B_1^{E_0=10E_{\mathrm{s}}}=B_{\mathrm{0}}-2.47$ G.

Figure 3 shows the loss rate coefficients as a function of the magnetic field for different laser frequencies around ${\omega }_0^{E_0=10E_{\mathrm{s}}}$. The loss rate coefficient behaves like the Autler–Townes doublet, which was observed in [28]. With laser frequency detuned away from ${\omega }_0^{E_0=10E_{\mathrm{s}}}$, one of the two loss rate coefficient peaks increases and the other decreases. As laser frequency decreases from ${\omega }_0^{E_0=10E_{\mathrm{s}}}$, the loss rate coefficient peak on the left side decreases and the peak on the right side increases. As laser frequency increases from ${\omega }_0^{E_0=10E_{\mathrm{s}}}$, the loss rate coefficient peak on the left side increases and the peak on the right side decreases. Different from the case observed in [28], it can be seen from Figure 3 that the loss rate coefficient peak on the left side increases much faster than that on the right side. We then calculate the loss rate coefficients at the two resonances versus laser frequency for E₀ = 10E_s, as shown in Figure 4. As laser frequency increases from ${\omega }_0^{E_0=10E_{\mathrm{s}}}$ to ${\omega }_0^{E_0=10E_{\mathrm{s}}}+80.5$ MHz, the resonance on the left side is shifted to the magnetic field position $B_1^{E_0=10E_{\mathrm{s}}}$, where the bound state in the continuum occurs and the resonance width decreases. The loss rate coefficient at the left side resonance increases rapidly and reaches its maximum when the laser frequency ω is tuned close to ${\omega }_0^{E_0=10E_{\mathrm{s}}}+80.5$ MHz. According to $|A_3^{\prime }{|}^2=\frac{8}{\pi \mathrm{\Gamma }}|\frac{E_{\text{col}}-{ϵ}_2}{E_{\text{col}}-{ϵ}_2+E_{\text{col}}-{ϵ}_3}|$, the probability of being trapped in the excited molecular state increases as the resonance width decreases, so the loss rate coefficient at the left side resonance increases rapidly.

FIGURE 3

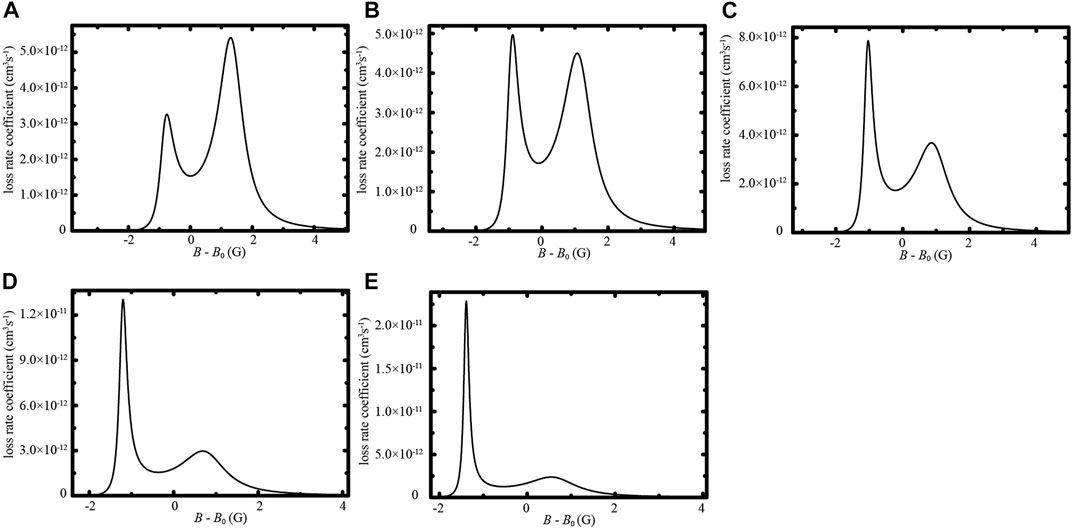
FIGURE 3. The loss rate coefficients versus magnetic field B for laser frequencies (A) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}-24.8$, (B) ${\omega }_0^{E_0=10E_{\mathrm{s}}}-12.4$, (C) ${\omega }_0^{E_0=10E_{\mathrm{s}}}$, (D) ${\omega }_0^{E_0=10E_{\mathrm{s}}}+12.4$, and (E) ${\omega }_0^{E_0=10E_{\mathrm{s}}}+24.8$ MHz. The laser amplitude E₀ is set at 10E_s.

FIGURE 4

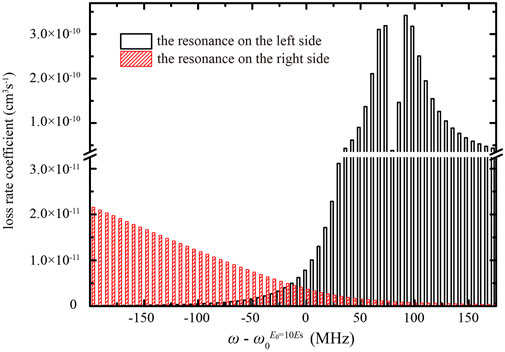
FIGURE 4. (Color online) Loss rate coefficients at the two resonances for different laser frequencies. The resonance on the left side of the magnetic field position is shown by a black bar with blank pattern. The resonance on the right side of the magnetic field position is shown by a red bar with dense pattern. The laser amplitude E₀ is set at 10E_s.

As shown in Figure 2, the magnetic field position of the resonances can be shifted by changing the laser frequency. However, the resonance widths are narrow in the neighborhood of the magnetic field position $B_1^{E_0=10E_{\mathrm{s}}}$, and the loss rate coefficients are large. Figure 5 shows the real part Re(a) of the scattering length and the loss rate coefficient at three resonances, when the laser frequency $\omega ={\omega }_0^{E_0=10E_{\mathrm{s}}}+142.3$, ${\omega }_0^{E_0=10E_{\mathrm{s}}}+86.6$, and ${\omega }_0^{E_0=10E_{\mathrm{s}}}-167.1$ MHz. These three resonances are located at the magnetic field positions B = B₀ − 3.8 G, B₀ − 2.6 G, and B₀ + 4.6 G, respectively. The real part Re(a) of the scattering length can be tuned by changing the magnetic field B or laser frequency. With the loss rate coefficient being limited below 10^–11 cm³s⁻¹, Re(a) can be tuned in the range from −430.27 to 572.10 a₀ for the resonance located at B = B₀ − 3.8 G. For the resonance located at B = B₀ + 4.6 G, Re(a) can be tuned in the range from −808.71 to 2719.43 a₀. However, for the very narrow resonance located at B = B₀ − 2.6 G, Re(a) can only be tuned in the range from −130.19 to −66.04 a₀. The tunability of Re(a) at narrow resonances is severely limited.

FIGURE 5

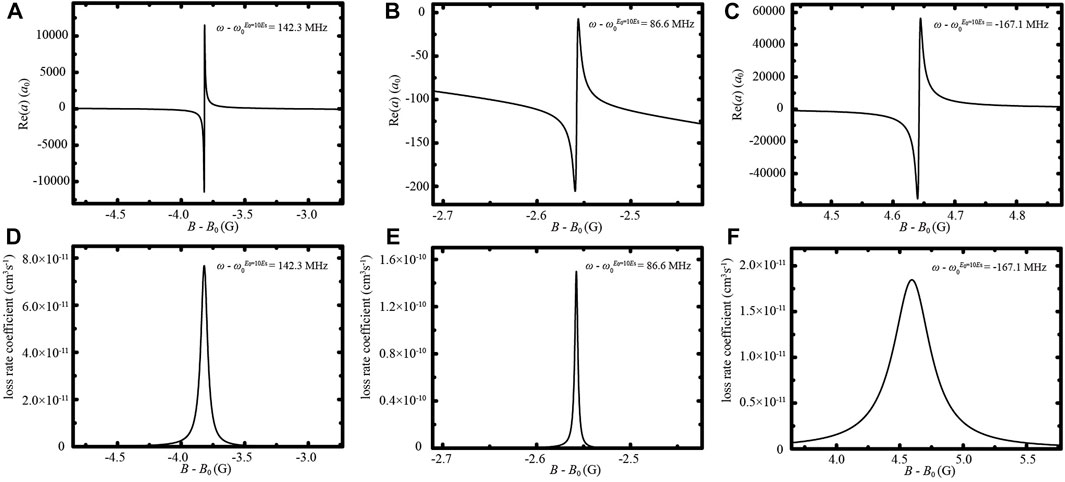
FIGURE 5. The real part Re (A) of the scattering length versus magnetic field B for laser frequencies (A) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}+142.3$ MHz, (B) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}+86.6$ MHz, and (C) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}-167.1$ MHz. The loss rate coefficients versus magnetic field B for laser frequencies (D) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}+142.3$ MHz, (E) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}+86.6$ MHz, and (F) ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}-167.1$ MHz. The laser amplitude E₀ is set at 10E_s.

Therefore, when laser amplitude E₀ = 10E_s, Re(a) cannot be tuned effectively in the neighborhood of the magnetic field position $B_1^{E_0=10E_{\mathrm{s}}}$. As mentioned previously, when stronger laser is applied, the wavefunction in channel 2 is more significantly changed by laser. When laser amplitude E₀ increases to 50E_s, compared with the cases of E₀ = 1 ∼ 10E_s, we find the magnetic field position where the bound state in the continuum occurs has been significantly shifted. The bound state in the continuum occurs at $B_1^{E_0=50E_{\mathrm{s}}}=B_{\mathrm{0}}+2.75$ G. With laser frequency being detuned, Re(a) = 280.05 a₀ at $B_1^{E_0=50E_{\mathrm{s}}}$, and the loss rate coefficient is lower than 10^–14 cm³s⁻¹. Comparing $u_2^0{(r)}_{|E_0=50E_{\mathrm{s}}}$ with $u_2^0{(r)}_{|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}$ at $B_1^{E_0=50E_{\mathrm{s}}}$, we obtain

$1-|⟨u_{2|E_0=50E_{\mathrm{s}}}^0|u_{2|\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}^0⟩{|}^2<2.5\times 10^{-3}.(29)$

By increasing laser amplitude from 10E_s to 50E_s, the bound state in the continuum is shifted from $B_1^{E_0=10E_{\mathrm{s}}}$ to $B_1^{E_0=50E_{\mathrm{s}}}$. Therefore, when laser amplitude E₀ = 50E_s, a wide resonance occurs at $B_1^{E_0=10E_{\mathrm{s}}}$. With the loss rate coefficient being limited below 10^–11 cm³s⁻¹, Re(a) can be tuned in the range from −461.90 to 478.00 a₀ at this wide resonance. The tunability of Re(a) in the neighborhood of $B_1^{E_0=10E_{\mathrm{s}}}$ is significantly improved.

Changing laser amplitude not only shifts the magnetic field position where the bound state in the continuum occurs but also adjusts the coupling W_2,3 between the ground and excited molecular states. A special case is that the coupling W_2,3 approaches zero due to the interference between the direct bound-to-bound coupling and the indirect coupling. Figure 6 shows the magnetic field positions of resonances at different laser frequencies when laser amplitude E₀ = 60E_s. One of the two resonances is linearly shifted, while the other resonance is unmoved. Due to the small |W_2,3|, the minimum difference between the magnetic field positions of the two resonances is only 0.21 G.

FIGURE 6

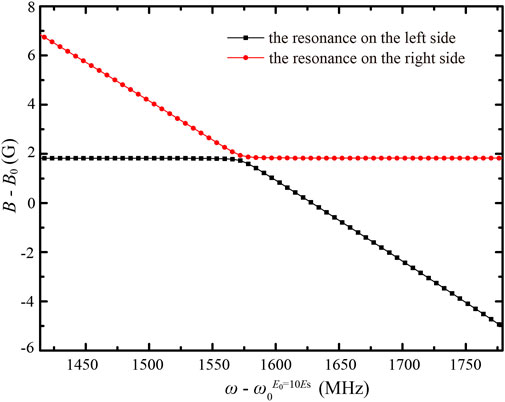
FIGURE 6. (Color online) Magnetic field positions of the two resonances split from the original Feshbach resonance versus laser frequency when E₀ = 60E_s.

We calculate the real part Re(a) of the scattering length versus the magnetic field B for different laser frequencies, as shown in Figure 7A. With |W_2,3| approaching zero, at the linearly shifted resonance |E_col − ϵ₂|≫|W_2,3|≫|E_col − ϵ₃| and the resonance width Γ ≈ 2π|W_3,1|². At the unmoved resonance, |E_col − ϵ₃|≫|W_2,3|≫|E_col − ϵ₂| and the resonance width Γ ≈ 2π|W_2,1|². We also calculate the loss rate coefficient at the two resonances for different laser frequencies. The maximum loss rate coefficients at the linearly shifted resonances for three frequencies are almost the same, which are 2.44 × 10⁻¹¹, 2.49 × 10⁻¹¹, and 2.59 × 10⁻¹¹ cm³s⁻¹, respectively. At the linearly shifted resonance $A_3^{\prime }\approx -2\sin {\delta }_{\text{res}}\frac{1}{W_{\mathrm{1,3}}}$ according to Eq. 25. The probability of being trapped in the excited molecular state is independent of the energy ϵ₂ of the ground molecular state and only dependent on the photoassociation coupling W_1,3. Thus, the maximum loss rate coefficient at the linearly shifted resonance changes little as the magnetic field position of this resonance is shifted. However, the loss rate coefficient peak does not occur at the unmoved resonance, as shown in Figure 7B. At the unmoved resonance $A_3^{\prime }\approx -2\sin {\delta }_{\text{res}}\frac{(E_{\text{col}}-{ϵ}_2)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}}{(E_{\text{col}}-{ϵ}_3)|W_{\mathrm{2,1}}{|}^2}$. The photoassociation transition and bound-to-bound transition are both suppressed because (E_col − ϵ₂) → 0 and |W_3,2| → 0. The real part Re(a) of the scattering length can be tuned over a large range without rapid losses.

FIGURE 7

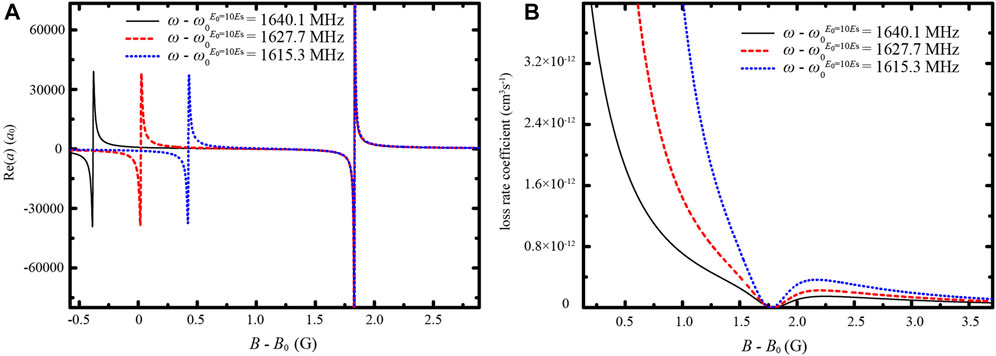
FIGURE 7. (Color online) (A) The real part Re (A) of the scattering length versus the magnetic field B for laser frequencies ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}+1640.1$ (black solid line), ${\omega }_0^{E_0=10E_{\mathrm{s}}}+1627.7$ (red dashed line), and ${\omega }_0^{E_0=10E_{\mathrm{s}}}+1615.3$ MHz (blue dotted line). (B) The loss rate coefficients versus the magnetic field B for laser frequencies ω = ${\omega }_0^{E_0=10E_{\mathrm{s}}}+1640.1$ (black solid line), ${\omega }_0^{E_0=10E_{\mathrm{s}}}+1627.7$ (red dashed line), and ${\omega }_0^{E_0=10E_{\mathrm{s}}}+1615.3$ MHz (blue dotted line).

Figure 8 is a schematic illustration of the variation of $A_3^{\prime }$ with the magnetic field B at the unmoved resonance, where |W_2,3| is much smaller than |W_1,3| and |W_1,2|, and |E_col − ϵ₃|≫|E_col − ϵ₂|. The two energies ϵ₂ and ϵ₃ decrease as B increases, and the energy interval between ϵ₂ and ϵ₃ at the resonance is altered by changing ϵ₃. At the resonance position, the position and width of the peak of | sin δ_res|² are almost unchanged when changing ϵ₃. As ϵ₃ gradually approaches ϵ₂, the value |E_col − ϵ₃| decreases at the resonance, and hence, |N (E_col)| decreases. The slope of $[(E_{\mathrm{c}\mathrm{o}\mathrm{l}}-{ϵ}_2)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}]/N(E_{\mathrm{c}\mathrm{o}\mathrm{l}})$ at the resonance increases gradually. As a result, $|A_3^{\prime }|$ increases faster on both sides of the resonance as ϵ₃ approaches ϵ₂. However, $|A_3\prime |$ at the resonance is still a small value because $|(E_{\mathrm{c}\mathrm{o}\mathrm{l}}-{ϵ}_2)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}|\to 0$. This explains the suppressed loss rate coefficient at the nearly immovable resonance in Figure 7 and the increase in the loss rate coefficient on both sides of this resonance as the two resonances are close to each other.

FIGURE 8

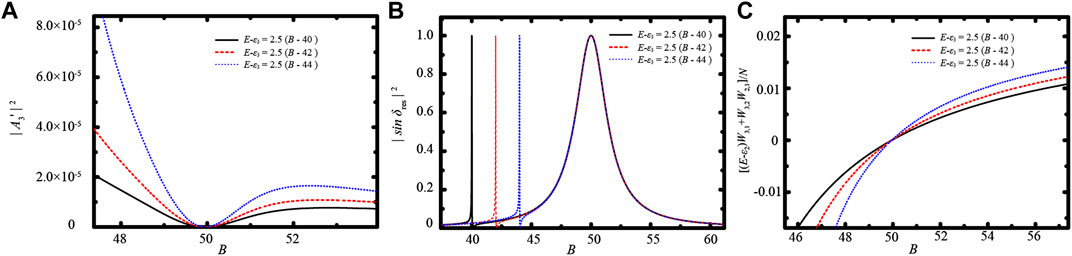
FIGURE 8. (Color online) Schematic illustration of (A) $|A_3^{\prime }{|}^2$, (B) | sin δ_res|², and (C) $[(E-{ϵ}_2)W_{\mathrm{3,1}}+W_{\mathrm{3,2}}{W}_{\mathrm{2,1}}]/N$ versus the magnetic field $B$ for E − ϵ₃ = 2.5(B − 40) (black solid line), 2.5(B − 42) (red dashed line), and 2.5(B − 44) (blue dotted line). The parameter values are taken to be E − ϵ₂ = 2.0(B − 50), W_1,3 = W_3,1 = 0.1, W_2,3 = W_3,2 = 0.01, and W_1,2 = W_2,1 = 1.0.

4 Conclusion

In this paper, we investigate the s-wave scattering of ultracold atoms controlled by the magnetic field and laser field in the neighborhood of the original magnetic Feshbach resonance. We find that the bound state in the continuum occurs at the magnetic field position B₁ near the original magnetic Feshbach resonance due to the interference between the photoassociation and bound-to-bound transitions. Changing the laser frequency can shift the magnetic field positions of resonances, and the widths of resonances in the neighborhood of B₁ become narrow. Because the probability of being trapped in the excited molecular state increases as the resonance width decreases, the loss rate coefficients at narrow resonances are large. The tunability of the real part Re(a) of the scattering length is severely limited at narrow resonances. The wavefunction of the ground molecular state is more significantly changed as laser intensity increases. Therefore, changing the laser intensity can shift the magnetic field position B₁ to induce wide resonances at desired magnetic field positions. This paves the way to tune the scattering length at a wide range of magnetic fields near the original magnetic Feshbach resonance. Changing the laser intensity also adjusts the coupling between the ground and excited molecular states. With the coupling canceled, a resonance is induced at which the loss rate coefficient is significantly suppressed. The scattering length can be tuned over a large range without causing rapid atomic losses. At the magnetic field position where the bound state in the continuum occurs, when the laser frequency is detuned away from the resonance condition, the scattering length does not change with the laser frequency and the spontaneous emission losses are significantly suppressed. Therefore, the laser frequency can be used as the control parameter to manipulate ultracold systems, for example, when other scattering lengths in this system need to be tuned. In this work, the s-wave scattering is manipulated by the magnetic field and one laser. In the future work, we would consider adding another laser to couple the excited molecular state with a deeply bound ground molecular state. In this way, more control parameters will be used to manipulate ultracold systems. Moreover, ultracold atoms are trapped in the deeply bound ground molecular state during the collision, which may be helpful in the preparation of ultracold molecules.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

B-KL performed research, analyzed data, and wrote the paper; B-WS analyzed data and wrote the paper; Z-HY wrote the paper; G-RW wrote the paper; S-LC designed the research study and wrote the paper. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Key R&D Program of China (No. 2018YFA0306503) and the National Natural Science Foundation (No. 11274056).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Guo Z, Jia F, Zhu B, Li L, Hutson JM, Wang D (2022). Improved characterization of Feshbach resonances and interaction potentials between ²³Na and ⁸⁷Rb atoms. Phys Rev A 105, 023313. doi:10.1103/PhysRevA.105.023313

CrossRef Full Text | Google Scholar

2. Hartmann T, Schulze TA, Voges KK, Gersema P, Gempel MW, Tiemann E, et al. Feshbach resonances in ²³Na +³⁹K mixtures and refined molecular potentials for the NaK molecule. Phys Rev A (2019) 99:032711. doi:10.1103/PhysRevA.99.032711

CrossRef Full Text | Google Scholar

3. Wang X-Y, Frye MD, Su Z, Cao J, Liu L, Zhang D-C, et al. Magnetic Feshbach resonances in collisions of ²³Na⁴⁰K with ⁴⁰K. New J Phys (2021) 23:115010. doi:10.1088/1367-2630/ac3318

CrossRef Full Text | Google Scholar

4. Weckesser P, Thielemann F, Wiater D, Wojciechowska A, Karpa L, Jachymski K, et al. Observation of Feshbach resonances between a single ion and ultracold atoms. Nature (2021) 600:429–33. doi:10.1038/s41586-021-04112-y

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yang H, Zhang D-C, Liu L, Liu Y-X, Nan J, Zhao B, et al. Observation of magnetically tunable Feshbach resonances in ultracold ²³Na⁴⁰K + ⁴⁰K collisions. Science (2019) 363:261–4. doi:10.1126/science.aau5322

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Krauser JS, Heinze J, Götze S, Langbecker M, Fläschner N, Cook L, et al. Investigation of Feshbach resonances in ultracold ⁴⁰K spin mixtures. Phys Rev A (2017) 95:042701. doi:10.1103/PhysRevA.95.042701

CrossRef Full Text | Google Scholar

7. Lyu B-K, Sun Z-X, Wang G-R, Cong SL. Suppression of interaction-induced loss rate coefficient near broad s-wave and p-wave Feshbach resonances by magnetic field. J Phys B: Mol Opt Phys (2022) 55:055201. doi:10.1088/1361-6455/ac5861

CrossRef Full Text | Google Scholar

8. Zhang Z, Chen L, Yao K-X, Chin C. Transition from an atomic to a molecular Bose–Einstein condensate. Nature (2021) 592:708–11. doi:10.1038/s41586-021-03443-0

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Boettcher I, Bayha L, Kedar D, Murthy PA, Neidig M, Ries MG, et al. Equation of state of ultracold fermions in the 2D BEC-BCS crossover region. Phys Rev Lett (2016) 116:045303. doi:10.1103/PhysRevLett.116.045303

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chen Y, Zhai H, Yu Z. Superradiant phase transition of Fermi gases in a cavity across a Feshbach resonance. Phys Rev A (2015) 91:021602. doi:10.1103/PhysRevA.91.021602

CrossRef Full Text | Google Scholar

11. Ries MG, Wenz AN, Zürn G, Bayha L, Boettcher I, Kedar D, et al. Observation of pair condensation in the quasi-2D BEC-BCS crossover. Phys Rev Lett (2015) 114:230401. doi:10.1103/PhysRevLett.114.230401

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kim M-S, Lee J, Lee JH, Shin Y, Mun J. Measurements of optical Feshbach resonances of ¹⁷⁴Yb atoms. Phys Rev A (2016) 94:042703. doi:10.1103/PhysRevA.94.042703

CrossRef Full Text | Google Scholar

13. Koch CP, Shapiro M. Coherent control of ultracold photoassociation. Chem Rev (2012) 112:4928–48. doi:10.1021/cr2003882

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lyu BK, Li JL, Wang M, Wang GR, Cong SL. Efficient formation of stable ultracold Cs₂ molecules in the ground electronic state via two-color photoassociation. Eur Phys J D (2019) 73:20. doi:10.1140/epjd/e2018-90314-5

CrossRef Full Text | Google Scholar

15. Arunkumar N, Jagannathan A, Thomas JE. Designer spatial control of interactions in ultracold gases. Phys Rev Lett (2019) 122:040405. doi:10.1103/PhysRevLett.122.040405

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Clark LW, Ha L-C, Xu C-Y, Chin C. Quantum dynamics with spatiotemporal control of interactions in a stable Bose-Einstein condensate. Phys Rev Lett (2015) 115:155301. doi:10.1103/PhysRevLett.115.155301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Schäfer F, Mizukami N, Yu P, Koibuchi S, Bouscal A, Takahashi Y. Experimental realization of ultracold Yb-⁷Li mixtures in mixed dimensions. Phys Rev A (2018) 98:051602. doi:10.1103/PhysRevA.98.051602

CrossRef Full Text | Google Scholar

18. Guo Z, Jia F, Li L, Ma Y, Hutson JM, Cui X, et al. Lee-Huang-Yang effects in the ultracold mixture of ²³Na and ⁸⁷Rb with attractive interspecies interactions. Phys Rev Res (2021) 3:033247. doi:10.1103/PhysRevResearch.3.033247

CrossRef Full Text | Google Scholar

19. Warner C, Lam AZ, Bigagli N, Liu HC, Stevenson I, Will S. Overlapping bose-einstein condensates of ²³Na and ¹³³Cs. Phys Rev A (2021) 104:033302. doi:10.1103/PhysRevA.104.033302

CrossRef Full Text | Google Scholar

20. Fava E, Bienaimé T, Mordini C, Colzi G, Qu C, Stringari S, et al. Observation of spin superfluidity in a Bose gas mixture. Phys Rev Lett (2018) 120:170401. doi:10.1103/PhysRevLett.120.170401

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Argüello-Luengo J, González-Tudela A, Shi T, Zoller P, Cirac JI. Analogue quantum chemistry simulation. Nature (2019) 574:215–8. doi:10.1038/s41586-019-1614-4

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Baier S, Petter D, Becher JH, Patscheider A, Natale G, Chomaz L, et al. Realization of a strongly interacting Fermi gas of dipolar atoms. Phys Rev Lett (2018) 121:093602. doi:10.1103/PhysRevLett.121.093602

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Goldman N, Budich JC, Zoller P. Topological quantum matter with ultracold gases in optical lattices. Nat Phys (2016) 12:639–45. doi:10.1038/nphys3803

CrossRef Full Text | Google Scholar

24. Moses SA, Covey JP, Miecnikowski MT, Yan B, Gadway B, Ye J, et al. Creation of a low-entropy quantum gas of polar molecules in an optical lattice. Science (2015) 350:659–62. doi:10.1126/science.aac6400

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Tomita T, Nakajima S, Danshita I, Takasu Y, Takahashi Y. Observation of the Mott insulator to superfluid crossover of a driven-dissipative Bose-Hubbard system. Sci Adv (2017) 3:e1701513. doi:10.1126/sciadv.1701513

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Dong G, Hu B, Lu W. Ground-state properties of a Bose-Einstein condensate tuned by a far-off-resonant optical field. Phys Rev A (2006) 74:063601. doi:10.1103/PhysRevA.74.063601

CrossRef Full Text | Google Scholar

27. Yamazaki R, Taie S, Sugawa S, Takahashi Y. Submicron spatial modulation of an interatomic interaction in a Bose-Einstein condensate. Phys Rev Lett (2010) 105:050405. doi:10.1103/PhysRevLett.105.050405

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Bauer DM, Lettner M, Vo C, Rempe G, Dürr S. Control of a magnetic Feshbach resonance with laser light. Nat Phys (2009) 5:339–42. doi:10.1038/nphys1232

CrossRef Full Text | Google Scholar

29. Theis M, Thalhammer G, Winkler K, Hellwig M, Ruff G, Grimm R, et al. Tuning the scattering length with an optically induced Feshbach resonance. Phys Rev Lett (2004) 93:123001. doi:10.1103/PhysRevLett.93.123001

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bauer DM, Lettner M, Vo C, Rempe G, Dürr S. Combination of a magnetic Feshbach resonance and an optical bound-to-bound transition. Phys Rev A (2009) 79:062713. doi:10.1103/PhysRevA.79.062713

CrossRef Full Text | Google Scholar

31. Fu Z, Wang P, Huang L, Meng Z, Hu H, Zhang J. Optical control of a magnetic Feshbach resonance in an ultracold Fermi gas. Phys Rev A (2013) 88:041601. doi:10.1103/PhysRevA.88.041601

CrossRef Full Text | Google Scholar

32. Zhang Y-C, Liu W-M, Hu H. Tuning a magnetic Feshbach resonance with spatially modulated laser light. Phys Rev A (2014) 90:052722. doi:10.1103/PhysRevA.90.052722

CrossRef Full Text | Google Scholar

33. Jagannathan A, Arunkumar N, Joseph JA, Thomas JE. Optical control of magnetic Feshbach resonances by closed-channel electromagnetically induced transparency. Phys Rev Lett (2016) 116:075301. doi:10.1103/PhysRevLett.116.075301

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Semczuk M, Gunton W, Bowden W, Madison KW. Anomalous behavior of dark states in quantum gases of ⁶Li. Phys Rev Lett (2014) 113:055302. doi:10.1103/PhysRevLett.113.055302

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wu H, Thomas JE. Optical control of Feshbach resonances in Fermi gases using molecular dark states. Phys Rev Lett (2012) 108:010401. doi:10.1103/PhysRevLett.108.010401

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wu H, Thomas JE. Optical control of the scattering length and effective range for magnetically tunable Feshbach resonances in ultracold gases. Phys Rev A (2012) 86:063625. doi:10.1103/PhysRevA.86.063625

CrossRef Full Text | Google Scholar

37. Friedrich H. Scattering theory, vol 872 of lecture notes in Physics. Berlin, Heidelberg: Springer Berlin Heidelberg (2013). doi:10.1007/978-3-642-38282-6

CrossRef Full Text | Google Scholar

38. Friedrich H, Wintgen D. Interfering resonances and bound states in the continuum. Phys Rev A (1985) 32:3231–42. doi:10.1103/PhysRevA.32.3231

CrossRef Full Text | Google Scholar

39. Sadreev AF, Bulgakov EN, Rotter I. Bound states in the continuum in open quantum billiards with a variable shape. Phys Rev B (2006) 73:235342. doi:10.1103/PhysRevB.73.235342

CrossRef Full Text | Google Scholar

40. Solís B, Ladrón de Guevara M, Orellana P. Friedel phase discontinuity and bound states in the continuum in quantum dot systems. PHYS LETT A (2008) 372:4736–9. doi:10.1016/j.physleta.2008.05.014

CrossRef Full Text | Google Scholar

41. Deb B, Agarwal GS. Creation and manipulation of bound states in the continuum with lasers: Applications to cold atoms and molecules. Phys Rev A (2014) 90:063417. doi:10.1103/PhysRevA.90.063417

CrossRef Full Text | Google Scholar

42. Naskar S, Sardar D, Deb B, Agarwal GS. Suppressing deleterious effects of spontaneous emission in creating bound states in cold atom continuum. J Phys B: Mol Opt Phys (2019) 52:245204. doi:10.1088/1361-6455/ab4ef2

CrossRef Full Text | Google Scholar

43. Alexander MH, Manolopoulos DE. A stable linear reference potential algorithm for solution of the quantum close-coupled equations in molecular scattering theory. J Chem Phys (1987) 86:2044–50. doi:10.1063/1.452154

CrossRef Full Text | Google Scholar

44. Bohn JL, Julienne PS. Prospects for influencing scattering lengths with far-off-resonant light. Phys Rev A (1997) 56:1486–91. doi:10.1103/PhysRevA.56.1486

CrossRef Full Text | Google Scholar

45. Hutson JM, Sueur CRL. Molscat: A program for non-reactive quantum scattering calculations on atomic and molecular collisions. Comput Phys Commun (2019) 241:9–18. doi:10.1016/j.cpc.2019.02.014

CrossRef Full Text | Google Scholar

46. Strauss C, Takekoshi T, Lang F, Winkler K, Grimm R, Hecker Denschlag J, et al. Hyperfine, rotational, and vibrational structure of the $a^3{\mathrm{\Sigma }}_u^{+}$ state of ⁸⁷Rb₂. Phys Rev A (2010) 82:052514. doi:10.1103/PhysRevA.82.052514

CrossRef Full Text | Google Scholar

47. Borisov AG. Solution of the radial Schrödinger equation in cylindrical and spherical coordinates by mapped Fourier transform algorithms. J Chem Phys (2001) 114:7770–7. doi:10.1063/1.1358867

CrossRef Full Text | Google Scholar

48. Willner K, Dulieu O, Masnou-Seeuws F. Mapped grid methods for long-range molecules and cold collisions. J Chem Phys (2004) 120:548–61. doi:10.1063/1.1630031

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix: interaction and coupling potentials in calculations

In our calculation, the interactions V_i (i = 1,2,3) are obtained from the interaction in the fourth, fifth, and sixth channels in the ⁸⁵Rb and ⁸⁷Rb s-wave system when the sum of the projection quantum numbers of ⁸⁵Rb and ⁸⁷Rb atoms equals +2 [46]. The order of the channels is sorted by the channel energy from low to high. The coupling potential V_1,2 (V_2,1) is obtained from the coupling between the fourth and fifth channels. For the case of minimal laser amplitude E_s, the coupling potentials V_1,3 (V_3,1) and V_2,3 (V_3,2) are obtained by multiplying the coupling between the fourth and sixth channels, and the coupling between the fifth and sixth channels by 0.001. The energy of the fifth channel is increased by 1237.8 MHz. In the case when laser frequency is ${\omega }_0^{E_0=10E_{\mathrm{s}}}$, the energy of the six channel is increased by 544.6 MHz. The energies of the fourth, fifth, and sixth channels are shifted together, letting the energy of the fourth channel be zero, and then used as E₁, E₂, and E₃, respectively. In the close-coupling calculation, the third channel in the ⁸⁵Rb and ⁸⁷Rb system is introduced to describe atomic losses, which is only coupled with the sixth channel. The coupling potential is obtained by multiplying the coupling between the third and sixth channels by 0.03. The energy of the third channel is reduced by 1856.7 MHz and then shifted together with the other three channels. The magnetic field is tuned to 265.65 G, where the original magnetic Feshbach resonance occurs.

FIGURE A1

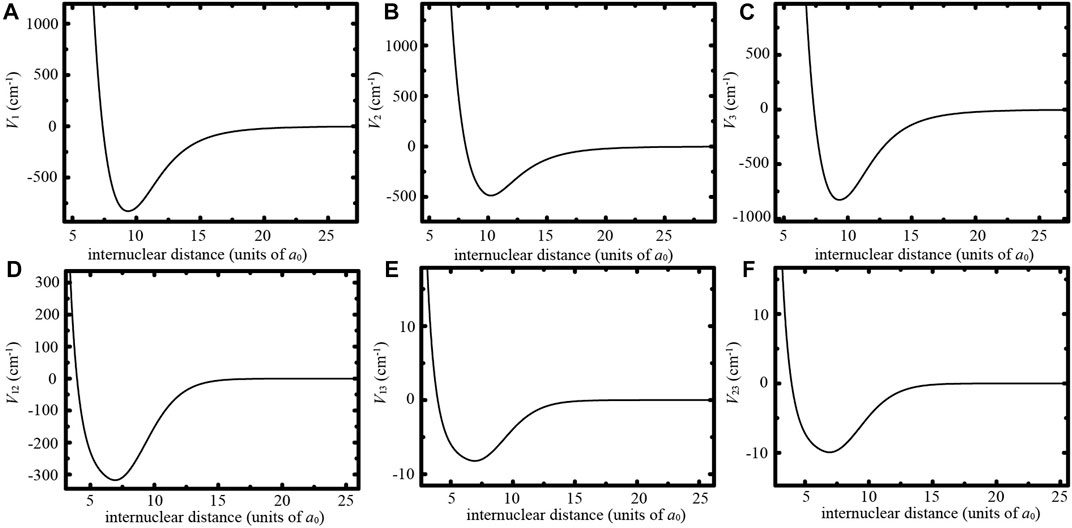
FIGURE A1. Interaction potentials and coupling potentials used in our calculation at B₀. (A) Interaction potential V₁. (B) Interaction potential V₂. (C) Interaction potential V₃. (D) Coupling potential V_1,2 between channels 1 and 2. (E) Coupling potential V_1,3 between channels 1 and 3 when laser amplitude E₀ = 10E_s. (F) Coupling potential V_2,3 between channels 2 and 3 when laser amplitude E₀ = 10E_s.