A theoretical model of high Curie temperature for N-type ferromagnetic diluted semiconductors based on iron-doped indium antimonide

In this paper, without using an external magnetic field, ferromagnetism on diluted InFeSb magnetic semiconductors is studied up to 317.65 K. The spin-wave model that the Heisenberg Hamiltonian translates into in the system has been developed using the green function formalism and the Holstein–Primakoff transformation estimate. The numbers of magnons, dispersion, Curie temperature, susceptibility, and specific heat capacity of the system have all been determined using the established model. The findings demonstrate that the ferromagnetic in ${In}_{0.893}{Fe}_{0.107}Sb$ has a Curie temperature that is significantly higher than those found in prior investigations (317.65 K).

1 Introduction

Before 1960, magnetic and semiconductor devices had different purposes: magnetic devices were used to store data, whereas semiconductor devices were used to transmit and analyze data [1–2]. The device made of these materials replaced two different devices made of magnetic and nonmagnetic semiconductors simultaneously around the time that EuO ferromagnetic semiconductors were discovered in the 1960s; however, since the device only works at low temperatures, we conducted the study to investigate for a different result [3–4]. Since spin-based electronics with diluted magnetic semiconductors have recently been developed, research to overcome this constraint has doped Mn in II-IV semiconductors [4–6]. Because of their potential as a novel material that will open the door to new applications, diluted magnetic semiconductors are of great interest to the industry [7]. Thus, diluted magnetic semiconductors are expected to play an important role in next-generation spin-based electronics, or spintronics technology [8–11]. This type of technology is required if the DMS Curie temperature (T_C) is higher than the room temperature for the application [9]. As is observed, diluted magnetic semiconductor devices not only fill the gap between the magnet and the semiconductor devices but also use it to store, process, and transmit data simultaneously, saving time, space, and money [12–18].

Manganese doped on II–IV, one of the 3D transition elements according to the study, has been the subject of numerous studies. The Curie temperature is promising compared to an intrinsically magnetic semiconductor, but because it is very low compared to room temperature [4, 18], it has attracted the attention of other researchers. In contrast, manganese doped in III–V has been able to achieve a higher Curie temperature than manganese doped in II–IV [10, 20]. However, its Curie temperature is less than the room temperature.

Some researchers have studied manganese-doped III-V narrow-band-gap semiconductors, with Curie temperatures higher than room temperature in some studies and lower Curie temperatures in others. Previous research has shown that a ferromagnetic Curie temperature is less than room temperature in the absence of an external magnetic field, as shown as follows: In [21–24], the Curie temperatures of (In, Mn) Sb are 2 K, 4 K, 20 K, and 130 K; in addition, in [25–29], the Curie temperatures of (In, Mn) As are 7.5 K, 35 K, 82 K, and 175 K. Previous research has shown that when an external magnetic field is used, the Curie temperature of the ferromagnetic is higher than the room temperature. In [8], [9], [12], [15],[22], [25], and [31–33], by setting a magnetic field from 1.6T to 15T, the (In, Mn) Sb curie temperatures were found to range from 300 K to 600 K. In addition, in [33–36], applying a magnetic field from 1.6T to 15T, the (In, Mn) As Curie temperatures from 293 K to 400 K have been found. However, Mn-doped III-V semiconductors have been found to exhibit ferromagnetism only from the origin of p-type carriers, so n-type diluted semiconductors may not be realized on this system. Most semiconductor devices, such as p-n junction diodes, spin light-emitting diodes, and field-effect transistors (semiconductor lasers), require a pair of n-type and p-type semiconductor materials to work. Due to this, we initiated the study of Fe doped on InSb with electrons exhibiting n-type electron-induced ferromagnetism, that is, filling the missing counterpart of p-type diluted magnetic semiconductors. Fe-doped InSb ferromagnetism originates from p-type carriers and shows electron-induced ferromagnetism, which is an n-type diluted semiconductor, making it easy to be used in real spin devices [37–40]. The n-type InSb (In, Fe) Sb ferromagnetic diluted magnetic semiconductor shows significance for next-generation nanoelectronic device [41] applications such as spintronics [42], biosensors to detect bacteria [43], Hall sensors [44], photonics [45], optoelectronics [46], infrared emitters [46,47], gas sensors [48], magneto resistors [49-50], and speed-sensitive sensors [51]. To use and apply the devices mentioned previously, it is necessary to understand the ferromagnetism properties of Fe-doped InSb.

Fe doped on InSb obtained an n-type diluted magnetic semiconductor; its curie temperature is higher than or less than the room temperature, with or without an applied external magnetic field; in [13], [19], and [37–52], the Curie temperatures of InFeSb are 131 K–385 K, when x = 5%–16% and 20%–35%.

When Fe³⁺ is replaced by a III-V semiconductor, the total spin quantum of Fe³⁺ (S = 5/2) [38], it is observed that the atomic mass of the pre-unit volume reaches from 6 $\times {10}^{18}{cm}^{-3}$ to 2.6 × 1 $\times {10}^{21}{cm}^{-3}$ [19, 38, 39] and that the number of atoms in the pre-unit volume reaches ${10}^{22}{cm}^{-3}$ to 2.2 $\times {10}^{22}{cm}^{-3}$ [11].

The Fe–Fe magnetic coupling impurity interaction value of an n-type semiconductor depends on the distance. In [53], when manganese is doped on CdTe, the maximum ferromagnetism value is 9.77 meV with a distance of 6.3 ± 0.3 and 0.810 meV with a distance 1.9 ± 1.1 using the RKKY model. The Fe–Co–Fe coupling interaction value, as cited in [54], is 10 meV using the RKKY model.

According to [55], there are three distinct energy ranges for spin waves. The lowest range, known as low-energy spin waves, is from 9 to 70 meV; the second ranges from 80 to 140 meV; and the third ranges from 180 meV to 230 meV. We can set quantitative limits on the effective exchange couplings in the Heisenberg Hamiltonian, thanks to the high-quality spin-wave data. As a result, our system developed on low-energy spin waves, and for our calculation, we took the value that is closest to the smallest range (9 meV), which is 10 meV.

The exceptional fact observed in this study is that we have found the Curie temperature of the ferromagnetism of InFeSb n-type diluted magnetic semiconductors to be 317.65 K without applying an external magnetic field. We used the green function formalism and the Holstein–Primakoff transformation estimate to develop the spin-wave model translated by the Heisenberg Hamiltonian into our system. According to the developed model, the number of magnons, dispersion, Curie temperature, specific heat capacity, and susceptibility were calculated. To obtain this result, we used the results of the Fe ion concentration from 5% to 10.7% from [19], the number of atoms per unit volume 1 $\times {10}^{21}{cm}^{-3}$ from [11, 19, 38, 39], and the lattice constant of a = 6.48 $A^0$ from [31], which had also been used for the theoretical analysis.

2 Hamiltonian model of the system and Green’s function formalism

In the presence of an applied magnetic field $B_O$ oriented in the z-direction, the Hamiltonian of the Heisenberg ferromagnetic model is written as follows [56]:

$H=-{\displaystyle \sum }_{〈i,j〉}J\left(R_i-R_j\right){\widehat{S}}_i.{\widehat{S}}_j-g{\mu }_B{B}_O{\displaystyle \sum }_i{S}_{iz}.(1)$

Without a magnetic field applied to the system, H becomes as follows [58]:

$H=-{\displaystyle \sum }_{〈i,j〉}J\left(R_i-R_j\right){\widehat{S}}_i.{\widehat{S}}_j,(2)$

where the symbol $〈i,j〉$ implies a sum over all distinct pairs of nearest neighbors, and $S_i$ is the total angular momentum of the $i^{th}$ ion and is parallel to the magnetic moment of the ion rather than opposite to the moment. If we write ${\widehat{S}}_i.{\widehat{S}}_j$ in terms of x, y, and z components of the spin operators, the Hamiltonian becomes

$\mathrm{H}=-{\displaystyle \sum }_{〈i,j〉}{J}_{ij}\left({\widehat{S}}_{ix}{\widehat{S}}_{jx}+{\widehat{S}}_{iy}{\widehat{S}}_{jy}+{\widehat{S}}_{iz}{\widehat{S}}_{jz}\right)=-{\displaystyle \sum }_{〈i.j〉}{J}_{ij}(\left(\frac{1}{2}{{\widehat{S}}_i}^{+}{{\widehat{S}}_j}^{-}+{{\widehat{S}}_i}^{-}{{\widehat{S}}_j}^{+})+{\widehat{S}}_{iz}{\widehat{S}}_{jz}\right),(3)$

where ${\widehat{S}}_{ix}{\widehat{S}}_{jx}+{\widehat{S}}_{iy}{\widehat{S}}_{jy}=\frac{1}{2}{{\widehat{S}}_i}^{+}{{\widehat{S}}_j}^{-}+\frac{1}{2}{{\widehat{S}}_i}^{-}{{\widehat{S}}_j}^{+}.$

Notice that ${a_j}^{+}$, which creates one spin deviation on site j, acts like lowering the operator ${S_j}^{-},$ while $a_j$ acts, by destroying one spin deviation on j, like ${S_j}^{+}$.

Using the Holstein–Primakoff transformation to boson creation and annihilation operators ${a_j}^{+}$ and $a_j$, and substituting in Eq. 3, it can be written as follows:

$H=-S{\displaystyle \sum }_{〈i,j〉}{J}_{ij}\left\{\sqrt{1-\frac{{\widehat{n}}_i}{2S}}{a}_i{a_j}^{+}\sqrt{1-\frac{{\widehat{n}}_j}{2S}}+{a_i}^{+}\sqrt{1-\frac{{\widehat{n}}_i}{2S}}\sqrt{1-\frac{{\widehat{n}}_j}{2S}}{a}_j+S\left(1-\frac{{\widehat{n}}_i}{S}\right)\left(1-\frac{{\widehat{n}}_j}{S}\right)\right\}.(4)$

This H can be expressed as follows:

$H=E_O+H_O+H_1.(5)$

Here, $E_O$ is the ground state energy, $H_O$ is the bilinear in spin-wave variables and magnon without an interaction, and $H_1$ is the part of the Hamiltonian that is quadratic in the spin deviation creation and annihilation operators. However, it is developed in our system by the bilinear in spin-wave variables and magnon without an interaction.

$H_O$ is the bilinear in spin wave variable and magnon without an interaction, then $H_0$ can be written as

$H_0=-zS{\displaystyle \sum }_{jk}{J}_{ij}\left\{\left\{{\gamma }_k{b}_k{b_k}^{+}+{\gamma }_{-k}{b_k}^{+}{b}_k-2{b_k}^{+}{b}_k\right\}\right\}.(6)$

We introduce $\delta ,$ one of the nearest neighbor vectors connecting neighboring sites, and write $x_l=x_j+\delta$ in the summation; then, taking the term ${\displaystyle \sum }_j{J}_{ij}$ and considering the contact type of the interaction, we get the following [4]:

${\displaystyle \sum }_j{J}_{ij}={\displaystyle \sum }_{j}J\left({\overrightarrow{R}}_{ij}\right)=J{\displaystyle \sum }_j\delta \left(R_i{-R}_j\right).(7)$

Taking the average over j, we obtain

$<{\displaystyle \sum }_j\delta \left(R_i-R_j\right)>=x.(8)$

Substituting Eqs 7, Eqs 8 into Eq. 6, then we obtain Eq. 9 as follows:

$H_0=xzSJ{\displaystyle \sum }_{jk}\left\{{-\gamma }_k{b}_k{b_k}^{+}-{\gamma }_{-k}{b_k}^{+}{b}_k+2{b_k}^{+}{b}_k\right\}.(9)$

If the center of symmetry $\gamma -k={\gamma }_k.$ further, since ${\displaystyle \sum }_k{e}^{ik.R}=0$ unless R $=0$, it is apparent that ${\displaystyle \sum }_k{\gamma }_k=0$, for which

$H_0={\displaystyle \sum }_K{\omega }_k{b_k}^{+}{b}_k={\displaystyle \sum }_{K}2zxJS\left(1-{\gamma }_k\right){b_k}^{+}{b}_k.(10)$

For a long wavelength $\left[k.\delta \right]\ll 1$, in this region, we can expand $e^{ik.\delta }$ in powers of k. Therefore,

${\gamma }_k=z^{-1}{\displaystyle \sum }_{\delta }\left(1+ik.\delta -{\frac{\left(k.\delta \right)}{2}}^2+\dots \right).(11)$

Using ${\displaystyle \sum }_{\delta }1=z$ and ${\displaystyle \sum }_{\delta }\delta =0,$ the aforementioned expansion gives the following formula:

$\left(1-{\gamma }_k\right)\backsimeq \frac{1}{2z}{\displaystyle \sum }_{\delta }{\left(k.\delta \right)}^2.(12)$

For a simple cubic lattice $\left|\delta \right|=a$ and ${\displaystyle \sum }_{\delta }{\left(k.\delta \right)}^2=2k^2{a}^2$, Formula 10 is written as follows:

$H_0={\displaystyle \sum }_K{\omega }_k{b_k}^{+}{b}_k={\displaystyle \sum }_{K}2JxS{a}^2{k}^2{b_k}^{+}{b}_k.(13)$

Taking average over the impurity concentration, $H_0$ becomes $〈H_{magnon}〉$:

$〈H_{magnon}〉=〈{\displaystyle \sum }_{k}2JxS{a}^2{k}^2{b_k}^{+}{b}_k〉={\displaystyle \sum }_k{\widehat{n}}_k{\omega }_k,(14)$

where $n_k={b_k}^{+}{b}_k$ in the number of magnons in the state k,

${\omega }_k=2JxS{a}^2{k}^2.(15)$

Eq. 15 is the ferromagnetism magnon dispersion relation for the magnetic impurity concentration x.

For our present application, it is convenient to separate $\mathrm{G}\left(\mathrm{t},{\mathrm{t}}^{\prime }\right)$ into two parts that propagate a state forward or backward in time. Hence, in general, we define the retarded Green function and advanced Green’s function [59]:

${\mathrm{G}}_{\mathrm{r}}\left(\mathrm{t},{\mathrm{t}}^{\prime }\right)=\ll \mathrm{B}\left(\mathrm{t}\right),\mathrm{C}\left({\mathrm{t}}^{\prime }\right){\gg }_{\mathrm{r}}=-i\mathrm{\theta }\left(\mathrm{t}-{\mathrm{t}}^{\prime }\right)<\left[B\left(\mathrm{t}\right),\mathrm{C}\left({\mathrm{t}}^{\prime }\right)\right]>.(16)$

We consider the operators B = $b_k$ and C = ${b_k}^{+}$, then Formula 16 is written as follows:

${\mathrm{G}}_{\mathrm{k}{\mathrm{k}}^{\prime }}\left(\mathrm{t},{\mathrm{t}}^{\prime }\right)=\ll {\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right),{{\mathrm{b}}_{\mathrm{k}}}^{+}\left({\mathrm{t}}^{\prime }\right)\gg =-i\mathrm{\theta }\left(\mathrm{t}-{\mathrm{t}}^{\prime }\right)<\left[{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right),{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}\left({\mathrm{t}}^{\prime }\right)\right]>.(17)$

Assuming it is ${\left[\mathrm{b}\right.}_{\mathrm{k}}\left(\mathrm{t}\right),{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}\left({\mathrm{t}}^{\prime }\right)]={\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right){{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}\left({\mathrm{t}}^{\prime }\right)-\mathrm{\zeta }{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}\left({\mathrm{t}}^{\prime }\right)}^{+}{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right)={\mathrm{b}}_{\mathrm{k}}{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}-\mathrm{\zeta }{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}{\mathrm{b}}_{\mathrm{k}}$, $\zeta =\pm 1.$

Simplifying Eq. 17, we obtain the following:

$G_{k{k}^{\prime }}\left(t,t^{\prime }\right)=-i\theta \left(t,t^{\prime }\right)\left[<{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right){{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}\left({\mathrm{t}}^{\prime }\right)>-\mathrm{\zeta }<{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}\left({\mathrm{t}}^{\prime }\right)}^{+}{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right)>\right].(18)$

After different Formula 18 with respect to t, multiplying both sides of the result by i and substituting $\left.\begin{array}{c}{\widehat{\mathrm{H}}}_{magnon}={\displaystyle \sum }_{\mathrm{k}}{\mathrm{\omega }}_{\mathrm{k}}{{\mathrm{b}}_{\mathrm{k}}\left({\mathrm{t}}^{\prime }\right)}^{+}{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right)\\ i\frac{d}{dt}{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right)=\left[{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right),{\widehat{\mathrm{H}}}_{magnon}\right]\end{array}\right\}$, we obtain the following formula:

$\frac{d}{dt}{G}_{k{k}^{\prime }}\left(t,t^{\prime }\right)=\delta \left(t-t^{\prime }\right)<\left[{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right),{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}\left({\mathrm{t}}^{\prime }\right)\right]>-i\theta \left(t-t^{\prime }\right)\left\{<\left[{\mathrm{\omega }}_{\mathrm{k}}{\mathrm{b}}_{\mathrm{k}}\left(\mathrm{t}\right),{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}\left({\mathrm{t}}^{\prime }\right)\right]>\right\}.(19)$

Simplifying Eq. 18 using the Fourier transformation and considering k = k’, then Eq. 19 can be obtained as follows:

${\mathrm{G}}_{\mathrm{k}{\mathrm{k}}^{\prime }}\left(\mathrm{\omega }\right)=\frac{1}{2\mathrm{\pi }\left(\mathrm{\omega }-{\mathrm{\omega }}_{\mathrm{k}}\right)}.(20)$

When $\mathrm{\omega }-{\mathrm{\omega }}_{\mathrm{k}}$ = 0, we obtain the dispersion relation.

The correlation function $〈{{\mathrm{b}}_{{\mathrm{k}}^{\prime }}}^{+}{\mathrm{b}}_{\mathrm{k}}〉$ is related to the analytic property of Green’s function, written as follows:

$\left.〈{{\mathrm{b}}_{\mathrm{k}}}^{+}{\mathrm{b}}_{\mathrm{k}}〉=i\underset{\delta \to 0}{\mathit{lim}}i{\int }_{-\infty }^{\infty }\frac{{{〈〈b}_k,{b_k}^{+}〉〉}_{\omega +i\delta }-{{〈〈b}_k,{b_k}^{+}〉〉}_{\omega -i\delta }}{e^{\sigma \omega }-1}{e}^{\left(-i\omega \left\{t-t^{\prime }\right\}\right)}d\omega \right\}.(21)$

Let ω = ${\mathrm{\omega }}_{\mathrm{k}}$ be considered the dispersion relation, then simplifying Eq. 21, we obtain the following:

${〈{\mathrm{b}}_{\mathrm{k}}}^{+}{\mathrm{b}}_{\mathrm{k}}〉=\underset{\mathrm{\delta }\to 0}{\lim }\mathrm{i}\int \frac{\mathrm{\delta }\left({\mathrm{\omega }}_{\mathrm{k}}-{\mathrm{\omega }}_{\mathrm{k}}\right)}{{\mathrm{e}}^{\mathrm{\sigma }{\mathrm{\omega }}_{\mathrm{k}}}-1}d\omega =\frac{1}{{\mathrm{e}}^{\mathrm{\sigma }{\mathrm{\omega }}_{\mathrm{k}}}-1}.(22)$

Substituting Eq. 13 and $\sigma =\frac{1}{K_{B}T}$ in Eq. 22, we obtain the following:

${〈{\widehat{\mathrm{n}}}_{\mathrm{k}}〉=〈{\mathrm{b}}_{\mathrm{k}}}^{+}{\mathrm{b}}_{\mathrm{k}}〉=\frac{1}{{\mathrm{e}}^{\frac{2JxS{a}^2{k}^2}{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}}-1}.(23)$

The total number of magnons in all modes excited at temperature T can be calculated as follows:

${\displaystyle \sum }_k{\overline{n}}_k=\int D\left(\omega \right)n\left(\omega \right)d\omega .(24)$

$D\left(\omega \right)$ with frequency $d\omega$ at $\omega$ is calculated as follows:

$D\left(\omega \right)={\left(\frac{1}{2\pi }\right)}^3\left(4\pi k^2\right)\left(\frac{dk}{d\omega }\right).(25)$

Substituting Eqs 23, Eqs 25 into Eq. 24, we obtain the following:

${\displaystyle \sum }_k{\overline{n}}_k={\int }_0^{\infty }\frac{1}{{\mathrm{e}}^{\frac{2JxS{a}^2{k}^2}{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}}-1}{\left(\frac{1}{2\pi }\right)}^3\left(4\pi k^2\right)\left(\frac{dk}{d\omega }\right)d\omega =0.0587{\left(\frac{K_{B}T}{2JxS{a}^2}\right)}^{\frac{3}{2}}.(26)$

Eq. 26 gives us the number of reversed spins given by the ensemble average of the spin-wave occupancy numbers.

Thermal magnetization as a function of T is referred to as spontaneous magnetization; it is expressed as [57, 60]

${\mathrm{M}}_{\mathrm{S}}\left(\mathrm{T}\right)=\frac{g{\mu }_B{S}_Z}{V}=\frac{g{\mu }_B}{V}\left(NS-{\displaystyle \sum }_k{〈b_k}^{+}{b}_k〉\right)=M_s\left(0\right)-\frac{g{\mu }_B}{V}{\displaystyle \sum }_k〈{\widehat{n}}_k〉,(27)$

$M_S\left(T\right)=M_S\left(0\right)\left(1-\frac{1}{nSV}0.0587{\left(\frac{K_{B}T}{2JxS{a}^2}\right)}^{\frac{3}{2}}\right),(28)$

$\frac{M_S\left(T\right)}{M_S\left(0\right)}=1-\frac{1}{nSV}0.0587{\left(\frac{K_{B}T}{2JxS{a}^2}\right)}^{\frac{3}{2}}.(29)$

For a primitive unit cell, the aforementioned equation is expressed as follows:

$\frac{M_S\left(T\right)}{M_S\left(0\right)}=1-\frac{1}{nS}0.0587{\left(\frac{K_{B}T}{2JxS{a}^2}\right)}^{\frac{3}{2}}=1-{\left(\frac{T}{T_c}\right)}^{\frac{3}{2}}.(30)$

Eq. 30 indicates that reduced magnetization rapidly changes and is inversely proportional to temperature.

To find the Curie temperature, we assume that reduced magnetization becomes zero, and it is expressed as $\frac{M_S\left(T\right)}{M_S\left(0\right)}=0.$

$0=1-\frac{1}{nS}0.0587{\left(\frac{K_{B}T}{2JxS{a}^2}\right)}^{\frac{3}{2}}=1-{\left(\frac{T}{T_c}\right)}^{\frac{3}{2}}.(31)$

Rearranging it, we get the Curie temperature as follows:

$T_c=x\left(\frac{2JS}{K_B}\right){\left(\frac{nS{a}^3}{0.0587}\right)}^{\frac{2}{3}}.(32)$

If the external magnetic field is zero and if magnon–magnon interactions are neglected, then we can write the magnon frequency as ${\omega }_k=2xJS{a}^2{k}^2$ for small values of k.

The internal energy per unit volume associated with this excitation is given by [56]

$U=\frac{1}{V}{\displaystyle \sum }_k{\omega }_k〈{\widehat{n}}_k〉,(33)$

where $〈{\widehat{n}}_k〉=\frac{1}{{\mathrm{e}}^{\frac{2JxS{a}^2{k}^2}{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}}-1}=\frac{1}{{\mathrm{e}}^{{\mathrm{\omega }}_{\mathrm{k}}/⊝}-1}$, $⊝={\mathrm{K}}_{\mathrm{B}}\mathrm{T},$ and ${\omega }_k=2JxS{a}^2{k}^2.$

Converting the sum to an integral over K and simplifying it by part gives the following:

$U=\frac{1}{{\left(2\pi \right)}^3}{\displaystyle \underset{0}{\overset{\infty }{\int }}}{d}^{3}k\frac{{\omega }_k}{{\mathrm{e}}^{\frac{2JxS{a}^2{k}^2}{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}}-1}=\frac{1}{{\left(2\pi \right)}^3}{\displaystyle \underset{0}{\overset{\infty }{\int }}}{d}^{3}k\frac{D{k}^2}{e^{\raisebox{1ex}{$D{k}^2$}\!\left/ \!\raisebox{-1ex}{$⊝$}\right.}-1}=0.0456\frac{{\left(K_{B}T\right)}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\left(2JxS{a}^2\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}.(34)$

The heat capacity of magnons will be calculated as follows:

$c_{magnon}=\frac{\partial U}{\partial T}=\frac{\partial }{\partial T}\left(0.0456\frac{{\left(K_{B}T\right)}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\left(2JxS{a}^2\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right)=0.113\left(\frac{1}{{\left(2JxS{a}^2\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right){K_B}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{T}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.(35)$

The specific heat capacity of magnons will also be calculated as follows:

$C_{magnon}=\frac{c_{magnon}}{unitmass}=0.113\left(\frac{1}{{\left(2JxS{a}^2\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right){K_B}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{T}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}/K\mathrm{g}.(36)$

The basic equation of magnetization for ferromagnetic material as a Brillouin function is given by

$M\left(H,T\right)=N{\mu }_{B}S{B}_S\left(x\right),(37)$

where the Brillouin function that varies from −1 to 1 is defined as

$B_S\left(x\right)=\frac{2S+1}{2S}\coth \left(\frac{2S+1}{2S}x\right)-\frac{1}{2S}\coth \left(\frac{1}{2S}x\right)=\frac{1}{S}\left(S+\frac{1}{2}\right)\coth \left(S+\frac{1}{2}\right)x-\frac{1}{2}\coth \left(\frac{x}{2}\right).(38)$

For spontaneous magnetization,

$x=\frac{g{\mu }_B{H}_{eff}}{K_{B}T}=\frac{g{\mu }_B\left(H+\lambda M\right)}{K_{B}T}.(39)$

For using expanded power series expanded for $y\ll 1,\mathit{coth}y=\frac{e^y+e^{-y}}{e^y-e^{-y}}=\frac{1}{y}+\frac{1}{3}y,$

$\begin{array}{c}{\mathrm{B}}_{\mathrm{S}}\left(\mathrm{x}\right)=\frac{1}{\mathrm{S}}\left\{\left(\mathrm{S}+\frac{1}{2}\right)\left(\frac{1}{\left(\mathrm{S}+\frac{1}{2}\right)x}+\frac{1}{3}\left(\mathrm{S}+\frac{1}{2}\right)x\right)-\frac{1}{2}\left(\frac{2}{\mathrm{x}}+\frac{x}{6}\right)\right\}\\ =\frac{1}{S}\left\{\frac{1}{x}+\frac{1}{3}{\left(\mathrm{S}+\frac{1}{2}\right)}^{2}x-\frac{1}{x}-\frac{x}{12}\right\}=\frac{1}{3S}\left(S^{2}x+Sx+\frac{1}{4}x-\frac{1}{4}x\right)=\frac{x}{3}\left(S+1\right).\end{array}(40)$

Substituting Eqs 35, Eqs 36 into Eq. 33, we obtain

$\frac{M}{H}=\frac{N{g}^2{{\mu }_B}^2\frac{S\left(S+1\right)}{3K_B}}{\left(T-N{g}^2{{\mu }_B}^2\frac{S\left(S+1\right)}{3K_B}\lambda \right)}=\frac{C}{T-C\lambda }=\frac{C}{T-T_c}.(41)$

Since $N{g}^2{{\mu }_B}^2\frac{S\left(S+1\right)}{3K_B}$ = c and $g^2{{\mu }_B}^2\frac{S\left(S+1\right)}{3K_B}\lambda$ = $T_c,$

$\chi =\frac{M}{H}=\frac{C}{T-T_c}.(42)$

This is the Curie–Weiss law.

3 Results and discussion

In the previous section, we formulated the spin-wave model translated by Hamiltonian and explored the ferromagnetism dispersion, using Green function formalism change, and comparing the dispersion with the magnitude of the ferromagnetism magnons, Curie temperature, susceptibility, and specific heat capacity (In, Fe), Sb formulas have been obtained. In this section, we have used the following parameters to analyze and graphically describe the ferromagnetism parameters mentioned previously: $J_{nm}=10meV$;the lattice constant of an InSb $a=6.48A^o$; atom $S=\frac{5}{2}$; $k_B=0.08625meV/K$; Bohr magneton = ${\mu }_B=5.49\times {10}^{-23}J/T$, the Fe ion concentration x = 0.055–0.107; and the number of lattice points per unit volume n $\approx 1\times {10}^{27}{m}^{-3}$ [11, 20, 30, 56–60]. Finally, the are plotted based on the lab cod mat, and the findings of the study are summarized in relation to the previous study on the ferromagnetism property of diluted magnetic semiconductors.

The magnon magnetic order is obtained in In_1-xFe_xSb when the manganese ion concentration is 0.05–0.107. We calculated the Curie temperature with this concentration in Eq. 32 by substituting a numerical estimation constant, and the graph plotted of the Fe concentration range with the Curie temperature is illustrated in the following paragraphs.

Figure 1 shows that the Curie temperature of (In, Fe) Sb is linearly proportional to the iron ion concentration in the given range. It meant that (In, Fe) Sb has a ferromagnetic order only in the region of the iron ion concentration from 0.05 to 0.107 and the temperature less than 317.65 K. The minimum Curie temperature of ${\mathrm{I}\mathrm{n}}_{1-\mathrm{x}}{\mathrm{F}\mathrm{e}}_{\mathrm{x}}\mathrm{S}\mathrm{b}$ is 163.4 K when we use x = 0.05, and the maximum Curie temperature is also 317.65 K when we use x = 0.107. When the temperature reaches Curie’s temperature, the phase change takes place; it becomes par magnetism. The calculated curve fits the experimental results obtained [39, 40] and [57, 58].

FIGURE 1

FIGURE 1. Curie temperature versus Mn concentration impurity.

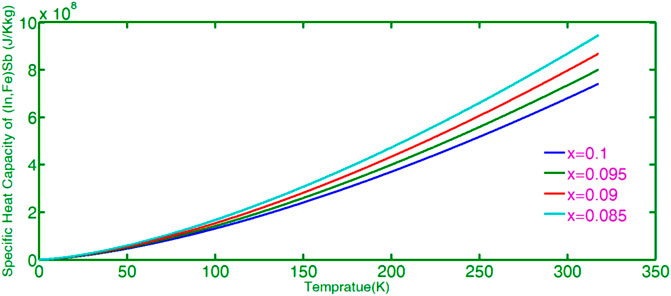
The specific heat capacity of the (In, Fe) Sb formula is expressed in Eq. 36 by substituting the numerical estimation constant in this equation; the graph of specific heat capacity versus temperature with a constant concentration of Fe impurity is plotted.

Figure 2 indicates that the internal energy and the specific heat capacity of the ferromagnetic order in In_1-xFe_xSb vanish when the temperature reaches the Curie temperature, which is 317.65 K. With a constant manganese ion concentration, the specific heat capacity is directly proportional to temperature ($T^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$), but it is inversely proportional to the manganese ion concentration ($x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$), with the temperature constant.

FIGURE 2

FIGURE 2. Specific heat capacity versus temperature with a constant concentration of impurity x.

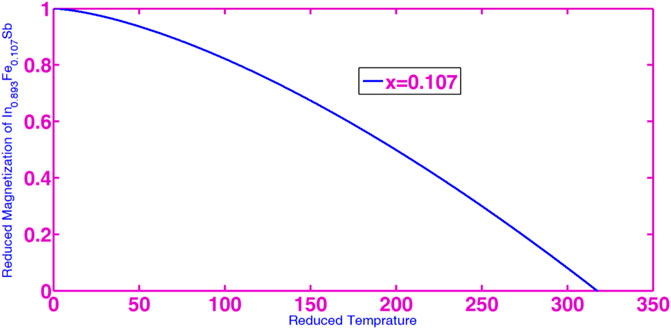
The reduced magnetization of the ferromagnetic magnon as a function of temperature is calculated in Eq. 34; we have plotted the graph.

As shown in Figure 3, the reduced magnetization rapidly changes and is inversely proportional to the reduced temperature, up to the Curie temperature. Thus, when the temperature approaches the Curie temperature, magnetization goes to zero. When the temperature is equal to 317.65 K, the $\frac{M_s\left(T\right)}{M_s\left(0\right)}$ becomes zero, that is, the spontaneous magnetization disappears. When the temperature is equal to 0 K, $\frac{M_s\left(T\right)}{M_s\left(0\right)}$ approaches 1, that is, the atomic magnetic moments alignment will be completely parallel. The calculated curves fit wonderfully well with the experimental results reported.

FIGURE 3

FIGURE 3. Reduced magnetization versus reduced temperature at constant x = 0.107.

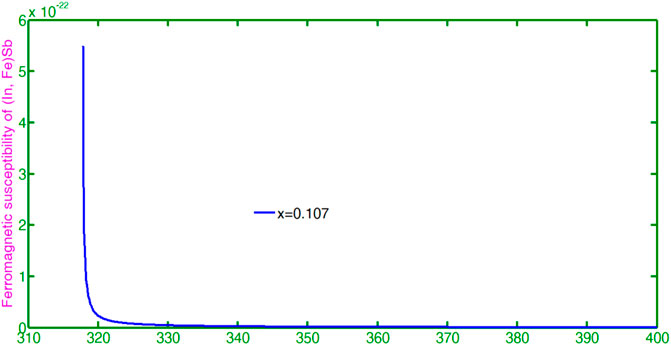
The ferromagnetic susceptibility of the (In, Fe) Sb formula is expressed in Eq. 42 by substituting the numerical estimation constant in this equation, and the ferromagnetic susceptibility of ${In}_{0.893}{Fe}_{0.107}Sb$ versus temperature is plotted.

As we observed in this figure, the susceptibility of the ferromagnetic magneton increases when the temperature decreases with a constant concentration of iron at a temperature greater than the Curie temperature. The temperature approaches 317.65 K on the right side, the susceptibility becomes infinite, and when the temperature is equal to 317.65 K, the ferromagnetic susceptibility of ${In}_{0.893}{Fe}_{0.107}Sb$ is undefined.

In this study, we used the spin-wave model of the Heisenberg Hamiltonian magnetic coupling interaction (J) without applying magnetic fields, electric fields, or chemical potential to get the Curie temperature of (In, Fe) Sb above room temperature, which is 317.65 K. If we used magnetic field, electric field, and chemical potential by using the RKKY interaction model, the Curie temperature of (In, Fe) Sb may be higher than that investigated in this study.

4 Conclusion

This study’s primary goal is to calculate the indium iron antimonide Curie temperature at temperatures higher than room temperature without the application of an external magnetic field. Indium iron antimonide material has a ferromagnetic Curie temperature that is lower than room temperature in the absence of an external magnetic field, according to earlier studies.

The unique aspect of our study is that we were able to determine the Curie temperature of the diluted (In, Fe) Sb n-type ferromagnetism without using an external magnetic field.

We developed the spin-wave model utilizing Hamiltonian translation and investigated the ferromagnetism dispersion. By comparing the dispersion with the magnitude of the ferromagnetism magnons, we were able to determine the Curie temperature, susceptibility, and specific heat capacity (In, Fe) Sb formula.

As the temperature approaches the Curie point, which is 317.65 K, the internal energy and specific heat capacity of the ferromagnetic order in ${In}_{0.893}{Fe}_{0.107}Sb$ disappear. This is shown by the relationship between specific heat capacity and temperature with a constant concentration of impurity x. With constant $x=0.107$, as illustrated in Figure 3, the relationship between reduced magnetization and lowered temperature is inversely proportional up to the Curie temperature. As seen in Figure 4, the susceptibility of ferromagnetic magnets increases as the temperature decreases while maintaining a constant iron concentration for temperatures higher than the Curie temperature.

FIGURE 4

FIGURE 4. Susceptibility versus temperature to ferromagnetism.

This n-type ferromagnetic semiconductor indium iron antimonide material exists at room temperature and is surprisingly used in modern and sophisticated spintronic devices.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary materials; further inquiries can be directed to the corresponding author.

Author contributions

BM participated in writing the initial draft. BA is responsible for editing the language. Finally, the final draft was authorized by both BA and BM. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors acknowledge the typesetters for this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Singh J, Electronic and optoelectronic properties of semiconductor structures. England: Cambridge University Press (2007).

Google Scholar

2. Adhikarya FLDMC. Innovative fields of ballistics & applied physics, 1. India: Allied Publishers (2012).

Google Scholar

3. Marius G. The physics of semiconductors: An introduction including devices and nanophysics. Berlin, Germany (2006).

Google Scholar

4. Tadesse G. The study of antiferromagnetic in diluted magnetic semiconductor" CDMNTE" (doctoral dissertation. Ethiopia: Addis Ababa University (2006).

Google Scholar

5. Vasilache V, Apostol NG, Lungu GA, Macovei D, Teodorescu CM. Manganese-based room temperature ferromagnetism in gallium arsenide. Optoelectronics Adv Materials-Rapid Commun (2012) 6(2012):1054–60.

Google Scholar

6. Prucnal S, Gao K, Skorupa I, Rebohle L, Vines L, Schmidt H, et al. Band-gap narrowing in Mn-doped GaAs probed by room-temperature photoluminescence. Phys Rev B (2015) 92(22):224407. doi:10.1103/PhysRevB.92.224407

CrossRef Full Text | Google Scholar

7. Tegegne MT. The study of diluted magnetic semiconductor: The case of manganese doped gallium nitride. World (2022) 17(1):1–10. doi:10.11648/j.wjap.20220701.11

CrossRef Full Text | Google Scholar

8. Rednic L, Deac IG, Dorolti E, Coldea M, Rednic V, Neumann M. Magnetic cluster developement in In1−x Mn x Sb semiconductor alloys. Cent Eur J Phys (2010) 8(4):620–7. doi:10.2478/s11534-009-0140-7

CrossRef Full Text | Google Scholar

9. Kulatov ET, Titov A, &Uspenskii YA. Ab initio study of electronic and magneto-optical properties of InSb: Mn and InAs: Mn. In: Solid state phenomena, 190. Trans Tech Publications Ltd (2012). p. 113–6. doi:10.4028/www.scientific.net/SSP.190.113

CrossRef Full Text | Google Scholar

10. Shamsul MA, Shahjahan M, &Rahman MM. Calculation of ferromagnetic state and critical temperature in transition metal doped III-V wurtzite semiconductors. J Bangladesh Acad Sci (2017) 41(2):217–25. doi:10.3329/jbas.v41i2.35499

CrossRef Full Text | Google Scholar

11. Chernet A. Enhancement of TC of the (Ga, Mn) as: Diluted magnetic semiconductor by photoinduced exchange coupling of the Mn2+ spins. Int J Phys Sci (2010) 5(6):671–4.

Google Scholar

12. Okano R, Hotta T, Takeda T, Araki K, Takase K, Anh LD, et al. Ferromagnetism induced by hybridization of Fe 3d orbitals with ligand InSb bands in n-type ferromagnetic semiconductor (In, Fe) Sb (2022). arXiv preprint arXiv:2202.04286.

Google Scholar

13. Kudrin AV, Lesnikov VP, Pavlov DA, Usov YV, Danilov YA, Dorokhin MV, et al. Formation of epitaxial pin structures on the basis of (In, Fe) Sb and (Ga, Fe) Sb diluted magnetic semiconductors layers. J Magnetism Magn Mater (2019) 487:165321. doi:10.1016/j.jmmm.2019.165321

CrossRef Full Text | Google Scholar

14. Mauger SJ, Bocquel J, Koenraad PM, Feeser CE, Parashar ND, Wessels BW. Mn doped InSb studied at the atomic scale by cross-sectional scanning tunneling microscopy. Appl Phys Lett (2015) 107(22):222102. doi:10.1063/1.4936754

CrossRef Full Text | Google Scholar

15. Bououdina M, Song Y, Azzaza S. Nano-structured diluted magnetic semiconductors (2023).

Google Scholar

16. Amente C, Dharamvir K. Ferromagnetism indiluted magnetic semiconductor (Ga, Mn) as quantum wires and quantum wells under the influence of photo-excitation and spin wave scattering. J Mod Phys (2013) 04:1563–8. doi:10.4236/jmp.2013.412192

CrossRef Full Text | Google Scholar

17. Zhou S. Dilute ferromagnetic semiconductors prepared by the combination of ion implantation with pulse laser melting. J Phys D: Appl Phys (2015) 48(26):263001. doi:10.1088/0022-3727/48/26/263001

CrossRef Full Text | Google Scholar

18. Chen W, Buyanova I. Handbook of spintronic semiconductors. Florida: CRC Press (2019). doi:10.1201/9780429065507

CrossRef Full Text | Google Scholar

19. Tu NT, Hai PN, Anh LD, Tanaka M. A new class of ferromagnetic semiconductors with high Curie temperatures (2017) arXiv preprint arXiv:1706.00735.2017 Jun 2.

Google Scholar

20. Dietl T, Fukushima AT, Bonanni A, Jamet M, Barski A, Kuroda S, et al. Spinodal nanodecomposition in semiconductors doped with transition metals. Rev Mod Phys (2015) 87(4):1311–77. doi:10.1103/RevModPhys.87.1311

CrossRef Full Text | Google Scholar

21. Hollingsworth J, Bandaru PR. Increasing Mn substitution in magnetic semiconductors through controlled ambient annealing processes. Mater Sci Eng B (2008) 151(2):152–6. doi:10.1016/j.mseb.2008.05.020

CrossRef Full Text | Google Scholar

22. Verma UP, Devi N, Sharma S, Jensen P. Spin-polarized first-principles study of ferromagnetism in zinc-blende In1−xMnxSb. The Eur Phys J B (2011) 81(4):381–6. doi:10.1140/epjb/e2011-20047-8

CrossRef Full Text | Google Scholar

23. Peters JA, Parashar ND, Rangaraju N, &Wessels BW. Magnetotransport properties of InMnSb magnetic semiconductor thin films. Phys Rev B (2010) 82(20):205207. doi:10.1103/PhysRevB.82.205207

CrossRef Full Text | Google Scholar

24. Khodaparast GA, Matsuda YH, Saha D, Sanders GD, Stanton CJ, Saito H, et al. Cyclotron resonance in ferromagnetic InMnAs and InMnSb. Phys Rev B (2013) 88(23):235204. doi:10.1103/PhysRevB.88.235204

CrossRef Full Text | Google Scholar

25. Yuan Y. The interplay between localization and magnetism in III-Mn-V dilute ferromagnetic semiconductors (2023).

Google Scholar

26. Jungwirth T, Sinova J, Mašek J, Kučera J, MacDonald AH. Theory of ferromagnetic (III, Mn) V semiconductors. Rev Mod Phys (2006) 78(3):809–64. doi:10.1103/revmodphys.78.809

CrossRef Full Text | Google Scholar

27. Iye Y, Oiwa A, Endo A, Katsumoto S, Matsukura F, Shen A, et al. Metal-insulator transition and magnetotransport in III-V compound diluted magnetic semiconductors. Mater Sci Eng B (1999) 63(1-2):88–95. doi:10.1016/s0921-5107(99)00057-4

CrossRef Full Text | Google Scholar

28. Yoon IT, Lee S, Shon Y, Lee SW, Kang TW. Magnetic and optical properties of self-organized InMnAs quantum dots. J Phys Chem Sol (2011) 72(3):181–4. doi:10.1016/j.jpcs.2010.12.008

CrossRef Full Text | Google Scholar

29. Anna K, Jacek AM. On origin of room temperature ferromagnetism in wide gap semiconductors. Физика низких темпеpатуp (2009) 35(1):70–4.

Google Scholar

30. Kuzmina K, Aronzon BA, Kochura AV, Lashkul AV, Lisunov KG, Lähderanta E, et al. Magnetotransport of indium antimonide doped with manganese. In: EPJ Web of Conferences, 75. France: EDP Sciences (2014). p. 05014.

CrossRef Full Text | Google Scholar

31. Rednic L. Electronic structure and magnetic properties of metallic systems based on rare earths and D transition elements. Doctoral dissertation (2010).

Google Scholar

32. Kochura AV, Aronzon BA, Lisunov KG, Lashkul AV, Sidorenko AA, De Renzi R, et al. Structural and magnetic properties of In1−xMnxSb: Effect of Mn complexes and MnSbnanoprecipitates. J Appl Phys (2013) 113(8):083905. doi:10.1063/1.4792652

CrossRef Full Text | Google Scholar

33. Danilov Y, Drozdov Y, Kudrin A, Vikhrova O, Zvonkov B, Sapozhnikov M, et al. Room-temperature ferromagnetic behaviour of InMnAs films grown by laser ablation technique. In: Journal of Physics: Conference Series, 200. United Kingdom: IOP Publishing (2010). 062025. doi:10.1088/1742-6596/200/6/062025.6

CrossRef Full Text | Google Scholar

34. Danilov YA, Demidov ES, Drosdov YN, Lesnikov VP, Podolskii VV, Sapozhnikov MV, et al. Ferromagnetism in epitaxial layers of gallium and indium antimonides and indium arsenide supersaturated by manganese impurity. J Magnetism Magn Mater (2006) 300(1):e24–7. doi:10.1016/j.jmmm.2005.10.141

CrossRef Full Text | Google Scholar

35. Blattner AJ, Wessels BW. Ferromagnetism in (In, Mn) as alloy thin films grown by metalorganic vapor phase epitaxy. Appl Surf Sci (2004) 221(1-4):155–9. doi:10.1016/s0169-4332(03)00873-0

CrossRef Full Text | Google Scholar

36. Kulbachinskii VA, Gurin PV, Vikhrova OV, Danilov YA, Zvonkov BN. Ferromagnetism and magnetotransport in GaAs structures with InAs quantum dot layer or InxGa1-xAs quantum well delta-doped with Mn and C, In Journal of Physics: Conference Series 100. United Kingdom: IOP Publishing (2008). 042025. No. 4.

CrossRef Full Text | Google Scholar

37. Shinya H, Fukushima T, Masago A, Sato K, Katayama-Yoshida H. First-principles prediction of the control of magnetic properties in Fe-doped GaSb and InSb. J Appl Phys (2018) 124(10):103902. doi:10.1063/1.5046912

CrossRef Full Text | Google Scholar

38. Kobayashi M, Minár J, Khan W, Borek S, Hai PN, Harada Y, et al. Minority-spin impurity band in n-type (in, Fe) as: A materials perspective for ferromagnetic semiconductors. Phys Rev B (2021) 103(11):115111. doi:10.1103/PhysRevB.103.115111

CrossRef Full Text | Google Scholar

39. Hai PN, Anh LD, Tanaka M. Iron-based n-type electron-induced ferromagnetic semiconductor (2011) arXiv preprint arXiv: 1106.0561.

Google Scholar

40. Nam Hai P, Duc Anh L, Mohan S, Tamegai T, Kodzuka M, Ohkubo T, et al. Growth and characterization of n-type electron-induced ferromagnetic semiconductor (In, Fe) as. Appl Phys Lett (2012) 101(18):182403. doi:10.1063/1.4764947

CrossRef Full Text | Google Scholar

41. Gui R, Jin H, Sun Y, Jiang X, Sun Z. Two-dimensional group-VA nanomaterials beyond black phosphorus: Synthetic methods, properties, functional nanostructures and applications. J Mater Chem A (2019) 7(45):25712–71. doi:10.1039/C9TA09582A

CrossRef Full Text | Google Scholar

42. Tu NT, Hai PN, Anh LD, Tanaka M. Heavily Fe-doped n-type ferromagnetic semiconductor (In,Fe) Sb with high Curie temperature and large magnetic anisotropy (2019). arXiv preprint arXiv:1901.01996. doi:10.7567/1882-0786/ab3f4b

CrossRef Full Text | Google Scholar

43. Zhang H, Xue L, Huang F, Wang S, Wang L, Liu , et al. A capillary biosensor for rapid detection of Salmonella using Fe-nanocluster amplification and smart phone imaging. Biosens Bioelectron (2019) 127:142–9. doi:10.1016/j.bios.2018.11.042

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Nishijima K, Tu NT, Tanaka M, Hai P. NFe delta-doped (In, Fe) Sb ferromagnetic semiconductor thin films for magnetic-field sensors with ultrahigh Hall sensitivity. J Cryst Growth (2019) 511:127–31. doi:10.1016/j.jcrysgro.2019.01.030

CrossRef Full Text | Google Scholar

45. Galkin NG, Goroshko DL, Chusovitin EA, Galkin KN, Dotsenko SA. Silicon-silicide quasi-zero dimensional heterostructures for silicon based photonics, opto- and thermoelectronics. physica status solidi (c) (2013) 10(12):1670–6. doi:10.1002/pssc.201300501

CrossRef Full Text | Google Scholar

46. Capper P, Elliott CT. Infrared detectors and emitters: Materials and devices. Springer Science & Business Media (2013).

Google Scholar

47. Gershon G, Avnon E, Brumer M, Freiman W, Karni Y, Niderman T, et al. 10um pitch family of InSb and XBn detectors for MWIR imaging. In: Infrared technology and applications XLIII 2017 may 16, 10177. United states: SPIE (2017). p. 334–49. doi:10.1117/12.2261703

CrossRef Full Text | Google Scholar

48. Camargo EG, Tokuo S, Goto H, Kuze N. Nondispersive infrared gas sensor using InSb-based photovoltaic-type Infrared Sensor. Sensors Mater (2014) 26(4):253–62. doi:10.18494/SAM.2014.970

CrossRef Full Text | Google Scholar

49. Agrawal N, Sarkar M, Nagar P, Dhruv DK. Structural and optical properties of Fe doped InSb bulk systems. Mater Today Proc (2022) 55:39–41. doi:10.1016/j.matpr.2021.12.098

CrossRef Full Text | Google Scholar

50. Singh J, Chandel T, Rajaram P. Structural, morphological and Raman studies of pulse electrosynthesised indium antimonide thin films. In: InAIP Conference Proceedings, 1675. New York, NY: AIP Publishing LLC (2015). 030008. No. 1. doi:10.1063/1.4929224

CrossRef Full Text | Google Scholar

51. Singh J, Poolla R. Study of InSb thin films grown on different substrates by the pulsed electrodeposition technique. J Mater Sci Mater Elect (2017) 28:13716–26. doi:10.1007/s10854-017-7216-8

CrossRef Full Text | Google Scholar

52. You JY, Gu B, Maekawa S, Su G. Microscopic mechanism of high-temperature ferromagnetism in Fe, Mn, and Cr-doped InSb, InAs, and GaSb magnetic semiconductors. Phys Rev B (2020) 102(9):094432. doi:10.1103/PhysRevB.102.094432

CrossRef Full Text | Google Scholar

53. Śliwa C. Superexchange dominates in magnetic topological insulators. Phys Rev B (2021) 104(22):L220404. doi:10.1103/PhysRevB.104.L220404

CrossRef Full Text | Google Scholar

54. Huang Z, Liu D, Mansikkamäki A, et al. Ferromagnetic kinetic exchange interaction in magnetic insulators. Phys Rev Res (2020) 2(3):033430. doi:10.1103/PhysRevResearch.2.033430

CrossRef Full Text | Google Scholar

55. Wang M, Fang C, Yao DX, Tan G, Harriger LW, Song Y, et al. Spin waves and magnetic exchange interactions in insulating Rb0.89Fe1.58Se2. Nat Commun (2011) 2(1):580–6. doi:10.1038/ncomms1573

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Quinn JJ, Yi KS. Solid state physics: Principles and modern applications. Springer Science & Business Media (2009). doi:10.1007/978-3-540-92231-5

CrossRef Full Text | Google Scholar

57. Ghosh S. Experimental studies on magnetic nano structures and anti-ferromagnetic thin films. United states: University of Florida (2012).

Google Scholar

58. Solomon Y. The study of ferro and antiferromagnetism. In: Diluted magnetic semiconductor (GaMnAs). LAP LAMBERT Academic Publishing (2018).

Google Scholar

59. Woldetsadik MB, Amente C, Singh P. Magnon specific heat and magnetic susceptibility of Fe/Gasb diluted magnetic semiconductor in the presence of applied electric field, magnetic field, and anisotropic energy. SINET: Ethiopian J Sci (2020) 43(2):125–33.

Google Scholar

60. Marino EC, Neto MB. Effective sublattice magnetization and Néel temperature in quantum antiferromagnets. Phys Rev B (2000) 62(1):142–5. doi:10.1103/PhysRevB.62.142

CrossRef Full Text | Google Scholar