Information geometry of Markov Kernels: a survey

Information geometry and Markov chains are two powerful tools used in modern fields such as finance, physics, computer science, and epidemiology. In this survey, we explore their intersection, focusing on the theoretical framework. We attempt to provide a self-contained treatment of the foundations without requiring a solid background in differential geometry. We present the core concepts of information geometry of Markov chains, including information projections and the pivotal information geometric construction of Nagaoka. We then delve into recent advances in the field, such as geometric structures arising from time reversibility, lumpability of Markov chains, or tree models. Finally, we highlight practical applications of this framework, such as parameter estimation, hypothesis testing, large deviation theory, and the maximum entropy principle.

1 Introduction

Markov chains are stochastic models that describe the probabilistic evolution of a system over time and have been successfully used in a wide variety of fields, including physics, engineering, and computer science. Conversely, information geometry is a mathematical framework that provides a geometric interpretation of probability distributions and their properties, with applications in diverse areas such as statistics, machine learning, and neuroscience. By combining the insights and methods from both fields, researchers have, in recent years, developed novel approaches for analyzing and modeling systems with time dependencies.

1.1 Outline and scope

As the fields of information geometry and Markov chains are broad, it is not possible to review all topics exhaustively, and we had to confine the scope of our survey to certain basic topics. Our focus will be on time-discrete, time-homogeneous Markov chains that take values from a finite alphabet. In particular, we will not cover time-continuous Markov chains [1, 2] nor discuss quantum information geometry or hidden Markov models [3, 4]. Our introduction to information geometry in the distribution setting will be limited to the basics. For a more comprehensive treatment, we recommend referring to the monographs [5, 6].

This survey is structured into five sections.

Section 1 is a brief introduction that provides an outline, lists the main concepts and results found in this survey, and clarifies its scope.

In Section 2, we lay out the notation that will be used throughout this paper and provide a primer on irreducible Markov chains and information geometry in the context of distributions. Along the way, we recall how to extend notions of entropy and Kullback–Leibler (KL) divergence from distributions to Markov chains.

In Section 3, following Nagaoka [7], we introduce a Fisher metric and a pair of dual affine connections on the set of irreducible stochastic matrices, which allows us to define the orthogonality of curves and parallel transport. We then proceed to define exponential families (e-families) and mixture families (m-families) of Markov chains. Importantly, the set of irreducible stochastic matrices is shown to form both an e-family and m-family, endowing it with the structure of a dually flat manifold. We explore minimality conditions for exponential families and chart transition maps between their natural and expectation parameters. Additionally, we define geodesics and their generalizations and conclude the section with a discussion on information projections and decomposition theorems. Specifically, similar to the distribution setting, the dual affine connections induce two notions of convexity, leading to Pythagorean identities.

In Section 4, we explore some recent developments in the field. First, we list and analyze the geometric properties of important subfamilies of stochastic matrices, such as symmetric or bistochastic Markov chains. The highlights of this section include the analysis of geometric properties induced by the time reversibility of Markov chains. This analysis leads to the establishment of the em-family structure of the reversible set, the derivation of closed-form expressions for reversible information projections, and the characterization of the reversible set as geodesic hulls of contained families. We continue this section by discussing some notable advancements in the context of data processing of Markov chains. Mirroring congruent embeddings in a distribution setting, we present a construction of embeddings of families of stochastic matrices that are congruent with respect to the lumping operation of Markov chains. These embeddings preserve the Fisher metric, the pair of dual affine connections, and the e-family structure. Additionally, we explore the establishment of a foliation structure on the manifold of lumpable stochastic matrices. Lastly, we conclude this section by presenting results in the context of tree models.

Section 5 is devoted to applications of the information geometry framework to large deviations, estimation theory, hypothesis testing, and the maximum entropy principle.

2 Preliminaries

2.1 Notation

Let $\mathcal{X}$ be a finite space of symbols. All vectors will be written as row vectors. A vector $v\in {\mathbb{R}}^{\mathcal{X}}$ is non-negative (resp., positive), indicated by v ≥ 0 (resp., v > 0), when v(x) ≥ 0 (resp., v(x) > 0) for any $x\in \mathcal{X}$. For $x\in \mathcal{X}$, the vector $e_x\in {\mathbb{R}}^{\mathcal{X}}$ is defined by $e_x(x^{\prime })=\delta \left[x=x^{\prime }\right]$ for $x^{\prime }\in \mathcal{X}$, where $\delta \left[\cdot \right]$ is the function that takes the value 1 when the predicate in the argument is true and 0 otherwise. For two vectors $u,v\in {\mathbb{R}}^{\mathcal{X}}$, the Hadamard product of u and v is defined by (u∘v)(x) = u(x)v(x), and we will also use the shorthand (u/v)(x) = u(x)/v(x). For convenience, for k vectors u₁, …, u_k, we write ${○}_{i=1}^k{u}_i=u_1\circ u_2\circ \dots \circ u_k$, and for vector u and positive real number α, u^∘α is such that u^∘α(x) = u(x)^α. For p ≥ 0, we write ${‖v‖}_p={\left({\sum }_{x\in \mathcal{X}}{\left|v(x)\right|}^p\right)}^{1/p}$. We denote by $\mathcal{P}(\mathcal{X})$ the set of all distributions over $\mathcal{X}$,

$\mathcal{P}\left(\mathcal{X}\right)\triangleq \left\{\mu \in {\mathbb{R}}^{\mathcal{X}}:\mu \ge 0,{‖\mu ‖}_1=1\right\},$

and ${\mathcal{P}}_{+}(\mathcal{X})\subset \mathcal{P}(\mathcal{X})$ refers to the positive subset. X ∼ μ means that the random variable X is distributed according to a distribution $\mu \in \mathcal{P}(\mathcal{X})$, and for $\mu ,\nu \in \mathcal{P}(\mathcal{X})$, the absolute continuity of ν with respect to μ is denoted by ν ≪ μ.

2.2 Irreducible Markov chains

A time-discrete, time-homogeneous Markov chain is a random process $X={\left\{X_t\right\}}_{t\in \mathbb{N}}$ that takes values on the state space $\mathcal{X}$ and satisfies the Markov property. Namely, for t ≥ 2 and for any $x_1,\dots ,x_t,x_{t+1}\in \mathcal{X}$,

${\mathbb{P}}_{\mu }\left(X_{t+1}=x_{t+1}|X_t=x_t,\dots ,X_1=x_1\right)=\mathbb{P}\left(X_{t+1}=x_{t+1}|X_t=x_t\right),$

with $\mathbb{P}\left(X_1=x_1\right)=\mu (x_1)$ for an initial distribution $\mu \in \mathcal{P}(\mathcal{X})$. The transition probabilities of the process can be organized in a row-stochastic matrix P, where $P(x,x^{\prime })=\mathbb{P}\left(X_{t+1}=x^{\prime }|X_t=x\right)$. We write X ∼ (μ, P) for the Markov chain started from μ and with transition matrix P. Let the vector space $\mathcal{F}(\mathcal{X})\triangleq {\mathbb{R}}^{{\mathcal{X}}^2}$, whose elements can be conveniently represented by real square matrices of size $\left|\mathcal{X}\right|$, simultaneously understood as linear operators on ${\mathbb{R}}^{\mathcal{X}}$. We introduce the set of all row-stochastic matrices over the space $\mathcal{X}$,

$\mathcal{W}\left(\mathcal{X}\right)\triangleq \left\{P\in \mathcal{F}\left(\mathcal{X}\right):\forall x\in \mathcal{X},e_{x}P\in \mathcal{P}\left(\mathcal{X}\right)\right\}.(1)$

As we assume $\left|\mathcal{X}\right|<\infty$, for any member P of $\mathcal{W}(\mathcal{X})$, there exists a fixed point $\pi \in \mathcal{P}(\mathcal{X})$ such that πP = π, and we call π a stationary distribution for P. Let $\mathcal{E}\subset {\mathcal{X}}^2$ define the set of positive probability transitions on the state space. When $(\mathcal{X},\mathcal{E})$ is a fully connected digraph, we say that P is irreducible. Algebraically, this means that for any pair of states $x,x^{\prime }\in \mathcal{X}$, there exists $p\in \mathbb{N}$ such that P^p(x, x′) > 0, or less tersely, there exists a path on the graph $(\mathcal{X},\mathcal{E})$ from x to x′. When P defines an irreducible Markov chain, the stationary distribution π is unique and positive. Moreover, when the initial distribution μ = π, we say that the chain is stationary, write ${\mathbb{P}}_{\pi }\left(\cdot \right)$ for probability statements over a stationary trajectory and X ∼ P as a shorthand for X ∼ (π, P). We denote the irreducible set:

$\mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\triangleq \left\{P\in \mathcal{W}\left(\mathcal{X}\right):P\text{\hspace{0.17em}is\hspace{0.17em}irreducible\hspace{0.17em}over\hspace{0.17em}}\left(\mathcal{X},\mathcal{E}\right)\right\}.$

It will also be convenient to define $\mathcal{F}(\mathcal{X},\mathcal{E})$, the real functions over $\mathcal{E}$, and identify this set with all functions over ${\mathcal{X}}^2$ that are null outside of $\mathcal{E}$. Note that $\mathcal{F}(\mathcal{X},\mathcal{E})$ can be endowed with the structure of a $\left|\mathcal{E}\right|$-dimensional vector space. We write ${\mathcal{F}}_{+}(\mathcal{X},\mathcal{E})\subset \mathcal{F}(\mathcal{X},\mathcal{E})$ for the positive subset. For $n\in \mathbb{N}$, the probability of observing a stationary path x₁ → x₂ → ⋯ → x_n induced from a π-stationary P is given by

$Q^{\left(n\right)}\left(x_1,x_2,\dots ,x_n\right)\triangleq {\mathbb{P}}_{\pi }\left(X_1=x_1,\dots ,X_n=x_n\right)=\pi \left(x_1\right)\prod _{t=1}^{n-1}P\left(x_t,x_{t+1}\right).(2)$

In particular,

$Q\triangleq Q^{\left(2\right)}\in \mathcal{P}\left({\mathcal{X}}^2\right)$

is called the edge measure pertaining to P. Observe that the map from an irreducible transition matrix P to its edge measure is one-to-one (see, e.g., [8]) and that the set of all edge measures $\mathcal{Q}(\mathcal{X},\mathcal{E})$ can be expressed as

$\mathcal{Q}\left(\mathcal{X},\mathcal{E}\right)=\left\{Q\in \mathcal{P}\left({\mathcal{X}}^2\right)\cap {\mathcal{F}}_{+}\left(\mathcal{X},\mathcal{E}\right):{\displaystyle \sum _{x^{\prime }\in \mathcal{X}}}Q\left(x,x^{\prime }\right)={\displaystyle \sum _{x^{\prime }\in \mathcal{X}}}Q\left(x^{\prime },x\right),\forall x\in \mathcal{X}\right\}.(3)$

We refer the reader to Levin et al. [9] for a thorough treatment of Markov chains.

2.3 Entropy and divergence rates for Markov chains

Let us first recall the definition of the Shannon entropy of a random variable. We let $\mu \in \mathcal{P}(\mathcal{X})$ and X ∼ μ. The entropy H of the random variable X, which measures the average level of surprise inherent to the possible outcomes, is defined by

$H\left(X\right)=-{\displaystyle \sum _{x\in \mathcal{X}}}\mu \left(x\right)\log \mu \left(x\right),$

and where by convention 0 log 0 = 0. The entropy rate of a stationary stochastic process $X={(X_t)}_{t\in \mathbb{N}}$ corresponds to the number of bits to describe one random variable in a stochastic process averaged over time. Namely,

$H\left(X\right)\triangleq \underset{n\to \infty }{\lim }\frac{1}{n}H\left(X_1,X_2,\dots ,X_n\right),(4)$

where for any $n\in \mathbb{N}$, H(X₁, X₂, …, X_n) is the joint entropy of the random variables X₁, X₂, …, X_n. Particularly, when X forms an irreducible Markov chain with transition matrix $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ and stationary distribution π, the entropy rate can be written as

$H\left(X\right)=-{\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}Q\left(x,x^{\prime }\right)\log P\left(x,x^{\prime }\right),$

where Q is the edge measure pertaining to P. In other words, the entropy rate of the process is computed from P only. We can thus overload H to define

$\begin{array}{cc}\hfill H:\mathcal{W}\left(\mathcal{X},\mathcal{E}\right)& \to {\mathbb{R}}_{+}\hfill \\ \hfill P& \mapsto H\left(P\right)=H\left(X\right),\text{\hspace{0.17em}for}X\sim P.\hfill \end{array}$

For two random variables X ∼ μ, X′ ∼ μ′ with $\mu ,{\mu }^{\prime }\in \mathcal{P}(\mathcal{X})$, we define the Kullback–Leibler divergence from X′ to X by

$D\left(X\Vert X^{\prime }\right)\triangleq \left\{\begin{array}{cc}{\sum }_{x\in \mathcal{X}}\mu \left(x\right)\log \frac{\mu \left(x\right)}{{\mu }^{\prime }\left(x\right)}\hfill & \text{\hspace{0.17em}when\hspace{0.17em}}\mu \ll {\mu }^{\prime },\hfill \\ \infty \hfill & \text{\hspace{0.17em}otherwise}.\hfill \end{array}\right.(5)$

Extending the aforementioned definition to Markov processes, the information divergence rate [10] (see also [73, Section 3.5]) of $X\sim P\in \mathcal{W}(\mathcal{X},\mathcal{E})$, from another chain $X^{\prime }\sim P^{\prime }\in \mathcal{W}(\mathcal{X},{\mathcal{E}}^{\prime })$, is given by

$\begin{array}{cc}\hfill D\left(X\Vert X^{\prime }\right)& =\underset{n\to \infty }{\lim }\frac{1}{n}D\left(X_1,X_2,\dots ,X_n\Vert X_1^{\prime },X_2^{\prime },\dots ,X_n^{\prime }\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}{\sum }_{\left(x,x^{\prime }\right)\in \mathcal{E}}Q\left(x,x^{\prime }\right)\log \frac{P\left(x,x^{\prime }\right)}{P^{\prime }\left(x,x^{\prime }\right)}\hfill & \text{\hspace{0.17em}when\hspace{0.17em}}\mathcal{E}\subset {\mathcal{E}}^{\prime },\hfill \\ \infty \hfill & \text{\hspace{0.17em}otherwise,}\hfill \end{array}\right.\hfill \end{array}$

which is also agnostic on initial distributions, inviting us to lift the definition of D to stochastic matrices:

$\begin{array}{cc}\hfill D:\mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\times \mathcal{W}\left(\mathcal{X},{\mathcal{E}}^{\prime }\right)& \to {\mathbb{R}}_{+}\cup \left\{\infty \right\}\hfill \\ \hfill P,P^{\prime }& \mapsto D\left(X\Vert X^{\prime }\right)\text{\hspace{0.17em}for\hspace{0.17em}}X\sim P\text{\hspace{0.17em}and\hspace{0.17em}}{X}^{\prime }\sim P^{\prime }.\hfill \end{array}(6)$

2.4 Information geometry

We briefly introduce basic concepts related to information geometry in the context of distributions. The central idea is to regard ${\mathcal{P}}_{+}(\mathcal{X})$ as a $(\left|\mathcal{X}\right|-1)$-dimensional smooth manifold and statistical models, i.e., parametric families of distributions $\mathcal{M}={\left\{{\mu }_{\theta }\right\}}_{\theta \in \mathrm{\Theta }\subset {\mathbb{R}}^d}$, as smooth submanifolds of ${\mathcal{P}}_{+}(\mathcal{X})$. At each point $\mu \in {\mathcal{P}}_{+}(\mathcal{X})$, we define a (0,2)-tensor,

$\begin{array}{c}{\mathfrak{g}}_{\mu }:T_{\mu }{\mathcal{P}}_{+}\left(\mathcal{X}\right)\times T_{\mu }{\mathcal{P}}_{+}\left(\mathcal{X}\right)\to \mathbb{R}\hfill \\ U_{\mu },V_{\mu }\mapsto {\mathfrak{g}}_{\mu }\left(U_{\mu },V_{\mu }\right)={\displaystyle \sum _{x\in \mathcal{X}}}\mu \left(x\right)\left(U_{\mu }\log \mu \left(x\right)\right)\left(V_{\mu }\log \mu \left(x\right)\right),\hfill \end{array}$

where $T_{\mu }{\mathcal{P}}_{+}(\mathcal{X})$ is the tangent plane at the point μ, and U_μ log  μ(x) is the directional derivative of the $C^{\infty }({\mathcal{P}}_{+}(\mathcal{X}))$ function, μ↦ log  μ(x) with respect to the tangent vector U_μ. This leads to the definition of a Riemannian metric, termed Fisher metric [5, Section 2.2]:

$\begin{array}{c}\mathfrak{g}:\mathrm{\Gamma }\left(T{\mathcal{P}}_{+}\left(\mathcal{X}\right)\right)\times \mathrm{\Gamma }\left(T{\mathcal{P}}_{+}\left(\mathcal{X}\right)\right)\to C^{\infty }\left({\mathcal{P}}_{+}\left(\mathcal{X}\right)\right)\hfill \\ U,V\mapsto \mathfrak{g}\left(U,V\right):{\mathcal{P}}_{+}\left(\mathcal{X}\right)\to \mathbb{R},\mu \mapsto \mathfrak{g}\left(U,V\right)\left(\mu \right)={\mathfrak{g}}_{\mu }\left(U_{\mu },V_{\mu }\right),\hfill \end{array}$

where $\mathrm{\Gamma }(T{\mathcal{P}}_{+}(\mathcal{X}))$ is the set of all vector fields [5, Section 1.3] and $C^{\infty }({\mathcal{P}}_{+}(\mathcal{X}))$ the set of all smooth real functions on ${\mathcal{P}}_{+}(\mathcal{X})$. Letting $\theta :\mathcal{M}\to \mathrm{\Theta }\subset \mathbb{R}$ be a chart map¹, μ_θ denote the distribution at coordinates θ = (θ¹, …, θ^d), and ∂_i = ∂ ⋅/∂θⁱ, we write ${({\partial }_i)}_{i\in [d]}$ for the θ-induced basis of $T_{{\mu }_{\theta }}{\mathcal{P}}_{+}(\mathcal{X})$. We can express the Fisher metric at coordinates θ as

${\mathfrak{g}}_{ij}\left(\theta \right)={\displaystyle \sum _{x\in \mathcal{X}}}{\mu }_{\theta }\left(x\right){\partial }_i\log {\mu }_{\theta }\left(x\right){\partial }_j\log {\mu }_{\theta }\left(x\right).$

In addition to $\mathfrak{g}$, we define a pair of affine connections by their associated covariant derivatives [5, Chapter 1, (1.38)]:

${\nabla }^{(e)},{\nabla }^{(m)}:\mathrm{\Gamma }\left(T{\mathcal{P}}_{+}\left(\mathcal{X}\right)\right)\times \mathrm{\Gamma }\left(T{\mathcal{P}}_{+}\left(\mathcal{X}\right)\right)\to \mathrm{\Gamma }\left(T{\mathcal{P}}_{+}\left(\mathcal{X}\right)\right).$

In the parametrization θ, the connections are specified by their coefficients (Christoffel symbols):

$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_{ij,k}^{(e)}\left(\theta \right)& \triangleq {\mathfrak{g}}_{{\mu }_{\theta }}\left({\nabla }_{{\partial }_i}^{(e)}{\partial }_j,{\partial }_k\right)={\displaystyle \sum _{x\in \mathcal{X}}}{\mu }_{\theta }\left(x\right){\partial }_i{\partial }_j\log {\mu }_{\theta }\left(x\right){\partial }_k{\mu }_{\theta }\left(x\right),\hfill \\ \hfill {\mathrm{\Gamma }}_{ij,k}^{(m)}\left(\theta \right)& \triangleq {\mathfrak{g}}_{{\mu }_{\theta }}\left({\nabla }_{{\partial }_i}^{(m)}{\partial }_j,{\partial }_k\right)={\displaystyle \sum _{x\in \mathcal{X}}}{\mu }_{\theta }\left(x\right){\partial }_i{\partial }_j{\mu }_{\theta }\left(x\right){\partial }_k\log {\mu }_{\theta }\left(x\right),\hfill \end{array}$

where ${\nabla }_{{\partial }_i}^{(e)}{\partial }_j$ is the covariant derivative of ∂_j with respect to ∂_i. The canonical divergence associated with $\mathfrak{g},{\nabla }^{(e)}$ and ∇^(m) is the Kullback–Leibler divergence (5). The connections ∇^(e) and ∇^(m) are conjugate [5, Chapter 3, (3.1)] in the sense where for any vector fields $U,V,W\in \mathrm{\Gamma }(T{\mathcal{P}}_{+}(\mathcal{X}))$,

$U\mathfrak{g}\left(V,W\right)=\mathfrak{g}\left({\nabla }_U^{(e)}V,W\right)+\mathfrak{g}\left(V,{\nabla }_U^{(m)}W\right).$

As a consequence, the curvature tensors associated with ∇^(e), ∇^(m) vanish simultaneously. In particular, they vanish for ${\mathcal{P}}_{+}(\mathcal{X})$, and we say that the manifold is dually flat. A complete review of the distribution setting, including exponential and mixture families, is outside the scope of this survey. We refer the reader to Amari and Nagaoka [5] for a complete treatment of the topic.

3 The dually flat manifold of irreducible stochastic matrices

Similar to the distributional setting, we regard $\mathcal{W}(\mathcal{X},\mathcal{E})$, the set of irreducible stochastic matrices over some prescribed fully connected digraph $(\mathcal{X},\mathcal{E})$, as a smooth manifold, on which we introduce a Riemannian metric together with a dually flat structure (Section 2.3). In turn, we will define exponential and mixture families of stochastic matrices. We will further examine notions of geodesic convexity and information projections.

3.1 The information manifold

Our first order of business is to establish a dually flat structure on the set of stochastic matrices, following Nagaoka [7]. A smooth manifold structure can be established on $\mathcal{W}(\mathcal{X},\mathcal{E})$, using the map introduced by Nagaoka [7, p.2], reported in (15). One possible construction is based on the definition of the informational divergence between two Markov processes at (6) and gives rise to a metric and dual affine connections [11, 12]. We proceed to confirm that while the structure can be defined without invoking asymptotic notions, the obtained Fisher metric and affine connections are indeed asymptotically consistent with their distributional counterparts for path measures.

3.1.1 Divergence as a general contrast function

Recall the definition of the information divergence from one stochastic matrix $P^{\prime }\in \mathcal{W}(\mathcal{X},{\mathcal{E}}^{\prime })$ to another $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ given at (6). We henceforth focus on the setting where the supports are identical $\mathcal{E}={\mathcal{E}}^{\prime }$; that is, stochastic matrices P, P′ belong to $\mathcal{W}(\mathcal{X},\mathcal{E})$ and $D\left(P\Vert P^{\prime }\right)<\infty$. We are interested in parametric families of irreducible matrices. Namely, for some open and connected parameter space $\mathrm{\Theta }\subset {\mathbb{R}}^d$, we define

$\mathcal{V}=\left\{P_{\theta }:\theta \in \mathrm{\Theta }\right\}\subset \mathcal{W}\left(\mathcal{X},\mathcal{E}\right),$

and regard $\mathcal{V}$ as a smooth submanifold of $\mathcal{W}(\mathcal{X},\mathcal{E})$ with a global coordinate system θ. For $P,P^{\prime }\in \mathcal{V}$, for simplicity, let us write θ = (θ¹, …, θ^d) = θ(P), θ′ = θ(P′), ${\partial }_i=\partial /{\partial }_{{\theta }^i}$, and ${\partial }_i^{\prime }=\partial /{\partial }_{{\theta }^{\prime i}}$ and use the shorthand $D\left(\theta \Vert {\theta }^{\prime }\right)=D\left(P_{\theta }\Vert P_{{\theta }^{\prime }}\right)$. The information divergence rate $D:\mathcal{V}\times \mathcal{V}\to {\mathbb{R}}_{+}$ we defined in (6) is C³ and satisfies the following properties of a contrast function:

(i) $D\left(\theta \Vert {\theta }^{\prime }\right)\ge 0$ for any θ, θ′ ∈ Θ (non-negativity).

(ii) $D\left(\theta \Vert {\theta }^{\prime }\right)=0$ if and only if θ = θ′ (identity of indiscernibles).

(iii) ${\partial }_{i}D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }}={\partial }_j^{\prime }D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }}=0$ for any i, j ∈ [d] (vanishing gradient on the diagonal).

(iv) $-{\partial }_i{\partial }_j^{\prime }D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }}={\partial }_i^{\prime }{\partial }_j^{\prime }D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }}={\partial }_i{\partial }_{j}D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }}$ is positive definite.

We call

$\begin{array}{cc}\hfill D^{*}:\mathcal{V}\times \mathcal{V}& \to \mathbb{R}\hfill \\ \hfill \left(P,P^{\prime }\right)& \mapsto D^{*}\left(\theta \Vert {\theta }^{\prime }\right)=D\left({\theta }^{\prime }\Vert \theta \right),\hfill \end{array}$

the dual divergence of D.

3.1.2 Fisher metric and dual affine connections

From any divergence function D on a manifold $\mathcal{V}$ verifying the aforementioned properties (i), (ii), (iii), and (iv), one can construct a conjugate connection manifold:

$\left(\mathcal{V},\mathfrak{g},\nabla ,{\nabla }^{*}\right),$

where the Riemannian metric $\mathfrak{g}$ and Christoffel symbols of ∇ and ∇^* are expressed in the chart $\theta :\mathcal{V}\to \mathrm{\Theta }$ and for any i, j, k ∈ [d] as

$\begin{array}{cc}\hfill {\mathfrak{g}}_{ij}\left(\theta \right)& ={\mathfrak{g}}_{P_{\theta }}\left({\partial }_i,{\partial }_j\right)=-{\partial }_i{\partial }_j^{\prime }D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }},\hfill \\ \hfill {\mathrm{\Gamma }}_{ij,k}\left(\theta \right)& ={\mathfrak{g}}_{P_{\theta }}\left({\nabla }_{{\partial }_i}^{(e)}{\partial }_j,{\partial }_k\right)=-{\partial }_i{\partial }_j{\partial }_k^{\prime }D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }},\hfill \\ \hfill {\mathrm{\Gamma }}_{ij,k}^{*}\left(\theta \right)& ={\mathfrak{g}}_{P_{\theta }}\left({\nabla }_{{\partial }_i}^{(m)}{\partial }_j,{\partial }_k\right)=-{\partial }_i^{\prime }{\partial }_j^{\prime }{\partial }_{k}D\left(\theta \Vert {\theta }^{\prime }\right){\left.\right|}_{\theta ={\theta }^{\prime }}.\hfill \end{array}(7)$

As the metric and connections are derived from the KL divergence, they all depend solely on the transition matrices and are, in particular, agnostic of initial distributions. From calculations, we obtain the Fisher metric [7, (9)]:

$\begin{array}{c}\hfill {\mathfrak{g}}_{ij}\left(\theta \right)={\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}{Q}_{\theta }\left(x,x^{\prime }\right){\partial }_i\log P_{\theta }\left(x,x^{\prime }\right){\partial }_j\log P_{\theta }\left(x,x^{\prime }\right),\end{array}(8)$

and the coefficients for the pair of torsion-free affine connections ∇^(e) (e-connection) and ∇^(m) (m-connection) [7, (19, 20)]:

$\begin{array}{c}\hfill {\mathrm{\Gamma }}_{ij,k}^{(e)}\left(\theta \right)={\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}{\partial }_i{\partial }_j\log P_{\theta }\left(x,x^{\prime }\right){\partial }_k{Q}_{\theta }\left(x,x^{\prime }\right),\\ \hfill {\mathrm{\Gamma }}_{ij,k}^{(m)}\left(\theta \right)={\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}{\partial }_i{\partial }_j{Q}_{\theta }\left(x,x^{\prime }\right){\partial }_k\log P_{\theta }\left(x,x^{\prime }\right).\end{array}(9)$

On the one hand, the metric encodes notions of distance and angles on the manifold. In particular, the information divergence D locally corresponds to the Fisher metric. In other words, for $\theta \in \mathrm{\Theta }\subset {\mathbb{R}}^d$ and $\delta \theta \in {\mathbb{R}}^d$ such that θ + δθ ∈ Θ,

$\begin{array}{cc}\hfill D\left(\theta +\delta \theta \Vert \theta \right)& =\frac{1}{2}{\displaystyle \sum _{i,j\in \left[d\right]}}\delta {\theta }^i\delta {\theta }^j{\partial }_i^{\prime }{\partial }_j^{\prime }D\left({\theta }^{\prime }\Vert \theta \right){|}_{{\theta }^{\prime }=\theta }+o\left({‖\delta \theta ‖}_2^2\right)=\frac{1}{2}\delta \theta \mathfrak{g}\left(\theta \right)\delta {\theta }^{⊺}+o\left({‖\delta \theta ‖}_2^2\right),\hfill \\ \hfill D\left(\theta \Vert \theta +\delta \theta \right)& =\frac{1}{2}{\displaystyle \sum _{i,j\in \left[d\right]}}\delta {\theta }^i\delta {\theta }^j{\partial }_i^{\prime }{\partial }_j^{\prime }D\left(\theta \Vert {\theta }^{\prime }\right){|}_{{\theta }^{\prime }=\theta }+o\left({‖\delta \theta ‖}_2^2\right)=\frac{1}{2}\delta \theta \mathfrak{g}\left(\theta \right)\delta {\theta }^{⊺}+o\left({‖\delta \theta ‖}_2^2\right).\hfill \end{array}$

Consider two curves $\gamma ,\sigma :\mathbb{R}\to \mathcal{V}$, and suppose that they intersect at some point $P_0\in \mathcal{V}$, achieved without loss of generality at γ(0) and σ(0). We define the angle between the curves γ and σ at P₀ as the angle formed by the two curves in the tangent space at P₀:

${\mathfrak{g}}_{P_0}\left(\dot{\gamma }\left(0\right),\dot{\sigma }\left(0\right)\right),$

and we will say that the two curves are orthogonal at P₀ when the inner product is null. On the other hand, affine connections define notions of straightness on the manifold. The fact that the connections are coupled with the metric $\mathfrak{g}$ introduces a generalization of the invariance of the inner product under the parallel translation of Euclidean geometry. Letting ${\mathrm{\Pi }}_{\gamma }^{(e)},{\mathrm{\Pi }}_{\gamma }^{(m)}:T_P\mathcal{V}\to T_{P^{\prime }}\mathcal{V}$ denote parallel translations along a curve γ from P to P′ with respect to ∇^(e) and ∇^(m), for any $U,V\in T_P\mathcal{V}$,

${\mathfrak{g}}_{P^{\prime }}\left({\mathrm{\Pi }}_{\gamma }^{\left(e\right)}\left(U\right),{\mathrm{\Pi }}_{\gamma }^{\left(m\right)}\left(V\right)\right)={\mathfrak{g}}_P\left(U,V\right).$

3.1.3 Asymptotic consistency with information rates

Recall from (2) that a stationary Markovian trajectory has a probability described by the path measure Q⁽ⁿ⁾. For every $n\in \mathbb{N}$, one can consider the manifold ${\mathcal{Q}}^{(n)}\subset \mathcal{P}({\mathcal{X}}^n)$ of all path measures of length n. Computing the limit of the metric and connection coefficients [7, 13],

$\begin{array}{cc}\hfill \underset{n\to \infty }{\lim }\frac{1}{n}{\mathfrak{g}}_{ij}^{\left[n\right]}\left(\theta \right)& ={\mathfrak{g}}_{ij}\left(\theta \right),\hfill \\ \hfill \underset{n\to \infty }{\lim }\frac{1}{n}{\mathrm{\Gamma }}_{ij,k}^{\left[n\right],\left(e\right)}\left(\theta \right)& ={\mathrm{\Gamma }}_{ij,k}^{(e)}\left(\theta \right),\hfill \\ \hfill \underset{n\to \infty }{\lim }\frac{1}{n}{\mathrm{\Gamma }}_{ij,k}^{\left[n\right],\left(m\right)}\left(\theta \right)& ={\mathrm{\Gamma }}_{ij,k}^{(m)}\left(\theta \right),\hfill \end{array}(10)$

where ${\mathfrak{g}}^{[n]}$, ∇^[n],(e), and ∇^[n],(m) are the Fisher metric and e/m-connections on $\mathcal{P}({\mathcal{X}}^n)$, with ${\mathfrak{g}}^n(\theta )={\mathfrak{g}}_{Q_{\theta }^{(n)}}$. Therefore, the Fisher metric for stochastic matrices essentially corresponds to the time density of the average Fisher metric, and a similar interpretation can be proposed for the affine connections.

3.2 Exponential families and mixture families

Similar to the distribution setting, we proceed to define exponential families (e-families) and mixture families (m-families) of stochastic matrices.

3.2.1 Definition of exponential families

Definition 3.1. (e-family of stochastic matrices [7]). Let $\mathrm{\Theta }={\mathbb{R}}^d$. We say that the parametric family of stochastic matrices

${\mathcal{V}}_e=\left\{P_{\theta }:\theta =\left({\theta }^1,\dots ,{\theta }^d\right)\in \mathrm{\Theta }\right\}\subset \mathcal{W}\left(\mathcal{X},\mathcal{E}\right)$

is an exponential family (e-family) of stochastic matrices with natural parameter θ, when there exist functions $K,g_1,\dots ,g_d\in \mathcal{F}(\mathcal{X},\mathcal{E})$ and $R\in {\mathbb{R}}^{\mathrm{\Theta }\times \mathcal{X}},\psi \in {\mathbb{R}}^{\mathrm{\Theta }}$, such that, for any $(x,x^{\prime })\in \mathcal{E}$ and θ ∈ Θ,

$\log P_{\theta }\left(x,x^{\prime }\right)=K\left(x,x^{\prime }\right)+{\displaystyle \sum _{i=1}^d}{\theta }^i{g}_i\left(x,x^{\prime }\right)+R\left(\theta ,x^{\prime }\right)-R\left(\theta ,x\right)-\psi \left(\theta \right).(11)$

For some fixed θ ∈ Θ, we may write for convenience ψ_θ for ψ(θ) and R_θ for $R(\theta ,\cdot )\in {\mathbb{R}}^{\mathcal{X}}$.

Note that R and ψ are analytic functions of θ and that ψ is a convex potential function. R and ψ are completely determined from g₁, …, g_d and K by the Perron–Frobenius (PF) theory, and we can introduce a stochastic rescaling mapping [7, 13]:

$\begin{array}{cc}\hfill \mathfrak{s}:{\mathcal{F}}_{+}\left(\mathcal{X},\mathcal{E}\right)& \to \mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\hfill \\ \hfill \tilde{P}\left(x,x^{\prime }\right)& \mapsto P\left(x,x^{\prime }\right)=\frac{\tilde{P}\left(x,x^{\prime }\right)v\left(x^{\prime }\right)}{\rho v\left(x\right)},\hfill \end{array}(12)$

where ρ and v are, respectively, the PF root and right PF eigenvector of $\tilde{P}$. Following this notation, we can rewrite Definition 3.1 more simply as

$P_{\theta }=\mathfrak{s}\left(\exp \left(K+{\displaystyle \sum _{i=1}^d}{\theta }^i{g}_i\right)\right),$

where exp is understood to be entry-wise. In particular, $\mathcal{W}(\mathcal{X},\mathcal{E})$ forms an e-family. Indeed, with $\mathcal{X}\cong [m]$ and $m\in \mathbb{N}$ in the parametrization proposed by Ito and Amari [14], we pick an arbitrary $x_{*}\in \mathcal{X}$ and write

$\begin{array}{ll}\hfill \log P\left(x,x^{\prime }\right)& ={\displaystyle \sum _{i=1,i\ne x_{*}}^m}\log \frac{P\left(x_{*},i\right)P\left(i,x_{*}\right)}{P\left(x_{*},x_{*}\right)P\left(x_{*},x_{*}\right)}{\delta }_i\left(x^{\prime }\right)\hfill \\ \hfill & +{\displaystyle \sum _{i=1,i\ne x_{*}}^m\sum _{j=1,j\ne x_{*}}^m}\log \frac{P\left(i,j\right)P\left(x_{*},x_{*}\right)}{P\left(x_{*},j\right)P\left(i,x_{*}\right)}{\delta }_i\left(x\right){\delta }_j\left(x^{\prime }\right)\hfill \\ \hfill & +\log P\left(x,x_{*}\right)-\log P\left(x^{\prime },x_{*}\right)+\log P\left(x_{*},x_{*}\right).\hfill \end{array}(13)$

The basis is given by

$\begin{array}{cc}\hfill g_i& =1^{⊺}{\delta }_i,i\in \left[m\right],i\ne x_{*}\hfill \\ \hfill g_{ij}& ={\delta }_i^{⊺}{\delta }_j,i,j\in \left[m\right],i,j\ne x_{*}\hfill \end{array}$

and the parameters are

$\begin{array}{c}\hfill {\theta }^i=\log \frac{P\left(x_{*},i\right)P\left(i,x_{*}\right)}{P\left(x_{*},x_{*}\right)P\left(x_{*},x_{*}\right)},{\theta }^{ij}=\log \frac{P\left(i,j\right)P\left(x_{*},x_{*}\right)}{P\left(x_{*},j\right)P\left(i,x_{*}\right)}.\end{array}$

We can alternatively define e-families as e-autoparallel submanifolds of $\mathcal{W}(\mathcal{X},\mathcal{E})$ [7, Theorem 6], where a submanifold $\mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$ is said to be autoparallel with respect to an affine connection ∇ when for any $U,V\in \mathrm{\Gamma }(T\mathcal{V})$, it holds that ${\nabla }_{U}V\in \mathrm{\Gamma }(T\mathcal{V})$.

3.2.2 Affine structures and characterization of minimal exponential families

We define the set of functions [7, 13, 15]

$\mathcal{N}\left(\mathcal{X},\mathcal{E}\right)\triangleq \left\{f\in \mathcal{F}\left(\mathcal{X},\mathcal{E}\right):\exists \left(f,c\right)\in \left({\mathbb{R}}^{\mathcal{X}},\mathbb{R}\right),h\left(x,x^{\prime }\right)=f\left(x^{\prime }\right)-f\left(x\right)+c\right\},(14)$

and observe that we can endow $\mathcal{N}(\mathcal{X},\mathcal{E})$ with the structure of a $\left|\mathcal{X}\right|$-dimensional vector subspace of the $\left|\mathcal{E}\right|$-dimensional space $\mathcal{F}(\mathcal{X},\mathcal{E})$. We can thus define the quotient space of generators

$\mathcal{G}\left(\mathcal{X},\mathcal{E}\right)\triangleq \mathcal{F}\left(\mathcal{X},\mathcal{E}\right)/\mathcal{N}\left(\mathcal{X},\mathcal{E}\right),$

of dimension $\left|\mathcal{E}\right|-\left|\mathcal{X}\right|$ and the diffeomorphism

$\begin{array}{cc}\hfill \mathrm{\Delta }:\mathcal{G}\left(\mathcal{X},\mathcal{E}\right)& \to \mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\hfill \\ \hfill g& \mapsto \mathrm{\Delta }\left(g\right)=\mathfrak{s}\left(\exp \circ g\right),\hfill \end{array}(15)$

where ∘ stands here for function composition. Essentially, there is a one-to-one correspondence between vector subspaces of $\mathcal{G}(\mathcal{X},\mathcal{E})$ and e-families.

Theorem 3.1. ([7, Theorem 2]). A submanifold $\mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$ forms an e-family if and only if there exists an affine subspace $\mathcal{A}\subset \mathcal{G}(\mathcal{X},\mathcal{E})$ such that $\mathrm{\Delta }(\mathcal{A})=\mathcal{V}$. In this case, $\dim \mathcal{V}=\dim \mathcal{A}$.

As a corollary [7, Corollary 1], $\mathcal{W}(\mathcal{X},\mathcal{E})$ is trivially an exponential family of dimension $\left|\mathcal{E}\right|-\left|\mathcal{X}\right|$. A family $\mathcal{V}$ will be called minimal (or full) whenever the functions g₁, …, g_d in Definition 3.1 are linearly independent in $\mathcal{G}(\mathcal{X},\mathcal{E})$. In this case, we will say that g₁, …, g_d form a basis for $\mathcal{V}$.

3.2.3 Mixture families

In the stochastic matrix setting, the notion of a mixture family is naturally defined in terms of edge measures.

Definition 3.2. (m-family of stochastic matrices [15]). We say that a family of irreducible stochastic matrices ${\mathcal{V}}_m$ is a mixture family (m-family) of irreducible stochastic matrices on $(\mathcal{X},\mathcal{E})$ when the following holds.There exists affinely independent $Q_0,Q_1,\dots ,Q_d\in \mathcal{Q}(\mathcal{X},\mathcal{E})$, and

${\mathcal{V}}_m=\left\{P_{\xi }\in \mathcal{W}\left(\mathcal{X},\mathcal{E}\right):Q_{\xi }=\left(1-{\displaystyle \sum _{i=1}^d}{\xi }^i\right)Q_0+{\displaystyle \sum _{i=1}^d}{\xi }^i{Q}_i,\xi \in \mathrm{\Xi }\right\},$

where $\mathrm{\Xi }=\left\{\xi \in {\mathbb{R}}^d:Q_{\xi }(x,x^{\prime })>0,\forall (x,x^{\prime })\in \mathcal{E}\right\}$, and Q_ξ is the edge measure that pertains to P_ξ. Note that Ξ is an open set, ξ is called the mixture parameter, and d is the dimension² of the family ${\mathcal{V}}_m$.

It is easy to verify that $\mathcal{W}(\mathcal{X},\mathcal{E})$ also forms an m-family, and it is possible to define m-families as m-autoparallel submanifolds of $\mathcal{W}(\mathcal{X},\mathcal{E})$.

3.2.4 Dual expectation parameter and chart transition maps

For an exponential family ${\mathcal{V}}_e$ with natural parametrization [θⁱ], following Definition 3.1, one may introduce [7] the expectation parameter [η_i] as follows. For i ∈ [d] and θ ∈ Θ,

${\eta }_i\left(\theta \right)={\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}{Q}_{\theta }\left(x,x^{\prime }\right)g_i\left(x,x^{\prime }\right)={\mathbb{E}}_{\left(X,X^{\prime }\right)\sim Q_{\theta }}\left[g_i\left(X,X^{\prime }\right)\right],(16)$

where Q_θ is the edge measure corresponding to the stochastic matrix at coordinates θ. When ${\mathcal{V}}_e$ is minimal, η defines an alternative coordinate system to the natural parametrization θ for ${\mathcal{V}}_e$.

Theorem 3.2. [15, Lemma 4.1] The following statements are equivalent:

(i) The functions g₁, …, g_d are linearly independent in $\mathcal{G}(\mathcal{X},\mathcal{E})$.

(ii) The mappings θ∘η⁻¹ and η∘θ⁻¹ are one-to-one.

(iii) The Hessian matrix ${[{\partial }_i{\partial }_j\psi (\theta )]}_{ij}\succ 0$ for any θ ∈ Θ.

(iv) The Hessian matrix ${[{\partial }_i{\partial }_j\psi (\theta )]}_{ij}\succ 0$ for θ = 0.

(v) The parametrization $\theta :\mathcal{V}\to \mathrm{\Theta }$ is faithful.

Defining the Shannon negentropy³ potential function $\phi :{\mathbb{R}}^d\to \mathbb{R}$ to satisfy

$\phi \left(\eta \right)+\psi \left(\theta \right)=⟨\theta ,\eta ⟩,$

we can express [7, Theorem 4] the chart transition maps (see Figure 1) between the expectation [η_i] and natural [θⁱ] parameters of the e-family ${\mathcal{V}}_e$ as

$\begin{array}{cc}\hfill \eta ◦{\theta }^{-1}:{\mathbb{R}}^d& \to {\mathbb{R}}^d\hfill \\ \hfill \theta & \mapsto {\eta }_i\left(\theta \right)={\partial }_i\psi \left(\theta \right),\hfill \\ \hfill \theta ◦{\eta }^{-1}:{\mathbb{R}}^d& \to {\mathbb{R}}^d\hfill \\ \hfill \eta & \mapsto {\theta }^i\left(\eta \right)={\partial }^i\phi \left(\eta \right),\hfill \end{array}$

where we wrote ∂ⁱ⋅ = ∂ ⋅/∂η_i. We can also obtain the counterpart [13, Lemma 5] of (16) for θ◦η⁻¹,

$\begin{array}{c}\hfill {\theta }^i\left(\eta \right)={\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}{\partial }^i{Q}_{\eta }\left(x,x^{\prime }\right)\left(\log P_{\eta }\left(x,x^{\prime }\right)-K\left(x,x^{\prime }\right)\right).\end{array}(17)$

FIGURE 1

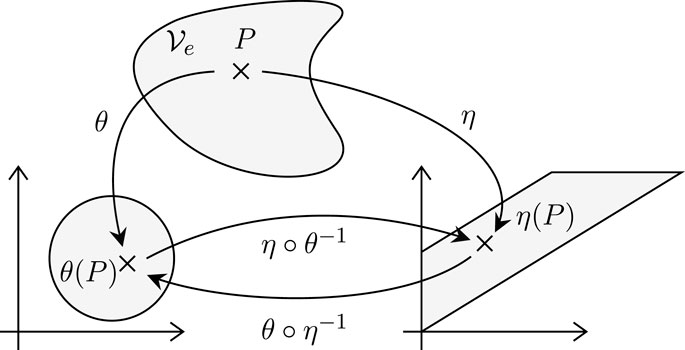
FIGURE 1. Natural and expectation parametrizations of an e-family ${\mathcal{V}}_e$, together with their chart transition maps.

3.2.5 Dual flatness

A straightforward computation shows that all the e-connection coefficients ${\mathrm{\Gamma }}_{ij,k}^{(e)}$ for an e-family ${\mathcal{V}}_e$ and all the m-connection coefficients ${\mathrm{\Gamma }}_{ij,k}^{(m)}$ for an m-family ${\mathcal{V}}_m$ are null. We say that ${\mathcal{V}}_e$ is e-flat and that ${\mathcal{V}}_m$ is m-flat. From the conjugacy of the affine connections, curvature tensors associated with ∇^(e) and ∇^(m) vanish simultaneously. As a consequence, for any smooth submanifold $\mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$,

$\mathcal{V}\text{\hspace{0.17em}is\hspace{0.17em}}\mathrm{m}-\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{t}\iff \mathcal{V}\text{\hspace{0.17em}is\hspace{0.17em}}\mathrm{e}-\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{t},$

which is sometimes called the fundamental theorem of information geometry [79, Theorem 3]. In other words, e-families and m-families are both e-flat and m-flat [7, Theorem 5], and for any $\mathcal{V}$, it is enough to find an affine coordinate system in which either the e-connection or m-connection coefficients are null for it to be dually flat. For i, j ∈ [d], recall that ${\mathfrak{g}}_{ij}(\theta )={\mathfrak{g}}_{P_{\theta }}({\partial }_i,{\partial }_j)$. Similarly, we define ${\mathfrak{g}}^{ij}(\eta )={\mathfrak{g}}_{P_{\eta }}({\partial }^i,{\partial }^j)$. The coefficients of the Fisher metric and its inverse are recovered by

$\begin{array}{cc}\hfill {\mathfrak{g}}_{ij}\left(\theta \right)& ={\partial }_i{\partial }_j\psi \left(\theta \right),\hfill \\ \hfill {\mathfrak{g}}^{ij}\left(\eta \right)& ={\partial }^i{\partial }^j\phi \left(\eta \right),\hfill \\ \hfill {\left[{\mathfrak{g}}^{ij}\left(\eta \right)\right]}^{ij}& ={\left[{\mathfrak{g}}_{ij}\left(\theta \right)\right]}_{ij}^{-1}.\hfill \end{array}(18)$

Thus, φ is also strictly convex, and the coordinate systems [θⁱ] and [ηⁱ] are mutually dual with respect to $\mathfrak{g}$. The two coordinate systems are related by the Legendre transformation, and we can express their dual potential functions as

$\begin{array}{c}\hfill \phi \left(\eta \right)=\underset{\theta \in \mathrm{\Theta }}{\max }\left\{\langle \theta ,\eta \rangle -\psi \left(\theta \right)\right\},\psi \left(\theta \right)=\underset{\eta \in H}{\max }\left\{\langle \theta ,\eta \rangle -\phi \left(\eta \right)\right\}.\end{array}$

3.2.6 Geodesics and geodesic hulls

An affine connection ∇ defines a notion of the straightness of curves. Namely, a curve γ is called a ∇-geodesic whenever it is ∇-autoparallel, ${\nabla }_{\dot{\gamma }}\dot{\gamma }=0$, where $\dot{\gamma }(t)$ is the velocity vector at time parameter t. The geodesic between two points $P_0,P_1\in \mathcal{W}(\mathcal{X},\mathcal{E})$ is the straight curve that goes through the two points. As our manifold is equipped with two dual connections, there are two distinct notions of straight lines, and the arc between the two points will not necessarily correspond to the shortest path between the two elements with respect to the Riemannian metric, unlike in Euclidean geometry. Specifically, the e-geodesic going through P₀ and P₁ is given [7, Corollary 2] by

${\gamma }_{P_0,P_1}^{\left(e\right)}\triangleq \left\{P_t=\mathfrak{s}\left(P_0^{◦1-t}◦P_1^{◦t}\right):t\in \mathbb{R}\right\},(19)$

and the m-geodesic [7, Theorem 7] by

${\gamma }_{P_0,P_1}^{\left(m\right)}\triangleq \left\{P_t:Q_t=\left(1-t\right)Q_0+t{Q}_1,t\in \mathbb{R},Q_t\in \mathcal{Q}\left(\mathcal{X},\mathcal{E}\right)\right\},(20)$

where $\mathcal{Q}(\mathcal{X},\mathcal{E})$ is the set of all edge measures introduced in (3). A submanifold $\mathcal{V}\in \mathcal{W}(\mathcal{X},\mathcal{E})$ forms an e-family if and only if for any two points $P_0,P_1\in \mathcal{V}$, ${\gamma }_{P_0,P_1}^{(e)}$ lies entirely in $\mathcal{V}$ [7, Corollary 3], and a similar claim holds for m-families. We generalize the aforementioned objects beyond two points to more general subsets of $\mathcal{W}(\mathcal{X},\mathcal{E})$, by defining geodesic hulls [13] (see Figure 2).

FIGURE 2

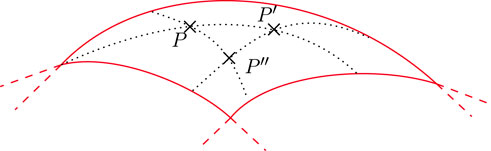
FIGURE 2. E-hull $\mathrm{e}-\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}(\left\{P,P^{\prime },P^{″}\right\})$ of three points. It is instructive to note that although a set of three points forms a zero-dimensional manifold, we construct a manifold of dimensions possibly up to two.

Definition 3.3. (Exponential hull [13, Definition 7]). Let $\mathcal{V}\subset \mathcal{W}$:

$\begin{array}{c}\hfill \mathrm{e}-\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}\left(\mathcal{V}\right)=\left\{\mathfrak{s}\left(\tilde{P}\right):\tilde{P}={○}_{i=1}^k{P}_i^{o{\alpha }_i},k\in \mathbb{N},{\alpha }_1,\dots ,{\alpha }_k\in \mathbb{R},{\displaystyle \sum _{i=1}^k}{\alpha }_i=1,P_1,\dots P_k\in \mathcal{V}\right\},\end{array}$

where $\mathfrak{s}$ is defined in (12).

Definition 3.4. (Mixture hull [13, Definition 8]). Let $\mathcal{V}\subset \mathcal{W}$:

$\begin{array}{c}\hfill \mathrm{m}-\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}\left(\mathcal{V}\right)=\left\{P:Q\in \mathcal{Q},Q={\displaystyle \sum _{i=1}^k}{\alpha }_i{Q}_i,k\in \mathbb{N},{\alpha }_1,\dots ,{\alpha }_k\in \mathbb{R},P_1,\dots ,P_k\in \mathcal{V}\right\},\end{array}$

where Q (resp., Q_i) is the edge measure that pertains to P (resp., P_i).

When a family $\mathcal{V}$ forms both an m-family and an e-family, we say it forms an em-family.

3.3 Information projections and decomposition theorems

The projection of a point onto a surface is among the most natural geometric concepts. In Euclidean geometry, projecting on a connected convex body leads to a unique closest solution point. However, the dually flat geometry on $\mathcal{W}(\mathcal{X},\mathcal{E})$ is based on two different notions of straightness, inducing two different flavors of geodesic convexity. Furthermore, the divergence function we consider is not symmetric in its arguments, hence the need for two definitions of projections as minimizer with respect to the first and second arguments. This section goes back to and hinges around the notion of divergence defined in (6), projection, and orthogonality and explores the Bregman geometry of $\mathcal{W}(\mathcal{X},\mathcal{E})$.

3.3.1 Information divergence as a Bregman divergence

For a continuously differentiable and strictly convex function $f:\mathrm{\Xi }\to \mathbb{R}$ on a convex domain $\mathrm{\Xi }\subset {\mathbb{R}}^d$, we call Bregman divergence B_f [16] with generator f (see Figure 3) the function

$\begin{array}{cc}\hfill B_f:\mathrm{\Xi }\times \mathrm{\Xi }& \to {\mathbb{R}}_{+}\hfill \\ \hfill \left(\xi ,{\xi }^{\prime }\right)& \mapsto B_f\left(\xi :{\xi }^{\prime }\right)=f\left(\xi \right)-f\left({\xi }^{\prime }\right)-{\displaystyle \sum _{i\in \left[d\right]}}{\partial }_{i}f\left({\xi }^{\prime }\right)\left({\xi }^i-{\xi }^i\right).\hfill \end{array}$

FIGURE 3

FIGURE 3. Geometrical interpretation of a Bregman divergence.

When we let $P_{\theta },P_{{\theta }^{\prime }}\in {\mathcal{V}}_e$ some e-family following Definition 3.1, one can verify with direct computations [15, 17] that

$\begin{array}{cc}\hfill D\left(\theta \Vert {\theta }^{\prime }\right)& =\psi \left({\theta }^{\prime }\right)-\psi \left(\theta \right)-{\displaystyle \sum _{i\in \left[d\right]}}{\partial }_i\psi \left(\theta \right)\left({\theta }^{\prime i}-{\theta }^i\right)=B_{\psi }\left({\theta }^{\prime }:\theta \right),\hfill \\ \hfill H\left(\theta \right)& =\psi \left(\theta \right)-{\displaystyle \sum _{i\in \left[d\right]}}{\eta }_i{\theta }^i=-\phi \left(\eta \right).\hfill \end{array}(21)$

As ψ and φ are convex conjugate,

$\begin{array}{c}\hfill D\left(\theta \Vert {\theta }^{\prime }\right)=B_{{\psi }^{*}}\left(\eta :{\eta }^{\prime }\right)=B_{\phi }\left(\eta :{\eta }^{\prime }\right),\end{array}$

where we used the shorthands η = η(θ) and η′ = η(θ′); hence, the KL divergence is the Bregman divergence associated with the Shannon negentropy function, and as any Bregman divergence, it verifies the law of cosines:

$\begin{array}{c}\hfill B_{\phi }\left(\eta ,{\eta }^{\prime }\right)+B_{\phi }\left({\eta }^{\prime },{\eta }^{″}\right)=B_{\phi }\left(\eta ,{\eta }^{″}\right)+{\displaystyle \sum _{i\in \left[d\right]}}\left({\partial }^i\phi \left({\eta }^{″}\right)-{\partial }^i\phi \left({\eta }^{\prime }\right)\right)\left({\eta }_i-{\eta }_i^{\prime }\right),\end{array}(22)$

which can be re-expressed [7, (23)] as

$\begin{array}{cc}\hfill D\left(\theta \Vert {\theta }^{\prime }\right)+D\left({\theta }^{\prime }\Vert {\theta }^{″}\right)& =D\left(\theta \Vert {\theta }^{″}\right)+{\displaystyle \sum _{i\in \left[d\right]}}\left({\theta }^{\prime \prime i}-{\theta }^{\prime i}\right)\left({\eta }_i-{\eta }_i^{\prime }\right)\hfill \\ \hfill & =D\left(\theta \Vert {\theta }^{″}\right)+{\mathfrak{g}}_{P_{{\theta }^{\prime }}}\left(\dot{\gamma }\left(0\right),\dot{\sigma }\left(0\right)\right),\hfill \end{array}$

for γ an m-geodesic going through P_θ and P_θ′ and σ an e-geodesic going through P_θ′ and P_θ″.

3.3.2 Canonical divergence

One may naturally wonder whether it is possible to recover the divergence D defined at (6) from $\mathfrak{g}$ and ∇^(e), ∇^(m) only. This is referred to as the inverse problem in information geometry. It is easily understood that such a divergence is not unique. In fact, there exist an infinity of divergence functions that could have given rise to the dually flat geometry on $\mathcal{W}(\mathcal{X},\mathcal{E})$ [18]. However, it is possible to single out one particular divergence, termed canonical divergence [5], which is uniquely defined from $\mathfrak{g}$ and ∇^(e), ∇^(m). For $P,P^{\prime }\in \mathcal{W}(\mathcal{X},\mathcal{E})$, its expression is given in a dual coordinate system [θⁱ], [η_i] by

$D\left(P\Vert P^{\prime }\right)=\phi \left(\eta \right)+\psi \left({\theta }^{\prime }\right)-{\displaystyle \sum _{i\in \left[d\right]}}{\eta }_i{\theta }^{\prime i},$

where η = η(P) and θ′ = θ(P′). One can verify from (21) that we indeed recover the expression at (6).

3.3.3 Geodesic convexity and convexity properties of information divergence

Geodesic convexity is a natural generalization of convexity in Euclidean geometry for subsets of Riemannian manifolds and functions defined on them. As straight lines are defined with respect to an affine connection ∇, a subset $\mathcal{C}$ of $\mathcal{W}(\mathcal{X},\mathcal{E})$ is said to be geodesically convex with respect to ∇ when ∇-geodesic joining⁴ two points in $\mathcal{C}$ remain in $\mathcal{C}$ at all times. In particular, $\mathcal{C}$ is e-convex (resp., m-convex), when for any $P_0,P_1\in \mathcal{C}$ and any t ∈ [0, 1], it holds that ${\gamma }_{P_0,P_1}^{(e)}(t)\in \mathcal{C}$ (resp., ${\gamma }_{P_0,P_1}^{(m)}(t)\in \mathcal{C}$), where ${\gamma }_{P_0,P_1}^{(e)}$ and ${\gamma }_{P_0,P_1}^{(m)}$ are defined in (19, 20). An immediate consequence is that an e-family (resp., m-family) $\mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$ is e-convex (resp., m-convex). On a geodesically convex domain $\mathcal{C}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$, a function $f:\mathcal{C}\to \mathbb{R}$ is said to be a geodesically convex (resp., strictly geodesically convex) if the composition $f◦\gamma :[\mathrm{0,1}]\to \mathbb{R}$ is a convex (resp., strictly convex) function for any geodesic $\gamma :[\mathrm{0,1}]\to \mathcal{C}$ contained within $\mathcal{C}$. In particular, the information divergence defined in (6) is strictly m-convex in its first argument and strictly e-convex in its second argument [15, Theorem 3.3]. Namely, for t ∈ (0,1), $P,P_0,P_1\in \mathcal{W}(\mathcal{X},\mathcal{E})$, with P₀ ≠ P₁,

$\begin{array}{cc}\hfill D\left({\gamma }_{P_0,P_1}^{\left(m\right)}\left(t\right)\Vert P\right)& <\left(1-t\right)D\left(P_0\Vert P\right)+tD\left(P_1\Vert P\right),\hfill \\ \hfill D\left(P\Vert {\gamma }_{P_0,P_1}^{\left(e\right)}\left(t\right)\right)& <\left(1-t\right)D\left(P\Vert P_0\right)+tD\left(P\Vert P_1\right).\hfill \end{array}$

However, for $\left|t\right|>1$, the opposite inequality holds [13]:

$\begin{array}{c}\hfill D\left(P\Vert {\gamma }_{P_0,P_1}^{\left(e\right)}\left(t\right)\right)>\left(1-t\right)D\left(P\Vert P_0\right)+tD\left(P\Vert P_1\right).\end{array}$

Unlike in the distribution setting, where the KL divergence is jointly m-convex, this property does not hold true for stochastic matrices [21, Remark 4.2].

3.3.4 Pythagorean inequalities

In the more familiar Euclidean geometry, projecting a point P onto a subset $\mathcal{C}$ of ${\mathbb{R}}^d$ consists in finding the point in $\mathcal{C}$ that minimizes the Euclidean distance between P and $\mathcal{C}$. If $\mathcal{C}$ is convex, the minimization problem admits a unique solution and a Pythagorean inequality holds between the point, its projection, and any other point in $\mathcal{C}$. Similar ideas are made possible on $\mathcal{W}(\mathcal{X},\mathcal{E})$ by the Bregman geometry induced from D. Let ${\mathcal{C}}_m\subset \mathcal{W}(\mathcal{X},{\mathcal{E}}^{\prime })$ (resp., ${\mathcal{C}}_e\subset \mathcal{W}(\mathcal{X},{\mathcal{E}}^{\prime })$) with ${\mathcal{E}}^{\prime }\subset \mathcal{E}$ be non-empty, closed, and m-convex (resp., e-convex). We define the e-projection onto ${\mathcal{C}}_m$ as the mapping

$\begin{array}{c}\hfill P_e:\mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\to {\mathcal{C}}_m,P\mapsto \underset{\bar{P}\in {\mathcal{C}}_m}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}D\left(\bar{P}\Vert P\right),\end{array}$

and the m-projection onto ${\mathcal{C}}_e$ as the mapping

$\begin{array}{c}\hfill P_m:\mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\to {\mathcal{C}}_e,P\mapsto \underset{\bar{P}\in {\mathcal{C}}_e}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}D\left(P\Vert \bar{P}\right).\end{array}$

For a point P in context, we simply write P_e = P_e(P) and P_m = P_m(P).

Theorem 3.3. (Pythagorean inequalities for geodesic e-convex [21, Proposition 4.2], m-convex sets [23, Lemma 1]). The following statements hold.

(i) P_e exists in the sense where the minimum is attained for a unique element in ${\mathcal{C}}_m$.

(ii) For $P_0\in {\mathcal{C}}_m$, P₀ = P_e if and only if

$\forall \bar{P}\in \mathcal{C},D\left(\bar{P}\Vert P\right)\ge D\left(\bar{P}\Vert P_0\right)+D\left(P_0\Vert P\right).$

(iii) P_m exists in the sense where the minimum is attained for a unique element in ${\mathcal{C}}_e$.

(iv) For $P_0\in {\mathcal{C}}_e$, P₀ = P_m if and only if

$\forall \bar{P}\in \mathcal{C},D\left(P\Vert \bar{P}\right)=D\left(P\Vert P_0\right)+D\left(P_0\Vert \bar{P}\right).$

3.3.5 Pythagorean equality for linear families

Inequalities become equalities when projecting onto e-families and m-families.

Theorem 3.4. (Pythagorean theorem for e-families, m-families [19], [15, Section 4.4]). The following statements hold.

(i) P_e exists in the sense where the minimum is attained for a unique element in ${\mathcal{C}}_m$.

(ii) For $P_0\in {\mathcal{C}}_m$, P₀ = P_e if and only if

$\forall \bar{P}\in \mathcal{C},D\left(\bar{P}\Vert P\right)=D\left(\bar{P}\Vert P_0\right)+D\left(P_0\Vert P\right).$

(iii) P_m exists in the sense where the minimum is attained for a unique element in ${\mathcal{C}}_e$.

(iv) For $P_0\in {\mathcal{C}}_e$, P₀ = P_m if and only if

$\forall \bar{P}\in \mathcal{C},D\left(P\Vert \bar{P}\right)=D\left(P\Vert P_0\right)+D\left(P_0\Vert \bar{P}\right).$

3.4 Bibliographical remarks

The construction of the conjugate connection manifold from a general contrast function in Section 3.1.1 and Section 3.1.2 follows the general scheme of Eguchi [11, 12], which can also be found in [79, Definition 5, Theorem 4]. The expression for the Fisher metric at (Eq. 8) and the conjugate affine connections at (Eq. 8) were introduced by Nagaoka [7, (9), (19), (20)]. One-dimensional e-families of stochastic matrices were first introduced by Nakagawa and Kanaya [19], whereas the general construction in the multi-dimensional setting was done by Nagaoka [7], who also established the characterization in Theorem 3.1 of minimal e-families in terms of affine structures of in [7, Theorem 2]. Curved exponential families of transition matrices and mixture families make their first named appearances in Hayashi and Watanabe [15; Section 8.3; Section 4.2]. See also [13, Definition 1] for two alternative equivalent definitions of an m-family. The expectation parameter for exponential families in (16) and its expression as the gradient of the potential function were discussed on multiple occasions [7, Theorem 4], [19, (28)], [15, Lemma 5.1]. Theorem 3.2 was taken from [15, Lemma 4.1]. The expression for the chart transition map from expectation to natural parameters in (17) was obtained from [13, Lemma 5]. Geodesics discussed in Section 3.2.6 were introduced in one-dimension in [19] and multiple dimensions in [7], whereas mixture and exponential hulls of sets first appeared in [13]. Nagaoka [7] established the dual flatness of the manifold discussed in Section 3.2.5 and matched the information divergence with the canonical divergence. The expression of the informational divergence and entropy for exponential families in (21) was given in [15, 17]. The law of cosines was also mentioned by Adamčík [20] for general Bregman projections. The convexity properties of the divergence appeared in Hayashi and Watanabe [15, Theorem 3.3] and Hayashi and Watanabe [15, Lemma 4.5], and their strict version was discussed in [21, Section 4] together with the case $\left|t\right|>1$. The Pythagorean inequality for projections onto m-convex sets [Theorem 3.3 (i), (ii)] was shown to hold by Csiszár et al. [23, Lemma 1]. The inequality for the “reversed projection” onto e-convex sets was found in [21]. The equality in the Pythagorean theorem for e-families and m-families was first found in [19, Lemma 5] for the one-dimensional setting and in [15, Corollary 4.7, Corollary 4.8] for multiple dimensions.

3.4.1 Timeline

The idea of tilting or exponential change of measure, which gives rise to e-families in the context of distributions, can be traced back to Miller [22]. However, in this section, we focused on the milestones toward the geometric construction of Nagaoka [7], and we deferred the history of the development of the large deviation theory to Section 5.2. The first to recognize the exponential family structure of stochastic matrices is Csiszár et al. [23] by considering information projections onto linearly constrained sets and inferring exponential families as the solution to the maximum entropy problem, as discussed in more detail in Section 5.1. The notion of an asymptotic exponential family was implicitly described by Ito and Amari [14] and was formalized by Takeuchi and Barron [24] and Takeuchi and Kawabata [25]. A later result by Takeuchi and Nagaoka [26] proved that asymptotic exponential families and their non-asymptotic counterparts are in fact equivalent.

3.4.2 Alternative constructions

Some alternative definitions of exponential families of Markov chains include [27–32]. However, they do not enjoy the same geometric properties as the one of Definition 3.1. Thus, we do not discuss them in detail.

4 Recent advances

One area of recent progress has been the analysis of the geometric properties of significant submanifolds of $\mathcal{W}(\mathcal{X},\mathcal{E})$. In Section 4.1, we briefly discuss symmetric, bistochastic, and memoryless classes. In Section 4.2, we turn the spotlight onto the structure-rich family of irreducible and reversible stochastic matrices. In Section 4.3, we mention some recent progress in connecting the dually flat geometry of Section 3.1 to the theory of lumpability of Markov chains. We end with a discussion on finite state machine (FSMX) models in Section 4.4.

4.1 Symmetric, bistochastic, and memoryless stochastic matrices

In this section, we briefly survey known geometric properties of notable submanifolds of $\mathcal{W}(\mathcal{X},\mathcal{E})$. We also refer the reader to Table 1, adapted from [13, Table 1], for a more visual classification.

TABLE 1

TABLE 1. Geometry of submanifolds of irreducible Markov kernels for $\left|\mathcal{X}\right|\ge 3$.

4.1.1 Memoryless class

We say that a stochastic matrix $P\in \mathcal{W}(\mathcal{X})$ is memoryless, when it can be expressed as

$P=\left(\begin{array}{ccc}\hfill \text{——}\hfill & \hfill \pi \hfill & \hfill \text{——}\hfill \\ \hfill \text{——}\hfill & \hfill \pi \hfill & \hfill \text{——}\hfill \\ \hfill \text{——}\hfill & \hfill \pi \hfill & \hfill \text{——}\hfill \end{array}\right),$

for $\pi \in \mathcal{P}(\mathcal{X})$. We note that π is the stationary distribution of P, and that for such P to be irreducible, it is necessary that π > 0; hence, $P\in \mathcal{W}(\mathcal{X},{\mathcal{X}}^2)$. Markov chains defined by a memoryless stochastic matrix correspond in fact to an iid process. We write ${\mathcal{W}}_{\mathsf{i}\mathsf{i}\mathsf{d}}(\mathcal{X},{\mathcal{X}}^2)$ for the set of all memoryless stochastic matrices.

Lemma 4.1. ([13, Lemma 7, Lemma 8]). The two following statements hold:

(i) ${\mathcal{W}}_{\mathsf{i}\mathsf{i}\mathsf{d}}(\mathcal{X},{\mathcal{X}}^2)$ forms an e-family of dimension $\left|\mathcal{X}\right|-1$.

(ii) ${\mathcal{W}}_{\mathsf{i}\mathsf{i}\mathsf{d}}(\mathcal{X},{\mathcal{X}}^2)$ does not form an m-family.

Recall the parametrization of Ito and Amari [14], reported in (13). Coefficients θ^ij in the expression represent memory in the process, and thus vanish. For $\mathcal{X}\cong [m]$ and an arbitrary x_* ∈ [m], we can re-write

$\begin{array}{cc}\hfill \log P\left(x,x^{\prime }\right)=& {\displaystyle \sum _{\begin{array}{c}i=1\\ i\ne x_{*}\end{array}}^m}{\theta }^i{g}_i\left(x,x^{\prime }\right)+\log \pi \left(x_{*}\right),\hfill \end{array}(23)$

where for i ∈ [m], i ≠ x _*,

${\theta }^i=\log \frac{\pi \left(i\right)}{\pi \left(x_{*}\right)},g_i\left(x,x^{\prime }\right)={\delta }_i\left(x^{\prime }\right).$

4.1.2 Bistochastic class

Bistochastic matrices, also called doubly stochastic matrices, are row- and column-stochastic. In other words, $P\in \mathcal{W}(\mathcal{X})$ is bistochastic if and only if the transposition $P^{⊺}\in \mathcal{W}(\mathcal{X})$ . In particular, the stationary distribution of a bistochastic matrix is uniform. We denote ${\mathcal{W}}_{\mathsf{b}\mathsf{i}\mathsf{s}}(\mathcal{X},{\mathcal{X}}^2)$ as the set of positive bistochastic matrices.

Lemma 4.2. The two following statements hold:

(i) ${\mathcal{W}}_{\mathsf{b}\mathsf{i}\mathsf{s}}(\mathcal{X},{\mathcal{X}}^2)$ forms an m-family of dimension ${(\left|\mathcal{X}\right|-1)}^2$ [15, Example 4].

(ii) For $\left|\mathcal{X}\right|>2$ , ${\mathcal{W}}_{\mathsf{b}\mathsf{i}\mathsf{s}}(\mathcal{X},{\mathcal{X}}^2)$ does not form an e-family [13, Lemma 10].

4.1.3 Symmetric class

A symmetric stochastic matrix P satisfies P(x, x′) = P(x′, x) for any pair of states $x,x^{\prime }\in \mathcal{X}$ . Writing ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ for the set of positive symmetric matrices, note that ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ lies at the intersection of reversible (see Section 4.2) and doubly stochastic matrices, enjoying all their properties (e.g., uniform stationary distribution, self-adjointness). However, perhaps surprisingly, ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ does not form an e-family.

Lemma 4.3. ([13, Lemma 9, Lemma 10]). The two following statements hold:

(i) ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ forms an m-family of dimension $\left|\mathcal{X}\right|(\left|\mathcal{X}\right|-1)/2$ ,

(ii) For $\left|\mathcal{X}\right|>2$ , ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ does not form an e-family.

4.2 Time-reversible stochastic matrices

In Section 4.2.1, we begin by briefly introducing time reversals and time reversibility in the context of Markov chains. In Section 4.2.2, we proceed to analyze geometric structures that are invariant under the time reversal operation. In Section 4.2.3, we inspect the e-family and m-family nature of the submanifold of reversible stochastic matrices and reversible edge measures. In Section 4.2.4 and Section 4.2.5, we, respectively, discuss reversible information projections and how to generate the reversible set as a geodesic hull of structured subfamilies.

4.2.1 Reversibility

Consider a Markov chain ${(X_t)}_{1\le t\le n}$ with transition matrix $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ , started from its stationary distribution π. When we look at the random process in reverse time ${(X_{n+1-t})}_{1\le t\le n}$ , the Markov property is still verified. In fact, the transition matrix P ^* of this time-reversed Markov chain is given by P ^*(x, x′) = π(x′)P(x′, x)/π(x). The time reversal P ^* shares the same stationary distribution as the original chain, and irreducibility is preserved, although $P^{*}\in \mathcal{W}(\mathcal{X},{\mathcal{E}}^{*})$ , where ${\mathcal{E}}^{*}=\left\{(x^{\prime },x):(x,x^{\prime })\in \mathcal{E}\right\}$ is the symmetric image of the connection digraph $\mathcal{E}$ . When P ^* = P, the transition probabilities of the chain forward and backward in time coincide, and we say that the chain is time-reversible. Equivalently, we may say that P verifies the detailed balance equation:

$\pi \left(x\right)P\left(x,x^{\prime }\right)=\pi \left(x^{\prime }\right)P\left(x^{\prime },x\right).$

We write ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ for the set of reversible chains that are irreducible with connection digraph $(\mathcal{X},\mathcal{E})$ . Note that the edge set must necessarily satisfy $\mathcal{E}={\mathcal{E}}^{*}$ ; otherwise, ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})=\varnothing$ .

Time-reversibility is a central concept across a myriad of scientific fields, from computer science (queuing networks [33], storage models, Markov Chain Monte Carlo algorithms [34], etc.) to physics (many classical or quantum natural laws appear as being time-reversible [35]). The theory of reversibility for Markov chains was originally developed by Kolmogorov [36, 37], and we refer the reader to [38] for a more complete historical exposition.

Reversible Markov chains enjoy a particularly rich mathematical structure. Perhaps first and foremost, reversibility implies self-adjointness of P with respect to the Hilbert space ℓ ₂(π) of real functions over $\mathcal{X}$ endowed with the weighted inner product ${⟨f,g⟩}_{\pi }={\sum }_{x\in \mathcal{X}}f(x)g(x)\pi (x)$ . Key properties of reversible stochastic matrices induced from self-adjointness include a real spectrum, control from above and below the mixing time by the inverse of the absolute spectral gap [9, Chapter 12], and stability of spectrum estimation procedures [39]. Reversibility has also been explored in the context of algebraic statistics [40] or Bayesian statistics [41]. In this section, we focus on the properties of reversibility and families of reversible stochastic matrices from an information geometric viewpoint.

4.2.2 Geometric invariants

The time reversal operation is known to preserve some geometric properties of families of transition matrices. Consider $\mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$ , a family of irreducible stochastic matrices. The time-reversal family [13, Definition 3], denoted as ${\mathcal{V}}^{*}$ , is defined by

${\mathcal{V}}^{*}\triangleq \left\{P^{*}:P\in \mathcal{V}\right\}.$

Lemma 4.4. ([13, Proposition 1]). Let ${\mathcal{V}}_e$ (resp., ${\mathcal{V}}_m$ ) be an e-family (resp., m-family) in $\mathcal{W}(\mathcal{X},\mathcal{E})$ . Then, ${\mathcal{V}}_e$ (resp., ${\mathcal{V}}_m$ ) forms an e-family (resp., m-family) in $\mathcal{W}(\mathcal{X},{\mathcal{E}}^{*})$ .

Moreover, the time reversal operation leaves the divergence between stochastic matrices unchanged [80, Proof of Proposition 2]:

$P_1,P_2\in \mathcal{W}\left(\mathcal{X},\mathcal{E}\right)\Rightarrow D\left(P_1\Vert P_2\right)=D\left(P_1^{*}\Vert P_2^{*}\right).(24)$

When ${\mathcal{V}}_r\subset {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ , we say that the family ${\mathcal{V}}_r$ is reversible, and in this case ${\mathcal{V}}_r^{*}={\mathcal{V}}_r$ , with ${\mathcal{E}}^{*}=\mathcal{E}$ . From the definition of an e-family ${\mathcal{V}}_e$ , it is possible to determine whether ${\mathcal{V}}_e$ is reversible. It is convenient to first introduce the class of log-reversible functions [13, Definition 4, Corollary 1]:

$\begin{array}{c}\hfill {\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)\triangleq \left\{h\in \mathcal{F}\left(\mathcal{X},\mathcal{E}\right):\exists f\in {\mathbb{R}}^{\mathcal{X}},\forall x,x^{\prime }\in \mathcal{X},h\left(x,x^{\prime }\right)=h\left(x^{\prime },x\right)+f\left(x^{\prime }\right)-f\left(x\right)\right\}.\end{array}(25)$

Lemma 4.5. ([13, Theorem 2]). Let ${\mathcal{V}}_e\subset \mathcal{W}(\mathcal{X},\mathcal{E})$ be an e-family that follows the expression of (11). Then $\mathcal{V}={\mathcal{V}}^{*}$ if and only if $\mathcal{E}={\mathcal{E}}^{*}$ and $K\in {\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ and for all i ∈ [d], $g_i\in {\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ .

4.2.3 The em-family of reversible stochastic matrices

The class of functions ${\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ introduced in (25) can be endowed with the structure of a vector space [13, Lemma 4], which verifies the following inclusions:

$\mathcal{N}\left(\mathcal{X},\mathcal{E}\right)\subset {\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)\subset \mathcal{F}\left(\mathcal{X},\mathcal{E}\right),$

where $\mathcal{N}(\mathcal{X},\mathcal{E})$ was defined in (14). Immediately, $\left|\mathcal{X}\right|\le \dim {\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})\le \left|\mathcal{E}\right|$ , and this enables us to further define the quotient space of reversible generators:

${\mathcal{G}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)\triangleq {\mathcal{F}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)/\mathcal{N}\left(\mathcal{X},\mathcal{E}\right).$

It is possible to verify that

${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)=\mathrm{\Delta }\left({\mathcal{G}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)\right),$

where Δ is the diffeomorphism defined in (15). The following result is then a consequence of Theorem 3.1.

Theorem 4.1. ([13, Theorem 3, Theorem 5, Theorem 6]). ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ forms an e-family and an m-family of dimension

$\begin{array}{c}\hfill \dim {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)=\frac{\left|\mathcal{E}\right|+\left|\ell \left(\mathcal{E}\right)\right|}{2}-1,\end{array}(26)$

where $\ell (\mathcal{E})\triangleq \left\{(x,x^{\prime })\in \mathcal{E}:x^{\prime }=x\right\}$ is the set of loops in the connection graph $(\mathcal{X},\mathcal{E})$ .

Theorem 4.2. ([13, Theorem 4, Theorem 5]). Let $P\in {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ , with stationary distribution π. Pick an arbitrary element $e_{*}=(x_{*},x_{*}^{\prime })\in \mathcal{E}\backslash \ell (\mathcal{E})$ , and define

$\begin{array}{cc}\hfill T\left(\mathcal{E}\right)& \triangleq \left\{\left(x,x^{\prime }\right)\in \mathcal{E}:x^{\prime }\le x,\left(x,x^{\prime }\right)\ne e_{*}\right\},\hfill \\ \hfill g_{*}& \triangleq {\delta }_{x_{*}}^{⊺}{\delta }_{x_{*}^{\prime }}+{\delta }_{x_{*}^{\prime }}^{⊺}{\delta }_{x_{*}}.\hfill \end{array}$

For $(i,j)\in T(\mathcal{E})$ , the collection of functions

$g_{ij}={\delta }_i^{⊺}{\delta }_j+{\delta }_j^{⊺}{\delta }_i,$

forms a basis for ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ . We can write P as a member of the m-family of reversible stochastic matrices by expressing its edge measure Q as

$\begin{array}{c}\hfill Q=\frac{g_{*}}{2}+{\displaystyle \sum _{\left(i,j\right)\in T\left(\mathcal{E}\right)}}\left(g_{ij}-g_{*}\right)\frac{Q\left(i,j\right)}{1+{\delta }_i\left(j\right)},\end{array}$

and we can write P as a member of the e-family,

$\begin{array}{ll}\hfill \log P\left(x,x^{\prime }\right)& ={\displaystyle \sum _{\left(i,j\right)\in T\left(\mathcal{E}\right)}}\frac{1}{2\left(1+{\delta }_i\left(j\right)\right)}\log \frac{P\left(i,j\right)P\left(j,i\right)}{P\left(x_{*},x_{*}^{\prime }\right)P\left(x_{*}^{\prime },x_{*}\right)}{g}_{ij}\left(x,x^{\prime }\right)\hfill \\ \hfill & +\frac{1}{2}\log \pi \left(x^{\prime }\right)-\frac{1}{2}\log \pi \left(x\right)+\frac{1}{2}\log P\left(x_{*},x_{*}^{\prime }\right)P\left(x_{*}^{\prime },x_{*}\right),\hfill \end{array}$

when $(x,x^{\prime })\in \mathcal{E}$ , and P(x, x′) = 0 otherwise.

4.2.4 Reversible information projections

Let $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ with ${\mathcal{E}}^{*}=\mathcal{E}$ . We recall the definitions (see Section 3.3) of the m-projection P _m and the e-projection P _e of P onto ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ ,

$\begin{array}{c}\hfill P_m\triangleq \underset{\bar{P}\in {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}D\left(P\Vert \bar{P}\right),P_e\triangleq \underset{\bar{P}\in {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},\mathcal{E}\right)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}D\left(\bar{P}\Vert P\right).\end{array}$

There are known closed-form expressions for P _m and P _e . Moreover, the fact that ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ forms an em-family (Theorem 4.1) leads to a pair of Pythagorean inequalities (see Figure 4), and the invariance of D under time reversals highlighted in (24) implies a bisection property.

FIGURE 4

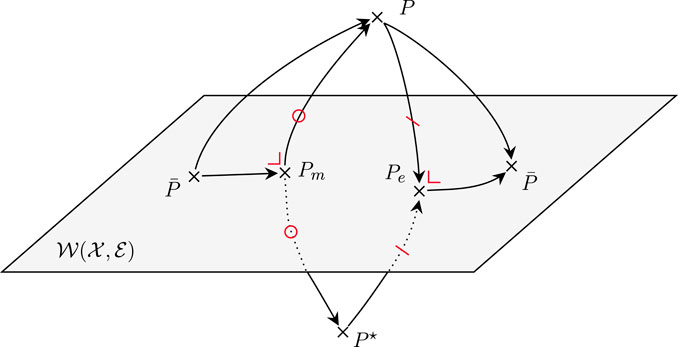
FIGURE 4. Information projections onto ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ , and illustrations of Pythagorean identities and bisection property of Theorem 4.3.

Theorem 4.3. ([13, Theorem 7, Proposition 2]). Let $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ with ${\mathcal{E}}^{*}=\mathcal{E}$ :

$\begin{array}{cc}\hfill P_m& =\frac{P+P^{*}}{2},\hfill \\ \hfill P_e& =\mathfrak{s}\left({\tilde{P}}_e\right),\text{\hspace{0.17em}with\hspace{0.17em}}{\tilde{P}}_e\left(x,x^{\prime }\right)=\sqrt{P\left(x,x^{\prime }\right)P^{*}\left(x,x^{\prime }\right)},\hfill \end{array}$

where $\mathfrak{s}$ is defined in Eq. (12). Moreover, for any $\bar{P}\in {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},\mathcal{E})$ , P _m and P _e satisfy the following Pythagorean identities:

$\begin{array}{cc}\hfill D\left(P\Vert \bar{P}\right)& =D\left(P\Vert P_m\right)+D\left(P_m\Vert \bar{P}\right),\hfill \\ \hfill D\left(\bar{P}\Vert P\right)& =D\left(\bar{P}\Vert P_e\right)+D\left(P_e\Vert P\right).\hfill \end{array}$

Furthermore, the following bisection property holds

$\begin{array}{c}\hfill D\left(P\Vert P_m\right)=D\left(P^{*}\Vert P_m\right),D\left(P_e\Vert P\right)=D\left(P_e\Vert P^{*}\right).\end{array}$

Finally, we mention that the entropy production σ(P) for a Markov chain with transition matrix P, which plays a central role in discussing irreversible phenomena in non-equilibrium systems, can be expressed in terms of the canonical divergence [81, (22)] as follows:

$\sigma \left(P\right)=\frac{1}{2}{\displaystyle \sum _{x,x^{\prime }\in \mathcal{X}}}\left(Q\left(x,x^{\prime }\right)-Q\left(x^{\prime },x\right)\right)\log \frac{Q\left(x,x^{\prime }\right)}{Q\left(x^{\prime },x\right)}=\frac{1}{2}\left(D\left(P\Vert P^{*}\right)+D\left(P^{*}\Vert P\right)\right).$

4.2.5 Characterization of the reversible family as geodesic hulls

It is known that the set of bistochastic matrices—also known as the Birkhoff polytope—is the convex hull of the set of permutation matrices (theorem of Birkhoff and von Neumann [42–44]). By recalling from Section 3.2.6 the definition of geodesic hulls (Definition 3.3, Definition 3.4) of families of stochastic matrices, results in a similar spirit are known for generating the positive and reversible family as geodesic hulls of particular subfamilies.

Theorem 4.4. ([13, Theorem 9, Theorem 10]). It holds that

(i)

$\mathrm{m}-\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}\left({\mathcal{W}}_{\mathsf{i}\mathsf{i}\mathsf{d}}\left(\mathcal{X},{\mathcal{X}}^2\right)\right)={\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},{\mathcal{X}}^2\right),$

where ${\mathcal{W}}_{\mathsf{i}\mathsf{i}\mathsf{d}}(\mathcal{X},{\mathcal{X}}^2)$ is the family of memoryless stochastic matrices discussed in Section 4.1.1 .

(ii) For $\left|\mathcal{X}\right|\ge 3$ , ⁵

$\mathrm{e}-\mathrm{h}\mathrm{u}\mathrm{l}\mathrm{l}\left({\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}\left(\mathcal{X},{\mathcal{X}}^2\right)\right)={\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}\left(\mathcal{X},{\mathcal{X}}^2\right),$

where ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ is the family of positive symmetric stochastic matrices discussed in Section 4.1.3.

4.3 Markov morphisms, lumping, and embeddings of Markov chains

In the context of distributions, Čencov [45] introduced Markov morphisms in an axiomatic manner as the natural mappings to consider for statistics. The Fisher information metric can then be characterized as the unique invariant metric tensor under Markov morphisms [45–47]. In the context of stochastic matrices, we saw that the metric and connections introduced in Section 3 were asymptotically consistent with Markov models. This section connects with the axiomatic approach of Čencov and proposes a class of data processing operations that are arguably natural in the Markov setting.

4.3.1 Lumpability

We briefly recall lumpability in the context of distributions and data processing. Consider a distribution $\mu \in \mathcal{P}(\mathcal{Y})$ , and let Y ₁, Y ₂, …, be a sequence of random variables independently sampled from μ. Suppose we define a deterministic, surjective map $\kappa :\mathcal{Y}\to \mathcal{X}$ , where $\mathcal{X}$ is a space not larger than $\mathcal{Y}$ , and we inspect the random process defined by ${(\kappa (Y_t))}_{t\in \mathbb{N}}$ . Note that κ induces a partition of the space $\mathcal{Y}={\bigcup }_{x\in \mathcal{X}}{\mathcal{S}}_x$ , $x\ne x^{\prime }\Rightarrow {\mathcal{S}}_x\cap {\mathcal{S}}_{x^{\prime }}=\varnothing$ with ${\mathcal{S}}_x=\left\{y\in \mathcal{Y}:\kappa (y)=x\right\}={\kappa }^{-1}(\left\{x\right\})$ . The new process is again a sequence of independent random variables sampled identically from the push-forward distribution κ(μ) = μ◦κ ⁻¹, where we used an overloaded definition $\kappa :\mathcal{P}(\mathcal{Y})\to \mathcal{P}(\mathcal{X})$ . Namely, the probability of the realization $x\in \mathcal{X}$ is the probability of the preimage ${\mathcal{S}}_x$ ; for $x\in \mathcal{X}$ ,

$\kappa \left(\mu \right)\left(x\right)={\displaystyle \sum _{y\in \mathcal{Y}}}\delta \left[\kappa \left(y\right)=x\right]\mu \left(y\right).$

When $\mathcal{X}=\mathcal{Y}$ , symbols are merely being permuted. As with any data-processing operation, monotonicity of information dictates that two distributions can only be brought closer together with respect to D by the action of κ:

$D\left(\kappa \left(\mu \right)\Vert \kappa \left(\nu \right)\right)\le D\left(\mu \Vert \nu \right).$

Crucially, in the independent and identically distributed setting, the lumping operation can be understood both as a form of processing of the stream of observations and as an algebraic manipulation of the distribution that generated the random process.

For Markov chains, the concept of lumpability is vastly richer. The first fact one must come to terms with is that a Markov chain may lose its Markov property after a processing operation on the data stream [48, 49], even for an operation as basic as a lumping. A chain is said to be lumpable [50] with respect to a lumping map $\kappa :\mathcal{Y}\to \mathcal{X}$ , when the Markov property is preserved for the lumped process.

Theorem 4.5. ([50, Theorem 6.3.2]). Let $P\in \mathcal{W}(\mathcal{Y},\mathcal{E})$ . P is lumpable if and only if for all $x,x^{\prime }\in \mathcal{X}$ and for all $y_1,y_2\in {\mathcal{S}}_x$ , it holds that $P(y_1,{\mathcal{S}}_{x^{\prime }})=P(y_2,{\mathcal{S}}_{x^{\prime }})$ , where for $y\in \mathcal{Y},\mathcal{S}\subset \mathcal{Y}$ , $P(y,\mathcal{S})={\sum }_{y^{\prime }\in \mathcal{S}}P(y,y^{\prime })$ .

The subset of $\mathcal{W}(\mathcal{Y},\mathcal{E})$ of all lumpable stochastic matrices is written ${\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ . We overload the operation $\kappa :{\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})\to \mathcal{W}(\mathcal{X},\mathcal{D})$ and the κ-lumped stochastic matrix is denoted as κ(P) with, for any $x,x^{\prime }\in \mathcal{X}$ ,

$\kappa \left(P\right)\left(x,x^{\prime }\right)=P\left(y,{\mathcal{S}}_{x^{\prime }}\right),y\in {\mathcal{S}}_x.$

4.3.2 Embeddings of Markov chains

Embeddings of stochastic matrices that correspond to conditional models were proposed and analyzed in [51–53]. However, the question of Markov chains, where one considers the stochastic process, was only recently explored in [21]. Looking at reverse operations to lumping, we are interested in embedding an irreducible family of chains $\mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{D})$ into a space of irreducible chains $\mathcal{W}(\mathcal{Y},\mathcal{E})$ defined on a larger state space $\mathcal{Y}$ , with some compatible edge set $\mathcal{E}$ . In [21], it is postulated that natural morphisms should satisfy the following requirements:

A.1 Morphisms should preserve the Markov property.

A.2 Morphisms should be expressible as algebraic operations on stochastic matrices.

A.3 Morphisms should have operational meaning on trajectories of observations.

The following definition of a Markov morphism was proposed in [21].

Definition 4.1. (Markov morphism for stochastic matrices [21, Definition 3.2]). A map $\lambda :\mathcal{W}(\mathcal{X},\mathcal{D})\to {\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ is called a κ-compatible Markov morphism for stochastic matrices when for any $y,y^{\prime }\in \mathcal{E}$ ,

$\lambda \left(P\right)\left(y,y^{\prime }\right)=P\left(\kappa \left(y\right),\kappa \left(y^{\prime }\right)\right)\mathrm{\Lambda }\left(y,y^{\prime }\right),$

where $\mathrm{\Lambda }\in {\mathcal{F}}_{+}(\mathcal{Y},\mathcal{E})$ , and for any $y\in \mathcal{Y},x^{\prime }\in \mathcal{X}$ , it holds that

$\left(\kappa \left(y\right),x^{\prime }\right)\in \mathcal{D}\Rightarrow {\left(\mathrm{\Lambda }\left(y,y^{\prime }\right)\right)}_{y^{\prime }\in {\mathcal{S}}_{x^{\prime }}}\in \mathcal{P}\left({\mathcal{S}}_{x^{\prime }}\right).$

The constraints on the function Λ in Definition 4.1 ensure that the objects produced by λ are stochastic matrices and are κ-lumpable. Furthermore, given the full description of P and Λ, one can directly compute the embedded λ(P), thereby satisfying A.1 and A.2. Alternatively, when given a sequence of observations ${\left\{X_t\right\}}_{1\le t\le n}\sim P$ and without even knowing P, one can apply a random mapping ϕ _Λ on the trajectory and simulate a trajectory ${\left\{{\varphi }_{\mathrm{\Lambda }}(X_t)\right\}}_{1\le t\le n}\sim \lambda (P)$ generated from the embedded chain, essentially satisfying axiom A.3. A key feature of a Markov morphism λ is that the divergence between two points and their image is unchanged [21, Lemma 3.1]. Namely, for two points $P,P^{\prime }\in \mathcal{V}\subset \mathcal{W}(\mathcal{X},\mathcal{D})$ ,

$D\left(\lambda \left(P\right)\Vert \lambda \left(P^{\prime }\right)\right)=D\left(P\Vert P^{\prime }\right).$

As a consequence, the Fisher metric and affine connections are preserved [21, Lemma 3.1] (see Figure 5), in the sense where for $U_P,V_P\in T_P\mathcal{V}$ ,

$\begin{array}{c}\hfill {\mathfrak{g}}_P\left(U_P,V_P\right)={\mathfrak{g}}_{\lambda \left(P\right)}\left({\lambda }_{*}\left(U_P\right),{\lambda }_{*}\left(V_P\right)\right),\end{array}$

and for any vector fields $U,V\in \mathrm{\Gamma }(T\mathcal{V})$ ,

$\begin{array}{cc}\hfill {\lambda }_{*}\left({\nabla }_U^{\left(m\right)}V\right)& ={\nabla }_{{\lambda }_{*}\left(U\right)}^{\left(m\right)}{\lambda }_{*}\left(V\right),\hfill \\ \hfill {\lambda }_{*}\left({\nabla }_U^{\left(e\right)}V\right)& ={\nabla }_{{\lambda }_{*}\left(U\right)}^{\left(e\right)}{\lambda }_{*}\left(V\right),\hfill \end{array}$

where

${\lambda }_{*}:T_P\mathcal{V}\to T_{\lambda \left(P\right)}\lambda \left(\mathcal{V}\right)$

defined by ${({\lambda }_{*}(U_P))}_{{\lambda }_{*}(P)}={(d\lambda )}_P(U_P)$ is the pushforward map associated with the diffeomorphism λ. Furthermore, Markov morphisms are e-geodesic affine maps [21, Theorem 3.2]. Namely, for any $P_0,P_1\in \mathcal{W}(\mathcal{X},\mathcal{D})$ ,

$\lambda \left({\gamma }_{P_0,P_1}^{\left(e\right)}\right)={\gamma }_{\lambda \left(P_0\right),\lambda \left(P_1\right)}^{\left(e\right)}.$

FIGURE 5

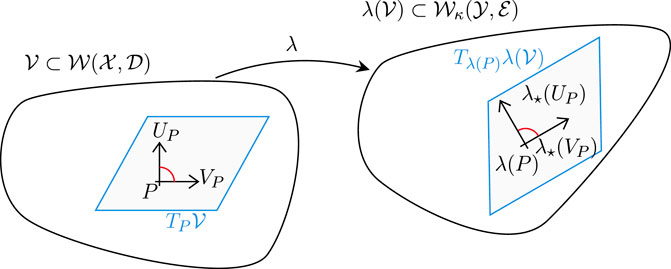
FIGURE 5. Markov morphisms (Definition 4.1) preserve the Fisher metric and the pair of dual affine connections.

However, they are no m-geodesic affine, which means that generally

$\lambda \left({\gamma }_{P_0,P_1}^{\left(m\right)}\right)\ne {\gamma }_{\lambda \left(P_0\right),\lambda \left(P_1\right)}^{\left(m\right)}.$

A more restricted class of embeddings, termed memoryless embeddings, preserve m-geodesics [21, Lemma 3.6], whereas e-geodesics are even preserved by the more general class of exponential embeddings [21, Theorem 3.2]. The concept of lumpability is easily extended to bivariate functions [21, Definition 3.3].

Definition 4.2. (κ-lumpable function). $f\in \mathcal{F}(\mathcal{Y},\mathcal{E})$ is a κ-lumpable function if and only if for any $x,x^{\prime }\in \mathcal{X}$ and for any $y_1,y_2\in {\mathcal{S}}_x$ , it holds that

$f\left(y_1,{\mathcal{S}}_{x^{\prime }}\right)=f\left(y_2,{\mathcal{S}}_{x^{\prime }}\right).$

The set of all κ-lumpable functions is denoted as ${\mathcal{F}}_{\kappa }(\mathcal{Y},\mathcal{E})$ .

Lumpable functions ${\mathcal{F}}_{\kappa }(\mathcal{Y},\mathcal{E})$ form a vector space of dimension $\left|\mathcal{E}\right|+\left|\mathcal{D}\right|-{\sum }_{(x,x^{\prime })\in \mathcal{D}}\left|{\mathcal{S}}_x\right|$ [21, Lemma 3.3].

Definition 4.3. (Linear congruent embedding). A linear map $\varphi :\mathcal{F}(\mathcal{X},\mathcal{D})\to {\mathcal{F}}_{\kappa }(\mathcal{Y},\mathcal{E})$ is called a κ-congruent embedding when it is a right inverse of κ and satisfies the two following monotonicity conditions. For any lumpable function $f\in \mathcal{F}(\mathcal{X},\mathcal{D})$ ,

$\begin{array}{cc}\hfill f\ge 0& \Rightarrow \varphi \left(f\right)\ge 0,\hfill \\ \hfill f>0& \Rightarrow \varphi \left(f\right)>0.\hfill \end{array}$

Theorem 4.6. (Characterization of Markov morphisms as congruent linear embeddings). Let $\varphi :\mathcal{W}(\mathcal{X},\mathcal{D})\to {\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ . The two following statements are equivalent:

(i) ϕ is a κ-congruent linear embedding.

(ii) ϕ is a κ-compatible Markov morphism.

Theorem 4.6 is a counterpart for a similar fact for finite measure spaces in the distribution setting, which can be found in Ay et al. [6, Example 5.2].

As Markov morphisms and linear congruent embeddings can be identified, it will be convenient to refer to them simply as Markov embeddings. We proceed to give two examples of embeddings.

4.3.2.1 Hudson expansions

Let ${\left\{X_t\right\}}_{t\in \mathbb{N}}$ be a Markov chain with transition matrix $\bar{P}\in \mathcal{W}(\mathcal{X},{\mathcal{X}}^2)$ . The stochastic process ${\left\{(X_t,X_{t+1})\right\}}_{t\in \mathbb{N}}$ also forms a Markov chain on state space ${\mathcal{X}}^2$ . Considered by Kemeny and Snell [50] to be the natural reverse operation of lumping, the Hudson [21, 50] expansion can be expressed as a Markov embedding [21, Theorem 3.4]. In particular, this yields an example of an embedding that is not m-geodesically convex [21, Lemma 3.4].

4.3.2.2 Symmetrization embedding for grained reversible stochastic matrices

Suppose a given stochastic matrix $\bar{P}\in {\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}([n],\mathcal{D})$ with stationary distribution $\bar{\pi }(x)=p(x)/m$ for $p\in {\mathbb{N}}^n$ and $m\in \mathbb{N}$ . The embedding $\lambda :\mathcal{W}(\mathcal{X},\mathcal{D})\to {\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ constructed [21, Corollary 3.2] by

$\begin{array}{cc}\hfill \kappa \left(j\right)& =\underset{i\in \left[n\right]}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\left\{{\displaystyle \sum _{k=1}^i}p\left(k\right)\ge j\right\},j\in \left[m\right],\hfill \\ \hfill \mathrm{\Lambda }\left(j,j^{\prime }\right)& =\frac{\delta \left[\left(\kappa \left(j\right),\kappa \left(j^{\prime }\right)\right)\in \mathcal{D}\right]}{p\left(\kappa \left(j^{\prime }\right)\right)},\hfill \end{array}$

is such that $\lambda (\bar{P})\in {\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}([m],\mathcal{E})$ , with $\mathcal{E}=\left\{(j,j^{\prime })\in {[m]}^2:(\kappa (j),\kappa (j^{\prime }))\in \mathcal{D}\right\}$ . The constructed embedding is memoryless, thus m-geodesically affine. This approach can be used to reduce inference problems in Markov chains from a reversible to a symmetric setting [54].

4.3.3 The foliated manifold of lumpable stochastic matrices

There is generally no left inverse for a lumping map κ. However, for any κ-lumpable $P_0\in {\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ , there always exists a Markov morphism ${\lambda }^{(P_0)}:\mathcal{W}(\mathcal{X},\mathcal{D})\to {\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ , termed canonical embedding [21, Lemma 3.2], such that

$P_0=\left({\lambda }^{\left(P_0\right)}◦\kappa \right)\left(P_0\right).(27)$

For fixed ${\bar{P}}_0\in \mathcal{W}(\mathcal{X},\mathcal{D})$ and $P_0\in \mathcal{W}(\mathcal{Y},\mathcal{E})$ , it is interesting to introduce the two following submanifolds:

$\begin{array}{cc}\hfill \mathcal{L}\left({\bar{P}}_0\right)& \triangleq {\kappa }^{-1}\left(\left\{{\bar{P}}_0\right\}\right),\hfill \\ \hfill \mathcal{J}\left(P_0\right)& \triangleq {\lambda }^{\left(P_0\right)}\left(\mathcal{W}\left(\mathcal{X},\mathcal{D}\right)\right).\hfill \end{array}$

Less tersely, $\mathcal{L}({\bar{P}}_0)$ corresponds to the set of stochastic matrices that lump into ${\bar{P}}_0$ , whereas $\mathcal{J}(P_0)$ is the image of the entire set $\mathcal{W}(\mathcal{X},\mathcal{D})$ by the canonical embedding (27) associated with P ₀. It can be shown [21, Lemma 5.1] that $\mathcal{L}({\bar{P}}_0)$ and $\mathcal{J}(P_0)$ , respectively, form an m-family and an e-family in $\mathcal{W}(\mathcal{Y},\mathcal{E})$ , of dimensions

$\begin{array}{cc}\hfill \dim \mathcal{L}\left({\bar{P}}_0\right)& =\left|\mathcal{D}\right|-\left|\mathcal{X}\right|,\hfill \\ \hfill \dim \mathcal{J}\left(P_0\right)& =\left|\mathcal{E}\right|-{\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{D}}}\left|{\mathcal{S}}_x\right|.\hfill \end{array}$

It is not hard to show that the submanifold ${\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ of $\mathcal{W}(\mathcal{Y},\mathcal{E})$ is generally not autoparallel with respect to either the e-connection or the m-connection. Perhaps surprisingly, it is nevertheless possible to construct a mutually dual foliated structure on ${\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ (see Figure 6).

FIGURE 6

FIGURE 6. Mutually dual foliated structure on ${\mathcal{W}}_{\kappa }(\mathcal{Y},\mathcal{E})$ .

Theorem 4.7. ([21, Theorem 5.1]). Let ${\bar{P}}_0\in \mathcal{W}(\mathcal{X},\mathcal{D})$ . Then,

$\begin{array}{cc}\hfill {\mathcal{W}}_{\kappa }\left(\mathcal{Y},\mathcal{E}\right)& =\bigcup _{P_0\in \mathcal{L}\left({\bar{P}}_0\right)}\mathcal{J}\left(P_0\right)\hfill \\ \hfill \forall P_0,P_0^{\prime }\in \mathcal{L}\left({\bar{P}}_0\right),P_0,\ne P_0^{\prime }& \Rightarrow \mathcal{J}\left(P_0\right)\cap \mathcal{J}\left(P_0^{\prime }\right)=\varnothing ,\hfill \\ \hfill \dim {\mathcal{W}}_{\kappa }\left(\mathcal{Y},\mathcal{E}\right)& =\left|\mathcal{E}\right|-{\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{D}}}\left|{\mathcal{S}}_x\right|+\left|\mathcal{D}\right|-\left|\mathcal{X}\right|.\hfill \end{array}$

The following Pythagorean identity [21, Theorem 5.2] follows as a direct application of Theorem 4.7. For ${\bar{P}}_0\in \mathcal{W}(\mathcal{X},\mathcal{D})$ , $P_0,P_0^{\prime }\in \mathcal{L}({\bar{P}}_0)$ , and $P^{\prime }\in \mathcal{J}(P_0)$ ,

$D\left(P_0^{\prime }\Vert P^{\prime }\right)=D\left(P_0^{\prime }\Vert P_0\right)+D\left(P_0\Vert P^{\prime }\right),$

and P ₀ is both the e-projection onto $\mathcal{L}({\bar{P}}_0)$ and the m-projection onto $\mathcal{J}(P_0)$ (see Figure 6).

4.4 Tree models

For a finite alphabet $\mathcal{Y}$ , let ${\mathcal{Y}}^{\ast }=\{ϵ\}\cup \mathcal{Y}\cup {\mathcal{Y}}^2\cup \cdots$ be the set of all finite length sequences on $\mathcal{Y}$ , where ϵ is the null string. For a string $y_1^n=(y_1,\dots ,y_n)$ , strings $y_1^n,y_2^n,\dots ,y_{n-1}^n,y_n$ and ϵ are called postfixes of $y_1^n$ . A finite subset $T\subset {\mathcal{Y}}^{\ast }$ is termed a tree if all postfixes of any element of T belong to T. An element of T is termed a leaf if it is not a postfix of any other element of T. The set of all leaves of T is denoted by ∂T.

For a string $s\in {\mathcal{Y}}^{\ast }$ , let γ(s) be the element of ∂T that matches a postfix of s, if it exists. We refer to γ(s) as the context of the string s, and $\left|s\right|$ denotes the length of the string s. When $|s|\ge \underset{s^{\prime }\in \partial T}{\max }|s^{\prime }|$ , γ(s) is uniquely defined.

Definition 4.4. (Tree model). For a given tree T and

$k=\underset{s^{\prime }\in \partial T}{\max }|s^{\prime }|,(28)$

let us consider the set $\mathcal{W}({\mathcal{Y}}^k,\mathcal{E})$ of kth order Markov transition matrices, where

$\mathcal{E}=\left\{\left(\left(y_1,\dots ,y_k\right),\left(y_1^{\prime },\dots ,y_k^{\prime }\right)\right):y_i=y_{i-1}^{\prime }\forall i=2,\dots ,k\right\}.(29)$

The tree model induced by the tree T is

${\mathcal{M}}_T≔\left\{P\in \mathcal{W}\left({\mathcal{Y}}^k,\mathcal{E}\right):\forall y^k,{\tilde{y}}^k\in {\mathcal{Y}}^k,\gamma \left(y^k\right)=\gamma \left({\tilde{y}}^k\right)\Rightarrow P\left(y^k,\cdot \right)=P\left({\tilde{y}}^k,\cdot \right)\right\}.(30)$

The tree model is a well-studied model of Markov sources in the context of data compression [55, 56], and it can be categorized based on the structure of the underlying tree as follows:

Definition 4.5. (Finite State Machine X (FSMX) model). For a tree model ${\mathcal{M}}_T$ induced by tree T, if ∂T satisfies the condition that γ(sy) is defined for all $(s,y)\in \partial T\times \mathcal{Y}$ (this means that sy is not an internal node of T for every $(s,y)\in \partial T\times \mathcal{Y}$ ), then the tree model ${\mathcal{M}}_T$ is referred to as FSMX model. If a tree model is not FSMX, it is referred to as non-FSMX (see Figure 7).

FIGURE 7

FIGURE 7. Example of an FSMX tree (left) and a non-FSMX tree (right).

Theorem 4.8. ([25, 57]). A tree model ${\mathcal{M}}_T$ is an e-family if and only if it is an FSMX model.

5 Applications

In this section, we give details of some application domains of the geometric perspective.

5.1 Maximum entropy principle

Recall that the maximum entropy probability distribution over a fixed alphabet $\mathcal{X}$ is uniform. In the Markovian setting, for a fixed fully connected digraph $(\mathcal{X},\mathcal{E})$ , the stochastic matrix $U\in \mathcal{W}(\mathcal{X},\mathcal{E})$ , which maximizes the entropy rate [58–61] of the process H defined in (4), is given by $\mathfrak{s}({\delta }_{\mathcal{E}})$ , where ${\delta }_{\mathcal{E}}:\mathcal{X}\to \left\{\mathrm{0,1}\right\}$ is defined by ${\delta }_{\mathcal{E}}(x,x^{\prime })=\delta \left[(x,x^{\prime })\in \mathcal{E}\right]$ , and where $\mathfrak{s}$ is the stochastic rescaling map introduced in (12). Let $\mathcal{L}\subset \mathcal{W}(\mathcal{X},\mathcal{E})$ be an m-family of stochastic matrices. One can express $\mathcal{L}$ as a polytope generated by a set of linear constraints:

$\mathcal{L}=\left\{P\in \mathcal{W}\left(\mathcal{X},\mathcal{E}\right):\forall i\in \left[d\right],{\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}Q\left(x,x^{\prime }\right)g_i\left(x,x^{\prime }\right)=c_i\right\}.$

It is known [23] that the e-projection (Section 3.3) of an arbitrary $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ onto $\mathcal{L}$ belongs to an e-family. Namely, for $\xi \in \mathbb{R}$ , let

$P_{\xi }=\mathfrak{s}\left({\tilde{P}}_{\xi }\right),{\tilde{P}}_{\xi }=Po\exp \left({\displaystyle \sum _{i\in \left[d\right]}}{\xi }^i{g}_i\right),$

and write ψ(ξ) for the logarithm of the PF root of ${\tilde{P}}_{\xi }$ . By the Lagrange multiplier method, the solution to the minimization problem is readily obtained to be at ${\xi }^{*}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_{\xi \in {\mathbb{R}}^d}\left\{⟨\xi ,c⟩-\psi (\xi )\right\}$ . By rewriting,

$\underset{\bar{P}\in \mathcal{L}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}D\left(\bar{P}\Vert P\right)=\underset{\bar{P}\in \mathcal{L}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}\left\{H\left(\bar{P}\right)+{\mathbb{E}}_{\left(X,X^{\prime }\right)\sim \bar{Q}}\log P\left(X,X^{\prime }\right)\right\},$

and observing that for P = U the maxentropic chain ${\mathbb{E}}_{(X,X^{\prime })\sim \bar{Q}}\log P(X,X^{\prime })$ is a function of the edge graph $(\mathcal{X},\mathcal{E})$ only ⁶ , we obtain that

$\underset{\bar{P}\in \mathcal{L}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}D\left(\bar{P}\Vert U\right)=\underset{\bar{P}\in \mathcal{L}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}H\left(\bar{P}\right).$

In other words, the e-projection onto $\mathcal{L}$ follows the principle of maximum entropy.

5.2 Large deviation theory

The topic of large deviation theory is the study of the probabilities of rare events or fluctuations in stochastic systems, where the likelihood of these events occurring is exponentially small in the system parameters. In this context, we provide a concise overview of the classical asymptotic results and offer references to recent developments of finite sample upper bounds for the probability of large deviations. For X ₁, …, X _n , a Markov chain started from an initial distribution μ and with transition matrix P, a function $f:\mathcal{X}\to \mathbb{R}$ , and for some $\eta \ge {\mathbb{E}}_{\pi }f$ , we are interested in the rate of decay of the following probability:

${\mathbb{P}}_{\mu }\left(\frac{1}{n}{\displaystyle \sum _{t=1}^n}f\left(X_t\right)\ge \eta \right).$

Similar in spirit to the heart of the approach taken in the iid setting, we proceed with an exponential change of measure (also known as tilting or twisting) of P and define for $\theta \in \mathbb{R}$ ,

${\tilde{P}}_{\theta }\left(x,x^{\prime }\right)=P\left(x,x^{\prime }\right)e^{\theta f\left(x^{\prime }\right)}.$

We denote by ρ _θ the Perron–Frobenius root of the matrix ${\tilde{P}}_{\theta }$ , its logarithm by ψ(θ) = log  ρ _θ , and its associated right eigenvector by v _θ . We then define $P_{\theta }=\mathfrak{s}({\tilde{P}}_{\theta })\in \mathcal{W}(\mathcal{X},\mathcal{E})$ and note that ${\left\{P_{\theta }\right\}}_{\theta \in \mathbb{R}}$ corresponds to constructing a one-dimensional exponential family of transition matrices generated by f.

5.2.1 Asymptotic theory

The large deviation rate is given by the convex conjugate (Fenchel–Legendre dual) of the log-Perron–Frobenius eigenvalue of the matrix ${\tilde{P}}_{\theta }$ .

Theorem 5.1. ([64, Theorem 3.1.2]). For $\eta \ge {\mathbb{E}}_{\pi }f$ ,

$\underset{n\to \infty }{\lim }-\frac{1}{n}\log {\mathbb{P}}_{\mu }\left(\frac{1}{n}{\displaystyle \sum _{t=1}^n}f\left(X_t\right)\ge \eta \right)=R^{*}\left(\eta \right)=\underset{\theta \in \mathbb{R}}{\sup }\left\{\theta \eta -\psi \left(\theta \right)\right\}.$

Theorem 5.2. ([75, Theorem 6.3]). When

$\underset{\theta \in \mathbb{R}}{\sup }\left\{\theta \eta -\psi \left(\theta \right)\right\}=R^{*}\left(\eta \right),$

is achieved for θ = θ ^* , as n → ∞,

${\mathbb{P}}_{\mu }\left(\frac{1}{n}{\displaystyle \sum _{t=1}^n}f\left(X_t\right)\ge \eta \right)\sim \frac{{\mathbb{E}}_{X\sim \mu }\left[v_{{\theta }^{*}}\left(X\right)\right]}{{\theta }^{*}\sqrt{2\pi n{\sigma }_{{\theta }^{*}}^2}}{e}^{-n{R}^{*}\left(\eta \right)},$

where ${\sigma }_{{\theta }^{*}}^2={\partial }^2\psi (\theta ){\left.\right|}_{\theta ={\theta }^{*}}$ is the asymptotic variance ⁷ of f, and $v_{{\theta }^{*}}$ is the right Perron–Frobenius eigenvector of ${\tilde{P}}_{{\theta }^{*}}$ .

5.2.2 Finite sample theory

Moulos and Anantharam [62] achieved the most recent and tightest result. They established a finite sample bound with a prefactor that does not depend on the deviation η, which holds for a large class of Markov chains, surpassing the earlier results [17, 63, 64].

Theorem 5.3. ([62, Theorem 1]). Let $P\in \mathcal{W}(\mathcal{X},{\mathcal{X}}^2)$ , with stationary distribution π and a function $f:\mathcal{X}\to \mathbb{R}$ . Then, for $\eta \ge {\mathbb{E}}_{\pi }f$ ,

$\mathbb{P}\left(\frac{1}{n}{\displaystyle \sum _{t=1}^n}f\left(X_t\right)\ge \eta \right)\le C\left(P,f\right)e^{-n{R}^{*}\left(\eta \right)},$

with

$C\left(P,f\right)\triangleq \underset{x,x^{\prime },x^{″}\in \mathcal{X}}{\max }\frac{P\left(x,x^{\prime }\right)}{P\left(x,x^{″}\right)}.$

Lastly, the subsequent uniform multiplicative ergodic theorem is known to hold.

Theorem 5.4. ([62, Theorem 3]). For $P\in \mathcal{W}(\mathcal{X},{\mathcal{X}}^2)$ and $f:\mathcal{X}\to \mathbb{R}$ ,

$\underset{\theta \in \mathbb{R}}{\sup }\left|{\psi }_n\left(\theta \right)-\psi \left(\theta \right)\right|\le \frac{\log C\left(P,f\right)}{n},$

where ψ _n is the scaled log-moment-generating-function,

${\psi }_n\left(\theta \right)\triangleq \frac{1}{n}\log {\mathbb{E}}_{\mu }\left[\exp \left(\theta {\displaystyle \sum _{t=1}^n}f\left(X_t\right)\right)\right],$

and C(P, f) is the constant defined in Theorem 5.3.

For a more detailed exposition of the aforementioned results in a broader context, please refer to [62].

5.2.3 Timeline

5.3 Parameter estimation

Let $g:{\mathcal{X}}^2\to \mathbb{R}$ , and suppose we wish to estimate ${\mathbb{E}}_{(X,X^{\prime })\sim Q}\left[g(X,X^{\prime })\right]$ , from one trajectory X ₁, …, X _n from a stationary Markov chain with transition matrix $P\in \mathcal{W}(\mathcal{X},\mathcal{E})$ and stationary distribution $\pi \in {\mathcal{P}}_{+}(\mathcal{X})$ . An important special case is when there exists $f\in {\mathbb{R}}^{\mathcal{X}}$ such that for any $x,x^{\prime }\in \mathcal{X}$ , g(x, x′) = f(x′). Then, the quantity of interest is simply ${\mathbb{E}}_{\pi }f$ . The sample mean evaluated on a stationary Markov trajectory X ₁, …, X _n is defined by

${\widehat{f}}_n\left(X_1,\dots ,X_n\right)=\frac{1}{n}{\displaystyle \sum _{t=1}^n}f\left(X_t\right).$

The statistical behavior of ${\widehat{f}}_n$ is of particular interest for the topic of Markov Chain Monte Carlo methods. By using the strong law of large numbers, the almost sure convergence to the true expectation holds:

${\widehat{f}}_n\left(X_1,\dots ,X_n\right)\stackrel{\mathsf{a}.\mathsf{s}.}{\to }{\mathbb{E}}_{\pi }f\left(X_1\right).$

Furthermore, defining the asymptotic variance of f as

${\sigma }_{\infty }^2\left(f\right)\triangleq \underset{m\to \infty }{\lim }\mathbb{V}\mathbf{a}\mathbf{r}\left[\frac{1}{\sqrt{m}}{\displaystyle \sum _{t=1}^m}f\left(X_t\right)\right],(31)$

the following Markov chain version of the central limit theorem [65] holds

$\sqrt{n}\left({\widehat{f}}_n\left(X_1,\dots ,X_n\right)-{\mathbb{E}}_{\pi }f\right)\stackrel{\mathsf{a}.\mathsf{s}.}{\to }\mathcal{N}\left(0,{\sigma }_{\infty }^2\left(f\right)\right).$

Although asymptotic analysis may be of mathematical interest, for modern tasks, it is crucial to have a finite sample theory that explains the behavior of the sample mean. With regard to the original bivariate function problem, the sample mean for a sliding window of pairs of observations can be defined as follows:

${\widehat{g}}_n\left(X_1,\dots ,X_n\right)\triangleq \frac{1}{n-1}{\displaystyle \sum _{t=1}^{n-1}}g\left(X_t,X_{t+1}\right).$

One can construct by exponential tilting the following one-dimensional parametric family of transition matrices:

${\mathcal{V}}_e=\left\{P_{\theta }\left(x,x^{\prime }\right)=P\left(x,x^{\prime }\right)\exp \left(\theta g\left(x,x^{\prime }\right)+R_{\theta }\left(x^{\prime }\right)-R_{\theta }\left(x\right)-\psi \left(\theta \right)\right):\theta \in \mathbb{R}\right\},$

where R _θ and ψ are fixed using the PF theory (see Section 3.2). Essentially, ${\mathcal{V}}_e$ is a one-dimensional e-family of transition matrices, and for θ = 0, the original P is recovered. At any natural parameter $\theta \in \mathbb{R}$ , the quantity of interest ${\mathbb{E}}_{(X,X^{\prime })\sim Q_{\theta }}\left[g(X,X^{\prime })\right]$ is the expectation parameter η(θ) of P _θ . Recall from (18) that the Fisher information at coordinates θ can be expressed as the second derivative of the potential function, that is, ${\partial }^2\psi (\theta )=\mathfrak{g}(\theta )$ . There exists [15, Lemma 6.2] a constant $C\in \mathbb{R}$ such that

$\frac{1}{n}\mathfrak{g}\left(0\right){\left(1-\frac{C}{\sqrt{n}}\right)}^2\le \mathbb{V}\mathbf{a}\mathbf{r}\left[{\widehat{g}}_n\left(X_1,\dots ,X_n\right)\right]\le \frac{1}{n}\mathfrak{g}\left(0\right){\left(1+\frac{C}{\sqrt{n}}\right)}^2.$

Defining the asymptotic variance for the bivariate g as

${\sigma }_{\infty }^2\left(g\right)\triangleq \underset{m\to \infty }{\lim }\mathbb{V}\mathbf{a}\mathbf{r}\left[\frac{1}{\sqrt{m}}{\displaystyle \sum _{t=1}^{m-1}}g\left(X_t,X_{t+1}\right)\right],$

it follows that

${\sigma }_{\infty }^2\left(g\right)=\mathfrak{g}\left(0\right).$

Note that it coincides with the reciprocal of the Fisher information with respect to the expectation parameter; see Eq. 18. Essentially, this establishes that the sample mean evaluated on pairs of observations ${\widehat{g}}_n(X_1,\dots ,X_n)$ is asymptotically efficient; it attains the Markov counterpart of the Cramér–Rao lower bound. Similar results for the multi-parametric case, non-stationary case, and curved exponential families are obtained in [15].

5.4 Hypothesis testing

We let $P_0,P_1\in \mathcal{W}(\mathcal{X},\mathcal{E})$ be two irreducible stochastic matrices with respective stationary distributions π ₀ and π ₁. We call P ₀ the null hypothesis and P ₁ the alternative hypothesis. We observe a trajectory X ₀, X ₁, …, X _n sampled from an unknown Markov chain (P ₀ or P ₁). A randomized test function is defined by

$\begin{array}{cc}\hfill {\mathcal{T}}_n:{\mathcal{X}}^n& \to \left[\mathrm{0,1}\right]\hfill \\ \hfill \left(x_0,x_1,\dots ,x_n\right)& \mapsto {\mathcal{T}}_n\left(x_0,x_1,\dots ,x_n\right).\hfill \end{array}$

We interpret ${\mathcal{T}}_n$ as the probability of rejecting the null hypothesis ⁸ under a random experiment [76, p.58]. In particular, if the range of ${\mathcal{T}}_n$ is $\left\{\mathrm{0,1}\right\}$ , the randomized test becomes deterministic. The set of all test functions will be denoted by

${\mathfrak{T}}_n\left(\mathcal{X}\right)\triangleq \left\{{\mathcal{T}}_n:{\mathcal{X}}^n\to \left\{\mathrm{0,1}\right\}\right\}.$

We write ${\mathbb{P}}_0,{\mathbb{P}}_1,{\mathbb{E}}_0,{\mathbb{E}}_1$ to denote probability statements and expectations under the null and alternative hypotheses. We define the error probability of the first kind α (also known as the size of the test, type I error, or significance) and second kind β (type II error), respectively, as follows:

$\begin{array}{cc}\hfill \alpha \left({\mathcal{T}}_n\right)& \triangleq {\mathbb{E}}_0\left[{\mathcal{T}}_n\left(X_0,\dots ,X_n\right)\right]\hfill \\ \hfill \beta \left({\mathcal{T}}_n\right)& \triangleq {\mathbb{E}}_1\left[1-{\mathcal{T}}_n\left(X_0,\dots ,X_n\right)\right].\hfill \end{array}$

Then, 1 − β is called the power of the test. Fixing $\bar{\alpha }\in {\mathbb{R}}^{+}$ , we define the most powerful test to be the test function ${\mathcal{T}}_n^{*}$ that maximizes the power under the size constraint $\alpha ({\mathcal{T}}_n)\le \bar{\alpha }$ :

(i) $\alpha ({\mathcal{T}}_n)\le \bar{\alpha }$ .

(ii) $\beta ({\mathcal{T}}_n^{*})\le \beta ({\mathcal{T}}_n)$ for any ${\mathcal{T}}_n\in {\mathfrak{T}}_n(\mathcal{X})$ .

The Neyman–Pearson lemma asserts the existence of a test, which can be achieved through the likelihood ratio test.

Lemma 5.1. [78]. There exist ${\mathcal{T}}_n^{*}\in {\mathfrak{T}}_n(\mathcal{X})$ and $\eta \in {\mathbb{R}}^{+}$ such that

(i)

(a) $\alpha ({\mathcal{T}}_n^{*})=\alpha$ .

(b) ${\mathcal{T}}_n^{*}(x_0,x_1,\dots ,x_n)=\left\{\begin{array}{c}\frac{{\mathbb{P}}_1\left(X_0=x_0,\dots ,X_n=x_n\right)}{{\mathbb{P}}_0\left(X_0=x_0,\dots ,X_n=x_n\right)}>\eta \hfill \\ \frac{{\mathbb{P}}_1\left(X_0=x_0,\dots ,X_n=x_n\right)}{{\mathbb{P}}_0\left(X_0=x_0,\dots ,X_n=x_n\right)}\le \eta ,\hfill \end{array}\right.$

(ii) If ${\mathcal{T}}_n\in {\mathfrak{T}}_n(\mathcal{X})$ satisfies (a) and (b) for $\eta \in {\mathbb{R}}^{+}$ , then ${\mathcal{T}}_n$ is most powerful at level α.

If we ignore the effect of the initial distribution that is negligible asymptotically, the Neyman–Pearson accepts the null hypothesis if

$\frac{1}{n}{\displaystyle \sum _{t=1}^{n-1}}\log \frac{P_0\left(x_t,x_{t+1}\right)}{P_1\left(x_t,x_{t+1}\right)}\ge \eta$

for a threshold η and observation (x ₁, …, x _n ). Employing the large deviation bound (e.g., [17, Section 8]), we can evaluate the Neyman-Pearson test’s performance in terms of rare events as follows:

$\begin{array}{ll}\hfill \underset{n\to \infty }{\lim }-\log {\mathbb{P}}_0\left(\frac{1}{n}{\displaystyle \sum _{t=1}^{n-1}}\log \frac{P_0\left(X_t,X_{t+1}\right)}{P_1\left(X_t,X_{t+1}\right)}\le \eta \right)& =D\left(P_{\theta \left(\eta \right)}\Vert P_0\right),\hfill \\ \hfill \underset{n\to \infty }{\lim }-\log {\mathbb{P}}_1\left(\frac{1}{n}{\displaystyle \sum _{t=1}^{n-1}}\log \frac{P_0\left(X_t,X_{t+1}\right)}{P_1\left(X_t,X_{t+1}\right)}>\eta \right)& =D\left(P_{\theta \left(\eta \right)}\Vert P_1\right),\hfill \end{array}$

where

${\mathcal{V}}_e\triangleq \left\{P_{\theta }\left(x,x^{\prime }\right)≔\mathfrak{s}\left[\exp \left(\theta \log P_0\left(x,x^{\prime }\right)+\left(1-\theta \right)\log P_1\left(x,x^{\prime }\right)\right)\right]:\theta \in \mathbb{R}\right\}$

is the exponential family passing through P ₀ and P ₁ (see Figure 8), and $P_{\theta (\eta )}\in {\mathcal{V}}_e$ is the intersection of ${\mathcal{V}}_e$ and the mixture family ${\mathcal{V}}_m$ given by

${\mathcal{V}}_m\triangleq \left\{P\in \mathcal{W}\left(\mathcal{X},\mathcal{E}\right):{\displaystyle \sum _{\left(x,x^{\prime }\right)\in \mathcal{E}}}P\left(x,x^{\prime }\right)\log \frac{P_0\left(x,x^{\prime }\right)}{P_1\left(x,x^{\prime }\right)}=\eta \right\}.$

FIGURE 8

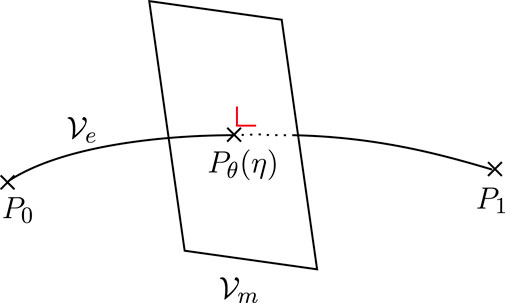
FIGURE 8. Geometric interpretation of the Neyman–Pearson test as the orthogonal bisector to the e-geodesic passing through both the null and alternative hypotheses.

Note that the e-family ${\mathcal{V}}_e$ and the m-family ${\mathcal{V}}_m$ are orthogonal in that the Pythagorean identity holds

$D\left(P\Vert P_{\theta }\right)=D\left(P\Vert P_{\theta \left(\eta \right)}\right)+D\left(P_{\theta \left(\eta \right)}\Vert P_{\theta }\right),$

for any $P\in {\mathcal{V}}_m$ and $P_{\theta }\in {\mathcal{V}}_e$ . The Neyman–Pearson test can be understood as a method that bisects the space $\mathcal{W}(\mathcal{X},\mathcal{E})$ by means of an m-family, which is perpendicular to the e-family that links the two hypotheses. For a given 0 < r < D(P ₀‖P ₁), if we set the threshold η = η(r) so that D(P _θ(η(r))‖P ₀) = r, the Neyman–Pearson test attains the exponential trade-off:

$\begin{array}{ll}\hfill \underset{n\to \infty }{\lim }-\log {\mathbb{P}}_0\left(\frac{1}{n}{\displaystyle \sum _{t=1}^{n-1}}\log \frac{P_0\left(X_t,X_{t+1}\right)}{P_1\left(X_t,X_{t+1}\right)}\le \eta \left(r\right)\right)& =r,\hfill \\ \hfill \underset{n\to \infty }{\lim }-\log {\mathbb{P}}_1\left(\frac{1}{n}{\displaystyle \sum _{t=1}^{n-1}}\log \frac{P_0\left(X_t,X_{t+1}\right)}{P_1\left(X_t,X_{t+1}\right)}>\eta \left(r\right)\right)& =D\left(P_{\theta \left(\eta \left(r\right)\right)}\Vert P_1\right).\hfill \end{array}$

In fact, it can be proved that D(P _θ(η(r))‖P ₁) is the optimal attainable exponent of the type II error probability among any tests such that the type I error probability is less than e ^−nr . Furthermore, it also holds that

$D\left(P_{\theta \left(\eta \left(r\right)\right)}\Vert P_1\right)=\min \left\{D\left(P\Vert P_1\right):P\in \mathcal{W}\left(\mathcal{X},\mathcal{E}\right),D\left(P\Vert P_0\right)\le r\right\},$

and the optimal exponential trade-off between the type I and type II error probability can be attained by the so-called Hoeffding test. For a more detailed derivation of these results and finite length analysis, see [17, 19].

5.4.1 Historical remarks and timeline

Binary hypothesis testing is one of the well-studied problems in information theory. The use of the Perron–Frobenius theory in this context can be traced back to the 1970s and 1980s [63, 66–68]. The geometrical interpretation of the binary hypothesis testing for Markov chains was first studied in [19]. More recently, the finite length analysis of the binary hypothesis testing for Markov chains was developed in [17] using tools from the information geometry. The binary hypothesis testing is also well studied for quantum systems; for results on quantum systems with memory, see [69].

Author contributions

GW drafted the initial version, which was subsequently reviewed and edited by both authors. All authors contributed to the article and approved the submitted version.

Funding

GW was supported by the Special Postdoctoral Researcher Program (SPDR) of RIKEN and the Japan Society for the Promotion of Science KAKENHI under Grant 23K13024. SW was supported in part by JSPS KAKENHI under Grant 20H02144.

Acknowledgments

The authors are thankful to the referees for their numerous comments, which helped improve the quality of this manuscript, and for bringing reference [81] to their attention.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹ As is customary in the literature, θ denotes both the coordinates of a point in context and the corresponding chart map.

² In our definition of m-family, we do not allow a redundant choice of Q ₀, Q ₁, …, Q _d to express ${\mathcal{V}}_m$ ; if we allow a redundant choice, Ξ need not be an open set and d need not coincide with the dimension of ${\mathcal{V}}_m$ .

³ The reason for this name will become clear in (21).

⁴ When discussing geodesic convexity in this section, we only consider the section of the geodesic joining the two points, achieved for parameter t ∈ [0, 1], not the entire geodesic.

⁵ For $\left|\mathcal{X}\right|=2$ , ${\mathcal{W}}_{\mathsf{s}\mathsf{y}\mathsf{m}}(\mathcal{X},{\mathcal{X}}^2)$ itself is an e-family, which is a strict submanifold of ${\mathcal{W}}_{\mathsf{r}\mathsf{e}\mathsf{v}}(\mathcal{X},{\mathcal{X}}^2)=\mathcal{W}(\mathcal{X},{\mathcal{X}}^2)$ .

⁶ Note that log  U is of the form f(x′) − f(x) + c for some function f and constant c.

⁷ The fact that the second derivative of ψ(θ) coincides with the asymptotic variance was clarified in [15].

⁸ Note that Nakagawa and Kanaya [19] used a different notation convention, where ${\mathcal{T}}_n$ outputs the probability of accepting the null hypothesis.

References

1. Diaconis P, Miclo L. On characterizations of Metropolis type algorithms in continuous time. ALEA: Latin Am J Probab Math Stat (2009) 6:199–238.

Google Scholar

2. Choi MCH, Wolfer G. Systematic approaches to generate reversiblizations of non-reversible Markov chains (2023). arXiv:2303.03650.

Google Scholar

3. Hayashi M. Local equivalence problem in hidden Markov model. Inf Geometry (2019) 2, 1–42. doi:10.1007/s41884-019-00016-z

CrossRef Full Text | Google Scholar

4. Hayashi M. Information geometry approach to parameter estimation in hidden Markov model. Bernoulli (2022) 28, 307–42. doi:10.3150/21-BEJ1344

CrossRef Full Text | Google Scholar

5. Amari S-i., Nagaoka H. Methods of information geometry, 191. American Mathematical Soc. (2007).

Google Scholar

6. Ay N, Jost J, Vân Lê H, Schwachhöfer L. Information geometry, 64. Springer (2017).

Google Scholar

7. Nagaoka H. The exponential family of Markov chains and its information geometry. In: The proceedings of the symposium on information theory and its applications, 28-2 (2005). p. 601–604.

Google Scholar

8. Vidyasagar M. An elementary derivation of the large deviation rate function for finite state Markov chains. Asian J Control (2014) 16:1–19. doi:10.1002/asjc.806

CrossRef Full Text | Google Scholar

9. Levin DA, Peres Y, Wilmer EL. Markov chains and mixing times. second edition. American Mathematical Soc. (2009).

Google Scholar

10. Rached Z, Alajaji F, Campbell LL. The Kullback-Leibler divergence rate between Markov sources. IEEE Trans Inf Theor (2004) 50:917–21. doi:10.1109/TIT.2004.826687

CrossRef Full Text | Google Scholar

11. Eguchi S. Second order efficiency of minimum contrast estimators in a curved exponential family. Ann Stat (1983) 11:793–803. doi:10.1214/aos/1176346246

CrossRef Full Text | Google Scholar

12. Eguchi S. A differential geometric approach to statistical inference on the basis of contrast functionals. Hiroshima Math J (1985) 15:341–91. doi:10.32917/hmj/1206130775

CrossRef Full Text | Google Scholar

13. Wolfer G, Watanabe S. Information geometry of reversible Markov chains. Inf Geometry (2021) 4:393–433. doi:10.1007/s41884-021-00061-7

CrossRef Full Text | Google Scholar

14. Ito H, Amari S. Geometry of information sources. In: Proceedings of the 11th symposium on information theory and its applications. SITA ’88 (1988). p. 57–60.

Google Scholar

15. Hayashi M, Watanabe S. Information geometry approach to parameter estimation in Markov chains. Ann Stat (2016) 44:1495–535. doi:10.1214/15-AOS1420

CrossRef Full Text | Google Scholar

16. Bregman LM. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput Math Math Phys (1967) 7:200–17. doi:10.1016/0041-5553(67)90040-7

CrossRef Full Text | Google Scholar

17. Watanabe S, Hayashi M. Finite-length analysis on tail probability for Markov chain and application to simple hypothesis testing. Ann Appl Probab (2017) 27:811–45. doi:10.1214/16-AAP1216

CrossRef Full Text | Google Scholar

18. Matumoto T Any statistical manifold has a contrast function—On the C3-functions taking the minimum at the diagonal of the product manifold. Hiroshima Math J (1993) 23:327–32. doi:10.32917/hmj/1206128255

CrossRef Full Text | Google Scholar

19. Nakagawa K, Kanaya F. On the converse theorem in statistical hypothesis testing for Markov chains. IEEE Trans Inf Theor (1993) 39:629–33. doi:10.1109/18.212294

CrossRef Full Text | Google Scholar

20. Adamčík M. The information geometry of Bregman divergences and some applications in multi-expert reasoning. Entropy (2014) 16:6338–81. doi:10.3390/e16126338

CrossRef Full Text | Google Scholar

21. Wolfer G, Watanabe S. Geometric aspects of data-processing of Markov chains (2022). arXiv:2203.04575.

Google Scholar

22. Miller H. A convexity property in the theory of random variables defined on a finite Markov chain. Ann Math Stat (1961) 32:1260–70. doi:10.1214/aoms/1177704865

CrossRef Full Text | Google Scholar

23. Csiszár I, Cover T, Choi B-S. Conditional limit theorems under Markov conditioning. IEEE Trans Inf Theor (1987) 33:788–801. doi:10.1109/TIT.1987.1057385

CrossRef Full Text | Google Scholar

24. Takeuchi J-i., Barron AR. Asymptotically minimax regret by Bayes mixtures. In: Proceedings 1998 IEEE International Symposium on Information Theory (Cat No 98CH36252). IEEE (1998). p. 318.

Google Scholar

25. Takeuchi J, Kawabata T. Exponential curvature of Markov models. In: Proceedings. 2007 IEEE International Symposium on Information Theory; June 2007; Nice, France. IEEE (2007). p. 2891–5.

CrossRef Full Text | Google Scholar

26. Takeuchi J, Nagaoka H. On asymptotic exponential family of Markov sources and exponential family of Markov kernels (2017). [Dataset].

Google Scholar

27. Feigin PD Conditional exponential families and a representation theorem for asympotic inference. Ann Stat (1981) 9:597–603. doi:10.1214/aos/1176345463

CrossRef Full Text | Google Scholar

28. Küchler U, Sørensen M. On exponential families of Markov processes. J Stat Plann inference (1998) 66:3–19. doi:10.1016/S0378-3758(97)00072-4

CrossRef Full Text | Google Scholar

29. Hudson IL. Large sample inference for Markovian exponential families with application to branching processes with immigration. Aust J Stat (1982) 24:98–112. doi:10.1111/j.1467-842X.1982.tb00811.x

CrossRef Full Text | Google Scholar

30. Stefanov VT. Explicit limit results for minimal sufficient statistics and maximum likelihood estimators in some Markov processes: Exponential families approach. Ann Stat (1995) 23:1073–101. doi:10.1214/aos/1176324699

CrossRef Full Text | Google Scholar

31. Küchler U, Sørensen M. Exponential families of stochastic processes: A unifying semimartingale approach. Int Stat Review/Revue Internationale de Statistique (1989) 57:123–44. doi:10.2307/1403382

CrossRef Full Text | Google Scholar

32. Sørensen M. On sequential maximum likelihood estimation for exponential families of stochastic processes. Int Stat Review/Revue Internationale de Statistique (1986) 54:191–210. doi:10.2307/1403144

CrossRef Full Text | Google Scholar

33. Kelly FP. Reversibility and stochastic networks. Cambridge University Press (2011).

Google Scholar

34. Brooks S, Gelman A, Jones G, Meng X-L. Handbook of Markov chain Monte Carlo. Chapman & Hall/CRC Press (2011).

Google Scholar

35. Schrödinger E. Über die umkehrung der naturgesetze. Sitzungsberichte der preussischen Akademie der Wissenschaften, physikalische mathematische Klasse (1931) 8:144–53.

Google Scholar

36. Kolmogorov A. Zur theorie der Markoffschen ketten. Mathematische Annalen (1936) 112:155–60. doi:10.1007/BF01565412

CrossRef Full Text | Google Scholar

37. Kolmogorov A. Zur umkehrbarkeit der statistischen naturgesetze. Mathematische Annalen (1937) 113:766–72. doi:10.1007/BF01571664

CrossRef Full Text | Google Scholar

38. Dobrushin RL, Sukhov YM, Fritz J. A.N. Kolmogorov - the founder of the theory of reversible Markov processes. Russ Math Surv (1988) 43:157–82. doi:10.1070/RM1988v043n06ABEH001985

CrossRef Full Text | Google Scholar

39. Hsu D, Kontorovich A, Levin DA, Peres Y, Szepesvári C, Wolfer G. Mixing time estimation in reversible Markov chains from a single sample path. Ann Appl Probab (2019) 29:2439–80. doi:10.1214/18-AAP1457

CrossRef Full Text | Google Scholar

40. Pistone G, Rogantin MP. The algebra of reversible Markov chains. Ann Inst Stat Math (2013) 65:269–93. doi:10.1007/s10463-012-0368-7

CrossRef Full Text | Google Scholar

41. Diaconis P, Rolles SW. Bayesian analysis for reversible Markov chains. Ann Stat (2006) 34:1270–92. doi:10.1214/009053606000000290

CrossRef Full Text | Google Scholar

42. König D. Theorie der endlichen und unendlichen Graphen: Kombinatorische Topologie der Streckenkomplexe, 16. Akademische Verlagsgesellschaft mbh (1936).

Google Scholar

43. Birkhoff G. Three observations on linear algebra. Univ Nac Tacuman, Rev Ser A (1946) 5:147–51.

Google Scholar

44. Von Neumann J. A certain zero-sum two-person game equivalent to the optimal assignment problem. Contrib Theor Games (1953) 2:5–12. doi:10.1515/9781400881970-002

CrossRef Full Text | Google Scholar

45. Čencov NN. Statistical decision rules and optimal inference, Transl. Math. Monographs, 53. Providence-RI: Amer. Math. Soc. (1981).

Google Scholar

46. Campbell LL. An extended Čencov characterization of the information metric. Proc Am Math Soc (1986) 98:135–41. doi:10.1090/S0002-9939-1986-0848890-5

CrossRef Full Text | Google Scholar

47. Lê HV. The uniqueness of the Fisher metric as information metric. Ann Inst Stat Math (2017) 69:879–96. doi:10.1007/s10463-016-0562-0

CrossRef Full Text | Google Scholar

48. Burke C, Rosenblatt M. A Markovian function of a Markov chain. Ann Math Stat (1958) 29:1112–22. doi:10.1214/aoms/1177706444

CrossRef Full Text | Google Scholar

49. Rogers LC, Pitman J. Markov functions. Ann Probab (1981) 9:573–82. doi:10.1214/aop/1176994363

CrossRef Full Text | Google Scholar

50. Kemeny JG, Snell JL Markov chains, 6. New York: Springer-Verlag (1976).

Google Scholar

51. Lebanon G. An extended Čencov-Campbell characterization of conditional information geometry. In: Proceedings of the 20th conference on Uncertainty in artificial intelligence; July 2004 (2004). p. 341–8.

Google Scholar

52. Lebanon G. Axiomatic geometry of conditional models. IEEE Trans Inf Theor (2005) 51:1283–94. doi:10.1109/TIT.2005.844060

CrossRef Full Text | Google Scholar

53. Montúfar G, Rauh J, Ay N. On the Fisher metric of conditional probability polytopes. Entropy (2014) 16:3207–33. doi:10.3390/e16063207

CrossRef Full Text | Google Scholar

54. Wolfer G, Watanabe S. A geometric reduction approach for identity testing of reversible Markov chains. In: Geometric Science of Information (to appear): 6th International Conference, GSI 2023; August–September, 2023; Saint-Malo, France. Springer (2023). Proceedings 6.

Google Scholar

55. Weinberger MJ, Rissanen J, Feder M. A universal finite memory source. IEEE Trans Inf Theor (1995) 41:643–52. doi:10.1109/18.382011

CrossRef Full Text | Google Scholar

56. Willems F, Shtar’kov Y, Tjalkens T. The context tree weighting method: Basic properties. IEEE Trans Inf Theor (1995) 41:653–64. doi:10.1109/18.382012

CrossRef Full Text | Google Scholar

57. Takeuchi J, Nagaoka H. Information geometry of the family of Markov kernels defined by a context tree. In: 2017 IEEE Information Theory Workshop (ITW). IEEE (2017). p. 429–33.

CrossRef Full Text | Google Scholar

58. Spitzer F. A variational characterization of finite Markov chains. Ann Math Stat (1972) 43:303–7. doi:10.1214/aoms/1177692723

CrossRef Full Text | Google Scholar

59. Justesen J, Hoholdt T. Maxentropic Markov chains (corresp). IEEE Trans Inf Theor (1984) 30:665–7. doi:10.1109/TIT.1984.1056939

CrossRef Full Text | Google Scholar

60. Duda J. Optimal encoding on discrete lattice with translational invariant constrains using statistical algorithms (2007). arXiv preprint arXiv:0710.3861.

Google Scholar

61. Burda Z, Duda J, Luck J-M, Waclaw B. Localization of the maximal entropy random walk. Phys Rev Lett (2009) 102:160602. doi:10.1103/PhysRevLett.102.160602

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Moulos V, Anantharam V. Optimal chernoff and hoeffding bounds for finite state Markov chains (2019). arXiv preprint arXiv:1907.04467.

Google Scholar

63. Davisson L, Longo G, Sgarro A. The error exponent for the noiseless encoding of finite ergodic Markov sources. IEEE Trans Inf Theor (1981) 27:431–8. doi:10.1109/TIT.1981.1056377

CrossRef Full Text | Google Scholar

64. Dembo A, Zeitouni O. Large deviations techniques and applications. Springer (1998).

Google Scholar

65. Jones GL. On the Markov chain central limit theorem. Probab Surv (2004) 1:299–320. doi:10.1214/154957804100000051

CrossRef Full Text | Google Scholar

66. Boza LB. Asymptotically optimal tests for finite Markov chains. Ann Math Stat (1971) 42:1992–2007. doi:10.1214/aoms/1177693067

CrossRef Full Text | Google Scholar

67. Vašek K. On the error exponent for ergodic Markov source. Kybernetika (1980) 16:318–29. doi:10.1109/TIT.1981.1056377

CrossRef Full Text | Google Scholar

68. Natarajan S. Large deviations, hypotheses testing, and source coding for finite Markov chains. IEEE Trans Inf Theor (1985) 31:360–5. doi:10.1109/TIT.1985.1057036

CrossRef Full Text | Google Scholar

69. Mosonyi M, Ogawa T. Two approaches to obtain the strong converse exponent of quantum hypothesis testing for general sequences of quantum states. IEEE Trans Inf Theor (2015) 61:6975–94. doi:10.1109/TIT.2015.2489259

CrossRef Full Text | Google Scholar

70. Donsker MD, Varadhan SS. Asymptotic evaluation of certain Markov process expectations for large time, i. Commun Pure Appl Math (1975) 28:1–47. doi:10.1109/TIT.2015.2489259

CrossRef Full Text | Google Scholar

71. Ellis RS. Large deviations for a general class of random vectors. Ann Probab (1984) 12:1–12. doi:10.1214/aop/1176993370

CrossRef Full Text | Google Scholar

72. Gärtner J. On large deviations from the invariant measure. Theor Probab Its Appl (1977) 22:24–39. doi:10.1137/1122003

CrossRef Full Text | Google Scholar

73. Gray RM. Entropy and information theory. Springer Science & Business Media (2011).

Google Scholar

74. Balaji S, Meyn SP. Multiplicative ergodicity and large deviations for an irreducible Markov chain. Stochastic Process their Appl (2000) 90:123–44. doi:10.1016/S0304-4149(00)00032-6

CrossRef Full Text | Google Scholar

75. Kontoyiannis I, Meyn SP. Spectral theory and limit theorems for geometrically ergodic Markov processes. Ann Appl Probab (2003) 13:304–62. doi:10.1214/aoap/1042765670

CrossRef Full Text | Google Scholar

76. Lehmann EL, Romano JP, Casella G Testing statistical hypotheses, 3. Springer (2005).

Google Scholar

77. Nakagawa K. The geometry of m/d/1 queues and large deviation. Int Trans Oper Res (2002) 9:213–22. doi:10.1111/1475-3995.00351

CrossRef Full Text | Google Scholar

78. Neyman J, Pearson ES. Ix. on the problem of the most efficient tests of statistical hypotheses. Philosophical Trans R Soc Lond Ser A, Containing Pap a Math or Phys Character (1933) 231:289–337. doi:10.1098/rsta.1933.0009

CrossRef Full Text | Google Scholar

79. Nielsen F. An elementary introduction to information geometry. Entropy (2020) 22:1100. doi:10.3390/e22101100

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Čencov NN. Algebraic foundation of mathematical statistics. Ser Stat (1978) 9:267–76. doi:10.1080/02331887808801428

CrossRef Full Text | Google Scholar

81. Gaspard P. Time-reversed dynamical entropy and irreversibility in Markovian random processes. J Stat Phys (2004) 117:599–615. doi:10.1007/s10955-004-3455-1

CrossRef Full Text | Google Scholar