Neutron generation enhanced by a femtosecond laser irradiating on multi-channel target

A novel scheme has been proposed to enhance neutron yields, in which a multi-channel target consisting of a row of parallel micro-wires and a plane substrate is irradiated by a relativistic femtosecond laser. Two-dimensional particle-in-cell simulations show that the multi-channel target can significantly enhance the neutron yield, which is about 4 orders of magnitude greater than the plane target. Different from the case of nanowire target, we find that when the laser penetrates into the channel, the excited transverse sheath electric field can effectively accelerate the D⁺ ions in the transverse direction. When these energetic D⁺ ions move towards the nearby wire, they will collide with the bulk D⁺ ions to trigger D-D fusion reaction and produce neutrons, which is much more effective than the plane target case. Due to the unique trajectory of the incident D⁺ ions, the angular distribution of the produced neutrons is modulated from isotropic to two peaks around ±90°. Meanwhile, this enhancement and modulation is further verified in a wide range of target parameters.

1 Introduction

The laser intensity has increased significantly since the invention of the chirped pulse amplification (CPA) technology [1] in 1985. Recently the laser peak power has broken through 10 PW [2,3] and laser peak intensity has reached 10²³W/cm² [4], with corresponding electric field intensity of approximately 10¹⁴V/m. It enables us to create extreme physical conditions with ultra-high temperature and ultra-high density in the laboratory and promotes the development of many branches of physics, such as the laser-plasma accelerator [5,6], fast ignition in inertial confinement fusion (ICF) [7,8], laboratory astrophysics [9,10], and laser nuclear physics [11,12], etc.

In recent years, efforts have been made to exploit ultrashort and ultrahigh laser systems to generate neutron beam. The production of neutrons with a relativistic femtosecond laser has been realized by using different materials of targets that include thin foils of deuterated materials [13–15], deuterated clusters [16–18], and heavy water jets and spray [19] in recent years. Many theoretical simulations and experimental studies have proved the superiority of nanowire-array (NWA) targets with diameters and gaps of hundreds of nanometers (i.e., the subwavelength-scale target) in enhancing the energy conversion efficiency between femtosecond relativistic laser and plasma, and have been widely used in the research of electron and ion acceleration [20,21], X/γ ray generation [22,23] and terahertz radiation [24,25]. Besides, the above target structure has also been proved to be able to create an extremely high-energy-density plasma (HEDP) environment [26] and to greatly improve the neutron yield compared with the plane target [27,28]. In addition to the subwavelength micro-target, recent research [29] shows that, for the targets with diameter and gap of micrometers (i.e., the wavelength-scale target), the energy conversion efficiency of laser can also be significantly improved, and thus ions with higher energy can be produced. Therein, the higher energy gain of ions may be employed to enhance the fusion efficiency and neutron yield, which is still an open question.

In this work, the neutron generation by the interaction of a femtosecond laser with the multi-channel target (MCT) is investigated via the particle-in-cell (PIC) simulations. Our results show that with the introduction of the MCT, the neutron yield can be significantly enhanced, which is about 4 orders of magnitude higher than that from a plane target. Meanwhile, we also find that the generated neutrons are not isotropic, and peak in the perpendicular direction of the laser incidence. The paper is organized as follows. Section 2 outlines the target configurations, simulation parameters and results. Besides, the physical mechanism of the neutron yield enhancement is analyzed in detail. Section 3 discusses the impact of target parameters on neutron yield. Lastly, a summary is given in Section 4.

2 Simulation setup, results and analysis

To reveal the basic physics and mechanism of interaction between MCT target with the relativistic femtosecond pulse, two-dimensional (2D) PIC simulations are performed by using the Smilei code [30], which has included the nuclear reaction module for D (D, n)³He to produce neutrons. The simulation box is 48λ₀ × 48λ₀ with 2560 × 2560 cells and 49 particles per cell, where λ₀ = 1 μm is the laser wavelength. A linearly polarized laser pulse with a Gaussian profile in the $\widehat{y}$ direction, i.e., $\vec{a}=a_0\cdot \exp (-{(y-y_0)}^2/r_0^2)\cdot \exp (\log 2\cdot {(t-\tau /2)}^2/{(\tau /6)}^2)\cdot \overrightarrow{e_y}$, travels along the x-axis from the left side and normally incident on the MCT target, where a₀ = eE₀/m_ecω₀ = 5 is the normalized amplitude, y₀ = 24 μm is the laser central location, r₀ = 10 μm is the laser spot radius, and τ = 10T₀ = 33fs is the pulse duration. The corresponding peak intensity and total light energy are thus 3.4 × 10¹⁹W/cm² and 1.17J, respectively, which is commonly used in the laboratory.

Figure 1A shows a schematic diagram of the MCT target. The typical diameter (D), length (L), and spacing (S) of the MCT are 1 ∼ 3λ₀, 5 ∼ 15λ₀, and 1 ∼ 3λ₀, respectively. For a typical MCT, the cylindrical deuterated polyethylene (CD₂) wires of length L = 10.0λ₀, diameter D = 1.0λ₀, and space length between the adjacent wires S = 2.0λ₀, are located from x₀ = 15λ₀ to x₁ = 25λ₀. A CD₂ substrate of thickness L₁ = 5.0λ₀ is used to support the wires and is attached directly to the wire array. The corresponding 2D diagram is shown in Figure 1B. As the target containes deuterium, neutrons are generated via D-D fusion reaction: D + D → n +³He (Q = 3.27 MeV). It assumes that the ions are fully ionized since the laser intensity is much higher than the ionization potential of the carbon and deuterium ions [31,32], with carbon ions (C⁶⁺), deuterium ions (D⁺) and electrons (e⁻) densities 20 n_c, 40 n_c, 160 n_c, respectively, where $n_c=m_e{\omega }_0^2/4\pi e^2$ is the electron’s critical density. For comparison, we also perform simulations for a plane CD₂ target (PT), as shown in Figure 1C.

FIGURE 1

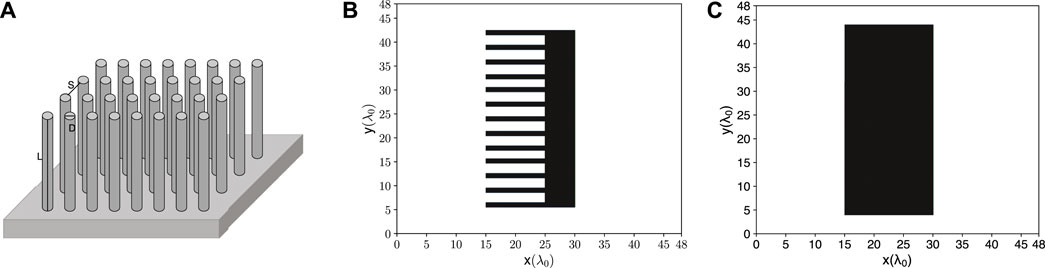
FIGURE 1. Schematic diagram of the multi-channel target (A) 3D configurations. L, D, and S are the channel length, diameter, and spacing, respectively. (B) Corresponding 2D configurations. (C) A flat target 2D configurations.

To show the effect of MCT target on neutron generation, the results of neutron production in the cases of MCT and PT are shown in Figure 2. One could find that in the case of MCT, the neutrons are produced in the large volume range of the wires rather than in the area near the substrate and that more neutrons are distributed on the wire during the production process than in the gap area between the wires; see Figure 2A. While in the case of PT, neutrons are mainly produced near the target surface interacting with the laser and extend to the surrounding area, and the distribution area is far smaller than that in the case of MCT; see Figure 2B. At the same time, the neutron yield in MCT is 4 orders of magnitude higher than that in PT, i.e., the MCT can greatly improve the neutron yield with the same input laser energy. Besides, in the PT case, the emission of neutrons along the laser axis is about 1.2 times higher than in the transverse direction, which is consistent with the experimental results.[33]. However, when the laser interacts with the MCT, as shown by the black solid line in Figure 2C, the number of neutrons peaks around ±90° (i.e., in the perpendicular direction of laser propagation). This result is obviously different from that of accelerated D⁺ colliding with the substrate along the laser propagation direction [28] or being used in the pitcher-catcher configuration with a conversion target such as Be [34,35] to produce directed beams of higher energy neutrons in which more neutrons are mainly located along the laser propagation direction rather than its vertical direction.

FIGURE 2

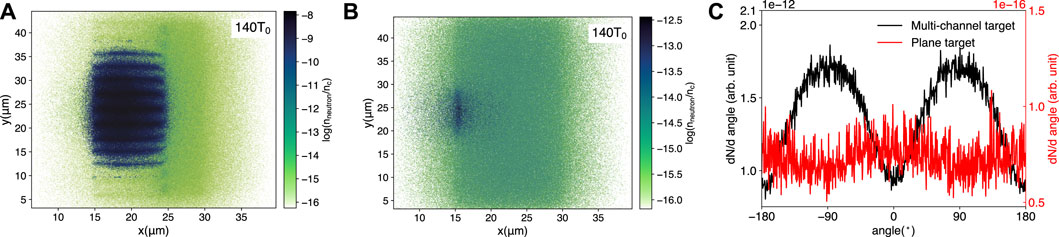
FIGURE 2. (A) The neutron number density of the multi-channel target. (B) The neutron number density of the plane target. (C) Neutron angular spectrum for different targets, where the black line represents the MCT and the red line represents the PT.

In order to reveal the reason why MCT enhances the neutron yield and why the angular distribution is anisotropic, we have made a detailed analysis of the progress at different times. Neutron is the product of D-D fusion reaction. Therefore, to understand the effect of MCT on neutron production, the dynamics of high-energy D⁺ ions need to be analyzed in detail. Figure 3 shows the energy density of D⁺ ions in the wires region and the corresponding neutron yield at 60T₀, 80T₀, 100T₀. From Figure 3A, one can see that at 60T₀, because the wire is relatively thick, the target does not explode after strong laser irradiation like the nanowire target [27] but maintains its shape, and the ions from the wire surface expand radially and gradually fill the gaps. Correspondingly, the neutron yield of the MCT is not obvious in Figure 3D. Only the tip of the wires and the substrate surface, which are irradiated directly by the laser, produce a small number of neutrons. From the value of the color bar in Figure 3D, it shows that the neutron yield is about two orders of magnitude lower than that of the subsequent generation. Over time, the high-energy deuterons expand further and collide with each other in the gaps, as shown in Figure 3B. It should be noted that even the gaps have been filled with high-energy D⁺ ions, but in Figure 3E, there is no significant neutron generation in the gaps. The average density of D⁺ ions between gaps is estimated to be 0.21n_c, which is much lower than the target density. This indicates that with the current laser pulse and the gaps in the micrometer scale, the plasma between the gaps cannot form a high-energy-density environment for effective nuclear reactions. As the high-energy deuterons expand further between the gaps, a portion of the ions reach the surface of the adjacent wires, as shown in Figure 3C. This process is like the “pitcher-catcher” configuration, where deuterium ions are pitched from the wire surface, accelerated in the gaps, and catched by the adjacent wires. As a result, in Figure 3F, significant neutron generation on the wires can be observed.

FIGURE 3

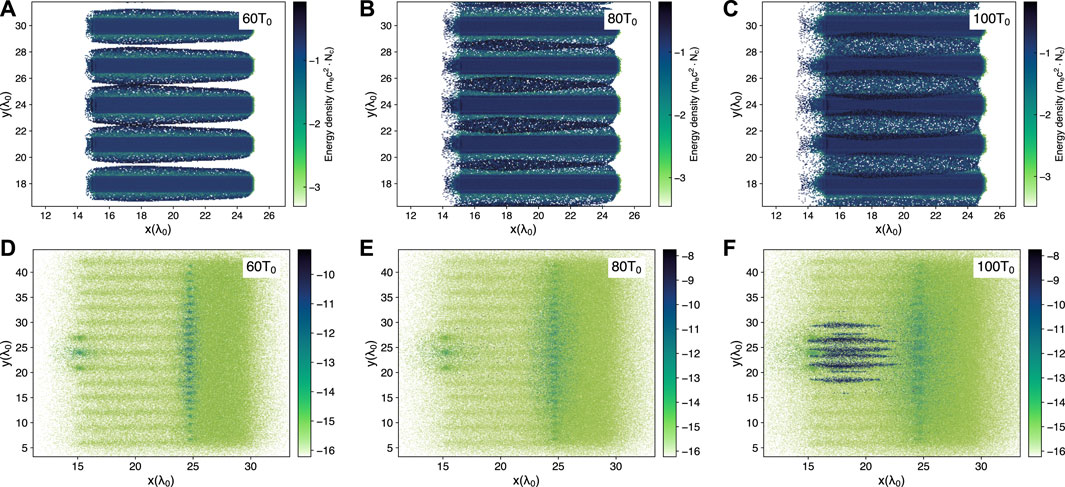
FIGURE 3. The deuterons energy density of the multi-channel target at (A) 60T₀, (B) 80T₀ and (C) 100T₀. The neutron number density of the multi-channel target at (D) 60T₀, (E) 80T₀ and (F) 100T₀.

The above results show that the acceleration of D⁺ ions in the $\widehat{y}$ direction and the subsequent collision with adjacent wire targets are the main factors for enhancing neutron production. Here, the space-charge field (sheath field) normal to the surfaces of the wires dominates the acceleration of D⁺ ions, which is shown in Figure 4a1. As the laser propagates through the gaps between wires, channels act as closely packed waveguides [36–38], and a large number of high-energy-density electrons are dragged out from the wires by the periodic laser electric field [39,40]. From Figure 4B, one can find that the upper half of the gap is filled with charge separation field of E_sy < 0, and the lower half with E_sy > 0. This field is against the effect of the laser and directs electrons back into the wires [41]. At the same time, D⁺ ions in the surface of the wires are dragged out and accelerated in the transverse direction. The energy spectrum from different snapshots and the x-p_x phase diagram, x-p_y phase diagram of D⁺ ions at 40T₀ are shown in Figure 4C and Figures 4d1, d2, which confirms that the acceleration of D⁺ ions in the transverse direction is dominant, while the acceleration along the laser propagation is negligible. Most importantly, this sheath field does not disappear right away after the laser is completely finished but decays gradually due to the remaining electrons filling in the gaps. Figure 4a2 demonstrates that at 40T₀ there is still a fairly strong field remaining along the gap surface, which is equivalent to almost 10% of the field strength when the laser exists.

FIGURE 4

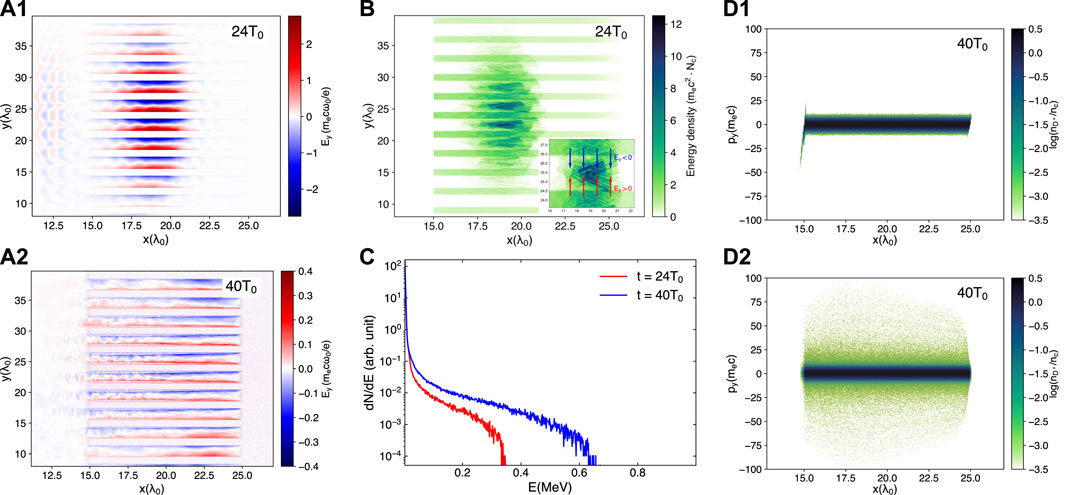
FIGURE 4. Spatial distribution of the transverse sheath field E_sy at (A1) 24T₀ and (A2) 40T₀. (B) The electron energy density averaged over a laser cycle. The field formed by the charge separation is represented by a subfigure in the lower right corner. (C) Energy spectrum of wires deuterons at different times. (D1) The x-p_x phase diagrams and (D2) The x-p_y phase diagrams of the D⁺ ions at 40T₀.

As shown in Figures 5a1, a2, the D⁺ ions on the surface of the wires see the unscreened electric field of the electrons in the gaps and are continuously accelerated in the gaps from 40T₀–68T₀, until the moment when the gaps are filled with high-energy deuterium ions and the sheath field disappears, as shown in Figure 5a3. This means that the effective acceleration distance of D⁺ ions is limited by the length of the gap, which is about half of the interwire separation, i.e., l_acc ≃ S/2. Correspondingly, there is a significant increase in the number of D⁺ ions in the range of 0.4 MeV–0.8 MeV, with a cut-off energy of 0.87 MeV at 68T₀; see Figure 5B. Besides, from Figure 5B, it should be noted that the energy spectrum represented by the black line at the 100T₀ differs from the blue line at 68T₀ in two ways: (1) the number of deuterium ions at t = 100T₀ is larger than that of t = 68T₀ in the range of 10 KeV to 60 keV, and (2) t = 100T₀ has higher cut-off energy. The former is due to the heating of wires when energetic deuterium ions collide with neighboring wires, which is beneficial for subsequent D-D fusion reaction. The latter is mainly attributed to the TNSA acceleration in the front surface of the target [46] rather than the radial acceleration in the region of the wires. And the contribution of these ions to neutron production is minimal since the number of trailing high-energy deuterium ions is very small. Meanwhile, the angular distribution of the accelerated deuterons is closely related to the angular profile of the neutrons. Figure 5C shows the D⁺ ions are accelerated perpendicular to the direction of the laser, rather than along the direction of the laser like the plane target. This coincides with the angular distribution of the produced neutrons which is not isotropic but peaks around ±90°. Moreover, both the experimental data [42–44] and the theoretical calculations [45] show that the D-D reaction cross-section increases rapidly with the increase of energy when less than 1 MeV; see Figure 5D. For deutrons thermonuclear reactions, the volumetric reaction rate is given by [47].

$R=n_{D^{+}}^2⟨\sigma v⟩/\left(1+\delta \right)(1)$

where $n_{D^{+}}$ is the number density of D⁺ ions, δ is the Kronecker symbol of 1, σ is the D-D reaction cross-section, v is deuterium–deuterium relative velocity, and ⟨σv⟩ is an average of reaction cross-section and relative velocity. Then multiplied by the reaction volume V and reaction time τ, the reaction number can be roughtly estimated as

$N=V{n}_{D^{+}}^2⟨\sigma v⟩\mathrm{\tau }/2(2)$

From Equation 2, we can see that the MCT irradiated by the laser forms a larger volume V, and a higher-energy-density environment, i.e., a higher density $n_{D^{+}}$ and larger ⟨σv⟩, so the neutron yield has increased dramatically.

FIGURE 5

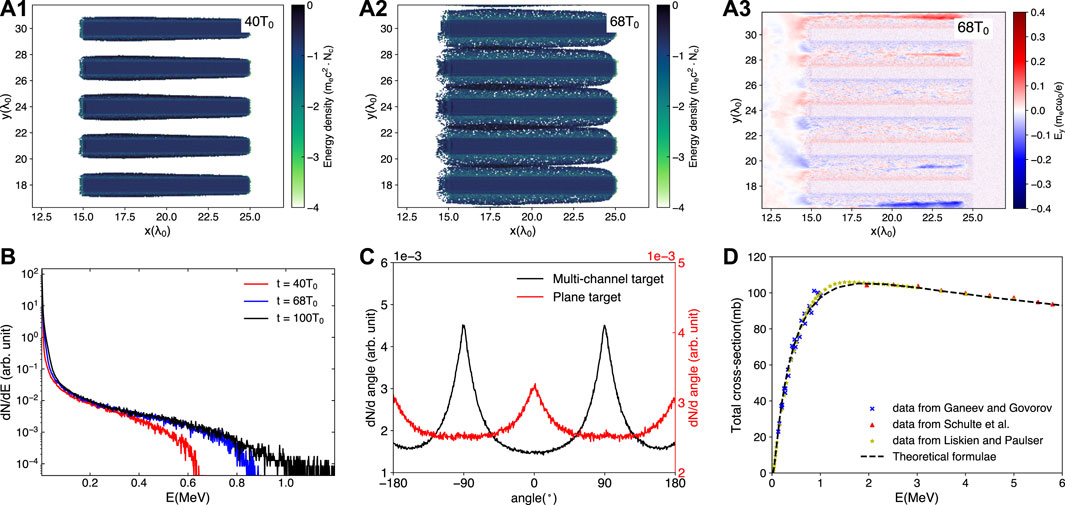
FIGURE 5. (A1,A2) The energy spectrum of wires deuterium ions at 40T₀ and 80T₀. (A3) Spatial distribution of the transverse sheath field E_sy at 80T₀. (B) Energy spectrum of wires deuterons at different times. (C) Angular spectrum of wires deuterons for different targets at 100T₀, where the black line represents the MCT and the red line represents the PT. (D) The total cross-section of D-D reaction. The experimental data came from [42–44] and theoretical calculation [45] is the method used in Smilei code.

3 Target parameters effect on neutron yield

The target parameters play crucial roles in the D⁺ ions acceleration and subsequent neutron generation. Figure 6 shows the influence of wire length L, diameter D, and spacing between the adjacent wires S on D⁺ cut-off energy when the gaps are enclosed due to the expansion of D⁺ ions and neutron yield. Apparently, in order to reduce the laser reflection, a smaller diameter D is better, as shown in Figure 6A. However, D = 1.0λ₀ is optimal because much smaller D (i.e., nanowire target) requires the laser system with very high contrast and makes it harder for wires to grow longer when the target is prepared by chemical methods. For given D = 1.0λ₀, Figure 6B illustrates the impact of spacing S on the neutron yield and D⁺ cut-off energy. For larger S, the laser can penetrate deeper into the target and produce a stronger sheath field, and the D⁺ ions are accelerated over a longer distance to higher energy. However, take into consideration that the laser’s spot radius is fixed in the simulation, which is also in line with the experimental conditions, the wider gaps will reduce the number of wires within the area of laser spot irradiation, resulting in a dramatic decrease of the D⁺ ions number and D-D collision events. Therefore, in order to maximize the neutron yield, one needs to make a trade-off between the cut-off energy to increase the cross-section and high-energy number density of the D+ ions, i.e., $N_{\text{fusion}}\propto n_{D^{+}}^2\cdot {\sigma }_{DD}$. Here, S = 2.8λ₀ is a good choice.

FIGURE 6

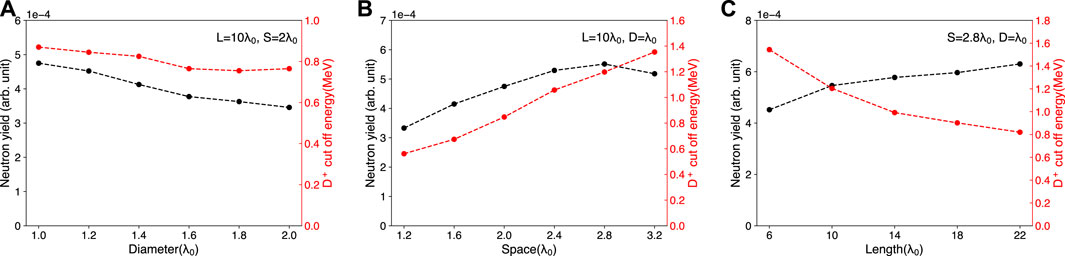
FIGURE 6. (A) For the fixed L = 10.0λ₀ and S = 2.0λ₀, the neutron yield and D⁺ cut-off energy when channels are closed vary with the wire diameter D. (B) For the fixed L = 10.0λ₀ and D = 1.0λ₀, the neutron yield and D⁺ cut-off energy when channels are closed vary with space length S. (C) For the fixed S = 2.8λ₀ and D = 1.0λ₀, the neutron yield and D⁺ cut-off energy when channels are closed vary with wire length L.

In addition to D and S, L is also of great importance for particle acceleration and neutron generation. Note that neutron yield and D⁺ cut-off energy show completely opposite trends in Figure 6C. Detailed simulations show that in the early stage of laser-target interaction, the energy spectra of deuterium ions are nearly the same for both cases of L = 10λ₀ and L = 18λ₀, but deviate from each other at 36T₀. In the case of L = 10λ₀, the laser is reflected by the substrate and propagates backward in the channels, and the reflected intensity is about 31% of the initial intensity; see Figure 7A. In the case of L = 18λ₀, the laser continues to propagate forward in the channels, so we do not see the laser main pulse in Figure 7B. This difference will induce different sheath fields within the channel shown in Figure 7C, further leading to different deuterium ions acceleration. For longer L, even if the energy of deuterium ions decreases, as shown in Figure 6C, the number of deuterium ions increases due to the larger heating volume, so neutron production increases. Therefore, taking into account factors such as neutron yield and experimental conditions, the wire length between 14λ₀ and 18λ₀ is appropriate. For example, given S = 2.8λ₀, D = 1.0λ₀, L = 15.0λ₀, which is considered to be optimal in our simulation, a deuterium ion cut-off energy of 1.0 MeV and a high neutron yield can be obtained.

FIGURE 7

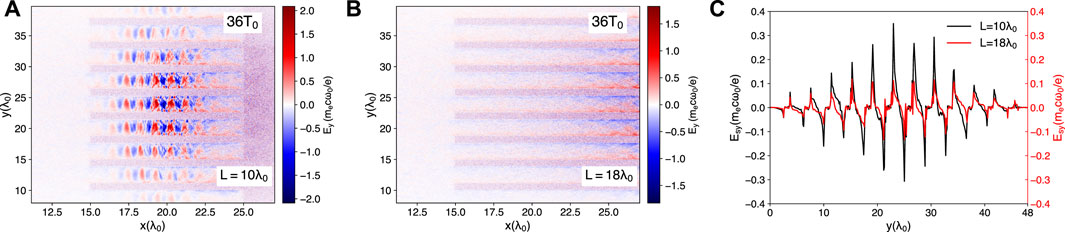
FIGURE 7. (A) For the fixed L = 10.0λ₀, S = 2.8λ₀, D = 1.0λ₀, the laser electric field at t = 36T₀. (B) For the fixed L = 18.0λ₀, S = 2.8λ₀, D = 1.0λ₀, the laser electric field at t = 36T₀. (C) The transverse sheath field E_sy along the line x = 20λ₀ at 36T₀.

4 Summary

In summary, we have proposed a multi-channel target which is highly efficient for neutron yield by using a relativistic femtosecond laser pulse. With a laser pulse of intensity a₀ = 5, duration τ = 33 fs and energy 1.17 J, the neutron yield of the MCT target is estimated to be 4 orders of magnitude larger than that of the plane target. Detailed analysis shows that the sheath field, which is normal to the surfaces of the wires, can effectively accelerate the D⁺ ions transversely inside the region of the wires. A cut-off energy up to 1.0 MeV is achieved, at which the total cross-section of the D-D fusion reaction almost approaches its maximum. As a result, the fusion probability is significantly enhanced and a large number of neutrons are produced in the region of the wires. Besides, due to the special acceleration mechanism of D⁺, the produced neutrons directionally peaked around ±90°. Moreover, this proposal is quite robust with respect to a wide range of target parameters, which should facilitate its experimental implementation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

CL and FW proposed this study and led the simulations, data analysis, and the interpretation of the results. YY, WS, XB, and QL carried out the PIC simulations. YY and CL wrote the text. CL, FW, and BZ led the discussion. JL and WZ are the principle investigator of the research. All listed authors contributed to discussion and helped to improve the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 12005305, U2267204, U2241281, 12275209, the Foundation under Grant Nos. FY222506000201, FC232412000201, and Foundation of China Institute of Atomic Energy under Grant Nos. YZ222402000401 and YC212212000301.

Acknowledgments

The PIC simulations were performed on the Beijing Super Cloud Computing Center (China).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Strickland D, Mourou G. Compression of amplified chirped optical pulses. Opt Commun (1985) 55:219–21. doi:10.1016/0030-4018(85)90120-8

CrossRef Full Text | Google Scholar

2. Li W, Gan Z, Yu L, Wang C, Liu Y, Guo Z, et al. 339 j high-energy ti: Sapphire chirped-pulse amplifier for 10 pw laser facility. Opt Lett (2018) 43:5681–4. doi:10.1364/ol.43.005681

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Radier C, Chalus O, Charbonneau M, Thambirajah S, Deschamps G, David S, et al. 10 pw peak power femtosecond laser pulses at eli-np. High Power Laser Sci Eng (2022) 10:e21. doi:10.1017/hpl.2022.11

CrossRef Full Text | Google Scholar

4. Yoon JW, Kim YG, Choi IW, Sung JH, Lee HW, Lee SK, et al. Realization of laser intensity over 10 23 w/cm 2. Optica (2021) 8:630–5. doi:10.1364/optica.420520

CrossRef Full Text | Google Scholar

5. Esarey E, Schroeder C, Leemans W. Physics of laser-driven plasma-based electron accelerators. Rev Mod Phys (2009) 81:1229–85. doi:10.1103/revmodphys.81.1229

CrossRef Full Text | Google Scholar

6. Macchi A, Borghesi M, Passoni M. Ion acceleration by superintense laser-plasma interaction. Rev Mod Phys (2013) 85:751–93. doi:10.1103/revmodphys.85.751

CrossRef Full Text | Google Scholar

7. Betti R, Hurricane O. Inertial-confinement fusion with lasers. Nat Phys (2016) 12:435–48. doi:10.1038/nphys3736

CrossRef Full Text | Google Scholar

8. Hurricane O, Callahan D, Casey D, Celliers P, Cerjan C, Dewald E, et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature (2014) 506:343–8. doi:10.1038/nature13008

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Takabe H, Kuramitsu Y. Recent progress of laboratory astrophysics with intense lasers. High Power Laser Sci Eng (2021) 9:e49. doi:10.1017/hpl.2021.35

CrossRef Full Text | Google Scholar

10. Bulanov S, Esirkepov TZ, Habs D, Pegoraro F, Tajima T. Relativistic laser-matter interaction and relativistic laboratory astrophysics. The Eur Phys J D (2009) 55:483–507. doi:10.1140/epjd/e2009-00138-1

CrossRef Full Text | Google Scholar

11. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun (2013) 4:2506–6. doi:10.1038/ncomms3506

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hofmann I. Review of accelerator driven heavy ion nuclear fusion. Matter Radiat Extremes (2018) 3:1. doi:10.1016/j.mre.2017.12.001

CrossRef Full Text | Google Scholar

13. Pretzler G, Saemann A, Pukhov A, Rudolph D, Schätz T, Schramm U, et al. Neutron production by 200 mj ultrashort laser pulses. Phys Rev E (1998) 58:1165–8. doi:10.1103/physreve.58.1165

CrossRef Full Text | Google Scholar

14. Willingale L, Petrov G, Maksimchuk A, Davis J, Freeman R, Joglekar A, et al. Comparison of bulk and pitcher-catcher targets for laser-driven neutron production. Phys Plasmas (2011) 18:083106. doi:10.1063/1.3624769

CrossRef Full Text | Google Scholar

15. Gillich DJ, Kovanen A, Danon Y. Deuterated target comparison for pyroelectric crystal d–d nuclear fusion experiments. J Nucl Mater (2010) 405:181–5. doi:10.1016/j.jnucmat.2010.08.012

CrossRef Full Text | Google Scholar

16. Ditmire T, Zweiback J, Yanovsky V, Cowan T, Hays G, Wharton K. Nuclear fusion from explosions of femtosecond laser-heated deuterium clusters. Nature (1999) 398:489–92. doi:10.1038/19037

CrossRef Full Text | Google Scholar

17. Grillon G, Balcou P, Chambaret J-P, Hulin D, Martino J, Moustaizis S, et al. Deuterium-deuterium fusion dynamics in low-density molecular-cluster jets irradiated by intense ultrafast laser pulses. Phys Rev Lett (2002) 89:065005. doi:10.1103/physrevlett.89.065005

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Bang W, Dyer G, Quevedo H, Bernstein A, Gaul E, Rougk J, et al. Optimum laser intensity for the production of energetic deuterium ions from laser-cluster interaction. Phys Plasmas (2013) 20:093104. doi:10.1063/1.4821611

CrossRef Full Text | Google Scholar

19. Ter-Avetisyan S, Schnürer M, Hilscher D, Jahnke U, Busch S, Nickles P, et al. Fusion neutron yield from a laser-irradiated heavy-water spray. Phys Plasmas (2005) 12:012702–5. doi:10.1063/1.1815001

CrossRef Full Text | Google Scholar

20. Moreau A, Hollinger R, Calvi C, Wang S, Wang Y, Capeluto MG, et al. Enhanced electron acceleration in aligned nanowire arrays irradiated at highly relativistic intensities. Plasma Phys Controlled Fusion (2019) 62:014013. doi:10.1088/1361-6587/ab4d0c

CrossRef Full Text | Google Scholar

21. Dozières M, Petrov G, Forestier-Colleoni P, Campbell P, Krushelnick K, Maksimchuk A, et al. Optimization of laser-nanowire target interaction to increase the proton acceleration efficiency. Plasma Phys Controlled Fusion (2019) 61:065016. doi:10.1088/1361-6587/ab157c

CrossRef Full Text | Google Scholar

22. Eftekhari-Zadeh E, Blümcke M, Samsonova Z, Loetzsch R, Uschmann I, Zapf M, et al. Laser energy absorption and x-ray generation in nanowire arrays irradiated by relativistically intense ultra-high contrast femtosecond laser pulses. Phys Plasmas (2022) 29:013301. doi:10.1063/5.0064364

CrossRef Full Text | Google Scholar

23. Serebryakov D, Volkova T, Nerush E, Kostyukov IY. Efficient gamma-ray source from solid-state microstructures irradiated by relativistic laser pulses. Plasma Phys Controlled Fusion (2019) 61:074007. doi:10.1088/1361-6587/ab209b

CrossRef Full Text | Google Scholar

24. Seletskiy DV, Hasselbeck MP, Cederberg JG, Katzenmeyer A, Toimil-Molares ME, Léonard F, et al. Efficient terahertz emission from inas nanowires. Phys Rev B (2011) 84:115421. doi:10.1103/physrevb.84.115421

CrossRef Full Text | Google Scholar

25. Beleckaitė I, Treu J, Morkötter S, Döblinger M, Xu X, Adomavičius R, et al. Enhanced thz emission efficiency of composition-tunable ingaas nanowire arrays. Appl Phys Lett (2017) 110:201106. doi:10.1063/1.4983641

CrossRef Full Text | Google Scholar

26. Kong D, Zhang G, Shou Y, Xu S, Mei Z, Cao Z, et al. High-energy-density plasma in femtosecond-laser-irradiated nanowire-array targets for nuclear reactions. Matter Radiat Extremes (2022) 7:064403. doi:10.1063/5.0120845

CrossRef Full Text | Google Scholar

27. Curtis A, Calvi C, Tinsley J, Hollinger R, Kaymak V, Pukhov A, et al. Micro-scale fusion in dense relativistic nanowire array plasmas. Nat Commun (2018) 9:1077–7. doi:10.1038/s41467-018-03445-z

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Curtis A, Hollinger R, Calvi C, Wang S, Huanyu S, Wang Y, et al. Ion acceleration and dd fusion neutron generation in relativistically transparent deuterated nanowire arrays. Phys Rev Res (2021) 3:043181. doi:10.1103/physrevresearch.3.043181

CrossRef Full Text | Google Scholar

29. Zou D, Yu D, Jiang X, Yu M, Chen Z, Deng Z, et al. Enhancement of target normal sheath acceleration in laser multi-channel target interaction. Phys Plasmas (2019) 26:123105. doi:10.1063/1.5096902

CrossRef Full Text | Google Scholar

30. Derouillat J, Beck A, Pérez F, Vinci T, Chiaramello M, Grassi A, et al. Smilei: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comp Phys Commun (2018) 222:351–73. doi:10.1016/j.cpc.2017.09.024

CrossRef Full Text | Google Scholar

31. Ammosov MV, Delone NB, Krainov VP. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Soviet J Exp Theor Phys (1986) 64:1191.

Google Scholar

32. Shen X, Qiao B, Zhang H, Xie Y, Kar S, Borghesi M, et al. Electrostatic capacitance-type acceleration of ions with an intense few-cycle laser pulse. Appl Phys Lett (2019) 114:144102. doi:10.1063/1.5088340

CrossRef Full Text | Google Scholar

33. Disdier L, Garconnet J, Malka G, Miquel J. Fast neutron emission from a high-energy ion beam produced by a high-intensity subpicosecond laser pulse. Phys Rev Lett (1999) 82:1454–7. doi:10.1103/physrevlett.82.1454

CrossRef Full Text | Google Scholar

34. Roth M, Jung D, Falk K, Guler N, Deppert O, Devlin M, et al. Bright laser-driven neutron source based on the relativistic transparency of solids. Phys Rev Lett (2013) 110:044802. doi:10.1103/physrevlett.110.044802

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Huang C-K, Broughton DP, Palaniyappan S, Junghans A, Iliev M, Batha S, et al. High-yield and high-angular-fluence neutron generation from deuterons accelerated by laser-driven collisionless shock. Appl Phys Lett (2022) 120:024102. doi:10.1063/5.0075960

CrossRef Full Text | Google Scholar

36. Yi L, Pukhov A, Luu-Thanh P, Shen B. Bright x-ray source from a laser-driven microplasma waveguide. Phys Rev Lett (2016) 116:115001. doi:10.1103/physrevlett.116.115001

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zou D, Pukhov A, Yi L, Zhuo H, Yu T, Yin Y, et al. Laser-driven ion acceleration from plasma micro-channel targets. Scientific Rep (2017) 7:42666–9. doi:10.1038/srep42666

CrossRef Full Text | Google Scholar

38. Zou D, Yu D, Yu M, Huang T, Pukhov A, Zhuo H, et al. Efficient generation of 100 mev ions from ultrashort 1021 w cm- 2 laser pulse interaction with a waveguide target. Nucl Fusion (2019) 59:066034. doi:10.1088/1741-4326/ab1121

CrossRef Full Text | Google Scholar

39. Jiang S, Krygier A, Schumacher D, Akli K, Freeman R. Effects of front-surface target structures on properties of relativistic laser-plasma electrons. Phys Rev E (2014) 89:013106. doi:10.1103/physreve.89.013106

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Ong J, Ghenuche P, Tanaka K. Electron transport in a nanowire irradiated by an intense laser pulse. Phys Rev Res (2021) 3:033262. doi:10.1103/physrevresearch.3.033262

CrossRef Full Text | Google Scholar

41. Gong Z, Robinson A, Yan X, Arefiev A. Highly collimated electron acceleration by longitudinal laser fields in a hollow-core target. Plasma Phys Controlled Fusion (2019) 61:035012. doi:10.1088/1361-6587/aaf94b

CrossRef Full Text | Google Scholar

42. Ganeev A, Govorov A. The dd reaction in the deuteron energy range 100-1000 kev. Soviet J At Energ (1958). (English Translation).

Google Scholar

43. Schulte RL, Cosack M, Obst AW, Weil JL. 2H+ reactions from 1.96 to 6.20 meV. Nucl Phys A. Elsevier (1972) 192:609–624. doi:10.1016/0375-9474(72)90093-0

CrossRef Full Text | Google Scholar

44. Liskien H, Paulsen A (1973). Neutron production cross sections and energies for the reactions t (p, n) 3he, d (d,n) 3he, and t (d,n) 4he. At Data Nucl Data Tables 11, 569–619.

CrossRef Full Text | Google Scholar

45. Goncharov P (2018). Differential and total cross sections and astrophysical s-factors for ²h (d,n) ³he and ²h (d,p) ³h reactions in a wide energy range. At Data Nucl Data Tables 120, 121–51. doi:10.1016/j.adt.2017.05.006

CrossRef Full Text | Google Scholar

46. Fuchs J, Sentoku Y, d’Humières E, Cowan T, Cobble J, Audebert P, et al. Comparative spectra and efficiencies of ions laser-accelerated forward from the front and rear surfaces of thin solid foils. Phys Plasmas (2007) 14:053105. doi:10.1063/1.2720373

CrossRef Full Text | Google Scholar

47. Thompson W. Thermonuclear reaction rates. Proc Phys Soc Section B (1957) 70:1–5. doi:10.1088/0370-1301/70/1/302

CrossRef Full Text | Google Scholar