
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys., 26 May 2023
Sec. Atomic and Molecular Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1187537
This article is part of the Research TopicEditor’s Challenge in Atomic and Molecular Physics: Applications and Advances in Fundamental PhysicsView all 4 articles
Antihydrogen atoms,
Antihydrogen atoms,
In Section 2, developments required for the inner region, the boundary and outer regions of the R-matrix method are outlined. In Section 3 an initial study of the required mixed coordinate systems for the general effective 3-body case and their transformations at the R-matrix boundary surfaces is reported. These systems, which combine coordinates from each arrangement, are needed in the R-matrix inner region with associated links to the separate coordinate systems for each collisional and reactive arrangement outer region on the boundary hypersurface. In Section 4, we report some preliminary bound-state calculations on the {p,p,
We propose to overcome a major bottleneck in understanding matter-antimatter collisions by developing the capability to calculate in full dimension and fully quantum mechanically, the scattering cross sections for molecular matter-antimatter rearrangements. Theory and simulation of antimatter formation and trapping are crucial in designing and interpreting experiments [9] but the necessary accurate scattering cross sections are lacking. We will make use of recent R-matrix developments [8] in the EPSRC High-End Computing (HEC) Consortium UK-AMOR [10], combined with recent variational approaches to solving matter-antimatter collision problems [5–7, 11].
Our early objectives are to adapt existing codes for the inner region, the boundary and outer regions of the R-matrix method for the adiabatic treatment of molecular matter-antimatter problems We will validate this work with test calculations on Pn + p which we can compare with mass-scaled literature Ps + e− results, then apply the methods and codes to calculate rearrangement cross sections for a system of high priority for experiments:
Our later objectives are to further adapt the inner region, boundary and outer region codes for non-adiabatic processes, such as Ps formation and apply the methods and codes to calculate rearrangement cross sections for other systems of high priority for experimentalists, in particular H2 +
Our general approach to tackle the heavy-projectile/molecular-target systems of interest will be to adapt and combine existing R-matrix methodologies from three areas: normal chemical reactions, light-particle (electron/positron/positronium) collisions with atoms and molecules; and antiproton-atom collisions. We will adapt the new UK-AMOR RmatReact code package [8]. Initially, the adiabatic approach will be adopted but this will be adaptable to the later non-adiabatic treatments. This will be essential as collisions involving excited states of
In R-matrix theory the inner region contains the interacting systems at close range and a full ab initio approach accounts for all interactions. As developed for electron atom/molecule scattering with excitation, the inner region boundary is a sphere centred on the nuclear centre of mass with radius r = a such that the “target” atomic or molecular states are contained within the sphere and the colliding electron is the only particle which crosses the boundary—see Figure 1.
The outer region Schrödinger equation is a set of multichannel coupled differential equations and the R-matrix is the inverse log-derivative matrix of the wavefunction at the boundary radius. At larger distances (the asymptotic region) the propagated solutions are matched to known forms consistent with non-vanishing potential interactions and the scattering parameters are calculated.
For low-energy atom-molecule collisions without rearrangement, the theory is applied in the centre of mass frame, using Jacobi coordinates for the three-body nuclear problem, or internal molecular coordinates and a collision vector between the atom and the molecular centre of mass in the N-body case. The boundary radius is determined by the requirement that the colliding bodies are distinguishable from the boundary outwards, that is, their component electronic and rovibrational states have negligible overlap. The outer region interaction is made up of inverse power potentials in the collision vector, R, for |R| > A. This defines the inner region for non-reactive collisions, with the intramolecular coordinates taken either over all space or to a radial value at which the included molecular wavefunctions effectively vanish. The inner region requires electronic and nuclear states for the all-body system (in practice expanded in bases of target state wavefunctions).
For reactive scattering the boundary definition is extended to a mixed coordinate system which includes Rα for each arrangement α. The inner region part of the solution is a bound-state problem for all the interacting particles with modified finite-range boundary conditions to allow non-zero probability amplitudes associated with the Rα in the initial and final arrangements.
The calculations in the outer regions for the different arrangements may be considered separately, linked together by the full R-matrix defined on the multidimensional boundary surface. This is chosen such that the pre- and post-reaction components are distinct entities outside the corresponding parts of the boundary surface, with no overlap between probability amplitudes for different arrangements [4, 8, 16]. The divisions of configuration space for the
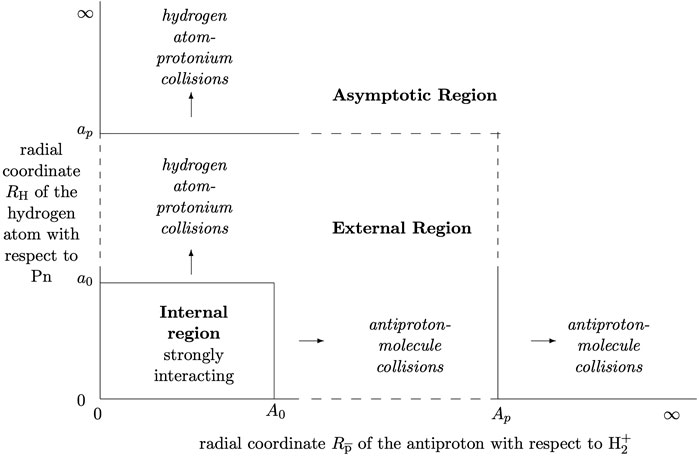
FIGURE 2. Separation of R-matrix configuration space for the
Our non-adiabatic treatment will make use of and expand established theories. Burke [4] details an R-matrix formalism for dissociative attachment and vibrational excitation in electron molecule collisions: the treatment of Le Dourneuf et al [17], extended by Gillan et al [18] allows for Born-Oppenheimer electronic calculations on a grid of nuclear configurations to be combined non-adiabatically with motion of the nuclei. Alternatively, R-matrix calculations using the “energy balance adiabatic nuclei” method of Stibbe and Tennyson [19] include impact dissociation for electron collisions with H2 (see also Scarlett et al [20]). For antimatter interactions, Sakimoto [5–7] has investigated
The first task would be to adapt the bound-state code DVR3D [21] to tackle, adiabatically, closely interacting matter-antimatter atoms (with positively and negatively charged nuclei). The strongly attractive potentials will require large well-designed basis sets. The extension to rearrangement collisions will use theory for mixed coordinate systems [16, 22, 23]. DVR3D can use Lobatto shape functions and quadrature for the inner region basis functions of the Rα, as utilized by Manolopoulos et al. [16], which (as do B-splines) have particularly useful properties to treat both bound-state and continuum basis requirements and which have been applied as a discrete variable representation (DVR) to the atom-atom code DUO in RmatReact ([8] and references). Burke [4] includes a rearrangement formalism for positronium formation in positron atom collisions, and an early calculation [24] includes explicit formulation of the “Bloch operators”, added to the inner region Hamiltonian in R-matrix and log-derivative Kohn [16] calculations to ensure Hermiticity with non-vanishing continuum functions at the boundary, for the mixed coordinate systems.
We will generate the multiple-arrangement boundary surface as indicated in ([4, 8, 16]), given in terms of the chosen magnitudes Rα = Aα of the collision vectors Rα for each arrangement. We have studied the mixed coordinate systems and their transformations at the boundary surfaces for our requirements, guided by related work with Jacobi and hyperspherical coordinates [22, 25, 26]–see Section 3 below. For the different arrangements to be treated as uncoupled outside the inner region, while linked by the boundary R-matrix [4], the values of Aα are constrained by the kinematics. For example, for
The outer region RmatReact codes PFARM ([8, 27, 28] form asymptotic solutions for charged and neutral collision products and when needed, can propagate R-matrices to suitable matching distances (Ap and ap in Figure 2). Minor adaptations are needed for propagation with two or more arrangement matrix blocks [4]. PFARM can already propagate two uncoupled sets of states linked only by off-diagonal block terms.
Following initial test calculations on Pn + p scattering, elastic, inelastic, rearrangement and (in-flight) annihilation cross-sections for
For our treatment of non-adiabatic processes and additional rearrangements such as {Pn + Ps} + H, we aim to incorporate Sakimoto’s DVR grid methods into our mixed Jacobi-type bases for all particles. Our experience with adiabatic applications will act as a guide to the feasibility of this approach. The sizes of basis set required will determine how many further dimensions for the light particles can be included explicitly.
Following Sakimoto’s approach [5–7], we will further adapt DVR3D to include electronic/positronic basis functions and matrix elements. The inner region boundary and outer region treatment for two-body break up channels would be defined as for the adiabatic cases but three-body break up, including
While [8] considers various approaches, bases and coordinates for the RmatReact inner region in useful detail for many-particle (atom-molecule) interacting systems, it does not give explicit details of how the boundary requirements for rearrangement affect the physical shape of the inner region shown in Figure 1. The [8] discussions build on [4] chapters 7 (positron atom collisions with positronium formation) and 11 (non-adiabatic electron molecule collisions with dissociation) which set out details of internal region basis expansions in both arrangements, and transformations at the boundaries chosen so that the one relevant expansion has non-zero surface amplitudes at each boundary. However it is assumed that the inner region integrals over the mixed coordinate hypervolume can be carried out without undue difficulty. Sakimoto’s atomic rearrangement calculations [5–7] are able to use the product channel Jacobi coordinates to describe both arrangements in the inner region and boundary definitions by taking advantage of the lightness of the electron. Reference [16] gives a general description of the mixed-coordinate approach. We may briefly illustrate the kind of necessary coordinate changes and make-up of the R-matrix inner region hypervolume and boundary transformations between internal and external regions using the example of three spinless (for ease of notation) interacting particles A, B, and C, with an initial arrangement of A colliding with molecular (ionic) structure BC and an additional final arrangement B + CA. The standard Jacobi coordinate structure is shown in Figure 3, which also establishes notation.
In the centre of mass frame, as described by Miller [22] the six coordinates Ra, ra describe the system in arrangement a (A + BC), while Rb, rb describe the system in arrangement b (B + CA). In arrangement a, it is convenient [22] to use the revised coordinates {Ra, ra, γa} and {θa, ϕa, ψa} where θa and ϕa are the spherical polar angle coordinates of Ra and ψa (0-2π) is the orientation of the ABC triangle about Ra. The inner region basis functions of {ra, γa} and {θa, ϕa, ψa}, in R-matrix terms the target states combined with the colliding particle angular coordinate functions, with label i and angular quantum numbers {J, MJ, li} can be summarized as products of rotation matrix angular momentum functions
[22] and its successor papers perform integrals over all space, whereas in the R-matrix method all three particles interact in a finite volume which must interface with two (to begin with) exit arrangements, a and b. This finite volume is bounded by a hypersurface defined by Ra = Aa and Rb = Ab, thus both of these conditions must be included in the coordinates defining the inner region. That this approach is feasible can be illustrated by our ABC example. The coordinates {ra, γa} may be replaced by {Rb, γab}, with γab (0-π) as shown in Figure 3. The relation between the volume elements is given in [22] (equation between (25) and (26)), or in [23] equation (2.18d).
We note the reduced mass factors can be removed by switching to mass-scaled Jacobi coordinates: details are given in our Supplementary Material along with the full set of transformations from the a coordinates to the b coordinates ([22] Appendix A). With (for example) particle A having mass MA and total mass M, the B − C reduced mass ma = MBMC/(MB + MC) and the A plus BC collisional reduced mass μa = MAMBMC/(maM) with cyclic permutation for the b and c arrangements.
There is no problem in performing the transformed integrals over all space, however we are interested in the transformation at the R-matrix boundaries from the mixed coordinate system to the a and b systems. We note that for the orientation coordinates the transformation of the rotation matrices of {θa, ϕa, ψa} to corresponding rotation matrices of coordinates {θb, ϕb, ψb}, dependent on angle γab, given by equation (24) in [22], is standard angular momentum theory [33].
At the Ra = Aa boundary, the {Ra, Rb, γab} mixed coordinates need to be related to arrangement a coordinates:
where we may take θab = π and (Ra dependent) aa can be no larger than
([22] Appendix A). Our Supplementary Material gives expressions for θa, max and θa, min. As preliminary work, programs have been written to evaluate test integrals over a mixed Jacobi coordinate inner region volume using single arrangement coordinates: the single arrangement limits for a given hypervolume can be found for given numerical quadrature grid sizes on the fly.
The relevance of this work for the larger project with full description of the colliding atoms and molecules is that values of Aa and Ab must be chosen not only so that the reactants are separated at the boundary for a particular arrangement, but also so that the limits placed on ra and rb by the mixed coordinate system do not affect the surface transformations to the external regions. In practice this means that for initial calculations the wavefunctions decribing the target (or product) states should be effectively zero outside of the range indicated in the integral transformation to be fully consistent with the inner region, as the external region R-matrix formulation assumes all coordinates apart from Ra (or Rb) have been fully integrated over at the boundary. Thus the choice of Aa and Ab needs to take into account more factors than in standard R-matrix calculations. Example figures demonstrating geometrical constraints on coordinate limits are included in the Supplementary Material. The transformation of surface amplitudes from mixed coordinates to single arrangement coordinates is in principle sraightforward. The preliminary test work and programs on the 3-particle Jacobi coordinates included transformations of test function amplitudes at fixed boundary values.
The work summarized in the Supplementary Material also studied alternatives to the mixed coordinate systems, such as Delves coordinates and tangent sphere coordinates, and principal axis hyperspherical coordinates (see, for example [25, 26, 34]), which are formulated for composite systems. These can be employed in the antimatter work if the mixed coordinate inner region and boundary transformations prove to be problematic. However, in real problems, when combined with additional bases and states describing the component particles of the composite colliding systems, the mixed Jacobi-type coordinate system seems so far to be the most straightforward and natural extension to the existing R-matrix packages.
The RmatReact project [8] plans to modify existing nuclear motion programs [21, 35] to solve the inner region problem. Here we have used the unmodified Triatom code [36] (a finite basis representation code related to DVR3D) to conduct some preliminary bound-state calculations on {p,p,
Pn + p has only one bound state (by analogy with Ps−) so to make a more demanding test of the dynamics of this mixed matter-antimatter system that a code designed for normal molecules can reproduce, we have investigated the lowest-lying s-wave resonance states using a simple stabilization method [38, 39]. The radial basis functions consist of products of a Gaussian and associated Laguerre polynomials, all defined in terms of the quantity y = βr2 (where r is a p-
We report calculations here where β−1/2 is varied from 0.000859 to 0.008125 a0 - see Figure 4 and Supplementary Figure S4 in the Supplementary Material. The latter also includes a tabulation of the plotted data.
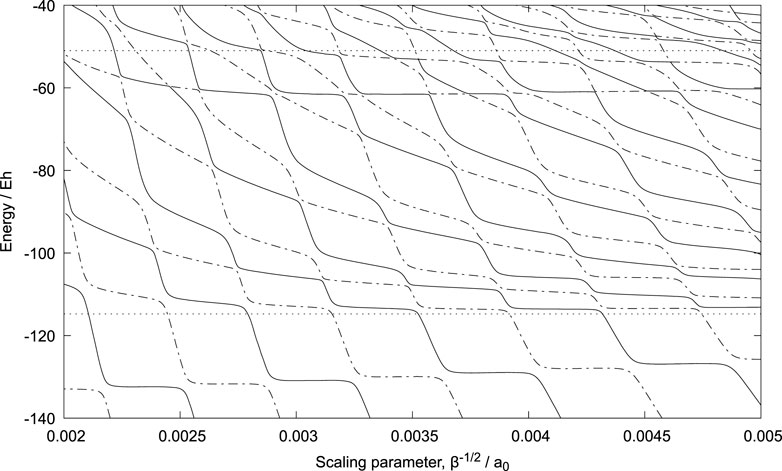
FIGURE 4. Stabilization diagram for the {p,p,
The energy of the bound state of Pn + p is minimised with respect to β at −483.1 Eh, that is below the expected −481.0 Eh. (Eh represents Hartree, the atomic unit of energy.) This discrepancy is due to inaccuracy in the numerical quadratures required for the Coulomb potential energy integrals. In the case of the integrals involving the proton-antiproton distances, Triatom uses Gauss-Laguerre quadrature and numerical problems were encountered when large numbers of quadrature points were used (that is greater than the 103 used for the reported results).
In spite of this issue, we pursued the exploration of Pn + p resonances to see if the chosen basis set could reproduce, at least qualitatively, the main features. Indeed the stabilization diagram, Figure 4, does show (near) horizontal regions, representing resonance states, at approximately −130, −113, −62 and −54 Eh. In every case they are higher in energy than expected from mass scaling of accurate calculations on Ps− (−139.6, −116.9, −64.9 and −54.8 Eh). Note also that the second lowest resonance should be below the protonium n = 2 energy (represented by the horizontal dotted line at −114.7 Eh). The mean energies of the horizontal regions vary with β and the values obtained for the largest β, giving a horizonal and stable region, are −132.5, −113.4, −61.5 and −53.5 Eh. See also Supplementary Table S1 where the present calculated energies of the {p,p,
We have set out a road-map for treatment of matter-antimatter scattering processes including rearrangement using the R-matrix method. We have described the complexities involved and set out an approach to solve these problems. This will be extendable to larger systems including for example molecular antimatter. We note that spectroscopic investigation of the antihydrogen molecular anion
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
MP and ML conceived and designed the study and developed the overall theoretical approach. The coordinate transformation studies were conducted by EK (with input from MP and ML), whilst the bound-state studies were conducted by LV (with input from ML). MP and ML wrote the manuscript with input from EK and LV. All authors contributed to the article and approved the submitted version.
The contribution of EK was supported by the Ada Lovelace Centre, UK Science and Technology Facilities Council. MP’s work made use of support by CoSeC, the Computational Science Centre for Research Communities, through Collaborative Computational Project Q and High-End-Consortium (HEC) UK-AMOR.
We are grateful for helpful discussions with Jonathan Tennyson and Mike Charlton. The bound-state calculations were performed using the Maxwell High Performance Computing Cluster of the University of Aberdeen IT Service.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1187537/full#supplementary-material
1. Ahmadi M, Alves BXR, Baker CJ, Bertsche W, Capra A, Carruth C, et al. Investigation of the fine structure of antihydrogen. Nature (2020) 578:375–80. doi:10.1038/s41586-020-2006-5
2. Baker CJ, Bertsche W, Capra A, Carruth C, Cesar CL, Charlton M, et al. Laser cooling of antihydrogen atoms. Nature (2021) 592:35–42. doi:10.1038/s41586-021-03289-6
3. Kolbinger B, Amsler C, Cuendis SA, Breuker H, Capon A, Costantini G, et al. Measurement of the principal quantum number distribution in a beam of antihydrogen atoms. Europ Phys J D (2021) 75:91. doi:10.1140/epjd/s10053-021-00101-y
5. Sakimoto K. R-matrix calculation of antiproton capture by helium ions. Phys Rev A (2007) 76:042513. doi:10.1103/physreva.76.042513
6. Sakimoto K. Cross sections for antiproton capture by helium ions. Phys Rev A (2010) 82:012501. doi:10.1103/physreva.82.012501
7. Sakimoto K. Unified treatment of hadronic annihilation and protonium formation in slow collisions of antiprotons with hydrogen atoms. Phys Rev A (2013) 88:012507. doi:10.1103/physreva.88.012507
8. McKemmish LK, Tennyson J. General mathematical formulation of scattering processes in atom–diatomic collisions in the RmatReact methodoogy. Phil Trans R Soc A (2019) 377:20180409. doi:10.1098/rsta.2018.0409
9. Jonsell S, Charlton M. On the binding energies of antihydrogen formed by the interactions of antiprotons in cold positron plasmas. J Phys B (2021) 54:025001. doi:10.1088/1361-6455/abcded
10.Available at: https://www.ukamor.com (Accessed May 16, 2023).
11. Mant BP, Law MM, Strasburger K. Hydrogen molecule-antihydrogen atom potential energy surface and scattering calculations. J Phys B (2019) 52:185201. doi:10.1088/1361-6455/ab312e
12. Lodi Rizzini E, Venturelli L, Zurlo N, Charlton M, Amsler C, Bonomi G, et al. Further evidence for low-energy protonium production in vacuum. E Phys J Plus (2012) 127:124. doi:10.1140/epjp/i2012-12124-9
13. Jonsell S, Saenz A, Froelich P, Zygelman B, Dalgarno A. Stability of hydrogen-antihydrogen mixtures at low energies. Phys Rev A (2001) 64:052712. doi:10.1103/physreva.64.052712
14. Jonsell S. Rearrangement and annihilation in antihydrogen-atom scattering. AIP Conf Proc (2008) 1037:347–357. doi:10.1063/1.2977853
15. Jonsell S, Armour EAG, Plummer M, Liu Y, Todd AC. Helium–antihydrogen scattering at low energies. New J Phys (2012) 14:035013. doi:10.1088/1367-2630/14/3/035013
16. Manolopoulos DE, D’Mello M, Wyatt RE. Quantum reactive scattering via the log derivative version of the Kohn variational principle: General theory for bimolecular chemical reactions. J Chem Phys (1989) 91:6096–102. doi:10.1063/1.457428
17. Le Dourneuf M, Schneider BI, Burke PG. Theory of vibrational excitation and dissociative attachment: An R-matrix approach. J Phys B (1979) 12:L365–9. doi:10.1088/0022-3700/12/12/008
18. Gillan CJ, Nagy O, Burke PG, Morgan LA, Noble CJ. Electron scattering by nitrogen molecules. J Phys B (1987) 20:4585–603. doi:10.1088/0022-3700/20/17/032
19. Stibbe DT, Tennyson J. Near-threshold electron impact dissociation of H2 within the adiabatic nuclei approximation. N J Phys (1998) 1:2. doi:10.1088/1367-2630/1/1/002
20. Scarlett LH, Fursa DV, Knol J, Zammit MC, Bray I. Isotopic and vibrational-level dependence of H2 dissociation by electron impact. Phys Rev A (2021) 103:L020801. doi:10.1103/physreva.103.l020801
21. Tennyson J, Kostin MA, Barletta P, Harris GJ, Polyansky OL, Ramanlal J, et al. DVR3D: A program suite for the calculation of rotation–vibration spectra of triatomic molecules. Comput Phys Commun (2004) 163:85–116. doi:10.1016/j.cpc.2003.10.003
22. Miller WH. Coupled equations and the minimum principle for collisions of an atom and a diatomic molecule, including rearrangements. J Chem Phys (1969) 50:407–18. doi:10.1063/1.1670812
23. Zhang JZH, Miller WH. Quantum reactive scattering via the S-mstrix version of the Kohn variational principle: Differential and integral cross sections for D + H2 → HD + H. J Chem Phys (1989) 91:1528–47. doi:10.1063/1.457650
24. Higgins K, Burke PG. Positron scattering by atomic hydrogen including positronium formation. J Phys B (1993) 26:4269–88. doi:10.1088/0953-4075/26/22/029
25. Carter S, Meyer W. A variational method for the calculation of vibrational energy levels of triatomic molecules using a Hamiltonian in hyperspherical coordinates. J Chem Phys (1990) 93:8902–14. doi:10.1063/1.459229
26. Parker GA, Keil M, Morrison MA, Crocchianti S. Quantum reactive scattering in three dimensions: Using tangent-sphere coordinates to smoothly transform from hyperspherical to Jacobi regions. J Chem Phys (2000) 113:957–70. doi:10.1063/1.481876
27. Sunderland AG, Noble CJ, Burke VM, Burke PG. A parallel R-matrix program PRMAT for electron–atom and electron–ion scattering calculations. Comp Phys Commun (2002) 145:311–40. doi:10.1016/s0010-4655(02)00140-6
28. Brigg WJ, Tennyson J, Plummer M. R-matrix calculations of low-energy electron collisions with methane. J Phys B (2014) 47:185203. doi:10.1088/0953-4075/47/18/185203
29. Cohen JS. Dissociation and ionization in capture of antiprotons and negative muons by the hydrogen molecular ion. J Phys B (2005) 38:441–56. doi:10.1088/0953-4075/38/4/011
30. Sakimoto K. Protonium formation in collisions of antiprotons with hydrogen molecular ions. J Phys B (2004) 37:2255–76. doi:10.1088/0953-4075/37/11/004
31. Cohen JS. Reactive collisions of atomic antihydrogen with the H2 and
32.UK engineering and physical science research Council Grant EP/T019530/1, Available at: https://gow.epsrc.ukri.org/NGBOViewGrant.aspx?GrantRef=EP/T019530/1 (Accessed May 16, 2023).
34. Pack RT, Parker GA. Quantum reactive scattering in three dimensions using hyperspherical (APH) coordinates. Theory. J Chem Phys (1987) 87:3888–921. doi:10.1063/1.452944
35. Kozin IN, Law MM, Tennyson J, Hutson JM. New vibration–rotation code for tetraatomic molecules exhibiting wide-amplitude motion: WAVR4. Comput Phys Commun (2004) 163:117–31. doi:10.1016/j.cpc.2004.07.005
36. Tennyson J, Miller S, Le Sueur CR. Triatom: Programs for the calculation of ro-vibrational spectra of triatomic molecules. Comp.Phys Commun (1993) 75:339–64. doi:10.1016/0010-4655(93)90048-h
37. Zhou Y, Lin CD. Comparative Studies of Excitations and Resonances in H−, Ps−, and e+ + H Systems. Phys Rev Lett (1995) 75:2296–9. doi:10.1103/physrevlett.75.2296
38. Hazi AU, Taylor HS. Stabilization method of calculating resonance energies: Model problem. Phys Rev A (1970) 1:1109–20. doi:10.1103/physreva.1.1109
39. Mandelshtam VA, Ravuri TR, Taylor HS. Calculation of the density of resonance states using the stabilization method. Phys Rev Lett (1993) 70:1932–5. doi:10.1103/physrevlett.70.1932
40. Myers EG. CPT tests with the antihydrogen molecular ion. Phys Rev A (2018) 98:010101(R). doi:10.1103/physreva.98.010101
Keywords: antihydrogen, antiproton, rearrangement scattering, matter-antimatter interactions, R-matrix method, coordinate transformations
Citation: Kasoar E, Plummer M, Van Lydon L and Law MM (2023) Matter-antimatter rearrangements using the R-matrix method. Front. Phys. 11:1187537. doi: 10.3389/fphy.2023.1187537
Received: 16 March 2023; Accepted: 10 May 2023;
Published: 26 May 2023.
Edited by:
Michael Charlton, Swansea University, United KingdomReviewed by:
Pedro Duarte Amaro, New University of Lisbon, PortugalCopyright © 2023 Kasoar, Plummer, Van Lydon and Law. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Plummer, bWFydGluLnBsdW1tZXJAc3RmYy5hYy51aw==; Mark M. Law, bS5tLmxhd0BhYmRuLmFjLnVr
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.