
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys., 16 May 2023
Sec. Nuclear Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1186457
In the mid-1980s, theoreticians predicted possible exotic states of an eta (η) meson and a nucleus bound by the strong interaction, so-called mesic nucleus. This led to extensive experimental efforts aimed at discovering such unstable states as well as understanding the underlying interactions via η meson production reactions. As experiments yielded new data, more and more sophisticated theoretical models were developed to understand the fundamental η-nucleon and η-nucleus interactions. After more than 35 years of research in this field, several signals have been identified as possible indications of hypothetical η-mesic nuclei, but there is still no general agreement or clear confirmation of their existence. In the paper, we review the study of the η-mesic nuclei with an emphasis on recent research activities.
The study of exotic atoms and exotic nuclei, new kinds of subatomic matter containing exotic particles like mesons or excited baryons, is one of the hottest topics in contemporary hadron and nuclear physics. A better understanding of these systems can offer valuable insight into the nature of strong forces and hadron-nucleus interaction. An example of such an object is a mesic atom, where a negatively charged pion [1] or kaon [2] replaces an electron in an outer orbital of a standard atom. The binding in this case is primarily due to the Coulomb interaction, but as the meson undergoes transitions, it eventually reaches the range of the strong nuclear interaction, resulting in its absorption by the nucleus or loss through a nuclear reaction. Another possible formation of meson-nucleus bound states is when the strong interaction between the meson and nucleus is attractive, as is the case with the neutral eta (η) meson. Its interaction with the nucleons has been found to be strong and attractive in the low-energy region (s-wave) [3]. Based upon this finding, Haider and Liu [4] predicted the possibility of the formation of strongly bound systems of the η meson and nuclei with mass number A ≥ 12, and called such systems η-mesic nuclei. This conclusion was supported by similar results from other studies [5, 6], while some analyses [7–16] have even suggested that light systems like 2H, 3H, 3He, and 4He could potentially form a bound state with η.
The η meson belongs to the pseudoscalar nonet of mesons with zero spin and negative parity (Jπ = 0−) [17]. It is an electrically neutral particle that can decay through both the strong and electromagnetic interactions. Its lifetime, τη, is
The attractive and strong character of the η-nucleon interaction led to the speculation of the existence of η-nucleus (quasi-)bound states. An initial theoretical prediction [4] prompted experimental searches for these unstable bound states. These searches have been conducted using various light and heavy nuclei targets and various beams such as pions [25–27], photons [28–32], protons [33–36] and deuterons [37–41]. With advancements in experimental research, new and more sophisticated models have emerged to shed light on the fundamental ηN interaction and the multi-body systems of η mesons and nuclei. Despite years of investigation, there is still no clear evidence of η-mesic nuclei and no consensus on the strength of the η-nucleon and η-nucleus interactions.
The search for η-mesic nuclei aims to investigate various important issues in η meson physics, including the interaction of the η meson with nucleons within nuclear matter. The discovery of such objects would allow for a more accurate determination of the poorly known ηN scattering length [22]. Furthermore, the examination of η-mesic nuclei would open up opportunities to study the structure of the η meson. The binding energy of the meson-nucleus system, as shown by Bass and Thomas [42], is sensitive to the flavor-singlet component and glue content of the η meson quark-gluon wave function. In a bound state, the wave function of the η meson overlaps with that of the nucleus, allowing for the observation of in-medium effects on meson properties. In particular, studies of η-mesic nuclei can provide precise information on the η meson mass shift, which is significant in understanding the dynamics of the axial UA (1) symmetry [42–44]. Additionally, the detection of η-mesic nuclei would also provide information regarding the properties of the N*(1,535) resonance in nuclear medium, useful in verifying different theoretical models related to the structure of the resonance [45–49].
The purpose of the article is to provide a comprehensive overview of the current status of research on η-mesic bound states. It begins with a discussion of theoretical approaches and predictions, followed by a review of experimental efforts aimed at detecting the η-mesic nuclei. The paper focuses on summarizing recent investigations and highlighting areas for future research.
The study of the η-nucleus bound states is related to the η meson interactions with nucleons and nuclei. Recent reviews on this topic can be found in Refs. [18, 22, 43, 50, 51, 52]. These interactions can only be probed through the study of reactions that produce η mesons in the final state. The knowledge of the reaction mechanisms plays a significant role in both understanding this interaction and predicting the existence of η-mesic unstable nuclear states. The strong effects of the η-nucleus interaction are particularly pronounced close to the threshold of the η production reactions, where off-shell rescattering becomes relevant [53]. Since the η meson has an extremely short lifetime, data on elastic scattering of the η-nucleon or η-nucleus are not available. Instead, a more efficient approach in a theoretical search for η-mesic nuclei involves using information on the ηN interaction obtained from models that fit the η meson production reactions data to construct a complex η-nucleus elastic scattering matrix (S-matrix) [54–56].
The scattering matrix elements are treated as functions of complex incident momentum p. The analytical properties of matrix elements are determined by the interaction potential, specifically its asymptotic behavior. If the potential decreases exponentially at large distances r and is analytic for
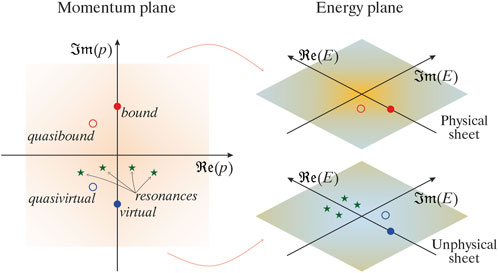
FIGURE 1. The diagram displays the complex momentum plane (left) and energy plane (right) with markers indicating the positions of poles in the scattering matrix. The poles correspond to various states: bound (red full circle), quasibound (red empty circle), virtual (blue full circle), quasivirtual (blue empty circle), and resonances (green stars).
The poles located on the physical sheet
The possible binding energy of the meson-nucleus state is determined by both the η-nucleon optical potential and the value of the η-nucleon scattering length aηN [57]. The real part of aηN has a broad range of phenomenological estimates that vary by up to six times depending on the underlying model assumptions [18, 21, 23, 24]. Consequently, this significant uncertainty in the value of aηN results in different predictions regarding the potential existence of η-mesic nuclei.
One of the commonly used theoretical approaches to study the interaction between the η meson and atomic nuclei involves constructing an appropriate optical potential Uη-nucleus = V(r) + iW(r) based on the η-nucleon scattering length aηN, and then using it to solve the wave equation. A negative real part of the optical potential
The binding energies and widths of possible η-mesic states in 12C, 40Ca, and 208Pb nuclei were also calculated using the self-energies of the η meson in the nuclear medium [60]. The results obtained by applying the local density approximation (LDA) showed that the optical potential generates bound states with a very large width, which makes it unlikely to experimentally observe narrow peaks corresponding to η-mesic states in these nuclei. Another study [6], which used a chiral unitary approach [47] to evaluate the self-energy of the η meson, similarly reported that the resulting bound states have a half width larger than the separation of the levels.
An alternative method is the quark-meson coupling (QMC) model, based on quantum chromodynamics. Within this model, the η meson is considered to be embedded in the nuclear medium and couples to quarks, mixing with its heavier partner, η′ meson [42, 61, 62]. The in-medium mass of the η meson
The feasibility of forming η-mesic bound state in light nuclei is closely related to the constraints on the complex η-nucleus scattering length aη-nucleus. Specifically, to create such a state, the imaginary part of aη-nucleus must be positive, i.e.,
Using the optical potential approach, Wilkin [8] has investigated the 3He-η system, which is the final state of the
Theoretical models based on few-body equations for systems consisting of η meson and two, three, or four nucleons can be useful for studying light η-mesic nuclei. One of the initial calculations considered the ηNN-πNN coupled system in a three-body equation and predicted a quasibound 2H-η state near the threshold with a mass of 2,430 MeV and a width of 10–20 MeV [63]. Few years later, further investigations were conducted within the framework of the finite-rank approximation (FRA) to explore the possibility of forming 2H-η, 3H-η, 3He-η, and 4He-η bound states [7, 64]. The analysis suggested that η-nucleus quasibound states are possible for A ≥ 2 when the value of
The Wigner’s time delay and dwell time delay concepts have been used as an alternative approach to search for light η-mesic nuclei [10, 11, 68]. The delay times for η-nucleus elastic scattering were calculated to locate quasibound states in 2H-η, 3He-η, and 4He-η systems. By varying the strength of the ηN interaction, quasibound states were found to be more favorable for small ηN scattering lengths, while higher values corresponded to resonances [68].
In Ref. [12], the stochastic variational method (SVM) was used to study the NNN-η and NNNN-η systems within a pionless effective field theory. Based on the η-nucleon scattering lengths, the authors found that the formation of a bound state of the η meson and 3He nucleus requires a value of
A recent theoretical analysis of the η meson interaction with the 3He nucleus considered the total cross sections and asymmetry parameter for the
The theoretical model presented by Ikeno et al. in Ref. [15] describes the formation of 4He-η bond states in the dd fusion reaction. The model takes into account the experimental data on the production of the η meson near the
In contrast, Fix and Kolesnikov [70] used a non-relativistic five-body problem to investigate the 4He-η interaction and solved the corresponding AGS equations. Their analysis showed that the predicted parameters of the ηN interaction do not provide enough attraction in the NNNN-η system to support the existence of the 4He-η bound state. The authors subsequently expanded their analysis to include the 2H-η and 3He-η systems [71]. Their new calculations once again did not confirm the hypothesis of an η-mesic bound state in 4He, while the status of the 3He-η system remains ambiguous. Significantly, the analysis revealed that the interaction between the η meson and 4He is unexpectedly less attractive compared to the 3He-η case. In turn, the weaker attraction in the case of deuteron was attributed to the smaller number of nucleons.
In summary, while some theoretical analyses suggest that the formation of certain η-nucleus bound states is unlikely, many others predict their existence. The significant variation in input parameters used in different calculations results in a wide range of predicted outcomes regarding the potential existence or non-existence of η-mesic nuclei.
The concept of mesic nuclei, first introduced by Haider and Liu in 1986 [4], has garnered significant attention and has prompted numerous experimental and theoretical investigations aimed at discovering both light and heavy mesic nuclei. The experimental searches for this exotic form of nuclear matter involve the production of η mesons, analyzing their interaction with nuclei, and detecting η-mesic states through their possible decay modes. This section provides an overview of previous measurements in this area.
The initial theoretical predictions indicated that η mesons could be bound in nuclei with a mass number greater than 12 [4, 5], leading to initial experimental searches for these bound states being conducted in heavy nuclei region.
The first proposal of an experiment devoted to the search for η-mesic nuclei was introduced by Liu and Haider in Ref. [58]. They suggested using a positively charged pion beam to induce the reaction
An alternative proposal to investigate the η production induced by pions on lithium and carbon targets was presented at the Japan Proton Accelerator Research Complex (J-PARC) [72, 73]. In contrast to previous experiments [25, 26], this proposed study would focus on the (π−, n) reaction, with the aim of optimizing the conditions for recoilless kinematics using a pion beam momentum in the range of 0.7–1.0 GeV/c. Additionally, the cross-sections of the π+d → ppη reaction were also proposed to be studied, in order to obtain an exclusive measurement and estimate background from π−p pairs [72]. Unfortunately, this experiment has not been carried out.
Another attempt to search for such exotic states using the LAMPF accelerator [27], inspired by the prior work of Haider and Liu [74], was focused on the production of the η-mesic fluorine nucleus
The research group at the Lebedev Physical Institute (LPI) reported the first observation of η-mesic nuclei formed in the photoproduction process induced by bremsstrahlung γ rays from the electron synchrotron [28, 29]. In the experiment, a beam of photons with energy of 650–850 MeV was used together with a carbon target. The study was performed through the reaction
A similar experiment on the photoproduction of η-mesic nuclei was conducted at the LPI via the observation of the two-nucleon decay that results from the two-nucleon absorption of the captured η meson in the nucleus [30]. An experimental setup consisting of two TOF spectrometers was used to detect correlated π+n and pn pairs from the annihilation of η mesons that were stopped in the nuclear matter, and the velocity distributions of these particles were measured. For a photon energy of Eγ = 850 MeV (above the η meson photoproduction threshold), the velocity of protons was found to peak in the βC ∼ 0.6–0.7 region. This observation was interpreted as evidence of the production of low-energy η mesons followed by their two-nucleon absorption (ηNN → NN). In contrast, no such effect was observed in standard photoproduction with a photon energy of 650 MeV, when high-momentum particles are not produced. Based on the assumption that the π+n and pn pairs were primarily produced through the formation and decay of η-mesic nuclei with A = 11, the upper limit of the total cross section of the studied reaction was estimated to be 10 μb. It is worth noting, however, that the energy resolution of the measurement was not sufficient to definitively confirm the position and width of a possible bound state, so the results of this experiment are not conclusive.
The formation of η-mesic nuclei in a reaction induced by deuterons was investigated at the Joint Institute for Nuclear Research (JINR) [37, 75]. The experiment was performed using an internal deuteron beam at the NUCLOTRON accelerator with a primary beam energy ranging from 1.5 to 2.2 GeV/nucleon. The d + C → π− + p + X reaction was studied by measuring the velocities, masses, and angles of emitted particles. The results of the experiment showed clear back-to-back π−p correlation and a resonance-like peak below the η production threshold. This finding was interpreted as a signature of the decay of the N* resonance, which is related to the formation of an η-mesic nucleus. However, further investigation required to confirm these results needs more intense beam and higher spectrometer acceptance.
Investigating the existence of η-mesic nuclei can also be done through transfer reaction experiments. In these reactions, the entire beam momentum is transferred to one or multiple nucleons, leaving a remaining system at rest and increasing the chance of the produced η meson binding to the nucleus. The experiment of this type was conducted at the GSI Helmholtz Centre for Heavy Ion Research in Darmstadt [38]. The study used a recoil-free transfer reaction
The COSY-GEM Collaboration at the Forschungszentrum Jülich conducted an experiment examining the transfer reaction
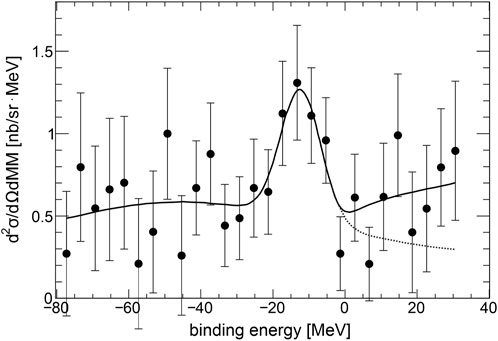
FIGURE 2. Missing mass spectrum converted to the binding energy of the bound state 25Mg-η measured by the COSY-GEM Collaboration. The solid curve represents a fit with a constant background, two Gaussians, and a phase space behavior for the unbound system, while the dotted curve shows the same fit without the phase space contribution (The figure is adapted from Ref. [34]).
The COSY-GEM group has also investigated the
As previously mentioned, studies on the production of η mesons in various processes have resulted in a wide range of possible values for the η-nucleon scattering lengths (aηN) [18, 21, 23, 24]. This opens the possibility for the formation of η-mesic states in light nuclei like helium (3He, 4He) [8, 9] or hydrogen isotopes (2H, 3H) [7, 65]. The smaller absorption of η mesons in the light nuclei causes an increase in their lifetime in the nuclear medium, resulting in the formation of narrower bound states [52] that may be easier to observe compared to those in heavy nuclei. Additionally, there are no complications in interpreting results related to excitation of higher nuclear levels.
The existence of η-mesic bound states in helium is supported by several indirect experimental observations. In particular, the studies of the
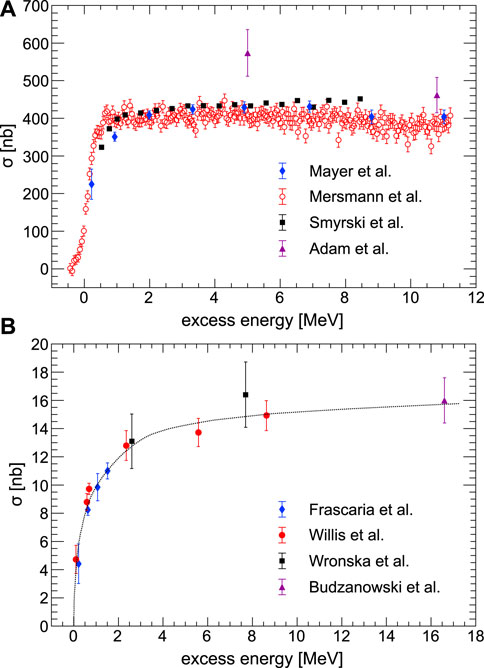
FIGURE 3. The close-to-threshold total cross section for the η meson production reactions plotted as a function of excess energy. (A) Data for the
The first experiment to directly search for a bound state of the η meson with a light nucleus was conducted using the Two-Arm Photon Spectrometer (TAPS) at the Mainz Microtron (MAMI) accelerator facility [31]. The experiment studied the
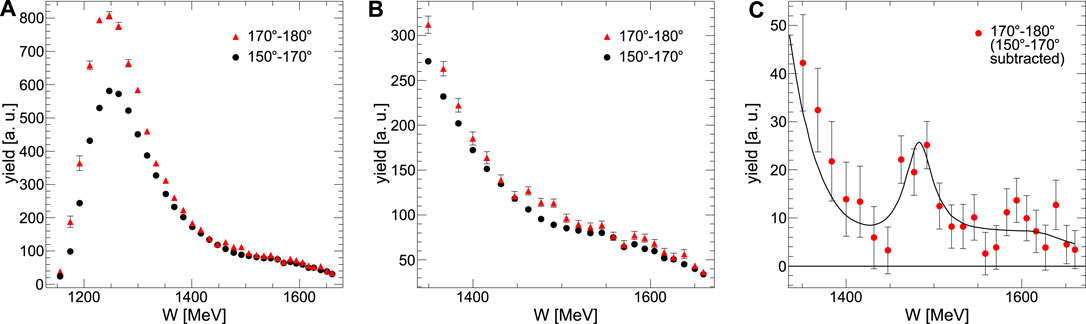
FIGURE 4. (A) and (B) Excitation function of the π0-proton pairs production in the γ3He → π0pX process for relative angles of 170°–180° (red triangles) and 150°–170° (black circles) in the γ-3He center-of-momentum frame. (C) Difference spectrum between both distributions with a line indicating the results of fitting the Breit-Wigner distribution plus background (The figure is adapted from Ref. [31]).
The search for η-mesic helium nuclei was also carried out using the internal deuteron beam of the Cooler Synchrotron (COSY) [51] at the Forschungszentrum Jülich. During the experiment [39, 91–94], the deuterons were scattered on a proton target of the cluster-jet type, and the resulting charged products of the reaction were detected by the COSY-11 facility [95]. The beam momentum was continuously ramped within each acceleration cycle, crossing the threshold for the
In more recent experiments, the search for hypothetical η-bound states in helium nuclei has been carried out employing the Wide Angle Shower Apparatus (WASA) [96] at the COSY accelerator. Three high-statistics, exclusive measurements were performed in 2008, 2010, and 2014, using a deuteron pellet target and deuteron and proton beams to study the possible formation of 4He-η and 3He-η bound states, respectively [97]. During each experiment, data were collected as the beam was slowly and continuously accelerated in each cycle, crossing the kinematic threshold for the production of the η meson (corresponding to the η-helium excess energy range Q ∈ (−70, 30) MeV).
The study of η-mesic nuclei involves investigating the physical processes in which a virtual η meson is produced and then forms a bound state with the nucleus, which eventually decays. In the WASA-at-COSY experiments, two mechanisms for η-mesic helium decay were tested. The first hypothesis involves the absorption of the η meson by a nucleon inside helium, exciting it to the N*(1,535) resonance, which subsequently decays into a nucleon-pion pair, causing the disintegration of the mesic nucleus. Three reactions were analyzed to test this mechanism:
In the reactions that proceed via the excitation of the N* resonance, the accuracy of determining the cross section depends on the momentum distributions of the N* inside the mesic nuclei, which determine the kinematics of the particles in the final state. Calculations, based on elementary NN* → NN* amplitudes within a π plus η meson exchange model, allowed to determine the momentum distributions of N* in the N*-3He and N*-NN systems [98–100]. These distributions were used in the analysis of the experimental data.
To search for 4He-η bound states, the WASA-at-COSY Collaboration measured the excitation functions for the
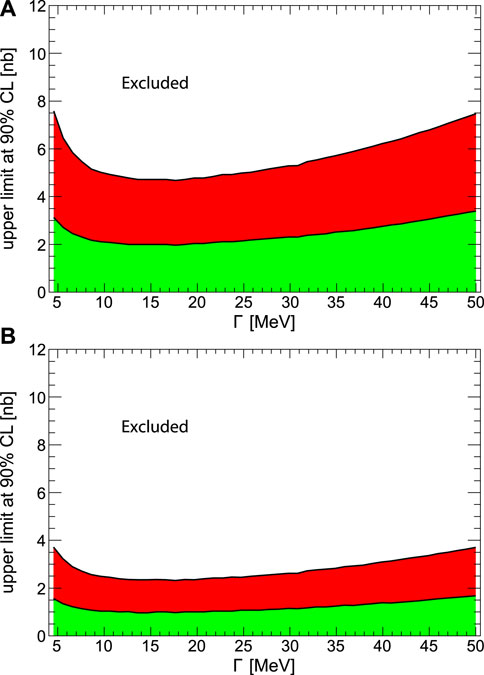
FIGURE 5. The upper limit (at the 90% confidence level) of the total cross section as a function of the width of the bound state for the
A recently developed phenomenological model describing subthreshold cross sections for the
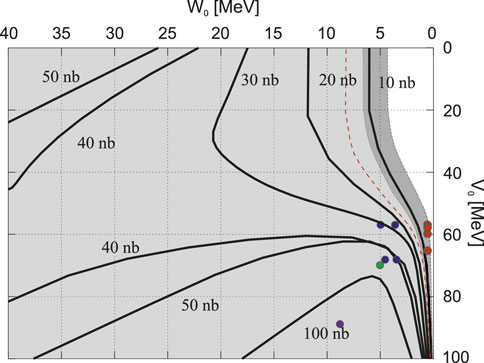
FIGURE 6. Contour plot of the theoretically determined conversion cross section for the η-mesic 4He production in dd reaction, shown in the V0− W0 plane [15]. The light shaded area represents the region of excluded optical potential parameters, while the dark shaded area shows the systematic uncertainties. The dashed red line extends the region of allowed parameters based on an error estimate that considered the recent model of the N* momentum distribution in 4He [98]. The color dots in the plot correspond to the optical potential parameters that are associated with the predicted 4He-η bound states (The figure is adapted from Ref. [101]).
In particular, Figure 6 shows predictions based on a few-body formalism and an optical model [13] that uses the η-nucleon scattering amplitude obtained from two different models described in Ref. [102] (purple dot) and [103] (green dot). Results for a class of potentials, which include Gaussian, exponential and Hulthen potentials [104], are shown as blue dots. The analysis [101] suggested that the η-mesic helium states within these models are excluded. Finally, the study also predicted very narrow and weakly bound states of 4He-η with binding energies and widths of
The final experimental campaign conducted by WASA-at-COSY Collaboration in 2014 aimed to search for η-mesic 3He state in the proton-deuteron nuclear fusion [35, 36, 105–108]. This run resulted in the world’s largest data sample collected thus far [105]. As previously mentioned, phenomenological calculations indicate the potential existence of a weakly bound 3He-η state with an estimated binding energy of approximately 0.3 MeV and a width of approximately 3 MeV [14]. Analysis of this data, assuming the 3He-η bound state decays through the creation of the N* resonance, allowed for the establishment of an excitation function for the pd → dpπ0 reaction in the region of the η meson production thresholds. However, no narrow resonance-like structure associated with an η-mesic helium was observed. Therefore, an upper limit for the total cross section of the
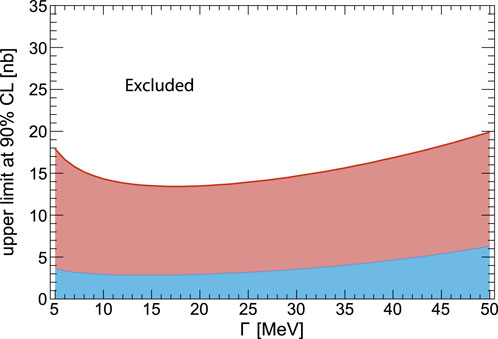
FIGURE 7. The upper limit (at the 90% confidence level) of the total cross section for formation of the η-mesic 3He and its decay via the
The data obtained from this experiment also allowed the investigation of the second proposed mechanism for the decay of 3He-η bound state, which involves the direct decay of the η meson. This mechanism was studied for the first time by analysing the
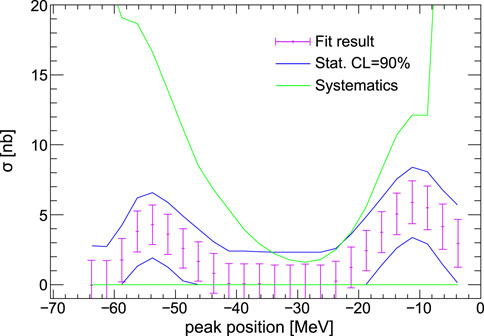
FIGURE 8. The upper limits for the cross-section of the
In summary, while some research efforts suggests the existence of η-mesic nuclei, none of these findings have been independently confirmed. Some of the experiments mentioned above require higher precision or improved detection systems. Conducting new experiments with better statistics and less background uncertainty would provide more conclusive evidence for the existence of η-mesic nuclei in the future.
Mesic nuclei would represent a novel form of nuclear matter in which a meson is bound with a nucleus solely through the strong interaction, without the influence of electromagnetic Coulomb effects. The η meson is a particularly promising candidate for exploring such bound states, due to its strong attractive interaction with nucleons [3]. Mesic nuclei would serve as a unique laboratory for investigating the behavior of mesons and their possible modifications in the nuclear medium, offering valuable insights for hadron physics research.
As previously mentioned, the value of ηN scattering length is significant dependent on the chosen model [18], resulting in a wide range of predictions for the possible η-nuclear states. Therefore, distinguishing between different theoretical approaches can be challenging. Some models suggest the existence of narrow, easily observable bound states, while others predict widths that are too large or too weak to generate bound states. Despite numerous experiments aimed at discovering η-mesic nuclei using pion, photon, proton, and deuteron beams, conclusive results have not been obtained. The absence of a clear positive signal may be due to significant non-η background. The uncertainty related to the predictions of possible η-nuclear states from different theoretical models and inconclusive experimental results leave the question of the existence of hypothetical η-mesic nuclei unanswered. Therefore, new strategies and measurements with higher statistics are necessary to advance in this field.
Transfer reactions have been identified as a particularly intriguing topic for further investigation due to current evidence that supports the existence of the 25Mg-η mesic nucleus [33]. Moreover, it is possible that mesic nuclei could be discovered in lighter systems such as 3He, 4He, and 11B [21]. Analysis of the excitation function of the pion DCX reaction
Research on hypothetical mesic nuclei involves also investigating the formation of bound states of atomic nuclei and the η′ meson, which is the heavier partner of the η meson and has a mass of 957.78 MeV [17]. The η′ meson is a promising candidate for mesic nuclei searches due to its strong and attractive interactions with nucleons [18, 110]. Ongoing experimental [111, 112] and theoretical [44, 113–115] studies are actively pursuing this research direction. In 2014, the pioneering experiment aimed at detecting η′-mesic bound states was conducted using the 12C (p, d) reaction at the Fragment Separator (FRS) facility located at the GSI [111]. Despite the excellent statistics, no narrow structure was observed, and an upper limit for the formation cross-section of η′-mesic nuclei of
A detailed account of the various theoretical and experimental efforts for the search for bound η meson in nuclei was given in this review.
Initially, based on the assumption of a relatively small η-nucleon scattering length aηN, theorists estimated that the lightest nucleus on which the η meson might bind is 12C [4, 5, 58]. The larger value of aηN [18, 21, 23, 24] suggested later indicates that η could tightly bind with heavy nuclei, resulting in large and overlapping widths, making it difficult to detect, but also raises the possibility of binding even in lighter systems, such as helium [9–16]. Numerous experimental attempts and theoretical investigations have been conducted since the first prediction, but most searches for signals of η-mesic nuclei have been unsuccessful.
Due to limited knowledge about the η-nucleon and η-nucleus interactions, diverse theoretical predictions of mesic nuclei have been proposed, using various assumptions and considerations. Binding energies and widths of several heavy η-mesic nuclei have been calculated using techniques based on different approaches, such as η-nucleus optical potentials [4, 58, 59], self-energies of the η meson in the nuclear medium [60], or unitarized chiral perturbation theory [6]. The QMC approach has also been applied to study the behavior of η-mesons in the nuclear medium, where it mixes with the η′ meson [42, 61, 62], which allowed to predict of bound states in several closed-shell nuclei. Exploring the existence of η binding in light nuclei typically involves identifying poles in the scattering matrix and calculating corresponding η-nucleus scattering lengths. A bound state requires a large, negative real component of the scattering length [59]. Calculations based on few-body equations have been performed for the 2H-η, 3H-η, 3He-η, and 4He-η systems [7, 13, 63]. The time delay concept has also been applied to locate these bound states [10, 11, 68]. More recent studies based on optical potential [14] and pionless effective field theory [12] suggest the possibility of bound η-mesic states in 3He and 4He. However, some works [70, 71] indicate that the attraction in these systems is very weak, which makes their detection unlikely.
Early experiments with low statistics using pion [25–27], photon [28–32], proton [33, 34], or deuteron [37–39] beams provided some indications of potential η-mesic bound states, but no definitive evidence was found due to limited sensitivity. Recent searches with using the COSY [51] accelerator have concentrated on the possibility of η-mesic bound states in 3He and 4He isotopes. Evidence of possible mesic helium nuclei was indicated by a sharp rise in cross sections near threshold observed in photoproduction [31, 32], proton-deuteron (pd) [79–82], and deuteron-deuteron (dd) [83–86] experiments. These hypothetical states in helium require a η-nucleon scattering length with a real part lager than 0.7 to 1 fm [12, 13]. Experimental efforts to search for the η-mesic 3He have been conducted by the COSY-11 Collaboration [39, 91–94] and resulted in the upper limits of the cross section of 270 nb and 70 nb for the
In conclusion, despite more than 35 years of theoretical and experimental efforts, the search for unambiguous evidence of η-mesic states has proven to be challenging task. The lack of a conclusive signal highlights the difficulty of this field of research. Therefore, the development of novel experimental strategies with higher statistics measurements is crucial to make significant progress in this direction.
The manuscript was initially drafted by AK, and later edited and contributed to by MS and PM. All authors contributed to the final editing and proofreading of the manuscript and approved it for submission. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The work is financially supported by the SciMat and qLife Priority Research Area budget under the program Excellence Initiative—Research University at Jagiellonian University.
The authors would like to thank the WASA-at-COSY Collaboration and the WASA-FRS/Super-FRS Experiment Collaboration.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Yamazaki T, Hirenzaki S, Hayano RS, Toki H. Deeply bound pionic states in heavy nuclei. Phys Rep (2012) 514:1–87. doi:10.1016/j.physrep.2012.01.003
2. Curceanu C, Guaraldo C, Iliescu M, Cargnelli M, Hayano R, Marton J, et al. The modern era of light kaonic atom experiments. Rev Mod Phys (2019) 91:025006. doi:10.1103/RevModPhys.91.025006
3. Bhalerao RS, Liu LC. Off-shell model for threshold pionic η production on a nucleon and for ηN scattering. Phys Rev Lett (1985) 54:865–8. doi:10.1103/PhysRevLett.54.865
4. Haider Q, Liu LC. Formation of an eta-mesic nucleus. Phys Lett B (1986) 172:257–60. doi:10.1016/0370-2693(86)90846-4
5. Li GL, Cheng WK, Kuo TTS. On formation of η-meson-nucleus bound states. Phys Lett B (1987) 195:515–20. doi:10.1016/0370-2693(87)91564-4
6. Garcia-Recio C, Inoue T, Nieves J, Oset E. η bound states in nuclei. Phys Lett B (2002) 550:47–54. doi:10.1016/S0370-2693(02)02960-X
7. Rakityansky SA, Sofianos SA, Braun M, Belyaev VB, Sandhas W. Quasibound states of η-nucleus systems. Phys Rev C (1996) 53:R2043–R2047. doi:10.1103/PhysRevC.53.R2043
8. Wilkin C. Near-threshold production of η mesons. Phys Rev C (1993) 47:R938–R940. doi:10.1103/PhysRevC.47.R938
9. Wycech S, Green AM, Niskanen JA. Are there η-helium bound states? Phys Rev C (1995) 52:544–53. doi:10.1103/PhysRevC.52.544
10. Kelkar NG, Khemchandani KP, Jain BK. Possible η-mesic 3He states within the finite rank approximation. J Phys G: Nucl Part Phys (2006) 32:L19–L26. doi:10.1088/0954-3899/32/3/L01
11. Kelkar NG, Khemchandani KP, Jain BK. ηN scattering lengths favor ηd and ηα states. J Phys G: Nucl Part Phys (2006) 32:1157–70. doi:10.1088/0954-3899/32/8/007
12. Barnea N, Bazak B, Friedman E, Gal A. Onset of η-nuclear binding in a pionless EFT approach. Phys Lett B (2017) 771:297–302. doi:10.1016/j.physletb.2017.05.066
13. Barnea N, Friedman E, Gal A. Onset of η-meson binding in the He isotopes. Nucl Phys A (2017) 968:35–47. doi:10.1016/j.nuclphysa.2017.07.021
14. Xie JJ, Liang WH, Oset E, Moskal P, Skurzok M, Wilkin C. Determination of the η3He threshold structure from the low energy pd → η3He reaction. Phys Rev C (2017) 95:015202. doi:10.1103/PhysRevC.95.015202
15. Ikeno N, Nagahiro H, Jido D, Hirenzaki S. η-nucleus interaction from the d + d reaction around the η production threshold. Eur Phys J A (2017) 53:194. doi:10.1140/epja/i2017-12381-7
16. Xie JJ, Liang WH, Oset E. η-4He interaction from the dd → η4He reaction near threshold. Eur Phys J A (2019) 55:6. doi:10.1140/epja/i2019-12693-6
17. Workman RL, Burkert VD, Crede V, Klempt E, Thoma U, Tiator L, et al. Review of particle physics. Prog Theor Exp Phys (2022) 2022:083C01. doi:10.1093/ptep/ptac097
18. Metag V, Nanova M, Paryev EY. Meson-nucleus potentials and the search for meson-nucleus bound states. Prog Part Nucl Phys (2017) 97:199–260. doi:10.1016/j.ppnp.2017.08.002
19. Christ NH, Dawson C, Izubuchi T, Jung C, Liu Q, Mawhinney RD, et al. η and η′ mesons from lattice QCD. Phys Rev Lett (2010) 105:241601. doi:10.1103/PhysRevLett.105.241601
20. Moskal P, Wolke M, Khoukaz A, Oelert W. Close-to-threshold meson production in hadronic interactions. Prog Part Nucl Phys (2002) 49:1–90. doi:10.1016/S0146-6410(02)00143-6
21. Haider Q, Liu LC. Eta-mesic nuclei: Past, present, future. Int J Mod Phys E (2015) 24:1530009. doi:10.1142/S021830131530009X
22. Kelkar NG, Khemchandani KP, Upadhyay NJ, Jain BK. Interaction of eta mesons with nuclei. Rep Prog Phys (2013) 76:066301. doi:10.1088/0034-4885/76/6/066301
23. Sibirtsev A, Schneider S, Elster C, Haidenbauer J, Krewald S, Speth J. ηN final state interaction in incoherent photoproduction of η mesons from the deuteron near threshold. Phys Rev C (2002) 65:044007. doi:10.1103/PhysRevC.65.044007
24. Arndt RA, Briscoe WJ, Morrison TW, Strakovsky , Workman RL, Gridnev AB. Low-energy ηN interactions: Scattering lengths and resonance parameters. Phys Rev C (2005) 72:045202. doi:10.1103/PhysRevC.72.045202
25. Chrien RE, Bart S, Pile P, Sutter R, Tsoupas N, Funsten HO, et al. Search for bound states of the η meson in light nuclei. Phys Rev Lett (1988) 60:2595–8. doi:10.1103/PhysRevLett.60.2595
26. Lieb B, Liu L. Search for nuclear bound states of the eta meson. In: Progress at LAMPF. Los Alamos National Laboratory (1988). p. 52–5. LA-11670-PR.
27. Johnson JD, Burleson GR, Edwards C, El-Ghossain M, Espy MA, Garnett R, et al. Search for an η bound state in pion double charge exchange on 18O. Phys Rev C (1993) 47:2571–3. doi:10.1103/PhysRevC.47.2571
28. Sokol GA, L’vov AI, Pavlyuchenko LN. Discovery of η-mesic nuclei. In: AI Studenikin, editor. Frontiers of particle physics. World Scientific (2003). p. 188–96. doi:10.1142/9789812704948_0024
29. Sokol G, Pavlyuchenko L. Discovery and investigation of η-mesic nuclei in photoproduction processes. Phys Atom Nuclei (2008) 71:509–19. doi:10.1134/S1063778808030113
30. Baskov V, Koltsov A, L’vov A, Lebedev A, Pavlyuchenko L, Polyanskiy V, et al. Studies of eta-mesic nuclei at the LPI electron synchrotron. In: Proceedings of XXI International Baldin Seminar on High Energy Physics Problems – PoS Baldin-ISHEPP-XXI, 173 (2013). p. 102. doi:10.22323/1.173.0102
31. Pfeiffer M, Ahrens J, Annand JRM, Beck R, Caselotti G, Cherepnya S, et al. Photoproduction of η-mesic 3He. Phys Rev Lett (2004) 92:252001. doi:10.1103/PhysRevLett.92.252001
32. Pheron F, Ahrens J, Annand J, Arends H, Bantawa K, Bartolome P, et al. Coherent photoproduction of η-mesons off 3He – search for η-mesic nuclei. Phys Lett B (2012) 709:21–7. doi:10.1016/j.physletb.2012.01.075
33. Budzanowski A, Chatterjee A, Hawranek P, Jahn R, Jain BK, Jha V, et al. Search for η-mesic nuclei in a recoil-free transfer reaction. Phys Rev C (2009) 79:012201. doi:10.1103/PhysRevC.79.012201
35. Adlarson P, Augustyniak W, Bashkanov M, Bass SD, Bergmann FS, Berłowski M, et al. Search for the η mesic 3He in the pd → dpπ0 reaction with the WASA-at-COSY facility. Phys Rev C (2020) 102:044322. doi:10.1103/PhysRevC.102.044322
36. Adlarson P, Augustyniak W, Bardan W, Bashkanov M, Bass S, Berłowski M, et al. Search for η mesic 3He with the WASA-at-COSY facility in the pd → 3He2γ and pd → 3He6γ reactions. Phys Lett B (2020) 802:135205. doi:10.1016/j.physletb.2020.135205
37. Afanasiev V, Artiomov AS, Bekmirzaev RN, Dryablov DK, Igamkulov ZA, Ivanov VI, et al. Search for η-mesic nuclei in the reaction d + C at JINR. Phys Part Nucl Lett (2011) 8:1073–7. doi:10.1134/S1547477111100025
39. Moskal P, Smyrski J. Search for the η-mesic nuclei by means of COSY-11, WASA-at-COSY and COSY-TOF detector systems. Acta Phys Pol B (2010) 41:2281–92.
40. Adlarson P, Augustyniak W, Bardan W, Bashkanov M, Bednarski T, Bergmann FS, et al. Search for η-mesic 4He with the WASA-at-COSY detector. Phys Rev C (2013) 87:035204. doi:10.1103/PhysRevC.87.035204
41. Adlarson P, Augustyniak W, Bardan W, Bashkanov M, Bergmann F, Berłowski M, et al. Search for η-mesic 4He in the dd→3Henπ0 and dd→3Hepπ− reactions with the WASA-at-COSY facility. Nucl Phys A (2017) 959:102–15. doi:10.1016/j.nuclphysa.2017.01.001
42. Bass SD, Thomas AW. η bound states in nuclei: A probe of flavour-singlet dynamics. Phys Lett B (2006) 634:368–73. doi:10.1016/j.physletb.2006.01.071
43. Bass SD, Moskal P. η′ and η mesons with connection to anomalous glue. Rev Mod Phys (2019) 91:015003. doi:10.1103/RevModPhys.91.015003
44. Nagahiro H, Takizawa M, Hirenzaki S. η- and η′-mesic nuclei and UA(1) anomaly at finite density. Phys Rev C (2006) 74:045203. doi:10.1103/PhysRevC.74.045203
45. Jido D, Nagahiro H, Hirenzaki S. Medium effects to the N(1535) resonance and η mesic nuclei. Phys Rev C (2002) 66:045202. doi:10.1103/PhysRevC.66.045202
46. Jido D, Nagahiro H, Hirenzaki S. Medium effects to the N(1535) resonance and η mesic nuclei. Nucl Phys A (2003) 721:C665–C668. doi:10.1016/S0375-9474(03)01148-5
47. Inoue T, Oset E. η in the nuclear medium within a chiral unitary approach. Nucl Phys A (2002) 710:354–70. doi:10.1016/S0375-9474(02)01167-3
48. Nagahiro H, Jido D, Hirenzaki S. η-nucleus interactions and in-medium properties of N*(1535) in chiral models. Phys Rev C (2003) 68:035205. doi:10.1103/PhysRevC.68.035205
49. Nagahiro H, Jido D, Hirenzaki S. Formation of η-mesic nuclei by the (π, N) reaction and properties of N*(1535) in medium. Phys Rev C (2009) 80:025205. doi:10.1103/PhysRevC.80.025205
50. Krusche B, Wilkin C. Production of η and η′ mesons on nucleons and nuclei. Prog Part Nucl Phys (2015) 80:43–95. doi:10.1016/j.ppnp.2014.10.001
51. Wilkin C. The legacy of the experimental hadron physics programme at COSY. Eur Phys J A (2017) 53:114. doi:10.1140/epja/i2017-12295-4
52. Bass SD, Metag V, Moskal P. “The η- and η′-nucleus interactions and the search for η, η′-mesic states,” in Handbook of Nuclear Physics. Editors I Tanihata, H Toki, and T Kajino (Singapore: Springer)(2022):1–8. doi:10.1007/978-981-15-8818-1_39-1
53. Kelkar NG. Unresolved issues in the search for eta-mesic nuclei. Acta Phys Pol B (2015) 46:113–20. doi:10.5506/APhysPolB.46.113
54. Taylor JR. Scattering theory: The quantum theory of nonrelativistic collisions. New York, London, Sydney, Toronto: John Wiley & Sons (1972). p. 478.
55. Newton RG. Scattering theory of waves and particles. 2nd ed. New York, Heidelberg, Berlin: Springer-Verlag (1982). p. 743.
56. Cassing W, Stingl M, Weiguny A. Scattering with absorptive interaction. Phys Rev C (1982) 26:22–33. doi:10.1103/PhysRevC.26.22
57. Ericson TEO, Weise W. Pions and nuclei. In: International series of monographs on physics, 74. Oxford: Clarendon Press (1988). p. 479.
58. Liu LC, Haider Q. Signature for the existence of eta-mesic nucleus. Phys Rev C (1986) 34:1845–54. doi:10.1103/PhysRevC.34.1845
59. Haider Q, Liu LC. Dependence of calculated binding energies and widths of η-mesic nuclei on treatment of subthreshold η-nucleon interaction. Phys Rev C (2002) 66:045208. doi:10.1103/PhysRevC.66.045208
60. Chiang HC, Oset E, Liu LC. Width of bound eta in nuclei. Phys Rev C (1991) 44:738–46. doi:10.1103/PhysRevC.44.738
61. Tsushima K, Lu DH, Thomas AW, Saito K. Are η- and ω-nuclear states bound? Phys Lett B (1998) 443:26–32. doi:10.1016/S0370-2693(98)01336-7
62. Tsushima K. Study of ω-η-η′- and D−-mesic nuclei. Nucl Phys A (2000) 670:198–201. doi:10.1016/S0375-9474(00)00098-1
63. Ueda T. I = 0, JP = 1− quasibound state in the ηNN-πNN coupled system. Phys Rev Lett (1991) 66:297–300. doi:10.1103/PhysRevLett.66.297
64. Rakityansky SA, Sofianos SA, Sandhas W, Belyaev VB. Threshold scattering of the η-meson off light nuclei. Phys Lett B (1995) 359:33–8. doi:10.1016/0370-2693(95)01057-W
65. Green AM, Niskanen JA, Wycech S. η-deuteron scattering. Phys Rev C (1996) 54:1970–5. doi:10.1103/PhysRevC.54.1970
66. Shevchenko NV, Rakityansky SA, Sofianos SA, Belyaev VB, Sandhas W. Faddeev-type calculation of ηd threshold scattering. Phys Rev C (1998) 58:R3055–R3059. doi:10.1103/PhysRevC.58.R3055
67. Shevchenko N, Belyaev V, Rakityansky S, Sofianos SA, Sandhas W. Low-energy ηd-resonance. Eur Phys J A (2000) 9:143–6. doi:10.1007/s100500070064
68. Kelkar NG. Quantum reflection and dwell times of metastable states. Phys Rev Lett (2007) 99:210403. doi:10.1103/PhysRevLett.99.210403
69. Wycech S, Krzemień W. Studies of mesic nuclei via decay reactions. Acta Phys Pol B (2014) 45:745–51. doi:10.5506/APhysPolB.45.745
70. Fix A, Kolesnikov O. Solution of the five-body η4He problem with separable pole expansion method. Phys Lett B (2017) 772:663–8. doi:10.1016/j.physletb.2017.07.034
71. Fix A, Kolesnikov O. Systematic few-body analysis of ηd, η3He, and η4He interaction at low energies. Phys Rev C (2018) 97:044001. doi:10.1103/PhysRevC.97.044001
73. Fujioka H. Search for mesic nuclei at J-PARC. J Phys Conf Ser (2012) 374:012015. doi:10.1088/1742-6596/374/1/012015
74. Haider Q, Liu LC. Nuclear bound states of the η0 meson and pion double-charge-exchange reactions. Phys Rev C (1987) 36:1636–9. doi:10.1103/PhysRevC.36.1636
75. Afanasiev SV, Bekmirzaev RN, Baskov VA, Cruceru I, Constantin F, Cruceru M, et al. New status of the project “η-nuclei” at the Nuclotron. Nucl Phys B Proc Suppl 245 (2013) 173–6. doi:10.1016/j.nuclphysbps.2013.10.034
76. Haider Q, Liu LC. Interference and nuclear medium effects on the eta-mesic nuclear spectrum. J Phys G: Nucl Part Phys (2010) 37–125104. doi:10.1088/0954-3899/37/12/125104
77. Budzanowski A, Chatterjee A, Hawranek P, Jahn R, Jha V, Kilian K, et al. Experimental study of the p +6Li → η +7Be reaction 11.3 MeV above threshold. Phys Rev C (2010) 82:041001. doi:10.1103/PhysRevC.82.041001
78. Upadhyay NJ, Kelkar NG, Jain BK. Eta meson rescattering effects in the p + 6Li → η + 7Be reaction near threshold. Nucl Phys A (2009) 824:70–85. doi:10.1016/j.nuclphysa.2009.03.010
79. Mayer B, Boudard A, Fabbro B, Garçon M, Kerboul C, Poitou J, et al. Reactions pd→ 3He η and pd→3He pi + pi - near the η threshold. Phys Rev C (1996) 53:2068–74. doi:10.1103/PhysRevC.53.2068
80. Mersmann T, Khoukaz A, Büscher M, Chiladze D, Dymov S, Hartmann M, et al. Precision study of the η3He system using the dp→ 3Heη reaction. Phys Rev Lett (2007) 98:242301. doi:10.1103/PhysRevLett.98.242301
81. Smyrski J, Adam HH, Budzanowski A, Czerwiński E, Czyżykiewicz R, Gil D, et al. Measurement of the d p →3Heη reaction near threshold. Phys Lett B (2007) 649:258–62. doi:10.1016/j.physletb.2007.04.021
82. Adam HH, Geck I, Khoukaz A, Lister T, Santo R, Steltenkamp S, et al. Hadronic 3Heη production near threshold. Phys Rev C (2007) 75:014004. doi:10.1103/PhysRevC.75.014004
83. Frascaria R, Roudot F, Wurzinger R, Duval MA, Ernst J, Goldzahl L, et al. Total d + d → α + η cross sections near threshold. Phys Rev C (1994) 50:R537–R540. doi:10.1103/PhysRevC.50.R537
84. Willis N, Le Bornec Y, Zghiche A, Wilkin C, Wurzinger R, Bing O, et al. η-helium quasi-bound states. Phys Lett B (1997) 406:14–9. doi:10.1016/S0370-2693(97)00650-3
85. Wrońska A, Hejny V, Wilkin C, Dymov S, Hanhart C, Komarov V, et al. Near-threshold η-meson production in the dd↦He η reaction. Eur Phys J A (2005) 26:421–8. doi:10.1140/epja/i2005-10185-0
86. Budzanowski A, Chatterjee A, Gebel R, Hawranek P, Jahn R, Jha V, et al. Cross section and tensor analysing power of the dd → ηα reaction near threshold. Nucl Phys A (2009) 821:193–209. doi:10.1016/j.nuclphysa.2009.02.004
87. Papenbrock M, Barsov S, Burmeister I, Chiladze D, Dymov S, Fritzsch C, et al. Absence of spin dependence in the final state interaction of the d→p→He3η reaction. Phys Lett B (2014) 734:333–7. doi:10.1016/j.physletb.2014.05.079
88. Wilkin C, Büscher M, Chiladze D, Dymov S, Hanhart C, Hartmann M, et al. Is there an η3He quasi-bound state? Phys Lett B (2007) 654:92–6. doi:10.1016/j.physletb.2007.08.041
89. Hanhart C. Comment on “photoproduction of η-mesic 3He. Phys Rev Lett (2005) 94:049101. doi:10.1103/PhysRevLett.94.049101
90. Pfeiffer M, Thoma U, van Pee H, Ahrens J, Annand JRM, Beck R, et al. Reply to the comment by C. Hanhart. Phys Rev Lett (2005) 94:049102. doi:10.1103/PhysRevLett.94.049102
91. Smyrski J, Adam HH, Budzanowski A, Czerwiński E, Czyżykiewicz R, Gil D, et al. Study of the 3He-η system in d-p collisions at COSY-11. Acta Physica Slovaca (2006) 56:213–9.
92. Smyrski J, Adam HH, Budzanowski A, Czerwiński E, Czyżykiewicz R, Gil D, et al. Study of the 3He-η system in d-p collisions. Nucl Phys A (2007) 790:438c–41c. doi:10.1016/j.nuclphysa.2007.03.137
93. Smyrski J, Krzemień W, Moskal P. Study of the dp → pppπ− reaction near the η production threshold. Acta Phys Pol B Proc Suppl (2009) 2:133–40.
94. Krzemień W, Smyrski J, Budzanowski A, Czerwiński E, Czyżykiewicz R, Gil D, et al. Search for the 3He-η bound state at COSY-11. Int J Mod Phys A (2009) 24:576–80. doi:10.1142/S0217751X09044115
95. Brauksiepe S, Grzonka D, Kilian K, Oelert W, Roderburg E, Rook M, et al. COSY-11, an internal experimental facility for threshold measurements. Nucl Instrum Methods Phys Res A (1996) 376:397–410. doi:10.1016/0168-9002(96)00080-0
96. Adam HH, Bashkanov M, Bechstedt U, Bisplinghoff J, Bogoslovski D, Bondar A, et al. Proposal for the wide angle shower apparatus (WASA) at COSY-jüelich – “WASA at COSY”. [Preprint] (2004). doi:10.48550/arXiv.nucl-ex/0411038
97. Skurzok M. Status of the search for η-mesic nuclei with particular focus on η-helium bound states. Few-body Syst (2021) 62:5. doi:10.1007/s00601-020-01585-x
98. Kelkar NG. Momentum distribution of N* in nuclei. Eur Phys J A (2016) 52:309. doi:10.1140/epja/i2016-16309-5
99. Kelkar NG, Kamada H, Skurzok M. N-N-N* model calculations for experimental η-mesic 3He searches. Int J Mod Phys E (2019) 28:1950066. doi:10.1142/S0218301319500666
100. Kelkar NG, Bedoya Fierro D, Kamada H, Skurzok M. Study of the N* momentum distribution for experimental η-mesic 3He searches. Nucl Phys A (2020) 996:121698. doi:10.1016/j.nuclphysa.2020.121698
101. Skurzok M, Moskal P, Kelkar NG, Hirenzaki S, Nagahiro H, Ikeno N. Constraining the optical potential in the search for η-mesic 4He. Phys Lett B (2018) 782:6–12. doi:10.1016/j.physletb.2018.04.047
102. Green AM, Wycech S. η-nucleon scattering length and effective range uncertainties. Phys Rev C (2005) 71:014001. doi:10.1103/PhysRevC.71.014001
103. Cieplý A, Smejkal J. Chirally motivated separable potential model for ηN amplitudes. Nucl Phys A (2013) 919:46–66. doi:10.1016/j.nuclphysa.2013.10.003,
104. Liverts EZ, Barnea N. Transition states and the critical parameters of central potentials. J Phys A: Math Theor (2011) 44:375303. doi:10.1088/1751-8113/44/37/375303
105. Rundel O, Skurzok M, Khreptak A, Moskal P. Search for the η-mesic helium in proton-deuteron reaction. Acta Phys Pol B (2017) 48:1807–12. doi:10.5506/APhysPolB.48.1807
106. Khreptak A, Rundel O, Skurzok M. Luminosity determination for the proton-deutron reactions using quasi-free reactions with WASA-at-COSY facility. EPJ Web Conf (2019) 199:05026. doi:10.1051/epjconf/201919905026
107. Khreptak A, Skurzok M, Rundel O. Search for the 3He-η bound state via pd → pdπ0 reaction. Acta Phys Pol B (2020) 51:361–6. doi:10.5506/APhysPolB.51.361
108. Khreptak A, Skurzok M, Rundel O, Moskal P. Analysis of the pd → pdπ0 reaction measured with WASA-at-COSY facility in order to search for η-mesic helium. Acta Phys Pol B Proc Suppl (2020) 13:835–40. doi:10.5506/APhysPolBSupp.13.835
109. Skurzok M, Hirenzaki S, Kinutani S, Konishi H, Moskal P, Nagahiro H, et al. Non-mesonic decay of the η-mesic 3He via pd→(3He-η)bound→ 3He2γ(6γ) reaction. Nucl Phys A (2020) 993:121647. doi:10.1016/j.nuclphysa.2019.121647
110. Czerwiński E, Moskal P, Silarski M, Bass SD, Grzonka D, Kamys B, et al. Determination of the η′-proton scattering length in free space. Phys Rev Lett (2014) 113:062004. doi:10.1103/PhysRevLett.113.062004
111. Tanaka YK, Itahashi K, Fujioka H, Ayyad Y, Benlliure J, Brinkmann KT, et al. Measurement of excitation spectra in the 12C(p, d) reaction near the η′ emission threshold. Phys Rev Lett (2016) 117:202501. doi:10.1103/PhysRevLett.117.202501
112. Tanaka Y, Bagchi S, Benlliure J, Dickel T, Drozd V, Ekawa H, et al. Spectroscopy of η′-mesic nuclei with WASA at GSI/FAIR. Acta Phys Pol B (2020) 51:39–44. doi:10.5506/APhysPolB.51.39
113. Nagahiro H, Hirenzaki S. Formation of η′(958)-mesic nuclei and axial UA(1) anomaly at finite density. Phys Rev Lett (2005) 94:232503. doi:10.1103/PhysRevLett.94.232503
114. Nagahiro H. Formation of possible η′(958)-nucleus bound states and η′N interaction. In: JPS Conference Proceedings (2017). p. 010010. doi:10.7566/JPSCP.13.010010
Keywords: exotic nuclei, η meson, η-mesic nucleus, bound state, η-nucleon interaction, η-nucleus interaction, η meson production reaction
Citation: Khreptak A, Skurzok M and Moskal P (2023) Search for η-mesic nuclei: a review of experimental and theoretical advances. Front. Phys. 11:1186457. doi: 10.3389/fphy.2023.1186457
Received: 14 March 2023; Accepted: 03 May 2023;
Published: 16 May 2023.
Edited by:
Michele Viviani, National Institute of Nuclear Physics of Pisa, ItalyCopyright © 2023 Khreptak, Skurzok and Moskal. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aleksander Khreptak, YWxla3NhbmRlci5raHJlcHRha0BsbmYuaW5mbi5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.