- Department of Psychology, University of Groningen, Groningen, Netherlands
The aim of this article is to present a very basic dynamic systems model of L2 learning based on a number of basic principles 1) at any moment in time, a learner’s L2 proficiency is a distribution of potentialities (possible levels of L2 production), 2) the distribution changes as a result of experienced L2-events such as conversations, 3) L2 proficiency and L2 events are represented on the same underlying array of linguistic proficiency (from 0, i.e., inexistent, to 1, i.e., maximal under the currently available linguistic resources); 4) learning processes are “normative” in the sense that they are governed by a process of convergence on the language spoken by a particular L2 community, this process depends on an optimum between familiarity and novelty; 5) the parameters governing the systems dynamic differ among individual learners and L2 learning contexts (e.g., highly adaptive versus non-adaptive communicative interactions with native L2 speakers).
Modeling L2 learning as a process of change
A lack of process models
There is surprisingly little dynamic—or processual—modeling in the behavioral and learning sciences. Researchers who focus on building dynamic or agent-based modeling of psychological and social phenomena are rarely cited by their “mainstream” colleagues (see, for example, the articles in the JASSS Journal). There are several explanations for this—actually rather remarkable—fact. The mainstream praxis of the behavioral and educational sciences, treats modeling as something that becomes only relevant after the collection of major sets of generalizable, representative data, i.e., the crowning achievement of extensive and laborious empirical reserach. The notions representative or general data refer to their being representative of populations characterized by some important feature or natural kind (e.g., the natural kind “adult learners of English as a foreign language”). That is, in order to refer to some form of nomothetic truth, a model must refer to an important general feature, e.g., a general class of learners. In order to achieve this form of representativeness, the data must consist of extensive samples of independent cases, for instance a case being a particular learner of English as a foreign language. Because of its obvious relation to actual, specific data, the main praxis of psychological and learning sciences research places an almost exclusive emphasis on statistical models, consisting of statistical relationships between the main variables of a particular data set (for a general discussion on the need for processual models in the behavioral and learning sciences, see [1]).
The question is whether this praxis - first data, then models - is also typical of important nomothetic—i.e., law-seeking—sciences such as physics. Not being a physicist myself, I am not in the position to answer this question, but my hinge is that it is not (but the answer depends on what one considers a “model”). Of course, the statistical modeling of large and (in the population sense) representative data sets is and remains an important goal of modeling. However, the position I have tried to defend so far is that this is not the most important goal of modeling. And neither is this form of modeling—statistical relationships among variables based on interindividual variability—the most suitable for the kind of phenomena that the behavioral and learning sciences are trying to explain. In my view, models–and dynamic models in particular–should be expressions of the most basic defendable assumptions about a particular kind of process, for instance the learning of a second language.
By using mathematical or formal ways of expression, dynamic models are primarily tools for understanding the consequences of the recursive application of basic principles of change, typical of a particular (sub)discipline, such as the applied linguistics of L2 learning. The construction of such models can help us understand our own general theoretical assumptions better: it compels us to make our theoretical intuitions explicit, because the model must “do” something we intend it to do, by following the rules and principles we believe are plausible of the way nature works for a particular phenomenon and context (e.g., [2]).
In line with the spirit of theoretical and mathematical models in physics, I start this dynamic systems model of L2 learning from first principles, i.e., from what I consider to be the fundamental facts or assumptions about L2 learning.
General facts or general assumptions about L2 learning
Taking the learning of a second language as my example—and I assume this example represents a great variety of phenomena that are typical of the behavioral and learning sciences in general—I think the fundamental facts are the following.
The processual nature of L2 learning
First, learning a second language is a process. Processes are sequences of conditionally connected events or flows that are governed by process causality. That is, next states (the relevant properties of the process at any particular moment in time) are conditioned by previous states. A process is a temporal evolution of some specific property or set of properties. In the case of L2, I define the process as the temporal evolution of the state of L2 proficiency in a particular learner over the course of time.
L2 learning as a process of convergence and assimilation
Second, learning a second language is a process of active social convergence, driven by a need to assimilate the language spoken by an L2 community (a real community, or one that is represented in the form of an educational teaching-learning context). This drive towards assimilation and convergence explains why processes of learning and development are normative. They have a particular direction, that is, they aim towards adaptation to a particular norm [3]. In the case of L2 learning this norm is the language use of proficient speakers, and in principle the language use of native speakers of the learner’s L2. The process of convergence is often bidirectional, but it is not symmetric. L2 learners adapt to the language spoken by the L2 community, that is, for every moment in time, they assimilate features of L2, given the assimilation possibilities associated with the level of L2 they have already achieved. This process of adaptation is, broadly speaking, irreversible (not excluding the process of L2 attrition, however, e.g., [4]). L2 speakers communicating with L2 learners tend to locally and temporarily adapt to the learner’s level of L2 understanding, for instance to facilitate communication. However, this form of adaptation or convergence is transient and depending on the occasion (for an application to L1, see [5]). As a result of these processes of convergence, a learner’s emerging verb-argument constructions in English as a second language reflect properties of the changing linguistic input [6].
The situatedness of L2 learning
Third, learning a second language is a concrete, physically and semiotically situated process. That is to say, it takes place in a concrete, embodied learner acting in a concrete physical and semiotic context (e.g., a particular context of speakers of a language, for instance the context of a Moroccan immigrant worker in a particular Scottish town, or a Dutch speaking student learning English in an English course given by a particular teacher, using particular educational materials). An embodied learner enters the situation of L2 learning with person-specific dispositions, e.g., the learner’s sensitivity to linguistic information, the ability to assimilate L2 and so forth. These person-specific dispositions change as a consequence of the L2 learning process. The situatedness of L2 learning, including the specificities of the learner and the learning contexts, is a major source of variation between L2 learners.
Idiosyncrasy and non-ergodicity of L2 learning
Fourth, given its concrete situatedness, actual processes of L2 learning will most likely be idiosyncratic, that is to say case-specific (by case I mean a concrete person in a concrete context). Whether or not these idiosyncratic properties actually converge on a set of commonalities is a question to be answered by the modeling and, in the end, by the empirical person-specific data [7]. As a general rule however, we can expect those processes to be non-ergodic, that is to say that statistical properties based on a comparison of independent individuals in a representative sample of persons do not generalize to individual processes, i.e., sequences of conditionally coupled states, steps or events [8]). However, although the resulting processes of L2 learning may be idiosyncratic, the underlying dynamic system, i.e., the system describing the basic process mechanisms, may be universal, that is to say generalizable to all actual processes of L2 learning. If such a general dynamic system exists, it forms the nomothetic base of the variety of idiosyncratic and non-ergodic processes of actual L2 learning.
L2 learning as a complex system
Fifth, the process of L2 learning, as virtually all forms of human learning and development, constitutes a complex system. Put differently, it is a process that should be understood against the backdrop of a complexity epistemology and ontology [1, 9]. The main arguments for interpreting L2 learning as an instantiation of complex dynamic systems principles have been amply discussed in a variety of articles (for instance, [9–12]).
A complex system consists of many components (it is easy to imagine the many components involved in a particular L2 learning process) that interact and, as a result of these interactions, self-organize into patterns that are characteristic of the totality of interacting components. These patterns have emergent properties, i.e., properties not reducible to properties of the components. Emergent properties have conditional or causal effects on the component interactions from which these properties are a result. That is to say, the complex system is characterized by a cyclical relationship between bottom-up causality (from components to overarching emergent properties) and top-down causality (from emergent properties to underlying components). The complexity of the process of L2 learning depends on the fact that it is an embodied process (there is a physical, concretely situated learner), that it is enacted (the learning takes place in the form of interest-driven, intertwined activities of a learner and a concrete linguistic environment, for instance a particular speech partner), that it is embedded (emerged in a specific material, cultural and normative context), and that it is extended (the actual processes of L2 learning, for instance a learner uttering a particular sentence in a specific context, is the result of intertwining processes that take place in the learner as well as in the context). Dynamic systems models model system dynamics, that is to say the evolution of particular properties over time. However, in their form and assumptions they should reckon with the fact that what they are referring to are complex systems, i.e., systems with emergent properties and cyclical causality.
As a result of this embodied-enacted-embedded-extended format of the learning process, a particular learner’s L2 proficiency cannot be represented by a specific point value, that is, the learner’s “true score” on the proficiency dimension. The learner’s proficiency should rather be seen as a potentiality distribution stretched out across the entire proficiency dimension (which ranges from virtually absent L2 proficiency to the level of proficiency that is maximally attainable under the resources and possibilities provided in a specific L2 learning context). By potentiality distribution I mean the total of potential levels of proficiency performance that an L2 learner can show at a particular moment in the learning process. These levels differ in terms of degrees of characteristicness or typicality of the levels of L2 usage by a particular L2 learner at a particular moment. These degrees of characteristicness or typicality are represented by a weight function or membership function (if one uses the tools of fuzzy logic), which, in practice, boil down to the probability of a particular level of proficiency being actualized at a particular moment in time. If the potentiality distribution at time t is unimodal, the top of the distribution corresponds with the most typical, and probably also the most likely level of proficiency at time t. If it is multimodal, i.e., if it has more than one local peak, it corresponds with more than one typical proficiency level and potential discontinuities in the learning process (e.g., [13]). During a specific communicative interaction, which yields a particular expression of linguistic proficiency of a learner in a specific, momentary communicative context, this potentiality distribution collapses into a considerably narrower region of actual, performed proficiency (similar to a point value). An L2 proficiency test—or any psychological ability test for that matter—is an interaction that collapses the current probability distribution of a complex system, characterizing the particular L2 learner at a particular moment in time, into a point value. Tests customarily provide a confidence interval around this point value that superficially looks like the potentiality distribution discussed above. A confidence interval, however, refers to the measurer’s uncertainty about the true point value of the proficiency, whereas a potentiality wave represents the current proficiency potential of an L2 learner, which is a set of such point values associated with a weight or probability scalar. There is a distant but not uninteresting similarity here with the notion of a wave function in quantum mechanics that collapses into an observable particle state as a result of a measurement activity, which is a form of interaction with the wave function. The mechanisms underlying the notion of a potentiality distribution of a particular complex system and those of the wave function in quantum mechanics are of course entirely different, but there is an interesting metaphorical similarity here (and maybe an answer to the possible objection that all the variables in nature must by necessity have a determinate point value, and that any deviation from this principle is due to measurement uncertainty or lack of precise knowledge1).
L2 learning is governed by feedback loops
Sixth, L2 learning has a typical feature of a complex system, namely, the occurrence of feedback loops between the interacting components. For instance, the language used in a particular environment by L1 speakers influences (in fact drives) the L2 learning of a speaker for whom this L1 is L2, whereas the current linguistic proficiency of the learner influences the “input” that is to say the language addressed to the L2 learner by the L1 community. This feedback loop comes about as a result of the communicative processes that take place between learners and their concrete and momentary linguistic environments, and that form the backbone of the L2 learning process. Of course, one can imagine a completely protocolized form of L2 learning, where the learner is presented with a fixed, gradual sequence of examples and exercises, and where any kind of interaction is avoided (in principle, this condition could be modeled as one out of many possible conditions in a dynamic systems model). Feedback loops are at the heart of co-adaptive processes, for instance in which learners adapt to the language (L2) spoken to them, and that the native L2 speakers adapt to the level of understanding of the learners with whom they communicate.
L2 learning is characterized by fluctuations and variability
Seventh, L2 proficiency as expressed in actual L2 use and understanding by a concrete L2 learner shows typical fluctuations and variability over time. These fluctuations and variability can of course be interpreted as random external influences on the real or true point-value proficiency that is supposed to show long-term learning changes in a basically smooth manner (this is in a nutshell the assumption of fluctuation-as-measurement-error). However, as L2 proficiency is a feature of a complex dynamic system, its variability is intrinsic to the system itself, and should be conceived of as a direct consequence of the fact that the state of proficiency in a concrete L2 learner is a potentiality wave of arbitrary complexity instead of a point value.
The aim of this article is to discuss a dynamic systems model of the process of change in proficiency in L2 learners, reckoning with the basic facts, or maybe more precisely, the basic assumptions discussed above.
The basic components of the process model
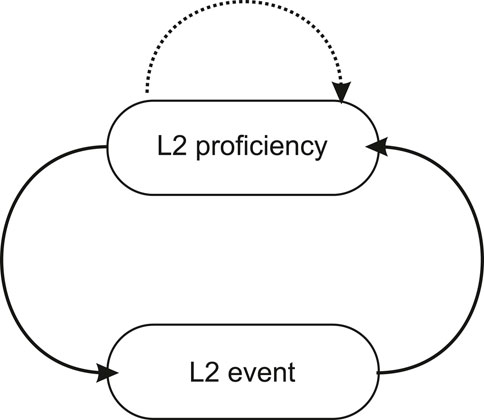
The model contains two components: one is the L2 learner, represented by the process of changing L2 proficiency, defined over a dimension or array of proficiency levels ranging from zero (absent) to 1 (highest possible proficiency level given the current learning resources in context). The other component is the L2 environment with whom the L2 learner interacts. The L2 environment may consist of speakers for whom the learner’s L2 is their first language, other speakers who are in the process of learning L2, professional educators teaching L2 to a variety of learners, didactic and educational L2 materials and so forth. Hence, although the dynamic model describes the trajectory of L2 learning in a single learner, it does so in the form of a socially interactive process, in which a learner and an L2 environment affect one another.
This environment is not a fixed variable: it is itself a dynamic process as it is presented to the learner in the form of a sequence of what I shall call L2-events. In the great majority of cases, those L2 events will consist of conversations in L2 between the learner and various conversation partners, such as native speakers, teachers or other L2 learners. L2 events may also consist of formal exercises in L2 courses. They may or may not contain explicit activities aimed at correcting an L2 learner’s mistakes or imperfections (see [14] for discussion). With the current modeling purposes, I shall confine myself to more or less informal L2 events such as spontaneous L2 conversations. Aspects of these conversations such as explicit educational methods, assignments and feedback can eventually be incorporated into general parameters of the model, such as the parameter(s) moderating the learning effects of L2 events (for instance, operationalizing the assumption that adequate corrective feedback accelerates L2 learning). In the model, the main influence goes from the environment to the learner, as the environment is the source of the learner’s developing L2 proficiency.
However, in the model I assume a feedback loop from the learner to the learner’s environment. It is important to note that the L2 events are by definition L2 experiences: their properties in terms of the information and meaning they provide depend on the learner’s experience of those events. The learner’s current experience potential greatly depends on the currently available L2 knowledge that is expressed in form of the learner’s current proficiency distribution. To the extent that the linguistic event is interactional, e.g., in the form of a conversation, a considerable part of the linguistic event will consist of the contributions of the learner him- or herself, and those contributions depend on the learner’s current L2 proficiency and the scaffolding of L2 use in the form of the activities of the conversational partners. Conversational partners may be sensitive to the learner’s current linguistic proficiency to different extents: some will adapt their learner-directed speech to what they perceive as the learner’s ability to understand and respond, whereas others might be totally insensitive to the learner’s current L2 abilities and use learner-directed speech that is in no way different from the way they converse with other native speakers of their language (their L1, which is the learner’s L2). That is, the learner’s L2 proficiency and the L2 environment in the form of a process of speech interaction events are mutually coupled (see Figure 1).
Finally, as learning is a recursive or iterative process—the next step is conditioned by the preceding step or steps—the model also contains a self-referential coupling in the L2 learner component. If the conversation partner is a fixed person (or persons; as in L1 learning with parents as major conversation partners, or formal L2 learning with a fixed teacher) a self-referential coupling might also be added to the L2 environment (see [5] for a discussion of a dynamic model in L1, involving a coupling between child speech and child directed speech). For the current purposes, I assume that since in L2 learning conversation partners are variable, the second self-referential coupling (involving the L2 events) can be omitted (if there is basically only one conversation partner, as in formal L2 learning with an L2 teacher, the iterative coupling of L2 events must be introduced as a component of the model).
Note that this mathematical model deliberately has been greatly simplified, and in fact reduced to the bare essentials of the assumed processes of L2 learning. It is what physicists call a toy model, and although this term might evoke negative connotations (“it should not be taken seriously”) it provides in fact possibilities, first, to check whether the highly simplified, basic assumptions suffice to generate major qualitative properties of actual L2 learning and second, to see what variation in essential parameters generates in terms of idiosyncratic learning trajectories (e.g., under conditions of sub-optimal or even adverse parameter settings, corresponding with suboptimal or adverse conditions of L2 learning).
Dynamic systems as process models
What is a dynamic system?
Learning a second language is a process with properties as defined above. Dynamic systems provide an appropriate formal framework for modeling such processes, given that certain requirements are met.
To see which requirements they are, we begin with a general definition of a dynamic system: “A dynamical system is a state space S, a set of times T and a rule R for evolution, R:S×T→S that gives the consequent(s) to a state s∈S. A dynamical system can be considered to be a model describing the temporal evolution of a system.” [15]. The state space is the set of all possible states of a particular dynamic system, for instance the set of all possible states of L2 proficiency in a particular L2 learner on the one hand, and the state of all possible L2 events (conversations, etc.) on the other hand. In principle, we can represent each set of possible states by means of a one-dimensional ratio scale, a dimension of real numbers referring to particular levels of L2 proficiency. This dimension is a useful abstraction of actual measurement scales that capture L2 proficiency of a particular type. Examples are measures of spoken language proficiency, syntactic or semantic complexity and correctness of a learner’s L2 speech, or a main principal component of a variety of proficiency scales comprising syntactic, semantic, lexical and pragmatic abilities. For the purposes of modeling—as I understand its function in the scientific understanding of a particular phenomenon such as L2 learning—issues and difficulties of measurement are not conditional. They would be so if modeling would be confined to modeling existing data sets, which are of course dependent on the measurement issues they faced. However, if modeling is primarily serving the goal of theoretical understanding of the way processes unfold, it may assume that the state spaces it requires can in principle be represented by ratio scales, irrespective of whether such ratio scales are available in the empirical researchers’ toolkits. In principle, dynamic systems models may be extended towards categorical dimensions, for instance in the form of symbol dynamics. Such symbol dynamics may be modeled in the form of agent-based models, but for the current purposes, I will confine myself to system dynamics based on ratio scales.
It is important to note that this ratio scale of linguistic proficiency in spoken L2 in conversations and interactions applies to both components of the model, or, to put it differently to both dimensions of its state space. That is, L2 proficiency applies to the L2 learner but also to the L2 events that represent the learner’s environment. That is, each such event corresponds with a particular distribution of L2 proficiency levels. The width of this distribution depends on the nature of the L2 event: compare for instance a very simplified conversation with very short, extremely simple sentences with highly limited vocabulary, to a conversation as would occur with two native speakers; or compare a conversation between two inexperienced L2 learners with a conversation between an L2 learner and a native speaker.
In the current litterature on the modeling of L2 learning, the focus is on the application of connectionist networks, which are self-organizing computational processes extracting structure from inputs, e.g., a linguistic corpus, generating outputs that conform to the inputs (e.g., [6, 16, 17]). Although connectionist networks are examples of dynamic models, a discussion of differences and similarities from typical dynamic systems models exceeds the scope of the current article [18].
The starting point: the (initial) proficiency distribution
I shall assume that the state space—or phase space in this particular case—consists of dimensions in the form of a ratio scale ranging from 0 to 1. Let us focus on the dimension specifying the L2 proficiency of the learner. The value 0 represents the absence of any L2 proficiency, and the value 1 represents a maximum level of proficiency available under the given learning resources, including examples from native speakers, help from educators, cognitive variables in the learner relating to sensitivity for linguistic patterns and so forth. I have stated that since the learner is a complex system, the ability to produce and understand a particular second language is an embodied, enacted, embedded and extended ability. This implies that it is highly unlikely that a learner’s current L2 ability—or L2 proficiency—can be validly represented by a point value, that is to say by a single “true and unique” level on the proficiency axis. Instead, recognizing the complexity and dynamic nature of this proficiency it should be represented as a distribution of potentialities, i.e., a distribution of potential, more or less typical levels of L2 proficiency of a learner at any given time. The distribution is a scalar field, i.e., for each value of the proficiency dimension there is a characteristic value for the L2 learner’s proficiency, corresponding with a probability that this particular value will be expressed in the learner’s L2 use. This distribution of potentialities forms a dynamic field, that is to say a field that can change under the influence of internal and external events. The notion of dynamic fields is a central feature of Dynamic Field Theory [19]. It “ … provides an explanation for how the brain gives rise to behavior via the coordinated activity of populations of neurons. These neural populations […], make local decisions about behaviorally relevant events in the world2.” Both events in the world and the neuronal populations that reacted on them are represented in the form of scalar fields, corresponding with potentials to react. The concept of dynamic fields, representing a particular skill, knowledge, developmental or proficiency level in the form of a distribution of potential levels, can also be applied to any cognitive, linguistic or skill dimension to which learning or developmental change can apply [20].
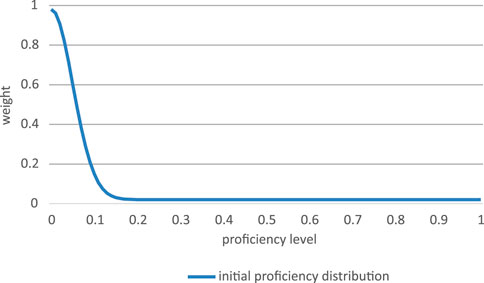
The simplest way to represent the initial state of this distribution—that is the point at which L2 learning begins with a novice—is by means of a symmetric distribution, such as a typical bell curve or normal distribution (see Figure 2). In the simulation model, this initial proficiency is the non-negative half of a normal distribution with a mean of zero and a particular standard deviation (which I customarily set to 5% of the total reach of possible linguistic proficiency, for technical details see Supplementary Appendix).
Figure 2 shows a typical starting level for a particular L2 learner, in the form of a dynamic field, i.e., a distribution of potential expressions of L2 proficiency.
Let us call this distribution ψt which is the distribution of potential proficiency levels of a learner L at time t. The development of L2 proficiency amounts to the change and transformation of this distribution over the course of time. This change and transformation apply, first, to the form of the distribution, for instance from unimodal it may become bimodal or multimodal (similar to the shift from one to various attractor states) and, second, to the position of the distribution across the proficiency dimension (from occupying mainly the lower levels to occupying the higher to highest levels of proficiency). A distribution that begins in a unimodal format can eventually evolve towards a multimodal distribution, corresponding with discontinuities in the major mode (i.e., the preferred proficiency level at a partiular moment in time; see Figure 3).
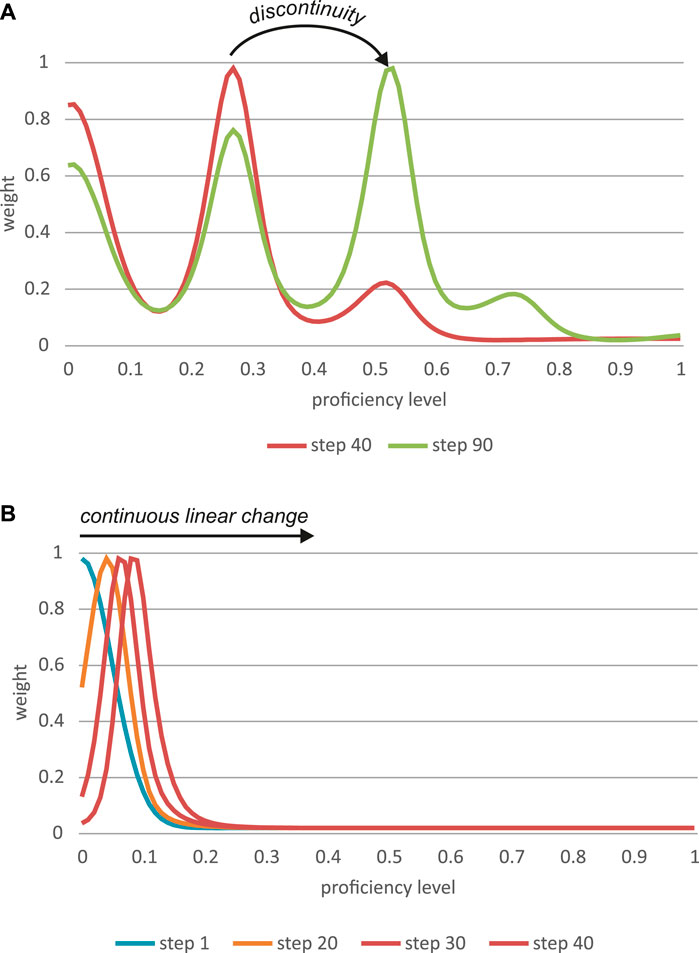
FIGURE 3. (A) unimodal distribution turns into a multimodal distribution over the course of time corresponding with a discontinuity in L2 learning. (B) under different parameter values, an initial unimodal distribution remains unimodal over the course of time (typical of linear change).
The L2 learning dynamic system’s evolution rule
The dynamic model intends to describe the transformation of Ψt over the course of time. To do so it needs “… a rule R for evolution, R:S×T→S that gives the consequent(s) to a state s∈S” [15]. As stated earlier, the model assumes that L2 learners learn a second language to the extent that they are confronted with tokens from the second language, for instance in the form of conversations with a native speaker, exercises given by a second language teacher, or passive participation in L2 use (perception of L2 spoken by others). In the typical case, these L2 tokens are interaction events that present the L2 learner with a range of examples of L2 that correspond with a range of levels of proficiency. For instance, they range from simple short sentences to long and complicated ones, and they will even contain typical errors as the L2 learner’s contribution to an interaction is part of the linguistic token. That is, in most of these L2 tokens, especially those that take place in the form of conversations (or educational assignments), the learner’s own L2 production is part of the set of linguistic tokens from which the L2 learner appropriates the second language. These wholes of linguistic tokens are the L2 events (or events for short) mentioned before, and they are determined by the way they are experienced by the L2 learner (they are experienced events). Similar to the way in which the L2 learner’s current proficiency is represented as a distribution rather than a point value, these events are also represented as a distribution on the proficiency dimension. A typical event such as a conversation or a discussion piece in an L2 class, provides a variety of examples of proficiency levels–for instance, sentences of various levels of grammatical and semantic complexity. This event-proficiency distribution at time t is referred to by the Greek letter epsilon, εt (referring to “event”).
For simplicity, this proficiency distribution is modeled by a standard normal distribution with a mean drawn from the current proficiency distribution of the learner Ψt and a randomly varying standard deviation representing the amount of L2 variety present in the experienced L2 event. For instance, events may contain one or a few L2 sentences, in which case they are represented by a distribution with a very small standard deviation. Other events consisting of lengthy conversations or L2 class exercises will be represented by a distribution with a considerably bigger standard deviation.
In a standard dynamic growth model where the change in variable X depends on the value of a variable Y, the change in variable X is typically represented by ΔX/Δt = a *x *y (for a a particular change parameter). This principle also applies to the current model where the variables are represented by distributions rather than point values: Δψ/Δt = a *ψ *ε. In the model, this basically means that for every value of the proficiency dimension, the corresponding values of ψ and ε are multiplied.
An additional assumption is that a particular linguistic event such as an L2 conversation or extensive exercise does not only have positive, but also negative effects. That is, its core will have an increasing effect on the corresponding values of the learner’s proficiency distribution. Its extremes (i.e., its lateral values) however will have a decreasing or reducing effect on the proficiency values that correspond with these extreme ranges (see Figure 4). That is, an experienced L2 event increases the weight or probability of its central range of proficiency and decreases the weight or probability of the proficiency levels at its extremes.
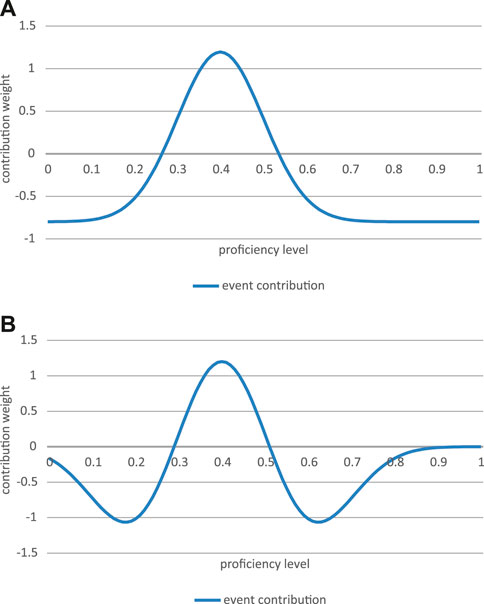
FIGURE 4. The effect of an L2 event, e.g., a conversation, on the change in the learner’s current proficiency distribution. (A) A simple “inundated” effect distribution. (B) a Mexican hat function.
This inhibitory effect of the extremes can be modeled in the form of a so-called Mexican hat function (see Figure 4B). A much simpler solution, which I followed in the very basic simulation model I am presenting here, is to subtract a constant from every value of the event distribution: Δψ/Δt = a *ψ * (ε-c) (Figure 4A).
In earlier publications (in particular [20]) I have argued that the normative aspect of learning and development—its being drawn towards a particular normative state, e.g., L2 as a spoken by native speakers of L2—can be explained by the dynamics of two antagonistic properties, namely, familiarity versus novelty. Familiarity depends on what the learner has already mastered, which is represented by the learner’s proficiency distribution at a particular moment in time. Familiarity can be represented as a distribution over the proficiency dimension, more precisely by a sigmoid curve denoted by the Greek letter Phi, φ, which has a maximum value for the maximum value of the proficiency distribution and for all proficiency levels lower than that. In the model, the curve has two fixed parameters (1 as its maximum, 0 as its minimun) and two free parameters, governing its steepness and flex point. Novelty, represented by the Greek letter Nu, ν, is defined as the inverse of familiarity and is represented by a sigmoid curve defined by (1–φ). For any given L2 event as defined above, the more it represents a familiar level of proficiency, the easier it is to learn, but also the less important it is to learn (since it largely corresponds to what is already there). On the contrary, the more novel an L2 event is, the more important it is to learn it, but also the more difficult it is to learn it (to the point of being impossible to learn if the L2 event is too novel). Hence, the effect of an L2 event on the proficiency distribution of an L2 learner is a simple compromise between familiarity and novelty. It can be modeled by the product of the familiarity sygmoid (descending) and the novelty symoid (ascending). The effect of the familiarity/novelty compromise can further be modified by adding a fixed parameter d (see Figures 5A, B for familiarity, novelty and familiarity*novelty product curves).
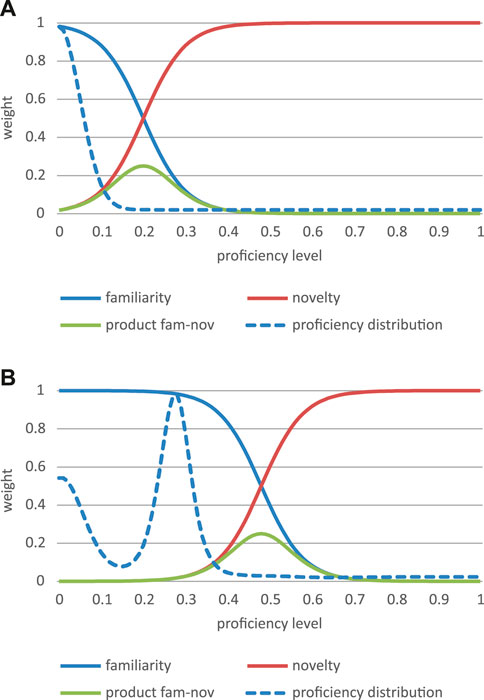
FIGURE 5. (A) familiarity, novelty and familiarity*novelty product distributions for an initial proficiency distribution. (B) familiarity, novelty and familiarity*novelty product distributions for a multimodal proficiency distribution.
The familiarity/novelty optimality function is a generalization of fundamental properties of learning and development described in classic theories of (cognitive) development, notably those of Vygotsky and Piaget. Both theories postulate a function that runs ahead of the current developmental or learning level of a particular learner. Vygotsky does so with the concept of a zone of proximal development, which defines what a learner can do with the help of a more competent other. Piaget makes a distinction between processes of assimilation (basically a reduction of the content of an experience to what is already known or mastered) and processes of accommodation (basically an adaptation to what is new in a given experience, vis-à-vis what is currently familiar). The dynamics of these processes have been amply discussed in earlier publications [20, 21]. A detailed study of the properties of a dynamic systems model based on Vygotskyan principles of learning reveals a rich landscape of possible outcomes (for a mathematical analysis, see [22]).
In the present model, novelty and familiarity are “elastic” properties. That is to say, they depend on person-specific abilities and on context-specific events. For instance, some learners can, on average, tolerate more novelty than others, which implies that they can profit from information that lies relatively far ahead of their current level of maximal L2 proficiency. This ability to profit from relatively new information is, very broadly speaking, an expression of (linguistic) learning ability. Other learners have a familiarity curve that goes down quite rapidly, which means that their optimal level of novelty lies quite close to their current maximal level of familiarity. They can only profit from L2 experiences that are close to what they have already achieved. However, some L2 contexts provide learners with L2 experiences that correspond with high levels of novelty, that is, with experiences that are quite far from a particular learner’s current maximal L2 proficiency. In this sense, they overcharge the learner’s current L2 learning capacity, or to put it differently, they require more familiarity with novel features of L2 than the learner can currently muster. In principle, an optimally adaptive L2 learning environment will provide L2 experiences with levels of novelty and familiarity that are relatively close to the learner’s optimal levels, given a particular level of linguistic proficiency. In the current, simplified model, what counts as the optimal level of familiarity/novelty is implicit (it is the range of levels for which L2 learning occurs rapidly and smoothly; Van Geert and Steenbeek [21], presented a model of Vygotsky’s zone of proximal development, in which this optimal level is a free parameter). However, in the current model it is easy to experiment with the effect of different distances between the current proficiency level and the point where the familiarity and novelty curves cross by manipulating the free parameters of the familiarity curve (see the next section, step two).
A description of the dynamic model of L2 learning
In order to keep the dynamic systems model as a simple and transparent as possible, I will present it in the form of a spreadsheet model, with a few simple functions added, the syntax of which will be given in Supplementary Appendix. The spreadsheet model provides an overview of its basic structure and can be rewritten in any programming language the reader prefers, in order to improve speed and flexibility. I will describe the model in the form of its consecutive steps.
The steps in the model
1. Step 0: Define the L2 proficiency array: the array consists of values from 0 to 1, with step size 0.01: {0, 0.01, 0.02, … }; This array corresponds with the basic dimensions of the dynamic system and defines the state of the system in terms of a distribution of weights or probabilities.
2. Step 1: Define the initial proficiency range for the L2 learner at time 1 (which corresponds with the first step in the simulation process);
a. Define a probability density function for every value of the L2 proficiency array, in the form of the non-negative part of a normal distribution (use mean of 0 and standard deviation of 0.05; both are free parameters that can be modified to model different initial states);
b. Normalize the values of the probability density function to a number close to but bigger than 0 and close to but smaller than 1 (default limits are 0.02 and 0.96).
c. Determine the proficiency level for the maximum value of the learner’s proficiency range maxp; for the initial proficiency range this maximum is the corresponding proficiency value for the mean of the proficiency probability density function, which is set to 0; store maxp
d. Randomly draw 50 proficiency levels from the proficiency density function (by means of a Visual Basic function called rand_dist_array(); the syntax is given in Supplementary Appendix); these 50 levels correspond for instance with 50 utterances produced by the learner at this point in time, for instance in the context of a conversation; they are thus a randomized expression of the learner’s current L2 proficiency
e. Calculate the mean, mode, 0.75th percentile, distance between 10th and 90th percentile, and the proficiency value corresponding with the maximum value of the original proficiency density function of these 50 levels; store for final output; to determine the mode, the simulation model uses a kernel density function to calculate frequencies and determine the maximum frequency (see Supplementary Appendix)
3. Step 2: Define familiarity and novelty functions and their product
a. Determine the density function for familiarity: for each value of the proficiency array, calculate the value of a sigmoid curve with minimum value 0 and maximum value 1, and two free parameters, one for the midpoint value (equal to a constant, e.g., 0.1, plus the value of maxp) and the slope parameter (which in the case of the familiarity function must be a negative value, e.g., −0.05);
b. For every value p of the proficiency array, define the density function for novelty as 1–famp;
c. For each value of the proficiency array ranging from 0 to 1, multiply the familiarity and novelty value;
d. Normalize all multiplied values by dividing by the maximum value of the curve obtained in step c
4. Step 3: Define an L2 event;
a. Randomly draw a proficiency value me from the current learner’s proficiency range with the rand_dist_array() function (note that after a few steps in the learning process, the proficiency range is often no longer a unimodal or symmetric distribution, as its properties have been updated by every step in the simulation process); randomly draw a value sde for a standard deviation between a minimum and maximum value (the current model uses 0.15 and 0.35)
b. For every value of the L2 proficiency array, calculate the value of a probability density function with mean me and standard deviation sde
c. Determine how the event array will contribute to the change in the learner’s proficiency array by subtracting a constant from each value in the array; this constant is a free parameter; in the current model it most often varies between 0.2 and 0.4; instead of a simple subtraction, the effects may be determined by a Mexican hat function (see Supplementary Appendix for further explanation); the current model uses subtraction as the simplest, standard solution); this results in an event effect value evp for every point p on the proficiency array ranging from 0 to 1
5. Step 4: update the proficiency range based on the effect of the L2 event:
a. Multiply every value of the normalized familiarity-novelty product by a constant; this constant is a free parameter; the current model uses 0.25; this constant should never be 0: in order to model the absence of the familiarity-novelty effect, the current model uses an if-then parameter
b. For every value of the proficiency array ranging from 0 to 1, multiply each value from the preceding step by the corresponding value of the event contribution evp
c. For every value of the proficiency array ranging from 0 to 1, multiply each corresponding value from the preceding step by the corresponding value of the probability density function representing the L2 learner’s current L2 proficiency
d. For every value of the proficiency array ranging from 0 to 1, add the corresponding value from the preceding step to the corresponding value of the current probability density function representing the L2 learner’s current L2 proficiency
6. Step 5 to final number of simulation runs:
a. Repeat step 1b, update the learner’s L2 proficiency range with these new values, then repeat step 1c
b. Repeat all steps from step 2 on for the predetermined number of steps in the simulation; copy the results calculated in step 1e as final output
The model “output” representing the process of L2 learning
In order to determine the learning of L2, during each simulation step, the model generates 50 L2 expressions from the current L2 proficiency distribution of the learner. These “expressions” are in fact point values of the proficiency array (ranging from 0 to 1) drawn from the proficiency distribution, turned into a probability distribution, with the aid of the function described in step 1d. Think of these “expressions” as short L2 phrases, sentences, contributions to conversation, etc., produced by the L2 learner. Since the standard way of representing a learner’s current L2 proficiency is to take the average of the produced proficiency levels, the first output measure is the mean of the 50 randomly drawn proficiency levels. In addition to the average value of the 50 randomly drawn levels, I also took the most typical level of proficiency during that particular step in the simulation. The most typical level was defined as the level that occurred most frequently (which is a range of levels in fact, but I represented it by the central value of a frequency bin, calculated over the 50 levels by means of a kernel density estimator). The third way of representing the current proficiency level present in the 50 randomly drawn levels is to take a characteristic high level of proficiency, representing the more advanced proficiency levels, for which I used the 75th percentile level of the 50 expressions. In order to represent the within- (simulation) step variability, i.e., the amount of variation in the 50 expressions, I used the difference between the 90th and the 10th percentile (a standard measure would be the standard deviation, but this makes sense only if the variation is symmetrically distributed around a mean, which we cannot always justify in this particular case). Once all output has been generated, e.g., after the customary 500 simulation steps, between-step variability can be easily calculated by taking the absolute difference between any two consecutive measurements, e.g., the most typical level of proficiency at time t and t+1. This difference representation can then be smoothed by means of a Loess smoother (a smoothing function available in the simulation model; see Supplementary Appendix).
As a final measure for the current proficiency, the model determines the maximum value of the current proficiency curve. As this curve can take a multimodal form, e.g., with 3 peaks, the maximum level is the value of the dominant mode. This measure is particularly suited for showing discontinuities in the process, i.e., where one mode suddenly becomes dominant, replacing an earlier dominant mode. This process is the inverse of the typical attractor switch in models of behavioral potentials, for instance modeled by means of the so-called cusp catastrophe (e.g., [23]). In this sense, the dominant mode of the proficiency distribution is reminiscent of the dominant (deepest, widest) attractor in an attractor landscape.
In addition to the values of the 50 randomly drawn expressions and the dominant mode of the current proficiency distribution, the model keeps track of the proficiency distributions taken every 10th simulation step. Given the default number of simulation steps has been set to 500, every simulation is represented by 50 consecutive proficiency distributions.
An overview of some typical simulation results
A hypothetical default case
I hypothesize that, in a typical progressive learning model, the familiarity curve should neither be too close nor too far away from the current proficiency distribution of an L2 learner at a particular moment in time. That is, given a particular L2 event presenting levels of L2 proficiency that the learner does not yet master, what a learner perceives as learnable, or recognizes as new and higher levels of proficiency in this event, should not be too similar to the learner’s own, current proficiency. This description is of course extremely vague, but it can be operationalized in the form of different familiarity curves for a given proficiency distribution. For instance, in Figure 6A, I defined the peak of the familiarity-novelty product too close to the learner’s current (initial) proficiency distribution, in Figure 6B the distance is adequate, and in Figure 6C it is too far. That is, for the case in Figure 6B learning will be optimal (smooth and relatively fast), given all other parameter values are similar.
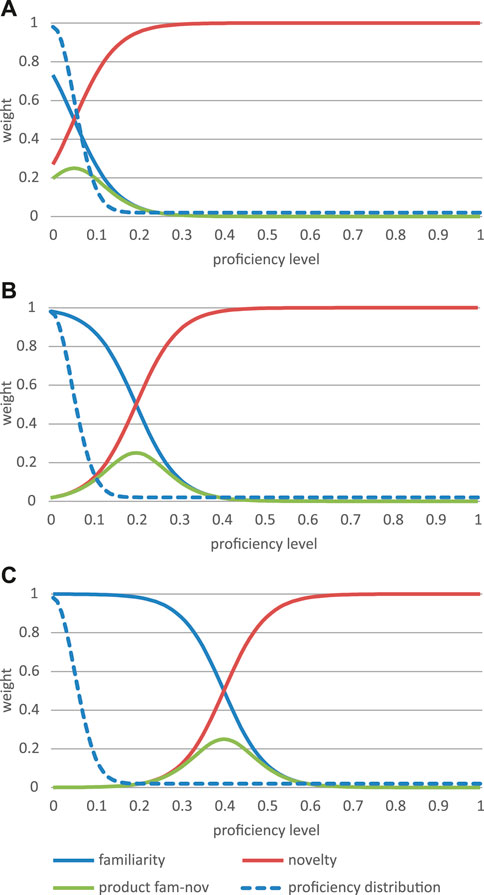
FIGURE 6. Optimal and suboptimal familiarity-novelty distances: An example of a familiarity-novelty function that is too close to the learner’s proficiency distribution (A), one that is an example of an optimal distance (B) and one in which the distance is too great (C).
Figure 7 show the result of a simulation based on optimal parameter settings, given the number of 500 simulation steps. Optimality is defined in terms of whether or not the simulation reaches the maximum level within the time range of this simulation, where the maximum level corresponds with maximum L2 proficiency, given the L2 proficiency demonstrated in the L2 events that the learner is confronted with in his or her given L2 context. The simulation shows how the maximum level of the proficiency curve changes in a discontinuous fashion, which is due to the fact that the proficiency curve becomes multimodal (it has more than one local maximum suggesting more than one attractor state). The discontinuity is most clearly visible in the mode of the L2 production, i.e., in the trajectory of the most frequent levels occurring in the changing corpus of 50 L2 expressions at any particular moment in time. These discontinuities relate to the discontinuities in the maximum point of the proficiency curve. The curve of the averages shows a slightly scalloped pattern, corresponding with the discontinuities in the most frequent level, in the maximum point of the proficiency curve, or in the discontinuities of the maximum of the changing proficiency distributions.
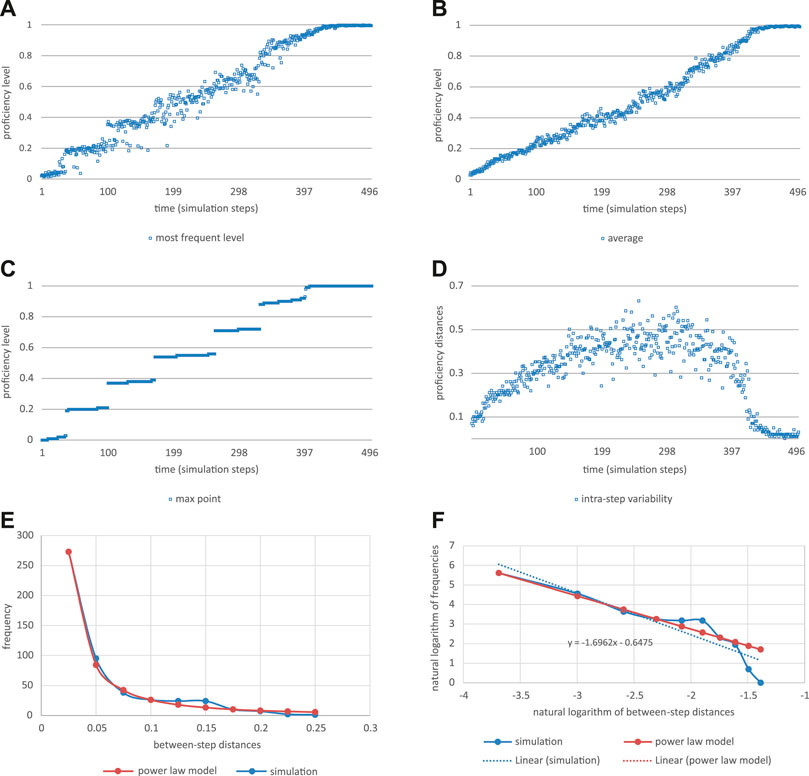
FIGURE 7. (A–F) Results of a simulation with a familiarity-novelty curve considered optimal. (A) The most frequent level changes in a more or less discontinuous fashion, relating to the discontinuities in the maximum point of the proficiency curve; (B) the curve of the step averages shows a slightly scalloped pattern; (C) the maximum level of the proficiency curve changes in a discontinuous fashion, which is due to the fact that the proficiency curve is multimodal (it has more than one local maximum suggesting more than one attractor state); (D) within-step variability is highest around the middle of the learning trajectory; (E) the frequency of between-step differences follows a power law distribution; (F) a log-log plot of the simulated between-step differences and of their power law model, including the linear trend equation for the simulated differences.
Within-step variability, that is, differences between the proficiency levels of the recurrent 50-utterances corpus, is highest around the middle of the learning trajectory. Between-step variability peaks after the points of discontinuous change. That is, distances between successive steps in the simulation, i.e., between proficiency indicators of the successive samples of 50 expressions, are greatest immediately after the discontinuity.
It is interesting to note that in the simulated optimal L2 learning (e.g., Figure 7C), the frequency distribution of the between-step variability values closely follows a power law distribution. Power law distributions are typical of complex systems whose behavior is governed by interactions between their components (for instance in psychological reaction times [24]). Let y be the frequency with which a value x of between-step variability occurs, then y = k * xa (a constant k multiplied by x to the power a). In the distribution of between-step distances in the simulated trajectory represented by Figure 7C, a = −1.7 and k = 0.52; the correlation between the logarithms of the frequencies based on the simulation and those predicted by the power law model is 0.93. Power law distributions (also called Zipfian distributions) have been found in data from L2 learning, for instance in the frequency distributions for types of verb-argument constructions and verb lemmas [6, 25]. These data are of course different from the between-step variability discussed above, but they illustrate the ubiquity of power law (or Zipfian) distributions in L2 (and language in general for that matter).
The proficiency curves change from a unimodal distribution (the initial distribution) to multimodal distributions representing different attractors for the mode (i.e., most frequently occurring level; Figures 8A, B).
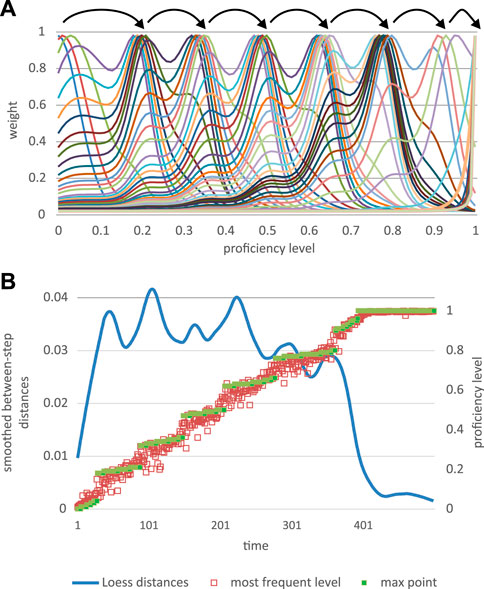
FIGURE 8. (A) The proficiency curves change from a unimodal distribution (initial distribution) to multimodal distributions, representing different attractors for the mode (i.e., most frequently occurring level); shifts between peaks represent discontinuities in L2 development (B) Between step variability peaks after the points of discontinuous change.
Simulation results under non-optimal parameter values
The following results refer to a model in which the familiarity-novelty function is too far away from the learner’s current proficiency level (see Figure 9). It might be compared with the situation in which a learner is only confronted with linguistically complex L2 use, without any form of adaptation or simplification towards the learner’s current proficiency. Note however that, whatever the complexity of the L2 use in the L2 event1 the learner is confronted with, these events will always be drawn from the learner’s current proficiency distribution. That is to say, irrespective of how complex the actual L2 input might be, the learner will always assimilate this to what he or she is able to understand or process (but eventually only with great difficulty). That being said however, a non-optimal familiarity-novelty distance will result in a process of learning that takes about 3 times as long to reach a maximum proficiency level. In addition, the model generates only 2 discontinuities, one from the initial level to some middle level of proficiency, which remains unchanged for a very long time. Finally, towards the end of this extended learning trajectory (1,500 simulation steps) a new discontinuity emerges leading to the final, that is maximum level of proficiency the L2 learner may contain (see Figures 9A–C). Within-step variability (i.e., variability within the samples of 50 L2 expressions) is complex and highly nonlinear (see Figure 9D). Between-step variability typically peaks before the discontinuity arises (this can best be seen in the trajectory of the 75th percentile level).
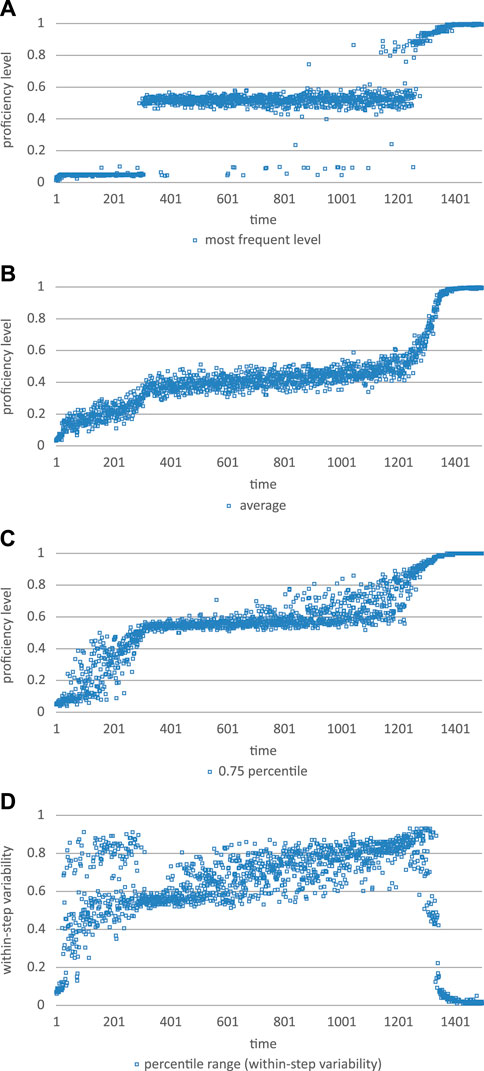
FIGURE 9. If the familiarity-novelty distance from the current proficiency level is too great, the learning process shows a prolonged, self-sustaining sub-optimal proficiency level (around level 0.5) and complex forms of variability (note that the simulation covers 1500 instead of 500 time steps, as in the optimal case).
If the familiarity novelty curve is too close to the current familiarity-novelty level of the L2 learner, the resulting learner trajectory is strictly linear (Figure 10). Around 500 simulation steps, it reaches a level of 0.45 (as compared to the level I, which represents the maximally attainable proficiency under the given range of L2 events). Note also that the within- and between-step variability are stationary.
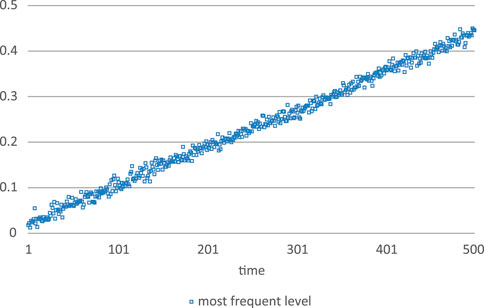
FIGURE 10. A strictly linear increase occurring with a familiarity-novelty function too close to the current proficiency level of the learner.
If there is no effect of a familiarity-novelty function (which is different from this function being too close or equal to the current proficiency distribution of the L2 learner) the result is an erratic trajectory of local ups and downs, stabilizing around a value of about 0.5 of the maximum proficiency level, with a stationary within-step variability (see Figure 11).
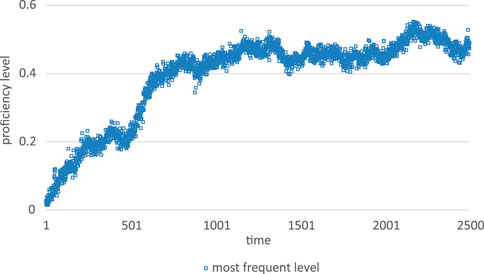
FIGURE 11. Deficient temporal trajectory of L2 proficiency over a duration of 2,500 steps if the effect of familiarity-novelty function is disabled.
Some preliminary conclusions
The aim of this article was to present a very basic dynamic systems model of L2 learning based on a number of fundamental principles: 1) at any moment in time, a learner’s L2 proficiency is a distribution of potentialities (possible levels of L2 production), 2) the distribution changes as a result of experienced L2-events such as conversations or L2 instruction, 3) L2 proficiency and L2 events are represented on the same underlying array of linguistic proficiency (from 0, i.e., inexistent, to 1, i.e., maximal under the currently available linguistic resources); 4) learning processes are “normative” in the sense that they are governed by a process of convergence on the language spoken by a particular L2 community, this process depends on an optimum between familiarity and novelty; 5) the parameters governing the systems dynamic differ among individual learners and L2 learning contexts.
Optimal parameter values are those that generate an L2 trajectory from close to 0 (L2 proficiency is minimal) to close to 1 (L2 proficiency as maximal under the given learning resources), over a duration of time represented by 500 simulation steps (the number of simulation steps is arbitrary, but it should be defendable under the interpretation of L2 events, for instance in the form of conversations or other repeated events that foster L2 learning). Significant deviance from optimal parameter values leads to “degenerate” learning trajectories, such as continuous self-reproduction of suboptimal proficiency levels.
Under these optimal parameter values, the model also yields some interesting additional effects.
First, the model provides evidence of discontinuous change, that is to say, of leaps from one mode to another (modes are defined as the local maxima of the proficiency distribution at any one point in time). In the model’s L2 “output” (i.e.; the expressions of L2 proficiency by the learner in the form of utterances or contributions to conversations), discontinuities are best observable in the most frequently occurring L2-levels at any moment in time (the “typical” level at a particular moment in time). This simulation result is directly in line with findings on L2 development by Rastelli [13, 26]. Rastelli explains the occurrence of discontinuities by the combination of statistical and grammatical learning in L2. This type of functional explanation does not contradict the validity of a dynamic systems model such as the one presented in the current article. Dynamic systems models try to capture the evolution rules of a particular state space, whereas functional explanations explain how the learning actually works (by way of an analogy, think about the difference and compatibility between a dynamic systems model of the growth of a biological population on the one hand and a functional-physiological model of biological reproduction and death of organisms on the other hand). Discontinuities in L2 proficiency are also in line with the existence of qualitatively different stages in L2 learning: a shift from one stage to another is likely to correspond with a discontinuous change in L2 proficiency (e.g., [25]).
Second, the simulation model under optimal values generates nonlinear trajectories of variability. That is, within-step variability increases towards the middle of the learning process, and then sharply decreases as the level of “full” mastery is achieved (note that this is defined relative to the available L2 resources). Nonstationary variability is an important property of the dynamics of L2 learning [27–29]. As to between-step variability, magnitudes of differences between steps are distributed in accordance with a power law (similar to a Zipf distribution). This distribution is typical of a wide range of linguistic phenomena, and also occurs under various forms in L2 learning [6]. The simulation model shows increased between-steps variability in the vicinity of discontinuous changes. This is a typical nonlinear feature of variability in discontinuous development [23], which can also be found in L1 acquisition [30]. The co-occurrence of increased variability with developmental jumps has also been shown to occur in L2 learning [27, 31].
With this—in fact extremely simple—dynamic systems model of L2 learning, based on the general assumptions discussed in the introduction of this article, I have tried to provide a “proof of concept” or proof of possibility of a dynamic systems model that is based on the idea of L2 proficiency as a distribution of possible proficiency levels, instead of L2 proficiency as a point value on some measurement dimension. As with all such models, the connection with the empirical data poses interesting problems (for a discussion of L2 proficiency measurement, see [32]). As regards the measurement of abilities represented by distributions instead of point values, some practical tools have been suggested for time-serial observational data, for instance in L1 and L2 [33–35]. However, I believe that models such as this one should, in the first place, provide a correspondence with major, empirically observed, qualitative properties, such as nonlinear variability, discontinuity, and inter-individual differences based on different parameter sets. If the general correspondences apply, simple models can further be elaborated to account for individual, time-serial data sets and for the complexities of L2 learning as a social, co-adaptive process.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, upon reasonable request.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1186136/full#supplementary-material
Footnotes
1I thank the first reviewer for pointing out that a comparable idea has been formulated to long time ago by the distinguished linguist Kenneth Pike [36].
2https://dynamicfieldtheory.org/
References
1. van Geert P, de Ruiter N. Toward a process approach in psychology: Stepping of into heraclitus. River. Cambridge: Cambridge University Press (2022).
2. Van Geert P. Dynamic systems of development. Change between complexity and chaos. New York: Harvester (1994).
3. Christensen WD, Bickhard MH. The process dynamics of normative function. The Monist (2002) 85(1):3–28. doi:10.5840/monist20028516
4. Park ES “Language attrition,” In: Language attrition. The TESOL encyclopedia of English language teaching, (2018), 1–12.
5. Van Dijk M, van Geert P, Korecky-Kröll K, Maillochon I, Laaha S, Dressler WU, et al. Dynamic adaptation in child–adult language interaction. Lang Learn (2013) 63(2):243–70. doi:10.1111/lang.12002
6. Ellis NC, Larsen-Freeman D. Constructing a second language: Analyses and computational simulations of the emergence of linguistic constructions from usage. Lang Learn (2009) 59(Suppl. l):90–125. doi:10.1111/j.1467-9922.2009.00537.x
7. Molenaar PC, Campbell CG. The new person-specific paradigm in psychology. Curr Dir Psychol Sci (2009) 18(2):112–7. doi:10.1111/j.1467-8721.2009.01619.x
8. Lowie WM, Verspoor MH. Individual differences and the ergodicity problem. Lang Learn (2019) 69:184–206. doi:10.1111/lang.12324
9. Han Z, Kang EY, Sok S. The complexity epistemology and ontology in second language acquisition: A critical review. In: Studies in second language acquisition (2022). p. 1–25.
10. Larsen-Freeman D, Cameron L. Complex systems and applied linguistics. Oxford: Oxford University Press (2008). p. 287.
11. de Bot K, Lowie W, Verspoor M. A dynamic systems theory approach to second language acquisition. Bilingualism: Lang Cogn (2007) 10:7–21. doi:10.1017/s1366728906002732
12. Van Dijk M, van Geert P. Dynamic system approaches to language acquisition. In: RJ Tierney, F Rizvi, and K Erkican, editors. International encyclopedia of education, 10. Elsevier (2023). doi:10.1016/B978-0-12-818630-5.07041-X
13. Rastelli S. The discontinuity model: Statistical and grammatical learning in adult second-language acquisition. Lang Acquis (2019) 26(4):387–415. doi:10.1080/10489223.2019.1571594
14. Han Z. Corrective feedback from behaviorist and innatist perspectives. In: H Nassaji, and E Kartchava, editors. The cambridge handbook of corrective feedback in second language learning and teaching. Cambridge: Cambridge University Press (2021). p. 23–44.
16. Ellis NC. Constructions, chunking, and connectionism: The emergence of second language structure. In: The handbook of second language acquisition (2003). p. 63–103.
18.In:JP Spencer, MS Thomas, and JL McClelland, editors. Toward a unified theory of development: Connectionism and dynamic systems theory re-considered. Oxford: Oxford University Press (2009).
19. Schöner G, Spencer JP. Dynamic thinking: A primer on dynamic field theory. Oxford: Oxford University Press (2016).
20. Van Geert P. A dynamic systems model of basic developmental mechanisms: Piaget, Vygotsky, and beyond. Psychol Rev (1998) 105(4):634–77. doi:10.1037/0033-295x.105.4.634-677
21. van Geert P, Steenbeek H. The dynamics of scaffolding. New ideas Psychol (2005) 23(3):115–28. doi:10.1016/j.newideapsych.2006.05.003
22. Merlone U, Panchuk A, van Geert P. Modeling learning and teaching interaction by a map with vanishing denominators: Fixed points stability and bifurcations. Chaos, Solitons Fractals (2019) 126:253–65. doi:10.1016/j.chaos.2019.06.008
23. van der Maas HL, Molenaar PC. Catastrophe analysis of discontinuous development. In: Categorical variables in developmental research: Methods of analysis (1996). p. 77–105.
24. Holden JG, Van Orden GC, Turvey MT. Dispersion of response times reveals cognitive dynamics. Psychol Rev (2009) 116(2):318–42. doi:10.1037/a0014849
25. Ellis NC. Formulaic language and second language acquisition: Zipf and the phrasal teddy bear. Annu Rev Appl Linguist (2012) 32:17–44. doi:10.1017/s0267190512000025
26. Rastelli S. Discontinuity in second language acquisition: The switch between statistical and grammatical learning. In: Bristol/Buffalo/Toronto: Multilingual matters, 80 (2014).
27. van Dijk M, Verspoor MH, Lowie W. Variability and DST. In: M Verspoor, K de Bot, and W Lowie, editors. A dynamic approach to second language development: Methods and techniques. Amsterdam: John Benjamins (2011). p. 55–84.
28. Lowie W, Verspoor M. Variability and variation in second language acquisition orders: A dynamic reevaluation. Lang Learn (2015) 65(1):63–88. doi:10.1111/lang.12093
29. Verspoor M, Lowie W, Van Dijk M. Variability in second language development from a dynamic systems perspective. Mod Lang J (2008) 92(2):214–31. doi:10.1111/j.1540-4781.2008.00715.x
30. Bassano D, Van Geert P. Modeling continuity and discontinuity in utterance length: A quantitative approach to changes, transitions and intra-individual variability in early grammatical development. Dev Sci (2007) 10(5):588–612. doi:10.1111/j.1467-7687.2006.00629.x
31. Spoelman M, Verspoor M. Dynamic patterns in development of accuracy and complexity: A longitudinal case study in the acquisition of Finnish. Appl Linguistics (2010) 31:532–53. (increased variability). doi:10.1093/applin/amq001
32.In:P Leclercq, A Edmonds, and H Hilton, editors. Measuring L2 proficiency: Perspectives from SLA. Multilingual matters, 78. Berlin: De Gruyter (2014).
33. Van Dijk M, Van Geert P. Wobbles, humps and sudden jumps: A case study of continuity, discontinuity and variability in early language development. Infant Child Dev Int J Res Pract (2007) 16(1):7–33. doi:10.1002/icd.506
34. Van Dijk M, Van Geert P. Heuristic techniques for the analysis of variability as a dynamic aspect of change. Infancia y Aprendiz (2011) 34(2):151–67. doi:10.1174/021037011795377557
35. Van Geert P, Van Dijk M. Focus on variability: New tools to study intra-individual variability in developmental data. Infant Behav Dev (2002) 25(4):340–74. doi:10.1016/s0163-6383(02)00140-6
Keywords: second language (L2), dynamic system, modeling, learning, variability, discontiuity
Citation: Van Geert PLC (2023) Some thoughts on dynamic systems modeling of L2 learning. Front. Phys. 11:1186136. doi: 10.3389/fphy.2023.1186136
Received: 14 March 2023; Accepted: 15 May 2023;
Published: 08 June 2023.
Edited by:
ZhaoHong Han, Columbia University, United StatesReviewed by:
Diane Larsen-Freeman, University of Michigan, United StatesPaul Wiita, The College of New Jersey, United States
Copyright © 2023 Van Geert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Paul L.C. Van Geert, cGF1bEB2YW5nZWVydC5ubA==, cC5sLmMudmFuLmdlZXJ0QHJ1Zy5ubA==
 Paul L.C. Van Geert
Paul L.C. Van Geert