Junyu Chai1,2,3
Wenguang Liu1,2,3*
Yujun Wen1,2,3
Xiaolin Wang1,2,3*Kun Xie4Qiong Zhou1,2,3
Hanwei Zhang1,2,3
Jiangbin Zhang1,2,3*Pengfei Liu1,2,3Dan Zhang1,2,3
Yao Lu1,2,3Zongfu Jiang1,2,3Guomin Zhao1,2,3- 1College of Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha, China
- 2Nanhu Laser Laboratory, National University of Defense Technology, Changsha, China
- 3Hunan Provincial Key Laboratory of High Energy Laser Technology, National University of Defense Technology, Changsha, China
- 4Xi’an Satellite Control Center, Xi’an, China
In recent years, transverse mode instability (TMI) has been widely observed in fiber laser amplifier systems. The transverse mode instability phenomenon in fiber laser oscillators is less studied. Here, we focus on the dynamical output properties, i.e., its temporal signal and modal characteristics in a 30-μm-core-diameter ytterbium (Yb)-doped fiber laser oscillator. The TMI occurs at a pumping power around 310 W. Different from amplifiers, the basic oscillation frequency is quite low, at around 100 Hz, changing with time and pump power. When the fiber laser oscillator operates beyond TMI threshold at 357 W or 377 W for a while, the temporal fluctuation slowly disappears together with a decreased oscillation frequency, and appears again later. Based on the mode decomposition technique, we find that during the period of fluctuation disappearance at 357 W, the power output stays low and the output beam is still a mixture of fundamental mode and higher-order modes. The fundamental mode content is calculated to be averagely higher when temporal fluctuation disappears, increasing from ∼57% to ∼63%. Our results indicate complex interaction between the fiber laser oscillation and the TMI effect, and calls for more attention into understanding TMI in fiber laser oscillators.
1 Introduction
High power fiber lasers (HPFLs) have attracted much attention in scientific research and industrial field due to their high conversion efficiency, excellent beam quality and convenient heat management [1–3]. There are currently three operations of fiber lasers, including pulse wave, quasi continuous wave (QCW), and continuous wave (CW). The progress of ultra-fast optics and ultra-intense laser technology has promoted the development of pulsed wave fiber laser [4–8]. They provide the advantages of high repetition rate and high peak power, which can be widely used in laser cutting. QCW fiber laser refers to a pulsed laser of ms magnitude with a duty cycle of 10%, which can be applied in drilling [9–11]. By contrast, CW fiber laser can continuously output light with stable power and play an important role in welding [12–14].
The rapid progress of high-brightness laser diodes (LDs) and large-mode-area (LMA) fiber fabrication technology quickly pushed the CW fiber laser power to exceed 20 kW in a multimode fiber [15–20]. However, such trend was prohibited by a thermo-optical effect called transverse mode instability (TMI). In this effect, the heat generated from the amplification affects the refractive index of the fiber, inducing dynamical energy transfer between the fundamental mode and higher-order modes. This coupling typically results in unstable output beam profile, which exhibits temporal fluctuations up to a few kHz. Therefore, the beam quality and laser output performance degrade. As mentioned in the field of ultrafast photonics, pulsed optical fiber laser is generated from complex interactions among photons, electrons, and phonons under laser excitation conditions [21–23]. TMI process in CW fiber laser is also related to the dynamics of complex non-linear systems [24]. In order to mitigate TMI effect, researchers use several methods, such as imposing external bend loss of HOMs for mode selection [25–27], optimizing the fiber parameters [28–30], changing the fiber laser architecture as well as changing pumping schemes [31–33]. These mitigation strategies using passive optical devices are promising, but are only applicable in specific operation regimes [34]. Considering the physical origin of TMI (dynamic in nature) and taking the idea from adaptive optics, active mode control in a closed-loop system may provide a universal way to stabilize the beam beyond TMI threshold [35]. In principle, active mode control aims to control the direction of mode coupling, allowing energy transfer to flow between fundamental mode and higher-order modes.
In order to accurately measure the direction of energy, different methods have been developed to detect the TMI effect, such as utilizing photodiode (PD) [30] and high-speed camera (HSC) [36–38]. The PD is widely used to detect power fluctuation. The HSC method, in combination with modal analysis algorithm can measure the beam fluctuation spatially and temporally, but is not cheap. The fluctuation of power and modal analysis can provide the detailed information about dynamic mode coupling, showing the dynamic energy transfer between two or more modes. Such information is prior to perform proper mode control.
What’s more, there are usually two configurations for CW fiber lasers, including master oscillator power amplifier (MOPA) and fiber laser oscillator. Currently, the MOPA architecture is more studied due to its high-power output [39–41]. In comparison with MOPA, the monolithic fiber laser oscillators exhibit the advantages of simpler structure, easier manipulation, and less sensitivity against backward coupled light. The output power level from the fiber oscillators has reached over 8 kW [42]. Therefore, more attention should be paid on investigating and suppressing TMI effect in fiber laser oscillators.
In this paper, we characterize TMI in a co-pumping fiber laser oscillator by measuring its temporal variation and performing modal analysis. We first describe the adopted all-fiber laser oscillator configuration and methods to characterize TMI properties. Then, we measure the laser output performance and observe transverse mode coupling. Furthermore, proper physical explanations are provided according to the experimental phenomenon.
2 Experimental setup
We build a co-pumping all-fiber laser oscillator with a low TMI threshold. The advantage of researching such laser is that the TMI process can be carefully observed at a low output power. Thus, the laser system is safe to operate around and beyond TMI threshold for a long time. The fiber laser oscillator setup is shown in Figure 1. We use fiber-coupled LDs with a stabilized emission wavelength of 976 nm as optical pump sources. A forward (6 + 1)×1 pump-signal combiner (PSC) enables a number of pump LDs to inject into the laser oscillation cavity. Six pump ports of the PSC are used, while the unoccupied central pump port of the PSC is angle cleaved to avoid facet reflection. The co-pumping light is launched into the laser oscillation cavity via the high-reflection fiber Bragg grating (HR-FBG). A length of ∼20 m Ytterbium (Yb)-doped fiber (YDF) with 30/400 μm core/cladding diameters (NAcore = 0.064) is applied as gain fiber. The HR-FBG is inscribed on the end of YDF, and it provides a reflectivity of ∼99.9% with a 3 dB bandwidth of ∼4 nm at the central wavelength of ∼1,080 nm. An output coupler fiber Bragg grating (OC-FBG) provides a reflectivity of ∼10% with a 3 dB bandwidth of ∼1.7 nm at the central wavelength of ∼1,080 nm. After the OC-FBG, a length of 3 m 30/400 μm delivery fiber is spliced and a quartz endcap is used to output the signal laser without facet reflection. A cladding light stripper (CLS) is realized by removing the polymer cladding of delivery fiber and coating the inner cladding with high refractive index ointment. Thus, the CLS ensures the cladding light to leak into the air and only the amplified signal light reaches the fiber output. To avoid the heat accumulation, the whole all-fiber laser oscillator is attached on a water-cooled plate, and the gain fiber is coiled in a figure-8 shape with a minimum bend diameter of 85 mm.
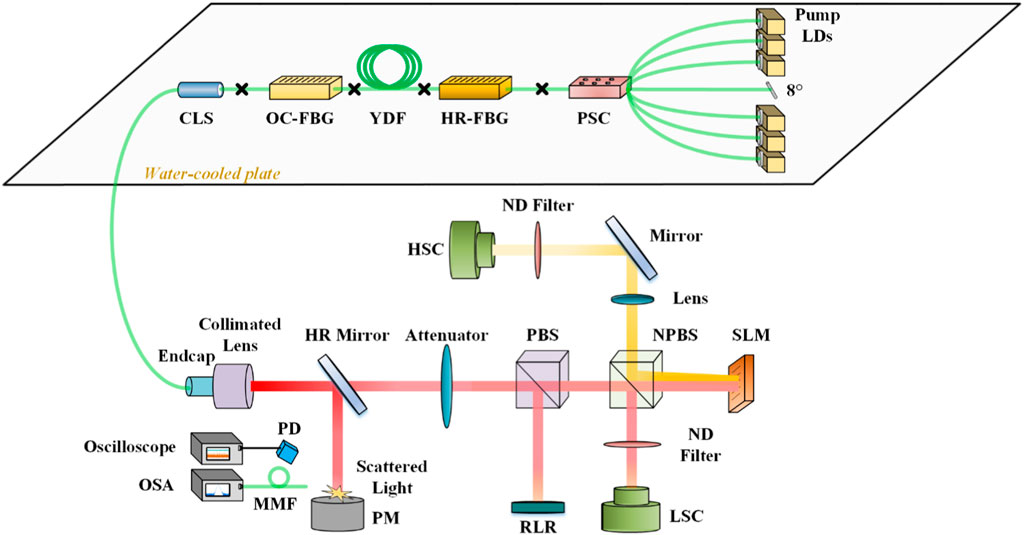
FIGURE 1. A schematic diagram of all-fiber laser oscillator and measurement system. (LDs, Laser diodes; PSC, Pump-signal combiner; HR, High reflection; FBG, Fiber Bragg grating; OC, Output coupler; YDF, Ytterbium-doped fiber; CLS, Cladding light stripper; PD, Photo-diode; OSA, Optical spectrum analyzer; MMF, Multi-mode fiber; PM, Power meter; PBS, Polarizing beam splitter; NPBS, Non-Polarizing beam splitter; SLM, Spatial light modulator; ND, Neutral density; RLR, Residual light receiver; LSC, Low-speed camera; HSC, High-speed camera).
As depicted in Figure 1, we employ several methods to characterize TMI. In the experiment, the output beam is collimated by a lens, and then a high reflection (HR) mirror reflects ∼99.99% of the laser into the power meter (PM). A photodiode (PD) receives the scattered lights to monitor the temporal traces of output power via the oscilloscope. Part of the light is coupled into multimode fiber and transmitted to an optical spectrum analyzer (OSA) for recording spectral information. A mode decomposition system is applied to analyze the real-time modal variation of the co-pumping optical fiber oscillator. A spatial light modulator (SLM) and a HSC are the main components of the mode decomposition device with optical correlation filter (OCF) method [43]. To match the polarization requirement of the SLM, the incident light passes through a polarized beam splitter (PBS). A computer-generated-hologram containing the first six linearly polarized (LP) modes (LP01, LP11e, LP11o, LP21e, LP21o and LP02) related transmission functions is loaded on the SLM. The first order of the diffracted light is captured via a HSC. The neutral density filters (NDF) and optical bandpass filters are applied to adjust the incident power level onto the HSC and remove any residual pump light. A low-speed camera (LSC), which assists in judging the accuracy of the placement position and tilt angle of optical components, is used to calibrate the measurement system. A residual light receiver (RLR) is applied to receive the unused polarized light during the entire measurement.
3 Results and discussion
3.1 Laser output characteristic
In the experiment, we first measure the spectrum and output power of the fiber laser oscillator. As depicted in Figure 2A, the central wavelength is around 1,080 nm at 155 W, and there are no pump light or ASE in the spectrum. Figure 2B depicts the output power dependence on the pump power and the standard deviations (STD) of the temporal signals at different power levels. The fiber laser oscillator shows a rollover output power of 180 W at the co-pumping power of 318 W, along with a rising instability, quantified by the STD of the temporal signal. We set the fiber laser oscillator to operate at three pumping powers (318, 357, and 377 W) over TMI threshold for 60 s, and recorded their temporal fluctuations using a PD per 10 s, as shown in Figure 2C. When the pumping power is 318 W, the time domain STD suddenly increases after 10 s, marking the appearance of TMI, and the intensity of STD fluctuates with time. When the pumping power reaches 357 and 377 W, we observe there is no fluctuation for the temporal signal at 40 and 50 s, respectively. Each stable period lasts for more than 10 s, and then the fluctuation re-appears again with the varied intensity over times.
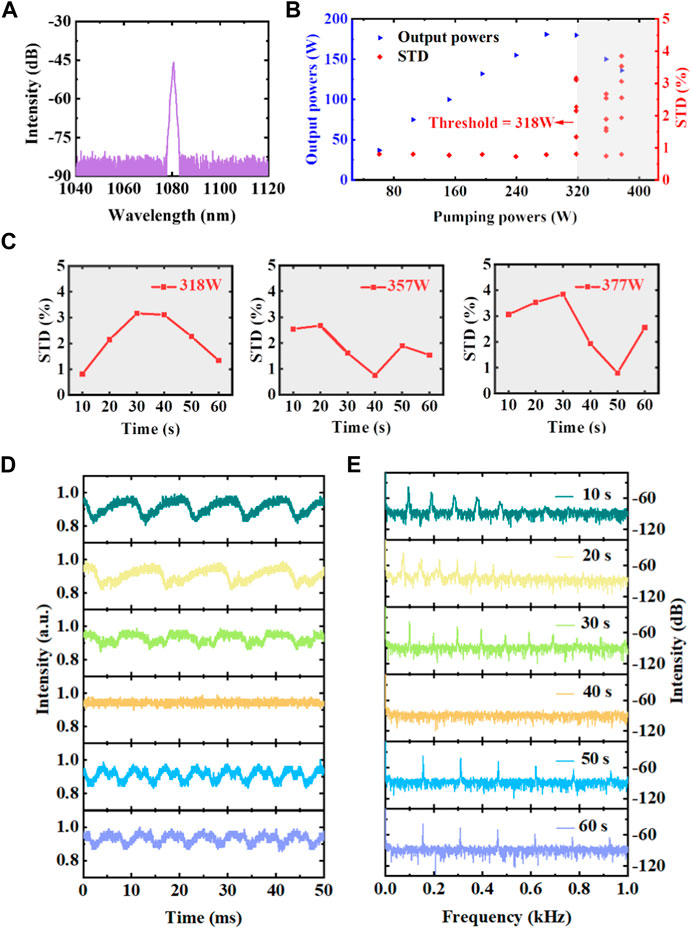
FIGURE 2. The spectrum and evolution of the output power and stability of the beam emitted by the co-pumping fiber laser oscillator: (A) The output spectrum at the output power of 155 W. (B) The output power and STD of the temporal signal at distinct pumping power. (C) Six recordings within 60 s of the time domain STDs at three pumping powers of 318, 357, and 377 W (The data is collected every 10 s). (D) Six temporal traces with first 50 ms in every 10 s in sequence at the pumping power of 357 W. (E) Fourier spectra of intensity variations.
In order to watch the time variation at the pumping power beyond TMI, we take the 357 W power input, and plot six normalized temporal intensities in a short period of 50 ms (The data is recorded every 10 s), as shown in Figure 2D. The signal shows periodic change, except at 40 s when the signal becomes quite stable. To better visualize the related frequency information, we perform Fourier transformation in Figure 2E. The fundamental frequency is initially 100 Hz, which decreases to around 75 Hz at 20 s, and returns to 100 Hz at 30 s. There is no obvious peak signal around 100 Hz at 40 s, but reappears at 150 Hz afterwards. We see that the signal variation frequency changes with time. Interestingly, there is a period which lasts around 10 s, when the time variation disappears. This indicates that TMI may be suppressed at power beyond the threshold.
3.2 Transverse modal properties
To research the transverse mode coupling process when TMI occurs, the temporal variation of the laser output profile is recorded. The far-field spot for mixed modes and the +1st diffraction pattern from mode decomposition is simultaneously captured via a HSC at 2,000 fps. A hole with a diameter of 4.5 μm is chosen at the centroid of the far-field spot, and the power change in this circle is monitored. When the pumping power is 357 W, we record the quasi-periodic fluctuation of power in the far-field bucket at selected time slices, as shown in Figures 3A–F. The waveform presents a superposition of two sine waves with a certain phase difference. When there are no distinct temporal fluctuations (Figure 3D), the normalized intensity is relatively stable but at a low level around 0.6. Although the temporal fluctuation disappears, the TMI still occurs due to the reduced output power. This low output power is assumed a dynamic multimode coupling of some frequency combinations or a static energy transfer (mode coupling).
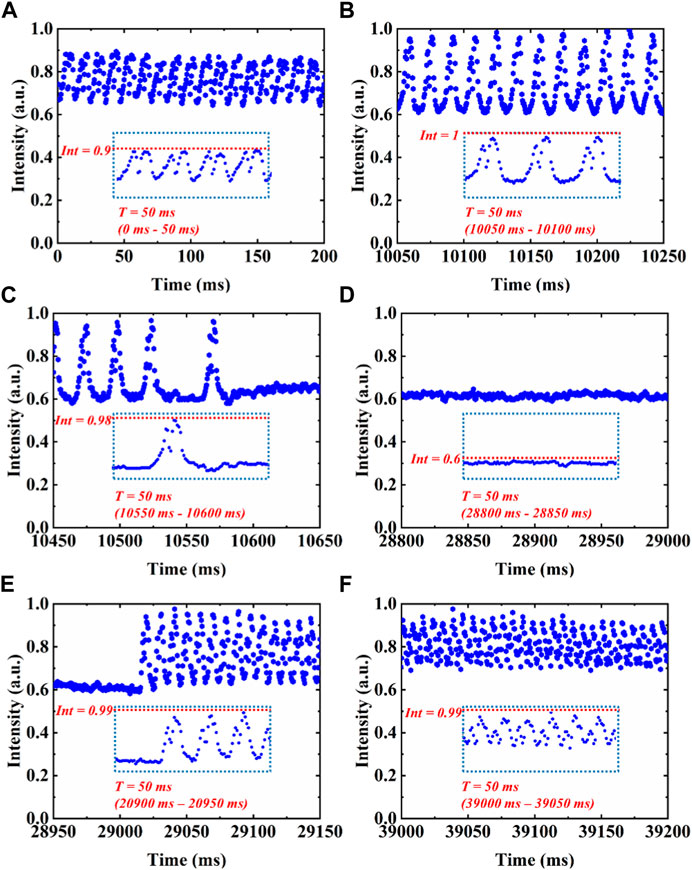
FIGURE 3. Variation of power in the far-field bucket within multiple 200 ms at the pumping power of 357 W. Inset: selected 50 ms time window, where Int denotes the maximum intensity.
We then perform mode decomposition and the corresponding modal content is shown in Figures 4A–F. The accuracy of mode decomposition can be up to 98% in our experiment. When the modal coupling occurs at adjacent modes, these two modes are recognized as a coupling pair. According to the variation of modal contents, the modal coupling presents a reverse periodic change among one coupling pair. When one mode intensity decreases, the other mode in the coupling pair will increase in a similar trend. It can be clearly seen that there is a strong coupling between LP01 and LP11e mode in the state of TMI. The degenerate modes (LP11e and LP11o, LP21e and LP21o) have mutual energy exchange. Besides, the results of the modal analysis demonstrate that the periodic modal coupling changes with time. In Figure 4D, when the laser output is relatively stable which lasts for about 18 s, the mode content of the fundamental mode stays around 65%, increasing from 58% in the unstable case. This result demonstrates a static mode coupling in the time range of 18 s. And then the output power oscillates again, accompanied by dynamic mode coupling.
FIGURE 4. The variation of transverse mode coupling at the pumping power of 357 W.
To figure out the properties of the modal coupling frequencies, we compute Fourier spectrum of the individual mode content in 30 s. We compare it with the frequency of the power in the far-field bucket. The power fluctuation of the far-field bucket in 50 ms is shown in Figure 5A. The intensity has a periodic quasi-triangle waveform in this time window. The characteristic peaks of the Fourier spectrum are independent below 1 kHz. As depicted in Figure 5B, the characteristic frequencies of the individual modes are similar as that of the power change of the far-field mixed modes. The basic frequencies are all around 150 Hz. Thus, we consider 1.5 kHz may be an essential frequency for controlling mode coupling for this fiber laser oscillator in an active control system.
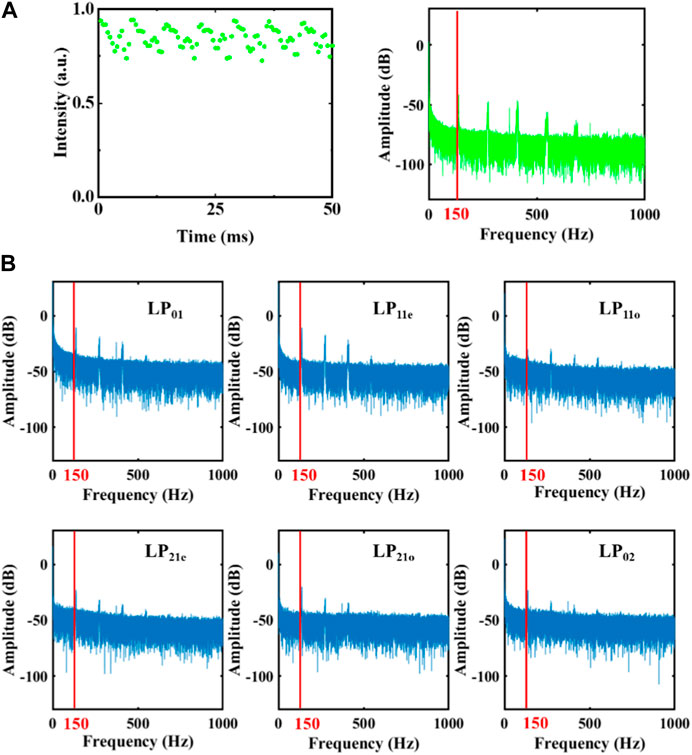
FIGURE 5. The variation of the power fluctuation in the bucket of far-field spot and modal coupling frequencies. (A) The power fluctuation of the far-field bucket in 50 ms and the related Fourier spectrum; (B) The characteristic frequencies of the individual modes (LP01, LP11e, LP11o, LP21e, LP21o, LP02) in 30 s.
3.3 Physical explanations and analysis
The above experimental results show that the frequencies of the temporal fluctuation are several times lower than the dynamic TMI in fiber amplifiers, which are mostly in kHz level. This phenomenon is consistent with that of Ref. [44] that the characteristic frequency of a fiber laser oscillator is lower than that of a fiber laser amplifier.
In recent years, it is generally agreed that TMI is induced by the refractive index gratings (RIG) [11]. But there are still two different theories explaining the physical origin of TMI. One of the theories is based on non-adiabatic waveguide changes which are thermally induced [39]. The other theory relies on modal interference pattern (MIP) between fundamental mode and higher-order modes with slightly different frequencies [45].
The energy transfer between the transverse modes for the dynamic TMI is related to the non-adiabatic longitudinal change of the transverse refractive index distribution along the fiber. From the Ref. [39] and the results of our experiments, the energy exchange is a ripple-shape in one cycle. This ripple-shape will change slightly over time compared with the previous ones. That is to say, the energy oscillation can remain unchanged within a certain time range, but it will suddenly vary to a new state, and then keep this state for a moment. What’s more, the net energy transfer after each period will be equal to zero, since the energy transfer in the first half cycle will be completely reversed in the second half cycle.
We observe that the TMI effect switches from an unstable temporal state to a stable temporal state. Even though, this phenomenon is demonstrated as a static mode coupling in the selected time window at 357 W (Figure 4D). When the system operates for a period at the pumping power point above TMI threshold, it is also recorded that the system switches back and forth between the stable and the unstable state (at 357 and 377 W). This may be still a dynamic energy transfer with a certain set of the coupling frequencies, which can induce a plausible balanced state. Otherwise, the temporal stability may be occurred when the dynamic energy transfer relaxes to a stable state of the system over time. A weak external perturbation, such as air turbulence/convection, mechanical vibration, or the thermally-induced change, is enough to trigger the modal interference conditions and induce the unstable evolution of the system again. Besides, the RIG at the fiber end amplifies the impact of these perturbations. The TMI will occur when this amplification factor is higher than the damping of perturbation. This also requires in-depth researches to explore the physical origin of this relaxation.
In additon, according to Ref. [46], Hui Cao from Yale University calculated that multiple mode excitation can reduce the thermo-optical non-linearity and instability compared to two mode excitation. As there are at least 6 supported modes in 30 μm Yb-doped fiber, multiple mode excitation is highly likely to exist and may change over time. When the mode coupling results in more mode distribution, the TMI threshold increases so that TMI phenomenon may not occur. On the other hand, when the mode coupling reduces the number of modes, the TMI may jump in again due to the reduced threshold.
4 Conclusion
In summary, we have experimentally studied the TMI phenomenon in a 30 μm Yb-doped fiber laser oscillator in detail and validate the modal energy transfer during TMI using temporal analysis and mode decomposition. The TMI threshold is measured at a pumping power around 310 W. The basic characteristic frequency is quite low, around 100 Hz, changing with time and pump power. When the fiber laser oscillator operates above TMI threshold at 357 W or 377 W, to our surprise, the temporal fluctuation slowly disappears with a reduced frequency, and re-appears after more than 10 s. During the period of fluctuation disappearance at 357 W, the mode content of fundamental mode increases from 57% to 63%, while the output power stays low. This demonstrates a static mode coupling in the selected time window. We provide proper physical explanations and analysis for several complex non-linear dynamics of TMI, which could be helpful for the recognition and suppression of TMI in the fiber laser oscillator.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
Investigation, JC, WL, and XW; resources, YW, KX, QZ, PL, HZ, DZ, YL, and ZJ; writing—original draft preparation, JC; writing—review and editing, JC, JZ, and XW; supervision, WL, XW, and GZ. All authors have read and agreed to the submitted version of the manuscript.
Funding
The authors appreciate the financial support from the National Natural Science Foundation of China (NSFC) under Grant Nos. 12074432 and 12204540; Science and Technology Innovation Program of Hunan Province under Grant No. 2021RC3038.
Acknowledgments
The authors would like to thank Lingfa Zeng, Penglin Zhong, and Xiaoyong Xu for their assistance in the whole experiment.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Jauregui C, Limpert J, Tünnermann A. High-power fibre lasers. Nat Photon (2013) 7(11):861–7. doi:10.1038/nphoton.2013.273
2. Nilsson J, Payne D. High-power fiber lasers. Science (2011) 332(6032):921–2. doi:10.1126/science.1194863
3. Zervas M, Codemard C. High power fiber lasers: A review. IEEE J Sel Top Quan Electron. (2014) 20(5):219–41. doi:10.1109/jstqe.2014.2321279
4. Zhang C, Liu J, Gao Y, Li X, Lu H, Wang Y, et al. Porous nickel oxide micron polyhedral particles for high-performance ultrafast photonics. Opt Laser Technol (2022) 146:P107546. doi:10.1016/j.optlastec.2021.107546
5. Li X, Feng J, Mao W, Yin F, Jiang J. Emerging uniform Cu2O nanocubes for 251st harmonic ultrashort pulse generation. J Mater Chem C (2022) 8(41):14386–92. doi:10.1039/d0tc03622f
6. Li X, Xu W, Wang Y, Zhang X, Hui Z, Zhang H, et al. Optical-intensity modulators with PbTe thermoelectric nanopowders for ultrafast photonics. Appl Mater Today (2022) 28:101546. doi:10.1016/j.apmt.2022.101546
7. Zhao Y, Wang W, Li X, Lu H, Shi Z, Wang Y, et al. Functional porous MOF-Derived CuO octahedra for harmonic soliton molecule pulses generation. ACS Photon (2022) 7(9):2440–7. doi:10.1021/acsphotonics.0c00520
8. Zhang C, Li X, Chen E, Liu H, Shum P, Chen X. Hydrazone organics with third-order nonlinear optical effect for femtosecond pulse generation and control in the L-band. Opt Laser Technol (2022) 151:108016. doi:10.1016/j.optlastec.2022.108016
9. Wang L, Zhang H, Wang P, Yang B, Wang X, Ning Y, et al. A 6.4-kw peak power near-single-mode quasi-continuous wave fiber laser oscillator employing spindle-shaped ytterbium-doped fiber. Opt Laser Technol (2022) 154.
10. Hong Z, Wan Y, Xi X, Zhang H, Wang X, Xu X. High-peak-power pump-modulated quasi-CW fiber laser. Appl Opt (2022) 61(7):1826–33. doi:10.1364/ao.452604
11. Leone C, Mingione E, Genna S. Laser cutting of CFRP by quasi-continuous wave (QCW) fibre laser: Effect of process parameters and analysis of the HAZ index. Compos B-eng (2021) 0224:109146. doi:10.1016/j.compositesb.2021.109146
12. Limpert J, Liem A, Zellmer H, Tünnermann A. 500 W continuous-wave fibre laser with excellent beam quality. Electron Lett (2003) 39:645–7. doi:10.1049/el:20030447
13. Jeong Y, Sahu J, Payne D, Nilsson J. Ytterbium-doped large-core fiber laser with 1.36 kW continuous-wave output power. Opt Express (2004) 12:6088–92. doi:10.1364/opex.12.006088
14. Pakniat M, Ghaini F, Torkamany M. Hot cracking in laser welding of Hastelloy X with pulsed Nd:YAG and continuous wave fiber lasers. Mater Des. (2016) 16:177–83. doi:10.1016/j.matdes.2016.05.124
15. Richardson D, Nilsson J, Clarkson W. High power fiber lasers: Current status and future perspectives [invited]. J Opt Soc Am B (2010) 27(11):B63. B63–B92. doi:10.1364/josab.27.000b63
16. Fang Q, Shi W, Qin Y, Meng X, Zhang Q. 2.5 kw monolithic continuous wave (cw) near diffraction-limited fiber laser at 1080 nm. Laser Phys Lett (2014) 11(10):105102. doi:10.1088/1612-2011/11/10/105102
17. Yu H, Zhang H, Lv H, Wang X, Leng J, Xiao H, et al. 315 kW direct diode-pumped near diffraction-limited all-fiber-integrated fiber laser. Appl Opt (2015) 54(14):4556–60. doi:10.1364/ao.54.004556
18. Shi C, Su R, Zhang H, Yang B, Wang X, Zhou P, et al. Experimental study of output characteristics of bi-directional pumping high power fiber amplifier in different pumping schemes. IEEE Photon J (2017) 9(3):1–10. doi:10.1109/jphot.2017.2679753
19. Beier F, Hupel C, Kuhn S, Hein S, Nold J, Proske F, et al. Single mode 4.3 kw output power from a diode-pumped yb-doped fiber amplifier. Opt Express (2017) 25(13):14892. doi:10.1364/oe.25.014892
20. Beier F, Hupel C, Nold J, Kuhn S, Hein S, Ihring J, et al. Narrow linewidth, single mode 3 kw average power from a directly diode pumped ytterbium-doped low na fiber amplifier. Opt Express (2016) 24(6):6011. doi:10.1364/oe.24.006011
21. Guan M, Chen D, Hu S, Zhao H, You P, Meng S. Theoretical insights into ultrafast dynamics in quantum materials. Ultrafast Sci (2022) 16:9767251. doi:10.34133/2022/9767251
22. Liu X, Yao X, Cui Y. Real-time observation of the buildup of soliton molecules. Phys Rev Lett (2018) 121(2):023905. doi:10.1103/physrevlett.121.023905
23. Liu X, Popa D, Akhmediev N. Revealing the transition dynamics from Q switching to mode locking in a soliton laser. Phys Rev Lett (2019) 123(9):093901. doi:10.1103/physrevlett.123.093901
24. Hansen K, Alkeskjold T, Broeng J, Lægsgaard J. Theoretical analysis of mode instability in high-power fiber amplifiers. Opt Express (2013) 21:1944–71. doi:10.1364/oe.21.001944
25. Hejaz K, Norouzey A, Poozesh R, Heidariazar A, Roohforouz A, Nasirabad R, et al. Controlling mode instability in a 500 W ytterbium-doped fiber laser. Laser Phys (2014) 24(2):025102. doi:10.1088/1054-660x/24/2/025102
26. Smith A, Smith J. Mode instability in high power fiber amplifiers. Opt Express (2011) 19(11):10180–92. doi:10.1364/oe.19.010180
27. Ward B, Robin C, Dajani I. Origin of thermal modal instabilities in large mode area fiber amplifiers. Opt Express (2012) 20(10):11407–22. doi:10.1364/oe.20.011407
28. Haarlammert N, Sattler B, Liam A, Strecker M, Nold J, Schreiber T, et al. Optimizing mode instability in low NA fibers by passive strategies. Opt Lett (2015) 40(10):2317–20. doi:10.1364/ol.40.002317
29. Brar K, Savage-Leuchs M, Henrie J, Courtney S, Dilley C, Afzal R, et al. “Threshold power and fiber degradation induced modal instabilities in high-power fiber amplifiers based on large mode area fibers,” In Proc. SPIE (2014) San Francisco, California, USA. 8961.
30. Otto H, Stutzki F, Jansen F, Eidam T, Jauregui C, Limpert J, et al. Temporal dynamics of mode instabilities in high-power fiber lasers and amplifiers. Opt Express (2012) 20(14):15710–22. doi:10.1364/oe.20.015710
31. Tao R, Wang X, Zhou P. Comprehensive theoretical study of mode instability in high-power fiber lasers by employing a universal model and its implications. IEEE J Sel Top Quan Electron. (2018) 24(3):1–19. doi:10.1109/jstqe.2018.2811909
32. Smith A, Smith J. Increasing mode instability thresholds of fiber amplifiers by gain saturation. Opt Express (2013) 21(13):15168–82. doi:10.1364/oe.21.015168
33. Jauregui C, Otto H, Stutzki F, Jansen F, Limpert J, Tünnermann A. Passive mitigation strategies for mode instabilities in high-power fiber laser systems. Opt Express (2013) 21(16):19375–86. doi:10.1364/oe.21.019375
34. Jauregui C, Stihler C, Limpert J. Transverse mode instability. Adv Opt Photon (2020) 12(2):429–84. doi:10.1364/aop.385184
35. Chai J, Liu W, Zhang J, Xie K, Lu Y, Li C, et al. Influence of aberrations on modal decomposition for LMA fiber laser systems. Front Phys (2022) 9:9. doi:10.3389/fphy.2021.796666
36. Eidam T, Wirth C, Jauregui C, Stutzki F, Jansen F, Otto H, et al. Experimental observations of the threshold-like onset of mode instabilities in high power fiber amplifiers. Opt Express (2011) 19(14):13218–24. doi:10.1364/oe.19.013218
37. Christensen S, Johansen M, Michieletto M, Triches M, Maack M, Lægsgaard J. Experimental investigations of seeding mechanisms of TMI in rod fiber amplifier using spatially and temporally resolved imaging. Opt Express (2020) 28(18):26690–705. doi:10.1364/oe.400520
38. Stutzki F, Otto H, Jansen F, Gaida C, Jauregui C, Limpert J, et al. High-speed modal decomposition of mode instabilities in high-power fiber lasers. Opt Lett (2011) 36(23):4572–4. doi:10.1364/ol.36.004572
39. Jauregui C, Eidam T, Otto H, Stutzki F, Jansen F, Limpert J, et al. Physical origin of mode instabilities in high-power fiber laser systems. Opt Express (2012) 20(12):12912–25. doi:10.1364/oe.20.012912
40. Karow M, Tünnermann H, Neumann J, Kracht D, Wessels P. Beam quality degradation of a singlefrequency Yb-doped photonic crystal fiber amplifier with low mode instability threshold power. Opt Lett (2012) 37(20):4242–4. doi:10.1364/ol.37.004242
41. Naderi S, Dajani I, Madden T, Robin C. Investigations of modal instabilities in fiber amplifiers through detailed numerical simulations. Opt Express (2013) 21(13):16111–29. doi:10.1364/oe.21.016111
42. Wang Y, Kitahara R, Kiyoyama W, Shirakura Y, Kurihara T, Nakanishi Y, et al. “8-kW single-stage all-fiber Yb-doped fiber laser with a BPP of 0.50 mm-mrad.” In Proc. SPIE (2020) San Francisco, California, USA, 1126022.
43. Xie K, Liu W, Zhou Q, Huang L, Jiang Z, Xi F, et al. Adaptive phase correction of dynamic multimode beam based on modal decomposition. Opt Express (2019) 27(10):13793–802. doi:10.1364/oe.27.013793
44. Yang B, Zhang H, Shi C, Wang X, Zhou P, Xu X, et al. Mitigating transverse mode instability in all-fiber laser oscillator and scaling power up to 2.5 kW employing bidirectional-pump scheme. Opt Express (2016) 24(24):27828–35. doi:10.1364/oe.24.027828
45. Smith A, Smith J. Spontaneous Rayleigh seed for stimulated Rayleigh scattering in high power fiber amplifiers. IEEE Photon J (2013) 5(5):7100807. doi:10.1109/jphot.2013.2280526
Keywords: transverse mode instability, fiber laser oscillator, modal coupling, refractive index gratings, modal interference pattern
Citation: Chai J, Liu W, Wen Y, Wang X, Xie K, Zhou Q, Zhang H, Zhang J, Liu P, Zhang D, Lu Y, Jiang Z and Zhao G (2023) Dynamic modal characteristics of transverse mode instabilities in ytterbium-doped fiber laser oscillator. Front. Phys. 11:1181692. doi: 10.3389/fphy.2023.1181692
Received: 07 March 2023; Accepted: 28 March 2023;
Published: 06 April 2023.
Edited by:
Zhenxu Bai, Hebei University of Technology, ChinaReviewed by:
Andrey Pryamikov, Prokhorov General Physics Institute (RAS), RussiaXiaohui Li, Shaanxi Normal University, China
Copyright © 2023 Chai, Liu, Wen, Wang, Xie, Zhou, Zhang, Zhang, Liu, Zhang, Lu, Jiang and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenguang Liu, bHdnLmtldmluQDE2My5jb20=; Xiaolin Wang, Y2hpbmFwaG90b25pY3NAMTYzLmNvbQ== Jiangbin Zhang, emhhbmdqaWFuZ2JpbkBudWR0LmVkdS5jbiYjeDAyMDBhOw==