Moment-based analysis of pinning synchronization in complex networks with sign inner-coupling configurations

In this paper, pinning synchronization of complex networks with sign inner-coupling configurations is investigated from a moment-based analysis approach. First, two representative non-linear systems with varying dynamics parameters are presented to illustrate the bifurcation of the synchronized regions. The influence of sign inner-coupling configurations on network synchronizability is then studied in detail. It is found that adding negative parameters in the inner-coupling matrix can significantly enhance the network synchronizability. Furthermore, the eigenvalue distribution of the coupling and control matrix in the pinned network is estimated using the spectral moment analysis. Finally, numerical simulations are given for illustration.

1 Introduction

Synchronization is a typical collective behavior in complex networks [1–5]. In the past two decades, the issues of synchronization, control, and optimization in complex network systems have become focal subjects in network science and engineering [6–31], and numerous works have been reported on such topics as complete synchronization [6], near-synchronization [32], phase synchronization [33], bounded synchronization [34], fixed-time synchronization [35, 36], heterogeneous node dynamics [37], multiplex networks [38], time-delay systems [39–41], and time-varying networks [42, 43].

It has been demonstrated that the local stability of a complex dynamical network under the pinning control can be converted into two independent sub-problems: identifying the synchronized regions of the pinned network and analyzing the scaled eigenvalues of the coupling and control matrix [44]. On one hand, the bifurcation behavior of the synchronized regions has been observed in complex networks with varying node parameters [39, 40, 45]. Various rich bifurcation patterns of the synchronized regions have been found in the pioneer work [45]. On the other hand, the moment-based analysis approach [46–48] has been introduced to successfully estimate the eigenvalue distribution of the coupling and control matrix [49]. Therein, without performing explicit eigenvalue decomposition, the eigenvalue distribution can be estimated only from the network structural parameters and the control mechanism.

It is worth noting that most of the above-reviewed works on network synchronization assume that the inner-coupling matrix consists of zeros and positive parameters. However, less attention has been paid to the case that the elements in the inner-coupling matrix are negative [50]. Interestingly, negative interactions among the nodes will lead to the enhancement of the synchronization in complex networks [51]. Moreover, a recent work on network controllability has revealed that adding negatively-weighted edges in a signed network can significantly change its average controllability [52]. Indeed, in real-world scenarios, it is more reasonable and accurate to model a complex system using a network with both negative and positive weights on edges. For instance, in social networks, positive edge weights can denote the relations of like and friendships, while negative edge weights on can represent the relations of dislike and foe [53]. Inspired by these observations, a sign inner-coupling matrix with positive and negative parameters is introduced to denote the cooperation and competition relationships, respectively, between the node variables.

The main contributions of this paper are two-fold. First, the influence of sign inner-coupling configurations on network synchronizability is studied. The interesting bifurcation behavior of the synchronized regions is observed in the pinned network with a varying node dynamics parameter. It is shown that the network synchronizability can be improved by adding negative parameters in the inner-coupling matrix, while blindly adding inner-coupling elements with positive parameters may weaken it. This finding provides a good alternative to optimize the network synchronizability. Second, the eigenvalue distribution of the pinned network is analyzed from the moment-based approach. The analytical expressions of the spectral moments for a globally coupled network and a nearest-neighbor coupled network are derived, respectively. It is found that the expected moments depend not only on the structural parameters of the network but also on the control mechanism. The derived expected moments are then used to estimate the eigenvalue distribution. Numerical examples demonstrate the efficiency of the proposed spectral estimation method.

The rest of the paper is organized as follows. Notation and preliminaries are given in Section 2. The influence of sign inner-coupling configurations on network synchronizability is investigated in Section 3. In Section 4, the estimation of the eigenvalues of the coupling and control matrix for two representative regular networks is provided. Section 5 shows the numerical results. Finally, Section 6 concludes the paper.

2 Notation and preliminaries

2.1 Notation

Throughout the paper, let $\mathbb{R}$ denote the set of real numbers, ${\mathbb{R}}^n$ the vector space of n-dimensional real vectors, and ${\mathbb{R}}^{m\times n}$ the set of m × n real matrices. Let I_m be an m × m identity matrix and diag{a₁, a₂, …, a_n} an n × n diagonal matrix. Let ⊗ indicate the Kronecker product and tr(A) the trace of matrix A.

2.2 Graph theory

Let $\mathcal{G}=(\mathcal{V},\mathcal{E})$ be an undirected graph with a node set $\mathcal{V}=\{\mathrm{1,2},\dots ,N\}$ and an edge set $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$. A path between two nodes, say i and j, is given by the node sequence v₁, v₂, …, v_k, where v₁ = i, v_k = j, and $(v_l,v_{l+1})\in \mathcal{E}$. An undirected graph $\mathcal{G}$ is connected if, for any two nodes, there exists a path connecting them. Let $A=(A_{ij})\in {\mathbb{R}}^{N\times N}$ denote the adjacency matrix of the undirected graph $\mathcal{G}$. If there is an edge between nodes i and j, then A_ij = A_ji = 1, and A_ij = 0 (j ≠ i) otherwise. The degree of node i is the number of edges directly connected to it and can be denoted by $d_i={\sum }_{j=1}^N{A}_{ij}$. The degree sequence of $\mathcal{G}$ is the list of node degrees, denoted by {d₁, d₂, …, d_N}. The degree matrix is, thus, defined as D = diag{d₁, d₂, …, d_N}. The corresponding Laplacian matrix is given by L = D − A.

2.3 Problem statement

We consider a complex dynamical network of N nodes described by

${\dot{x}}_i\left(t\right)=F\left(x_i\left(t\right)\right)-\sigma \sum _{j=1}^N{L}_{ij}H{x}_j\left(t\right),i=\mathrm{1,2},\dots ,N,(1)$

where $x_i(t)={[x_{i1}(t),x_{i2}(t),\dots ,x_{im}(t)]}^T\in {\mathbb{R}}^m$ is the state vector of node i. The non-linear function F(⋅) is continuously differentiable denoting the self-dynamics of the nodes. σ > 0 is the global coupling strength. The matrix $H\in {\mathbb{R}}^{m\times m}$ describes the inner-coupling of the state variables of nodes, while the Laplacian matrix $L=(L_{ij})\in {\mathbb{R}}^{N\times N}$ describes the outer-coupling among the nodes. We assume that the network is undirected and connected. If there is a connection between node i and node j, then L_ij = L_ji = −1; otherwise, L_ij = L_ji = 0 (j ≠ i). In addition, the diagonal elements of L are given by

$L_{ii}=-\sum _{j=1,j\ne i}^N{L}_{ij},i=\mathrm{1,2},\dots ,N,(2)$

which satisfy the diffusion condition ${\sum }_{j=1}^N{L}_{ij}=0$. It can be verified that L is a symmetric and diagonalizable matrix.

Suppose that all the nodes have a common equilibrium $\bar{x}$, satisfying $F(\bar{x})=0$. In order to synchronize network (1) at the state $\bar{x}$, pinning control is applied. The pinned network is, thus, described as follows:

$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)& =F\left(x_i\left(t\right)\right)-\sigma \sum _{j=1}^N{L}_{ij}H{x}_j\left(t\right)-{\delta }_i\sigma b_{i}H\left(x_i\left(t\right)-\bar{x}\right),\hfill \\ \hfill i& =\mathrm{1,2},\dots ,N,\hfill \end{array}(3)$

where the variable δ_i denotes whether node i is under control. If control is directly applied to node i, then δ_i = 1 with b_i = b > 0, otherwise δ_i = b_i = 0. Here, b denotes the feedback gain to be designed. Let l (1 ≤ l < N) be the number of pinned nodes. Therefore, ∑_iδ_i = l.

Let $e_i(t)=x_i(t)-\bar{x}$ and $E(t)={[e_1^T(t),e_2^T(t),\dots ,e_N^T(t)]}^T\in {\mathbb{R}}^{mN}$. Linearizing system (3) at $\bar{x}$ leads to the following error system:

$\dot{E}\left(t\right)=\left(I_N\otimes J_F\left(\bar{x}\right)-\sigma C\otimes H\right)E\left(t\right),(4)$

where $J_F(\bar{x})$ is the Jacobian matrix of F(⋅) evaluated at $\bar{x}$, C = L + B is the coupling and control matrix, and B = diag{b₁, b₂, …, b_N} is the feedback gain matrix.

It is worth noting that the matrix C is a real symmetric matrix, which can be written as Λ = Φ⁻¹CΦ, where Λ = diag{λ₁, λ₂, …, λ_N} with λ_i, i = 1, 2, …, N being the eigenvalues of C, and the columns of Φ are the set of the corresponding eigenvectors. It can be verified that the eigenvalues of the matrix $I_N\otimes J_F(\bar{x})-\sigma C\otimes H$ and those of $J_F(\bar{x})-\sigma {\lambda }_{i}H,i=\mathrm{1,2},\dots ,N$ are identical. For convenience, let α_i = σλ_i, i = 1, 2, …, N. It has been demonstrated in the literature that the local stability of the pinned network (3) is determined by the following generic system [49]:

$\dot{\eta }\left(t\right)=\left(J_F\left(\bar{x}\right)-\alpha H\right)\eta \left(t\right),(5)$

where η(t) is a new auxiliary variable.

λ_m(α) denotes the maximal real part of the eigenvalues of $J_F(\bar{x})-\alpha H$. The synchronized region $\mathcal{S}$ is defined as the range of α with λ_m(α) < 0. The synchronization will be achieved if all the eigenvalues of σC are located inside $\mathcal{S}$.

In summary, pinning synchronization in network (3) is separated into two sub-problems: 1) identifying the synchronized regions and 2) analyzing the eigenvalue distribution of σC. Previous works on the types and bifurcation behavior of synchronized regions assume that the elements in the inner-coupling matrix are either zeros or positive parameters. Here, a zero indicates the absence of a relation between some state variables of nodes, while a positive parameter characterizes the cooperative relationship between two corresponding state variables. However, less attention has been paid to the case of negative or competitive interactions between node variables. In this paper, a more general inner-coupling matrix including negative parameters is considered.

Definition 1. If the elements of matrix H consist of the symbols +, −, and 0, H is then called the sign pattern matrix [50].For example,

$H=\left[\begin{array}{ccc}\hfill -\hfill & \hfill +\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill +\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\hfill \end{array}\right](6)$

is called a sign pattern matrix, in which 0, +, and − represent zero, positive, and negative parameters, respectively.If the state variables of nodes are coupled through a sign pattern matrix, the networked system is said to have a sign inner-coupling configuration. Without loss of generality, in what follows, the elements of H are denoted by 1, −1, and 0, where “1” indicates cooperative relationship, “−1” indicates competitive relationship, and “0” indicates that there is no relation between some state variables of nodes.

3 Bifurcation of the synchronized regions

In this section, the influence of sign inner-coupling configurations on network synchronizability is studied in detail. In particular, two representative non-linear systems with varying parameters are given to illustrate the bifurcation of the synchronized regions.

3.1 Lü system

A single Lü system [54] is described as

$\left[\begin{array}{c}\hfill {\dot{x}}_1\hfill \\ \hfill {\dot{x}}_2\hfill \\ \hfill {\dot{x}}_3\hfill \end{array}\right]=\left[\begin{array}{c}\hfill a\left(x_2-x_1\right)\hfill \\ \hfill -x_1{x}_3+\gamma x_2\hfill \\ \hfill x_1{x}_2-\beta x_3\hfill \end{array}\right],$

where β = 3 and γ = 20. Obviously, $\bar{x}={[\mathrm{0,0,0}]}^T$ is an equilibrium point of the aforementioned Lü system, and the Jacobian matrix of the system is as follows:

$J_F\left(\bar{x}\right)=\left[\begin{array}{ccc}\hfill -a\hfill & \hfill a\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 20\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -3\hfill \end{array}\right].$

In what follows, three different types of inner-coupling matrices are considered.

(i) When the inner-coupling matrix is chosen as

$H_{l1}=\left[\begin{array}{ccc}\hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$

the corresponding characteristic equation is obtained as follows:

$f\left(\lambda ,\alpha ,a\right)=\left(\lambda +3\right)\left[{\lambda }^2+\left(a-20\right)\lambda -{\alpha }^2+\left(2a+20\right)\alpha -20a\right]=0.$

One has λ₁ = −3 < 0. If a − 20 > 0 and −α² + (2a + 20)α − 20a > 0, then λ_2,3 < 0; that is, the pinned network can synchronize at $\bar{x}={[\mathrm{0,0,0}]}^T$. Here, the boundary curves of the synchronized region are represented by ${\alpha }_1=-\sqrt{a^2+100}+a+10$, ${\alpha }_2=\sqrt{a^2+100}+a+10$, and a > 20. In this situation, the synchronized region of the Lü system with varying dynamics parameter a and its boundary curves are given as shown in Figure 1A. The cyan-shaded area denotes the synchronized region in which λ_m(α) < 0. The magenta line denotes the corresponding boundary curve. These notations will be used for Figures 1B, C and Figure 2.

FIGURE 1

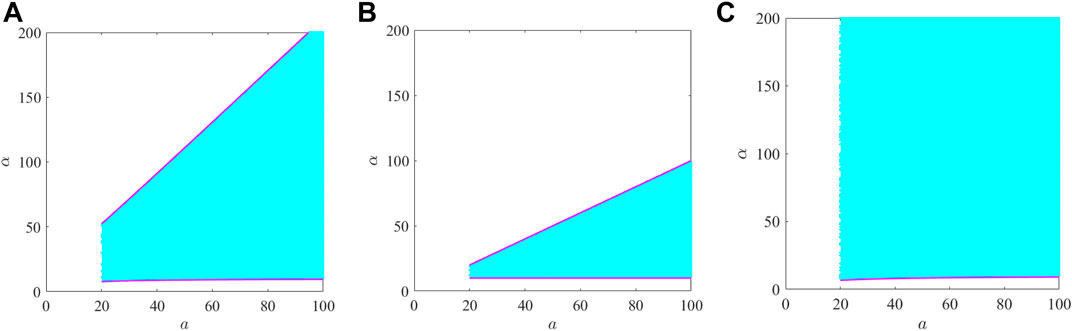
FIGURE 1. Synchronized regions of the Lü system with varying dynamics parameter a and its boundary curves.

FIGURE 2

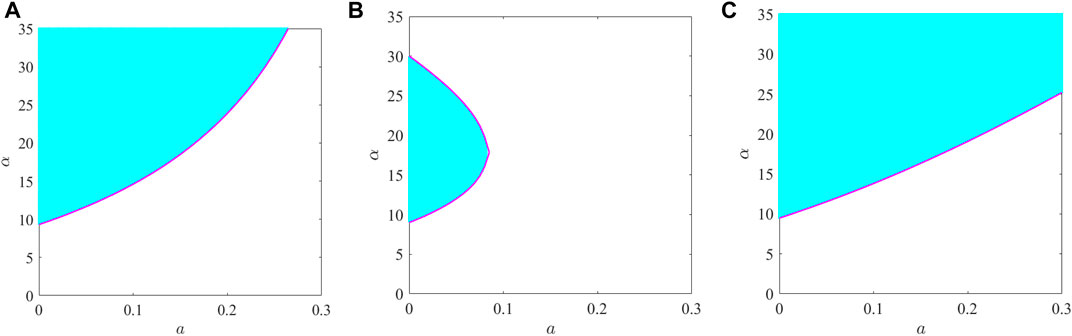
FIGURE 2. Synchronized regions of the unified chaotic system with varying dynamics parameter a and its boundary curves.

(ii) When the inner-coupling matrix is chosen as

$H_{l2}=\left[\begin{array}{ccc}\hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$

the corresponding characteristic equation is obtained as follows:

$f\left(\lambda ,\alpha ,a\right)=\left(\lambda +3\right)\left[{\lambda }^2+\left(a-20\right)\lambda -2{\alpha }^2+\left(2a+20\right)\alpha -20a\right]=0.$

One has λ₁ = −3 < 0. If a − 20 > 0 and −2α² + (2a + 20)α − 20a > 0, then λ_2,3 < 0; that is, the pinned network can synchronize at $\bar{x}={[\mathrm{0,0,0}]}^T$. Here, the boundary curves of the synchronized region are represented by ${\alpha }_1=-\sqrt{a^2/4-5a+25}+a/2+5$, ${\alpha }_2=\sqrt{a^2/4-5a+25}+a/2+5$ and a > 20. In this situation, the synchronized region of the Lü system with varying dynamics parameter a and its boundary curves are given as shown in Figure 1B.

(iii) When the inner-coupling matrix is chosen as

$H_{l3}=\left[\begin{array}{ccc}\hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$

the corresponding characteristic equation is obtained as follows:

$f\left(\lambda ,\alpha ,a\right)=\left(\lambda +3\right)\left[{\lambda }^2+\left(a-20\right)\lambda +\left(2a+20\right)\alpha -20a\right]=0.$

One has λ₁ = −3 < 0. If a − 20 > 0 and (2a + 20)α − 20a > 0, then λ_2,3 < 0; that is, the pinned network can synchronize at $\bar{x}={[\mathrm{0,0,0}]}^T$. Here, the boundary curves of the synchronized region are represented by ${\alpha }_0=\frac{20a}{2a+20}$ and a > 20. In this situation, the synchronized region of the Lü system with varying dynamics parameter a and its boundary curves are given as shown in Figure 1C.

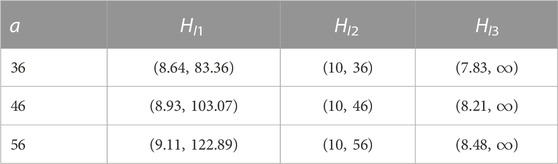
Figure 1 shows the synchronized regions of Lü system for three different sign inter-coupling matrices. Table 1 further summarizes the synchronized regions for three specific values of a. It can be observed from Figures 1A, B that the synchronized region switches from “empty set” to “bounded region” with the increase in the dynamics parameter a, while in Figure 1C, the synchronized region switches from “empty set” to “unbounded region.”

TABLE 1

TABLE 1. Synchronized regions of the Lü system under different sign inter-coupling matrices.

3.2 Unified chaotic system

A single unified chaotic system [55] is described as

$\left[\begin{array}{c}\hfill {\dot{x}}_1\hfill \\ \hfill {\dot{x}}_2\hfill \\ \hfill {\dot{x}}_3\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \left(25a+10\right)\left(x_2-x_1\right)\hfill \\ \hfill \left(28-35a\right)x_1-x_1{x}_3+\left(29a-1\right)x_2\hfill \\ \hfill x_1{x}_2-\frac{a+8}{3}{x}_3\hfill \end{array}\right],$

where a ∈ [0, 1]. Obviously, $\bar{x}={[\mathrm{0,0,0}]}^T$ is an equilibrium point of the aforementioned unified chaotic system, and the Jacobian matrix of the system is as follows:

$J_F\left(\bar{x}\right)=\left[\begin{array}{ccc}\hfill -\left(25a+10\right)\hfill & \hfill \left(25a+10\right)\hfill & \hfill 0\hfill \\ \hfill 28-35a\hfill & \hfill 29a-1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{a+8}{3}\hfill \end{array}\right].$

Then, we consider the following three types of different inner-coupling matrices:

(i) We set the inner-coupling matrix as

$H_{u1}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$

The corresponding characteristic equation is obtained as follows:

$\begin{array}{c}f\left(\lambda ,\alpha ,a\right)=\left(\lambda +\frac{a+8}{3}\right)\left[{\lambda }^2+\left(11-4a+\alpha \right)\lambda +\left(29-64a\right)\alpha -\left(25a+10\right)\left(27-6a\right)\right]=0.\hfill \end{array}$

One obtains ${\lambda }_1=-\frac{a+8}{3}<0$. If 11 − 4a + α > 0 and (29 − 64a)α − (25a + 10)(27 − 6a) > 0, then λ_2,3 < 0; that is, the pinned network can synchronize at $\bar{x}={[\mathrm{0,0,0}]}^T$. Here, the boundary curve of the synchronized region is represented by α₀ = (25a + 10)(27 − 6a)/29 − 64a. When the inner-coupling matrix is set as H_u1, the synchronized region of unified chaotic system with varying dynamics parameter a and its boundary curve are illustrated in Figure 2A.

(ii) We set the inner-coupling matrix as

$H_{u2}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$

The corresponding characteristic equation is obtained as follows:

$\begin{array}{cc}\hfill f\left(\lambda ,\alpha ,a\right)& =\left(\lambda +\frac{a+8}{3}\right)\left[{\lambda }^2+\left(11-4a+\alpha \right)\lambda -{\alpha }^2-\left(39a-39\right)\alpha -\left(25a+10\right)\left(27-6a\right)\right]\hfill \\ \hfill & =0.\hfill \end{array}$

One has ${\lambda }_1=-\frac{a+8}{3}<0$. If 11 − 4a + α > 0 and −α² − (39a − 39)α − (25a + 10)(27 − 6a) > 0, then λ_2,3 < 0; that is, the pinned network can synchronize at $\bar{x}={[\mathrm{0,0,0}]}^T$. Here, the boundary curves of the synchronized region are represented by ${\alpha }_1=\sqrt{4(25a+10)(6a-27)+{(39a-39)}^2}/2-(39a-39)/2$, ${\alpha }_2=-\sqrt{4(25a+10)(6a-27)+{(39a-39)}^2}/2-(39a-39)/2$. When the inner-coupling matrix is set as H_u2, the synchronized region of the unified chaotic system with varying dynamics parameter a and its boundary curves are shown in Figure 2B.

(iii) We set the inner-coupling matrix as

$H_{u3}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$

The corresponding characteristic equation is obtained as

$\begin{array}{cc}\hfill f\left(\lambda ,\alpha ,a\right)& =\left(\lambda +\frac{a+8}{3}\right)\left[{\lambda }^2+\left(11-4a+\alpha \right)\lambda +{\alpha }^2+\left(19-89a\right)\alpha -\left(25a+10\right)\left(27-6a\right)\right]\hfill \\ \hfill & =0.\hfill \end{array}$

One has ${\lambda }_1=-\frac{a+8}{3}<0$. If 11 − 4a + α > 0 and α² + (19 − 89a)α − (25a + 10)(27 − 6a) > 0, then λ_2,3 < 0; that is, the pinned network can synchronize at $\bar{x}={[\mathrm{0,0,0}]}^T$. Here, the boundary curves of the synchronized region are represented by ${\alpha }_1=\sqrt{4(25a+10)(6a-27)+{(19-89a)}^2}/2-(19-89a)/2$ and ${\alpha }_2=-\sqrt{4(25a+10)(6a-27)+{(19-89a)}^2}/2-(19-89a)/2$. When the inner-coupling matrix is set as H_u3, the synchronized region of the unified chaotic system with varying dynamics parameter a and its boundary curves are shown in Figure 2C.

Figure 2 shows the synchronized regions of the unified chaotic system for three different sign inter-coupling matrices. Table 2 further summarizes the synchronized regions for three specific values of a. It can be observed from Figures 2A, C that the synchronized region switches from “unbounded region” to “empty set” with the increase in the dynamics parameter a, while in Figure 2B, the synchronized region switches from “bounded region” to “empty set.”

TABLE 2

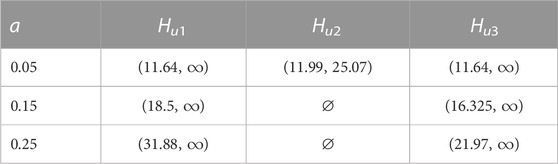
TABLE 2. Synchronized regions of the unified chaotic system under different sign inter-coupling matrices.

In summary, there exist bifurcation phenomena in the synchronized regions of complex networks for some specific inner-coupling matrices. The synchronized region can evolve with the varying node dynamics parameter and switch from one type to another type.

Given the node dynamics, the larger the range of the synchronized region corresponding to the sign inner-coupling matrix, the easier it is for the network to achieve synchronization. From the aforementioned simulations, the following conclusions can be drawn:

(i) From Figure 1, it can be seen that when the inner-coupling matrix is chosen as H_l2, the synchronized region is smaller than that of H_l1. In Figure 2, when the inner-coupling matrix is chosen as H_u2, the synchronized region is smaller than that of H_u1. It can be seen that H_l2 and H_u2 add a cooperative inner-coupling element to H_l1 and H_u1, respectively. This means that blindly adding positive parameters in the inner-coupling matrix may weaken the synchronizability of the network.

(ii) From Figure 1, it can be seen that when the inner-coupling matrix is chosen as H_l3, a larger synchronized region is obtained compared to H_l1. From Figure 2, it can be seen that when the inner-coupling matrix is chosen as H_u3, a larger synchronized region is obtained compared to H_u1. It can be observed that H_l3 and H_u3 add a competitive inner-coupling element to H_l1 and H_u1, respectively. This implies that the network synchronizability can be significantly enhanced by adding a small number of negative parameters in the inner-coupling matrix.

Remark 1. It should be pointed out that although numerical simulations are performed with the aforementioned two chaotic systems, the extension to other general systems is straightforward.

Remark 2. Recall that the bifurcation behavior of the synchronized regions in a network with a varying node dynamics parameter is analyzed in this section. The assumption that all the nodes have a common equilibrium can ensure that the boundary curves of the synchronized region can be analytically derived. It is found that the boundary curves of the synchronized region are related to the varying node dynamics parameter.

4 Spectral analysis of pinned networks

In this section, the spectral moment method [46] is applied to estimate the eigenvalues of C [49].

4.1 Spectral moments of the matrix C

The nth-order spectral moment of C is defined as

${\mathcal{Q}}_n\left(C\right)=\frac{1}{N}\sum _{i=1}^N{\lambda }_i^n=\frac{1}{N}\mathbf{t}\mathbf{r}\left(C^n\right)=\frac{1}{N}\mathbf{t}\mathbf{r}{\left(L+B\right)}^n.(7)$

The first three spectral moments of C can be obtained as follows:

$\left\{\begin{array}{c}{\mathcal{Q}}_1\left(C\right)=\frac{1}{N}\sum _{i=1}^N\left(d_i+b_i\right),\hfill \\ {\mathcal{Q}}_2\left(C\right)=\frac{1}{N}\sum _{i=1}^N\left(d_i^2+d_i+2d_i{b}_i+b_i^2\right),\hfill \\ {\mathcal{Q}}_3\left(C\right)=\frac{1}{N}\sum _{i=1}^N\left(d_i^3+3d_i^2+3d_i^2{b}_i+3d_i{b}_i+3d_i{b}_i^2+b_i^3-2t_i\right),\hfill \end{array}\right.(8)$

where b_i is the feedback gain, d_i is the degree of node i, and t_i is the number of triangles touching node i.

4.2 Globally coupled network

We consider a globally coupled network composed of N nodes, in which any two nodes are directly connected by an edge. The degree distribution of nodes of the globally coupled network is

$\begin{array}{cc}\hfill {\delta }_{N-1}& =\delta \left(d_i-\left(N-1\right)\right)=0,\text{for}{d}_i\ne N-1,\hfill \\ \hfill {\int }_{-\infty }^{\infty }{\delta }_{N-1}\left(d_i\right)dx& =1,\text{for}{d}_i=N-1.\hfill \end{array}(9)$

The first three expected moments of node degree are obtained by

$\left\{\begin{array}{c}\mathbb{E}\left[d_i\right]=\left(N-1\right),\hfill \\ \mathbb{E}\left[d_i^2\right]={\left(N-1\right)}^2,\hfill \\ \mathbb{E}\left[d_i^3\right]={\left(N-1\right)}^3.\hfill \end{array}\right.(10)$

The number of connected triples centered on any node in the globally coupled network is

$\left(\genfrac{}{}{0.0pt}{}{N-1}{2}\right)=\frac{1}{2}\left(N-1\right)\left(N-2\right).(11)$

When the pinned nodes are consecutively distributed in the network, the first three expected moments of C can, thus, be derived as

$\left\{\begin{array}{cc}\hfill \mathbb{E}\left[{\mathcal{Q}}_1\left(C\right)\right]& =N-1+b\frac{l}{N},\hfill \\ \hfill \mathbb{E}\left[{\mathcal{Q}}_2\left(C\right)\right]& ={\left(N-1\right)}^2+N-1+2\left(N-1\right)b\frac{l}{N}+b^2\frac{l}{N},\hfill \\ \hfill \mathbb{E}\left[{\mathcal{Q}}_3\left(C\right)\right]& ={\left(N-1\right)}^3+3{\left(N-1\right)}^2-\left(N-1\right)\left(N-2\right)\hfill \\ \hfill & +3\left[{\left(N-1\right)}^2+N-1\right]b\frac{l}{N}+3\left(N-1\right)b^2\frac{l}{N}+b^3\frac{l}{N}.\hfill \end{array}\right.(12)$

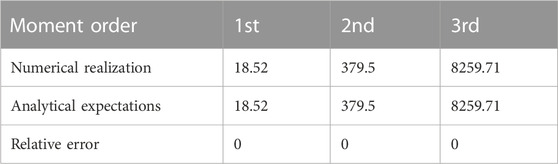
Example 1. We consider a globally coupled network of N = 17 nodes. Here, only l = 4 consecutively distributed nodes are pinned with b = 10.4. Table 3 compares the numerical values of the moments of C with the analytical predictions in (13). It shows that the analytical expectations of the moments are exactly the same as the numerical realizations.

TABLE 3

TABLE 3. Moments for a globally coupled network.

4.3 Nearest-neighbor coupled network

Consider a nearest-neighbor coupled network of N nodes, in which each node is only connected to its 2k nearest-neighbor nodes. The degree distribution of nodes of the nearest-neighbor coupled network is

$\begin{array}{cc}\hfill {\delta }_{2k}=\delta \left(d_i-2k\right)=0,& \text{for}{d}_i\ne 2k,\hfill \\ \hfill {\int }_{-\infty }^{\infty }{\delta }_{2k}\left(d_i\right)dx=1& \text{for}{d}_i=2k.\hfill \end{array}(13)$

Then, one obtains the first three expected moments of node degree as follows:

$\left\{\begin{array}{c}\mathbb{E}\left[d_i\right]=2k,\hfill \\ \mathbb{E}\left[d_i^2\right]=4k^2,\hfill \\ \mathbb{E}\left[d_i^3\right]=8k^3.\hfill \end{array}\right.(14)$

The number of connected triples centered on any node in the network is

$\left(\genfrac{}{}{0.0pt}{}{2k}{2}\right)=k\left(2k-1\right).(15)$

When the pinning nodes are uniformly distributed in the network, the first three expected moments of C are then obtained by

$\left\{\begin{array}{cc}\hfill \mathbb{E}\left[{\mathcal{Q}}_1\left(C\right)\right]& =2k+b\frac{l}{N},\hfill \\ \hfill \mathbb{E}\left[{\mathcal{Q}}_2\left(C\right)\right]& =4k^2+2k+2kb\frac{l}{N}+b^2\frac{l}{N},\hfill \\ \hfill \mathbb{E}\left[{\mathcal{Q}}_3\left(C\right)\right]& =8k^3+8k^2+2k+12k^{2}b\frac{l}{N}\hfill \\ \hfill & +6kb\frac{l}{N}+6k{b}^2\frac{l}{N}+b^3\frac{l}{N}.\hfill \end{array}\right.(16)$

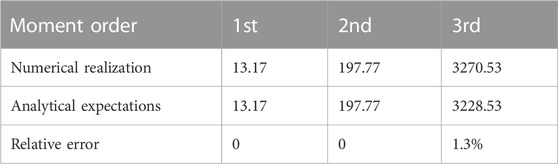
Example 2. We consider a nearest-neighbor coupled network with N = 200 and k = 6. It is assumed that l = ∑_iδ_i = 20 uniformly distributed nodes are pinned with i = 1, 11, …, 191. We set b = 11.7. Table 4 compares the numerical values of the moments with the analytical predictions in (17). It shows clearly that the analytical expectations of the moments are suited to capture the spectral property of the matrix C.

TABLE 4

TABLE 4. Moments for a nearest-neighbor coupled network.

Remark 3. In this paper, the spectral moment method is extended to the aforementioned two kinds of regular networks. The relationship between the lower-order expected moments and the local structural properties, control scheme including feedback gain and the number of pinned nodes, together with their distributions (i.e., the positions of pinned nodes in the whole network), is established. Note that other network models, such as ER random networks, Chung-Lu random networks, and NW small-world networks, have been given to verify the efficiency of the moment-based estimation method [49].

4.4 Triangular reconstruction of matrix C

In this section, the triangular reconstruction method [56] is generalized to estimate the bounds of the eigenvalues.

We define a triangular distribution T(λ) based on a set of abscissas p₁ ≤ p₂ ≤ p₃ as

$T\left(\lambda \right)=\{\begin{array}{ccc}\hfill \frac{h}{p_2-p_1}\left(\lambda -p_1\right),& \hfill & \hfill \text{for}\lambda \in \left[p_1,p_2\right),\\ \hfill \frac{h}{p_2-p_3}\left(\lambda -p_3\right),& \hfill & \hfill \text{for}\lambda \in \left[p_2{p}_3\right],\\ \hfill 0,& \hfill & \hfill \text{otherwise,}\end{array}$

with h = K/(p₃ − p₁) and K > 0. The expected moments of C are obtained as follows:

$\left\{\begin{array}{cc}\hfill \mathbb{E}\left[{\mathcal{Q}}_1\left(C\right)\right]& =\frac{1}{3}\left(p_1+p_2+p_3\right),\hfill \\ \hfill \mathbb{E}\left[{\mathcal{Q}}_2\left(C\right)\right]& =\frac{1}{6}\left(p_1^2+p_2^2+p_3^2+p_1{p}_2+p_1{p}_3+p_2{p}_3\right),\hfill \\ \hfill \mathbb{E}\left[{\mathcal{Q}}_3\left(C\right)\right]& =\frac{1}{10}\left(p_1^3+p_1^2{p}_2+p_1^2{p}_3+p_2^3+p_2^2{p}_1\right.\hfill \\ \hfill & +\left.p_2^2{p}_3+p_3^3+p_3^2{p}_1+p_3^2{p}_2+p_1{p}_2{p}_3\right).\hfill \end{array}\right.(17)$

For simplicity, we use $\bar{\mathcal{Q}}$ to represent $\mathbb{E}[\mathcal{Q}(C)]$. The aim is to find a set of abscissas {p₁, p₂, p₃} so as to fit a given set of expected moments $\{{\bar{\mathcal{Q}}}_1,{\bar{\mathcal{Q}}}_2,{\bar{\mathcal{Q}}}_3\}$. Using the symmetries of the polynomials, the values of {p₁, p₂, p₃} can be determined as roots of the polynomial

$p^3-s_1{p}^2+s_{2}p-s_3=0,(18)$

with

$\left\{\begin{array}{c}{s}_1=3{\bar{\mathcal{Q}}}_1,\hfill \\ s_2=9{\bar{\mathcal{Q}}}_1^2-6{\bar{\mathcal{Q}}}_2,\hfill \\ s_3=27{\bar{\mathcal{Q}}}_1^3-36{\bar{\mathcal{Q}}}_1{\bar{\mathcal{Q}}}_2+10{\bar{\mathcal{Q}}}_3.\hfill \end{array}\right.(19)$

Example 3. We consider again a 17-node globally coupled network (as shown in Example 1) and a 200-node nearest-neighbor coupled network (as shown in Example 2), respectively. For the globally coupled network, the abscissas for the triangular function are p₁ = 1.4359, p₂ = 26.1860, and p₃ = 27.9311 with h = 20/(p₃ − p₁). For the nearest-neighbor coupled network, the abscissas for the triangular function are p₁ = 0.5547, p₂ = 14.3239, and p₃ = 24.6314 with h = 3/(p₃ − p₁). Figures 3, 4 show the eigenvalue histograms of C and triangular approximations for the globally coupled network and the nearest-neighbor coupled network, respectively. The ordinate μ(λ) denotes the percentage of the eigenvalue with a certain value in all eigenvalues. It can be seen from Figures 3, 4 that the triangular function can well fit the eigenvalue distribution of the matrix C.

FIGURE 3

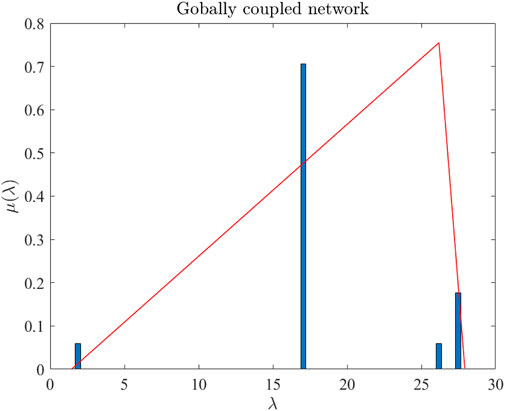
FIGURE 3. Eigenvalue histograms of C and its triangular approximations for a globally coupled network.

FIGURE 4

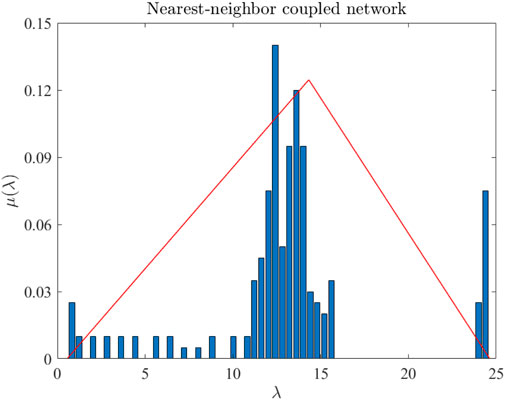
FIGURE 4. Eigenvalue histograms of C and its triangular approximations for a nearest-neighbor coupled network.

5 Numerical results

We consider the globally coupled network in Example 1 and set the Lü system as the node dynamics. When the node dynamics parameter a = 36 and the inner-coupling matrix is chosen as H_l3, it can be obtained from Table 1 that the corresponding synchronized region of the Lü system is (7.83, ∞). According to Example 3, ${\bar{\lambda }}_1=1.4359$ and ${\bar{\lambda }}_N=27.9311$ are good estimations of the lower and upper bounds of the eigenvalues, respectively. The 17-node globally coupled network of Lü systems can achieve synchronization if $\sigma \in (7.83/{\bar{\lambda }}_1,\infty )=(5.45,\infty )$. Figures 5A, B show the evolution of the node states with σ = 5∉(5.45, ∞) and σ = 6 ∈ (5.45, ∞), respectively. The numerical results are in good agreement with the theoretical results.

FIGURE 5

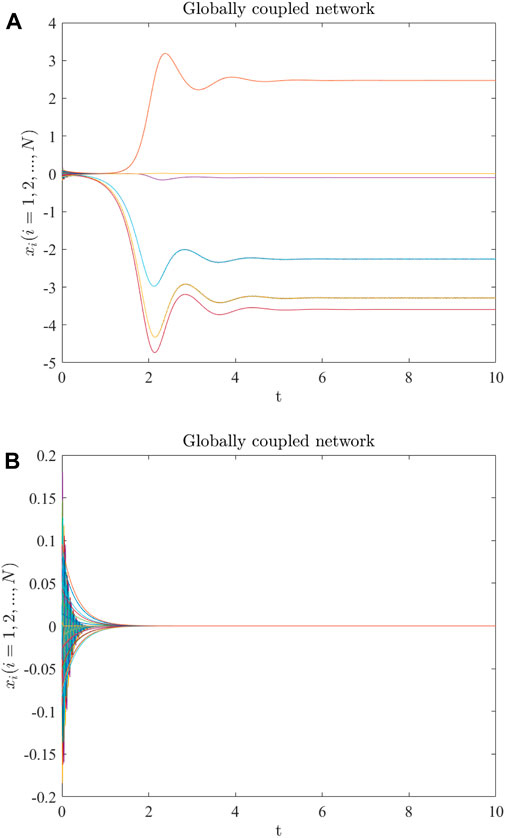
FIGURE 5. Evolution of the node states in a 17-node globally coupled network of Lü systems with (A) σ = 5; (B) σ = 6.

We consider the nearest-neighbor coupled network in Example 2 and set the unified chaotic system as the node dynamics. When the parameter a = 0.05 and the inner-coupling matrix is set as H_u3, it can be obtained from Table 2 that the corresponding synchronized region of the unified chaotic system is (11.64, ∞). From Example 3, ${\bar{\lambda }}_1=0.5547$ and ${\bar{\lambda }}_N=24.6314$ are the bound estimations of the eigenvalues. The nearest-neighbor coupled network of unified chaotic systems can achieve synchronization if $\sigma \in (11.64/{\bar{\lambda }}_1,\infty )=(20.98,\infty )$. Figures 6A, B show the evolution of the node states with σ = 15∉(20.98, ∞) and σ = 22 ∈ (20.98, ∞), respectively. The numerical simulations are in good agreement with the theoretical results.

FIGURE 6

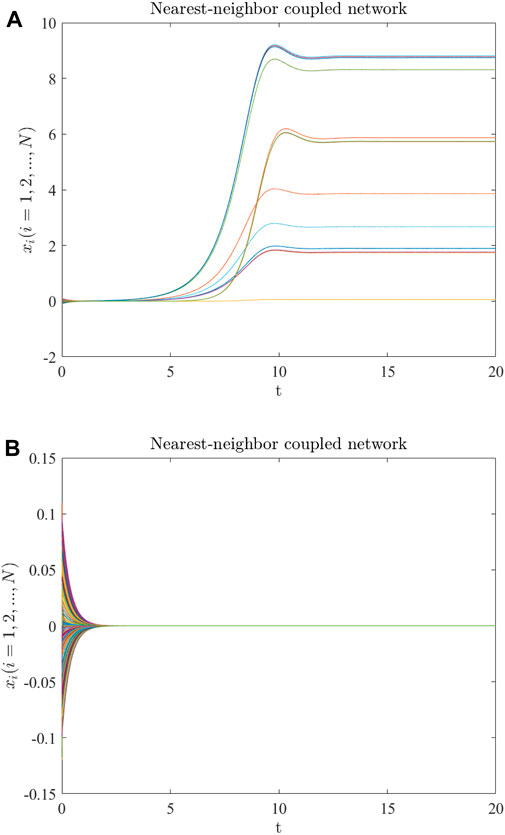
FIGURE 6. Evolution of the node states in a 200-node nearest-neighbor coupled network of unified chaotic systems with (A) σ = 15; (B) σ = 22.

6 Conclusion

In this paper, pinning synchronization of complex networks with sign inner-coupling configurations has been investigated. The bifurcation behavior of the synchronized regions has been observed, and the effect of sign inner-coupling configurations on network synchronizability has been studied in detail. It is shown that the synchronized region can evolve with the varying node dynamics parameter and switch from one type to another type. It is also found that the network synchronizability can be significantly improved by adding negative parameters in the inner-coupling matrix, while blindly adding inner-coupling elements with positive parameters may weaken it. The expected moments of C for the globally coupled network and nearest-neighbor coupled network have been derived. The shape of the eigenvalue distribution of C for each of the aforementioned regular networks can, thus, be estimated to predict pinning synchronization of the network.

It is worth noting that the obtained results in this paper can be generalized to handle control problems with directed topologies or switching topologies. However, directed topology implies that the network is not symmetric, and switching topology means that the network is time-varying. From a technical perspective, this introduces more challenges than its undirected and time-invariant counterpart. In the future, it will be interesting to study the higher-order moments of the matrix C and their corresponding fitting functions. Moreover, pinning synchronization of multiplex networks with time delays [57, 58], noise [59], and disturbances [60, 61] is more challenging but worthy of deep investigation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors designed and conducted the research. YY and LX performed the analytical and numerical calculations. YY, LX, BL, and CX were the lead writers of the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China (Nos. 61973064 and 62173355), Natural Science Foundation of Tianjin (No. 22JCZDJC00550), and Natural Science Found ation of Hebei Province of China (Nos. F2022501024 and F2019501126).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chen G. Pinning control of complex dynamical networks. IEEE Trans Consum Electron (2022) 68(4):336–43. doi:10.1109/tce.2022.3200488

CrossRef Full Text | Google Scholar

2. Chen G. Searching for best network topologies with optimal synchronizability: A brief review. IEEE/CAA J Autom Sin (2022) 9(4):573–7. doi:10.1109/jas.2022.105443

CrossRef Full Text | Google Scholar

3. Chen G. Pinning control and synchronization on complex dynamical networks. Int J Control Autom Syst (2014) 12:221–30. doi:10.1007/s12555-014-9001-2

CrossRef Full Text | Google Scholar

4. Tang Y, Jin X, Shi Y, Du W. Event-triggered attitude synchronization of multiple rigid body systems with velocity-free measurements. Automatica (2022) 143:110460. doi:10.1016/j.automatica.2022.110460

CrossRef Full Text | Google Scholar

5. Wu Y, Liu L, Hu J, Feng G. Adaptive antisynchronization of multilayer reaction-diffusion neural networks. IEEE Trans Neural Networks Learn Syst (2018) 29(4):807–18. doi:10.1109/tnnls.2017.2647811

CrossRef Full Text | Google Scholar

6. Pecora LM, Carroll TL. Master stability functions for synchronized coupled systems. Phys Rev Lett (1998) 80:2109–12. doi:10.1103/physrevlett.80.2109

CrossRef Full Text | Google Scholar

7. Wen G, Yu W, Hu G, Cao J, Yu X. Pinning synchronization of directed networks with switching topologies: A multiple lyapunov functions approach. IEEE Trans Neural Networks Learn Syst (2015) 26(12):3239–50. doi:10.1109/tnnls.2015.2443064

CrossRef Full Text | Google Scholar

8. Yu F, Shen H, Yu Q, Kong X, Kumar Sharma P, Cai S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans Netw Sci Eng (2023) 10(2):845–58. doi:10.1109/tnse.2022.3223930

CrossRef Full Text | Google Scholar

9. Yu F, Kong X, Mokbel AAM, Yao W, Cai S. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive Hopfield neural network with a novel local active memeristor. IEEE Trans Circuits Systems-II: Express Briefs (2023) 70(1):326–30. doi:10.1109/tcsii.2022.3218468

CrossRef Full Text | Google Scholar

10. Wan Q, Li F, Chen S, Yang Q. Symmetric multi-scroll attractors in magnetized Hopfield neural network under pulse controlled memristor and pulse current stimulation. Chaos, Solitons Fractals (2023) 169:113259. doi:10.1016/j.chaos.2023.113259

CrossRef Full Text | Google Scholar

11. Wang F, Ni Y, Liu Z, Chen Z. Containment control for general second-order multiagent systems with switched dynamics. IEEE Trans Cybern (2020) 50(2):550–60. doi:10.1109/tcyb.2018.2869706

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jiang Y, Wang F, Liu Z, Chen Z. Composite learning adaptive tracking control for full-state constrained multiagent systems without using the feasibility condition. IEEE Trans Neural Networks Learn Syst (2022) 1–13. doi:10.1109/tnnls.2022.3190286

CrossRef Full Text | Google Scholar

13. Xia C, Hu Z, Zhao D. Costly reputation building still promotes the collective trust within the networked population. New J Phys (2022) 24:083041. doi:10.1088/1367-2630/ac8898

CrossRef Full Text | Google Scholar

14. Li C, Feng B, Li S, Kurths J, Chen G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans Circuits Syst Regular Pap (2019) 66(6):2322–35. doi:10.1109/tcsi.2018.2888688

CrossRef Full Text | Google Scholar

15. Feng J, Zhang L, Wang J, Zhao Y. The synchronization of complex dynamical networks with discontinuous dynamics and exogenous disturbances. Asian J Control (2021) 23(6):2837–48. doi:10.1002/asjc.2414

CrossRef Full Text | Google Scholar

16. Liao H, Mariani MS, Medo M, Zhang Y-C, Zhou M-Y. Ranking in evolving complex networks. Phys Rep (2017) 689:1–54. doi:10.1016/j.physrep.2017.05.001

CrossRef Full Text | Google Scholar

17. Zhou M-Y, Zhuo Z, Liao H, Fu Z-Q, Cai S-M. Enhancing speed of pinning synchronizability: Low-degree nodes with high feedback gains. Sci Rep (2015) 5:17459. doi:10.1038/srep17459

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ruan X, Feng J, Xu C, Wang J, Zhao Y. Dynamic event-triggered pinning synchronization for switched impulsive complex networks with asynchronous switching. IEEE Trans Circuits Syst Express Briefs (2022) 69(4):2211–5. doi:10.1109/tcsii.2021.3123285

CrossRef Full Text | Google Scholar

19. Chen F, Chen J. Minimum-energy distributed consensus control of multi-agent systems: A network approximation approach. IEEE Trans Autom Control (2020) 65(3):1144–59. doi:10.1109/tac.2019.2917279

CrossRef Full Text | Google Scholar

20. Chen F, Feng G, Liu L, Ren W. Distributed average tracking of networked Euler-Lagrange systems. IEEE Trans Autom Control (2015) 60(2):547–52. doi:10.1109/tac.2014.2343111

CrossRef Full Text | Google Scholar

21. Wen G, Yu X, Yu W, Lü J. Coordination and control of complex network systems with switching topologies: A survey. IEEE Trans Syst Man, Cybern Syst (2021) 51(10):6342–57. doi:10.1109/tsmc.2019.2961753

CrossRef Full Text | Google Scholar

22. Chen K, He W, Han Q-L, Xue M, Tang Y. Leader selection in networks under switching topologies with antagonistic interactions. Automatica (2022) 142:110334. doi:10.1016/j.automatica.2022.110334

CrossRef Full Text | Google Scholar

23. Yi X, Yang T, Wu J, Johansson KH. Distributed event-triggered control for global consensus of multi-agent systems with input saturation. Automatica (2019) 100:1–9. doi:10.1016/j.automatica.2018.10.032

CrossRef Full Text | Google Scholar

24. Wang X, Chen G. Synchronization in scale-free dynamical networks: Robustness and fragility. IEEE Trans Circuits Syst Fundam Theor Appl (2002) 49(1):54–62. doi:10.1109/81.974874

CrossRef Full Text | Google Scholar

25. Barahona M, Pecora LM. Synchronization in small-world systems. Phys Rev Lett (2002) 89(5):054101. doi:10.1103/physrevlett.89.054101

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Li X, Wang X, Chen G. Pinning a complex dynamical network to its equilibrium. IEEE Trans Circuits Syst Regular Pap (2004) 51(10):2074–87. doi:10.1109/tcsi.2004.835655

CrossRef Full Text | Google Scholar

27. Wang X, Chen G. Pinning control of scale-free dynamical networks. Physica A: Stat Mech its Appl (2002) 310(3-4):521–31. doi:10.1016/s0378-4371(02)00772-0

CrossRef Full Text | Google Scholar

28. Moradi Amani A, Jalili M, Yu X, Stone L. Finding the most influential nodes in pinning controllability of complex networks. IEEE Trans Circuits Syst Express Briefs (2017) 64(6):685–9. doi:10.1109/tcsii.2016.2601565

CrossRef Full Text | Google Scholar

29. Liu H, Xu X, Lu J-A, Chen G, Zeng Z. Optimizing pinning control of complex dynamical networks based on spectral properties of grounded Laplacian matrices. IEEE Trans Syst Man, Cybern Syst (2021) 51(2):786–96. doi:10.1109/tsmc.2018.2882620

CrossRef Full Text | Google Scholar

30. Shao S, Cao J, Hu Y, Liu X. Prespecified-time distributed synchronization of Lur’e networks with smooth controllers. Asian J Control (2022) 24(1):125–36. doi:10.1002/asjc.2422

CrossRef Full Text | Google Scholar

31. He S, Wang H, Yu W. Distributed fast finite-time tracking consensus of multi-agent systems with a dynamic leader. IEEE Trans Circuits Syst Express Briefs (2022) 69(4):2176–80. doi:10.1109/tcsii.2021.3125700

CrossRef Full Text | Google Scholar

32. Sun J, Bollt EM, Nishikawa T. Master stability functions for coupled nearly identical dynamical systems. EPL (2016) 85(6):60011. doi:10.1209/0295-5075/85/60011

CrossRef Full Text | Google Scholar

33. Zhou C, Kurths J. Noise-induced phase synchronization and synchronization transitions in Chaotic oscillators. Phys Rev Lett (2002) 88:230602. doi:10.1103/physrevlett.88.230602

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhu S, Zhou J, Yu X, Lu J-A. Bounded synchronization of heterogeneous complex dynamical networks: A unified approach. IEEE Trans Autom Control (2021) 66(4):1756–62. doi:10.1109/tac.2020.2995822

CrossRef Full Text | Google Scholar

35. Liu X, Ho D, Song Q, Xu W. Finite/fixed-time pinning synchronization of complex networks with stochastic disturbances. IEEE Trans Cybern (2019) 49(6):2398–403. doi:10.1109/tcyb.2018.2821119

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Li N, Wu X, Feng J, Xu Y, Lü J. Fixed-time synchronization of coupled neural networks with discontinuous activation and mismatched parameters. IEEE Trans Neural Networks Learn Syst (2021) 32(6):2470–82. doi:10.1109/tnnls.2020.3005945

CrossRef Full Text | Google Scholar

37. Xiang J, Chen G. On the V-stability of complex dynamical networks. Automatica (2007) 43(6):1049–57. doi:10.1016/j.automatica.2006.11.014

CrossRef Full Text | Google Scholar

38. Tang L, Wu X, Lü J, Lu J-A, D’Souza RM. Master stability functions for complete, intralayer, and interlayer synchronization in multiplex networks of coupled Rössler oscillators. Phys Rev E (2019) 99(1):012304. doi:10.1103/physreve.99.012304

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Tang L, Lu J-A, Lü J, Wu X. Bifurcation analysis of synchronized regions in complex dynamical networks with coupling delay. Int J Bifurcation Chaos (2014) 24(1):1450011. doi:10.1142/s0218127414500114

CrossRef Full Text | Google Scholar

40. Tang L, Wu X, Lü J, Lu J-A. Bifurcation behaviors of synchronized regions in logistic map networks with coupling delay. Chaos (2015) 25:033101. doi:10.1063/1.4913854

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Yao W, Wang C, Sun Y, Zhou C. Robust multimode function synchronization of memristive neural networks with parameter perturbations and time-varying delays. IEEE Trans Syst Man, Cybern Syst (2022) 52(1):260–74. doi:10.1109/tsmc.2020.2997930

CrossRef Full Text | Google Scholar

42. Ghosh D, Frasca M, Rizzo A, Majhi S, Rakshit S, Alfaro-Bittner K, et al. The synchronized dynamics of time-varying networks. Phys Rep (2022) 949:1–63. doi:10.1016/j.physrep.2021.10.006

CrossRef Full Text | Google Scholar

43. Wen G, Zheng W. On constructing multiple Lyapunov functions for tracking control of multiple agents with switching topologies. IEEE Trans Autom Control (2019) 64(9):3796–803. doi:10.1109/tac.2018.2885079

CrossRef Full Text | Google Scholar

44. Xiang L, Chen F, Chen G. Synchronized regions of pinned complex networks: Spectral analysis. Nonlinear Dyn (2014) 78(3):1609–28. doi:10.1007/s11071-014-1538-3

CrossRef Full Text | Google Scholar

45. Tang L, Lu J-A, Lü J, Yu X. Bifurcation analysis of synchronized regions in complex dynamical networks. Int J Bifurcation Chaos (2012) 22(11):1250282. doi:10.1142/s0218127412502823

CrossRef Full Text | Google Scholar

46. Preciado VM, Verghese GC. Low-order spectral analysis of the Kirchhoff matrix for a probabilistic graph with a prescribed expected degree sequence. IEEE Trans Circuits Syst Regular Pap (2009) 56(6):1231–40. doi:10.1109/tcsi.2009.2023758

CrossRef Full Text | Google Scholar

47. Preciado VM, Jadbabaie A, Verghese GC. Structural analysis of Laplacian spectral properties of large-Scale networks. IEEE Trans Autom Control (2013) 58(9):2338–43. doi:10.1109/tac.2013.2261187

CrossRef Full Text | Google Scholar

48. Preciado VM, Jadbabaie A. Moment-based spectral analysis of large-scale networks using local structural information. IEEE/ACM Trans Networking (2013) 21(2):373–82. doi:10.1109/tnet.2012.2217152

CrossRef Full Text | Google Scholar

49. Xiang L, Yu Y, Zhu J. Moment-based analysis of pinning synchronization in complex networks. Asian J Control (2022) 24(2):669–85. doi:10.1002/asjc.2590

CrossRef Full Text | Google Scholar

50. Yin J, Xiang L, Chen F. Pinning synchronization and optimization of complex networks with sign inner-coupling configurations. In: 13th IEEE International Conference on Control and Automation (ICCA). (2017).

CrossRef Full Text | Google Scholar

51. Nishikawa T, Motter AE. Network synchronization landscape reveals compensatory structures, quantization, and the positive effect of negative interactions. PNAS (2010) 107(23):10342–7. doi:10.1073/pnas.0912444107

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Zhu J, Xiang L, Yu Y, Chen F, Chen G. Average controllability of complex networks with Laplacian dynamics. IEEE Trans Circuits Syst Regular Pap (2022) 69(4):1704–14. doi:10.1109/tcsi.2021.3133650

CrossRef Full Text | Google Scholar

53. Xiang L, Chen G. Minimal edge controllability of directed networks. Adv Complex Syst (2019) 22(7 and 8):1950017. doi:10.1142/s0219525919500176

CrossRef Full Text | Google Scholar

54. Lü J, Chen G. A new chaotic attractor coined. Int J Bifurcation Chaos (2002) 12(3):659–61. doi:10.1142/s0218127402004620

CrossRef Full Text | Google Scholar

55. Lü J, Chen G, Cheng D, Celikovský S. Bridge the gap between the Lorenz system and the Chen system. Int J Bifurcation Chaos (2002) 12(12):2917–26. doi:10.1142/s021812740200631x

CrossRef Full Text | Google Scholar

56. Preciado VM. Spectral analysis for stochastic models of large-scale complex dynamical networks. Massachusetts Institute of Technology (2009).

Google Scholar

57. Liu S, Li C, Hu Q. Cryptanalyzing two image encryption algorithms based on a first-order time-delay system. IEEE MultiMedia (2022) 29(1):74–84. doi:10.1109/mmul.2021.3114589

CrossRef Full Text | Google Scholar

58. Wang D, Wang D, Wang W. Necessary and sufficient conditions for containment control of multi-agent systems with time delay. Automatica (2019) 103:418–23. doi:10.1016/j.automatica.2018.12.029

CrossRef Full Text | Google Scholar

59. Chen L, Wang Y, Ren W, Hou Z-G, Tan M. On convergence rate of leader-following consensus of linear multi-agent systems with communication noises. IEEE Trans Automatic Control (2016) 61(11):3586–92. doi:10.1109/tac.2016.2522647

CrossRef Full Text | Google Scholar

60. Ye M, Li D, Han Q-L, Ding L. Distributed Nash equilibrium seeking for general networked games with bounded disturbances. IEEE/CAA J Autom Sin (2022) 9.

Google Scholar

61. Sun H, Sun Q, Sun M, Tao J, Chen Z. Accurate modeling and homing control for parafoil delivery system based on wind disturbance rejection. IEEE Trans Aerospace Electron Syst (2022) 58(4):2916–34. doi:10.1109/taes.2022.3141033

CrossRef Full Text | Google Scholar