Controlling multiple returnings in non-sequential double ionization with orthogonal two-color laser pulses

With the three-dimensional semi-classical ensemble model, we studied the non-sequential double ionization by orthogonal two-color laser pulses. Our calculations show that the proportion of events experiencing multiple returnings, the sum of the final energies of two electrons, and the ion momentum distribution depend on the relative phase of the two-color fields, exhibiting oscillatory behavior with a period of π. Back analysis of these trajectories reveals that we can control the recollision energy of the electron by changing the relative phase of the two-color laser pulse. As a consequence, the trajectories of multiple-returning ions change with the relative phase, resulting in relative-phase-dependent ion momentum distributions. The result shows that the momentum distribution of the ions in the trajectories of multiple returnings is clearly wider than that for the case of single returning. For the multiple-returning events, the binary recollision leads to a smaller scattering angle of the first electron.

1 Introduction

It is well known that when in a strong laser field, two electrons in an atom may leave the parent nucleus, and the atom gets doubly ionized. For the ionization of two electrons in atoms and molecules in a strong laser field, the simplest and most direct physical picture is that the two electrons get ionized independently one after another; that is, the ionization of the first electron has no effect on the ionization of the second electron. This process is often called sequential double ionization [1, 2]. However, in 1992, Fittinghoff et al. accurately measured the ionization rate of He and found that when the laser intensity is not too high, the experimental double ionization yield shows a knee-like structure with varying laser intensity [3]. For different laser parameters and different targets, this knee-like structure is also observed, which is considered a feature of non-sequential double ionization [4–7]. This kind of double ionization, which is contrary to the theory of sequential ionization and reflects electronic correlation, is called non-sequential double ionization (NSDI). The strong-field NSDI provides a simple and clear model for studying the effect of electron correlation [8, 9]. The study of the strong-field NSDI enables us to deeply understand electron correlation and gain insight into the essence of many physical phenomena [10–15]. Therefore, the strong-field NSDI has become one of the research hot spots in strong-field physics.

Later, experimental and theoretical studies showed that the recollision model was in good agreement with the experiment [16]. In addition, it was widely recognized that the strong-field NSDI occurs mainly through two different pathways: recollision impact ionization (RII) and recollision excitation with subsequent field ionization (RESI) [17]. Cold target recoil ion momentum spectroscopy (COLTRIMS) [18, 19], combined with recent progress in laser development, succeeded in measuring three-dimensional momentum distributions of multiple electrons and ions simultaneously. From the momentum spectrum, we can obtain more information about the detailed ultrafast dynamics in the NSDI [20–22]. Staudte et al. accurately measured the NSDI of helium atoms [23]. With an intensity just slightly higher than the threshold of collision ionization, they observed a finger-like structure that had not been found before on the measured correlated electron momentum spectrum. Through a classical kinematics analysis, they suggested that this structure reflects two different collision mechanisms: recoil collision and binary collision. In the recoil collision, the incoming electrons are backscattered after the collision, and the scattering angle is close to 180°, which may produce electrons with energy greater than 2Up (Up ∝Iλ² is the ponderomotive energy [16]). For the two-body collision, the direction of the incoming electron is almost unchanged after the collision; that is, the scattering angle is around 0°, and the energy of the photoelectron generated by this mechanism will always be less than 2Up. Further research found that the Coulomb attraction of the nucleus to electrons and the Coulomb repulsion between the two electrons after ionization are also important reasons for the formation of finger-like structures [12, 24, 25]. In later research, it was found that there were multiple recollisions and multiple returns in NSDI generally [26–30]. At low laser intensity, Liu et al. found multiple recollisions leading to back-to-back emission of the electrons and a significant cutoff in the sum-energy spectra [26].^.Ye et al. discussed that multiple recollisions strongly enhance the energy exchange between two electrons [27]. In an experiment with doubly ionized Xe with mid-IR fields, Wolter et al. found several small peak structures in the electron momentum spectrum, which indicated that electrons undergo multiple recollisions during double ionization [31]. Later, we found that the various multiple-returning recollision trajectories correspond to different windows of the initial transverse velocity [29]. In these multiple-returning recollision processes, the Coulomb focusing effect plays an important role. It can be said that multiple returnings play an important role in NSDI. The electron dynamics of multiple-returning recollision in the NSDI by a multi-cycle orthogonal two-color laser field had not been investigated before.

In this paper, we theoretically study the correlated electron dynamics in strong-field NSDI of Ar with a two-color laser pulse consisting of a strong 800 nm field and a weak orthogonal-polarized 400 nm field. We focus on the single-returning and multiple-returning processes in NSDI using a semi-classical ensemble model. Results show that the process of multiple-returning recollision can be controlled by changing the relative phase of the two-color fields. Back analysis of the NSDI trajectories shows that lower return energy causes the first electron to collide after multiple returnings. Then, the binary collision causes the electron to scatter at a small angle after the collision; thus, the momentum direction of the first electron is unchanged. The final ion momentum distribution is wide.

2 Theoretical model

Among many theoretical research methods for describing double ionization in strong fields, solving the time-dependent Schrodinger equation is undoubtedly the most accurate [32–36]. However, for multi-electron systems, the computational requirement of this method is huge [21, 37, 38]. In the past decades, the classical and semi-classical ensemble models have been well established [39–44]. Compared with solving the Schrödinger equation, the classical and semi-classical ensemble models have some advantages: the amount of corresponding computation is much less; they can be used to reproduce the basic dynamic characteristics of the quantized two-electron system; and the double-ionization track of any atom at any time can be obtained by backward analysis. It has been proven that these models are reliable tools for investigating electron dynamics in strong-field double ionization [45–47]. Thus, in this paper, we employ the two-dimensional semi-classical ensemble model to study the electron dynamics of the NSDI using two-color pulses.

In this semi-classical ensemble model, the process of NSDI is divided into two steps. The first step is the ionization of the first electron, which is described by the tunneling ionization theory [48]. The second step is the classical motion of two electrons; that is, the first ionized electron and the second electron in the bound state are both regarded as classically charged particles that move under the joint action of the laser field and Coulomb field. The motion of electrons is determined by the following equation (atomic units are used throughout until stated otherwise):

$\frac{d^2{\mathbf{r}}_i}{d{t}^2}=-\nabla \left[V_{ne}\left({\mathbf{r}}_i\right)+V_{ee}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\right]-\mathbf{E}\left(t\right),(1)$

where the subscript i = 1,2 is the label of the two electrons and E(t) is the electric field. The electric field of the orthogonal two-color pulse is written as

$\mathbf{E}\left(t\right)=f\left(t\right)\left[E_x\left(t\right)\widehat{x}+E_y\left(t\right)\widehat{y}\right],(2)$

where $\widehat{x}$ and $\widehat{y}$ are the polarization vectors. The pulse envelope f(t) has a constant amplitude for the first eight cycles and is linearly turned off with a two-cycle ramp of the 800 nm field. $E_x\left(t\right)=E_{x0}\cos \left(wt\right)$ and $E_y\left(t\right)=E_{y0}\cos \left(2wt+\Delta \mathrm{\varphi }\right)$, where Δϕ is the relative phase between the 400 nm and 800 nm fields. w is the frequency of the 800 nm laser field. Ex0 and Ey0 are the amplitudes of the 800 nm and 400 nm fields, respectively. $V_{ne}\left({\mathit{r}}_i\right)=-2/\sqrt{{{\mathit{r}}_i}^2+a^2}$ and $V_{ee}\left({\mathit{r}}_1,{\mathit{r}}_2\right)=1/\sqrt{{\left({\mathit{r}}_1-{\mathit{r}}_2\right)}^2+b^2}$ represent the ion-electron and electron-electron interaction potentials, respectively. Here, we set a = 1.5 to avoid auto-ionization [24]. The parameter b in the electron–electron interaction potential is not important as long as it is sufficiently small. In this paper, the intensity of the 800 nm field is set to be 4.0 × 10¹⁴ W/cm². The intensity ratio of the 800 nm to 400 nm fields is 40.

The initial state of the first electron is determined by the tunneling ionization theory, and the weight of each track is determined by $w\left(t_0,v_{\perp 0}^i\right)=w\left(t_0\right)w\left(v_{\perp 0}\right)$ [49], in which

$w\left(t_0\right)={\left[\frac{2{\left(2{\mathrm{I}}_{\mathrm{p}1}\right)}^{1/2}}{\left|\mathbf{E}\left(t_0\right)\right|}\right]}^{\frac{2}{\sqrt{2{\mathrm{I}}_{p1}}}-1}\exp \left[\frac{-2{\left(2{\mathrm{I}}_{p1}\right)}^{3/2}}{3\left|\mathbf{E}\left(t_0\right)\right|}\right],(3)$

$w\left(v_{\perp 0}\right)=\frac{1}{\left|\mathbf{E}\left(t_0\right)\right|}\exp \left[-\frac{{\mathrm{v}}_{\perp 0}^2{\left(2{\mathrm{I}}_{p1}\right)}^{1/2}}{\left|\mathbf{E}\left(t_0\right)\right|}\right],(4)$

where $w\left(t_0\right)$ represents the instantaneous tunneling probability in the quasistatic approximation and $w\left(v_{\perp 0}\right)$ is the distribution of initial transverse velocity $v_{\perp 0}$. I_p1 = −0.58 a.u. is the negative ionization potential of the first electron.

The initial distribution of the second electron is the regular ensemble distribution of the ground state for Ar⁺. After the laser field, we analyze the energy of two electrons in every trajectory. If the energy of both electrons is greater than zero, the corresponding atom is considered to have undergone double ionization.

Here, the first electron is defined as the ionized and returned electron. Recollision is defined when this distance is less than 3.0 a.u. after the tunneling of the first electron. The recollision time is defined as the instant of the closest approach of the two electrons, and the double ionization time is defined as the instant when both electrons achieve positive energies. In our calculations, for almost all of the double ionization events, the closest distance is less than 2.5 a.u., meaning that double ionization occurs through the recollision. We have checked that a small change in this criterion does not influence the final results.

3 Results and discussion

Figure 1A shows the relative yields of Ar²⁺ as a function of the relative phase of the two-color laser pulse. It shows that the ratio of Ar²⁺ exhibits an oscillating behavior with a period of π. It indicates that NSDI has indeed been controlled by the orthogonal two-color laser fields. The distribution shows that the ratio is minimum for about Δϕ = 0.4π and 1.4π and maximum for about Δϕ = 0.9π and 1.9π. In Figure 1B, we can see that the proportion of events experiencing single returning (blue triangles) and multiple returnings (yellow circles) in all double-ionization events also experiences oscillation changes with a period of π, but they are in the opposite trend. The proportion of events experiencing single returning is higher for about Δϕ = 0.6π and 1.6π, but the proportion of events experiencing multiple returnings is higher for about Δϕ = 0.1π and 1.1π.

FIGURE 1

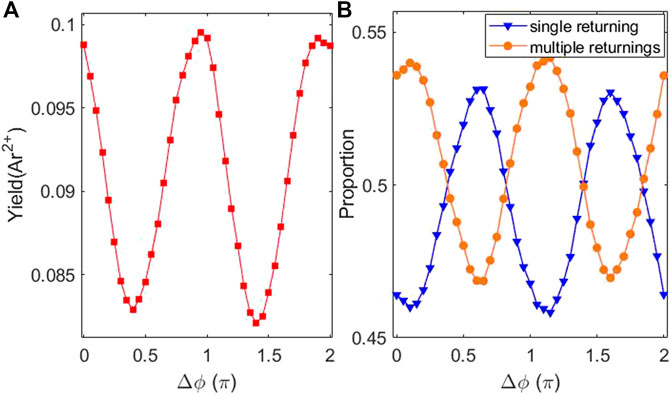
FIGURE 1. (A) Relative yields of Ar²⁺ as a function of the relative phase of the two-color laser pulse. (B) The proportion of events experiencing single returning (blue triangles) and multiple returnings (yellow circles) in all double-ionization events as a function of the relative phase of the two-color laser pulse.

Figures 2A,B show the sum of the final energies of two electrons and the ion momentum distribution along the 800 nm laser polarization direction after recollision. In Figure 2A, the sum of the energies of two electrons exhibits an oscillating behavior with a period of π. For near Δϕ = 0.1π and 1.1π, the energy distribution exhibits a peak located at 0.5 a.u. For near Δϕ = 0.6π and 1.6π, the energy distribution extends to about 1.5 a.u. We show the momentum distribution of the ion along the 800 nm laser polarization direction as a function of the relative phase in Figure 2B. The distribution also oscillates with the relative phase, with a period of π. For about Δϕ = 0.6π and 1.6π, the momentum distribution exhibits a narrow structure around 0 a.u. However, for about Δϕ = 0.1π and 1.1π, the distribution exhibits a wide structure.

FIGURE 2

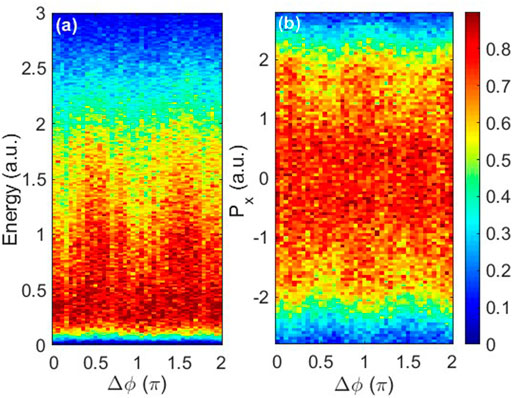
FIGURE 2. Distributions of the sum of the final energies of two electrons (A) and ion momentum distribution along the 800 nm laser polarization direction (B) as a function of the relative phase of the two-color laser pulse.

In order to reveal the corresponding dynamics of electrons in the two-color fields, we back-trace the classical trajectories and perform statistical analysis. Figure 3 shows the distributions of the energy of the bound electron versus the recolliding electron at time 0.02 T₁ after recollision at the relative phases Δϕ = 0.6π (Figures 3A–C) and 1.1π (Figures 3B, D). The first line of pictures represents the trajectories of recollision occurring at the first returning, and the second line of pictures represents the trajectories of recollision occurring at later returnings. Here, the energy of each electron is defined to contain the kinetic energy, the potential energy of the electron-ion interaction, and half electron–electron potential energy. Figure 3 shows that the distributions are away from the main diagonal, indicating asymmetric energy sharing during recollision. Especially for the trajectories of single-returning recollision (Figures 3A B), after recollision, the first electron possesses most of the returning energy. The extremely unequal energy sharing leads to a recoil collision between the two electrons [23]. Relatively speaking, for trajectories of multiple returnings (Figures 3C,D), the asymmetry of energy sharing is weaker, so binary collision makes a major contribution to double ionization.

FIGURE 3

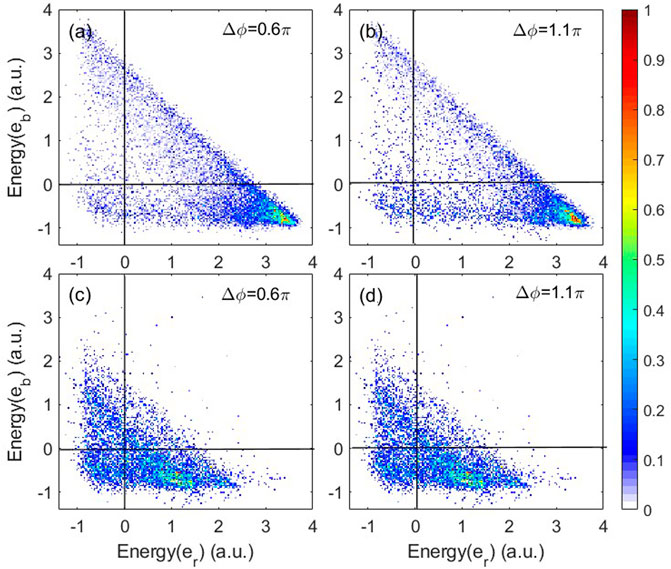
FIGURE 3. Distributions of the energy of the bound electron versus the recolliding electron at time 0.02 T₁ after recollision at the relative phases Δϕ = 0.6π[(A), (C)] and 1.1π[(B), (D)]. (A, B); (C, D) The events that recollision occurs at the first returning and later returning, respectively.

More information on the ionization dynamics can be obtained from the distributions of the traveling time, the recollision energy of the first electron, and the sum of the energy of two electrons after recollision as a function of the relative phase of the two-color laser pulse in Figures 4A–C. The traveling time is the time difference between recollision and tunneling of the first electron. Here, it should be noted that we only consider the NSDI events where tunneling of the first electron occurs within the optical cycle of −1.0T₁ to 0T₁ (T₁ is the laser cycle of the 800 nm field), and we find almost all of the events occur through RII (the delay time is less than 0.15T₁). Clearly, the positions of these distributions change gradually with the relative phases. For example, the window in Figure 4A located from 0.6T₁ to 0.8T₁ moves from 0.45T₁ to 0.75T₁ as Δϕ changes from 0π to 0.5π. It means that the traveling time of the first electron has been controlled with attosecond accuracy by the two-color fields. The traveling time distribution shows that for most of the events, the first electron returns to the nucleus within 0.75T₁, indicating recollision occurs at the first returning of the first electron. The other population is at about 1.2T₁ and 1.85T₁, corresponding to the events where recollision occurs at the second and third returnings, respectively. Events of the multiple returnings are rarely distributed for about Δϕ = 0.6π and 1.6π, which is in good agreement with Figure 1B. This means that with the orthogonal two-color pulses, electron trajectories with multiple returnings can be regulated and controlled to make contributions to double ionization; Figure 4B shows that the recollision energy of the first electron exhibits a stronger peak located at about 2.7 a.u. and two weak peaks located at 1.95 a.u. and 1.1 a.u., respectively. In consideration of the fact that second ionization potential of Ar is −1.01 a.u. and the sum of the first and second ionization potentials is −1.59 a.u., we can deduce that the events corresponding to the two weak peaks of the recollision energy occur through many times of returning. The energy transmitted during the first returning is not high enough to induce the ionization of the second electron. According to the recollision model, the returning electron possesses the highest energy at the first return and the second (third) highest energy at the third (fifth) return [50]. Thus, for the multiple-return trajectory, the first electron needs the second or even the third return to transfer enough energy to cause ionization of the second electron. This is more clearly seen in the sum of the energies of two electrons after recollision, as shown in Figure 4C. For most of the events, recollision occurs at the first returning, and the corresponding energy distribution is located at about 2.3 a.u. For the multiple-returning recollision event, the sum of energy decreases to 0.35 a.u. at the relative phase change between 0 and 0.4π, 0.8π and 1.4π, or 0.8π and 2.0π. This is the phase range where multiple returning trajectories make less contribution, indicating the control of the multiple-returning recollision by the two-color fields. As a consequence, the relative yield of Ar²⁺ is higher when the relative phase is within these ranges, which is consistent with Figure 1.

FIGURE 4

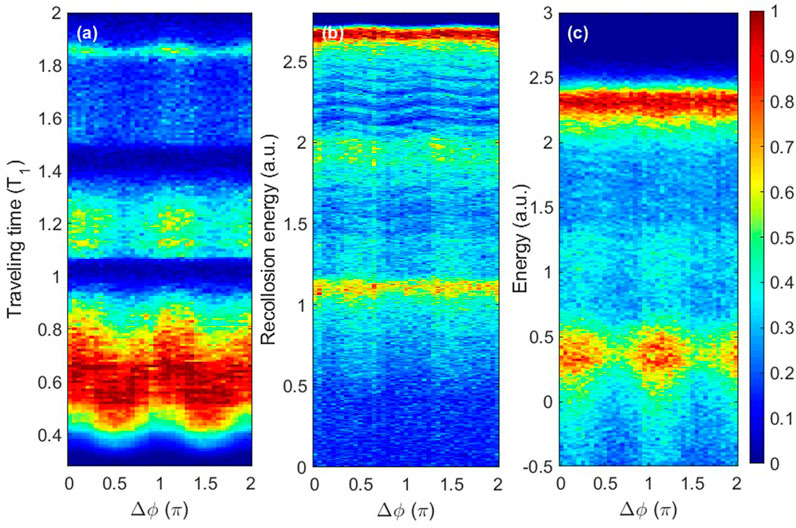
FIGURE 4. (A, B) Distributions of the traveling time and the recollision energy of the first electron as a function of the relative phase. (C) The sum of the energies of two electrons after recollision as a function of the relative phase of the two-color laser pulse.

Figures 5A–D show the momentum distributions of the ion as a function of the relative phase. We can see that the momentum of Ar²⁺ along the polarization direction of the 800 nm field oscillates with a period of π with the relative phase of the orthogonal two-color field changing, and the width along the 400 nm direction is constant with the relative phase, which is qualitatively consistent with the experimental results [51]. In Figures 5A,C, we show the NSDI events where recollision occurs through only one returning along the 800 nm laser polarization direction and 400 nm laser polarization direction, respectively. In contrast; Figures 5B,D show the NSDI events that occur through multiple-returning recollision along the 800 nm and 400 nm laser polarization directions, respectively. The distribution of the ion momentum in the single-returning recollision case is narrower than in the multiple-returning recollision case. Combined with Figures 4B,C, it can be easily deduced that for a single-returning recollision case, higher return energy leads to stronger recollision; thus, the energy sharing between two electrons is unequal at the instant of recollision. This is consistent with the recoil collision scenario. However, for the multiple-returning recollision case, lower return energy causes the momentum direction of the first electron to remain unchanged before and after the collision, which corresponds to the binary collision scenario. The binary collision scenario leads to a broad momentum distribution of Ar²⁺ [23], which is shown in Figure 5B.

FIGURE 5

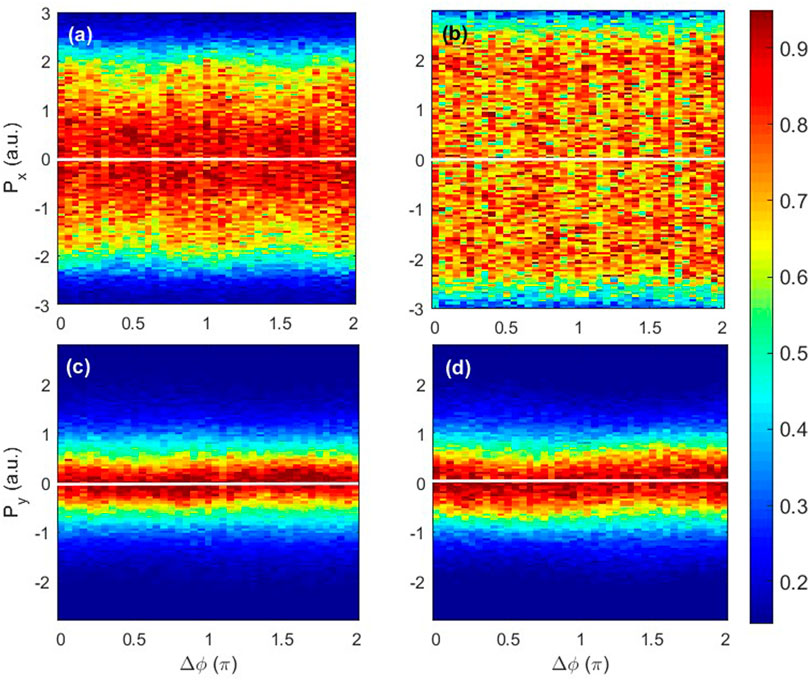
FIGURE 5. (A, B) Momentum distribution of Ar²⁺ along the polarization direction of the 800 nm field as a function of the relative phase of the two-color laser pulse. (C, D) Momentum distribution of Ar²⁺ along the polarization direction of the 400 nm field as a function of the relative phase of the two-color laser pulse. The events in the left column and the right column correspond to the blue triangles and yellow circles in Figure 1B, respectively. The white lines show zero value of momentum.

In Figure 6 we show two representative trajectories to provide an intuitive picture of the recollision process of NSDI in the orthogonal two-color laser fields. The trajectories in Figure 6A–C show that the first electron collides and ionizes at the first returning to the nucleus. After recollision, the direction of the momentum of the first electron changes compared with the direction before the recollision in Figure 6A, which means that the first electron is backscattered by recoil collision. In Figures 6D–F, the first electron experiences three times of returning before recollision. Figure 6F shows the first electron was in an excited state after collision for about 0.13T₁ before ionization, which means the recollision energy is low, resulting in a weak collision, and the scattering angle of the first electron is very small.

FIGURE 6

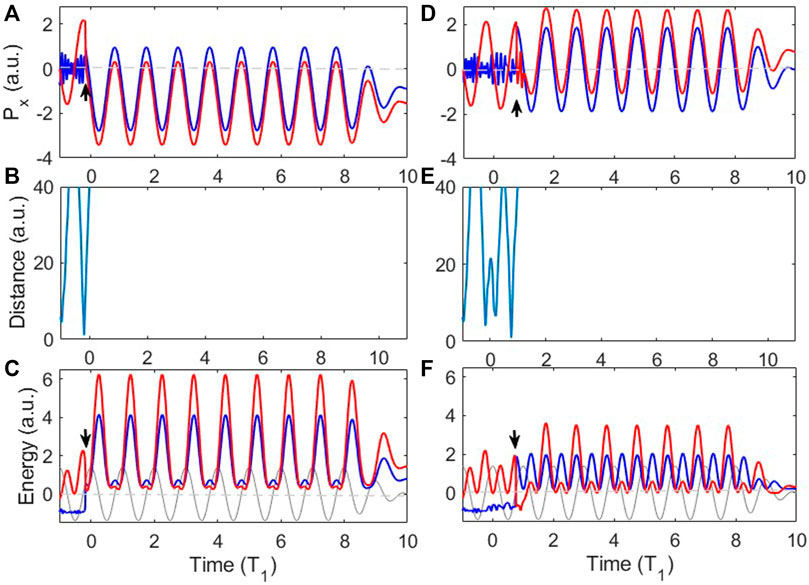
FIGURE 6. Two representative NSDI trajectories of single return and multiple returns (A–C); (D–F). (A, D) Time evolution of the momenta of the two electrons along the 800 nm laser polarization direction. (B, E) Time evolution of the distance between each electron. (C, F) Time evolution of the energies of the two electrons. The solid gray curves show the electric field of the 800 nm laser pulse. In (A), (D), (C), and (F), the black arrows indicate the instant of recollision.

4 Conclusion

In conclusion, we have theoretically studied the correlated electron dynamics in the orthogonal two-color laser fields. Our calculations show that the momentum distributions of Ar²⁺ in the direction parallel to the 800 nm polarization of the laser field exhibit a narrow or wide structure, depending on the relative phase of the two-color fields. The recollision energy of the first electron is accurately controlled with the two-color fields. Back analysis of the NSDI trajectories reveals that before recollision, the first electron with different recollision energies experiences single returning or multiple returnings, which can be controlled by changing the relative phase of the two-color field. Thus, trajectories of single or multiple returnings lead to a recoil collision or binary collision between two electrons, respectively, resulting in relative-phase-dependent ion momentum distributions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XM conceived the idea, conducted the simulations, and wrote the manuscript. Data were analyzed by XZ and AT. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (Grants No. 11904269), the Natural Science Foundation of Hubei Province under Grant No. 2021CFB300, the Scientific Research Program of the Hubei Provincial Department of Education under Grant No. B2020176, and the 2022nd talent introduction research start-up fund project of Hubei University of Education under Grant No. 27.

Acknowledgments

The authors thank Profs. Yueming Zhou and Min Li for the helpful discussion.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fleischer A, Worner HJ, Arissian L, Liu LR, Meckel M, Rippert A, et al. Probing angular correlations in sequential double ionization. Phys Rev Lett (2011) 107(11):113003. doi:10.1103/PhysRevLett.107.113003

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Shvetsov-Shilovski NI, Sayler AM, Rathje T, Paulus GG. Momentum distributions of sequential ionization generated by an intense laser pulse. Phys Rev A (2011) 83(3):033401. doi:10.1103/physreva.83.033401

CrossRef Full Text | Google Scholar

3. Fittinghoff DN, Bolton PR, Chang B, Kulander KC. Observation of nonsequential double ionization of helium with optical tunneling. Phys Rev Lett (1992) 69:2642–5. doi:10.1103/PhysRevLett.69.2642

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Walker B, Sheehy B, DiMauro LF, Agostini P, Schafer KJ, Kulander KC. Precision measurement of strong field double ionization of helium. Phys Rev Lett (1994) 73(9):1227–30. doi:10.1103/PhysRevLett.73.1227

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Talebpour A, Chien CY, Liang Y, Larochelle S, Cin SL, Chin SL. Non-sequential ionization of Xe and Kr in an intense femtosecond Ti:sapphire laser pulse. J Phys B: Mol Opt Phys (1997) 30(7):1721–30. doi:10.1088/0953-4075/30/7/010

CrossRef Full Text | Google Scholar

6. Guo C, Li M, Nibarger JP, Gibson GN. Single and double ionization of diatomic molecules in strong laser fields. Phys Rev A (1998) 58(6):R4271–4. doi:10.1103/physreva.58.r4271

CrossRef Full Text | Google Scholar

7. Cornaggia C, Hering P. Nonsequential double ionization of small molecules induced by a femtosecond laser field. Phys Rev A (2000) 62(2):023403. doi:10.1103/PhysRevA.62.023403

CrossRef Full Text | Google Scholar

8. Weber T, Giessen H, Weckenbrock M, Urbasch G, Staudte A, Spielberger L, et al. Correlated electron emission in multiphoton double ionization. Nature (2000) 405(6788):658–61. doi:10.1038/35015033

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Haan SL, Smith ZS, Shomsky KN, Plantinga PW. Anticorrelated electrons from weak recollisions in nonsequential double ionization. J Phys B: Mol Opt Phys (2008) 41(21):211002. doi:10.1088/0953-4075/41/21/211002

CrossRef Full Text | Google Scholar

10. Liu X, Rottke H, Eremina E, Sandner W, Goulielmakis E, Keeffe KO, et al. Nonsequential double ionization at the single-optical-cycle limit. Phys Rev Lett (2004) 93(26):263001. doi:10.1103/PhysRevLett.93.263001

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Rudenko A, de Jesus VLB, Ergler T, Zrost K, Feuerstein B, Schröter CD, et al. Correlated two-electron momentum spectra for strong-field nonsequential double ionization of He at 800 nm. Phys Rev Lett (2007) 99(26):263003. doi:10.1103/PhysRevLett.99.263003

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Chen Z, Liang Y, Lin CD. Quantum Theory of Recollisional (e, 2e) Process in Strong Field Nonsequential Double Ionization of Helium. Phys Rev Lett (2010) 104(25):253201. doi:10.1103/PhysRevLett.104.253201

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhou Y, Liao Q, Lu P. Asymmetric electron energy sharing in strong-field double ionization of helium. Phys Rev A (2010) 82(5):053402. doi:10.1103/PhysRevA.82.053402

CrossRef Full Text | Google Scholar

14. Huang C, Zhou Y, Zhang Q, Lu P. Contribution of recollision ionization to the cross-shaped structure in nonsequential double ionization. Opt Express (2013) 21(9):11382–90. doi:10.1364/OE.21.011382

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ma X, Tong A, Wang Z, Zhai C. Multiple recollisions in nonsequential double ionization below the recollision-ionization threshold. Chin Phys B (2021) 30(12):123402. doi:10.1088/1674-1056/ac2d1e

CrossRef Full Text | Google Scholar

16. Corkum PB. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71(13):1994–7. doi:10.1103/PhysRevLett.71.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Feuerstein B, Moshammer R, Fischer D, Dorn A, Schröter CD, Deipenwisch J, et al. Separation of recollision mechanisms in nonsequential strong field double ionization of Ar: The role of excitation tunneling. Phys Rev Lett (2001) 87(4):043003. doi:10.1103/PhysRevLett.87.043003

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Dörner R, Mergel V, Jagutzki O, Spielberger L, Ullrich J, Moshammer R, et al. Cold target recoil ion momentum spectroscopy: A ‘momentum microscope’ to view atomic collision dynamics. Phys Rep (2000) 330:95–192. doi:10.1016/S0370-1573(99)00109-X

CrossRef Full Text | Google Scholar

19. Ullrich J, Schmidt-Bocking H, Moshammer R, Dorn A, Dorner R, Schmidt LSH. Recoil-ion and electron momentum spectroscopy: Reaction-microscopes. Rep Prog Phys (2003) 66(9):1463–545. doi:10.1088/0034-4885/66/9/203

CrossRef Full Text | Google Scholar

20. Ho PJ, Eberly JH. Different rescattering trajectories related to different total electron momenta in nonsequential double ionization. Opt Express (2003) 11(22):2826–31. doi:10.1364/OE.11.002826

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Liao Q, Lu P, Zhang Q, Hong W, Yang Z. Phase-dependent nonsequential double ionization by few-cycle laser pulses. J Phys B: At Mol Opt Phys (2008) 41(12):125601. doi:10.1088/0953-4075/41/12/125601

CrossRef Full Text | Google Scholar

22. Hao XL, Qi Wang G, Jia XY, Li WD, Liu J, Chen J. Nonsequential double ionization of Ne in an elliptically polarized intense laser field. Phys Rev A (2009) 80(2):023408. doi:10.1103/PhysRevA.80.023408

CrossRef Full Text | Google Scholar

23. Staudte A, Ruiz C, Schöffler M, Schössler S, Zeidler D, Weber T, et al. Binary and recoil collisions in strong field double ionization of helium. Phys Rev Lett (2007) 99(26):263002. doi:10.1103/PhysRevLett.99.263002

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Haan SL, Van Dyke JS, Smith ZS. Recollision excitation, electron correlation, and the production of high-momentum electrons in double ionization. Phys Rev Lett (2008) 101(11):113001. doi:10.1103/PhysRevLett.101.113001

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ye DF, Liu X, Liu J. Classical trajectory diagnosis of a fingerlike pattern in the correlated electron momentum distribution in strong field double ionization of helium. Phys Rev Lett (2008) 101(23):233003. doi:10.1103/PhysRevLett.101.233003

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Liu Y, Tschuch S, Rudenko A, Dürr M, Siegel M, Morgner U, et al. Strong-field double ionization of Ar below the recollision threshold. Phys Rev Lett (2008) 101(3):053001. doi:10.1103/PhysRevLett.101.053001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ye D, Li M, Fu L, Liu J, Gong Q, Liu Y, et al. Scaling laws of the two-electron sum-energy spectrum in strong-field double ionization. Phys Rev Lett (2015) 115(15):123001. doi:10.1103/PhysRevLett.115.123001

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ma X, Zhou Y, Lu P. Multiple recollisions in strong-field nonsequential double ionization. Phys Rev A (2016) 93:013425. doi:10.1103/PhysRevA.93.013425

CrossRef Full Text | Google Scholar

29. Ma X, Li M, Zhou Y, Lu P. Nonsequential double ionization of Xe by mid-infrared laser pulses. Opt Quant Electron (2017) 49:170. doi:10.1007/s11082-017-1002-y

CrossRef Full Text | Google Scholar

30. Xu T, Zhu Q, Chen J, Ben S, Zhang J, Liu X. Multiple recollisions in nonsequential double ionization by counter-rotating two-color circularly polarized laser fields. Opt Express (2018) 26(2):1645–54. doi:10.1364/OE.26.001645

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wolter B, Pullen MG, Baudisch M, Sclafani M, Hemmer M, Senftleben A, et al. Strong-field physics with Mid-IR fields. Phys Rev (2015) X:021034. doi:10.1103/PhysRevX.5.021034

CrossRef Full Text | Google Scholar

32. Smyth ES, Parker JS, Taylor KT. Numerical integration of the time-dependent Schrödinger equation for laser-driven helium. Comp Phys Commun (1998) 114:1–14. doi:10.1016/S0010-4655(98)00083-6

CrossRef Full Text | Google Scholar

33. Parker JS, Smyth ES, Taylor KT. Intense-field multiphoton ionization of helium. J Phys B: Mol Opt Phys (1998) 31(14):L571–8. doi:10.1088/0953-4075/31/14/001

CrossRef Full Text | Google Scholar

34. Parker JS, Doherty BJS, Taylor KT, Schultz KD, Blaga CI, DiMauro LF. High-energy cutoff in the spectrum of strong-field nonsequential double ionization. Phys Rev Lett (2006) 96(13):133001. doi:10.1103/PhysRevLett.96.133001

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Hu S. Boosting photoabsorption by attosecond control of electron correlation. Phys Rev Lett (2013) 111(12):123003. doi:10.1103/PhysRevLett.111.123003

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Liu A, Thumm U. Laser-assisted XUV few-photon double ionization of helium: Joint angular distributions. Phys. Rev. A (2014) 89(6):063423. doi:10.1103/PhysRevA.89.063423

CrossRef Full Text | Google Scholar

37. Lein M, Gross EKU, Engel V. Intense-field double ionization of helium: Identifying the mechanism. Phys Rev Lett (2000) 85(22):4707–10. doi:10.1103/PhysRevLett.85.4707

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Prauzner-Bechcicki JS, Sacha K, Eckhardt B, Zakrzewski J. Time-resolved quantum dynamics of double ionization in strong laser fields. Phys Rev Lett (2007) 98(20):203002. doi:10.1103/PhysRevLett.98.203002

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Chen J, Liu J, Fu LB, Zheng WM. Interpretation of momentum distribution of recoil ions from laser-induced nonsequential double ionization by semiclassical rescattering model. Phys Rev A (2000) 63(1):011404. doi:10.1103/PhysRevA.63.011404

CrossRef Full Text | Google Scholar

40. Fu LB, Liu J, Chen J, Chen SG. Classical collisional trajectories as the source of strong-field double ionization of helium in the knee regime. Phys Rev A (2001) 63(4):043416. doi:10.1103/PhysRevA.63.043416

CrossRef Full Text | Google Scholar

41. Fu LB, Liu J, Chen SG. Correlated electron emission in laser-induced nonsequence double ionization of helium. Phys Rev A (2002) 65(2):021406. doi:10.1103/PhysRevA.65.021406

CrossRef Full Text | Google Scholar

42. Liu J, Ye DF, Chen J, Liu X. Complex dynamics of correlated electrons in molecular double ionization by an ultrashort intense laser pulse. Phys Rev Lett (2007) 99(1):013003. doi:10.1103/PhysRevLett.99.013003

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wang X, Eberly JH. Effects of elliptical polarization on strong-field short-pulse double ionization. Phys Rev Lett (2009) 103(10):103007. doi:10.1103/PhysRevLett.103.103007

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Tong A, Zhou Y, Lu P. Resolving subcycle electron emission in strong-field sequential double ionization. Opt Express (2015) 23(12):15774–83. doi:10.1364/OE.23.015774

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Ma X, Zhou Y, Chen Y, Li M, Li Y, Zhang Q, et al. Timing the release of the correlated electrons in strong-field nonsequential double ionization by circularly polarized two-color laser fields. Opt Express (2019) 27(3):1825–37. doi:10.1364/oe.27.001825

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Chen Z, Wang Y, Zhang L, Jia X. Revisiting the recollisional (e, 2e) process in strong-field nonsequential double ionization of helium. Phys Rev A (2019) 99:033401. doi:10.1103/PhysRevA.99.033401

CrossRef Full Text | Google Scholar

47. Tong A, Li Q, Ma X, Zhou Y, Lu P. Internal collision induced strong-field nonsequential double ionization in molecules. Opt Express (2019) 27(5):6415–25. doi:10.1364/OE.27.006415

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Ammosov MV, Delone NB, Krainov VP. Tunnel ionization of complex atoms and atomic ions in electromagnetic field. Zh Eksp Teor Fiz (1986) 91:2008–13. doi:10.1117/12.938695

CrossRef Full Text | Google Scholar

49. Delone NB, Krainov VP. Energy and angular electron spectra for the tunnel ionization of atoms by strong low-frequency radiation. J Opt Soc Am B (1991) 8(6):1207–11. doi:10.1364/JOSAB.8.001207

CrossRef Full Text | Google Scholar

50. Becker W, Grasbon F, Kopold R, Milosevic D, Paulus G, Walther H. Above-threshold ionization: From classical features to quantum effects. Adv Mol Opt Phys (2002) 48:35–98. doi:10.1016/S1049-250X(02)80006-4

CrossRef Full Text | Google Scholar

51. Zhang L, Xie X, Roither S, Zhou Y, Lu P, Kartashov D, et al. Subcycle control of electron-electron correlation in double ionization. Phys Rev Lett (2014) 112(19):193002. doi:10.1103/PhysRevLett.112.193002

PubMed Abstract | CrossRef Full Text | Google Scholar