A spin model for intrinsic antiferromagnetic skyrmions on a triangular lattice

Skyrmions are prospected as the potential future of data storage due to their topologically protected spin structures. However, traditional ferromagnetic (FM) skyrmions experience deflection when driven with an electric current, hindering their usage in spintronics. Antiferromagnetic (AFM) skyrmions, consisting of two FM solitons coupled antiferromagnetically, are predicted to have zero Magnus force, making them promising candidates for spintronic racetrack memories. Currently, they have been stabilized in synthetic AFM structures, i.e., multilayers hosting FM skyrmions, which couple antiferromagnetically through a non-magnetic spacer, while recent first-principle simulations predict their emergence in an intrinsic form, within a row-wise AFM single monolayer of Cr deposited on a PdFe bilayer grown on Ir (111) surfaces. The latter material forms a triangular lattice, where single and interlinked AFM skyrmions can be stabilized. Here, we explore the minimal Heisenberg model, enabling the occurrence of such AFM solitons and the underlying phase diagrams by accounting for the interplay between the Dzyaloshinskii–Moriya and Heisenberg exchange interactions, as well as the magnetic anisotropy and impact of the magnetic field. By providing the fundamental basis to identify and understand the behavior of intrinsic AFM skyrmions, we anticipate our model to become a powerful tool for exploring and designing new topological magnetic materials to conceptualize devices for AFM spintronics.

Introduction

Since their early observation [1–4], skyrmions, which are magnetic textures with unique properties, have garnered the attention of the condensed matter community. They are seen as potential bit representatives for future spintronic devices due to their nontrivial topological twists and exotic properties [5–21]. Skyrmion-based racetrack memory devices are expected to remarkably reduce the power consumption in data flow compared to domain walls [22, 23]. However, ferromagnetic (FM) skyrmions are afflicted with various drawbacks that limit their optimal utilization, such as their sensitivity to stray fields and suffering from dipolar interactions [24, 25], in addition to their complex response to applied currents leading to unwanted deflections [8, 26], which can become even more elaborated under the presence of defects [24, 26–29]. In contrast, antiferromagnetic (AFM) skyrmions have several advantages over their FM counterparts since the stray field cancels out [30, 31], augmented with an immunity to the Magnus force [32–37] with their potential for ultrafast dynamics [38] and ability to overcome defects [39, 40].

Several recent theoretical studies has inspected the realization of individual AFM skyrmions or their periodic arrangements assuming a squared [32, 33, 35, 37, 41], a triangular [42, 43], or a honeycomb lattice [36]. On the experimental side, synthetic AFM skyrmions were unveiled experimentally in multilayers, where FM films host regular FM skyrmions with an interfilm coupling of AFM nature through various spacers [44–48], while fractional antiferromagnetic skyrmion lattice was stabilized in MnSc₂S₄ [49, 50], and complex topological AFM objects were found in a bulk phase [51]. As proposed in Ref. [52], we predicted the emergence of intrinsic single and interchained AFM skyrmions on a triangular lattice of a row-wise AFM (RW-AFM) Cr layer deposited on PdFe/Ir (111). The latter substrate became, over the last decade, a perfect bed system for a plethora of phenomena pertaining to FM skyrmions [4, 11, 14, 15, 20, 53–58].

The goal of the current work is to introduce a Heisenberg model that incorporates the essential magnetic interactions required to produce AFM skyrmions on a triangular lattice. We perform atomistic spin simulations on the basis of the Landau–Lifschitz–Gilbert (LLG) equations as implemented in the Spirit code [59]. We consider the interplay between the exchange interactions, Dzyaloshinskii–Moriya interactions (DMI), the magnetic anisotropy, and the impact of an external magnetic field to establish the phase diagrams of the intrinsic AFM skyrmions while inspecting their stability via simulations based on the geodesic nudged elastic band (GNEB) method [59–61]. Our model offers a robust approach to comprehending the behavior of AFM skyrmions in a triangular lattice with the aim of understanding the required ingredients for their stabilization and to creating novel materials and devices for AFM spintronics.

Materials and methods

In our study, we consider a two-dimensional Heisenberg model on a triangular lattice, equipped with Heisenberg exchange coupling, DMI, magnetic anisotropy energy (MAE), and Zeeman term. The energy functional reads are as follows:

$H=-\sum _{<i,j>}{J}_{ij}{\mathbf{S}}_i\cdot {\mathbf{S}}_j-\sum _{<i,j>}{\mathbf{D}}_{ij}\cdot \left({\mathbf{S}}_i\times {\mathbf{S}}_j\right)-K\sum _i{\left(S_i^z\right)}^2-\sum _i{h}_i{S}_i^z,(1)$

where i and j are site indices, each carrying a magnetic moment. S is the unit vector of the magnetic moment. J is the Heisenberg exchange coupling strength, being negative for an AFM interaction, while D is the DMI vector, and K is the magnetic anisotropy energy per atom favoring an out-of-plane orientation if positive. h_i = μ_iB describes the Zeeman coupling to the atomic spin moment μ at site i, assuming μ = 1 μ_B and an out-of-plane field. To explore the magnetic properties and emerging complex states, we utilize the (LLG) equation as implemented in the Spirit code [59]. The simulations were carried out with 100², 200², and 300² sites, assuming periodic boundary conditions to model the extended two-dimensional Heisenberg Hamiltonian at 0 K.

Results

Phase diagrams

We start our investigations by determining the conditions to form an RW-AFM spin state, which was observed experimentally in Mn/Re (0001) [62, 63]. As established in Ref. [64, 65], the minimum set of Heisenberg exchange interactions involves the interactions with the first (J₁) and second (J₂) nearest neighboring interactions, as shown in the upper inset of Figure 1A. The formation of the FM skyrmions building up our AFM skyrmions requires, as demonstrated in Ref. [52], a third nearest neighboring interaction J₃, which should mediate a ferromagnetic coupling. Figure 1A illustrates the underlying phase diagram, where we expect four regions that can host either a Néel, FM, spin spiraling, or RW-AFM spin state. The dark blue color indicates the region of interest, where the magnetic moments are distributed into four sublattices, namely, L1, L2, L3, and L4, as shown in the lower inset of Figure 1A. J₃ mediates the magnetic interaction within each sublattice and must be positive, i.e., favoring an FM alignment, to enable the stabilization of the RW-AFM state. If too weak with respect to J₁ or if it is of AFM nature, either spin spirals or a Néel state is favored depending on the strength of J₂. We observe that the RW-AFM configuration occupies a larger phase area when J₂ is of AFM nature. In the RW-AFM state, J₃ is thus positive, which together with the DMI vector D₃, that is, connecting the third n.n. similarly to J₃, enables the formation of sublattice FM skyrmions. D₃ lies in-plane and is perpendicular to the bond connecting neighboring atoms, as shown in Supplementary Figure S1. The AFM interaction among the FM skyrmions is mediated by J₁ such that the presence of J₂ is not requested. As predicted in Ref. [52], the single AFM skyrmion consists of FM skyrmions that are present in two sublattices (L1 and L2) with the other two sublattices remaining collinear, while for the double AFM skyrmions, the building blocks of FM skyrmions reside in each of the four sublattices (L1, L2, L3, and L4), as illustrated in Figures 1B, C.

FIGURE 1

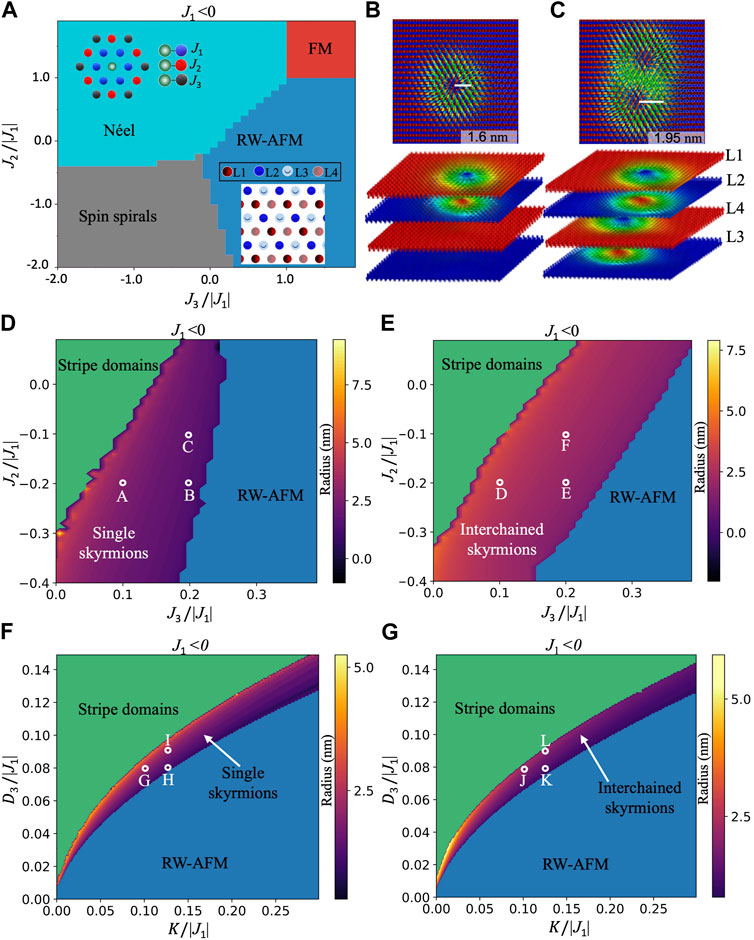
FIGURE 1. Phase diagrams for AFM skyrmions. (A) Phase diagram for the Heisenberg model of a triangular lattice without spin–orbit-induced interactions. The impact of magnetic interactions up to the third nearest neighbors is considered assuming an antiferromagnetic coupling J₁ among first nearest neighbors. The upper inset shows the triangular lattice indicating the considered magnetic exchange interactions, while the lower inset illustrates the four sublattices building up the RW-AFM ground state. (B) The single AFM skyrmion is made of two FM skyrmions, each hosted by sublattices L1 and L2, while L3 and L4 remain collinear, whereas the latter can host a second AFM skyrmion in case of the overlapped skyrmion scenario (C). Note that the separation of the four sublattices in (B,C) is carried out for the illustration purpose only since all skyrmions reside in the same layer. Phase diagrams showing the range of interactions J₂/|J₁| and J₃/|J₁| at which the single (D) and double (E) AFM skyrmions can be stabilized with D₃/|J₁| = 0.03 and K/|J₁| = 0.024. The color code indicates the radius of the stabilized AFM skyrmion. (F,G) Phase diagrams obtained by changing the D₃/|J₁| magnitude along with that of K/|J₁| while fixing J₂/|J₁| at −0.2 and J₃/|J₁| at 0.2, for single and double AFM skyrmions, respectively. The letters A–L shown in the diagrams indicate skyrmions, which are plotted in Supplementary Figure S2.

After setting the base for the magnetic interactions needed to realize our AFM solitons, we inspect the range of parameters (J₂, J₃, D₃, and K) normalized to the absolute value of J₁, within which the single and double interchained AFM skyrmions can be stabilized (Figures 1D–G). The building blocks of the AFM solitons are FM skyrmions. The region hosting the skyrmions, color coded in terms of their radius, is sandwiched between the RW-AFM and stripe domain phases. Thus, the impact of the underlying interactions is similar to what is expected from the FM topological objects. For instance, increasing J₃ (Figures 1D, E, with K/|J₁| and D₃/|J₁| equal to 0.024 and 0.03, respectively), which defines the FM interaction among the spins of the FM skyrmions, or K (Figures 1F, G, with J₂/|J₁| and J₃/|J₁| equal to −0.2 and 0.2, respectively), shrinks the size of the spin-texture by ultimately leading to its annihilation, while the DM interaction D₃ induces the opposite behavior (Figures 1F, G). Interestingly, J₂ counteracts J₃ by amplifying the skyrmion size, which at some point can be deformed into stripe domains. For completeness, snapshots of skyrmions, labeled from A to L in Figure 1, are presented in Supplementary Figure S2.

It is significant to point out that the shape of the AFM skyrmions is determined by the specific interaction parameters involved. While the interactions between spins in one sublattice L_i, characterized by J₃ and D₃, lead to the formation of an FM skyrmion in that sublattice, the interactions with spins in the other FM skyrmions hosting the sublattice, governed by J₁ and J₂, have a substantial impact on shaping the resulting AFM skyrmion, as illustrated in Supplementary Figure S3 and discussed in detail in Supplementary Data S1. Without J₂, there is an anisotropic cancellation of contributing magnetic interactions induced by the AFM alignment of the spins around the skyrmion, which triggers shape elongation. A finite J₂ helps establishing a balance in the magnetic interaction, which reduces the aforementioned skyrmion asymmetry. However, interlinking of the AFM skyrmions results in a slight deformation in the overlap region, as the spins in the overlapping area interact with the non-collinear spins of the second AFM skyrmion, which is not the case for the other spins on the free side of the AFM skyrmion.

It is worth mentioning that the size of the single AFM skyrmion is smaller than those participating in the formation of the interchained magnetic textures (see, for example, the radius given in Figures 1B, C), which impacts on the details of the phase diagrams. On the one hand, the window in which double AFM skyrmions are stabilized while varying J₂ and J₃ is larger than that of the single magnetic objects (Figures 1D, E). On the other hand, the single skyrmion phase seems wider and shifted to the upper region of the diagram while tuning D₃ and K.

Response to external magnetic fields

The stability of skyrmions when exposed to an external magnetic field is an essential aspect for their utilization in future spintronics. Here, we investigate the responses of the single and double AFM skyrmions to a magnetic field perpendicular to the lattice. Within our model, as theoretically expected [42, 52, 66, 67], and in contrast to their FM counterparts, the size of the AFM skyrmions increases with the external magnetic field, until its magnitude approaches a critical value (B_c), after which the skyrmion deforms into the stripe domain phase. It has been shown that the single and interlinked AFM skyrmions formed with the realistic interactions among Cr atoms bear high magnetic fields [52]. At the model level, the critical value of the normalized magnetic field (μB_c/|J1|) can be enhanced by increasing the anisotropy magnitude, as depicted in Figure 2A, for both single and double AFM skyrmions. In contrast, the DMI lessens the highest magnetic field survived by the AFM solitons, as shown in Figure 2C. Various formulas have been proposed to describe the impact of DMI and anisotropy magnitude on the radius of the FM skyrmions [12, 68–70]. Inspired by Ref. [70], and utilizing the fact that |J₁|≫ D₃, K, our results on the dependence of the AFM skyrmion radius R on the anisotropy (Figure 2B) and DMI (Figure 2D), when the external field is switched off, can be fitted with $R_0=a+b\frac{D_3}{K}\left(1+c\frac{D_3^2}{|J_1|K}\right)$, where a, b, and c are fitting parameters.

FIGURE 2

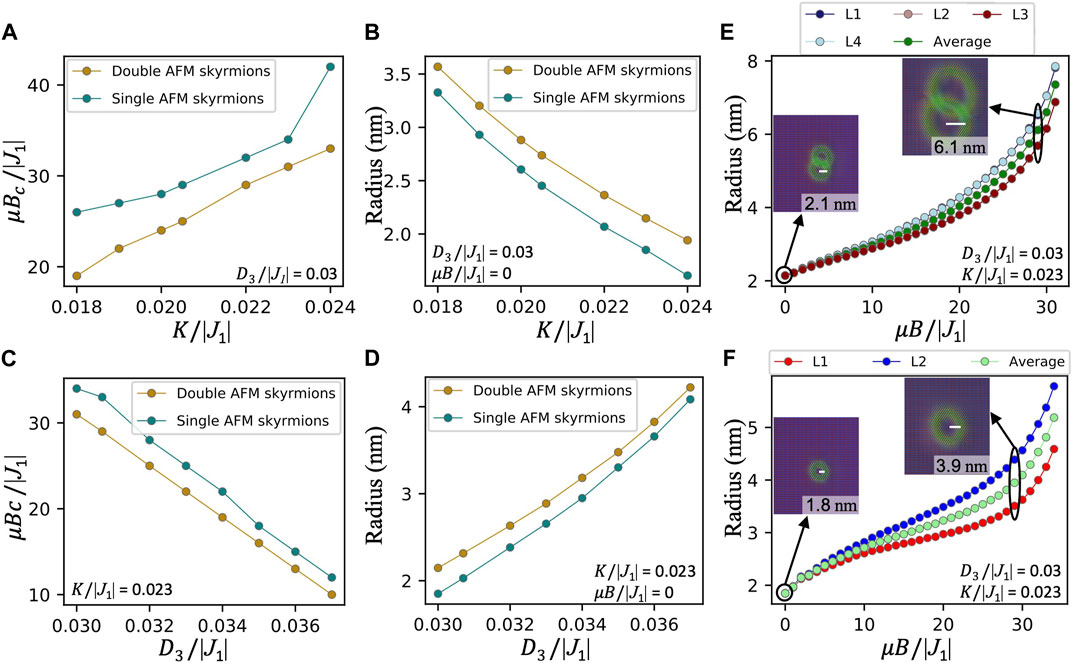
FIGURE 2. The critical magnetic field μB_c/|J₁| tolerated by the single (green dots) and double (golden dots) AFM skyrmions as a function of (A) the normalized values of the anisotropy K/|J₁|, and (C) the normalized values of DMI D₃/|J₁|. (B) Increasing K/|J₁| shrinks the radii of both the double and single AFM skyrmions, while (D) increasing D₃/|J₁| expands them. (E, F) Impact of the external magnetic field on the radii of both types of AFM skyrmions.

Upon the application of the magnetic field, we found that the form proposed in Ref. [66] has to be amended with a linear field-dependent term. After a Taylor expansion in the regime where the field is smaller than the rest of the magnetic interactions, we find $R=a+b\frac{D_3}{K}\left(1+c\frac{D_3^2}{|J_1|K}\right)\left(1+\alpha \frac{B}{|J_1|}+\beta \frac{B^2}{|J_1{|}^2}+\gamma \frac{B^3}{|J_1{|}^3}\right)$, where α, β, and γ are additional fitting parameters, grasping reasonably the dependencies reported in Figures 2E, F (with D₃/|J₁| = 0.03 and K/|J₁| = 0.023).

Overall, the magnetic interactions reducing (increasing) the size of the skyrmions, as the magnetic anisotropy (DMI) does, enable an enhanced (reduced) stability with respect to an external magnetic field.

Thermal stability of AFM skyrmions

Now, we turn to the stability of the AFM skyrmions against thermal fluctuations by calculating the energy barrier which is needed for the collapse of the single and double interchained AFM skyrmions into the RW-AFM ground state utilizing the GNEB method [59–61]. To inspect their stability, we calculate the energy barrier for both single and double interlinked AFM skyrmions assuming J₂/|J₁| = −0.2, J₃/|J₁| = 0.2, D₃/|J₁| = 0.03, and K/|J₁| = 0.024. The barrier is determined by the energy difference between the local minimum magnetic state hosting the AFM skyrmion and its relevant saddle point, which lies on the path of minimum energy connecting the skyrmion configuration to the RW-AFM ground state. In the absence of the external magnetic field, the double AFM skyrmions, with a radius of 1.95 nm, have an energy barrier of 0.67 meV, which translates to ≈ 7.8 K, while for the single AFM skyrmion, with a radius of 1.6 nm, the energy barrier is 0.055 meV (≈0.64 K). For both cases, the major key for the stability of the AFM skyrmions is the DMI, which contributes ΔE_DMI = 15.66 meV to the energy barrier of the double AFM skyrmion and 4.33 meV for the single case, while the anisotropy and exchange interactions prefer the collapse of the AFM solitons by contributing ΔE_K = −9.21 meV (−2.53 meV) and ΔE_J = −5.79 meV (−1.71 meV) for double (single) AFM skyrmions. Moreover, we address another important aspect, the impact of the magnetic field, by carrying out a systematic study with results illustrated in Figure 3. The thermal stability is obviously enhanced with the magnetic field, which impacts more efficiently the double than the single AFM skyrmion (Figure 3A). For μB/|J₁| = 1, the energy barrier of the double (single) AFM skyrmions increased to 0.81 meV (0.12 meV) ≈ 9.4 K (1.3 K). By increasing the magnetic field, the skyrmions expand (Figure 3F), which in contrast to the DMI and Zeeman contributions (Figures 3C, D) is disfavored by those of the exchange and anisotropy (Figures 3B, E). Snapshots of various states prospected in defining the energy barriers are presented in Supplementary Figure S4.

FIGURE 3

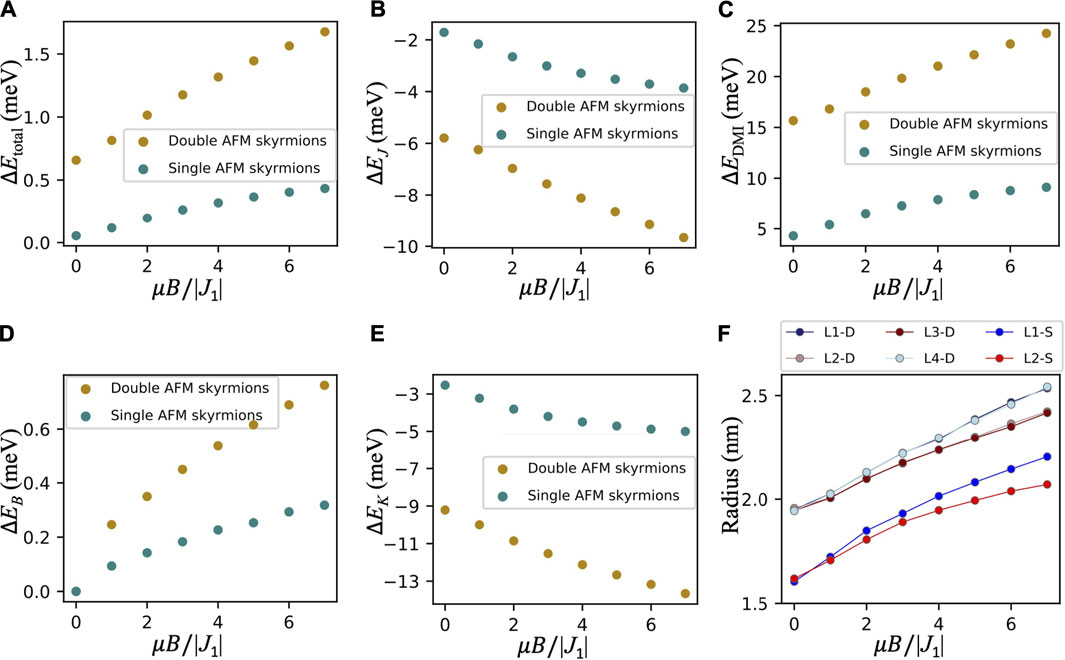
FIGURE 3. Thermal stability of the single and double AFM skyrmions in the presence of an external magnetic field. (A) Total energy barrier for double (golden) and single (green) AFM skyrmions as a function of the normalized value of the external magnetic field. The different contributions to the energy barrier are shown in (B) exchange, (C) DMI, (D) Zeeman, and (E) magnetic anisotropy. (F) The radii of the single and double AFM skyrmions are plotted as functions of the magnetic field.

Discussion

Inspired by our recent findings on the emergence of single and interchained AFM skyrmions on a triangular lattice, we propose here a spin model with the minimum set of magnetic interactions needed to realize such intriguing solitons. They form in an RW-AFM state, which can be decomposed into four sublattices. The exchange interaction within each sublattice, mediating the coupling between the third n.n., is of FM nature which along with the associated DMI and out-of-plane anisotropy permits the formation of FM skyrmions within the sublattices. The first n.n. has to be AFM to impose the emergence of AFM skyrmions. We identify the phase diagrams of the latter entities as well as their dependencies on the magnitude of various magnetic interactions and sensitivity to an external magnetic field.

The identification of AFM spin-textures requires specific experimental techniques. We expect the recently proposed all-electrical detection based on the tunneling spin-mixing magnetoresistance (TXMR) [11, 71], with its different possible modes [20] that can be enhanced by the proper implantation of atomic defects [15], to be useful for the exploration of AFM states. In this context, the predicted non-collinear Hall effect [72], the topological spin Hall effect for antiferromagnets [73], and the spin-resolved inelastic electron scattering approaches could be valuable [74, 75]. Obviously spin-polarized scanning tunneling microscopy is capable of resolving AFM states via atomic resolution [76, 77], while enormous progress has been made with X-ray magnetic microscopy [47] and all-optical relaxometry with a scanning quantum sensor based on a single nitrogen-vacancy (NV) defect in diamond, which were applied to identify variuos synthetic AFM textures, among which skyrmions [46].

We expect our work to facilitate the search and the identification of single or overlapping AFM skyrmions while contributing to the detailed understanding of their various properties, which is a corner stone in the field of topological antiferromagnetism and its potential use in devices for information technology.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

SL initiated, designed, and supervised the project. AA performed the simulations with support and supervision from MS. AA, MS, MA, and SL discussed the results. AA and SL wrote the manuscript to which all co-authors contributed.

Funding

This work was supported by the Federal Ministry of Education and Research of Germany in the framework of the Palestinian-German Science Bridge (BMBF grant number 01DH16027) and the Deutsche Forschungsgemeinschaft (DFG) through SPP 2137 “Skyrmionics” (Project LO 1659/8-1).

Acknowledgments

The authors gratefully acknowledge the computing time granted through JARA on the supercomputer JURECA at Forschungszentrum Jülich.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1175317/full#supplementary-material

References

1. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, et al. Skyrmion lattice in a chiral magnet. Science (2009) 323:915–9. doi:10.1126/science.1166767

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yu X, Onose Y, Kanazawa N, Park JH, Han JH, Matsui Y, et al. Real-space observation of a two-dimensional skyrmion crystal. Nature (2010) 465:901–4. doi:10.1038/nature09124

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Heinze S, von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R, et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat Phys (2011) 7:713–8. doi:10.1038/nphys2045

CrossRef Full Text | Google Scholar

4. Romming N, Hanneken C, Menzel M, Bickel JE, Wolter B, von Bergmann K, et al. Writing and deleting single magnetic skyrmions. Science (2013) 341:636–9. doi:10.1126/science.1240573

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bogdanov A, Hubert A. Thermodynamically stable magnetic vortex states in magnetic crystals. J Magn Magn Mater (1994) 138:255–69. doi:10.1016/0304-8853(94)90046-9

CrossRef Full Text | Google Scholar

6. Rössler UK, Bogdanov AN, Pfleiderer C. Spontaneous skyrmion ground states in magnetic metals. Nature (2006) 442:797–801. doi:10.1038/nature05056

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kiselev N, Bogdanov A, Schäfer R, Rößler U. Chiral skyrmions in thin magnetic films: New objects for magnetic storage technologies? J Phys D (2011) 44:392001. doi:10.1088/0022-3727/44/39/392001

CrossRef Full Text | Google Scholar

8. Nagaosa N, Tokura Y. Topological properties and dynamics of magnetic skyrmions. Nat Nanotechnol (2013) 8:899–911. doi:10.1038/nnano.2013.243

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Iwasaki J, Mochizuki M, Nagaosa N. Universal current-velocity relation of skyrmion motion in chiral magnets. Nat Commun (2013) 4:1463. doi:10.1038/ncomms2442

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Fert A, Cros V, Sampaio J. Skyrmions on the track. Nat Nanotechnol (2013) 8:152–6. doi:10.1038/nnano.2013.29

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Crum DM, Bouhassoune M, Bouaziz J, Schweflinghaus B, Blügel S, Lounis S. Perpendicular reading of single confined magnetic skyrmions. Nat Commun (2015) 6:8541. doi:10.1038/ncomms9541

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Fert A, Reyren N, Cros V. Magnetic skyrmions: Advances in physics and potential applications. Nat Rev Mater (2017) 2:17031. doi:10.1038/natrevmats.2017.31

CrossRef Full Text | Google Scholar

13. Lai P, Zhao GP, Tang H, Ran N, Wu SQ, Xia J, et al. An improved racetrack structure for transporting a skyrmion. Sci Rep (2017) 7:45330. doi:10.1038/srep45330

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Fernandes IL, Bouaziz J, Blügel S, Lounis S. Universality of defect-skyrmion interaction profiles. Nat Commun (2018) 9:4395. doi:10.1038/s41467-018-06827-5

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Fernandes IL, Bouhassoune M, Lounis S. Defect-implantation for the all-electrical detection of non-collinear spin-textures. Nat Commun (2020) 11:1602. doi:10.1038/s41467-020-15379-6

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhang X, Zhou Y, Mee Song K, Park TE, Xia J, Ezawa M, et al. Skyrmion-electronics: Writing, deleting, reading and processing magnetic skyrmions toward spintronic applications. J Phys Condens Matter (2020) 32:143001. doi:10.1088/1361-648x/ab5488

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bogdanov AN, Panagopoulos C. Physical foundations and basic properties of magnetic skyrmions. Nat Rev Phys (2020) 2:492–8. doi:10.1038/s42254-020-0203-7

CrossRef Full Text | Google Scholar

18. Luo S, You L. Skyrmion devices for memory and logic applications. APL Mater (2021) 9:050901. doi:10.1063/5.0042917

CrossRef Full Text | Google Scholar

19. Göbel B, Mertig I, Tretiakov OA. Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles. Phys Rep (2021) 895:1–28. doi:10.1016/j.physrep.2020.10.001

CrossRef Full Text | Google Scholar

20. Lima Fernandes I, Blügel S, Lounis S. Spin-orbit enabled all-electrical readout of chiral spin-textures. Nat Commun (2022) 13:1576. doi:10.1038/s41467-022-29237-0

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang K, Bheemarasetty V, Duan J, Zhou S, Xiao G. Fundamental physics and applications of skyrmions: A review. J Magn Magn Mater (2022) 169905:169905. doi:10.1016/j.jmmm.2022.169905

CrossRef Full Text | Google Scholar

22. Jonietz F, Mühlbauer S, Pfleiderer C, Neubauer A, Münzer W, Bauer A, et al. Spin transfer torques in MnSi at ultralow current densities. Science (2010) 330:1648–51. doi:10.1126/science.1195709

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yu X, Kanazawa N, Zhang W, Nagai T, Hara T, Kimoto K, et al. Skyrmion flow near room temperature in an ultralow current density. Nat Commun (2012) 3:988. doi:10.1038/ncomms1990

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Woo S, Litzius K, Krüger B, Im MY, Caretta L, Richter K, et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat Mater (2016) 15:501–6. doi:10.1038/nmat4593

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Büttner F, Lemesh I, Beach GSD. Theory of isolated magnetic skyrmions: From fundamentals to room temperature applications. Sci Rep (2018) 8:4464. doi:10.1038/s41598-018-22242-8

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jiang W, Zhang X, Yu G, Zhang W, Wang X, Benjamin Jungfleisch M, et al. Direct observation of the skyrmion Hall effect. Nat Phys (2017) 13:162–9. doi:10.1038/nphys3883

CrossRef Full Text | Google Scholar

27. Lin S-Z, Reichhardt C, Batista CD, Saxena A. Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep. Phys Rev B (2013) 87:214419. doi:10.1103/physrevb.87.214419

CrossRef Full Text | Google Scholar

28. Fernandes IL, Chico J, Lounis S. Impurity-dependent gyrotropic motion, deflection and pinning of current-driven ultrasmall skyrmions in PdFe/Ir (111) surface. J Phys Condens Matter (2020) 32:425802. doi:10.1088/1361-648x/ab9cf0

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Reichhardt C, Reichhardt CJO, Milošević M. Statics and dynamics of skyrmions interacting with disorder and nanostructures. Rev Mod Phys (2022) 94:035005. doi:10.1103/revmodphys.94.035005

CrossRef Full Text | Google Scholar

30. Olejník K, Seifert T, Kašpar Z, Novák V, Wadley P, Campion RP, et al. Terahertz electrical writing speed in an antiferromagnetic memory. Sci Adv (2018) 4:eaar3566. doi:10.1126/sciadv.aar3566

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Fang W, Raeliarijaona A, Chang P-H, Kovalev AA, Belashchenko KD. Spirals and skyrmions in antiferromagnetic triangular lattices. Phys Rev Mater (2021) 5:054401. doi:10.1103/physrevmaterials.5.054401

CrossRef Full Text | Google Scholar

32. Barker J, Tretiakov OA. Static and dynamical properties of antiferromagnetic skyrmions in the presence of applied current and temperature. Phys Rev Lett (2016) 116:147203. doi:10.1103/physrevlett.116.147203

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhang X, Zhou Y, Ezawa M. Antiferromagnetic skyrmion: Stability, creation and manipulation. Sci Rep (2016) 6:24795. doi:10.1038/srep24795

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Velkov H, Gomonay O, Beens M, Schwiete G, Brataas A, Sinova J, et al. Phenomenology of current-induced skyrmion motion in antiferromagnets. New J Phys (2016) 18:075016. doi:10.1088/1367-2630/18/7/075016

CrossRef Full Text | Google Scholar

35. Jin C, Song C, Wang J, Liu Q. Dynamics of antiferromagnetic skyrmion driven by the spin hall effect. Appl Phys Lett (2016) 109:182404. doi:10.1063/1.4967006

CrossRef Full Text | Google Scholar

36. Göbel B, Mook A, Henk J, Mertig I. Antiferromagnetic skyrmion crystals: Generation, topological hall, and topological spin hall effect. Phys Rev B (2017) 96:060406. doi:10.1103/physrevb.96.060406

CrossRef Full Text | Google Scholar

37. Akosa CA, Tretiakov O, Tatara G, Manchon A. Theory of the topological spin hall effect in antiferromagnetic skyrmions: Impact on current-induced motion. Phys Rev Lett (2018) 121:097204. doi:10.1103/physrevlett.121.097204

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Gomonay O, Baltz V, Brataas A, Tserkovnyak Y. Antiferromagnetic spin textures and dynamics. Nat Phys (2018) 14:213–6. doi:10.1038/s41567-018-0049-4

CrossRef Full Text | Google Scholar

39. Tomasello R, Puliafito V, Martinez E, Manchon A, Ricci M, Carpentieri M, et al. Performance of synthetic antiferromagnetic racetrack memory: Domain wall versus skyrmion. J Phys D (2017) 50:325302. doi:10.1088/1361-6463/aa7a98

CrossRef Full Text | Google Scholar

40. Silva R, Silva R, Pereira A, Moura-Melo W. Antiferromagnetic skyrmions overcoming obstacles in a racetrack. J Phys Condens Matter (2019) 31:225802. doi:10.1088/1361-648x/ab0abd

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Keesman R, Raaijmakers M, Baerends A, Barkema G, Duine R. Skyrmions in square-lattice antiferromagnets. Phys Rev B (2016) 94:054402. doi:10.1103/physrevb.94.054402

CrossRef Full Text | Google Scholar

42. Rosales HD, Cabra DC, Pujol P. Three-sublattice skyrmion crystal in the antiferromagnetic triangular lattice. Phys Rev B (2015) 92:214439. doi:10.1103/physrevb.92.214439

CrossRef Full Text | Google Scholar

43. Mohylna M, Albarracín FG, Žukovič M, Rosales H. Spontaneous antiferromagnetic skyrmion/antiskyrmion lattice and spiral spin-liquid states in the frustrated triangular lattice. Phys Rev B (2022) 106:224406. doi:10.1103/physrevb.106.224406

CrossRef Full Text | Google Scholar

44. Dohi T, DuttaGupta S, Fukami S, Ohno H. Formation and current-induced motion of synthetic antiferromagnetic skyrmion bubbles. Nat Commun (2019) 10:5153. doi:10.1038/s41467-019-13182-6

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Legrand W, Maccariello D, Ajejas F, Collin S, Vecchiola A, Bouzehouane K, et al. Room-temperature stabilization of antiferromagnetic skyrmions in synthetic antiferromagnets. Nat Mater (2020) 19:34–42. doi:10.1038/s41563-019-0468-3

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Finco A, Haykal A, Tanos R, Fabre F, Chouaieb S, Akhtar W, et al. Imaging non-collinear antiferromagnetic textures via single spin relaxometry. Nat Commun (2021) 12:767. doi:10.1038/s41467-021-20995-x

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Juge R, Sisodia N, Larrañaga JU, Zhang Q, Pham VT, Rana KG, et al. Skyrmions in synthetic antiferromagnets and their nucleation via electrical current and ultra-fast laser illumination. Nat Commun (2022) 13:4807. doi:10.1038/s41467-022-32525-4

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Chen R, Cui Q, Han L, Xue X, Liang J, Bai H, et al. Controllable generation of antiferromagnetic skyrmions in synthetic antiferromagnets with thermal effect. Adv Funct Mater (2022) 32:2111906. doi:10.1002/adfm.202111906

CrossRef Full Text | Google Scholar

49. Gao S, Rosales HD, Gómez Albarracín FA, Tsurkan V, Kaur G, Fennell T, et al. Fractional antiferromagnetic skyrmion lattice induced by anisotropic couplings. Nature (2020) 586:37–41. doi:10.1038/s41586-020-2716-8

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Rosales H, Albarracín FAG, Guratinder K, Tsurkan V, Prodan L, Ressouche E, et al. Anisotropy-driven response of the fractional antiferromagnetic skyrmion lattice in MnSc₂S₄ to applied magnetic fields. Phys Rev B (2022) 105:224402. doi:10.1103/physrevb.105.224402

CrossRef Full Text | Google Scholar

51. Jani H, Lin JC, Chen J, Harrison J, Maccherozzi F, Schad J, et al. Antiferromagnetic half-skyrmions and bimerons at room temperature. Nature (2021) 590:74–9. doi:10.1038/s41586-021-03219-6

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Aldarawsheh A, Fernandes IL, Brinker S, Sallermann M, Abusaa M, Blügel S, et al. Emergence of zero-field non-synthetic single and interchained antiferromagnetic skyrmions in thin films. Nat Commun (2022) 13:7369. doi:10.1038/s41467-022-35102-x

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Dupé B, Hoffmann M, Paillard C, Heinze S. Tailoring magnetic skyrmions in ultra-thin transition metal films. Nat Commun (2014) 5:4030. doi:10.1038/ncomms5030

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Simon E, Palotás K, Rózsa L, Udvardi L, Szunyogh L. Formation of magnetic skyrmions with tunable properties in PdFe bilayer deposited on Ir (111). Phys Rev B (2014) 90:094410. doi:10.1103/physrevb.90.094410

CrossRef Full Text | Google Scholar

55. Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R. Field-dependent size and shape of single magnetic skyrmions. Phys Rev Lett (2015) 114:177203. doi:10.1103/physrevlett.114.177203

PubMed Abstract | CrossRef Full Text | Google Scholar

56. dos Santos Dias M, Bouaziz J, Bouhassoune M, Blügel S, Lounis S. Chirality-driven orbital magnetic moments as a new probe for topological magnetic structures. Nat Commun (2016) 7:13613. doi:10.1038/ncomms13613

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Arjana IG, Lima Fernandes I, Chico J, Lounis S. Sub-nanoscale atom-by-atom crafting of skyrmion-defect interaction profiles. Sci Rep (2020) 10:14655. doi:10.1038/s41598-020-71232-2

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Bouhassoune M, Lounis S. Friedel oscillations induced by magnetic skyrmions: From scattering properties to all-electrical detection. Nanomaterials (2021) 11:194. doi:10.3390/nano11010194

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Müller GP, Hoffmann M, Dißelkamp C, Schürhoff D, Mavros S, Sallermann M, et al. Spirit: Multifunctional framework for atomistic spin simulations. Phys Rev B (2019) 99:224414. doi:10.1103/physrevb.99.224414

CrossRef Full Text | Google Scholar

60. Bessarab PF, Uzdin VM, Jónsson H. Method for finding mechanism and activation energy of magnetic transitions, applied to skyrmion and antivortex annihilation. Comput Phys Commun (2015) 196:335–47. doi:10.1016/j.cpc.2015.07.001

CrossRef Full Text | Google Scholar

61. Müller GP, Bessarab PF, Vlasov SM, Lux F, Kiselev NS, Blügel S, et al. Duplication, collapse, and escape of magnetic skyrmions revealed using a systematic saddle point search method. Phys Rev Lett (2018) 121:197202. doi:10.1103/physrevlett.121.197202

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Spethmann J, Meyer S, von Bergmann K, Wiesendanger R, Heinze S, Kubetzka A. Discovery of magnetic single-and triple-q states in Mn/Re (0001). Phys Rev Lett (2020) 124:227203. doi:10.1103/physrevlett.124.227203

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Spethmann J, Grünebohm M, Wiesendanger R, von Bergmann K, Kubetzka A. Discovery and characterization of a new type of domain wall in a row-wise antiferromagnet. Nat Commun (2021) 12:3488. doi:10.1038/s41467-021-23760-2

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Kurz P. Non-collinear magnetism at surfaces and in ultrathin films. Ph.D. thesis. Elektronische Eigenschaften (2001).

65. Hardrat B, Al-Zubi A, Ferriani P, Blügel S, Bihlmayer G, Heinze S. Complex magnetism of iron monolayers on hexagonal transition metal surfaces from first principles. Phys Rev B (2009) 79:094411. doi:10.1103/physrevb.79.094411

CrossRef Full Text | Google Scholar

66. Bessarab P, Yudin D, Gulevich DR, Wadley P, Titov M, Tretiakov OA. Stability and lifetime of antiferromagnetic skyrmions. Phys Rev B (2019) 99:140411. doi:10.1103/physrevb.99.140411

CrossRef Full Text | Google Scholar

67. Potkina MN, Lobanov IS, Jónsson H, Uzdin VM. Skyrmions in antiferromagnets: Thermal stability and the effect of external field and impurities. J Appl Phys (2020) 127:213906. doi:10.1063/5.0009559

CrossRef Full Text | Google Scholar

68. Rohart S, Thiaville A. Skyrmion confinement in ultrathin film nanostructures in the presence of Dzyaloshinskii-Moriya interaction. Phys Rev B (2013) 88:184422. doi:10.1103/physrevb.88.184422

CrossRef Full Text | Google Scholar

69. Zhang X, Zhou Y, Ezawa M, Zhao G, Zhao W. Magnetic skyrmion transistor: Skyrmion motion in a voltage-gated nanotrack. Sci Rep (2015) 5:11369. doi:10.1038/srep11369

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Wang X, Yuan H, Wang X. A theory on skyrmion size. Commun Phys (2018) 1:31. doi:10.1038/s42005-018-0029-0

CrossRef Full Text | Google Scholar

71. Hanneken C, Otte F, Kubetzka A, Dupé B, Romming N, von Bergmann K, et al. Electrical detection of magnetic skyrmions by tunnelling non-collinear magnetoresistance. Nat Nanotechnol (2015) 10:1039–42. doi:10.1038/nnano.2015.218

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Bouaziz J, Ishida H, Lounis S, Blügel S. Transverse transport in two-dimensional relativistic systems with nontrivial spin textures. Phys Rev Lett (2021) 126:147203. doi:10.1103/physrevlett.126.147203

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Nakazawa K, Hoshi K, Nakane JJ, Ohe J-i., Kohno H. Topological spin hall effect in antiferromagnets driven by vector Néel chirality (2023). arXiv preprint arXiv:2304.02850.

Google Scholar

74. Dos Santos FJ, dos Santos Dias M, Guimaraes FSM, Bouaziz J, Lounis S. Spin-resolved inelastic electron scattering by spin waves in noncollinear magnets. Phys Rev B (2018) 97:024431. doi:10.1103/physrevb.97.024431

CrossRef Full Text | Google Scholar

75. Dos Santos FJ, dos Santos Dias M, Lounis S. Modeling spin waves in noncollinear antiferromagnets: Spin-flop states, spin spirals, skyrmions, and antiskyrmions. Phys Rev B (2020) 102:104436. doi:10.1103/physrevb.102.104436

CrossRef Full Text | Google Scholar

76. Wortmann D, Heinze S, Kurz P, Bihlmayer G, Blügel S. Resolving complex atomic-scale spin structures by spin-polarized scanning tunneling microscopy. Phys Rev Lett (2001) 86:4132–5. doi:10.1103/physrevlett.86.4132

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Schmitt M, Moras P, Bihlmayer G, Cotsakis R, Vogt M, Kemmer J, et al. Indirect chiral magnetic exchange through Dzyaloshinskii–Moriya-enhanced RKKY interactions in manganese oxide chains on Ir (100). Nat Commun (2019) 10:2610. doi:10.1038/s41467-019-10515-3

PubMed Abstract | CrossRef Full Text | Google Scholar