- 1School of Science, Jiangnan University, Wuxi, China
- 2School of Artificial Intelligence and Computer Science, Jiangnan University, Wuxi, China
We present a novel approach that combines the power of pix2pix, an image-to-image translation framework, with the advanced capabilities of isogeometric multi-patch analysis for topology optimization. The proposed method adds the Nitsche’s methods into the advantages of Isogeometric analysis (IGA), thus gaining the ability to handle complex geometries by generating locally smooth and well-converged results. Additionally, the usage of generative adversarial network based pix2pix allows for a more efficient representation of the design space, reducing the computational cost of the optimization process. This approach has shown promising results in various numerical examples. This technique aims to improve the efficiency of conceptual design in complex engineering applications.
1 Introduction
Nowadays, topology optimization is becoming a powerful computational technique for designing structures with optimal properties by iteratively redistributing material within a given design space. It has many practical applications in the design of structures for aerospace, automotive, civil engineering and many other projects [1]. However, accurately representing complex geometries can be challenging, especially when utilizing traditional finite element methods (FEM) that require a high number of elements. Isogeometric analysis (IGA), which uses the same basis functions for both the geometry field and displacement field, has emerged as a promising alternative to traditional FEM [2]. Isogeometric based topology optimization offers several advantages over traditional topology optimization methods. Firstly, the usage of Non-Uniform Rational B-Splines (NURBS) basis functions offers improved accuracy, as NURBS provide a smooth and flexible representation of geometry that can accurately capture complex features. Additionally, isogeometric topology optimization reduces meshing efforts and achieves faster convergence rates than traditional topology optimization methods, thanks to the higher accuracy of the NURBS-based representation. Finally, isogeometric topology optimization can be seamlessly integrated with CAD systems, making it a potential tool for designers and engineers to create more accurate and efficient designs for a wide range of engineering applications [3]. However, one significant issue with isogeometric topology optimization is its computational cost. The NURBS basis functions bring a high number of control points, leading to an increased number of degrees of freedom and computational complexity, especially for large-scale problems. Additionally, the optimization iteration itself is time consuming, especially when convergence issues occur, the computational costs could be badly increased.
To address these challenges, the deep learning technique is introduced into the IGA and topology optimization. Liao et.al. [4]. Proposed a deep-learning-based inverse design approach for auxetic materials, using a surrogate model based on deep neural networks. The deep learning framework called IGA-Reuse-Net was presented by Wang [5], which combined IGA and UNet3+ architecture, and achieved a good trade-off between accuracy and efficiency in solving Poisson equations on different topologies. Gasick and Qian [6] introduced a physics-based machine learning approach that combines isogeometric representation with deep learning to solve parameterized PDEs over changing domains. As for topology optimization, Sosnovik and Oseledets [7] proposed a deep learning-based approach to accelerate topology optimization by treating it as an image segmentation problem, which demonstrates significant acceleration. In the study of Sasaki and Igarashi [8], a novel approach of topology optimization was proposed, which combined the power of deep learning with traditional optimization techniques to accelerate the design process and achieved optimal solutions for complex electromagnetic systems. Nie et al. [9] proposed a new method for topology optimization using generative adversarial networks, leveraging physical fields over the initial design domain to generate high-quality optimized structures. In the recent contribution of Yan et al. [10], a new method for real-time topology optimization driven by deep learning is introduced, by utilizing initial stress learning to achieve efficient and accurate optimization, marking a significant step forward in the development of intelligent design systems.
The pix2pix framework is a type of conditional generative adversarial network (cGAN) that maps an input image to an output image with high resolution, in our case, an optimized topology of a structure [11]. It has been specifically designed for image-to-image translation, such as converting a black-white image to a color image or converting a low-resolution image to a high-resolution image. The generator network produces a high-resolution image of the optimized structure, while the discriminator network evaluates the generated image and provides feedback to the generator network to iteratively improve its performance. Pix2pix has been successfully used in a variety of applications, including the translation of sketches to photorealistic images, the generation of realistic images of 3D objects from 2D images, and the restoration of degraded or low-resolution images [12]. By considering the mechanical structures in the form of images as input, the pix2pix proves its effectiveness in topology optimization applications. Hertlein et al. [13] presented an approach for topology optimization, which enables designers to explore design flexibility in the early stages of the additive manufacturing process. Ye et al. [14] accelerated the topology optimization process by utilizing a pix2pix network to generate high-quality optimized designs. Li et al. [15] developed a cross-resolution Pix2pix neural network, enabling efficient and accurate optimization of geometrically nonlinear systems.
In engineering common practice, complex design spaces are usually represented by a set of NURBS patches, and each patch has its own parameterization, such as different degrees of continuity or geometric shape. Isogeometric multi-patch methods have been proposed to address the challenges of complex geometries. Ruess et al. [16] utilized weak coupling to enable accurate analysis of complex multi-patch geometries with non-matching and trimmed boundaries. Brivadis et al. [17] used the mortar method for the coupling between different subdomains, paving the way for advanced numerical simulation in a variety of fields. In the study of Kargaran et al. [18], a new approach to isogeometric analysis using overlapping multi-patch structures is proposed, which enables efficient and accurate simulation of complex geometries.
The Nitsche’s method is usually adopted in FEM for weakly imposing boundary conditions and handling non-matching meshes between different subdomains. The method involves adding energy terms to the weak form of the partial differential equation being solved, which helps to enforce the boundary conditions and reduce the effect of the non-matching meshes. The Nitsche’s method has been shown to be robust, accurate, and flexible, and has become a popular method in the FEM community. Chouly and Hild [19] solved unilateral contact problems using a Nitsche-based approach, enabling accurate and efficient numerical analysis of complex systems. Nguyen et al. [20] presented a new approach to patch coupling using the Nitsche’s method, allowing for efficient and accurate analysis of complex two and three-dimensional systems. Guo and Ruess [21] tried to couple isogeometric thin shells and blended shell structures using the Nitsche’s method, facilitating efficient and accurate simulation of complex structures. Du et al. [22] presented a new approach to isogeometric analysis of Reissner-Mindlin plates with non-conforming multi-patches by the Nitsche’s method. Back to our study in 2018 [23], we proposed a skew-symmetric Nitsche’s formulation for isogeometric analysis, which allows for the incorporation of Dirichlet and symmetry conditions, patch coupling, and frictionless contact in IGA simulations.
In this research, the pix2pix framework is adopted for fast topology optimization in the context of multi-patch IGA. Our goal is to expedite the conceptual design process and enhance efficiency. The analysis process begins with multiple NURBS patches, each with its own local isogeometric basis functions. These patches are then merged by the Nitsche’s method under a continuity condition to ensure a smooth and seamless design across patch interfaces. Subsequently, a well-trained pix2pix network is used to generate an image of the desired design from an initial image of element-wise strain energy distribution. Finally, the generated image is projected back onto the multi-patch domain together with some post-processing treatment. This approach offers multiple benefits. Firstly, the isogeometric basis functions and multi-patch technique provide a more accurate representation of the geometry, resulting in clear designs. Secondly, the adoption of the pix2pix significantly reduces the computational efforts of the calculation process while maintaining relatively high-quality outcomes. Lastly, combining these techniques leads to an efficient and accurate topology optimization process, enabling faster and more cost-effective design iterations. This method has yielded promising results in various problems.
2 Isogeometric multi-patch analysis
2.1 Basic theory of IGA
FEM is widely utilized in structural mechanics, but it requires careful consideration of mesh quality in order to keep good analysis accuracy. IGA, on the other hand, overcomes this drawback using the inherent meshes naturally from the CAD model. Moreover, by utilizing NURBS as shape functions, IGA gains the ability to construct high-order continuous approximations. This paper focuses specifically on two-dimensional structures. For three-dimensional problems, the extension can be naturally achieved by incorporating an additional dimension.
The IGA process starts with a parametric representation for its geometric model, which is constructed by the NURBS interpolation as
where
IGA can be considered as a special isoparametric version of FEM, meaning that the interpolation basis functions used in geometry discretization, i.e., NURBS, are consistent with the shape functions used in displacement discretization. Then the following formula expresses the physical field
where
Isogeometric analysis offers superior accuracy in representing the geometric features of a given model. Unlike traditional FEM, it provides a wider range of mesh refinement strategies, including the commonly used h-refinement and p-refinement, as well as the unique k-refinement strategy. This innovative approach allows for higher accuracy and faster refinement speeds. From an optimization perspective, isogeometric analysis offers an integrated approach to design and simulation. In this way, the geometry of the structure being designed gains the potential to be directly modified based on the results of the simulation, resulting in greater efficiency in structural design optimization.
2.2 Multi-patch analysis based on the Nitsche’s method
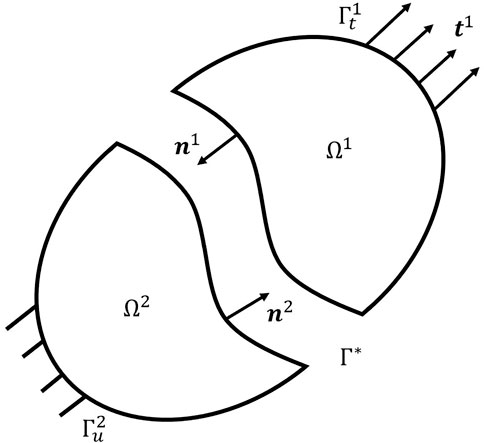
In practice, most complex geometric models are represented by multiple patches of distinct material properties. Furthermore, patches with different meshes reveal the potential of parallel computation, although not considered in this study. Consider an interface problem, as indicated in Figure 1, the domain
Where the
In order to glue the two patches, according to the Nitsche’s method [23], we define the trial function on the domain
Find
By defining the displacement jump and stress average operators as
and
we obtain the Nitsche’s formulation as
Find
where the
For the Nitsche parameter
From the matrix point of view, original discrete IGA formula in matrix form is given by
where
where the superscripts are used to show the patch indexes as before. After marking the interface elements by subscripts
here the tilde indicates the remaining elements which are not involved into the interface coupling, for illustration
3 Topology optimization based on pix2pix
3.1 Pix2pix driven topology optimization
Structural topology optimization is a more advanced optimization technique than size and shape optimization, which operates at the conceptual design stage of a structure, and its output serves as the foundation for future designs. This study focuses on the topology optimization of elastic structures, aiming to identify the optimal structural type generated within the design domain under given conditions. This paper uses the minimum structural compliance as the objective function to optimize the topology, i.e., the density distribution. The optimization formula is written by
where subscript
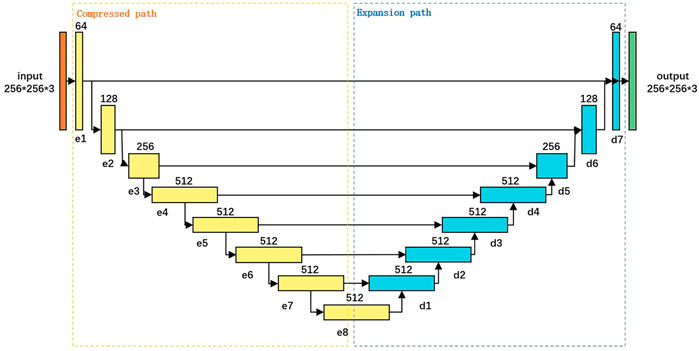
Pix2pix algorithm, proposed by Phillip Isola of the AI Laboratory in Berkeley, is a typical image migration algorithm based on GAN [11]. The pix2pix algorithm consists of two components: a generator network and a discriminator network. The generator network takes an input image and attempts to generate a corresponding output image, while the discriminator network evaluates the output image to determine whether it is a qualitied image or not, according to the training data. During the training process, the generator network is trained to generate output images that the discriminator network is unable to distinguish from qualified images, while the discriminator network is trained to accurately differentiate between qualitied and unqualified images. Figure 2 shows the network structure of pix2pix, which includes 8 convolution layers and 7 deconvolution layers. In order to better retain the information of the input image, a jump connection structure is added between the convolution layers and the deconvolution layers.
In this paper, we are using pix2pix to accelerate the topology optimization process. This approach is divided into the following three steps:
i. We calculate the strain energy for each element by
from the first iteration of topology optimization through (multi-patch) IGA, since the strain energy is a part of the structural compliance, and it reveals the sensitivities of the objective function to a certain extent. The strain energy matrix is normalized and then scaled as an input image for pix2pix.
ii. The pix2pix model is trained together with the well-calculated topology optimization results served as reference for the discriminator. In the model, the strain energy data is used as the training image, and the topology optimization results obtained by the sequential integer programming and canonical relaxation algorithm proposed by Liang and Cheng [25], are used as the reference results, since it provides clear black-white results.
iii. Based on the well-trained pix2pix model obtained in step ii, for the topology optimization problem that needs to be predicted, we carry out isogeometric analysis, and input the strain energy heat map into the trained pix2pix model. According to the input, the model will quickly output the probable distribution of the element densities of the structure. Finally, we convert this distribution into topology optimization results.
3.2 Data training and testing
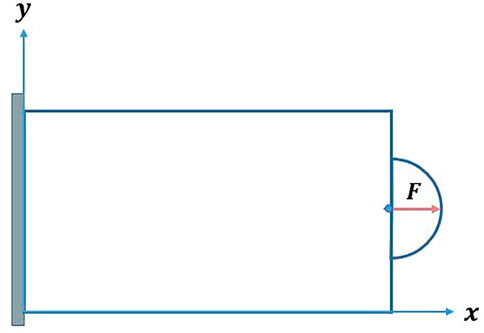
As illustrated in Figure 3, the pix2pix network is trained by a single-patch cantilever beam example. In order to provide training and testing samples for the pix2pix model, and to get as many data as possible, we fix the left side of the cantilever beam and apply a variable concentrated force at the midpoint of the right side of the beam, with a force magnitude of
In this study, we trained the input data using a batch size of 1 and a maximum epoch of 200, and the final prediction result comprises images measuring

FIGURE 4. A glance during the early stage of the train process. (A) element-wise strain energy heat map. (B) predicted results by pix2pix. (C) reference results.
3.3 Special treatment for multi-patch cases and post-processing
For multi-patch topology optimization in IGA, the Nitsche’s method is firstly adopted to couple patches. Since the mesh resolutions of different patches are usually different, the magnitudes of the sensitivity values corresponding to meshes of different densities are also different. If these sensitivities are directly substituted into the topology optimization algorithm, it could lead to inappropriate optimization results, especially along the coupling interfaces. To overcome this problem, a simple method to filter the interface sensitivities is used [26].
The deep learning toolbox is commonly used as a black box, it just learns from big data and predicts a result according to a given input, thus it is difficult to impose direct constrains, such as volume constrains in our topology optimization applications. In our practice, the pix2pix accepts a heat map of the element-wise strain energy matrix, then feeds back an element-wise density distribution matrix. To address this matter, we firstly sort the densities by their numbers, then keep and drop out the elements according to the desired volume constrain.
4 Numerical examples
4.1 Cantilever beam
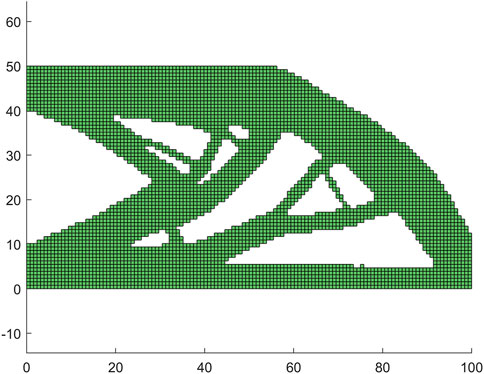
In this study, we present the results of testing our proposed method on a cantilever beam model, the left side of the beam is fixed, and the bottom right is subjected to a downward concentrated force. The model is fixed at the left end and subject to a concentrated force at the lower right corner. The mesh is shown in Figure 5. The topology optimization result obtained by the pix2pix method is shown in Figure 6. By comparing the result obtained through normal calculation (Figure 7) and our proposed method, we observed that the material topology of both results is similar, with the pix2pix result exhibiting some jagged boundaries and finer details.
However, the pix2pix result accurately reflects the material distribution. Our method demonstrates significant potential for accelerating the optimization process, while simultaneously maintaining high accuracy and generalizability.
4.2 One-quarter ring
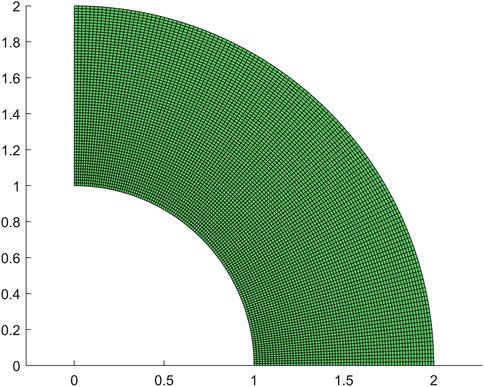
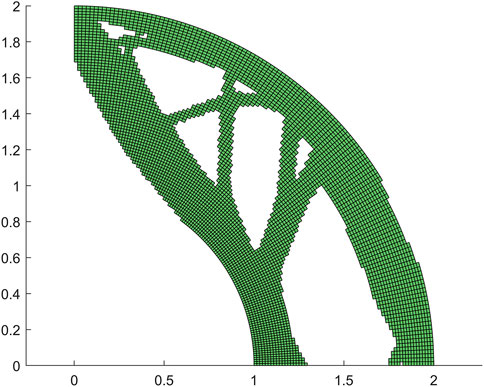
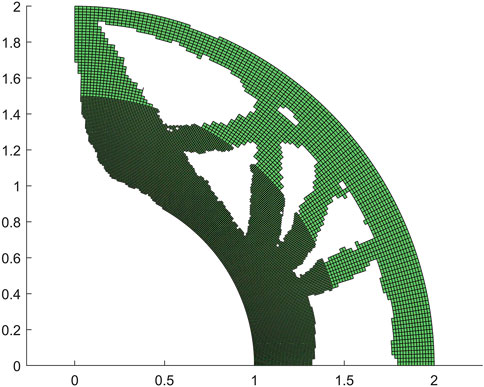
As our next example, the proposed method is used to test the one-quarter ring model. The bottom of the ring is fixed to the ground, and its upper left corner is applied by a concentrated force. This model serves to evaluate the efficacy of isogeometric analysis for models with curved edges. The mesh partitioning is presented in Figure 8, and the topology optimization result obtained through the application of pix2pix can be found in Figure 9.
Despite the inherent limitations of the method, such as the occurrence of unsmoothness at certain boundaries and occasional holes at individual locations, the pix2pix results are still commendable, especially when compared to the reference result obtained through conventional calculations in Figure 10. However, it is worth noting that the use of the element-wise strain energy as the sole predictor in pix2pix does make it challenging to obtain entirely smooth boundaries even with post-processing.
4.3 Double-beam structure
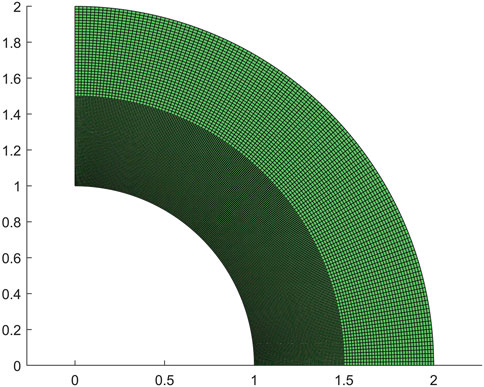
To further assess the performance of our proposed method in multi-path scenarios, we conducted experiments on a divided cantilever beam model, as depicted in Figure 11. The upper patch of the beam is subjected to a sparser mesh division, while the lower patch is subjected to a denser mesh division. The result obtained from pix2pix prediction are presented in Figure 12.
Notably, the two patches exhibit a seamless connection, indicating that the pix2pix prediction is able to maintain the smoothness of the overall structure despite the differing mesh divisions in the separate patches. These results highlight the potential of our method to provide accurate predictions for complex, multi-patch models. The approach we propose not only resolves the topology optimization problem for the training model but also accomplishes a range of topology optimization problems within a shorter computational time compared to conventional optimization procedures.
4.4 Double-ring structure
The double one-quarter ring problem, as depicted in the accompanying Figure 13, has been partitioned into two distinct segments, with corresponding mesh divisions, in order to address its computational complexity. However, despite its utility, the performance of the pix2pix model in predicting the outcome of this problem is suboptimal, as evidenced by the accompanying predicted outcome of Figure 14. The model’s limited efficacy is characterized by a heavily jagged boundary and localized discontinuities arising from a lack of edge connectivity, which compromises the accuracy of its predictive capacity.
Despite these shortcomings, the material distribution resultant from this exercise provides a clear conceptual framework for further analyses and serves as a dependable guide for subsequent investigations. By generating a clear and coherent spatial representation of the material distribution, it enables researchers to identify relevant features of the problem and evaluate its overall complexity. Thus, while the pix2pix model may not be fully optimized for this task, the insights gleaned from this exercise demonstrate its potential for application in a range of related problems, and serve as a stepping stone for further research in this area.
5 Conclusion
In this article, we provide a comprehensive evaluation of the isogeometric multi-patch topology optimization based on the pix2pix method and discuss its potential applications in the design of complex structures.
The Nitsche’s method is adopted for multi-patch coupling, enabling isogeometric analysis (IGA) to analyze complex geometries. Within the IGA framework, element density is treated as the design variable, resulting in topology optimization geometries with smooth, curved boundaries that are used as training data for the generative adversarial network (GAN). Finally, the pix2pix algorithm is used to quickly evaluate a complex model by inputting a heat map of element-wise energy. However, due to the limitations of GANs, controlling the volume constraint directly is not straightforward. Therefore, a post-processing step is applied by sorting and filtering the element densities. Our results demonstrate the efficiency and the effectiveness of the proposed approach.
Overall, the combination of IGA, Nitsche-based multi-patch technique, and pix2pix image-to-image translation provides a powerful tool for engineers and designers to efficiently and effectively optimize complex engineering designs, and we believe that it represents an exciting area of research for topology optimization with a wide range of potential applications.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, upon reasonable request.
Author contributions
QH, XM, and YY contributed to the conception and design of the study. QH proposed the original idea and the code framework. XM developed further the algorithm, performed the computation, and wrote the draft. YY helped with the training and computation, the result analysis, as well as the draft of the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version.
Funding
QH is supported by the National Natural Science Foundation of China (No. 12102146), the Natural Science Foundation of Jiangsu Province (No. BK20200611), and the Fundamental Research Funds for the Central Universities (No. JUSRP12038).
Acknowledgments
The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bendsoe MP, Sigmund O. Topology optimization: Theory, methods, and applications. Berlin: Springer Science and Business Media (2003). doi:10.1007/978-3-662-05086-6
2. Hughes TJ, Cottrell JA, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comp Methods Appl Mech Eng (2005) 194(39-41):4135–95. doi:10.1016/j.cma.2004.10.008
3. Cottrell JA, Hughes TJ, Bazilevs Y. Isogeometric analysis: Toward integration of CAD and FEA. Chichester: John Wiley and Sons (2009). doi:10.1002/9780470749081
4. Liao Z, Wang Y, Gao L, Wang ZP. Deep-learning-based isogeometric inverse design for tetra-chiral auxetics. Compos Structures (2022) 280:114808. doi:10.1016/j.compstruct.2021.114808
5. Wang D, Xu J, Gao F, Wang CC, Gu R, Lin F, et al. IGA-reuse-NET: A deep-learning-based isogeometric analysis-reuse approach with topology-consistent parameterization. Comp Aided Geometric Des (2022) 95:102087. doi:10.1016/j.cagd.2022.102087
6. Gasick J, Qian X. Isogeometric neural networks: A new deep learning approach for solving parameterized partial differential equations. Comp Methods Appl Mech Eng (2023) 405:115839. doi:10.1016/j.cma.2022.115839
7. Sosnovik I, Oseledets I. Neural networks for topology optimization. Russ J Numer Anal Math Model (2019) 34(4):215–23. doi:10.1515/rnam-2019-0018
8. Sasaki H, Igarashi H. Topology optimization accelerated by deep learning. IEEE Trans Magnetics (2019) 55(6):1–5. doi:10.1109/TMAG.2019.2901906
9. Nie Z, Lin T, Jiang H, Kara LB. Topologygan: Topology optimization using generative adversarial networks based on physical fields over the initial domain. J Mech Des (2021) 143(3). doi:10.1115/detc2020-22675
10. Yan J, Zhang Q, Xu Q, Fan Z, Li H, Sun W, et al. Deep learning driven real time topology optimisation based on initial stress learning. Adv Eng Inform (2022) 51:101472. doi:10.1016/j.aei.2021.101472
11. Isola P, Zhu JY, Zhou T, Efros AA. Image-to-image translation with conditional adversarial networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017). doi:10.1109/CVPR.2017.632
12. Pan W, Torres-Verdín C, Pyrcz MJ. Stochastic pix2pix: A new machine learning method for geophysical and well conditioning of rule-based channel reservoir models. Nat Resour Res (2021) 30:1319–45. doi:10.1007/s11053-020-09778-1
13. Hertlein N, Buskohl PR, Gillman A, Vemaganti K, Anand S. Generative adversarial network for early-stage design flexibility in topology optimization for additive manufacturing. J Manufacturing Syst (2021) 59:675–85. doi:10.1016/j.jmsy.2021.04.007
14. Ye HL, Li JC, Yuan BS, Wei N, Sui YK. Acceleration design for continuum topology optimization by using Pix2pix neural network. Int J Appl Mech (2021) 13(04):2150042. doi:10.1142/S1758825121500423
15. Li J, Ye H, Yuan B, Wei N. Cross-resolution topology optimization for geometrical non-linearity by using deep learning. Struct Multidisciplinary Optimization (2022) 65(4):133. doi:10.1007/s00158-022-03231-y
16. Ruess M, Schillinger D, Oezcan AI, Rank E. Weak coupling for isogeometric analysis of non-matching and trimmed multi-patch geometries. Comp Methods Appl Mech Eng (2014) 269:46–71. doi:10.1016/j.cma.2013.10.009
17. Brivadis E, Buffa A, Wohlmuth B, Wunderlich L. Isogeometric mortar methods. Comp Methods Appl Mech Eng (2015) 284:292–319. doi:10.1016/j.cma.2014.09.012
18. Kargaran S, Jüttler B, Kleiss SK, Mantzaflaris A, Takacs T. Overlapping multi-patch structures in isogeometric analysis. Comp Methods Appl Mech Eng (2019) 356:325–53. doi:10.1016/j.cma.2019.07.010
19. Chouly F, Hild P. A nitsche-based method for unilateral contact problems: Numerical analysis. SIAM J Numer Anal (2013) 51(2):1295–307. doi:10.1137/12088344X
20. Nguyen VP, Kerfriden P, Brino M, Bordas SP, Bonisoli E. Nitsche’s method for two and three dimensional NURBS patch coupling. Comput Mech (2014) 53:1163–82. doi:10.1007/s00466-013-0955-3
21. Guo Y, Ruess M. Nitsche’s method for a coupling of isogeometric thin shells and blended shell structures. Comp Methods Appl Mech Eng (2015) 284:881–905. doi:10.1016/j.cma.2014.11.014
22. Du X, Zhao G, Wang W. Nitsche method for isogeometric analysis of Reissner–Mindlin plate with non-conforming multi-patches. Comp Aided Geometric Des (2015) 35:121–36. doi:10.1016/j.cagd.2015.03.005
23. Hu Q, Chouly F, Hu P, Cheng G, Bordas SP. Skew-symmetric Nitsche’s formulation in isogeometric analysis: Dirichlet and symmetry conditions, patch coupling and frictionless contact. Comp Methods Appl Mech Eng (2018) 341:188–220. doi:10.1016/j.cma.2018.05.024
24. Hu Q, Baroli D, Rao S. Isogeometric analysis of multi-patch solid-shells in large deformation. Acta Mechanica Sinica (2021) 37:844–60. doi:10.1007/s10409-020-01046-y
25. Liang Y, Cheng G. Topology optimization via sequential integer programming and canonical relaxation algorithm. Comp Methods Appl Mech Eng (2019) 348:64–96. doi:10.1016/j.cma.2018.10.050
Keywords: isogeometric, topology optimization, Nitsche, GaN, pix2pix
Citation: Hu Q, Meng X and You Y (2023) Isogeometric multi-patch topology optimization based on pix2pix. Front. Phys. 11:1174262. doi: 10.3389/fphy.2023.1174262
Received: 26 February 2023; Accepted: 21 March 2023;
Published: 31 March 2023.
Edited by:
Leilei Chen, Huanghuai University, ChinaReviewed by:
Haifeng Gao, Taiyuan University of Technology, ChinaZhao Binghao, Beijing Institute of Technology, China
Copyright © 2023 Hu, Meng and You. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingyuan Hu, cWluZ3l1YW5odUBqaWFuZ25hbi5lZHUuY24=
 Qingyuan Hu
Qingyuan Hu Xin Meng
Xin Meng Yangxiu You2
Yangxiu You2